Study Tentang Strategi Murni dari Dua Pemain dengan Nash
Equilibrium
(2-Player Pure Strategy Nash Equilibrium)
SKRIPSI
Ramidin Sinaga
040803042
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
Study Tentang Strategi Murni dari Dua Pemain dengan Nash Equilibrium
(2-Player Pure Strategy Nash Equilibrium)
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
Ramidin Sinaga
040803042
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
MEDAN
PERSETUJUAN
Judul : STUDY TENTANG STRATEGI MURNI DARI DUA PEMAIN DENGAN NASH EQUILIBRIUM ( TWO
PLAYERS PURE STRATEGY NASH EQUILIBRIUM)
Kategori : SKRIPSI
Nama : RAMIDIN SINAGA
Nomor Induk Mahasiswa : 040803042
Program Studi : SARJANA (S1) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA
UTARA
Diluluskan di
Medan, Desember 2010 Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Dra. Ester Nababan, M. Sc Prof. Dr. Herman Mawengkang NIP. 196103181987112001 NIP : 194611281974031001
Diketahui/Disetujui oleh
Departeman Matematika FMIPA USU Ketua.
PERNYATAAN
Study Tentang Strategi Murni dari Dua Pemain dengan Nash
Equilibrium
(2-Player Pure Strategy Nash Equilibrium)
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Desember 2010
PENGHARGAAN
Segala puji dan syukur penulis haturkan atas kehadirat Allah Subhanna Wa Ta’ala yang telah melimpahkan Nikmat dan karunia-Nya, sehingga penulis berhasil menyelesaikan skripsi ini dalam waktu yang telah ditetapkan. Dan tak lupa pula shalawat dan salam senantiasa tercurah kepada Nabi Allah, Muhammad Shalallahu
‘Alaihi Wassalam yang diutus sebagai rahmat untuk sekalian alam serta keluarga dan
sahabat beliau serta orang-orang yang berpegang teguh dengan petunjuk Sunnah beliau hingga hari kiamat.
Dalam kesempatan ini, penulis ingin mengucapkan jazakumullahu khairan
katsiran kepada semua pihak yang telah membantu dan membimbing penulis dalam
penyusunan skripsi ini, ucapan terima kasih saya sampaikan kepada :
1. Bapak Prof. Dr. Herman Mawengkang selaku pembimbing I dan Dra. Ester Nababan, M.Sc selaku pembimbing II yang telah memberikan bimbingan dan pengarahan kepada saya sehingga skripsi ini dapat saya selesaikan.
2. Bapak Drs. Henry Rani Sitepu, M.Si. dan Drs. H. Haluddin Panjaitan selaku dosen penguji saya.
3. Bapak Dr. Saib Suwilo, M.Sc. dan Drs. Henry Rani Sitepu, M.Sc. selaku Ketua dan Sekretaris Departemen Matematika
4. Dekan dan Pembantu Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumetera Utara.
5. Semua Dosen pada Departemen Matematika FMIPA USU, pegawai di FMIPA USU
6. Terkhusus kedua orangtua tercinta, Bapak J.Sinaga dan S.Manihuruk, dan kepada kakak, abang dan adik saya serta semua keluarga besar J.Sinaga yang selama ini memberikan bantuan dan dorongan yang diperlukan.
7. Seluruh teman-teman kuliah dan junior Matematika khususnya stambuk 2004 dan juga teman terdekat saya Deni, Taufiq, Robby, Revin, Indra, Jali, Darto, Juhri, Nova, Ila dan Shari serta sahabat-sahabat dan rekan-rekan saya di MMC,yang telah memberikan semangat, dorongan dan saran dalam pengerjaan skripsi ini.
ABSTRAK
ABSTRACT
DAFTAR ISI
2.5.2 Metode Strategi Campuran 23
2.6 Nash Equilibrium 29
Bab 3 PEMBAHASAN 35
3.1 Nash Equilibrium Dan Dominan Strategi 35
3.2 Prisoner’s Dilemma 36
3.3Penghapusan Berulang Strategi didominasi 37
3.4 Multiple Nash Equilibria 38
3.5 Menggunakan Fungsi Tanggapan Terbaik Untuk Menghitung Pure Strategi Nash Equilibria 40
Bab 4 KESIMPULAN DAN SARAN 46
4.1 Kesimpulan 46
4.2 Saran 47
ABSTRAK
ABSTRACT
BAB I
PENDAHULUAN
1.1 Latar Belakang
Beberapa tahun terakhir ini, banyak peneliti tertarik mempelajari teori permainan. Teori permainan yang mula-mula dikembangkan oleh ilmuan Prancis bernama Emile Borel ini, secara umum digunakan untuk menyelesaikan masalah yang berkaitan dengan tindakan sebuah unit bisnis (misalnya) untuk memenangkan persaingan dalam usaha yang digelutinya. Seperti diketahui, bahwa dalam praktek sehari-hari, setiap unit usaha atau organisasi pada umumnya harus berhadapan dengan para pesaing. Untuk memenangkan persaingan itulah, diperlukan analisis dan pemilihan strategi pemasaran tepat, khususnya strategi bersaing yang paling optimal bagi unit usaha atau organisasi yang bersangkutan.
Teori permainan bertitik tolak dari keadaan dimana seseorang mengambil keputusan harus berhadapan dengan orang lain dengan kepentingan yang bertentangan. Masa depan yang dilandasi keputusan yang ia pilih dipengaruhi oleh keputusan yang dipilih orang lain. Ini mengandung arti, bahwa perolehan dari seseorang adalah sama dengan kerugian bagi orang lain. Penyelesaian dari pertentangan dari dua pihak yang bersaing ini adalah inti dari teori permainan. Dengan kata lain, pengambilan keputusan dalam suatu pertentangan umumnya disebut teori permainan. Jadi, teori permainan mengandung dua pihak yang bertentangan, pihak I (Pemain) dan pihak II (Lawan main). Teori matematika dalam permainan ini ditujukkan untuk menjelaskan bagaimana tiap pihak yang bertentangan atau pemain memilih strategi terbaik bagi mereka.
(decision maker) selalu dihadapkan pada permasalahan yang relevan dengan dunia bisnis sebagai pesaing. Mereka harus mempelajari atau paling tidak memperkirakan langkah-langkah pihak pesaingnya.
Apabila mereka dapat melakukannya dengan baik, para pengambil keputusan itu dapat mengetahui atau memperkirakan langkah apa yang dilakukan oleh pihak pesaing, maka mereka akan menjadi lebih mudah dan efektif didalam menyusun perencanaan, misalnya untuk menyusun strategi untuk merebut pasar. Pengalaman tentang tingkah laku dari pihak pesaing akan memudahkan pemain untuk memperkirakan strategi terbaik yang harus dilakukan.
Ada bebrapa ketentuan-ketentuan dalam Teori Permainan. Misalkan dari matriks perolehan pada table 1.1 di bawah ini
Tabel 1.1
Dari contoh tabel matrik pay off (matrik permainan) di atas, dapat dijelaskan beberapa ketentuan dasar yang terpenting dalam teori permainan, yakni :
1. Nilai-nilai yang ada dalam tabel tersebut (yakni angka , , di baris pertama dan , , di baris kedua dan , , di baris ketiga ), merupakan hasil yang diperoleh dari penggunaan berbagai strategi
yang dipilih oleh kedua perusahaan. Satuan nilai tersebut merupakan efektifitas yang dapat berupa uang, persentase pangsa pasar, jumlah pelanggandan sejenisnya. Nilai positif menunjukkan keuntungan bagi pemain baris dan kerugian bagi pemain kolom, begitu pula sebaliknya nilai negatif menunjukkan kerugian bagi pemain baris dan keuntungan bagi pemain kolom. Sebagai contoh, nilai pada sel C12 menunjukkan apabila pemain/perusahaan A menggunakan strategi harga murah (S1) dan perusahaan B meresponnya dengan strategi harga sedang (S2), maka perusahaan A akan mendapatkan keuntungan sebesar yang berarti perusahaan B akan mengalami kerugian sebesar ,
2. Suatu strategi dari sebuah pemain/perusahaan dianggap tidak dapat dirusak oleh perusahaan lainnya,
3. Setiap pemain/perusahaan akan memilih strategi-strategi tersebut secara terus menerus selama perusahaan masih memiliki keinginan melanjutkan usahanya.
4. Suatu permainan/persaingan dikatakan adil atau ‘fair’ apabila hasil akhir permainan atau persaingan menghasilkan nilai nol (0), atau tidak ada pemain atau perusahaan yang menang/kalah atau mendapat keuntungan/kerugian.
5. Suatu strategi dikatakan dominan terhadap strategi lainnya apabila memiliki nilai pay off yang lebih baik dari strategi lainnya. Maksudnya, bagi pemain/perusahaan baris, nilai positif (keuntungan) yang diperoleh dari suatu strategi yang digunakan, menghasilkan nilai positif yang lebih besar dari hasil penggunaan strategi lainnya. Bagi pemain kolom, nilai negatif (kerugaian) yang diperoleh dari suatu strategi yang digunakan, menghasilkan nilai negatif yang lebih kecil dari hasil penggunaan strategi lainnya.
6. Tujuan dari teori permainan ini adalah mengidentifikasi strategi yang paling optimal untuk setiap perusahaan.
kerugian tersebut adalah paling kecil). Agar sebuah permainan atau persaingan menjadi optimal, setiap strategi yang dipergunakan berusaha untuk mendapatkan nilai permainan (sadle point) yang sama. Dari table 1.1, Setelah pemain baris menggunakan aturan maximin dan pemain kolom menggunakan aturan minimax, andaikan bahwa pilihan pemain baris A dan pemain kolom-B tidak sama, dimana pemain atau perusahaan A memilih nilai dan perusahaan B memilih nilai , dengan demikian maka permainan ini dapat dikatakan belum optimal atau stabil, karena belum ditemukan saddle point yang sama. Karena penggunaan strategi murni belum mampu menemukan nilai permainan yang sama, maka penyelesaian masalah permainan/persaingan di atas dilanjutkan dengan digunakannya strategi campuran. Penggunaan strategi campuran mampu menemukan nilai permainan yang sama, strategi campuran juga mampu memberikan hasil yang lebih baik bagi masing-masing perusahaan. Namun dalam hal ini, penulis hanya akan membahas tentang strategi murni aturan dengan aturan dominansi.
Jhon Nash (1950), dalam bukunya yang berjudul Equilibrium points in
n-person games, menyertakan satu paper yang sangat menarik perhatian dunia
dan sampai saat ini dinyatakan sebagai Nash Equilibrium. Nash Equilibrium adalah istilah yang digunakan dalam teori permainan untuk menggambarkan suatu keseimbangan dimana setiap pemain memilih strategi yang merupakan strategi yang optimal dari semua pemain. Nash Equilibrium ada ketika tidak
ada penyimpangan menguntungkan sepihak dari salah satu pemain yang
terlibat. Dengan kata lain, tidak ada pemain dalam permainan akan
mengambil tindakan yang berbeda selama setiap pemain lain tetap sama. Ketika pemain berada pada Nash Equilibrium, mereka tidak memiliki keinginan untuk pindah karena mereka akan menerima hasil yang lebih buruk. Sehingga diperlukan persyaratan untuk keseimbangan ini, yaitu bahwa setiap pemain harus memainkan respon terbaik terhadap dugaan strategi lawan mainnya, dan dugaan tersebut harus benar.
dapat menentukan strategi yang akan dilaksanakan untuk memperoleh keuntungan optimum.
1.2 Perumusan Masalah
Yang menjadi permasalahan dalam penelitian ini adalah bagaimana peranan Nash Equilibrium dalam menyelesaikan masalah teory permainan dengan menggunakan strategi Murni (Pure Strategy)
1.2 Tujuan Penelitian
Tujuan dari penelitian ini adalah untuk membantu pemain (decicion maker) membuat keputusan terbaik, yakni strategi optimal Nash Equilibrium bagi pemain/pesaing dalam permainan dengan aturan dominansi dalam strategi murni.
1.4 Tinjauan Pustaka
Sebagai sumber pendukung teori dalam penulisan ini, maka penulis mengggunakan beberapa pustaka antara lain :
1) Suprapto, Johannes. 1988. Riset Operasi Untuk Pengambilam Keputusan menyatakan bahwa Secara matematis, defenisi dari strategi murni sebagai berikut :
Suatu srategi murni untuk pemain pertama (P1) adalah sebuah vector A =
( , , …, ) dimana entri-entrinya adalah bilangan riil positif. Sehingga
+ + ⋯ + = 1, dengan pengertian bahwa P1 akan memainkan strategi S1 dengan peluang , 1 ≤ ≤ m.
2) Andrew. W.Moore (1921) Non Zero Sum Game Theory, menyatakan bahwa pasangan strategi ( M , M ) merupakan suatu Nash Equilibrium jika, M
adalah strategi terbaik dari pemain A sebagai balasan/tanggapan terhadap M , dan M adalah strategi terbaik dari pemain B sebagai balasan/tanggapan terhadap M .
1.4. Kontribusi Penelitian
1. Hasil penelitian ini diharapkan dapat memberikan kontribusi pada penggunaan permainan dari dua orang/instansi dengan Nash equilibrium. 2. Hasil penelitian ini diharapkan dapat menjadi suatu landasan berpikir
pembaca dalam mengambil kebijakan strategi permainan yang terbaik dan terstruktur.
3. Hasil penelitian ini diharapkan dapat bermanfaat sebagai tambahan literatur dan pengetahuan pembaca yang sedang mempelajari teori permainan.
1.5. Metodologi Penelitian
Penelitian ini bersifat studi literatur yang disusun berdasarkan rujukan pustaka dengan langkah-langkah sebagai berikut:
Langkah-1 : Menguraikan definisi teori permainan dan strategi murni dan strategi campuran dari dua orang pemain.
Langkah-2 : Menjelaskan dan menguraikan peranan Nash Equilibrium dalam menyelesaikan problema permainan.
BAB 2
LANDASAN TEORI
Pada bab ini akan dibahas beberapa konsep teori permainan pada permainan berstrategi murni dan campuran dari dua pemain dengan yang akan digunakan sebagai landasan berfikir dalam melakukan penelitian ini. Juga akan dibahas Keseimbangan Nash (Nash Equilibrium) yang akan menjadi pertimbangan dalam mengambil keputusan dari permainan dari dua pemain. Beberapa konsep dan metode teori permainan dalam menentukan keseimbangan atau titik optimal dari permainan berstrategi murni dan aturan dominansi dengan Nash Equilibrium akan dipergunakan pada bab pembahasan.
2.1 Riset Operasi
Permasalahan yang dihadapi pada dunia industri, perdagangan, pemerintahan, dan sebagainya semakin hari semakin komplek dan rumit. Dari permasalahan tersebut diperlukan pengembangan dalam metodologi permecahan masalah tersebut. Cara yang baik dalam memecahkannya menimbulkan kebutuhan akan teknik-teknik riset operasi (operation
research).
Riset operasi diartikan sebagai peralatan manajemen yang menyatukan ilmu pengetahuan, matematika, dan logika dalam rangka memecahkan masalahmasalah yang dihadapi sehari-hari, sehingga akirnya permasalahan tersebut dapat dipecahkan secara optimal (Subagyo,1993:4).
Operation Research juga diartikan sebagai aplikasi metode ilmiah pada
sumber daya yang terbatas sehingga lebih efektif dan efisien. Tujuan utama adalah membantu manajemen menentukan kebijakan dan tindakan ilmiah.
Riset operasi merupakan suatu metode untuk memecahkan masalah optimasi. Dalam riset operasi yang dibahas meliputi dynamic programing,
network analis, markov chain, games theory, nonlinier programing, dan
interger linier programing.
Suatu model dikatakan baik jika model tersebut bermanfaat dalam menjawab permasalahan yang menjadi perhatian. Hal ini perlu diperhatikan dalam membangun model dalam Operasi Riset. Prinsip dasar itu sebagai berikut. : 1. Jangan membangun model yang rumit jika dapat dibuat model yang lebih
sederhana.
2. Jangan mengubah permasalahan agar cocok dengan teknik atau metoda yang ingin digunakan.
3. Proses deduksi harus dilakukan secara baik.
4. Proses validasi terhadap model harus dilakukan sebelum model tersebut diimplementasikan.
5. Jangan memaksakan untuk menjawab suatu pertanyaan (permasalahan) tertentu dari suatu model yang akan dirancang untuk menjawab pertanyaan itu.
6. Suatu model punya karakteristik tertentu, sehingga jangan terlalu menjual model yang dikembangkan. Suatu model sering kali menghasilkan suatu kesimpulan yang sederhana dan menarik.
7. Suatu model yang dikembangkan memerlukan input /entry (data) yang cermat.
2.2 Program Linear
1947. Selanjutnya berbagai alat dan metode dikembangkan untuk menyelesaikan masalah program linear bahkan sampai pada masalah riset operasi hingga tahun 1950 an sepertipemrogramandinamik,teori antrian, dan teori persediaan.
Program Linear banyak digunakan untuk menyelesaikan masalah optimasi didalam industri, perbankkan, pendidikan dan masalah-masalah lain yang dapat dinyatakan dalam bentuk linear. Bentuk linear di sini berarti bahwa seluruh fungsi dalam model ini merupakan fungsi linear.
Secara umum, fungsi pada model ini ada dua macam yaitu fungsi tujuan dan fungsi pembatas. Fungsi tujuan dimaksudkan untuk menentukan nilai optimum dari funsi tersebut yaitu nilai maksimal untuk masalah keuntungan dan nilai minimal untuk masalah biaya. Fungsi pembatas diperlukan berkenaan dengan adanya keterbatasan sumber daya yang tersedia, misalnya jumlah bahan baku yang terbatas, waktu kerja, jumlah tenaga kerja, luas gudang persediaan. Tujuan utama dari program linear ini adalah menentukan nilai optimum (maksimal/minimal) dari fungsi tujuan yang telah ditetapkan.
2.3 Teori Permainan
Teori permainan (Game Theory) merupakan teori yang menggunakan pendekatan matematis dalam merumuskan situasi persaingan dan konflik antara berbagai kepentingan (Fien Zulkariyah: 2004). Teori ini dikembangkan dengan menganalisa proses pengambilan keputusan dari situasi-situasi persaingan yang berbeda-beda dan melibatkan dua atau lebih kepentingan.
Ide dasar dari teori permainan adalah tingkah laku strategis dari pemain atau pengambil keputusan (player or decision maker). Setiap pemain diasumsikan mempunyai suatu seri rencana atau model tingkah laku dari mana pemain bisa memilih, kalau memiliki suatu himpunan strategi. Pemain dimaksudkan sebagai gerakan khusus yang harus dipilih dari himpunan strategi yang ada. Anggapannya bahwa, setiap pemain mempunyai kemampuan untuk mengambil keputusan secara bebas dan rasional. Konsep teori permainan menyediakan sebuah bahasa untuk memformulasi, menstruktur, menganalisa dan mengerti scenario strategi.
Tujuan teori ini adalah menganalisa proses pengambilan keputusan dari persaingan yang berbeda-beda dan melibatkan dua atau lebih pemain/kepentingan. Kegunaan dari teori permainan adalah metodologi yang disediakan untuk menstruktur dan menganalisa masalah pemilihan strategi. Untuk menggunakan teori permainan, maka langkah pertama adalah menentukan secara explicit pemain, strategi ayng ada, dan juga menentukan preferensi serta reaksi dari stiap pemain.
penurunan harga, pemberian hadiah, peningkatan mutu produk, memilih media advertasi yang efektif. Disinilah peranan teori permainan untuk menentukan strategi mana yang akan diputuskan oleh dirktur pemasaran tersebut untuk merebut pasar.
Persaingan yang dicontohkan diatas dapat diidentifikasi untuk menjelaskan konsep teori permainan yang terdiri dari beberapa unsur-unsur dasar, yaitu:
1. Angka-angka dalam matriks pay-off, atau biasa disebut matriks permainan, menunjukkan hasil-hasil (pay-off) dari strategi–strategi permainan yang berbeda-beda, hasil-hasil ini dinyatakan dalam suatu bentuk ukuran efektifitas seperti uang, persentase market share, atau utilitas.
2. Maximizing player adalah pemain yang berada di baris dan yang
memenangkan/memperoleh keuntungan permainan, sedangkan minimizing
player adalah pemain yang berada di kolom dan yang menderita
kekalahan/kerugian.
3. Strategi permainan adalah rangkaian kegiatan atau rencana yang menyeluruh dari seorang pemain, sebagai reaksi atas perilaku pesaingnya. Dalam hal ini, strategi atau rencana tidak dapat dirusak oleh pesaing lainya.
4. Aturan-aturan permainan adalah pola dimana para pemain memilih strategi mereka
5. Nilai permainan adalah hasil pay-off yang diperkirakan oleh pemain sepanjang rangkaian permainan dimana masing-masing pemain menggunakan strategi terbaiknya. Permainan dikatakan adil apabila nilai permainan sama dengan nol dan sebaliknya.
6. Dominan adalah kondisi dimana pemain dengan setiap pay-offnya dalam strategi superior terhadap setiap pay-off yang berhubungan dalam suatu strategi alternative. Aturan dominan digunakan untuk mengurangi ukuran matriks pay-off dan upaya perhitungan.
7. Strategi optimal adalah kondisi dimana dalam rangkaian kegiatan permainan seorang pemain berada dalam posisi yang paling menguntungkan tanpa menghiraukan kondisi pesaingnya.
Dengan demikian, terlihat bahwa unsur-unsur diatas menunjukkan nilai praktis teori keputusan agak terbatas. Tetapi ide dan konsep teori permainan ini untuk beberapa hal berikut :
a. Mengembangkan suatu kerangka untuk analisis pengambilan keputusan dalam situasi-situasi persaingan.
b. Menguraikan suatu metoda kuantitatif yang sistematis yang memungkinkan para pemain yang terlibat persaingan untuk memilih strategi-strategi yang rasional dalam pencapaian tujuan mereka.
c. Memberikan gambaran dan penjelasan situasi-situasi persaingan atau konflik, seperti tawar-menawar dan perumusan koalisi.
Model-model teori permainan dapat diklasifikasikan dengan sejumlah cara, seperti jumlah pemain, jumlah keuntungan dan kerugian, dan jumlah strategi yang diganankan dalam permainan. Sebagai contoh, bila jumlah pemain ada dua, maka permainan disebut sebagai permainan dua-orang. Begitu juga, bila jumlah pemain adalah N (dengan N>2), maka disebut permainan N-orang.
Sebelum kasus game theory diselesaikan dengan mengunakan salah satu metode game theory, diidentifikasi terlebih dahulu berdasarkan jumlah pemain, jumlah keuntungan dan kerugiaan atau yang biasa disebut nilai permainan, dan jenis strategi yan digunakan. Pada game theory berdasarkan jumlah pemainnya terbagi menjadi dua jenis games yang terkenal, yaitu two
person games dan N person games. Two person games jumlah pemainnya
sebanyak dua orang, sedangkan N person games jumlah pemainnya lebih dari dua orang. Berdasarkan jumlah keuntungan dan kerugiaan dikenal dua jenis games, yaitu zero sum games dan non zero sum games. Nilai permainan pada zero sum games adalah nol, sedangka non zero sum games nilai permainannya tidak sama dengan nol.
berbagai strategi yang berbeda-beda). Pure strategy digunakan untuk jenis permainan yang hasil optimalnya mempunyai saddle point (semacam titik keseimbangan antara nilai permainan kedua pemain). Sedangkan mixed
strategy digunakan untuk mencari solusi optimal dari kasus game theory
yang tidak mempunyai saddle point.
2.3 Unsur-Unsur Dasar Teori Permainan
Ada beberapa unsur atau konsep dasar yang sangat penting dalam penyelesaian setiap kasus dengan teori permainan yaitu:
a) Jumlah Pemain
Permainan diklasifikasikan menurut jumlah kepentingan atau tujuan yang ada dalam permainan tersebut. Dalam hal ini perlu dipahami, bahwa pengertian “ jumlah pemain” tidak selalu sama artinya dengan “jumlah Orang” yang terlibat dalam permainan. jumlah pemain disini berarti jumlah kelompok pemain berdasarkan masing-masing kepentingan atau tujuannya. Dengan demikian dua orang atau lebih yang mempunyai kepentingan yang sama dapat diperhitungkan sebagai satu kelompok pemain.
b) Ganjaran /Payoff
Ganjaran/payoff adalah hasil akhir yang terjadi pada akhir permainan berkenaan dengan ganjaran ini, permainan digolongkan menjadi 2 macam kategori, yaitu permainan jumlah-nol (zero-sum games) dan permainan jumlah-bukan-nol (non-zero-sum games). permainan jumlah-nol terjadi jika jumlah ganjaran dari seluruh pemain adalah nol, yaitu dengan memperhitungkan setiap keuntungan sebagai bilangan positif dan setiap kerugian sebagai bilangan negatif. selain dari itu adalah permainan jumlah – bukan-nol.
permainan pada dasarnya merupakan permainan jumlah-nol. berbagai situasi dapat dianalisis sebagai permainan jumlah-nol.
c) Strategi Permainan
Strategi permainan dalam teori permainan adalah suatu siasat atau rencana tertentu dari seorang pemain, sebagai reaksi atas aksi yang mungkin dilakukan oleh pemain yang menjadi saingannya. permainan diklasifikasikan menurut jumlah strategi yang tersedia bagi masing-masing pemain. jika pemain pertama memiliki m kemungkinan strategi dan pemain kedua memiliki n kemungkinan strategi, maka permainan tersebut dinamakan permainan m x n. letak arti penting dari perbedaan jenis permainan berdasarkan jumlah strategi ini adalah bahwa permainan dibedakan menjadi permainan berhingga dan permainan tak berhingga.
Permainan berhingga terjadi apabila jumlah terbesar dari strategi yang dimiliki oleh setiap pemain berhingga atau tertentu, sedangkan permainan tak berhingga terjadi jika setidak-tidaknya seorang pemain memiliki jumlah strategi yang tak berhingga atau tidak tertentu.
d) Matriks Permainan
Setiap permainan yang dianalisis dengan teori permainan selalu dapat disajikan dalam bentuk sebuah matriks permainan. matriks permainan disebut juga matriks ganjaran yaitu sebuah matriks yang semua unsur berupa ganjaran dari para pemain yang terlibat dalam permainan tersebut. baris-barisnya melambangkan strategi –strategi yang dimiliki pemain pertama, sedangkan kolom-kolomnya melambangkan strategi-strategi yang dimiliki pemain lain. dengan demikian, permainan berstrategi mxn dilambangkan dengan matriks permainan m x n .
keuntungannya yang minimum (maksimin) atau meminimumkan kerugiannya yang maksimum (minimaks).
Nilai dari suatu permainan adalah ganjaran rata-rata/ganjaran yang diharapkan dari sepanjang rangkaian permainan, dengan menganggap kedua pemain selalu berusaha memainkan strateginya yang optimum. secara konvensional , nilai permainan dilihat dari pihak pemain yang strategi-strateginya dilambangkan oleh baris-baris matriks ganjaran, dengan kata lain dilihat dari sudut pandang pemain tertentu. pemain dikatakan adil (fair) apabila nilainya nol, dimana takseorang pemain pun yang memperoleh keuntungan atau kemenangan dalam permainan yang tidak adil (unfair) seorang pemain akan memperoleh kemenangan atas pemain lain, yaitu jika nilai permainan tersebut bukan nol, dalam hal ini nilai pemain adalah positif jika pemain pertam (pemain Baris) memperoleh kemenangan, sebaliknya nilai permainan negatif jika pemain lain (pemain kolom ) memperoleh kemenangan.
e) Titik Pelana (Saddle Poin )
Titik pelana adalah suatu unsur didalam matriks permainan yang sekaligus sebagai maksimin baris dan minimaks kolom. permainan dikatakan bersaing ketat (Strictly determined) jika matriksnya memiliki titik pelana. strategi yang optimum bagi masing-masing pemain adalah strategi pada baris dan kolom yang mengandung titik pelana tersebut. dalam hal ini baris yang mengandung titik pelana merupakan strategi optimum bagi pemain pertama, sedangkan kolom yang mengandung titik pelana merupakan strategi optimum bagi pemain lain.
Contoh:
Terdapat sebuah titik pelana pada perpotongan baris kedua dengan kolom ketiga. Nilai permainan adalah 5, mengingat titik plananya 5. Baris kedua merupakan strategi optimum bagi pemain pertama atau pemain baris, sedangkan kolom ketiga merupakan stragi optimum bagi pemain lain atau pemain kolom.
Terdapat sebuah titik pelana pada perpotongan baris ketiga (strategi optimum bagi pemain pertama) dengan kolom ketiga (strategi optimum bagi pemain lain), nilai permainan adalah -2.
2.5 Permainan Berjumlah Nol Dari Dua Orang Pemain
campuran berlakunya hubungan. Ada beberapa metode untuk menyelesaikan permainan jenis ini, diantaranya adalah dengan cara grafis dengan menggunakan program linier.
Permainan dengan 2 pemain dengan perolehan (keuntungan)bagi salah satu pemain merupakan kehilangan (kerugian) bagi pemain lainnya. Konsep dari game ini dapat dilihat dari aturan yang berlaku dalam permainan ini . Pada dasarnya jenis ini adalah game dengan interaksi antar pemain yang berkelanjutan. Zero-Sum Game berakibat setiap aksi dari satu pemain selalu berdampak pada pemain lain. Sebagai contoh adalah suatu permanan kartu dengan taruhan. Dengan memisalkan terdapat 2 orang pemain, bila suatu pemain A memenangkan sebanyak 5 poin maka pemain B akan kehilangan sebanyak 5 poin juga. Dengan menganggap bahwa kekalahan adalah suatu minus dari menang, maka pada permainan tadi hanya akan menghasilkan nol pada akhirnya karena (5 – 5 = 0). Berikut ini adalah gambarannya :
(mixed strategy game) dimana kedua pemain menjalankan strategi yang berbeda-beda.
1. Metode Pure Stategy (Strategi Murni)
Hasil yang optimal dari suatu permainan yang mempunyai saddle point dapat diperoleh dengan menggunakan pure strategy. yang dimaksud dengan saddle point adalah semacam titik keseimbangan antara nilai permainan kedua pemain Dalam pure strategy digunakan criteria maksimin dan minimaks. Maksimin adalah nilai maksimum dari nilai-nilai minimum, dan minimaks adalah nilai minimum dari nilai-nilai maksimum
Langkah-langkah penyelesaian dengan pure strategy
1. Terjemahkan setiap kasus ke dalam bentuk matriks segi, dimana satu pemain berperan sebagai pemain baris dan yang lain berperan sebagai pemain kolom.
2. Pay-off bernilai positif berarti keuntungan bagi pemain baris 3. Pay-off bernilai negative berarti keuntungan bagi pemain kolom 4. Tentukan nilai minimum setiap baris
5. Tentukan nilai maksimum dari langkah ke-4 6. Tentukan nilai maksimum setiap kolom 7. Tentukan nilai minimum dari langkah ke-6
jika nilai maksimin = minimaks, maka ada saddle point, yaitu nilai maksimin atau minimaks = a. Bisa juga dilakukan penyederhanaan matriks pay-off terlebih dahulu dengan berdasarkan pada criteria superioritas, baru kemudian dianalisa dengan menggunakan criteria minimaks dan maksimin. Superioritas adalah suatu criteria penghilangan suatu kolom atau baris dari suatu matriks pay-off sehingga menjadi lebih sederhana berdasarkan pada pendominasian suatu baris/kolom oleh baris/kolom lainnya.
- Untuk pemain baris >> if pay-off dari suatu strategi > strategi lain - Untuk pemain kolom >> if pay-off dari satu strategi < strategi lain
maksimin
contoh kasus 1 (Kartono. 1994)
Tentukan strategi terbaik dari masing-masing pemain!!
Contoh kasus 2 (Teguh Akbar, 2006)
Dari kasus di atas, bagaimana strategi yang harus digunakan oleh masing-masing pemain atau perusahaan, agar masing-masing-masing-masing mendapatkan hasil yang optimal (kalau untung, keuntungan tersebut besar, dan kalau harus rugi maka kerugian tersebut adalah paling kecil).
Seperti telah dijelaskan di atas, bagi pemain baris akan menggunakan aturan maximin dan pemain kolom akan menggunakan aturan minimax.
Langkah 1
Untuk pemain baris (perusahaan A), pilih nilai yang paling kecil untuk setiap baris (Baris satu nilai terkecilnya 1 dan baris dua nilai terkecilnya 4). Selanjutnya dari dua nilai terkecil tersebut, pilih nilai yang paling baik atau besar, yakni nilai 4.
Langkah 2
Langkah 3
Karena pilihan pemain baris-A dan pemain kolom-B sudah sama, yakni masingmasing memilih nilai 4, maka permainan ini sudah dapat dikatakan optimal à sudah ditemukan nilai permainan (sadle point) yang sama.
Hasil optimal di atas, dimana masing-masing pemain memilih nilai 4 mengandung arti bahwa pemain A meskipun menginginkan keuntungan yang lebih besar, namun A hanya akan mendapat keuntungan maksimal sebesar 4, bila ia menggunakan strategi harga mahal (S2). Sedangkan pemain B, meskipun menginginkan kerugian yang dideritanya adalah sekecil mungkin, namun kerugian yang paling baik bagi B adalah sebesar 4, dan itu bisa diperoleh dengan merespon strategi yang digunakan A dengan juga menerapkan strategi harga mahal (S3).
2. Metode strategi campuran (Mixed Strategy)
John von Neumann mengatakan bahwa kalau himpunan kemungkinan strategi dari para pemain diperluas sampai diluar strategi murni yang mencakup seluruh kemungkinan strategi campuran, selalu ada beberapa strategi campuran untuk pemain pertama yang minimum pay off-nya akan >
dari nilai maksimin dan selalu ada beberapa strategi campuran untuk pemain kedua yang maksimum pay off-nya < dari nilai minimaks dan dua nilai pay off itu sama.
Suatu srategi campuran untuk pemain pertama (P1) adalah sebuah vector A = ( , , …, ) dimana entri-entrinya adalah bilangan riil positif. Sehingga
+ + ⋯ + = 1, dengan pengertian bahwa P1 akan memainkan strategi S1 dengan peluang , 1 ≤ ≤ m. (Suprapto, Johannes. 1988).
Mixed strategy digunakan untuk mencari solusi optimal dari kasus game theory yang tidak mempunyai saddle point (jika permainan tidak seimbang). Pemilihan strategy dilakukan dengan mengevaluasi kombinasi strategy lawan menggunakan prinsip peluang. Ciri permaian dengan strategy campuran :
1. Nilai maximin tidak sama dengan nilai minimax 2. Tidak ada saddle point
3. Permainan tekstabil (unstable game)
Penyelesaian masalah dengan strategi campuran dilakukan apabila strategi murni yang digunakan belum mampu menyelesaikan masalah permainan atau belum mampu memberikan pilihan strategi yang optimal bagi masing-masing pemain/perusahaan. Dalam strategi ini seorang pemain atau perusahaan akan menggunakan campuran/lebih dari satu strategi untuk mendapatkan hasil optimal.
mengeluarkan produk berharga sedang, dan hasil yang diperoleh tampak pada tabel berikut ini :
Langkah 1
Mula-mula akan dicoba dulu dengan menggunakan strategi murni. Seperti telah dijelaskan di atas, bagi pemain baris akan menggunakan aturan maximin dan pemain kolom akan menggunakan aturan minimax. Untuk
pemain baris, pilih nilai yang paling kecil untuk setiap baris (Baris satu nilai terkecilnya 2 , untuk baris kedua nilai terkecilnya -1 dan baris tiga nilai terkecilnya 1). Selanjutnya dari dua nilai terkecil tersebut, pilih nilai yang paling baik atau besar, yakni nilai 2.
Langkah 2
Untuk pemain kolom, pilih nilai yang paling besar untuk setiap kolom (kolom satu nilai terbesarnya 6, kolom dua nilai terbesarnya 5, dan kolom tiga nilai terbesarnya 9). Selanjutnya dari tiga nilai terbesar tersebut, pilih nilai yang paling baik atau kecil bagi B, yakni nilai 5 (rugi yang paling kecil).
Langkah 3
Dari tabel di atas terlihat bahwa pilihan pemain baris-A dan pemain kolom-B tidak sama, dimana pemain atau perusahaan A memilih nilai 2 dan perusahaan B memilih nilai 5, dengan demikian maka permainan ini dapat dikatakan belum optimal à karena belum
Langkah 4
Masing-masing pemain akan menghilangkan strategi yang menghasilkan keuntungan atau kerugian paling buruk. Bila diperhatikan pada tabel sebelumnya, untuk pemain A, strategi S2 adalah paling buruk, karena bisa menimbulkan kemungkinan kerugian bagi A (ada nilai negatif / -1 nya). Dan bagi pemain B, strategi S3 adalah paling buruk karena kerugiannya yang bisa terjadi paling besar (perhatikan nilai-nilai kerugian di strategi S3 pemain/perusahaan B)
Langkah 5
Setelah pemain A membuang strategi S2 dan pemain B membuang stretgi S3, diperoleh tabel sebagiai berikut :
Perhatikan bahwa setelah masing-masing membuang strategi yang paling buruk, maka sekarang persaingan atau permainan dilakukan dengan kondisi, perusahaan A menggunakan strategi S1 dan S3, sementara perusahaan B menggunakan strategi S1 dan S2.
Langkah 6
Langkah selanjutnya adalah dengan memberikan nilai probabilitas terhadap kemugkinan digunakannya kedua strategi bagi masing-masing perusahaan. Untuk perusahaan A, bila kemungkinan keberhasilan penggunaan strategi S1 adalah sebesar p, maka kemungkinan keberhasilan digunakannya strategi S3 adalah (1-p). Begitu pula dengan pemain B, bila kemungkinan keberhasilan penggunaan strategi S1 adalah sebesar q, maka kemungkinan keberhasilan digunakannya strategi S2 adalah (1-q).
Langkah 7
masing-masing strategi untuk menghitung sadle point yang optimal, dengan cara sebagai berikut :
Untuk perusahaan A
Bila, apapun strategi yang digunakan A, perusahaan B meresponnya dengan strategi S1, maka :
2p + 6(1-p) = 2p + 6 – 6p = 6 – 4p ………...(1)
Bila, apapun strategi yang digunakan A, perusahaan B meresponnya dengan strategi S2, maka :
5p + 1(1-p) = 5p + 1 – 1p = 1 + 4p…………(2) Bila kedua hasil persamaan tersebut digabung, maka : 6 – 4p = 1 + 4p
5 = 8p
P = 5/8 = 0,625
Dan apabila nilai p = 0,625, maka nilai (1-p) adalah (1 – 0,625) = 0,375, sehingga kedua nilai probabilitas untuk strategi S1 dan S3 milik perusahaan A sudah diketahui nilainya. Apabila kedua nilai probabilitas tersebut dimasukkan dalam kedua persamaan di atas, maka keuntungan yang diharapkan oleh perusahaan A adalah :
Dengan persamaan ke-1 Dengan persamaan ke-2
= 2p + 6(1-p) = 5p + 1(1-p)
= 2 (0,625) + 6 (0,375) = 5 (0,625) + 1 (0,375)
= 3,5 = 3,5
Perhatikan, bahwa keduanya menghasilkan keuntungan yang diharapkan adalah sama, yakni sebesar 3,5. Coba diingat di atas, bahwa sebelum menggunakan strategi campuran ini keuntungan perusahaan A hanya sebesar 2, berarti dengan digunakan strategi campuran ini, keuntungan perusahaan A bisa meningkat 1,5 menjadi 3,5.
Bagaimana dengan perusahaan B ?
Untuk perusahaan B
2q + 5(1-q) = 2q + 5 – 5q = 5 – 3p ………..(1)
Bila, apapun strategi yang digunakan B, perusahaan A meresponnya dengan strategi S3, maka :
6q + 1(1-q) = 6q + 1 – 1q = 1 + 5p ………..(2) Bila kedua hasil persamaan tersebut digabung, maka : 5 – 3q = 1 + 5q
4 = 8q q = 4/8 = 0,5
Dan apabila nilai p = 0,5, maka nilai (1-p) adalah (1 – 0,5) = 0,5, sehingga kedua nilai probabilitas untuk strategi S1 dan S2 milik perusahaan B sudah diketahui nilainya. Apabila kedua nilai probabilitas tersebut dimasukkan dalam kedua persamaan di atas, maka kerugian minimal yang diharapkan oleh perusahaan B adalah :
Dengan persamaan ke-1 Dengan persamaan ke-2
= 2q + 5(1-q) = 6q + 1(1-q)
= 2 (0,5) + 5 (0,5) = 6 (0,5) + 1 (0,5)
= 3,5 = 3,5
Perhatikan, bahwa keduanya menghasilkan kerugian minimal yang diharapkan adalah sama, yakni sebesar 3,5. Coba diingat di atas, bahwa sebelum menggunakan strategi campuran ini kerugian minimal perusahaan
B adalah sebesar 5, berarti dengan digunakan strategi campuran ini, kerugian
minimal perusahaan B bisa menurun sebesar 1,5 menjadi 3,5.
2.6 Nash Equilibrium (Keseimbangan Nash)
Jadi untuk menuju titik ekuilibrium dalam pendekatan Nash, pertanyaan utama yang harus dijawab kedua pihak adalah apakah dengan mengetahui strategi lawan, dengan asumsi bahwa strategi lawan adalah konstan, apakah negosiator itu dapat memperoleh keuntungan dengan cara mengubah strateginya? Negosiator berada dalam titik ekuilibrium jika perubahan strategi oleh salah satu pihak akan membawa dampak yang menguntungkan dengan biaya yang lebih rendah jika dibandingkan dengan jika negosiator itu tetap pada strategi semula. Negosiasi yang ideal menurut Nash tidak harus menguntungkan kedua belah pihak, yang penting dalam pendekatan ini adalah ketika kedua pihak mendapat bagian dalam pencapaian kepentingannya, tidak mempermasalahkan prosentase kepentingan yang terakomodasi. Jadi dalam hal ini keadaan win-lose dapat diterima.
Nash Equilibrium mengakomodasi keadaan negosiasi yang non-cooperatif dan dilaksanakan secara terbuka. Di katakan non cooperatif karena dianggap tidak membentuk dan menjaga suatu urutan alur, tidak memperhatikan variabel diluar fokus pada kepentingan masing-masing, langsung pada sasaran dan telah ada pertukaran informasi dan strategi pada fase pre-negosiasi.
Gagasan utamanya adalah negosiator dapat memperjuangkan kepentingan secara rasional, dimana hasil akhirnya adalah tercapainya sebuah kesepakatan. Dalam negosiasi non-cooperatif ada tiga karakteristik khusus yaitu adanya informasi secara terbuka dengan terbukanya kepentingan yang mengarah pada bentuk koalisi bila pihak yang terlibat lebih dari dua, sifatnya tidak mengikat, dan adanya pemaksaan pada dirinya sendiri untuk melakukan suatu tindakan yang diinginkan (self enforcing).
sendiri dimana negosiator menganalisis strategi lawan dan menentukan perubahan strategi yang dianggap lebih baik.
Pendekatan kedua adalah A Coalition-Proof Nash Equilibrium (CPNE). CPNE ini muncul ketika negosiator tidak dapat melakukan hal yang lebih baik lagi walaupun mereka dapat saling bertukar informasi pada tahap pre-negosiasi. Nilai lebih dari teori ini adalah untuk merevisi asumsi dan pandangan dangkal dari gagasan mengenai bukti keseimbangan Nash dalam koalisi serta proses negosiasi yang disusun dengan grafik untuk membantu perluasan sifat dasar pendekatan dari model persiapan komunikasi dengan permainan yang lebih variatif.
Ketika pemain-pemain meramalkan secara benar dan masuk akal akan strategi dari lawan-lawan mereka, mereka tidak hanyalah memainkan tanggapan-tanggapan terbaik kepada kepercayaan-kepercayaan mereka tentang permainan lawan mereka; mereka sedang memainkan tanggapan-tanggapan terbaik kepada permainan yang nyata dari lawan-lawan mereka. Ketika semua pemain secara benar meramalkan strategi lawan mereka, dan tanggapan-tanggapan permainan terbaik untuk peramalan-peramalan ini, profil strategi yang hasilnya adalah suatu keseimbangan Nash. (Ratliff, Jim. 1992)
Contoh Dasar: Dilema Narapidana
Dilema narapidana adalah yang sangat popular sebagai dasar atau ilustrasi contoh dari teori permainan Nash. Ada dua tahanan, Jack dan Tom, yang baru saja ditangkap untuk merampok bank. Polisi tidak memiliki cukup bukti untuk menghukum mereka, tetapi tahu bahwa mereka melakukan kejahatan. Mereka menempatkan Jack dan Tom di kamar interogasi secara terpisah dan berbeda konsekuensi.
Jika kedua Jack dan Tom mengaku mereka masing-masing akan mendapatkan 10 tahun penjara.
Jika tidak ada yang mengaku, mereka akan sama-sama mendapatkan hukuman 5 tahun untuk kejahatan yang berbeda yang mereka inginkan.
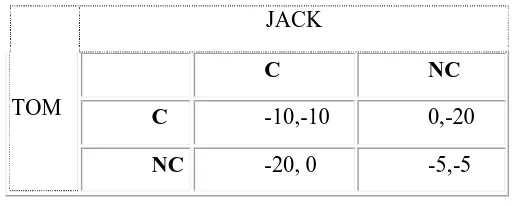
Lebih mudah untuk melihat dan membandingkan hasil ini jika kita masukkan ke dalam matriks:
Jack
TOM
C NC
C -10,-10 0,-20
NC -20, 0 -5,-5
Karena strategi Tom terdaftar dalam baris, atau sumbu x, dengan hadiah
pertama terdaftar. Jack terdaftar hadiah kedua karena strategi-nya di kolom,
atau pada sumbu-y. "C" berarti "mengaku" dan "NC" berarti "tidak
mengaku.". Matriks ini disebut "Normal Form" dalam teori permainan. Bergerak yang simultan, yang berarti bahwa baik pemain tahu keputusan yang lain dan keputusan yang dibuat pada waktu yang sama (dalam contoh ini, kedua tahanan tersebut di kamar terpisah dan tidak akan dibiarkan keluar sampai mereka memiliki membuat keputusan mereka).
Pada pandangan pertama, tampaknya bahwa kedua pemain tidak mengaku adalah pilihan terbaik karena setiap tahanan hanya akan mendapatkan 5 tahun, tetapi yang lebih mendalam akan tampak menunjukkan bahwa hal ini tidak terjadi.
Dominan Strategi
Tom untuk mengaku. Mari kita menyoroti hasil ini dalam matriks untuk melacak.
JACK
TOM
C C NC
C -10 ,-10 0,-20
NC -20, 0 -5,-5
Sekarang mari kita asumsikan bahwa Jack tidak akan mengaku. Kalau Tom mengaku, ia akan bebas, jika ia tidak mengaku, dia akan mendapatkan 10 tahun. Sekali lagi, pilihan terbaiknya adalah dengan mengakui, tidak peduli apa yang Jack pilih. Karena dalam kedua kasus nya adalah pilihan terbaik untuk mengaku, mengakui adalah murni dominan strategi (itu juga benar untuk mengatakan tidak mengakui didominasi oleh mengaku). Sebuah strategi dominan adalah strategi yang memiliki hasil terbaik tidak peduli apa pilihan pemain lain.
JACK
TOM
C NC
C -10 ,-10 0 ,-20
NC -20,0 -5,-5
JACK
TOM
C NC
C -10 , -10 0 ,-20
NC -20, 0 -5,-5
Nash Equilibrium
Anda akan melihat bahwa hukuman untuk (mengaku, mengaku) keduanya disorot. Karena kedua tahanan yang sama dominan memiliki strategi murni, mengaku, mereka akan sama-sama mengaku dan masing-masing akan mendapatkan 10 tahun penjara. Ini adalah Nash Equilibrium, (John F. Nash) Sebuah Nash Equilibrium adalah setiap hasil di mana tidak ada penyimpangan menguntungkan sepihak - yaitu, memegang semua pemain lain secara konstan, satu pemain tidak dapat memilih strategi yang akan membuatnya lebih baik. Dalam kasus ini, jika salah satu pemain tidak mengaku, dia akan mendapatkan 20 tahun bukan 10. Kotak hasilnya (5,5) yang dihasilkan dari (NC, NC) adalah
bukan Nash Equilibrium, karena ada pemain yang mempunyai pilihan yang
BAB 3
PEMBAHASAN
3.1 Nash Equilibrium dan Dominan Strategi
Nash Equilibrium adalah istilah yang digunakan dalam teori permainan untuk menggambarkan suatu keseimbangan dimana setiap pemain diberikan strategi adalah strategi yang optimal dari semua pemain lain. A Nash Equilibrium ada
ketika tidak ada penyimpangan menguntungkan sepihak dari salah satu
pemain yang terlibat. Dengan kata lain, tidak ada pemain dalam permainan
akan mengambil tindakan yang berbeda selama setiap pemain lain tetap sama. Kesetimbangan Nash adalah memaksakan diri; ketika pemain berada pada Nash Equilibrium mereka tidak memiliki keinginan untuk pindah karena mereka akan lebih buruk.
Kondisi yang Diperlukan
L R
T a,b c,d
B e,f g,h
Tabel.3.1
Agar (B, L) menjadi ekuilibrium strategi dominan (yang juga merupakan Ekuilibrium Nash), berikut ini harus benar:
a > c c > g b > d f > h
Agar (B, L) untuk menjadi Nash Equilibrium, hanya harus berikut benar:
3.2 Prisoners 'Dilemma (Lagi)
Jika setiap pemain dalam memainkan permainan strategi murni dominannya (dengan asumsi setiap pemain memiliki strategi murni dominan), maka hasilnya akan menjadi kesetimbangan Nash. Pada Prisoners 'Dilemma adalah contoh yang sangat baik untuk permainan berikut ini (ingat bahwa dalam
Prisoners 'Dilemma, mewakili angka-angka hukuman penjara):
JACK
TOM
C NC
C -10,-10 0,-20
NC -20, 0 -5,-5
Table 3.2
Dalam permainan ini, kedua pemain tahu bahwa 10 tahun adalah lebih dari 20 dan 0 tahun adalah lebih baik daripada 5; karena itu, C adalah strategi dominan mereka dan mereka akan sama-sama memilih C. Karena kedua pemain memilih C, (10,10) adalah hasil dan juga Nash Equilibrium. Untuk memeriksa apakah ini adalah Nash Equilibrium, periksa apakah baik jika pemain ingin menyimpang dari posisi ini.. Jack tidak mau menyimpang, karena jika ia memilih NC dan Tom tinggal di C, Jack akan meningkatkan waktu penjara 10 tahun.
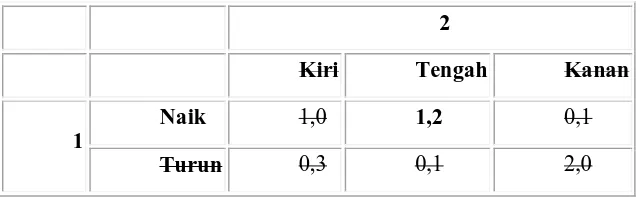
3.3 Penghapusan berulang strategi didominasi
2
Kiri Tengah Kanan
1
Naik 1,0 1,2 0,1
Turun 0,3 0,1 2,0
Table 3.3
Strategi pertama yang didominasi, adalah Kanan.. Pemain 2 akan selalu menjadi lebih baik dengan bermain Tengah, sehingga Kanan didominasi oleh Tengah. Pada titik ini kolom di bawah kanan bisa dihilangkan karena kanan tidak lagi menjadi pilihan. Hal ini akan ditampilkan dengan mencoret kolom:
2
Kiri Tengah Kanan
1
Naik 1,0 1,2 0,1
Turun 0,3 0,1 2,0
Ingat bahwa kedua pemain mengerti bahwa pemain 2 telah ada alasan untuk bermain Kanan. Pemain 1 memahami bahwa pemain 2 adalah mencoba mencari yang optimal, sehingga ia juga tidak lagi mempertimbangkan hadiah di kolom kanan. Dengan kolom kanan hilang, Hingga sekarang mendominasi Turun untuk pemain 1. Apakah pemain 2 memilih Kiri atau Tengah, pemain 1 akan mendapatkan hadiah dari pemain 2 selama ia memilih Naik. Jadi sekarang kita tidak lagi memilih strategi Turun:
2
Kiri Tengah Kanan
1
Naik 1,0 1,2 0,1
Sekarang kita tahu bahwa pemain 1 akan memilih Naik, dan pemain 2 akan memilih Kiri atau Tengah. Karena Tengah adalah lebih baik daripada kiri (sebuah hasil dari 2 vs 0), pemain 2 akan memilih Tengah dan telah terselesaikan permainan untuk Ekuilibrium Nash:
2
Kiri Tengah Kanan
1
Naik 1,0 1,2 0,1
Turun 0,3 0,1 2,0
Untuk memastikan bahwa jawaban ini (Atas, Tengah) adalah Nash Equilibrium, periksa untuk melihat apakah kedua pemain ingin menyimpang. Selama player 1 telah memilih Naik, pemain 2 akan memilih Tengah. Di sisi lain, asalkan telah memilih Tengah untuk pemain 2, pemain 1 akan memilih Atas.
3.4 Multiple Nash Equilibria
Berikut adalah beberapa permainan yang menunjukkan Multiple Nash Equilibrium. Dua driver bepergian dan berlawanan arah satu sama lain di jalan. Haruskah mereka mengemudi di kiri atau kanan? Mereka tidak ingin mengalami kecelakaan.
Driver 2 Kiri Kanan
Driver 1
kiri 1, 1 -1,-1
Kanan -1,-1 1, 1
Keduanya (Kiri, Kiri) dan (Kanan, Kanan) adalah kesetimbangan Nash. Selama mereka berada di sisi berlawanan jalan, driver yang bahagia dan tidak ingin menyimpang. Permainan seperti ini sering diselesaikan dengan konvensi social. Dahulu semua pemain setuju pada strategi itu sehingga setiap orang menjadi lebih baik. Tentu saja, semua orang tahu bahwa sisi kanan adalah yang terbaik untuk mengemudi di samping, sehingga permainan akan terlihat lebih seperti ini:
Driver 2
Kiri Kanan
Driver 1
kiri 1, 1 -1,-1
Kanan -1,-1 2, 2
Dalam kasus ini, permainan pemain itu sendiri memberikan petunjuk mengenai di mana pilihan yang baik untuk pemain lain, meskipun ada dua Nash Kesetimbangan.
Berikut adalah permainan dengan tiga Nash Kesetimbangan dan tidak ada strategi yang di dominasi:
2
a b c
1
A 1,1 2,0 3,0
B 0,2 3,3 0,0
C 0,3 0,0 10,10
Table 3.4
3.5 Menggunakan Fungsi Tanggapan Terbaik untuk Menghitung Pure Strategi Nash Equilibrium
Skripsi ini bertujuan untuk membantu kita menentukan strategi terbaik dalam permainan nash equilibrium 2x2. Juga untuk mencari apakah permainan itu suatu Nash Equilibrium atau tidak. Konsep strategi terbaik akan membantu kita untuk memilih strategi yang optimal bagi persaingan pasar, ekonomi, bisnis dan lain sebagainya. Dalam penerapan-penerapan yang praktis menunjukkan di sini adalah sangat fungsional maupun di bidang pendidikan, karena algoritma membantu ke arah penempatan keseimbangan di dalam game-game yang besar (lebih dari sekedar dua pemain dan lebih dari sekedar tiga strategi) melalui pemakaian program komputer yang mudah untuk menerapkan dan beroperasi. Lebih dari itu, prosedur memudahkan pemahaman konsep dari keseimbangan Nash dan strategi dominan di dalam game-game.
Oleh karena kebutuhan untuk mengidentifikasi pemain-pemain pada setiap aksi, tertentu jenis notasi harus diperkenalkan ke dalam prosedur, satu bahwa mengidentifikasi pemain-pemain dan pemberian imbalan mereka dengan mengabaikan jenis game yang dilibatkan secara bersama-sama. Notasi ini akan memberi pembaca satu kesan kompleksitas, tetapi contoh-contoh yang bersifat untuk menjelaskan yang diikuti keinginan menunjukkan kesederhanaan proses yang nyata.
i) N = {1, 2, 3, . . ., i, . . ., n}adalah suatu himpunan Jumlah pemain
ii) ai = {1, 2, 3, . . ., r, . . ., n} adalah suatu himpunan jumlah strategi yang dimainkan.
iii) Rk = {r1, r2, r3, ..., rn} adalah himpunan nilai permainan yang diperoleh oleh para pemain yang terhimpun dalam suatu matriks perolehan.
iv) R-ik = {r1, r2, r3,..., ri-1, ri+1, ..., rn} adalah himpunan nilai perolehan bersama dari pilihan strategi permainan yang optimal bagi n-pemain
v) Ji adalah identifikasi pemain ke- i.
vii) J-i R adalah himpunan dari semua pemain kecuali i, yang membuat pemain tersebut memilih asumsi untuk pindah strategi.
viii) (Ji r / J-i R) adalah imbalan yang diberikan untuk pemain i ketika dia memainkan strategi r, untuk memperbaiki perolehan sebagai pilihan yang tetap.
( / ) adalah daftar dari semua pemberian imbalan untuk pemain
i, yang memberikan hasil Rki sebagai hasil terpilih untuk strategi yang tetap atau optimal terhadap para pemain.
Contoh (Gibon, Robert 1992. “Game Theory for Applied Economists”.)
Player 2 Strategy 1 Strategy 2
Player 1 Strategy 1 ( 2, 1 ) ( 5,-1 ) Strategy 2 ( 3, 0 ) ( 4,-2 )
Sesuai dengan notasi yang telah diperkenalkan diatas, komponen dari game ini adalah:
a2 = {1, 2}; 1 untuk Strategy 1 dari player 2 and 2 untuk Strategy 2 dari player 2
r
L
rFungsi ini mempunyai tujuan untuk mengidentifikasi tanggapan-tanggapan terbaik suatu pemain kepada masing-masing dari himpunan yang diberi dari strategi untuk pemain-pemain lainnya. Ini merupakan suatu fungsi transformasi yang diterapkan ke atas pemberian imbalan pemain itu agar menghasilkan matriks pokok, di mana identifikasi Nash equilibria dan strategi yang dominan dengan mudah dapat diselesaikan.
(Gibon, Robert 1992. “Game Theory for Applied Economists”) Fungsi yang diperoleh dari masing-masing pemberian imbalan dari tiap pemain adalah:
Fungsi : F[ (Jir / J-iR)] = 1 ,
Masing-masing nomor 1 mengidentifikasi tanggapan terbaik dari pemain i kepada himpunan dari strategi yang diberikan oleh pemain lainnya. Seperti yang diberitahu sebelumnya, kompleksitas yang nyata dari fungsi ini akan dengan mudah diberlakukan bagi pemberian imbalan dari permainan itu. Setelah menggunakan fungsi tanggapan terbaik dalam contoh sebelumnya menggambarkan suatu keseimbangan Nash yang dikenali lewat statemen yang langsung terdefinisi. Ketika semua pemain memilih strategi terbaik yang mereka dapat, sesuai dengan strategi yang dimainkan oleh lawan mainnya. Jadi, dengan demikian, di dalam game yang diubah untuk F, suatu sel Rk dengan semua unsur-unsur sepadan dengan nilai 1 adalah suatu keseimbangan Nash. Secara Mathematic, (Gibon, Robert 1992. “Game Theory for Applied Economists”) suatu keseimbangan Nash terjadi ketika:
karena suatu titik Rk dari game yang diubah. Yaitu, ketika suatu sel berisi hanya 1's, itu mengidentifikasi satu set strategi yang merupakan tanggapan terbaik yang mungkin untuk masing-masing dari para pemain, sebagai tanggapan dari strategi yang dimainkan oleh pemain lainnya Ini adalah definisi yang klasik dari Nash.
Sebagai alternatif, hasil itu dapat ditulis dalam cara yang berikut:
i N
1 F[ (Jis / J-iS)] = NSuatu strategi yang dominan juga dapat dikenali dengan statemen definisi kepunyaan atau nilai permainan yang lebih menguntungkan, yaitu., ketika satu strategi pemain i adalah tanggapan terbaik dengan sendirinya dari apapun juga strategi yang dimainkan oleh pemain-pemain yang lain. Jadi; dengan demikian, di dalam bermain menurut aturan diubah oleh F, suatu strategi r dengan semua unsur-unsur sepadan dengan 1 adalah suatu strategi yang dominan. Secara Mathematic, (Gibon, Robert 1992. “Game Theory for Applied Economists”) suatu strategi yang dominan terjadi ketika:
F[ (Jir / J-iR)] = 1 to all Rk-i given.
Contoh :
Permainan akan berubah menjadi :
J2
J21 J22
J1 J11 (F[ (J11 / J21)], F[ (J21 / J11)]) (F[ (J11 / J22)], F[ (J22 / J11)])
J12 (F[ (J12 / J21)], F[ (J21 / J12)]) (F[ (J12 / J22)], F[ (J22 / J12)])
Dengan hasil :
Player 2 Strategy 1 Strategy 2 Player 1 Strategy 1 ( 0, 1 ) ( 1, 0 )
Strategy 2 ( 1, 1 ) ( 0, 0 )
Kita dapat mengidentifikasi satu keseimbangan Nash dan satu strategi yang dominan. keseimbangan Nash terjadi ketika:
player 1 memainkan strategi permainan 2 dan player 2 memainkan strategi permainan 1.
Karena :
F[ (J12 / J21)] = F[ (J21 / J12)] = 1, dan didalam table terlihat ada dua yang bernilai 1's.
Dan strategi 1 dominan untuk pemain 2, Karena:
BAB 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Kesimpulan yang dapat diproleh dari hasil penelitian yang telah dilakukan dalam tulisan ini adalah sebagai berikut :
1. Nash equilibrium adalah konsep solusi menggunakan serangkaian strategi dalam negosiasi dimana masing-masing pihak diasumsikan telah mengetahui strategi lawan, dan masing-masing pihak hanya dapat memperoleh keuntungan dengan mengubah strateginya sendiri.
2. Karena menitikberatkan pada pengambilan dan pengubahan strategi, negosiasi dalam Nash Equilibrium berlangsung dalam dua tahap.
a. Tahapan pertama sekaligus tahapan yang paling menentukan adalah pre-negosiasi dimana kedua pihak saling menginformasikan semua alternatif, penawaran dan permintaan ke lawan sehingga masing-masing pihak dapat menganalisis posisi diri sendiri dan lawan.
b. Tahapan kedua adalah negosiasi itu sendiri dimana negosiator menganalisis strategi lawan dan menentukan perubahan strategi yang dianggap lebih baik
3. Dalam negosiasi berkelanjutan, pengubahan strategi dapat membawa dampak non rasional karena pihak yang terlibat dapat mengancam lawan melalui aksi yang tidak rasional. Pihak yang satu dapat melakukan unfair play dengan tidak menginformasikan strategi yang sebenarnya pada pre-negosiasi dengan harapan lawan akan mengubah strateginya menuju ke keadaan yang lebih buruk.
2.4 Saran
Daftar Pustaka
1. Bronson, Richard. 1993. Teori dan Soal Operational Research. Erlangga : Jakarta.
2. Gibon, Robert 1992. “Game Theory for Applied Economists”. Pinceton University Press
3. Kartono. 1994. Teori Permainan. Andi Offset : Yogyakarta
4. Moore, Andrew.W. Diakses 20 januari 2010, Non-Zero-One Game Theory. http://www.cs.cmu.edu/~awm/tutorials.
5. Narahari, Y. 2008. Game Theory. Bangalore : India
6. Ratliff, Jim. 1992. Nash Equilibrium dan Finding Mixed Strategy Nash
Equilibria in 2-2 Games. http://virtualperfection.com/gametheory.
7. Siagian,P. 1987. Penelitian Operational. UI Press : Jakarta
8. Subagyo, Pangestu dkk. 1993. Dasar-dasar operational research. BPFE-Yogyakarta : BPFE-Yogyakarta.
9. Suprapto, Johannes. 1988. Riset Operasi Untuk Pengambilam Keputusan. UI press : Jakarta.
10.Turocy, Theodore L. and Stengel, Bernhard Von. 2001. Game Theory. Academic Press : CDAM
11.Wikipedia, http://en.wikipedia.org/wiki/Game Theory, waktu akses : 20 januari 2010, pukul 22.00.