Delineation of Potential and Actual Rice Planting Scheduling in Lampung and West Kalimantan

(1)

BIFURKASI SISTEM MANGSA-PEMANGSA

TIPE MICHAELIS-MENTEN DENGAN

TINGKAT PEMANENAN KONSTAN

FITRIA

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(2)

ABSTRAK

FITRIA. Bifurkasi Sistem Mangsa-Pemangsa Tipe Michaelis-Menten dengan Tingkat Pemanenan Konstan. Dibimbing oleh ENDAR HASAFAH NUGRAHANI dan ALI KUSNANTO.

(3)

ABSTRACT

FITRIA. Prey-Predator System Bifurcation Michaelis-Menten Type with Constant Harvesting Rate. Supervised by ENDAR HASAFAH NUGRAHANI and ALI KUSNANTO.

(4)

BIFURKASI SISTEM MANGSA-PEMANGSA

TIPE MICHAELIS-MENTEN DENGAN

TINGKAT PEMANENAN KONSTAN

FITRIA

G54060240

Skripsi

sebagai salah satu syarat untuk memperoleh gelar

Sarjana Sains

pada

Departemen Matematika

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

(5)

Judul

: Bifurkasi Sistem Mangsa-Pemangsa Tipe Michaelis-Menten dengan

Tingkat Pemanenan Konstan

Nama

: Fitria

NIM

: G54060240

Menyetujui

Pembimbing 1

Pembimbing II

Dr. Ir. Endar Hasafah Nugrahani, MS

Drs. Ali Kusnanto, M.Si

NIP. 19631228 198903 2 001

NIP. 19650820 199003 1 001

Mengetahui

Ketua Departemen Matematika

Dr. Berlian Setiawaty, MS

NIP. 19650505 198903 2 004

(6)

KATA PENGANTAR

Alhamdulillah

irobbil’alamin. Penulis mengucapkan syukur kehadirat Allah SWT atas segala limpahan rahmat dan karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Penyusunan karya ilmiah ini tidak terlepas dari dukungan dan bantuan dari berbagai pihak. Pada kesempatan ini, penulis juga ingin mengucapkan terimakasih yang sebesar-besarnya kepada:

1. Bapak dan Ibu tersayang, terima kasih atas didikan, kasih sayang, nasihat, semangat, serta

do’a yang tiada henti-hentinya. Do’a yang selalu menjadi penerang jalan penulis.

2. Dr. Ir. Endar Hasafah Nugrahani, MS. selaku dosen pembimbing I, Drs. Ali Kusnanto, M.Si. selaku pembimbing II. Terimakasih atas waktu, ilmu yang diberikan dan kesabarannyadalam membimbing penulis. Semua ilmu yang Bu Endar dan Pak Ali berikan sangat bermanfaat bagi penulis. Terima kasih.

3. Ir. N. K. Kutha Ardana, M.Sc. selaku dosen penguji. Terimakasih atas waktu dan ilmu yang sangat bermanfaat bagi penulis.

4. Kakak-kakakku tersayang (M. Ali Nasri, Iswandi, dan Risdiyanto), kakak ipar (Neneng Heni Sri Heryani dan Nuraini), terimakasih atas do’a, semangat dan dukungannya.

5. Adik-adikku tersayang (Elvi Rahayu dan Maulida Khairunnisa), terima kasih atas semangat dan senyum kebahagiaan yang selalu dirindukan. Segala bentuk ocehan dan larangan adalah kasih sayang yang suatu saat akan kalian kenang.

6. Keponakanku (Nabila, Rara, dan Quinza), terima kasih atas keceriaan dan senyum manis yang selalu hadir pada wajah mungil kalian.

7. Fauza Ronal, terima kasih atas semangat dan kasih sayang yang selama ini diberikan. Kesedihan dan kerinduan yang selalu terobati ketika mendengar tawa dan candamu.

8. Semua dosen Departemen Matematika, terimakasih atas ilmu yang telah diberikan.

9. Pak Yono, Bu Ade, Bu Susi, Mas Bono, Mas Heri, Mas Deni dan seluruh staf pegawai Departemen Matematika, terimakasih atas bantuannya dalam memperlancar administrasi akademik bagi penulis di departemen Matematika.

10. Guru-guru SMA N 1 Selatpanjang (Pak Yusuf, Pak Salman, dan lain-lain), SLTP N 1 Tebing Tinggi, dan SD N 013 Selatpanjang. Tanpamu, penulis takkan berdiri di sini. Terima Kasih. 11. Teman-teman satu bimbingan : Rias, Nene, dan Subro. Terima kasih atas doa, bantuan,

dukungan semangat, dan nasehatnya.

12. Kakak kelas angkatan 42 dan 41 yang tidak bisa penulis sebutkan satu per satu.

13. Teman-teman angkatan 43 : Margi Aa, Suci, Aini Radit, Nene Momogi, Putri Bagus, Lina, Lia, Erni Tyan, Rias Kriting, Arum Bayu, Nia, Destya, Resti, Nidya, Tami, Maria Herlina, Narsih, Desy, Ratna Agung, Cici, Vera, Rizki SN, Rizki NS, Kiki, Apri, Ace, Subro, Mamet, Supri, Irsyad, Copi, Wira, Peli, Arif, Mubarok, Ryan, Fardan, Nanu, Dwi, Adi, Ecka, Sendy, Dandi, Zul, Adam, Kunto, Syahrul, Faisol, Elly, Hendra, Razon, Kabil, Sabar, Gandi, Andrew, Ucok, dan Nobo. Terimakasih atas doa, dukungan dan semangatnya, terimakasih atas kebersamaannya selama 3 tahun di Math’43.

14. Adik kelas angkatan 44 dan 45 yang tidak bisa penulis sebutkan satu per satu.

15. Teman-temanku di Padasuka : Ferra, Emil, dan Dian (berawal dari sekamar di asrama TPB IPB sampai kost), Merry, Intan, Muti, Puma, Mei, Isti, Eka, Wulanda, Lina, Nabe, Molly, Ovi, dan lainnya yang tidak bisa ditulis satu per satu, terimakasih atas doa, bantuan, dan dukungan semangatnya.

16. Ella (sepupu), Eka, Yeyen, Yeni, Indah, Ayu, Jois, Amin, Agung, Agus, Topik, Lambok, Sri, Sinta, Ana, Ijah, Yuli, Eko, Nova, Ita, Bang Adek, Bang Iwan, Bang Roni, dan lain-lain. Penulis menyadari tulisan ini masih memiliki kekurangan dan jauh dari kesempurnaan. Oleh karena itu dibutuhkan kritik dan saran yang membangun dari pembaca.

Semoga karya ilmiah ini bermanfaat bagi kita semua, bagi dunia ilmu pengetahuan khususnya Matematika.

Bogor, Juli 2010

(7)

RIWAYAT HIDUP

Penulis lahir di Selatpanjang, Riau pada tanggal 26 Juni 1988 sebagai anak ke empat dari enam bersaudara, anak dari pasangan Arpan dan Yusniati. Tahun 2000 penulis lulus dari SDN 013 Selatpanjang. Tahun 2003 penulis lulus dari SLTPN 1 Tebing Tinggi. Tahun 2006 penulis lulus dari SMAN 1 Selatpanjang dan pada tahun yang sama penulis lulus seleksi masuk IPB melalui jalur Beasiswa Utusan Daerah (BUD), Tingkat Persiapan Bersama. Pada tahun 2007, penulis memilih jurusan Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.

Selama mengikuti perkuliahan, penulis pernah menjadi pengajar Pengantar Matematika dan Kalkulus I di bimbingan belajar Gumatika, Exacta, dan REC. Penulis pernah menjadi pengajar di SMA YPHB Bogor (bimbingan persiapan Ujian Nasional). Penulis aktif di Unit Kegiatan Mahasiswa Koperasi Mahasiswa (UKM Kopma) periode 2006/2007. Penulis pernah menjabat sebagai bendahara Organisasi Mahasiswa Daerah Rumpun Keluarga Pelajar Mahasiswa Bengkalis Bogor (OMDA RKPMB Bogor) periode 2008/2009. Penulis juga aktif pada kegiatan kemahasiswaan Gumatika (Gugus Mahasiswa Matematika) sebagai staf Departemen Keilmuan periode 2008/2009. Selain itu, penulis pernah terlibat dalam berbagai kegiatan mahasiswa, antara lain divisi acara Ice Cream Day, Campus Fair KOPMA IPB pada tahun 2007, divisi danus The Supremacy on The Stove, Campus Fair KOPMA IPB pada tahun 2008, divisi ticketing Try Out

(8)

DAFTAR ISI

Halaman

DAFTAR ISI ... vii

DAFTAR GAMBAR ... viii

DAFTAR TABEL ... viii

DAFTAR LAMPIRAN ... viii

I PENDAHULUAN 1.1 Latar Belakang ... 1

1.2 Tujuan Penulisan... 1

1.3 Sistematika Penulisan ... 1

II LANDASAN TEORI 2.1 Sistem Persamaan Diferensial Mandiri ... 2

2.2 Titik Tetap ... 2

2.3 Pelinearan ... 2

2.4 Nilai Eigen dan Vektor Eigen ... 2

2.5 Titik Tetap Hiperbolik dan Titik Tetap Non-Hiperbolik ... 2

2.6 Analisis Kestabilan Titik Tetap ... 2

2.7 Penondimensionalan ... 4

2.8 Siklus Limit ... 4

2.9 Bifurkasi ... 4

2.10 Bifurkasi Titik Sadel ... 4

2.11 Bifurkasi Hopf ... 4

III PEMBAHASAN 3.1 Model ... 6

3.2 Titik Tetap ... 6

3.3 Analisis Kestabilan Titik Tetap ... 7

3.4 Bifurkasi ... 8

3.5 Simulasi ... 10

IV SIMPULAN ... 14

V DAFTAR PUSTAKA ... 15

(9)

DAFTAR GAMBAR

Halaman

1 Jenis-jenis Kestabilan Titik Tetap ... 3

2 Plot Bidang Fase dan Bidang Solusi untuk Kasus 1 ... 11

3 Plot Bidang Fase dan Bidang Solusi untuk Kasus 2 ... 12

4 Bifurkasi Hopf ... 13

DAFTAR TABEL

Halaman 1 Kestabilan Titik Tetap Berdasarkan Jenis Titik Tetap ... 4

2 Ringkasan Keberadaan dan Kestabilan Titik Tetap ... 9

DAFTAR LAMPIRAN

Halaman 1 Penondimensionalan Persamaan Model Mangsa-Pemangsa Tipe Michaelis-Menten ... 17

2 Mencari Titik Tetap... 19

3 Pembuktian Lema 3.1... 21

4 Matriks Jacobi untuk Masing-masing Titik Tetap ... 24

5 Pembuktian Teorema 3.2 ... 26

9 Simulasi Bidang Fase dan Bidang Solusi Bifurkasi Titik Sadel Kasus 1... 33

10 Simulasi Bidang Fase dan Bidang Solusi Bifurkasi Titik Sadel Kasus 2... 37

(10)

1

I

PENDAHULUAN

1.1 Latar Belakang

Dalam suatu populasi, akan terjadi interaksi antar spesies, di mana dua spesies berinteraksi dalam suatu rantai makanan. Interaksi ini dapat berupa sistem mangsa- pemangsa atau sistem kompetisi. Abrams dan Ginzburg (2000) menyebutkan bahwa respon fungsional yang melebihi rentang waktu ekologi bergantung pada kepadatan populasi mangsa maupun pemangsa, terutama ketika pemangsa harus mencari makanan. Oleh karena itu, mangsa dan pemangsa harus berbagi atau bersaing untuk mendapatkan makanan.

Dalam dinamika populasi, beberapa ahli mengamati sistem mangsa-pemangsa yang memuat tipe Michaelis-Menten. Dinamika model ini telah dipelajari oleh beberapa peneliti dalam jurnalnya yaitu Kuang dan Beretta (1998) dan Kuang (1999) yang memperlihatkan adanya dinamika pada sistem ini.

Xiao (2005) menyebutkan bahwa dari sudut pandang biologi, jika ada titik tetap positif pada model, untuk beberapa nilai parameter tertentu baik mangsa maupun pemangsa masih bisa mengalami kepunahan. Kepunahan mangsa dan pemangsa terjadi dalam dua cara yang berbeda. Salah satu cara adalah kedua spesies akan mengalami kepunahan tanpa memperhatikan kepadatan awal populasi. Cara lain adalah kedua spesies akan punah hanya jika mangsa maupun pemangsa memiliki rasio awal yang terlalu rendah. Sedangkan dari sudut pandang kebutuhan manusia, perlu untuk mempertimbangkan adanya eksploitasi sumber daya alam hayati dan pemanenan populasi yang umumnya dipraktekkan di perikanan, kehutanan, dan pengelolaan satwa liar.

Dalam karya ilmiah ini, untuk penyederhanaan matematis, bentuk awal

sistem mangsa-pemangsa yang memuat tipe Michaelis-Menten akan dinondimensionalkan dengan skala tertentu. Faktor pemanenan diikutsertakan dalam model, namun diasumsikan bahwa tingkat pemanenan hanya berpengaruh terhadap populasi mangsa. Mengingat bahwa mangsa merupakan sumber makanan bagi pemangsa, maka secara otomatis pemanenan pada populasi mangsa akan mempengaruhi populasi pemangsa secara tidak langsung. Dinamika global dari sistem ini diprediksi dengan menunjukkan terjadinya perubahan struktur (bifurkasi) pada sistem [Xiao, 2005].

Secara matematis, dari sudut pandang bifurkasi, pertanyaan yang sangat menarik adalah jenis bifurkasi apa yang akan terjadi ketika model diganggu oleh perubahan nilai konstanta (tingkat pemanenan) yang kecil.

1.2 Tujuan Penulisan

Tujuan dari penulisan karya ilmiah ini adalah untuk memperlihatkan jenis bifurkasi yang terjadi pada sistem mangsa-pemangsa yang memuat tipe Michaelis-Menten dengan tingkat pemanenan konstan dan simulasi bifurkasi tersebut dalam berbagai parameter.

1.3 Sistematika Penulisan

(11)

2

II

LANDASAN TEORI

2.1 Sistem Persamaan Differensial Mandiri

Perhatikan sistem persamaan differensial (SPD) berikut :

= ,

(2.1)

= ,

dan adalah fungsi kontinu dari dan dengan turunan parsial pertama kontinu, dengan laju perubahan dan dinyatakan dengan fungsi eksplisit dari dan sendiri dan tidak mengandung di dalamnya. SPD (2.1) disebut sebagai sistem persamaan differensial autonomous/mandiri.

[Farlow, 1994]

2.2 Titik Tetap

Misalkan diberikan persamaan differensial (SPD) sebagai berikut :

= = , (2.2)

Titik ∗ disebut titik tetap jika memenuhi

∗ _{= 0}_{. Titik tetap disebut juga titik kritis}

atau titik kesetimbangan. Untuk selanjutnya akan digunakan istilah titik tetap.

[Tu, 1994]

2.3 Pelinearan

Misalkan :

= ,

Andaikan ∗, ∗ adalah titik tetap dari persamaan di atas, maka ∗, ∗ = 0 dan

∗_, ∗ _{= 0}_{. Misalkan} ₌ ₋ ∗_dan

= − ∗ maka didapatkan :

=

= ∗+ , ∗+

= ∗, ∗ + �

� + �

� + 2, 2,

= �

� + �

� + 2, 2,

=

= ∗+ , ∗+

= ∗, ∗ + �

� + �

� + 2, 2,

= �

� + �

� + 2, 2, Dalam bentuk matriks :

= � � � � � � � �

+ 2_, 2_,

Matriks

=

� � � � � � � � ∗_, ∗ disebut

matriks Jacobi pada titik tetap ∗, ∗ . Karena 2, 2, →0 maka dapat diabaikan sehingga didapat persamaan linear :

= � � � � � � � � (2.3) [Strogatz,1994]

2.4 Nilai Eigen dan Vektor Eigen

Misalkan matriks berukuran × . Suatu vektor tak nol � di disebut vektor eigen dari jika untuk suatu skalar, yang disebut nilai eigen dari berlaku :

�=�� (2.4) Vektor � disebut vektor eigen yang bersesuaian dengan nilai eigen �.

Untuk mencari nilai eigen dari matriks yang berukuran × , maka persamaan (2.4) dapat ditulis sebagai berikut :

− � �= 0 (2.5) Dengan adalah matriks identitas. Persamaan (2.5) mempunyai solusi tak nol jika dan hanya jika :

− � = 0 (2.6) Persamaan (2.6) disebut persamaan karakteristik dari .

[Tu, 1994]

2.5 Titik Tetap Hiperbolik dan Titik Tetap Non-Hiperbolik

Titik ∗disebut titik tetap hiperbolik jika pelinearan menghasilkan akar karakteristik dengan bagian real tak nol dan titik ∗ disebut titik tetap non-hiperbolik jika dari pelinearan ada akar karakteristik dengan bagian real sama dengan nol.

[Tu, 1994]

2.6 Analisis Kestabilan Titik Tetap

(12)

=

dengan persamaan karakteristik − � = 0, dan adalah matriks identitas, maka persamaan karakteristiknya menjadi − �

− � = 0, sedemikian sehingga diperoleh persamaan :

�2_{− ��}₊_Δ_{= 0} dengan

�= � = + =�1+�2 Δ= det = − =�1�2 Dengan demikian diperoleh nilai eigen dari adalah :

�1,2=�± � 2−₄∆

2

 Kasus Δ< 0.

Jika kedua nilai eigen real berbeda tanda maka titik tetap bersifat sadel.

 Kasus ∆ > 0.  �2₋₄_Δ_{> 0}_.

- Jika �> 0 dan kedua nilai eigen real bernilai positif maka titik tetap

bersifat “simpul tak stabil”.

- Jika �< 0 dan kedua nilai eigen real bernilai negatif maka titik tetap

bersifat “simpul stabil”.

 _�2₋₄_Δ_{< 0}_.

- Jika �> 0 dan kedua nilai eigen imajiner (�1,2= ± ) maka titik tetap bersifat “spiral tak stabil”. - Jika �< 0 dan kedua nilai eigen

imajiner (�1,2= ± ) maka titik

tetap bersifat “spiral stabil”.

- Jika �= 0 dan kedua nilai eigen imajiner murni (�1,2= ± ) maka

titik tetap bersifat “center”.

 �2₋₄_Δ_{= 0}_.

Parabola �2−4Δ= 0 adalah garis batas antara simpul dan spiral. Star nodes dan degenerate terletak pada parabola ini. Jika kedua nilai eigen bernilai sama maka titik tetap bersifat

“simpul sejati”.

 Kasus ∆ = 0.

Jika salah satu nilai eigen bernilai nol maka titik asal bersifat “titik tetap tak terisolasi”.

[Strogatz, 1994] Berikut diberikan gambar jenis-jenis kestabilan titik tetap :

Gambar 1. Jenis-jenis Kestabilan Titik Tetap

Diberikan juga ringkasan jenis-jenis kestabilan titik tetap berdasarkan jenis titik

tetapnya (hiperbolik dan non-hiperbolik) [Tu, 1994] :

Simpul stabil Simpul tak stabil

Center

Sadel Spiral tak stabil

(13)

4

Tabel 1 Kestabilan Titik Tetap Berdasarkan Jenis Titik Tetap

Titik Tetap Hiperbolik

Nilai eigen �1,�2 Sifat

Kasus 1 : �2₋₄_∆_{> 0}

(i) Real, � berbeda, sama tanda

(ii) Real, � berbeda, beda tanda

Simpul stabil atau simpul tak stabil

Titik sadel

Kasus 2 :

�2₋₄_∆_{= 0} �1=�2=�=

�

2< atau > 0 Simpul sejati

Kasus 3 :

�2₋₄_∆_{< 0} �= ± , ≠0≠ Spiral stabil atau spiral tak stabil

Titik Tetap Non-Hiperbolik

Nilai eigen �1,�2 Sifat

Kasus 4 : �2₋₄_∆_{> 0}

(i) � = 0≠ � ≠ → ∆ = 0 (ii) �1= 0 =�2→ ∆ = 0 =�

Simple degenerate Double degenerate

Kasus 5 :

�2₋₄_∆_{= 0} �1=�2= �

2= 0→ �= 0 Double degenerate

Kasus 6 :

�2₋₄_∆_{< 0} �= ± , �= 0 <∆ Center

2.7 Penondimensionalan

Penondimensionalan adalah suatu metode untuk menyederhanakan suatu persamaan banyak parameter menjadi persamaan dengan sedikit parameter.

[Strogatz, 1994]

2.8 Siklus Limit (Lymit Cycle)

Siklus limit adalah orbit tertutup yang terisolasi. Terisolasi artinya bahwa orbit di sekelilingnya menuju atau menjauhi siklus limit.

[Strogatz, 1994]

2.9 Bifurkasi

Bifurkasi adalah suatu kondisi di mana terjadinya perubahan pada sistem, bisa berupa perubahan banyaknya titik tetap atau perubahan kestabilan titik tetap. Titik yang mengalami kondisi ini disebut titik bifurkasi.

[Strogatz, 1994]

Pada bifurkasi satu-dimensi ditemukan kasus-kasus untuk bifurkasi saddle-node, bifurkasi transcritical, dan bifurkasi pitchfork

(supercritial dan subcritical). Sedangkan pada kasus dua-dimensi ditemukan kasus bifurkasi Hopf.

2.10 Bifurkasi Titik Sadel (Saddle-Node)

Bifurkasi saddle-node adalah bifurkasi yang terjadi jika salah satu sisi dari nilai parameter tidak terdapat titik tetap dan pada sisi lain terdapat dua titik tetap, dimana yang satu stabil dan yang lainnya tidak stabil.

[Strogatz, 1994]

2.11 Bifurkasi Hopf

Teorema : Misalkan :

= , (2.7)

(14)

− 0, 0 di mana 0 positif dan vektor fungsi 2 × − 0, 0 di mana adalah daerah asal pada 2_._{Misalkan bahwa} sistem (2.7) memiliki titik singular untuk masing-masing , sehingga :

, = 0 ⇒ = (2.8) Misalkan matriks pelinearan dari (2.7) untuk titik singular , maka :

= _x ( , ) _{= ( )} (2.9) Misalkan bahwa 0 memiliki nilai eigen imajiner murni ± , ≠0, sehingga :

tr 0 = 0, det 0 > 0 (2.10) Jika matriks , didefinisikan oleh :

= 0 + (2.11) maka tr (0)≠0 sehingga ada solusi periodik dari (2.7) untuk disekitar = 0 dan disekitar dengan periode =2� untuk yang kecil.

Bukti : Lihat Murray, 1993.

(15)

6

III

PEMBAHASAN

3.1 Model

Sistem mangsa-pemangsa telah dikenal luas dan dikembangkan dengan berbagai tipe seperti model mangsa-pemangsa klasik yang sering disebut Lotka-Volterra dan model mangsa-pemangsa Bazykin.

Dalam karya ilmiah ini akan dibahas tipe lain dari model mangsa-pemangsa yaitu model mangsa-pemangsa yang memuat tipe Michaelis-Menten dengan tingkat pemanenan konstan.

Sistem mangsa-pemangsa yang memuat tipe Michaelis-Menten memiliki bentuk sebagai berikut :

=� 1− � − +

(3.1)

= − +

+ di mana :

= kepadatan populasi mangsa pada waktu

= kepadatan populasi pemangsa pada waktu

�= laju pertumbuhan intrinsik �= daya dukung lingkungan

= laju kematian pemangsa

= tingkat tertangkapnya mangsa oleh pemangsa

= konstanta tingkat kejenuhan = tingkat kemudahan pemangsaan oleh pemangsa

Untuk penyederhanaan matematis, dilakukan penondimensionalan dengan skala → � , → /�, dan → /� maka persamaan (3.1) menjadi :

= 1− − +

(3.2)

= − +

+ di mana =

� , =� , dan =� .

(Langkah-langkah penondimensionalannya dapat dilihat pada lampiran 1)

Untuk mempermudah dan menjaga dampak atau pengaruh biologis, parameter , , dan berturut-turut memiliki arti yang sama dengan , , dan .

Diasumsikan bahwa tingkat pemanenan konstan hanya berpengaruh pada perubahan populasi mangsa yang diambil secara kontinu. Aktivitas pemanenan tidak mempengaruhi populasi pemangsa secara langsung. Hal ini

jelas bahwa aktivitas pemanenan mengurangi populasi pemangsa secara tidak langsung dengan mengurangi ketersediaan mangsa untuk pemangsa.

Masalah tersebut diformulasikan sebagai berikut :

= 1− −

+ −

(3.3)

= − +

+ di mana :

= kepadatan populasi mangsa pada waktu

= kepadatan populasi pemangsa pada waktu

= tingkat tertangkapnya mangsa oleh pemangsa

= tingkat kemudahan pemangsaan oleh pemangsa

= laju kematian pemangsa = tingkat pemanenan

dengan , , , dan adalah konstanta positif. Berikut akan dicari titik tetap di +2 dari sistem (3.3) dengan mempertimbangkan bahwa kondisi awal yang bermakna secara biologis yaitu 0 0 dan 0 0. Kemudian akan dianalisis kestabilan di sekitar titik tetap tersebut serta bifurkasi yang terjadi.

3.2 Titik Tetap

Berikut akan ditentukan titik tetap dari persamaan (3.3) :

= = 0

dan

= = 0

Dari = = 0 diperoleh : = 0 atau

=( − )

Sehingga diperoleh :

1= , =

1 + (−1) 1−4

2 , 0

(3.4)

2= ∗, ∗

= − − + (−1) ∆

2 ,

(16)

di mana ∆ = − − 2₋₄ 2_dan = 1, 2.

(Penurunan rumusnya dapat dilihat pada lampiran 2)

Berikut lema yang menjelaskan jumlah dan lokasi titik tetap dari model (3.3) [Xiao, 2005].

Lema 3.1 :

1) Sistem (3.3) tidak memiliki titik tetap di +

2_jika _>1 4.

2) Sistem (3.3) memiliki satu titik tetap di +

2_{, yaitu} _, ₌ 1

2 , 0 jika = 1 4. 3) Sistem (3.3) memiliki dua dua titik tetap di

+ 2_{, yaitu}

1, 1 dan 2, 2 jika salah satu kondisi berikut ini terpenuhi:

(3.i) dan 0 < <1 4; (3.ii) − dan 0 < <1

4; (3.iii) 0 < − < dan − −

2 2

<

<1 4.

4) Sistem (3.3) memiliki tiga titik tetap di +2, yaitu ∗, ∗ = − −

2 ,

− _∗

,

1, 1 , dan 2, 2 jika 0 < − < dan − −

2 2

= <1 4.

5) Sistem (3.3) memiliki empat titik tetap di +

2_{, yaitu}

1∗, 1∗ , 2∗, 2∗ , 1, 1 dan

2, 2 , jika 0 < − < dan 0 < < − −₂ 2,1

4 .

(Pembuktian Lema 3.1 dapat dilihat pada lampiran 3)

Berdasarkan titik tetap yang diperoleh, berikut akan dianalisis kestabilan titik tetapnya.

3.3 Analisis Kestabilan Titik Tetap

Pada bagian ini akan dipertimbangkan sistem mangsa-pemangsa yang memuat tipe Michaelis-Menten dengan tingkat pemanenan konstan berikut :

= , = 1− −

+ −

(3.5)

= , = − +

+

Bentuk linear dari persamaan (3.5) yaitu : =

dengan = , dan matriks Jacobi berikut : = � � � � � � � � (3.6) =

1−2 − 2

+ 2 −

2

+ 2

2

+ 2 − +

2

+ 2

di mana dan masing-masing adalah koordinat titik tetap. Disubstitusikan hasil titik tetap (3.4) sehingga diperoleh :

, = −1

+1 ₁₋₄ ₋

0 −

(3.7)

∗_, ∗

=

− + −1 +1 ∆ 2

− 2

2 − 2

− − (Penurunan rumusnya dapat dilihat pada lampiran 4)

Dinamika model (3.5) di sekitar titik tetap secara langsung berasal dari sifat nilai eigen dari matriks

A

pada keseimbangan. Berikut diberikan Teorema 3.2 [Xiao, 2005] :

Teorema 3.2. Jika =1

4 , sistem (3.3) hanya memiliki satu titik tetap , = 1

2, 0 , dan (i) , merupakan degenerate jika ≠ ; (ii) , merupakan doubledegenerate jika

= .

Bukti : Lihat lampiran 5.

Dalam Teorema 3.2, =− −1 2

2 −

+ < 0 di

2

R

_ yang mengisyaratkan bahwa untuk beberapa nilai awal, spesies mangsa mungkin akan punah seiring dengan meningkatnya waktu. Dan jika , laju kematian pemangsa lebih besar dari tingkat kemudahan pemangsaan oleh pemangsa , < 0. Oleh karena itu untuk beberapa nilai awal tertentu spesies pemangsa akan punah seiring meningkatnya waktu. Tetapi keduanya tidak bisa punah secara bersamaan.

Untuk pembangunan sumber daya berkelanjutan, diasumsikan bahwa pihak yang melakukan pemanenan memiliki kewajiban terhadap masyarakat dan ekologi pelestarian spesies mangsa. Dengan demikian, laju pemanenan harus memenuhi 0 < <1

(17)

8

Berikut diberikan Teorema 3.3, Teorema 3.4, Teorema 3.5 [Xiao, 2005] :

Teorema 3.3. Sistem (3.3) hanya memiliki dua titik tetap dengan ketentuan :

(a) Jika < dan 0 < <1

4, maka sistem (3.3) memiliki dua titik tetap 1, 0 merupakan sadel, dan 2, 0 merupakan simpul stabil;

(b) Jika = dan 0 < <1

4 maka sistem (3.3) memiliki dua titik tetap 1, 0 dan 2, 0 keduanya merupakan degenerate; (c)Jika 0 < − < dan − −

2 2

<

<1

4 (atau − > dan 0 < < 1 4), maka sistem (3.3) memiliki dua titik tetap yaitu 1, 0 merupakan simpul tak stabil dan 2, 0 merupakan sadel. (Pembuktian Teorema 3.3 dapat dilihat pada lampiran 6)

Teorema 3.4. Misalkan 0= − −₂ 2

. Jika 0 < − < dan = 0<

1 4, maka sistem (3.3) mempunyai tiga titik tetap.

(I) Jika ≠ , maka sistem (3.3) memiliki tiga titik tetap di +2, yaitu ∗, ∗ =

− −

2 ,

− _∗

= 0, − 0

dan 2, 2 =

1+ 1−4 0

2 , 0 merupakan sadel, dan 1, 1 =

1₋1−4 0

2 , 0

merupakan simpul tak stabil.

(II) Jika = , maka sistem (3.3) memiliki tiga titik tetap di +2, yaitu ∗, ∗ =

− −

2 ,

− _∗

= 0, − 0 merupakan double degenerate,

1, 1 =

1₋1−4 0

2 , 0 merupakan simpul tak stabil, dan 2, 2 =

1+ 1−4 0

2 , 0 merupakan sadel.

(Pembuktian Teorema 3.3 dapat dilihat pada lampiran 7)

Teorema 3.5. Jika 0 < − < dan 0 < < ₀,1

4 maka sistem (3.3) memilki empat titik tetap di +2 seperti yang ditunjukkan pada Lemma 3.1. Selain itu, titik tetap 2, 0 dan 1∗, 1∗ merupakan sadel, titik tetap 1, 0 merupakan simpul tak stabil, dan titik tetap 2∗, 2∗ memiliki tiga kemungkinan berikut :

(i) 2∗, 2∗ adalah simpul atau spiral stabil jika :

0 < − 1 <

ataupun dimisalkan :

∗₌ − − 2− − − / 2

4 2 ,

0 < − < < 1, 0 < < min ₀,1

4,

∗ _;

(ii) 2∗, 2∗ adalah spiral atau center jika : 0 < − < < 1,

0 < = ∗< ₀,1 4 ;

(iii) 2∗, 2∗ adalah simpul atau spiral tak stabil jika 0 < − < < 1,

0 < < ∗< min ₀,1 4 .

(Pembuktian Teorema 3.3 dapat dilihat pada lampiran 8)

Ringkasan keberadaan dan kestabilan pada sistem (3.3) dapat dilihat pada Tabel 2.

Berdasarkan Lema dan Teorema yang telah dikemukakan di atas, berikut akan dibahas bifurkasi yang terjadi pada sistem (3.3).

3.4 Bifurkasi

3.4.1 Bifurkasi Titik Sadel

Dari Lema 3.1 dan Teorema 3.3, diperoleh sebagai berikut :

1= , , , : = 1

4, − 0,

> 0, > 0, > 0

yang merupakan batas dari bifurkasi titik sadel.

Ketika parameter meninggalkan satu sisi permukaan ke sisi yang lain, titik tetap dari sistem (3.3) akan berubah dari nol ke dua, dan kestabilan kedua titik tetap tersebut adalah sadel dan simpul. Ini merupakan permukaan bifurkasi titik sadel pertama dari sistem.

Di sisi lain, dari Teorema 3.4, diketahui bahwa permukaan :

2=

, , , : 0 < − < ,

= 0< 1

4, > 0, > 0, > 0 adalahbatas bifurkasi titik sadel yang kedua.

(18)

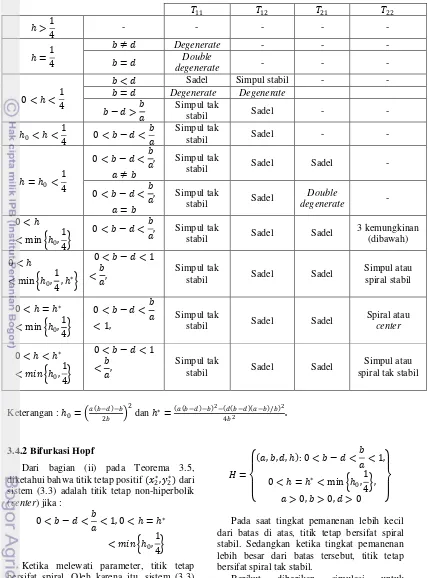
Tabel 2 Ringkasan Keberadaan dan Kestabilan Titik Tetap

11 12 21 22

>1

4 - - - - -

=1 4

≠ Degenerate - - -

= Double

degenerate - - -

0 < <1 4

< Sadel Simpul stabil - -

= Degenerate Degenerate

− > Simpul tak _stabil Sadel - -

0< < 1

4 0 < − <

Simpul tak

stabil Sadel - -

= 0< 1 4

0 < − < , ≠

Simpul tak

stabil Sadel Sadel -

0 < − < ,

=

Simpul tak

stabil Sadel

Double

degenerate -

0 <

< min 0, 1 4

0 < − < , Simpul tak

stabil Sadel Sadel

3 kemungkinan (dibawah)

0 <

< min 0, 1 4,

∗

0 < − < 1

< , Simpul tak _stabil Sadel Sadel Simpul atau spiral stabil

0 < = ∗

< min 0, 1 4

0 < − <

< 1,

Simpul tak

stabil Sadel Sadel

Spiral atau

center

0 < < ∗

< 0, 1 4

0 < − < 1

< , Simpul tak _stabil Sadel Sadel Simpul atau spiral tak stabil

Keterangan : 0= − −₂ 2

dan ∗= − −

2_{− − −}_/ 2

4 2 .

3.4.2 Bifurkasi Hopf

Dari bagian (ii) pada Teorema 3.5, diketahui bahwa titik tetap positif 2∗, 2∗ dari sistem (3.3) adalah titik tetap non-hiperbolik (center) jika :

0 < − < < 1, 0 < = ∗

< 0, 1 4

Ketika melewati parameter, titik tetap bersifat spiral. Oleh karena itu, sistem (3.3) dapat mengalami bifurkasi Hopf dengan batas sebagai berikut :

=

, , , : 0 < − < < 1,

0 < = ∗< min 0, 1 4 , > 0, > 0, > 0

Pada saat tingkat pemanenan lebih kecil dari batas di atas, titik tetap bersifat spiral stabil. Sedangkan ketika tingkat pemanenan lebih besar dari batas tersebut, titik tetap bersifat spiral tak stabil.

(19)

10

3.5 Simulasi

3.5.1 Bifurkasi Titik Sadel

Kasus 1 :

1= , , , : = 1

4, − < 0, > 0, > 0, > 0

Misalkan pada suatu sistem mangsa-pemangsa terdapat tingkat tertangkapnya mangsa oleh pemangsa 0.01, tingkat kemudahan pemangsaan oleh pemangsa 0.02, dan laju kematian pemangsa 0.03.

Untuk beberapa nilai diperoleh bidang fase dan bidang solusi seperti yang diberikan pada Gambar 2.

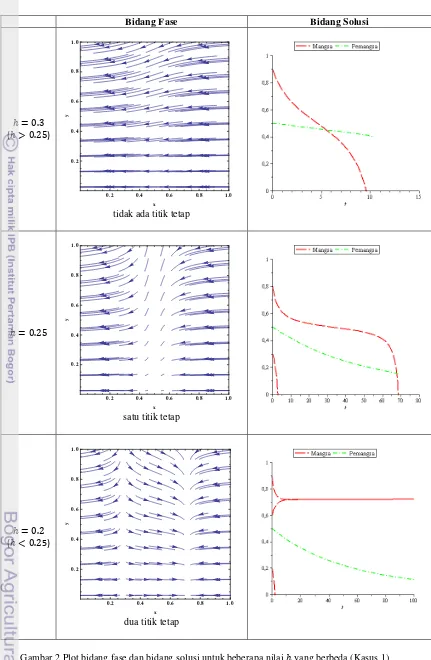
Dari Gambar 2 dapat dilihat bahwa dengan menggunakan nilai yang sedikit berbeda, maka akan didapat plot bidang fase dan bidang solusi yang berbeda sehingga akan menghasilkan simpulan yang berbeda juga. Dari plot bidang fase tersebut dapat disimpulkan bahwa telah terjadi bifurkasi titik sadel pada batas pertama. Dapat dilihat ketika melewati batas (saat = 0.25), sistem tidak mempunyai titik tetap pada saat = 0.3 ( > 0.25) namun pada saat = 0.2 ( < 0.25) sistem mempunyai dua buah titik tetap. Dari hasil bidang solusinya, untuk interpretasi biologis dari bifurkasi titik sadel yang pertama dapat disimpulkan bahwa pada saat tingkat pemanenan = 0.3 ( > 0.25) dapat dilihat bahwa dalam waktu yang lebih singkat spesies mangsa akan punah sehingga dapat dikatakan bahwa sistem runtuh/gagal. Pada tingkat pemanenan sebesar =1

4, dalam beberapa kurun waktu tertentu spesies mangsa menuju kepunahan sehingga lama-kelamaan akan disusul pula oleh punahnya pemangsa. Sedangkan pada saat tingkat pemanenan = 0.2 ( < 0.25) dapat dilihat bahwa spesies mangsa tidak menuju kepunahan ( 0 > 0.28), namun dalam kurun waktu tertentu, spesies pemangsa akan punah.

Kasus 2 :

2=

, , , : 0 < − < ,

= 0< 1

4, > 0, > 0, > 0 ,

dengan 0= − −₂ 2

.

Misalkan pada suatu sistem mangsa-pemangsa terdapat tingkat tertangkapnya mangsa oleh pemangsa 0.3, tingkat kemudahan pemangsaan oleh pemangsa 0.2, dan laju kematian pemangsa 0.1 sehingga

0= 0.180625.

Untuk beberapa nilai diperoleh bidang fase dan bidang solusi seperti yang diberikan pada Gambar 3.

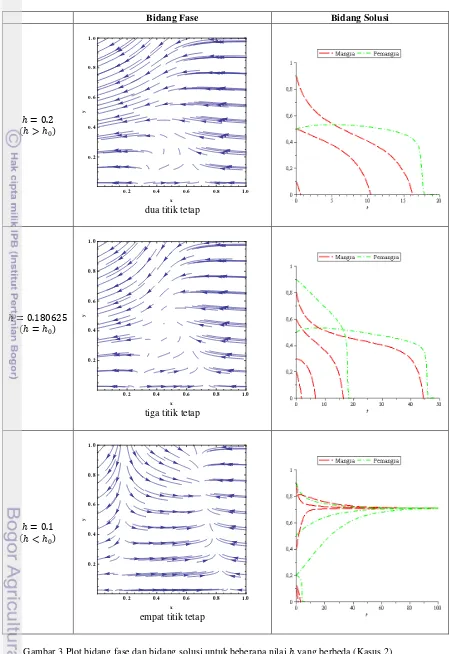
Dari Gambar 3, dapat dilihat bahwa telah terjadi bifurkasi titik sadel pada batas kedua. Hal ini dapat dilihat dari plot bidang fasenya, pada saat melewati batas ( = ₀=

− −

2 2

= 0.187778), titik tetap yang semula berjumlah dua buah pada saat = 0.2 ( > 0) menjadi empat buah pada saat

= 0.1 ( < ₀).

Dari hasil bidang solusi, dapat dilihat bahwa untuk interpretasi biologis dari bifurkasi titik sadel yang kedua ini dapat disimpulkan bahwa ketika tingkat pemanenan sama dengan besarnya tingkat pemanenan kritis = 0<

1

(20)

Bidang Fase Bidang Solusi

= 0.3 ( > 0.25)

tidak ada titik tetap

= 0.25

satu titik tetap

= 0.2 ( < 0.25)

dua titik tetap

Gambar 2 Plot bidang fase dan bidang solusi untuk beberapa nilai yang berbeda (Kasus 1)

0.2 0.4 0.6 0.8 1.0

x

y

0.2 0.4 0.6 0.8 1.0

x

y

0.2 0.4 0.6 0.8 1.0

x

(21)

12

Bidang Fase Bidang Solusi

= 0.2 > 0

dua titik tetap

= 0.180625 = 0

tiga titik tetap

= 0.1 < 0

empat titik tetap

Gambar 3 Plot bidang fase dan bidang solusi untuk beberapa nilai yang berbeda (Kasus 2)

0.2 0.4 0.6 0.8 1.0

x

y

0.2 0.4 0.6 0.8 1.0

x

y

0.2 0.4 0.6 0.8 1.0

x

(22)

3.5.2 Bifurkasi Hopf

Kasus :

=

, , , : 0 < − < < 1,

0 < = ∗< min 0, 1 4 , > 0, > 0, > 0

Misalkan pada suatu sistem mangsa-pemangsa terdapat tingkat tertangkapnya mangsa oleh pemangsa sebesar 1, tingkat kemudahan pemangsaan oleh pemangsa 0.5, dan laju kematian pemangsa 0.25 maka

∗_{= 0.05859375,}

0= 0.0625.

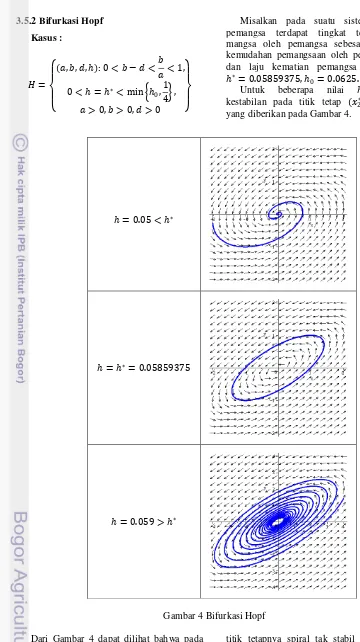
Untuk beberapa nilai diperoleh kestabilan pada titik tetap 2∗, 2∗ seperti yang diberikan pada Gambar 4.

= 0.05 < ∗

= ∗= 0.05859375

= 0.059 > ∗

Gambar 4 Bifurkasi Hopf

Dari Gambar 4 dapat dilihat bahwa pada saat < ∗, kestabilan titik tetap 2∗, 2∗ spiral stabil, pada saat = ∗, kestabilannya

center sedangkan pada saat > ∗, kestabilan

titik tetapnya spiral tak stabil dan terdapat

(23)

14

IV

SIMPULAN

Sistem mangsa-pemangsa tipe Michaelis-Menten dapat dikembangkan dengan melibatkan tingkat pemanenan konstan pada mangsa yang dilakukan secara terus-menerus. Perubahan besarnya tingkat pemanenan mengakibatkan adanya perbedaan banyaknya titik tetap beserta kestabilannya. Perubahan pada batas tingkat pemanenan tertentu dengan beberapa ketentuan parameter lainnya menyebabkan terjadinya bifurkasi titik sadel dimana model yang awalnya tidak memiliki titik tetap menjadi dua titik tetap, kemudian dari dua titik tetap menjadi empat titik tetap. Untuk batas tingkat pemanenan dan beberapa parameter tertentu lainnya, dengan mengubah menjadi lebih besar ataupun lebih kecil dari batas tingkat pemanenan tersebut menyebabkan terjadinya pertukaran kestabilan titik tetap. Titik tetap yang semula memiliki kestabilan spiral stabil menjadi spiral tak

stabil dan terdapat limit cycle tak stabil di dalamnya sehingga terjadi bifurkasi Hopf.

(24)

15

V

DAFTAR PUSTAKA

Abrams PA. dan Ginzburg LR. 2000. The Nature of Predation : Prey Dependent, Ratio-Dependent or Neither?. TREE. 15. pp. 337-341.

Farlow SJ. 1994. An Introduction to

Differential Equation and Their

Application. Mc Graw-Hill, New York.

Kuang Y. 1999. Rich Dynamics of Gause-Type Ratio-Dependent Predator-Prey System. In Differential Equations with Application to Biology. Fields Inst. Commun. 21. Ruan S., Wolkowicz GSK., dan J. Wu, eds., AMS. Providence. RI. pp. 325-337.

Kuang Y. dan Beretta E. 1998. Global Qualitative Analysis of A Ratio-Dependent Predator-Prey System. J. Math. Biol.. 36. pp. 389-406.

Murray JD. 1993. Mathematical Biology. Second, Corrected Edition. Springer-Verlag, New York.

Perko L. 1991. Differential Equations and Dynamical System, Texts in Applied Mathematics, vol. 7. Springer Verlag, New York.

Strogatz SH. 1994. Nonlinear Dynamics and Chaos, with Applications to Physics, Biology, Chemistry, and Engineering. Addison-Wesley Publishing Company, Reading, Massachusete.

Tu PNV. 1994. Dynamical System, An

Introduction with Application in

Economics and Biology. Springer-Verlag. Heidelberg, Germany.

Wiggins S. 1990. Introduction to Applied

Nonlinear Dynamical Systems and

Chaos, Springer-Verlag, New York.

(25)

(26)

Lampiran 1. Penondimensionalan Persamaan Model Mangsa Pemangsa Tipe Michaelis-Menten

=� 1− � −

+ , = − + + , Misal : = ∗ = ∗ = ∗�  Untuk

=� 1− � − +

∗

∗_� =� ∗ 1− ∗

� −

∗ ∗ ∗₊ ∗ ∗

∗∙ _�=� ∗ 1− ∗

� −

∗ ∗ ∗₊ ∗

�=� ∗ 1−

∗

� −

∗ ∗

∗ ₊ ∗

Dengan pemisalan ∗=1

�, ∗=�, ∗= �

, diperoleh :

�= 1− −

� � � +

�= 1− −

� +

�= 1− − +

di mana : =

�

Hasil penondimensionalannya adalah :

(27)

18

�= ∗ − +

∗

∗ ₊ ∗

Dengan pemisalan ∗=1

�, ∗=�, ∗= �

diperoleh :

�=� − + � � +

�= − + +

di mana : =

�, =�

Hasil penondimensionalannya adalah :

= − +

+

Sehingga rasio ketergantungan sistem mangsa-pemangsa dengan pemanenan konstan dapat disederhanakan menjadi :

= = 1− − +

= − +

+ dengan :

= �, =

�, =

(28)

Lampiran 2. Mencari Titik Tetap

Titik tetap diperoleh dengan menyederhanakan :

= = 0

Sehingga :

1− −

+ − = 0,

− +

+ = 0,

Dari − +

+ = 0, diperoleh :

 = 0,

Substitusi = 0 ke persaman 1− −

+ − = 0, didapat : 1− − = 0

2₋ ₊ _{= 0}

Sehingga :

1,2=

1 ± 1−4 2

Secara umum, diperoleh titik tetap :

1= , =

1 + −1 1−4

2 , 0

(L1) di mana = 1, 2.

 ₋ +

+ = 0,

Disederhanakan menjadi :

+ =

= +

= −

Substitusi = − ke persamaan 1− −

(29)

20

1− −

−

− ₊ − = 0

1− −

2₋

− + − = 0

1− −

2₋

− = 0

− 2₋ − ₋ _{= 0}

2₊ − − ₊ _{= 0}

2₊_{− −} ₊ _{= 0}

Sehingga :

1,2=

− − ± − − 2₋₄ 2 2

Secara umum diperoleh titik tetap :

2 ∗_, ∗ ₌ − − + −1 ∆

2 ,

−

(30)

Lampiran 3. Pembuktian Lema 3.1

Lihat persamaan titik tetap L1 dan L2 berikut :

1= , =

1 + −1 1−4

2 , 0

2= ∗, ∗ =

− − + −1 ∆

2 ,

− _∗

di mana ∆ = − − 2₋₄ 2_dan _{= 1,2.}

1) Jika >1 4 maka : Untuk 1 :

1−4 akan bernilai negatif sehingga tidak terdapat titik tetap di ₊2_.

Untuk 2 :

∆ = − − 2₋₄ 2

= − 2−2 − + 2₋₄ 2

= 1−4 2₋₂ ₋₊ 2 2₋₂ ₊ 2 = 1−4 2₋₂ ₋₊ 2 2₋₂ 2 ₊ 2 2 = 1−4 2−2 − −2 2 + 2 2+ 2

Dapat dilihat bahwa ∆ bernilai negatif sehingga tidak terdapat titik tetap di +2.

2) Jika =1 4 maka : Untuk 1 :

1−4 bernilai 0 sehingga ada satu titik tetap di +2 yaitu 1 2, 0 . Untuk 2 :

∆ = − − 2₋₄ 2

= − 2−2 − + 2₋₄ 2 =−2 − + 2 2−2 + 2 =−2 − + 2 2₋₂ 2 ₊ 2 2 =−2 − −2 2 + 2 2+ 2

3) Jika 0 < <1 4 maka : Untuk 1 :

1−4 akan bernilai positif dan < 1. Sehingga terdapat dua titik tetap di +2 yaitu : 1₋1−4

2 , 0 dan 1+ 1−4

2 , 0 .

Untuk 2 :

 Jika maka :

Untuk =

∆ = − − 2₋₄ 2 = 2₋₄ 2

= 1−4 2

(31)

22

− − + −1 ∆

2 =

+ −1 1−4 2 2

=1 + −1 1−4 2

Dapat dilihat bahwa untuk = pada 2 akan diperoleh dua titik tetap yang sama dengan 1.

Untuk < .

Dapat dilihat bahwa 1∗ dan 2∗ bernilai positif, namun karena < , maka 1∗ dan 2∗ akan bernilai negatif sehingga untuk 2 tidak terdapat titik tetap di +2.

 Jika − maka :

Untuk − =

∆ = − − 2−4 2 =−4 2

Untuk − >

Dapat dilihat bahwa − − + −1 − − 2

−4 2

2 bernilai negatif sehingga tidak terdapat titik tetap di +2.

 Jika 0 < − < dan − − 2

2

< <1

4 maka : Dapat dilihat bahwa :

− − + −1 − − 2−₄ 2 2

= − −

2 + −1

− − 2

2 −

Karena − − 2

2

< maka besarnya bilangan di dalam tanda akar bernilai negatif sehingga untuk 2 tidak terdapat titik tetap di +2.

4) Jika 0 < − < dan − − 2

2

= <1 4

Untuk 1 :

1−4 akan bernilai positif dan < 1 sehingga akan ada dua titik tetap di +2 yaitu : 1+ 1−4

2 , 0 dan 1− 1−4

2 , 0 .

Untuk 2 :

− − + −1 ∆

2 =

− − + −1 − − 2−₄ 2 2

=

− − + −1 − − 2−₄ − − 2

2 2

2

= − − + −1 − −

2_{− − −}2

2

= − −

2 ,

(32)

5) Jika 0 < − < dan 0 < < min − − 2

2 ,1

4 . Untuk 1 :

1−4 akan bernilai positif dan < 1 sehingga terdapat dua titik tetap di +2 yaitu : 1+ 1−4

2 , 0 dan 1− 1−4

2 , 0 .

Untuk 2 :

 0 < − < dan 0 < < − − 2

2

− − + −1 ∆

2 =

− − + −1 − − 2−₄ 2 2

Jika 0 < < − − 2

2

maka − − > − − 2−₄ 2_dan − − > 0 sehingga terdapat dua titik tetap di +2.

 0 < − < dan 0 < <1 4 − − + −1 ∆

2 =

− − + −1 − − 2−₄ 2 2

Jika 0 < <1

4 maka − − > − −

(33)

24

Lampiran 4. Matriks Jacobi untuk Masing-masing Titik Tetap (Persamaan (3.3))

Lihat persamaan titik tetap L1 dan L2 berikut :

1= , =

1 + −1 1−4

2 , 0

2= ∗, ∗ =

റ− − + −1 ∆

2 ,

− _∗

di mana ∆ = − − 2−4 2_dan _{= 1,2.}

Lihat juga persamaan (3.6) (matriks Jacobi persamaan (3.3)) berikut :

=

1−2 − 2

+ 2 −

2

+ 2

2

+ 2 − +

2

+ 2

(L3)

Untuk mendapatkan matriks Jacobi pada masing-masing titik tetap maka substitusikan persamaan L1 dan L2 ke persamaan matriks L3, diperoleh :

a. Untuk 1 :

, =

1−2 1 + −1 1−4

2 −0

− 2

2

0 − +

2

, = −1

+1 ₁₋₄ ₋

0 −

(L4) b. Untuk 2 :

∗_, ∗ =

1−2 ∗− −

∗ 2

− ∗₊ ∗ 2 −

∗2

− ∗₊ ∗ 2

− ∗ 2

− ∗₊ ∗ 2 −

+

∗2

− ∗₊ ∗ 2

=

1−2 ∗− −

∗ 2

∗ 2 −

∗2

∗ 2

− ∗ 2

∗ 2 −

+

∗2

∗ 2

=

1−2 ∗− − 2

2 −

2

2 − 2

− +

(34)

∗_, ∗ =

1−2 − − + −1 ∆

2 −

− 2

2 −

2

− 2

− +

2

=

2_{− − −}₊₋₁_{∆ − −}2

2 −

2

− 2 ₋ ₊ 2

=

2₋ 2₊ 2₋ ₊₋₁ +1 _{∆ −} 2_{+ 2} ₋ 2

2 −

2

2 − 2

− −

=

− 2₊₋₁ +1 _∆

2 −

2

2 − 2

− −

=

− + −1 +1 _∆

2 −

2

2 − 2

− −

(35)

26

Lampiran 5. Pembuktian Teorema 3.2

=1 4,

Dari Lema 3.1 diketahui bahwa jika =1

4, maka hanya ada satu titik tetap yaitu 1 2, 0 .

(i) Jika ≠

Substitusi titik tetap 1

2, 0 ke L1 sehingga matriks Jacobi menjadi :

1,0 =

0 −

Dengan demikian diperoleh :

�= − , berbentuk real (positif / negatif).

∆ = 0, sehingga dapat kita ketahui bahwa salah satu nilai eigen bernilai 0. �2₋₄_∆_{= (} ₋ ₎2_,_sehingga_�2₋₄_∆_{bernilai positif}_�2₋₄_∆_{> 0} _.

Dari hasil di atas, dapat disimpulkan bahwa titik tetap 1, 0 merupakan “degenerate”. (ii) Jika =

Substitusi titik tetap 1

2, 0 ke L1 sehingga matriks Jacobi menjadi : 1,0 = 0₀ −₀

Dengan demikian diperoleh : �= 0,

∆ = 0, sehingga dapat kita ketahui bahwa kedua nilai eigen bernilai 0. �2₋₄_∆_{= 0,}

(36)

Lampiran 6. Pembuktian Teorema 3.3

a) Jika < dan 0 < <1 4

Dari Lema 3.1 diketahui bahwa dengan syarat seperti di atas maka sistem (3.3) memiliki dua titik tetap, yaitu : 1, 0 =

1− 1−4

2 , 0 dan 2, 0 =

1+ 1−4

2 , 0 .

Untuk 1, 0 =

1₋1−4

2 , 0

Substitusi titik tetap 1, 0 ke L1 sehingga matriks Jacobi menjadi :

1,0 = 1−4 −

0 −

�= 1−4 + − , berbentuk real.

∆ = 1−4 − , akan bernilai negatif karena < sehingga dapat kita ketahui bahwa kedua nilai eigen beda tanda.

�2₋₄_∆₌₁₋_{4 +}₋2₋₄ ₁₋₄ ₋_,_dimana ₋₄ ₁₋₄ ₋ akan bernilai positif sehingga �2−4∆ bernilai positif �2−4∆> 0 .

Dari hasil di atas, dapat disimpulkan bahwa titik tetap 1, 0 merupakan “sadel”. Untuk 2, 0 =

1+ 1−4

2 , 0

1,0 = − 1−4 −

0 −

�=− 1−4 + − , berbentuk real negatif.

∆ =− 1−4 − , akan bernilai positif karena < sehingga dapat kita ketahui bahwa kedua nilai eigen sama tanda.

�2₋₄_∆₌₋₁₋_{4 +}₋2_{+ 4} ₁₋₄ ₋_,_dengan ₄ ₁₋₄ ₋

bernilai negative, dapat dilihat bahwa − 1−4 + − 2> 4 1−4 − sehingga �2−4∆ akan bernilai positif �2−4∆> 0 .

Dari hasil di atas, dapat disimpulkan bahwa titik tetap 1, 0 merupakan “simpul

stabil”.

b) Jika = dan 0 < <1 4

Dari Lema 3.1 dapat diketahui bahwa dengan syarat seperti di atas maka sistem (3.3) memiliki dua titik tetap, yaitu : 1, 0 =

1₋1−4

2 , 0 dan ฀2, 0 =

1+ 1−4

2 , 0 .

Untuk 1, 0 =

1₋1−4

2 , 0

1,0 = 1−4 −

0 0

(37)

28

∆ = 0, sehingga dapat kita ketahui bahwa salah satu nilai eigen bernilai 0. �2₋₄_∆₌₁₋₄ 2_,_{akan bernilai positif}_�2₋₄_∆_{> 0} _.

Dari hasil di atas, dapat disimpulkan bahwa titik tetap 1, 0 merupakan “degenerate”. Untuk 2, 0 =

1+ 1−4

2 , 0

1,0 = − 1−4 −

0 0

�=− 1−4 , berbentuk real negatif.

∆ = 0, sehingga dapat kita ketahui bahwa salah satu nilai eigen bernilai 0. �2₋₄_∆₌₋₁₋₄ 2_,_{akan bernilai positif}_�2₋₄_∆_{> 0}_.

Dari hasil di atas, dapat disimpulkan bahwa titik tetap 1, 0 merupakan “degenerate”. c) Jika 0 < − < dan − −

2 2

< <1 4.

Dari Lema 3.1 dapat diketahui bahwa dengan syarat seperti di atas maka sistem (3.3) memiliki dua titik tetap, yaitu : 1, 0 =

1₋1−4

2 , 0 dan 2, 0 =

1+ 1−4

2 , 0 .

Untuk 1, 0 =

1− 1−4

2 , 0

1,0 = 1−4 −

0 −

∆ = 1−4 − , akan bernilai positif karena − > 0 sehingga dapat kita ketahui bahwa kedua nilai eigen sama tanda.

�2₋₄_∆₌₁₋_{4 +}₋2₋₄ ₁₋₄ ₋_, _dapat _dilihat _bahwa 1−4 + − 2> 4 1−4 − sehingga �2−4∆ akan bernilai positif �2₋₄_∆_{> 0} _.

Dari hasil di atas, dapat disimpulkan bahwa titik tetap 1, 0 merupakan “simpul tak

stabil”.

Untuk 2, 0 =

1+ 1−4

2 , 0

1,0 = − 1−4 −

0 −

�=− 1−4 + − , berbentuk real.

(38)

�2₋₄_∆₌₋₁₋_{4 +}₋2_{+ 4} ₁₋₄ ₋_,_{dapat dilihat bahwa}_�2₋₄_∆ bernilai positif �2−4∆> 0 .

Dari hasil di atas, dapat disimpulkan bahwa titik tetap 1, 0 merupakan “sadel”. atau

Jika − > dan 0 < <1

4 maka akan diperoleh kesimpulan yang sama dengan yang di atas, yaitu ketika 0 < − < dan − −

2 2

(39)

30

Lampiran 7. Pembuktian Teorema 3.4

0=

− − 2

2 ,

= 0< 1 4,

Dari Lema 3.1 diketahui bahwa sistem (3.3) memiliki tiga titik tetap yaitu :

1, 0 =

1− 1−4

2 , 0 , 2, 0 =

1 + 1−4

2 , 0 ,

1∗, 1∗ =

− −

2 ,

−

1∗ = 0, −

0 .

di mana = 1,2, ∆ = − − 2₋₄ 2_. (I) Jika ≠

Untuk 1, 0 =

1− 1−4

2 , 0

1,0 =

1−4 −

0 −

�2₋₄_∆₌₁₋_{4 +}₋2₋₄ ₁₋₄ ₋_, _dapat _dilihat _bahwa 1−4 + − 2> 4 1−4 − sehingga �2₋₄_∆_{akan bernilai positif} �2₋₄_∆_{> 0} _.

Dari hasil di atas, dapat disimpulkan bahwa titik tetap 1, 0 merupakan “simpul tak stabil”. Untuk 2, 0 =

1+ 1−4

2 , 0

1,0 = − 1−4 −

0 −

∆ =− 1−4 − , akan bernilai negatif karena − > 0 sehingga dapat kita ketahui bahwa kedua nilai eigen beda tanda.

�2₋₄_∆₌₋₁₋_{4 +}₋2₋₄ ₁₋₄ ₋_,_{akan bernilai positif}_�2₋ 4∆> 0 .

Dari hasil di atas, dapat disimpulkan bahwa titik tetap 2, 0 merupakan “sadel”. Untuk 1∗, 1∗ = − − ₂ , − 1∗ = 0, − 0 .

(40)

1,∗ 1∗ =

−

2 −

2

2 − 2 ₋

�= − ₂ + − = − +₂ − , berbentuk real positif.

∆ =

2₋2

3 +

2₋2

3 =

2 2₋2

3 ,

akan bernilai positif sehingga dapat kita ketahui bahwa kedua nilai eigen sama tanda. �2₋₄_∆_{> 0.}

Dari hasil di atas, dapat disimpulkan bahwa titik tetap 1∗, 1∗ merupakan “simpul tak stabil”. (II) Jika =

Untuk 1, 0 =

1− 1−4

2 , 0

1,0 =

1−4 −

0 −

�2₋₄_∆₌₁₋_{4 +}₋2₋₄ ₁₋₄ ₋_, _dapat _dilihat _bahwa 1−4 + − 2> 4 1−4 − sehingga �2₋₄_∆_{akan bernilai positif} �2₋₄_∆_{> 0}_.

1+ 1−4

2 , 0

1,0 = − 1−4 −

0 −

(41)

32

Lampiran 8. Pembuktian Teorema 3.5

Jika 0 < − < dan 0 < < min 0, 1

4 maka berdasarkan Lema 3.1 sistem (3.3) memiliki empat titik tetap yaitu :

1, 0 =

1− 1−4

2 , 0 , 2, 0 =

1 + 1−4

2 , 0 ,

1∗, 1∗ = − − − ∆

2 ,

−

1∗ , 2∗, 2∗ =

− − + ∆

2 ,

− 2∗ .

di mana = 1,2, ∆ = − − 2₋₄ 2_.

Untuk 1, 0 =

1₋1−4

2 , 0

1,0 = 1−4 −

0 −

�2₋₄_∆₌₁₋_{4 +}₋2₋₄ ₁₋₄ ₋_, _dapat _dilihat _bahwa 1−4 + − 2> 4 1−4 − sehingga �2−4∆ akan bernilai positif �2₋₄_∆_{> 0} _.

1+ 1−4

2 , 0

1,0 = − 1−4 −

0 −

(42)

Lampiran 9. Simulasi Bidang Fase dan Bidang Solusi Bifurkasi Titik Sadel Kasus 1

Bidang Fase (menggunakan Software Mathematica7.0)

Load Package “CurvesGraphics6.nb”

a0.01;b0.02;d0.03;h0.3;

PhasePlotx1xaxy xy

h,y dbx

yx ,x, 0.001, 1,y, 0.001, 1,

2, 2,GridPoints10, FrameTrue, FrameLabel"x", "y", LabelStyleDirectiveBold , 11

0.2 0.4 0.6 0.8 1.0

x

y

a0.01;b0.02;d0.03;h0.25; PhasePlotx1xaxy

xy 

h,y dbx

yx 

,x, 0.001, 1,y, 0.001, 1,2, 2,GridPoints10, FrameTrue, FrameLabel"  LabelStyleDirectiveBold , 11

0.2 0.4 0.6 0.8 1.0

x

y

xy 

h,y dbx

yx 

(43)

34

Bidang Fase (menggunakan Software Maple12)

0.2 0.4 0.6 0.8 1.0

x

(44)

(45)

(46)

Lampiran 10. Simulasi Bidang Fase dan Bidang Solusi Bifurkasi Titik Sadel Kasus 2

Bidang Fase (menggunakan Software Mathematica7.0)

Load Package “CurvesGraphics6.nb”

xy 

h,y dbx

yx 

,x, 0.001, 1,y, 0.001, 1,2, 2,GridPoints10, FrameTrue, FrameLabel"  LabelStyleDirectiveBold , 11

0.2 0.4 0.6 0.8 1.0

x

y

a0.3;b0.2;d0.1;habdb 2b^ 2 PhasePlotx1xaxy

xy h,y d bx

yx ,x, 0.001, 1,y, 0.001, 1,2, 2,GridPoints10, FrameTrue, FrameLabel"  LabelStyleDirectiveBold , 11

0.2 0.4 0.6 0.8 1.0

x

y

xy h,y d bx

(47)

38

Bidang Solusi (menggunakan Software Maple12)

0.2 0.4 0.6 0.8 1.0

x

(48)

(49)

(50)

(51)

42

(52)