PEMBANGKIT ATURAN PADA FUZZY INFERENCE SYSTEM MENGGUNAKAN FUZZY DECISION TREE
UNTUK MEMPREDIKSI KEBERHASILAN STUDI MAHASISWA (STUDI KASUS : INSTITUT BISNIS DAN INFORMATIKA KWIK KIAN GIE)
HERI BAMBANG SANTOSO
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
Dengan ini saya menyatakan bahwa tesis yang berjudul Pembangkit Aturan pada Fuzzy Inference System menggunakan Fuzzy Decision Tree untuk Memprediksi Keberhasilan Studi Mahasiswa (Studi Kasus : Institut Bisnis dan Informatika Kwik Kian Gie) adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, Juni 2015
menggunakan Fuzzy Decision Tree untuk Memprediksi Keberhasilan Studi Mahasiswa (Studi Kasus : Institut Bisnis Dan Informatika Kwik Kian Gie). Dibimbing oleh AGUS BUONO dan WISNU ANANTA KUSUMA.
Kualitas lulusan dari sebuah perguruan tinggi selain dapat dilihat dari rata-rata lama lulusannya mendapatkan pekerjaan juga dapat dilihat dari rata-rata lama studi dari mahasiswanya. Jumlah mahasiswa yang lulus tepat waktu merupakan salah satu aspek penting dalam penilaian akreditasi dari suatu perguruan tinggi. Namun permasalahan yang muncul adalah masih banyak mahasiswa yang lulus melampaui target waktu lulus yakni 4 tahun. Oleh sebab itu, model prediksi kelulusan tepat waktu mahasiswa dapat
berperan sebagai early warning terhadap manajemen perguruan tinggi untuk
mempersiapkan strategi yang berkaitan dengan kebijakan preventif terkait pencegahan kasus Drop Out.
Tujuan pada penelitian ini adalah membangun model dengan menggunakan
metode fuzzy decision tree yaitu algoritme Fuzzy ID3 dalam membentuk aturan
klasifikasi yang kemudian digunakan untuk memprediksi keberhasilan studi mahasiswa
dengan menggunakan Fuzzy Inference System Mamdani. Pada penelitian ini juga
melakukan pengukuran tingkat akurasi dalam memprediksi kelulusan tepat waktu mahasiswa dari hasil model yang terbentuk. Selain itu, pada penelitian ini juga
melakukan perbandingan performansi antara algoritme Fuzzy ID3 dan algoritme ID3
dalam membentuk aturan klasifikasi yang digunakan untuk memprediksi keberhasilan studi mahasiswa. Hal ini bertujuan untuk mengetahui apakah dengan menggunakan
pendekatan fuzzy dalam membentuk model pohon keputusan akan lebih baik jika
dibandingkan dengan metode decision tree yang tidak menggunakan pendekatan fuzzy,
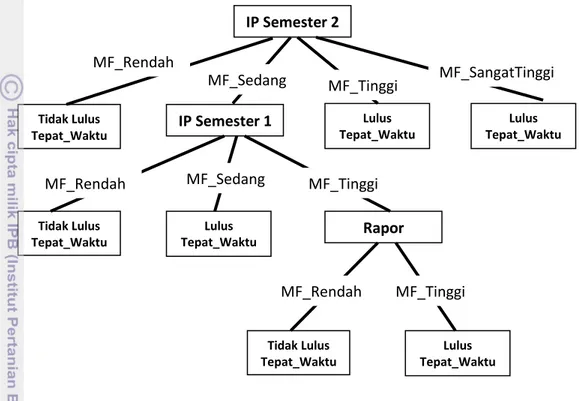
dalam penelitian ini adalah algoritme ID3. Pada penelitian ini, model klasifikasi kelulusan tepat waktu mahasiswa dibangun berdasarkan 5 faktor yakni IPK Semester 1, IPK Semester 2, Kedisiplinan, Prilaku, dan Rapor.
Hasil dari penelitian ini menghasilkan model klasifikasi kelulusan tepat waktu
mahasiswa dengan jumlah aturan klasifikasi sebanyak 28 aturan pada saat nilai fuzziness
control threshold (θr) sebesar 98% dan leaf decision threshold (θn) sebesar 3% dengan
tingkat akurasi sebesar 95.85%. Jika semakin tinggi nilai θr dan semakin rendah nilai θn
maka tingkat akurasi akan semakin tinggi. Berdasarkan dari aturan klasifikasi yang terbentuk, faktor yang paling menentukan mahasiswa akan lulus tepat waktu adalah IPK
Semester 2. Model yang dihasilkan dengan menggunakan fuzzy decision tree yakni
algoritme Fuzzy ID3 memiliki tingkat akurasi sebesar 95.85%, algoritma ini lebih baik
dibandingkan dengan algoritme decision tree yakni ID3 dengan tingkat akurasi sebesar
93.42%, dalam hal memprediksi keberhasilan studi mahasiswa.
Fuzzy Decision Tree to Predict Success of Graduation, Case Study: Kwik Kian Gie School of Business. Supervised by AGUS BUONO and WISNU ANANTA KUSUMA.
The quality of graduates from a university, can be seen from the average length of its graduates get a job and can also be seen from the average length of studies of students. The number of students who graduate on time is one of the important aspects in the assessment of accreditation of a university. But the problem is still a lot of students who pass beyond the target of the study period, which is 4 years. Therefore, the model predictions timely graduation students can act as an early warning to the college management to prepare strategies related to preventive policies related to the prevention of cases of Drop Out.
Our objective is to build a model using the fuzzy decision tree algorithms namely Fuzzy ID3, in the form of classification rules which are then used to predict the success of a student's study using Mamdani Fuzzy Inference System. In this study, also conducted measurement accuracy rate in predicting the timely graduation of students from the results of the model are formed. In addition, this study also did a comparison of performance between algorithms Fuzzy ID3 and ID3 algorithm in shaping the rules of classification that is used to predict the success of a student's study. It aims to determine whether using a fuzzy approach in forming a decision tree model would be better if compared with methods that do not use a decision tree or a fuzzy approach in this study is the ID3 algorithm. In this paper, the model classification timely graduation of students is built on five factors namely 1st Semester GPA 2nd Semester GPA, Discipline, Behavior, and Report Card.
Results from this study produced a model with a number of classification rules as much as 28 rules during the value fuzziness control threshold (θr) of 98% and leaf
decision threshold (θn) by 3% with an accuracy of 95.85%. If the higher value θr and
the lower the value θn then the accuracy will be higher. Based on the classification rules
are established, the most decisive factor of students will graduate on time is the 2nd Semester GPA. Models produced by using the fuzzy decision tree algorithm Fuzzy ID3 has an accuracy rate of 95.85%, this algorithm is better than the ID3 decision tree algorithm with an accuracy level of 93.42%, in terms of predicting the success of a student's study.
© Hak Cipta Milik IPB, Tahun 2015
Hak Cipta Dilindungi Undang-Undang
Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB
Tesis
sebagai salah satu syarat untuk memperoleh gelar Magister Ilmu Komputer
pada
Program Studi Ilmu Komputer
PEMBANGKIT ATURAN PADA FUZZY INFERENCE SYSTEM MENGGUNAKAN FUZZY DECISION TREE
UNTUK MEMPREDIKSI KEBERHASILAN STUDI MAHASISWA (STUDI KASUS : INSTITUT BISNIS DAN INFORMATIKA KWIK KIAN GIE)
HERI BAMBANG SANTOSO
SEKOLAH PASCA SARJANA INSTITUT PERTANIAN BOGOR
Nama : Heri Bambang Santoso
NIM : G651130664
Disetujui oleh
Komisi Pembimbing
Dr Ir Agus Buono, MSi MKom Ketua
Dr Eng Wisnu Ananta Kusuma, ST MT Anggota
Diketahui oleh
Ketua Program Studi Ilmu Komputer
Dr Eng Wisnu Ananta Kusuma, ST MT
Dekan Sekolah Pascasarjana
Dr Ir Dahrul Syah, MScAgr.
karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian ini ialah Kecerdasan Komputasional, dengan judul Pembangkit Aturan pada Fuzzy Inference System menggunakan Fuzzy Decision Tree untuk Memprediksi Keberhasilan Studi Mahasiswa (Studi Kasus : Institut Bisnis dan Informatika Kwik Kian Gie).
Penulis menyampaikan ucapan terima kasih, penghargaan, dan apresiasi kepada Bapak Dr Ir Agus Buono, MSi MKom selaku pembimbing utama dan Bapak Dr Eng Wisnu Ananta Kusuma, ST MT selaku pembimbing kedua, yang telah banyak memberikan saran, kritikan, motivasi dan kemudahan kepada penulis dalam menyelesaikan karya ilmiah ini. Terima kasih juga penulis ucapkan kepada Dr Imas Sukaesih Sitanggang, SSi MKom yang telah menguji, membimbing, dan memberikan saran dalam penulisan karya ilmiah ini.
Selanjutnya, penulis juga ingin mengucapkan terima kasih banyak kepada:
1. Mama Mulyani dan Papa Sunardi tercinta, terima kasih atas segala doa, cinta, kasih
sayang, dan dukungan yang tiada batasnya baik materil maupun spiritual.
2. Ayah mertuaku Bapak H. Hasan Bakri Sidik dan Ibu mertuaku Ibu Hj. Siti Nurhaya
(Alm), terima kasih atas segala doa, cinta, kasih sayang, dan dukungan yang tiada batasnya baik materil maupun spiritual.
3. Istriku tersayang Leny Christine dan putriku tersayang Zahira Latisha Azzahra,
terima kasih atas segala doa, cinta, kasih sayang dan dukungan yang tiada batasnya serta keceriaan yang selalu diberikan sehingga penulis memiliki semangat yang sangat tinggi dalam menyelesaikan karya ilmiah ini.
4. Adik-adikku tersayang Miranti Wahyuni dan Voni Apriyani, terima kasih atas doa
dan keceriaan yang telah menambah semangat atas terselesaikannya penulisan ini.
5. Kakak-kakak iparku yakni teteh Ifa Faulina, teteh Rita Lutfiah, SH, Aa‟ Indra
Ridarta, SE, dan Aa‟ Saeful Mujahid, SE, terima kasih banyak atas segala doa dan
dukungan yang selalu diberikan.
6. Adik iparku sekaligus teman, sahabat, dan partner fishing yakni Anugerah Sandy
Yudhastiya, SKom atas segala doa dan dukungan yang selalu diberikan.
7. Jajaran rektorat Institut Bisnis dan Informatika Kwik Kian Gie atas izin studi yang
telah diberikan.
8. Bapak Jesaja HB Waterkamp, SKom MKom, selaku ICT Manager Institut Bisnis
dan Informatika Kwik Kian Gie yang telah memberikan izin studi, motivasi dan dukungan.
9. Teman-teman seperjuangan Bu Tita, Pak Fajar, Kang Agus, Rendy, terima kasih
atas segala dukungan, kritik, dan sarannya.
10. Seluruh teman-teman Program Magister Ilmu Komputer kelas khusus angkatan
2013 atas segala doa dan dukungannya.
Akhirnya penulis berharap semoga karya ilmiah ini dapat bermanfaat bagi semua pihak yang membutuhkan. Amin.
Bogor, Juni 2015
DAFTAR TABEL iii
Ruang Lingkup Penelitian 3
2 TINJAUAN PUSTAKA 4
Penelitian Terkait 4
Transformasi Data 5
Korelasi Pearson Product Moment (PPM) 5
Decision Tree (Pohon Keputusan) 6
Iterative Dychotomizer Version 3(ID3) 7
Himpunan Fuzzy 8
Fungsi Keanggotaan 9
Fuzzy Decision Tree (FDT) 10
Fuzzy Iterative Dychotomizer Version 3(Fuzzy ID3) 10
Fuzzy Entropy dan Information Gain 11
Fuzzy Decision Tree Threshold 12
Sistem Inferensi Fuzzy 12
Metode Mamdani 13
Defuzzifikasi Metode Centroid 13
3 METODE PENELITIAN 14
Kerangka Pemikiran 14
Pengumpulan Data 14
Analisis Korelasi Atribut 15
Transformasi Data 16
Pembagian Data Training dan Data Testing 16
Pemilihan Nilai Threshold 17
Pembentukan Model 17
Evaluasi Model 17
Representasi Pengetahuan 18
Alat Bantu Penelitian 18
Hasil dan Analisa 18
4 HASIL DAN PEMBAHASAN 19
Pengumpulan dan Pembersihan Data 19
Uji Korelasi Atribut 21
Pembentukan Model (Proses Training) 25
Pengujian Model (Proses Testing) 32
Evaluasi Kinerja Fuzzy ID3 32
Representasi Pengetahuan 34
Perbandingan Performansi Fuzzy ID3 dan ID3 35
5 SIMPULAN DAN SARAN 37
1. Contoh hasil perhitungan uji korelasi pearson product moment 15
2. Contoh data hasil fuzzifikasi 16
3. Confusion matrix untuk prediksi kelululusan tepat waktu 17
4. Contoh record data IPK sebelum di transpose 19
5. Contoh record data IPK setelah di transpose 20
6. Contoh record data dengan missing value 20
7. Hasil uji korelasi antara atribut predictor terhadap masa studi 21
8. Aturan klasifikasi pada contoh data trainingset 29
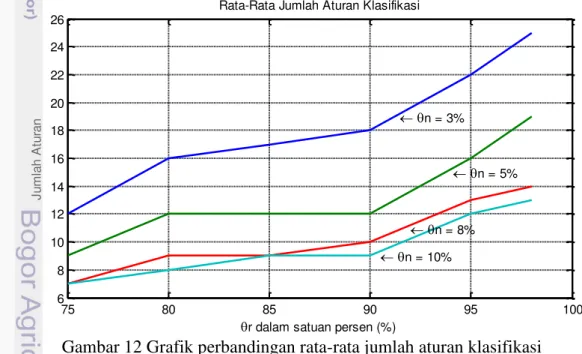
9. Rata-rata jumlah aturan 30
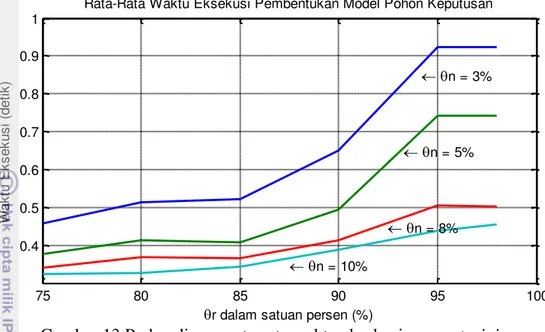
10.Rata-rata waktu eksekusi pembentukan model dalam satuan detik 31
11.Evaluasi akurasi rata-rata algoritme Fuzzy ID3 33
12.Transformasi data atribut untuk algoritme ID3 35
13.Perbandingan performansi Fuzzy ID3 dan ID3 35
DAFTAR GAMBAR
1. Pohon keputusan 6
2. Kurva segitiga 9
3. Kurva trapesium 9
4. Kerangka pemikiran 14
5. Himpunan fuzzy atribut IPK Semester 1 22
6. Himpunan fuzzy atribut IPK Semester 2 23
7. Himpunan fuzzy atribut Prilaku 23
8. Himpunan fuzzy atribut Rapor 24
9. Himpunan fuzzy atribut Kedisiplinan 24
10.Hasil ekspansi trainingset berdasarkan atribut IPK Semester 2 27
11.Fuzzy decision tree untuk contoh training set 29
14.Perbandingan rata-rata tingkat akurasi Fuzzy ID3 33
15.Tampilan utama aplikasi prediksi keberhasilan studi mahasiswa 34
16.Perbandingan jumlah aturan Fuzzy ID3 dan ID3 36
17.Perbandingan tingkat akurasi Fuzzy ID3 dan ID3 36
18.Tampilan form proses training algoritme Fuzzy ID3 55
19.Tampilan form proses testing algoritme Fuzzy Inference System 56
20.Tampilan form proses prediksi keberhasilan studi mahasiswa 57
DAFTAR LAMPIRAN
1. Contoh data hasil proses pembersihan data 40
2. Contoh data untuk proses training dan hasil fuzzifikasi data 41
3. Jumlah aturan klasifikasi yang dihasilkan oleh masing-masing training set 42
4. Waktu eksekusi algoritme Fuzzy ID3 untuk masing-masing training set
dalam satuan detik 43
5. Akurasi aturan klasifikasi setelah pengujian dengan menggunakan
testing set 45
6. Aturan klasifikasi dari hasil pembentukan model Fuzzy ID3 dengan θrdan
θn masing-masing 98% dan 3% 51
7. Aturan klasifikasi dari hasil pembentukan model algoritme ID3 53
8. Tampilan aplikasi prediksi keberhasilan studi mahasiswa menggunakan
1
PENDAHULUAN
Latar Belakang
Kualitas lulusan dari sebuah perguruan tinggi selain dapat dilihat dari rata-rata lama lulusannya mendapatkan pekerjaan juga dapat dilihat dari rata-rata lama studi dari mahasiswanya. Setiap program studi akan mempunyai variasi lama studi mahasiswa yang berbeda-beda. Program studi berkewajiban untuk memantau perkembangan studi
dari setiap mahasiswanya. Prediksi kelulusan tepat waktu dapat berperan sebagai early
warning bagi pihak terkait, seperti dosen wali atau ketua program studi terhadap kondisi performansi studi mahasiswa. Selanjutnya, hasil prediksi secara keseluruhan dapat digunakan sebagai acuan dalam mengevaluasi proses pendidikan, kurikulum, dan hal lain yang berkaitan dengan penyelenggaraan pendidikan. Untuk melakukan prediksi dapat dilakukan dengan berbagai cara, salah satunya dapat dilakukan dengan
menggunakan pendekatan teknik data mining. Institut Bisnis dan Informatika Kwik
Kian Gie mempunyai dataset pada SIMAK (Sistem Informasi Akademik) yang selama
ini belum dimanfaatkan secara maksimal. Sangat disayangkan jika dataset yang begitu
besar tersebut tidak dimanfaatkan untuk digali informasi apa yang terdapat di dalamnya. Data mining merupakan proses ekstraksi informasi atau pola penting dalam basis data berukuran besar (Han dan Kamber 2006). Klasifikasi merupakan salah satu metode
dalam data mining untuk mengetahui label kelas dari suatu record dalam data. Teknik
klasifikasi yang menjadi fokus pada penelitian ini adalah decision tree. Pada metode decision tree, jika atribut yang digunakan bertipe continuous maka harus dilakukan
diskritisasi untuk membagi range nilai pada atribut menggunakan titik potong, dimana
titik potong yang digunakan akan membedakan nilai suatu domain dengan batasan yang jelas sehingga dapat terjadi kesalahan klasifikasi (missclassification).
Pada penelitian ini salah satu atribut yang akan digunakan adalah Indeks Prestasi Akademik (IPK). Nilai IPK dari seorang mahasiswa dapat diekspresikan tidak saja secara numeris, tetapi juga dapat direpresentasikan dalam bentuk kualitatif secara linguistik. Contohnya, mahasiswa yang akan lulus tepat waktu adalah mahasiswa yang memiliki IPK tinggi. Penyajian secara linguistik ini dapat menimbulkan ambiguitas atau
keraguan. Konsep logika fuzzy merupakan alternatif untuk menyatakan sesuatu yang
tidak dapat didefinisikan dengan tepat. Pada himpunan fuzzy, peranan derajat
keanggotaan sebagai penentu keberadaan elemen dalam suatu himpunan sangatlah
penting. Nilai keanggotaan atau derajat keanggotaan (membership function) menjadi ciri
utama dalam penalaran logika fuzzy (Kusumadewi 2003). Penggunaan teknik fuzzy
memungkinkan untuk penentuan suatu objek yang dimiliki oleh lebih dari satu kelas. Beberapa penelitian dalam bidang akademik perguruan tinggi telah banyak
dilakukan dengan menggunakan teknik klasifikasi decision tree. Diantaranya penelitian
yang dilakukan oleh Vasani dan Gawali (2014) melakukan penelitian tentang klasifikasi
dan evaluasi performansi mahasiswa menggunakan algoritme decision tree C4.5 dan
Naive Bayesian. Adhatrao et al. (2013) menerapkan algoritme ID3 (Iterative Dichotomiser 3) dan C4.5 untuk memprediksi performansi mahasiswa pada semester pertama. Yadav dan Pal (2012) menerapkan algoritme C4.5, ID3, dan CART untuk
memprediksi performansi mahasiswa jurusan teknik. Yadav et al. (2012) memprediksi
Beberapa penelitian terkait penerapan teknik fuzzy inference system di antaranya penelitian yang dilakukan oleh Rahmadi dan Mustafidah (2014) melakukan penelitian
tentang fuzzy inference system untuk mengetahui pengaruh motivasi belajar dan
lingkungan belajar terhadap prestasi belajar mahasiswa. Mustafidah dan Aryanto (2012)
melakukan penelitian tentang fuzzy inference system untuk memprediksi prestasi belajar
mahasiswa berdasarkan nilai ujian nasional, tes potensi akademik dan motivasi belajar. Beberapa penelitian terkait penerapan teknik fuzzy decision tree di antaranya penelitian yang dilakukan oleh Yun et al. (2014) melakukan penelitian tentang fuzzy decision tree pada data bunga iris. Martin et al. (2012) melakukan penelitian tentang prediksi kebangkrutan sebuah perusahaan berdasarkan faktor kualitatif menggunakan
algoritme Fuzzy ID3. Li et al. (2012) melakukan penelitian tentang fuzzy decision tree
untuk mengevaluasi performansi kinerja karyawan. Idri dan Elyassami (2011)
melakukan penelitian tentang fuzzy decision tree untuk memperkirakan tingkat kesulitan
dalam pembuatan software. Romansyah et al. (2009) melakukan penelitian mengenai
penerapan teknik fuzzy decision tree dengan algoritme Fuzzy ID3 pada data diabetes.
Berdasarkan penelitian yang telah dilakukan dengan menggunakan teknik
klasifikasi decision tree (Vasani dan Gawali 2014; Adhatrao et al. 2013; Yadav dan Pal
2012; Yadav et al. 2012) maka pada penelitian ini akan dilakukan klasifikasi data
kelulusan mahasiswa menggunakan decision tree, namun pada penelitian ini akan
menggunakan pendekatan fuzzy, yakni dengan menggunakan salah satu teknik pada
fuzzy decision tree untuk memprediksi kelulusan tepat waktu mahasiswa dengan
menggunakan fuzzy inference system. Namun pada penelitian yang menggunakan fuzzy
inference system (Rahmadi dan Mustafidah 2014; Mustafidah dan Aryanto 2012), masih menggunakan sekumpulan aturan yang ditentukan sendiri atau bukan dibentuk berdasarkan data, sehingga apabila dalam pendefinisian aturan terdapat kesalahan maka dapat berpotensi akan menyebabkan tingkat akurasi yang dihasilkan tidak maksimal. Untuk itu pada penelitian ini akan membangun model klasifikasi data kelulusan
mahasiswa menggunakan metode fuzzy decision tree (Martin et al. 2012; Romansyah et
al. 2009). Hasil dari aturan-aturan klasifikasi dari fuzzy decision tree tersebut kemudian
digunakan pada fuzzy inference system sebagai sekumpulan aturan klasifikasi yang akan
digunakan untuk memprediksi kelulusan tepat waktu mahasiswa.
Perumusan Masalah
Berdasarkan latar belakang yang telah dijelaskan di atas, maka permasalahan yang bisa dirumuskan dalam penelitian ini adalah:
1. Bagaimana membangun model klasifikasi kelulusan tepat waktu mahasiswa
dengan menggunakan metode fuzzy decision tree.
2. Bagaimana cara memprediksi kelulusan tepat waktu mahasiswa dengan
menggunakan fuzzy inference system berdasarkan hasil pembentukan model
klasifikasi yang dihasilkan oleh fuzzy decision tree.
3. Bagaimana tingkat akurasi dari algoritme fuzzy decision tree dalam memprediksi
kelulusan tepat waktu mahasiswa berdasarkan dari hasil model yang terbentuk.
4. Bagaimana penggunaan pendekatan fuzzy dalam membentuk model pohon
keputusan. Apakah akan lebih baik jika dibandingkan dengan metode decision
Tujuan Penelitian
Berdasarkan permasalahan yang dirumuskan di atas, maka tujuan pada penelitian ini adalah:
1. Membangun model klasifikasi kelulusan tepat waktu mahasiswa dengan
menggunakan metode fuzzy decision tree (FDT).
2. Hasil dari pembentukan model tersebut kemudian digunakan untuk memprediksi
kelulusan tepat waktu mahasiswa dengan menggunakan fuzzy inference system
(FIS).
3. Melakukan pengukuran tingkat akurasi dari algoritme fuzzy decision tree dalam
memprediksi kelulusan tepat waktu mahasiswa berdasarkan dari hasil model yang terbentuk.
4. Melakukan perbandingan performansi antara algoritme Fuzzy ID3 dan algoritme
ID3 dalam membentuk aturan klasifikasi yang digunakan untuk memprediksi keberhasilan studi mahasiswa.
Manfaat Penelitian
Hasil dari model prediksi pada penelitian ini, dapat digunakan oleh manajemen perguruan tinggi dan dosen wali untuk memberikan perlakuan terhadap mahasiswa yang diprediksi memiliki masa studi akan melebihi batas waktu studi yakni 4 tahun. Diantaranya dengan cara memberikan bimbingan dan pengarahan agar mahasiswa bisa mengetahui bagaimana cara belajar mandiri yang efektif agar dapat memberikan hasil belajar yang optimal sehingga dapat lulus tepat waktu.
Ruang Lingkup Penelitian
Ruang lingkup pada penelitian ini dibatasi pada :
1. Seleksi atribut predictor atau atribut yang digunakan untuk melakukan prediksi akan
dilakukan dengan menggunakan metode korelasi pearson product moment, untuk
melihat hubungan antara atribut predictor tersebut terhadap kelulusan tepat waktu mahasiswa.
2. Membangun model untuk memprediksi apakah mahasiswa dapat lulus tepat waktu
atau tidak, dengan menggunakan data kelulusan mahasiswa Institut Bisnis dan Infomatika Kwik Kian Gie, jurusan S1-Akuntansi dan S1-Manajemen angkatan 2008-2010.
3. Menerapkan salah satu teknik klasifikasi pada fuzzy decision tree yaitu algoritme Fuzzy ID3.
4. Untuk memprediksi keberhasilan studi mahasiswa, dilakukan dengan menggunakan
2
TINJAUAN PUSTAKA
Penelitian Terkait
Penelitian yang dilakukan oleh Vasani dan Gawali (2014) melakukan klasifikasi
dan evaluasi performansi mahasiswa menggunakan algoritme data mining. Data yang
digunakan adalah 220 data mahasiswa dan diklasifikasikan kedalam tiga kategori yakni
Cerdas, Sedang, Lemah dengan menggunakan algoritme decision tree C4.5 dan Naive
Bayesian. Algoritme decision tree C4.5 memberikan hasil yang lebih baik dari pada
algoritme Naïve Bayesian dalam hal akurasi mengklasikasikan data.
Adhatrao et al. (2013) melakukan penelitian tentang prediksi performansi
mahasiswa menggunakan algoritme klasifikasi ID3 dan C4.5 yang bertujuan untuk memprediksi hasil belajar mahasiswa pada semester pertama berdasarkan atribut jenis kelamin, nilai rapor, nilai ujian masuk, jenis penerimaan. Hasil dari penelitian ini adalah algoritme ID3 dan C4.5 memiliki akurasi prediksi yang hampir sama, namun dalam hal waktu eksekusi, algoritme C4.5 lebih baik jika dibandingkan dengan algoritme ID3. Penelitian ini terbatas memprediksi hasil belajar mahasiswa pada semester pertama, belum memprediksi sampai mahasiswa tersebut lulus.
Yadav dan Pal (2012) melakukan penelitian tentang prediksi untuk meningkatkan performansi mahasiswa jurusan teknik menggunakan teknik klasifikasi. Algoritme yang digunakan adalah C4.5, ID3, dan CART, tujuannya adalah untuk memprediksi hasil ujian akhir semester mahasiswa dan diklasifikasikan menjadi tiga kategori yakni Promosi, Lulus, Gagal. Hasil dari penelitian ini adalah dapat memprediksi kemungkinan siswa yang akan mengalami gagal dalam ujian akhir berdasarkan data siswa pada tahun-tahun sebelumnya. Algoritme C4.5 memiliki akurasi prediksi yang lebih efektif dibandingkan ID3 dan CART. Namun dari sisi waktu eksekusi algoritme ID3 lebih efesien dibandingkan algoritme C4.5 dan CART.
Yadav et al. (2012) melakukan penelitian untuk memprediksi kinerja mahasiswa
dengan dataset 48 mahasiswa dan 7 atribut yang diperoleh dari VBS Purvachal
University, India. Data sampel yang digunakan adalah data mahasiswa Magister Ilmu Komputer angkatan 2008 sampai 2011. Algoritme yang digunakan adalah algoritme ID3, C4.5, CART yang digunakan untuk klasifikasi. Hasil penelitian menunjukkan bahwa CART adalah algoritme yang terbaik untuk klasifikasi data. Penelitian ini akan membantu dosen untuk mengidentifikasi mahasiswa yang membutuhkan perhatian khusus dan akan membantu untuk mengurangi rasio mahasiswa yang gagal.
Mustafidah dan Aryanto (2012) melakukan penelitian tentang sistem inferensi fuzzy untuk memprediksi prestasi belajar mahasiswa berdasarkan nilai ujian nasional, tes potensi akademik dan motivasi belajar. Penelitian ini bertujuan untuk memprediksi IPK berdasarkan 3 atribut prediktor yakni nilai TPA, NEM, dan tingkat motivasi.
Penelitian ini menunjukkan bahwa fuzzy mamdani dapat digunakan untuk memprediksi
prestasi belajar mahasiswa.
Romansyah et al. (2009) melakukan penelitian mengenai penerapan teknik fuzzy
pada data diabetes. Nilai akurasi terbaik dari model adalah 94.15% yang diperoleh pada
saat fuzziness control threshold = 75% dan leaf decision threshold = 8% atau 10%.
Transformasi Data
Sebelum menggunakan data dengan teknik fuzzy decision tree perlu dilakukan
praproses terhadap data. Hal ini dilakukan untuk mendapatkan hasil analisis yang lebih
akurat dalam pemakaian teknik fuzzy decision tree. Dalam beberapa hal, praproses bisa
membuat nilai data menjadi kecil tanpa merubah informasi yang dikandungnya. Beberapa cara antara lain adalah transformasi atau normalisasi data, yaitu prosedur mengubah data sehingga berada dalam skala tertentu. Skala ini bisa antara (0,1), (-1,1) atau skala lain yang dikehendaki. Salah satu metode yang umum dipakai untuk
transformasi data adalah Unary Encoding.
Unary Encoding merupakan metode transformasi data dengan mempresentasikan
data dengan kombinasi angka 1 dan 0 (numerical binary variable). Metode ini
digunakan untuk mentransformasi data kategorikal. Secara prinsip, data kategori dapat ditransformasi ke dalam bilangan numerik, dimana suatu bilangan numerik mewakili
nilai suatu kategori. Atribut kategori yang demikian disebut dengan “dummy variable”
(Kantardzic 2003). Misalnya „0‟ untuk kategori „melebih masa studi‟ dan „1‟ untuk
kategori „tepat waktu‟.
Korelasi Pearson Product Moment (PPM)
Korelasi merupakan angka yang menunjukkan arah dan kuatnya hubungan antara dua peubah atau lebih, arah dinyatakan dalam bentuk hubungan positif atau negatif. Kuatnya hubungan dinyatakan dalam besarnya koefisien korelasi (Sugiyono 2007). Korelasi ini dikemukakan oleh Karl Pearson tahun 1900. Rumus yang digunakan Korelasi PPM adalah:
= ∑ y−(∑ )(∑y)
∑ 2− (∑ )2 ∑ 2− (∑ )2 … … … …(1)
dimana:
= Koefisien korelasi antara variabel X dan variabel Y
∑ y = Jumlah perkalian antara variabel X dan Y
Kegunaan PPM adalah untuk mengetahui derajat hubungan dan kontribusi
variabel bebas (independent) dengan variabel terikat (dependent). Korelasi PPM
Decision Tree (Pohon Keputusan)
Pohon keputusan atau dikenal dengan decision tree adalah salah satu metode
klasifikasi yang menggunakan representasi suatu struktur pohon yang yang berisi alternatif-alternatif untuk pemecahan suatu masalah. Pohon ini juga menunjukkan faktor-faktor yang mempengaruhi hasil alternatif dari keputusan tersebut disertai dengan estimasi hasil akhir bila kita mengambil keputusan tersebut. Peranan pohon keputusan
ini adalah sebagai decision support tool untuk membantu manusia dalam mengambil
suatu keputusan (Tsang et al. 2009). Manfaat dari decision tree adalah melakukan break
down proses pengambilan keputusan yang kompleks menjadi lebih simpel sehingga
orang yang mengambil keputusan akan lebih mudah menginterpretasikan solusi dari
permasalahan. Konsep yang digunakan oleh decision tree adalah mengubah data
menjadi suatu keputusan pohon dan aturan-aturan keputusan (rule). Decision tree
menggunakan struktur hierarki untuk pembelajaran supervised. Proses dari decision tree
dimulai dari root node hingga leaf node yang dilakukan secara rekursif (Alpaydin 2004).
Setiap percabangan menyatakan suatu kondisi yang harus dipenuhi dan pada
setiap ujung pohon menyatakan kelas dari suatu data. Pada decision tree terdiri dari tiga
bagian yaitu (Alpaydin 2004) :
Root Node : Node ini merupakan node yang terletak paling atas dari suatu pohon.
Internal Node : Node ini merupakan node percabangan, hanya terdapat satu input serta mempunyai minimal dua output.
Leaf Node : Node ini merupakan node akhir, hanya memiliki satu input, dan tidak memiliki output.
Contoh dari pohon keputusan dapat dilihat di Gambar 1 berikut ini.
Iterative Dychotomizer Version 3(ID3)
Salah satu algoritme yang termasuk dalam teknik pembentukan pohon keputusan
adalah algoritme decision tree Iterative Dychotomizer Version 3 (ID3). Iterative
Dychotomizer Version 3 atau yang sering disebut dengan ID3 adalah salah satu
algoritme dalam decision tree learning. Algoritme ini ditemukan oleh J. Ross Quinlan
pada tahun 1986 yang berdasarkan algoritme CLS (Concept Learning System) (Liang
2005). ID3 merupakan penyempurnaan algoritme CLS dengan menambahkan feature
selection heuristic. ID3 akan melakukan pencarian secara rakus (greedy search) ke
semua kemungkinan pohon keputusan. Untuk menentukan root dan node atribut
lainnya, ID3 menghitung nilai entropy untuk mendapatkan information gain.
Entropy adalah parameter yang digunakan untuk mengetahui keberagaman (homogeneity) dari suatu kumpulan sampel data (Suyanto 2007). Semakin beragam kumpulan sampel data, maka nilai entropy nya semakin besar. Nilai entropy berada pada rentang 0 sampai dengan 1. Sampel data yang nilainya sama mempunyai nilai entropy 0, sedangkan dengan keberagaman yang seimbang (balanced) nilai entropy nya
sama dengan 1. Rumus perhitungan nilai entropy adalah sebagai berikut (Liang 2005):
= ∑ −� 2(�)………...(2)
dimana H (S) adalah nilai entropy dari sampel data S. N adalah jumlah kelas yang ada di atribut, sedangkan � adalah jumlah sampel untuk kelas i atau rasio dari kelas. Setelah mencari nilai entropy, maka selanjutnya dapat dihitung nilai information gain. Information gain adalah ukuran atau parameter keefektifitasan suatu atribut untuk
mengklasifikasikan data. Untuk menghitung information gain dapat digunakan rumus
berikut (Liang 2005):
H( ) : Entropy untuk sampel-sampel yang memiliki nilai v
Menurut Quinlan (1986) algoritme ID3 secara umum dapat dilihat sebagai berikut:
1. Buat simpul root
2. If semua sampel adalah kelas I, maka
Return pohon satu simpul Root dengan label=i
3. If Kumpulan Atribut kosong, Return pohon satu simpul Root dengan label=nilai
atribut target yang paling umum (yang paling sering muncul) Else
A←Atribut yang merupakan the best classifier (dengan information gain terbesar)
Atribut keputusan untuk Root←A
o Tambahkan suatu cabang di bawah Root sesuai dengan nilai
o Buat suatu variabel, misalnya Sample vi, sebagai himpunan bagian
(subset) dari kumpulan Sampel yang bernilai pada atribut A
o If Sample , kosong
Then dibawah cabang ini tambahkan suatu simpul daun (leaf node, simpul yang tidak punya anak di bawahnya) dengan label=nilai atribut target yang paling umum atau yang paling sering muncul)
Else dibawah cabang ini tambahkan subtree dengan memanggil fungsi ID3 (Sampel , Atribut Target, Atribut-{A})
End End End
4. Return Root
Himpunan Fuzzy
Himpunan fuzzy merupakan pengembangan dari himpunan biasa (crisp) (Marimin
2002). Pada himpunan biasa, fungsi karakteristik memetakan derajat keanggotaan ke nilai 1 jika suatu elemen masuk ke dalam suatu himpunan dan bernilai 0 jika elemen
tersebut tidak masuk ke dalam anggota himpunan tersebut. Himpunan fuzzy didasarkan
pada gagasan untuk memperluas jangkauan fungsi karakteristik sedemikian hingga fungsi tersebut akan mencakup bilangan real pada interval [0,1]. Derajat keanggotaan tidak hanya 0 atau 1, tetapi juga nilai yang terletak di antaranya (Kusumadewi 2002).
Ada beberapa hal yang perlu diketahui dalam memahami himpunan fuzzy, yaitu
(Kusumadewi 2003) :
a. Variabel Fuzzy
Variabel fuzzy merupakan variabel yang hendak dibahas dalam suatu sistem.
Contoh : temperatur, suhu, umur.
b. Himpunan Fuzzy
Himpunan fuzzy merupakan suatu grup yang mewakili suatu kondisi atau keadaan
tertentu dalam suatu variabel fuzzy.
Contoh : Variabel suhu, terbagi menjadi 3 himpunan fuzzy, yaitu Tinggi, Normal, dan Rendah.
c. Semesta pembicaraan
Semesta pembicaraan adalah keseluruhan nilai yang diperbolehkan untuk
dioperasikan dalam suatu variabel fuzzy. Semesta pembicaraan merupakan
himpunan bilangan real yang senantiasa naik (bertambah) secara monoton dari kiri kekanan. Nilai semesta pembicaraan dapat berupa bilangan positif maupun negatif. Adakalanya nilai semesta pembicaraan ini tidak dibatasi batas atasnya.
d. Domain
Domain himpunan fuzzy adalah keseluruhan nilai yang diizinkan dalam semesta
pembicaraan dan boleh dioperasikan dalam suatu himpunan fuzzy. Seperti halnya
semesta pembicaraan, domain merupakan himpunan bilangan real yang senantiasa
Fungsi Keanggotaan
Fungsi keanggotaan (membership function) adalah suatu kurva yang menunjukkan
pemetaan titik-titik masukan data ke dalam nilai keanggotaannya (Kusumadewi 2002). Pada sistem fuzzy, terdapat beberapa fungsi keanggotaan yang dapat digunakan untuk
pemberian nilai keanggotaan pada suatu elemen dalam himpunan fuzzy. Beberapa fungsi
keanggotaan yang umum digunakan adalah kurva segitiga dan kurva trapesium.
1. Representasi Kurva Segitiga (Triangle)
Representasi kurva segitiga merupakan gabungan dari dua garis linear seperti terlihat pada Gambar 2.
Gambar 2 Kurva Segitiga
Fungsi keanggotaan untuk kurva segitiga adalah sebagai berikut :
µ =
0 ; atau
−
− ; −
− ;
… … … …. . (4)
2. Representasi Kurva Trapesium
Representasi kurva trapesium pada dasarnya seperti bentuk segitiga, hanya saja ada beberapa titik yang memiliki nilai keanggotaan 1 seperti terlihat pada Gambar 3.
Gambar 3 Kurva Trapesium
Fungsi keanggotaan untuk kurva trapesium adalah sebagai berikut :
µ =
0 ; atau
−
− ;
1 ;
− − ;
Fuzzy Decision Tree (FDT)
Fuzzy decision tree adalah pengembangan dari algoritme ID3 dengan cara
menggabungkan algoritme klasik ID3 dengan teori fuzzy set yang efektif untuk
mendapatkan pengetahuan pada permasalahan yang tidak pasti. Dalam pohon
keputusan, leaf node diberikan sebuah label kelas. Non-terminal node, yang terdiri dari
root dan internal node lainnya, mengandung kondisi-kondisi uji atribut untuk
memisahkan record yang memiliki karakteristik yang berbeda. Edge-edge dapat
dilabelkan dengan nilai-nilai numeric-symbolic. Sebuah atribut numeric-symbolic adalah
sebuah atribut yang dapat bernilai numeric ataupun symbolic yang dihubungkan dengan
sebuah variable kuantitatif. Sebagai contoh, ukuran seseorang dapat dituliskan sebagai
atribut numeric-symbolic: dengan nilai kuantitatif, dituliskan dengan “1,72 meter”,
ataupun sebagai nilai numeric-symbolic seperti “tinggi” yang berkaitan dengan suatu
ukuran (size). Nilai-nilai seperti inilah yang menyebabkan perluasan dari decision tree
menjadi fuzzy decision tree (Yuan dan Shaw 1995). Penggunaan teknik fuzzy
memungkinkan untuk mengetahui suatu objek yang dimiliki oleh lebih dari satu kelas. Fuzzy decision tree memungkinkan untuk menggunakan nilai-nilai numeric-symbolic selama konstruksi atau saat mengklasifikasikan kasus-kasus baru. Manfaat dari
teori himpunan fuzzy dalam decision tree ialah meningkatkan kemampuan dalam
memahami decision tree ketika digunakan atribut-atribut kuantitatif. Bahkan, dengan
menggunakan teknik fuzzy dapat meningkatkan ketahanan saat melakukan klasifikasi
kasus-kasus baru (Marsala 1998).
Fuzzy Iterative Dychotomizer Version 3 (Fuzzy ID3)
Algoritme ID3 pertama kali diperkenalkan oleh Quinlan pada tahun 1986. Algoritme ini menggunakan teori informasi untuk menentukan atribut mana yang paling informatif, namun ID3 sangat tidak stabil dalam melakukan penggolongan berkenaan
dengan gangguan kecil pada data pelatihan. Logika fuzzy dapat memberikan suatu
peningkatan dalam melakukan penggolongan pada saat pelatihan (Liang 2005).
Algoritme Fuzzy ID3 merupakan algoritme yang efisien untuk membuat suatu
fuzzy decision tree. Algoritme Fuzzy ID3 adalah sebagai berikut (Liang 2005):
1. Buat root node yang memiliki dataset fuzzy dengan nilai membership 1.
2. Jika node t pada himpunan data fuzzy D memenuhi beberapa kondisi berikut maka
turunkan leaf node dan berikan label nama kelas:
Proporsi kelas lebih besar atau sama dengan threshold� ,
| |
� ………(6)
Jumlah record data lebih kecil dari threshold�
Tidak ada lagi atribut untuk klasifikasikan, maka leaf node diberi label nama
kelas.
3. Jika kondisi di atas tidak terpenuhi, maka itu bukan leaf-node. Sub-node baru akan
dihasilkan sebagai berikut:
Untuk setiap 1 s (i=1,2,...,L), hitung information gain G( 1, D) dan pilih
atribut yang nilai information gain nya paling besar.
Bagi D menjadi beberapa fuzzy subset 1,…, , sesuai dengan ,
dimana derajat keanggotaan data di adalah perkalian derajat keanggotaan
Buat node baru 1,..., , untuk fuzzy subset 1,..., , dan beri label
himpunan fuzzy j antara cabang yang menghubungkan node dan t.
Gantikan D dengan (j = 1,2,...,m) dan ulangi dari urutan nomor 2 secara rekursif.
Fuzzy Entropy dan Information Gain
Information gain adalah suatu nilai statistik yang digunakan untuk memilih atribut yang akan mengekspansi tree dan menghasilkan node baru pada algoritme ID3. Suatu entropy dipergunakan untuk mendefinisikan nilai information gain. Entropy dirumuskan sebagai berikut (Liang 2005):
Terdapat 2 kasus khusus yang terjadi pada klasifikasi boolean, yang pertama adalah jika
semua anggota dari himpunan S memiliki tipe yang sama, maka nilai entropy adalah 0
(nol). Hal ini berarti tidak terjadi ketidakpastian klasifikasi.
=−1∗ 2 1 −0∗ 2 0 = 0… … … …(9)
Kedua, jika jumlah contoh positif sama dengan jumlah contoh negatif, maka nilai entropy adalah 1 (satu), hal ini menandakan terjadi ketidakpastian klasifikasi maksimum.
=−0.5∗ 2 0.5 −0.5∗ 2 0.5 = 1… … …(10)
Untuk melakukan perluasan atribut, yang didasarkan pada data dari himpunan contoh, terlebih dahulu harus didefinisikan ukuran standar information gain. Information gain
digunakan sebagai ukuran seleksi atribut, yang merupakan hasil pengurangan entropy
dari himpunan contoh setelah membagi ukuran himpunan contoh dengan jumlah
atributnya. Information gain untuk atribut A didefinisikan sebagai berikut (Liang 2005):
, = −
… …. (11)
∈ ( )
dengan bobot = | |
| | adalah rasio dari data dengan atribut v pada himpunan contoh.
Pada himpunan data fuzzy, terdapat penyesuaian rumus untuk menghitung nilai entropy
untuk atribut dan information gain karena adanya ekspresi data fuzzy. Berikut adalah
= = −� ∗ 2(�)
�
… …. (12)
Untuk menentukan fuzzy entropy setelah dilakukan splitting data dan information gain
dari suatu atribut A pada algoritme Fuzzy ID3 digunakan persamaan sebagai berikut
entropy dari himpunan S dari data pelatihan pada node. | | adalah ukuran dari subset
⊆ S dari data pelatihan dengan atribut v. |S| menunjukkan ukuran dari himpunan S (Liang 2005).
Fuzzy Decision Tree Threshold
Jika proses learning dari fuzzy decision tree (FDT) dihentikan sampai semua data
contoh pada masing-masing leaf-node menjadi anggota sebuah kelas, akan dihasilkan
akurasi yang rendah. Oleh karena itu untuk meningkatkan akurasinya, proses learning
harus dihentikan lebih awal atau melakukan pemangkasan tree secara umum (Liang
2005). Untuk itu diberikan 2 (dua) buah threshold yang harus terpenuhi jika tree akan
diekspansi, yaitu (Liang 2005):
Fuzziness control threshold (FCT) / θr
Jika proporsi himpunan data dari kelas Ck lebih besar atau sama dengan nilai
threshold θr, maka ekspansi tree dihentikan. Sebagai contoh: jika diberikan θr
adalah 85%, pada sebuah sub-dataset rasio dari kelas 1 adalah 90% dan kelas 2
adalah 10%, maka ekspansi tree dihentikan.
Leaf decision threshold (LDT) / θn
Jika banyaknya anggota himpunan data pada suatu node lebih kecil dari
threshold θn, maka ekspansi tree dihentikan. Sebagai contoh: sebuah himpunan data memiliki 600 contoh dengan θn adalah 2%. Jika jumlah data contoh pada
sebuah node lebih kecil dari 12 (2% dari 600), maka ekspansi tree dihentikan.
Sistem Inferensi Fuzzy
Inferensi merupakan proses penarikan suatu kesimpulan berdasarkan data dan
aturan tertentu (Siler dan Buckley 2005). Sistem inferensi fuzzy merupakan sebuah
framework yang didasarkan pada konsep himpunan fuzzy, fuzzy if-then rules, dan fuzzy reasoning. Fuzzy Inference System (FIS) dapat menerima input berupa bilangan crisp
atau bilangan fuzzy, tapi outputnya hampir semua berupa himpunan fuzzy. Pada sistem
inferensi fuzzy yang outputnya berupa nilai crisp dibutuhkan metode defuzzifikasi untuk
Metode Mamdani
Metode Mamdani diperkenalkan oleh Ebrahim Mamdani pada tahun 1975. Metode ini sering juga dikenal dengan nama Metode Max-Min. Untuk mendapatkan output, diperlukan 4 tahapan (Kusumadewi 2002) :
1. Pembentukan himpunan fuzzy
Pada Metode Mamdani, baik variabel input maupun variabel output dibagi menjadi satu atau lebih himpunan fuzzy.
2. Aplikasi fungsi implikasi (aturan)
Pada Metode Mamdani, fungsi implikasi yang digunakan adalah Min.
3. Komposisi aturan
Tidak seperti penalaran monoton, apabila sistem terdiri-dari beberapa aturan, maka inferensi diperoleh dari kumpulan dan korelasi antar aturan. Ada 3 metode yang
digunakan dalam melakukan inferensi sistem fuzzy, yaitu: max, additive dan
probabilistik OR (probor). Pada penelitian ini, metode yang digunakan adalah
metode Max.
Metode Max (Maximum)
Pada metode ini, solusi himpunan fuzzy diperoleh dengan cara mengambil nilai
maksimum aturan, kemudian menggunakannya untuk memodifikasi daerah fuzzy,
dan mengaplikasikannya ke output dengan menggunakan operator OR (union).
Jika semua proposisi telah dievaluasi, maka output akan berisi suatu himpunan fuzzy yang merefleksikan konstribusi dari tiap-tiap proposisi. Secara umum dapat dituliskan:
Input dari proses defuzzifikasi adalah suatu himpunan fuzzy yang diperoleh dari
komposisi aturan-aturan fuzzy, sedangkan output yang dihasilkan merupakan suatu
bilangan pada domain himpunan fuzzy tersebut. Sehingga jika diberikan suatu
himpunan fuzzy dalam range tertentu, maka harus dapat diambil suatu nilai crisp tertentu sebagai output.
Defuzzifikasi Metode Centroid
Defuzzifikasi adalah merupakan proses pengubahan keluaran fuzzy ke dalam
keluaran yang bernilai tunggal (crisp). Oleh karena itu, masukan dari poses
defuzzifikasi adalah suatu himpunan fuzzy yang diperoleh dari komposisi aturan-aturan
fuzzy, sedangkan keluarannya adalah suatu bilangan pada domain himpunan fuzzy
tersebut (Kusumadewi 2002). Defuzzifikasi metode Centroid adalah teknik yang solusi
nilai tunggalnya didapatkan dengan mengambil titik pusat daerah fuzzy. Secara umum dapat diformulasikan sebagai berikut:
3
METODE PENELITIAN
Kerangka Pemikiran
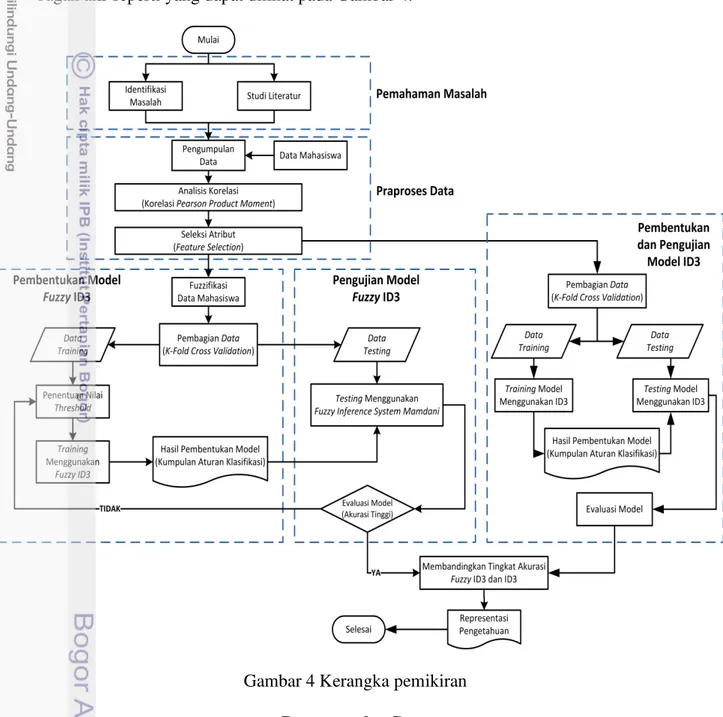
Adapun kerangka pemikiran pada penelitian ini dapat digambarkan dalam suatu bagan alir seperti yang dapat dilihat pada Gambar 4.
Gambar 4 Kerangka pemikiran
Pengumpulan Data
Sumber data yang digunakan diambil dari data kelulusan mahasiswa yang
diperoleh dari database SIMAK (Sistem Informasi Akademik) Institut Bisnis dan
Informatika Kwik Kian Gie pada tahun 2015, dari dua program studi dan dari tiga angkatan yaitu S1-Manajemen dan S1-Akuntansi angkatan 2008-2010. Data tersebut
merupakan gabungan dari beberapa tabel diantaranya berasal dari dari dataset identitas
Analisis Korelasi Atribut
Atribut predictor merupakan atribut-atribut yang akan digunakan untuk
melakukan prediksi terhadap kelulusan tepat waktu mahasiswa. Pemilihan atribut-atribut prediktor dilakukan dengan menggunakan pendekatan uji statistika yakni uji
korelasi pearson product moment menggunakan software IBM SPSS Statistics v.20 agar
dapat mengetahui apakah prediktor-prediktor tersebut memiliki hubungan terhadap kelulusan tepat waktu mahasiswa. Proses ini dilakukan untuk meningkatkan efisiensi dan skalabilitas dari sebuah sistem prediksi.
Tahap awal dalam menentukan korelasi antara atribut-atribut prediktor dengan kelulusan tepat waktu mahasiswa adalah menentukan hipotesis dari penelitian, sebagai contoh :
Ho : Tidak ada hubungan yang signifikan antara IPK Semester 1 dengan
kelulusan tepat waktu mahasiswa.
Ha : Ada hubungan yang signifikan antara IPK Semester 1 dengan kelulusan
tepat waktu mahasiswa.
Selanjutnya dihitung korelasinya menggunakan formula dari korelasi pearson
product moment hingga didapat nilai korelasi dari atribut IPK Semester 1 terhadap kelulusan tepat waktu mahasiswa. Dengan cara yang sama dilakukan perhitungan korelasi pada seluruh atribut yang akan digunakan dalam penelitian ini terhadap kelulusan tepat waktu mahasiswa. Tabel 1 menunjukkan contoh hasil perhitungan korelasi salah satu atribut prediktor yakni IP Semester 1 terhadap kelulusan tepat waktu mahasiswa.
Tabel 1 Contoh hasil perhitungan uji korelasi pearson product moment
Correlations
IPK Sem1 Lulus Tepat Waktu
IPK Sem1
**. Correlation is significant at the 0.01 level (2-tailed).
Transformasi Data
Proses transformasi data diantaranya dilakukan untuk data target yang bersifat
kategorikal, dengan menggunakan metode Unary Encoding, dimana data target
dipresentasikan dengan kombinasi angka 0 dan 1 (numerical binary variable). Dimana
„0‟ untuk kategori masa studi 8 semester atau ≤ 48 bulan dan „1‟ untuk kategori tidak
tepat waktu atau melebihi masa studi 8 semester atau > 48 bulan. Selain itu pada
penelitian ini juga menerapkan salah satu teknik data mining yaitu decision tree dengan
menggunakan pendekatan fuzzy dan algoritme yang digunakan adalah fuzzy decision
tree (FDT), Oleh karena itu data kelulusan yang digunakan harus direpresentasikan ke
dalam bentuk fuzzy. Proses ini diawali dengan membuat fungsi nilai keanggotaan
(membership function) pada masing-masing atribut yang dipakai. Hal ini merupakan
bagian dari penerapan prinsip fuzzy yang menjadi pedoman penelitian. Salah satu contoh
ilustrasi membership function yang digunakan untuk mentransformasi data IPK ke
dalam bentuk fuzzy adalah sebagai berikut :
� =
Berikut ini salah satu contoh ilustrasi hasil fuzzifikasi dari atribut IP Semester 1
terhadap kelulusan tepat waktu mahasiswa dengan menggunakan membership function
yang sudah didefinisikan sebelumnya, seperti yang dapat dilihat pada Tabel 2.
Tabel 2 Contoh data hasil fuzzifikasi
No_Data IPK_Sem1 MF_Rendah MF_Sedang MF_Tinggi MF_SangatTinggi Class Target
1 2.85 0 1 0 0 2
Pembagian Data Training dan Data Testing
Dalam penelitian ini metode yang digunakan untuk membagi data latih dan data uji adalah k-fold cross validation. Pembagian data latih dan data uji dengan proporsi
Pemilihan Nilai Threshold
Penentuan nilai fuzziness control threshold (θr ) dan nilai leaf decision threshold
(θn) hingga mendapatkan model yang terbaik dan dengan tingkat akurasi yang tinggi
(>80%) terhadap prediksi kelulusan tepat waktu mahasiswa. Sebagai contoh apabila nilai threshold yang digunakan untuk fuzziness control threshold (FDT) 80% dan leaf decision threshold (LDT) 20% namun masih menghasilkan akurasi model yang kurang
dari 80% maka dilakukan percobaan kombinasi threshold yang lain hingga mencapai
akurasi yang lebih tinggi dari 80%.
Pembentukan Model
Langkah-langkah pada metode fuzzy decision tree dalam pembentukan model
klasifikasi kelulusan tepat waktu mahasiswa adalah sebagai berikut :
o Menentukan atribut yang akan digunakan.
o Menentukan banyaknya fuzzy set untuk masing-masing atribut.
o Menentukan banyaknya training set yang akan digunakan.
o Menghitung membership value.
o Memilih besarnya threshold yang akan digunakan.
o Membangun fuzzy decision tree dengan algoritme Fuzzy ID3.
o Menguji model klasifikasi
Evaluasi Model
Dalam penelitian ini dipilih alat ukur evaluasi berupa confusion matrix dengan
tujuan untuk mempermudah dalam menganilisis performa algoritme Fuzzy ID3, karena
confusion matrix memberikan informasi dalam bentuk angka sehingga dapat dihitung rasio keberhasilan klasifikasi. Confusion matrix digunakan sebagai dasar dari variasi ukuran penilaian seperti akurasi, precision dan recall. Kombinasi precision dan recall
merepresentasikan nilai F-measure. Seperti terlihat pada Tabel 3 yang menunjukkan
tabel confision matrix untuk memprediksi kelulusan tepat waktu mahasiswa.
Tabel 3 Confusion matrix untuk prediksi kelulusan tepat waktu
Kelas Prediksi
Lulus Tepat Waktu
Ya Tidak
Ya True Positive (TP) False Negative (FN)
Tidak False Positive (FP) True Negative (TN)
Keterangan untuk Tabel 3 dinyatakan sebagai berikut :
True Positive (TP) : jumlah instance kelas positif yang diprediksi benar sebagai kelas positif.
False Positive (FP) : jumlah instance kelas negatif yang diprediksi salah sebagai kelas positif.
Tahapan representasi pengetahuan merupakan tahapan akhir pada penelitian ini, dimana pada tahap ini pola yang telah ditemukan dipresentasikan ke pengguna dengan teknik visualisasi agar pengguna dapat memahaminya. Deskripsi aturan klasifikasi akan dipresentasikan dalam bentuk aturan logika yang selanjutnya akan dievaluasi hasil dari pengetahuan yang didapatkan.
Alat Bantu Penelitian
Alat-alat bantu yang digunakan dalam penelitian ini adalah sebagai berikut :
a. Komputer Personal
Komputer personal dengan spesifikasi prosesor Intel® Core i5-2520M CPU @ 2.50 GHz, Memory (RAM) 4 GB.
b. Sistem Operasi Windows 7 Ultimate.
c. Aplikasi Microsoft Excel 2010 untuk melakukan praproses terhadap data sebelum
digunakan sebagai input model yang dikembangkan karena tampilan data dalam
bentuk datasheet maka aplikasi ini dapat digunakan unuk mempermudah dalam
pengolahan data.
d. Aplikasi IBM SPSS Statistics 20 untuk melakukan perhitungan korelasi pearson
product moment terhadap atribut-atribut predictor yang akan digunakan.
e. Aplikasi Matlab versi 7.04 digunakan dalam penelitian ini untuk pembentukan
model menggunakan algoritme Fuzzy ID3 dan visualisasi hasil.
Hasil dan Analisa
Analisa yang dilakukan terhadap predictor yang memiliki hubungan dengan
kelulusan tepat waktu mahasiswa menggunakan analisis korelasi pearson product
moment yang digunakan untuk membentuk model klasifikasi. Model yang paling bagus dari hasil pembentukan aturan klasifikasi yang dihasilkan menggunakan algoritme Fuzzy ID3 digunakan untuk memprediksi apakah seorang mahasiswa dapat lulus tepat
waktu atau tidak menggunakan Fuzzy Inference System Mamdani. Pada penelitian ini
juga dilakukan perbandingan akurasi dari beberapa rule yang dibentuk oleh Fuzzy ID3
berdasarkan nilai threshold yang ditentukan. Selain itu juga dilakukan perbandingan
performansi antara algoritme Fuzzy ID3 dan algoritme ID3 dalam membentuk aturan
4
HASIL DAN PEMBAHASAN
Pengumpulan dan Pembersihan Data
Data kelulusan mahasiswa diperoleh dari database SIMAK (Sistem Informasi
Akademik) Institut Bisnis dan Informatika Kwik Kian Gie pada tahun 2015, dari dua program studi dan dari tiga angkatan yaitu S1-Manajemen dan S1-Akuntansi angkatan 2008-2010. Data tersebut merupakan gabungan dari beberapa tabel diantaranya berasal dari dataset identitas mahasiswa, dataset transkrip nilai mahasiswa, dan dataset presensi mahasiswa.
Jumlah data yang diperoleh adalah sebanyak 957, dimana data IPK setiap
semester dari setiap mahasiswa sudah dilakukan transpose data sehingga didapat IPK
setiap semester dari masing-masing mahasiswa. Data yang diambil adalah data IPK
mahasiswa yang memiliki IPK ≥ 2.00. Dataset identitas mahasiswa terdiri dari 13 atribut yang menjelaskan identitas diri mahasiswa dan informasi tentang data mahasiswa yang bersangkutan saat mendaftar diri pada Institut Bisnis dan Informatika Kwik Kian Gie. Atribut-atribut tersebut diantaranya nomor induk mahasiswa (NIM), nama, jenis kelamin, tempat lahir, tanggal lahir, agama, pekerjaan orang tua, pendidikan orang tua, alamat, tanggal lulus, jurusan smu, nilai rata-rata rapor kelas 2 SMA, dan asal kota smu. Atribut tanggal lulus digunakan untuk menghitung masa studi yang ditempuh mahasiswa tersebut sehingga dapat menentukan apakah mahasiswa-mahasiswa tersebut
lulus tepat waktu atau tidak, yang nantinya akan digunakan sebagai atribut class target.
Mahasiswa dapat dinyatakan lulus tepat waktu adalah mahasiswa yang menempuh studi
dalam waktu tidak lebih dari 8 semester (≤ 48 bulan). Dataset presensi mahasiswa terdiri dari 3 atribut yakni NIM, semester dan jumlah kehadiran.
Dataset transkrip nilai terdiri dari 6 atribut yakni NIM, nama, nilai pendidikan kewarganegaraan, nilai pancasila, indeks prestasi komulatif (IPK) semester 1, IPK
semester 2. Dataset ini merupakan dataset yang sudah dilakukan perubahan dari kolom
menjadi baris atau dari baris menjadi kolom (transpose) data menggunakan structured
query language (SQL). Contoh query yang digunakan untuk transpose data IPK setiap semester adalah sebagai berikut :
SELECT a.idnim, b.fullname,
SUM(IF (a.idsemest=01, a.nilipk,0)) ipk_sem1, SUM(IF (a.idsemest=02, a.nilipk,0)) ipk_sem2,
FROM satr0000 a INNER JOIN satr0002 b ON b.idnim = a.idnim WHERE a.idangkat IN('2008','2009','2010') GROUP BY a.idnim, b.fullname
Contoh data sebelum di transpose dan yang sudah di transpose menggunakan
query diatas dapat dilihat pada Tabel 4 dan Tabel 5.
Tabel 4 Contoh record data IPK sebelum di transpose
NIM Nama Semester Indeks Prestasi
39100027 Kenneth Limindo 01 3.00
39100027 Kenneth Limindo 02 3.25
39100027 Kenneth Limindo 03 2.62
Tabel 5 Contoh record data IPK setelah di transpose
NIM Nama IP Sem 1 IP Sem 2 IP Sem 3 IP Sem 4
39100027 Kenneth Limindo 3.00 3.25 2.62 2.71
Data yang diambil ini adalah data yang sudah bersih atau tidak mengandung missing value, relevan, dan tidak redundant. Dikatakan missing value jika nilai dari salah satu atau beberapa dari atribut tersebut tidak berisi nilai atau kosong.
Tabel 6 Contoh record data dengan missing value
No Nama Jenis Kelamin Agama Jumlah Kehadiran
1 Jimmy Leonard Laki-Laki Khatolik 0
2 Nitha Oktavianty Perempuan Kristen 190
3 Caterine Gunawan Perempuan Khatolik 187
4 Henricus Leonard Laki-Laki Kristen 172
5 Shiela Agustine Y. Perempuan Kristen 0
6 Norma Juwita Perempuan Buddha 191
7 Wiwin Perempuan Khonghucu 178
Pada Tabel 6 di atas terlihat bahwa record ke 1 dan 5 terdapat atribut yang tidak
berisi data atau kosong, yakni pada atribut jumlah kehadiran. Maka keadaan seperti di atas dikatakan bahwa atribut tersebut missing value. Maka data seperti contoh di atas akan dihapus karena record tersebut dinilai tidak konsisten.
Selanjutnya dilakukan pemilihan atribut. Atribut yang tidak relevan dan atribut
yang banyak mengandung missing value akan dihilangkan. Semua atribut yang terpilih
adalah atribut yang kontinu. Sementara untuk kelas target dikategorikan menjadi dua
kategori yakni Lulus Tepat Waktu (masa studi ≤ 48 bulan) dan kategori Tidak Lulus
Tepat Waktu (masa studi > 48 bulan). Record yang mengandung nilai kosong dan atau
duplikat dihapus, karena akan berpotensi menyebabkan kesalahan terhadap hasil dari model klasifikasi kelulusan tepat waktu mahasiswa yang terbentuk.
Dari hasil akhir penggabungan antara dataset identitas mahasiswa, dataset
transkrip nilai mahasiswa, dan dataset presensi mahasiswa terdiri dari 410 record yang
Uji Korelasi Atribut
Dari 5 atribut yang ada akan dilakukan pemilihan atribut lagi menggunakan uji hipotesis statistika yaitu dengan menggunakan pendekatan uji statistika yakni uji
korelasi pearson product moment (PPM) agar dapat mengetahui apakah
prediktor-prediktor tersebut memiliki hubungan terhadap kelulusan tepat waktu mahasiswa. Berdasarkan uji korelasi yang telah dilakukan terhadap seluruh atribut
menggunakan metode pearson product moment diperoleh hasil harga indeks korelasi
setiap atribut yang dirangkum pada Tabel 7. Seperti yang terlihat pada Tabel 7, semua atribut memiliki korelasi negatif terhadap lulus tepat waktu. Atribut IPK semester 2 memiliki korelasi yang paling tinggi dengan besar koefisien -0.740 (74%). Korelasi negatif memiliki makna bahwa semakin tinggi nilai dari suatu atribut prediktor maka lama masa studi yang ditempuh akan semakin kecil atau semakin cepat. Atribut-atribut inilah yang selanjutnya akan digunakan pada penelitian ini.
Tabel 7 Hasil uji korelasi antara atribut predictor terhadap masa studi
Fuzzifikasi Data
Penelitian ini menerapkan salah satu teknik pada data mining, yaitu fuzzy decision
tree, oleh karena itu data yang digunakan harus direpresentasikan ke dalam bentuk fuzzy. Proses diawali dengan membuat fungsi nilai keanggotaan (membership function) pada masing-masing atribut yang dipakai. Dari 5 (lima) atribut yang digunakan pada penelitian ini semuanya merupakan atribut yang bersifat kontinu, yaitu IPK Semester 1,
IPK Semester 2, Kedisiplinan, Prilaku, dan Rapor. Pada penelitian ini, range nilai dari
setiap atribut didapatkan berdasarkan hasil diskusi bersama pakar yakni beberapa orang
dosen dan management dari Institut Bisnis dan Informatika Kwik Kian Gie. Atribut
yang telah ditransformasi ke dalam bentuk fuzzy antara lain:
Correlations
IPK Sem1 IPK Sem2 Prilaku Kedisiplinan Rapor Lulus Tepat Waktu
Atribut IPK Semester 1
Atribut IPK Semester 1 dibagi menjadi 4 kelompok atau linguistic term, yaitu rendah
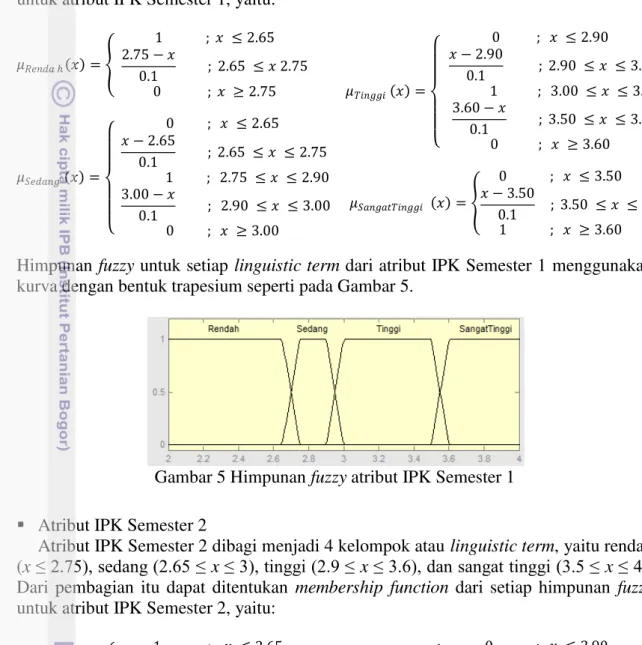
(x≤ 2.75), sedang (2.65 ≤ x≤ 3), tinggi (2.9 ≤ x≤ 3.6), dan sangat tinggi (3.5 ≤ x ≤ 4). Dari pembagian itu dapat ditentukan membership function dari setiap himpunan fuzzy untuk atribut IPK Semester 1, yaitu:
� =
Himpunan fuzzy untuk setiap linguistic term dari atribut IPK Semester 1 menggunakan
kurva dengan bentuk trapesium seperti pada Gambar 5.
Gambar 5 Himpunan fuzzy atribut IPK Semester 1
Atribut IPK Semester 2
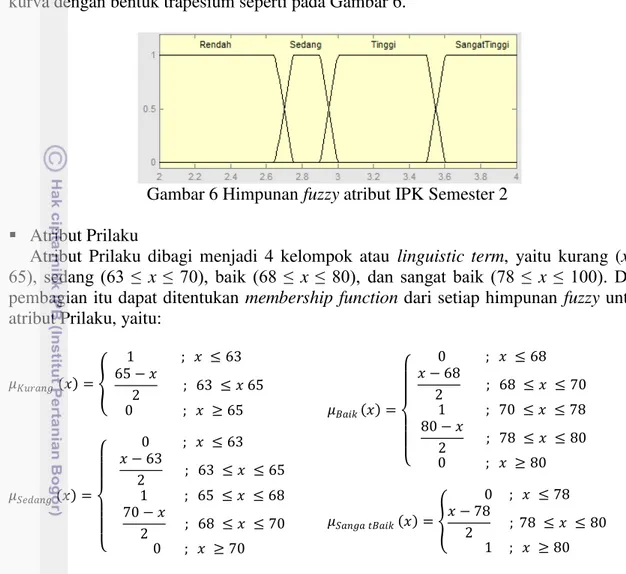
Atribut IPK Semester 2 dibagi menjadi 4 kelompok atau linguistic term, yaitu rendah
(x≤ 2.75), sedang (2.65 ≤ x≤ 3), tinggi (2.9 ≤ x≤ 3.6), dan sangat tinggi (3.5 ≤ x ≤ 4). Dari pembagian itu dapat ditentukan membership function dari setiap himpunan fuzzy untuk atribut IPK Semester 2, yaitu:
Himpunan fuzzy untuk setiap linguistic term dari atribut IPK Semester 2 menggunakan kurva dengan bentuk trapesium seperti pada Gambar 6.
Gambar 6 Himpunan fuzzy atribut IPK Semester 2
Atribut Prilaku
Atribut Prilaku dibagi menjadi 4 kelompok atau linguistic term, yaitu kurang (x ≤
65), sedang (63 ≤ x ≤ 70), baik (68 ≤ x ≤ 80), dan sangat baik (78 ≤ x ≤ 100). Dari
pembagian itu dapat ditentukan membership function dari setiap himpunan fuzzy untuk
atribut Prilaku, yaitu:
Himpunan fuzzy untuk setiap linguistic term dari atribut Prilaku menggunakan kurva dengan bentuk trapesium seperti pada Gambar 7.
Gambar 7 Himpunan fuzzy atribut Prilaku
Atribut Rapor
Atribut Rapor dibagi menjadi 4 kelompok atau linguistic term, yaitu rendah (x≤ 7),
sedang (6.75 ≤ x ≤ 7.5), tinggi (7.25 ≤ x ≤ 8.25), dan sangat tinggi (8 ≤ x ≤ 10). Dari
pembagian itu dapat ditentukan membership function dari setiap himpunan fuzzy untuk
� =
dengan bentuk trapesium seperti pada Gambar 8.
Gambar 8 Himpunan fuzzy atribut Rapor
Atribut Kedisiplinan
Atribut Kedisiplinan dibagi menjadi 3 kelompok atau linguistic term, yaitu kurang (x
≤ 180 hadir), sedang (175 hadir ≤ x≤ 190 hadir), dan baik (185 hadir ≤ x ≤ 196 hadir). Dari pembagian itu dapat ditentukan membership function dari setiap himpunan fuzzy untuk atribut Kedisiplinan, yaitu:
Himpunan fuzzy untuk setiap linguistic term dari atribut Kedisiplinan menggunakan
kurva dengan bentuk trapesium seperti pada Gambar 9.