MODEL MATEMATIKA
PERPINDAHAN KELOMPOK BELALANG
DENGAN METODE GELOMBANG BERJALAN
NURUDIN MAHMUD
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI TESIS DAN
SUMBER INFORMASI
Dengan ini saya menyatakan bahwa tesis Model Matematika Perpindahan Kelompok Belalang dengan Metode Gelombang Berjalan adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Bogor, Agustus 2008
ABSTRACT
NURUDIN MAHMUD. The Mathematical Models for Migratory Locust Swarms with Travelling Band. Under direction of PAIAN SIANTURI and MOCHAMAD TITO JULIANTO
Mathematical models for the swarming behaviour of locusts are developed with a goal of understanding how swarm cohesion can be maintained by the huge population of insects over long distances and long periods of time. The types of model to consider are local and nonlocal. The purposes of this thesis are to apply the diffusion models and to determine numerical solutions of the models. The matematical models are generally partial differential equations that can be analyzed by travelling wave solutions. These solutions are directed to travelling band (pulse) solutions. The analytical solution of the nonlocal model gives information that long-range interactions can contribute to group cohesion, but have limited ability to prevent the loss of individuals from the swarm. This result shows that nonlocal model is better than the local models. Furthermore, the numerical solution of the nonlocal model gives information that if the initial values are given differently, then the figures will also be different. If the distance between the smaller swarm and the larger swarm is relatively small, then the smaller swarm will join to the larger one. Otherwise, both groups will be separated.
RINGKASAN
NURUDIN MAHMUD. Model Matematika Perpindahan Kelompok Belalang dengan Metode Gelombang Berjalan. Dibimbing oleh PAIAN SIANTURI, dan MOCHAMAD TITO JULIANTO.
Dalam kehidupan sehari-hari banyak fenomena yang dapat dimodelkan dengan melihat perilaku dari subyek yang diamati. Pada fenomena belalang yang suka berkelompok dan berpindah tempat (di antara udara dan tanah) secara kontinu, dibangun beberapa model matematika (Edelstein-Keshet et al. 1998) secara berturut-turut, yaitu model I (kepaduan belalang bergantung pada konveksi difusi dan kecepatan belalang terbang), model II (gerakan terbang belalang bergantung pada kepadatan lokal), model III (gerakan belalang di tanah bergantung pada kepadatan lokal), model IV (perubahan arah terbang bergantung kepadatan), dan model V (gerakan aktif belalang terbang bergantung pada kepadatan individu). Tujuannya untuk memahami bagaimana kepaduan kelompok dapat dipertahankan dalam populasi yang besar (diatas 109 individu) pada jarak tempuh yang jauh (di atas ribuan mil) dan dalam periode waktu yang lama. Model I, II, III dan IV dibangun secara lokal dan model V secara non lokal.Modellokal mengamati tentang pengaruh kepadatan kelompok terhadap gerakan belalang, sedangkan model non lokal mengamati tentang kepadatan individu (pengaruh penggunaan rangsangan) terhadap gerakan belalang.
Tujuan tesis ini adalah mengkaji penerapan model difusi pada perpindahan belalang dan menentukan solusi numeriknya.
Metode gelombang berjalan digunakan dalam tiap model untuk menentukan solusi dengan beberapa langkah, yaitu peralihan koordinat persamaan diferensial parsial ke dalam koordinat persamaan diferensial biasa, melakukan penondimensionalan, pelinearan, menentukan nilai eigen dan vektor eigen. Dari nilai eigen dan vektor eigen dapat ditelusuri solusi model yang mengarah ke solusi gelombang berjalan. Untuk mempermudah menentukan solusi dari sistem persamaan, dilakukan pembatasan pada gelombang berjalan. Batas gelombang (orbit trayektori) dalam tesis ini dibagi menjadi dua, yaitu orbit heteroklinik yang mengarah ke solusi travelling front dan orbit homoklinik yang mengarah ke solusi travellingband.
Pada dasarnya, pergerakan belalang berkelompok mengarah ke solusi
travelling band. Tetapi, beberapa model banyak yang gagal untuk menghasilkan perilaku ideal kecuali dibuat asumsi-asumsi yang tidak biasa dan tidak realistis. Oleh karena itu, pendekatan untuk mengurangi masalah kegagalan ini perlu dideskripsikan (Edelstein-Keshet et al. 1998).
Dari penelusuran yang dilakukan Edelstein-Keshet et al. (1998), model I, II, III dan IV yang dibangun secara lokal tidak dapat menjaga kepaduan kelompok dengan memuaskan, maka dalam tesis ini diamati model V dengan pengamatan kepaduan kelompok secara non lokal.
v
Langkah selanjutnya adalah melakukan simulasi model V. Untuk keperluan ini, maka terlebih dahulu dikaji analisis model V dan ditetapkan parameter-parameter realistis yang berkaitan dengan model.
Hasil pengkajian secara analitik terhadap model V memberikan informasi bahwa interaksi dalam range yang panjang dapat memberi kontribusi terhadap kepaduan kelompok, tetapi mempunyai keterbatasan untuk menjaga hilangnya individu dalam kelompok.
Hasil pendekatan numerik menunjukkan bahwa jika nilai awal yang diberikan berbeda, maka menghasilkan gambar yang berbeda pula. Populasi yang lebih kecil akan bergabung dengan populasi yang lebih besar, bila jarak antar kedua populasi cukup dekat. Bila tidak, akan terpisah dari populasi yang lebih besar.
© Hak cipta milik Institut Pertanian Bogor, tahun 2008 Hak cipta dilindungi Undang-undang
1 Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber
a Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik atau
tinjauan suatu masalah.
b Pengutipan tidak merugikan kepentingan yang wajar Institut Pertanian Bogor.
MODEL MATEMATIKA
PERPINDAHAN KELOMPOK BELALANG
DENGAN METODE GELOMBANG BERJALAN
NURUDIN MAHMUD
Tesis
sebagai salah satu syarat untuk memperoleh gelar
Magister Sains pada
Departemen Matematika
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
Judul Tesis : Model Matematika Perpindahan Kelompok Belalang dengan Metode Gelombang Berjalan
Nama : Nurudin Mahmud NIM : G551060201
Disetujui
Komisi Pembimbing
Dr. Paian Sianturi
Mochamad Tito Julianto, M.Kom. Ketua Anggota
Diketahui
Ketua Program Studi Dekan Sekolah Pascasarjana Matematika Terapan
Dr. Ir. Endar H. Nugrahani, M.S. Prof. Dr. Ir. Khairil A. Notodiputro, M.S.
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Maret 2008 ini ialah masalah perpindahan kelompok belalang, dengan judul Model Matematika Perpindahan Kelompok Belalang dengan Metode Gelombang Berjalan.
Ucapan terima kasih atas pengorbanan dan permohonan maaf atas kurangnya perhatian serta kasih sayang penulis sampaikan kepada istri tercinta
Anita Ellyana Hardiyati. Selanjutnya ucapan terima kasih dengan iringan doa penulis semoga Allah SWT membalas dengan kebaikan kepada:
1 Dr. Paian Sianturi dan Mochamad Tito Julianto, M.Kom. selaku pembimbing yang dengan penuh kesabaran Memberikan bimbingan dan motivasi kepada penulis.
2 Drs. Ali Kusnanto, M.Si. selaku penguji yang telah memberikan saran dan kritiknya.
3 Departemen Agama Republik Indonesia, yang telah memberikan biaya kepada penulis selama menempuh pendidikan program magister di Institut Pertanian Bogor.
4 Ibu, ibu mertua, kakak ipar, dan seluruh keluarga di Piyaman, Wonosari, GK. 5 Teman-teman mahasiswa S-2 Matematika Terapan IPB angkatan 2006. 6 Semua pihak yang telah membantu penulis, yang tidak bisa penulis sebutkan
satu persatu.
Akhirnya penulis menyadari bahwa tulisan ini masih jauh dari sempurna. Oleh karena itu sumbangsih kritik dan saran demi kemajuan tulisan selanjutnya sangat penulis dambakan.
Semoga karya ilmiah ini bermanfaat.
Bogor, Agustus 2008 Penulis,
MODEL MATEMATIKA
PERPINDAHAN KELOMPOK BELALANG
DENGAN METODE GELOMBANG BERJALAN
NURUDIN MAHMUD
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI TESIS DAN
SUMBER INFORMASI
Dengan ini saya menyatakan bahwa tesis Model Matematika Perpindahan Kelompok Belalang dengan Metode Gelombang Berjalan adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Bogor, Agustus 2008
ABSTRACT
NURUDIN MAHMUD. The Mathematical Models for Migratory Locust Swarms with Travelling Band. Under direction of PAIAN SIANTURI and MOCHAMAD TITO JULIANTO
Mathematical models for the swarming behaviour of locusts are developed with a goal of understanding how swarm cohesion can be maintained by the huge population of insects over long distances and long periods of time. The types of model to consider are local and nonlocal. The purposes of this thesis are to apply the diffusion models and to determine numerical solutions of the models. The matematical models are generally partial differential equations that can be analyzed by travelling wave solutions. These solutions are directed to travelling band (pulse) solutions. The analytical solution of the nonlocal model gives information that long-range interactions can contribute to group cohesion, but have limited ability to prevent the loss of individuals from the swarm. This result shows that nonlocal model is better than the local models. Furthermore, the numerical solution of the nonlocal model gives information that if the initial values are given differently, then the figures will also be different. If the distance between the smaller swarm and the larger swarm is relatively small, then the smaller swarm will join to the larger one. Otherwise, both groups will be separated.
RINGKASAN
NURUDIN MAHMUD. Model Matematika Perpindahan Kelompok Belalang dengan Metode Gelombang Berjalan. Dibimbing oleh PAIAN SIANTURI, dan MOCHAMAD TITO JULIANTO.
Dalam kehidupan sehari-hari banyak fenomena yang dapat dimodelkan dengan melihat perilaku dari subyek yang diamati. Pada fenomena belalang yang suka berkelompok dan berpindah tempat (di antara udara dan tanah) secara kontinu, dibangun beberapa model matematika (Edelstein-Keshet et al. 1998) secara berturut-turut, yaitu model I (kepaduan belalang bergantung pada konveksi difusi dan kecepatan belalang terbang), model II (gerakan terbang belalang bergantung pada kepadatan lokal), model III (gerakan belalang di tanah bergantung pada kepadatan lokal), model IV (perubahan arah terbang bergantung kepadatan), dan model V (gerakan aktif belalang terbang bergantung pada kepadatan individu). Tujuannya untuk memahami bagaimana kepaduan kelompok dapat dipertahankan dalam populasi yang besar (diatas 109 individu) pada jarak tempuh yang jauh (di atas ribuan mil) dan dalam periode waktu yang lama. Model I, II, III dan IV dibangun secara lokal dan model V secara non lokal.Modellokal mengamati tentang pengaruh kepadatan kelompok terhadap gerakan belalang, sedangkan model non lokal mengamati tentang kepadatan individu (pengaruh penggunaan rangsangan) terhadap gerakan belalang.
Tujuan tesis ini adalah mengkaji penerapan model difusi pada perpindahan belalang dan menentukan solusi numeriknya.
Metode gelombang berjalan digunakan dalam tiap model untuk menentukan solusi dengan beberapa langkah, yaitu peralihan koordinat persamaan diferensial parsial ke dalam koordinat persamaan diferensial biasa, melakukan penondimensionalan, pelinearan, menentukan nilai eigen dan vektor eigen. Dari nilai eigen dan vektor eigen dapat ditelusuri solusi model yang mengarah ke solusi gelombang berjalan. Untuk mempermudah menentukan solusi dari sistem persamaan, dilakukan pembatasan pada gelombang berjalan. Batas gelombang (orbit trayektori) dalam tesis ini dibagi menjadi dua, yaitu orbit heteroklinik yang mengarah ke solusi travelling front dan orbit homoklinik yang mengarah ke solusi travellingband.
Pada dasarnya, pergerakan belalang berkelompok mengarah ke solusi
travelling band. Tetapi, beberapa model banyak yang gagal untuk menghasilkan perilaku ideal kecuali dibuat asumsi-asumsi yang tidak biasa dan tidak realistis. Oleh karena itu, pendekatan untuk mengurangi masalah kegagalan ini perlu dideskripsikan (Edelstein-Keshet et al. 1998).
Dari penelusuran yang dilakukan Edelstein-Keshet et al. (1998), model I, II, III dan IV yang dibangun secara lokal tidak dapat menjaga kepaduan kelompok dengan memuaskan, maka dalam tesis ini diamati model V dengan pengamatan kepaduan kelompok secara non lokal.
v
Langkah selanjutnya adalah melakukan simulasi model V. Untuk keperluan ini, maka terlebih dahulu dikaji analisis model V dan ditetapkan parameter-parameter realistis yang berkaitan dengan model.
Hasil pengkajian secara analitik terhadap model V memberikan informasi bahwa interaksi dalam range yang panjang dapat memberi kontribusi terhadap kepaduan kelompok, tetapi mempunyai keterbatasan untuk menjaga hilangnya individu dalam kelompok.
Hasil pendekatan numerik menunjukkan bahwa jika nilai awal yang diberikan berbeda, maka menghasilkan gambar yang berbeda pula. Populasi yang lebih kecil akan bergabung dengan populasi yang lebih besar, bila jarak antar kedua populasi cukup dekat. Bila tidak, akan terpisah dari populasi yang lebih besar.
© Hak cipta milik Institut Pertanian Bogor, tahun 2008 Hak cipta dilindungi Undang-undang
1 Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber
a Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik atau
tinjauan suatu masalah.
b Pengutipan tidak merugikan kepentingan yang wajar Institut Pertanian Bogor.
MODEL MATEMATIKA
PERPINDAHAN KELOMPOK BELALANG
DENGAN METODE GELOMBANG BERJALAN
NURUDIN MAHMUD
Tesis
sebagai salah satu syarat untuk memperoleh gelar
Magister Sains pada
Departemen Matematika
SEKOLAH PASCASARJANA
INSTITUT PERTANIAN BOGOR
Judul Tesis : Model Matematika Perpindahan Kelompok Belalang dengan Metode Gelombang Berjalan
Nama : Nurudin Mahmud NIM : G551060201
Disetujui
Komisi Pembimbing
Dr. Paian Sianturi
Mochamad Tito Julianto, M.Kom. Ketua Anggota
Diketahui
Ketua Program Studi Dekan Sekolah Pascasarjana Matematika Terapan
Dr. Ir. Endar H. Nugrahani, M.S. Prof. Dr. Ir. Khairil A. Notodiputro, M.S.
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah SWT atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Maret 2008 ini ialah masalah perpindahan kelompok belalang, dengan judul Model Matematika Perpindahan Kelompok Belalang dengan Metode Gelombang Berjalan.
Ucapan terima kasih atas pengorbanan dan permohonan maaf atas kurangnya perhatian serta kasih sayang penulis sampaikan kepada istri tercinta
Anita Ellyana Hardiyati. Selanjutnya ucapan terima kasih dengan iringan doa penulis semoga Allah SWT membalas dengan kebaikan kepada:
1 Dr. Paian Sianturi dan Mochamad Tito Julianto, M.Kom. selaku pembimbing yang dengan penuh kesabaran Memberikan bimbingan dan motivasi kepada penulis.
2 Drs. Ali Kusnanto, M.Si. selaku penguji yang telah memberikan saran dan kritiknya.
3 Departemen Agama Republik Indonesia, yang telah memberikan biaya kepada penulis selama menempuh pendidikan program magister di Institut Pertanian Bogor.
4 Ibu, ibu mertua, kakak ipar, dan seluruh keluarga di Piyaman, Wonosari, GK. 5 Teman-teman mahasiswa S-2 Matematika Terapan IPB angkatan 2006. 6 Semua pihak yang telah membantu penulis, yang tidak bisa penulis sebutkan
satu persatu.
Akhirnya penulis menyadari bahwa tulisan ini masih jauh dari sempurna. Oleh karena itu sumbangsih kritik dan saran demi kemajuan tulisan selanjutnya sangat penulis dambakan.
Semoga karya ilmiah ini bermanfaat.
Bogor, Agustus 2008 Penulis,
RIWAYAT HIDUP
Penulis dilahirkan di Gunungkidul pada tanggal 10 Oktober 1978 dari ayah Suradi dan ibu Ngakisah. Penulis merupakan putra ketiga dari enam bersaudara.
Tahun 1997 penulis lulus dari SMU Negeri 2 Playen Gunungkidul dan pada tahun 1998 masuk Universitas Ahmad Dahlan Yogyakarta. Penulis memilih Jurusan Pendidikan Matematika pada Fakultas Keguruan dan Ilmu Pendidikan Program Sarjana dan selesai pada tahun 2004.
x
DAFTAR ISI
DAFTAR TABEL ... xii DAFTAR GAMBAR ... xiii DAFTAR LAMPIRAN ... xiv I PENDAHULUAN ... 1 1.1 Latar Belakang dan Perumusan Masalah ... 1 1.2 Tujuan Penelitian ... 2 II LANDASAN TEORI ... 3
2.1 Persamaan Keseimbangan ... 3 2.2 Konveksi ... 3 2.3 Matematika Difusi ... 4 2.4 Hukum Ficks ... 4 2.5 Persamaan Difusi Kelompok Belalang ... 4 2.6 Pola Penyebaran Belalang ... 5 2.7 Tarikan (Attraction) dan Tolakan (Repulsion) ... 5 2.8 Gelombang Berjalan ... 5
2.8.1 Persamaan Fisher ... 6 2.8.2 Penondimensionalan ... 7 2.8.3 Proses Pelinearan ... 7 2.8.4 Orbit ... 9 2.9 Momen Sebaran Belalang ... 9 2.10 Konvolusi Fungsi ... 10 2.11 Fungsi Kernel ... 11 III MODEL MATEMATIKA KEPADUANKELOMPOK BELALANG ... 12
3.1 Model I: Kepaduan Belalang Bergantung pada Konveksi Difusi dan
Kecepatan Belalang Terbang ... 14 3.1.1 Gelombang Berjalan (TravellingFront dan TravellingBand) . 15 3.1.2 Analisis Persamaan Gelombang Berjalan ... 16 3.2 Model II: Kecepatan Terbang Bergantung pada Kepadatan Lokal (Local
Density) ... 20 3.3 Model III: Kecepatan Terbang dan Gerakan Belalang di Tanah
Bergantung kepadatan lokal ... 21 3.4 Model IV: Perubahan Arah Terbang Bergantung Kepadatan (Density
Dependent) ... 23 3.5 Model V: Gerakan Aktif Belalang Terbang Bergantung Kepadatan
Individu ... 25
xi
IV METODE DAN PEMBAHASAN ... 28 4.1 Analisis Model V ... 28 4.2 Nilai-Nilai Parameter untuk Model V ... 32 4.3 Simulasi Model V ... 33 4.4 Hasil Simulasi Model V ... 34 V KESIMPULAN DAN SARAN ... 40
5.1 Kesimpulan ... 40 5.2 Saran ... 40 DAFTAR PUSTAKA ... 41 LAMPIRAN ... 42
xii
DAFTAR TABEL
Halaman
4.1 Nilai-nilai parameter model V ... 37
4.2 Klasifikasi model belalang berkelompok………... 38
xiii
DAFTAR GAMBAR
Halaman
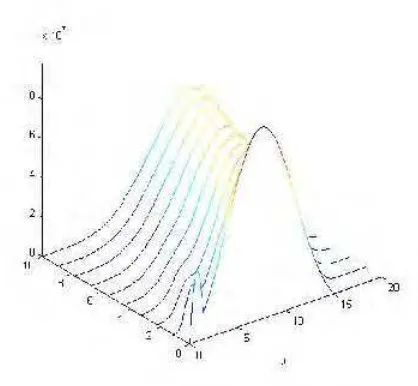
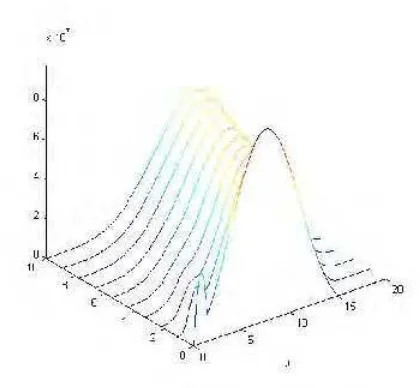
1 Struktur perputaran tipe kelompok belalang Schistocerca ... 13 2 Populasi kelompok belalang terbang dengan kepadatan lebih kecil
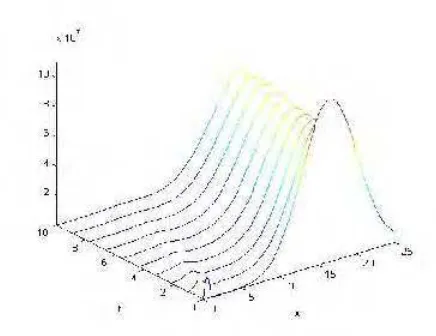
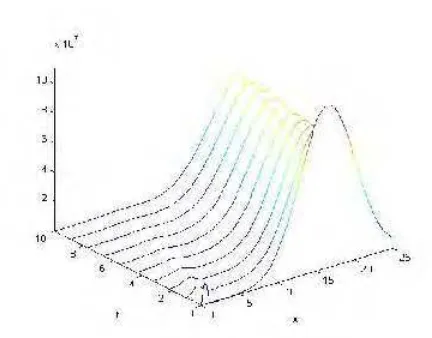
bergabung ke kelompok belalang yang mempunyai kepadatan lebih besar. 34 3 Populasi kelompok belalang terbang dengan kepadatan lebih kecil terpisah
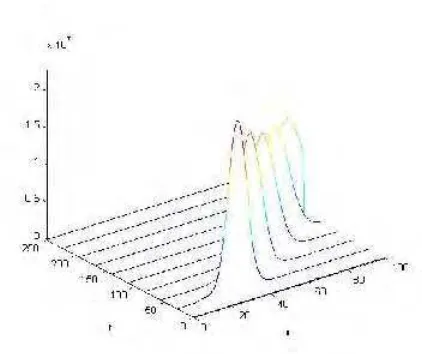
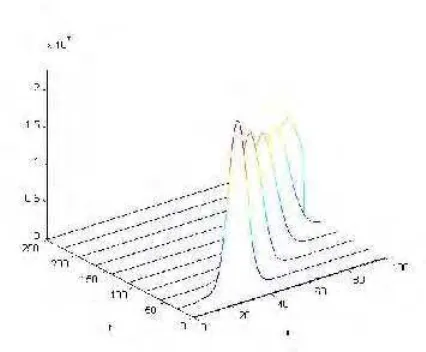
dari kelompok belalang yang mempunyai kepadatan lebih besar ... 35 4 Populasi kelompok belalang di tanah pada saat t = 100 ... 36 5 Populasi kelompok belalang di tanah pada saat t = 250 ... 36
xiv
DAFTAR LAMPIRAN
Halaman
1 Hubungan antara momen kedua dan ragam (persamaan (4.5)) ... 43 2 Pusat massa (persamaan (4.7)) ... 44 3 Ragam sebaran (persamaan (4.8)) ... 46 4 Nilai konvolusi (persamaan (4.8)) ... 48 5 Nilai ragam dari persamaan (4.19) ... 52 6 Prosedur simulasi model V ... 53 7 Prosedur penelitian ... 54 8 Program untuk simulasi model V ... 55
I PENDAHULUAN
1.1 Latar Belakang dan Perumusan Masalah
Penelusuran tentang fenomena belalang merupakan bahasan yang baik untuk dipelajari karena belalang dikenal suka berkelompok dan berpindah. Dalam kelompok, gerakan internal individu-individu tidak sepenuhnya dipahami. Ketika berpindah terjadi pertukaran tempat yang kontinu di antara belalang yang berada di tanah dan belalang yang terbang.
Beberapa model perilaku kelompok belalang disusun oleh Edelstein-Keshet
et al. (1998) dengan tujuan memahami bagaimana kepaduan kelompok dapat dipertahankan dalam populasi yang besar (diatas 109 individu) pada jarak yang jauh (di atas ribuan mil) dan dalam periode waktu yang lama (di atas satu minggu). Untuk merefleksikan hal tersebut, Edelstein-Keshet L (1988) menggunakan variasi spasial (ruang) dasar. Variasi spasial dasar tersebut membahas tentang pengaruh gerakan, sebaran, dan kekompakan kelompok.
Pada umumnya, beberapa populasi tersebar dengan tidak memperhatikan variasi lingkungan, kepadatan populasi dan gerakan dari belalang. Pada tingkat populasi yang besar (kelompok), hal tersebut mempengaruhi kekompakan kelompok dalam melakukan perpindahan. Beberapa populasi yang bergabung dalam kelompok mempunyai ukuran awal yang tidak sama. Dalam beberapa kasus tundaan atau periodik, dapat mempunyai ukuran awal yang sama. Ketika ukuran awalnya sama, setiap populasi bergerak menyerupai gerakan populasi yang besar seiring berjalannya waktu.
Pada penelitian ini, diasumsikan bahwa ukuran sebaran masing-masing populasi sama, populasi bergerak dengan laju jarak yang konstan, dan tidak ada ukuran panjang populasi yang lebih kecil dari jarak tempuh yang ditentukan. Hal ini menyebabkan laju perubahan ukuran populasi belalang analog dengan kecepatan atau laju perubahan lokasi belalang. Setelah dilakukan pentranslasian dari peubah spasial populasi ke ukuran peubah kelompok, dilakukan penghitungan akumulasi kelompok untuk menunjukkan besar rataan dan ragamnya (Edelstein-Keshet L 1988).
2 dengan dua tahap. Pertama, pembuatan argumen sederhana dalam satu dimensi. Kedua, menunjukkan beberapa fenomena dengan memasukkan konveksi, difusi, dan tarikan karena adanya gerakan dari individu. Agar lebih sederhana, turunan persamaan difusi menggunakan hukum Ficks dengan pendekatan yang didasarkan pada model gerakan acak sehingga model direpresentasikan ke dalam Persamaan Diferensial Parsial (PDP). Kemudian dilakukan peralihan koordinat pada model ini, yaitu koordinat PDP ke dalam koordinat Persamaan Diferensial Biasa (PDB) untuk mengurangi kesulitan pencarian solusi yang kompleks. Sehingga diperoleh dua tipe solusi, yaitu solusi di sekitar titik tetap dan solusi gelombang berjalan (travelling wave).
Pada dasarnya kelompok mengarah ke solusi travelling band (pulse). Beberapa model biologi banyak yang gagal untuk menghasilkan perilaku ideal kecuali dibuat asumsi-asumsi yang tidak biasa dan tidak realistis. Kegagalan ini disebabkan karena kesulitan menemukan model yang serupa dengan fenomena perpindahan dan kesulitan melakukan pendekatan kelompok untuk mengurangi masalah ini. Oleh karena itu, perlu pengkajian ulang penerapan difusi pada model dan penentuan solusi numerik agar diperoleh pendeskripsian yang lebih baik.
1.2 Tujuan Penelitian
Berdasarkan latar belakang dan perumusan masalah di atas, maka tujuan penelitian ini adalah:
II LANDASAN TEORI
2.1 Persamaan Keseimbangan
Edelstein-Keshet L (1988) menyatakan bahwa persamaan keseimbangan adalah dasar dalam sebaran spasial. Dideskripsikan bahwa F x t( , ) adalah kepadatan belalang pada posisi x dan waktu t, J adalah banyaknya belalang yang masuk ke dalam kelompok, x adalah panjang perubahan kepadatan, dan adalah banyaknya belalang masuk dan keluar dari kelompok (source-sink). Berdasarkan pendeskripsian ini, persamaan keseimbangan dapat dinyatakan sebagai
( , ) ( , ) ( , )
( , ).
F x t J x t J x x t
x t
t x (2.1)
Bila pada persamaan (2.1) diambil limit x 0, maka diperoleh persamaan keseimbangan satu dimensi berikut
( , ) ( , )
( , ).
=
F x t J x t
x t
t x (2.2)
Tanda min pada J x t( , )
x menyatakan bahwa rumus beda hingga dalam
persamaan (2.1) mempunyai tanda yang berlawanan dengan tanda pada definisi turunannya.
2.2 Konveksi
Menurut Edelstein-Keshet L (1988), gerakan belalang dalam kelompok dipengaruhi oleh kecepatan angin dan kepadatan kelompok. Jika w adalah kecepatan angin, maka banyaknya belalang yang masuk ke dalam kelompok adalah
,
J Fw (2.3)
Jika persamaan (2.3) disubstitusikan ke persamaan (2.2), maka diperoleh persamaan perpindahan (transport) satu dimensi sebagai berikut:
( , )
( , ) ( , ) .
F x t
F x t w x t
4 Kokasih PB (2006) menuliskan persamaan konveksi difusi penyebaran F
yang disebabkan oleh koefisien difusi (D) bergantung pada konveksi karena bergeraknya populasi dengan kecepatan (U), sebagai berikut:
2
2 .
F F F
D U
t x x (2.5)
2.3 Matematika Difusi
Difusi adalah fenomena dari populasi yang menyebar secara keseluruhan menurut gerakan acak tiap individu.
(Okubo A 1980)
2.4 Hukum Ficks
Menurut hukum Ficks, jumlah perpindahan populasi di posisi x dalam satu unit area terhadap satu unit waktu, yakni fluks J x t( , )
x adalah proporsi gradien
kepadatan populasi. Selanjutnya, didefinisikan bahwa J x t( , ) D F
x x , dengan
F adalah kepadatan populasi dan Dadalah laju penyebaran atau koefisien difusi. Tanda negatif menunjukkan bahwa difusi terjadi dari kepadatan tinggi menuju kepadatan rendah. Penggunaan hukum Ficks ada dalam persamaan difusi berikut:
( ( , ) / )
.
F J x t x F
D
t x x x (2.6)
(Okubo A 1980)
2.5 Persamaan Difusi Kelompok Belalang
Model matematika untuk sebaran spasial populasi dari belalang seperti pola kepadatan kelompok tidak dapat didasarkan pada gerakan acak sederhana. Dalam hal ini harus dimasukkan mekanisme pergerakan populasi belalang yang melawan aksi difusi. Jadi fluks populasi melalui bidang yang tegak lurus dengan sumbu
x yang berisi dua komponen, yakni acak dan tak acak.
Jika proses difusi diasumsikan sebagai komponen acak dan proses adveksi sebagai komponen tak acak, maka fluks dapat di formulasikan D F
5 proses difusi dan uF sebagai proses adveksi. Dalam hal ini, D menyatakan koefisien difusi dan u menyatakan kecepatan rata-rata individu yang melewati bidang.
Pergerakan acak populasi terjadi dari kepadatan tinggi ke kepadatan rendah, sedangkan pergerakan tak acak terjadi dalam arah kecepatan rata-rata. Secara umum D dan u mempengaruhi kekompakan kelompok. Hal ini tergantung pada kepadatan populasi. Total fluks dapat dituliskan
.
F
J uS D
x
(2.7)
(Okubo A 1980)
2.6 Pola Penyebaran Belalang
Individu dalam populasi ada yang keluar masuk dalam kelompok ketika kelompok tersebut bergerak. Adanya individu yang keluar masuk dalam kelompok membentuk suatu pola sebaran tertentu. Dengan mengacu pada hukum Ficks tentang perbedaan kedifusian dan ragam dari dua populasi, Okubo A (1980) menyatakan bentuk pola penyebaran tiap populasi sebagai berikut:
2 1 2exp[ ( / ) ],
A
l x a
a (2.8)
2 2 2exp[ ( / ) ],
b
B
l x b (2.9)
dalam hal ini, b a.
2.7 Tarikan (Attraction) dan Tolakan (Repulsion)
Dalam persamaan (2.8) dan (2.9), simbol l1 menyatakan tarikan dan l2
menyatakan tolakan. Bentuk keseimbangan akibat adanya dua sumber (tarikan dan tolakan) yang berlawanan arah diberikan Okubo A (1980) sebagai berikut:
1 2,
L l l (2.10)
2.8 Gelombang Berjalan (GB)
6 (1988) menyatakan bahwa f x t( , ) disebut GB jika fungsi tersebut mempertahankan bentuk gelombang pada laju konstan c ketika gelombang bergerak ke kanan. Pengamat bergerak dengan kecepatan sama dan searah dengan gerakan gelombang sehingga terlihat bentuk gelombang yang tidak berubah. Hubungan antara fungsi gelombang yang bergerak ke kanan f x t( , ) dengan fungsi pengamat yang bergerak F z( ) adalah:
( ) ( , ),
F z f x t dengan syarat z x ct, (2.11)
( )
F z adalah fungsi dari peubah tunggal, yaitu jarak sepanjang gelombang dari beberapa titik tetap yang dipilih menuju z 0.
Dengan aturan rantai diferensiasi, persamaan (2.11) dapat diubah ke dalam bentuk berikut:
,
.
F F z F
x z x z
F F z F
c
t z t z
(2.12)
Sehingga diperoleh bentuk Persamaan Diferensial Biasa (PDB) dari suatu sistem PDP, yang dapat diketahui eksistensi dan sifat yang dimiliki solusi GB.
2.8.1 Persamaan Fisher
Mengenai eksistensi dan sifat yang dimiliki solusi GB, Edelstein-Keshet L (1988) mengutip Fisher (1937) mengamati gerakan acak dari populasi individu pada suatu daerah tertentu. Ia memisalkan F sebagai proporsi populasi individu yang bergerak acak, S 1 F sebagai proporsi populasi individu pada saat awal,
sebagai koefisien konstan proporsi populasi, dan D sebagai koefisien difusi. Laju perubahan F pada suatu lokasi tertentu dapat dinyatakan ke dalam bentuk persamaan berikut:
2
2 1 .
F F
D F F
t x (2.13)
7 peralihan koordinat z x ct dan perubahan bentuk persamaan menjadi PDB, maka solusi GB dapat dicari dengan lebih mudah. Pada penelitian ini, diasumsikan bahwa domain gelombang berada pada daerah yang tak terbatas. Gelombang penyebaran individu dalam kelompok yang dideskripsikan pada persamaan (2.13) diharapkan sesuai realitas biologis. Untuk menemukan solusi sistem PDP berdimensi kecil dapat digunakan analisis bidang fase.
2.8.2 Penondimensionalan
Dalam suatu sistem PDP, bentuk peubah-peubah ada yang berdimensi tak sama. Oleh karena itu, peubah-peubah tersebut perlu diekspresikan sama agar solusi mudah diperoleh.
Menurut Edelstein-Keshet L (1988), pengekspresian peubah dapat dilakukan dengan cara berikut:
2.8.3 Proses Pelinearan
Untuk menentukan solusi tertutup steady state (solusi yang didekati oleh pelinearan) dari sistem PDP, Edelstein-Keshet L. (1988) memisalkan PDB sebagai berikut:
( , ),
dX
F X Y
dt (2.14)
( , ),
dY
G X Y
dt (2.15)
di mana F dan G adalah fungsi tak linear. Diasumsikan bahwa X dan Y
adalah solusi steady state, yang memenuhi ( , ) ( , ) 0.
F X Y G X Y (2.16)
Solusi tertutup steady state yang sering disebut gangguan (pertubation) memenuhi
( ) ( ),
X t X x t (2.17)
( ) ( ).
Y t Y y t (2.18)
Kuantitas
ukuran = Skalar pengali
8 Setelah disubtitusi ke persamaan (2.14) dan (2.15), diperoleh
( ) ( , ),
d
X x F X x Y y
dt (2.19)
( ) ( , ).
d
Y y G X x Y y
dt (2.20)
Sisi kiri diperluas dan dibentuk turunannya oleh definisi dX dt 0 dan 0.
dY dt Sisi kanan diperluas oleh F dan G dalam deret Taylor pada titik (X Y, ). Sehingga diperoleh
2 2
( , ) ( , ) ( , )
bentuk orde , , , dan yang lain,
x y
dx
F X Y F X Y x F X Y y
dt
x y xy
(2.21)
2 2
( , ) ( , ) ( , )
bentuk orde , , , dan yang lain,
x y
dy
G X Y G X Y x G X Y y
dt
x y xy
(2.22)
di mana F X Yx( , ) adalah F x yang dievaluasi pada (X Y, ). Untuk , , ,
y x y
F G G dievaluasi dengan cara yang sama. Oleh definisi F X Y( , ) G X Y( , ) 0 diperoleh
11 12 ,
dx
a x a y
dt (2.23)
21 22 ,
dy
a x a y
dt (2.24)
dalam bentuk matriks
11 12
21 22 ( , )
.
x y
x y X Y
F F
a a
A a a G G (2.25)
9
2.8.4 Orbit
Ketika suatu sistem PDP berdimensi kecil, maka solusi sistem tersebut dapat dicari dengan menggunakan pendekatan analisis bidang fase. Pendekatan analisis bidang fase merupakan teknik untuk mencari solusi dari sistem PDB yang luas cakupan solusinya. Oleh karena itu, untuk mempermudah mencari solusi dari sistem tersebut perlu dilakukan pembatasan pada GB yang diberikan. Batas gelombang ini merupakan batas trayektori untuk sistem persamaan pada ruang fase yang berdimensi tinggi. Edelstein-Keshet L (1988) menyatakan bahwa orbit trayektori heteroklinik merupakan cerminan batas gelombang yang menghubungkan dua titik tetap. B atas trayektori yang lain adalah:
i Orbit homoklinik (trayektori yang meninggalkan sebuah titik sadel ketika tak stabil dan kembali ke titik sadel ketika stabil) akan menghasilkan gelombang asimtotik yang mendekati nilai z .
ii Suatu cycle atau orbit periodik yang mencerminkan osilasi penyebaran melimpah pada ruang.
2.9 Momen Sebaran Belalang
Dougherty RD (1990) mendefinisikan nilai awal momen sebaran sebagai berikut:
i Untuk beberapa bilangan bulat tak negatif k, maka nilai awal momen dari peubah acak X adalah:
' k .
k E X (2.26)
ii Jika X kontinu, maka
' k k / .
k E X x f x x dx (2.27)
iii Jika '
0 1, dengan jumlah keseluruhan peluang adalah satu dan '
1 E X x, maka nilai awal momen kedua adalah:
' 2 2
10 Edelstein-Keshet et al. (1998), menuliskan hal tersebut ke dalam bentuk berikut ini:
i F ti( ) x F x t dxi ( , ) , (2.29)
ii V t( ) 1 x X 2F x t dx( , ) ,
N (2.30)
dalam hal ini, F merupakan ukuran sebaran. V adalah ragam, N adalah jumlah total individu dan X adalah pusat massa (kepadatan tertinggi) kelompok.
2.10 Konvolusi Fungsi
Menurut Riley et al. (2006), selain dipengaruhi penyebaran populasi, laju kepadatan populasi juga dipengaruhi kecepatan kelompok. Kecepatan kelompok ini merupakan sebaran yang diamati, yakni dengan memisalkan F x( ') sebagai fungsi yang akan diukur, K y( )sebagai fungsi resolusi yang digunakan sebagai alat ukur, dan v x( ) hasil penghitungan sebaran yang diamati. Fungsi resolusi tidak memberikan nilai keluaran yang benar, maka dimungkinkan bahwa nilai keluaran y 0 akan diganti oleh nilai di antara y dan y dy dan dinyatakan dengan K y dy( ) . Simbol x', , x dan y adalah peubah berukuran sama (panjang atau sudut), tetapi mempunyai perbedaan peran.
Diasumsikan bahwa F x dx( ') ' bergerak menuju ke interval dz, yaitu ke
( ') ,
K x x dx karena adanya resolusi x x '. Kombinasi yang mungkin ada adalah bahwa interval dx 'akan meningkat dalam interval dx, yaitu menuju
( ') ( ') '.
K x x F x dx Penambahan kontribusi dari semua nilai x' mengarah ke dalam range x menuju x dx, sehingga diperoleh bentuk
( ) ( ') ( ') '.
v x K x x F x dx (2.31)
Bentuk ini disebut konvolusi dari fungsi F dan ,K yang sering ditulis dalam bentuk
* .
v K F (2.32)
11
2.11 Fungsi Kernel
Dalam penelitian ini, untuk fungsi resolusi menggunakan bentuk kernel ganjil karena adanya trayektori homoklinik. Edelstein-Keshet et al. (1998) memberikan definisi fungsi resolusi dalam konvolusi dengan bentuk kernel ganjil sebagai berikut:
2 2
2exp[ ( / ) ] 2exp[ ( / ) ] ,
A B
K x x a x b
a b (2.33)
dalam hal ini, A adalah repulsion (tolakan), B adalah attraction (tarikan), a
III MODEL MATEMATIKA KEPADUAN
KELOMPOK BELALANG
Berdasarkan orbit trayektori yang dimiliki, Gelombang Berjalan (GB) di bagi menjadi 2, yaitu Travelling Front (TF) yang dideskripsikan sebagai trayektori heteroklinik dan Travelling Pulse (TP) digunakan sebagai pengganti dari Travelling Band (TB) yang dideskripsikan oleh trayektori homoklinik pada saat awal. Dalam penelitian digunakan trayektori homoklinik sebagai batasnya.
Untuk menghubungkan model penyebaran populasi secara geografis digunakan gelombang invasi. Edelstein-Keshet et al. (1998) mengutip Skellam JG (1951) mendeskripsikan model ini berdasarkan hasil pengamatan Fisher (1937), yakni mendeskripsikan kejadian beberapa generasi dengan laju kecepatan sebaran spasial yang merupakan laju pertumbuhan yang tak nol. Ketika berpindah secara acak, terjadi peningkatan secara lokal yang menyebabkan kepadatan populasi yang besar pada daerah tengahnya sehingga model mengarah ke solusi TF, yakni bagian belakang gelombang mewakili ruang yang pernah dilewati, sedangkan bagian depan gelombang adalah daerah yang belum pernah dilewati. Jumlah organisme dalam populasi bertambah seperti bagian depan yang menyebar dalam daerah baru.
Bagaimana menghubungkan gerakan individu dengan gerakan kelompok sebagai satu keutuhan adalah masalah mendasar yang perlu diamati. Menurut Edelstein-Keshet et al. (1998), model pada skala kecil dapat menghubungkan gerakan organisme ke beberapa pengaruh eksternal seperti nutrisi atau makanan. Adanya gradien eksternal (seperti nutrisi, tarikan, atau pengaruh lain) membuat ketaksimetrian yang dapat memberi pengaruh penting. Hal ini tidak kelihatan karena belalang dapat berpindah secara berkelompok tanpa makanan atau gradien eksternal. Sedangkan dalam skala yang besar, skala waktu lebih pendek daripada waktu reproduksi organisme. Oleh sebab itu, tipe solusi diperoleh dengan membuat perkiraan, yaitu dengan membuat jumlah organisme konstan. Artinya, agar TB terlihat, maka perlu menentukan batasan perilaku yang mungkin.
13
Arah Angin
Persinggahan Zona Interior
Zona Keberangkatan (Settlement)
(Take-off Zone)
tidak sosial dan menjauh dari yang lain. Tetapi, ketika perubahan untuk suka berkawan muncul, individu menjadi lebih kuat sosialnya dan bergabung dengan kelompok yang besar.
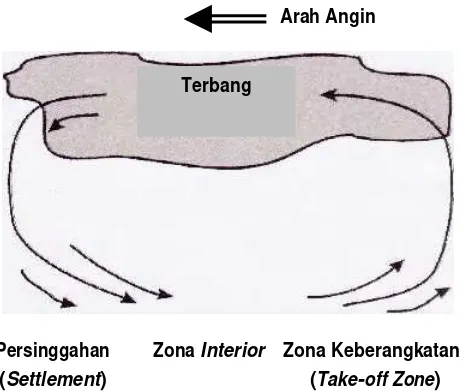
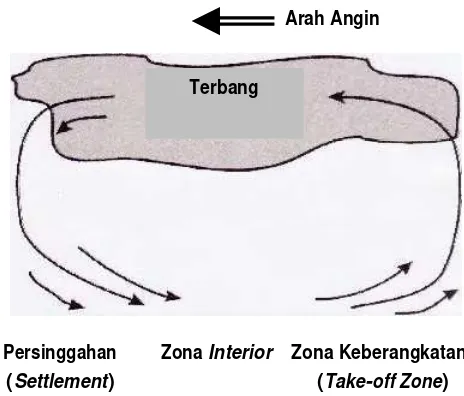
[image:39.612.222.452.301.497.2]Edelstein-Keshet et al. (1998), gerakan kelompok terarah dengan kecepatan konstan dengan skala waktu yang lebih lama dari skala waktu gerakan individu. Pengamatan ini direfleksikan dalam asumsi pendekatan model, yakni pendekatan dinamis kelompok sebagai proses satu dimensi. Individu berada dalam salah satu dari dua kategori, yaitu bergerak dan tidak bergerak. Edelstein-Keshet et al. (1998) mengutip Albrecht FO (1967) menyatakan bahwa belalang secara berkelompok mengalami perpindahan terus menerus dengan struktur perputaran yang dilukiskan dalam skema gambar 1.
Gambar 1 Struktur perputaran tipe kelompok belalang Schistocerca. (Edelstein-Keshet et al. 1998)
Sedangkan struktur kelompok mempertahankan bentuk yang tetap dengan kecepatan konstan. Individu dalam kelompok sebenarnya berputar melalui urutan perilaku sebagai berikut:
(i) terbang menuju ke bawah secara berkelompok (biasanya turun bersamaan), (ii) mendarat di tanah, kebanyakan ketika mereka mencapai bagian depan
kelompok,
14 (iii) makan dan beristirahat sampai menyusul bagian tepi kelompok, dan
(iv) berangkat terbang dan naik menuju ketinggian, sesudah itu berputar kembali ke awal lagi.
Belalang-belalang yang terbang di atas memicu pasangan mereka yang berada di tanah sehingga menyebabkan belalang di tanah terbang secara besar-besaran. Kelompok belalang ini diperkirakan menghabiskan waktu untuk terbang pada pendekatan 20 s.d 40 %.
3.1 Model I: Kepaduan Belalang Bergantung pada Konveksi Difusi dan
Kecepatan Belalang Terbang
Pendekatan pertama adalah menunjukkan belalang di tanah bergerak tak leluasa dibandingkan pasangan terbang mereka. Sehingga dapat dibangun sebuah model sebagai berikut:
( , ) ( , ) ,
S
R S F S G S F F
t (3.1)
2
2 ( , ) ( , ) .
F F F
D U R S F S G S F F
t x x (3.2)
Dalam hal ini, ( , )
F x t = populasi belalang yang terbang pada , ,x t
( , )
S x t = populasi belalang yang tidak terbang (standing) pada , ,x t
( , )
R S F = proporsi belalang berangkat (take-off), ( , )
G S F = proporsi belalang mendarat (landing),
D = laju gerakan acak belalang saat di udara,
U = kecepatan terbang (kecepatan angin + kecepatan terbang aktif) belalang. Laju gerakan acak dan kecepatan terbang belalang yang dipengaruhi kecepatan angin, dan kecepatan terbang aktif diasumsikan konstan. Sesuai pembahasan sebelumnya, digunakan solusi TP dengan jumlah total individu yang terbatas dengan syarat fungsi kepadatan F dan S terbatas dan positif di mana-mana. Untuk TP, nilai fungsi kepadatan F dan S menuju nol ketika peubah x
menjauh ke depan dari kelompok dan menjauh ke belakang dari kelompok
( , 0 untuk )
15
3.1.1 Gelombang Berjalan (TravellingFront dan TravellingBand)
Sistem persamaan model I ditransformasikan ke dalam koordinat GB ,
z x ct dengan c adalah kecepatan gelombang yang konstan, sehingga diperoleh
( , ) ( , ) ,
S
c R S F S G S F F
z (3.3)
2
2 ( , ) ( , ) .
F F F
c D U R S F S G S F F
z z z (3.4)
. Kedimensionalan sistem persamaan ini dapat dikurangi dengan cara menambahkan kedua persamaan, mengintegralkan dari ke z, dan mensubstitusikan ke dalam sistem persamaan sehingga diperoleh
( , ) ( , ) ,
S
c R S F S G S F F
z (3.5)
( ) konstanta.
F
D cS U c F
z (3.6)
Hasil ini dapat dipelajari dengan metode bidang fase. Tetapi solusi secara rinci (nilai pada konstanta acak) akan bergantung pada syarat bantu. Syarat bantu dalam kasus TF dan TB saling berlawanan. Kemungkinan himpunan yang relevan dengan syarat bantu untuk TF dan TB adalah:
(i) lim , 0,
z F S
(ii) lim , 0,
z F S
(iii) F S, 0 untuk semua .z
Arti syarat-syarat di atas adalah: (i) tidak ada individu yang jauh di depan gelombang, (ii) tidak ada individu yang jauh di belakang gelombang, dan (iii) kepadatannya tak negatif.
16 Pada saat awal (F S 0) mempunyai satu titik sadel atau satu titik stabil, yaitu satu nilai eigen real negatif ( ) untuk menerangkan sifat pertama di atas.
Pada ruang state, vektor eigen yang berkorespondensi dengan berada di kuadran pertama.
Pada kuadran positif, paling sedikit mempunyai satu keseimbangan, yaitu satu sadel, titik tak stabil, atau spiral tak stabil. Keseimbangan ini merepresentasikan kepadatan F dan S yang jauh di belakang gelombang. Untuk solusi TB memenuhi syarat (i), (ii), dan (iii), direpresentasikan oleh trayektori homoklinik yang berada pada kuadran positif di bidang SF. Oleh karena itu, solusinya memenuhi beberapa kriteria berikut:
Pada saat awal trayektorinya dapat keluar dan masuk ke titik tetap, artinya harus ada satu titik sadel, yaitu satu nilai eigen positif dan satu nilai eigen negatif.
Pada ruang state, vektor eigen tidak dapat diarahkan ke kuadran II dan IV karena solusi dibatasi pada daerah tak negatif.
Nullcline F dan S melewati kuadran I karena mempunyai maksima di kuadran ini.
Selanjutnya adalah memeriksa syarat bantu yang dipenuhi. Jika memenuhi solusi TF, maka solusi TB ditiadakan. Artinya jika solusi pulse ada pada solusi TF, maka dimana-mana tidak tak negatif dan tidak akan ada representasi kelompok secara biologi.
3.1.2 Analisis Persamaan Gelombang Berjalan Diasumsikan bahwa
lim 0,
z F zlim 0.
F
z (3.7)
17
( , ) ( , ) ,
S
c R S F S G S F F
z (3.8)
( ) .
F
D cS U c F
z (3.9)
Selanjutnya adalah menguji perilaku dari sistem persamaan ini dengan tujuan menunjukkan trayektori homoklinik pada saat awal dapat terjadi di bawah beberapa asumsi yang sesuai. Sistem persamaan memenuhi nullcline sebagai berikut:
0 R S F S( , ) G S F F( , ) , (3.10)
0 cS (U c F) . (3.11)
Sehingga nullcline F memenuhi (U c F) cS
(U c)
F S
c
( )
0.
U c
F S
c (3.12)
Karena nullcline ini melewati kuadran I, maka hal ini mengimplikasikan bahwa gradien bernilai positif (U c) 0.
c Dari gradien positif ini diperoleh
0.
U Dengan asumsi bahwa arah angin menuju ke ke sumbu x positif dan 0,
U diperoleh batasan berikut:
0 c U. (3.13)
Sehingga dapat disimpulkan bahwa jika GB dari beberapa tipe ada, maka kecepatan kelompok lebih pelan dari pada kecepatan angin. Pernyataan ini mengikuti fakta bahwa belalang menghabiskan waktu di antara tanah dan langit secara berkelompok dengan gerakan ke depan lebih pelan dari pada ketika di bawa ke depan oleh angin.
Persamaan diferensial yang ada dapat diubah ke dalam formulasi tanpa dimensi berikut:
( , ) ( , ) ,
18 .
f s f (3.15)
dengan, , s S
(3.16) , U c f F c (3.17) , ( ) D
U c z (3.18)
( , ) ( ), ( ) ,
( )
D
R s f R S s F f
c U c (3.19)
2
( , ) ( ), ( ) .
( )
D
G s f G S s F f
c U c (3.20)
Pelinearan sistem dengan titik tetap f s 0 adalah:
0 0 .
1 1
s R G s
f
f (3.21)
Parameter R0 R(0, 0) 0 dan G0 G(0, 0) 0 merepresentasikan bentuk interaksi pada titik tetap (0, 0) yang ekuivalen dengan laju pendaratan dan laju berangkat untuk terbang ketika kepadatan belalang rendah. Nilai eigen dari sistem linear ini adalah:
1 / 2 2
0 0 0 0
1
1 (1 ) 4
2 R R R G (3.22)
Karena R0 positif, maka 1 R0 juga positif. Untuk R0 G0 0 tidak konsisten dengan GB pada beberapa bentuk karena nilai eigennya positif dan pada saat awal tak stabil. Keadaan ini tidak diakui pendekatannya pada trayektori dari beberapa titik tetap lain sehingga tidak sesuai untuk TF dan TB. Oleh karena itu, diasumsikan syarat perlu untuk solusi GB sebagai berikut:
0 0.
R G
19
0
0 0
.
R U
c
G R (3.24)
Artinya bahwa kuantitas pada sisi kiri menyatakan kecepatan rata-rata belalang pada daerah berkepadatan rendah. Rasio R0/ G0 R0 adalah jumlah relatif belalang yang terbang dengan kecepatan U. Jika ketaksamaan ini tidak dipenuhi, maka belalang yang berada jauh di depan kelompok akan terbang lebih cepat dari pada yang berada dalam kelompok. Ini mengimplikasikan bahwa gelombang pada beberapa tipe (front atau band) akan mempunyai kecepatan gelombang minimum. Sedangkan kecepatan gelombang maksimum di c U.
Ketika syarat (3.24) dipenuhi, diperoleh R0 G0 0 dan satu titik sadel pada saat awal (kemungkinan ketika dibangkitkan). Keberadaan satu titik sadel pada saat awal adalah salah satu syarat untuk terjadinya solusi TB dan konsisten dengan solusi TF. Tetapi, terlihat bahwa kriteria lain untuk solusi band tidak dapat dipenuhi.
Untuk melihat ada tidaknya solusi TB, maka vektor eigen pada saat awal harus diarahkan ke dalam kuadran I dan III. Vektor eigen yang diperoleh
1 ,
1
(3.25)
Sehingga untuk titik sadelnya memenuhi nilai eigen 1 R0 > 1 dan < 0. Dalam kasus tak dibangkitkan, yaitu jika R0 G0, maka vektor eigen yang stabil berkorespondensi dengan titik di kuadran I dan III sedangkan vektor eigen tak stabil berkorespondensi dengan titik di kuadran II dan IV. Pada keadaan ini, beberapa trayektori homoklinik pada saat awal merupakan titik tetap pada bidang fase F atau S yang bernilai negatif. Artinya beberapa solusi bukan biologi harus dibuang ketika menunjukkan kepadatan populasi.
20 seperti pembahasan sebelumnya. Jika R0 G0 0, maka analisis tidak berperan memunculkan trayektori homoklinik dan pengamatan dapat diteruskan.
Hasil di atas menunjukkan keberadaan solusi TB tetapi kemungkinan dalam kasus pembangkitan, sehingga dapat disimpulkan bahwa
Interaksi lokal belalang yang terbang dan tidak terbang, konveksi difusi sederhana pada belalang yang terbang tidak dapat menjelaskan kepaduan kelompok yang berpindah pada TB-nya.
Model I berhenti, karena analisis tidak mendukung.
Kegagalan model I, kemungkinan karena difusi dan kecepatan yang konstan terlalu umum sehingga mengarahkan untuk memunculkan model II.
3.2 Model II: Kecepatan Terbang Bergantung pada Kepadatan Lokal
(Local Density)
Belalang merespon variasi kepadatan kelompok lokal dengan cara mengubah laju acak atau arah gerakan. Perubahan kecepatan terbang menentukan kepaduan kelompok. Pada model ini digunakan bentuk kumpulan persamaan pada saat awal. Bentuk ini melukiskan tendensi belalang untuk berkelompok dan tendensi untuk menyesuaikan gerakan dalam respon untuk bergabung dan berpencar pada kelompok. Bentuk gerakan penerbang menjadi fungsi kepadatan. Sistem secara umum mempunyai bentuk sebagai berikut:
( , ) ( , ) ,
S
R S F S G S F F
t (3.26)
.
( , ) ( , ) ( , )
( , ) ( , )
F F S
D E F U F
t x x x
R S G F
S F S F S F
S F S F
(3.27)
( , )
21 Dalam sistem koordinat GB, setelah penambahan dua persamaan dan pengintegralan seperti langkah sebelumnya, diperoleh sistem sebagai berikut:
( , ) ( , ) ,
S
c R S F S G S F F
z (3.28)
( ) ( , ) F ( , ) S ( , ) .
c F S D S F E S F F U S F F
z z (3.29)
Pendekatan vektor eigen dilakukan untuk menemukan pusat pulse pada perilaku awal dan titik sadel pada (0, 0), sehingga trayektori homoklinik dapat dibangun. Ketika pulse ditemukan, pelinearan sistem persamaan mengarah ke himpunan eksak yang sama pada PDB dengan laju difusi D(0, 0) dan kecepatan
(0, 0).
u U Fakta ini menunjukkan bahwa U dan D adalah fungsi yang apabila dibandingkan dengan konstanta tidak akan relevan. Perilaku fungsi ini (pada kepadatan rendah) merupakan batas (contohnya pada gelombang balik atau gelombang ke depan) masuk ke dalam analisis. Bentuk model yang baru ini tidak menolong untuk menghilangkan masalah pada saat awal karena hasilnya identik dengan pendefinisian ulang konstanta.
Kesimpulan yang dapat di buat:
ModeI perubahan belalang yang terbang maupun yang tidak terbang secara sederhana, taxis (gaya pergerakan belalang dalam merespon rangsangan), kecepatan tak linear, dan difusi tak linear pada belalang yang terbang tidak mampu menjelaskan kepaduan kelompok.
Analisis tidak mendukung model II.
3.3 Model III: Kecepatan Terbang dan Gerakan Belalang di Tanah
Bergantung kepadatan lokal
22 pada laju yang lebih pelan. Gerakan mengarah ke koordinat GB dan menuju sistem dimensi tingkat tinggi sehingga solusi TP dapat dielakkan.
Persamaan-persamaan yang dikaji adalah:
( , ) ( , ) ( , ) ( , ) ,
S S F
A S F B S F S R S F S G S F F
t x x x (3.30)
.
( , ) ( , ) ( , )
( , ) ( , )
F F S
D E F U F
t x x x
R S G F
S F S F S F
S F S F
(3.31)
Dalam hal ini, A S F( , ) adalah motility (koefisien difusi) dengan adveksi (kecepatan rata-rata dalam berpindah) belalang yang ada di zona interior kecil atau nol.
Analisis bergantung fakta bahwa nilai eigen tanpa dimensi pada sistem ini adalah persamaan akar kubik
3 2
0,
R G R G (3.32)
dalam hal ini, parameter (tanpa dimensi) adalah 2
2
/( ), / , /( ) , /
c U c A D R RD U c G GD U c dan semua fungsi
dievaluasi pada T F S, , 0, 0, 0 .
Dari pengamatan bentuk vektor eigen dan nilai eigen pada saat awal diperoleh sekumpulan syarat yang mendeskripsikan bahwa 1 sebagai nilai eigen yang tak stabil, dan 2 sebagai nilai eigen yang stabil, dengan batas
1 2
0 1,
/ 0.
Nilai eigen harus tak stabil dan kurang dari 1 atau stabil dan lebih dari 2. Dengan penyusunan ulang secara sederhana, dapat diperoleh syarat sebagai berikut:
2 1
3 1
/ 0 1
.
23 Secara ringkas, syarat perlu untuk TP adalah persamaan (3.32) yang mempunyai tiga solusi real dan solusi ini memenuhi (3.33).
Untuk 0, sistem terkurangi menjadi sistem dua dimensi. Untuk kecil, sistem merupakan gangguan tunggal dari sistem dua dimensi yang di analisis sebelumnya (untuk belalang yang tidak terbang di tanah). Dua nilai eigen tertutup menuju nilai eigen sistem dua dimensi dan nilai eigen ketiga adalah:
/ R / ( ). (3.34)
Karena / , maka dua nilai eigen harus memenuhi syarat persamaan (3.33). Tetapi, analisis gangguan sederhana dari persamaan (3.32) menunjukkan bahwa syarat ini tidak dijumpai jika 1. Ketika nilai eigen positif ( )1 dan lebih besar dari 1 untuk memenuhi kecilnya , maka TB tidak akan terjadi sehingga dibangunlah model IV.
3.4 Model IV: Perubahan Arah Terbang Bergantung Kepadatan
(DensityDependent)
Edelstein-Keshet et al. (1998) mengutip Waloff Z (1962) menyatakan bahwa kelompok belalang memelihara kepaduan karena individu atau kelompok kecil yang keluar mendadak dari kelompok mengubah orientasi mereka dan kembali menuju kelompok. Pernyataan ini didasarkan pendekatan pada ide bahwa belalang secara kontinu bergabung kembali dan terbang menuju kelompok, atau berputar pada respon kepadatan lokal. Untuk menjelajahi ide ini, diasumsikan bahwa interaksi di tanah diabaikan. Sehingga yang diamati kepada hal yang lebih perlu, yaitu difokuskan pada belalang yang terbang itu sendiri. Belalang yang terbang di bagi dua, yaitu belalang dengan gerakan ke depan A x t( , ) dan belalang dengan gerakan balik B x t( , ) . Diasumsikan bahwa kecepatan terbang ( )v sama. Laju perputaran rab dan rba juga diasumsikan bergantung pada kepadatan lokal. Persamaan yang dikaji adalah:
( ) ab ba ,
A A
v w r A r B
24
( ) ba ab .
B B
v w r B r A
t x (3.36)
Dalam hal ini, rab rab( ,A B), rba rba( ,A B) adalah fungsi kepadatan dan kecepatan angin ( )w diasumsikan konstan.
Dengan penerapan sistem peralihan koordinat z x ct pada persamaan (3.35) dan (3.36) diperoleh
( ) ,
ab ba
dA
v w c r A r B
dz (3.37)
( ) .
ab ba
dB
v w c r A r B
dz (3.38)
Kurangkan kedua persamaan di atas untuk mengeliminasi bentuk kinetik, sehingga diperoleh
(v w c)dA (v w c)dB 0.
dz dz (3.39)
Integralkan dan gunakan syarat batas (yaitu tidak ada individu jauh ke depan atau jauh di belakang gelombang) sehingga menghasilkan
(v w c A) (v w c B) 0, (3.40)
yang mengimplikasikan bahwa kepadatan gerakan individu ke depan dan gerakan balik adalah proposional dimana-mana.
Kemudian dieliminasi satu peubah (semisal B ), oleh substitusi berikut:
( )
,
( )
v w c
B A
v w c (3.41)
dalam bentuk pendekatan persamaan untuk A. Ini berarti bahwa sistem persamaan terkurangi menjadi persamaan tunggal, yang mempunyai bentuk dasar
( ),
dA
A f A
dz (3.42)
dalam hal ini, f A( ) adalah ungkapan dengan laju perputaran awal rab dan rba
25 (yakni titik tetap dari Af A( )) adalah dapat ada, tetapi tidak bermula dan berakhir pada A 0. Artinya TF dapat terjadi, tetapi bukan pulse. Sehingga dapat disimpulkan bahwa:
bergabung kembali dan terbang bersama kelompok memungkinkan untuk mempertahankan kelompok maju ke depan, tetapi bukan TB karena berlawanan dengan pernyataan Waloff. Hal ini tidak akan mengarah ke kepaduan kelompok, karena mekanisme untuk kembali ke kelompok belalang yang tidak terbang tidak dijaga.
analisis tidak mendukung model IV.
Karena TB tidak terjadi, maka dibangunlah model V.
3.5 Model V: Gerakan Aktif Belalang Terbang Bergantung Kepadatan
Individu
Interaksi untuk memelihara kepaduan kelompok tidak hanya lokal, termasuk belalang yang menggunakan rangsangan yang nampak untuk bergabung dan merespon kepadatan kelompok pada jarak yang jauh. Dalam hal ini, belalang dapat menyesuaikan kecepatan untuk tetap bergabung dengan kelompok sehingga terjaga kepaduan kelompok.
Model ini didasarkan pada asumsi realistis biologi dengan kajian matematis yang mengarah ke tipe perbedaan dasar model yang lebih menantang analisisnya. Dalam model ini, kecepatan individu diasumsikan untuk mengatur besarnya kepadatan rata-rata kelompok.
Persamaan untuk gerakan kelompok dalam model ini adalah: 2
2 ( ) ,
F F
D w v F
t x x (3.43)
dalam hal ini, ada dua kecepatan yang dilapiskan, yaitu kecepatan angin dan gerakan aktif kelompok yang bergantung kepadatan individu. Gerakan aktif ini mengarah ke bentuk konvolusi berikut:
* ( ') ( ') '.
26 Pengaruh untuk keluar dari kelompok dan bergabung ke kelompok dapat digantikan dalam bentuk kernel berikut:
2 2
2exp[ ( / ) ] 2exp[ ( / ) ] ,
A B
K x x a x b
a b (3.45)
dalam hal ini, besarnya A adalah kepadatan belalang yang keluar kelompok dan B adalah kepadatan belalang yang kembali ke kelompok sedangkan a adalah jarak yang ditempuh ketika belalang keluar dari kelompok dan b adalah jarak yang ditempuh ketika belalang kembali ke kelompok. Kesimetrian antara gelombang yang bergerak ke depan dan gelombang balik tidak mempunyai makna
* 0 untuk konstanta
K F F . Artinya bahwa belalang yang keluar dari kelompok sama jumlahnya dengan yang bergabung ke kelompok, sehingga interaksi tidak mempunyai pengaruh.
Menurut Edelstein-Keshet et al. (1998), model serupa tetapi dengan w 0 dan dengan interpretasi berbeda telah dianalisis oleh Mogilner et al. (1996), yakni dengan memperhatikan perilaku puncak sebagai solusi ketika difusi konstan atau bernilai kecil. Ketika difusi kecil (D ), hasil mengarah ke peralihan koordinat
z x ct dengan menggunakan ekspansi gangguan dalam bentuk berikut:
2
'(0)
( ) exp ,
2
K N
F z z (3.46)
dalam hal ini,
.
N F s ds (3.47)
Penggunaan bentuk kernel yang diberikan persamaan (3.46) menghasilkan bentuk berikut:
2 2
'(0) A B .
K
a b (3.48)
Ini berarti bahwa lebar puncak yang diprediksi menjadi 1 2
1 2 1 2
2 2 .
B A
L N
27 Hasil ini harus diinterpretasikan dengan hati-hati, karena hanya mengarah ke orde hasil saja. Hasil solusi perilaku puncak ini berada pada batasan berikut:
2 2.
A B
28
IV METODE DAN PEMBAHASAN
Karena model I, II, III dan IV yang dibangun secara lokal tidak dapat menjaga kepaduan kelompok dengan memuaskan, maka dalam penelitian ini diamati model V dengan pengamatan kepaduan kelompok secara non lokal. Langkah pertama adalah mencari solusi model V dengan beberapa sifat seperti pusat massa atau luasan kelompok menggunakan bentuk kernel secara rinci untuk mengimbangi pengaruh bentuk difusi sehingga dapat menyelesaikan beberapa perluasan dari persamaan (3.49). Langkah selanjutnya adalah melakukan simulasi model V dengan pendekatan syarat awal menggunakan fungsi sebaran normal. Untuk keperluan ini, maka terlebih dahulu dikaji analisis model non lokal dan menetapkan parameter-parameter realistis yang berkaitan dengan model. Selanjutnya dilakukan simulasi dengan bantuan software Matlab R2008a untuk melihat hasilnya.
4.1 Analisis Model V
Menurut Edelstein-Keshet et al. (1998), pusat massa atau luasan kelompok dinyatakan sebagai berikut:
0( ) ( , ) ,
F t F x t dx
(4.1)
1( ) ( , ) ,
F t xF x t dx (4.2)
2
2( ) ( , ) ,
F t x F x t dx (4.3)
dengan jumlah total individu N F t0( ) dan pusat massa (kelompok) adalah:
1
( ) .
X t F N
Ragamnya adalah:
2 1
( ) ( , ) .
V t x X F x t dx
N (4.4)
Hubungan antara momen kedua dan ragam (lihat lampiran 1) adalah: 2
2 ,
29 Jumlah keseluruhan individu dipertahankan oleh pengintegralan kedua sisi persamaan (3.43) dengan bentuk sisi kanan bernilai nol dengan pendekatan perilaku pada . Karena N konstan, maka F0 juga konstan sehingga
0 0.
dF dt
(4.6)
Ini memperkuat fakta bahwa persamaan (3.43) bukan bentuk source-sink, hanya bentuk ulang sebaran pada ruang yang luas sehingga jumlah total individu pada daerah yang tak terbatas adalah konstan.
Untuk pusat massa yang diperoleh dari persamaan (3.43) (lihat lampiran 2) adalah:
1
( * ) .
d X
w K F Fdx
dt N (4.7)
Pusat massa bergerak karena adanya kecepatan angin dan kecepatan kelompok. Tetapi, ketika K ganjil, bentuk kelompok tidak memberikan kontribusi untuk kecepatan pada pusat massa.
Ragam diperoleh dari persamaan (3.43) (lihat lampiran 3) adalah: ( )
( )
dV t<