Studi Perbandingan Algoritma Prim, Algoritma Kruskal, Dan Algoritma Sollin Dalam Menentukan Pohon Merentang Maksimum

(1)

MERENTANG MAKSIMUM

SKRIPSI

IBNU HARIS LUBIS 050803059

MATEMATIKA KOMPUTASI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

(2)

STUDI PERBANDINGAN ALGORITMA PRIM, ALGORITMA KRUSKAL, DAN ALGORITMA SOLLIN DALAM MENENTUKAN POHON

MERENTANG MAKSIMUM

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

IBNU HARIS LUBIS 050803059

MATEMATIKA KOMPUTASI

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

(3)

PERSETUJUAN

Judul : STUDI PERBANDINGAN ALGORITMA PRIM,

ALGORITMA KRUSKAL, DAN ALGORITMA

SOLLIN DALAM MENENTUKAN POHON

MERENTANG MAKSIMUM

Kategori : SKRIPSI

Nama : IBNU HARIS LUBIS

Nomor Induk Mahasiswa : 050803059

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN

ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di

Medan, Juni 2011

Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Drs. Sawaluddin, M.IT Prof. Drs. Tulus, M.Si.

NIP. 195912311998021001 NIP. 196209011988031002

Diketahui/Disetujui oleh

Departeman Matematika FMIPA USU Ketua.

(4)

PERNYATAAN

STUDI PERBANDINGAN ALGORITMA PRIM, ALGORITMA KRUSKAL, DAN ALGORITMA SOLLIN DALAM MENENTUKAN MAKSIMUM

SPANNING TREE

SKRIPSI

Saya mengaku bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Juni 2011

Ibnu Haris Lubis

(5)

PENGHARGAAN

Puji dan syukur penulis panjatkan kehadirat Allah SWT yang Maha Pemurah

dan Maha Penyayang, karena atas rahmat dan hidayah-Nya sehingga penulis dapat menyelesaikan skripsi ini dalam waktu yang telah ditetapkan.

Ucapan terima kasih penulis sampaikan kepada Bapak Prof. Dr. Tulus, M.Si dan Bapak Drs. Sawaluddin, M.I.T, selaku pembimbing pada penyelesaian skripsi ini yang telah memberikan panduan dan penuh kepercayaan kepada saya untuk

menyempurnakan skripsi ini. Panduan ringkas, padat dan bermanfaat telah diberikan agar saya dapat menyelesaikan skripsi ini. Ucapan terima kasih juga ditujukan kepada Ketua dan Sekretaris Departemen Prof. Dr. Tulus, M.Si dan Dra. Mardiningsih, M.Si, Dekan dan Pembantu Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara, semua Dosen pada Departemen Matematika FMIPA USU, Pegawai di FMIPA USU dan teman-teman seangkatan 2005. Tidak terlupakan

kepada Ayah, Ibunda tercinta dan adik-adik yang selama ini memberikan dukungan dan doa. Spesial terima kasih buat Adinda Nur Aidar atas bantuan dan inspirasinya dari awal hingga selesainya skripsi ini. Terima kasih kepada sahabat-sahabatku Novi Yuanda Lubis, Muhammad Haikal, Supardi, Riko Azhari, Irfan Affandi, Taufik Zuhri,

dan Abang Abdul Syukur. Penulis juga mengucapkan terima kasih kepada Abang dan Kakak stambuk atas nasehat dan bantuannya selama perkuliahan serta Adik stambuk yang memberikan motivasi kepada penulis.

(6)

ABSTRAK

Hasil penelitian ini merupakan pendeskripsian langkah-langkah dalam

menentukan maximum spanning treedengan menggunakan tiga algoritma. Setelah itu

dilanjutkan dengan analisis perbandingan dari tiga algoritma tersebut. Hasil penelitian

menunjukkan bahwa bentuk spanning tree dan jumlah bobot merentangnya

mempunyai kesamaan untuk setiap graf berbobot tersebut. Yang membedakan antara algoritma Prim, algoritma Kruskal, dan algoritma Sollin adalah algoritmanya beda sehingga jumlah langkah yang digunakan ketiga algoritma tersebut berbeda- berbeda-beda. Untuk graf G dengan jumlah sisi = 2(p – 1) algoritma Sollin paling efektif dan efisien dibandingkan algoritma Prim dan algoritma Kruskal. Untuk graf G dengan jumlah sisi = 2(p – 1) namum terdapat sisi yang memiliki bobot yang sama algoritma

Prim dan algoritma Sollin paling efektif dan efisien dibandingkan algoritma Kruskal. Untuk graf G dengan jumlah sisi < 2(p – 1) algoritma Sollin paling efektif dan efisien dibandingkan algoritma Prim dan algoritma Kruskal. Untuk graf G dengan jumlah sisi > 2(p – 1) algoritma Kruskal paling efektif dan efisien dibandingkan algoritma Prim

dan algoritma Sollin. Pembahasan mengenai maximum spanning treeini masih dapat

(7)

ABSTRACT

The result of this research is description of steps in determining minimum spanning tree by using four algorithms. Then is continued with comparative analysis out of the three algorithms. The result of this research indicates that the form of spanning tree and the number of weight spanning it is having equality for every

weighted graph. What differentiates between Prim algorithm, Kruskal algorithm, and Sollin algorithm are different so algorithm the that number of steps applied by fourth of algorithms are different. For graph G with number of sides = 2(p - 1), algoritma Sollin is the most efficient and effectively compared to Prim algorithm, and Kruskal algorithm. For graph G with number of sides = 2(p - 1) but there is side having the same weight, Prim algorithm and Sollin algorithm are the most efficient and

effectively compared to Kruskal algorithm. For graph G with number of sides < 2(p -1), Sollin algoritma is more efficient and effectively compared to Prim algorithm, and Kruskal algorithm. For graph G with number of sides > 2(p - 1), Kruskal algorithm is the most efficient and effectively compared to Prim algorithm, and Sollin algorithm.

Discussion about the maximum spanning tree admits of continued for research of

(8)

DAFTAR ISI

Halaman

PERSETUJUAN...i

PERNYATAAN...ii

PENGHARGAAN...iii

ABSTRAK...iv

ABSTRACT...v

DAFTAR ISI...vi

DAFTAR GAMBAR...vii

BAB 1 PENDAHULUAN... 13

1.1 Latar belakang... 13

1.2 Perumusan Masalah... 16

1.3 Pembatasan Masalah... 16

1.4 Tinjauan Pustaka... 16

1.5 Tujuan Penelitian... 17

1.6 Kontribusi Penelitian... 17

1.7 Metode Penelitian... 17

BAB 2 LANDASAN TEORI... 19

2.1 Teori Graf... 19

2.1.1 Defenisi Graf... 19

2.1.2 Macam-macam Graf... 20

2.1.3 Terminologi dalam Graf... 20

2.2 Graf Terhubung, Graf Berbobot, dan Sub-graf... 21

2.2.1 Graf Terhubung (Connected Graph)... 21

(9)

2.2.3 Sub Graf... 23

2.3 Pohon dan Hutan... 24

2.3.1 Pohon (Tree)... 24

2.3.2 Hutan (Forest)... 25

2.4 Pohon Merentang dan Pohon Merentang Minimum... 26

2.4.1 Defenisi Pohon Merentang (Spanning Tree)... 26

2.4.2 Pohon Merentang Maksimum (Maximum Spanning Tree)... 27

2.5 Algoritma Prim... 28

2.6 Algoritma Kruskal... 28

2.7 Algoritma Sollin... 29

BAB 3 HASIL DAN PEMBAHASAN... 30

3.1 Perhitungan Maximum Spanning TreeMenggunakan Algoritma Prim... 33

3.1.1 Perhitungan Maximum Spanning Treepada graf G dengan banyak edge = 2(p–1)... 33

3.1.2 Perhitungan Maximum Spanning Treepada graf G dengan banyak edge = 2(p – 1) dan terdapat edge yang memiliki bobot sama... 36

3.1.3 Perhitungan Maximum Spanning Treepada graf Gdengan edge < 2(p-1). ... 39

3.1.4 Perhitungan Maximum Spanning Treepada graf G dengan banyak edge > 2(p – 1)... 42

3.3 Perhitungan Maximum Spanning TreeMenggunakan Algoritma Kruskal 45 3.3.1 Perhitungan Maximum Spanning Treepada Graf G dengan Banyak Sisi = 2(p - 1)... 45

3.3.2 Perhitungan Maximum Spanning Treepada Graf G dengan Banyak Sisi = 2(p – 1) dan Terdapat Sisi yang Memiliki Bobot Sama... 48

3.3.3 Perhitungan Maximum Spanning Treepada Graf G dengan Banyak Sisi < 2(p – 1)... 51

(10)

3.4.1 Perhitungan Maximum Spanning Treepada Graf G dengan Banyak Sisi =

2(p – 1)... 58

3.4.2 Perhitungan Maximum Spanning Treepada Graf G dengan Banyak Sisi = 2(p – 1) dan Terdapat Sisi yang Memiliki Bobot Sama... 62

3.4.3 Perhitungan Maximum Spanning Treepada Graf G dengan Banyak Sisi < 2(p – 1)... 66

3.4.4 Perhitungan Maximum Spanning Treepada Graf G dengan Banyak Sisi >2(p–1)... 69

3.5 Perbandingan... 74

BAB 4 KESIMPULAN DAN SARAN... 77

4.1 Kesimpulan... 77

4.2 Saran... 77

(11)

DAFTAR GAMBAR

Gambar 2.1 Contoh Graf G(6, 9) ... ... 20

Gambar 2.2 Graf Terhubung (Connected Graph) ... ... 22

Gambar 2.3 Graf Berbobot (Weighted Graph) ... ... 22

Gambar 2.4 Graf dan Subgraf-nya ... ... 23

Gambar 2.5 Pohon dengan 1, 2, 3, dan 4 verteks ... ... 24

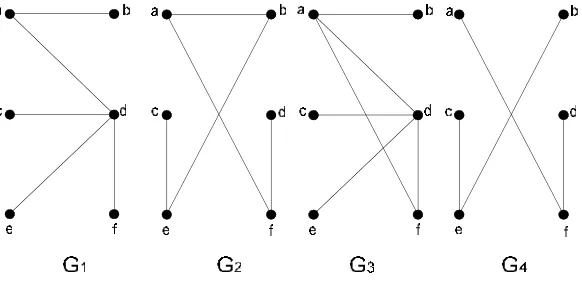
Gambar 2.6 G1dan G2adalah Pohon, sedangkan G3dan G4bukan Pohon ... 25

Gambar 2.7 Hutan (Forest) yang terdiri dari tiga buah Pohon (Tree)... ... 25

Gambar 2.8 Graf Lengkap G dan empat buah pohon merentangnya, T1, T2, T3, dan T4 ...26

Gambar 3.1 Graf dengan verteks 8 dan edge 14 ... ... 30

Gambar 3.2 Graf dengan verteks 8 dan edge 14 dan ada bobot yang bernilai sama .. 31

Gambar 3.5 Maximum Spanning Treedengan Algoritma Prim pada graf G dengan Banyak Sisi = 2(p – 1) ... ... 35

Gambar 3.6 Maximum Spanning Treedengan Algoritma Prim pada graf G dengan Banyak Sisi = 2(p – 1) dan terdapat Sisi yang Memiliki Bobot Sama ... ... 38

Gambar 3.7Maximum Spanning Treedengan Algoritma Prim pada graf G dengan Banyak Sisi < 2(p – 1) ... ... 41

Gambar 3.8Maximum Spanning Treedengan Algoritma Prim pada graf G dengan Banyak Sisi > 2(p – 1) ... ... 44

Gambar 3.9 Maximum Spanning Treedengan Algoritma Kruskal pada graf G dengan Banyak Sisi = 2(p – 1) ... 47

(12)

Banyak Sisi = 2(p – 1) dan terdapat Sisi yang Memiliki Bobot Sama

... 51

Gambar 3.11 Maximum Spanning Treedengan Algoritma Kruskal pada graf G dengan

Banyak Sisi < 2(p – 1) ... ... 54

Gambar 3.12Maximum Spanning Treedengan Algoritma Kruskal pada graf G dengan

Banyak Sisi > 2(p – 1) ... ... 58

Gambar 3.13 Maximum Spanning Treedengan Algoritma Sollin pada graf G dengan

Banyak Sisi = 2(p – 1) ... ... 60

Gambar 3.14Maximum Spanning Treedengan Algoritma Sollin pada graf G dengan

Banyak Sisi = 2(p – 1) dan terdapat Sisi yang Memiliki Bobot Sama

... ... 65

Banyak Sisi < 2(p – 1) ... ... 68

(13)

ABSTRAK

Hasil penelitian ini merupakan pendeskripsian langkah-langkah dalam

menentukan maximum spanning treedengan menggunakan tiga algoritma. Setelah itu

dilanjutkan dengan analisis perbandingan dari tiga algoritma tersebut. Hasil penelitian

menunjukkan bahwa bentuk spanning tree dan jumlah bobot merentangnya

mempunyai kesamaan untuk setiap graf berbobot tersebut. Yang membedakan antara algoritma Prim, algoritma Kruskal, dan algoritma Sollin adalah algoritmanya beda sehingga jumlah langkah yang digunakan ketiga algoritma tersebut berbeda- berbeda-beda. Untuk graf G dengan jumlah sisi = 2(p – 1) algoritma Sollin paling efektif dan efisien dibandingkan algoritma Prim dan algoritma Kruskal. Untuk graf G dengan jumlah sisi = 2(p – 1) namum terdapat sisi yang memiliki bobot yang sama algoritma

Prim dan algoritma Sollin paling efektif dan efisien dibandingkan algoritma Kruskal. Untuk graf G dengan jumlah sisi < 2(p – 1) algoritma Sollin paling efektif dan efisien dibandingkan algoritma Prim dan algoritma Kruskal. Untuk graf G dengan jumlah sisi > 2(p – 1) algoritma Kruskal paling efektif dan efisien dibandingkan algoritma Prim

dan algoritma Sollin. Pembahasan mengenai maximum spanning treeini masih dapat

(14)

ABSTRACT

The result of this research is description of steps in determining minimum spanning tree by using four algorithms. Then is continued with comparative analysis out of the three algorithms. The result of this research indicates that the form of spanning tree and the number of weight spanning it is having equality for every

weighted graph. What differentiates between Prim algorithm, Kruskal algorithm, and Sollin algorithm are different so algorithm the that number of steps applied by fourth of algorithms are different. For graph G with number of sides = 2(p - 1), algoritma Sollin is the most efficient and effectively compared to Prim algorithm, and Kruskal algorithm. For graph G with number of sides = 2(p - 1) but there is side having the same weight, Prim algorithm and Sollin algorithm are the most efficient and

effectively compared to Kruskal algorithm. For graph G with number of sides < 2(p -1), Sollin algoritma is more efficient and effectively compared to Prim algorithm, and Kruskal algorithm. For graph G with number of sides > 2(p - 1), Kruskal algorithm is the most efficient and effectively compared to Prim algorithm, and Sollin algorithm.

Discussion about the maximum spanning tree admits of continued for research of

(15)

BAB 1

PENDAHULUAN

1.1 Latar belakang

Perkembangan ilmu pengetahuan dan teknologi yang sangat pesat, tidak lepas dari peran ilmu matematika, yaitu ilmu yang menjadi solusi secara konseptual dalam menyelesaikan berbagai permasalahan yang terjadi dalam kehidupan di dunia. Dewasa ini semakin banyak muncul penggunaan model matematika maupun penalaran matematika sebagai alat bantu dalam meyelesaikan permasalahan yang dihadapi

dalam berbagai disiplin ilmu.

Teori graf merupakan salah satu cabang ilmu matematika yang bermanfaat dengan teori-teorinya dapat diterapkan untuk memecahkan masalah dalam kehidupan sehari-hari. Dengan mengkaji dan menganalisis model atau rumusan teori graf, dapat

diperlihatkan peranan dan kegunaannya dalam memecahkan permasalahan. Permasalahan yang dirumuskan dengan teori graf dibuat sederhana, yaitu diambil aspek-aspek yang diperlukan dan dibuang aspek-aspek lainnya (Purwanto, 1998). Dalam kehidupan sehari-hari terdapat permasalahan mengenai optimasi yang dapat diselesaikan menggunakan pohon merentang minimum, atau dikenal dengan istilah

(16)

Problema kita dapat pula berupa penentuan pohon rentang dari G dengan

bobot maksimal. Sebagai contoh, simpul dan ruas dari G menyajikan berturut-turut kota dan jalan raya yang menghubungkan dua kota. Kita akan membangun system transportasi antar semua kota tersebut. Kita akan mengambil sejumlah jalan raya yang paling cocok dilalui sistem tersebut. Untuk itu mula-mula kita harus memberi bobot kepada masing-masing jalan raya. Di sini kita menggolongkan setiap jalan raya itu,

misalkan berdasarkan kualitas jalan, potensi ekonomi, keadaan social, potensi pariwisata sepanjang jalan, dan lain sebagainya dengan memberi suatu bobot tertentu. Semakin baik kondisi jalan raya tersebut, maka semakin tinggi bobotnya. Pemecahan bobot ini pada hakekatnya sama dengan problema mencari pohon rentang maksimal

dari G, atau dikenal dengan istilah Maximum Spanning Tree. Metode untuk

menentukan minimum spanning tree dapat juga digunakan saat kita membutuhkan

sebuah maximum spanning tree.

Terkait dengan pernyataan di atas, maka perlu adanya pemecahan untuk masalah-masalah tersebut. Salah satu teori yang dapat diaplikasikan dalam

menyelesaikan permasalahan-permasalahan tersebut adalah dengan penerapan teori graf. Penyelesaiaan masalah-masalah tersebut di atas, pada dasarnya menentukan

terjadinya semua maximum spanning tree yang mungkin dan memperhitungkan

maximum spanning tree. Di dalam sebuah graf mungkin saja terdapat lebih dari satu spanning tree. Maka harus dicari spanning tree yang mempunyai jumlah jarak

terpanjang, dengan kata lain harus dicari maximum spanning tree. Mencari maksimum

dari suatu spanning tree merupakan suatu masalah yang sudah cukup dikenal dalam

pokok bahasan graf dan mempunyai terapan yang luas dalam praktek. Terkait dengan pernyataan di atas, dalam menentukan algoritma yang paling efektif dalam

menentukan maximum spanning tree. Pentingnya aplikasi graf dalam menentukan

maximum spanning tree, untuk itu diperlukan suatu algoritma yang tepat untuk

menentukan maximum spanning treedalam suatu graf terhubung, berbobot, dan tidak

berarah. Dalam bahasan ini akan dikaji tentang algoritma-algoritma dalam

(17)

Peneliti merasa bahwa penelitian ini merupakan salah satu penelitian yang

menarik untuk dikaji, karena terdapat beberapa macam algoritma yang dapat

digunakan dalam menentukan maximum spanning tree. Di sini, peneliti meneliti 3

macam algoritma yang dapat digunakan dalam menentukan maximum spanning tree

yaitu algoritma Prim, algoritma Kruskal, dan algoritma Sollin, yang masing-masing

algoritma memiliki aturan yang berbeda-beda dalam menentukan maximum spanning

tree, sehingga peneliti merasa perlu mengkaji algoritma manakah yang paling efektif

dalam menentukan maximum spanning treeagar mendapatkan perbedaan dari ketiga

algoritma tersebut.

Konsep dasar yang digunakan dalam algoritma Prim dalam menentukan

maximum spanning tree adalah dalam setiap langkah memilih sisi dari graf G yang berbobot maksimum, yang terhubung dengan pohon merentang T yang telah terbentuk, dan tidak membentuk sirkuit. Langkah awal dalam algoritma Prim yaitu menentukan sebarang titik awal dan dilanjutkan mengambil sisi dari graf G yang berbobot maksimum dari titik awal yang telah dipilih tadi, masukkan ke dalam T yang

kosong.

Konsep dasar yang digunakan dalam algoritma Kruskal dalam menentukan maximum spanning tree adalah pada setiap langkah memilih sisi dari graf G yang berbobot maksimum, tetapi sisi tersebut tidak membentuk sirkuit di T. Langkah awal yang sangat penting dalam algoritma ini adalah pengurutan terhadap setiap sisi pada graf G, mulai dari sisi dengan bobot terbesar hingga bobot terkecil.

Konsep dasar yang digunakan algoritma Sollin dalam menentukan maximum

spanning tree adalah penghapusan sisi-sisi yang tidak menyebabkan graf menjadi tidak terhubung. Algoritma ini sangat memperhatikan urutan sisi-sisi berbobot. Dalam

menentukan maximum spanning tree, algoritma ini mengurutkan sisi-sisi mulai dari

(18)

Berdasarkan penjelasan tersebut, dalam penelitian ini akan membahas tentang:

“Perbandingan Algoritma Prim, Algoritma Kruskal, dan Algoritma Sollin dalam Menentukan Pohon Merentang Maksimum”.

1.2 Perumusan Masalah

Berdasarkan latar belakang yang telah dipaparkan sebelumnya, didapat rumusan masalah yaitu menentukan algoritma manakah yang lebih efektif diantara algoritma

Prim, algoritma Kruskal, dan algoritma Sollin dalam menentukan maximum spanning

tree.

1.3 Pembatasan Masalah

Pada penelitian ini, batasan masalahnya adalah sebagai berikut :

1. Graf berbobot dan tak berarah.

2. Graf yang memuat titik yang banyaknya 8 dan sisi yang banyaknya 14. 3. Graf yang memuat titik yang banyaknya 8 dan sisi yang banyaknya tetap 14

namun terdapat sisi yang memilki bobot sama.

4. Graf yang memuat titik yang banyaknya 8 dan sisi yang banyaknya < 14 yakni 11.

5. Graf yang memuat titik yang banyaknya 8 dan sisi yang banyaknya > 14 yakni 20.

1.4 Tinjauan Pustaka

J.J Siang (2002) dalam bukunya yang berjudul Matematika Diskrit dan

(19)

Berbeda dengan Algoritma Kruskal yang dimulai dengan graf tanpa garis,

algoritma Prim dimulai dari graf yang kosong sama sekali.

Khoiroh (2010) menjelaskan bahwa algoritma Prim lebih efektif dibandingkan algoritma Sollin, algoritma Kruskal maupun algoritma Boruvka dalam menentukan pohon perentang minimum dengan banyak verteks 8 dan banyak edge 14.

1.5 Tujuan Penelitian

Tujuan dari penelitian ini adalah membandingkan algoritma Prim, algoritma Kruskal,

dan algoritma Sollin dalam menyelesaikan masalah maximum spanning tree pada

kasus graf yang telah ditentukan.

1.6 Kontribusi Penelitian

Penelitian ini digunakan sebagai informasi dan wawasan pengetahuan tentang teori graf, khususnya tentang pohon merentang maksimum, algoritma Prim, algoritma Kruskal, dan algoritma Sollin.

1.7 Metode Penelitian

Jenis dari penelitian ini adalah deskriptif kualitatif. Pendekatan yang digunakan adalah pendekatan kualitatif dengan metode kepustakaan. Dalam pendekatan deskriptif

(20)

Dalam skripsi ini membahas tentang algoritma Prim, algoritma Kruskal, dan

algoritma Sollin beserta langkah-langkahnya dalam menentukan maximum spanning

tree dalam suatu graf sederhana terhubung, berbobot, dan tidak berarah. Beberapa

langkah yang harus dilakukan untuk menyelesaikan masalah maksimum spanning tree

adalah :

1. Penentuan titik-titik dalam pembentukan graf 2. Penentuan bobot dari setiap sisi

3. Perhitungan maximum spanning tree dari hasil pembentukan graf

menggunakan algoritma Prim

4. Perhitungan maximum spanning treedari hasil pembentuka graf menggunakan

algoritma Kruskal

5. Perhitungan maximum spanning treedari hasil pembentuka graf menggunakan

algoritma Sollin

(21)

LANDASAN TEORI

2.1 Teori Graf

2.1.1 Defenisi Graf

Suatu graf G adalah suatu himpunan berhingga tak kosong dari objek-objek yang

disebut verteks (titik/simpul) dengan suatu himpunan yang anggotanya adalah

pasangan tak berurut dari verteks yang berbeda pada G yang disebut edge(mungkin

kosong), dan dinotasikan dengan G{V(G),E(G)}. Himpunan verteks dari G

dinotasikan dengan V(G) dan himpunan edge(sisi) dinotasikan dengan E(G).

Banyaknya anggota dari himpunan verteks pada G disebut order G dan dinotasikan

dengan p(G), atau dengan singkat ditulis p.

Edge e = {u,v} atau juga dapat ditulis e= uv adalah sebuah edge dalam G,

yaitu u dan vadalah titik-titik ujung dari e, maka udan vdikatakan adjacent(berelasi)

dimana u dan eadalah incident(terhubung), begitu juga dengan vdan w. Banyaknya

edge yang incidentdengan verteks u disebut degree / valensi / derajat dari u, dengan

kata lain degree uadalah banyaknya edge yang memuat usebagai titik ujung. Degree

udinotasikan dengan deg(u).

Suatu graf biasanya dipresentasikan secara grafis, dengan setiap verteks

dipresentasikan sebagai titik atau lingkaran kecil, dan setiap edge e = uv

dipresentasikan dengan sebuah garis atau kurva yang menghubungkan titik-titik yang

(22)

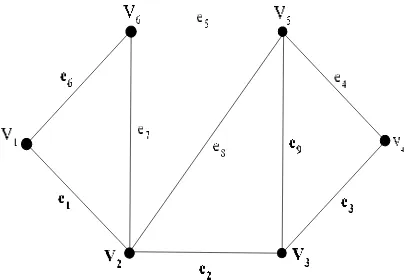
Gambar 2.1 Contoh Graf G(6, 9)

Gambar 2.1 menunjukkan bahwa graf G = G(V, E), di mana V(G) = {v1, v2, v3, v4, v5,

v6} dan E(G) = {e1, e2, e3, e4, e5, e6, e7, e8, e9}.

2.1.2 Macam-macam Graf

Berdasarkan arah dan bobotnya, graf digolongkan atas 4 jenis, yaitu :

1. Graf berarah dan berbobot graf yang setiap sisinya mempunyai orientasi arah

dan bobot.

2. Graf berarah dan tak berbobot  graf yang setiap sisinya mempuyai arah dan

tidak berbobot.

3. Graf tidak berarah dan berbobot  graf yang setiap sisinya tidak mempunyai

arah tetapi memiliki bobot.

4. Graf tidak berarah dan tidak berbobot graf yang setiap sisinya tidak memiliki

arah dan bobot.

2.1.3 Terminologi dalam Graf

(23)

1. Walk adalah suatu barisan berhingga dari verteks dan edge secara bergantian,

yang diawali dari verteks dan diakhiri dengan verteks. Bentuk umum dari walk:

0 0 1 1 n1 n n

v e v e v e v_

Dalam hal ini v0 merupakan verteks awal dan vn merupakan vertex akhir. Jika

verteks awal dan vertex akhir dari suatu walk adalah sama, maka walk disebut

close walk(walk tertutup).

2. Trailadalah suatu walkdengan setiap edgenya berlainan.

3. Pathadalah suatu walkdengan setiap verteksnya berbeda.

4. Cycleadalah suatu pathyang memiliki verteks awal sama denga verteks akhir. 5. Length (panjang) adalah bilangan yang menyatakan banyaknya edge yang

muncul dalam suatu walk.

6. Edge e adalah sebuah jembatan untuk G jika G – e tidak terhubung. Secara

umum edge e adalah jembatan untuk suatu graf G jika G-e mempunyai

komponen terhubung lebih dari G.

2.2 Graf Terhubung, Graf Berbobot, dan Sub-graf

2.2.1 Graf Terhubung (Connected Graph)

Misalkan u dan v adalah titik yang berbeda pada graf G. Maka titik u dan v dapat

dikatakan terhubung (connected), jika terdapat lintasan u-v di G. Sedangkan suatu graf

G dapat dikatakan terhubung (connected), jika untuk setiap titik u dan v di G

terhubung (Chartrand dan Lesniak, 1986:28). Keterhubungan adalah sifat yang dimiliki graf. Graf terhubung dapat dilihat atau dibuktikan dari keterhubungan antara

(24)

Gambar 2.2 Graf Terhubung (Connected Graph)

2.2.2 Graf Berbobot (Weighted Graph)

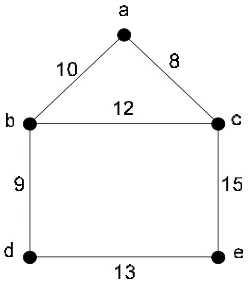
Graf berbobot adalah graf yang setiap sisinya diberi sebuah bobot. Bobot pada tiap sisi dapat berbeda-beda bergantung pada masalah yang dimodelkan dengan graf (Munir, 2005:376)

Contoh 2.1 :

Gambar 2.3 Graf Berbobot (Weighted Graph)

(25)

2.2.3 Sub Graf

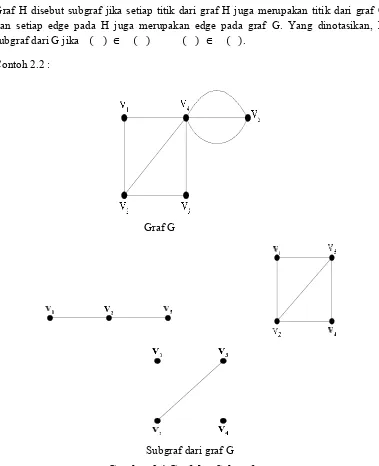
Graf H disebut subgraf jika setiap titik dari graf H juga merupakan titik dari graf G dan setiap edge pada H juga merupakan edge pada graf G. Yang dinotasikan, H

subgraf dari G jika ( ) ∈ ( ) ( ) ∈ ( ).

Contoh 2.2 :

Graf G

Subgraf dari graf G

(26)

2.3.1 Pohon (Tree)

Sejumlah masalah yang berhubungan dengan graf yang ditemukan manusia dalam kehidupan nyata menimbulkan penemuan konsep-konsep pemecahan masalah graf. Konsep pohon pernah diterapkan pada tahun 1870-an oleh Matematikawan Inggris yang bernama Arthur Cayley dalam penghitungan molekul kimia. Karya yang lebih

baru membuktikan bahwa pohon digunakan di banyak bidang, mulai dari linguistik

sampai komputer. Pohon adalah suatu graf terhubung yang tidak memuat sirkuit.Tree

dinotasikan dengan T.

Sebuah graf G dengan nverteks dikatakan sebuah treejika :

1. G terhubung dan tak memuat sirkuit,atau

2. G terhubung dan memiliki n – 1edge,atau

3. G tak memuat sirkuit dan memiliki n – 1edge,atau

4. Terdapat tepat satu pathdiantara setiap pasangan verteks-verteks di G,atau

5. G setidaknya merupakan sebuah graf terhubung.

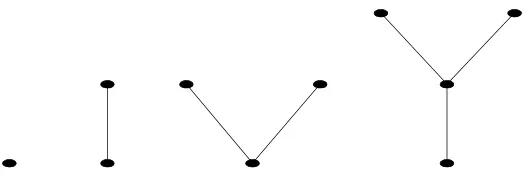
Gambar 2.5 Pohon dengan 1, 2, 3, dan 4 verteks

(27)

Pada Gambar 2.6, hanya G1 dan G2 merupakan pohon, sedangkan G3 dan

G4 bukan pohon. G3 bukan pohon karena mengandung sirkuit a, d, f, a sedangkan G4 bukan pohon karena merupakan graf tak-terhubung.

Gambar 2.6 G1 dan G2adalah Pohon, sedangkan G3dan G4bukan Pohon

2.3.2 Hutan (Forest)

Hutan merupakan :

 Kumpulan pohon yang saling lepas.

 Graf tidak terhubung yang tidak mengandung sirkuit. Setiap komponen di

dalam graf terhubung tersebut adalah pohon.

Contoh 2.3 :

(28)

2.4.1 Defenisi Pohon Merentang (Spanning Tree)

Pohon rentang suatu graf G adalah subgraf G yang merupakan pohon dan semua memuat titik dalam G. Disebut pohon merentang karena semua simpul pada pohon T

sama dengan semua simpul pada graf G, dan sisi-sisi pada pohon T sisi-sisi pada

graf G. Dengan kata lain, V1 = V dan E1 E.

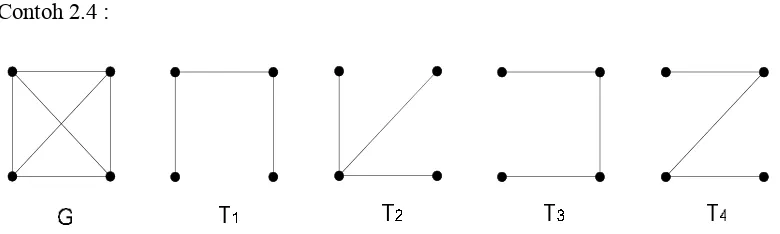
Pada Contoh 2.4 berikut akan diberikan bagaimana cara menentukan pohon merentang dari sebuah graf.

Contoh 2.4 :

Gambar 2.8 Graf lengkap G dan empat buah pohon merentangnya, T1, T2, T3, dan T4

Perlu dicermati bahwa spanning tree didefenisikan hanya untuk graf

terhubung, karena pohon selalu terhubung. Pada graf tak terhubung dengan n buah

simpul kita tidak dapat ditemukan subgraf terhubung dengan n buah titik. Tiap

komponen dari graf tak-terhubung mempunyai satu buah spanning tree. Dengan

demikian, graf tak-terhubung dengan k komponen mempunyai hutan merentang

(29)

Graf G Spanning Tree

n verteks n vertex

m edge n – 1 ruas

Cabang (Branch)

m – (n – 1) Chord(Tali-hubung)

Contoh 2.6 :

Keterangan : = Branch --- = Chord

2.4.2 Pohon Merentang Maksimum (Maximum Spanning Tree)

Jika G adalah graf berbobot, maka bobot pohon merentang T dari G didefenisikan

sebagai jumlah bobot semua sisi di T. Pohon merentang yang berbeda mempunyai bobot yang berbeda pula. Di antara semua pohon merentang di G, pohon merentang

yang berbobot maksimum dinamakan pohon merentang maksimum atau maximum

(30)

Masalah pohon merentang minimum dapat dipecahkan dengan bantuan suatu pohon yang ditemukan oleh Prim (1957). Algoritma ini biasa disebut dengan Algoritma Prim. Algoritma Prim adalah suatu algoritma di dalam teori graf yang bertujuan menentukan suatu pohon merentang minimum dari suatu graf terhubung yang

berbobot. Metode ini digunakan untuk menemukan suatu subset dari sisi yang

membentuk suatu pohon yang melibatkan tiap-tiap titik, dimana total bobot dari semua sisi di dalam pohon adalah minimum. Algoritma Prim juga dapat digunakan

dalam menentukan maximum spanning tree. Secara terurut, algoritma Prim untuk

mencari maximum spanning treedapat dituliskan sebagai berikut :

1. Menentukan sebarang titik awal dan dilanjutkan mengambil sisi dari graf G yang berbobot maksimum dari titik awal yang dipilih tadi, masukkan ke dalam T yang kosong.

2. Pilih sisi eyang mempunyai bobot maksimum berikutnya dan bersisian dengan

titik di T, tetapi etidak membentuk sirkuit di T. Masukkan eke dalam T.

3. Ulangi langkah 2 hingga terbentuk maximum spanning tree.

2.6 Algoritma Kruskal

Algoritma Kruskal adalah suatu algoritma di dalam teori graf yang digunakan untuk mengkonstruksi pohon merentang minimum di di dalam graf berbobot terhubung

secara berurutan dari sisi yang berbobot kecil sampai berbobot besar hingga tidak

terbentuk cycle. Algoritma Kruskal dapat diasumsikan dengan memilih sisi dari graf

secara berurutan berdasarkan bobotnya dari bobot kecil ke bobot besar. Algoritma

Kruskal juga dapat digunakan dalam menentukan maximum spanning tree. Secara

terurut, algoritma Kruskal untuk mencari maximum spanning tree dapat dituliskan

sebagai berikut :

1. Urutkan sisi-sisi graf dari besar ke kecil. T merupakan himpunan kosong.

2. Pilih sisi e dengan bobot maksimum yang tidak membentuk sirkuit di T.

(31)

3. Ulangi langkah 2 sebanyak n – 1 kali hingga terbentuk maximum spanning tree.

2.7 Algoritma Sollin

Algoritma Sollin adalah suatu algoritma dalam teori graf yang digunakan untuk menentukan pohon merentang minimum di dalam graf berbobot terhubung dengan cara melakukan penghapusan sisi-sisi yang tidak menyebabkan graf menjadi tidak

berhubung atau membentuk sirkuit. Penghapusan tersebut dimulai dari sisi yang memiliki bobot terbesar hingga terkecil. Algoritma Sollin juga dapat digunakan

dalam menentukan maximum spanning tree. Untuk menentukan maximum spanning

tree dari sebuah graf dengan menggunakan Algoritma Sollin maka diperlukan

langkah-langkah sebagai berikut :

1. Urutkan sisi-sisi pada graf berdasarkan bobotnya dari kecil ke besar.

2. Lakukan penghapusan setiap sisi yang tidak menyebabkan graf menjadi

tidak terhubung. Penghapusan dimulai dari sisi yang memiliki bobot terkecil.

(32)

BAB 3

HASIL DAN PEMBAHASAN

Pada bab ini akan dibahas tentang pencarian maximum spanning tree dengan

menggunakan algoritma Prim, algoritma Kruskal, dan algotirma Sollin, yang kemudian dilanjutkan dengan menentukan algoritma manakah yang lebih efektif

digunakan dalam menentukan maximum spanning tree.

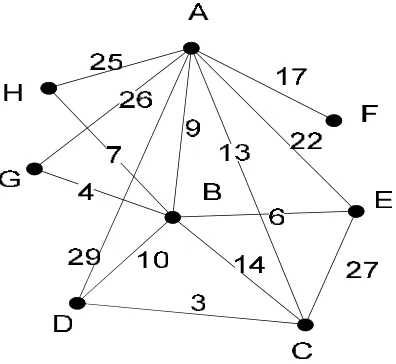
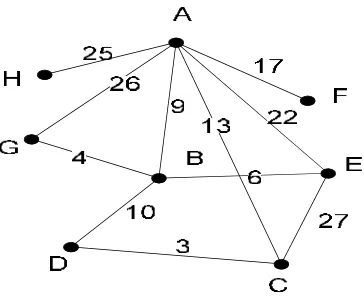
[image:32.612.222.420.378.560.2]

Berikut ini akan ditunjukkan graf berbobot G yang memuat 8 titik dan 14 edge

Gambar 3.1 Graf dengan verteks 8 dan edge 14

Gambar 3.1 adalah graf G dengan banyak sisi = 2(p – 1) dengan p adalah

banyak titik, dan diketahui banyak titik adalah 8 sehingga diperoleh graf G dimana

banyak sisinya 14. Untuk mencari dan mendapatkan maximum spanning treedari graf

tersebut, digunakan algoritma Prim, algoritma Kruskal, dan algoritma Sollin. Ketiga

algoritma tersebut mempunyai metodologi yang berbeda, tetapi keduanya memang

(33)

maximum spanning tree, maka akan diperoleh jarak maksimum terpanjang yang menghubungkan antara titik yang satu dengan titik yang lain.

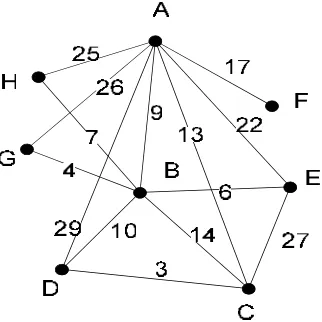
Berikut ini akan ditunjukkan graf berbobot G yang memuat 8 verteks dan 14

[image:33.612.233.409.163.326.2]

edge, namun terdapat edge yang memiliki bobot sama.

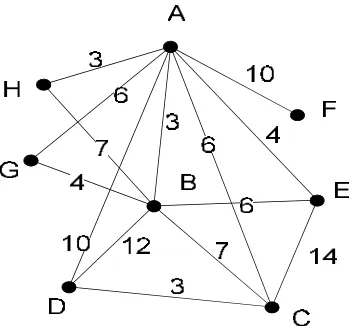
Gambar 3.2 Graf dengan verteks 8 dan edge 14 dan ada bobot yang bernilai sama

Gambar 3.2 adalah graf G dengan banyak sisi = 2(p – 1) dan terdapat edge

yang memiliki bobot yang sama, dengan p adalah banyak titik, dan diketahui banyak

titik adalah 8 sehingga diperoleh graf Gdimana banyak sisinya 14. Untuk mencari dan

mendapatkan maximum spanning tree dari graf tersebut, digunakan algoritma Prim,

algoritma Kruskal, dan algoritma Sollin. Ketiga algoritma tersebut mempunyai metodologi yang berbeda tetapi keduanya memang dikontruksikan untuk

mendapatkan maximum spanning tree. Setelah diperoleh maximum spanning tree,

maka akan diperoleh jarak maksimum terpanjang yang menghubungkan antara titik satu dengan titik yang lain.

(34)

[image:34.612.230.412.83.232.2]

Gambar 3.3 Graf dengan verteks 8 dan edge 11

Gambar 3.3 adalah graf G dengan banyak edge < 2(p – 1) dengan p adalah

banyak verteks, dan diketahui banyak verteks adalah 8 sehingga diperoleh graf G di

mana banyak sisinya kurang dari 14, dan pada graf ini memuat 8 verteks dan 11 edge.

Untuk mencari dan mendapatkan maximum spanning tree dari graf tersebut,

digunakan algoritma Prim, algoritma Kruskal, dan algoritma Sollin. Ketiga algoritma tersebut mempunyai metodologi yang berbeda tetapi keduanya memang

dikontruksikan untuk mendapatkan maximum spanning tree. Setelah diperoleh

maximum spanning tree, maka akan diperoleh jarak maksimum terpanjang yang menghubungkan antara titik satu dengan titik yang lain.

Berikut ini akan ditunjukkan graf berbobot Gyang memuat 8 verteks dan 20

[image:34.612.232.412.519.677.2]

edge.

(35)

Gambar 3.4 adalah graf G dengan banyak edge > 2(p – 1) dengan p adalah

banyak verteks, dan diketahui banyak verteks adalah 8 sehingga diperoleh graf G di

mana banyak edgenya lebih dari 14, dan pada graf ini memuat 8 verteks dan 20 edge.

Untuk mencari dan mendapatkan maximum spanning tree dari graf tersebut,

digunakan algoritma Prim, algoritma Kruskal, dan algoritma Sollin. Ketiga algoritma tersebut mempunyai metodologi yang berbeda tetapi keduanya memang

dikontruksikan untuk mendapatkan maximum spanning tree. Setelah diperoleh

maximum spanning tree, maka akan diperoleh jarak maksimum terpanjang yang menghubungkan antara titik satu dengan titik yang lain.

3.1 Perhitungan Maximum Spanning TreeMenggunakan Algoritma Prim

3.1.1 Perhitungan Maximum Spanning Treepada graf G dengan banyak edge = 2(p–1)

Untuk menentukan maximum spanning tree dengan menggunakan algoritma Prim

dapat dilakukan dengan prosedur dalam langkah-langkah di bawah ini :

Langkah 1: Pilih sebarang titik awal yaitu titik Alalu dilanjutkan mengambil sisi

berbobot maksimum dari graf G, masukkan titik Ake dalam T. T ={A}

Langkah 2: Pilih sisi dengan bobot maksimum berikutnya dan bersisian dengan titik di

T. Sisi yang dipilih adalah AD dengan bobot 29. Letakkan sisi AD ke

dalam T.T= {A,D}

[image:35.612.241.402.359.520.2]

(36)

dipilih adalah sisi AH. Letakkan sisi AHke dalam T.T = {A,D,G,H} Langkah 5: Ulangi langkah 2. Pilih sisi dengan bobot maksimal berikutnya. Sisi yang

dipilih adalah sisi AE. Letakkan sisi AEke dalam T.T = {A,D,G,H,E}

Langkah 6: Ulangi langkah 2. Pilih sisi dengan bobot maksimal berikutnya. Sisi yang

dipilih adalah sisi CE. Letakkan sisi CEke dalam T.T = {A,D,G,H,E,C}

dipilih adalah sisi AF.T = {A,D,G,H,E,C,F}

dipilih adalah sisi CB.T = {A,D,G,H,E,C,F,B}

Langkah 1 Langkah 2

Langkah 3

(37)

Langkah 5 Langkah 6

Langkah 7 Langkah 8

Karena sudah diperoleh maximum spanning tree, maka langkah dapat

dihentikan. Hasil maximum spanning tree yang diperoleh dari perhitungan

[image:37.612.129.516.79.407.2]

menggunakan algoritma Prim pada gambar di bawah ini :

(38)

dengan jumlah bobot sebagai berikut :

W(T) = W(A, D) + W(A, E) + W(A, F) + W(A, G) + W(A, H) + W(B, C) + W(C, E) = 29 + 22 + 17 + + 26 + 25 + 14 + 27 = 160

Jadi diperoleh maximum spanning treedengan W = {A, B, C, D, E, F, G, H }

dengan bobot 160, dan dari 8 verteks serta 14 edge, setelah diperoleh maximum

spanning tree-nya diperoleh 8 verteks dan 7 edge, dan banyak langkah yang ditempuh adalah 8.

Catatan : Meskipun dalam menentukan titik awal adalah sebarang, banyak

kemungkinan maximum spanning tree yang tebentuk hanya satu.

3.1.2 Perhitungan Maximum Spanning Treepada graf G dengan banyak edge =

2(p – 1) dan terdapat edge yang memiliki bobot sama.

Langkah 1: Pilih sebarang titik awal yaitu titik Alalu dilanjutkan mengambil sisi

(39)

T. Sisi yang dipilih adalah AF dengan bobot 10. Letakkan sisi AD ke

dalam T.T= {A,F}

Langkah 3: Ulangi langkah 2. AGadalah sisi yang dipilih selanjutnya. Letakkan sisi

AGke dalam T.T= {A,F,D}

Langkah 4: Ulangi langkah 2. Masih sama dengan langkah sebelumnya. Sisi yang

dipilih adalah sisi AB. Letakkan sisi ABke dalam T.T = {A,F,D,B}

Langkah 5: Ulangi langkah 2. Pilih sisi dengan bobot maksimal berikutnya. Sisi yang dipilih adalah sisi BH.Letakkan sisi BHke dalam T.T = {A,F,D,B,H} Langkah 6: Ulangi langkah 2. Pilih sisi dengan bobot maksimal berikutnya. Sisi yang

dipilih adalah sisi BC. Letakkan sisi BCke dalam T.T = {A,F,D,B,H,C} Langkah 7: Ulangi langkah 2. Pilih sisi dengan bobot maksimal berikutnya. Sisi yang

dipilih adalah sisi CE.T = {A,F,D,B,H,C,E}

Langkah 8: Ulangi langkah 2. Pilih sisi dengan bobot maksimal berikutnya. Sisi yang dipilih adalah sisi AG.T = {A,F,D,B,H,C,E,G}

Langkah 1 Langkah 2

(40)

Langkah 5

Langkah 6

Langkah 7 Langkah 8

Karena sudah diperoleh maximum spanning tree-nya, maka langkah dapat

[image:40.612.127.519.76.349.2]

Gambar 3.7 Maximum Spanning Tree dengan Algoritma Prim pada Graf G dengan Banyak Sisi = 2(p – 1) dan terdapat Sisi yang Memiliki Bobot Sama

Dari perhitungan algoritma Prim di atas, diperoleh maximum spanning tree

W(T) = W(A,D) + W(A,F) + W(A,G) + W(B,C) + W(B,D) + W(B,H) + W(C,E)

(41)

Jadi diperoleh maximum spanning treedengan W = {A, B, C, D, E, F, G, H }

dengan bobot 66, dan dari 8 titik serta 14 sisi, setelah diperoleh maximum spanning

treenyadiperoleh 8 titik dan 7 sisi, dan banyak langkah yang ditempuh adalah 8.

Catatan : Meskipun dalam menentukan titik awal adalah sebarang, banyak

kemungkinan maximum spanning tree yang tebentuk hanya satu.

3.1.3 Perhitungan Pohon Merentang Minimum pada graf Gdengan edge < 2(p-1).

Langkah 1: Sisi yang dipilih pertama adalah AGdengan bobot 26. Letakkan sisi AG

ke dalam T.T= {A,G}

T. AH adalah sisi yang dipilih selanjutnya. Letakkan sisi AHke dalam T. T= {A,G,H}

Langkah 3: Ulangi langkah 2. Masih sama dengan langkah sebelumnya. Sisi yang dipilih adalah sisi AE. Letakkan sisi AEke dalam T.T = {A,G,H,E} Langkah 4: Ulangi langkah 2. Pilih sisi dengan bobot maksimal berikutnya. Sisi yang

dipilih adalah sisi CE.Letakkan sisi CEke dalam T.T = {A,G,H,E,C} Langkah 5: Ulangi langkah 2. Pilih sisi dengan bobot maksimal berikutnya. Sisi yang

(42)

adalah sisi dengan bobot maksimum berikutnya, tetapi jika AC dipilih

maka akan berakibat terjadi cycle.

Langkah 7: Ulangi langkah 2. Pilih sisi dengan bobot maksimal berikutnya. Sisi yang dipilih adalah sisi AB.T = {A,G,H,E,C,B}

dipilih adalah sisi AG.T = {A,F,D,B,H,C,E,G}

Langkah 1 Langkah 2

Langkah 3 Langkah 4

(43)

Langkah 7 Langkah 8

Karena sudah diperoleh maximum spanning treenya, maka langkah dapat

dihentikan. Maximum spanning tree yang diperoleh dari perhitungan menggunakan

[image:43.612.124.525.78.212.2]

algoritma Prim pada gambar di bawah ini :

Gambar 3.9 Maximum Spanning Tree dengan Algoritma Prim pada Graf G dengan Banyak Sisi < 2(p – 1)

Dari perhitungan algoritma Prim di atas diperoleh pohon merentang minimum dengan jumlah bobot sebagai berikut :

W(T) =W(A, B) + W(A, E) + W(A, F) + W(A, G) + W(A,H) + W(B, D) + W(C, E)

= 9 + 22 + 17 + 26 + 25 + 10 + 27 = 136

Jadi diperoleh maximum spanning tree dengan T = {A, B, C, D, E, F, G, H)

tree-nya diperoleh 8 titik dan 7 sisi, dan banyak langkah yang ditempuh adalah 8.

(44)

3.1.4 Perhitungan Pohon Merentang Minimum pada graf G dengan banyak edge > 2(p – 1).

Langkah 1: Sisi yang dipilih pertama adalah ADdengan bobot 29. Letakkan sisi AD

ke dalam T.T= {A,D}

Langkah 2: Pilih sisi dengan bobot maksimum berikutnya dan bersisian dengan titik di T. AG adalah sisi yang dipilih selanjutnya. Letakkan sisi AGke dalam T. T= {A,D,G}

Langkah 3: Ulangi langkah 2. Masih sama dengan langkah sebelumnya. Sisi yang

dipilih adalah sisi GF. Letakkan sisi GFke dalam T.T = {A,D,G,F} Langkah 4: Ulangi langkah 2. Pilih sisi dengan bobot maksimal berikutnya. Sisi yang

dipilih adalah sisi AH.Letakkan sisi CEke dalam T.T = {A,D,G,F,H}

dipilih adalah sisi HE.Letakkan sisi HEke dalam T.T = {A,D,G,F,H,E}

dipilih adalah sisi CE. Letakkan sisi HE ke dalam T. T =

{A,D,G,F,H,E,C}

Langkah 7: Ulangi langkah 2. Pilih sisi dengan bobot maksimal berikutnya. Sisi AE adalah sisi dengan bobot maksimum berikutnya, tetapi jika AE dipilih

(45)

Langkah 8: Ulangi langkah 2. Pilih sisi dengan bobot maksimal berikutnya. Sisi CF

adalah sisi dengan bobot maksimum berikutnya, tetapi jika CF dipilih

Langkah 9: Ulangi langkah 2. Pilih sisi dengan bobot maksimal berikutnya. Sisi AF adalah sisi dengan bobot maksimum berikutnya, tetapi jika AF dipilih

Langkah10: Ulangi langkah 2. Pilih sisi dengan bobot maksimal berikutnya. Sisi yang dipilih adalah sisi FB.T = {A,D,G,F,H,E,C,B}

Langkah 1 Langkah 2

Langkah 3 Langkah 4

Langkah 5 Langkah 6

(46)

Langkah 9 Langkah 10

Karena sudah diperoleh maximum spanning treenya, maka langkah dapat

dihentikan. Hasil maximum spanning tree-nya yang diperoleh dari perhitungan

[image:46.612.126.517.78.204.2]

Gambar 3.10 Maximum Spanning Tree dengan Algoritma Prim pada Graf G dengan Banyak Sisi > 2(p – 1)

Dari perhitungan algoritma Prim di atas diperoleh pohon merentang minimum

W(T) = W(A,D) + W(A,G) + W(A,H) + W(B,F) + W(C,E) + W(E,H) + W(F,G) = 29 + 26 + 25 + 15 + 27 + 33 + 28 = 183

Jadi diperoleh maximum spanning tree dengan T = {A, B, C, D, E, F, G, H }dengan

bobot 183, dan dari 8 titik serta 20 sisi, setelah diperoleh maximum spanning treenya

diperoleh adalah 8 titik dan 7 sisi, dan banyak langkah yang ditempuh adalah 10.

(47)

3.3 Perhitungan Maximum Spanning TreeMenggunakan Algoritma Kruskal

3.3.1 Perhitungan Maximum Spanning Treepada Graf G dengan Banyak Sisi = 2(p

- 1)

Untuk menentukan maximum spanning treedengan menggunakan Algoritma Kruskal

dapat dilakukan dengan mengikuti prosedur dalam langkah-langkah di bawah ini :

Langkah 1 : Urutkan sisi-sisi graf dari besar ke kecil.

AD = 29 CE = 27

AG = 26 AH = 25

AE = 22 AF = 17

BC = 14 AC = 13

BD = 10 AB = 9

BH = 7 BE = 6

BG = 4 DC = 3

Langkah 2 : Mulai dari sisi dengan bobot paling maksimum, yaitu sisi AD dengan

bobot 29. Simpan sisi AD ke dalam T. T = {AD}

Langkah 3 : Pilih sisi berbobot maksimum selanjutnya dan pastikan tidak terjadi cycle. AG sisi yang dipilih. T = { AD, CE}

Langkah 4 : Pilih sisi berbobot maksimum selanjutnya dan pastikan tidak terjadi cycle. AG sisi yang dipilih. T = { AD, CE, AG}

(48)

tidak terjadi cycle. AE sisi yang dipilih. T = { AD, CE, AG, AH, AE} Langkah 7 : Ulangi langkah 3. Pilih sisi berbobot maksimum selanjutnya dan pastikan

tidak terjadi cycle. AF sisi yang dipilih. T = { AD, CE, AG, AH, AE, AF}

Langkah 8 : Ulangi langkah 3. Pilih sisi berbobot maksimum selanjutnya dan pastikan

tidak terjadi cycle. BC sisi yang dipilih. T = { AD, CE, AG, AH, AE, AF, BC}

Langkah 1 Langkah 2

Langkah 3 Langkah 4

(49)

Langkah 7 Langkah 8

Karena sudah diperoleh maximum spanning tree, maka langkah dapat dihentikan.

Hasil maximum spanning treeyang diperoleh dari perhitungan menggunaka algoritma

[image:49.612.122.526.75.236.2]

Kruskal dapat dilihat pada gambar di bawah ini.

Gambar 3. 5 Maximum Spanning Tree dengan Algoritma Kruskal pada Graf G dengan Banyak Sisi = 2(p – 1)

Dari perhitungan Algoritma Kruskal di atas diperoleh maximum spanning treedengan

jumlah bobot sebagai berikut :

W(T) = W(A,D) + W(A,E) + W(A,F) + W(A,G) + W(A,H) + W(B,C) + W(C,E)

= 29 + 22 + 17 + 26 + 25 + 14 + 27 = 160

Jadi diperoleh maximum spanning tree dengan T = { AD, CE, AG, AH, AE,

(50)

tree-nya diperoleh 8 titik dan 7 sisi, dan banyak langkah yang ditempuh adalah 7.

Catatan : Karena dalam mencari maximum spanning tree langkahnya adalah

dilakukan pengurutan terlebih dahulun pada setiap bobot dari terbesar hingga terkecil, dan dilanjutkan dengan menambahkan bobot yang telah diurutkan tadi hingga terbentuk maximum spanning tree. Jadi banyak kemungkinan maximum spanning tree yang dapat terbentuk hanya satu.

3.3.2 Perhitungan Maximum Spanning Tree pada Graf G dengan Banyak Sisi = 2(p – 1) dan Terdapat Sisi yang Memiliki Bobot Sama

dapat dilakukan dengan mengikuti prosedur dalam langkah-langkah di bawah ini:

CE = 14 BD = 12

AD = 10 AF = 10

BC = 7 BH = 7

AC = 6 AG = 6

BE = 6 AE = 4

BG = 4 AB = 3

(51)

Langkah 1 : Mulai dari sisi dengan bobot paling maksimum, yaitu sisi CE dengan

bobot 14. Simpan sisi CE ke dalam T. T = {CE}

Langkah 2 : Pilih sisi berbobot maksimum selanjutnya dan pastikan tidak terjadi cycle. BD sisi yang dipilih. T = {CE,BD}

Langkah 3 : Pilih sisi berbobot maksimum selanjutnya dan pastikan tidak terjadi cycle. AD sisi yang dipilih. T = { CE,BD,AD }

Langkah 4 : Pilih sisi berbobot maksimum selanjutnya dan pastikan tidak terjadi cycle. AF sisi yang dipilih. T = { CE,BD,AD,AF }

tidak terjadi cycle. BC sisi yang dipilih. T = { CE,BD,AD,AF,BC }

tidak terjadi cycle. BH sisi yang dipilih. T = { CE,BD,AD,AF,BC,BH }

tidak terjadi cycle. AC berbobot maksimum selanjutnya, tetapi akan

mengakibatkan cyclesehingga sisi AC tidak yang dipilih.

tidak terjadi cycle. AG sisi yang dipilih. T = { CE,BD,AD,AF,BC,BH,

AG }

(52)

Langkah 3 Langkah 4

Langkah 5 Langkah 6

Langkah 7 Langkah 8

Karena sudah diperoleh maximum spanning tree-nya, maka langkah dapat dihentikan.

Hasil maximum spanning tree yang diperoleh dari perhitungan menggunakan

(53)

[image:53.612.241.402.85.214.2]

Gambar 3. 6 Maximum Spanning Tree dengan Algoritma Kruskal pada Graf G dengan Banyak Sisi = 2(p – 1) dan terdapat Sisi yang Memiliki Bobot Sama

Dari perhitungan Algoritma Kruskal di atas diperoleh maximum spanning tree

W(T) = W(A,D) + W(A,F) + W(A,G) + W(B,C) + W(B,D) + W(B,H) + W(C,E) = 10 + 10 + 6 + 7 + 12 + 7 + 14 = 66

Jadi diperoleh maximum spanning tree dengan T =

{AD,AF,AG,BC,BD,BH,CE}

dengan bobot 66, dan dari 8 titik serta 14 sisi dan terdapat sisi yang memiliki bobot

sama, setelah diperoleh maximum spanning treenya diperoleh 8 titik dan 7 sisi, dan banyak langkah yang ditempuh adalah 9.

Catatan : Karena dalam mencari maximum spanning tree langkahnya adalah dilakukan pengurutan terlebih dahulu pada setiap bobot dari terbesar hingga terkecil, dan dilanjutkan dengan menambahkan bobot yang telah diurutkan tadi hingga terbentuk maximum spanning tree, Jadi banyak kemungkinan maximum spanning tree yang dapat terbentuk hanya satu.

3.3.3 Perhitungan Maximum Spanning Tree pada Graf G dengan Banyak Sisi <

(54)

CE = 27 AG = 26

AH = 25 AE = 22

AF = 17 AC = 13

BD = 10 AB = 9

BE = 6 BG = 4

CD = 3

Langkah 1 : Mulai dari sisi dengan bobot paling maksimum, yaitu sisi CE dengan

bobot 27. Simpan sisi CE ke dalam T. T = {CE}

Langkah 2 : Pilih sisi berbobot maksimum selanjutnya dan pastikan tidak terjadi cycle. AG sisi yang dipilih. T = {CE,AG}

Langkah 3 : Ulangi langkah 2.Pilih sisi berbobot maksimum selanjutnya dan pastikan

tidak terjadi cycle. AH sisi yang dipilih. T = { CE,AG,AH }

Langkah 4 : Ulangi langkah 2.Pilih sisi berbobot maksimum selanjutnya dan pastikan

tidak terjadi cycle. AE sisi yang dipilih. T = { CE,AG,AH,AE }

tidak terjadi cycle. AF sisi yang dipilih. T = { CE,AG,AH,AE,AF }

tidak terjadi cycle. AC berbobot maksimum selanjutnya, tetapi akan

mengakibatkan cyclesehingga sisi AC tidak yang dipilih.

tidak terjadi cycle. BD sisi yang dipilih. T = { CE,AG,AH,AE,AF,BD }

(55)

Langkah 1 Langkah 2

Langkah 3 Langkah 4

Langkah 5 Langkah 6

(56)

[image:56.612.270.375.141.240.2]

dihentikan. Hasil maximum spanning tree yang diperoleh dari perhitungan menggunakan Algoritma Kruskal dapat dilihat pada gambar di bawah ini :

Gambar 3.7 Maximum Spanning Tree dengan Algoritma Kruskal pada Graf G dengan Banyak Sisi < 2(p – 1)

Dari perhitungan Algoritma Kruskal di atas diperoleh maximum spanning treedengan

W(T) = W(A,B) + W(A,E) + W(A,F) + W(A,G) + W(A,H) + W(B,D) + W(C,E) = 9 + 22 + 17 + 26 + 25 + 10 + 27 = 136

Jadi diperoleh maximum spanning tree dengan T =

{CE,AG,AH,AE,AF,BD,AB} dengan bobot 136, dan dari 8 titik serta 11 sisi, setalah

diperoleh maximum spanning tree-nya diperoleh adalah 8 titik dan 7 sisi, dan banyak

langkah yang ditempuh adalah 8.

(57)

3.3.4 Perhitungan Maximum Spanning Tree pada Graf G dengan Banyak Sisi > 2(p – 1)

EH = 33 AD = 29

FG = 28 CE = 27

AG = 26 AH = 25

AE = 22 CF = 21

AF = 17 BF = 15

BC = 14 AC = 13

DE = 12 BD = 10

AB = 9 EF = 8

BH = 7 BE = 6

BG = 4 CD = 3

Langkah 1 : Mulai dari sisi dengan bobot paling maksimum, yaitu sisi EH dengan bobot 33. Simpan sisi EH ke dalam T. T = {EH}

Langkah 2 : Pilih sisi berbobot maksimum selanjutnya dan pastikan tidak terjadi cycle. AD sisi yang dipilih. T = {EH,AD}

(58)

tidak terjadi cycle. CE sisi yang dipilih. T = { EH,AD,FG,CE }

tidak terjadi cycle. AG sisi yang dipilih. T = { EH,AD,FG,CE,AG }

tidak terjadi cycle. AH sisi yang dipilih. T = { EH,AD,FG,CE,AG,AH }

tidak terjadi cycle. AE berbobot maksimum selanjutnya, tetapi akan

mengakibatkan cyclesehingga sisi AE tidak yang dipilih.

tidak terjadi cycle. CF berbobot maksimum selanjutnya, tetapi akan

mengakibatkan cyclesehingga sisi CF tidak yang dipilih.

tidak terjadi cycle. AF berbobot maksimum selanjutnya, tetapi akan

mengakibatkan cyclesehingga sisi AF tidak yang dipilih.

Langkah 10: Ulangi langkah 2. Pilih sisi berbobot maksimum selanjutnya dan pastikan

tidak terjadi cycle. BF sisi yang dipilih. T={EH,AD,FG,CE,AG,AH,BF}

(59)

Langkah 3 Langkah 4

Langkah 5

Langkah 6

Langkah 7 _{Langkah 8}

Langkah 9 Langkah 10

Karena sudah diperoleh minimum spanning tree-nya, maka langkah dapat dihentikan.

Hasil maximum spanning tree yang diperoleh dari perhitungan menggunakan

(60)

[image:60.612.248.404.80.200.2]

Gambar 3.8 Maximum Spanning Tree dengan Algoritma Kruskal pada Graf G dengan Banyak Sisi > 2(p – 1)

Dari perhitungan Algoritma Kruskal di atas diperoleh maximum spanning tree dengan jumlah bobot sebagai berikut :

W(T) = W(A,D) + W(A,G) + W(A,H) + W(B,F) + W(C,E) + W(E,H) + W(F,G) = 29 + 26 + 25 + 15 + 27 + 33 + 28 = 183

Jadi diperoleh maximum spanning treedenga T = {AD,AG,AH,BF,CE,EH,FG}

tree-nyadiperoleh adalah 8 titik dan 7 sisi, dan banyak langkah yang ditempuh adalah

10.

Catatan: Karena dalam mencari maximum spanning tree langkahnya adalah dilakukan pengurutan terlebih dahulu pada setiap bobot dari terbesar hingga tekecil, dan dilanjutkan dengan menambahkan bobot yang telah diurutkan tadi hingga terbentuk maximum spanning tree. Jadi banyak kemungkinan maximum spanning tree yang dapat terbentuk hanya satu.

3.4 Perhitungan Maximum Spanning Tree Menggunakan Algoritma Sollin

3.4.1 Perhitungan Maximum Spanning Tree pada Graf G dengan Banyak Sisi = 2(p –

1)

Untuk menetukan maximum spanning tree dengan menggunakan Algoritma Sollin

(61)

Langkah 0 : T = himpunan semua sisi.

Urutkan sisi-sisi graf dari besar ke kecil.

AD = 29 CE = 27

AG = 26 AH = 25

AE = 22 AF = 17

BC = 14 AC = 13

BD = 10 AB = 9

BH = 7 BE = 6

BG = 4 DC = 3

Langkah 1 : Mulai dari sisi dengan bobot paling minimum, yaitu sisi DC dengan bobot 3. Hapus sisi DC dari T.

Langkah 2 : Pastikan semua vertex terhubung. Pilih sisi berbobot minimum selanjutnya. BG sisi terpilih. Hapus sisi BG di T.

Langkah 3 : Ulangi langkah 2. Pilih sisi berbobot minimum selanjutnya. BG sisi terpilih. Hapus sisi BE di T.

Langkah 4 : Ulangi langkah 2. Pilih sisi berbobot minimum selanjutnya. BH sisi

terpilih. Hapus sisi BH di T.

Langkah 5 : Ulangi langkah 2. Pilih sisi berbobot minimum selanjutnya. BG sisi terpilih. Hapus sisi BG di T.

Langkah 6 : Ulangi langkah 2.Pilih sisi berbobot minimum selanjutnya. AB sisi terpilih. Hapus sisi AB di T.

Langkah 7 : Ulangi langkah 2.Pilih sisi berbobot minimum selanjutnya. BD sisi

(62)

Langkah 1 Langkah 2

Langkah 3 Langkah 4

(63)

Langkah 7

Karena sudah tidak terdapat lagi sisi yang dihapus dan itu artinya semua titik sudah

terhubung dan sudah diperoleh maximum spanning tree-nya, maka langkah dapat

[image:63.612.126.519.75.233.2]

menggunakan Algoritma Sollin dapat dilihat pada gambar di bawh ini :

Gambar 3.9 Maximum Spanning Tree dengan Algoritma Sollin pada Graf G dengan Banyak Sisi = 2(p – 1)

Dari perhitungan Algoritma Sollin di atas diperoleh Maximum Spanning Tree dengan

W(T) = W(A,D) + W(A,E) + W(A,F) + W(A,G) + W(A,H) + W(B,C) + W(C,E) = 29 + 22 + 17 + 26 + 25 + 14 + 27 = 160

Jadi diperoleh maximum spanning treedengan T = { A, B, C, D, E, F, G, H } dengan

bobot 160, dan dari 8 titik serta 14 sisi, setelah diperoleh maximum spanning tree-nya

(64)

dilakukan pengurutan terlebih dahulu pada setiap bobot dari terkecil hingga terbesar, dan dilanjutkan dengan menghapus bobot yang telah diurutkan tadi hingga terbentuk maximum spanning tree. Jadi banyak kemungkinan maximum spanning tree yang dapat terbentuk hanya satu.

3.4.2 Perhitungan Maximum Spanning Tree pada Graf G dengan Banyak Sisi = 2(p – 1) dan Terdapat Sisi yang Memiliki Bobot Sama

Urutkan sisi-sisi graf dari besar ke kecil.

CE = 14 BD = 12

AD = 10 AF = 10

BC = 7 BH = 7

AC = 6 AG = 6

BE = 6 AE = 4

BG = 4 AB = 3

AH = 3 DC = 3

Langkah 1 : Mulai dari sisi dengan bobot paling minimum, yaitu sisi DC dengan bobot 3. Hapus sisi DC dari T.

Langkah 2 : Pastikan semua vertex terhubung. Pilih sisi berbobot minimum selanjutnya. AH sisi terpilih. Hapus sisi AH di T.

Langkah 3 : Ulangi langkah 2. Pilih sisi berbobot minimum selanjutnya. AB sisi terpilih. Hapus sisi AB di T.

Langkah 4 : Ulangi langkah 2. Pilih sisi berbobot minimum selanjutnya. BG sisi terpilih. Hapus sisi BG di T.

(65)

Langkah 6 : Ulangi langkah 2. Pilih sisi berbobot minimum selanjutnya. BE sisi

terpilih. Hapus sisi BE di T.

Langkah 7 : Ulangi langkah 2. Pilih sisi berbobot minimum selanjutnya. AG sisi terpilih. Tetapi itu jika sisi AG dihapus, maka titik G akan terisolasi, sehingga sisi AG tidak dihapus T.

Langkah 8 : Ulangi langkah 2. Pilih sisi berbobot minimum selanjutnya. AC sisi

terpilih. Hapus sisi AC di T.

Langkah 1 Langkah 2

(66)

Langkah 5

Langkah 6

Langkah 7

Karena sudah tidak terdapat lagi sisi yang dihapus dan itu artinya semua titik sudah

terhubung dan sudah diperoleh maximum spanning tree-nya, maka langkah dapat

(67)

[image:67.612.255.387.85.218.2]

Gambar 3.11 Maximum Spanning Tree dengan Algoritma Sollin pada Graf G dengan Banyak Sisi = 2(p – 1) dan Terdapat Sisi yang Memiliki Bobot Sama

Dari perhitungan Algoritma Sollin di atas diperoleh maximum spanning tree

W(T) = W(A,D) + W(A,F) + W(A,G) + W(B,C) + W(B,D) + W(B,H) + W(C,E) = 10 + 10 + 6 + 7 + 12 + 7 + 14 = 66

Jadi diperoleh maximum spanning tree dengan T = { A, B, C, D, E, F, G, H }

dengan bobot 66, dan dari 8 titik dan 14 sisi dan terdapat sisi yang memiliki bobot

sama, setelah diperoleh maximum spanning tree-nya diperoleh 8 titik dan 7 sisi, dan

banyak langkah yang ditempuh adalah 7.

(68)

1)

Urutkan sisi-sisi graf dari kecil ke besar.

CE = 27 AG = 26

AH = 25 AE = 22

AF = 17 AC = 13

BD = 10 AB = 9

BE = 6 BG = 4

CD = 3

Langkah 1 : Mulai dari sisi dengan bobot paling minimum, yaitu sisi CD dengan

bobot 3. Hapus sisi CD dari T.

Langkah 2 : Pastikan semua verteks terhubung. Pilih sisi berbobot minimum selanjutnya. BG sisi terpilih. Hapus sisi BG di T.

Langkah 3 : Ulangi langkah 2. Pilih sisi berbobot minimum selanjutnya. BG sisi terpilih. Hapus sisi BE di T.

Langkah 4 : Ulangi langkah 2. Pilih sisi berbobot minimum selanjutnya. AB sisi

(69)

Langkah 5 : Ulangi langkah 2. Pilih sisi berbobot minimum selanjutnya. BD sisi

terpilih. Tetapi hal ini menyebabkan titik D terisolasi, sehingga sisi BD tidak dihapus dari T.

Langkah 6 : Ulangi langkah 2. Pilih sisi berbobot minimum selanjutnya. AC sisi terpilih. Hapus sisi AC di T.

Langkah 1 Langkah 2

(70)

Langkah 5

Langkah 6

Karena sudah tidak terdapat lagi sisi yang dapat dihapus dan itu artinya semua titik

sudah terhubung dan sudah diperoleh maximum spanning tree-nya, maka langkah

dapat dihentikan. Hasil maximum spanning tree yang diperoleh dari perhitungan

[image:70.612.123.525.77.283.2]

menggunakan Algoritma Sollin dapat dilihat pada gambar di bawah ini :

Gambar 3.11 Maximum Spanning Tree dengan Algoritma Sollin pada Graf G dengan banyak sisi < 2(p – 1)

Dari perhitungan Algoritma Sollin di atas diperoleh maximum spanning tree

(71)

Jadi diperoleh maximum spanning tree dengan T = { A, B, C, D, E, F, G, H }

dengan bobot 136, dan dari 8 titik dan 11 sisi, setelah diperoleh maximum spanning

tree-nya diperoleh 8 titik dan 7 sisi, dan banyak langkah yang ditempuh adalah 6.

Catatan: Karena dalam mencari maximum spanning tree langkahnya adalah dilakukan pengurutan terlebih dahulu pada setiap bobot dari terbesar hingga terkecil, dan dilanjutkan dengan menghapus bobot yang telah diurutkan tadi hingga terbentuk maximum spanning tree. Jadi banyak kemungkinan maximum spanning tree yang dapat terbentuk hanya satu.

3.4.4 Perhitungan Maximum Spanning Tree pada Graf G dengan Banyak Sisi >2(p–1)

Urutkan sisi-sisi graf dari kecil ke besar.

EH = 33 AD = 29

FG = 28 CE = 27

AG = 26 AH = 25

AE = 22 CF = 21

AF = 17 BF = 15

BC = 14 AC = 13

(72)

BH = 7 BE = 6