ANALISIS RISIKO OPERASIONAL MENGGUNAKAN
PENDEKATAN DISTRIBUSI KERUGIAN
DENGAN METODE AGREGAT
YUSUFI ARBI
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ABSTRAK
YUSUFI ARBI. Analisis Risiko Operasional Menggunakan Pendekatan Distribusi Kerugian dengan Metode Agregat. Dibimbing oleh RETNO BUDIARTI dan I GUSTI PUTU PURNABA.
Risiko operasional didefinisikan sebagai risiko kerugian yang disebabkan oleh kesalahan proses internal atau eksternal. Asuransi sebagai institusi keuangan juga dihadapkan pada risiko ini. Pencatatan kerugian operasional di perusahaan asuransi, masih belum terlaksana dengan baik sehingga berdampak pada terbatasnya data kerugian operasional. Pada karya ilmiah ini data kerugian operasional yang diamati diperoleh dari pembayaran klaim. Secara umum, banyaknya klaim asuransi dapat dimodelkan dengan menggunakan sebaran Poisson, dengan nilai harapan dari klaim sama dengan ragamnya dan sebaran binomial negatif, dengan nilai harapan lebih kecil dari ragamnya.
Alat analisis yang digunakan dalam pengukuran potensi kerugian adalah pendekatan distribusi kerugian dengan metode agregat di mana data kerugian dikelompokkan dalam distribusi frekuensi dan severitas. Dengan melakukan simulasi sebanyak kali dihasilkan nilai total klaim yang merupakan jumlah dari potensi kerugian klaim individu dari setiap simulasi yang dilakukan. Kemudian, dari hasil tersebut ditetapkan nilai potensi kerugian (OpVar) pada tingkat kepercayaan tertentu.
ABSTRACT
YUSUFI ARBI. Operational Risk Analysis Using Loss Distribution Approach with Aggregate Method. Supervised by RETNO BUDIARTI and I GUSTI PUTU PURNABA.
Operational risk is defined as the risk of loss resulting from inadequate or failed internal processes or external problems. Insurance companies as financial institution that also faced at risk. Recording of operating losses in insurance companies, were not properly conducted so that the impact on the limited data for operational losses. In this work, the data of operational loss observed from the payment of the claim. In general, the number of insurance claims can be modelled using the Poisson distribution, where the expected value of the claims is similar with variance, while the negative binomial distribution, the expected value was bound to be less than the variance.
Analysis tools are used in the measurement of the potential loss is the loss distribution approach with the aggregate method. In the aggregate method, loss data grouped in a frequency distribution and severity distribution. After doing 10.000 times simulation are resulted total loss of claim value, which is total from individual claim every simulation. Then from the result was set the value of potential loss (OpVar) at a certain level confidence.
ANALISIS RISIKO OPERASIONAL MENGGUNAKAN
PENDEKATAN DISTRIBUSI KERUGIAN
DENGAN METODE AGREGAT
YUSUFI ARBI
Skripsi
sebagai salah satu syarat untuk memperoleh gelar
Sarjana Sains pada
Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Judul Skripsi : Analisis
Risiko
Operasional
Menggunakan
Pendekatan
Distribusi Kerugian dengan Metode Agregat
.Nama
: Yusufi Arbi
NIM
: G54080011
Menyetujui
Tanggal Lulus:
Pembimbing I,
Ir. Retno Budiarti, MS.
NIP: 19610729 198903 2 001
Pembimbing II,
Dr. Ir. I Gusti Putu Purnaba, DEA.
NIP: 19651218 199002 1 001
Mengetahui:
Ketua Departemen,
KATA PENGANTAR
Puji syukur penulis panjatkan kepada Allah swt atas berkat, rahmat dan kasih sayang-Nya sehingga penulis mampu menyelesaikan karya ilmiah ini. Berbagai kendala dialami oleh penulis sehingga banyak sekali orang yang membantu dan berkontribusi dalam pembuatan karya ilmiah ini. Oleh karena itu, dalam kesempatan ini penulis mengucapkan terima kasih kepada:
1. keluarga tercinta: Apa dan Ama. Ama sebagai pemberi motivasi dan Apa sebagai sumber inspirasi, adikku Novetra Subuhadi dan Islamia Fuada (terima kasih atas doa, dukungan, kesabaran dan kasih sayangnya), Alm. Atuak Amat yang pasti selalu mendoakanku, Enek Ina, Enek Marlianis, Pak Odang Aznil, Pak Odang Meh, Pak Ongah, Ante Wati, Ante Ina, Ibu Yeni, Ni Pipi, Ciat dan Ira (terima kasih atas doa, semangat, motivasi dan dukungannya), Sepupuku Tesi, Titik, Pian, Icha, dhani dan Andien (Terimakasih atas doa dan keceriannya), Rahmadini Suryani (terima kasih atas kasih sayang, dan doanya), 2. Ir. Retno Budiarti, MS. selaku dosen pembimbing I yang telah meluangkan waktu dan
pikiran dalam membimbing, memberi motivasi, semangat dan doa,
3. Dr. Ir. I Gusti Putu Purnaba, DEA. selaku dosen pembimbing II yang telah memberikan ilmu, kritik dan saran, motivasi serta doanya,
4. Dr. Ir. I Wayan Mangku, M.Sc. selaku dosen penguji yang telah memberikan ilmu, saran dan doanya,
5. semua dosen Departemen Matematika, terima kasih atas semua ilmu yang telah diberikan, 6. staf Departemen Matematika: Bapak Yono, Ibu Susi, Ibu Ade, Alm. Bapak Bono, Bapak
Deni, Mas Hery, Ibu Yanti atas semangat dan doanya,
7. Bari, Fachri dan Hendra yang telah meluangkan waktu untuk menjadi pembahas pada seminar karya ilmiah saya,
8. teman-teman satu bimbingan: Khafidz, Yunda, Fitriah dan Edi,
9. sahabatku Hardono, Dahen, Herlan, Irwan, Ridwan, Haryanto, Ari, Izzudin, Beni, Fuka, Khafidz, Nova, Fenny, Achi, Gita, Rischa, Mega (terimakasih atas kebersamaannya), 10. teman-teman mahasiswa Matematika angkatan 45 (terimakasih atas doa, dukungan
semangatnya serta kebersamaannya selama 3 tahun),
11. kakak-kakak Matematika angkatan 43, dan 44 yang menjadi cermin untuk menjadi pribadi yang lebih baik,
12. adik-adik Matematika angkatan 46 dan 47 yang terus mendukung agar berkembang, 13. Gumatika Ceria, Gumakusi dan IKMP yang menunjukkan sebuah hal yang baru, 14. semua pihak yang telah membantu dalam penyusunan karya ilmiah ini.
Semoga karya ilmiah ini dapat bermanfaat bagi dunia ilmu pengetahuan khususnya bidang matematika dan menjadi inspirasi bagi penelitian selanjutnya.
Bogor, Januari 2013
RIWAYAT HIDUP
Penulis dilahirkan di Tiakar Sumatera Barat, pada tanggal 30 Desember 1989 dari Bapak H. Aldiwarman dan Ibu Nirmeli. Penulis merupakan putra Sulung dari tiga bersaudara.
Pada tahun 1996 penulis lulus dari TK Aisyiah Anding, tahun 2002 penulis lulus dari SD Negeri 43 Tiakar, tahun 2005 penulis lulus dari SMP Negeri 1 Kecamatan Guguak, tahun 2008 penulis lulus dari SMA Negeri 1 Kecamatan Guguak. Penulis diterima sebagai mahasiswa Institut Pertanian Bogor pada tahun 2008 melalui jalur Undangan Seleksi Masuk IPB (USMI), Tingkat Persiapan Bersama. Pada tahun 2009, penulis memilih mayor Matematika pada Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
Selama mengikuti perkuliahan, penulis menjadi asisten mata kuliah Metode Statistika dan Pemograman Linear (S1) pada tahun akademik 2010-2011. Tahun 2008-2009 penulis mendapatkan beasiswa POM (Persatuan Orng tua Mahasiswa) dari Institut Pertanian Bogor dan Beasiswa Bank Indonesia pada tahun 2011-2012.
Penulis aktif dalam organisasi kemahasiswaan di kampus, seperti organisasi himpunan profesi Departemen Matematika yang dikenal dengan GUMATIKA (Gugus Mahasiswa Matematika) sebagai Staf Divisi Sosial Komunikasi tahun 2009-2010 dan sebagai Ketua organisasi mahasiswa daerah Payakumbuh yang dikenal dengan IKMP (Ikatan Kekeluargaan Mahasiswa Payakumbuh). Penulis juga aktif dalam organisasi komunitas GEN BI (Generasi Baru Indonesia) yang dibentuk oleh Bank Indonesia pada tahun 2011-2013.
DAFTAR ISI
Halaman
DAFTAR TABEL ... ix
DAFTAR GAMBAR ... ix
DAFTAR LAMPIRAN ... ix
I PENDAHULUAN 1.1 Latar Belakang ... 1
1.2 Tujuan Penulisan ... 1
II LANDASAN TEORI 2.1 Pengukuran Risiko Operasional ... 2
2.2 Percobaan Acak, Ruang Contoh, Kejadian, dan Peluang ... 2
2.3 Peubah Acak dan Fungsi Sebaran ... 2
2.4 Nilai Harapan, Ragam dan Momen ... 4
2.5 Proses Stokastik ... 4
2.6 Metode Konvolusi ... 5
III PEMBAHASAN 3.1 Distribusi Total Kerugian ... 7
3.2 Proses Compound Poisson ... 8
3.3 Sifat Sebaran Compound Poisson ... 11
3.3 Pendekatan Distribusi Total Klaim ... 12
3.3 Pengukuran Risiko Operasional Klaim ... 13
IV SIMPULAN ... 16
DAFTAR PUSTAKA ... 17
LAMPIRAN ... 18
DAFTAR TABEL
Halaman
1 Nilai OpVaR pada tingkat kepercayaan 99% dan 95% (hasil dalam sepuluh ribuan) ... 14 2 Statistik simulasi dengan 100 kali ulangan ... 15 3 Simulasi ulangan ke-1 ... 20
DAFTAR GAMBAR
Halaman
1 Nilai OpVaR pada tingkat kepercayaan 99% dan 95%. ... 15 2 Grafik simulasi total kerugian pada ulangan pertama dengan n = 10.000
(hasil dalam sepuluh ribuan). ... 21
DAFTAR LAMPIRAN
Halaman
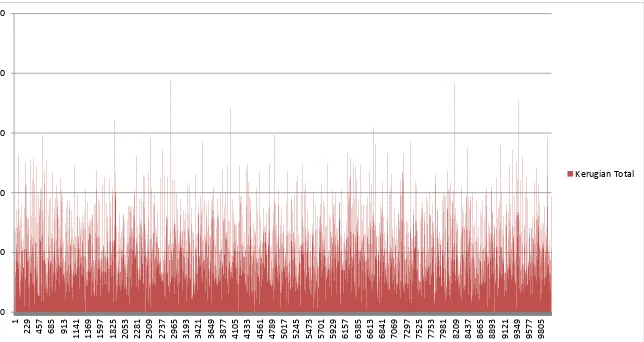
1 Sifat-sifat fungsi pembangkit momen ... 19 2 Hasil simulasi dengan MATLAB ... 20 3 Grafik simulasi total kerugian pada ulangan pertama dengan n = 10.000
(hasil dalam sepuluh ribuan). ... 21
1
I PENDAHULUAN
1.1 Latar belakang
Sektor jasa keuangan merupakan salah satu sektor industri yang sering menghadapi hambatan strategis. Industri keuangan menghadapi perubahan peraturan seiring dengan perkembangan teknologi. Asuransi sebagai institusi keuangan yang sedang berkembang saat ini dalam menjalankan aktivitasnya juga dihadapkan pada risiko, karena pada dasarnya risiko selalu melekat pada seluruh aktivitas perusahaan. Besarnya risiko dalam suatu perusahaan pada hakikatnya menunjukkan besarnya potensi masalah oleh perusahaan tersebut.
Salah satu risiko yang belum banyak diketahui karakteristiknya dibandingkan beberapa risiko lainnya adalah risiko operasional. Risiko operasional adalah risiko yang antara lain disebabkan oleh adanya ketidakcukupan atau tidak berfungsi proses internal, kesalahan manusia, kegagalan sistem, atau adanya masalah eksternal yang mempengaruhi operasional perusahaan. Meskipun terlihat sederhana, jika tidak dikelola dengan baik risiko ini akan menimbulkan dampak yang besar. Menurut BASEL II (peraturan perbankan internasional) ukuran besarnya risiko operasional (Operational Value at Risk) disingkat dengan OpVaR.
BASEL II memberikan beberapa metode pengukuran risiko operasional, di antaranya
Basic Indicator Approach (pendekatan indikator dasar), Standardized Approach
(pendekatan standar) dan Advance
Measurement Approach (pendekatan
pengukuran lanjutan). Pada dua metode pertama mensyaratkan sebaran normal, padahal dalam kenyataannya kerugian seringkali menyebar tidak normal (Situngkir dan Surya 2006). Oleh karena itu, dalam peraturan BASEL II ini diperbolehkan menggunakan metode alternatif (pendekatan pengukuran lanjutan). Salah satu teknik yang digunakan yaitu Loss Distribution Approach
(pendekatan distribusi kerugian) yang dipercaya sangat relevan dalam pengukuran risiko operasional pada perusahaan asuransi.
Pencatatan kerugian operasional khususnya di perusahaan asuransi, masih belum terlaksana dengan baik sehingga berdampak pada terbatasnya data untuk kerugian dalam risiko operasional. Pada karya ilmiah ini data kerugian operasional yang diamati diperoleh dari pembayaran klaim. Secara umum, klaim asuransi dapat dimodelkan dengan menggunakan sebaran yang memiliki sifat yang sama seperti sebaran Poisson, di mana nilai harapan dari klaim sama dengan ragamnya dan sebaran binomial negatif, di mana nilai harapan lebih kecil dari ragamnya.
1.2 Tujuan
Tujuan dari karya ilmiah ini yaitu: 1. Mempelajari karakteristik statistik risiko
operasional (OpVaR) pada perusahaan asuransi.
2
II LANDASAN TEORI
2.1 Pengukuran Risiko Operasional
Terdapat beberapa pendekatan untuk mengukur risiko operasional sebagaimana yang disarankan oleh lembaga keuangan internasional (Bank for International Settlement, BIS) yaitu:
a. Pendekatan indikator dasar. b. Pendekatan standar.
c. Pendekatan pengukuran lanjutan. Pada dua pendekatan pertama, lembaga keuangan internasional (BIS) telah menentukan standar baku perhitungan risiko operasionalnya, sementara untuk pendekatan pengukuran lanjutan, lembaga keuangan internasional (BIS) menyerahkan pada internal bank atau perusahaan untuk perhitungannya, dengan syarat metode ini memenuhi kriteria kelayakan perhitungan.
Salah satu teknik dari pendekatan pengukuran lanjutan adalah pendekatan distribusi kerugian. Pendekatan distribusi kerugian didasarkan pada data kerugian operasional internal. Data kerugian operasional dikelompokkan dalam distribusi frekuensi kejadian atau events dan distribusi severitas (besarnya kerugian operasional). Distribusi data frekuensi kejadian operasional merupakan distribusi yang bersifat diskret dan proses stokastik data umumnya mengikuti distribusi Poisson. Sedangkan distribusi data severitas kerugian operasional merupakan distribusi yang bersifat kontinu. Distribusi severitas kerugian operasional umumnya mengikuti karakteristik distribusi eksponensial (Muslich 2007).
Alat analisis yang digunakan dalam pengukuran potensi kerugian adalah pendekatan distribusi kerugian dengan metode agregat. Dalam metode agregat, data kerugian operasional didistribusikan dalam distribusi frekuensi dan severitas. Dengan dua jenis distribusi frekuensi dan severitas tersebut, distribusi total kerugian operasional tinggal menggabungkannya menjadi satu distribusi total kerugian. Distribusi total kerugian ini yang kemudian digunakan untuk memproyeksikan potensi kerugian risiko operasional.
2.2 Percobaan Acak, Ruang Contoh, Kejadian, dan Peluang
Definisi 1 (Percobaan Acak)
Percobaan acak adalah percobaan yang dapat dilakukan berulang-ulang dalam kondisi yang sama. Semua kemungkinan hasil yang
akan muncul dapat diketahui, tetapi hasil pada percobaan berikutnya tidak dapat ditebak dengan tepat.
(Hogg et al. 2005)
Definisi 2 (Ruang Contoh)
Ruang contoh adalah himpunan semua hasil yang mungkin dari suatu percobaan acak, dan dinotasikan dengan Ω.
(Grimmet dan Stirzaker 1992)
Definisi 3 (Kejadian)
Kejadian adalah suatu himpunan bagian dari ruang contoh Ω.
(Grimmet dan Stirzaker 1992)
Definisi 4 (Kejadian Saling Lepas)
Kejadian A dan B disebut saling lepas jika irisan dari keduanya adalah himpunan kosong ( .
(Grimmet dan Stirzaker 1992)
Definisi 5 (Medan- )
Medan- adalah suatu himpunan yang anggotanya terdiri atas himpunan bagian ruang contoh , yang memenuhi syarat berikut:
1. .
2. Jika , maka
3. Jika , maka ⋃ (Grimmet dan Stirzaker 1992)
Definisi 6 (Ukuran Peluang)
Ukuran peluang P pada ( merupakan fungsi yang memenuhi:
1. ( (
2. bersifat aditif tak hingga, yaitu jika dengan maka
( ∑ (
Pasangan ( disebut ruang peluang. (Grimmet dan Stirzaker 1992)
2.3 Peubah Acak dan Fungsi Sebaran
Definisi 7 (Peubah Acak)
Misalkan Ω adalah ruang contoh dari suatu percobaan acak. Fungsi terdefinisi pada yang memetakan setiap unsur ke satu dan hanya satu bilangan real ( disebut peubah acak.
Ruang dari adalah himpunan bagian bilangan real ( .
3
Catatan :
Peubah acak dinotasikan dengan huruf kapital, misalnya sedangkan nilai peubah acak dinotasikan dengan huruf kecil seperti
Definisi 8 (Fungsi Sebaran)
Misalkan adalah peubah acak dengan ruang . Misalkan kejadian ( , maka peluang dari kejadian adalah
( (
Fungsi disebut fungsi sebaran dari peubah acak
(Hogg et al. 2005)
Definisi 9 (Peubah Acak Diskret)
Peubah acak dikatakan diskret jika nilainya hanya berada pada himpunan bagian yang terhitung dari .
(Grimmet dan Stirzaker 1992) Catatan :
Suatu himpunan bilangan disebut terhitung jika terdiri atas terhingga bilangan atau dapat dikorespondensikan 1-1 dengan bilangan bulat positif.
Definisi 10 (Peubah Acak Kontinu)
Peubah acak dikatakan kontinu jika fungsi sebarannya dapat diekspresikan sebagai ( ∫ ( ,
untuk suatu fungsi yang dapat diintegralkan. Selanjutnya fungsi disebut fungsi kepekatan peluang (probability density function) bagi
(Hogg et al. 2005)
Definisi 11 (Fungsi Massa Peluang)
Fungsi massa peluang dari peubah acak diskret adalah fungsi yang diberikan oleh : ( (
(Hogg et al. 2005)
Definisi 12 (Fungsi Kepekatan Peluang Bersyarat)
Misalkan dan adalah peubah acak kontinu, yang menyebar bersama dengan fungsi kepekatan peluang bersama dan fungsi kepekatan peluang marginal dari adalah
( Fungsi kepekatan peluang bersyarat dari dengan syarat adalah ( ( ( .
(Grimmet dan Stirzaker 1992)
Definisi 13 (Kejadian Saling Bebas)
Misalkan kejadian tidak memengaruhi kejadian dengan peluang (
sedemikian sehingga peluang bersyarat jika diketahui adalah
( (
maka kejadian dan dikatakan saling bebas. Kemudian dapat diperoleh peluang bersamanya
( ( ( ( ( dan untuk ( peluang bersyarat jika diketahui adalah
( ( ( ( (Grimmet dan Stirzaker 1992)
Definisi 14 (Peubah Acak Binomial Negatif)
Peubah acak dikatakan menyebar binomial negatif dengan parameter ( dan jika memiliki fungsi massa peluang
( { (
(Grimmet dan Stirzaker 1992)
Definisi 15 (Peubah Acak Poisson)
Peubah acak dikatakan menyebar Poisson dengan parameter , jika memiliki fungsi massa peluang
( ( dengan .
(Hogg et al. 2005)
Definisi 16 (Sebaran Multinomial)
Peubah acak diskret disebut menyebar multinomial dengan parameter dan adalah bilangan bulat positif, untuk semua dan jika fungsi massa peluangnya
( =
(
(Hogg et al. 2005)
Definisi 17 (Peubah Acak Eksponensial)
Suatu peubah acak disebut peubah acak eksponensial dengan parameter jika nilainya terletak pada dan memiliki fungsi kepekatan peluang
(
4
Definisi 18 (Peubah Acak Gamma)
Suatu peubah acak kontinu dikatakan menyebar Gamma ( , jika fungsi kepekatan peluangnya diberikan oleh
(
⁄
(
dengan dan ( , di mana ( ∫
(Hogg et al. 2005)
2.4 Nilai Harapan, Ragam dan Momen
Definisi 19 (Nilai Harapan)
i. Jika adalah peubah acak diskret dengan fungsi massa peluang ( maka nilai harapan , dinotasikan dengan ( adalah
( ∑ (
asalkan jumlah di atas konvergen mutlak. ii. Jika adalah peubah acak kontinu
dengan fungsi kepekatan peluang ( maka nilai harapan dari , dinotasikan dengan ( adalah
( ∫ (
asalkan integral di atas konvergen. Jika integral di atas divergen, maka nilai harapan dari tidak ada.
(Hogg et al. 2005)
Definisi 20 (Ragam)
Ragam dari peubah acak adalah nilai harapan kuadrat selisih antara dengan nilai harapannya. Secara matematis dapat dituliskan sebagai
( ( ( jika nilai harapannya ada. Jika nilai harapannya tidak ada, maka ragam dari peubah acak tidak ada.
(Hogg et al. 2005)
Definisi 21 (Momen)
a) Jika adalah peubah acak diskret dengan fungsi massa peluang ( maka
momen ke- atau dari ,
didefinisikan sebagai ( ∑
(
jika jumlah di atas konvergen. Jika jumlah di atas divergen, momen ke- dari peubah acak tidak ada.
b) Jika adalah peubah acak kontinu dengan fungsi kepekatan peluang (
maka momen ke- dari didefinisikan sebagai
( ∫
( jika integral di atas konvergen. Jika integral di atas divergen, maka momen ke- dari peubah acak tidak ada.
(Grimmet dan Stirzaker 1992)
Definisi 22 (Fungsi Pembangkit Momen)
Fungsi pembangkit momen dari suatu peubah acak didefinisikan sebagai
( (
untuk sehingga nilai harapan di atas ada.
Fungsi pembangkit momen mempunyai sifat-sifat sebagai berikut:
1. ( ( (
2. Jika mempunyai fungsi pembangkit momen ( dan maka mempunyai fungsi pembangkit momen
( (
3. Jika dan peubah acak yang saling bebas dengan fungsi pembangkit momen dan maka mempunyai fungsi pembangkit momen
( ( (
Bukti sifat 1, 2 dan 3 di lampiran 1.
(Grimmet dan Stirzaker 1992)
2.5 Proses Stokastik
Definisi 23 (Proses Stokastik)
Proses stokastik (stochastic process) ( adalah koleksi dari peubah acak. Untuk setiap dalam indeks , ( merupakan peubah acak. Jika menyatakan waktu , maka ( menyatakan kondisi proses saat . Jika T merupakan himpunan indeks terhitung maka, ( disebut proses stokastik waktu diskret dan jika T kontinu, maka ( disebut proses stokastik waktu kontinu.
(Ross 1996)
Definisi 24 (Proses Pencacahan)
Suatu proses stokastik ( disebut sebagai proses pencacahan (counting process) jika ( menyatakan banyaknya kejadian yang terjadi dalam selang waktu [0,t] dan ( harus memenuhi:
i. (
ii. ( bernilai bulat.
5
iv. Untuk ( ( menyatakan banyaknya kejadian yang terjadi dalam selang waktu ( .
(Ross 1996)
Definisi 25 (Proses Poisson)
Suatu proses pencacahan ( disebut proses Poisson (Poisson process) dengan laju , jika:
(i) (
(ii) Proses memiliki kenaikan bebas. (iii) Banyaknya kejadian yang terjadi dalam
setiap selang waktu sepanjang menyebar Poisson dengan nilai harapan . Sehingga untuk semua berlaku
( (
( untuk
(Ross 1996)
Definisi 26 (Proses Poisson Majemuk)
Suatu proses stokastik ( disebut sebagai proses Poisson majemuk (compound Poisson process), jika dapat dinyatakan sebagai
( ∑
(
dengan ( adalah proses Poisson dengan laju , dan adalah suatu barisan peubah acak independent and identically distribution (i.i.d) dengan suau fungsi sebaran , yang juga bebas terhadap (
(Ross 1996)
2.6 Metode Konvolusi
Metode Konvolusi Untuk Dua Peubah Acak
Misalkan dan adalah dua peubah acak yang saling bebas. Jumlah keduanya didefinisikan sebagai :
Untuk mencari fungsi distribusi dari , yaitu , adalah sebagai berikut :
Ambil dan
Garis dan daerah di bawah garis itu merupakan daerah
( ( ( . Untuk dan yang diskret dan non negatif maka menurut hukum peluang total :
( (
∑ ( (
∑ ( (
Karena dan saling bebas maka ( ∑ (
( (
sehingga fungsi peluang yang berkaitan dengan fungsi distribusi ini adalah :
( ∑ ( (
∑ ( ( =∑ ( (
Pernyataan (2.6.1) tersebut merupakan konvolusi dari dua peubah acak diskret.
Untuk dan peubah acak kontinu dan non negatif maka fungsi distribusi dari analog dengan peubah acak diskret, tetapi tanda ∑ diganti dengan tanda ∫, sehingga didapat :
( ∫ ( (
( ∫ ( (
Pernyataan di atas merupakan konvolusi dua peubah kontinu.
Notasi konvolusi untuk dua peubah acak adalah : ( ( (
Metode Konvolusi Secara Umum
Dalam menentukan distribusi jumlah dari peubah acak dapat digunakan proses konvolusi secara rekursif atau berulang-ulang. Misalkan peubah-peubah acak yang saling bebas dan non negatif yang menyatakan uang klaim dalam suatu polis asuransi. Jumlah uang klaim dari polis tersebut dilambangkan dengan :
merupakan peubah acak yang saling bebas
merupakan fungsi peluang dari ( merupakan fungsi distribusi dari
. Untuk model ini berlaku :
6
1. Dalam hal tepat dua peubah acak klaim, jika salah satu uang klaim dinotasikan dengan , maka kemungkinan bahwa uang klaim bernilai adalah ( dengan demikian
( ( (
2. Jika salah satu uang klaim mempunyai nilai , maka kemungkinan total uang dua klaim yang kurang dari atau sama dengan adalah sama dengan kemungkinan uang klaim lain yang kurang dari atau sama dengan ( atau dengan kata lain
( ( Notasinya adalah ( (
3. Dengan demikian kemungkinan untuk dua uang klaim adalah
( ( (
4. Untuk suatu nilai tertentu, bernilai antara 0 dan maka
( ( ∑ ( ( (
5. Untuk tepat tiga peubah acak klaim, di mana salah satu uang bernilai dan besar untuk dua klaim yang lain bernilai ( maka
( ( ∑ ( ( (
6. Untuk tepat empat peubah acak klaim ( ( ∑ ( ( (
Sehingga untuk peubah acak klaim ( ( ∑ ( ( (
Untuk memudahkan, maka konvolusi peubah acak dinotasikan sebagai berikut: ( ( (
jika ( mempunyai distribusi yang sama, misal maka distribusi jumlahnya dilambangkan .
Apabila diasumsikan bahwa banyaknya peubah acak misalnya dan saling bebas terhadap atau terhadap , dalam hal seperti ini dapat dicari fungsi distribusi dari
( ( ∑ (
(
∑ (
(
Karena dan saling bebas maka ( menjadi :
∑ ( (
(
(
Untuk ( yang berdistribusi sama maka:
( ∑ (
dengan
∑ ( (
(
(Ester 1998)
2.7 Value at Risk (VaR)
Value at risk adalah pengukuran suatu risiko yang dilakukan secara kuantitatif dengan memperkirakan potensi maksimum kerugian yang mungkin terjadi dengan suatu tingkat keyakinan tertentu.
7
III PEMBAHASAN
Pada hakikatnya, risiko dalam sektorkeuangan dibagi menjadi tiga bagian yaitu risiko pasar, risiko kredit dan risiko operasional. Risiko operasional, tidak sebagaimana dengan risiko pasar dan risiko kredit, terjadi pada setiap orang yang ada dalam perusahaan karena orang merupakan salah satu sumber dari risiko operasional. Risiko operasional mempunyai dimensi yang luas dan kompleks dengan sumber risiko yang merupakan gabungan dari berbagai sumber yang ada dalam organisasi, proses dan kebijakan, sistem dan teknologi, orang dan faktor lainnya (Muslich 2007).
Pencatatan kerugian operasional, khususnya di perusahaan asuransi masih belum terlaksana dengan baik sehingga berdampak pada terbatasnya data untuk kerugian dalam risiko operasional. Oleh karena itu pada karya ilmiah ini data kerugian operasional yang diamati diperoleh dari pembayaran klaim.
Metode pengukuran risiko operasional yang digunakan dalam karya ilmiah ini adalah metode alternatif (pendekatan pengukuran lanjutan). Salah satu teknik yang digunakan yaitu pendekatan distribusi kerugian dengan metode agregat yang dipercaya sangat relevan dalam pengukuran risiko operasional pada perusahaan asuransi (McNeil et al. 2005). Berikut ini adalah bentuk dari model risiko padapendekatan distribusi kerugian:
Misalkan :
banyaknya klaim yang dihasilkan dari portofolio polis pada waktu tertentu. = besarnya klaim ke- Sehingga model dari total kerugian risiko operasional dapat dituliskan sebagai berikut
. (1)
Model ini sering disebut juga model risiko kolektif Secara umum model (1) merepresentasikan klaim secara keseluruhan dari portofolio pada waktu tertentu. Peubah acak menyatakan banyaknya klaim dan erat kaitan dengan frekuensi klaim. Peubah acak menyatakan besarnya klaim ke-. Agar model lebih mudah diselesaikan maka diperlukan asumsi berikut(i) Peubah acak dan ( ) saling bebas.
(ii) Peubah acak saling bebas. (iii)Peubah acak memiliki
sebaran yang sama.
(Bowers et al. 1997)
3.1 Distribusi Total Kerugian
Distribusi total klaim dalam periode waktu tertentu dapat diperoleh dari distribusi banyaknya klaim dan distribusi besar klaim individu .
Misalkan merupakan peubah acak yang menyatakan besarnya klaim. Diketahui fungsi distribusi adalah . Bila terjadi klaim sebanyak maka besarnya total klaim adalah dan distribusi dinyatakan dengan ( .
Momen ke-k = . Fungsi pembangkit momen dari
(
Fungsi pembangkit momen dari (
Fungsi pembangkit momen dari (
Untuk menentukan nilai harapan dan ragam dari maka diperlukan dua teorema berikut
Teorema 1
Misalkan ( adalah peubah acak dua dimensi maka nilai harapan dari dapat ditentukan lewat nilai harapan dengan syarat sebagai berikut :
.
Bukti (Teorema 1)
Jika dan adalah peubah acak diskret, maka [ ] ∑ ( ∑ ∑ ( ( ∑ ∑ ( ( ( ∑ ∑ ( ∑ ∑ ( ∑ (
8 ∫ ∫ ( ( ( ∫ ∫ ( ∫ ∫ ( ∫ (
Jadi, terbukti .
Teorema 2
Misalkan ( adalah peubah acak dua dimensi maka:
[ ]
Bukti (Teorema 2)
( [ ] ( ] ( ( ( ( ( ( { ( ( [ ] } [ ] Jadi terbukti [ ] [ ]
Atas dasar Teorema 1 dan Teorema 2 dan dalam kaitannya dengan ketiga asumsi yang digunakan, maka diperoleh nilai harapan dari : (2) Bukti (2)
dan ragam :
(3) Bukti (3) [ ] [ ] [ ] di mana
Selanjutnya akan diperlihatkan rumus fungsi pembangkit momen dari .
( ( ( ( (4)
Bukti (4)
(
[ ( ]
[ ] karena saling bebas, maka
( [ ] dan berdistribusi identik, diperoleh:
(
( (
( ( (
Selanjutnya untuk menentukan fungsi distribusi dari dapat dilihat sebagai berikut:
( ( ∑ ( ( ∑ ( (
Menurut operasi konvolusi untuk risiko kolektif dan sesuai dengan asumsi berdistribusi sama ,
( ∑ (
(
Jika distribusi besarnya klaim individu adalah diskret dengan fungsi probabilitas ( ( maka distribusi dari total klaim juga diskret, sehingga fungsi probabilitas dari dapat diperoleh sebagai berikut : ( ∑ ( ( ∑ ( ( (
3.2 Proses Compound Poisson
Pada umumnya, sebaran dari peubah acak (banyaknya klaim) adalah sebaran Poisson dengan fungsi massa peluang
( ( dengan
Nilai harapan dan ragam dari sebaran Poisson berturut-turut adalah
Misalkan dan merupakan nilai harapan dan momen ke-2 dari , dapat dinyatakan dan
9
compound Poisson. Sehingga, nilai harapan dan ragam dari sebaran compound Poisson adalah
(8) dan
(9)
Bukti (8)
Diketahui S= + +…+ , dengan , ,… menyebar i.i.d dan menyebar Poisson. Akan dibuktikan .
( (∑ ∑ [∑ ] ( ∑ [∑ ] ( ∑ [∑ ( ] ( ∑ ( ∑ ( ( Bukti (9)
Diketahui S= + +…+ , dengan , ,… menyebar i.i.d dan menyebar Poisson. Akan dibuktikan : . ( ((∑ ∑ (∑ ) ( ∑ ∑ ( ) ∑ ∑ ( ( ( ∑ ( ) ( ( ( ∑ ( ( ∑( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( Fungsi pembangkit momen untuk sebaran Poisson yaitu:
( (
Dengan mensubstitusikan fungsi pembangkit momen Poisson diperoleh persamaan berikut
(
(
( (10)
( ( Sehingga, fungsi pembangkit momen untuk sebaran compound Poisson dapat dituliskan sebagai berikut:
( ( ( (
( ( ( (11) Sebaran Poisson hanya dapat dipakai jika nilai ragamnya sama dengan nilai harapannya. Namun jika nilai ragam dari banyaknya kerugian lebih besar dari nilai harapannya maka sebaran yang digunakan untuk peubah acak N (banyaknya klaim) adalah sebaran binomial negatif dengan fungsi massa peluang (
(12) dengan
.
Nilai harapan dan ragam dari sebaran binomial negatif berturut-turut sebagai berikut
10
Misalkan dan berturut-turut merupakan nilai harapan dan momen ke-2 dari , dapat dinyatakan
Jika peubah acak (banyaknya klaim) memiliki sebaran binomial negatif maka peubah acak S pada persamaan (1) memiliki sebaran compound binomial negatif. Sehingga, diperoleh nilai harapan dan ragam dari sebaran compound binomial negatif sebagai berikut
(13) dan
(14)
Bukti (13)
Diketahui: dengan menyebar i.i.d dan menyebar binomial negatif.
Akan dibuktikan : . ( (∑ ∑ [∑ ] ( ∑ [∑ ] ( ∑ [∑ ( ] ( ∑ ( ∑ ( Bukti (14)
Diketahui: dengan menyebar i.i.d dan menyebar binomial negatif Akan dibuktikan: ( (∑ ) | ∑ (∑ ) | ( ∑ [ ∑ ( ) ∑ ∑ ( ( ) ] ( ∑[ ( ) ( ( ] ( ∑ ( ( ∑( ( ( ( { } ( ( ( { } ( ( ( { } ( ( ( ( { ( } ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( (
11
(
Dengan mensubstitusikan fungsi pembangkit momen binomial negatif pada persamaan (4) maka diperoleh fungsi pembangkit momen untuk sebaran compound
binomial negatif adalah sebagai berikut: ( ( (
(
( ( ( (15)
3.3 Sifat Sebaran Compound Poisson
Sebaran compound Poisson memiliki dua sifat, yaitu:
1. Jika setiap peubah acak menyebar
compound Poisson, maka jumlah dari peubah acak tersebut juga menyebar
compound Poisson.
2. Jika peubah acak S dinyatakan S= N1+ N2+…+
maka peubah acak S memiliki sebaran
compound Poisson
Berikut akan dijelaskan lebih lanjut sifat-sifat dari sebaran compound Poisson.
1. Jika setiap peubah acak menyebar
compound Poisson, maka jumlah dari peubah acak tersebut juga menyebar
compound Poisson ( ∏ ( ∑ ( ( ( ∑ ( ) (
untuk lebih jelasnya maka sifat 1 dirangkum dalam Teorema 3 berikut :
Teorema 3
Jika peubah acak saling bebas, dan menyebar compound Poisson dengan parameter dan fungsi kepekatan peluang dari kerugian ( , maka , menyebar compound
Poisson dengan ∑ ( ( ∑ ( (
Bukti (Teorema 3)
Diketahui :
(
Berdasarkan persamaan (10), maka ( ( ( ( Akan dibuktikan ( maka ( ( ∑ ( ( ( ( ( ( ( ( ( ( ( ( ∏ ( ∏ ( ( ( ∑ ( ( ( ( [∑ ( ( ]) (
Persamaan di atas merepresentasikan dua peranan penting dalam memodelkan klaim. Pertama, jika portofolio menyebar
compound Poisson dan saling bebas, maka klaim majemuk dari portofolio yang dikombinasikan juga menyebar compound
Poisson. Kedua, misal sebuah portofolio tunggal dengan jangka waktu tahun. Diasumsikan klaim agregat tahunan untuk jangka waktu tahun dan klaim majemuk tiap tahun saling bebas dan menyebar
compound Poisson. Sebaran tahunan untuk klaim majemuk tidak harus selalu sama. Menurut Teorema 3, total klaim untuk jangka waktu tahun menyebar compound Poisson. 2. Jika peubah acak S dinyatakan
maka peubah acak S memiliki sebaran
compound Poisson. Misalkan
merupakan peubah acak diskret dari sejumlah kerugian (klaim).
12
peubah acak yang menyatakan banyaknya klaim.
Peubah acak dinyatakan sebagai
(21) Menurut Teorema 4 berikut, peubah acak S
menyebar compound Poisson. Namun, untuk dapat menggunakan Teorema 4 diperlukan pemahaman dasar mengenai sebaran multinomial.
Teorema 4
Jika peubah acak S seperti pada persamaan (21) menyebar compound Poisson dengan parameter dan fungsi peluang kerugian (klaim) diskret seperti pada persamaan (20) maka
saling bebas.
menyebar Poisson dengan parameter
Bukti (Teorema 4)
Diketahui :
∑
( ∑
Fungsi peluang dan pembangkit momen untuk sebaran multinomial adalah
( ( [ (∑ )] ( Akan dibuktikan ( ( . [ (∑ )] (∑ ) ∑ [ (∑ ) ] ( ∑( ( ∑( ( ∑( ∑ ( ( ∑ ( ∑ ( ∑ ) [ (∑ )] ∏ ( (22)
Fungsi pembangkit momen seperti persamaaan (22) menunjukkan adanya kebebasan untuk setiap Sehingga jika dimisalkan maka fungsi pembangkit momen pada persamaan (22) akan menjadi ( (
3.4 Pendekatan Distribusi Total Klaim
Terdapat dua pendekatan yang digunakan untuk distribusi total klaim, yaitu pendekatan normal dan pendekatan translasi Gamma. Berikut akan dijelaskan lebih lanjut kedua pendekatan tersebut.
Pendekatan Normal
Berdasarkan teorema limit pusat perhatikan 2 hal berikut :
1. Jika memiliki distribusi Poisson majemuk dengan parameter dan fungsi distribusi yaitu ( maka peubah acak √ , akan berdistribusi normal baku bila . Dua parameter untuk pendekatan normal ini adalah
dan
2. Jika mimiliki distribusi binomial negatif mejemuk dengan parameter dan fungsi distribusi yaitu ( maka peubah acak (
√ (
berdistribusi normal baku bila . Dua parameter untuk pendekatan normal ini adalah
dan
Pendekatan normal ini akan lebih baik digunakan jika ekspektasi banyaknya klaim yang terjadi besar atau dengan kata lain jika besar untuk distribusi Poisson majemuk atau jika besar untuk distribusi binomial majemuk.
Karena distribusi normal adalah simetris maka sebagai akibatnya sentral momen ketiganya sama dengan nol atau dapat dituliskan sebagai berikut (
13
yang kedua ini dilakukan pendekatan translasi distribusi Gamma.
Pendekatan Translasi Gamma
Bila ( dinotasikan sebagai fungsi distribusi Gamma dengan parameter dan , maka
( ∫ (
Kemudian untuk suatu definisikan fungsi distribusi baru dengan notasi ( ( yang merupakan translasi distribusi Gamma ( terhadap . Gambar di bawah menggambarkan tentang ( dengan dan ( dengan dan di mana ( dan ( berturut-turut menyatakan fungsi kepekatan peluang dari ( dan (
Pada pendekatan translasi Gamma, parameter dipilih dengan menyamakan sentral momen pertama, sentral momen kedua dan sentral momen ketiga dari dengan sentral momen-sentral momen yang berkaitan untuk translasi distribusi Gamma. Oleh karena itu sentral momen dari translasi distribusi Gamma standar maka :
( Sehingga diperoleh : (
( (
( (
Untuk distribusi Poisson majemuk, prosedur di atas dengan , dan ( akan menghasilkan parameter sebagai berikut :
( )
3.5 Pengukuran Risiko Operasional Klaim
Pada dasarnya asuransi selalu berkaitan dengan risiko. Klaim dari peserta asuransi merupakan salah satu risiko yang harus dikelola dengan baik. Agar perusahaan dapat mengelola klaim dengan baik, diperlukan cara untuk mengukur cadangan klaim tersebut. Salah satu cara yang dapat digunakan untuk mengukur cadangan klaim asuransi adalah dengan menggunakan pendekatan pengukuran lanjutan. Salah satu teknik yang digunakan dalam pendekatan pengukuran lanjutan adalah pendekatan distribusi kerugian dengan metode agregat.
Pada awalnya pendekatan distribusi kerugian merupakan bagian metodologi pengukuran risiko operasional yang dianjurkan pada industri keuangan. Pada perkembangan selanjutnya, pendekatan distribusi kerugian juga bisa diterapkan pada industri asuransi.
Dalam metode agregat, data klaim asuransi dibentuk dalam distribusi frekuensi (banyaknya klaim) yang dapat memiliki karakteristik distribusi Poisson, binomial, binomial negatif atau geometrik; dan distribusi severitas yang memiliki karakteristik distribusi eksponensial, normal, Pareto, Weibul dan beta.
Total klaim dari metode agregat ini adalah pengabungan antara distribusi frekuensi dan severitas. Distribusi total klaim ini kemudian digunakan untuk memproyeksikan potensi kerugian (risiko). Kombinasi antara distribusi frekuensi klaim dengan distribusi severitas (besarnya klaim) dapat dihasilkan dengan menggunakan simulasi.
Secara teoritis ada beberapa langkah yang harus dilakukan dalam menghitung cadangan klaim dengan pendekatan distribusi kerugian dengan metode agregat. Langkah-langkah tersebut adalah sebagai berikut
1. Pengumpulan data klaim asuransi. 2. Pengelompokan data klaim asuransi
berdasarkan distribusi dan severitas. 3. Menentukan jenis distribusi frekuensi dan
distribusi severitas.
4. Menentukan parameter dari distribusi frekuensi dan distribusi severitas.
5. Simulasikan parameter frekuensi dan parameter severitas dengan . 6. Hitung total kerugian dari pembayaran
klaim untuk setiap .
14
8. Menghitung unexpected loss (OpVaR klaim asuransi).
9. Lakukan langkah 5, 6, 7 dan 8 sebanyak 100 kali untuk mendapatkan rata-rata dari
unexpected loss (potensi kerugian dari klaim asuransi).
Tahap akhir adalah menghitung nilai
unexpected loss, dengan cara memilih tingkat kepercayaan yang dikehendaki, misalnya 95% atau 99%. Untuk 95% maka nilai unexpected loss adalah 5%x10.000 (banyaknya simulasi) =500, artinya data ke-500 adalah nilai
unexpected loss dengan tingkat kepercayaan 95%. Sedangkan tingkat kepercayaan 99% dapat dilakukan hal yang sama yaitu data ke-100 adalah nilai unexpected loss dengan tingkat kepercayaan 99% atau dapat juga dilakukan secara langsung dengan melihat pada kolom aggregate quartile yang telah diurutkan dari yang terbesar (99.99%) sampai yang terkecil (0%).
Pada karya ilmiah ini data yang diperoleh merupakan data hipotetik dari asuransi kendaraan bermotor (frekuensi dan besarnya
klaim perhari). Oleh karena itu, langkah 1-4 pada perhitungan cadangan klaim tidak dilakukan. Langkah berikutnya, membangkitkan data dengan distribusi frekuensi menyebar Poisson dengan parameter 3,7 sebanyak n = 10.000 dan membangkitkan data dengan distribusi severitas menyebar eksponensial dengan parameter 100,1 sebanyak data frekuensi yang telah diperoleh untuk setiap n, di mana .
(Perhitungan langkah 5-8 ada di Lampiran 2), (Grafik simulasi total kerugian ada di lampiran 3).
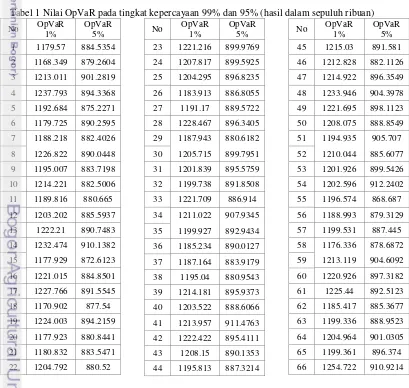
[image:23.595.104.513.377.765.2]Setelah langkah 5-8 dilakukan ulangan sebanyak 100 kali, maka nilai OpVar (potensi kerugian dari klaim asuransi) pada tingkat kepercayaan 99% dan tingkat kepercayaan 95% dapat dirangkum dalam Tabel 1 sebagaimana berikut
Tabel 1 Nilai OpVaR pada tingkat kepercayaan 99% dan 95% (hasil dalam sepuluh ribuan)
No OpVaR
1%
OpVaR 5% 1 1179.57 884.5354 2 1168.349 879.2604
3 1213.011 901.2819
4 1237.793 894.3368
5 1192.684 875.2271
6 1179.725 890.2595
7 1188.218 882.4026
8 1226.822 890.0448
9 1195.007 883.7198
10 1214.221 882.5006 11 1189.816 880.665
12 1203.202 885.5937
13 1222.21 890.7483
14 1232.474 910.1382
15 1177.929 872.6123
16 1221.015 884.8501
17 1227.766 891.5545 18 1170.902 877.54
19 1224.003 894.2159 20 1177.923 880.8441
21 1180.832 883.5471
22 1204.792 880.52
No OpVaR
1%
OpVaR 5% 23 1221.216 899.9769 24 1207.817 899.5925
25 1204.295 896.8235
26 1183.913 886.8055
27 1191.17 889.5722
28 1228.467 896.3405
29 1187.943 880.6182
30 1205.715 899.7951
31 1201.839 895.5759
32 1199.738 891.8508 33 1221.709 886.914
34 1211.022 907.9345
35 1199.927 892.9434
36 1185.234 890.0127
37 1187.164 883.9179
38 1195.04 880.9543 39 1214.181 895.9373
40 1203.522 888.6066
41 1213.957 911.4763
42 1222.422 895.4111
43 1208.15 890.1353
44 1195.813 887.3214
No OpVaR
1%
OpVaR 5% 45 1215.03 891.581 46 1212.828 882.1126
47 1214.922 896.3549
48 1233.946 904.3978
49 1221.695 898.1123
50 1208.075 888.8549
51 1194.935 905.707
52 1210.044 885.6077
53 1201.926 899.5426
54 1202.596 912.2402 55 1196.574 868.687
56 1188.993 879.3129
57 1199.531 887.445
58 1176.336 878.6872
59 1213.119 904.6092
60 1220.926 897.3182
61 1225.44 892.5123 62 1185.417 885.3677
63 1199.336 888.9523 64 1204.964 901.0305
65 1199.361 896.374
15
No OpVaR
1%
OpVaR 5% 67 1243.561 889.6035
68 1202.311 875.0372
69 1165.936 866.7547
70 1217.812 891.7538 71 1212.552 879.9491
72 1213.443 890.924
73 1189.527 888.5262
74 1211.039 897.7229
75 1216.792 890.8233
76 1224.24 885.7001
77 1189.349 874.1484
78 1232.666 894.7878
No OpVaR
1%
OpVaR 5% 79 1217.254 881.723
80 1172.345 891.6238
81 1210.35 903.9724 82 1208.486 896.0464
83 1198.613 880.6819
84 1229.491 881.9569
85 1197.104 898.5799
86 1212.241 889.0343
87 1216.21 886.9924
88 1215.623 886.9123
89 1197.621 882.9609
90 1213.361 892.7376
No OpVaR
1%
OpVaR 5% 91 1205.714 884.3733
92 1205.714 884.3733
93 1226.738 896.0856 94 1197.84 883.3441
95 1213.06 878.8313
96 1221.839 906.2982
97 1183.92 887.4438
98 1182.508 884.1437
99 1182.483 890.1959
100 1213.982 885.7684
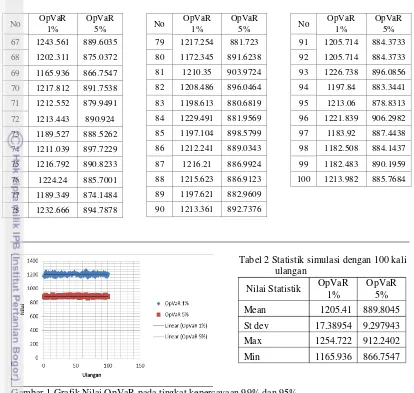
Gambar 1 Grafik Nilai OpVaR pada tingkat kepercayaan 99% dan 95%. Dari Gambar 1 dan Tabel 2 dapat diperoleh
informasi berikut
Nilai unexpected loss klaim asuransi kendaraan bermotor pada satu hari ke depan dengan menggunakan pendekatan distribusi kerugian dengan metode agregat pada atau tingkat kepercayaan 99% sebesar Rp 12.054.100,00. Artinya potensi klaim asuransi kendaraan bermotor maksimum dapat ditoleransi dengan tingkat kepercayaan 99% pada satu hari mendatang adalah sebesar Rp 12.054.100,00. Dengan kata lain, besarnya cadangan klaim yang harus disediakan perusahaan asuransi untuk
menutup klaim asuransi kendaraan bermotor maksimal untuk 1 hari mendatang sebesar Rp 12.054.100,00.
[image:24.595.102.516.72.465.2]Unexpected loss klaim asuransi kendaraan bermotor dengan atau tingkat kepercayaan 95% pada satu hari kedepan sebesar Rp 8.898.045,00. Artinya potensi klaim asuransi kendaraan bermotor yang dapat ditolerir pada tingkat kepercayaan 95% pada satu hari ke depan adalah sebesar Rp 8.898.045,00 sehingga perusahaan asuransi harus menyediakan cadangan klaim asuransi kendaraan bermotor pada satu hari ke depan sebesar Rp 8.898.045,00.
Tabel 2 Statistik simulasi dengan 100 kali ulangan
Nilai Statistik OpVaR 1%
OpVaR 5%
Mean 1205.41 889.8045
St dev 17.38954 9.297943
Max 1254.722 912.2402
16
KESIMPULAN
1. Karakteristik statistik risiko operasional pada perusahaan asuransi didasarkan pada pemahaman tentang konsep risiko kolektif sebagaimana berikut :
Distribusi total klaim dari sebuah polis yang merupakan kejadian acak dapat dicari dengan Teori Risiko dengan terlebih dahulu menentukan bentuk distribusi frekuensi (banyaknya klaim) dan distribusi severitas (besarnya klaim).
Distribusi total klaim dapat dihitung dengan metode konvolusi, pendekatan normal dan pendekatan translasi Gamma.
Secara umum, banyaknya klaim asuransi dapat dimodelkan dengan menggunakan sebaran yang memiliki sifat yang sama seperti sebaran Poisson, di mana nilai harapan dari klaim sama dengan ragamnya dan sebaran binomial negatif, di mana nilai harapan lebih kecil dari ragamnya.
17
DAFTAR PUSTAKA
Bowers NL, Gerber HU, Hickman JC, JonesDA, Nesbitt CJ. 1997. Actuarial Mathematics. 2nd Ed. The Society of Actuaries. Schaumburg.
Ester D. 1998. Penentuan Distribusi Total Klaim Dengan Menggunakan Teori Resiko Kolektif [Skripsi]. Bogor: Program Sarjana Institut Pertanian Bogor. Grimmett GR, Stirzaker DR. 1992.
Probability and Random Processes. 2nd
Ed. Clarendon Press. Oxford.
Hogg RV, Craig AT, McKean JW. 2005.
Introduction to Mathematical Statistics.
6th Ed. Prentice Hall, Englewood Clifft. New Jersey.
Jorion P. 2001. Value at Risk: The New Benchmark for Managing Financial Risk.
2nd Ed. McGraw-Hill. California.
McNeil AJ, Frey R, Embrechts P. 2005.
Quantitative Risk Management. Princeton University Press. New Jersey.
Muslich M. 2007. Manajemen Risiko Operasional. Bumi Aksara. Jakarta. Ross SM.1996. Stochastic Processes. 2nd Ed.
John Wiley & Sons. New York.
18
19
Lampiran 1
Sifat-sifat fungsi pembangkit momen
1. ( ( ( Bukti :
(
(
( ( ( ( (
( (
(
(
( (
( (
(
( (
( (
(
( (
. .
( ( ( Jadi, sifat 1 terbukti
2. Jika mempunyai fungsi pembangkit momen ( dan maka mempunyai fungsi pembangkit momen ( (
Bukti: ( (
(
(
( ( Jadi, sifat 2 terbukti
3. Jika dan peubah acak yang saling bebas dengan fungsi pembangkit momen dan maka mempunyai fungsi pembangkit momen
( ( ( Bukti :
( (
(
(
( (
20
Lampiran 2
Hasil simulasi dengan
MATLAB
A=poissrnd(3.7,10000,1)
for i=1:10000
t=exprnd(100.1,1,A(i,1));
[image:29.842.79.759.183.511.2]end
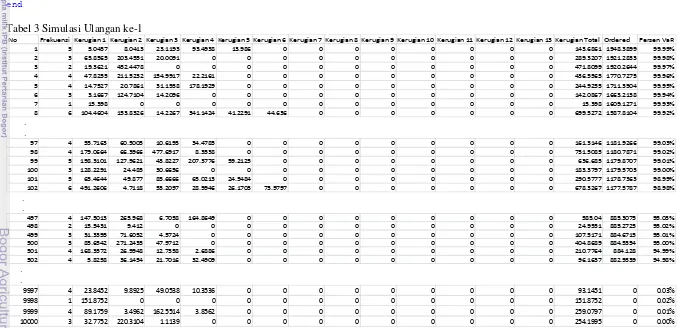
Tabel 3 Simulasi Ulangan ke-1
. .
. .
. .
No Frekuensi Kerugian 1 Kerugian 2 Kerugian 3 Kerugian 4 Kerugian 5 Kerugian 6 Kerugian 7 Kerugian 8 Kerugian 9 Kerugian 10 Kerugian 11 Kerugian 12 Kerugian 13 Kerugian Total Ordered Persen VaR
1 5 5.0457 8.0413 23.1193 93.4938 13.986 0 0 0 0 0 0 0 0 143.6861 1948.3899 99.99%
2 3 65.8565 203.4551 20.0091 0 0 0 0 0 0 0 0 0 0 289.3207 1921.2833 99.98%
3 2 19.3621 452.4478 0 0 0 0 0 0 0 0 0 0 0 471.8099 1920.2644 99.97%
4 4 47.8255 211.5232 154.9917 22.2161 0 0 0 0 0 0 0 0 0 436.5565 1770.7275 99.96%
5 4 14.7527 20.7861 31.1938 178.1929 0 0 0 0 0 0 0 0 0 244.9255 1711.3904 99.95%
6 3 3.1667 124.7104 14.2096 0 0 0 0 0 0 0 0 0 0 142.0867 1663.2138 99.94%
7 1 15.398 0 0 0 0 0 0 0 0 0 0 0 0 15.398 1609.1271 99.93%
8 6 104.4604 153.8326 14.2267 341.1424 41.2291 44.636 0 0 0 0 0 0 0 699.5272 1587.8104 99.92%
97 4 55.7163 60.5005 10.6193 34.4785 0 0 0 0 0 0 0 0 0 161.3146 1181.9266 99.03%
98 4 179.0664 66.3966 477.6917 8.3538 0 0 0 0 0 0 0 0 0 731.5085 1180.7871 99.02%
99 5 198.3101 127.9621 43.8227 207.3776 59.2125 0 0 0 0 0 0 0 0 636.685 1179.8707 99.01%
100 3 128.2291 24.485 30.6656 0 0 0 0 0 0 0 0 0 0 183.3797 1179.5703 99.00%
101 5 65.4644 49.877 85.6666 65.0213 24.5484 0 0 0 0 0 0 0 0 290.5777 1178.7363 98.99%
102 6 491.2606 4.7118 53.2097 28.9946 26.1703 73.9797 0 0 0 0 0 0 0 678.3267 1177.5787 98.98%
497 4 147.5013 265.968 6.7058 164.8649 0 0 0 0 0 0 0 0 0 585.04 885.3075 95.03%
498 2 15.5431 9.412 0 0 0 0 0 0 0 0 0 0 0 24.9551 885.2725 95.02%
499 3 31.3395 71.6052 4.5724 0 0 0 0 0 0 0 0 0 0 107.5171 884.6715 95.01%
500 3 85.6542 271.2435 47.9712 0 0 0 0 0 0 0 0 0 0 404.8689 884.5354 95.00%
501 4 168.3572 26.9948 12.7358 2.6886 0 0 0 0 0 0 0 0 0 210.7764 884.128 94.99%
502 4 5.8258 36.1454 21.7016 32.4909 0 0 0 0 0 0 0 0 0 96.1637 882.9339 94.98%
9997 4 23.8452 9.8925 49.0538 10.3536 0 0 0 0 0 0 0 0 0 93.1451 0 0.03%
9998 1 151.8752 0 0 0 0 0 0 0 0 0 0 0 0 151.8752 0 0.02%
9999 4 89.1759 3.4962 162.5514 3.8562 0 0 0 0 0 0 0 0 0 259.0797 0 0.01%
21
[image:30.842.107.751.134.476.2]