DINAMIKA PENYEBARAN PENYAKIT KOLERA
OLEH BAKTERI VIBRIO CHOLERAE
BERTIPE HYPERINFECTIOUS
NUR RAHMI
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI TESIS DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa tesis berjudul Dinamika Penyebaran Penyakit Kolera oleh Bakteri Vibrio cholerae Bertipe Hyperinfectious adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
RINGKASAN
NUR RAHMI. Dinamika Penyebaran Penyakit Kolera oleh Bakteri Vibrio cholerae Bertipe Hyperinfectious. Dibimbing oleh JAHARUDDIN dan ENDAR H. NUGRAHANI.
Kolera adalah infeksi akut yang disebabkan oleh bakteri Vibrio cholerae yang masuk ke dalam tubuh melalui makanan dan minuman yang dikonsumsi. Setelah terinfeksi, penderita akan mengeluarkan bakteri bersama fesesnya. Bakteri yang baru saja keluar dari saluran pencernaan manusia memiliki kekuatan infeksi yang tinggi, yang disebut hyperinfectious. Untungnya, kekuatan infeksi dari bakteri hyperinfectious hanya berlangsung dalam selang waktu singkat karena dalam hitungan jam akan meluruh menjadi bakteri less infectious. Dengan demikian, kondisi bakteri, hyperinfectious atau less infectious, merupakan kunci untuk memahami sifat penyebaran penyakit kolera dari manusia-ke-manusia.
Penelitian ini bertujuan memodifikasi model dengan melibatkan bakteri hyperinfectious dan memperhatikan pengaruh vaksinasi, pengobatan, dan sanitasi air. Selain itu, penelitian ini juga bertujuan untuk melakukan analisis kestabilan titik tetap. Akhirnya, beberapa simulasi numerik dari model diberikan untuk mengilustrasikan dinamika penyebaran penyakit kolera.
Model yang diajukan dalam penelitian ini merupakan hasil modifikasi dari model yang telah ada, yaitu dengan menambahkan asumsi bahwa populasi manusia tidak konstan dan adanya pengaruh vaksinasi, pengobatan, dan sanitasi air. Populasi manusia dibagi menjadi tiga kelas, yaitu manusia yang rentan (susceptible), manusia yang terkena infeksi (infected), dan manusia yang sembuh (recovered). Manusia yang rentan adalah manusia yang tak imun dan belum terkena infeksi. Manusia yang terkena infeksi adalah manusia yang terinfeksi bakteri V. cholera sehingga dapat menularkan kepada individu lain. Manusia sembuh adalah manusia yang sembuh dari penyakit dan tidak dapat tertular lagi. Di lain pihak, populasi bakteri dibagi menjadi dua kelas, yaitu bakteri hyperinfectious dan bakteri less infectious.
Analisis terhadap sistem dinamik ini menunjukkan bahwa terdapat dua titik tetap, yaitu titik tetap tanpa penyakit dan titik tetap endemik. Titik tetap endemik positif akan ada jika bilangan reproduksi dasar lebih dari satu. Titik tetap tanpa penyakit akan bersifat stabil asimtotik lokal jika dan hanya jika bilangan reproduksi dasar kurang dari satu, sedangkan titik tetap endemik bersifat stabil asimtotik lokal jika bilangan reproduksi dasar lebih dari satu.
itu, hasil simulasi juga menunjukkan bahwa meningkatnya laju cerna bakteri hyperinfectious menyebabkan bilangan reproduksi dasar naik, sehingga mempercepat laju penyebaran penyakit. Di lain pihak, meningkatnya laju vaksinasi, pengobatan, atau sanitasi menyebabkan bilangan reproduksi dasar turun, sehingga dapat menekan laju penyebaran penyakit.
SUMMARY
NUR RAHMI. Dynamics of Cholera Disease Transmission by Vibrio cholerae bacteria in Hyperinfectious State. Supervised by JAHARUDDIN and ENDAR H. NUGRAHANI.
Cholera is an acute infection caused by Vibrio cholerae bacteria that enter the body through consumed food and beverages. After getting infected, cholera sufferers will shed the bacteria together with their feces. Freshly shed bacteria from the human gastrointestinal tract has high infectivity, which is called hyperinfectious. Fortunately, the hyperinfectious state decays in a matter of hours into a lower infectious state. So, the state of bacteria, whether hyperinfectious or less infectious, is the key to understanding the nature of the spread of cholera from human-to-human.
This study aims to modify the model of cholera transmission by involving hyperinfectious bacteria and taking into account the effect of vaccination control, treatment and water sanitation. Moreover, this study also intended to perform the stability analysis of equilibrium points. Finally, some numerical simulations of models are given to illustrate the dynamics of the transmission of cholera disease.
The model proposed in this study is a modification of the existing model, i.e. there is additional assumption that the human population is not constant and that there are some effects of vaccination, treatment, and water sanitation. The human population is divided into three classes, namely susceptible, infected, and recovered. Susceptible humans are people who are not immune and not yet exposed to the infection. Infected humans are humans infected by the bacteria and, therefore, can infect another. Recovered humans are people who recovered from the disease and can not be infected again. On the other hand, bacterial population is divided into two classes, namely hyperinfectious bacteria and less infectious bacteria.
Analysis of this dynamic system shows that there are two equilibria, namely disease free and endemic equilibrium. A positive endemic equilibrium exists if and only if the basic reproduction number is greater than one. Moreover, the disease free equilibrium of system is locally asymptotically stable if and only if the basic reproduction number is less than one. The endemic equilibrium is positive and locally asymptotically stable if the basic reproduction number is greater than one.
hyperinfectious bacteria ingestion causes the basic reproduction number also increased, thus it can speed up the rate of spread of the cholera disease. On the other hand, improving force of vaccination, medical treatment, or sanitation causes the basic reproduction number decreased, so that it can also decrease the cholera transmission.
© Hak Cipta Milik IPB, Tahun 2016
Hak Cipta Dilindungi Undang-Undang
Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB
Tesis
sebagai salah satu syarat untuk memperoleh gelar Magister Sains
pada
Program Studi Matematika Terapan
DINAMIKA PENYEBARAN PENYAKIT KOLERA
OLEH BAKTERI VIBRIO CHOLERAE
BERTIPE HYPERINFECTIOUS
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Tema yang dipilih dalam penelitian ini ialah pemodelan matematika, dengan judul: Dinamika Penyebaran Penyakit Kolera oleh Bakteri Vibrio cholerae Bertipe Hyperinfectious.
Penulisan tesis ini merupakan salah satu syarat memperoleh gelar Magister Sains pada Program Studi Magister Matematika Terapan Sekolah Pascasarjana Institut Pertanian Bogor. Penulis menyadari bahwa bantuan dan bimbingan dari kedua pembimbing sangat membantu dalam menyelesaikan karya tulis ini. Terima kasih penulis ucapkan kepada Bapak Dr Jaharuddin, MS dan Ibu Dr Ir Endar H Nugrahani, MS selaku pembimbing yang telah banyak memberi saran dan bimbingan dalam menyelesaikan tesisi ini.
Penulis juga menyampaikan terima kasih kepada:
1. Orang tua, saudara, dan seluruh keluarga yang selalu memberikan doa dan semangat selama masa studi penulis.
2. Sponsor Beasiswa Fresh Graduate Direktorat Jenderal Pendidikan Tinggi (DIKTI)
3. Seluruh dosen dan staf pegawai Tata Usaha Departemen Matematika.
4. Seluruh mahasiswa Program Studi Magister Matematika Terapan Sekolah Pascasarjana IPB, terutama angkatan 2014 dan 2013.
5. Sahabat-sahabat yang telah membantu secara moril maupun materil.
Jazakumullah khairan katsira, semoga semua bantuan, doa, dan motivasi yang telah diberikan pada penulis mendapat balasan dari Allah SWT.
Akhirnya, penulis berharap semoga karya ilmiah ini bermanfaat dan memperkaya wawasan bagi semua pembaca.
DAFTAR ISI
Model Penyebaran Penyakit Kolera Hasil Modifikasi 11
Daerah Solusi Model Penyebaran Penyakit Kolera 13
DAFTAR TABEL
1 Notasi pada model modifikasi penyebaran penyakit kolera 12
2 Sifat kestabilan titik tetap 24
3 Nilai parameter yang digunakan dalam simulasi 25
4 Nilai parameter dan dalam simulasi laju cerna bakteri
hyperinfectious 26
5 Nilai parameter dan dalam simulasi laju vaksinasi 28 6 Nilai parameter dan dalam simulasi laju pengobatan 31 7 Nilai parameter dan dalam simulasi laju sanitasi 33
DAFTAR GAMBAR
1 Kasus kolera di Indonesia periode tahun 1986-2012 1 2 Diagram kompartemen model Hartley et al. (2006) 8 3 Diagram kompartemen model Wang dan Modnak (2011) 10
4 Diagram kompartemen model modifikasi 11
5 Dinamika populasi saat dan 26
6 Dinamika populasi saat dan 27
7 Pengaruh variasi laju cerna bakteri hyperinfectious terhadap manusia
terinfeksi 28
8 Dinamika populasi saat dan 29
9 Dinamika populasi saat dan 30
10 Pengaruh variasi laju vaksinasi terhadap manusia terinfeksi 30
11 Dinamika populasi saat dan 32
12 Dinamika populasi saat dan 32
13 Pengaruh variasi laju pengobatan terhadap manusia terinfeksi 33
14 Dinamika populasi saat dan 34
15 Dinamika populasi saat dan 34
16 Pengaruh variasi laju sanitasi terhadap manusia terinfeksi 35
DAFTAR LAMPIRAN
1 Penentuan Titik Tetap Endemik 39
2 Penentuan Nilai Kritis Laju Cerna Bakteri Hyperinfectious 40
3 Penentuan Nilai Kritis Laju Vaksinasi 41
4 Penentuan Nilai Kritis Laju Pengobatan 42
1
PENDAHULUAN
Latar Belakang
Kolera adalah infeksi akut yang disebabkan oleh bakteri Vibrio cholerae yang masuk ke dalam tubuh melalui makanan dan minuman yang dikonsumsi oleh penderita. Pada saat menginfeksi seseorang, bakteri ini memproduksi enterotoxin yang mengakibatkan keluarnya cairan tubuh dalam jumlah yang banyak, sehingga tanpa penanganan yang tepat, seseorang yang terjangkit oleh bakteri ini dapat meninggal dunia. Ketika di suatu daerah dengan tingkat sanitasi yang sangat rendah terdapat seorang penderita diare yang membawa bakteri Vibrio cholerae, maka sangat memungkinkan terjadi penyebaran bakteri Vibrio cholerae ini di sumber air daerah setempat. Hal ini dapat mengakibatkan terkontaminasinya seluruh daerah tersebut, dan menyebabkan kemungkinan terjadinya tiga kasus, yaitu tidak ada outbreak (bebas kolera), terjadi epidemik atau terjadi endemik di wilayah yang terjangkiti tersebut.
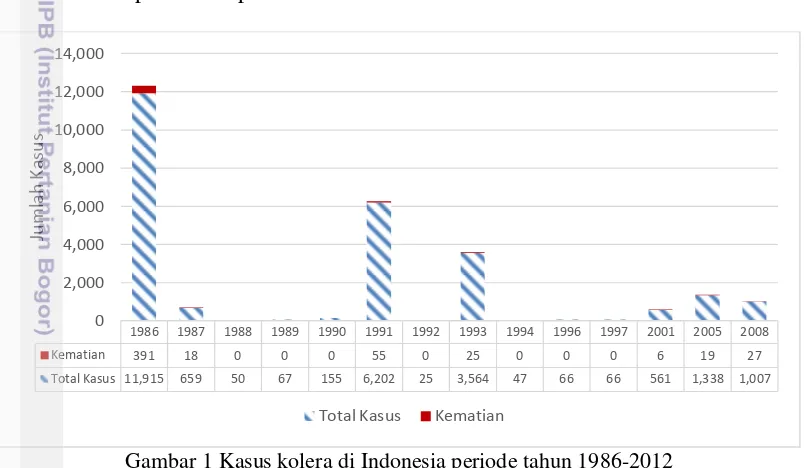
Di Indonesia, perkembangan jumlah kasus kolera dari tahun 1986 sampai tahun 2012 dapat dilihat pada Gambar 1.
Gambar 1 Kasus kolera di Indonesia periode tahun 1986-2012 Gambar direproduksi dari Knoema (2014)
Gambar 1 menunjukkan bahwa kasus kolera di Indonesia terbanyak sepanjang periode tersebut terjadi pada tahun 1986 dengan 11,915 kasus dan 391 kematian. Setelah itu jumlah kasus menurun setiap tahun setelahnya hingga akhirnya mulai naik tajam pada tahun 1991. Kasus kolera di Indonesia yang terbaru terjadi pada tahun 2008 sebanyak seribu tujuh kasus dengan 27 kematian. Selanjutnya tidak ada laporan kolera lagi sejak tahun 2009 hingga 2012.
2
Kasus kolera yang dilaporkan ini hanya menggambarkan sebagian kecil dari kasus yang sebenarnya terjadi. Diduga terdapat lebih dari dua juta kasus dan hampir seratus ribu kematian karena kolera setiap tahunnya. Berdasarkan uraian tersebut kolera masih menjadi masalah kesehatan utama di beberapa belahan dunia. Untuk itu, dibutuhkan suatu model matematika yang mampu menggambarkan dan menganalisis dinamika penyebaran penyakit kolera dalam suatu populasi agar diperoleh solusi strategi optimal dalam penanganan penyebaran penyakit kolera.
Bakteri Vibrio cholerae dapat masuk ke dalam tubuh melalui makanan atau minuman. Pada saat menginfeksi, bakteri ini memproduksi enterotoksin yang menyebabkan keluarnya cairan tubuh dalam jumlah besar. Bakteri ini kemudian keluar bersama dengan kotoran. Bakteri V. cholerae yang baru saja keluar dari saluran pencernaan manusia memiliki infektivitas tinggi (bersifat hyperinfectious). Namun kekuatan infeksi dari bakteri hyperinfectious hanya berlangsung untuk selang waktu singkat karena dalam hitungan jam akan meluruh menjadi bakteri less infectious (infeksi lemah). Ini berarti bakteri hyperinfectious hanya akan tercerna jika terjadi pertemuan (menggunakan toilet yang sama pada hari yang sama) dengan individu yang telah terinfeksi. Peralihan kondisi bakteri hyperinfectious menjadi less infectious merupakan kunci untuk memahami penyebaran penyakit kolera dari manusia-ke-manusia (Merrell et al. 2002).
Sejak diperkenalkan oleh Edward Jenner untuk penyakit cacar (Fenner et al. 1988), vaksinasi telah menjadi metode yang umum digunakan untuk mengontrol penyakit dan bekerja dengan mengurangi jumlah individu yang rentan dalam suatu populasi (Hethcote 1998; Hethcote 2000; Tian 2012). Untuk penyakit kolera, vaksin kolera oral (OCV) telah diusulkan sebagai strategi efektif dalam mengontrol endemik dan epidemik (WHO 2010; Ivers et al. 2010). Selain itu, kontrol sanitasi, seperti klorinasi, telah lama dikenal sebagai tindakan pencegahan yang efektif terhadap kolera dan penyakit diare lainnya (Waldman et al. 2013; Fung et al. 2013). Di sisi lain, pengobatan adalah hal yang paling penting untuk memberantas penyakit ini. Oleh karena itu, vaksinasi, pengobatan, dan sanitasi dapat memainkan peran penting dalam penekanan penyebaran kolera.
Penelitian mengenai dinamika penyebaran kolera telah banyak dilakukan. Model pertama dibangun oleh Capasso dan Paveri-Fontana (1979) yang menggambarkan epidemik kolera di Italia pada tahun 1973. Model ini terdiri dari dua persamaan yang menggambarkan dinamika orang yang terinfeksi dalam komunitas dan dinamika populasi bakteri patogenik dalam air. Codeco (2001) mengembangkan dengan memasukkan dinamika populasi yang rentan terhadap penyakit serta secara eksplisit mempertimbangkan komponen lingkungan, yaitu konsentrasi bakteri pada persediaan air, ke dalam model epidemik SIR. Selanjutnya, model Codeco (2001) dikembangkan oleh Hartley et al. (2006) dengan memasukkan tahap hyperinfectious dari patogen. Di lain pihak, Wang dan Modnak (2011) menyajikan model penyebaran kolera dengan rute penularan lingkungan-ke-manusia dan manusia-ke-manusia dengan memasukkan parameter kontrol, yaitu vaksinasi, pengobatan, dan sanitasi air.
3
Tujuan Penelitian
Berdasarkan uraian latar belakang di atas, tujuan yang akan dicapai pada penelitian ini adalah sebagai berikut:
a. Memodifikasi model penyebaran penyakit kolera dengan memperhatikan kondisi hyperinfectious bakteri dengan kontrol vaksinasi, pengobatan, dan sanitasi.
b. Melakukan analisis kestabilan di sekitar titik tetap pada model hasil modifikasi. c. Melakukan simulasi numerik terhadap model yang telah dimodifikasi untuk melihat dinamika penyebaran penyakit kolera yang terjadi berdasarkan perubahan nilai-nilai parameter laju cerna bakteri hyperinfectious, laju vaksinasi, laju pengobatan, dan laju kematian bakteri karena sanitasi.
2
TINJAUAN PUSTAKA
Sistem Dinamik
Sistem dinamik adalah suatu sistem yang berubah sesuai dengan waktu. Sistem dinamik penyebaran penyakit kolera merupakan sistem persamaan diferensial taklinear orde satu.
Misalkan suatu sistem persamaan diferensial biasa dinyatakan sebagai berikut
Sistem persamaan (2.1) disebut sistem persamaan diferensial biasa taklinear (Braun 1983).
4
dengan fungsi kontinu bernilai real dari x. Sistem (2.2) disebut sistem persamaan differensial biasa mandiri (autonomous) karena tidak memuat secara eksplisit di dalamnya (Tu 1994).
Titik Tetap
Diberikan sistem persamaan diferensial mandiri seperti pada sistem (2.2). Titik disebut titik tetap, jika . Titik tetap disebut juga titik kritis atau titik kesetimbangan atau titik ekuilibrium (Tu 1994). Untuk selanjutnya digunakan istilah titik tetap.
Pelinearan
Misalkan diberikan sistem persamaan diferensial biasa taklinear sebagaimana sistem (2.2). Dengan menggunakan ekspansi Taylor di sekitar titik tetap, maka sistem persamaan (2.2) dapat ditulis sebagai berikut:
(2.3) dengan adalah matriks Jacobi yang dinyatakan sebagai berikut :
Persamaan (2.4) disebut sistem persamaan diferensial linear dari sistem (2.2). Selanjutnya pada persamaan (2.3) disebut pelinearan dari sistem persamaan Nilai skalar dinamakan nilai eigen dari . Untuk mencari nilai dari , maka sistem persamaan (2.5) dapat ditulis:
(2.6) dengan adalah matriks identitas. Sistem persamaan (2.6) mempunyai solusi tak nol jika dan hanya jika
5 Persamaan (2.7) merupakan persamaan karakteristik matriks (Anton dan Rorres 1995).
Kestabilan Titik Tetap
Misalkan diberikan sistem persamaan diferensial mandiri sebagaimana pada sistem (2.2). Kestabilan titik tetap dari sistem (2.2) diberikan dalam definisi
3. Titik tetap yang tidak stabil disebut takstabil.
Berdasarkan definisi tersebut, titik tetap dikatakan stabil jika solusi sistem persamaan pada saat selalu berada pada jarak yang cukup dekat dengan titik tetap tersebut, sedangkan titik tetap dikatakan stabil asimtotik jika solusi sistem persamaan pada saat akan menuju ke titik tetap, dan titik tetap dikatakan tidak stabil jika solusi sistem persamaan pada saat bergerak menjauhi titik tetap tersebut.
Titik tetap yang stabil atau stabil asimtotik hanya berlaku pada suatu daerah tertentu dalam lingkungan sistem dikatakan sebagai stabil lokal atau stabil asimtotik lokal. Titik tetap dikatakan stabil global atau stabil asimtotik global jika titik tetap tersebut stabil atau stabil asimtotik pada setiap lingkungan solusi sistem.
Selanjutnya, untuk mengetahui kestabilan lokal titik tetap sistem (2.2) dilakukan pelinearan di sekitar titik tetap sesuai dengan persamaan (2.3) sehingga diperoleh persamaan (2.4). Analisis kestabilan sistem persamaan diferensial (2.2) dilakukan melalui analisis kestabilan sistem persamaan diferensial (2.4).
Penentuan kestabilan titik tetap didapat dengan melihat nilai-nilai eigen dari matriks yaitu: yang diperoleh dari persamaan (2.7).
Secara umum kestabilan titik tetap mempunyai perilaku sebagai berikut: 1. Stabil, jika setiap nilai eigen kompleks memiliki bagian real negatif atau sama
dengan nol ( ≤ 0 untuk setiap ).
2. Stabil asimtotik, jika setiap nilai eigen kompleks memiliki bagian real negatif ( < 0 untuk setiap ).
3. Takstabil, jika terdapat komponen bagian real dari nilai eigen kompleks yang positif ( > 0 untuk suatu ).
Teorema Castillo-Chaves dan Song (2004)
6 sedangkan nilai eigen lainnya memiliki bagian real yang negatif;
A2: Matriks memiliki satu vektor eigen kanan dan satu vektor eigen kiri yang berkorespondensi dengan nilai eigen nol.
Misalkan adalah komponen ke- dari dan dinotasikan
kestabilannya dari stabil menjadi tidak stabil. Begitu pula titik tetap negatif takstabil berubah menjadi positif dan stabil asimtotik lokal.
Bilangan Reproduksi Dasar
7 adalah bilangan yang menyatakan banyaknya rata-rata individu infektif sekunder akibat tertular individu infektif primer yang berlangsung di dalam populasi yang rentan (Diekmann dan Heesterbeek 2000).
Pendekatan untuk menentukan bilangan reproduksi dasar yang digunakan dalam penelitian ini mengikuti Driessche dan Watmough (2002), yaitu dengan menggunakan matriks next generation dengan nilai . Hal ini dikarenakan banyaknya individu yang terinfeksi tidak mungkin bernilai negatif. Selanjutnya didefinisikan sebagai nilai eigen dominan dari matriks next generation. Matriks ini merupakan matriks yang dikonstruksi dari sub-subpopulasi yang menyebabkan infeksi saja.
Misalkan ada n kelas terinfeksi dan m kelas yang tidak terinfeksi, dan misalkan adalah subpopulasi dari masing-masing kelas. Model kompartemen (kelas) dapat dituliskan dalam bentuk berikut:
dengan merupakan matriks fungsi yang menunjukkan tingkat kemunculan infeksi baru di kompartemen ke- dan adalah matriks yang menunjukkan selisih laju perpindahan yang keluar ke dalam kompartemen ke- dengan laju perpindahan yang masuk ke dalam kelas ke- Selanjutnya perhatikan model penyebaran penyakit berikut.
Perhitungan bilangan reproduksi dasar berdasarkan linearisasi sistem (2.10) pada titik tetap tanpa penyakit . Hasil linearisasi dari kelas terinfeksi pada titik tetap tanpa penyakit adalah sebagai berikut
dengan F dan V matriks berukuran ,
dan .
Selanjutnya disebut matriks next generation. Nilai eigen terbesar dari matriks next generation merupakan bilangan reproduksi dasar sistem.
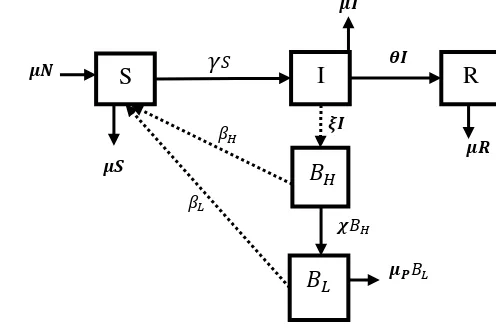
Model Hartley et al. (2006)
Model yang diajukan oleh Hartley et al. (2006) adalah model kolera SIR (Susceptible – Infected – Recovered) dan kelompok bakteri yang terbagi menjadi dua, yaitu hyperinfectious dan less infectious. Total populasi manusia yang setelah terinfeksi akan menjadi sembuh dan tidak rentan lagi.
8
Diagram kompartemen model Hartley et al. (2006) diberikan pada Gambar 2 sebagai berikut.
Gambar 2 Diagram kompartemen model Hartley et al. (2006) disesuaikan dari Hartley et al. (2006)
Pada model ini, diasumsikan total populasi manusia konstan dan laju
dengan subskrip dan masing-masing menunjukkan kategori bakteri hyperinfectious dan less infectious. Pada model ini dan menunjukkan laju cerna bakteri hyperinfectious dan less infectious, sedangkan dan adalah konsentrasi bakteri hyperinfectious dan less infectious dalam air yang menyebabkan 50% kemungkinan terkena kolera. Saat sama dengan , peluang mencerna bakteri yang dapat menyebabkan kolera adalah 0.5, dan hal yang sama saat sama dengan
Kelas I menyatakan individu yang terinfeksi dan dapat menularkan kolera kepada orang lain. Berkurangnya populasi ini disebabkan oleh kematian alamiah dengan laju . Individu yang terinfeksi kolera dapat sembuh kembali dengan laju dan masuk ke dalam populasi R sehingga menyebabkan berkurangnya populasi I. Individu dalam kelas R diasumsikan tidak akan terinfeksi penyakit lagi. Berkurangnya populasi ini disebabkan oleh kematian alamiah dengan laju .
9 Hartley et al. (2006) menekankan pentingnya peran bakteri hyperinfectious dalam penyebaran penyakit kolera. Penelitian terkait bakteri hyperinfectious menunjukkan bahwa terdapat hubungan antara jalur penyebaran lingkungan-ke-manusia dengan jalur penyebaran dari lingkungan-ke-manusia-ke-lingkungan-ke-manusia. Oleh karena itu dalam model (2.11) penyebaran penyakit hanya memperhatikan penyebaran lingkungan-ke-manusia. Namun model ini masih relatif sederhana karena belum mempertimbangkan pengaruh kontrol penyebaran penyakit seperti vaksinasi, pengobatan, dan sanitasi air. Oleh karena itu, dalam penelitian ini model Hartley et al. (2006) akan dimodifikasi dengan menambahkan parameter vaksinasi, pengobatan, dan sanitasi pada model.
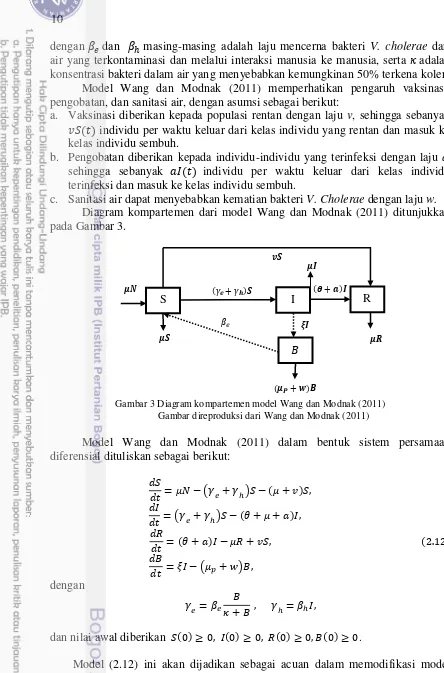
Model Wang dan Modnak (2011)
Wang dan Modnak (2011) dalam penelitiannya menyajikan model penyebaran penyakit kolera dengan memperhatikan pengaruh vaksinasi, pengobatan dan sanitasi. Model ini melibatkan empat variabel yaitu dan Misalkan dan masing-masing menyatakan kelas individu rentan terserang penyakit (susceptible), kelas individu yang terinfeksi (infected), dan kelas individu yang sembuh (recovered). Total populasi diasumsikan konstan. Misalkan pula B sebagai konsentrasi bakteri V. Cholerae di lingkungan (misalnya air yang terkontaminasi). Model Wang dan Modnak (2011) dibangun sebagai kombinasi dari sistem populasi manusia dan komponen lingkungan (SIR-B), dengan penularan lingkungan-ke-manusia direpresentasikan dalam fungsi logistik dan penularan dari manusia-ke-manusia. Pada sistem ini, dinotasikan sebagai laju kelahiran/kematian alamiah, adalah laju kontribusi setiap orang yang terinfeksi pada populasi bakteri V. cholerae, adalah laju penyembuhan dari kolera. Subpopulasi akan berkurang karena terinfeksi kolera baik karena mencerna bakteri di lingkungan atau melalui interaksi manusia ke manusia dengan laju
10
dengan dan masing-masing adalah laju mencerna bakteri V. cholerae dari air yang terkontaminasi dan melalui interaksi manusia ke manusia, serta adalah konsentrasi bakteri dalam air yang menyebabkan kemungkinan 50% terkena kolera.
Model Wang dan Modnak (2011) memperhatikan pengaruh vaksinasi, pengobatan, dan sanitasi air, dengan asumsi sebagai berikut:
a. Vaksinasi diberikan kepada populasi rentan dengan laju v, sehingga sebanyak individu per waktu keluar dari kelas individu yang rentan dan masuk ke kelas individu sembuh.
b. Pengobatan diberikan kepada individu-individu yang terinfeksi dengan laju a, sehingga sebanyak individu per waktu keluar dari kelas individu terinfeksi dan masuk ke kelas individu sembuh.
c. Sanitasi air dapat menyebabkan kematian bakteri V. Cholerae dengan laju w. Diagram kompartemen dari model Wang dan Modnak (2011) ditunjukkan pada Gambar 3.
Gambar 3 Diagram kompartemen model Wang dan Modnak (2011) Gambar direproduksi dari Wang dan Modnak (2011) (2.11) berkaitan dengan penambahan parameter vaksinasi, pengobatan, dan sanitasi.
11
3
HASIL DAN PEMBAHASAN
Model Penyebaran Penyakit Kolera Hasil Modifikasi
Pada bagian ini dilakukan modifikasi model penyebaran penyakit kolera yang mengacu pada model yang disajikan oleh Hartley et al. (2006) dengan melihat adanya pengaruh dari vaksinasi, pengobatan, dan sanitasi air seperti model yang diperkenalkan oleh Wang dan Modnak (2011). Asumsi yang digunakan pada model ini antara lain:
a. Total populasi manusia tidak konstan.
b. Individu yang baru lahir/ masuk ke populasi rentan terhadap kolera.
c. Individu bisa terinfeksi kolera karena mengonsumsi makanan/minuman terkontaminasi oleh bakteri V. choleraehyperinfectious (disebabkan pertemuan individu yang terinfeksi dengan individu yang rentan) atau bakteri V. cholerae less infectious (mengonsumsi makanan/minuman terkontamiasi tanpa adanya pertemuan individu yang terinfeksi dengan individu yang rentan).
d. Individu yang telah sembuh tidak akan terinfeksi kembali karena adanya kekebalan tubuh.
e. Vaksinasi diberikan kepada populasi rentan efektif membuat individu rentan menjadi sembuh.
f. Pengobatan diberikan kepada individu-individu yang terinfeksi. g. Sanitasi air dapat menyebabkan kematian bakteri V. cholera. h. Kolera dapat menyebabkan kematian pada penderitanya.
i. Bakteri hyperinfectious dapat bertransisi secara alami menjadi less infectious. Secara skematis pola penyebaran penyakit kolera dengan asumsi-asumsi di atas digambarkan dalam diagram kompartemen pada Gambar 4.
Gambar 4 Diagram kompartemen model modifikasi
12
Penjelasan notasi yang digunakan pada model (3.1) dapat dilihat pada tabel berikut.
Tabel 1 Notasi pada model modifikasi penyebaran penyakit kolera
Notasi Keterangan Laju kematian alamiah manusia (hari-1)
Laju kematian manusia karena penyakit kolera (hari-1) Laju kematian alamiah untuk bakteri (hari-1)
Laju bakteri hyperinfectious yang tercerna oleh individu S dari air yang terkontaminasi (hari-1)
Laju bakteri less infectious yang tercerna oleh individu S dari air yang terkontaminasi (hari-1)
Konsentrasi bakteri hyperinfectious dalam air yang menyebabkan 50 % dari kemungkinan terkena kolera (sel/ml)
Konsentrasi bakteri less infectious dalam air yang menyebabkan 50 % dari kemungkinan terkena kolera (sel/ml)
v Laju per kapita pada orang yang rentan yang divaksinasi (hari-1) Laju per kapita penyembuhan dari kolera (hari-1)
Laju per kapita pengobatan penyakit kolera (hari-1)
Laju kontribusi setiap orang yang terinfeksi pada populasi bakteri V.
cholera hyperinfectious dalam lingkungan perairan (sel/ml/hari)
13
Daerah Solusi Model Penyebaran Penyakit Kolera
Daerah solusi model penyebaran penyakit kolera pada sistem (3.1) adalah taknegatif dan terbatas untuk setiap waktu, hal ini ditunjukkan berdasarkan Lemma 1 berikut.
Lemma 1. Himpunan dan adalah daerah solusi yang taknegatif dan terbatas dari model pada sistem (3.1), dimana dan masing-masing adalah total populasi manusia dan total populasi bakteri saat .
Bukti. Misalkan , berdasarkan sistem persamaan (3.1) diperoleh
Karena taknegatif, maka dari persamaan (3.2) diperoleh
Pertidaksamaan (3.3) diselesaikan menggunakan faktor integrasi sehingga diperoleh
Karena untuk setiap , maka diperoleh
atau
Karena dan taknegatif, maka untuk setiap diperoleh
Selanjutnya akan ditunjukkan bahwa populasi bakteri juga taknegatif dan terbatas. Misalkan , maka berdasarkan sistem persamaan (3.1) diperoleh
Karena taknegatif, maka berdasarkan persamaan (3.4) dan (3.5) diperoleh
14
dengan Karena untuk setiap , maka diperoleh
atau
Karena dan taknegatif untuk setiap maka diperoleh
Berdasarkan pertidaksamaan (3.5) dan (3.7) diperoleh bahwa
dan
Titik Tetap
Titik tetap dari SPD (3.1) di atas akan diperoleh dengan menetapkan
sehingga diperoleh persamaan-persamaan sebagai berikut:
Dengan menyelesaikan persamaan ( ) akan diperoleh dua titik tetap, yaitu titik tetap tanpa penyakit dan titik tetap endemik.
Matriks Jacobi
15
Titik tetap tanpa penyakit merupakan kondisi ketika semua individu menjadi sehat atau dapat dikatakan tidak terdapat penyakit. Titik tetap ini diperoleh ketika banyaknya individu yang terinfeksi sama dengan nol ( ).
Titik tetap endemik merupakan kondisi ketika penyakit terdapat di dalam populasi manusia. Dari sistem persamaan (3.1) diperoleh titik tetap endemik
16
periode menular, dan infeksi tidak bisa tumbuh. Sebaliknya, jika maka setiap individu yang terinfeksi menghasilkan rata-rata lebih dari satu infeksi baru, dan penyakit dapat menyerang penduduk.
Pendekatan untuk menentukan bilangan reproduksi dasar yang digunakan dalam penelitian ini mengikuti Driessche dan Watmough (2002). Bilangan reproduksi dasar dihitung dengan menggunakan the next generation matrix untuk sistem (3.1). Bilangan reproduksi dasar diperoleh dari nilai eigen dominan dari
dimana adalah fungsi yang menunjukkan tingkat kemunculan infeksi baru di
kompartemen i, adalah fungsi yang menunjukkan transfer infeksi dari satu kompartemen i ke kompartemen lain, dan adalah titik tetap tanpa penyakit.
Dari sistem (3.1) tuliskan kembali persamaan-persamaan untuk kelas infeksi, dan ke dalam sistem (3.14).
Berdasarkan sistem (3.14), diperoleh fungsi dan sebagai berikut:
17
dimana
Bilangan reproduksi dasar diperoleh dari nilai eigen dominan dari matriks , yaitu
Makna biologis dari hasil bilangan reproduksi dasar ini adalah sebagai berikut. adalah banyaknya orang yang rentan pada saat kesetimbangan tanpa penyakit. adalah rata-rata banyaknya bakteri hyperinfectious yang dikeluarkan oleh setiap individu yang sakit. dan
masing-masing adalah banyaknya kasus baru setiap satuan waktu karena bakteri hyperinfectious dan bakteri less infectious. dan adalah rata-rata lama bakteri berada pada kondisi hyperinfectious dan less infectious.
adalah hasil kali dari laju transisi bakteri hyperinfectious menjadi less infectious dengan rata-rata lama bakteri berada pada kondisi less infectious. Dari penjelasan tersebut, maka dan masing-masing adalah rata-rata banyaknya bakteri hyperinfectious dan less infectious yang dikeluarkan ke lingkungan. Dengan demikian, suku pertama dari bilangan reproduksi dasar menunjukkan banyaknya infeksi baru karena bakteri hyperinfectious. Sedangkan suku kedua menunjukkan banyaknya infeksi baru karena bakteri less infectious.
Kestabilan sistem selanjutnya dianalisis dengan mempeerhatikan bilangan reproduksi dasar tersebut. Seelanjutnya akan disajikan teorema mengenai kestabilan lokal dari masing-masing titik tetap.
Analisis Kestabilan Titik Tetap Tanpa Penyakit
Teorema 1. Titik tetap tanpa penyakit untuk sistem (3.1) bersifal stabil asimtotik lokal jika dan tidak stabil jika .
18
dan persamaan karakteristiknya berbentuk
(3.16)
Karena
maka persamaan karakteristik (3.16) menjadi
Berdasarkan persamaan karakteristik (3.17), maka diperoleh lima nilai eigen. Dua nilai eigen negatif adalah:
Sedangkan ketiga nilai eigen lain diperoleh dengan menyelesaikan persamaaan kubik
berikut.
dengan
19
Akar-akar persamaan (3.19) ini merupakan nilai-nilai eigen lain dari persamaan karakteristik (3.17) yaitu . Berdasarkan sifat akar persamaan kubik, diperoleh sistem persamaan berikut
,
Karena , maka jumlah dari ketiga nilai eigen tersebut bernilai negatif Hal ini menandakan di antara ketiga nilai eigen tersebut, selalu ada yang bernilai negatif, anggap Selanjutnya untuk memeriksa kestabilan titik tetap cukup dengan memperhatikan dan Jika dan maka titik tetap akan stabil, sedangkan jika atau maka titik tetap tidak stabil Berdasarkan persamaan (3.15), mengakibatkan
tanpa penyakit bersifat stabil asimtotik lokal.
Selanjutnya akan dibuktikan jika , maka titik tetap tanpa penyakit tidak stabil. Berdasarkan persamaan (3.15), mengakibatkan
Dari pertidaksamaan (3.26) diperoleh sehingga persamaan ketiga dari sistem (3.20) memenuhi
20
Berdasarkan kondisi (3.27) dan selalu negatif, maka diperoleh . Hal ini berarti dan memiliki tanda yang berlawanan. Dengan kata lain, terdapat nilai eigen yang positif sehingga titik tetap tanpa penyakit bersifat tidak stabil.
Jadi, titik tetap tanpa penyakit untuk sistem (3.1) bersifal stabil asimtotik lokal jika dan tidak stabil jika
Analisis Kestabilan Titik Tetap Endemik
Teorema 2. Titik tetap endemik untuk sistem (3.1) unik dan positif jika dan hanya jika
Bukti. Tinjau titik tetap endemik berikut.
21 Berdasarkan sifat akar persamaan kubik, maka akar-akar dari persamaan (3.33) memenuhi sifat berikut:
Karena maka persamaan (3.36) bernilai nol sehingga dapat dipastikan terdapat akar dari persamaan (3.33) yang bernilai nol, misalkan =0. Selanjutnya
mengakibatkan bernilai positif. Selanjutnya karena =0, maka diperoleh
22 mungkin. Dengan demikian tidak ada titik tetap endemik positif diperoleh. Kontradiksi.
Dengan cara yang sama dapat dibuktikan jika maka persamaan (3.33) mempunyai dua akar nol dan satu akar negatif, yang secara biologis juga tidak mungkin. Jadi, titik tetap endemik positif ada dan tunggal untuk sistem (3.1)
jika dan hanya jika .
Berdasarkan teorema 2, jika titik tetap endemik tidak positif (secara biologis tidak mungkin). Teorema berikut menyatakan bahwa, jika , maka titik titik tetap endemik bersifat stabil asimtotik lokal. Bukti teorema dilakukan dengan cara membuktikan bahwa jika maka terjadi bifurkasi. Bifurkasi adalah perubahan kestabilan titik tetap suatu sistem persamaan akibat berubahnya nilai parameter.
Teorema 3. Jika maka titik tetap endemik bersifat stabil asimtotik lokal.
23 bebas,
bebas.
Berdasarkan persamaan (2.11) didefinisikan
dengan
Berdasarkan sistem (3.1) diperoleh
24
maka berdasarkan sistem persamaan (3.44) diperoleh
= 2
Karena maka diperoleh Akibatnya kasus 4 adalah satu-satunya yang berlaku untuk sistem (3.1). Ini berarti saat berubah dari menjadi , titik tetap berubah dari stabil menjadi tidak stabil dan titik tetap endemik berubah dari negatif menjadi positif dan menjadi stabil asimtotik lokal. Dengan kata lain, jika maka titik tetap endemik stabil asimtotik lokal.
25 Tabel 2 Sifat kestabilan titik tetap
Kondisi Titik Tetap Tanpa Penyakit Titik Tetap Endemik Ada dan stabil asimtotik lokal Tidak ada
Ada dan tidak stabil Ada dan stabil asimtotik lokal
Simulasi Model
Simulasi model dilakukan untuk memperlihatkan kembali sifat kestabilan dari masing-masing titik tetap dan untuk mempelajari hal-hal yang terjadi dalam sistem dinamik. Simulasi menggunakan software berbasis fungsional yaitu Maple 13. Dalam hal ini, dinamika populasi manusia dan bakteri dianalisis dengan mengubah-ubah parameter-parameter yang masih memungkinkan untuk dikontrol oleh manusia dalam upaya penekanan penyebaran kolera, yaitu laju cerna bakteri hyperinfectious ( ), laju vaksinasi ( ), laju pengobatan ( ), dan laju kematian bakteri karena sanitasi air Nilai untuk setiap parameter yang digunakan dapat dilihat pada tabel berikut.
Tabel 3 Nilai parameter yang digunakan dalam simulasi
Parameter Nilai Satuan Sumber
Dinamika Populasi dengan Variasi Laju Cerna Bakteri Hyperinfectious
26
Pada bagian ini akan dilakukan simulasi pada kondisi dan Simulasi pertama dan kedua untuk mengecek kestabilan titik tetap sistem (3.1). Simulasi ketiga untuk mengetahui pengaruh variasi parameter laju cerna bakteri hyperinfectious ( ).,Ketiga simulasi dilakukan dengan memberi variasi nilai parameter Nilai parameter dan yang digunakan dalam simulasi laju cerna bakteri hyperinfectious dapat dilihat pada Tabel 4.
27
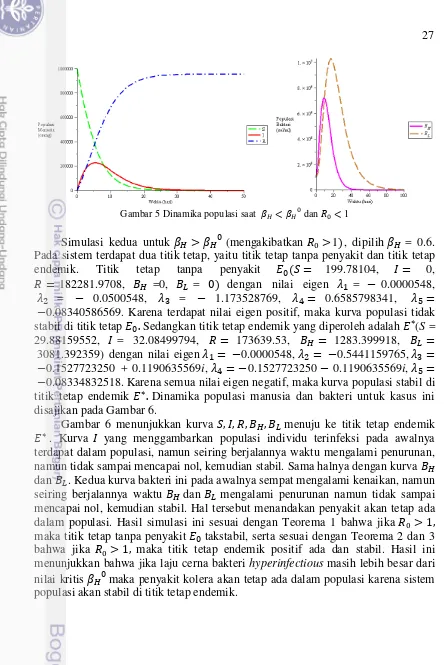
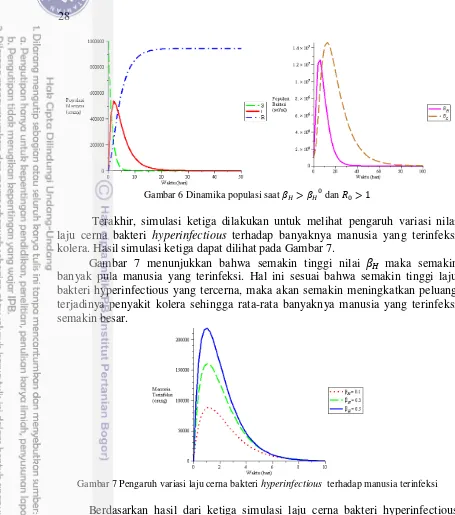
Gambar 5 Dinamika populasi saat dan 1
Simulasi kedua untuk (mengakibatkan 1 , dipilih = 0.6. Pada sistem terdapat dua titik tetap, yaitu titik tetap tanpa penyakit dan titik tetap endemik. Titik tetap tanpa penyakit 199.78104, 0, 182281.9708, =0, = dengan nilai eigen = 0.0000548, = 0.0500548, = 1.173528769, 0.6585798341, 0.08340586569. Karena terdapat nilai eigen positif, maka kurva populasi tidak stabil di titik tetap Sedangkan titik tetap endemik yang diperoleh adalah (S = 29.88159552, = 32.08499794, 173639.53, 1283.399918,
3081.392359) dengan nilai eigen 0.0000548, 0.5441159765, 0.1527723250 + 0.1190635569i, 0.1527723250 0.1190635569i, 0.08334832518.Karena semua nilai eigen negatif, maka kurva populasi stabil di titik tetap endemik Dinamika populasi manusia dan bakteri untuk kasus ini disajikan pada Gambar 6.
28
Gambar 6 Dinamika populasi saat dan
Terakhir, simulasi ketiga dilakukan untuk melihat pengaruh variasi nilai laju cerna bakteri hyperinfectious terhadap banyaknya manusia yang terinfeksi kolera. Hasil simulasi ketiga dapat dilihat pada Gambar 7.
Gambar 7 menunjukkan bahwa semakin tinggi nilai maka semakin banyak pula manusia yang terinfeksi. Hal ini sesuai bahwa semakin tinggi laju bakteri hyperinfectious yang tercerna, maka akan semakin meningkatkan peluang terjadinya penyakit kolera sehingga rata-rata banyaknya manusia yang terinfeksi semakin besar.
Gambar 7 Pengaruh variasi laju cerna bakteri hyperinfectious terhadap manusia terinfeksi
Berdasarkan hasil dari ketiga simulasi laju cerna bakteri hyperinfectious ( dapat disimpulkan semakin tinggi nilai , semakin tinggi pula nilai yang berarti semakin sulit mengatasi wabah penyakit kolera. Ketika nilai masih di bawah satu, kurva akan stabil menuju titik tetap tanpa penyakit, dalam hal ini penyakit akan hilang seiring berjalannya waktu. Sedangkan ketika nilai lebih besar dari satu, kurva akan stabil menuju titik tetap endemik, dalam hal ini penyakit akan tetap ada dalam populasi.
Dinamika Populasi dengan Variasi Laju Vaksinasi
29 tetap sistem (3.1), sedangkan simulasi ketiga untuk mengetahui pengaruh variasi parameter laju vaksinasi ( ). Ketiga simulasi dilakukan dengan memberikan variasi pada nilai parameter Nilai parameter dan yang digunakan dalam simulasi laju cerna bakteri hyperinfectious dapat dilihat pada Tabel 5 berikut.
Tabel 5 Nilai parameter dan dalam simulasi laju vaksinasi
Simulasi
ke-1 0.1 0.2 0.05 0.05 <1
2 0.1 0.02 0.05 0.05 >1
3 0.1 0.1 0.05 0.05 <1
0.1 0.3 0.05 0.05 <1
0.1 0.5 0.05 0.05 <1
Pada simulasi ini ditetapkan nilai , sedangkan diubah-ubah nilainya. Nilai kritis laju vaksinasi diperoleh saat yaitu 0.1063602164 (Penentuan nilai kritis laju vaksinasi bisa dilihat pada Lampiran 3). Simulasi dilakukan dengan mengevaluasi pada yang mengakibatkan
dan yang mengakibatkan .
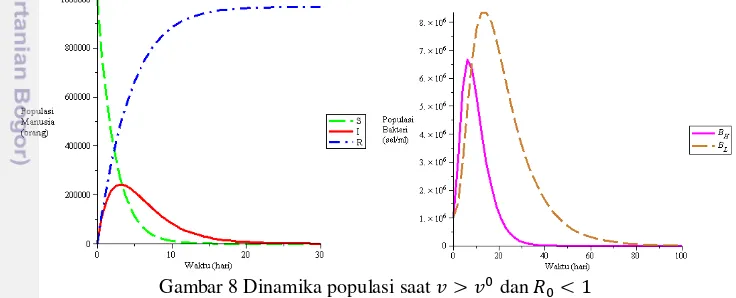
Simulasi pertama untuk (mengakibatkan dipilih 0.2, maka diperoleh satu titik tetap yaitu titik tetap tanpa penyakit = 49.98630375
= 0 = 182431.7655, = 0 = 0) dengan nilai eigen = 0.0000548 = 0.2000548 = 0.44457759138 = 0.0686827432, = 0.08690893442. Dinamika populasi manusia dan bakteri untuk kasus ini disajikan pada Gambar 8.
Gambar 8 Dinamika populasi saat dan
30
nilai kritis maka penyakit kolera bisa hilang dari populasi karena sistem populasi akan stabil di titik tetap tanpa penyakit.
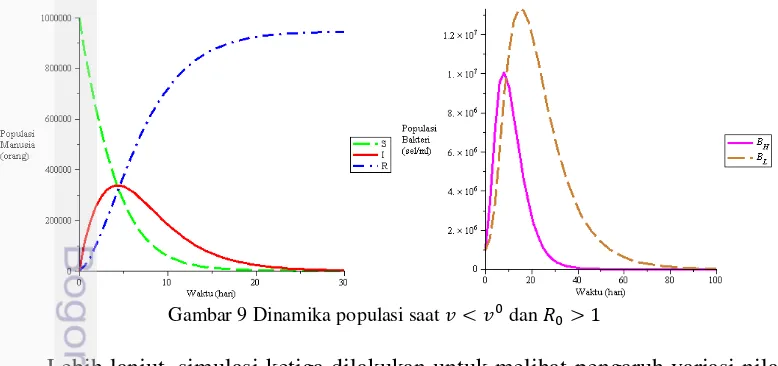
Simulasi kedua untuk dan 1, dipilih = 0.02. Pada sistem dan bakteri untuk kasus ini disajikan pada Gambar 9.
Gambar 9 menunjukkan kurva secara asimtotik menuju ke titik tetap endemik . Kurva yang menggambarkan populasi individu terinfeksi pada awalnya terdapat dalam populasi, awalnya mengalami peningkatan namun seiring berjalannya waktu mengalami penurunan namun tidak mencapai titik nol, lalu stabil. Sama halnya dengan kurva dan , kedua kurva bakteri ini pada awalnya sempat mengalami kenaikan, namun seiring berjalannya waktu dan mengalami penurunan namun tidak mencapai titik nol dan stabil secara asimtotik di titik yang bernilai positif. Dalam hal ini sistem stabil di titik tetap endemik. Hasil simulasi ini sesuai dengan Teorema 1 bahwa titik tetap tanpa penyakit stabil jika dan hanya jika sehingga ketika titik tetap tanpa penyakit
tidak stabil. Hal ini juga sesuai dengan Teorema 2 dan Teorema 3 bahwa jika maka ada titik tetap endemik positif yang diperoleh, dan bersifat stabil asimtotik lokal. Hasil ini menunjukkan bahwa jika laju vaksinasi diturunkan hingga lebih rendah dari nilai kritis maka penyakit kolera akan meningkat dan penyakit akan menetap dalam populasi.
Gambar 9 Dinamika populasi saat dan
31
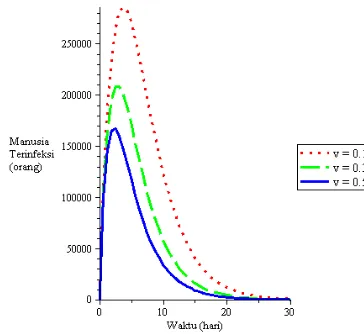
Gambar 10 Pengaruh variasi laju vaksinasi terhadap manusia terinfeksi
Gambar 10 menunjukkan bahwa semakin tinggi nilai maka semakin sedikit manusia yang terinfeksi. Hal ini sesuai bahwa peningkatan kontrol vaksinasi dapat mengendalikan penyakit.
Berdasarkan ketiga simulasi variasi laju vaksinasi tersebut, dapat disimpulkan semakin tinggi nilai semakin rendah nilai maka kurva akan semakin mendekati ke titik tetap tanpa penyakit Ketika nilai masih di bawah satu, kurva akan stabil menuju titik tetap tanpa penyakit, dalam hal ini penyakit akan hilang seiring berjalanya waktu. Sedangkan ketika nilai lebih besar dari satu, kurva akan stabil menuju titik tetap endemik, dalam hal ini penyakit akan tetap ada. Dengan demikian tingkat vaksinasi memiliki peran penting dalam menekan penyebaran penyakit kolera.
Dinamika Populasi dengan Variasi Laju Pengobatan
Definisikan adalah laju pengobatan, yaitu laju per kapita pengobatan penyakit kolera untuk individu terinfeksi/terjangkit kolera. Simulasi pertama dan kedua dilakukan untuk mengecek kestabilan titik tetap sistem (3.1), sedangkan simulasi ketiga untuk mengetahui pengaruh variasi parameter laju pengobatan ( ). Ketiga simulasi dilakukan dengan memberikan variasi pada nilai parameter Nilai parameter dan yang digunakan dalam simulasi laju pengobatan dapat dilihat pada Tabel 6 berikut.
Tabel 6 Nilai parameter dan dalam simulasi laju vaksinasi
Simulasi
ke-1 0.1 0.05 0.05 0.05 <1
2 0.1 0.05 0.005 0.05 >1
3 0.1 0.05 0.1 0.05 >1
0.1 0.05 0.3 0.05 >1
0.1 0.05 0.5 0.05 <1
32
yaitu 0.3484438233 (Penentuan nilai kritis laju pengobatan bisa dilihat pada Lampiran 4). Simulasi dilakukan dengan mengevaluasi pada yang mengakibatkan dan yang mengakibatkan .
Simulasi pertama dengan (mengakibatkan dipilih 0.5, maka diperoleh satu titik tetap yaitu titik tetap tanpa penyakit = 199.78104 = 0 = 182281.9708, = 0 = 0) dengan nilai eigen = 0.0000548 =
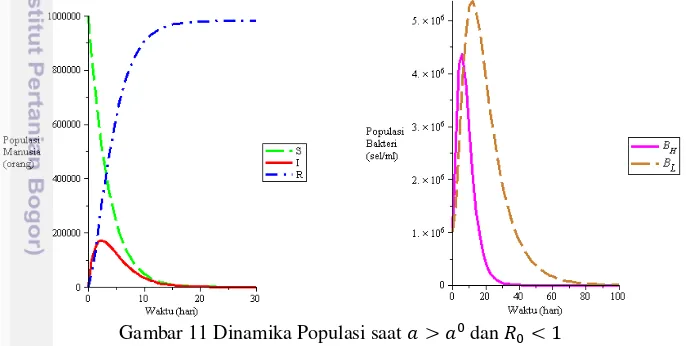
0.0500548 = 0.9227701993 = 0.03993259837, = 0.08565200235. Dinamika populasi manusia dan bakteri untuk kasus ini disajikan pada Gambar 11.
Gambar 11 menunjukkan kurva menuju ke titik tetap tanpa penyakit . Kurva yang menggambarkan populasi individu terinfeksi pada awalnya terdapat dalam populasi, namun seiring berjalannya waktu mengalami penurunan hingga mencapai nol dan stabil. Sama halnya dengan kurva dan , kedua kurva bakteri ini pada awalnya sempat mengalami kenaikan, namun seiring berjalannya waktu dan mengalami penurunan hingga mencapai nol dan stabil. Hasil simulasi ini sesuai dengan Teorema 1 bahwa jika maka titik tetap tanpa penyakit stabil, serta sesuai dengan Teorema 2 bahwa jika maka tidak ada titik tetap endemik positif yang diperoleh. Hasil ini menunjukkan bahwa jika laju pengobatan ditingkatkan hingga lebih besar dari nilai kritis maka penyakit kolera bisa hilang dari populasi karena sistem populasi akan stabil di titik tetap tanpa penyakit.
Gambar 11 Dinamika Populasi saat dan
Simulasi kedua untuk ( 1 , dipilih = 0.05. Hasil yang diperoleh dapat dilihat pada Gambar 12. Pada simulasi ini diperoleh dua titik tetap yaitu titik tetap tanpa penyakit 199.78104, 0, 182281.9708, =0, = dan
titik tetap endemik (S = 128.8607425, =
33
Gambar 12 Dinamika Populasi saat dan
Lebih lanjut, simulasi ketiga menunjukkan pengaruh perubahan nilai laju pengobatan terhadap banyaknya manusia terinfeksi kolera. Hasil yang diperoleh dapat dilihat pada gambar berikut
Gambar 13 Pengaruh variasi laju pengobatan terhadap manusia terinfeksi
Berdasarkan simulasi dengan variasi laju pengobatan tersebut, dapat disimpulkan semakin tinggi nilai , semakin rendah nilai maka kurva akan semakin mendekat ke titik tetap tanpa penyakit Ketika nilai masih di bawah satu, kurva akan stabil menuju titik tetap tanpa penyakit, dalam hal ini penyakit akan hilang seiring berjalannya waktu. Sedangkan ketika nilai di atas 1, kurva akan stabil menuju titik tetap endemik, pada kondisi ini penyakit akan tetap ada (tidak menghilang). Dengan demikian tingkat pengobatan memiliki peran penting dalam mengurangi penyebaran penyakit kolera.
Dinamika Populasi dengan Variasi Laju Sanitasi
Definisikan laju sanitasi adalah laju kematian bakteri karena sanitasi air. Variasi nilai berhubungan dengan tingkat klorinasi dan kebersihan cadangan air masyarakat.
34
pada nilai parameter Nilai parameter dan yang digunakan dalam simulasi laju sanitasi dapat dilihat pada Tabel 7 berikut.
Tabel 7 Nilai parameter dan dalam simulasi laju sanitasi
Simulasi
ke-1 0.1 0.05 0.05 0.5 <1
2 0.1 0.05 0.05 0.05 >1
3 0.1 0.05 0.05 0.1 >1
0.1 0.05 0.05 0.3 >1
0.1 0.05 0.05 0.5 <1
Pada simulasi ini ditetapkan nilai , sedangkan laju sanitasi, diubah-ubah nilainya. Nilai kritis laju sanitasi diperoleh saat yaitu 0.32850728643 (Penentuan nilai kritis sanitasi bisa dilihat pada Lampiran 5). Simulasi dilakukan dengan mengevaluasi pada yang mengakibatkan dan yang mengakibatkan .
Simulasi pertama dengan (mengakibatkan dipilih 0.5, maka diperoleh satu titik tetap yaitu titik tetap tanpa penyakit = 199.78104 = 0 = 182281.9708, = 0 = 0) dengan nilai eigen = 0.0000548 =
0.0500548 = 0.04972475273 = 0.9148659888, = 05337640585. Dinamika populasi manusia dan bakteri untuk kasus ini disajikan pada Gambar 14.
Gambar 14 Dinamika populasi saat dan
35 Selanjutnya, simulasi dilakukan dengan mengganti nilai laju sanitasi yang lebih kecil dari nilai kritis , yaitu dengan . Hasil yang diperoleh ditunjukkan pada Gambar 15.
Gambar 15 Dinamika populasi saat dan
Pada simulasi kedua diperoleh dua titik tetap yaitu titik tetap tanpa penyakit dengan nilai eigen dan titik tetap endemik (S = 141.7999448, = 10.94955506, 179331.8613, 364.9851685,
547.6146565) dengan nilai eigen 0.0000548, 0.5391814997, 0.04754647259+0.04698620621i, 0.04754647259 0.04698620621i
. Titik tetap tanpa penyakit memiliki empat nilai eigen negatif dan satu nilai eigen positif kurva populasi tidak stabil di titik tetap Sedangkan untuk titik tetap endemik , semua nilai eigen negatif, maka kurva populasi stabil di titik tetap endemik . Hal ini berarti jika laju pengobatan lebih rendah dari nilai kritis , maka sistem populasi akan stabil dalam keadaan selalu ada penyakit kolera.
Lebih lanjut, simulasi ketiga menunjukkan pengaruh perubahan nilai laju sanitasi terhadap banyaknya manusia terinfeksi kolera ditunjukkan pada Gambar 16 berikut.
36
Pada Gambar 16 terlihat bahwa walaupun ada perbedaan nyata dalam nilai laju sanitasi, pada awalnya ketiga kurva hampir berimpit. Namun jika dilihat untuk jangka panjang, laju sanitasi yang lebih besar dari nilai kritis akan membuat sistem populasi stabil dalam keadaan tanpa penyakit. Sedangkan jika laju sanitasi lebih rendah dari nilai kritis, sistem populasi stabil dalam keadaan masih ada penyakit. Dengan demikian peningkatan sanitasi merupakan alternatif strategi untuk menekan terjadinya kolera.
4
SIMPULAN DAN SARAN
Simpulan
Dalam tesis ini telah dilakukan modifikasi terhadap model matematika penyebaran penyakit kolera. Model tersebut mempertimbangkan adanya tahap hyperinfectious dari bakteri dan pengaruh vaksinasi, pengobatan, dan sanitasi. Rincian hasil utama dalam tesis ini disimpulkan sebagai berikut:
1. Analisis model menunjukkan bahwa model matematika penyebaran penyakit kolera memiliki dua titik tetap, yaitu titik tetap tanpa penyakit dan titik tetap endemik. Titik tetap tanpa penyakit bersifat stabil asimtotik lokal jika , sedangkan titik tetap endemik yang positif ada dan stabil asimtotik lokal jika . Hasil ini juga telah dijustifikasi melalui simulasi numerik yang telah dilakukan.
2. Hasil simulasi numerik menunjukkan bahwa
a. Jika laju cerna bakteri hyperinfectious ditekan hingga lebih kecil dari nilai kritisnya, maka sistem akan stabil di titik tetap tanpa penyakit, dengan kata lain, penyakit kolera bisa hilang dari populasi. Sebaliknya, jika laju cerna bakteri hyperinfectious masih lebih besar dari nilai kritisnya, maka sistem akan stabil di titik tetap endemik, dengan kata lain, penyakit kolera akan menetap dalam populasi.
b. Jika laju vaksinasi ditingkatkan hingga lebih besar dari nilai kritisnya, maka sistem akan stabil di titik tetap tanpa penyakit, dengan kata lain, penyakit kolera bisa hilang dari populasi. Sebaliknya, jika laju vaksinasi lebih rendah dari nilai kritisnya, maka sistem akan stabil di titik tetap endemik, dengan kata lain, penyakit kolera akan menetap dalam populasi. Hal yang sama juga berlaku untuk laju pengobatan dan laju sanitasi.
3. Hasil simulasi numerik juga menunjukkan bahwa meningkatnya laju cerna bakteri hyperinfectious menyebabkan naik, sehingga mempercepat laju penyebaran penyakit. Di lain pihak, meningkatnya laju vaksinasi, pengobatan, dan sanitasi menyebabkan turun, sehingga menekan laju penyebaran penyakit.
Saran
37 terinfeksi, adanya pertumbuhan logistik dari bakteri, serta mempertimbangkan faktor lain seperti edukasi dan nutrisi, yang mungkin mempunyai peran penting dalam menyebarkan penyakit kolera dalam komunitas masyarakat miskin.
DAFTAR PUSTAKA
Anton H, Rorres C. 1995. Elementary Linear Algebra. New York: John Wiley & Son Inc.
Braun M. 1983. Differential Equations and Their Applications. New York: Springer-Verlag.
Capasso V, Paveri-Fontana SL. 1979. A Mathematical Model for the 1973 Cholera Epidemic in The European Mediterranean Region. Rev Epidém et Santé Pub.
27:121-132.
Castillo-Chaves C, Song B. 2004. Dynamical Models of Tuberculosis and Their Applications. Mathematical Biosciences and Engineering. 1(2):361-404. Codeco CT. 2001. Endemic and Epidemic Dynamics of Cholera: The Role of The
Aquatic Reservoir. BMC Infectious Diseases. 1:1.
Diekman O, Heesterbeek JAP, Metz JAP. 1990. On the Definition and Computation of The Basic Reproduction Ratio in The Model of Infectious Disease in Heterogeneous Populations. Journal of Mathematical Biology.
2(1):265-382.
Driessche PVD, Watmough J. 2002. Reproduction numbers and sub-thresh-old endemic equilibria for compartmental models of disease transmission. Math-Biosci. 180. 29-48.
Fenner F, Henderson DA, Arita I, Jezek Z, dan Ladnyi ID. 1988. Smallpox and Its Eradication. Journal of Community Health. 18(4):245-592.
Fung ICH, Fitter DL, Borse RH, Meltzer MI, dan Tappero JW. 2013. Modeling the Effect of Water, Sanitation, and Hygiene and Oral Cholera Vaccine Implementation in Haiti. American Journal Tropical Medicine and Hygiene.
89(4):633–640.
Hartley DM, Morris Jr JG , Smith DL. 2006. Hiperinfectivity: A Critical Element in the Ability of V. Cholerae to Cause Epidemics? PLoS Med. 3(1):63-68. Hethcote HW. 1998. Oscilations in an Endemic Model for Pertussis. The Canadian
Applied Mathematics Quarterly. 6(1):61-88.
Hethcote HW. 2000. The Mathematics of Infectious Disease. SIAM Review.
42(4):599-653.
Hove-Musekwa SD, Nyabadza F, Chiyaka C, Das P, Tripathi A, Mukandavire Z. 2011. Modelling and Analysis of The Effects of Malnutrition in The Spread of Cholera. Mathematical and Computer Modelling. 53: 1583–1595.
Ivers LC, Farner P, Almazor CP, Leandre F. 2010. Five Complementary Interventions to Slow Cholerae: Haiti. Lancet. 376:2048–2051.
38
Tian XH. 2012. Stability Analysis of A Delayed SIRS Epidemic Model with Vaccination and Nonlinear Incidence. International Journal of Biomathematics. 5(6).
Tu PNV. 1994. Dynamic System: An Introduction with Application in Economics and Biology. New York: Springer-Verlag.
Waldman RJ, Mintz ED, Papountz HE. 2013. The Cure for Cholera: Improving Access to Safe Water and Sanitation. New England Journal Medicine.
368:592-594.
Wang J, Modnak C. 2011. Modelling Cholera Dynamics with Controls. Canadian Applied. 3: 255-272.
[WHO] World Health Organization. 2010. Cholera Vaccines: WHO position paper. Weekly Epidemiological Record. 85:117-128.
39 Kemudian hasil yang diperoleh untuk
40
Lampiran 2 Penentuan Nilai Kritis Laju Cerna Bakteri Hyperinfectious
Nilai kritis laju cerna bakteri hyperinfectious diperoleh saat , yaitu saat peralihan kondisi kestabilan titik tetap.
Berdasarkan persamaan (3.15), jika maka akan diperoleh nilai kritis sebagai berikut
41
Lampiran 3 Penentuan Nilai Kritis Laju Vaksinasi
Nilai kritis laju vaksinasi diperoleh saat , yaitu saat peralihan kondisi kestabilan titik tetap.
Berdasarkan persamaan (3.15), jika maka akan diperoleh nilai kritis sebagai berikut
42
Lampiran 4 Penentuan Nilai Kritis Laju Pengobatan
Nilai kritis laju pengobatan diperoleh saat , yaitu saat peralihan kondisi kestabilan titik tetap.
Berdasarkan persamaan (3.15), jika maka akan diperoleh nilai kritis sebagai berikut
43
Lampiran 5 Penentuan Nilai Kritis Laju Kematian Bakteri Karena Sanitasi
Nilai kritis laju kematian bakteri karena sanitasi diperoleh saat , yaitu saat peralihan kondisi kestabilan titik tetap.
Berdasarkan persamaan (3.15), jika maka akan diperoleh nilai kritis yang memenuhi persamaan berikut.
Misalkan
Persamaan kuadrat untuk nilai kritis menjadi
Untuk nilai parameter pada tabel 2 dan maka diperoleh
Sehingga persamaan kuadrat untuk nilai kritis diperoleh
Akar-akar yang memenuhi adalah
dan (secara biologis tidak mungkin).
44
RIWAYAT HIDUP
Penulis dilahirkan di Sungguminasa, Kabupaten Gowa, Provinsi Sulawesi Selatan pada tanggal 6 Oktober 1992 dan merupakan anak keempat dari empat bersaudara. Penulis lahir dari pasangan Bapak Arifuddin dan Rabiah.