ANALISIS DINAMIKA MODEL
PENYEBARAN PENYAKIT KOLERA
ANDI FITRIANAH
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI SKRIPSI DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA
Dengan ini saya menyatakan bahwa skripsi berjudul Analisis Dinamika Model Penyebaran Penyakit Kolera adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
Bogor, Februari 2015
Andi Fitrianah
ABSTRAK
ANDI FITRIANAH. Analisis Dinamika Model Penyebaran Penyakit Kolera. Dibimbing oleh ELIS KHATIZAH dan ALI KUSNANTO.
Model matematika SIR penyakit kolera yang dikembangkan oleh Liao & Wang (2011) dengan populasi bakteri terbagi dua yaitu bakteri yang sangat berbahaya (hyper infectious) dan bakteri yang kurang berbahaya (less infectious). Model ini menghasilkan dua titik tetap, yaitu titik tetap tanpa penyakit dan titik tetap endemik. Analisis kestabilan bagi titik tetap tersebut ditentukan menggunakan kriteria Routh-Hurwitz. Dengan asumsi total populasi konstan, dinamika populasi bagi titik tetap endemik menunjukkan bahwa peningkatan laju infeksi bakteri akan mempercepat terjadinya wabah penyakit. Kecepatan terjadinya wabah akan lebih besar pada saat laju infeksi bakteri hyper infectious
meningkat dibandingkan pada saat laju infeksi bakteri less infectious meningkat. Di sisi lain, laju kelahiran/kematian populasi manusia yang besar akan memperbesar pula kecepatan terjadinya wabah.
Kata kunci: model SIR, kolera, dan kriteria kestabilan Routh-Hurwitz
ABSTRACT
ANDI FITRIANAH. Dynamics Analysis of Cholera’s Spreading Model Supervised byELIS KHATIZAHandALI KUSNANTO.
A mathematical model developed by Liao & Wang (2011) for cholera disease was categorized within a SIR model, where bacteria concentration were grouped into hyper infectious and less infectious groups. This model provides two equilibrium points i.e., disease-free and endemic states. Analysis of stability of those equilibrium points were determined by using the Routh-Hurwitz stability criterion. The population dynamics at endemic equilibrium under a constant total of population shows that the increase of the infection rate of bacteria will increase the disease victims. The disease outbreak were found to be faster when the infection rate of hyper infectious bacteria increase, compared with increase of the infection rate of less infectious bacteria. Also, a high birth rate and/or human mortality rate would increase the outbreak of the disease.
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada
Departemen Matematika
ANALISIS DINAMIKA MODEL
PENYEBARAN PENYAKIT KOLERA
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM INSTITUT PERTANIAN BOGOR
BOGOR 2015
PRAKATA
Puji dan syukur penulis panjatkan kepada Allah subhanahu wa ta’ala atas segala karunia-Nya sehingga karya ilmiah ini berhasil diselesaikan. Judul yang dipilih dalam penelitian yang dilaksanakan sejak bulan Januari 2014 ini ialah Analisis Dinamika Model Penyebaran Penyakit Kolera.
Terima kasih penulis ucapkan kepada semua pihak yang telah membantu dalam penyelesaian karya ilmiah ini khususnya Ibu Elis Khatizah, MSi dan Bapak Drs Ali Kusnanto, MSi selaku pembimbing, serta Bapak Dr Paian Sianturi yang telah banyak memberi saran. Di samping itu, penghargaan penulis sampaikan kepada Bapak Darwin dan Ibu Nonon Mulyanah selaku orangtua yang memberikan dukungan, semangat, dan doa tanpa henti. Ungkapan terima kasih juga disampaikan kepada adik, kakak, seluruh keluarga, serta teman-teman atas segala doa dan kasih sayangnya.
Semoga karya ilmiah ini bermanfaat.
Bogor, Februari 2015
DAFTAR ISI
DAFTAR GAMBAR viii
DAFTAR TABEL viii
DAFTAR LAMPIRAN viii
PENDAHULUAN
Latar Belakang 1
Tujuan Penelitian 1
TINJAUAN PUSTAKA 2
HASIL DAN PEMBAHASAN 4
Perumusan Model 4
Titik Tetap 6
Analisis Kestabilan Titik Tetap 7
SIMULASI MODEL 10
SIMPULAN 18
DAFTAR PUSTAKA 18
LAMPIRAN 19
DAFTAR GAMBAR
1 Diagram kompartemen model matematika penyakit kolera 5
2 Dinamika populasi pada saat 11
3 Dinamika populasi pada saat 11
4 Dinamika populasi pada saat 12
5 Dinamika populasi pada saat 12
6 Perbandingan populasi I ketika dan 12
7 Dinamika populasi pada saat 13
8 Dinamika populasi pada saat 13
9 Dinamika populasi pada saat 14
10 Dinamika populasi pada saat 14
11 Perbandingan populasi I ketika dan 15
12 Dinamika populasi pada saat 15
13 Dinamika populasi pada saat 16
14 Dinamika populasi pada saat 17
15 Dinamika populasi pada saat 17
16 Perbandingan populasi I ketika dan 17
DAFTAR TABEL
1 Notasi pada sistem persamaan (3) beserta satuannya 6
2 Nilai parameter , dan dalam simulasi 10
DAFTAR LAMPIRAN
1 Bukti untuk kasus menurut kondisi Routh-Hurwitz 19
2 Pencarian titik tetap tanpa penyakit 19
3 Pencarian titik tetap endemik 19
4 Bukti untuk memeriksa kestabilan titik tetap endemik dengan kriteria
Routh-Hurwitz 20
5 Contoh simulasi bidang solusi dinamika populasi pada Gambar 2
PENDAHULUAN
Latar Belakang
Penyakit infeksi seperti kolera dan hepatitis merupakan penyakit infeksi yang berbahaya. Penyakit tersebut disebabkan oleh bakteri atau virus yang dapat menyebar melalui kontak langsung dengan penderita.
Perkembangan ilmu di bidang matematika turut memberikan peranan penting dalam menggambarkan fenomena penyebaran penyakit. Menurut Hetchcote (2000), model penyebaran penyakit infeksi salah satunya adalah model SIR. Pada model SIR, individu yang telah sembuh dari suatu penyakit tidak akan terinfeksi lagi karena telah memiliki kekebalan tubuh.
Menurut Johnson (2004), kolera adalah penyakit yang telah lama menyerang manusia dan terus menjadi masalah bagi kesehatan masyarakat dunia. Penyakit kolera merupakan penyakit infeksi saluran usus bersifat akut yang disebabkan oleh bakteri Vibrio cholerae. Bakteri ini masuk ke dalam tubuh seseorang melalui makanan atau minuman yang terkontaminasi. Bakteri tersebut mengeluarkan enterotoksin (racun) pada saluran usus sehingga menimbulkan diare disertai muntah yang akut dan hebat.Akibatnya, seseorang dalam waktu hanya beberapa hari akan kehilangan banyak cairan tubuh dan masuk pada kondisi dehidrasi. Apabila dehidrasi tidak segera ditangani, maka akan berlanjut ke arah hipovolemik dan asidosis metabolik dalam waktu yang relatif singkat. Kondisi ini dapat menyebabkan kematian bila tidak cepat ditangani. Penyakit kolera dapat menjadi penyakit yang mengancam jiwa, tetapi dapat dicegah dan diobati.
Pada penelitian ini, akan dibahas model matematika untuk penyakit kolera yang disusun oleh Liao dan Wang pada tahun 2011 dalam artikel yang berjudul
Stability analysis and application of a mathematical cholera modeldengan model populasi manusia berbentuk SIR dan model konsentrasi bakteri yang terbagi menjadi dua yaitu bakteri yang sangat berbahaya (hyperinfectious) dan bakteri yang tidak begitu berbahaya (less infectious). Dari model tersebut akan dilakukan analisis dinamika populasi terhadap penyakit dengan asumsi total populasi konstan.
Tujuan Penelitian
2
TINJAUAN PUSTAKA
Sistem Persamaan Diferensial dan Solusi Kesetimbangan
Persamaan yang digunakan pada pendekatan model ini adalah sistem persamaan diferensial taklinear orde satu.
Perhatikan sistem persamaan diferensial linear (SPD) berikut:
( , ),
Sedangkan titik lain disebut titik biasa. Selanjutnya akan dibahas analisis kestabilan dari suatu titik tetap.
Definisi 1 Titik Tetap Stabil
Titik adalah titik tetap sebuah SPD dan adalah solusi yang memenuhi kondisi awal dengan Titik dikatakan stabil jika terdapat yang memenuhi sifat berikut: untuk setiap
terdapat sehingga jika maka , untuk
setiap
Definisi 2 Titik Tetap Tidak Stabil
Misalkan titik tetap sebuah SPD mandiri dan adalah sebuah solusi SPD mandiri dengan nilai awal dengan Titik dikatakan tak stabil jika terdapat radius dengan ciri sebagai berikut: untuk sebarang terdapat posisi awal yang memenuhi berakibat solusi memenuhi untuk paling sedikit satu
(Verhulst 1990) Selain menggunakan definisi, kestabilan titik tetap dapat ditentukan dengan mencari nilai eigen yang diperoleh dari penyelesaian solusi taknol matriks yang berukuran .Persamaan (1) dikatakan sistem persamaan diferensial linear jika
F dan G merupakan fungsi linear dan persamaan (1) dikatakan sistem persamaan diferensial taklinear jika F atau G merupakan fungsi taklinear. Untuk suatu sistem persamaan diferensial taklinear, analisis kestabilannya dilakukan melalui pelinearan. Tahap pertama dalam pelinearan terhadap persamaan (1) adalah mengasumsikan persamaan (1) sebagai persamaan taklinear dengan turunan parsial dari persamaan (1) kontinu di . Menggunakan ekspansi Taylor di sekitar titik tetapnya diperoleh
, (2)
dengan ,
dan adalah suku berorde tinggi yang memiliki sifat Bentuk disebut pelinearan persamaan (2)
3 hanya jika memenuhi persamaan karakteristik berikut:
det
(Leon 1998) Misalkan diberikan matriks berukuran sebagai berikut:
Persamaan karakteristik diberikan oleh: det
sedemikian sehingga akan diperoleh nilai eigen dari matriks tersebut. Setelah diperoleh nilai eigen, didapat empat kasus sebagai berikut: 1 Jika nilai eigennya real dan berbeda tanda, maka titik tetap bersifat sadel. 2 Jika semua nilai eigennya real dan bertanda sama, maka titik tetapnya
merupakan simpul tidak sejati (nodes). Jika nilai eigen bertanda positif, maka simpul tidak stabil. Jika nilai eigen bertanda negatif, maka simpul stabil. 3 Jika nilai eigennya merupakan complexconjugate dengan bagian realnya
positif, maka titik tetap bersifat spiral tak stabil. Jika bagian realnya negatif, maka titik tetap bersifat spiral stabil.
4 Jika nilai eigen merupakan imajiner murni, maka titik tetap bersifat center
yang selalu stabil.
(Verhulst 1990) Dalam permasalahan tertentu, tidak mudah menentukan kestabilan titik kesetimbangan hanya menggunakan tanda bagian real nilai eigen. Oleh karena itu, diperlukan metode penentuan kestabilan titik kesetimbangan lain yang dapat menentukan tanda bagian real nilai eigen suatu persamaan karakteristik. Salah satu metode yang dapat digunakan adalah metode kestabilan Routh-Hurwitz, yaitu suatu metode untuk menunjukkan kestabilan dengan tidak harus menghitung akar-akar persamaan karakteristik secara langsung.
Kriteria Kestabilan Routh-Hurwitz. Misalkan bilangan-bilangan real dan jika Semua nilai eigen dari persamaan karakteristik
4
A
adalah positif, dengan .
Menurut kondisi Routh-Hurwitz, untuk suatu disebutkan bahwa titik tetap stabil jika dan hanya jika,
(Fisher 1990) (Bukti untuk kasus pada Lampiran 1)
Bilangan Reproduksi Dasar
Bilangan reproduksi dasar adalah rata-rata banyaknya individu yang rentan terinfeksi secara langsung oleh individu lain yang telah terinfeksi bila individu yang telah terinfeksi tersebut masuk ke dalam populasi yang seluruhnya masih rentan. Bilangan reproduksi dasar dapat diperoleh dari titik tetap tanpa penyakit. Bilangan reproduksi dasar dilambangkan dengan
Beberapa kondisi yang akan timbul, yaitu 1 Jika maka penyakit akan menghilang. 2 Jika maka penyakit akan menetap.
3 Jika maka penyakit akan meningkat menjadi wabah.
(Gieseacke 1994)
dibagi menjadi tiga kelas, yaitu: kelas individu terserang penyakit (susceptible) yang dinotasikan dengan , kelas individu yang terinfeksi (infected) yang dinotasikan dengan , dan kelas individu yang sembuh (recovered) yang dinotasikan dengan , atau dapat juga ditulis: Ini menjelaskan bahwa individu yang rentan, setelah terinfeksi akan menjadi sembuh dan tidak rentan lagi.
5 terinfeksi dan akan masuk menjadi populasi I sehingga mengakibatkan berkurangnya populasi S. Laju bakteri yang menginfeksi sebesar dan . Kelas
I menyatakan individu yang terinfeksi dan dapat menularkan kolera kepada orang lain. Berkurangnya populasi ini disebabkan oleh kematian dengan laju . Individu yang terinfeksi kolera dapat sembuh kembali dengan laju dan masuk dalam populasi R sehingga menyebabkan berkurangnya populasi I. Individu dalam kelas
R diasumsikan tidak akan terinfeksi penyakit lagi. Berkurangnya populasi ini disebabkan oleh kematian dengan laju .
Bakteri hyperinfectious yang dinotasikan dengan akan bertambah karena adanya kontribusi orang yang terinfeksi populasi Vibrio cholerae dalam perairan dengan laju . Berkurangnya populasi ini disebabkan oleh laju transisi bakteri sebesar yang kemudian masuk dalam populasi bakteri less infectious yang dinotasikan dengan . Bakteri dalam kelas akan berkurang disebabkan oleh kematian bakteri dengan laju sebesar .
Dari asumsi-asumsi tersebut dapat dibuat diagram model matematika penyakit kolera seperti terlihat pada Gambar 1.
b
H HGambar 1 Diagram kompartemen model matematika penyakit kolera Selanjutnya, berdasarkan diagram kompartemen model matematika penyakit kolera dapat dibentuk sistem persamaan berikut.
,
6
Tabel 1 Notasi pada sistem persamaan (3) beserta satuannya
Notasi Keterangan Satuan
Variabel
banyaknya individu sehat namun rentan terhadap penyakit
b laju kelahiran/kematian dalam populasi manusia konsentrasi bakteri hyperinfectious dalam air yang menyebabkan 50 % dari kemungkinan terkena kolera konsentrasi bakteri less infectious dalam air yang menyebabkan 50 % dari kemungkinan terkena kolera laju bakteri hyperinfectious yang tercerna oleh individu S
laju bakteri less infectiousyang tercerna oleh individu S
laju kesembuhan
kontribusi setiap orang yang terinfeksi pada populasi
V. cholerae dalam lingkungan perairan laju transisi bakteri
laju kematian bakteri
(
)
Untuk sistem ini, semua parameter bernilai positif.
Selanjutnya, akan dicari titik tetap untuk sistem persamaan di atas dan dianalisis kestabilan di sekitar titik tetap tersebut.
7 Titik Tetap Tanpa Penyakit
Titik tetap tanpa penyakit merupakan kondisi ketika semua individu menjadi sehat atau dapat dikatakan tidak terdapat penyakit. Titik tetap ini diperoleh ketika banyaknya individu yang terinfeksi sama dengan nol ( ) yang didapat dari persamaan (6) dan (7). Kemudian, substitusikan penyelesaian yang diambil dari persamaan (6) dan (7) ke persamaan (4), (5), dan (8) sehingga diperoleh titik tetap
. Penurunan titik tetap ini dapat dilihat pada Lampiran 2. Titik Tetap Endemik
Titik tetap endemik merupakan kondisi ketika penyakit terdapat di dalam populasi manusia. Dari sistem persamaan (3) diperoleh titik tetap endemik
Penurunan titik tetap ini dapat dilihat pada Lampiran 3.
Analisis Kestabilan Titik Tetap
Kestabilan Titik Tetap Tanpa Penyakit
8
Nilai eigen akan diperoleh dengan menyelesaikan persamaan karakteristik dengan
.
Titik tetap dengan kondisi stabil akan diperoleh jika akar ciri bernilai negatif, yaitu dan untuk menganalisis polinomial pangkat tiga, didefinisikan
,
, .
Berdasarkan kondisi Routh-Hurwitz, kondisi yang diperlukan agar memenuhi kriteria kestabilan adalah dan . Jelas bahwa karena semua parameter bernilai positif. Untuk akan diperoleh jika dan hanya jika
(
)
H L0
untuk total populasi (yang diasumsikan benar-benar rentan pada awalnya), yaitu
9 tidak stabil dan penyakit yang memasuki populasi akan bertahan serta menyebabkan epidemik.
Selanjutnya, diperoleh bilangan reproduksi dasar
Kondisi setara dengan . Kestabilan Titik Tetap Endemik
Ketika , titik tetap endemik positif dari persamaan
adalah stabil asimtotik lokal. Sederhanakan bentuk pada titik keseimbangan endemik menjadi titik tetap endemik menjadi
2
Nilai eigen akan diperoleh dengan menyelesaikan persamaan karakteristik dengan
.
Jelas persamaan ini memiliki salah satu akar negatifnya yaitu Selanjutnya, mengekspresikan
Untuk memastikan bahwa semua akar persamaan tersebut memiliki bagian-bagian real negatif, maka menurut kriteria Routh-Hurwitz, ,
. (Pembuktian ini dapat dilihat pada Lampiran 4)
10
SIMULASI MODEL
Untuk mengamati pengaruh masuknya bakteri ke dalam populasi manusia, diperlukan kurva bidang solusi yang menunjukkan hubungan banyaknya populasi terhadap waktu. Hal ini membutuhkan nilai tertentu untuk setiap parameter dan nilai awal untuk setiap variabel dalam sistem persamaan (3). Dalam karya ilmiah ini dianalisis dinamika populasi dengan mengubah-ubah nilai , dan . Dengan demikian, akan didapatkan dua kondisi untuk menganalisis dinamika populasi, yaitu dan . adalah kondisi ketika penyakit akan hilang dari populasi. Sebaliknya, adalah kondisi ketika penyakit bertahan dalam populasi dan menjadi wabah. Nilai untuk setiap parameter yang digunakan,
yaitu , , , , , dan . Nilai
Dinamika populasi dengan mengubah laju bakteri hyper infectious ( ) Definisikan bahwa laju infeksi bakterihyper infectious ( ) adalah laju bakteri hyper infectiousyang tercerna oleh individu yang rentan terhadap penyakit. Pada kondisi ini, nilai diubah-ubah sedangkan nilai dan nilai tetap, yaitu
dan . Ketika dievaluasi pada nilai dan
menghasilkan , sedangkan pada nilai dan
menghasilkan . Ketika , kurva akan stabil menuju titik tetap tanpa penyakit. Ketika , kurva stabil menuju titik tetap endemik
11
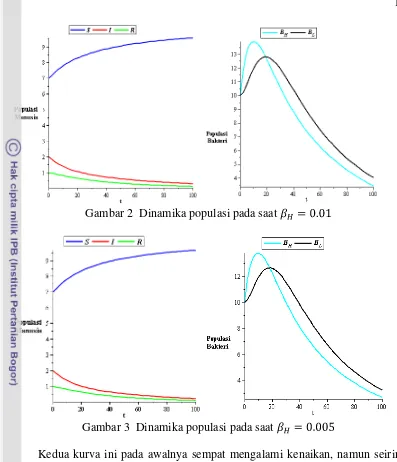
Gambar 2 Dinamika populasi pada saat
Gambar 3 Dinamika populasi pada saat
Kedua kurva ini pada awalnya sempat mengalami kenaikan, namun seiring berjalannya waktu mengalami penurunan hingga menuju nol. Hal tersebut menandakan bahwa penyakit mengalami penurunan atau kepunahan seiring berjalannya waktu.
Pada Gambar 4 yaitu ketika , diperoleh titik tetap endemik (6, 4, 1, 35, 35). Pada Gambar 4 dapat dilihat pada bahwa kurva S, I, R, , dan menuju ke titik tetap endemik, yaitu (6, 4, 1, 35, 35). Kurva S mengalami penurunan sedangkan kurva I mengalami peningkatan. Kurva R mengalami perubahan yang tidak terlalu signifikan. Selain itu, kurva dan terus mengalami peningkatan. Hal ini menandakan bahwa penyakit menetap di dalam populasi.
12
Gambar 4 Dinamika populasi pada saat
Gambar 5 Dinamika populasi pada saat
13 Pada Gambar 6 dapat dilihat bahwa ketika nilai ditingkatkan dari menjadi , populasi I semakin mengalami peningkatan. Ini berarti bahwa individu yang terinfeksi akan semakin bertambah ketika nilai laju bakteri hyper infectioussemakin ditingkatkan pula. Selain itu, dapat dilihat pula pada Gambar 6 bahwa kurva dengan nilai lebih cepat menuju kestabilan di titik tetapnya, sedangkan kurva dengan nilai lebih lambat menuju kestabilannya. Ini berarti bahwa semakin besar laju bakteri hyper infectious, maka semakin cepat penyakit menjadi wabah endemik.
Dinamika populasi dengan mengubah laju bakteri less infectious ( )
Definisikan bahwa laju bakteriless infectious ( ) adalah laju bakteri less infectiousyang tercerna oleh individu yang rentan terhadap penyakit. Pada kondisi ini, nilai diubah-ubah sedangkan nilai dan nilai tetap, yaitu
dan . Ketika dievaluasi pada nilai dan
menghasilkan , sedangkan pada nilai dan menghasilkan . Ketika , kurva akan stabil menuju titik tetap tanpa penyakit. Ketika , kurva stabil menuju titik tetap endemik.
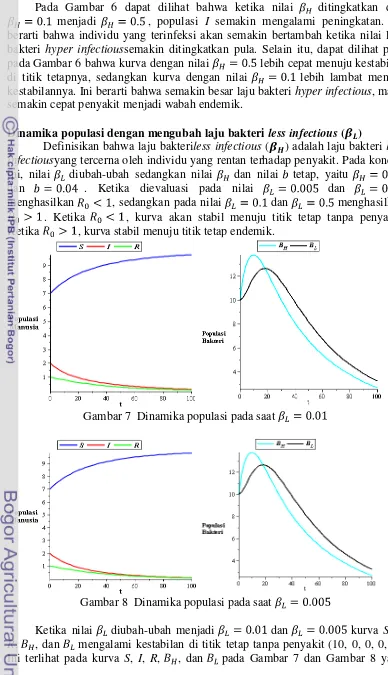
Gambar 7 Dinamika populasi pada saat
Gambar 8 Dinamika populasi pada saat
Ketika nilai diubah-ubah menjadi dan kurva S, I,
14
menuju titik tetap tanpa penyakit. Hal ini menandakan bahwa penyakit yang pada awalnya terdapat dalam populasi, mengalami kepunahan seiring berjalannya waktu.
Gambar 9 Dinamika populasi pada saat
Gambar 10 Dinamika populasi pada saat
Pada Gambar 9 dan Gambar 10, nilai yang digunakan yaitu
dan yang kemudian menghasilkan . Kedua kondisi tersebut mengakibatkan kurva S, I, R, , dan stabil menuju titik tetap endemik. Dapat pula dilihat kurva I serta kurva dan yang mengalami peningkatan dan stabil pada titik tetap endemik. Ini berarti bahwa penyakit menetap di dalam populasi. Sama halnya ketika nilai ditingkatkan. Ketika nilai ditingkatkan pula, akan menghasilkan kurva I yang yang semakin meningkat. Artinya, individu yang terinfeksi akan semakin meningkat ketika nilai dan ditingkatkan. Sedangkan pada kurva S, kurva S semakin mengalami penurunan ketika nilai dan ditingkatkan.
15
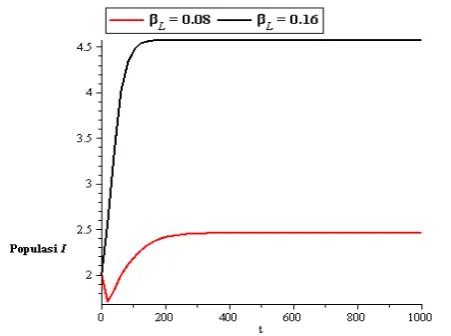
Gambar 11 Perbandingan populasi I ketika dan
Selain itu, dapat dilihat pula bahwa kurva dengan nilai lebih cepat menuju kestabilan dibandingkan kurva dengan nilai . Ini berarti bahwa semakin besar laju bakteri less infectious, maka semakin cepat penyakit menjadi wabah endemik.
Dinamika populasi dengan mengubah laju kelahiran/kematian manusia ( ) Pada kondisi ini, nilai diubah-ubah sedangkan nilai dan nilai tetap,
yaitu dan . Ketika dievaluasi pada nilai dan
menghasilkan yang artinya bahwa kurva akan stabil menuju titik tetap tanpa penyakit.
Pada Gambar 12 menunjukkan bahwa seluruh kurva menuju kestabilan di titik tetap tanpa penyakit, yaitu titik tetap (10, 0, 0, 0, 0). Kurva I dan kurva R
semakin mengalami penurunan hingga menuju nol, sedangkan kurva S mengalami peningkatan. Kurva dan yang menunjukkan banyaknya populasi bakteri, mengalami penurunan yang cukup signifikan hingga menuju nol meskipun sebelumnya sempat mengalami peningkatan dalam jangka waktu tertentu.
Gambar 12 Dinamika populasi pada saat
16
Gambar 13 menandakan bahwa penyakit yang sempat ada dalam populasi akan mengalami kepunahan seiring berjalannya waktu.
Gambar 13 Dinamika populasi pada saat
Pada kondisi selanjutnya, nilai dan menghasilkan yang artinya bahwa kurva akan stabil menuju titik tetap endemik.
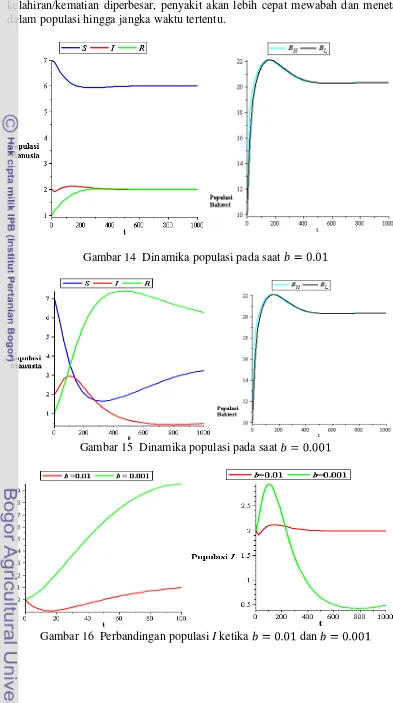
Gambar 14 merupakan dinamika populasi ketika dievaluasi pada . Gambar 15 merupakan dinamika populasi ketika dievaluasi pada . Gambar 14 dan Gambar 15 menunjukkan bahwa masing-masing bidang solusi menghasilkan kurva yang stabil menuju titik tetap endemik. Kurva S, I, R, , dan pada Gambar 14 dan Gambar 15 tidak stabil menuju titik tetap tanpa penyakit (10, 0, 0, 0, 0). Pada Gambar 14, kurva S, I, R, , dan stabil menuju titik tetap endemik (6, 2, 2, 20, 20). Pada Gambar 15, kurva S, I, R, , dan stabil menuju titik tetap endemik (3, 1, 6, 20, 20). Pada Gambar 14 kurva S mengalami penurunan, sedangkan kurva R mengalami peningkatan. Kurva I menunjukkan perubahan yang tidak cukup signifikan, yaitu sempat mengalami peningkatan kemudian stabil pada titik tetap endemik. Kurva dan terus mengalami peningkatan kemudian mengalami sedikit penurunan hingga menuju titik tetap endemik. Hal ini menandakan bahwa penyakit menetap dalam populasi. Pada Gambar 15, kurva S mengalami penurunan yang cukup signifikan, sedangkan kurva R mengalami peningkatan. Kurva I mengalami peningkatan hingga jangka waktu tertentu kemudian mengalami penurunan. Ketiga kurva tersebut akhirnya menuju titik tetap endemik meskipun sempat mengalami perubahan kurva yang naik dan turun. Hal berarti bahwa penyakit menetap dalam populasi dan menjadi wabah.
17 kelahiran/kematian diperbesar, penyakit akan lebih cepat mewabah dan menetap dalam populasi hingga jangka waktu tertentu.
Gambar 14 Dinamika populasi pada saat
Gambar 15 Dinamika populasi pada saat
18
SIMPULAN
Dalam karya ilmiah ini telah dipelajari model matematika penyebaran penyakit kolera, SIR- . Dari model tersebut dihasilkan dua titik tetap, yaitu titik tetap tanpa penyakit dan titik tetap endemik. Ketika dilakukan analisis bidang solusi, dinamika populasi bergantung pada bilangan reproduksi dasar ( ). Titik tetap tanpa penyakit berada dalam kestabilan ketika dan titik tetap endemik berada dalam kestabilan ketika .
Melalui analisis , pada simulasi dinamika populasi dengan mengubah nilai laju bakteri hyper infectious, disimpulkan bahwa semakin besar laju bakteri
hyper infectious, semakin cepat penyakit menjadi wabah endemik. Pada simulasi dinamika populasi dengan mengubah nilai laju bakteri less infectious, disimpulkan bahwa semakin besar laju bakteri less infectious, semakin cepat penyakit menjadi wabah endemik. Walaupun begitu, untuk bakteri less infectious, penginfeksian menjadi wabah endemik lebih rendah dibandingkan bakteri hyper infectious. Pada simulasi dinamika populasi dengan mengubah nilai laju kelahiran/kematian manusia, disimpulkan bahwa semakin besar laju kelahiran/kematian, penyakit akan lebih cepat mewabah dan menetap dalam populasi hingga jangka waktu tertentu karena kurva yang semakin cepat menuju kestabilannya di titik tetap endemik.
Leon SJ. 1998. Aljabar Linear dan Aplikasinya. Ed. Alit Bondan, penerjemah. Jakarta (ID): Erlangga.
Liao S, Wang J. 2011. Stability analysis and application of a mathematical cholera model. Mathematical Biosciences and Engineering. 8(3):733-752. DOI:10.3934/mbe.2011.8.733.
TuPNV.1994. Dynamic System: An Introduction with Application in Economics and Biology.Hiedelberg(DE):Springer-Verlag.
19 Lampiran 1 Bukti untuk kasus menurut kondisi Routh-Hurwitz.
Misalkan dan bilangan-bilangan real. Bagian real dari setiap nilai eigen
persamaan karakteristik adalah negatif jika dan
hanya jika bernilai positif dan Bukti:
Dari persamaan , maka
dan jika selainnya. Berdasarkan kriteria Routh-Hurwitz, maka
bagian real dari setiap akar polinomial adalah
negatif jika dan hanya jika positif dengan
(9) sehingga dari (10) diperoleh nilai
Dengan demikian diperoleh bahwa bagian real dari setiap akar polinomial adalah negatif jika dan hanya jika
serta
Terbukti Lampiran 2 Pencarian titik tetap tanpa penyakit
Titik tetap akan diperoleh dengan menetapkan
, (12)
, (13)
, (14)
, (15)
. (16)
Kemudian titik tetap tanpa penyakit diperoleh dengan membuat pada persamaan (14) dan (15) sebagai berikut:
, sehingga didapatkan , , sehingga didapatkan .
Selanjutnya disubstitusikan ke persamaan (16) dan (13) sehingga didapatkan Dari hasil-hasil yang telah diperoleh tersebut disubstitusikan kembali ke persamaan (12), sehingga didapatkan Titik tetap tanpa penyakit yang didapatkan yaitu ( ).
Lampiran 3 Pencarian titik tetap endemik
20
. , sehingga didapatkan .
Dari persamaan (16) dan dengan mensubstitusikan ke persamaan (16) diperoleh
.
, sehingga didapatkan . Dari persamaan (14) diperoleh sebagai berikut
.
, sehingga didapatkan .
Selanjutnya mensubstitusikan hasil-hasil yang didapatkan ke persamaan (12) dan
(13) sehingga didapatkan dan .
Titik tetap tanpa penyakit yang diperoleh yaitu
21
Pelinearan pada titik tetap endemik diperoleh matriks .
Nilai eigen akan diperoleh dengan menyelesaikan persamaan karakteristik .
Untuk memastikan bahwa semua akar persamaan tersebut memiliki bagian-bagian real negatif, maka menurut kriteria Routh-Hurwitz, ,
22
. (23) Dengan menggunakan persamaan (22) dan (23), diperoleh
.
.
. (24)
Bagian bernilai positif.
Setelah mensubstitusikan (22) dan (23),
= =
. dan
.
Sehingga terpenuhi.
Untuk membuktikan dibuat menjadi dua pertaksamaan
, (25)
. (26)
Untuk menunjukkan (25) ditulis menjadi penjumlahan empat bagian: +(3P
23
.
Dengan cara yang sama, dapat dibuktikan dan , sehingga pertaksamaan (25) terpenuhi.
Terakhir, untuk menunjukkan pertaksamaan (26), ditulis menjadi penjumlahan beberapa bagian sebagai berikut:
)+(
sehingga terpenuhi.
Lampiran 5 Contoh simulasi bidang solusi dinamika populasi pada Gambar 2 (dengan menggunakan software Maple)
>
25
RIWAYAT HIDUP
Penulis dilahirkan di Jakarta pada tanggal 7 Maret 1992, anak ketiga dari lima bersaudara, anak dari Bapak Darwin dan Ibu Nonon Mulyanah.
Tahun 2010 Penulis lulus dari SMAN 1 Sukaresmi Kabupaten Cianjur dan melanjutkan pendidikan di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam (FMIPA), Institut Pertanian Bogor (IPB) melalui jalur Undangan Seleksi Masuk IPB (USMI).