Analisa Kelakuan Partikel Berdasarkan Statistik Maxwell- Boltzmann, Bose-Einstein dan Fermi-Dirac

ANALISA KELAKUAN PARTIKEL BERDASARKAN STATISTIK MAXWELL-BOLZTMANN BOSE-EINSTEIN DAN FERMI-DIRAC

SKRIPSI

Diajukan Sebagai Salah Satu Syarat Untuk Memperoleh Gelar Sarjana Sains

Rio Tambunan 040801024

DEPARTEMEN FISIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

LEMBAR PERSETUJUAN

Judul : Analisa Kelakuan Partikel Berdasarkan Statistik Maxwell- Boltzmann, Bose-Einstein dan Fermi-Dirac

Nama : Rio Tambunan

Nim : 040801024

Skripsi ini telah diperiksa dan disetujui oleh :

Pembimbing I Pembimbing II

(Dra Manis Sembiring,Ms) (Drs Tenang Ginting,Ms) Nip: 195511291987032001 Nip: 194806101976031003

Disahkan oleh Ketua Departemen Fisika

Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara

Medan 25 Januari 2010

PERNYATAAN

ANALISA KELAKUAN PARTIKEL BERDASARKAN STATISTIK MAXWELL-BOLZTMANN BOSE-EINSTEIN DAN FERMI-DIRAC

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, 2 maret-2010

PENGHARGAAN

Puji dan syukur saya ucapkan kehadirat Tuhan Yang Maha Pengasih, dimana hanya karena kekuatan dariNya saya dapat menyelesaikan skripsi ini dengan baik.

Ucapan terimakasih juga saya sampaikan kepada dosen pembimbing saya, yakni Dra Manis Sembiring MS, dan Bapak Drs Tenang Ginting MS, yang telah banyak memberikan bimbingan, pengarahan dan masukan kepada penulis selama mengerjakan tugas akhir ini, Ucapan terimakasih juga saya sampaikan kepada ketua dan sekretaris departemen fisika DR. Marhaposan situmorang dan Dra Justinon,MS. Ucapan terimakasih juga ditujukan kepada dosen wali saya Drs Kurnia Sembiring MS, Dekan dan pembantu Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Smatera Utara, semua dosen pada departemen Fisika USU dan Pegawai di FMIPA USU. Ucapan terimakasih juga ditujukan kepada kawan-kawan kuliah terkhusus stambuk 2004 yang banyak membantu saya dalam penyelesaian tugas akhir ini, Merry tati riama siagian yang menjadi sahabat dan memberi dukungan baik dalam motivasi maupun materi.

ABSTRAK

Mekanika statistik menunjukkan bagaimana sifat makrospik sistem banyak partikel berhubungan dengan sifat mikrospik partikel itu sendiri, mekanika statistik tidak mempersoalkan gerak sebenarnya atau interaksi antara partikel individual, melainkan mempersoalkan kelakuan partikel dengan peluang terbesar untuk menempati suatu keadaan energi tertentu.

Particle Behavior Analysis Based on Maxwell-Statistics Boltzmann, Bose-Einstein and Fermi-Dirac.

ABSTRACT

Statistical mechanics to show how the nature of many particle systems makrospic touch with nature itself mikrospic particles, statistical mechanics do not question the actual movement or interaction the individual particles, but questioned the behavior of particles with the greatest opportunity to occupy a particular energy state.

Maxwell-Bolztmann statistics applied to the identical system with distinguishable particles, each particle is enough to spin away from where the wave function does not clasping and categorized as classical particles, for example, the gas molecules. Bose-Enstein statistics applied to systems that are identical and indistinguishable particles that do not meet the exclusion principle, each spin particles: 0,1,2, ... with a symmetric wave function for the exchange of labels and categorized Boson particle, for example: liquid helium in solids , photons in the cavity, and Phonon in a solid. Fermi-Dirac statistics apply to systems that are identical and indistinguishable particles that satisfy the exclusion principle, each spin of particles: 1/ 2, 3 / 2, 5 / 2, ... with the anti-symmetric wave function for the exchange of particles and particle labels categorized fermions.

DAFTAR ISI

LEMBAR PERSETUJUAN i

LEMBAR PERNYATAAN ii

PENGHARGAAN iii

ABSTRAK iv ABSTRACT v

DAFTAR ISI vi

DAFTAR TABEL vii DAFTAR GAMBAR viii

DAFTAR BESARAN ix

BAB I : PENDAHULUAN 1.1Latar Belakang 1 1.2Sistematika Pembahasan 2

1.3Batasan Masalah 2

1.4Tujuan Penelitian 2

1.5Metodologi Penelitian 3

BAB II : TINJAUAN PUSTAKA 2.1 Sifat partikel dari gelombang 2.1.1 Efek foto listrik 6 2.1.2 Efek Compton 7

2.2 Hukum Distribusi statistik 7

2.2.1 Ruang Fase 7

2.2.2 Distribusi Maxwell-Bolztmann 9

2.2.3 Distribusi Bose-Einstein 14

2.2.4 Distribusi Fermi_Dirac 17

2.2.5 Fungsi Gelombang 18

2.2.6 Asas Larangan Pauli 20

BAB III : HASIL DAN PEMBAHASAN 3.1 Mekanika Statistik 22

3.1.1 Perlakuan partikel berdasarkan statistik Maxwell-Bolztmann 22

3.1.2 Perlakuan partikel berdasarkan statistik kuantum 26

3.1.3 Tabel perbandingan Fungsi Distribusi statistik 31

BAB IV : KESIMPULAN 33 DAFTAR PUSTAKA 34

DAFTAR TABEL

DAFTAR GAMBAR

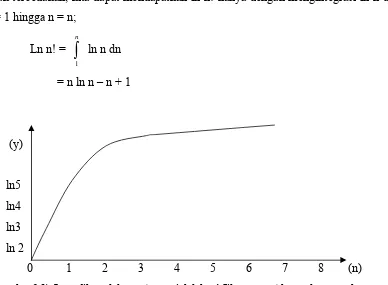
Gambar 2.1 Luas dibawah kurva tangga ialah n! jika n sangat besar , kurva malar merupakan aproksimasi yang baik dari kurva tangga, dan ln n! dapat dicari dengan

integrasi ln n dari n = 1 hingga n = n 12

Gambar 2.2 Jumlah partikel dalam keadaan(jumlah total = n_i) 14

Gambar 3.1 Distribusi energi Maxwell-Bolztmann untuk molekul

gas ideal 25

Gambar 3.2 Distribusi kelajuan molekul oksigen dan hydrogen 25

Gambar 3.3 Perbandingan tiga fungsi distribusi untuk α = 1 28

DAFTAR BESARAN

ψ fungsi gelombang

) (ε

n Jumlah partikel berenergi ε )

(ε

f Fungsi distribusi

) (ε

g Banyaknya keadaan berenergi ε

mb

f Fungsi distribusi Maxwell-Bolztmann

be

f Fungsi distribusi Bose-Einstein

fd

f Fungsi distribusi Fermi-Dirac

T Temperature

α Multiplier(kuantitas/pengali)

β Multiplier(kuantitas/pengali)

X Jumlah total cara pengisian keadaan sistem

E Energi total molekul

N Jumlah molekul

ε Energi tunggal

n molekul

) (ε

p momentum sebuah molekul yang berenergi ε Γ volume masing-masing sel(dalam ruang fase)

2 h ≥ ∆

∆x p Prinsip ketaktentuan

W Banyaknya cara N molekul yang dapat didistribusikan

dE

n(ε) Banyaknya molekul yang energinya diantara ε dan ε +dε h konstanta planck (6,6262 x 10−34) Js−1

k konstanta Bolztmann (1,3806 x 10−23 jk-1

ev

1 1,6022 x 10−19 J

e 2,7183

π 3,1416

1 −

ABSTRAK

Mekanika statistik menunjukkan bagaimana sifat makrospik sistem banyak partikel berhubungan dengan sifat mikrospik partikel itu sendiri, mekanika statistik tidak mempersoalkan gerak sebenarnya atau interaksi antara partikel individual, melainkan mempersoalkan kelakuan partikel dengan peluang terbesar untuk menempati suatu keadaan energi tertentu.

Particle Behavior Analysis Based on Maxwell-Statistics Boltzmann, Bose-Einstein and Fermi-Dirac.

ABSTRACT

Statistical mechanics to show how the nature of many particle systems makrospic touch with nature itself mikrospic particles, statistical mechanics do not question the actual movement or interaction the individual particles, but questioned the behavior of particles with the greatest opportunity to occupy a particular energy state.

Maxwell-Bolztmann statistics applied to the identical system with distinguishable particles, each particle is enough to spin away from where the wave function does not clasping and categorized as classical particles, for example, the gas molecules. Bose-Enstein statistics applied to systems that are identical and indistinguishable particles that do not meet the exclusion principle, each spin particles: 0,1,2, ... with a symmetric wave function for the exchange of labels and categorized Boson particle, for example: liquid helium in solids , photons in the cavity, and Phonon in a solid. Fermi-Dirac statistics apply to systems that are identical and indistinguishable particles that satisfy the exclusion principle, each spin of particles: 1/ 2, 3 / 2, 5 / 2, ... with the anti-symmetric wave function for the exchange of particles and particle labels categorized fermions.

BAB I

PENDAHULUAN

1.1 Latar Belakang

1.2 Sistematika Pembahasan

Studi pustaka ini meliputi kelakuan dan sifat-sifat partikel yang dikaji berdasarkan mekanika statistik. Mekanika statistik dihimpun dari statistik Maxwel-Boltzmann, statistik Bose-Einstein dan statistik Fermi-Dirac yang ketiganya mengkategorikan partikel dengan sifat yang berbeda-beda. Kemudian didigitasi untuk memudahkan analisis distribusi partikel dalam suatu sistem. Analisis hubungan variabel-variabel yang menyusun komponen mekanika statistik menggunakan pendekatan deskriptif kuantitatif. Perlakuan partikel diteliti melalui fungsi distribusi, sifat distribusi, sifat partikel, kategori partikel dan sistem dari partikel itu sendiri. Fungsi distribusi partikel ditentukan berdasarkan jumlah partikel pada setiap keadaan berenergi ∈ untuk temperatur T melalui statistik Maxwel-Boltzmann, Bose-Einstein dan Fermi-Dirac. Sifat distribusi partikel ditentukan berdasarkan ada tidaknya batas pada jumlah partikel per keadaan. Sifat partikel ditentukan berdasarkan jarak spin yang dimiliki oleh partikel itu sendiri melalui statistik Maxwel-Boltzmann, Bose-Einstein, dan Fermi-Dirac. Kategori partikel ditentukan secara klasik dan kuantum. Sistem dari pertikel ditentukan berdasarkan prinsip eksklusi dan jarak dari partikel itu sendiri.

1.3 Batasan Masalah

Masalah yang dikaji meliputi: Statistik klasik(Maxwell-Boltzmann) dan statistik kuantum (Fermi-Dirac, Bose-Einstein)

1.4 Tujuan Penelitian

1.5 Metodologi Penelitian

BAB II

TINJAUAN PUSTAKA

2.1 Sifat Partikel Dari Gelombang

Seperti yang kita ketahui partikel memiliki sifat-sifat, yaitu muatan, massa, dan spin. Tiap-tiap partikel memiliki antipartikelnya yang memiliki muatan yang berbeda satu dengan yang lainnya. Dari sifat dualisme gelombang yang mengatakan bahwa partikel juga memiliki sifat gelombang, tak heran jika partikel memiliki fungsi gelombang, dimana dari fungsi gelombang kita dapat menentukan pergerakan dari partikel tersebut.

Berdasarkan bilangan spinnya partikel dibagi menjadi dua bagian yaitu fermion dan boson, dimana partikel fermion yang memiliki spin setengah bilangan bulat yang menggunakan statistik Fermi-Dirac, dan Boson adalah partikel yang memiliki spin bilangan bulat yang mengikuti statistic Bose-Einstein. Dan jika menggunakan momentum sudut spin tersebut berarti partikel diklasifikasikan dengan meninjau teorema statistic spin. Dari statistik yang digunakan oleh partikel dapat menentukan kesimetrisan antara dua buah partikel. Suatu partikel dikatakan boson identitas ialah jika ia memiliki bilangan spin bilangan bulat dan fungsi-fungsi gelombang dari kedua partikel tidak berubah ketika saling bertukaran, seperti berikut:

ψ ψ 1 →⇔2

ilangan

Begitu juga suatu partikel dikatakan sebagai fermion identitas jika ia memiliki bilangan spin setengah bulat ganjil dan fungsi-fungsi gelombang dari kedua partikel berubah ketika saling bertukaran, seperti berikut :

ψ ψ 1 →⇔2 −

Berikut fungsi gelombang yang diwakili dengan ψ menggambarkan sifat identitas dari kesimetrisan partikel

Fermion identitas ψ(1,2)=−ψ(2,1) antisimetris

ψ = α(ruang)β(spin) ) , ( (r)Y ) , (r, )

( ψ θ φ χ _lm θ φ

α ruang = = (2.2)

φ θ π χ φ θ ψ

α m im

l e P m l m l l r

ruang (cos )

) ( 4 ) )( 1 2 ( (r) ) , , ( ) ( +− + =

= (2.3)

Dimana α menggambarkan gerakan orbital partikel 1 mengitari partikel laiinnya dan

α dapat dirumuskan sebagai fungsi harmonik bola yang dirumuskan sebagai berikut: ) , (θ φ α m l Y =

Dimana θ dan φ adalah kordinat bola. Perubahan kordinat ruang antara partikel 1 dan partikel 2 (tanpa memperhatikan faktor spin) adalah sebagai berikut:

θ π

θ → −

π φ

φ → + (2.5)

Akan menghasilkan persamaan :

) , ( (r)Y ) , (r, )

( ψ θ φ χ _lm θ φ

α ruang = =

φ θ π χ φ θ ψ

α m im

l e P m l m l l r

ruang (cos )

) ( 4 ) )( 1 2 ( (r) ) , , ( ) ( +− + =

= (2.6)

Pada persamaan (2.3)akibat faktor rotasi, maka akan terdapat faktor pengali (-1)l yang diperlihatkan pada persmaan (2.6), jika l bernilai genap maka α bersifat simetris dan sebaliknya jika l bernilai ganjil makaα bersifat antisimetris. Demikian juga dengan fungsi spin β akan bersifat simetris jika spin pararel dan bersifat dan bersifat antisimetris jika spin antipararel. Jika dihubungkan dengan partikel pada persamaan(2.2) maka untuk boson identitas harus memenuhi α dan β bersifat simetris atau antisimetris sedangkan pada fermion identitasα bersifat simetris sedangkan β bersifat antisimetris atau sebaliknya. Jika kedua partikel memiliki muatan, maka persamaan (2.2) menjadi:

isospin) atau tan ( ) ( )

(ruang β spin γ mua

α ψ =

2.1.1 Efek Foto Listrik

Efek fotolistrik adalah terlepasnya elektron dari suatu permukaan (biasanya logam) akibat penyinaran. ketika dikenai, dan menyerap, radiasi elektromagnetik (seperti cahaya tampak dan radiasi ultraungu) yang berada di atas frekuensi ambang tergantung pada jenis permukaan. Istilah lama untuk efek fotolistrik adalah efek Hertz (yang saat ini tidak digunakan lagi).

Tidak ada elektron yang dilepaskan oleh radiasi di bawah frekuensi ambang, karena elektron tidak mendapatkan energi yang cukup untuk mengatasi ikatan atom. Elektron yang dipancarkan biasanya disebut fotoelektron dalam banyak buku pelajaran. Efek fotolistrik banyak membantu dualisme gelombang-partikel, dimana sistem fisika (seperti foton dalam kasus ini) dapat menunjukkan kedua sifat dan kelakuan seperti-gelombang dan seperti-partikel, sebuah konsep yang banyak digunakan oleh pencipta mekanika kuantum. Efek fotolistrik dijelaskan secara matematis oleh Albert Einstein yang memperluas kuanta yang dikembangkan oleh Max Planck .

Hukum emisi fotolistrik:

1. Untuk logam dan radiasi tertentu, jumlah fotoelektron yang dikeluarkan berbanding lurus dengan intensitas cahaya yg digunakan.

2. Untuk logam tertentu, terdapat frekuensi minimum radiasi. di bawah frekuensi ini fotoelektron tidak bisa dipancarkan.

3. Di atas frekuensi tersebut, energi kinetik yang dipancarkan fotoelektron tidak bergantung pada intensitas cahaya, namun bergantung pada frekuensi cahaya. 4. Perbedaan waktu dari radiasi dan pemancaran fotoelektron sangat kecil,

2.1.2 Efek Compton

Pada efek fotolistrik, cahaya dapat dipandang sebagai kuantum energi dengan energi yang diskrit. Kuantum energi tidak dapat digambarkan sebagai gelombang tetapi lebih mendekati bentuk partikel. Partikel cahaya dalam bentuk kuantum dikenal dengan sebutan foton. Pandangan cahaya sebagai foton diperkuat lagi melalui gejala yang dikenal sebagai efek Compton. Jika seberkas sinar-X ditembakkan ke sebuah elektron bebas yang diam, sinar-X akan mengalami perubahan panjang gelombang dimana panjang gelombang sinar-X menjadi lebih besar. Gejala ini dikenal sebagai efek Compton, sesuai dengan nama penemunya, yaitu Arthur Holly Compton.

Sinar-X digambarkan sebagai foton yang bertumbukan dengan elektron (seperti halnya dua bola bilyar yang bertumbukan). Elektron bebas yang diam menyerap sebagian energi foton sehingga bergerak ke arah membentuk sudut terhadap arah foton mula-mula. Foton yang menumbuk elektron pun terhambur dengan sudut θ terhadap arah semula dan panjang gelombangnya menjadi lebih besar. Perubahan panjang gelombang foton setelah terhambur dinyatakan sebagai

Dimana m adalah massa diam elektron, c adalah kecepatan cahaya, dan h adalah konstanta Planck.

2.2 Hukum Distribusi Statisitik

Hukum distribusi Maxwell-Bolztmann, Bose-Einstein, dan Fermi-Dirac akan diturunkan di sini.

kedudukan dan momentum merupakan vektor dengan tiga komponen masing-masing, kita harus mengetahui enam kuantitas X,Y,Z,Px,Py,Pz untuk masing-masing partikel.

Kedudukan sebuah partikel ialah suatu titik berkordinat x,y,z dalam ruang tiga- dimensional yang biasa. Supaya memudahkan kita rambatkan konsep ini dengan membayangkan ruang enam-dimensional; dalam ruang ini setiap titik memeiliki enam kordinat X,Y,Z,Px,Py,Pz. Kombinasi ruang kedudukan dan momentum ini disebut ruang fase. Pengertian ruang fase diperkenalkan supaya kita dapat mengembangkan mekanika statistik dalam keangka geometris, sehingga mengijinkan metoda analisis yang lebih sederhana dan langsung dipakai alih-alih metoda analisis yang setara tetapi sifatnya lebih abstark. Satu titik dalam ruang fase bersesuaian dengan kedudukan dan momentum tertentu, sedangkan titik dalam ruang biasa bersesuaian dengan hanya dengan kedudukan tertentu saja. Jadi setiap partikel terspesifikasi lengkap dengan satu titik dalam ruang fase, dan keadaan suatu sistem partikel bersesuaian dengan distribusi titil dalam ruang fase.

Prinsip ketaktentuan memaksa kita untuk menguraikan lebih lanjut apa yang kita maksudkan dengan titik dalam ruang fase. Marilah kita bagi ruang fase menjadi sel enam-dimensional yang kecil-kecil yang panjang sisi masing-masing dx,dy,dz,dpx,dpy,dpz. Ketika kita mereduksi ini sel ini, lita mendekati limit titik dalam ruang fase. Namun, volume masing-masing sel ialah:

Г = dx dy dz dp_xdp_y dpz

Dan menurut prinsip ketaktentuan

dx dp_x

2 h ≥

dy dp_y

2 h ≥

dz dp_z

2 h ≥

Jika kita lihat bahwa

Γ

8

3

Suatu titik dalam ruang fase sebetulnya suatu sel yang volume minimumnya dalam orde

8

3

h

. Kita harus membayangkan partikel dalam ruang fase terletak dalam sel semacam itu berpusat pada titik x,y,p_x,p_y, p_z alih-alih tepat pada titik itu.

Analisis yang lebih terperinci menunjukkan bahwa masing-masing sel dslsm rung fase sebetulnya bervolume h3; hal ini tidak bertentangan dengan prinsip ketaktentuan, karena h3>

8

3

h

Pada umumnya, masing-masing sel dalam ruang fase

terdiri dari k kordinat dan k momentum yang menempati volume hk. Tugas mekanika statistik ialah menentukan keadaan sistem dengan memeriksa bagaimana partikel pembangun sistem itu mendistribusikan dirinya dalam sel-sel dalam ruang fase.

Pengertian titik dengan ukuran infinitesimal dalam ruang fase tidal mempunyai peranan fisis karena melanggar prinsip ketaktentuan, hanya pengertian titik berukuran infinitesimal pada ruang biasa saja atau ruang momentum saja yang dapat diterima secara prinsip kita dapat menetukan kedudukan suatu partikel dengan tepat menurut yang kita inginkan jika kita mau menerima ketaktentuan yang tak terbatas mengenai momentum, atau sebaliknya.

2.2.2 Distribusi Maxwell-Bolztmann

Distribusi statistik Maxwell-boltzmann menggunakan pandangan klasik, dimana sesuai dengan asumsi :

1. Partikel penyusun dapat dibedakan

2. Dalam satu keadaan energy dapat diisi oleh lebih dari satu partikel

• Karena tidak menutup kemungkinan setiap partikel penyusun gas ideal bergerak dengan energy yang sama (dengan mengabaikan interaksi antara partikel satu dengan yang lainnya serta terjadi tumbukan lenting sempurna), maka tidak menutup kemungkinan adanya keadaan energy yang sama dimiliki oleh beberapa partikel.

Untuk setiap keadaan energinya, dapat terdegenerasi atau tidak. Sebagai contoh : tinjau 4 partikel terbedakan (a, b, c, d) mempunyai 2 tingkat energy non degenerasi. Tuliskan kemungkinan keadaan energy yang mungkin. Untuk menggambarkannya, buatlah kemungkinan-kemungkinan kombinasi yang mungkin untuk setiap keadaan makro (rincian banyak partikel pada tiap tingkat energy) dan keadaan mikronya (rincian banyak partikel pada tiap keadaan energy).

Marilah kita tinjau kumpulan N molekul yang energinya terbatas pada harga

, 2 , 1 ε

ε ………, ε_i, … Energi ini dapat menyatakan keadaan kuantum yang diskrit atau energi rata-rata untuk sederetan selang energi, dan lebih dari satu sel dalam ruang fase bersesuain dengan energi tertentu. Apa yang kita ingin ketahui ialah peluang terbesar dari distribusi molekul diantara berbagai energi yang mungkin.

Suatu anggapan dasar dalam mekanika statistik ialah lebih besar bilangan W

yang menyatakan banyaknya cara molekul dapat di tata diantara sel dalam ruang fase untuk menghasilkan distribusi molekul dianatara tingkat energi yang berbeda-beda, lebik besar pula peluang distribusi tertsebut. Jadi distribusi berpeluang terbesar ialah distribusi yang bersesuain dengan W maksimum. Langkah kita yang pertama ialah mencari bentuk umum dari W. Kita anggap bahwa setiap sel dalam ruang fase berpeluang berpeluang sama untuk ditempati; anggapan ini berkemungkinan besar memang terjadi, tetapi pembultiannya (seperti juga dalam kasus persamaan schrodinger) didapatkan dari kesimpulan mengenai kecocokan dengan hasil eksperimental.

Jika terdapat g_i sel dengan ε_i, banyaknya cara sebuah molekul dapat memiliki energi ε_i ialah g_i. Banyaknya cara total dua molekul dapat memiliki energi

i

ε masing-masing ialah g_i2, dan banyaknya cara total n_i molekul masing-masing

( ) ( ) ( )

1 2 3

3 2 1 g

n n n

g

g …… (2.7)

Dengan syarat

N .... n n

n₁+ ₂ + ₃ + =

=

∑ni (2.8)

Persamaan (2.7) tidak sama dengan W, karena kita masih harus memperhitungkan permutasi yang mungkin dari molekul dianatara energi yang berbeda, dengan perkataan lain, N molekul diatur dalam N! urutan yang berbeda. Sebahai contoh jika kita memiliki empat molekul a, b, c, dan d. banyaknya permutasi 4! Sama dengan:

4! = 4 x 3 x 2 x 1 = 24

Namun, jika lebih dari satu molekul boleh menempati satu tingkat energi, mempermutasikan di antara molekul itu tidak berperan dalam situasi ini. Misalnya, jika molekul a,b dan c berada dalam tingkat j, disini tidak apa-apa jika kita menyatakannya sebagai abc, acb, bac, cab, atau cba; keenam distribusi ini setara, karena semuanya menyatakan fakta bahwa n_j= 3. Jadi n_i molekul dalam tingkat –i memberi konstribusi (sumbangan) n_i! permutasi tak relevan. Jika ada n₁ molekul dalam tingkat 1, n₂ molekul dalam tingkat 2, dan sebagainya, maka terdapat n₁!n₂!....permutasi tak relevan. Apa yang kita inginkan ialah N! permutasi yang mungkin dibagi dengan banyaknya permutasi yang tak-relevan, atau

!.... ! !

!

3 1n₂ n

n N

(2.9)

Banyaknya cara N molekul dapat didistribusikan diantara tingkat energi yang dihasilkan persamaan (2.7) dan (2.9)

=

W

!.... ! !

!

3 1n2 n

n

N

( )

1

( ) ( )

2 3

1 2 3

n n n

g g

g (2.10)

Yang harus kita lakukan sekarang ialah menentukan distribusi mana yang berpeluang terbesar, yaitu distribusi yang mengkasilkan harga W terbesar. Langkah kita yang pertama ialah mendapatkan aproksimasi analitis yang memadai untuk faktorial dari suatu bilangan besar. Kita perhatikan, karena

Gambar (I-i ) ialah plot ln n terhadap n. Luas dibawah kurva malar dari ln n menjadi tak terbedakan, kita dapat mendapatkan ln n! hanya dengan mengintegrasi ln n dari n = 1 hingga n = n;

Ln n! =

∫

n

1

ln n dn

= n ln n – n + 1

(y)

ln5 ln4 ln3 ln 2

0 1 2 3 4 5 6 7 8 (n)

(gambar 2.1) Luas dibawah kurva tangga ialah ln n! Jika n sangat besar, kurva malar

merupakan aproksimasi yang baik dari kurva tangga, dan ln n! Dapat dicari dengan integrasi ln

n dari n = 1 hingga n = n

Karena kita anggap n > 1, kita dapat mengabaikan 1 dalam hasil atas, dan kita peroleh

Ln n! = n ln n – n n >> 1 (2.11)

Persamaan diatas dikenal sebagai rumus strilling. Logaritma natural persamaan (2.10) adalah: Ln W = ln N! -

∑

lnn_i! +

∑

n_i ln g_j

Rumus strilling memungkinkan kita untuk menulis persamaan itu menjadi Ln W = N ln N – N -

∑

n_iln n_i +

∑ ∑

n_i + n_iln g_j

Karena

∑

n_i =N

ln W = N ln N -

∑

n_i ln n_i +

∑

n_i ln g_j (2.12)

Kita mempunyai persamaan untuk ln W alih-alih W sendiri, tetapi ini tidakmerupakan penghalang karena:

Persyaratan supaya suatu distribusi berpeluang terbesar ialah perubahan kecil

i

n

δ pada setiap n_itidak mempengaruhi harga W. Jika perubahan ln W bersesuaian dengan perubahan n_i yaitu δn_i ialah δ ln W , dari persamaan (2,12) kita dapatkan.

δ ln W = -

∑

n_iδ ln n_i -

∑

lnn_iδn_i +

∑

ln gδn_i = 0 (2.13) Karena N ln N konstan. Sekarang

δln n_i= _i

i

n

n δ

1

Sehingga δ

∑

ni ln ni=

∑

δni

Karena banyaknya molekul total konstan, jumlah

∑

δn_i untuk semua perubahan banyaknya molekul tiap-tiap tingkat energi harus 0, ini berarti

δ

∑

ni ln ni= 0

Jadi persamaan (2.14) menjadi:

-

∑

ln n_iδn_i+

∑

lng_iδn_i = 0 (2.14)

Persamaan (2.14) harus dipenuhi oleh distribusi molekul antara tingkat energi, yang berpeluang terbesar, namun persamaan itu. Kita harus memperhitungkan kekalahan jumlah partikel

∑

n_i= n₁ + n₂+ n₃+ …….= N

Dan kekekalan energi,

∑

n1ε1= ...n1ε1+n2ε2 +n3ε3+ = E (2.15)

Dengan E menyatakan energi total kumpulan molekul itu. Akibatnya variasi δn₁,

2

n

δ ,……. Dari jumlah molekul masing-masing tingkat energi tidak bebas satu terhadap lainnya tetapi harus memenuhi hubungan

∑

δn_i =δn₁+δn₂ +δn₃ +...= 0 (2.16)

-bebas dari n_i, dan menambahkannya pada persamaan (2.14) kita dapatkan hailnya sebagai berikut:

∑

(lnni +lngi −α −βεi)δni = 0 (2.18)

Dalam masing-masing persamaan yang harus dijumlahkan menjadi persamaan (2.18) variasi δn_i secara efektif merupakan variabel bebas. Supaya persamaan (2.18) di penuhi, kuantitas dalam tanda kurung harus 0 untuk setiap harga I, jadi

- ln n_i +ln g_i -α-βε_i = 0

sehingga kita dapatkan hukum distribusi Maxwell-Boltzmann

n_i = g_ie−αe−βε (2.19)

Rumus ini memberi banyaknya molekul n_i yang memiliki energi ε_i dinyatakan dalam banyaknya sel dalam ruang fase g_i yang memiliki energi ε_i dan kuantitas α serta β. Kuantitas e−αe−βε dalam persamaan (2.19) menjadi fungsi distribusi Ae−εkT dari persamaan eα =A, suatu cara untuk menulis e−α, dan jika β=1/kT. Hubungan yang terakhir ini dapat diturunkan dengan memberi syarat bahwa energi interanal total dari sebuah sistem dari N molekul pada temperature mutlak T ialah

2 3

NkT.

2.2.3 Distribusi Bose-Einstein

Dasar pembeda antara statistika Maxwell-Boltzmann dan statistika Bose-Einstein ialah yang terdahulu mengatur partikel identik yang dapat dibedakan dengan suatu cara tertentu, sedangkan yang mengatur partikel identik yang tidak dapat dibedakan, walaupun partikel itu dapat dicacah. Dalam statistika Bose-Einstein, semua keadaan kuantum dianggap berpeluang sama untuk di

Partikel

pembatas

2 0 1 3 6 2 2 0 1 2 1

Banyaknya partikel tak terbedakan = ni = 20

Banyaknya pembatas = g_i - 1 = 11

Banyaknya sel g_i= 12

Sehingga g_i menyatakan banyaknya keadaan yang memiliki energi sama ε _i. Setiap keadaan kuantum bersesuain dengan satu sel dalam ruang fase, dan langkah kita yang pertama ialah menetukan banyaknya cara n_i partikel tak terbedakan dapat didistribusikan dalam sel g_i.

Untuk mencarinya, kita anggap deretan n_i + g_i - 1 benda yang diletakkan dalam gambar (I-ii) . Kita perhatikan bahwa g_i - 1 benda dapat dianggap sebagai pembatas yang memisahkan g_i selang, sedangkan seluruh deretan mengambarkan n_i partikel yang diatur dalam g_i sel. Dalam gambar itu g_i= 12 dan n_i= 20; 11 pembatas memisahkan 20 partikel menjadi 12 sel. Sel pertama berisi dua partikel, yang kedua tidak ada, yang ketiga satu partikel, yang keempat tiga partikel, dan seterusnya. Terdapat (n_i + g_i- 1)! Permutasi n_i partikel diantara mereka dan (g_i-1)! Permutasi dari g_i- 1 pembatas yang tidak mempengaruhi distribusi dan tak relevan. Jadi terdapat

)! 1 ( !

)! 1 g

( _i

−− +

i i i

g n n

Pengaturan yang berbeda mungkin dari n_i partikel tak terbedakan diantara g_isel. Banyaknya cara W supaya N partikel dapat didistribusikan ialah perkalian W = Π

)! 1 ( !

)! 1 g

( _i

−− +

i i i

g n n

(2.20)

Dari banyaknya pengaturan yang berbeda dari partikel diantara keadaan yang memiliki energi tertentu. Kita anggap

(n_i+ g_i) >> 1

Sehingga (n_i+ g_i - 1) dapat diganti dengan (n_i+ g_i), dan dianggap mengambil logaritma natural dari persamaan (2.20) didapatkan

Ln W =

∑

[(n_i +g_i)ln(n_i +g_i)−n_ilnn_i −ln(g_i −1)!−g_i] (2.21) Persyaratan supaya distribusi ini berpeluang terbesar ialah perubahan kecil δn_i dalam setiap n_i individual tidak mempengaruhi harga W. Jika perubahan ln W yaitu δ ln W terjadi ketika n_i berubah dengan δn_i, persyaratan tersebut dapat ditulis sebagai berikut:

max

lnW

δ = 0

Jadi, jika W dari persamaan (2.21) menyatakan maksimum maka:

max

lnW

δ =

∑

[ln(n_i +g_i)−lnn_i]δn_i = 0 Disini kita telah membahas fakta

n n

n δ

δln = 1 (2.22)

Seperti sebelumnya kita memasukkan kekekalan jumlah partikel dengan menyatakan dalam bentuk

∑

δni = 0

Dan kekekalan energi, dalam bentuk

∑

εiδni= 0

Dengan mengalikan persamaan yang terdahulu dengan -α dan yang kemudian -β dan menambahkannya pada persamaan δlnW_max=

∑

[ln(n_i +g_i)−lnn_i]δn_i = 0 kita dapatkan:

∑

[ln(n_i +g_i)−lnn_i −α −βε_i]δn_i = 0

Karena secara efektif δn_i bebas, maka kuantitas dalam tanda kurung harus nol untuk setiap harga i. Jadi

Ln + − − _i =0

i i i

n g n

βε α

1 +

i i n g

= eαeβ

Dan

n

i

=

1

−

i

e e

g_i

βε

α

(2.23)

n

_i

=

1

/kT / −

i

e e

g_i

ε

α

(

2.24)

2.2.4 Distribusi Fermi-Dirac

Statistika Fermi-Dirac berlaku untuk partikel takterbedakan yang diatur oleh prinsip eksklusi. Penurunan kita mengenai hokum distribusi Fermi-Dirac akan sejajar denagn hokum distribusi Bose-Einstein kecuali sekarang setiap (yaitu, keadaan kuantum) dapat diisi paling banyak 1 partikel.

Jika ada g_isel yang berenergi sama ε_i dan ada n_ipartikel, maka n_isel terisi dan (g_i- n_i)! Permutasi sel kosong di antara mereka yang tak relevan karena sel itu tidak ada isinya. Jadi banyaknya pengaturan partikel diantara sel ialah

)! (

!

i i i

i n g n

g

−

Peluang W dari seluruh distribusi partikel ialah perkalian

W = Π

)! (

!

i i i

i n g n

g

− (2.25)

Dengan mengambil logaritma natural dari kedua ruas,

ln W =

∑

[lng_i!−lnn_i!−ln(g_i −n_i)!] (2.26) kemudian dengan memakai rumus stirling ln n! = n ln n-n, kita dapat menulisnya dalam bentuk

ln W =

∑

[g_ilng_i!−n_ilnn_i −(g_i −n_i)ln(g_i −n_i)] (2.27) supaya distribusi ini menyatakan peluang terbesar, perubahan kecil δn_i dari setiap n_i individual harus tidak berubah W. Jadi

max

lnW

δ =

∑

[−lnn_i +ln(g₁−n₁)]δn_i = 0 (2.28)

Kita memperhitungkan kekekalan jumlah partikel dan kekekalan energi dengan menambahkan

∑

[−lnni +ln(gi −ni)−α −βεi]δni = 0 (2.29)

Karena δn_i secara efektif bebas, kuantitas dalam tanda kurung harus nol untuk setiap I, sehingga

ln − − − _i =0

i i i

n n g

βε α

ln − =_{ln e}α-βεi

i i i

n n g

i

e n

g

i

i −₁= α−βε

1

+ =_e − i

n g

i

i α βε

i

g = )_n(_e + i +1

i

βε α

n_i=

1

+ + i

e g_i

βε α

subsitusi β =−1/kT, dan α =ε_f /kT

n

_i

=

1

/kT + i

i

e e

g

ε

α

(2.30)

2.2.5 Fungsi Gelombang

Keberatan tersebut tidak berlaku untuk ψ 2, kuadrat dari harga mutlak fungsi gelombang yang dikenal sebagai kerapatan peluang. Peluang untuk secara eksperimental mendapatkan benda yang diberikan oleh fungsi gelombang ψ pada titik x,y,z pada saat t berbanding lurus dengan harga ψ 2 di tempat itu pada saat t. Harga

2

ψ yang besar menyatakan peluang yang besar untuk mendapatkan benda itu.

Selama ψ 2 tidak nol, terdapat peluang tertentu untuk mendapatkan benda tersebut disitu.

Pada pihak lain, bila eksperimennya berkaitan dengan banyak benda identik yang semuanya diberikan dengan fungsi gelombang yang sama ψ , kerapatan yang sebenarnya dari benda itu di x,y,z pada saat t berbanding dengan harga ψ 2.

Panjang-panjang gelombang de Broglie yang berkaitan dengan sebuah benda bergerak dinyatakan dengan rumus sederhana

= λ

mv h

Menentukan amplitude ψ sebagai fungsi kedudukan dan waktu biasanya merupakan persoalan sulit. Pada kejadian dengan fungsi gelombang ψ kompleks dengan bagian nyata (real) dan khayal!(imaginer) nya tidak nol, kerapatan peluang dinyatakan dengan perkalian ψ *ψ dari konjugate ψ kompleks ψ *. Konjugate kompleks suatu fungsi diperoleh dengan mengganti I = ( −1) dengan –i bilamana huruf itu muncul dalam fungsi gelombang. Setiap fungsi kompleks ψ dapat ditulis dalam bentuk

ψ = A + iB

Dengan A dan B menyatakan fungsi real. Konjugate kompleks ψ * dapat ditulis dalam bentuk :

ψ * = A – iy Sehingga

2.2.6 Asas Larangan Pauli

Asas larangan pauli secara sederhana didefenisikan sebagai berikut:

Dua electron dalam sebuah atom tidak boleh memiliki himpunan bilangan kuantum (n,l,m_l,m_s) yang sama. Asas larangan Pauli merupakan aturan paling penting yang mengatur structure atom, dan kajian terhadap sifat-sifat atom hanya akan berhasil melalui pemahaman secara mendalam terhadap asas ini.

Oleh karena itu suatu ketidakpastian ∆k dalam jumlah gelombang pada-pada gelombang de Broglie berhubungan dengan hasil-hasil partikel dalam suatu ketidakpastian ∆pdalam momentum partikel menurut rumus

π 2

k h

p= ∆

∆

Karena x k ,maka

2 1

≥ ∆ ∆

x k

∆ ≥ ∆

2 1

dan

π 4

h p

x∆ ≥

∆

Persamaan ini merupakan salah satu bentuk prinsip ketaktentuan ini menyatakan perkalian ketaktentuan kedudukan benda ∆x pada suatu saat dan ketaktentuan komponen komponen momentum dalam arah x atau ∆ppada saat yang sama lebih besar sama dengan

π 4

h

. Ketaktentuan ini bukan ditimbulkan oleh alat yang kuran baik melainkan ditimbulkan oleh sifat ketaktentuan alamiah dari kuantitas yang tersangkut ketaktentuan instrumental atau statistic. Kuantitas

π 2

h

sering muncul dari fisika modern, karena ternyata kuantitas itu merupakan satuan dasar dari momentum sudut atau disingkat dengan

π 2

h

dengan lambang h

h = π 2

h

= 1,504 x 10−34 J.s

Selanjutnya kita akan memakai hsebagai pengganti dari π 2

h

dinyatakan dalam h prinsip ketaktentuan menjadi

2

h p

x∆ ≥

BAB III

HASIL DAN PEMBAHASAN

3.1 Mekanika statistik

Mekanika statistika adalah aplikasi teori probabilitas, yang memasukkan matematika untuk menangani populasi besar, ke bidang mekanika, yang menangani gerakan partikel atau objek yang dikenai suatu gaya. Bidang ini memberikan kerangka untuk menghubungkan sifat mikroskopis atom dan molekul individu dengan sifat makroskopis atau limbak (bulk) materi yang diamati sehari-hari, dan menjelaskan termodinamika sebagai produk alami dari statistika dan mekanika (klasik dan kuantum) pada tingkat mikroskopis. Mekanika statistika khususnya dapat digunakan untuk menghitung sifat termodinamika materi limbak berdasarkan data spektroskopis dari molekul individual.

Kemampuan untuk membuat prediksi makroskopis berdasarkan sifat mikroskopis merupakan kelebihan utama mekanika statistika terhadap termodinamika. Kedua teori diatur oleh hukum kedua termodinamika melalui media entropi. Meskipun demikian, entropi dalam termodinamika hanya dapat diketahui secara empiris, sedangkan dalam mekanika statistika, entropi merupakan fungsi distribusi sistem pada kondisi mikro.

3.1.1 Perlakuan Partikel Berdasarkan Statistik Maxwell- Boltzmann

jenis partikel yang sedang ditinjau, kemudian memaksimumkan W dengan syarat bahwa sistem itu terdiri dari sejumlah partikel tertentu (kecuali dalam sistem fonon dan equivalensi aquistiknya fonon) dan bahwa sistem itu berenergi tertentu. Hasil dalam setiap kasus ialah rumusan n(∈), jumlah partikel berenergi ∈ yang bentuknya

) ( ) ( )

(∈ = g ∈ f ∈

n ………...(3.1)

dengan )g(∈ = banyaknya keadaan berenergi ∈ atau bobot statistik yang bersesuaian dengan energi ∈

) (∈

f = fungsi distribusi atau banyaknya partikel rata-rata untuk setiap keadaan berenergi ∈ atau peluang terisinya setiap keadaan berenergi ∈

Jika yang terlibat adalah distribusi malar (kontinue), alih-alih distribusi diskrit dan energi )g(∈ diganti

dengan g(∈)d(∈) yang menyatakan banyaknya keadaan dengan energi antara

∈ + ∈

∈dan d . Dengan meninjau sistem partikel identik yang jaraknya cukup

berjauhan sehingga satu sama lainnya dapat dibedakan (menurut istilah kuantum, partikel ini berkelakuan klasik dengan spinnya tidak relevan). Molekul gas merupakn partikel sejenis ini, dan fungsi distribusi Maxwel-Boltzmann berlaku untuknya

kT

MB Ae

f (∈)= −ε/ ………...……(3.2)

Harga A bergantung dari jumlah partikel dalam sistem dan disini memegang peranan yang serupa dengan konstanta normalisasi suatu fungsi gelombang.

Fungsi distribusi f(ε) juga berubah terhadap temperatur T. Faktor 3/2kT dalam eksponen jelas mungkin, karena peluang bahwa sebuah partikel memiliki energi tinggi harus bertambah dengan bertambahnya energi, tetapi ini bukan satu-satunya faktor yang memilki sifat seperti itu. Test yang lebih meyakinkan ialah penggunaan persamaan (2) untuk menghitung energi internal total E dari sebuah sistem partikel yang harga E nya diketahui dan melihatnya apakah cocok. Sistem yang sesuai untuk diperiksa ialah sampel gas ideal yang terdiri dari N molekul. Teori kinetik elementer dari gas menunjukkan bahwa jika hanya energi kinetik molekullar rata-ratanya 3/2kT hukum gas ideal mempunyai bentuk yang benar pV=nkT sehingga energi molekul total haruslah E=3/2kT.

1

∈ ,∈₂,∈₃,….Jika )n(∈)d(∈ menyatakan banyaknya molekul yang energinya terletak antara ∈dan∈+d∈ maka persamaan (1) dapat ditulis menjadi

∈ ∈ = ∈ ∈ ∈ ∈=

∈_{d g d xf Ag e}−∈ _d

n( ) ( ) ( ) ( ) ( ) /kT ………..…...(3.3)

Sebuah molekul berenergi ∈ memiliki momentum p yang besarnya

2 2 2

2mc p_x p_y p_z

p= = + + ………...(3.4)

Setiep kumpulan komponen momentum p_x,p_y,p_z memberi ciri suatu keadaan gerak dalam ruang momentum. Banyaknya keadaan g(∈)dp dengan momentum yang besarnya ada diantara pdan p+dp berbanding lurus dengan volume kulit bola (bentuk partikel) dalam ruang momentum tiga dimensi yang berjari-jari p dan tebalnya

dp p yaitu

dp_{, 4}π 2 _jadi

dp Bp dp p

g( ) = 2 ………..…(3.5)

dengan B merupakan konstanta. Karena setiap besar momentum pbersesuaian dengan energi tunggal ∈, banyaknya keadaan energi g(∈)d∈antara∈dan∈+d∈ sama dengan banyaknya keadaan momentum g(p)dpantara pdan p+dp, sehingga

∈ ∈ ∈=

∈ ∈=

∈d Bp dpatau g d m B d

g( ) 2 ( ) 2 3/2 ………...(3.6)

dan untuk jumlah molekul dengan energi antara ∈dand∈

∈ ∈

∈=

∈_{d C e}−∈ _d

n( ) /kT ………...(3.7)

dengan C=₂m3/2AB _{merupakan konstanta yang harus dicari dengan menggunakan}

syarat normalisasi bahwa jumlah molekulnya N, sehingga

∫

∫

∞ ∞ ∈ − _∈ ∈ ∈= ∈ = 0 0 / )

( d C e d

n

N kT _diperoleh

2 / 3 ) ( 2 kT N C π π = ,sehingga: ∈ ∈ ∈=

∈ _e−∈ _d

kT N d

n /kT

2 / 3 ) ( 2 ) (

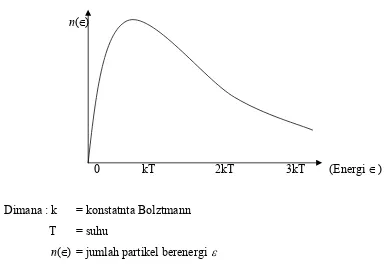
n(∈)

0 kT 2kT 3kT (Energi ∈)

Dimana : k = konstatnta Bolztmann T = suhu

n(∈) = jumlah partikel berenergi ε

Gambar (3.1) Distribusi energi Maxwel-Boltzmann untuk molekul gas ideal

Energi rat-rata sebuah molekul gas ideal ternyata tidak bergantung pada massa molekul, molekul ringan memiliki kelajuan rata-rata yang lebih besar pada suatu temperatur tertentu daripada molekul berat, seperti gambar berikut:

persentase molekul de ngan kelajuan dalam kisaran 10 m/s pada

kelajuan yang ditunjuk O₂(73 K)

(O₂)(273 K)

(H) (273K)

[image:37.595.104.494.91.366.2]

Gambar(3.2) Distribusi kelajuan molekul dalam oksigen dan hidrogen

Distribusi kelajuan molekular dapat diperoleh dari persamaan (3.8) dengan

mensubtitusikan 2

2 1

mv

∈= sehingga d∈=mvdv. Hasil untuk sejumlah molekul

dalam kelajuan antara v dan v + dv ialah

dv e

v kT

Nm dv

v

n _3/2 2 mv /2kT

2 / 3

2 )

( 2 )

( = −

ππ ………...…(3.9)

3.2. Perlakuan Partikel Berdasarkan Statistik Kuantum

Jika fungsi gelombang cukup banyak saling bertumpangan maka partikel itu tidak dapat dibedakan walaupun partikel itu tetap dapat dicacah. Sistem partikel dengan fungsi gelombang saling bertumpangan jatuh dalam dua kategori:

1. Partikel dengan spin 0 atau bilangan bulat yang disebut boson. Boson tidak memenuhi prinsip eksklusi, dan fungsi gelombang boson tidak terpengaruh oleh pertukaran setiap pasangan partikel. Fungsi gelombang semacam ini disebut simetrik. Setiap jumlah Boson bisa terdapat dalam keadaan kuantum yang sama dari sistem itu. 2. Partikel dengan spin setengah bilangan bulat ganjil (1/2, 3/2, 5/2,…) disebut fermion. Fermion memenuhi prinsip eksklusi dan fungsi gelombang sistem fermion berubah tanda terhadap pertukaran setiap pasangan partikel. Fungsi gelombang semacam ini disebut antisimetrik. Hanya satu fermion bisa terdapat pada keadaan kuantum tertentu dari sistem itu.

Dengan meninjau sistem dua partikel, 1 dan 2, salah satu partikel itu berbeda dalam keadaan a dan yang lainnya dalam keadaan b. Jika kedua partikel itu tidak terbedakan, terdapat dua kemungkinan terisinya keadaan yang diberikan oleh fungsi gelombang

) 2 ( ) 1

( _b

a

I ψ ψ

ψ = ………...…..(310)

) 1 ( ) 2

( _b

a

II ψ ψ

ψ = ………..…..(3.11)

II

I danψ

ψ untuk mencerminkan peluang yang sama Jika partikelnya boson, sistem

itu diberikan oleh fungsi gelombang simetik

[

(1) (2) (2) (1)

]

2 1 b a b a

B ψ ψ ψ ψ

ψ = + ………...(3.12)

dan jika partikelnya fermion, sistem itu diberikan oleh fungsi gelombang antisimetrik

[

(1) (2) (2) (1)

]

2 1 b a b a

F ψ ψ ψ ψ

ψ = − ………....….(3.13)

Faktor 1/ 2diperlukan untuk menormalisasi fungsi gelombang itu.

Dalam hal ini dapat ditentukan berapa kemungkinan untuk masing-masing kasus untuk mendapatkan kedua partikel dalam keadaan yang sama, misalakan a. Untuk partikel yang terbedakan, keduanya ψ_I danψ_II menjadi

) 2 ( ) 1 ( _a a

M ψ ψ

ψ = ………...………(3.14)

sehingga menghasilkan kerapatan peluang ) 2 ( ) 1 ( ) 2 ( ) 1 ( * * * a a a a M

Mψ ψ ψ ψ ψ

ψ = ………..…...(3.15)

Untuk boson fungsi gelombangnya menjadi

[

(1) (2) (1) (2)

]

2 (1) (2) 2 1 a a a a a a

B ψ ψ ψ ψ ψ ψ

ψ = + = ………...(3.16)

Sehingga menghasilkan kerapatan peluang

M M a a a a B

Bψ ψ ψ ψ ψ ψ ψ

ψ* * * * 2 ) 2 ( ) 1 ( ) 2 ( ) 1 ( 2 = = ……….…...(3.17)

Jadi peluang untuk mendapatkan kedua boson dalam keadaan yang sama dua kali untuk partikel yang terbedakan. Untuk fermion fungsi gelombangnya menjadi

[

(1) (2) (2) (1)

]

0 2

1

= −

= a a a a

F ψ ψ ψ ψ

ψ ………....……...(3.18)

Peluang untuk mendapatkan kedua partikel dalam keadaan yang sama menjadi nol,ini merupakan pernyataan prinsip eksklusi.

1 1 )

(

/ −

=

∈ _∈kT

BE

e e

f _α ………....…………(3.19

) dan peluang untuk fermion ternyata sama dengan

1 1 )

(

/ +

=

∈ _∈kT

FD

e e

f _α ………...……(3.20)

Kuantitas α bergantung dari sifat sistem tertentu dan dapat merupakan fungsi dari T. f(∈)

2 (B-E) (M-B)

1 (F-D)

0 kT 2kT 3kT 4kT 5kT (∈)

Gambar (3.3). Perbandingan tiga fungsi distribusi untuk α =−1

Terlihat bahwa fungsi Bose-Einstein selalu lebih tinggi dari fungsi Maxwel-Boltzmann yang merupakan eksponensial murni, dan fungsi Fermi-Dirac selalu lebih rendah. Fungsi tersebut memberikan peluang terisinya keadaan berenergi ∈ pada temperatur mutlak T.

Suku –1 pada penyebut dari persamaan (3.19) menyatakan bertambahnya peluang pengisian jamak keadaan energi oleh boson dibandingkan dengan peluang untuk pertikel terbedakan seperti molekul. Suku +1 pada persamaan (3.20) merupakan akibat prinsip ketaktentuan. Hargaα,edanT, f(∈)tidak pernahlebihbesar dari1. Dalam kedua kasus tersebut , jika ∈≥kT, fungsi f(∈) mendekati statistik Maxwel-Boltzman. Untuk boson f_BE selalu lebih besar dari untuk molekul pada suatu harga

kT

/

yang merupakan suatu kuantitas yang sangat penting dalam sistem fermion, seperti elektron dalam logam. Dinyatakan dalam ∈_F fungsi distribusi Fermi-Dirac menjadi

1 1 ) ( / ) ( + =

∈ _∈−∈ kT

FD _F

e

f ………...…(3.21)

Untuk suatu tingkat energi ∈_itertentu dari suatu fermion, akan terdapat sejumlah g_i keadaan yang memiliki energi ini yakni, ∈_i memiliki suatu degenerasi berorde g_i. Jumlah fermion maksimum yang dapat menempati tingkat energi ini dengan demikian akan sebanyak g_i, karena menurut asas larangan Pauli, tak boleh terdapat lebih dari satu partikel dalam satu keadaan. Dalam hal ini akan dapat ditentukan cara yang berbeda untuk mendistribusikan N fermion tak terbedakan pada tingkat-tingkat energi ∈₁,∈₂,...,∈_i,...,sedemikian rupa sehingga tingkat energi ke-i

akan memiliki keadaan terisi penuh sebanyak n_i ≤ g_i(n₁+n₂ +...= N).Berikut, dari

1

g keadaan dalam ∈₁, diambil n₁ keadaan yang akan diisi oleh n₁ partikel; ini dapat dilakukan dalam )! ( ! ! 1 1 1 1 1 1 n g n g n g − =     _{………....…(3.22)}

cara yang berbeda. Dengan demikian jumlah total cara pengisian keadaan-keadaan sistem fermion ini adalah

... )! ( ! ! )! ( ! ! ... 1 2 2 2 2 1 1 1 1 2 2 1 1 n g n g n g n g n g n g x X − − =         = ………...(3.23)

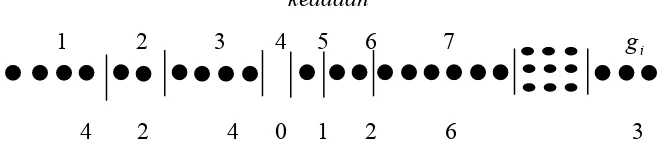
keadaan

1 2 3 4 5 6 7 g_i

4 2 4 0 1 2 6 3

Gambar (3.4). Jumlah partikel dalam keadaan (jumlah totalnya adalah n_i) untuk mendapatkan n_i boson dalam keadaan-keadaan g_i, tanpa ada batasan terhadap jumlah partikel dalam satu keadaan dan juga partikel-partikelnya tak terbedakan, adalah sama dengan jumlah cara mempermutasikan n_i +g_i −1 partikel dan garis-garis pembagi , yakni (n_i +g_i −1)!, dibagi dengan jumlah cara ke (g_i −1) garis yang dapat dipermutasikan, yakni (g_i −1)!:

)! 1 ( )! 1 ( − − + i i i g g n ………..….…(3.24)

Tetapi, karena partikel-partikelnya tak terbedakan, sehingga pertukaran dua partikel tetap memberi distribusi yang sama, maka pernyataan diatas harus dibagi dengan

!

n cara berbeda partikel-partikel itu dapat dipermutasikan. Dengan demikian jumlah cara berbeda sebenarnya, dimana tingkat ke-i dapat dibentuk adalah

)! 1 ( ! )! 1 ( −− + i i i g n g n ………....…..(3.25)

Oleh karena itu, jumlah total X cara berbeda , untuk menyusun n₁,n₂,...,boson dalam tingkat-tingkat energi ∈₁,∈₂,....jika terdapat g₁,g₂,...keadaan dalam tiap-tiap tingkat energi itu adalah

[image:42.595.152.488.93.166.2]

3.3 Tabel Perbandinan Fungsi Distribusi Statistik

(Tabel I-1) Ketiga Fungsi Distribusi Statistik

Maxwell-Boltzmann Bose-Einstein Fermi-Dirac Dapat diterapkan untuk sistem Identik, Partikel terbedakan

Identik, Partikel tak terbedakan dan tidak memenuhi prinsip eksklusi

Identil, Partikel tak terbedakan dan memenuhi prinsip eksklusi

Kategori partikel

klasik Boson Fermion

Sifat partikel Setiap spin, partiekel berjarak cukup berjauhan sehingga fungsi gelombang tidak bertumpangan

Spin 0,1,2.. fungsi gelombang nya simetrik terhadap pertukaran label partikel Spin 2 1 , 2 3 , 2 5 Fungsi gelombang antisimetrik terhadap pertukaran label partikel

Contoh Molekul gas, ion dan atom

Foton dalam rongga; fonon dalam zat padat

Elektron bebas dalam logam Persamaan distribusi s s s e

n =g_s α+βε

1

) ( −

= _{− + s}

e g

n s

s _{α βε}

1

) ( +

= _{− + s}

e g

n s

s _{α βε}

Fungsi

distribusi

f

_mb(ε)=Ae-ε/kT

f

1 e 1 ) ( / − = kT be eε α ε

f

1 e 1 ) ( / ) -( f +

= kT

Sifat distribusi

Tidak ada batas pada jumlah partikel perkeadaan

Tidak ada batas pada jumlah partikel per keadaan; lebih banyak partikel perkeadaan f_mb

pada E rendah mendekati

mb

f pada E tinggi

Tidak lebih dari satu partikel per

keadaan;lebih sedikit jumlah partikel per keadaan dari f_mb

BAB IV

KESIMPULAN

1. Berdasarkan statisitik Maxwell-Bolztmann; setiap spin partikel berjarak cukup berjauhan sehingga fungsi gelombang tidak bertumpangan, partikel di kategorikan klasik contohnya molekul gas. Fungsi distribusinya dirumuskan dengan

kT

MB Ae

f (∈)= −∈/ yang sifatnya tidak ada batas pada jumlah partikel perkeadaan. Hukum distribusi statistik yang dihasilkan adalah: _{n e} s

s

βε α

s

g +

=

.

2. Berdasarkan statistik Bose-Einstein; Partikel memiliki spin bilangan bulat 0,1,2,…. dengan fungsi gelombang simetris, tidak memenuhi prinsip eksklusi dan partikel di kategorikan boson contohnya foton dalam rongga, fonon dalam zat padat, fungsi distribusinya dirumuskan dengan

1 1 )

( _/

− =

∈ _∈ kT

BE

e e

f _α yang sifatnya

tidak ada batas pada jumlah partikel perkeadaan dari f_MB pada energi rendah dan mendekati f_MB pada energi tinggi. Hukum distribusi statistik yang dihasilkan

adalah :

1 e

g

) (

-s

s − = _α+βε

s n

3. Berdasarkan statistik Fermi-Dirac; partikel memiliki spin setengah bilangan bulat ganjil ½, 3/2, 5/2,…dengan fungsi gelombang antisimetris, memenuhi prinsip eksklusi dan partikel dikategorikan fermion contohnya elektron bebas dalam logam. Fungsi distribusinya dirumuskan dengan

1 1 )

( _/

+ =

∈ _∈kT

FD

e e

f _α yang

sifatnya tidak lebih dari satu partikel perkeadaan, lebih sedikit jumlah partikel perkeadaan dari dari f_MB pada energi rendah dan mendekati f_MB pada energi

tinggi. Hukum distribusi yang dihasilkan adalah :

1 e

g

/

s

+ = _{i kT}

e

DAFTAR PUSTAKA

A.PICH. (2006-2007). The Standard Model Electroweaks Interactions, European

School of High Energi Physics (Aronsborg, Sweden, 18 june – 1 July 2006)

and at the 4th CERN – CLAF School of High Energi Physics (Vina Del Mar, Chile, 18

ARHTUR BEISER. 1992. Konsep Fisika Modern, Cetakan kedua, Terjemahan The How Liong, Erlangga, Jakarta,

CRIS QUIGG. 1983 Gauge Theories of The Strong, weak and Electromagnetic

Interaction, The Benjamin Publishing Company, Canada .

GRAHAM G. ROSS. 1985. Grand Unified Theories, The Benjamin Publishing CompanyCanada.

KERSON HUANG. 1971. Statistical Mechanics. New york.

KITTEL. JHON WILLEY & SONS. 1961. Elementary Statistical Physics. New York

VANTOURNHOUT, N. JACHOWICZ, J.RYCKEBUSCH. 2006. Electroweak

interaction in relativistic Fermi Gas, Departemen of Subatomic and Radiation

Physics, Ghent University, Belgium, Phys.Rev. c74(2006) 035501,

arXiv:nucleth/0602045v2.

RONALD GAUTREU. 1995. Teori dan Soal-soal Fisika Modern, Terjemahan Hans

J.Wosparkirk, Erlangga, Jakarta.

S.M BILENKY. 2004. A Lecture On Neutrinos< Joint Institute For Nuclear

Research, Dubna, R-141980, Russia SISSA, Via Beirut 2-4, Trieste, 34014,

T.MART. 2006. From Pauli Principle to Hypernucleus, Neutron Star, and

EconoPhysics, Departemen Fisika FMIPA UI, Keynote talk given at 3rd

LAMPIRAN

Pengali

α

A = eα n_s= Ag_seβεs

N = A

∑

s s

s

e

g βε dan

A =

∑

_s s

s

e g

N

βε

A =

ε ε

π _{m BV e}βε_d

N

∫

∞ 0 2 1 2 3 ) 2 ( 2

Karena : -βε = x

2 -3 0 2 1 ) (-β ε ε βε ₌

∫

∞ d e ) 2 3 ( ) (- 2 3 0 2 1 Γ = − ∞

∫

x e xdx β

=(-2 ) 2

3 π

β −

A =

2 3 ) 2 ( β πm BV N −

Karena β = -1/kT

A =

2 3 ) 2 ( mkT BV N π

Sehingga pengali α adalah:

Pengali β

E =

∑

+

∑

s ii s s i s i n s ii s n ε ε

Dimana : dNi=0 dNii=0 dE = 0 karena dNi= 0 =

∑

s

s i s i

n ε = 0 dan

dNii=

∑

s ii s

dn = 0

maka:

dE =

∑

s i s s i dn ε +

∑

s s ii ii s dn

ε = 0

W_T=WiWii

d log W_T+αidNi +αiidNii +βdE =0

karena W i ii

T=W W maka:

d log Wi=

∑

∂ ∂ s i s s i i dn n W log dan,

d logWii=

∑

∂ ∂ s ii s ii n W log ii s dn 0 ) ( log log = + + + + ∂ ∂ + ∂ ∂

∑

_s

∑

_sii i

∑

_{s s}i ii

∑

_s iis

∑

_{s s}i _si

∑

_s iis iis

s s ii s i s i s i dn dn dn dn dn n W dn n W

ε

ε

β

α

α

Atau :

∑

∑

+ = ∂ ∂ + + + ∂ ∂ s ii s ii s

s iis

ii s i s i s i s i dn n W dn n W 0 } log { } log { α βε α βε

dE = dQ - ρdV dE = d

∑

s s s n ε =

∑

+

∑

s s s

sdn d

s s n ε ε

∑

= s s sd

n ε -ρdV

∑

=

s s

sdn dQ

ε

d log W + αdN+βdQ=0 d log W = -βdQ=0

dS =

T dQ kT 1 -= β

Banyaknya cara molekul yang dapat didistribusikan

n

n_{C =}

)! (

! !

1 1 N n

n N

−

(n-n₁)C_n2 =

)! ( ! )! ( 2 1 2 1 n n N n n N − −− )! ( ! ! ! )! ( ! )! ( )! ( ! 2 1 2 1 2 1 2 1 1 !

1 n n N n n

N n n N n n N x n N n N − − = − −− −

n₃= (N−n₁ −n₂)

! ! ! ! 3 2 1 n n

n N ! !... !... ! ! ! 3 2

1 n n ns nr

n

N

n₁;n₂;n₃;…..n_s;….n_r

= W r s n n n n n N ... !.... ! ! ! 3 1 2

( )

1

( ) ( )

2 3

1 2 3