MODEL EPIDEMI SEIV
PENYEBARAN PENYAKIT POLIO
PADA POPULASI TAK KONSTAN
SKRIPSI
disajikan sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
Program Studi Matematika
oleh
Yanuar Chaerul Umam 4150408013
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
ii
pernah diajukan untuk memperoleh gelar kesarjanaan di suatu Perguruan Tinggi, dan sepanjang pengetahuan saya juga tidak terdapat karya atau pendapat yang pernah ditulis atau diterbitkan oleh orang lain, kecuali yang secara tertulis dirujuk dalam skripsi ini dan disebutkan dalam daftar pustaka.
Semarang, Mei 2014
iii
Model Epidemi SEIV Penyebaran Penyakit Polio pada Polpulasi Tak Konstan disusun oleh
Yanuar Chaerul Umam 4150408013
telah dipertahankan di hadapan sidang Panitia Ujian Skripsi Fakultas MIPA, Universitas Negeri Semarang pada:
Hari : Jumat Tanggal : 16 Mei 2014 Panitia :
Ketua Sekretaris
Prof. Dr. Wiyanto, M.Si Drs. Arief Agoestanto, M.Si
NIP. 196310121988031001 NIP. 196807221993031005
Ketua Penguji
Drs. Wuryanto, M.Si. NIP. 195302051983031003
Anggota Penguji/ Anggota Penguji/
Pembimbing Utama Pembimbing Pendamping
Muhammad Kharis,S.Si., M.Sc. Drs. Supriyono, M.Si.
iv
“Maka sesungguhnya bersama kesulitan ada kemudahan (Asy-Syarh: 5)”.
Berusaha menjadi lebih baik untuk kebaikan diriku sendiri, bukan untuk mengalahkan orang lain.
Jangan patah semangat walaupun apapun yang terjadi, jika kita menyerah maka habislah sudah.Skripsi ini aku persembahkan untuk : 1. Orang tuaku tercinta
2. Kakak-kakakku dan keluarga besarku 3. Teman-teman Matematika’08 UNNES
4. Semua sahabatku di EX kontrakan
v
karunia-Nya, sehingga penulis dapat menyelesaikan penulisan skripsi yang berjudul “Model Epidemi SEIV Penyebaran Penyakit Polio Pada Populasi Tak Konstan”. Penulisan skripsi ini sebagai syarat mutlak yang harus dipenuhi oleh penulis untuk memperoleh gelar sarjana sains di Universitas Negeri Semarang.
Penulisan skripsi ini dapat terselesaikan karena adanya bimbingan, bantuan, dan dukungan dari berbagai pihak baik secara langsung maupun tidak langsung. Oleh karena itu, penulis mengucapkan terima kasih kepada:
1. Prof. Dr. Fahtur Rakhman, M.Hum, Rektor Universitas Negeri Semarang. 2. Prof. Dr. Wiyanto, M.Si, Dekan FMIPA Universitas Negeri Semarang.
3. Drs. Arief Agoestanto, M.Si, Ketua Jurusan Matematika FMIPA Universitas Negeri Semarang.
4. Muhammad Kharis, S.Si., M.Sc, Pembimbing Utama yang telah memberikan bimbingan, motivasi, dan pengarahan.
5. Drs. Supriyono, M.Si, Pembimbing Pendamping yang telah memberikan bimbingan, motivasi, dan pengarahan.
6. Drs. Wuryanto, M.Si, Dosen Penguji Utama yang telah memberikan inspirasi, kritik, saran, dan motivasi kepada penulis, sehingga penulis dapat menyelesaikan skripsi.
vi
Simbah, Alip, Very, Borok, dan Nurul Ardiansyah) yang telah memberikan banyak motivasi, kritik, usulan yang menjadikan terselesaikannya penulisan skripsi ini.
10.Mahasiswa matematika angkatan 2008 yang telah memberikan dorongan dan motivasi.
11.Semua pihak yang telah membantu terselesaikannya penulisan skripsi ini. Penulis sadar dengan apa yang telah disusun dan disampaikan masih banyak kekurangan dan jauh dari sempurna. Untuk itu penulis menerima segala kritik dan saran yang sifatnya membangun untuk skripsi ini. Semoga skripsi ini dapat bermanfaat bagi pembaca.
Semarang, Mei 2014
vii
Utama Muhammad Kharis, S.Si., M.Sc dan Pembimbing Pendamping Drs. Supriyono, M.Si.
Kata kunci: Polio, epidemi SEIV, titik kesetimbangan, vaksinasi.
Penelitian ini membahas model matematika untuk penyebaran penyakit polio. Model matematika yang digunakan berupa model epidemi SEIV dengan laju rekruitmen tidak sama dengan laju kematian. Sebagai upaya dalam mencegah penyebaran penyakit polio maka dalam model juga diperhatikan faktor vaksinasi.
Permasalahan yang diangkat dalam penelitian ini adalah bagaimana membentuk model epidemi SEIV penyebaran penyakit polio pada populasi tak konstan, bagaimana menentukan titik kesetimbangan dan analisis kestabilan penyebaran penyakit polio pada populasi tak konstan, bagaimana simulasi model dan interpretasi perilaku model penyebaran penyakit polio pada populasi tak konstan menggunakan program Maple. Metode yang digunakan untuk menganalisis masalah adalah dengan studi pustaka. Langkah-langkah yang dilakukan adalah menentukan masalah, merumuskan masalah, studi pustaka, analisis pemecahan masalah, dan penarikan kesimpulan.
Sebagai hasil penelitian, model yang diperoleh adalah
Dari model tersebut diperoleh dua titik kesetimbangan yaitu titik kesetimbangan bebas penyakit dan titik kesetimbangan endemik. Analisis yang dilakukan menghasilkan angka rasio reproduksi dasar Setelah dianalisis kestabilan pada titik kesetimbangan, titik kesetimbangan bebas penyakit akan stabil asimtotis untuk R0 1. Sedangkan titik kesetimbangan endemik akan
stabil asimtotis jika R0 1 dan . Selanjutnya, untuk mengilustrasikan
viii
PERNYATAAN ... ii
PENGESAHAN ... iii
MOTTO DAN PERSEMBAHAN ... iv
KATA PENGANTAR ... v
ABSTRAK ... vii
DAFTAR ISI ... viii
DAFTAR GAMBAR ... xi
DAFTAR TABEL ... xii
DAFTAR LAMPIRAN ... xiii
BAB 1 PENDAHULUAN ... 1
1.1 Latar Belakang ... 1
1.2 Rumusan Masalah ... 4
1.3 Tujuan Penulisan ... 4
1.4 Manfaat Penulisan ... 5
1.5 Batasan Masalah ... 5
1.6 Sistematika Penulisan ... 6
BAB 2 TINJAUAN PUSTAKA ... 8
2.1 Persamaan Diferensial ... 8
2.2 Sistem Persamaan Diferensial Linear dan Tak Linear ... 9
ix
2.7 Pemodelan Matematika ... 23
2.8 Pendekatan pada Pemodelan Matematika ... 24
2.9 Tahap Pemodelan ... 25
2.10 Model Epidemi SEIV ... 26
2.11 Penyakit Polio ... 27
2.12 Titik Kesetimbangan (Ekuilibrium) ... 33
2.13 Nilai Eigen dan Vector Eigen ... 34
2.14 Kriteria Routh-Hurwitz ... 35
2.15 Kriteria Kestabilan ... 39
2.16 Maple ... 40
BAB 3 METODE PENELITIAN ... 43
3.1 Menentukan Masalah ... 43
3.2 Merumuskan Masalah ... 43
3.3 Studi Pustaka ... 43
3.4 Analisis dan Pemecahan Masalah ... 44
3.5 Penarikan Kesimpulan ... 44
BAB 4 HASIL DAN PEMBAHASAN ... 45
4.1 Model Matematika untuk Penyebaran Penyakit Polio ... 45
4.2 Titik Kesetimbangan ... 49
x
5.1 Simpulan ... 69
5.2 Saran ... 70
DAFTAR PUSTAKA ... 71
xi
Gambar 2.1. Diagram Transfer Penyebaran Penyakit Polio ... 27 Gambar 2.2. Tipe Kestabilan dari Titik Kesetimbangan... 40 Gambar 4.1. Diagram Transfer Penyebaran Penyakit Polio ... 48 Gambar 4.2. Dinamika Populasi S(t), E(t), I(t) dan V(t) terhadap waktu t
pada saat dan
. ... 64 Gambar 4.3. Dinamika Populasi S*(t), E*(t), I*(t) dan V*(t) terhadap
xii
Tabel 2.1. Kriteria kestabilan berdasarkan nilai eigen ... 39
Tabel 4.1. Daftar Variabel-variabel ... 47
Tabel 4.2. Daftar Parameter-parameter ... 47
Tabel 4.3. Nilai Parameter Tetap untuk Simulasi Model ... 62
Tabel 4.4. Titik Kesetimbangan , Rasio Reproduksi Dasar R0 ... 63
xiii
1
BAB 1
PENDAHULUAN
1.1
Latar Belakang
Matematika bersifat universal dan sangat erat dengan kehidupan nyata, dan merupakan ilmu pengetahuan yang bersifat deduktif. Konsep-konsep yang ada di dalam matematika bersifat hierarkis, terstruktur, logis dan sistematis dari konsep yang paling sederhana sampai konsep yang paling kompleks (Suherman, 1993:124). Setiap konsep dapat dibangun berdasarkan konsep terdahulu atau dengan kata lain konsep sebelumya sebagai prasyarat yang harus dipenuhi untuk dapat memahami konsep-konsep selanjutnya.
Selain itu matematika juga dapat berperan sebagai ratu ilmu sekaligus pelayan (Suherman, 1993:127). Matematika dikatakan sebagai ratu ilmu karena matematika dapat tumbuh dan berkembang untuk dirinya sendiri sebagai suatu ilmu tanpa adanya bantuan dari ilmu lain. Selanjutnya matematika dikatakan sebagai pelayan ilmu lain karena matematika mendukung pertumbuhan dan perkembangan ilmu lain. Kajian matematika yang berperan sebagai pelayan ilmu-ilmu lain biasa disebut matematika terapan.
pengenalan konsep maupun pemecahan masalah yang berkaitan dengan dunia nyata. Kebanyakan masalah-masalah yang muncul di dalam persamaan diferensial adalah bagaimana menemukan solusi eksak (analitik) dari model-model matematika yang diperoleh dari masalah nyata (Waluya, 2006: 1).
Dewasa ini semakin banyak disiplin ilmu yang menggunakan model matematika ataupun penalaran matematika sebagai alat bantu dalam menyelesaikan permasalahan yang dihadapi. Penggunaan model matematika telah banyak membantu menyelesaikan masalah-masalah di berbagai bidang sains, ekonomi dan teknik. Secara umum pengertian model adalah suatu usaha menciptakan suatu replika/tiruan dari suatu fenomena alam. Pada model matematika replika/tiruan tersebut dilaksanakan dengan mendeskripsikan fenomena alam dengan satu set persamaan. Kecocokan model terhadap fenomena tersebut tergantung dari ketetapan formulasi persamaan matematis dalam mendeskripsikan fenomena alam yang ditirukan. Pemodelan matematika adalah suatu proses yang menjalani tiga tahap yaitu perumusan model matematika, penyelesaian dan/atau analisis model matematika dan pengiterpretasian hasil ke situasi nyata (Pamuntjak, 1990:1).
nyata. Kebanyakan masalah-masalah yang muncul di dalam persamaan diferensial adalah bagaimana menemukan solusi eksak (analitik) dari model-model matematika yang diperoleh dari masalah nyata (Waluya, 2006:1).
Konsep persamaan diferensial juga seringkali digunakan untuk memodelkan masalah-masalah yang berkaitan dengan ilmu kesehatan. Ilmu kesehatan yang dibahas salah satunya adalah masalah penyebaran penyakit. Salah satu masalah penyebaran penyakit yang dapat dimodelkan dengan persamaan diferensial adalah pemodelan matematika pada penyakit polio.
Polio adalah suatu penyakit yang disebabkan oleh virus polio yang dapat mengakibatkan terjadinya kelumpuhan yang permanen. Penyakit ini dapat menyerang pada semua kelompok umur, namun yang peling rentan adalah kelompok umur kurang dari 3 tahun. Gejala meliputi demam, lemas, sakit kepala, muntah, sulit buang air besar, nyeri pada kaki, tangan, kadang disertai diare. Kemudian virus menyerang dan merusakkan jaringan syaraf, sehingga menimbulkan kelumpuhan yang permanen. Penyakit polio pertama terjadi di Eropa pada abad ke-18, dan menyebar ke Amerika Serikat beberapa tahun kemudian. Penyakit polio juga menyebar ke negara maju belahan bumi utara yang bermusim panas. Penyakit polio menjadi terus meningkat dan rata-rata orang yang menderita penyakit polio meninggal, sehingga jumlah kematian meningkat akibat penyakit ini. Penyakit polio menyebar luas di Amerika Serikat tahun 1952, dengan penderita 20,000 orang yang terkena penyakit ini (Miller, 2004 ).
sebagai cara yang paling efektif dalam menekan penyebaran penyakit polio. Oleh karena itu, vaksinasi perlu diperhatikan dalam model sebagai upaya untuk mencegah meluasnya penyakit.
Pada karya ilmiah ini, model tersebut akan dikembangkan dengan memperhatikan kenyataan bahwa laju rekruitmen (penambahan populasi) sama dengan laju kematian (jumlah populasi konstan). Berdasarkan pemikiran tersebut, maka penulis mencoba melakukan pembahasan yang berjudul “Model Epidemi
SEIV Penyebaran Penyakit Polio pada Populasi Tak Konstan”.
1.2
Rumusan Masalah
Berdasarkan uraian pada latar belakang di atas, maka masalah dalam penelitian ini dirumuskan sebagai berikut.
1. Bagaimana membentuk model epidemi SEIV penyebaran penyakit polio pada populasi tak konstan?
2. Bagaimana menentukan titik kesetimbangan dan analisis kestabilan dari model matematika penyebaran penyakit polio pada populasi tak konstan?
3. Bagaimana simulasi model matematika penyebaran penyakit polio pada populasi tak konstan menggunakan program MAPLE?
1.3
Tujuan Penelitian
Sejalan dengan rumusan masalah di atas, tujuan penelitian ini adalah untuk mengetahui :
2. Mengetahui kestabilan titik tetap dari model matematika penyebaran penyakit polio pada populasi tak konstan.
3. Mengetahui simulasi model matematika penyebaran penyakit polio pada populasi tak konstan menggunakan program Maple.
1.4
Manfaat Penelitian
Manfaat dari penelitian ini adalah sebagai berikut: 1. Bagi Penulis
Sebagai sarana untuk memperdalam pengetahuan mengenai pemodelan matematika khususnya dari model matematika penyebaran penyakit polio pada
populasi tak konstan sekaligus sebagai sarana untuk memenuhi syarat kelulusan program studi Matematika, S1 FMIPA Unnes.
2. Bagi Mahasiswa Matematika
Sebagai referensi untuk menambah wawasan mengenai pemodelan matematika khususnya dari model matematika penyebaran penyakit polio pada populasi tak konstan.
3. Bagi Pembaca
Sebagai wacana dan pengetahuan tentang model penyakit dalam kasus
penyebaran penyakit polio pada populasi tak konstan.
1.5
Batasan Masalah
menyederhanakan permasalahan konstanta pembanding laju kematian murni pada populasi infective akan digunakan sebagai konstanta pembanding untuk laju pengurangan populasi misalnya karena sudah melewati batas usia yang diamati.
1.6
Sistematika Penulisan
Secara garis besar penulisan skripsi ini dibagi menjadi tiga bagian, yaitu bagian awal skripsi, bagian isi skripsi dan bagian akhir skripsi. Berikut ini penjelasan masing-masing bagian skripsi:
1. Bagian awal skripsi
Bagian awal skripsi meliputi halaman judul, abstrak, halaman pengesahan, motto dan persembahan, kata pengantar, daftar isi, daftar gambar, daftar tabel, daftar lampiran.
2. Bagian isi skripsi
Secara garis besar bagian isi skripsi terdiri dari lima bab, yaitu:
BAB 1 PENDAHULUAN
Dalam bab ini dikemukakan latar belakang, permasalahan, tujuan penelitian, manfaat penelitian, batasan masalah, dan sistematika penulisan skripsi.
BAB 2 LANDASAN SKRIPSI
homogen, orde persamaan diferensial sistem persamaan diferensial, model epidemi SEIV, penyakit polio, titik kesetimbangan (ekuilibrium), nilai eigen dan vaktor eigen, kriteria routh-hurwitz, kriteria kestabilan, maple.
BAB 3 METODE PENELITIAN
Bab ini berisi tentang metode-metode yang digunakan dalam penelitian untuk memecahkan masalah yang meliputi ruang lingkup penelitian, metode pengumpulan data, perumusan masalah, analisis dan pemecahan masalah, serta penarikan kesimpulan.
BAB 4 HASIL PENELITIAN DAN PEMBAHASAN
Berisi tentang konstruksi model matematika untuk penyakit polio, titik kesetimbangan, analisis kestabilan, hasil simulasi model dengan software Maple.
BAB 5 PENUTUP
Bab ini dikemukakan simpulan dari pembahasan dan saran yang berkaitan dengan simpulan.
3. Bagian akhir skripsi
8 BAB 2
TINJAUAN PUSTAKA
2.1 Persamaan Differensial
Persamaan differensial adalah persamaan matematika untuk fungsi satu variabel atau lebih yang menghubungkan nilai fungsi itu sendiri dan turunannya dalam berbagai orde. Selain itu, persamaan diferensial juga didefinisikan sebagai persamaan yang memuat satu atau beberapa turunan fungsi yang tak diketahui (Waluya, 2006: 1). Menurut peubah bebas, persamaan diferensial dapat dibedakan menjadi dua macam yaitu persamaan differensial biasa dan parsial sedangkan persamaan differensial dilihat dari bentuk fungsi atau pangkatnya juga dibedakan menjadi dua yaitu persamaan differensial linear dan persamaan differensial non linear.
Persamaan diferensial biasa adalah persamaan yang mengandung satu atau beberapa turunan dari variabel tak bebas terhadap satu variabel bebas. Persamaan diferensial parsial adalah persamaan yang mengandung turunan parsial dari variabel tak bebas terhadap dua variabel bebas atau lebih. Berikut ini adalah beberapa contoh persamaan diferensial.
(1) y 4y 0 merupakan persamaan diferesial biasa,orde satu (2) y y 2y 0 merupakan persamaan diferensial biasa,orde dua
(3) 0
merupakan persamaan diferensial parsial,orde dua
(4) x y
y u x u
2.2 Persamaan Diferensial Linear dan Tak Linear
Klasifikasi persamaan diferensial dilihat dari bentuk fungsi atau pangkatnya juga dibedakan menjadi dua yaitu persamaan diferensial linear dan persamaan diferensial non linear
Definisi 2.1
Diberikan persamaan diferensial biasa
, F dikatakan linear dalam variabel . Definisi serupa juga berlaku untuk persamaan diferensial parsial. Jadi secara umum persamaan diferensial biasa orde n diberikan dengan
Persamaan yang tidak dalam bentuk tersebut merupakan persamaan tak linear (Waluya, 2006).
Contoh:
(1) merupakan persamaan diferensial linear
(2) merupakan persamaan diferensial
tak linear, karena suku dan 2.3 Solusi Persamaan Diferensial
Definisi 2.2
Diberikan persamaan diferensial
, dx
f t x
dt (2.1)
, , ,..., n 0
F t y y y y y, ,..., yn
1
0 1 ...
n n
n
Dimana f adalah fungsi dalam dua variabel yang diberikan. Sebarang fungsi terturunkan x t yang memenuhi persamaan ini untuk semua t dalam suatu interval disebut solusi.(Waluya, 2006)
2.4 Persamaan Diferensial Linear Homogen dan Tak Homogen Definisi 2.3
Persamaan diferensial linear (PDL)
x a t x g t (2.2)
Dengan a t dan g t adalah fungsi dari waktu t. Pada saat a t a dengan a adalah konstanta, maka a t disebut koefisen dari PDL. Jika g t 0maka persamaan (2.2) disebut PDL Homogen dan jika g t 0, disebut PDL tak homogen (Waluya, 2006).
2.5 Orde Persamaan Diferensial Definisi 2.4
Orde dari persamaan diferensial adalah derajat atau pangkat tertinggi dari turunan yang muncul dalam persamaan. Secara umum persamaan diferensial berorde n dapat dituliskan sebagai
'
, ,..., n 0
F t u t u t
Persamaan di atas menyatakan relasi antara variabel bebas dan nilai-nilai dari fungsi u t' ,...,un t (Waluya, 2006:4).
' 2.5.1 Persamaan Diferensial Biasa Orde Satu Diberikan bentuk persamaan diferensial biasa
, dx
f t x dt
Dimana f adalah fungsi dalam dua variabel, sembarang fungsi terturunkan x t yang memenuhi persamaan itu untuk semua t disebut solusi persamaan diferensial biasa orde satu.
Contoh:
Tentukan solusi umum dari persamaan diferensial berikut ini:
4 2
2.5.1.1 Persamaan differensial eksak
Definisi 2.5
Persamaan diferensial orde satu berbentuk
, , 0
M x t dt N x t dx , (2.3)
Persamaan (2.3) disebut persamaan eksak apabila f x t, Csehingga
, , ,
df x t M x t dt N x t dx (2.4)
Dari definisi dan hubungan (2.4) terlihat bahwa df x t, 0.
Dengan mengintegralkan ini diperoleh solusi umum persamaan diferensial (PD) yaitu f x t, C. Selanjutnya dari definisi total, terlihat bahwa
,
2
Jika f memiliki turunan parsial kedua yang kontinu maka
M N
x t (2.7)
Syarat (2.7) persamaan diferensial (2.3) dikatakan eksak. Juga syarat cukup , sehingga hubungan (2.3) dapat dipergunakan untuk menentukan f x t, C yang merupakan solusi umum untuk PD (2.3) (Supriyono, 2012: 14).
Disisi lain df M x t, x 2.5.1.2 Faktor Integrasi
Definisi 2.6
Misalkan PD : M x t dt, N x t dx, 0 tidak eksak.
Fungsi x t, sehingga x t M x t dt, , x t N x t dx, , 0 PD eksak, ,
x t disebut faktor integrasi (Waluya, 2006).
Perhatikan langkah untuk menentukan faktor integrasi pada
M N
sekarang kita tinjau beberapa kasus.
g t dt
e
Diperoleh faktor integrasi e g t dt
Contoh:
Perhatikan PD: 2
0
Jadi faktor integrasi pada PD di atas adalah
1 M N Tentukan faktor integrasinya!
2
Jadi faktor integrasi untuk PD di atas adalah 4
4
Dengan substitusi y xt diperoleh
1
3 xt
3 g y y
Jadi faktor integrasi PD di atas adalah
3
Berikut ini contoh penerapan faktor integrasi untuk mencari solusi umum PD orde satu.
Contoh:
Tentukan solusi dari persamaan diferensial biasa linear orde satu dari dx Selanjutnya kedua ruas kita kalikan dengan e t
t t 2.6 Sistem Persamaan Differensial
Sistem persamaan differensial adalah suatu persamaan differensial bentuk sebagai berikut:
)
Sistem persamaan differensial adalah gabungan dari n buah persamaan differensial dengan n buah fungsi tak diketahui, dalam hal ini, n merupakan bilangan bulat positif 2. Sistem persamaan differensial juga dibedakan menjadi dua yaitu sistem persamaan differensial linear dan tak linear.
Sistem persamaaan diferensial linear adalah persamaan yang terdiri dari lebih dari satu persamaan yang saling terikat. Sistem dari dua persamaan diferensial dengan dua fungsi yang tak diketahui berbentuk.
t penyelesaian eksplisit jika koefisien a11,a12,a21, dana22 semuanya konstanta. Sistem persamaan diferensial linear dengan n buah fungsi-fungsi yang tak
Atau secara singkat:
Sistem persamaan yang terdiri dari n buah persamaan differensial tak linear dengan n buah fungsi tak diketahui. Bentuk umum sistem persamaan differensial tak linear dapat ditulis:
) kualitatif dibanding kuantitatif (Waluya, 2006: 159).
2.7 Pemodelan Matematika
Pemodelan matematika merupakan bidang matematika yang berusaha untuk mempresentasi dan menjelaskan sistem-sistem fisik atau problem pada dunia real dalam pernyataan matematik, sehingga diperoleh pemahaman dari dunia real ini menjadi lebih tepat. Representasi matematika yang dihasilkan dari proses ini dikenal sebagai model matematika. Kontruksi, analisis dan penggunaan model matematika dipandang sebagai salah satu aplikasi matematika yang paling penting.
2.8 Pendekatan Pada Pemodelan Matematika
Perlu diketahui bahwa terdapat perbedaan pendekatan pemodelan
matematika dalam memformulasikan model matematika. Terdapat beberapa jenis-jenis model matematika yang meliputi model empiris, model simulasi, model stokastik dan deterministik.
a. Model Empiris
Pada model empiris, data yang berhubungan dengan problem menentukan peran yang penting. Dalam pendekatan ini, gagasan yang utama adalah mengkonstruksi formula (persamaan) matematika yang dapat menghasilkan grafik yang terbaik untuk mencocokan data.
b. Model Simulasi
Dalam pendekatan ini program komputer dituliskan didasarkan aturan-aturan. Aturan-aturan ini dipercaya untuk membentuk bagaimana suatu proses atau fenomena akan berjalan terhadap waktu dalam kehidupan nyata. Program komputer ini dijalankan terhadap waktu sehingga implikasi interaksi dari berbagai variabel dan komponen yang dikaji dan diuji.
c. Model Deterministik dan Stokastik
awal yang sesuai, persamaan differensial dapat diselesaikan untuk memprediksi perilaku sistem model.
Dalam model deterministik, variasi random diabaikan. Dengan kata lain persamaan ini digunakan untuk menyatakan problem dunia nyata yang diformulasikan berdasarkan pada hubungan dasar faktor-faktor yang terlibat dalam problem ini (Widowati & Sutimin, 2007:1-2).
2.9 Tahap Pemodelan
Tahapan mencari solusi permasalahan kehidupan sehari-hari maupun pada ilmu-ilmu lain dengan menggunakan bantuan matematika diberikan sebagai berikut.
1. Pemodelan matematika untuk menyelesaikan masalah kehidupan sehari-hari diawali dengan mengenali masalah tersebut terlebih dahulu yaitu melalui beberapa langkah yaitu identifikasi masalah, lambang, satuan dan variabel atau konstanta serta menentukan besaran yang terlibat, selain itu dalam proses penterjemahan masalah selalu terdapat hukum yang mengendalikan.
2. Menentukan variabel atau konstanta yang penting dan merinci keterkaitan antara variabel atau konstanta tersebut sehingga dapat disusun model matematika. Model matematika yang terbentuk harus bebas satuan.
3. Dengan memanfaatkan teori-teori dalam matematika dapat diperoleh solusi model.
2.10 Model Epidemi SEIV
Model epidemi memodelkan epidemi dalam populasi terbuka. Hal dasar dalam model epidemi adalah jika penyebab penyakit menjangkiti satu individu dalam suatu populasi, maka pertanyaan berikutnya (Diekmann, 2000):
(1) apakah hal tersebut menyebabkan epidemi
(2) jika menyebabkan epidemi, dengan kecepatan berapa banyaknya individu yang terinfeksi bertambah
(3) apakah populasi pada akhirnya akan terinfeksi seluruhnya.
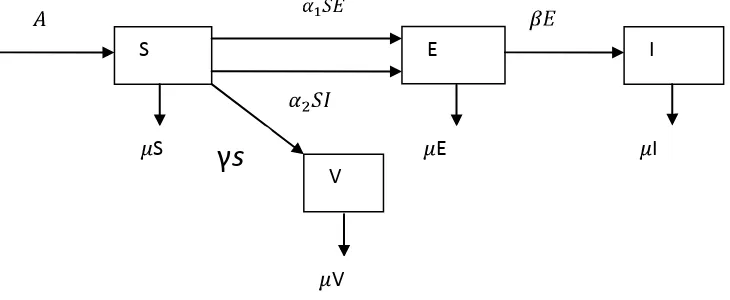
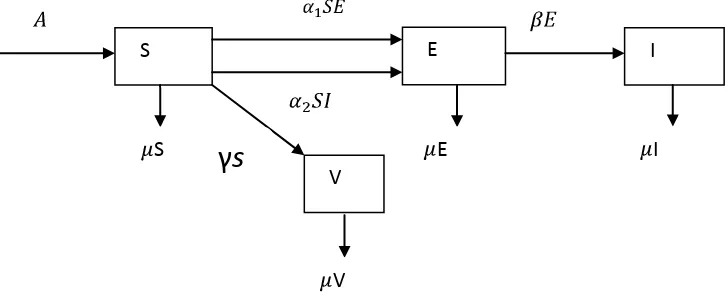
Pembentukan model epidemi SEIV didasari oleh adanya penyakit menular yang memiliki periode laten. Misal, populasi yang diberikan dibagi ke dalam empat kelas, yakni kelas populasi rentan (susceptibles), kelas populasi laten (exposed), kelas populasi terinfeksi (infectious), dan kelas populasi vaksinasi (Vaccination). Perhatikan diagram alir perubahan keadaan suatu populasi akibat adanya penyebaran penyakit pada Gambar 2.1(Agarawal & Bhadauria, 2011).
Gambar 2.1 Diagram Transfer Penyebaran Penyakit Polio.
S E I
S E I
V V
Dari Gambar 2.1 diperoleh model dalam bentuk sistem persamaan diferensial berikut.
2.11 Penyakit Polio
Polio adalah penyakit yang sangat menular yang disebabkan oleh virus. Ini menyerang sistem saraf, dan dapat menyebabkan kelumpuhan total dalam hitungan jam. Individu yang terkena polio mempunyai gejala demam disertai lumpuh layuh mendadak dan pada pemeriksaan tinja ditemukan virus polio.
2.11.1 Etiologi
Penyakit Polio disebabkan oleh infeksi polio virus yang berasal dari genus Enterovirus dan family Picorna viridae. Virus ini menular melalui kotoran(feses) atau sekret tenggorokan orang yang terinfeksi. Virus polio masuk melalui ludah sehingga menyebabkan infeksi. Hal ini dapat terjadi dengan mudah bila tangan terkontaminasi atau benda-benda yang terkontaminasi dimasukkan ke dalam mulut. Jenis – jenis Polio antara lain :
1. Polio Non-Paralisis
Polio non-paralisis menyebabkan demam, muntah, saki perut, lesu dan sensitif. Terjadi kram otot pada leher dan punggung, otot terasa lembek jika disentuh.
2. Polio Paralisis Spinal
Strain poliovirus ini menyerang saraf tulang belakang, menghancurkan sel tanduk anterior yang mengontrol pergerakan pada batang tubuh dan otot tungkai. Meskipun strain ini dapat menyebabkan kelumpuhan permanen, kurang dari satu penderita dari 200 penderita akan mengalami kelumpuhan. Kelumpuhan paling sering ditemukan terjadi pada kaki. Setelah poliovirus menyerang usus, virus ini akan diserap oleh kapiler darah pada dinding usus dan diangkut seluruh tubuh. Poliovirus menyerang saraf tulang belakang dan neuron motor yang mengontrol gerak fisik. Pada periode inilah muncul gejala seperti flu. Namun, pada penderita yang tidak memiliki kekebalan atau belum divaksinasi, virus ini biasanya akan menyerang seluruh bagian batang saraf tulang belakang dan batang otak. Infeksi ini akan mempengaruhi sistem saraf pusat menyebar sepanjang serabut saraf. Seiring dengan berkembang biaknya virus dalam sistem saraf pusat, virus akan menghancurkan neuron motor. Neuron motor tidak memiliki kemampuan regenerasi dan otot yang berhubungan dengannya tidak akan bereaksi terhadap perintah dari sistem saraf pusat. Kelumpuhan pada kaki menyebabkan tungkai menjadi lemas kondisi ini disebut acute flaccid paralysis (AFP). Infeksi parah pada sistem saraf pusat dapat menyebabkan kelumpuhan pada batang tubuh dan otot pada toraks (dada) dan abdomen (perut), disebut quadriplegia.
3. Polio Bulbar
pergerakan bola mata saraf trigeminal dan saraf muka yang berhubungan dengan pipi, kelenjar air mata, gusi, dan otot muka, saraf auditori yang mengatur pendengaran, saraf glossofaringeal yang membantu proses menelan dan berbgai fungsi di kerongkongan; pergerakan lidah dan rasa; dan saraf yang mengirim sinyal ke jantung, usus, paru-paru, dan saraf tambahan yang mengatur pergerakan leher (Wilson, 2001 ).
Ketiga jenis tersebut bisa menyebabkan kelumpuhan. Tipe 1 adalah tipe yang paling mudah di isolasi , diikuti tipe 3, sedangkan tipe 2 paling jarang diisolasi. Tipe yang sering menyebabkan wabah adalah tipe 1, sedangkan kasus yang dihubungkan dengan vaksin yang disebabkan oleh tipe 2 dan tipe 3.
2.11.2 Penularan
Virus polio masuk melalui mulut dan hidung, berkembang biak di dalam tenggorokan dan saluran pencernaan, diserap dan disebarkan melalui system pembuluh darah dan pembuluh getah bening. Virus ini dapat memasuki aliran darah dan mengalir ke system saraf pusat menyebabkan melemahnya otot dan kadang kelumpuhan (paralisis).
2.11.3 Gejala dan tanda
Virus polio masuk kedalam tubuh manusia melalui mulut dan berkembang biak ditenggorokan dan usus. Berkembang biak selama 4 sampai 35 hari, kemudian akan dikeluarkan melalu tinja selama beberapa minggu kemudian.
Gejala awal biasanya terjadi selama 1-4 hari, yang kemudian menghilang. Gejala lain yang biasanya muncul adalah nyeri tenggorokan, rasa tidak enak diperut disertai demam ringan, lemas dan nyeri kepala ringan.
Gejala klinis yang mengarah pada serangan virus polio adalah adanya demam dan kelumpuhan akut, kaki biasanya lemas tanpa gangguan saraf perasa, terutama terjadi pada tungkai bawah, asimetris dan dapat menetap selamanya yang bisa disertai dengan segala nyeri kepala dan muntah. Biasanya terdapat kekakuan pada leher dan punggung setelah 24 jam.
Kelumpuhan sifatnya mendadak dan layuh, sehingga sering dihubungkan dengan lumpuh layu akut, (AFP, acud flacide paralysis)menyerang satu tungkai lemas sampai tidak ada gerakan. Otot biasanya mengecil, reflex fisiologis dan reflex patologis negative.
WHO mengatakan bahwa kelumpuhan dapat disebabkan oleh lebih dari 100 macam penyebab. Namun di Indonesia sampai saat ini di laporkan disebebkan oleh 23 penyakit. Sebanyak 60%-70% kelumpuhan disebabkan oleh Gulain Baree Syndrome (GBS). Untuk membuktikan apakah kelumpuhan disebabkan oleh polio
Diagnosis banding yang mirip dengan polio adalah Mielitis Transversa, yaitu tentang peradangan sum-sum tulang belakang . kumpulan layu biasanya menyerang kedua tungkai, bersifat akut, dan lemas flefleksi fisiologi dan reflex patologis negative, bisa disertai dengan gangguan buang air kecil dan besar.
Diagnosis banding lainnya adalah GBS, dimana terjadi demam disertai gejala khas kelumpuhan yang berangsur dari ujung jari naik keatas dengan batas tegas bila sudah sampai pergelangan membentuk gambaran seperti sarung tangan/kaki (glove phenomenon). Kelumpuhan menyerang kedua tungkaim, reflex fisiologis negative sedangkan reflex patologi positif bila kelumpuhan menyerang otot saluran pernafasan, maka penderita dapat mengalami sesak nafas sampai meninggal.
2.11.4 Vaksinasi
Pencegahan dan pemberantasan virus polio sebenaraya sangat mudah karena sudah ada vaksin yang sangat bagus dan efektif yaitu vaksin polio oral (OPV) dan vaksin polio inaktif (IPV), dan hanya manusia satu-satunya reservoire untuk penyebaran virus polio. Penyebaran virus polio melalui fecal-oral. Anak yang terinfeksi virus polio mengekskresi virus polio melalui feces selama 14 hari, tetapi dapat juga ditemukan sampai 30 hari meskipun kemungkinannya sangat kecil. OPV biasa digunakan di negara berkembang karena harganya terjangkau dan mudah pemberiannya, sedangkan IPV biasa digunakan di negara maju karena efektivitasnya tinggi, tidak menimbulkan masalah kelumpuhan pada penerima vaksin (WHO, 2008).
tajam. Saat ini upaya imunisasi di banyak negara dibantu oelh Rotary International UNICEF dan WHO untuk mempercepat eradikasi global polio (Widoyono, 2008).
Dalam World Health Assembly tahun 1998 yang diikuti oleh sebagian besar negara di penjuru dunia dibuat kesepakatan untuk melakukan Eradikasi Polio (Erapo) tahun 2000, artinya dunia bebas polio tahun 2000. Program Eropa pertama yang dilakukan adalah
1. Melakukan cakupan imunisasi yang tinggi dan menyeluruh
2. Pekan Imunisasi Nasional yang telah dilakukan Depkes tahun 1995, 1996, dan 1997. Pemberian imunisasi polio yang sesuai dengan rekomendasi WHO adalah diberikan sejak lahir sebanyak 4 kali dengan interval 6-8 minggu. Kemudian diulang usia 1½ tahun, 5 tahun, dan usia 15 tahun
3. Survailance Acute Flaccid Paralysis atau penemuan penderita yang dicurigai lumpuh layuh pada usia di bawah 15 tahun harus diperiksa tinjanya untuk memastikan karena polio atau bukan.
4. Melakukan Mopping Up, artinya pemberian vaksinasi massal di daerah yang ditemukan penderita polio terhadap anak di bawah 5 tahun tanpa melihat status imunisasi polio sebelumnya (WHO, 2005).
2.12 Titik Kesetimbangan (Ekuilibrium) Definisi 2.7
Titik n
R
x disebut titik ekuilibrium x f(x) jika f(x) 0 (Perko, 1991). Definisi 2.8
(a) Stabil lokal jika untuk setiap 0 terdapat d 0sedemikian hingga untuk setiap solusi x(t) yang memenuhi x(t0) x berlaku x(t) x untuk setiap t t0.
(b) Stabil asimtotik lokal jika titik ekuilibrium n
R
(c) Tidak stabil jika titik ekuilibrium n
R
x tidak memenuhi a (Wiggins, 2003). Definisi 2.9
(a) Jika semua bagian real nilai eigen dari matriks Jf(x) bernilai negatif, maka titik ekuilibrium x dari Sistem nonlinear x f(x) stabil asimtotik lokal. (b) Jika terdapat paling sedikit satu nilai eigen matriks Jf(x) yang bagian realnya
positif, maka titik ekulibrium x dari sistem nonlinear x f(x) tidak stabil (Olsder, 1994).
2.13 Nilai Eigen dan Vektor Eigen
Misalkan A adalah matriks n x n, maka suatu vektor taknol x di dalam n disebut vektor eigen dari A, jika untuk suatu skalar λ, yang disebut nilai eigen dari
A, berlaku:
Ax = λx. (2.13)
Vektor x disebut vektor eigen yang bersesuaian dengan nilai eigen λ. Untuk mencari nilai eigen dari matriks A yang berukuran n x n, maka persamaan (2.13) dapat dituliskan sebagai berikut:
(λI - A) x = 0. (2.14)
Dengan I matriks identitas. Persamaan (2.13) mempunyai solusi tak nol jika dan hanya jika,
det(λI - A) = 0. (2.15)
Persamaan (2.15) disebut persamaan karakteristik (Anton, 1995: 277). 2.14 Kriteria Routh-Hurwitz
Teorema 2.2
Jika pembuat nol pada persamaan
n
Mempunyai bagian real negatif, maka
0
Selanjutnya tanpa mengurangi keumuman diambil a0 positif sehingga seluruh koefisien dari polinomial (2.16) bertanda sama, sehingga dapat dibentuk
Teorema 2.3
Pembuat nol dari polinomial (2.16) mempunyai bagian real negatif jika dan hanya jika pertidaksamaan (2.17) dipenuhi dan
0 Matriks Hurwitz untuk persamaan (2.16) didefinisikan sebagai matriks bujur sangkar berukuran n x n yang berbentuk sebagai berikut.
n dibentuk dari matriks Hurwitz (2.19), didefinisikan sebagai berikut.
n
Berikut ini teorema yang menjamin pembuat nol Polinomial (2.16) mempunyai bagian real negatif.
Teorema 2.5
Pembuat nol dari Polinomial (2.16) mempunyai bagian real negatif jika dan hanya jika Pertidaksamaan (2.17) dipenuhi dan
0 Matriks Hurwitz dari polinomial tersebut adalah
3
Dari matriks H diperoleh
)
Agar semua akar polinomial tersebut mempunyai bagian real negatif maka harus memenuhi:
2.15 Kriteria Kestabilan
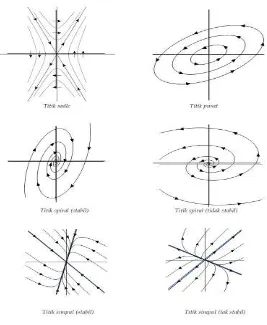
Tabel 2.1 menunjukan bahwa sistem akan stabil asimtotis jika kedua nilai eigen matriks Jacobian J(x) berupa bilangan real negatif atau bilangan kompleks dengan bagian real bernilai negatif. Jika salah satu atau kedua nilai eigen berupa bilangan real positif atau bilangan kompleks dengan bagian real bernilai positif maka sistem akan tidak stabil.
Tipe kestabilan dari titik kesetimbangan pada Tabel 2.1 dapat dilihat dengan mengamati trayektori pada bidang fase. Gambar 2.2 menunjukan contoh trayektori dari tipe kestabilan yang telah disajikan pada Tabel 2.1.
Tabel 2.1 Kriteria kestabilan berdasarkan nilai eigen
Nilai eigen Nama Kestabilan
real, tidak sama, bertanda sama
simpul
stabil asimtotik: semuanya negatif tidak stabil: semuanya positif real, tidak sama,
berlawanan tanda
sadel tidak stabil
real, sama simpul
stabil asimtotik: semuanya negatif tidak stabil: jika semuanya positif kompleks konjugate
bukan imajiner murni
spiral
Gambar 2.2 Tipe kestabilan dari titik kesetimbangan
Gambar 2.2 menunjukan titik pusat (kanan atas), titik sadel (kiri atas), titik spiral stabil (kanan bawah) dan titik spiral yang tak stabil (kiri bawah).
2.16 Maple
Maple sering digunakan untuk keperluan penyelesaian permasalahan persamaan diferensial dan visualisasinya, karena Maple memiliki kemampuan menyederhanakan persamaan, hingga suatu solusi persamaan diferensial dapat dipahami dengan baik. Keunggulan lain dari Maple untuk aplikasi persamaan diferensial adalah kemampuan melakukan animasi grafik dari suatu fenomena gerakan yang dimodelkan ke dalam persamaan diferensial yang memiliki nilai awal dan syarat batas (Kartono, 2001).
Pernyataan yang sering digunakan untuk keperluan menyelesaikan permasalahan persamaan diferensial antara lain: diff digunakan untuk mendiferensialkan (menurunkan) suatu fungsi, dsolve digunakan untuk menyelesaikan persamaan diferensial, evalf memberikan nilai numeric dari suatu persamaan, dan simplify digunakan untuk menyederhanakan suatu persamaan. Namun tentu saja pernyataan-pernyataan awal seperti restart dan deklarasi variabel/konstanta yang diperlukan tidak boleh diabaikan. Untuk membuat grafik pada Maple digunakan perintah plot, plot2d, plot3d, tergantung dimensi dari pernyataan yang dimiliki. Untuk membuat gerakan animasi digunakan perintah animate3d (Kartono, 2001).
42 BAB 3
METODE PENELITIAN
Metode penelitian yang dilakukan dalam penelitian ini meliputi beberapa tahap sebagai berikut:
3.1 Menentukan Masalah
Dalam tahap ini dilakukan pencarian sumber pustaka dan memilih bagian dalam sumber pustaka tersebut yang dapat dijadikan sebagai permasalahan yang akan dikaji.
3.2 Merumuskan Masalah
Tahap ini dimaksudkan untuk merumuskan permasalahan dengan jelas sehingga mempermudah pembahasan, permasalahan yang dibahas adalah:
(1) bagaimana model matematika epidemi SEIV penyebaran penyakit polio pada populasi tak konstan,
(2) bagaimana menentukan titik kesetimbangan dan analisis kestabilan model matematika penyebaran penyakit polio pada populasi tak konstan, dan
(3) bagaimana simulasi model dan interpretasi perilaku model matematika penyebaran penyakit polio pada populasi tak konstan menggunakan program Maple.
3.3 Studi Pustaka
makalah, dsb. Setelah sumber pustaka terkumpul dilanjutkan dengan penelaahan dari sumber pustaka tersebut. Pada akhirnya sumber pustaka ini dijadikan landasan untuk menganalisis permasalahan.
3.4 Analisis dan Pemecahan Masalah
Dari berbagai sumber pustaka yang menjadi bahan kajian, diperoleh suatu pemecahan masalah diatas. Selanjutnya dilakukan langkah-langkah pemecahan masalah sebagai berikut:
(1) Menjelaskan bagaimana model matematika epidemi SEIV penyebaran penyakit polio pada populasi tak konstan.
(2) Menjelaskan bagaimana menentukan titik kesetimbangan dan analisis kestabilan model matematika penyebaran penyakit polio pada populasi tak konstan.
(3) Menjelaskan bagaimana simulasi model dan interpretasi perilaku model matematika penyebaran penyakit polio pada populasi tak konstan menggunakan program Maple.
Dalam proses pemecahan masalah tersebut, diterangkan berbagai cara menyelesaikan masalah dengan pendekatan yang ditetapkan sebelumnya berdasarkan tinjauan pustaka yang sudah ada.
3.5 Penarikan Kesimpulan
44 BAB 4
HASIL DAN PEMBAHASAN
4.1 Model Matematika Penyakit Polio
Model yang diturunkan dan dibahas pada bab ini adalah model SEIV (Susceptibles, Exposed, Infectious, Vaccination) penyakit polio pada populasi tak konstan dengan memperhatikan fakta- fakta dan asumsi-asumsi.
4.1.1 Fakta-fakta
(1) Informasi mengenai masa inkubasi pada penyebaran penyakit polio diperoleh dari Paul (2004) dan Kunoli (2013). Dalam Paul (2004) dan Kunoli (2013) disebutkan masa inkubasi penyakit polio umumnya 7-14 hari.
(2) Informasi mengenai individu yang terinfeksi polio tidak dapat sembuh dan tidak mematikan diperoleh dari Wilson(2001). Disebutkan bahwa individu yang terjangkit polio jenis paralisis spinal tidak akan sembuh disebabkan vaksinasi hanya dapat dilakukan sebelum tertular. Strain poliovirus jenis ini menyerang saraf tulang belakang yang dapat menyebabkan kelumpuhan pada kaki secara permanen. Akan tetapi polio jenis ini tidak mematikan karena tidak menyerang organ vital.
4.1.2 Asumsi-asumsi
Dalam pembentukan model ini dibatasi oleh beberapa asumsi. Asumsi-asumsi yang digunakan dalam model penyakit polio sebagai berikut.
(1) Jumlah populasi diasumsikan cukup besar.
(3) Penyakit polio memiliki masa inkubasi.
(4) Individu yang terinfeksi tidak dapat sembuh dan tidak mematikan.
Selanjutnya, asumsi yang digunakan terhadap vaksinasi dalam model ini adalah sebagai berikut.
(1) Vaksin hanya diberikan pada individu yang baru lahir.
(2) Keampuhan vaksinasi adalah 100%. Hal tersebut berarti setiap individu yang telah mendapatkan vaksin akan kebal dari penyakit.
(3) Kekebalan yang terjadi karena vaksin bersifat permanen. Hal tersebut berarti individu yang mendapat vaksin tidak dapat terinfeksi oleh penyakit yang sama sampai waktu yang tidak terbatas.
(4) Biaya vaksin tidak diperhatikan dalam model sehingga pemberian vaksin diasumsikan tidak terkendala oleh faktor biaya.
Dari asumsi-asumsi dan fakta-fakta di atas, pembentukkan model matematika untuk penyakit polio pada populasi tak konstan dapat dibatasi.
4.1.3 Pembentukkan Model Matematika
Pembentukan model epidemi SEIV didasari oleh adanya penyakit menular yang memiliki periode laten. Populasi yang diberikan dibagi ke dalam empat kelas yakni kelas sub populasi rentan (susceptibles), kelas sub populasi laten (exposed), kelas sub populasi terinfeksi (infectious), dan kelas sub vaksinasi(Vaccination).
Tabel 4.1Daftar Variabel-variabel
No Variabel Keterangan
1. S(t)
Banyak individu yang rentan terinfeksi penyakit pada waktu t
2. E(t)
Banyak individu terinfeksi pada waktu t
3. I(t)
Banyak individu yang terinfeksi penyakit pada waktu t
4. V(t)
Banyak individu yang mendapat vaksinasi pada waktu t
Tabel 4.2Daftar Parameter-parameter
No Parameter Keterangan Syarat
1. µ Laju kematian alami
2.
Probabilitas penularan penyakit akibat kontak dengan individu
laten
3.
Probabilitas penularan penyakit akibat kontak dengan individu
terinfeksi
4.
5.
Laju transfer individu dari kelas laten menjadi kelas terinfeksi
6. A Laju pertambahan populasi A>1
Secara skematis proses penyebaran penyakit polio dengan vaksinasi dalam suatu populasi dapat disajikan dalam diagram transfer pada
Gambar 4.1 Diagram Transfer Penyebaran Penyakit polio. Model Matematika
Model matematika yang dibentuk merupakan suatu sistem persamaan diferensial diberikan di bawah ini
(4.1)
S E I
S E I
V V
4.2 Titik Kesetimbangan
Dari sistem (4.1) dapat dicari titik kesetimbangannya, sebagai berikut:
Persamaan ketiga dari sistem (4.2) dapat menjadi
(4.3) Substitusikan persamaan (4.3) kedalam persamaan kedua dari sistem (4.2)
(4.4)
Untuk kasus E=0.
Persamaan (4.3) dapat diperoleh
Persamaan pertama dari sistem (4.2) dapat diperoleh
Persamaan keempat dari sistem (4.2) dapat diperoleh
Dengan demikian diperoleh titik kesetimbangan bebas penyakit yaitu
Selanjutnya, untuk menentukan titik kesetimbangan endemik, diasumsikan . Misalkan merupakan titik kesetimbangan endemik, sehingga sistem (4.1) menjadi
Untuk kasus , dari persamaan (4.4) diperoleh (4.6) Penyederhanaan persamaan (4.6)
(4.7)
Persamaan keempat dari sistem (4.5) dapat menjadi .
Maka diperoleh
Persamaan ketiga dari sistem (4.5) dapat menjadi (4.8) Substitusikan persamaan (4.8) ke persamaan pertama dari sistem (4.5)
Maka diperoleh
(4.9)
Substitusikan persamaan (4.7) ke persamaan (4.8) Maka diperoleh
Jadi diperoleh titik kesetimbangan endemik dengan
4.3 Angka Rasio ReproduksiDasar
Untuk menentukan angka rasio reproduksi dasar yaitu dengan mengasumsikan . Berdasarkan titik kesetimbangan endemik diperoleh
Didefinisikan
4.4 Titik Kestabilan
Analisis kestabilan ditentukan berdasarkan nilai eigen dari matriks Jacobian yang diperoleh melalui metode linearisasi. Matriks Jacobian dari sistem (4.1) adalah sebagai berikut.
Dengan
4.4.1 Analisis Kestabilan di Titik Kesetimbangan Bebas Penyakit Untuk titik kesetimbangan bebas penyakit
Mencari nilai eigen dari matriks tersebut adalah
(4.10) Dari persamaan (4.10) diperoleh nilai eigen sebagai berikut:
Diperoleh:
Berdasarkan nilai-nilai eigen tersebut terlihat bahwa bagian real dari nilai eigen
2
Ditunjukan
Jelas
Jadi
Untuk menunjukkan nilai 4 0, maka
Ditunjukkan
Dipunyai
+ 1− 1 + + 2
1 + + 2
+ 1− 1 + + 2
Jadi 1 0, 2 0,dan 3 0untuk setiap kondisi R0, sedangkan nilai 0
4.4.2 Analisis Kestabilan di Titik Kesetimbangan Endemik
Untuk titik kesetimbangan endemik dengan
, , dan .
Diperoleh
Mencari nilai eigen dari matriks tersebut adalah
Karena nilai eigennya tidak dapat dicari secara langsung, untuk itu akan dengan menggunakan kriteria Ruth Hurwizt. Persamaan karakteristik dari matrik J*( adalah
dengan
Ditunjukkan mempunyai akar-akar dengan bagian real
negatif yaitu dengan menunjukkan :
Diasumsikan: 1)
2)
Jadi Diperoleh:
Jelas
Ditunjukkan
Jelas
Ditunjukan Dipunyai
Diperoleh Ditunjukkan Jelas
Diperoleh Ditunjukkan Jelas
Diperoleh
Ditunjukkan
Jelas
Karena
Jadi berdasarkan kriteria Routh Hurwisz untuk polinom pangkat 3 diperoleh
simpulan bahwa mempunyai akar-akar dengan bagian
real negatif, maka titik kesetimbangan stabil asimtotik lokal. Teorema 2
1. Jika maka titik ekuilibrium stabil asimtotik lokal. 2. Jika maka titik ekuilibrium tidak stabil.
3. Jika , dan maka titik ekuilibrium stabil asimtotik lokal.
4.5 Hasil Simulasi
Simulasi dilakukan dengan memberikan nilai-nilai untuk masing-masing parameter sesuai dengan kondisi dengan teorema yang telah diberikan di atas.Simulasi ini diberikan untuk memberikan gambaran geometris dari teorema eksistensi dan kestabilan dari titik-titik ekuilibrium model ini.
Berdasarkan penjelasan makna nilai-nilai parameter, nilai laju manusia yang lahir dan mati tiap satuan waktu, menyatakan probabilitas penularan penyakit akibat kontak dengan individu laten, menyatakan probabiltas penularan penyakit akibat kontak dengan individu terinfeksi, menyatakan rata proporsi jumlah dari kelas rentan menjadi kelas vaksinasi, menyatakan rata-rata proporsi jumlah pada masa laten menjadi masa terinfeksi, menyatakan laju pertambahan populasi.
4.5.1 Untuk Model Penyakit di Titik Kesetimbangan Bebas Penyakit
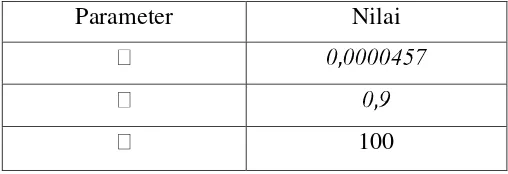
Jika diasumsikan nilai artinya yang diinterpretasikan sebagai waktu rata-rata seseorang berada dalam sistem yang diamati yaitu selama 60 tahun, nilai diperoleh dari jurnal Agarawal & Bhaduria (2011), nilai A= 100 artinya penambahan populasi sejumlah 100 orang tiap harinya.
Nilai-nilai parameter tetap yang diberikan untuk membuat simulasi dari model penyebaran penyakit polio, disajikan dalam Tabel 4.3.
Tabel 4.3. Nilai Parameter tetap untuk Simulasi Model
Parameter Nilai
100
Selanjutnya, peluang seseorang tertular penyaki polio jika seseorang yang rentan mempunyai kontak dengan sebagian populasi laten atau seseorang dari populasi terinfeksi . Nilai-nilai , dan γ diberikan pada tabel 4.4. Selanjutnya, program vaksinasi dilakukan untuk mencegah meluasnya penyakit. Vaksinasi dianggap berhasil jika pada waktu tertentu penyakit akan menghilang dari populasi. Rasio reproduksi dasar dapat digunakan untuk menentukan apakah penyakit tersebut akan menghilang dari populasi. Penyakit akan menghilang dari populasi pada waktu tertentu jika R0 1.
Berikut ini akan dianalisis untuk empat kondisi R0 1 dengan mengubah nilai , dan di titik ekuilibrium bebas penyakit
Tabel 4.4 Titik kesetimbangan , rasio reproduksi dasar R0 . Titik Kestimbangan P0 R0
(3328.3,0,0,2184855.544)
0.72832216 0.00000002 0.00000001 0.03 (2497.14701,0,0,2185686.66)
0.54644941 0.00000002 0.00000001 0.04 (1998.173669,0,0,2186185.634)
0.874452053 0.00000001 0.00000002 0.05 (1665.398188,0,0,2186518.409)
0.729542602 0.00000004 0.00000002 0.06
Sebagai contoh kondisi pada saat diperoleh dengan
mengubah nilai dan sehingga
diperoleh nilai .
b. Grafik E(t) terhadap t
c. Grafik L(t)=I(t) terhadap t
d. Grafik V(t) terhadap t
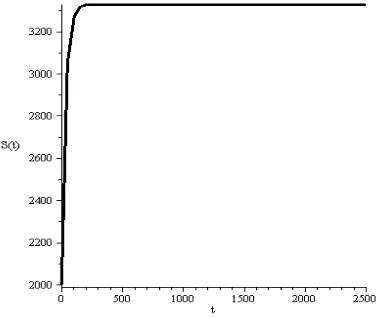
Gambar 4.2 Dinamika populasi S(t), E(t), I(t) dan V(t) terhadap waktu t
Berdasarkan hasil simulasi pada Gambar 4.2 untuk <1. Artinya jumlah individu pada sub populasi S(t) akan bertambah seiring pertambahan populasi susceptibles yang tidak terinfeksi oleh penyakit polio. Jumlah pada sub populasi E(t) akan menuju ke titik kesetimbangan 0 artinya jumlah populasi Exposed yang tertular oleh kelompok Exposed atau infective berkurang, disebabkan karena kelompok manusia Exposed menjadi kelompok manusia infective. Pada sub populasi I(t) kelompok manusia infective semakin lama hilang, ini dapat terjadi ketika tidak ada individu pada kelas Exposed maka semakin lama individu yang menderita sakit berkurang dan hilang karena meninggal karena usia. Pada sub populasi V(t) akan semakin bertambah dikarenakan banyak populasi susceptibles yang divaksinasi. Ini berarti untuk jangka waktu tertentu penyakit polio akan menghilang dalam populasi dikarenakan semua individu akan tervaksinasi. Hal ini berarti tidak terjadi epidemi pada populasi. 4.5.2 Untuk Model Penyakit di Titik Kesetimbangan Endemik
Pada saat nilai R0 1 akan dianalisis untuk empat kondisi dengan memberikan nilai parameter seperti diatas tetapi dengan asumsi dan akan memperlihatkan bahwa untuk jangka waktu yang lama dalam lingkungan atau komunitas tertentu akan selalu ada individu yang terkena penyakit polio.
Berikut ini akan dianalisis untuk empat kondisi R0 1 , dengan mengubah
nilai dan di titik kesetimbangan endemik dengan
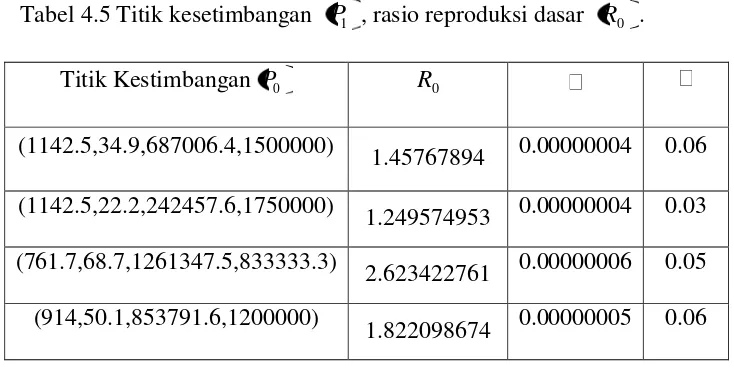
Tabel 4.5 Titik kesetimbangan P1 , rasio reproduksi dasar R0 . Titik Kestimbangan P0 R0
(1142.5,34.9,687006.4,1500000)
1.45767894 0.00000004 0.06 (1142.5,22.2,242457.6,1750000)
1.249574953 0.00000004 0.03 (761.7,68.7,1261347.5,833333.3)
2.623422761 0.00000006 0.05 (914,50.1,853791.6,1200000)
1.822098674 0.00000005 0.06
Sebagai contoh kondisi pada saat pada saat diperoleh dengan
mengubah nilai dan sehingga diperoleh nilai
(1142.5,34.9, 687006.4,1500000)
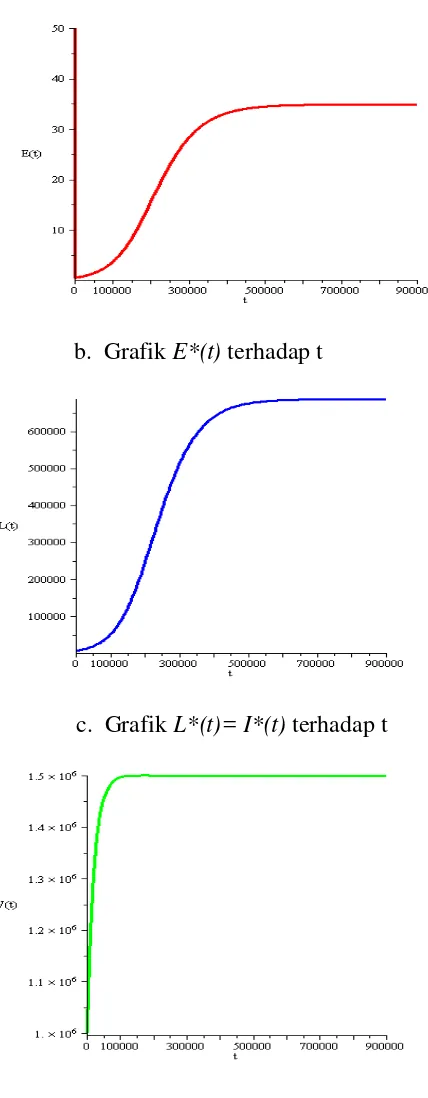
b. Grafik E*(t) terhadap t
c. Grafik L*(t)= I*(t) terhadap t
d. Grafik V*(t) terhadap t
Gambar 4.3 Dinamika populasi S*(t), E*(t), I*(t) dan V*(t) terhadap waktu t
69 BAB 5 PENUTUP
5.1 Simpulan
Dari pembahasan pada bab sebelumnya, dapat disimpulkan bahwa
(1) Model matematika untuk model kestabilan SEIV penyebaran penyakit polio pada populasi tak konstan membentuk sebuah sistem persamaan diferensial yang terdiri dai 4 persamaan, yaitu:
(5.1) (2) Analisis kestabilan penyebaran penyakit polio pada suatu populasi
menghasilkan angka rasio reproduksi dasar yang didefinisikan sebagai . Diperoleh dua titik kesetimbangan yaitu titik
kesetimbangan bebas penyakit polio dan
titik kesetimbangan endemik dengan
. Titik
0
(3) Dinamik dari sistem ini ditentukan oleh beberapa parameter pada R0. Jika
, dan dengan
,maka R0 1 artinya untuk jangka waktu yang lama populasi penyakit polio akan hilang dikarenakan semua individu tervaksinasi dan populasi laten dan terinfeksi hilang (I=0). Sedangkan jika
dan dengan maka R0 1 artinya untuk jangka waktu yang lama populasi penyakit polio akan tetap ada namun jumlahnya lebih kecil daripada populasi yang tervaksinasi (I*<V*).
5.2 Saran
71
DAFTAR PUSTAKA
Agarawal, M & Bhaduria, A.S. 2011. Modeling Spread of Polio with the Role of Vaccination. AAM:Intern. J. Vol.6 ,issue 2:552-571
Anton, H. 1995. Aljabar Linier Elementer. Edisi kelima. (diterjemahan oleh: Silaban, P. dan Susila, I. N.). Jakarta: Erlangga.
Bellomo, N. & L. Preziosi. 1995. Modeling Mathematical Methods and Scientific Computation. Florida: CRC Press.
Conte, S. & C. Boor. 1993. Dasar-Dasar Analisis Numerik Suatu Pendekatan Algoritma. Jakarta: Erlangga.
Diekmann, J.A.P. 2000. Mathematical Epidemology of Infectious Diseases. West Sussex: John Wiley & Sons Ltd.
Gantmacher, F.R. 1959. The Theory of Matrices. New York: Chelsea Publishing Company.
Hanh, W. 1967. Stability of Motion. New York: Springer-Verlag.
Kartono. 2001. Maple untuk Persamaan Diferensial. Yogyakarta: J&J Learning. Kocak, H. & Hole, J. K. 1991. Dynamic and Bifurcation. New York:
Springer-Verlag.
Kunoli, F.J. 2013. Epidemologi penyakit menular. Jakarta: Trans Info Media. Miller, N.Z. 2004. The polio vaccine: a critical assessment of its arcane history,
efficacy, and long-term health-related consequences. USA: Thinktwice Global Vaccine Institute.
Nagle, R.E & E.B. Saff. 1993. Fundamentals of Differential Equation and Boundary Value Problems. New York: Addison-wesley Publishing Company.
Olsder, G.J. 1994. Mathematics System Theory. The Netherlands: Delftse Uitgevers Maatscappij b.v.
Pamuntjak, R.J. & S. Widiarti. 1990. Persamaan Diferensial Biasa. Bandung: ITB. Paul, M.D.E. 2004. Poliomyelitis. Warm Springs : GA 31830.
Suherman. 1993. Strategi Belajar Mengajar Matematika. Jakarta: Universitas Terbuka Depdikbud.
Supriyono. 2012. Persamaan Diferensial Biasa. Semarang: Unnes. Waluya, S.B. 2006. Persamaan Diferensial. Yogyakarta: Graha Ilmu.
WHO. 2005. Framework for national policy makers in OPV-using countries. Geneva.p.l-10.
WHO-SEARO. 2008. Vaccine Preventable DiseaseSurveilance bulletin. Report for Week 38,2008.
Widowati & Sutimin. 2007. Buku Ajar Pemodelan Matematika. Jurusan Matematika Universitas Diponegoro.
Widoyono. 2008. PENYAKIT TROPIS Epidemiologi, Penularan, Pencegahan & Pemberantasannya. Jakarta: Erlangga.
Wiggins, S. 2003. Introduction to Applied Nonlinear Dynamical Systems and Chaos. Second Edition. New York: Springer-Verlag.
Lampiran 1
Lampiran 2