FAKUL
DENGAN R
D
LTAS MAT
IN
PEMADA
RANCANG
MUHA
G
DEPARTEM
TEMATIKA
NSTITUT P
ANAN BILA
GAN BUJUR
AMAD SYA
G54104023
MEN MATE
A DAN ILM
PERTANIA
BOGOR
2008
ATERAL
RSANGKA
AZALI
EMATIKA
MU PENGET
AN BOGOR
AR LATIN
TAHUAN A
R
ABSTRACT
MUHAMAD SYAZALI. Bilateral Matching with Latin Squares. Under the supervision of TONI BAKHTIAR and RETNO BUDIARTI.
In this paper we are interested in a particular type of matching process. We match everyone in the population to someone else exactly once. We view the bilateral matching process as a sequence of involutions from a population to itself. The bilateral matching process is then constructed by arranging the involutions by means of Latin square.
We perform the matching process into several steps. First, we describe how to construct meetings two different agents but the same size. Second, we reconsider the first step when agents belong to an odd-sized population. Finally, we exploit the two earlier steps to construct a matching procedure for any finite population.
ABSTRAK
MUHAMAD SYAZALI. Pemadanan Bilateral dengan Rancangan Bujursangkar Latin. Dibimbing oleh TONI BAKHTIAR dan RETNO BUDIARTI.
Di dalam karya ilmiah ini, yang dikaji adalah sebuah bentuk khusus dari proses pemadanan, yang bertujuan memadankan setiap orang di dalam suatu populasi ke setiap orang lainnya tepat satu kali. Proses pemadanan bilateral dipandang sebagai sebuah rangkaian berbagai involusi dari sebuah populasi itu sendiri. Proses pemadanan bilateral kemudian dikonstruksi oleh aturan involusi menggunakan bujursangkar latin.
Pembentukan proses pemadanan dibagi ke dalam beberapa tahap. Pertama, mendiskripsikan bagaimana menyusun pertemuan di antara dua agen yang berbeda tetapi memiliki ukuran populasi yang sama. Tahap kedua, mempertimbangkan kembali tahap pertama ketika agen-agen tersebut memiliki populasi yang berukuran ganjil. Terakhir, dua tahap sebelumnya digunakan untuk menyusun sebuah prosedur pemadanan untuk setiap populasi yang terbatas.
PEMADANAN BILATERAL
DENGAN RANCANGAN BUJURSANGKAR LATIN
Skripsi
sebagai salah satu syarat untuk memperoleh gelar sarjana sains
pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
Oleh :
MUHAMAD SYAZALI
G54104023
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Judul : Pemadanan Bilateral dengan Rancangan Bujursangkar Latin
Nama : Muhamad Syazali
NRP :
G54104023
Menyetujui:
Pembimbing
I,
Pembimbing
II,
Dr. Toni Bakhtiar, M.Sc.
Ir. Retno Budiarti, MS.
NIP. 132 158 750
NIP. 131 842 409
Mengetahui:
Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam
Institut Pertanian Bogor
Dr. drh. Hasim, DEA.
NIP. 131 578 806
PRAKATA
Puji Syukur penulis haturkan kepada Allah SWT yang telah memberikan limpahan ramat dan hidayahnya sehingga dapat terselesaikannya karya ilmiah ini. Shalawat serta salam senantiasa selalu tercurahkan teruntuk Nabi Muhamad SAW yang telah mengantarkan kita semua umatnya sehingga dapat memperoleh petunjuk jalan yang benar, beserta keluarganya, para sahabat, dan semoga tercurahkan juga untuk kita semua sebagai umatnya hingga akhir zaman.
Keberhasilan penyusunan karya ilmiah ini juga tidak lepas dari bantuan berbagai pihak. Untuk itu penulis mengucapkan terima kasih yang sebesar-besarnya kepada:
1. Bapak atas kerja keras bapak sehingga penulis dapat menyelesaikan studinya di sini, serta do’a, keikhlasan, nasehat dan semangat yang senantiasa diberikan. Ibu tercinta yang senantiasa menyokong semangat penulis, do’anya serta nasehat yang tak henti-hentinya. 2. Kakak-kakakku: Mas Edy Prasetyo dan Mas Rahmad Junaidi yang telah menjadi motifator
karena keberhasilan kalian yang telah lebih dahulu sehingga dapat menjadi contoh untuk adik-adiknya.
3. Adik-adikku: Istihana, Rofiqul Umam dan Fajri Farid yang menjadi inspirasi bagi penulis agar selalu menjadi contoh yang baik.
4. Bapak Toni Bakhtiar dan Ibu Retno Budiarti selaku dosen pembimbing dan Bapak Siswandi selaku dosen penguji, terima kasih atas kesabaran dan dukungan dalam membimbing dan mengarahkan penulis.
5. Semua dosen Departemen Matematika (terima kasih atas ilmunya selama ini). 6. Bu Ade, Bu Susi, Mas Bono, Bu Marisi, Mas Deny, Mas yono.
7. Rani Dwi Astuti, terima kasih atas do’anya, semangat dan dukungan yang selalu diberikan, serta kesabarannya untuk mendengarkan keluhan penulis.
8. Sahabat-sahabatku di rumah: Joko, Agus, Syahril, Yam-yam, Sopwanudin untuk do’a dan semangat kalian serta pertemanan selama ini.
9. Teman seperjuangan penulis dari MA Nurhamdani mudah-mudahan cepat menyusul, Verry Andriawan (terima kasih konsultasi ke dosen statistiknya).
10. The Al-father’s yang telah memberikan dukungan dan pertemanan serta kekeluargannya selama ini.
11. Nono hartono, SPi dan Erick yang sudah banyak meminjamkan banyak fasilitas. 12. Eci dan Fitrie atas bantuan proses editing.
13. Teman-teman Math 41: Mora (terima kasih terjemahannya), Uwie, Nurjannah, Ika, Sifa, Intan, Ahdiani, Diah, Mahar, Eva, Eni, Army, Ayu, Ani, Tities, Tia, Darwisah, Endit, Sita, Niken, Rizul, Rita, Fariz, Adji, Frederick, Rangga M, Mimin, Mahnur, Triyadi, Idris, Yaya dan teman-teman Math 41 lainnya yang tak dapat disebutkan satu per satu (terima kasih telah menjadi teman seperjuangan dan memberikan kenangan selama ini).
14. Math 42: Vino, Erlin, Eyyi, Niken, Jane, Idhun, Moko, dan math 42 lainnya. 15. Math 43: Putri Giani terima kasih buat diktat matdis dan grafnya.
16. Seluruh Pihak yang telah memberikan konstribusi dalam pembuatan karya ilmiah ini yang tak dapat disebutkan satu per satu.
Semoga karya ilmiah ini dapat bermanfaat dalam dunia Ilmu Pengetahuan khususnya matematika dan menjadi inspirasi bagi penelitian selanjutnya.
Bogor, Juli 2008
RIWAYAT HIDUP
Penulis dilahirkan di Bandar Lampung, pada tanggal 21 November 1986 sebagai anak ke tiga dari enam bersaudara, anak dari pasangan Prayitno dan Saiti.
Penulis menjalani jenjang pendidikan di SD Negeri 4 Sawah Brebes (1998), SLTP N 5 Bandar Lampung (2001), MAN 1 (MODEL) Bandar Lampung (2004) dan pada tahun yang sama berhasil masuk IPB melalui jalur USMI Fakultas Matematika dan Ilmu Pengetahuan Alam Departemen Matematika.
DAFTAR ISI
Halaman
DAFTAR ISI ... vii
DAFTAR TABEL ... viii
I. PENDAHULUAN ... 1
1.1 Latar Belakang ... 1
1.2 Tujuan ... 1
II. LANDASAN TEORI ... 1
2.1 Matriks ... 1
2.2 Bujursangkar Latin ... 1
2.2.1 Konstruksi Bujursangkar Latin 1 ... 2
2.2.2 Konstruksi Bujursangkar Latin 2 ... 2
2.2.3 Konstruksi Bujursangkar Latin 3 ... 3
2.3 Fungsi ... 4
2.4 Permutasi ... 4
2.5 Involusi ... 5
III. MATRIKS PEMADANAN DAN BUJURSANGKAR LATIN ... 6
IV. MATRIKS PEMADANAN MAKSIMAL ... 7
V. PENERAPAN DALAM BIDANG EKONOMI ... 11
VI. SIMPULAN DAN SARAN ... 13
DAFTAR TABEL
I PENDAHULUAN
1.1 Latar Belakang
Pada kondisi-kondisi tertentu keheterogenan unit percobaan tidak bisa dikendalikan hanya dengan pengelompokkan satu sisi keragaman unit-unit percobaan namun memerlukan penanganan yang lebih kompleks. Kondisi ini tentunya memerlukan bentuk rancangan yang lain. Salah satu rancangan yang mampu mengendalikan komponen keragaman unit-unit percobaan lebih dari satu sisi komponen adalah rancangan bujursangkar latin (latin square). Tulisan ini menawarkan prosedur sederhana yang dapat digunakan untuk membangun sekuen (rangkaian) dari petemuan berpasang-pasangan diantara pelaku yang berasal dari populasi yang finite
(terbatas) dengan menggunakan rancangan bujursangkar latin tersebut. Proses pertemuan yang dipelajari memiliki dua sifat, pertama rangkaian dari pertemuan tersebut adalah eksogen yang berarti bahwa setiap pelaku bertemu dengan pelaku yang lain tepat satu kali. Kedua, dalam setiap periode proses ini memaksimumkan banyaknya dari pemasangan dalam populasi.
Dalam ilmu ekonomi proses pertemuan berpasang-pasangan dengan sifat ini
digunakan untuk meyatakan konsep dari persaingan dagang secara eksplisit.
Dalam mengembangkan prosedur untuk menciptakan rangkaian pemasangan yang diinginkan digunakan bentuk khusus dari permutasi yang disebut involusi. Dengan memanfaatkan beberapa hasil matematis dari bujursangkar latin, alasan untuk bekerja dengan objek matematika ini adalah proses pemasangan yang merupakan cara untuk membagi populasi X ke dalam himpunan agen-agen yang disjoint secara berulang-ulang. Karena diketahui bahwa pertemuan yang dipandang adalah bilateral, maka proses pemasangan dapat dilihat sebagai rangkaian involusi dari X ke X.
1.2 Tujuan
Adapun tujuan dari penulisan makalah ini adalah memasangkan agen satu dengan agen lainnya dalam populasi yang terbatas di mana setiap agen bertemu dengan agen lainnya tepat satu kali dengan memperagakan bagaimana membangun bujursangkar latin sedemikian rupa sehingga setiap baris, pada awalnya adalah involusi dari baris pertama yang akhirnya didapatkan suatu matriks pemadanan.
II. LANDASAN TEORI
2.1 Matriks
Matriks adalah kumpulan bilangan yang disusun dalam bentuk persegi panjang atau bujur sangkar yang tersusun dalam baris dan kolom. Ukuran atau ordo dari suatu matriks ditentukan oleh banyaknya baris dan kolom yang membentuknya.
Secara umum matriks dapat ditulis sebagai berikut
= elemen matrik A yang terletak pada baris ke-i, kolom ke-j ; i=1,2,…,m ;
j=1,2,…..,n
= ukuran atau ordo matriks A, yaitu
11 12 1
21 22 2
1 2
n
n
m m mn
a
a
a
a
a
a
A
a
a
a
⎡
⎤
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎣
⎦
L
L
M
M
O
M
L
[Leon 2001]
2.2 Bujursangkar Latin Definisi 1 (Bujursangkar Latin)
Diketahui ada n symbol berbeda, bujursangkar latin adalah matriks
dengan entri simbol-simbol yang diketahui yang disusun sedemikian rupa sehingga setiap simbol muncul tepat satu kali dalam setiap baris dan kolom.
[Aliprantis, et al 2006]
Contoh 1 :
Diberikan himpunan simbol-simbol {1, 2, 3, 4} dan {@, #, $, &}, matriks
1 2 3 4 @ # $ & 2 3 4 1 $ & @ #
dan
3 4 1 2 # $ & @ 4 1 2 3 & @ # $
⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎣ ⎦ ⎣ ⎦
secara umum dapat diperoleh banyak bujursangkar latin yang berbeda, dan juga banyaknya bujursangkar latin yang terbentuk akan semakin bertambah bergantung pada n. Walaupun bujursangkar latin telah dipelajari secara rinci dalam matematika banyaknya bujursangkar latin yang ada telah dihitung hanya untuk .
[Aliprantis, et al 2006]
Diketahui himpunan populasi
, … … … , dengan n agen. Ada tiga prosedur pembangunan bujursangkar latin yang masing-masing menghasilkan matriks
yang spesifik.
2.2.1 KonstruksiBujursangkar Latin1 Bujursangkar latin ini dinotasikan dengan dan baris pertamanya adalah vektor (1, 2, . . . . , n). Baris lainnya dari dihasilkan secara rekursif dengan cara menggeser satu tempat ke kiri baris yang sebelumnya secara
siklik. Yang berarti baris kedua diperoleh dengan cara menggeser baris pertama satu tempat ke kiri, dalam contoh di atas baris kedua adalah (2, 3, . . . . , n, 1) dan baris ke tiga adalah vektor (3, 4, . . . ., n, 1, 2). Dengan demikian adalah matriks seperti berikut :
1 2 ... 2 1
2 3 1 1
3 4 1 2
1 4 3 2
1 3 2 1
n n n
n n
n
n n n n n
n n n n
− − − − − − − − − −
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
L LM M O M M M
L L
Jika menggunakan notasi standar untuk bujursangkar latin ini maka setiap entri diberikan formula sebagai berikut:
jika 1 dan 1
1 ( 1) 1 jika 2 dan 1
( ) 1 jika 2 dan 2
j i j n
aij i j n Y i j i j i i j n i
j n i i n i j n
χ = ≤ ≤ = + − − + − = + − ≥ ≤ ≤ − + − − − ≥ − + ≤ ≤
⎧⎪
⎨
⎪⎩
di mana χY N: →{0,1} adalah fungsi karakteristik dari himpunan
, , … dengan
( ) 1 jika dan ( ) 0 jika .
Y k k Y Y k k Y
χ = ∈ χ = ∉
Contoh 2
Saat konstruksi ini akan
menghasilkan bujursangkar latin
1 2 3 4 2 3 4 1 3 4 1 2 4 1 2 3
L− =
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
.2.2.2 KonstruksiBujursangkar Latin2 Misalkan notasi untuk bujursangkar latin ini adalah . Matriks ini memiliki baris pertama (1, 2, . . ., n) dan konstruksinya dibuat secara rekursif tepat seperti cara pertama, tetapi satu-satunya perbedaan terletak pada
cara penggeserannya yang ke arah kanan bukan ke arah kiri. Hal ini berarti baris kedua dari diperoleh dengan cara menggeser baris pertama ke kanan secara siklik, dalam contoh, baris ke dua adalah vektor (n, 1,…, n-2, n-1), dan baris ketiga adalah vektor (n-1, n, 1, …,
n-2), dan seterusnya. Bujursangkar latin yang terbentuk adalah
1 2 2 1
1 3 2 1
1 4 3 2
3 4 1 2
2 3 1 1
n n n
n n n n
n n n n n
L n n n − − − − − − − − − + = − ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ L L L
M M O M M M
L L
Dengan notasi maka formula untuk entri dari adalah
jika 1dan1
1 ( 1 1) ( ) 1 jika 2 dan1 1
1 jika 2 dan
j i j n
aij n j i n Y n j n i j i j i
j i i i j n
Contoh 3
Di mana saat kita mendapatkan
1 2 3 4
4 1 2 3 3 4 1 2 2 3 4 1
L+ =
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
.2.2.3 KonstruksiBujursangkar Latin3 Bujursangkar latin dinotasikan dengan
di mana baris pertama adalah (n, n-1, …1) dan baris lainnya dibentuk dengan cara mengikuti prosedur rekursif dengan cara menggeser baris pertama satu tempat ke kiri, sehingga baris ke dua yang terbentuk adalah (n-1,n-2, …, 1, n). Dengan mengulang proses
ini sebanyak maka diperoleh bujursangkar latin seperti berikut :
1 2 1
1 2 1
1 3 2
2 1 4 3
1 3 2
n n
n n n
L n i n i n i n i
n − − − = − + − − + − + ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ L L
M M O M M
L
M M O M M
M M
Dengan maka formula untuk entri dari L adalah
1 jika 1dan1
1 ( 1) ( 1) 2 jika 2dan1 1
2 2 jika 2dan 2
n j i j n
aij n i j n Y i j n i j i j n i
n i j i n i j n
χ + − = ≤ ≤ = + − + − + + − = + − − ≥ ≤ ≤ − + − + − ≥ − + ≤ ≤
⎧⎪
⎨
⎪⎩
Contoh 4Saat bujursangkar latin L adalah seperti berikut :
4 3 2 1 3 2 1 4 2 1 4 3
1 4 3 2
L=
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
Berdasarkan dari ketiga konstruksi bujursangkar latin di atas maka untuk sembarang populasi berukuran n terdapat beberapa bujursangkar latin yang dapat dibentuk. Banyaknya bujursangkar latin yang dapat dibentuk dari populasi berukuran n
dapat dilihat dari Tabel 1 berikut:
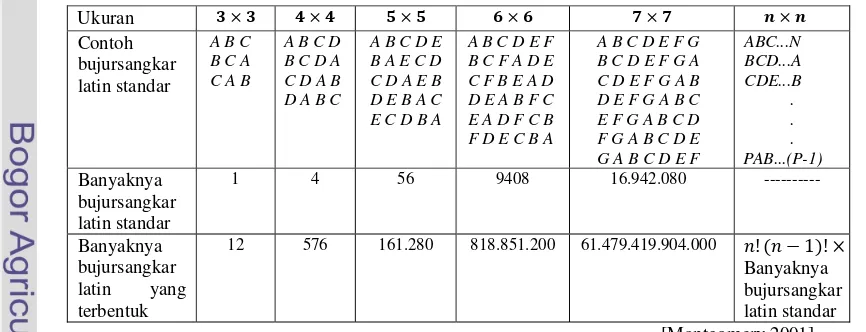
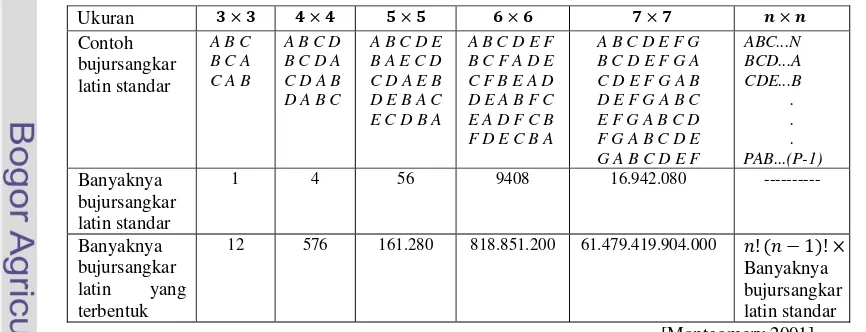
Tabel 1 Banyak bujursangkar latin dari populasi berukuran n sebarang.
Ukuran Contoh bujursangkar latin standar
A B C B C A C A B
A B C D B C D A C D A B D A B C
A B C D E B A E C D C D A E B D E B A C E C D B A
A B C D E F B C F A D E C F B E A D D E A B F C E A D F C B F D E C B A
A B C D E F G B C D E F G A C D E F G A B D E F G A B C E F G A B C D F G A B C D E G A B C D E F
ABC...N BCD...A CDE...B . . . PAB...(P-1) Banyaknya bujursangkar latin standar
1 4 56 9408 16.942.080 ---
Banyaknya bujursangkar latin yang terbentuk
2.3 Fungsi Definisi 2 (Fungsi)
Fungsi (pemetaan) f dari himpunan A ke himpunan B, dinotasikan , adalah suatu relasi dari A ke B yang setiap anggota dari A muncul hanya sekali sebagai komponen pertama dari pasangan terurut keanggotaan relasi yang bersangkutan.
Kurtz 1992]
Dari definisi dia atas, jika , , maka dapat ditulis b = f (a). Dalam hal ini b disebut imej dari a dibawa oleh f, sedangkan a
disebut preimej dari b oleh f. Penulisan ringkas dengan menerapkan lambang logika dari definisi di atas dapat dinyatakan sebagai berikut.
jika dan hanya jika
! , atau
: jika dan hanya jika ( )
[ ( ) ( )] maka .
f A B a A
b f a c f a b c
→ ∀ ∈
= ∧ = =
Contoh 5
Misalkan , , dan , , , , perhatikan bahwa , , , , ,
adalah fungsi dari A ke B, sedangkan
, , , dan
, , , , , , , bukan merupakan fungsi dari A ke B.
Definisi 3 (Fungsi Injektif)
Fungsi f disebut fungsi injektif (satu-satu) apabila f tidak pernah mencapai nilai yang sama dua kali; yakni,
jika maka
[Stewart 2001]
Contoh 6
Misalkan , , dan B = {a,b,c,d,e}.
fungsi , , , , , adalah
injektif, sedangkan fungsi
, , , , , bukan merupakan fungsi injektif.
Perhatikan Contoh 6 di atas komponen ke dua dari semua anggota f muncul hanya sekali, sehingga f adalah fungsi injektif. Sekarang perhatikan fungsi , unsur a muncul dua kali sebagai komponen ke dua di dalam kenggotaan , sehingga tidak injektif.
Definisi 4 (Fungsi Surjektif)
Suatu fungsi : disebut fungsi surjektif, jika , artinya
.
[Kurtz 1992]
Contoh 7
Jika , , , dan , , ,
, , , , , , , dan
, , , , , , , adalah dua fungsi surjektif dari A ke B, sedangkan fungsi
, , , , , , , tidak surjektif.
Dalam Contoh 7 terlihat bahwa semua anggota B muncul sebagai komponen ke dua di dalam ke anggotaan f1 dan f2, sehingga f1
dan f2 adalah fungsi surjektif. Sekarang
perhatikan fungsi , ada anggota B yaitu z
yang tidak muncul sebagai komponen ke dua di dalam kenggotaan , sehingga tidak surjektif.
Definisi 5 (Fungsi Bijektif)
f fungsi bijektif jika dan hanya jika f
fungsi injektif dan f fungsi surjektif
[Kurtz 1992]
Contoh 8
Jika , , dan , , ,
, , , , , adalah fungsi bijektif karena merupakan fungsi injektif dan surjektif.
Contoh 9
Jika , , dan , , , ,
, , , , , bukan fungsi bijektif karena merupakan fungsi injektif tetapi tidak surjektif.
2.4 Permutasi Definisi 6 (Permutasi)
Permutasi dari himpunan terbatas X yang tidak kosong adalah fungsi bijektif dari X ke
X.
[Biggs 1989]
Dalam pemasangan dari anggota X ke X
yang biasa dijumpai permutasi dapat dipandang sebagai suatu susunan yang dapat dibentuk dari sekumpulan objek yang dapat dipilih sebagian atau seluruhnya.
Jika ada n benda yang berbeda maka banyaknya susunan yang berbeda (permutasi) dari n benda tersebut adalah:
, ! … .
Permutasi merupakan penyusunan kembali suatu kumpulan objek dalam urutan yang berbeda dari urutan yang semula. Sebagai contoh, kata-kata dalam kalimat sebelumnya
berbeda dari urutan yang semula” dapat disusun kembali sebagai "merupakan Permutasi suatu urutan yangberbeda urutan yang kumpulan semula objek penyusunan kembali dalam dari". Proses mengembalikan objek-objek tersebut pada urutan yang baku (sesuai ketentuan) disebut sorting.
Jika terdapat suatu untai abjad abcd, maka untai itu dapat dituliskan kembali dengan urutan yang berbeda: acbd, dacb, dan seterusnya. Selengkapnya ada 24 cara menuliskan ke empat huruf tersebut dalam urutan yang berbeda satu sama lain. Setiap untai baru yang tertulis mengandung unsur-unsur yang sama dengan untai semula abcd, hanya saja ditulis dengan urutan yang berbeda. Maka setiap untai baru yang memiliki urutan berbeda dari untai semula ini disebut dengan permutasi dari abcd.
Contoh 10
Berikut ini adalah permutasi dari abcd abcd abdc acbd acdb adbc adcb bacd badc bcad bcda bdac bdca cabd cadb cbad cbda cdab cdba dabc dacb dbac dbca dcab dcba
[Wikipedia Indonesia 2008]
2.5 Involusi
Definisi 7 (Aturan pemadanan bilateral) Aturan pemadanan bilateral untuk populasi X adalah fungsi yang
memenuhi artinya
o untuk semua
, dengan yang merupakan pemetaan identitas pada X.
[Aliprantis, et al 2006]
Berdasarkan definisi di atas, jika merupakan aturan pemadanan bilateral, maka fungsi invertible dan adalah permutasi dari X karena adalah fungsi surjektif satu-satu. Bagaimanapun juga,
merupakan bentuk khusus dari permutasi yang inversnya adalah dirinya sendiri. Sebagai contoh ; fungsi ini dalam ilmu matematika kita kenal sebagai “involusi”. Secara sederhana dapat dikatakan bahwa cara apapun untuk memasangkan agen-agen dalam populasi haruslah sedemikian rupa sehingga
pasangan dari agen tersebut adalah agen itu sendiri.
Oleh karena itu, jika adalah aturan pemadanan dan agen x dipadankan dengan agen , maka kita sebut adalah pasangan dari x. Dengan cara serupa,
adalah pasangan dari jadi himpunan , dapat disebut aturan pemadanan bilateral.
Contoh 11
Berikut contoh sederhana dari aturan pemadanan bilateral (involusi)
Andaikan , ∞ dan didefinisikan
dengan .
[Aliprantis, et al 2006]
Contoh 12
Misal diberikan bujursangkar latin dengan
1 2 3 4 2 1 4 3 3 4 1 2 4 3 2 1
L=
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
III. MATRIKS PEMADANAN DAN BUJURSANGKAR LATIN
Tiga konstruksi bujursangkar latin yang telah dibahas sebelumnya akan digunakan untuk mencari model pemadanan bilateral yang diinginkan diantara agen-agen yang akan dipasangkan dalam populasi yang terhingga. Seperti pada Definisi 7 pemadanan bilateral pada populasi X adalah fungsi
yang memenuhi untuk semua
x
∈
X
, di mana merupakan bentuk permutasi yang disebut involusi. Dalam hal ini agen sebagai pasangan dari agen xsedemikian rupa sehingga pertemuan secara sederhana ini merupakan rangkaian dari pemadanan bilateral.
Proses pemadanan adalah memasangkan agen dengan agen lainnya yang feasible
dalam suatu populasi yang terbatas, di mana akan dipastikan bahwa agen-agen tersebut bertemu dengan setiap agen yang ada (kecuali dirinya sendiri) tepat satu kali. Hal tersebut akan mengakibatkan jika terdapat populasi yang terdiri atas n agen maka proses pemasangan yang diinginkan tidak dapat lebih dari periode. Hal itu dikarenakan setiap agen dapat dipasangkan paling banyak dengan
individu berbeda. Untuk memformalisasikan proses pemadanan yang demikian maka diperkenalkan bentuk khusus dari suatu matriks yaitu bujursangkar latin.
Definisi 8 (Matriks pemadanan)
Misal , , … , adalah populasi. Matriks berukuran dengan anggota yang berasal dari populasi X disebut matriks pemadanan bila:
1) Baris pertama adalah vektor (1,2,…,n). 2) Baris-baris lainnya merupakan involusi
dari baris pertama.
3) Jika n genap maka setiap kolom memiliki entri yang berbeda.
4) Jika n ganjil maka dalam setiap kolom j
agen j muncul paling banyak dua kali dan entri lainnya pada kolom tersebut seluruhnya berbeda yaitu agen X\{j}. Sebuah matriks pemadanan M dikatakan maksimal:
a) Jika n genap maka M berukuran dengan m = n.
b) Jika n ganjil maka M berukuran dengan m = n+1.
[Aliprantis, et al 2006]
Diberikan populasi , , … , , akan dilihat banyaknya matriks pemadanan
maksimal yang dapat dibuat dari populasi X. Untuk populasi X berukuran n dinotasikan matriks pemadanan maksimal dengan .
Perhatikan dua matriks berikut, misalkan populasi dengan dan . Dua matriks pemadanan maksimal dari populasi-populasi tersebut adalah:
1 2 3 1 2 3 4 3 2 1 2 1 4 3 3 2 1 3 4 4 3 2 1 1 3 2 3 4 1 2
μ = μ =
⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎣ ⎦ ⎣ ⎦
Baris pertama adalah semua agen dari populasi X, yang terurut dari 1, 2, …, n. Terlihat bahwa setiap baris yang berurutan membagi populasi ke dalam pasangan-pasangan pada beberapa periode. Untuk melihat hal ini terjadi, andaikan t=0 yang merupakan tahap awal di mana tak ada agen yang dipasangkan, dalam hal ini adalah baris pertama. Oleh karena itu, setiap baris i
menandakan periode pemasangan . Partisi pada periode t dengan demikian diindentifikasikan dengan mengasosiasikan setiap elemen dalam kolom j pada baris pertama dengan elemen yang terdapat pada kolom yang sama pada baris .
Contoh 13
Sebagai contoh, matriks pemadanan di atas menjelaskan rangkaian dari tiga pasangan pertemuan pada populasi X={1,2,3,4}, sehingga dapat dilihat matriks pemadanan berikut:
1 2 3 4
1 2 1 4 3 2 3 4 1 2 3 4 3 2 1
t
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
{(1,3),(2,4),(3,1),(4,2)} yang berarti pada periode ke dua yaitu baris ke tiga pada kolom pertama, agen 1 dipasangkan dengan agen 3. Lalu pada kolom dua agen 2 dipasangkan dengan agen 4, pada kolom berikutnya yaitu kolom tiga agen 3 dipasangkan dengan agen 1 dan kolom empat agen 4 dipasangkan dengan agen 2. Selanjutnya pada periode yaitu periode ke tiga diperoleh pemadanan {(1,4),(2,3),(3,2),(4,1)} artinya pada periode ke tiga yaitu baris ke empat pada kolom pertama agen 1 dipasangkan dengan agen 4, pada kolom dua agen 2 dipasangkan dengan agen 3, pada kolom tiga agen 3 dipasangkan dengan agen 2, dan pada kolom empat agen 4 dipasangkan dengan agen 1.
Matriks pemadanan maksimal menjelaskan pemasangan di antara n agen dengan tidak ada agen yang bertemu dengan pasangan yang sama lagi.
Perlu diketahui bahwa semua matriks pemadanan maksimal sembarang dengan n
genap adalah bujursangkar latin yang memenuhi batasan tambahan bahwa setiap baris adalah involusi dari baris pertama. Hal ini merupakan kasus khusus karena tidak semua bujursangkar latin memenuhi sifat involusi.
Contoh 14
Misal diberiakan matriks bujursangkar latin berikut dengan populasi , , ,
1 2 3 4 2 3 4 1 3 4 1 2 4 1 2 3
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
Perhatikan matriks bujursangkar latin pada Contoh 14 di atas, pada baris ke dua diperoleh
pemadanan {(1,2),(2,3),(3,4),(4,1)} yang artinya pada baris ke dua ini pada kolom satu agen 1 dipasangkan dengan agen 2 tetapi pada kolom dua agen 2 tidak dipasangkan dengan agen 1 melainkan dengan agen 3, hal ini bertentangan dengan sifat involusi sehingga matriks bujursangkar latin pada Contoh 14 ini bukan merupakan matriks pemadanan .
Untuk popolasi X saat jumlah agen n ganjil matriks pemadanan maksimal bukan merupakan bujursangkar latin karena matriks pemadanan maksimal memiliki baris sebanyak . Perlu diingat pada Definisi 8 merupakan matriks pemadanan jika pada saat n ganjil maka dalam setiap kolom j
agen j muncul paling banyak dua kali dan entri lainnya pada kolom tersebut seluruhnya berbeda yaitu agen X\{j}. Hal ini mengakibatkan jika n ganjil maka dengan mengeliminasi baris pertama dari matriks dapat diperoleh matriks bujursangkar latin.
Contoh 15
Misal n=3, didapatkan matriks pemadanan maksimal . Jika baris pertama dari dieliminasi, maka diperoleh bujursangkar latin
L.
1 2 3
3 2 1 3 2 1
2 1 3
3 2 1 3
1 3 2 1 3 2
L
μ = =
⎡
⎤
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
⎢
⎥
⎣
⎦
IV. MATRIKS
PEMADANAN MAKSIMAL
Bagian ini akan membahas eksistensi matriks pemadanan maksimal untuk sebarang populasi terbatas yang kemudian akan diperlihatkan bagaimana membentuk matriks pemadanan yang maksimal. Andaikan terdapat X populasi yang terdiri atas dua grup, sebut saja grup A dan grup B. Setiap grup memiliki anggota yang sama banyaknya misalkan n anggota. Untuk lebih mudahnya diinterpretasikan setiap grup tersusun atas agen yang homogen, sebagai contohnya, grup pembeli dan grup penjual. Tujuan selanjutnya adalah memasangkan tepat satu kali setiap
agen dari A dengan agen dari B, jadi setiap agen dari satu grup dipadankan dengan agen pada grup lainnya dalam keadaan mutlak saling asing, artinya setiap agen dipadankan dengan agen lainnya tepat satu kali dan dalam setiap periode pemadanan setiap agen yang diperoleh adalah maksimal artinya semua agen memperoleh pasangannya masing-masing.
dari grup lainnya. Permasalahan di sini adalah bagaimana membentuk pemadanan maksimal yang diharapkan dan bagaimana cara sistematis untuk memperoleh pemadanan yang maksimal tersebut. Dalam hal ini kita menggambarkan dalam sebuah matriks yang sebelumnya sudah disebutkan sebagai matriks pemadanan maksimal.
Terdapat dua hal yang diperoleh dari permasalahan di atas. Pertama hal tersebut menetapkan bahwa agen dipasangkan dalam keadaan mutlak saling asing paling banyak n
kali. Ke dua diperoleh prosedur untuk membentuk kaidah pemadanan pada sembarang populasi. Misal dinotasikan X =
AuB berarti dan ,
dengan kata lain X adalah union disjoint dari
A dan B.
Lema 1
Andaikan , . . . , dan
, . . . , , maka matriks M(A,B) berukuran .
1 2 1 1 2 2 1 2
1 2 2 1 2 1 2 1
( , ) 2 3 2 1 1 2 1
2 1 2 2 2 1 2 3 1
n n n n n n
n n n n n n
M A B n n n n n n n
n n n n n
− + + −
+ + − −
= + + + − −
+ − −
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
L L
L L
L L
M M O M M M M O M M
L L
adalah matriks pemadanan dari populasi
X=AuB sedemikian sehingga setiap agen di A
adalah pasangan yang terpadankan dengan setiap agen di B.
[Aliprantis, et al 2006]
Bukti
Notasi M(A,B) menggambarkan di mana agen pada himpunan A dipadankan dengan agen pada himpunan B dengan tidak memasangkan dengan dirinya sendiri. Andaikan adalah bujursangkar latin dari himpunan , . . . , yang dibangun berdasarkan konstruksi bujursangkar latin #1 pada Bab II, dan melambangkan bujursangkar latin dari himpunan , . . . , yang dibangun berdasarkan konstruksi bujursangkar latin #2. Sehingga dengan demikian diperoleh matriks
1... 1...2 ( , )
( ) ( )
n n n
M A B
L B L A
+
=
⎡
⎢
− +⎤
⎥
⎣
⎦
.Dengan demikian M(A,B) adalah matriks pemadanan yang sesuai untuk populasi X =
AuB.
Perlu diperhatikan pada matriks pemadanan M(A,B) yang diperoleh dari Lema 1 bukan merupakan matriks pemadanan yang maksimal, karena matriks M(A,B) tidak menggambarkan pemadanan antar agen dalam
himpunan itu sendiri melainkan pemadanan antar agen pada himpunan A dan B saja. Yang perlu diingat juga berdasarkan Definisi 8, matriks pemadanan maksimal M berukuran
di mana saat n ganjil maka
dan saat n genap maka . Untuk lebih jelas lihat Contoh 16 berikut.
Contoh 16
Andai , … . . , dengan
, , , dan , , , . Maka berdasarkan Lema 1 di atas diperoleh matriks berikut
1 2 3 4 5 6 7 8
5 6 7 8 1 2 3 4
( , ) 6 7 8 5 4 1 2 3
7 8 5 6 3 4 1 2
8 5 6 7 2 3 4 1
M A B =
⎡ ⎤
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎢ ⎥
⎣ ⎦
Perhatikan matriks pada Contoh 16 di atas, terlihat bahwa matriks pemadanan M(A,B)
yang terbentuk dari populasi , … . . , di mana . Matriks pemadanan M(A,B)
yang terbentuk tidak berukuran seperti yang didasarkan pada Definisi 8 sehingga dapat disimpulkan matriks pemadanan M(A,B)
yang diperoleh tidaklah maksimal.
yang diinginkan untuk memadankan setiap agen yang ada pada populasi yang terbatas.
Teorema 1
Setiap populasi yang terbatas mempunyai matriks pemadanan maksimal.
[Aliprantis, et al 2006]
Bukti
Pembuktian dari teorema ini terdiri atas dua bagian. Pada bagian pertama, akan ditunjukkan eksistensi matriks pemadanan maksimal untuk sebarang populasi ganjil, dan
pada bagian kedua akan ditunjukkan eksistensi dari matriks pemadanan maksimal untuk sebarang populasi genap.
Sekarang akan dibuktikan untuk bagian yang pertama untuk populasi ganjil. Misalkan diberikan populasi , … . , , di mana n
ganjil. Dengan menggunakan konstruksi bujursangkar latin 3 pada Bab II maka diperoleh bujursangkar latin L, sedemikian sehingga diperoleh matriks berukuran
sebagai berikut:
1 2 3 2 1
1 2 3 2 1
1 2 3 2 1
1...
2 3 4 1 1
2 1 5 4 3
1 1 4 3 2
n n n
n n n
n n n n
n
n n n n n
n L n n n μ − − − − − − − = − − − − = −
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥ ⎡ ⎤
⎢
⎥ ⎢ ⎥
⎣
⎦
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
L L L LM M M O M M M
L L
Matriks tersebut merupakan matriks pemadanan maksimal untuk populasi X di mana n ganjil.
Pada bagian ke dua untuk populasi genap, andaikan diberikan populasi , … . , , dan misalkan banyaknya populasi X adalah
, di mana p dan k adalah bilangan natural dengan p bilangan ganjil. Untuk menyelesaikannya dipandang dalam dua kasus. Pertama jika populasi dibagi menjadi dua populasi n yang sama banyak sebut saja menjadi populasi agen A dan agen
B maka masing-masing populasi agen pada A
dan B memiliki banyak anggota n dengan n
genap. Kedua kasus di mana jika
dibagi menjadi dua populasi n yang sama banyak juga maka masing-masing populasi A
dan B memiliki anggota n dengan n ganjil. Sekarang akan dibahas terlebih dahulu untuk kasus yang pertama
¾ Kasus 1 : p = 1
Sehingga diperoleh populasi banyaknya X
adalah . Akan dibuktikan adanya matriks pemadanan maksimal dengan menggunakan induksi matematika pada k. • Basis induksi:
Untuk , maka sehingga
diperoleh matriks
1 2
2 2 1
μ =
⎡
⎢
⎤
⎥
⎣
⎦
yang merupakan matriks pemadanan maksimal untuk populasi .
• Hipotesis Induksi:
Anggap benar untuk sehingga terdapat matriks pemadanan maksimal .
• Langkah Induksi
Akan dibuktikan benar terdapat matriks pemadanan maksimal untuk
sehingga . Untuk membuktikannya misalkan , … , = AuB di mana
, … , dan , … , . Dari hipotesis induksi diketahui bahwa terdapat matriks pemadanan maksimal berukuran untuk . Sehingga terdapat matriks pemadanan maksimal
untuk populasi , … , dan matriks pemadanan maksimal untuk populasi , … , . Berdasarkan Lema 1 maka diperoleh
( ) ( )
2 2
1 ( ) ( )
2
2 2
A B
h h
h B A
h h μ μ μ μ μ = +
⎡
⎤
⎢
⎥
⎢
⎥
⎣
⎦
yang merupakan matriks pemadanan maksimal untuk populasi , … , =
Selanjutnya akan dibahas keberadaan matriks pemadanan maksimal untuk kasus yang ke dua.
¾ Kasus 2 :
Dalam kasus dipilih , dan untuk membuktikannya masih dapat menggunakan induksi matematika pada k.
• Basis Induksi
Untuk k=1, maka diperoleh , akibatnya , … , . Misalkan X =
AuB dengan , … , dan
, … , di mana A dan B masing-masing memiliki p agen. Misalkan dan
adalah bujursangkar latin (p-1) x p
yang dibentuk dengan menghapus baris pertama dari dan .
Selanjutnya perlu diingat bahwa p ganjil.
Andaikan dan merupakan
matriks pemadanan maksimal
untuk A dan B yang dapat dibuat berdasarkan Definisi 8.
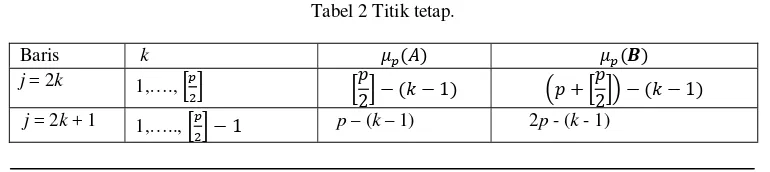
Perlu diingat juga, pada Definisi 8 diketahui bahwa jika n ganjil maka dalam setiap kolom j agen j muncul paling banyak dua kali. Kemunculan agen j untuk yang ke dua kalinya ini disebut titik tetap di mana pada periode ini agen j dipasangkan dengan dirinya sendiri. Untuk membuat supaya hal ini tidak terjadi maka dapat dilakukan dengan cara menukar titik tetap tersebut dengan titik tetap pada matriks pemadanan lainnya. Untuk lebih jelas titik tetap yang terdapat pada matriks pemadanan maksimal ditukar dengan titik tetap yang ada pada matriks pemadanan maksimal pada .
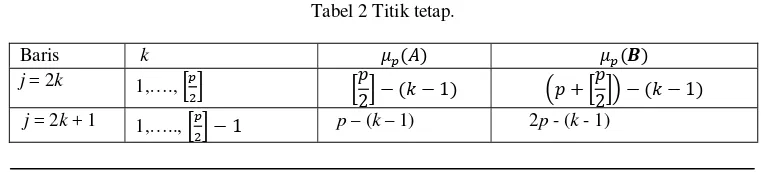
Untuk mengetahui letak titik tetap yang dimaksud, misalkan saja melambangkan yang dibulatkan ke integer yang lebih besar, dan . Sehingga diperoleh tabel untuk mencari titik tetap untuk setiap baris j
dari dan berikut.
Tabel 2 Titik tetap.
Baris k
j = 2k 1,….,
j = 2k + 1 1,….., p – (k – 1) 2p - (k - 1)
Lalu misalkan dan adalah matrik pemadanan maksimal yang diperoleh dengan menukar titik-titik tetap dari dan dalam setiap periode (baris). Sebagai contoh misalkan agent 1 yang muncul pada entri (p+1,1) dari yang dipasangkan dengan dirinya sendiri dengan kata lain tidak memiliki pasangan pada baris tersebut sementara itu agen yang juga muncul pada entri , dari juga tidak memiliki pasangan pada baris tersebut, maka dengan menukar agen 1 pada baris tersebut dari dengan agen p+1 pada baris yang sama dari . Dengan prosedur yang serupa untuk agen-agen lainnya sehingga diperoleh matriks pemadanan maksimal
dan .
Lalu berdasarkan Lema 1, maka diperoleh matriks 2p x 2p sebagai berikut
yang merupakan matriks pemadanan maksimal dari populasi , … . , .
• Hipotesisi Induksi
Misalkan terdapat matriks pemadanan maksimal untuk populasi 2n = 2h
p, di mana .
• Langkah Induksi
Sekarang akan diperlihatkan bahwa terdapat matriks pemadanan maksimal untuk populasi X pada saat sehingga populasi 2n = 2h+1
p. Untuk membuktikannya misalkan , … , = AuB di mana
, … , dan , … , . Dari hipotesis induksi diketahui bahwa terdapat matriks pemadanan maksimal berukuran untuk . Sehingga terdapat matriks pemadanan maksimal
untuk populasi , … , dan matriks pemadanan maksimal untuk populasi , … , . Berdasarkan Lema 1 maka diperoleh
( ) ( )
2 2
1 ( ) ( )
2
2 2
A B
h h
h B A
h h
μ μ
μ
μ μ
= +
⎡
⎤
⎢
⎥
⎢
⎥
yang merupakan matriks pemadanan maksimal untuk populasi , … , =
AuB.
Teorema 1 menunjukkan eksistensi dari matriks pemadanan maksimal untuk sembarang populasi terbatas dan pada beberapa kasus menyediakan algoritma untuk membangun matriks pemadanan maksimal pada populasi yang terbatas. Untuk lebih jelas perhatikan contoh-contoh berikut.
Contoh 17
Misal populasi yang ganjil dengan . Maka matriks pemadanan maksimal yang diperoleh adalah
1 2 3 3 2 1
3 2 1 3
1 3 2 μ =
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
Perhatikan matriks pada Contoh 17 di atas agen 1 muncul dua kali pada kolom pertama, kemunculan agen 1 pada baris selain baris pertama dalam Contoh 17 pada baris terakhir (ke empat) ini yang disebut sebagai titik tetap pada matriks pemadanan maksimal .
Contoh 18
Misalkan diberikan populasi genap
, , , , , , di mana k=1 dan p=3.
Misalkan , , dan , , .
Sehingga diperoleh matriks pemadanan maksimal untuk A dan B sebagai berikut
1 2 3 4 5 6
6 5 4 3 2 1
( ) , ( )
3 2 1 3 3 5 4 6
4 6 5 1 3 2
A B μ μ ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ = =
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
Selanjutnya dengan menukar titik-titik tetap pada dan akan diperoleh matriks pemadanan maksimal untuk A dan B berikut
,
3 3
1 2 3 4 5 6
3 5 1 6 2 4
' ( ) ' ( )
2 1 6 5 4 3
4 3 2 1 6 5
A B μ = μ =
⎡
⎤
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
Kemudian ingat kembali, berdasarkan defnisi dari dan , maka diperoleh matriks
3 1 2 ( ) 1 2 3 1
L+ A− =
⎡
⎢
⎤
⎥
⎣
⎦
dan5 6 4 ( ) 1 6 4 5
L− B − =
⎡
⎢
⎤
⎥
⎣
⎦
Dengan demikian matriks '( ) '( )
3 3
6
( ) 1 ( ) 1
1 2 3 4 5 6
3 5 1 6 2 4 2 1 6 5 4 3 4 3 2 1 6 5
5 6 4 3 1 2
6 4 5 2 3 1
A B
L B L A
μ μ μ = − + − − =
⎡
⎤
⎢
⎥
⎢
⎥
⎣
⎦
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
adalah matriks pemadanan maksimal dari populasi X.
V. PENERAPAN DALAM BIDANG EKONOMI
Dalam percobaan ekonomi matriks pemadanan ini dapat dikaitkan untuk mencari pemadanan di antara pelaku ekonomi. Misalkan saja penjual dan pembeli. Andaikan akan dijalankan percobaan untuk memasangkan penjual dan pembeli. Andaikan juga hanya terdapat delapan subyek yang terkumpul yang terdiri dari empat penjual dan empat pembeli. Selanjutnya akan dipasangkan masing-masing subyek sedemikian rupa sehingga setiap pembeli dapat bertemu setiap penjual tepat satu kali untuk paling banyak dalam empat periode. Yang perlu diingat
dengan menggunakan kaidah pemadanan menjadi kecil.
Untuk mengetahui kenapa hal tersebut terjadi, dimulai dengan mengetahui bahwa jumlah dari pemasangan yang muncul adalah (n!)n. Dengan menyadari bahwa semua matriks di mana simbol 1,…,n muncul tepat satu kali dalam tiap baris, tetapi dapat muncul lebih dari sekali dalam tiap kolom. Dengan demikian terdapat n! pilihan untuk baris pertama, n! untuk baris kedua , dan seterusnya sampai n! pilihan untuk baris ke-n.
Hal ini mengakibatkan jika diasumsikan bahwa setiap pemasangan memiliki peluang yang sama untuk muncul, peluang untuk memperoleh pemasangan dalam keadaan mutlak saling asing adalah
!
Dengan merupakan jumlah dari bujursangkar latin yang dapat diciptakan untuk populasi berukuran n. Misalkan
diberikan maka = 12 yang
mengakibatkan peluang bahwa pemadanan dalam keadaan mutlak saling asing . Untuk n=4 memiliki = 576 bujursangkar latin yang dapat dibentuk sehingga peluangnya adalah . Dari dua contoh populasi ini dapat dilihat jika semakin besar nilai n maka peluang terjadi pemadanan dalam keadaan mutlak saling asing semakin kecil. Jadi dapat disimpulakn jika ∞ maka
.
Hal ini bertujuan untuk mengetahui bagaimana membangun kaidah pemadanan dalam keadaan mutlak saling asing yang diperlukan, di mana kaidah tersebut sedemikian sehingga dapat digunakan untuk membangun beberapa matriks pemadanan. Hal ini menimbulkan fleksibilitas dalam mendesain kaidah pemadanan dan mendesain matriks pemadanan khususnya, sehingga dapat mengurangi peluang pemadanan yang berulang.
Untuk lebih jelas menggambarkan masalah ini, perhatikan Contoh 19 berikut. Di mana diketahui populasi berukuran delapan, akan dibangun beberapa bujursangkar latin berorde empat lalu secara acak memilih pemasangan yang terbentuk tersebut. Diperlukan lebih dari satu bujursangkar latin karena bila hanya menggunakan satu bujursangkar latin mengakibatkan jika pasangan berulang, maka partisi dari keseluruhan populasi juga berulang.
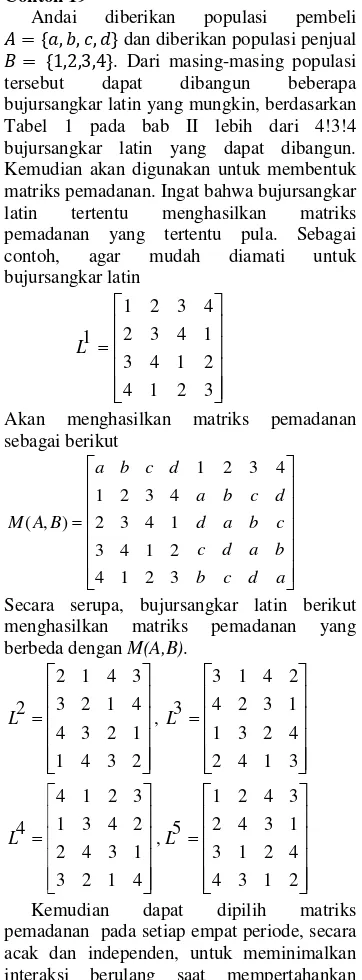
Contoh 19
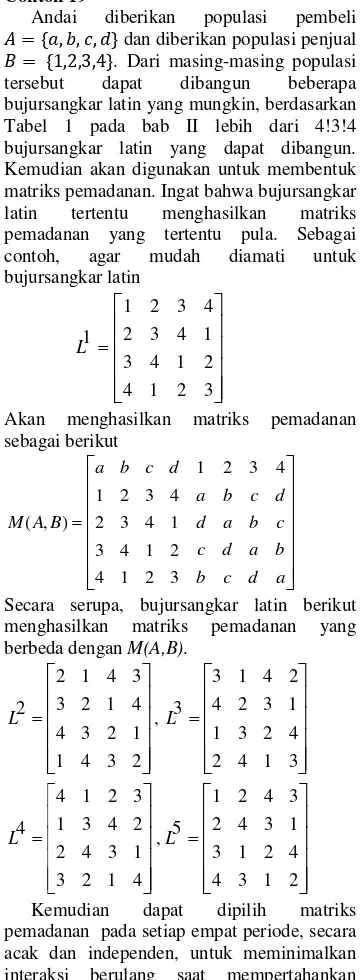
Andai diberikan populasi pembeli
, , , dan diberikan populasi penjual
, , , . Dari masing-masing populasi tersebut dapat dibangun beberapa bujursangkar latin yang mungkin, berdasarkan Tabel 1 pada bab II lebih dari 4!3!4 bujursangkar latin yang dapat dibangun. Kemudian akan digunakan untuk membentuk matrikspemadanan. Ingat bahwa bujursangkar latin tertentu menghasilkan matriks pemadanan yang tertentu pula. Sebagai contoh, agar mudah diamati untuk bujursangkar latin
1 2 3 4 2 3 4 1 1
3 4 1 2 4 1 2 3
L =
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
Akan menghasilkan matriks pemadanan sebagai berikut
1 2 3 4
1 2 3 4
( , ) 2 3 4 1
3 4 1 2 4 1 2 3 a b c d
a b c d
M A B d a b c
c d a b b c d a
=
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
Secara serupa, bujursangkar latin berikut menghasilkan matriks pemadanan yang berbeda dengan M(A,B).
2 1 4 3 3 1 4 2
3 2 1 4 4 2 3 1
2 3
,
4 3 2 1 1 3 2 4
1 4 3 2 2 4 1 3
L = L =
⎡
⎤
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
4 1 2 3 1 2 4 3
1 3 4 2 2 4 3 1
4 5
,
2 4 3 1 3 1 2 4
3 2 1 4 4 3 1 2
L = L =
⎡
⎤
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
⎣
⎦
VI. SIMPULAN DAN SARAN
6.1 Simpulan
Dalam proses pemadanan setiap agen dipadankan dengan agen lainnya tepat satu kali.
Jika banyaknya populasi (agen) yang ada adalah ganjil, maka dalam proses pemadanan pada periode tertentu terdapat agen yang tidak memiliki pasangan melainkan dipasangkan dengan dirinya sendiri.
Jika banyaknya populasi (agen) yang ada adalah genap, maka dalam proses pemasangan masing-masing agen akan bertemu dengan agen lain tepat satu kali.
Untuk masalah pemadanan antara n
penjual dan n pembeli maka matriks
pemadanan yang diperoleh akan berukuran .
6.2 Saran
Di dalam tulisan ini telah ditawarkan prosedur pembentukkan matriks pemadanan untuk populasi yang terbatas secara manual untuk selanjutnya pembentukan matriks pemadanan yang diinginkan dapat dibentuk dengan bantunan program komputer sehingga dapat memungkinkan membentuk matriks pemadanan untuk populasi yang besar.
VII DAFTAR PUSTAKA
Aliprantis CD, Camera G, Puzzello D, 2006. Matching and Anonymity.
Economic Theory.
Aliprantis CD, Camera G, Puzzello D, 2006. Bilateral Matching with Latin Squares. Departement of Economics, Purdue University. West Lafayette: USA.
Biggs, NL. 1989. Discrete mathematics, revised edition. Biddles ltd: London.
Kurtz, DC. 1992. Foundations of Abstract
Mathematics. McGraw-Hill, Inc:
Singapore.
Leon, SJ. 2001. Aljabar Linear dan Aplikasinya. Erlangga: Jakarta.
Montgomery, DC. 2001. Design and Analysis of Experiments. John Wiley &
Sons, INC: New York.
Stewart, J. 2001. Kalkulus, edisi ke-4 jilid 1. Gunawan H. & Susila I.N., alih bahasa; Hardani W. & Mahanani N., editor. Erlangga, Jakarta. Terjemahan dari
Calculus.
Wikipedi Indonesia. 2008. Permutasi.
FAKUL
DENGAN R
D
LTAS MAT
IN
PEMADA
RANCANG
MUHA
G
DEPARTEM
TEMATIKA
NSTITUT P
ANAN BILA
GAN BUJUR
AMAD SYA
G54104023
MEN MATE
A DAN ILM
PERTANIA
BOGOR
2008
ATERAL
RSANGKA
AZALI
EMATIKA
MU PENGET
AN BOGOR
AR LATIN
TAHUAN A
R
ABSTRACT
MUHAMAD SYAZALI. Bilateral Matching with Latin Squares. Under the supervision of TONI BAKHTIAR and RETNO BUDIARTI.
In this paper we are interested in a particular type of matching process. We match everyone in the population to someone else exactly once. We view the bilateral matching process as a sequence of involutions from a population to itself. The bilateral matching process is then constructed by arranging the involutions by means of Latin square.
We perform the matching process into several steps. First, we describe how to construct meetings two different agents but the same size. Second, we reconsider the first step when agents belong to an odd-sized population. Finally, we exploit the two earlier steps to construct a matching procedure for any finite population.
ABSTRAK
MUHAMAD SYAZALI. Pemadanan Bilateral dengan Rancangan Bujursangkar Latin. Dibimbing oleh TONI BAKHTIAR dan RETNO BUDIARTI.
Di dalam karya ilmiah ini, yang dikaji adalah sebuah bentuk khusus dari proses pemadanan, yang bertujuan memadankan setiap orang di dalam suatu populasi ke setiap orang lainnya tepat satu kali. Proses pemadanan bilateral dipandang sebagai sebuah rangkaian berbagai involusi dari sebuah populasi itu sendiri. Proses pemadanan bilateral kemudian dikonstruksi oleh aturan involusi menggunakan bujursangkar latin.
Pembentukan proses pemadanan dibagi ke dalam beberapa tahap. Pertama, mendiskripsikan bagaimana menyusun pertemuan di antara dua agen yang berbeda tetapi memiliki ukuran populasi yang sama. Tahap kedua, mempertimbangkan kembali tahap pertama ketika agen-agen tersebut memiliki populasi yang berukuran ganjil. Terakhir, dua tahap sebelumnya digunakan untuk menyusun sebuah prosedur pemadanan untuk setiap populasi yang terbatas.
I PENDAHULUAN
1.1 Latar Belakang
Pada kondisi-kondisi tertentu keheterogenan unit percobaan tidak bisa dikendalikan hanya dengan pengelompokkan satu sisi keragaman unit-unit percobaan namun memerlukan penanganan yang lebih kompleks. Kondisi ini tentunya memerlukan bentuk rancangan yang lain. Salah satu rancangan yang mampu mengendalikan komponen keragaman unit-unit percobaan lebih dari satu sisi komponen adalah rancangan bujursangkar latin (latin square). Tulisan ini menawarkan prosedur sederhana yang dapat digunakan untuk membangun sekuen (rangkaian) dari petemuan berpasang-pasangan diantara pelaku yang berasal dari populasi yang finite
(terbatas) dengan menggunakan rancangan bujursangkar latin tersebut. Proses pertemuan yang dipelajari memiliki dua sifat, pertama rangkaian dari pertemuan tersebut adalah eksogen yang berarti bahwa setiap pelaku bertemu dengan pelaku yang lain tepat satu kali. Kedua, dalam setiap periode proses ini memaksimumkan banyaknya dari pemasangan dalam populasi.
Dalam ilmu ekonomi proses pertemuan berpasang-pasangan dengan sifat ini
digunakan untuk meyatakan konsep dari persaingan dagang secara eksplisit.
Dalam mengembangkan prosedur untuk menciptakan rangkaian pemasangan yang diinginkan digunakan bentuk khusus dari permutasi yang disebut involusi. Dengan memanfaatkan beberapa hasil matematis dari bujursangkar latin, alasan untuk bekerja dengan objek matematika ini adalah proses pemasangan yang merupakan cara untuk membagi populasi X ke dalam himpunan agen-agen yang disjoint secara berulang-ulang. Karena diketahui bahwa pertemuan yang dipandang adalah bilateral, maka proses pemasangan dapat dilihat sebagai rangkaian involusi dari X ke X.
1.2 Tujuan
Adapun tujuan dari penulisan makalah ini adalah memasangkan agen satu dengan agen lainnya dalam populasi yang terbatas di mana setiap agen bertemu dengan agen lainnya tepat satu kali dengan memperagakan bagaimana membangun bujursangkar latin sedemikian rupa sehingga setiap baris, pada awalnya adalah involusi dari baris pertama yang akhirnya didapatkan suatu matriks pemadanan.
II. LANDASAN TEORI
2.1 Matriks
Matriks adalah kumpulan bilangan yang disusun dalam bentuk persegi panjang atau bujur sangkar yang tersusun dalam baris dan kolom. Ukuran atau ordo dari suatu matriks ditentukan oleh banyaknya baris dan kolom yang membentuknya.
Secara umum matriks dapat ditulis sebagai berikut
= elemen matrik A yang terletak pada baris ke-i, kolom ke-j ; i=1,2,…,m ;
j=1,2,…..,n
= ukuran atau ordo matriks A, yaitu
11 12 1
21 22 2
1 2
n
n
m m mn
a
a
a
a
a
a
A
a
a
a
⎡
⎤
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎣
⎦
L
L
M
M
O
M
L
[Leon 2001]
2.2 Bujursangkar Latin Definisi 1 (Bujursangkar Latin)
Diketahui ada n symbol berbeda, bujursangkar latin adalah matriks
dengan entri simbol-simbol yang diketahui yang disusun sedemikian rupa sehingga setiap simbol muncul tepat satu kali dalam setiap baris dan kolom.
[Aliprantis, et al 2006]
Contoh 1 :
Diberikan himpunan simbol-simbol {1, 2, 3, 4} dan {@, #, $, &}, matriks
1 2 3 4 @ # $ & 2 3 4 1 $ & @ #
dan
3 4 1 2 # $ & @ 4 1 2 3 & @ # $
⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎣ ⎦ ⎣ ⎦
I PENDAHULUAN
1.1 Latar Belakang
Pada kondisi-kondisi tertentu keheterogenan unit percobaan tidak bisa dikendalikan hanya dengan pengelompokkan satu sisi keragaman unit-unit percobaan namun memerlukan penanganan yang lebih kompleks. Kondisi ini tentunya memerlukan bentuk rancangan yang lain. Salah satu rancangan yang mampu mengendalikan komponen keragaman unit-unit percobaan lebih dari satu sisi komponen adalah rancangan bujursangkar latin (latin square). Tulisan ini menawarkan prosedur sederhana yang dapat digunakan untuk membangun sekuen (rangkaian) dari petemuan berpasang-pasangan diantara pelaku yang berasal dari populasi yang finite
(terbatas) dengan menggunakan rancangan bujursangkar latin tersebut. Proses pertemuan yang dipelajari memiliki dua sifat, pertama rangkaian dari pertemuan tersebut adalah eksogen yang berarti bahwa setiap pelaku bertemu dengan pelaku yang lain tepat satu kali. Kedua, dalam setiap periode proses ini memaksimumkan banyaknya dari pemasangan dalam populasi.
Dalam ilmu ekonomi proses pertemuan berpasang-pasangan dengan sifat ini
digunakan untuk meyatakan konsep dari persaingan dagang secara eksplisit.
Dalam mengembangkan prosedur untuk menciptakan rangkaian pemasangan yang diinginkan digunakan bentuk khusus dari permutasi yang disebut involusi. Dengan memanfaatkan beberapa hasil matematis dari bujursangkar latin, alasan untuk bekerja dengan objek matematika ini adalah proses pemasangan yang merupakan cara untuk membagi populasi X ke dalam himpunan agen-agen yang disjoint secara berulang-ulang. Karena diketahui bahwa pertemuan yang dipandang adalah bilateral, maka proses pemasangan dapat dilihat sebagai rangkaian involusi dari X ke X.
1.2 Tujuan
Adapun tujuan dari penulisan makalah ini adalah memasangkan agen satu dengan agen lainnya dalam populasi yang terbatas di mana setiap agen bertemu dengan agen lainnya tepat satu kali dengan memperagakan bagaimana membangun bujursangkar latin sedemikian rupa sehingga setiap baris, pada awalnya adalah involusi dari baris pertama yang akhirnya didapatkan suatu matriks pemadanan.
II. LANDASAN TEORI
2.1 Matriks
Matriks adalah kumpulan bilangan yang disusun dalam bentuk persegi panjang atau bujur sangkar yang tersusun dalam baris dan kolom. Ukuran atau ordo dari suatu matriks ditentukan oleh banyaknya baris dan kolom yang membentuknya.
Secara umum matriks dapat ditulis sebagai berikut
= elemen matrik A yang terletak pada baris ke-i, kolom ke-j ; i=1,2,…,m ;
j=1,2,…..,n
= ukuran atau ordo matriks A, yaitu
11 12 1
21 22 2
1 2
n
n
m m mn
a
a
a
a
a
a
A
a
a
a
⎡
⎤
⎢
⎥
⎢
⎥
=
⎢
⎥
⎢
⎥
⎣
⎦
L
L
M
M
O
M
L
[Leon 2001]
2.2 Bujursangkar Latin Definisi 1 (Bujursangkar Latin)
Diketahui ada n symbol berbeda, bujursangkar latin adalah matriks
dengan entri simbol-simbol yang diketahui yang disusun sedemikian rupa sehingga setiap simbol muncul tepat satu kali dalam setiap baris dan kolom.
[Aliprantis, et al 2006]
Contoh 1 :
Diberikan himpunan simbol-simbol {1, 2, 3, 4} dan {@, #, $, &}, matriks
1 2 3 4 @ # $ & 2 3 4 1 $ & @ #
dan
3 4 1 2 # $ & @ 4 1 2 3 & @ # $
⎡ ⎤ ⎡ ⎤
⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎢ ⎥ ⎢ ⎥
⎣ ⎦ ⎣ ⎦
secara umum dapat diperoleh banyak bujursangkar latin yang berbeda, dan juga banyaknya bujursangkar latin yang terbentuk akan semakin bertambah bergantung pada n. Walaupun bujursangkar latin telah dipelajari secara rinci dalam matematika banyaknya bujursangkar latin yang ada telah dihitung hanya untuk .
[Aliprantis, et al 2006]
Diketahui himpunan populasi
, … … … , dengan n agen. Ada tiga prosedur pembangunan bujursangkar latin yang masing-masing menghasilkan matriks
yang spesifik.
2.2.1 KonstruksiBujursangkar Latin1 Bujursangkar latin ini dinotasikan dengan dan baris pertamanya adalah vektor (1, 2, . . . . , n). Baris lainnya dari dihasilkan secara rekursif dengan cara menggeser satu tempat ke kiri baris yang sebelumnya secara
siklik. Yang berarti baris kedua diperoleh dengan cara menggeser baris pertama satu tempat ke kiri, dalam contoh di atas baris kedua adalah (2, 3, . . . . , n, 1) dan baris ke tiga adalah vektor (3, 4, . . . ., n, 1, 2). Dengan demikian adalah matriks seperti berikut :
1 2 ... 2 1
2 3 1 1
3 4 1 2
1 4 3 2
1 3 2 1
n n n
n n
n
n n n n n
n n n n
− − − − − − − − − −
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
L LM M O M M M
L L
Jika menggunakan notasi standar untuk bujursangkar latin ini maka setiap entri diberikan formula sebagai berikut:
jika 1 dan 1
1 ( 1) 1 jika 2 dan 1
( ) 1 jika 2 dan 2
j i j n
aij i j n Y i j i j i i j n i
j n i i n i j n
χ = ≤ ≤ = + − − + − = + − ≥ ≤ ≤ − + − − − ≥ − + ≤ ≤
⎧⎪
⎨
⎪⎩
di mana χY N: →{0,1} adalah fungsi karakteristik dari himpunan
, , … dengan
( ) 1 jika dan ( ) 0 jika .
Y k k Y Y k k Y
χ = ∈ χ = ∉
Contoh 2
Saat konstruksi ini akan
menghasilkan bujursangkar latin
1 2 3 4 2 3 4 1 3 4 1 2 4 1 2 3
L− =
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
.2.2.2 KonstruksiBujursangkar Latin2 Misalkan notasi untuk bujursangkar latin ini adalah . Matriks ini memiliki baris pertama (1, 2, . . ., n) dan konstruksinya dibuat secara rekursif tepat seperti cara pertama, tetapi satu-satunya perbedaan terletak pada
cara penggeserannya yang ke arah kanan bukan ke arah kiri. Hal ini berarti baris kedua dari diperoleh dengan cara menggeser baris pertama ke kanan secara siklik, dalam contoh, baris ke dua adalah vektor (n, 1,…, n-2, n-1), dan baris ketiga adalah vektor (n-1, n, 1, …,
n-2), dan seterusnya. Bujursangkar latin yang terbentuk adalah
1 2 2 1
1 3 2 1
1 4 3 2
3 4 1 2
2 3 1 1
n n n
n n n n
n n n n n
L n n n − − − − − − − − − + = − ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ L L L
M M O M M M
L L
Dengan notasi maka formula untuk entri dari adalah
jika 1dan1
1 ( 1 1) ( ) 1 jika 2 dan1 1
1 jika 2 dan
j i j n
aij n j i n Y n j n i j i j i
j i i i j n
Contoh 3
Di mana saat kita mendapatkan
1 2 3 4
4 1 2 3 3 4 1 2 2 3 4 1
L+ =
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
.2.2.3 KonstruksiBujursangkar Latin3 Bujursangkar latin dinotasikan dengan
di mana baris pertama adalah (n, n-1, …1) dan baris lainnya dibentuk dengan cara mengikuti prosedur rekursif dengan cara menggeser baris pertama satu tempat ke kiri, sehingga baris ke dua yang terbentuk adalah (n-1,n-2, …, 1, n). Dengan mengulang proses
ini sebanyak maka diperoleh bujursangkar latin seperti berikut :
1 2 1
1 2 1
1 3 2
2 1 4 3
1 3 2
n n
n n n
L n i n i n i n i
n − − − = − + − − + − + ⎡ ⎤ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ L L
M M O M M
L
M M O M M
M M
Dengan maka formula untuk entri dari L adalah
1 jika 1dan1
1 ( 1) ( 1) 2 jika 2dan1 1
2 2 jika 2dan 2
n j i j n
aij n i j n Y i j n i j i j n i
n i j i n i j n
χ + − = ≤ ≤ = + − + − + + − = + − − ≥ ≤ ≤ − + − + − ≥ − + ≤ ≤
⎧⎪
⎨
⎪⎩
Contoh 4Saat bujursangkar latin L adalah seperti berikut :
4 3 2 1 3 2 1 4 2 1 4 3
1 4 3 2
L=
⎡
⎤
⎢
⎥
⎢
⎥
⎢
⎥
⎢
⎥
⎣
⎦
Berdasarkan dari ketiga konstruksi bujursangkar latin di atas maka untuk sembarang populasi berukuran n terdapat beberapa bujursangkar latin yang dapat dibentuk. Banyaknya bujursangkar latin yang dapat dibentuk dari populasi berukuran n
dapat dilihat dari Tabel 1 berikut:
Tabel 1 Banyak bujursangkar latin dari populasi berukuran n sebarang.
Ukuran Contoh bujursangkar latin standar
A B C B C A C A B
A B C D B C D A C D A B D A B C
A B C D E B A E C D C D A E B D E B A C E C D B A
A B C D E F B C F A D E C F B E A D D E A B F C E A D F C B F D E C B A
A B C D E F G B C D E F G A C D E F G A B D E F G A B C E F G A B C D F G A B C D E G A B C D E F
ABC...N BCD...A CDE...B . . . PAB...(P-1) Banyaknya bujursangkar latin standar
1 4 56 9408 16.942.080 ---
Banyaknya bujursangkar latin yang terbentuk
2.3 Fungsi Definisi 2 (Fungsi)
Fungsi (pemetaan) f dari himpunan A ke himpunan B, dinotasikan , adalah suatu relasi dari A ke B yang setiap anggota dari A muncul hanya sekali sebagai komponen pertama dari pasangan terurut keanggotaan relasi yang bersangkutan.
Kurtz 1992]
Dari definisi dia atas, jika , , maka dapat ditulis b = f (a). Dalam hal ini b disebut imej dari a dibawa oleh f, sedangkan a
disebut preimej dari b oleh f. Penulisan ringkas dengan menerapkan lambang logika dari definisi di atas dapat dinyatakan sebagai berikut.
jika dan hanya jika
! , atau
: jika dan hanya jika ( )
[ ( ) ( )] maka .
f A B a A
b f a c f a b c
→ ∀ ∈
= ∧ = =
Contoh 5
Misalkan , , dan , , , , perhatikan bahwa , , , , ,
adalah fungsi dari A ke B, sedangkan
, , , dan
, , , , , , , bukan merupakan fungsi dari A ke B.
Definisi 3 (Fungsi Injektif)
Fungsi f disebut fungsi injektif (satu-satu) apabila f tidak pernah mencapai nilai yang sama dua kali; yakni,
jika maka
[Stewart 2001]
Contoh 6
Misalkan , , dan B = {a,b,c,d,e}.
fungsi , , , , , adalah
injektif, sedangkan fungsi
, , , , , bukan merupakan fungsi injektif.
Perhatikan Contoh 6 di atas komponen ke dua dari semua anggota f muncul hanya sekali, sehingga f adalah fungsi injektif. Sekarang perhatikan fungsi , unsur a muncul dua kali sebagai komponen ke dua di dalam kenggotaan , sehingga tidak inje