Penentuan Path Terpendek Dengan Algoritme Dekomposisi Jarvis-Tufekci

PENENTUAN PATH TERPENDEK DENGAN ALGORITME

DEKOMPOSISI JARVIS-TUFEKCI

Oleh:

DWI ADE RACHMA PUTRI

G05400050

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

ABSTRAK

DWI ADE RACHMA PUTRI. Penentuan Path Terpendek dengan Algoritme Dekomposisi

Jarvis-Tufekci. Dibimbing oleh FARIDA HANUM dan PRAPTO TRI SUPRIYO.

Salah satu masalah arus dalam suatu network adalah penentuan path terpendek. Masalah

path terpendek ini merupakan masalah pengoptimuman, karena dengan diperolehnya path

terpendek diharapkan dapat mengoptimumkan faktor yang lain (misalkan: waktu dan biaya). Secara umum, masalah path terpendek dalam suatu network ini terbagi menjadi 3 tipe, yakni menentukan

(1) path terpendek antara suatu simpul dan simpul lainnya,

(2) path terpendek antara suatu simpul dengan semua simpul lainnya, dan

(3) path terpendek antara semua pasang simpul yang terdapat pada network tersebut.

Salah satu algoritme yang dapat digunakan untuk menentukan path terpendek tipe (1) yakni path terpendek antara suatu simpul dan simpul lainnya adalah algoritme dekomposisi Jarvis-Tufekci. Dalam karya ilmiah ini kedua simpul tersebut masing-masing adalah simpul source

(sumber) dan sink (tujuan). Tahapan yang dilakukan dalam algoritme ini adalah mendekomposisi suatu network yang diberikan menjadi beberapa buah subnetwork yang bertindih secara linear (linearly overlapping). Lima tahap utama akan dilakukan dalam menyelesaikan masalah path

PENENTUAN PATH TERPENDEK DENGAN ALGORITME

DEKOMPOSISI JARVIS-TUFEKCI

Oleh:

DWI ADE RACHMA PUTRI

G05400050

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

Judul Skripsi : Penentuan Path Terpendek dengan Algoritme Dekomposisi Jarvis-Tufekci

Nama : Dwi Ade Rachma Putri

NIM : G05400050

Menyetujui:

Pembimbing I,

Dra. Farida Hanum, M.Si.

NIP. 131 956 709

Pembimbing II,

Drs. Prapto Tri Supriyo, M. Kom.

NIP. 131 878 952

Mengetahui:

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Pertanian Bogor

Prof.Dr.Ir. Yonny Koesmaryono, MS.

NIP. 131 473 999

PRAKATA

Alhamdulillaahirabbil’aalamin, Puji dan Syukur khadirat Allah SWT atas rahmat dan karunia-Nya penulis dapat menyelesaikan penulisan karya ilmiah ini. Pada kesempatan ini penulis ingin mengucapkan terima kasih kepada:

1. Dra. Farida Hanum, M.Si., dan Drs. Prapto Tri Supriyo, M. Kom. selaku dosen pembimbing yang telah banyak membantu, membimbing, memberi saran, kritik, serta kepercayaan dan kesabarannya selama penulis menyelesaikan tugas akhir ini.

2. Drs. Siswandi, M. Si. selaku dosen penguji, terima kasih.

3. Bapak, Mamah, Mbak Ria, Mas Yudi, Atin, Sitta, Athaya, Mas Iwan, dan seluruh keluarga atas do’a, dukungan, kasih sayang dan kesabarannya.

4. Mas Deni, Ibu Susi, Ibu Ade, Mas Yono, seluruh dosen dan staf Departemen Matematika IPB.

5. Nina, Ida, Nia, Echi, Ribut, Choi, Mbak Nine, dan semua teman ’37 yang masih selalu

memberikan semangat dukungan, dan persahabatan.

6. Lilis, Sri, Marlin, Indah, Hikmah, Desi, adik-adik angkatan terima kasih atas bantuannya. 7. Seluruh staf dan pengajar Bimbingan Belajar dan Les Privat Bina Ilmu Plus Depok.

Bogor, Januari 2007

RIWAYAT HIDUP

Penulis dilahirkan di Jakarta pada tanggal 1 Juli 1982 dan merupakan putri kedua dari empat bersaudara pasangan bapak Aris Sunaryo dan ibu Dyah Septi Sumarsiasih.

Pada tahun 2000 penulis menyelesaikan pendidikan di Sekolah Menengah Umum Negeri I Bogor. Pada tahun yang sama, penulis diterima di Institut Pertanian Bogor, Departemen Matematika melalui jalur Ujian Masuk Perguruan Tinggi Negeri (UMPTN).

DAFTAR ISI

Halaman

DAFTAR GAMBAR ... vii

PENDAHULUAN Latar Belakang... 1

Tujuan ... 1

LANDASAN TEORI Graf ... 1

Network... 5

Kompleksitas Algoritme ... 9

Algoritme Dekomposisi Hu ... 9

PEMBAHASAN Dekomposisi Network... 10

Contoh penerapan algoritme dekomposisi Jarvis-Tufekci untuk menentukan path terpendek ... 14

Penghitungan Kompleksitas Algoritme Dekomposisi Jarvis-Tufekci ... 18

SIMPULAN... 20

DAFTAR GAMBAR

Halaman

1 Graf dengan 4 simpul dan 5 sisi ... 1

2 G’ subgraf dari G... 2

3 Graf dengan 2 komponen... 2

4 Digraf ... 2

5 (a) Walk 1−2−3−4−5 adalah contoh walk berarah... 3

(b) Walk 1−2−3−4−5 adalah contoh walk tidak berarah... 3

6 Path... 3

7 Contoh subpath... 3

8 (a) Cycle 1−2−3−1 adalah cycle berarah... 3

(b) Cycle 1−2−3−1 adalah cycle tidak berarah ... 3

9 (a) Digraf terhubung... 4

(b) Digraf takterhubung... 4

10 Digraf terboboti... 4

11 Digraf yang mengandung cycle... 5

12 Network... 5

13 Contoh network yang longgar... 6

14 (a) Network dengan cut set... 6

(b) Network takterhubung setelah cut set dihilangkan... 6

15 Contoh minimal cut set pada suatu network... 7

16 Contoh path dengan 3 simpul ... 7

17 Contoh path dengan 5 simpul ... 7

18 Ilustrasi m buah subnetwork yang bertindih secara linear (linearly overlapping) ... 8

19 Contoh network dengan 3 buah subnetwork... 8

20 Network yang telah terdekomposisi... 8

21 Ilustrasi hasil akhir tahap dekomposisi pada suatu network menjadi m buah subnetwork yang bertindih secara linear ... 11

22 Contoh network N’ yang terbentuk... 12

23 Contoh path dalam network terdekomposisi ... 13

24 Network yang akan didekomposisi ... 15

25 Subnetwork N1_{... 15}

26 Subnetwork N2_{... 16}

27 Subnetwork N3_{... 17}

PENDAHULUAN

Latar Belakang

Salah satu masalah arus dalam suatu network

adalah penentuan path terpendek. Masalah

path terpendek ini merupakan masalah

pengoptimuman, karena dengan diperolehnya

path terpendek diharapkan dapat

mengoptimumkan faktor yang lain (misalkan: waktu dan biaya).

Secara umum, masalah path terpendek dalam suatu network ini terbagi menjadi 3 tipe, yakni:

(1) path terpendek antara suatu simpul dan simpul lainnya,

(2) path terpendek antara suatu simpul

dengan semua simpul lainnya, dan

(3) path terpendek antara semua pasang

simpul yang terdapat pada network

tersebut.

Pada karya ilmiah ini, yang menjadi masalah utama adalah masalah tipe (1), yaitu mencari

path terpendek antara suatu simpul, yaitu

source dan suatu simpul lainnya, yaitu sink.

Terdapat beberapa algoritme yang dapat digunakan untuk mencari path terpendek, salah satunya adalah algoritme dekomposisi. Algoritme dekomposisi dibahas di dalam [Hu, 1981], [Yen, 1968], dan [Shier et al., 1973].

Namun, tiap prosedur yang diperkenalkan memiliki keuntungan yang berbeda. Prosedur yang diperkenalkan oleh Hu akan tepat bila diaplikasikan pada network yang memiliki struktur linear. Prosedur yang diperkenalkan oleh Shier akan tepat bila diaplikasikan pada

network dengan struktur tree. Ada pula prosedur yang akan tepat bila diaplikasikan pada network berbentuk star, yaitu algoritme dekomposisi yang diperkenalkan oleh Land dan Stairs [Land & Stairs, 1967].

Dalam karya ilmiah yang merupakan rekonstruksi dari tulisan Jarvis dan Tufekci [Jarvis & Tufekci, 1982] ini, algoritme yang banyak diterapkan adalah algoritme dekomposisi yang diperkenalkan oleh Hu [Hu, 1981]. Dalam karya ilmiah ini juga dilakukan penghitungan kompleksitas dari algoritme dekomposisi yang digunakan.

Tujuan

Tujuan penulisan karya ilmiah ini adalah

mempelajari penyelesaian masalah path

terpendek antara simpul source (s) dan sink (t) dalam sebuah network dengan menggunakan Algoritme Dekomposisi Jarvis-Tufekci.

LANDASAN TEORI

Dalam mencari path terpendek antara source

(s) dan sink (t) dalam sebuah network dengan algoritme dekomposisi, diperlukan beberapa konsep sebagai berikut:

Graf Definisi 1 (Graf)

Suatu graf adalah pasangan terurut (V,E)

dengan V adalah himpunan berhingga dan

takkosong dari elemen-elemen graf, yang disebut simpul (node, verteks), dan E adalah himpunan pasangan takterurut dari simpul- simpul di V. Setiap {p,q}∈E (dengan p,q∈V)

disebut sisi (edge) dan dikatakan

menghubungkan simpul p dan simpul q. Sisi {p,q} dapat pula dituliskan dengan pq.

(Foulds, 1992)

Ilustrasi: G:

Gambar 1. Graf dengan 4 simpul dan 5 sisi.

v1 v2

v3 v4

e1

e2

e3 e₄

6

5

2

3

4 1

6

5

2

3 1

1

2

3

4

5 1

2

3

4

5

6 Graf G pada Gambar 1 mempunyai himpunan

simpul V={v1, v2, v3, v4} dan himpunan sisi

E={e1, e2, e3, e4, e5}.

Definisi 2 (Incident)

Misalkan diberikan graf G=(V,E). Jika sisi

e={p,q}∈E, maka simpul p dan q masing-masing dikatakan incident dengan sisi e. Dapat pula dikatakan bahwa sisi e incident

dengan simpul p dan q.

(Foulds, 1992)

Ilustrasi:

Berdasarkan graf pada Gambar 1, maka

e1 incident dengan simpul v1 dan v2,

e2incident dengan simpul v1 dan v3,

e3incident dengan simpul v2 dan v3, dan seterusnya.

Definisi 3 (Subgraf)

Suatu graf G’=(V’,E’) adalah suatu subgraf dari G=(V,E) jika V’⊆V dan E’⊆E.

(Ahuja et al., 1993)

Ilustrasi: G:

G’:

Gambar 2. G’ subgraf dari G.

Definisi 4 (Komponen)

Suatu subgraf maksimum yang terhubungkan dari graf G disebut komponen dari G.

(Foulds, 1992)

Ilustrasi: G:

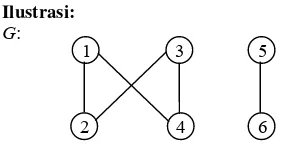
Gambar 3. Graf dengan 2 komponen.

Graf G pada Gambar 3 memiliki 2 buah

komponen, yaitu komponen yang mengandung himpunan simpul {1,2,3,4} dan yang mengandung himpunan simpul {5,6}.

Definisi 5 (Digraf)

Suatu graf berarah/digraf (directed graph) D

adalah pasangan terurut (V,A) dengan V

adalah himpunan takkosong dan hingga, dan A

adalah himpunan pasangan terurut elemen-elemen di V. Elemen dari A biasa disebut sisi berarah (arc).

Jika (u,v) (seringkali dituliskan dengan uv) adalah suatu sisi berarah pada digraf, maka u

dikatakan predecessor dari v, dan v adalah suatu successor dari u.

(Foulds, 1992)

Ilustrasi: D:

Gambar 4. Digraf.

Untuk digraf pada Gambar 4, V={1,2,3,4,5} dan A={(1,2), (1,3), (2,3), (2,4), (2,5), (3,5), (4,5)}.

Pada sisi berarah (1,2), maka simpul 1 adalah

predecessor bagi simpul 2, dan simpul 2 adalah successor bagi simpul 1. Hal yang sama berlaku bagi sisi berarah lainnya.

Definisi 6 (Walk)

Suatu walk pada suatu digraf D=(V,A) adalah suatu subgraf dari D=(V,A) yang berupa suatu barisan dari simpul dan sisi berarah i1−a1−i2−

a2−…−ir−1−ar−1−ir dan untuk semua 1≤ k ≤r−1

berlaku ak=(ik , ik+1)∈A atau dapat ditulis

Dapat pula dikatakan bahwa walk adalah suatu himpunan (barisan) dari sisi berarah atau simpul-simpul.

Walk dapat dibedakan menjadi 2, yakni:

a) Walk berarah yaitu suatu walk yang

memiliki satu arah, sehingga untuk sembarang 2 buah simpul ik dan ik+1 yang berurutan pada walk tersebut, (ik , ik+1)∈A. b) Walk tidak berarah yaitu suatu walk yang

tidak memenuhi definisi walk berarah. (Ahuja et al., 1993)

Ilustrasi:

Gambar 5(a). Walk 1−2−3−4−5 adalah contoh walk berarah.

Gambar 5(b). Walk 1−2−3−4−5 adalah contoh walk tidak berarah.

Definisi 7 (Path)

Suatu path dalam suatu digraf adalah suatu

walk dengan semua simpulnya berbeda (tidak ada yang berulang).

Berdasarkan definisi walk, maka path dapat pula dibedakan menjadi 2, yakni path berarah dan path tidak berarah.

(Ahuja et al., 1993)

Ilustrasi:

Gambar 6. Path.

Path 1−2−3−5 pada Gambar 6 merupakan contoh path yang dimiliki oleh digraf pada Gambar 4. Path ini merupakan contoh path

berarah.

Definisi 8 (Subpath)

Suatu subpath dari path v0−v1−v2−...−vk

adalah barisan simpul vi−vi+1−...−vj yang

terdapat dalam path tersebut sedemikian sehingga 0 ≤i ≤j ≤ k.

(Cormen et al., 1990)

Ilustrasi:

Dengan menggunakan path pada Gambar 6

dapat diperoleh contoh subpath, yakni:

Gambar 7. Contoh subpath.

Definisi 9 (Cycle)

Suatu cycle adalah suatu path i1−i2−...−ir dan

mengandung (i1, ir) atau (ir,i1), atau dapat dituliskan sebagai i1−i2−...−ir−i1. Suatu cycle dapat pula didefinisikan sebagai path yang tertutup.

Berdasarkan definisi path, maka cycle dapat dibedakan menjadi 2, yakni:

1) Cycle berarah yaitu path berarah

i1−i2−...−ir dan mengandung sisi berarah

(ir,i1).

2) Cycle tidak berarah yaitu path tidak berarah i1−i2−...−ir dan mengandung sisi

berarah (ir,i1).

(Ahuja et al., 1993)

Ilustrasi:

Gambar 8(a). Cycle 1−2−3−1 adalah

cycle berarah.

Gambar 8(b) Cycle 1−2−3−1 adalah

cycle tidak berarah. 1

2

3 5

1

2

3 4 5 1

2

3 4 5

1

2 3

1

2

3

1

1

2

3

4

3 1

1

1 5

Definisi 10 (Digraf Terhubungkan)

Suatu digraf D=(V,A) dikatakan terhubungkan (connected), jika terdapat paling sedikit satu buah path yang menghubungkan setiap pasang simpul pada digraf tersebut. Jika tidak, maka digraf tersebut dikatakan takterhubung.

(Foulds, 1992)

Ilustrasi:

Gambar 9(a). Digraf terhubung.

Gambar 9(b). Digraf takterhubung.

Definisi 11 (Graf terboboti)

Suatu graf G=(V,E) atau digraf D=(V,A) dikatakan terboboti jika terdapat fungsi

d:E→R atau d:A→R (dengan R adalah himpunan bilangan real) yang memetakan setiap bilangan real (yang disebut bobot) untuk setiap sisi di E (atau A). Setiap bobot

d(uv) dengan uv ∈ E (atau uv ∈ A) biasa dituliskan dengan duv.

(Foulds, 1992)

Ilustrasi:

Gambar 10. Digraf terboboti.

Definisi 12 (Panjang sisi berarah)

Misalkan diberikan suatu digraf terboboti dengan fungsi yang memetakan tiap sisi berarah dengan suatu bilangan real. Maka, bobot ini dapat pula dikatakan sebagai panjang sisi berarah. Panjang sisi berarah

yang menghubungkan simpul u dengan v

dinotasikan dengan duv=d(u,v), dan

didefinisikan pula bahwa d(u,u)=0, dan

d(u,v)=∞ (takhingga) jika tidak ada sisi berarah yang menghubungkan simpul u dan v

tersebut.

(Cormen et al., 1990)

Ilustrasi:

Bardasarkan digraf terboboti pada Gambar 10, maka dapat diperoleh:

d(1,1)=0 d(2,3)=1

d(1,2)=1 d(2,4)=5

d(1,3)=3 d(3,3)=0

d(1,4)=∞ d(3,4)=1

d(2,2)=0 d(4,4)=0.

Definisi 13 (Panjang path)

Misalkan diberikan path p, v0−v1−v2−...−vk.

Panjang path p adalah jumlah semua panjang sisi berarah yang terdapat pada path tersebut, atau dapat dituliskan sebagai:

∑

= −

=

= k

i

i i

k d v v

v v d p d

1 1

0, ) ( , )

( )

( .

(Cormen et al., 1990)

Ilustrasi:

Pada Gambar 10, terdapat beberapa path.

Berikut ini panjang path-path yang

menghubungkan simpul 1 dan simpul 4 pada digraf pada Gambar 10 tersebut:

Panjang path 1−2−4 =d(1,4)

=d(1,2)+d(2,4)

=1+5

=6 Panjang path 1−3−4 =d(1,4)

=d(1,3)+d(3,4)

=3+1

=4 Panjang path 1−2−3−4 =d(1,4)

=d(1,2)+d(2,3)+d(3,4)

=1+1+1

=3.

Definisi 14 (Path terpendek)

Path u−v dikatakan sebagai path terpendek jika path yang menghubungkan simpul u dan simpul v tersebut memiliki panjang minimum di antara path-path u−v lainnya.

(Hu, 1981)

Ilustrasi:

Berdasarkan digraf terboboti pada Gambar 10, dan panjang path-path yang menghubungkan simpul 1 dan 4 pada Ilustrasi Definisi 13, maka dapat ditentukan path terpendek yang menghubungkan simpul 1 dan 4 adalah path

1 2

3

4

5

1 2

3

4

1−2−3−4, karena memiliki panjang minimum di antara path-path 1−4 lainnya, yaitu 3.

Dalam karya ilmiah ini, definisi “panjang” dapat pula diartikan sebagai “jarak”.

Definisi 15 (Matriks jarak)

Misalkan D=(V,A) adalah suatu digraf dengan

} ,...., , {v1 v2 vn

V= dan A={a1,a2,....,am}.

Matriks jarak M didefinisikan dengan M=(mij)

dengan mij=d(vi,vj).

(Chartrand & Oellermann, 1993)

Ilustrasi:

Dengan menggunakan digraf terboboti pada Gambar 10, maka dapat diperoleh matriks jarak dari digraf tersebut, yakni sebagai berikut:

1 0 1 3

2 0 1 5

3 0 1

4 0

M

+∞

⎡ ⎤

⎢_+∞ ⎥

⎢ ⎥

=

⎢+∞ +∞ ⎥

⎢_{+∞ +∞ +∞} ⎥

⎣ ⎦

.

Definisi 16 (Panjang cycle)

Misalkan diberikan suatu cycle berarah c, yaitu v0−v1−v2−...−vk dengan v0 = vk. Panjang

cycle berarah c adalah jumlah panjang seluruh sisi berarah yang terdapat pada cycle tersebut, atau dapat dituliskan sebagai:

∑

= − −

−

= k

i

i i i

i v d v v

v d c

d

1

1

1, ) ( , )]

( [ )

( .

Panjang cycle dapat dibedakan sebagai

berikut:

•Panjang cycle dikatakan negatif jika d(c)< 0

•Panjang cycle dikatakan taknegatif jika

d(c) ≥ 0

•Panjang cycle dikatakan positif jika d(c) >0. (Ahuja et al., 1993)

Ilustrasi:

Gambar 11. Digraf yang mengandung cycle.

Berdasarkan Gambar 11, cycle 2−4−3−2

merupakan cycle negatif karena memiliki

panjang cycle:

d(c) = d(2,4) + d(4,3) + d(3,2) = (−11) + 2 +8

= −1 < 0.

Sedangkan cycle 1−3−2−1 merupakan cycle

taknegatif (dapat pula dikatakan positif), karena memiliki panjang cycle:

d(c) = d(1,3) + d(3,2) + d(2,1) = 5 + 8 + (−10)

= 3 ≥ 0.

Network

Definisi 17

Kasus khusus digraf terboboti adalah network

(jaringan kerja). Beberapa konsep pada

network adalah sebagai berikut:

1.

Jika a = (vi,vj) adalah suatu sisi berarah

pada digraf D=(V,A), maka a dikatakan sebagai sisi berarah yang menjauhi vi dan

mendekati vj.

2.

Suatu simpul sehingga tidak ada sisi

berarah yang mendekati dirinya disebut dengan sumber (source), sedangkan suatu simpul sehingga tidak ada sisi berarah yang menjauhi dirinya disebut dengan

sink

3.

Suatu network adalah suatu digraf yang mempunyai tepat satu source dan tepat satu sink.

Pada banyak aplikasi network, paling sedikit terdapat satu aliran/flow yang bergerak dari

source ke sink. Flow pada network merupakan bobot pada digraf.

(Foulds, 1992)

Ilustrasi:

Gambar 12. Network.

Definisi 18 (Kerapatan network)

Kerapatan suatu network adalah perbandingan banyaknya sisi berarah sebenarnya pada

network dengan banyaknya sisi berarah 1

2

3

4

2 5

8

−11 −10

1

s 3 2 _t

2

3 1

2 2

maksimum yang mungkin terdapat pada

network tersebut.

Jika suatu network N

=

(V,A) terdiri atas n

buah simpul dan n(n−1) buah sisi berarah, maka network seperti itu dikatakan memiliki kerapatan sebesar 100%. Namun, jika suatu

network memiliki nilai kerapatan yang lebih

kecil dari 0,20 maka network tersebut

dikatakan longgar.

(Jarvis & Tufekci, 1982)

Ilustrasi: N:

Gambar 13. Contoh network yang longgar.

Network N pada Gambar 13 memiliki n=7 buah simpul yaitu {s,1,2,3,4,5,t}, dan 7 buah sisi berarah yaitu {a1,a2,a3,a4,a5,a6,a7). Banyaknya sisi berarah maksimum yang

mungkin terdapat pada network tersebut

adalah n(n−1)=7(7−1) =42 buah sisi berarah.

Maka, kerapatan network tersebut adalah

17 , 0 42

7 ₌ . Nilai kerapatan yang kurang dari

0,20 tersebut menunjukkan bahwa network

tersebut merupakan network yang longgar.

Definisi 19 (Cut set)

Misalkan diberikan suatu network terhubung

N=(V,A) dan misalkan B dan X merupakan himpunan bagian dari V dengan X ≠ B. Himpunan X dikatakan sebagai cut set dari B

jika memenuhi kondisi-kondisi berikut:

(a) Jika X dan semua sisi berarah yang

incident dengan X dihilangkan, maka

network N=(V,A) tersebut menjadi takterhubung,

(b) Semua simpul pada B berada pada satu komponen yang sama dan tidak terdapat simpul lain yang bukan anggota B pada komponen ini.

(Hu & Torres, 1969)

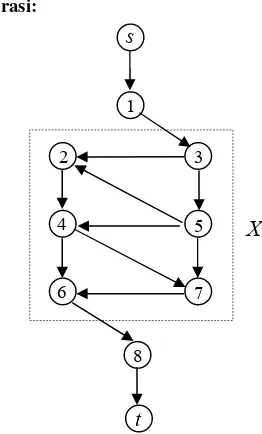
Ilustrasi: N:

Gambar 14(a). Network dengan cut set.

Gambar 14(b). Network takterhubung setelah

cut set dihilangkan.

Pada network N pada Gambar 14(a),

himpunan simpul X ={2,3,4,5,6,7} merupakan

cut set dari himpunan simpul {s,1}, atau cut set dari himpunan simpul {8,t}. Sedangkan Gambar 14(b) menunjukkan network tersebut menjadi takterhubung, jika himpunan simpul yang merupakan cut set tersebut dihilangkan.

Definisi 20 (Minimal cut set)

Misalkan X adalah cut set dari N. Maka, X

dikatakan sebagai minimal cut set jika tidak terdapat himpunan bagian sejati dari X yang juga merupakan cut set.

(Hu & Torres, 1969)

s

1

8 1

t

a

1

a

4

a

3

a

5

a

2

a

6

a

7

s

4

3

2

5

s

t

1

2 3

4 5

6 7

8

X

s

t

1

2 3

4 5

6 7

8

1

2

3

4

5 1

3

1

4 3

2

Ilustrasi:

X1

X2

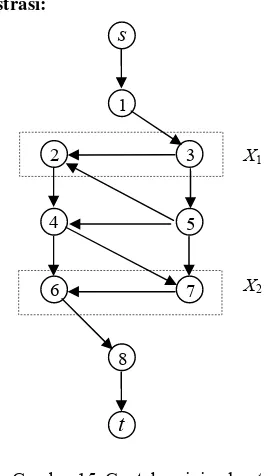
Gambar 15. Contoh minimal cut set

pada suatu network.

Berdasarkan Gambar 15, terlihat bahwa

X1={2,3} dan X2={6,7} adalah minimal cut

set pada network tersebut.

Berbeda halnya dengan cut set pada Gambar 14(a) yang tidak dapat dikatakan sebagai

minimal cut set karena masih memiliki

himpunan bagian sejati yang juga merupakan

cut set.

Definisi 21 (Operasi tripel)

Misalkan dij menyatakan panjang/jarak antara

simpul i dan simpul j pada digraf D. Maka, didefinisikan operasi tripel sebagai berikut:

dik ←min {dik, dij + djk}untuk i≠ j ≠k

dengan lambang “←” menyatakan “digantikan oleh”.

(Hu, 1981)

Ilustrasi:

Gambar 16. Contoh path dengan 3 simpul.

Untuk menentukan jarak terpendek antara

simpul i dan k pada Gambar 16, maka

dilakukan operasi tripel, yakni:

di k ← min {dik, dij+ djk}

= min {6,3+2}

= min {6,5}

= 5

∴di k ← 5.

Secara umum, operasi tripel dapat digunakan untuk lebih dari 3 simpul.

Ilustrasi:

Gambar 17. Contoh path dengan 5 simpul

Untuk menentukan jarak terpendek antara simpul 1 dan simpul 5, maka dilakukan operasi tripel sebagai berikut:

• d15 ← min {d15, d12 + d25}

• d15 ← min {d15, d13 + d35}

• d25 ← min {d25, d24 + d45} = min {+∞, 4 + 3}

= min {+∞, 7}

= 7

• d35 ← min {d35, d34 + d45} = min {2, 1 + 3} = min {2, 4}

= 2

• d15 ← min {d15, d13 + d35} = min {+∞, 3 + 2} = min {+∞, 5}

= 5

• d15 ← min {d15, d12 + d25} = min {5, 1 + 7} = min {5, 8}

= 5.

∴d15 ← 5.

Definisi 22 (Network terdekomposisi)

Misalkan Xi adalah himpunan simpul dan

diketahui Xi ≠ ∅, untuk setiap i. Suatu

network N=(V,A) dikatakan terdekomposisi

menjadi m buah subnetwork

m

N N N

N1, 2, 3,..., yang bertindih secara

linear (linearly overlapping) jika memenuhi kondisi-kondisi berikut:

(1) X_iIX_j= Ø ; i≠ j

(2) mN N

i i = =

U

1

i

j

k

3

2

s

t

1 2

3 4 2

2

1

1

3

3 5

4

X

(3)

⎪ ⎩ ⎪ ⎨ ⎧ =

−

Ø

1

i i

j

i X

X N

N I

). 1 ( ) 1 ( ;

1 ;

1 ;

+ − ≠

+ =

− =

i i, , i j

i j

i j

(Jarvis & Tufekci, 1982)

Gambar 18. Ilustrasi m buah subnetwork yang bertindih secara linear (linearly overlapping).

Berikut ini merupakan ilustrasi sebuah

network yang terdekomposisi menjadi 3 buah

subnetwork yang bertindih secara linear (linearly overlapping).

Ilustrasi: N:

Gambar 19. Contoh network dengan 3 buah subnetwork.

Network pada Gambar 19, terdekomposisi menjadi 3 buah subnetwork N1,N2,N3

dengan himpunan simpul di N1={s,1,2,3,4},

=

2

N {3,4,5,6}, dan N3 ={5,6,7,8}, dengan

X1 = {3,4} dan X2 = {5,6}.

Definisi 23 (Persamaan minisumasi)

Misalkan diberikan suatu network N=(V,A) yang terdekomposisi menjadi 2 buah

subnetwork N1 dan N2, maka N=N1∪X∪N2 dengan X adalah cut set pada network N.

Misalkan pula *

uv

d menyatakan jarak

terpendek antara simpul u dan simpul v.

Persamaan minisumasi didefinisikan sebagai berikut:

} {

min _{* *}

*

jk ij

ik d d

j

d = +

dengan i∈N1, j∈X, dan k∈N2.

(Hu & Torres, 1969)

Ilustrasi:

Misalkan diberikan suatu network N=(V,A) yang terdekomposisi menjadi 2 buah

subnetwork sebagai berikut:

N:

Gambar 20. Network yang telah terdekomposisi.

Network N pada Gambar 20 mempunyai 2 buah subnetwork dengan N1={s,1}, X={2,3}, dan N2={4,t}.

X1 X2 X3 ... Xm−1

1

N N2 N3 Nm

s

1

2

3

4

5

6

7

t

Untuk mengetahui jarak terpendek dari N1 ke

N2 dapat ditentukan dengan menggunakan

persamaan minisumasi berikut: )] ( ), min[( * 34 * 3 * 24 * 2 *

4 d d d d

d_s = _s + _s +

= min [(7 + 7), (3 + 1)] = min [14, 4]

= 4

)] ( ), min[( * 3 * 3 * 2 * 2 * t s t s

st d d d d

d = + +

= min [(7 + 1), (3 + 5)] = min [8, 8]

= 8

)] ( ), min[( * 34 * 13 * 24 * 12 *

14 d d d d

d = + +

= min [(6 + 7), (2 + 1)] = min [13, 3]

= 3

)] (

),

min[( 3*

* 13 * 2 * 12 *

1t d d t d d t

d = + +

= min [(6 + 1), (2 + 5)] = min [7, 7]

= 7.

Kompleksitas Algoritme Definisi 24 (Algoritme)

Algoritme adalah suatu tahapan/prosedur untuk menyelesaikan suatu masalah.

Langkah-langkah dari suatu algoritme dibedakan sebagai berikut:

1) Langkah penetapan.

Contoh: menetapkan beberapa nilai untuk suatu variabel.

2) Langkah aritmatika/penghitungan.

Contoh: penjumlahan, pengurangan, perkalian, dan pembagian.

3) Langkah logika.

Contoh: membandingkan 2 buah bilangan.

(Ahuja et al., 1993)

Definisi 25 (Kompleksitas Algoritme)

Fungsi kompleksitas waktu untuk suatu algoritme adalah fungsi dari ukuran masalah dan waktu yang diperlukan oleh algoritme tersebut untuk menyelesaikan masalah yang diberikan. Untuk selanjutnya, fungsi kompleksitas waktu ini disebut dengan kompleksitas algoritme.

(Ahuja et al., 1993)

Definisi 26 ( Notasi “big O”)

Notasi “big O” adalah suatu ekspresi yang menyatakan bahwa suatu algoritme

membutuhkan waktu cnm untuk beberapa

konstanta c. Pernyataan ini ekuivalen dengan pernyataan bahwa algoritme tersebut membutuhkan waktu O(nm). Secara formal dapat didefinisikan sebagai berikut:

“Suatu algoritme dikatakan bekerja dalam waktu O(f(n)) jika untuk beberapa bilangan c

dan no, maka waktu yang diperlukan oleh

algoritme tersebut paling banyak adalah cf(n) untuk semua n≥no”.

(Ahuja et al., 1993)

Algoritme Dekomposisi Hu

Hu adalah salah seorang tokoh yang memperkenalkan algoritme dekomposisi. Dalam karya ilmiah ini algoritme dekomposisi yang diperkenalkan oleh Hu berperan dalam penyelesaian masalah path terpendek pada suatu network yang diberikan.

Misalkan diberikan suatu network N=(V,A) yang longgar dan memiliki banyak simpul yang cukup besar (berskala besar). Untuk menyelesaikan masalah path terpendek dalam

network tersebut, Hu menggunakan algoritme dekomposisi. Langkah pertama pada algoritme dekomposisi Hu ini adalah

mendekomposisi network N=(V,A) yang

diberikan menjadi m buah subnetwork

m

N N N

N1, 2, 3,... , yang bertindih secara

linear (linearly overlapping).

Tahapan yang perlu dilakukan dalam mendekomposisi network N=(V,A) tersebut adalah:

1) Suatu himpunan simpul yang merupakan himpunan bagian dari V ditandai sebagai

N1.

2) Menentukan himpunan simpul yang

merupakan minimal cut set dari N1. 3) Menandai himpunan simpul berikutnya

yang merupakan cut set (tidak harus

merupakan minimal cut set) dari (N1∪X1) sebagai N2.

4) Menentukan himpunan simpul yang

merupakan minimal cut set dari

(N1∪X1∪N2) sebagai X2.

5) Hal yang sama dilakukan hingga network

tersebut terdekomposisi seluruhnya

menjadi m buah subnetwork

m

N N N

N1, 2, 3,..., dengan

1 1

1 N X

N = U ,

2 2 1

2 X N X

N = U U ,

3 3 2

3 X N X

1 1 2

1 _{− − −}

− = m m m

m X N X

N U U ,dan

m m

m X N

N = −₁U .

Jadi, N=N1∪X1∪N2∪....∪Xm−1∪Nm.

Misalkan didefinisikan Ni=Ni−(Xi−1UXi),

dan misalkan

j N i N

M menyatakan matriks jarak

dari Ni ke Nj, sedangkan *( )

k ij N

M menyatakan

matriks jarak terpendek dari Ni ke Nj yang

terletak pada Nk. Tahapan yang dilakukan

dalam algoritme dekomposisi Hu adalah sebagai berikut:

(1) Operasi tripel diaplikasikan pada m buah

subnetwork N1,N2,N3,...,Nm−1,Nm

secara bertahap. Jarak terpendek yang

diperoleh dari suatu subnetwork

menggantikan jarak aslinya pada

subnetwork berikutnya (yang akan dikenai operasi tripel), misalkan:

) ( 1 *

1 1 N

MXX yang diperoleh akan

menggantikan jarak

1 1X X

M sebelum

operasi tripel dilakukan pada subnetwork

2

N =N1∪X1∪N2. Hal yang sama

dilakukan hingga operasi tripel diaplikasikan pada subnetwork Nm. Pada

akhir tahap (1) ini diperoleh: )

( 1 *

1 1 N

M_NN , * ( 1 2)

2

2 N N

M_{N N} U , ...,

) ....

( 1 2 1

*

1

1 − −

−N m

N N N N

M

m

m U U U

, _M* (_N) m mN N .

(2) Operasi tripel diaplikasikan pada m−1 buah subnetwork Nm−1,Nm−2...,N2,N1

secara bertahap. Jarak yang diperoleh

pada suatu subnetwork menggantikan

jarak pada subnetwork selanjutnya (yang akan dikenai opersi tripel), misalkan:

) ( *

1 1 N

MXm−X_m− akan menggantikan jarak

) ( *

1 1Xm m m

X N N

M _{− −} − . Pada akhir tahap (2)

ini dapat diperoleh: M_N*_m−1Nm−1(N),..., )

(

*

2 2 N

M_{N N} , M*_N1N1(N).

(3) Jarak terpendek antara pasangan simpul

yang tidak terdapat pada subnetwork

yang sama ditentukan dengan menggunakan persamaan minisumasi.

(Hu & Torres, 1969)

PEMBAHASAN

Dekomposisi Network

Dalam bab ini akan diberikan beberapa asumsi yang diperlukan dan prosedur yang digunakan dalam algoritme dekomposisi Jarvis-Tufekci untuk dapat menyelesaikan masalah path terpendek antara source (s) dan

sink (t) pada suatu network. Selain itu, akan diberikan pula contoh penerapan algoritme dekomposisi tersebut dalam suatu network

yang diberikan. Pada akhirnya akan diuraikan penghitungan kompleksitas dari algoritme dekomposisi ini.

Penentuan path terpendek antara simpul

source dan sink pada suatu network berskala besar dengan menggunakan algoritme dekomposisi Jarvis-Tufekci memerlukan beberapa asumsi berikut:

1) Network yang akan didekomposisi

merupakan network yang longgar/tidak rapat.

2) Network tersebut tidak memuat cycle

yang negatif.

Berikut ini adalah prosedur yang digunakan dalam algoritme dekomposisi Jarvis-Tufekci dalam menyelesaikan masalah path terpendek pada suatu network.

Misalkan diberikan suatu network berskala

besar yang longgar N=(V,A) dengan

V={v1,v2,....,vn} dan A adalah himpunan sisi

berarah yang terdapat pada network tersebut, dengan tiap sisi berarah yang menghubungkan simpul vidan simpul vj memiliki panjang yang

dinotasikan dengan dij=d(vi,vj).

Misalkan network N=(V,A) yang diberikan terdekomposisi menjadi m buah subnetwork

m

N N N

N1, 2, 3,... , yang bertindih secara

linear (linearly overlapping). Tahapan yang dilakukan dalam mendekomposisi network N

yang diberikan tersebut tidak berbeda dengan tahapan yang dilakukan oleh algoritme Hu, sehingga pada akhir tahap diperoleh

N=N1∪X1∪N2∪....∪Xm−1∪Nmyang dapat pula

N:

Gambar 21. Ilustrasi hasil akhir tahap dekomposisi pada suatu network menjadi m buah subnetwork yang bertindih secara linear.

Misalkan didefinisikan Ni =Ni−(Xi−1UXi).

Matriks jarak yang terbentuk pada N1 adalah

) ( ₁₁

1

1N NN

N m

M = dengan tiap elemennya yaitu

1 1N N

m menyatakan panjang path berarah yang menghubungkan simpul di N1 dengan simpul di N1 pula. Matriks jarak dari N1 ke N2 adalah

)

( _{1 2}

2 1N NN

N m

M = dengan tiap

2 1N

N

m

menyatakan panjang path berarah yang

menghubungkan antara simpul di N1 dengan simpul lainnya di N2. Namun, seperti terlihat dalam ilustrasi pada Gambar 21, maka

Ni∩Nj=∅, untuk i≠j dengan i, j = 1,2,3,...,m.

Hal itu menunjukkan bahwa untuk i≠j, tidak

ada path berarah yang menghubungkan

simpul di Ni dengan simpul di Nj. Oleh sebab

itu, semua elemen matriks jarak j iN

N

M adalah

∞ (takhingga). Matriks jarak dari N1 ke X1 adalah MN₁X₁ =(mN₁X₁) dengan tiap mN1X1

menyatakan panjang path berarah yang

menghubungkan antara simpul di N1 dengan simpul di X1. Hal yang sama dilakukan hingga

m mN N

M , sehingga pada akhirnya diperoleh

matriks jarak dari seluruh subnetwork yang dapat dinyatakan dengan:

N1 X1 N2 X2 ... Xm−2 Nm−1 Xm−1 Nm

Berdasarkan matriks jarak dari seluruh

subnetwork tersebut, maka dapat terlihat bahwa hanya matriks jarak

i N i N

M dengan

i=1,2,....,m yang memiliki elemen hingga

(finite) dan ditunjukkan oleh daerah yang diarsir, sedangkan daerah yang tidak diarsir menyatakan matriks jarak yang memiliki elemen takhingga (infinite).

N1

1 1N N

M MN₁X₁ MN1N2 MN1X2 ... MN1Xm−2 MN1Nm−1 MN1Xm−1 MN1Nm

X1 1 1N X M 1 1X X M 2 1N X M 2 1X X M ... 2 1Xm−

X

M MX₁N_m−1 MX1Xm−1 MX1Nm

N2 1 2N N M 1 2X N M 2 2N N M 2 2X N M ... 2 2Xm−

N

M

1 2Nm−

N

M

1 2Xm−

N M m N N M 2 X2 1 2N X M 1 2X X M 2 2N X M 2 2X X M ... 2 2Xm−

X

M

1 2Nm−

X

M

1 2Xm−

X M m N X M 2 ... Nm m mN N M

X1 X2 X3 ... Xm−1

1

N N2 N3 Nm

Berikut ini adalah langkah-langkah yang dilakukan algoritme dekomposisi Jarvis-Tufekci untuk menyelesaikan masalah path

terpendek.

ƒ Tahap I:

Langkah pertama pada algoritme dekomposisi Jarvis-Tufekci adalah menggunakan tahap pertama dari algoritme dekomposisi Hu, yakni:

Operasi tripel diaplikasikan pada m buah

subnetwork N1,N2,N3,..., Nm−1,Nm

secara bertahap. Jarak terpendek yang

diperoleh dari suatu subnetwork

menggantikan jarak aslinya pada

subnetwork berikutnya (yang akan dikenai operasi tripel). Sebagai contoh, matriks jarak M*_X1X1(N1₎ yang diperoleh

akan menggantikan matriks jarak 1 1X X

M

sebelum operasi tripel dilakukan pada

subnetwork N =N2 1∪X1∪N2. Hal yang sama dilakukan hingga operasi tripel diaplikasikan pada subnetwork Nm,

sehingga pada akhir Tahap I ini diperoleh matriks-matriks jarak terpendek berikut:

) ( 1 *

1 1 N

M_NN , * ( 1 2)

2

2 N N

M_{N N} U , ....,

) ....

( 1 2 1

*

1

1 − −

−N m

N N N N

M

m

m U U U

, * _{( )}

N M_NmNm .

ƒ Tahap II:

Misalkan *( )

k ij N

d menyatakan jarak

terpendek antara simpul i dan simpul j

yang terletak pada Nk. Berdasarkan

matriks jarak terpendek yang diperoleh pada Tahap I, maka dapat didefinisikan matriks jarak M’=(mij) dengan

elemen-elemennya sebagai berikut:

⎪ ⎪ ⎩ ⎪ ⎪ ⎨ ⎧ ∞ = ) ( ) .... ( ) ( * 1 * 1 * N d N N d N d m it k ij sj ij U U

selainnya.

;

;

untuk

;

;

untuk

;

,

;

untuk

;

1 , 1 1

t

j

X

i

X

j

X

i

X

j

s

i

m k k

=

∈

∈

∈

∈

=

− −

dengan mij adalah elemen dari matriks jarak

M’ pada baris ke−i, dan kolom ke−j.

ƒ Tahap III:

Berdasarkan matriks jarak M’, maka

terbentuk network N’=(V’,A’) dengan

V’={s}∪X1∪X2∪...∪Xm−1∪{t} dan A’

merupakan himpunan sisi berarah ({s},X1), (X1,X2), ..., (Xm−2,Xm−1),

(Xm−1,{t}), atau dapat pula didefinisikan

A’ adalah himpunan sisi berarah ({s},X1),

(Xi,Xj), (Xm−1,{t}) dengan j=i+1 untuk

i=1,2,3,....,m−2. Namun, A’ tidak mengandung himpunan sisi dengan arah sebaliknya, yakni (X1,{s}), (Xj,Xi),

(t,Xm−1) dengan j=i+1, sehingga network

N’ tidak akan memuat cycle berarah.

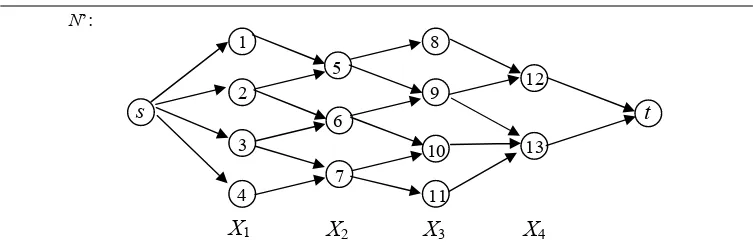
Berikut ini akan diberikan contoh network N’ yang terbentuk:

N’:

Gambar 22. Contoh network N’ yang terbentuk. 1 2 3 4 5 6 7 8 9 10 11 12 13

s

t

Pada network N’ pada Gambar 22, maka terlihat bahwa himpunan simpul X1={1,2,3,4},

X2={5,6,7}, X3={8,9,10,11}, dan X4={12,13}.

ƒ Tahap IV:

Berdasarkan jarak dari tiap sisi berarah

pada network N’, maka misalkan *

ij d

menyatakan jarak terpendek antara

simpul i dan simpul j. Misalkan pula wu

menyatakan jarak terpendek simpul

source ke simpul u. Penentuan jarak terpendek antara simpul source (s) dan simpul sink (t) dapat dilakukan dengan menggunakan algoritme A [Jarvis & Tufekci, 1982] berikut:

Algoritme A

Tahap awal :

w

_s

=

0

:

w

_i

=

*

si

d ; i∈Xk , k = 1

Tahap utama : (1) Untuk k⇐k + 1, jika k = m, Lanjutkan ke (3)

(2) wq =

{

*

}

1 min

iq i k

d w X

i∈ ₋ + ; untuk setiap q∈Xk,

lanjutkan ke (1)

(3) wt =

{

*

}

1 min

it i m

d w X

i∈ ₋ +

selesai.

Jarak terpendek dari s ke t telah diperoleh.

ƒ Tahap V:

Jarak terpendek antara simpul source dan

sink pada network N’ yang diperoleh dari algoritme A pada Tahap IV merupakan panjang path terpendek P’ dalam network N’. Path terpendek P’ tersebut adalah

s−x1−x2−...−xm−1−t, dengan xi∈Xi, atau

dapat dikatakan bahwa xi merupakan

salah satu simpul pada Xi. Path terpendek

P’ dalam network N’ ini berpadanan dengan path terpendek sebenarnya dalam

network N aslinya. Hal ini sesuai dengan teorema berikut:

Teorema 1

Jarak terpendek pada network N’=(V’,A’) berpadanan dengan jarak terpendek pada

network sebenarnya yaitu N=(V,A).

(Jarvis & Tufekci, 1982)

Bukti:

Misalkan path P yaitu s−i1−i2−...−iq−t,

merupakan path terpendek dalam network N

sebenarnya. Path P tersebut harus

mengandung paling sedikit satu buah simpul dari setiap Xi dengan i=1,2,3,...,m−1.

Misalkan path P’ s−j1−j2−....−jm−1−t

merupakan subpath dari path P sedemikian sehingga simpul jk merupakan simpul pertama

pada path P yang juga merupakan anggota Xk.

Berikut ini merupakan contoh path dalam suatu network terdekomposisi.

Ilustrasi:

s

8 9 10

12

14 15 7

4

6

5

11 2 3

1

13

Gambar 23. Contoh path dalam network terdekomposisi.

Berdasarkan contoh path pada Gambar 23, misalkan diperoleh path P yaitu s−1−2−3−4− 5−6−7−8−9−10−11−12−13−14−15−16−t, dan

path P’ yaitu s−1−3−8−10−16−t.

Hal yang ingin ditunjukkan adalah bahwa

path P’ mengandung informasi yang

diperlukan untuk menentukan path P dalam

network N sebenarnya.

Berdasarkan Tahap I algoritme dekomposisi Hu, maka jarak terpendek antara simpul

source (s) dan simpul j1 yang terletak pada

subnetwork N1 dapat ditentukan. Penentuan jarak terpendek antara simpul s dan simpul j1 tersebut menggunakan operasi tripel pada

subnetwork N1. Simpul j2 merupakan simpul pertama pada path P yang juga merupakan anggota X2, maka subpath dari path P yang menghubungkan simpul j1 ke simpul j2 akan terletak pada (N1UN2). Dengan mengganti jarak antara simpul-simpul di X1 sebenarnya dengan jarak terpendek yang diperolehnya pada subnetwork N1, maka jarak terpendek antara simpul j1 ke simpul j2 pada (N1UN2) dapat ditentukan, yakni dengan mengaplikasikan operasi tripel pada

subnetwork N2. Dengan menggunakan cara yang sama, maka jarak terpendek antara simpul ji−1 ke simpul ji pada subnetwork Ni

dapat ditentukan. Subpath tersebut akan

terletak pada (N1U....UNi). Pada langkah

akhir, dengan cara yang sama pula, maka jarak terpendek antara simpul jm−1 ke simpul

sink (t) pada subnetwork Nm dapat

ditentukan, sehingga terbentuklah path P’ yang termuat dalam network N’. Path P’ s−j1−j2−....−jm−1−t tersebut merupakan path

terpendek pada network N’. ▄

Jadi, berdasarkan informasi dari path

terpendek P’ dalam network N’, maka path

terpendek P dapat ditentukan. Path P’

merupakan subpath dari path P dalam

network N sebenarnya. Oleh karena itu, dengan memadankan path terpendek P’ tersebut dalam network N akan diperoleh path

terpendek P.

Berdasarkan tahapan-tahapan algoritme dekomposisi Jarvis-Tufekci, maka seluruh tahapan tersebut dapat pula dinyatakan dengan algoritme B [Jarvis & Tufekci, 1982].

Misalkan diberikan network N=(V,A) yang terdekomposisi menjadi m buah subnetwork

m

N N N

N1, 2, 3,..., yang bertindih secara

linear, maka penentuan path terpendek antara

simpul source dan simpul sink dapat

dilakukan dengan algoritme B berikut:

Algoritme B

Langkah 1 : Operasi tripel diaplikasikan pada tiap subnetwork N1,N2,N3,...,Nm secara

berurutan. Jarak terpendek yang dihasilkan pada suatu subnetwork akan menggantikan jarak sebenarnya pada subnetwork berikutnya.

Langkah 2 : Network N’=(V’,A’) dikonstruksi seperti yang telah dijelaskan pada Tahap III algoritme dekomposisi Jarvis-Tufekci. Algoritme A digunakan pada simpul-simpulyang terdapat pada network N’ untuk menentukan jarak terpendek antara simpul s ke simpul t. Jarak ini akan berpadanan dengan jarak sebenarnya pada

network N yang asli, sehingga path terpendek pada network N dapat ditentukan.

Berdasarkan algoritme B tersebut, maka penghitungan kompleksitas dari algoritme dekomposisi Jarvis-Tufekci ini dapat dilakukan. Penghitungan kompleksitas akan dibahas pada bab selanjutnya.

Pada bagian ini akan diberikan contoh penerapan algoritme dekomposisi Jarvis-Tufekci untuk menentukan path terpendek antara source (s) dan sink (t) pada suatu

networkN=(V,A) yang diberikan.

untuk menentukan path terpendek

Berikut ini diberikan contoh penyelesaian masalah path terpendek antara simpul source

dan sink pada suatu network dengan

menggunakan algoritme dekomposisi Jarvis-Tufekci.

Misalkan diberikan suatu network N=(V,A) dengan 15 buah simpul. Simpul 1 pada

network N merupakan source, dan simpul 13 merupakan sink.

N:

d

_ij*

X1 X2

Gambar 24. Network yang akan didekomposisi.

Misalkan: N1 = {1,2}, X1 = {3,4,5}, N2 = {6,7,8}, X2 = {9,15,12}, dan N3 = {10,11,14, 13}.

ƒ Tahap I:

Operasi tripel diaplikasikan pada m buah

subnetwork N1,N2,N3,...,Nm secara

bertahap.

Langkah pertama adalah operasi tripel diaplikasikan pada subnetwork N1=N₁UX₁,

dan matriks jarak terpendeknya ditunjukkan

oleh matriks _{( ).}

1 *

1

1 N

M_NN

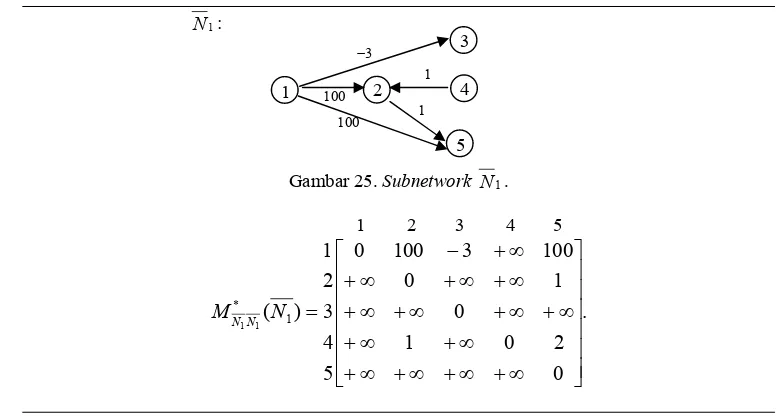
Berikut ini adalah subnetwork N1 dan matriks jarak terpendek yang diperoleh berdasarkan operasi tripel pada subnetwork tersebut.

N1:

Gambar 25. Subnetwork N1.

1 2 3 4 5

.

0 2 0 1

0

1 0

100 3

100 0

5 4 3 2 1

) ( ₁

*

1 1

⎥ ⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

∞ + ∞ + ∞ + ∞ +

∞ + ∞

+

∞ + ∞ + ∞

+ ∞ +

∞ + ∞ + ∞

+

∞ + −

=

N M

N N

1

2

3

4

5

6

7

8

9 10

11

12

13 14

15 100

-3

-3

1

1

1

1

3 1 1 1

1

1 15

3 100

100

-2

40

−3

100

100 1

1

1 2

3

4

5

Sebelum mengaplikasikan operasi tripel pada

2

N , maka jarak pada

1 1X

X

M pada subnetwork

2

N diganti dengan * ( 1)

1 1 N

MXX .

Berikut ini adalah matriks jarak

1 1X

X

M :

3 4 5

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + = 0 0 0 5 4 3 1 1X X M

yang akan digantikan oleh jarak pada matriks

jarak * ( 1)

1 1 N

MXX berikut:

3 4 5

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ∞ + ∞ + ∞ + ∞ + ∞ + = 0 2 0 0 5 4 3 ) ( 1 * 1 1 N

MXX ,

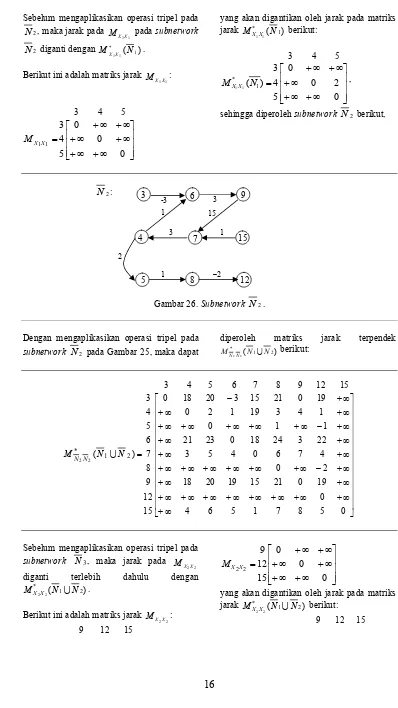
sehingga diperoleh subnetwork N2 berikut,

2

N :

Gambar 26. Subnetwork N2.

Dengan mengaplikasikan operasi tripel pada

subnetwork N2 pada Gambar 25, maka dapat

diperoleh matriks jarak terpendek )

( 1 2

*

2 2 N N

M_NN U berikut:

3 4 5 6 7 8 9 12 15

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + − ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + − ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + − = 0 5 8 7 1 5 6 4 0 19 0 21 15 19 20 18 2 0 4 7 6 0 4 5 3 22 3 24 18 0 23 21 1 1 0 1 4 3 19 1 2 0 19 0 21 15 3 20 18 0 15 12 9 8 7 6 5 4 3 )

( 1 2

*

2 2 N N

M_{N N} U

Sebelum mengaplikasikan operasi tripel pada

subnetwork N3, maka jarak pada

2 2X

X

M

diganti terlebih dahulu dengan )

( 1 2

*

2

2 N N

MX X U .

Berikut ini adalah matriks jarak

2 2X

X

M :

9 12 15

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + = 0 0 0 15 12 9 2 2X X M

yang akan digantikan oleh jarak pada matriks

jarak * ( 1 2)

2

2 N N

MXX U berikut:

⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎣ ⎡ ∞ + ∞ + ∞ + = 0 5 8 0 19 0 15 12 9 )

( 1 2

*

2

2 N N

M_{X X} U ,

sehingga diperoleh subnetwork N3 berikut,

3

N :

Gambar 27. Subnetwork N3.

Dengan mengaplikasikan operasi tripel pada

subnetwork N3 pada Gambar 27, maka dapat

diperoleh matriks jarak

3 3

*

( )

N N

M N terpendek

berikut:

9 15 12 10 11 14 13

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + = 0 7 0 10 109 6 1 9 8 1 0 7 2 10 40 0 1 0 6 10 9 5 0 8 9 2 1 100 8 3 0 13 14 11 10 12 15 9 ) ( * 3 3 N

M_{N N}

.

ƒ Tahap II:

Berdasarkan matriks-matriks jarak terpendek yang telah diperoleh dari Tahap I, maka dapat terbentuk matriks jarak M’=(mij) yang telah didefinisikan

sebelumnya.

Setelah diperoleh matriks jarak terpendek dari

seluruh subnetwork, yakni

1 1

* 1

( )

N N M N ,

2 2

*

1 2

( )

N N

M N UN , dan

3 3

*

( )

N N

M N , maka dapat

diperoleh matriks jarak M’ sebagai berikut:

⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + − ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + ∞ + − = 0 1 0 6 0 9 0 1 0 1 0 19 0 0 3 0 13 12 15 9 5 4 3 1 ' M .

ƒ Tahap III:

Berdasarkan matriks jarak M’, maka

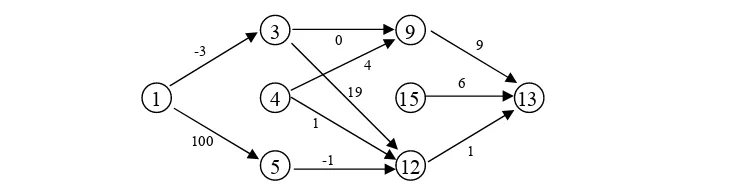
terbentuk network N’.

Berikut ini akan diberikan ilustrasi network N’ yang terbentuk berdasarkan matriks jarak M’ pada Tahap II.

Gambar 28. Network N’ yang terbentuk.

ƒ Tahap IV:

Berdasarkan jarak dari tiap sisi berarah pada network N’ yang dihasilkan pada Tahap III, maka jarak terpendek antara simpul source dan sink dapat ditentukan, yakni dengan menggunakan algoritme A.

Berdasarkan jarak dari tiap sisi berarah pada

network N’ pada Gambar 27, maka path

terpendek antara simpul 1 sebagai source dan simpul 13 sebagai sink pada network N’ dapat ditentukan dengan menggunakan algoritme A.

Berikut ini adalah penerapan algoritme A

untuk menentukan path terpendek pada

network N’ tersebut:

Algoritme A

Langkah 1: D

ari baris pada matriks jarak terpendek

1 1

* 1

( )

N N

M N , simpul yang berhubungan

dengan simpul 1 (dan juga terdapat pada network N’) adalah simpul 3, 4, dan simpul 5, sehingga diperoleh,

w3 = −3, w4 = + ∞, w5 = 100

Langkah 2: Dari baris pada * ( 1 2)

2

2 N N

M_{N N} U yang berhubungan dengan simpul 3, 4, dan 5 (dan

juga terdapat pada network N’) adalah simpul 9, 15, dan 12, sehingga diperoleh:

w9 = min {−3 + 0, +∞ + 4, 100 + ∞}= −3

w15 = min {−3 + ∞, +∞ + ∞, 100 + ∞}= +∞

w12 = min {−3 + 19, +∞ + 1, 100 – 1}= 16 Langkah 3: Dari baris pada

3 3

*

( )

N N

M N yang berhubungan dengan simpul 9, 15, dan 12 (dan

juga terdapat pada network N’) adalah simpul 13, sehingga diperoleh:

w13 = min {−3+9, +∞+6, 16+1}= 6.

Berdasarkan algoritme A yang telah dilakukan, maka diperoleh path terpendek P’ pada network N’ yakni path 1−3−9−13, dengan panjang path 6.

ƒ Tahap V:

Memadankan path terpendek P’ dalam

network N’ dengan path dalam network N

sebenarnya, sehingga path terpendek P

sebenarnya dapat ditentukan.

Bila path P’ dipadankan dengan network N

sebenarnya, maka diperoleh path P terpendek yang sebenarnya yakni path 1−3−6−9−11−14

−15−7−4−2−5−8−12−13.

PENGHITUNGAN KOMPLEKSITAS ALGORITME DEKOMPOSISI

JARVIS-TUFEKCI

Dengan menganggap bahwa suatu network

N=(V,A) dengan n buah simpul tersebut didekomposisi menjadi m buah subnetwork

m

N N N

N1, 2, 3,... , yang bertindih secara linear (linearly overlapping) seperti yang telah dijelaskan sebelumnya, maka tanpa menghilangkan sifat keumuman, diasumsikan bahwa:

⎢N1⎢=⎢N2⎢=...=⎢Nm⎢=u dan ⎢X1⎢= ⎢X2⎢=...= ⎢Xm−1⎢= v,

sehingga n = mu + (m−1)v.

Berdasarkan uraian yang telah dijelaskan sebelumnya, diketahui bahwa untuk mendapatkan jarak terpendek antara semua pasang simpul pada network yang memiliki n

buah simpul, dibutuhkan n(n−1)(n−2) aplikasi operasi tripel. Berdasarkan persamaan operasi tripel, setiap penggunaan operasi tripel tersebut, mengandung satu kali operasi penjumlahan dan satu kali operasi pembandingan untuk setiap i dan j, dan berlaku bagi k yang tetap, dengan i≠j≠ k.

Untuk dapat menentukan path terpendek dari

network tersebut diperlukan n(n−1)(n−2)

=O(n3_{) operasi penjumlahan dan}

perbandingan, sehingga dapat dikatakan bahwa diperlukan sebanyak n3=n.n.n aplikasi penjumlahan dan pembandingan dari operasi tripel tersebut.

Banyaknya seluruh operasi penjumlahan dan pembandingan yang dilakukan dapat terlihat dari algoritme B, yakni sebagai berikut:

ƒ Langkah 1: Pada N1:

Terdapat ⎟N1⎟+⎟X1⎟ = u+ v buah simpul, dan dengan menggunakan operasi tripel diperlukan (u+v)3 _{operasi penjumlahan dan} pembandingan.

Pada N2:

Terdapat ⎟X1⎟+⎟N2⎟+⎟X2⎟ = v+u+v = u+2v buah simpul, dan dengan menggunakan operasi tripel diperlukan (u+2v)3 _operasi penjumlahan dan pembandingan.

Sebanyak (u+2v)3 operasi penjumlahan dan pembandingan juga diperlukan pada setiap

k

N dengan k = 2,3,...,m−1. Sehingga dapat disimpulkan bahwa:

Pada Nk:

Terdapat ⎟Xk−1⎟+⎟Nk⎟+⎟Xk⎟ =v+u+v = u+2v

buah simpul dan dengan menggunakan operasi tripel, maka untuk seluruh subnetwork Nk dengan k = 2,3,...,m−1

diperlukan sebanyak (m−2)(u+v)3 operasi penjumlahan dan pembandingan.

Pada Nm:

Terdapat ⎟Xm−1⎟+⎟Nm⎟ = v+u = v+u buah

simpul, dan dengan menggunakan operasi tripel diperlukan sebanyak (u+v)3 operasi penjumlahan dan pembandingan.

ƒ Langkah 2:

Dengan menggunakan algoritme A, maka

path terpendek antara source (s) dan sink (t) pada N’ dapat diperoleh dengan cara: i) Pada setiap eksekusi yang terjadi pada

tahap utama algoritme A, diperlukan sebanyak v2 operasi penjumlahan dan pembandingan. Tahap utama ini dilakukan sebanyak (m−2) kali, karena yang ingin ditentukan adalah:

wq =

{

*

}

1 min

iq i k

d w X

i∈ − +

; untuk setiap

pada tahap ini diperlukan (m−2)v2 operasi penjumlahan dan pembandingan.

ii) Pada eksekusi yang dilakukan pada tahap terakhir, yakni menentukan wt, hanya

diperlukan sebanyak v operasi

penjumlahan dan pembandingan. Hal ini

dikarenakan, untuk menentukan wt

bergantung hanya pada ⎢Xm−1⎢= v.

Jadi, jumlah operasi penjumlahan dan pembandingan yang diperoleh dengan algoritme B tersebut dapat ditentukan.

Langkah 1 : (u+v)3+(m−2)(u+v)3+(u+v)3 Langkah 2 : (m−2)v2 _{+ v}

Dapat disimpulkan bahwa seluruh penjumlahan dan pembandingan yang diperlukan dalam algoritme B adalah sebanyak:

mu3+(6m−6)u2v+(12m−8)uv2+(8m+14)v3+ (m−2)v2_+v.

Berikut ini akan diberikan suatu tabel yang menunjukkan pembandingan kompleksitas antara algoritme dekomposisi Hu, Yen, dan algoritme yang diuraikan oleh Jarvis-Tufekci dalam karya ilmiah ini [Jarvis & Tufekci, 1982].

Tabel 1. Perbandingan penghitungan kompleksitas. Algoritme

dekomposisi

Penghitungan kompleksitas saat u≠v

Penghitungan kompleksitas saat u = v

Hu (2m−1)u3 + (m2+11m−15)u2v

+ (2m2+18m−35)uv2 + (m2+11m−23)v3

(4m2+42m−74)u3

Yen mu3 + (m2+6m−7)u2v + (2m2+10m−20)uv2

+ (m2+6m−14)v3

(4m2+23m−41)u3

Jarvis-Tufekci mu3 + (6m−6)u2v + (12m−8)uv2 + (8m−14)v3

+ (m−2)v2 _{+ v}

(27m−28)u3 + (m−2)u2 + u

Selain telah diberikan 2 buah kompleksitas algoritme dekomposisi lainnya (pada Tabel 1) sebagai pembandingan, maka akan diberikan pula kompleksitas dari suatu algoritme lain yang juga dapat digunakan untuk menentukan

path terpendek antara source dan sink dalam suat