MENDETEKSI CLIQUE DALAM SUATU GRAF
TESIS
Oleh
WIWIN APRIANI 117021015/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MENDETEKSI CLIQUE DALAM SUATU GRAF
T E S I S
Diajukan Sebagai Salah Satu Syarat
untuk Memperoleh Gelar Magister Sains dalam Program Studi Magister Matematika pada Fakultas Matematika dan Ilmu Pengetahuan Alam
Universitas Sumatera Utara
Oleh
WIWIN APRIANI
117021015/MT
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
Judul Tesis : MENDETEKSI CLIQUE DALAM SUATU GRAF Nama Mahasiswa : Wiwin Apriani
Nomor Pokok : 117021015
Program Studi : Magister Matematika
Menyetujui,
Komisi Pembimbing
(Prof. Dr. Saib Suwilo, M.Sc) (Prof. Dr. Opim Salim S, M.Sc)
Ketua Anggota
Ketua Program Studi Dekan
(Prof. Dr. Herman Mawengkang) (Dr. Sutarman, M.Sc)
Telah diuji pada Tanggal : 3 Juni 2013
PANITIA PENGUJI TESIS
Ketua : Prof. Dr. Saib Suwilo, M.Sc
Anggota : 1. Prof. Dr. Opim Salim S, M.Sc 2. Prof. Dr. Tulus, M.Si
PERNYATAAN
MENDETEKSI CLIQUE DALAM SUATU GRAF
TESIS
Saya mengakui bahwa tesis ini adalah hasil karya sendiri, kecuali beberapa kuti-pan dan ringkasan yang masing-masing dituliskan sumbernya
Medan, 3 Juni 2014 Penulis,
Wiwin Apriani
ABSTRAK
Diberikan suatu graf simple G dengan n buah verteks. Selanjutnya menjelaskan suatu algoritma untuk mendapatkan cliquemaksimal pada G. Semua graf Gdengan n buah verteks dan derajat minimum verteksδ akan memperolehcliquemaksimum yang berukuran sedikitnya⌈n/(n−δ)⌉. Clique QdariGmerupakan suatu himpunan verteks, dimana setiap verteks saling terhubung satu sama lain. Suatu clique dikatakan clique maksimal bila sudah tidak memiliki verteks-verteks yang adjoinablelagi. Untuk men-dapatkan clique maksimal Qi digunakan Algoritma Clique Maksimal. Algoritma ini
dibagi menjadi dua bagian, pada masing-masing bagian tersebut terdapat dua prosedur pengerjaan yang saling berkaitan satu sama lain. Prosedur pertama adalah bertujuan untuk mencaricliquemaksimalQi dan prosedur kedua bertujuan untuk mencariclique
maksimal Qi lain yang masih dapat ditemukan dari prosedur pertama.
Kata kunci : Clique, Clique maksimal, Verteks adjoinable
ABSTRACT
Given a simple graph G with n vertices. Furthermore, describes an algorithm to get maximum clique in graph G. Every graph G with n vertices and minimum vertex degree δ must have a maximum clique of size at least ⌈n/(n−δ)⌉. Clique Q of G is a set of vertices, where each vertex are connected to each other. Clique is called maximum clique when it does not have vertices that adjoinable again. For finding maximum clique
Qi used Algorithm Maximum Clique. This algorithm is divided into two parts, each part of the two procedure is that there are inter-related to each other. The first procedure to explore the maximum clique of the Qi, and the second procedure to find the another maximum clique Qi can be found from the first procedure.
Keyword : Clique, Maximum clique, Adjoinable vertices
KATA PENGANTAR
Syukur Alhamdulillah kehadirat ALLAH SWT, penulis panjatkan atas limpahan Rahmat dan KaruniaNya yang telah diberikan sehingga penulis dapat menyelesaikan tesis dengan judul : ”Mendeteksi Clique Dalam Suatu Graf”. Selawat dan salam kepada junjungan Nabi Muhammad SAW beserta keluarga dan sahabat sekalian.
Tesis ini merupakan salah satu persyaratan penyelesaian studi pada Program Stu-di Magister Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.
Pada kesempatan ini penulis menyampaikan terima kasih dan penghargaan yang sebesar-besarnya kepada:
Prof. Dr. dr. Syahril Pasaribu, DTM&H, M.Sc(CTM), Sp.A(K) selaku Rektor Univer-sitas Sumatera Utara
Dr. Sutarman, M.Sc selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam yang telah memberikan kesempatan kepada penulis untuk mengikuti Program Studi Magister Matematika di FMIPA Universitas Sumatera Utara
Prof. Dr. Herman Mawengkang selaku ketua Program Studi Magister Matematika FMIPA Universitas Sumatera Utara yang telah banyak memberikan bantuan dan do-rongan dalam penulisan tesis ini hingga selesai.
Prof. Dr. Saib Suwilo, M.Sc sebagai Sekretaris Program Studi Magister Matematika FMIPA Universitas Sumatera Utara pembimbing I dalam penulisan tesis ini, atas saran dan bantuan dari beliau hingga penulisan ini dapat diselesaikan.
Prof. Dr. Opim Salim S, M.Sc juga sebagai pembimbing II dalam penulisan tesis ini, atas saran dan bantuan dari beliau sehingga penulisan ini dapat diselesaikan.
Prof. Dr. Tulus, M.Si selaku pembanding atas saran dan bantuannya untuk kesempur-naan penulisan tesis ini.
Dr. Marwan Ramli, M.Si selaku pembanding atas saran dan bantuannya untuk kesem-purnaan penulisan tesis ini.
Seluruh Staf Pengajar pada Program Studi Magister Matematika FMIPA Universitas Sumatera Utara yang telah banyak memberikan ilmu pengetahuan selama masa perku-liahan.
Ibu Misiani, S.Si selaku Staf Administrasi Program Studi Magister Matematika FMIPA Universitas Sumatera Utara yang telah memberikan pelayanan yang baik kepada penulis selama mengikuti perkuliahan.
Ucapan terima kasih yang tak terhingga dan penghargaan setinggi-tingginya pe-nulis ucapkan kepada ayahanda Suparman dan Ibunda Sugiati yang telah mencurahkan kasih sayang dan dukungan kepada penulis. Selain itu, terima kasih juga kepada suami tercinta Indra Setiawan, S. Si dan sang buah hati Qonita Alifa Najwa serta seluruh keluarga yang telah membantu, memberikan semangat dan dorongan kepada penulis hingga penulisan tesis ini selesai.
Seluruh sahabat serta rekan-rekan seperjuangan mahasiswa angkatan 2011 ganjil atas kebersamaan dan bantuan dalam mengatasi masalah selama perkuliahan berlang-sung. Terima kasih juga kepada sahabat dan rekan-rekan lainnya yang tidak dapat disebutkan satu persatu, yang telah membantu dan memberikan semangat untuk pe-nulis hingga tesis ini selesai.
Akhir kata penulis menyadari bahwa tesis ini masih jauh dari sempurna. Untuk itu penulis mengharapkan kritik dan saran untuk penyempurnaan tesis ini. Semoga tesis ini dapat bermanfaat bagi pembaca dan pihakpihak lainnya yang memerlukannya.
Medan, Juli 2013
Penulis,
Wiwin Apriani
RIWAYAT HIDUP
Penulis di lahirkan di Desa Purwodadi Kabupaten Aceh Tamiang pada tanggal 10 April 1986 dan merupakan anak kedua dari tiga bersaudara, dari ayah Suparman dan ibu Sugiati. Penulis menamatkan Sekolah Dasar (SD), SD Negeri 2 Kejuruan Muda, Lulus tahun 1998. Sekolah Lanjutan Tingkat Pertama (SLTP), SLTP Negeri 2 Kejuruan Muda, Lulus tahun 2001. Sekolah Menengah Atas (SMA), SMA Negeri 2 Kejuruan Muda, Lulus tahun 2004. Pada tahun 2004 penulis melanjutkan pendidikan sarjana di Universitas Syiah Kuala Banda Aceh pada Fakultas Matematika dan Ilmu Pengetahuan Alam (MIPA) jurusan Matematika dan Lulus pada tahun 2009. Tahun 2011, penulis berkesempatan untuk melanjutkan Program Master pada Program Studi Magister Matematika Universitas Sumatera Utara Medan.
DAFTAR ISI
BAB 4 MENDETEKSI CLIQUE DALAM SUATU GRAF 13
4.1 AlgoritmaCliqueMaksimal 13
4.2 Keakuratan Algoritma 18
4.3 Kompleksitas 20
BAB 5 KESIMPULAN 22
DAFTAR PUSTAKA 23
DAFTAR TABEL
Nomor Judul Halaman
4.1 Vertek-verteks yang adjoinabledengan Q3 16
4.2 Vertek-verteks yang adjoinabledengan Q3,5 17
4.3 Vertek-verteks yang adjoinabledengan Q3,5,8 17
4.4 Vertek-verteks yang adjoinabledengan Q3,5,8,7 17
DAFTAR GAMBAR
Nomor Judul Halaman
3.1 Contoh clique dalam graf 10
4.1 Graf desa-desa yang terhubung 16
4.2 Graph with maximal cliquek = 5 18
ABSTRAK
Diberikan suatu graf simple G dengan n buah verteks. Selanjutnya menjelaskan suatu algoritma untuk mendapatkan cliquemaksimal pada G. Semua graf Gdengan n buah verteks dan derajat minimum verteksδ akan memperolehcliquemaksimum yang berukuran sedikitnya⌈n/(n−δ)⌉. Clique QdariGmerupakan suatu himpunan verteks, dimana setiap verteks saling terhubung satu sama lain. Suatu clique dikatakan clique maksimal bila sudah tidak memiliki verteks-verteks yang adjoinablelagi. Untuk men-dapatkan clique maksimal Qi digunakan Algoritma Clique Maksimal. Algoritma ini
dibagi menjadi dua bagian, pada masing-masing bagian tersebut terdapat dua prosedur pengerjaan yang saling berkaitan satu sama lain. Prosedur pertama adalah bertujuan untuk mencaricliquemaksimalQi dan prosedur kedua bertujuan untuk mencariclique
maksimal Qi lain yang masih dapat ditemukan dari prosedur pertama.
Kata kunci : Clique, Clique maksimal, Verteks adjoinable
ABSTRACT
Given a simple graph G with n vertices. Furthermore, describes an algorithm to get maximum clique in graph G. Every graph G with n vertices and minimum vertex degree δ must have a maximum clique of size at least ⌈n/(n−δ)⌉. Clique Q of G is a set of vertices, where each vertex are connected to each other. Clique is called maximum clique when it does not have vertices that adjoinable again. For finding maximum clique
Qi used Algorithm Maximum Clique. This algorithm is divided into two parts, each part of the two procedure is that there are inter-related to each other. The first procedure to explore the maximum clique of the Qi, and the second procedure to find the another maximum clique Qi can be found from the first procedure.
Keyword : Clique, Maximum clique, Adjoinable vertices
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Dalam kehidupan banyak hal yang dapat digambarkan dengan menggunakan su-atu diagram yang terdiri atas sekumpulan titik, dan garis untuk menghubungkan titik tersebut. Sebagai contoh, andaikan titik-titik direpresentasikan sebagai orang, dan garis direpresentasikan sebagai tingkat pertemanan. Selain itu, juga dapat dilihat pa-da pusat-pusat komunikasi yang disimbolkan dengan titik, pa-dan hubungan komunikasi disimbolkan sebagai garis yang menghubungkan tiap-tiap titik tersebut. Permasalahan tersebut dalam matematika dikenal sebagai konsep graf, karena dari titik-titik pada permasalahan tersebut dapat dilihat apakah dihubungkan dengan suatu garis ataukah tidak.
Brualdi dan Ryser (1991) merepresentasikan graf G dari suatu masalah yang digambarkan sebagai titik (verteks) yang dihubungkan dengan garis (edge). Sehing-ga suatu graf dapat disebut sebaSehing-gai Himpunan (V, E) dimana V adalah himpunan berhingga dan tidak kosong dari verteks v1, v2,· · · , vn, dan E adalah himpunan edge
yang menghubungkan vertekse1, e2,· · · , en atau dapat ditulis sebagai G= (V, E).
Diberikan suatu graf tak berarah G= (V, E), dimana V merupakan sekumpulan verteks dan E merupakan sekumpulan edge. Dua buah verteks dikatakan adjacent jika kedua verteks tersebut dihubungkan oleh sebuah edge. Suatu clique merupakan suatu subset dari verteks dalam graf G, sehingga tiap pasang verteks dalam G saling terhubung oleh edge. Permasalahan cliquemaksimum merupakan suatu permasalahan untuk mendapatkan clique dengan jumlah verteks terbanyak dalam suatu graf.
Permasalahan maksimumcliquemerupakan suatu permasalahan klasik dalam op-timisasi kombinatorial. Sehingga untuk mendapatkannya belum ditemukan solusi yang sangat efektif. Pada tahun 1972, karp memperkenalkan 21 data permasalahan lengkap NP (Non Polinomial), salah satunya adalah kasus bagaimana menemukan clique mak-simal dalam suatu graf.
2
Permasalahancliquemerupakan sebuah permasalahan graf NP-complete, dimana untuk mendapatkan penyelesaian eksak yang efisien dari permasalahan tersebut sangat susah. Clique juga merupakan suatu subgraf lengkap yang diperoleh dari suatu graf yang terdiri atas tiga atau lebih titik (verteks). Setiap titik tersebut saling berdekatan satu sama lain dengan titik lainnya. Pencarian maksimum clique telah diterapkan dalam sejumlah bidang keilmuan, keahlian teknik dan bahkan dalam bidang bisnis. Beberapa penerapan cliquebahkan mencapai bidang biologi meliputi solusi permasala-han struktur molekul DNA. Clique juga digunakan dalam pemrosesan citra dalam pengaturan jarak jauh, pencocokan titik koordinat dalam system informasi, permasala-han partisi data dalam kepingan memory dan lain-lain. Permasalapermasala-han ini juga meru-pakan suatu permasalahan pencarian solusi yang dianggap cukup sulit, sama seperti permasalahan knapsack, pewarnaan graf, sirkuit Hamilton, n−puzzledan Travelling Sales Person. Hingga sekarang belum ditemukan algoritma yang benar-benar sesuai untuk penyelesaian permasalahan tersebut meskipun untuk beberapa kasus telah dite-mukan algoritma solusi yang mendekati hasil optimal.
1.2 Perumusan Masalah
Adapun permasalahan yang akan dibahas dalam tesis ini adalah bagaimana menemukan cliquemaksimal pada sembarang graf simple yang terdiri darinbuah verteks berhingga.
1.3 Tujuan Penelitian
Tujuan dari tesis ini adalah memperoleh clique maksimum pada suatu graf simple dengan menggunakan algoritma cliquemaksimal.
1.4 Manfaat Penelitian
3
1.5 Metode Penelitian
Penelitian ini bersifat studi literatur ataupun studi kepustakaan dengan mengacu pada jurnal-jurnal internasional yang berhubungan dengan clique. Selain itu, untuk mencari
clique maksimal dapat dilakukan denga langkah-langkah sebagai berikut:
1. Menampilkan literatur-literatur yang berhubungan dengan clique.
2. Membahas masalah-masalah yang terjadi pada clique.
3. Mencariclique maksimalQi dalam suatu graf simple.
4. Mencariclique maksimalQi lain yang masih dapat ditemukan dari langkah 3.
BAB 2
TINJAUAN PUSTAKA
Permasalahan clique maksimum merupakan suatu permasalahan klasik dalam pen-dekatan kombinatorial. Permasalahan ini merupakan suatu permasalahanNP-complete, dimana untuk mendapatkan penyelesaian eksak yang efisien dari permasalahan terse-but sangat susah. Bron dan Kerbosch memberikan suatu algoritma untuk mendapatkan semua clique dalam graf tak berarah (Balas dan Yu, 1986).
Pengelompokan dianggap sebagai bagian dari subgraf G yang saling terhubung (clique), misalnya mengelompokkan jumlah bobot edge yang maksimum dalam suatu graf, atau mencari total minimum bobot edge pada graf tersebut. Model uncapacitated
biasa digunakan untuk analisis data kualitatif dari sejumlah item pada suatu graf, dimana item tersebut cenderung homogen dengan karakteristik yang dimiliki (Chopra dan Rao, 1991 dan 1993).
Dalam masalah pewarnaan yang dilakukan oleh Mehrotra dan Trick (1996), prose-dur enumerasi di implementasikan untuk menyelesaikan masalah bobot maksimum dari clique, dimana bobot dari clique tersebut diberikan oleh bobot pada node-node dalam clique yang tidak memiliki kendalacapacitated. Selain itu diberikan suatu prosedur un-tuk masalah pengelompokan bobot maksimum pada kendala knapsack. Dengan meng-gunakan metode kombinatorial, permasalahan ini dapat diselesaikan dengan menggu-nakan teknik innovative bounding, termasuk menggunakan prosedur tightening berda-sarkan aliran maksimum. Metode ini sangat cepat dalam menyelesaikan masalah yang berukuran kecil atau sedang.
Masalah maximum weight cluster problemmembagi verteksV kedalamsubclique, dengan tujuan agar jumlah bobot dari edge yang memiliki dua buah titik akhir dalam
subclique yang sama bernilai maksimum. Grotschel dan Wakabayasi (1989 dan 1990) mendeskripsikan secara detail beberapa jenis cutting planes, khususnya pada kendala
triangle dan kendala2-partition. Dari hasil yang diperoleh menunjukkan bahwa cukup hanya menggunakan triangle inequalities dan 2-partition inequalities. Suatu LP relax-tationterdiri dari semuatriangle inequalitiesdan beberapa2-partition inequalitiesyang keluar menjadi pengalaman yang sangat efektif. Pada kenyataannya bahwa hanya
5
BAB 3
LANDASAN TEORI
3.1 Graf
Menurut Teori Graf dalam Brualdi dan Ryser (1991) Graf G didefinisikan sebagai pa-sangan himpunan (V, E) dengan V adalah himpunan tak kosong dari titik (verteks), dan E adalah himpunan sisi (edge) yang menghubungkan sepasang titik pada graf G. Definisi tersebut menyatakan bahwa V tidak boleh kosong, sedangkan E boleh kosong. Dengan demikian sebuah graf dimungkinkan untuk tidak memiliki sebuah sisi pun, tetapi minimal satu buah titik harus dimiliki. Graf yang hanya memiliki sebuah titik tanpa memiliki sisi disebut graf trivial. Titik pada suatu graf dapat dinomori dengan huruf, sepertia, b,· · · , v, w,· · ·,dengan bilangan asli, seperti 1,2,3,· · · ,atau gabungan keduanya. Sedangkan sisi yang menghubungkan titik vi dan vj dinyatakan dengan
pa-sangan vivj atau dengan lambang e1, e2,· · · , en. Dengan kata lain, jika e adalah sisi
yang menghubungkan titik vi dengan vj, maka e dapat ditulis sebagai e=vivj.
Graf dapat dikelompokkan menjadi beberapa jenis tergantung sudut pandang pengelompokkannya yaitu sebagai berikut :
1. Berdasarkan ada tidaknya sisi ganda pada suatu graf
a. Graf sederhana (simple graph), berarti bahwa graf tidak mengandung loop
ataupun sisi ganda.
b. Graf tak sederhana (unsimple graph), berarti bahwa graf mengandung loop
ataupun sisi ganda.
2. Berdasarkan jumlah titik pada suatu graf
a. Graf berhingga (limited graph), yaitu graf yang jumlah titiknyan berhingga. b. Graf tak berhingga (unlimited graph), yaitu graf yang jumlah titiknyan tak
berhingga.
7
3. Berdasarkan orientasi arah pada sisinya
a. Graf berarah (directed graph), yaitu suatu graf yang sisinya tidak memiliki arah orientasi. Pada graf tak berarah, vjvk dan vkvj adalah sisi yang sama.
b. Graf tak berarah (undirected graph), yaitu suatu graf yang sisinya diberikan arah orientasi. Pada graf berarah, vjvk dan vkvj menyatakan dua buah sisi
yang berbeda, sehingga vjvk 6=vkvj.
Terdapat beberapa graf khusus yang sering digunakan dalam masalah teori graf, diantaranya adalah sebagai berikut:
a. Graf lengkap (Complete graph), yang berarti bahwa setiap verteks saling ter-hubung dengan semua verteks lainnya. Biasanya graf lengkap direpresentasikan dengan simbol Kn, dengan K adalah graf lengkap dan n adalah jumlah verteks.
Sebuah graf lengkap dengan n buah verteks akan mempunyai edge sebanyak
n(n−1)
2 .
b. Graf bipartisi (Bipartite graph), berarti bahwa graf yang satu verteksnya dibagi kedalam dua subset verteks m dan n, sedemikian sehingga tidak ada edge yang menyebabkan verteks-verteks dalam subset yang sama. Graf seperti ini biasanya direpresentasikan dengan simbol Km,n, dimana K adalah graf bipastisi dan m
adalah jumlah subset verteks m, dann adalah jumlah subset verteksn.
c. Graf lengkap bipartisi (Complete bipartite graph), yang berarti bahwa graf bipar-tisi yang setiap verteks dari m harus memiliki edge yang berhubungan ke semua verteks dari n. Biasanya graf ini direpresentasikan dengan simbol Km,n, sama
seperti pada graf bipartisi.
d. Graf reguler (Regular graph), yang berarti bahwa graf yang setiap verteksnya memiliki derajat yang sama.
e. Tree adalah graf yang tidak memilikicycle. Jika jumlah verteks padaTreeadalah n, maka jumlah edge pada tree adalah n−1.
8
a. Graf tidak berarah dan berbobot: Didefinisikan sebagai suatu graf yang setiap sisinya tidak mempunyai arah anak panah, akan tetapi memiliki bobot pada se-tiap sisinya. Urutan pasangan verteks yang terhubung oleh sese-tiap edge tidak diperhatikan. Sehingga (u, v) = (v, u) adalah sisi yang sama. Sehingga graf tak berarah sering dipakai pada jaringan saluran telepon karena sisi pada graf tak berarah menyatakan bahwa saluran telepon dapat beroperasi pada dua arah.
b. Graf berarah dan berbobot: Didefinisikan sebagai suatu graf yang setiap sisinya diberikan orientasi arah, yang disebut sebagai graf berarah. Secara umum sisi be-rarah disebut dengan busur (arc). Pada graf berarah (u, v) dan (v, u) menyatakan dua buah busur yang berbeda, dalam arti bahwa (u, v)6= (v, u). Jadi untuk busur (u, v) verteksudinamakan verteks asal dan verteksvdinamakan Verteks terminal atau verteks tujuan. Graf berarah sering dipakai untuk menggambarkan aliran proses, peta lintas kota dan lain sebagainya. Sehingga pada graf berarah gelang atau looping diperbolehkan tetapi sisi ganda tidak diperbolehkan.
c. Graf tidak berarah dan tidak berbobot: Didefinisikan sebagai suatu graf yang setiap sisinya tidak mempunyai arah dan tidak mempunyai bobot apapun.
d. Graf berarah dan tidak berbobot: Didefinisikan sebagai suatu graf yang setiap sisinya memiliki arah, akan tetapi tidak mempunyai bobot apapun.
Terdapat beberapa cara untuk mempresentasikan graf, diantaranya yang sering digu-nakan adalah matriks ketetanggaan, matriks bersisian dan senarai ketetanggaan.
1. Matriks ketetanggan (adjacency matrix)
Misalkan G= (V, E) adalah suatu graf dengan n verteks, dimana n ≥1. Sehing-ga matriks ketetangSehing-gaan G adalah matriks yang berukuran n×n. Bila matriks tersebut dinamakan A= [aij], maka aij = 1 jika verteksidan j bertetangga atau
terhubung, sebaliknya jika aij = 0 maka verteksi dan j tidak bertetangga atau
9
graf dengannbuah verteks atau titik adalahn2. Jika setiap elemen membutuhkan ruang memori sebesar N, maka ruang memori yang diperlukan seluruhnya adalah N =n2.
2. Matriks bersisian (incidency matrix)
Matriks bersisian menyatakan kebersisian verteks dengan edge. Misalkan G = (V, E) adalah graf dengan n buah verteks dan m buah edge. Matriks bersisian G adalah matriksn yang berukuran n ×m. Baris menunjukkan label verteks, sedangkan kolom menunjukkan label edge. Bila matriks tersebut dinamakan A= [aij], makaaij = 1 jika verteksibersisian denganj, sebaliknyaaij = 0 jika verteks
i tidak bersisian dengan verteks j. Matriks bersisian dapat digunakan untuk mempresentasikan graf yang mengandung sisi ganda atau sisi gelang. Derajat setiap verteks i dapat dihitung dengan menghitung jumlah seluruh elemen pada barisi(kecuali pada graf yang mengandung gelang ataulooping). Jumlah elemen matriks bersisian adalah n×m. Jika setiap elemen membutuhkan ruang memori sebesar N, maka ruang memori yang diperlukan seluruhnya adalah N =n×m.
3. Senarai ketetanggaan (adjacency list)
Jika dilihat dari segi implementasinya terhadap komputer, matriks ketetanggaan memiliki kebutuhan ruang memori yang boros. Hal ini dikarenakan matriksnya memiliki banyak elemen nol, sedangkan didalam komputer elemen nol tidak perlu disimpan. Untuk mengatasi hal tersebut maka senarai ketetanggaan yang lebih baik digunakan. Senarai ketetanggaan mengurutkan verteks-verteks yang berte-tangga dengan setiap verteks lainnya di dalam graf.
3.2 Clique
10
sebuah clique jika dalam graf tersebut setidaknya terdapat sebuah subgraf lengkap berjumlah k buah simpul yang dapat berdiri sendiri (Regneri, 2007).
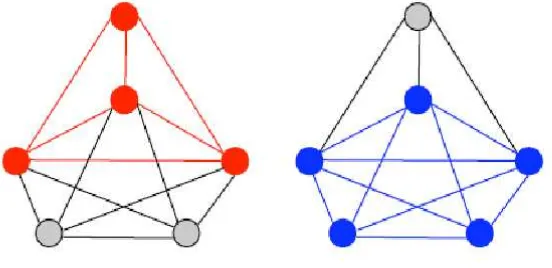
Gambar 3.1 Contohclique dalam graf
Pada gambar di atas, diberikan dua buah contoh clique yang dapat dibentuk dari graf tersebut. Dalam suatu graf akan terdapat sebuah clique jika dalam graf tersebut terdapat setidaknya sebuah subgraf lengkap berjumlah k buah verteks yang dapat berdiri sendiri. Adapun jumlah maksimum clique yang mungkin diperoleh dari suatu graf V dengan ukuran clique k dapat dirumuskan sebagai berikut:
V k
= V!
k!(V −k)! (3.1)
Terdapat 4 permasalahan yang paling umum dalam masalah cliqueyaitu sebagai berikut:
1. Pencarian maksimumclique
2. Pencarian bobot maksimum
3. List maximal clique
4. Memecahkan masalah putusan apakah sebuah graf memiliki subgraf(clique) de-ngan ukuran tertentu
11
kedalam unit-unit rectangular yang tidak overlapping. Identifikasi tentang kepadatan (density) unit dilakukan untuk setiap dimensi. Unit density tersebut kemudian diu-ji untuk menentukan cluster. Kedua, clique membuat deskripsi minimal untuk setiap
cluster. Untuk setiapcluster ditentukan daerah maksimum yang meliputiclustercluster
dari unit density yang tersambung. Selanjutnya menentukan minimal cover dari setiap
cluster. Adapun kelebihan dari clique yaitu secara otomatis dapat menemukansubspace
dengan dimensi tertinggi sehingga cluster-cluster dengan density tinggi muncul dalam
subspace tersebut, tidak sensitif terhadap urutan record yang masuk, skala inputnya linier dan skalabilitasnya baik sebagai jumlah dimensi data yang terus bertambah. Se-lain itu, kelemahanclique yaitu tingkat akurasinya masih rendah karena kesederhanaan dalam metode (Cavique et al, 2002).
3.3 Notasi dan Definisi
Dalam tesis ini akan menggunakan beberapa definisi dan notasi, sehingga berikut ini akan diberikan defenisi notasi yang tepat dari semua terminologi yang digunakan. Tulisan ini biasanya menggunakan notasi⌊x⌋untuk menyatakan bilangan bulat terbesar yang tidak lebih besar dari x dan fungsi ⌈x⌉ menunjukkan sedikitnya bilangan bulat yang tidak kurang dari x.
Sebuah simple graf Gdengan n verteks yang terdiri dari suatu himpunan verteks V, dengan|V|=n, dan suatu himpunan edgeE, sehingga setiap edge adalah pasangan tak berurut dari beberapa verteks yang berbeda . Pada definisiGsecara eksplisit mem-berikan bahwa tidak membolehkan adanya loop dalam graf G tersebut, dan beberapa edge yang terhubung dengan sepasang verteks, sehingga himpunan E juga harus ter-batas. Graf komplemenGC dari G adalah suatu graf simple dengan himpunan verteks
yang sama pada G tapi {u, v} adalah suatu edge dalam GC jika dan hanya jika {u, v}
12
Suatu matriks ketetanggaan dari G adalah suatu matriks n × n dengan input
baris udan kolomv, akan bernilai 1 jikauv∈E dan bernilai 0 jika sebaliknya. Sebuah
vertex cover C dari G merupakan sekumpulan verteks, sehingga untuk setiap edge {u, v} dari G sedikitnya terdapat satu u atau v di C. Sebuah clique Q dari G adalah sekumpulan verteks sedemikian sehingga setiap pasangan terurut dari verteks tersebut di Q terhubung oleh edge. Bila terdapat suatu clique Q pada G dan terdapat suatu vertex v luar Q, dapat dikatakan bahwa v adjoinable jika Q∪ {v} juga merupakan suatucliquepadaG. Hal ini dapat dilambangkan denganρ(Q) yang merupakan jumlah verteks yang adjoinable dari clique Q pada G. Suatu cliquemaksimal tidak memiliki verteks yang adjoinable lagi. Suatu clique maksimum adalah sebuah clique dengan jumlah verteks terbanyak.
BAB 4
MENDETEKSI CLIQUE DALAM SUATU GRAF
4.1 Algoritma Clique Maksimal
Algoritma merupakan suatu prosedur komputasi yang terdifinisi dengan baik de-ngan mengambil beberapa nilai atau seperangkat nilai sebagai masukan (input) dan menghasilkan beberapa nilai atau seperangkat nilai sebagai keluaran (output). Sebuah algoritma juga merupakan suatu langkah komputasi yang mengubah input menjadi output. Dengan demikian, algoritma dikatakan sebagai suatu urutan langkah-langkah logis dan sistematis untuk menyelesaikan suatu permasalahan.
Diberikan suatu graf simple G dengan n buah verteks, dimana |V| = n, dan setiap pasang verteks dihubungkan dengan sebuah edge. Suatu grafGC disebut sebagai
komplemen dari graf G dengan memiliki jumlah verteks yang sama pada G. Akan tetapi {u, v}merupakan edge dalamGC jika dan hanya jika {u, v}bukan anggota edge
dalam G. Jika sepasang verteks {u, v} terhubung oleh suatu edge dalam G, maka u disebut sebagai tetangga v dan dapat dinyatakan sebagai uv ∈ E. Dengan demikian neighborhood dapat dikatakan sebagai suatu hubungan simetris dari u dan v, dimana uv ∈E jika dan hanya jikavu ∈ E. Derajat dari verteksV dinotasikan dengan d(v), yang merupakan jumlah tetangga v. Derajat minimum pada semua verteks dalam G dinotasikan dengan δ.
Suatu matriks adjacency dari G merupakan suatu matriks n ×n dengan entri baris u dan kolomv, akan bernilai 1 jika uv∈E dan bernilai 0 jika sebaliknya. Clique Q dari G merupakan suatu himpunan verteks, dimana setiap verteks saling terhubung satu sama lain. Jika diberikan suatu clique Q pada G, dan terdapat suatu verteks v diluar Q, sehingga dapat dikatakan bahwa v adalah verteksadjoinablepada clique Q. ρ(Q) dinotasikan sebagai jumlah verteks yang adjoinable. Pada masalah maksimum clique, tidak lagi ditemukan verteks adjoinable dalam graf yang mengandung clique maksimal tersebut.
14
Devinisi: Diberikan sebuah clique Qpada grafG, dan terdapat suatu verteksv diluar Q, sehingga dapat dikatakan bahwa v adjoinable ke Qjika Q∪ {v} merupakan clique yang juga berada di G.
Proposisi 4.1: Qk adalah cliquemaksimal dariGjika setiapv∈G\Qk terhubung ke
paling banyak k−1 titik diQk.
Bukti: Apabila terdapat suatu titik v ∈G terhubung ke paling banyak k+ 1 titik di Qk, maka Qk bukanlah suatu clique maksimal diG.
Untuk mendeteksi clique maksimal dalam suatu graf tidak berbobot dapat di-lakukan dengan mengikuti dua prosedur berikut:
Prosedur 1:
1. Ambil sembarang graf simple G dengan n verteks, dan ambil sebuah clique Q pada G yang berukuran 2 verteks.
2. Ambil verteks awal Qi untuk memulai pencarian clique maksimal, dimana i =
1,2,3, ..., n.
3. Cari verteks-verteksv yang adjoinabledengan Qi.
4. Cari verteks-verteks yang adjoinablepada (Q∪ {v}).
5. Tentukan jumlah verteks-verteks yang adjoinable ρ(Q∪ {v}).
6. Cek letak maksimumρ(Q∪ {v}) divmax padaQi.
7. Gabungkan vmax keQi.
8. Ulangi langkah 3 sampai langkah 7 untuk pencarian selanjutnya.
9. Pencarian berhenti bila tidak terdapat lagi verteks yang adjoinable.
Prosedur 2:
15
2. Jika Qk memenuhi proposisi 4.1, maka akan diabaikan titik-titik yang tidak
ter-masuk kedalam k−1.
3. Cari verteks-verteks yang adjoinabledengan Qk dengan mengikuti prosedur 1.
Suatu graf simple G dengan n buah verteks disimbolkan dengan 1,2, ..., n, akan dicari sebuah clique maksimal yang berukuran k. Pada setiap langkah, jika diper-oleh clique maksimal berukuran k, maka proses pencarian berhenti. Adapun langkah-langkah algoritma dilakukan adalah:
I. Untuk i= 1,2, ..., n Inisialkan clique Qi ={i}
Lakukan prosedur 1 pada Qi
Jika pada G terdapat jumlah Qmax1, maka lakukan prosedur 2
Diperoleh hasil berupa cliquemaksimal Qk
II. Untuk tiap pasang maksimumclique Qi, Qj yang diperoleh pada bagian I,
Inisialkan clique Qi,j =Qi∩Qj
Lakukan prosedur 1 pada Qi,j
Jika pada G terdapat jumlah Qmax1, maka lakukan prosedur 2
Diperoleh hasil berupa cliquemaksimal Qki,j
16
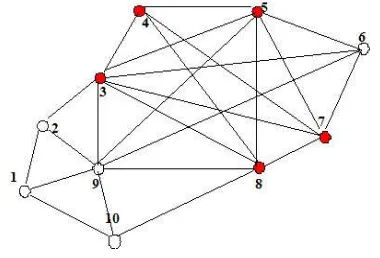
Gambar 4.1 Graf desa-desa yang terhubung
Pada gambar tersebut dapat dicari verteks-verteks yang saling adjoinable dan membentuk sebuah clique. Adapun proses pencarian clique dan maksimum clique berdasarkan pada prosedur 1 dan 2. Proses pencarian dapat dilihat sebagai berikut:
1. Pada gambar 4.1 diperoleh 10 buah verteks yaitu V ={1,2,3,4,5,6,7,8,9,10}
2. Diambil verteks awal i= 3, diperoleh clique Q3={i}={3} yang berukuran 1
3. Dicari verteks-verteks yangadjoinabledenganQ3, diperoleh hasil sebagai berikut:
Tabel 4.1 Vertek-verteks yang adjoinabledengan Q3
v adjoinablepadaQ3 Q3∪ {v} ρ(Q3∪ {v})
2 9 1
9 2,8,6,5 4
8 9,7,5,4 4
7 8,6,5,4 4
6 9,7,5 3
5 9,8,7,6,4 5
4 8,7,5 3
17
4. Dicari verteks-verteks yangadjoinabledenganQ3,5, diperoleh hasil sebagai berikut: Dari tabel 4.2 diperoleh bahwa jumlah verteks yangadjoinabledengan Q3,5yang
Tabel 4.2 Vertek-verteks yang adjoinabledengan Q3,5
v adjoinablepadaQ3,5 Q3,5∪ {v} ρ(Q3,5∪ {v})
maksimum berada pada vertek 8. Hal ini berarti bahwa verteks 8 dapat di ad-joinkan denganQ3,5. Sehingga diperolehcliquebaruQ3,5,8=Q3,5∪{v}={3,5,8} yang berukuran k = 3.
5. Dicari verteks-verteks yangadjoinabledenganQ3,5,8, diperoleh hasil sebagai berikut: Dari tabel 4.2 diperoleh bahwa jumlah verteks yang adjoinable dengan Q3,5,8 yang maksimum berada pada vertek 7. Hal ini berarti bahwa verteks 7 dapat di adjoinkan dengan Q3,5,8. Sehingga diperoleh cliquebaru Q3,5,8,7=Q3,5,8∪ {v}= {3,5,8,7} yang berukuran k = 4.
Tabel 4.3 Vertek-verteks yangadjoinabledengan Q3,5,8
v adjoinablepadaQ3,5,8 Q3,5,8∪ {v} ρ(Q3,5,8∪ {v})
9 None 0
7 4 1
4 7 1
5. Dicari verteks-verteks yang adjoinable dengan Q3,5,8,7, diperoleh hasil sebagai berikut:
Tabel 4.4 Vertek-verteks yangadjoinabledengan Q3,5,8,7
v adjoinablepadaQ3,5,8,7 Q3,5,8,7∪ {v} ρ(Q3,5,8,7∪ {v})
4 None 0
18
6. Proses pencarian selesai karena tidak terdapat lagi verteks yang adjoinable, dan diperoleh clique maksimal berukurank = 5.
Gambar 4.2 Graph with maximal clique k= 5
4.2 Keakuratan Algoritma
Algoritmaclique maksimal dapat diterapkan pada sembarang graf simple. Algo-ritma ini akan berhenti apabila telah mendapatkan cliqueyang berukuran maksimum. Proposisi berikut menunjukkan bahwa Algoritma yang digunakan pasti akan mene-mukancliquemaksimal bilacliqueada. Selanjutnya akan dibuktikan bahwa setiap graf dengan n buah verteks dan derajat minimum δ memiliki clique maksimum berukuran sedikitnya ⌈n/(n−δ)⌉.
Prinsip Sarang Merpati: jika terdapat l benda yang akan didistribusikan kedalam p sarang, maka ada sarang yang akan menerima paling sedikit ⌈l/p⌉ benda, dan ada sarang yang akan menerima paling banyak ⌊l/p⌋ benda.
Proposisi 4.2.1: Diberikan sembarang graf simple G dengan n buah verteks, dan diberikan suatu clique Q. Berdasarkan prosedur 1, jika terdapat verteks l diluar Q dan derajat minimum antar vertek dalamQ lebih besar darin− ⌈l/(n−l)⌉ −1, maka diperoleh clique maksimal dari prosedur 1.
Bukti: AndaikanQadalahcliquemaksimal, makaQtidak memiliki verteksadjoinable padaG. Pada graf komplemenGc, setiap verteks diluar Qharus memiliki tetangga Q.
Sehingga dalam graf komplemenGc paling sedikit terdapatl edge(benda) dengan satu
19
maksimum antar verteks dalamQlebih kecil dari⌈l/(n−l⌉=⌈l/p⌉dalamGc, sehingga
derajat minimum antar verteks dalam Qlebih besar darin− ⌈l/(n−l)⌉ −1 dalamG.
Proposisi 4.2.2: Diberikan suatu clique Q pada G, clique maksimal pada G akan diperoleh dari prosedur 1.
Bukti: Prosedur 1 akan berhenti pada saat tidak ada lagi verteks adjoinable. Berda-sarkan definisi, hasil yang diperoleh cliqueharus bernilai maksimal.
Proposisi 4.2.3: Diberikan graf simpleGdengan nverteks, dan terdapat clique mak-simum Q. Jika terdapat m verteks diluar clique maksimal Q dan derajat minimum antar verteks dalam Qlebih besar dari n− ⌈2m/(n−m)⌉ −1, maka terdapat verteksv diluar Q sedemikian sehingga ada satu verteksw dalam Qyang bukan tetangga v dan prosedur 2 menghasilkan clique maksimum yang berbeda dari Q dan berukuran lebih besar atau sama dengan ukuran Q.
Bukti: Pada saatQmaksimal, maka tidak ada verteks adjoinable lagi dalamG. Dalam graf komplemenGc, setiap verteks diluarQpaling sedikit memiliki satu tetangga dalam
Q. Andaikan dalam graf komplenenGc setiap verteks memiliki lebih dari satu tetangga
dalam Q, maka dalam Gc terdapat paling sedikit l = 2m edges (benda) dengan satu
verteks akhir diluar Q dan verteks akhir lainnya dalam Q terdapat p=n−m verteks dalam Q (sarang). Berdasarkan prinsip sarang merpati, ada verteks dalam Q harus masuk paling sedikit ⌈l/p⌉ edges dalam Gc. Hal ini kontradiksi, karena dari hipotesis
derajat minimum antar verteks dalamQlebih besar darin−⌈l/p⌉−1 dalamG, sehingga derajat maksimum antar verteks dalam Q lebih kecil dari⌈l/p⌉ dalamGc. Sedemikian
sehingga dalamGc terdapat verteksvdiluarQ, dimanavmemiliki satu tetangga dalam
20
Proposisi 4.2.4: Diberika suatu graf simpleGdengann verteks dan derajat minimum vertekδ, Algoritma pasti mendapatkan cliquemaksimal yang berukuran paling sedikit ⌈n/(n−δ⌉.
Bukti: Berdasarkan tiap langkah pada bagian I dalam algoritma, jika t verteks ber-dampingan dengan semuan, maka adal =n−tverteks diluarQdan derajat minimum antar verteks dalamQlebih besar atau sama denganδ. Berdasarkan proposisi 4.2.1, jika δlebih besar darin−⌈l/(n−l)⌉−1 =n−⌈(n−t)/(n−(n−t))⌉−1 = n−⌈(n−t)/t⌉−1 = n− ⌈(n/t)−1⌉ −1 =n− ⌈n/t⌉, maka diperolehcliquepaling besar dari penggabungan verteks yang adjoinable. Oleh karena itu, selama t kurang dari ⌈n/(n −δ)⌉, setiap verteks masih dapat digabungkan dan prosedur 1 berlanjut. Dengan demikian, paling sedikit ⌈n/(n−δ)⌉ verteks digabungkan dan menghasilkanclique ⌈n/(n−δ)⌉ beruku-ran paling kecil ⌈n/(n−δ)⌉. Dari proposisi 4.2.1, 4.2.2, dan 4.2.3, semua clique yang dihasilkan dari algoritma berukuran maksimum dan berukuran paling kecil⌈n/(n−δ)⌉.
4.3 Kompleksitas
Pada bagian ini akan menunjukkan bahwa algoritma berhenti pada waktu poly-nomial, dengan menentukan polynomial dari jumlah n verteks pada graf G.
Proposisi 4.3.1: Diberikan graf simpleG dengan n verteks dan clique Q, prosedur 1 memerlukan paling banyak n5 langkah.
Bukti: Memeriksa apakah pasangan verteks yangadjoinablemembutuhkan setidaknya n2 langkah, karena verteks yang diperoleh kurang darin verteks yang tidak bertetang-gaan, dan setiap verteks yang tidak bertetanggaan membutuhkan sedikitnyan langkah untuk mengecek apakah itu ada diluar clique tersebut. Untuk clique tertentu, men-dapatkan ρ pada verteks adjoinable membutuhkan n3 = nn2 langkah. Pada clique tertentu, mendapatkan verteks pada ρ maksimum membutuhkan sedikitny n4 = nn3 langkah, karena terdapat sebanyaknya n verteks diluar clique. Sehingga prosedur 1 berakhir pada saat n verteks yang terhubung paling banyak, jadi hal tersebut membu-tuhkan paling banyak n5 =nn4 langkah.
21
BAB 5
KESIMPULAN
Dari pembahasan yang telah dilakukan, maka dapat disimpulkan sebagai berikut:
1. Pencarian clique maksimal dapat dilakukan pada suatu graf simple yang terdiri dari n buah vertek berhingga.
2. Terdapat dua prosedur untuk mendapatkan clique maksimal, prosedur pertama bertujuan mencari clique maksimal Qi dan prosedur kedua bertujuan mencari
clique maksimal Qi lain yang masih dapat ditemukan pada prosedur pertama.
3. Semua grafG dengan nbuah verteks dan derajat minimum verteks δakan mem-peroleh clique maksimum yang berukuran sedikitnya ⌈n/(n−δ)⌉.
DAFTAR PUSTAKA
Balas, E dan Yu, C, S. (1986). Fincling a maximum clique in an arbitrary graph. SIAM J. COMPUT. 15(4) 10541068
Butenko, S dan wilhelm W. E.(2006). Clique-detection models in computational bio-chemistry and genomics,European Journal of Operational Research173, 1-17 Brualdi, R.A., dan Ryser H.J. (1991). Combinatorial Matrix Theory. Cambridge
Uni-versity Press, Cambridge.
Chopra, S. dan Rao, M. R. (1991). On the multiway cut polyhedron.Networks 21, 51-89 Chopra, S. dan Rao, M. R. (1993). The partition problem. Mathematical programming
59, 87-116.
Cavique, L., Rego. dan Themido, I. (2002). A Scatter Search Algorithm for Maximum Clique Problem.in:Essays and Surveys in Metahauristics. Kluwer Academic Pub-lishers. 227-244
Grotschel, M. dan Wakabayashi, Y. (1989). A cutting plane algorithm for a clustering problem.Mathematical Programming Series B 45, 59-96.
Grotschel, M. dan Wakabayashi, Y. (1990). Facets of the clique partitioning polytope.
Mathematical Programming, 47:367-387.
Janezic, D. dan Konc, J (2007). An improved branch and bound algorithm for the maximum cliqve problem.Journal of Mathematical and Computer Chemistry 0340-6253.
Karp, R. M. (1972).Reducibility among combinatorial problems, Research partially sup-ported by National sciense foundation grant, University of California at Berkeley. Mehrotra, A.,dan Trick, A. M. (1996). A column generation approach for graph coloring.
INFORMS J. Comput, 8:344-354.
Regneri, M. (2007). Finding all cliques of an undirected graph.Current trends in IE WS 06/07