GRAF BIPARTISI LENGKAP BERLABEL DALAM MENYELESAIKAN MASALAH PENUGASAN
SKRIPSI
RONAL GOMAR PURBA 040803061
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
GRAF BIPARTISI LENGKAP BERLABEL DALAM MENYELESAIKAN MASALAH PENUGASAN
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
RONAL GOMAR PURBA 040803061
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : GRAF BIPARTISI LENGKAP BERLABEL
DALAM MENYELESAIKAN MASALAH PENUGASAN
Kategori : SKRIPSI
Nama : RONAL G PURBA
Nomor Induk Mahasiswa : 040803061
Program Studi : SARJANA (S1) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN
ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Diluluskan di Medan, Juni 2010 Komisi Pembimbing:
Pembimbing 2 Pembimbing 1
Drs. Henry Rani Sitepu, M.Si Prof. Dr. Herman Mawengkang NIP. 19530303 198303 1 002 NIP. 19461128 1974403 1 001
Diketahui/ Disetujui oleh
Departemen Matematika FMIPA USU Ketua,
PERNYATAAN
GRAPH BIPARTISI LENGKAP BERLABEL DALAM MENYELESAIKAN MASALAH PENUGASAN
Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Juni 2010
PENGHARGAAN
Puji dan syukur penulis ucapkan serta panjatkan keapda Tuhan Yang Maha Kuasa atas kasih, berkat dan karuniaNya sehingga penulis dapat menyelesaikan ini.
Skripsi ini berjudul “ Graf Bipartisi Lengkap Berlabel dalam Menyelesaikan Masalah Penugasan” diajukan sebagai salah satu syarat untuk memperoleh gelar sarjana pada Departemen Matematika dan Ilmu Pengetahuan Alam Universitas Sumatera Utara.
Dalam kesempatan ini Penulis juga didukung dan dibantu oleh orang-orang yang ada di sekitar penulis. Oleh sebab itu penulis ingin mengucapkan terima kasih yang sebesar-besanya kepada:
1. Ayahanda dan Ibunda yang tersayang dan tercinta, Alm. M. Purba dan D br. Silaban yang telah mengasuh dan membesarkan penulis dengan rasa kasih dan sayang tulus yang tak terbatas.
2. Keluarga tercinta, T. Purba, E br. Purba, H. Purba, D br. Purba, L br. Purba, R br. Purba, James Edison Purba dan Lustina br. Purba yang selalu memberikan dukungan dan dorongan di setiap kondisi dan keadaan apa pun.
3. Rasdi Sirait yang selalu menemani penulis dalam langkah dan hari-hari penulis untuk menyelesaikan skripsi ini.
4. Bapak Prof. Herman Mawengkang dan Bapak Drs. Henry Rani Sitepu, M.Si selaku dosen pembimbing 1 dan dosen pembimbing 2 yang telah banyak memberikan masukan dan bantuan kepada penulis.
5. Bapak Drs. Djakaria Sebayang dan Bapak Drs. H Haluddin Panjaitan selaku dosen penguji buat penulis.
6. Teman-teman stambuk 2004 (Jekson, Golti, Jusian, Justinus, Darto, Domiatus, Halomoan, Mangasi, Lewin, Ukur Bangun, Hindra, Frans, Rista, Agnes, Kristin, Cani, Marta, Debo) dan lain-lain yang tidak dapat saya sebutkan satu per satu. Rekan-rekan stambuk 2005 khususnya Math ’05 FC (Marco, Jo, Paul, Mama, Sahat, Nixon, Nico, Doni, Cahaya, Opung, Reynold, Paskah, Andre, Firiska) serta Meilinda, Ester, Trisna, Christen Cs. Dan seluruh adik-adik stambuk 2006, 2007, 2008, dan 2009 thanks for all.
7. Untuk The Master College (TMC), Mr. Doni, S.Si, Miss Putri S.T, Miss Elisabet, S.P, Mr. Nelson, S.P, dan seluruh anak TMC serta Bapak Ir. Wesley Siagian (Sutomo 1 Medan).
Dalam penyusunan skripsi ini mungkin terdapat kekurangan dan kesalahan, untuk itu penulis mengharapkan kritik dan saran yang membangun dari pembaca guna perbaikan skripsi ini.
Akhirnya penulis berharap semoga skripsi ini dapat memberikan manfaat dan guna bagi para pembaca.
Medan, Juni 2010
Penulis
ABSTRAK
Pengambilan kebijakan dalam suatu perusahaan atau instansi membutuhkan metode-metode dalam penugasan n pekerja terhadap m penugasan. Dengan menggunakan matriks penugasan akan dihasilkan satu pekerja ditempatkan pada satu tugas. Diharapkan terbentuk penugasan yang akan memberikan total keuntungan maksimum. Akan tetapi, dengan menggunakan algoritma matching bobot maksimum dalam graf bipartisi lengkap berlabel dibutuhkan perulangan sebanyak jumlah verteks sampai berhenti ketika diperoleh Alternating Tree dengan Augmenting Path.
ABSTRACT
DAFTAR ISI
Halaman
PERSETUJUAN i
PERNYATAAN ii PENGHARGAAN iii
ABSTRAK iv ABSTRACT v DAFTAR ISI vi DAFTAR TABEL viii
DAFTAR GAMBAR ix BAB 1 PENDAHULUAN 1.1 Latar Belakang 1 1.2 Perumusan Masalah 2 1.3 Batasan Masalah 2 1.4 Tujuan Penelitian 2 1.5 Manfaat Penelitian 3 1.6 Metodologi Penelitian 3
1.7 Tinjauan Pustaka 3 BAB 2 LANDASAN TEORI 2.1 Penugasan Sebagai Masalah Matching Bobot Maksimum Dalam Graf Bipartisi Lengkap Berlabel 7
2.1.1 Loop Dan Edge Paralel 7
2.1.2 Graf Sederhana (Simple Graf) 7
2.1.3 Ketetanggaan (Adjacent) 8
2.1.4 Bersisian (Incident) 8
2.1.5 Simpul Terpencil (Isolated Vertex) 8
2.1.6 Graf Kosong (Null Graf) 9
2.1.7 Derajat (Degree) 2.3 Jenis-JenisGraf 9
2.4 Defenisi Dan Teori Matching Dalam Graf Bipartisi 13
2.5 Penyajian Masalah Penugasan Dalam Graf Bipartisi Lengkap Berlabel 19
BAB 3 PEMBAHASAN
3.1 Penyelesaian Masalah Penugasan Secara Klasik 26 3.2 Algoritma Untuk Mencari Matching Bobot Maksimum 26 3.3 Penyelesaian Masalah Penugasan dengan Menggunakan
Algoritma Matching Bobot Maksimum dalam Graf Bipartisi
Lengkap Berlabel 28
BAB 4 KESIMPULAN DAN SARAN
4.1 Kesimpulan 40
4.2 Saran 40
DAFTAR TABEL
Halaman Tabel 2.1 Matched edge, Unmatched edge, Matched Vertex dan Single Vertex 16
Tabel 2.2 Bobot 22
Tabel 3.1 Matriks Permutasi 24
Tabel 3.2 Matriks Permutasi Berderajat 3 Untuk Mencari Enam
Kemungkinan Penugasan 23
Tabel 3.3 Kemungkinan Penugasan 25
DAFTAR GAMBAR
Halaman
Gambar 2.1 Matriks Penugasan 4
Gambar 2.2 Simple Graf 8
Gambar 2.3 Graf Kosong 8
Gambar 2.4 Graf Berarah dan Graf Ganda Berarah 10
Gambar 2.5 Graf Lengkap 10
Gambar 2.6 Graf Lingkaran 10
Gambar 2.7 Graf Bipartite 11
Gambar 2.8 Graf Bipartisi Lengkap 11
Gambar 2.9 Graf Bipartisi Dan Bipartisi Lengkap 12
Gambar 2.10 Graf Bipartisi Berlabel 13
Gambar 2.11 Matching M1 13
Gambar 2.12 Matching M1 14
Gambar 2.13 Matching Sempurna 15
Gambar 2.14 Matching Bobot Maksimum 15
Gambar 2.15a Augmenting M sepanjang P 17
Gambar 2.15b Augmenting M sepanjang P 18
Gambar 2.16 Graf Bipartisi Tanpa Komplit Matching dari V1 ke V2 19
Gambar 2.17 Graph Lengkap Berlabel dari Masalah Penugasan 20
Gambar 3.1 Matching Awal M1={v1v5,v2v7} 29
Gambar 3.2 Alternating Tree tanpa Augmenting Path 31
Gambar 3.3 Alternating Tree Tanpa Augmenting Path 32
Gambar 3.4 Alternating Tree dengan Augmenting Path 33
Gambar 3.5 Alternating Tree tanpa Augmenting Path 35
Gambar 3.6 Alternating Tree tanpa Augmenting Path 36
Gambar 3.7 Alternating Tree dengan Augmenting Path 38
ABSTRAK
Pengambilan kebijakan dalam suatu perusahaan atau instansi membutuhkan metode-metode dalam penugasan n pekerja terhadap m penugasan. Dengan menggunakan matriks penugasan akan dihasilkan satu pekerja ditempatkan pada satu tugas. Diharapkan terbentuk penugasan yang akan memberikan total keuntungan maksimum. Akan tetapi, dengan menggunakan algoritma matching bobot maksimum dalam graf bipartisi lengkap berlabel dibutuhkan perulangan sebanyak jumlah verteks sampai berhenti ketika diperoleh Alternating Tree dengan Augmenting Path.
ABSTRACT
BAB 1 PENDAHULUAN
1.1Latar Belakang Masalah
Seiring dengan pertumbuhannya, setiap organisasi baik organisasi bisnis (perusahaan), industri, jasa dan sebagainya, menghadapi kenyataan bahwa sumber daya yang terbatas harus dialokasikan pada semua unit dalam organisasi. Manajer, selaku orang mengelola organisasi, tidak boleh berdiam diri dalam menghadapi kenyataan di atas. Manajer harus menyelesaikan masalah pengalokasian tersebut dengan membuat keputusan yang sangat layak. Manajer harus dapat mengalokasikan sumber daya organisasi sedemikian sehingga tidak ada unit organisasi yang kelebihan sumber daya dan tidak ada unit organisasi yang kekurangan sumber daya. Singkatnya, manajer perlu memainkan peranannya sebagai pengalokasi sumber (resource
allocator) dengan sebaik-baiknya.
Masalah penugasan merupakan salah satu masalah yang dihadapi oleh manajer sebagai pengalokasi sumber. Di sini manajer harus menugaskan sejumlah tenaga kerja yang memiliki kemampuan berbeda pada sejumlah tugas yang berbeda pula. Karena keterbatasan jumlah tenaga kerja, maka setiap pekerja hanya dapat ditugaskan pada satu tugas dan setiap tugas hanya dikerjakan oleh satu orang. Manajer akan menghadapi berbagai kemungkinan penugasan sejumlah pekerja pada sejumlah tugas. Masing-masing kemungkinan penugasan tersebut mempunyai total keuntungan yang berbeda satu dengan yang lain. Tentunya manajer harus memilih kemungkinan penugasan yang memiliki total keuntungan maksimum.
Dalam menyelesaikan suatu masalah, termasuk masalah penugasan, manajer tidak boleh mengandalkan kemampuan intuisinya saja, melainkan harus mempertimbangkan berbagai alat bantu untuk menyelesaikan masalah. Alat bantu tersebut dapat berupa metode kuantitatif maupun berbagai peralatan elektronik, khususnya komputer.
yaitu dengan memanfaatkan teori graf. Teori graf merupakan alat bantu dalam berbagai bidang ilmu. Sehubungan dengan masalah penugasan, dalam teori graf dikenal adanya masalah matching bobot maksimum dalam graf bipartisi lengkap berlabel. Jadi, masalah penugasan dapat dimodelkan ke dalam graf bipartisi lengkap berlabel dan kemudian diselesaikan dengan menerapkan algoritma untuk mencari
matching bobot maksimum dalam graf bipartisi lengkap berlabel.
1.2 Perumusan Masalah
Masalah dalam tugas akhir ini adalah bagaimana menyelesaikan masalah penugasan dengan menerapkan algoritma matching bobot maksimum dalam graf bipartisi lengkap berlabel.
1.3 Batasan Masalah
Masalah penugasan yang dibahas dalam tugas akhir ini dibatasi pada masalah maksimisasi. Penulis membatasi masalah penugasan dengan algoritma matching bobot maksimum dengan waktu tempuh sebagai contoh kasus dalam penelitian ini.
1.4 Tujuan Penelitian
Penulisan ini bertujuan untuk menunjukkan bahwa algoritma matching bobot maksimum dalam graf bipartisi lengkap berlabel dapat menyelesaikan masalah penugasan.
1.5 Manfaat Penelitian
Dapat merepresentasikan masalah graf bipartisi lengkap ke dalam model penugasan
1.6Metodologi Penelitian
Metodologi yang digunakan dalam rangka pembuatan dan penyusunan tugas akhir ini adalah penelitian literatur, guna memperoleh berbagai bahan referensi.
1.7 Tinjauan Pustaka
a. Pengenalan Terhadap Masalah Penugasan
Defenisi 1:
Masalah penugasan (assignment problem) merupakan masalah tentang menugaskan n elemen ke dalam n kategori dengan suatu cara yang optimal, sedemikian hingga tiap elemen yang ditugaskan pada satu dan hanya satu kategori dan tiap kategori memperoleh satu dan hanya satu elemen.
Penugasan elemen pada kategori yang dimaksud dalam defenisi 1 dapat berupa penugasan pelamar atau jabatan, awak kapal pada kapal, perenang pada gaya renang, dan sebagainya. Selanjutnya, kita sebut elemen dengan pekerja dan kategori dengan tugas.
Pada masalah penugasan, diasumsikan bahwa jumlah pekerja sama dengan jumlah tugas. Apabila terdapat suatu masalah penugasan yang tidak memenuhi asumsi ini, maka ditambahkan sejumlah pekerja khayal atau tugas khayal sedemikian hingga jumlah pekerja dan jumlah petugas sama.
Masalah penugasan dapat dikelompokkan menjadi dua, yaitu :
1. masalah maksimasi, yaitu masalah penugasan yang mencari total keuntungan maksimum.
2. masalah minimisasi, yaitu masalah penugasan yang mencari total kerugian minimum.
Data yang diperlukan oleh masalah penugasan dapat disajikan ke dalam matriks berordo n x n, yang disebut matriks penugasan. Setiap elemen cij menyatakan
tugas ke-n
Gambar 1.1 Matriks Penugasan
Matriks Penugasan
Penambahan pekerja/tugas khayal pada matriks penugasan dapat dilakukan dengan cara menambahkan baris yang semua elemennya nol, untuk penambahan pekerja khayal, atau menambahkan kolom yang semua elemennya nol, untuk penambahan tugas khayal.
Contoh :
a. Matriks penugasan dengan tambahan satu pekerja khayal menjadi
b. Matriks penugasan dengan tambahan dua tugas khayal
menjadi
Berdasarkan defenisi 1 dapat dilihat bahwa :
1. Tujuan yang akan dicapai dalam masalah penugasan adalah membentuk penugasan yang akan memberikan total keuntungan maksimum.
2. Batasan dalam masalah penugasan berupa terbatasnya sumber daya, yakni satu pekerja hanya ditempatkan pada tepat satu tugas, demikian pula setiap tugas hanya dapat memperoleh tepat satu pekerja.
b. Penugasan Sebagai Masalah Matching Bobot Maksimum Dalam Graf Bipartisi Lengkap Berlabel
Defenisi 2 :
Sebuah graf G adalah bipartisi jika V(G) dapat dipartisi ke dalam dua subset V1 dan V2
sedemikian sehingga semua sisi (edge) dalam G menghubungkan sebuah simpul
(vertex) dalam V1 dan sebuah simpul dalam V2.
Teori berikut menunjukkan karakteristik graf partisi : Teori :
Sebuah (nontrival) graf (V,E) adalah bipartisi jika dan hanya jika graf tersebut tidak mengandung cycle dengan panjang ganjil.
Dalam graf bipartisi, setiap simpul V1 tidak harus adjacent (berdampingan) ke
semua simpul dalam V2. Namun jika hal ini dipenuhi, maka graf bipartisi disebut “graf
bipartisi lengkap”. Contoh :
Pada gambar (1.1) diperlihatkan contoh graf bipartisi dan graf bipartisi lengkap. V1 V2 V3 V1 V2 V3
V4 V5 V6 V7 V4 V5 V6 V7
(a) Graf Bipartisi (b) Graf Bipartisi Lengkap
Gambar 1.2 Graf Bipartisi dan Bipartisi Lengkap
Contoh :
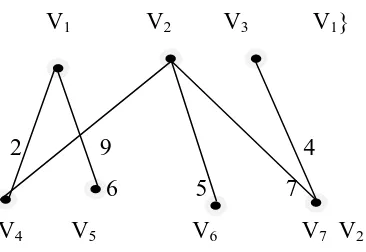
Sebuah contoh graf bipartisi berlabel dapat dilihat dalam gambar (1.2)
V1 V2 V3 V1}
2 9 4 6 6 5 7 V4 V5 V6 V7 V2
Gambar 1.3 Graf Bipartisi Berlabel
BAB 2
LANDASAN TEORI
2.1Penugasan Sebagai Masalah Matching Bobot Maksimum Dalam Graf Bipartisi Lengkap Berlabel
Teori Dasar Graf
Graf G adalah pasangan himpunan (V,E) di mana V adalah himpunan dari vertex dan E adalah himpunan dari edge yang menghubungkan sepasang simpul (Johnsonbaugh Richard, 2001; 265)
Atau graf G didefenisikan sebagai pasangan himpunan (V,E) dalam hal ini:
V=himpunan tidak kosong dari simpul-simpul (vertex)
V={ v1,v2,...,vn } dan
E= himpunan sisi (edge) yang menghubungkan sepasang simpul
E={ e2,e2,...,en }
Atau dapat ditulis singkat notasi G=(V,E) (Munir, 2003)
Definisi 2.1.1 Loop dan Edge Paralel
Sebuah edge yang menghubungkan pasangan vertex yang sama yakni (vi,vi)
disebut loop dan dua buah atau lebih edge yang mempunyai vertex -vertex ujung yang sama disebut edge-edge yang paralel atau multiple edge. Pada gambar 2.1 dapat dilihat, gambar G1 tidak memiliki loop maupun edge pararel, sedangkan pada gambar
G2 tidak memiliki loop tetapi memiliki edge paralel yaitu e3,e4 dan e1,e6. Dan pada
gambar G3 memiliki loop yaitu e8 dan edge pararel yaitu e3, e4 dan e1, e6.
Defenisi 2.1.2 Graf Sederhana (Simple Graf)
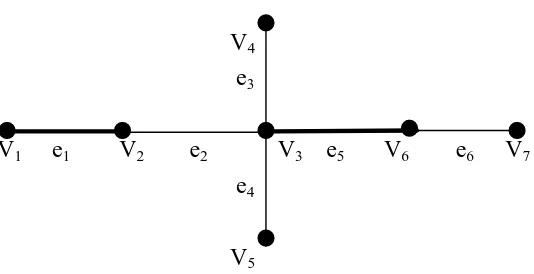
Simple graph adalah graf yang tidak memuat loop dan edge-edge yang
V4 e3 V3
e4 e2
V1 e1 V2
Gambar 2.1 Simple Graph
Definisi 2.1.3 Ketetanggaan (Adjacent)
Dua buah simpul pada graf dikatakan bertetangga bila kedua simpul tersebut terhubung langsung. Atau dapat kita sebut, vj bertetangga dengan vk pada graf G jika
(vj,vk ) adalah sisi pada sebuah graf G.
Definisi 2.1.4 Bersisian (Incident)
Untuk sembarang sisi e = ( vj, vk ) dikatakan e bersisian dengan simpul vj, atau
e bersisian dengan simpul vk.
Definisi 2.1.5 Simpul Terpencil (Isolated Vertex )
Simpul yang tidak memiliki sisi yang bersisian dengannya atau tidak bertetangga dengan simpul lainnya disebut dengan simpul terpencil.
Definisi 2.1.6 Graf Kosong (Null Graf)
Graf yang himpunan sisinya merupakan himpunan kosong (Nn) disebut graf
kosong, dimana n adalah jumlah simpul.
1 2
3
4
Defenisi 2.1.7 Derajat (Degree)
Derajat dari sebuah vertex vi dalam graf G adalah jumlah edge yang bersisian
dengan vi, dengan loop dihitung dua kali. Bila jumlah edge yang bersisian dengan jumlah vertex vi adalah n maka degree dari vi adalah n sehingga d(vi) = n.
2.2 Jenis-jenis Graf
Berdasarkan ada tidaknya gelang atau sisi ganda pada suatu graf, maka graf digolongkan menjadi dua jenis:
1. Graf sederhana (Simple Graf)
Graf yang tidak mengandung gelang maupun sisi-ganda dinamakan graf sederhana. 2. Graf tak-sederhana (Unsimple-Graf)
Graf yang mengandung sisi ganda atau gelang dinamakan graf tak-sederhana
(unsimple graf).
Berdasarkan jumlah simpul pada suatu graf, maka secara umum graf dapat digolongkan menjadi dua jenis:
1. Graf berhingga (Limited Graf)
Graf berhingga adalah graf yang jumlah simpulnya n berhingga. 2. Graf tak-berhingga (Unlimited Graf)
Graf yang jumlah simpulnya n tidak berhingga banyaknya disebut graf tak berhingga.
Berdasarkan orientasi arah pada sisi, maka secara umum graf dibedakan atas 2 jenis:
1. Graf tak-berarah (Undirected Graf)
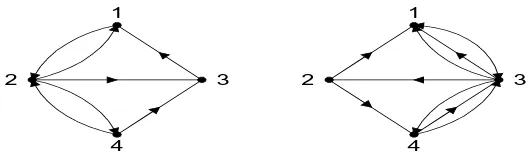
Graf yang sisinya tidak mempunyai orientasi arah disebut graf tak-berarah. 2. Graf berarah (Directed Graf atau Digraf)
Gambar 2.4 Graf Berarah dan Graf-Ganda Berarah
Ada juga graf sederhana khusus yang terdiri dari: a. Graf lengkap (Complete Graf)
Graf lengkap ialah graf sederhana yang setiap simpulnya mempunyai sisi ke semua simpul lainnya. Graf lengkap dengan n buah simpul dilambangkan dengan Kn.
Jumlah sisi pada graf lengkap yang terdiri dari n buah simpul adalah n(n – 1)/2.
K1 K2 K3 K4 K5 K6 Gambar 2.5 Graf Lengkap
b. Graf lingkaran
Graf lingkaran adalah graf sederhana yang setiap simpulnya berderajat dua. Graf lingkaran dengan n simpul dilambangkan dengan Cn.
Gambar 2.6 Graf Lingkaran
1 1
2 3
4
2 3
c. Graf teratur (Regular Graf)
Graf yang setiap simpulnya mempunyai derajat yang sama disebut graf
teratur. Apabila derajat setiap simpul adalah r, maka graf tersebut disebut sebagai graf
teratur derajat r. Jumlah sisi pada graf teratur adalah nr/2.
d. Graf bipartisi (Bipartite Graf)
Graf G yang himpunan simpulnya dapat dipisah menjadi dua himpunan bagian
V1 dan V2, sedemikian sehingga setiap sisi pada G menghubungkan sebuah simpul di
V1 ke sebuah simpul di V2 disebut graf bipartite dan dinyatakan sebagai G(V1, V2).
V1 V2
Gambar 2.7 Graf Bipartisi
e. Graf bipartisi Lengkap ( Complete Bipartite Graf )
Graf bipartisi yang tiap vertex pada V1 dihubungkan ke setiap vertex dari V2,
maka graf yang demikian disebut graf bipartisi lengkap dan dinotasikan dengan Km,n ;
dimana m dan n adalah jumlah vertex pada V1 dan V2.
Gambar 2.8 Graf Bipartisi Lengkap
Sebuah graf G adalah bipartisi jika V(G) dapat dipartisi ke dalam dua subset (tak hampa) V1 dan V2 sedemikian sehingga semua sisi (edge) dalam G
menghubungkan sebuah simpul (vertex) dalam sebuah simpul dalam V2.
Teori berikut menunjukkan karaktristik graf partisi : Teori :
Sebuah (nontrival) graf (V,E) adalah bipartisi jika dan hanya jika graf tersebut tidak mengandung cycle dengan panjang ganjil.
Dalam graf bipartisi, setiap simpul V1 tidak harus adjacent (berdampingan) ke
semua simpul dalam V2. Namun jika hal ini terpenuhi, maka graf bipartisi disebut
“graf bipartisi lengkap”. Contoh :
Pada gambar (2.9) diperlihatkan contoh graf bipartisi dan graf bipartisi lengkap.
V1 V2 V3 V1} V1 V2 V3 V1}
V4 V5 V6 V7 V2} V4 V5 V6 V7
(a) Graf Bipartisi (b) Graf Bipartisi Lengkap
Gambar 2.9 Graf Bipartisi dan Bipartisi Lengkap
Graf bipartisi akan disebut graf bipartisi berlabel jika sisinya diberi suatu bilangan non-negatif w, yang disebut label/bobot.
Contoh :
Sebuah contoh graf bipartisi berlabel dapat dilihat dalam gambar (2.10)
2 9 4 6 5 7
V4 V5 V6 V7 V2}
Gambar 2.10 Graf Bipartisi Berlabel
2.3 Defenisi dan Teori Matching dalam Graf Bipartisi
Sesungguhnya, konsep matching dalam graf bipartisi maupun dalam graf umum adalah sama, namun Matching dalam graf bipartisi mendapat perhatian khusus dalam teori graf, karena graf bipartisi sering digunakan dalam berbagai aplikasi. Pengertian Matching itu sendiri dapat dijelaskan dalam defenisi berikut.
Defenisi 2.3.1
Diberikan sebuah graf tak berarah G=(V,E). Matching adalah subset ruas ME di mana tidak ada ruas dalam M yang saling berdampingan.
Contoh :
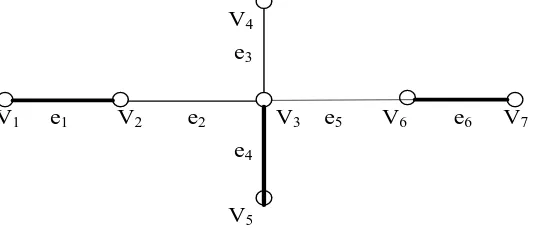
Dalam gambar bahwa M1 = {e1,e2} adalah Matching dalam graf G1, karena e3
dan e4 saling berdampingan.
V4 e3
V1 e1 V2 e2 V3 e5 V6 e6 V7 e4
V5
Bila kita perhatikan kembali contoh di atas, ternyata yang merupakan
Matching dalam graf bukan hanya M1={e1,e5}, melainkan juga {e1,e5}, {e1,e4}, {e1,e6},
{e2,e6}, {e3,e6}, {e4,e6}, {e1,e3,e6}, {e1,e4,e6}. Dengan demikian jelaslah bahwa sebuah
graf dapat saja memiliki lebih dari satu Matching, dengan kardinalitas/ukuran yang mungkin berbeda-beda pula, tergantung dari jumlah ruas yang dimiliki setiap
Matching.
Defenisi 2.3.2
Matching dengan kardinalitas maksimum dalam graf G disebut Matching
maksimum (maximum Matching), di mana untuk graf dengan order P, kardinalitasnya tidak akan melebihi p/2.
Contoh :
Graf G1 pada gambar 2.4 mempunyai order tujuh, sehingga kardinalitas
maksimumnya adalah tiga. Dalam graf G1 tersebut, Matching M2={e1,e4,e6}
merupakan Matching maksimum. Hal ini dapat dilihat gambar (2.12). V4
e3
V1 e1 V2 e2 V3 e5 V6 e6 V7
e4
V5
Gambar (2.12) Matching M2 = {e1,e4,e6} dalam graf G1
Dalam contoh dapat dilihat bahwa semua simpul dari graf G1 merupakan
simpul-simpul dalam Matching M2, kecuali simpul v4.
Defenisi 2.3.3
Matching yang memasangkan semua simpul dari graf disebut Matching
sempurna (perfect Matching).
Contoh :
V1 e1 V2 e2 V3 e3 V4 e4 V5 e5 V6
Gambar 2.13 Matching Sempurna M3={e1,e3,e5} dalam graf G2
Karena semua ruas dalam graf berlabel mempunyai bobot/label, maka setiap
Matching dalam graf berlabel juga mempunyai bobot, yang merupakan total dari
semua ruas dalam Matching.
Defenisi 2.3.4
Matching bobot maksimum (maximum weight matching) dalam graf berlabel
adalah Matching dengan bobot maksimum.
Matching bobot maksimum tidak harus memiliki kardinalitas maksimum.
Contoh :
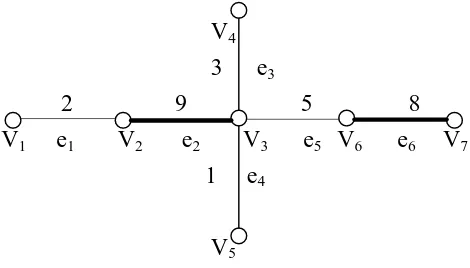
Dalam gambar (2.14) Matching M4 = {e4,e6} bukan merupakan Matching
dengan kardinalitas maksimum. Namun bobot dari Matching tersebut, yakni 17 merupakan bobot maksimum, sehingga Matching M4 merupakan bobot maksimum,
sehingga Matching M4 merupakan matching bobot maksimum dalam graf berlabel G3.
V4
3 e3
2 9 5 8
V1 e1 V2 e2 V3 e5 V6 e6 V7 1 e4
V5
Gambar 2.14 Matching Bobot Maksimum M4={e2,e6} dalam graf G3
Ruas yang dimiliki oleh Matching M disebut edge, sedangkan yang tidak disebut unmatched edge berkenaan dengan Matching M.
Defenisi 2.3.6
Simpul v dari G adalah matched vertex berkenaan dengan Matching M jika v
incident dengan ruas dari M, jika tidak y adalah single vertex berkenaan dengan
Matching M. Matched vertex dapat juga disebut saturated vertex. Single vertex dapat
juga disebut non-saturated vertex atau weak vertex atau free vertex (exposed vertex).
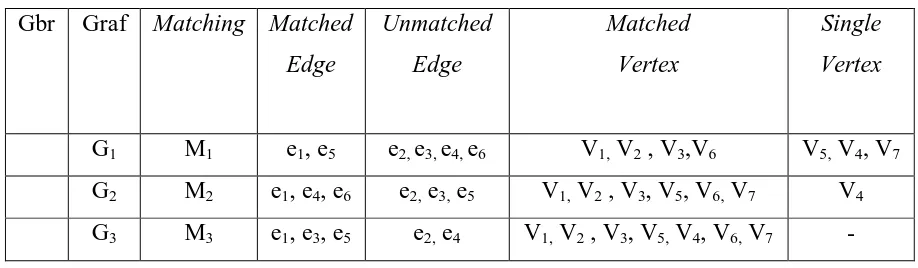
Tabel 2.1 Matched edge, Unmatched edge, Matched Vertex dan Single Vertex
Gbr Graf Matching Matched
Edge Unmatched Edge Matched Vertex Single Vertex
G1 M1 e1, e5 e2, e3, e4, e6 V1, V2 , V3,V6 V5, V4, V7 G2 M2 e1, e4, e6 e2, e3, e5 V1, V2 , V3, V5, V6, V7 V4 G3 M3 e1, e3, e5 e2, e4 V1, V2 , V3, V5, V4, V6, V7 -
Defenisi 2.3.7
Alternating path dalam graf adalah path yang ruas-ruasnnya berganti-ganti
matched dan unmatched. Nontrivial alternating path yang diawali dan diakhiri dengan
single vertex disebut augmenting path. Contoh :
Dalam gambar (2.11) path v1, v2 , v3, v6, v7 adalah Alternating path berkenaan
dengan Matching M1 tetapi bukan augmenting path. Sedangkan path v5, v3 , v6, v7
adalah augmenting path yang berkenaan dengan Matching M1.
Defenisi 2.3.8
M Matching dalam graf G dan P adalah augmenting path berkenaan dengan
M. M menandakan set dari P yang dimiliki oleh M dan M=E(P) – M. Maka M1
=(M-M)∪M adalah Matching untuk G dengan kardinalitas + 1. Dikatakan bahwa M1
Semua vertex yang single berkenaan dengan M1 juga single berdekatan dengan
M.
Contoh :
Dalam gambar 2.15a Matching M={e1, e4} mempunyai kardinalitas 2.
Augmenting path P nerkenaan dengan Matching M adalah v2, v1 , v5, v6. M={e1} dan
M={e1, e4}, maka M1={ e4, e2,e6} adalah Matching dengan kardinalitas 3 (gambar 2.8
(b)).
V1
e2
V2
V3
V4
V5
V7
e5
e6 e7
e3
e4
e
V1
e2
V2
V3
V4
V5
V7
e5
e6 e7
e3
e4
e
Gambar 2.15 (b) Augmenting M sepanjang P
Dalam suatu graf bipartisi, diharapkan menemukan Matching di mana semua simpul dalam V1 dipasangkan dengan simpul tertentu dalam V2 ataupun sebaliknya.
Defenisi 2.3.9
Dalam graf bipartisi simpul V1 dan V2, komplit Matching dari V1 dan V2 adalah
sebuah Matching di mana terdapat suatu ruas yang incident dengan semua simpul dalam V1, dengan kata lain semua simpul dalam V1 dipasangkan dengan simpul
tertentu dalam V2.
Agar graf bipartisi memiliki komplit matching dari V1 ke V2, paling tidak
jumlah simpul V2 harus sama pula dengan yang ada pada V1, namun syarat itu belum
cukup. Contoh :
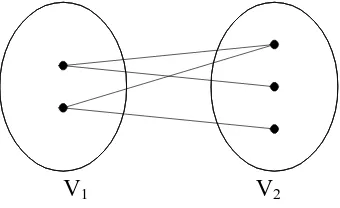
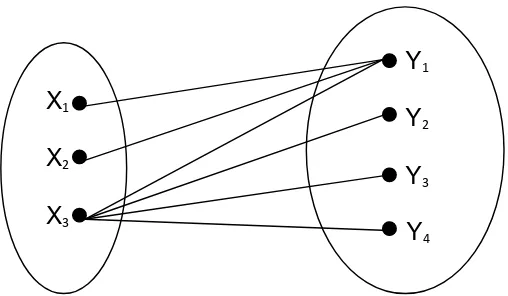
Graf pada gambar 2.15b , tidak memilik komplit matching dari V1 ke V2,
walaupun jumlah simpul dalam V2 lebih banyak daripada jumlah simpul V1. Dilihat
bahwa simpul x1 dan x2 dalam V1 sama-sama berdampingan dengan simpul y1 dalam
X1
X2
X3
Y1
Y2
Y3
Y4
[image:32.595.215.469.91.239.2]Gambar 2. 16 Graf Bipartisi Tanpa Komplit Matching dari V1 ke V2
Berarti diperlukan suatu kondisi lain untuk keberadaan komplit matching.
2.4 Penyajian Masalah Penugasan dalam Graf Bipartisi Lengkap Berlabel
Masalah penugasan dapat dimodelkan ke dalam graf bipartisi lengkap berlabel, di mana partisi V1 dan V2 masing-masing mengandung n simpul, mewakili n pekerja
dan n tugas. Bobot/label dalam graf bipartisi lengkap mewakili elemen-elemen matriks penugasan, tujuan masalah penugasan dapat dinyatakan sebagai Matching bobot maksimum dalam graf bipartisi lengkap berlabel. Matching itu sendiri menandakan kendala dalam masalah penugasan, yaitu penugasan satu ke satu. Matched edge dan unmatched edge berturut-turut mewakili nilai variabel keputusan ya dan tidak.
Contoh :
Suatu toko memiliki empat pekerja dengan kemampuan berbeda, yang akan ditugaskan pada empat tugas berbeda. Kemampuan setiap pekerja dalam mengerjakan suatu tugas tertentu, disajikan dalam matriks penugasan dan sebagai masalah mencari
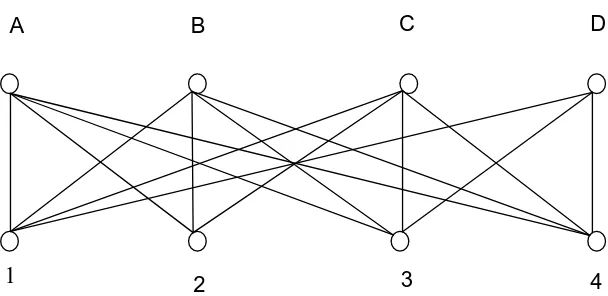
A B C D
[image:33.595.191.495.89.237.2]2 3 4
Gambar 2.17 Graf Lengkap Berlabel dari Masalah Penugasan
Tabel 2.2 bobot
A B C D
1 5 4 7 9
2 3 4 8 3
3 7 6 10 8
4 8 9 2 6
[image:33.595.103.531.306.419.2]BAB 3 PEMBAHASAN
3.1 Penyelesaian Masalah Penugasan Secara Klasik
Secara klasik, masalah penugasan diselesaikan dengan cara mencoba semua kemungkinan penugasan yang ada. Setelah menghitung besarnya total keuntungan yang dihasilkan oleh setiap kemungkinan penugasan, dapat dipilh penugasan yang memiliki total kemungkinan maksimum.
Semua kemungkinan penugasan n pekerja pada n tugas dapat dicari dengan bantuan matriks permutasi berderajat n, yaitu “suatu matriks P nxn yang kolom-kolomnya dan baris-barisnya merupakan suatu penyusunan kembali atau permutasi dari kolom-kolom dan baris-baris matriks identitas berordo n”. Berikut akan diberikan contoh dari matriks permutasi berderajat n.
Contoh 3.1 :
Matriks permutasi berderajat 3
Tabel 3.1 Matriks Permutasi No Penyusunan Baris-Baris Matriks
Identitas
Matriks Permutasi Berderajat 3
1 Baris-1, baris 2, baris 3
P=
2 Baris-1, baris 3, baris 2
P=
3 Baris-2, baris 1, baris 3
P=
4 Baris-2, baris 3, baris 1
P=
5 Baris-3, baris 1, baris 2
P=
6 Baris-3, baris 2, baris 1
P=
Permutasi n bilangan n!. demikian pula terdapat n! matriks permutasi berderajat n. Dari n! matriks permutasi diperoleh n! kemungkinan penugasan. Dari setiap matriks permutasi tersebut akan dibentuk setiap kemungkinan penugasan yaitu dengan melihat baris dan kolom dari semua elemen matriks permutasi bernilai 1. Jika elemen baris ke-i dan kolom ke-j bernilai 1, maka pekerja ke-i ditugaskan pada tugas ke-j dengan keuntungan sebesar elemen matriks penugasan baris ke-i kolom ke-j (i=j= 1,2, … , n).
Contoh 3.2 :
Matriks penugasan C=
Tabel 3.2 Matriks Permutasi berderajat 3 untuk mencari enam kemungkinan penugasan
No Matriks Permutasi Penugasan Total Keuntungan
1
P=
Pekerja 1 pada tugas ke-1
Pekerja 2 pada tugas ke-2
Pekerja 3 pada tugas ke-3
c11+c22+c33
2
P=
Pekerja 1 pada tugas ke-1
Pekerja 2 pada tugas ke-3
Pekerja 3 pada tugas ke-2
c11+c23+c32
3
P=
Pekerja 1 pada tugas ke-2
Pekerja 2 pada tugas ke-1
Pekerja 3 pada tugas ke-3
c11+c22+c32
4
P=
Pekerja 1 pada tugas ke-2
Pekerja 2 pada tugas ke-3
Pekerja 3 pada tugas ke-1
5
P=
Pekerja 1 pada tugas ke-3
Pekerja 2 pada tugas ke-1
Pekerja 3 pada tugas ke-2
c13+c21+c32
6
P=
Pekerja 1 pada tugas ke-3
Pekerja 2 pada tugas ke-2
Pekerja 3 pada tugas ke-1
c13+c22+c31
Berikut ini diberikan contoh penyelesaian masalah penugasan dengan cara klasik :
Contoh 3.3
Diketahui suatu matriks penugasan C :
t-1 t-2 t-3 t-4
Pekerja A Pekerja B Pekerja C Pekerja D
Penyelesaian :
Tabel 3.3 Kemungkinan Penugasan
No Penugasan Total Keuntungan
Dari tabel 3.3 dapat dilihat bahwa untuk mencari semua kemungkinan penugasan dari matriks penugasan berordo 4, dibutuhkan pengulangan sebanyak 4!=24 kali.
3.2 Algoritma Untuk Mencari Matching Bobot Maksimum
Algoritma untuk mencari matching bobot maksimum dalam (p,q) graf bipartisi G dengan V(G) = {v1, v2, …, vp} dan matching awal M1.
1. Variabel index I menunjukkan tahap dalam algoritma dimana root vi alternating tree berada. Set M akan berisi matching maksimum pada akhir algoritma. Langkah ini menginisialisasi I berisi 1 dan M mengandung ege-edge dari Mi.
I 1 M M1
2. Menentukan apakah matching M yang ada sekarang merupakan matching maksimum.
If i < p continiue otherwise
stop (M matching maksimum)
3. Langkah ini mencari sebuah vertex yang single berkenaan matching M yang ada dan yang sebelumnya bukan root dari alternating tree. Bila vertex v tersebut diperoleh, maka v akan diperoleh akan menjadi root dari alternating tree yang baru. Dalam hal ini sebuah barisan Q diinisialisasi yaitu hanya diisi oleh v saja. Barisan Q ini akan berisi vertex-vertex yang berada pada level genap dari alternating tree, yang vertex-vertexadjacent dengannnya masih harus diuji.
If vi = matched vertex I i+1
go to 2 otherwise v vi
4. Langkah ini membangun alternating tree dengan root v
4.1menginisialisasi array Boolean yang berisi tepat satu elemen untuk setiap vertex dalam G. array tree digunakan untuk menanda vertex-vertex yang sudah dimiliki oleh alternating tree yang sudah dibangun, dimana jika vertex w sudah dimiliki oleh alternating tree maka tree (w) = T, kalau tidak tree (w) = F
For j 1 to p
If j≠ I then tree (vj) F Otherwise tree (vj) T
4.2Menentukan apakah alternatingtree dengan root v = vi sudah selesai If Q = ∅ then
i = i +1 go to 2 otherwise
delete vertex x dari Q
4.3Langkah ini menguji semua vetex yang adjacent dengan x untuk menentukan apakah alternating tree dapat diperluas atau apakah sebuah augmenting path telah ditemukan.
4.3.1 Misalkan N(x) = {y1, y2, …, yk}. let j 1
4.3.2 if J ≤ k then y otherwise
go to 4.2
4.3.3 if tree (y) = T then J j+1 Go to 4.3.2
Otherwise continue
4.3.4 if y incident dengan sebuahmatched edge yz then Tree (y) T
go to 4.3.2 otherwise
y = single vertex continue
4.3.5 gunakan array parent untuk menentukan alternating v-x path P’ dalam alternating tree. P adalah augmenting path yang diperoleh dari P ‘ditambah path x-y.
5. Langkah ini melakukan augment M sepanjang P mengganti m dengan matching yang baru dibentuk.
Augment M sepanjang P untuk memperoleh matching baru M’ M M’
i i+1 go to 2
3.3 Penyelesaian Masalah Penugasan dengan Menggunakan Algoritma Matching Bobot Maksimum dalam graf Bipartisi Lengkap Berlabel
Sebelum dibahas dengan algoritma untuk mencari matching bobot maksimum dalam graf bipartisi lengkap berlabel, terlebih dahulu harus dipahami algoritma untuk mencari matching maksimum dalam graf bipartisi.
Matching maksimum dalam graf G dicari dengan membangun serangkaian
matching M1, M2, …, Mk, dimana M matching awal dalam G, sedangkan M diperoleh
dari Mi-1 (2 ≤ i ≥ k) dengan melakukan augmenting Mi-1 sepanjang augmenting path
yang bersangkutan, dan Mk merupakan matching yang tidak dapat diperbesar lagi
(matching maksimum).
Untuk mempermudah pencarian augmenting path yang berkenaan dengan
matching M dalam graf G, maka dibangun alternating tree dengan akar v, yakni tree
Contoh :
Mencari matching bobot maksimum dalam graf bipartisi pada gambar berikut dengan matching awal M1={v1v5,v2v7} (garis tebal)
V1 V5
V2 V6
V3 V7
[image:42.595.107.236.179.446.2]V4 V8
Gambar 3.1 Matching Awal M1={v1v5,v2v7}
i=1 M1={v1v5,v2v7} 1) 1<8 ? → Ya 2) v1 matched ? → ya
i=2
1) 2<8 ? → ya 2) v2 matched ? → ya
i=3 1) 3<8
2) v3 matched ? → tidak
Q : v3
4.1) tree = (F, F, T, F, F, F, F, F) 4.2) Q=∅ ? → tidak
Hapus x=v3 dari Q
Q : v3
4.3.1) N(x) = {x,y} N(v3) = {v5,v7}
j = 1
4.3.2) 1≤2 ? → ya y = v5
4.3.3) tree (y) = T ? → tidak
4.3.4) y incident dengan matched edge yz ? → ya (ya = v1) tree (v5) = T
tree (v1) = T parent (v5) = v3 parent (v1) = v5 tambahkan v1 dalam Q j = 2
jadi : tree = (T, F, T, F, T, F, F, F)
Alternating tree V3
V5
[image:44.595.112.211.87.240.2]V1
Gambar 3.2 Alternating Tree tanpa Augmenting Path
4.3.2) 2≤2 ? → ya y = v7
4.3.3) tree (y) = T → tidak
4.4.4) y incident dengan matched edge yz ? → ya (z = v2) tree (v1) = T
tree (v2) = T parent (v7) = v3 parent (v2) = v7 tambahkan v dalam Q j = 3
jadi : tree = (T, T, T, F, T, F, T, F)
alternating tree
V3
V5 V7
V1 V2
Gambar 3.3 Alternating Tree Tanpa Augmenting Path
4.3.2) 3≤ 2
4.2) Q = ∅ ? → tidak Hapus x = v1 dari Q
Q : v3 v1 v2
4.3.1) N(x) = (y1, y2, y3)
N(v1) = {v5, v6, v8}
j = 1
4.3.2) 1≤3 ? → ya
y = v5
4.3.3) tree (y) = T ? → ya
4.3.2) 2 ≤ 3 ? → ya
y = v6
4.3.3) tree (y) = T ? → tidak
4.3.4) y incident dengan matched edge yz ? → tidak
v6 = single vertex
alternating tree
V3
V5 V7
[image:46.595.108.277.595.799.2]V1 V2
Gambar 3.4 Alternating Tree dengan Augmenting Path
4.3.5) Augmenting Path : v3, v5, v1, v6
5) M = { v1 v6, v2v7, v3 v5 }
1 = 4
2) 4 < 8 ? → ya
3) v4 matched ? → tidak
v = v4
Q : v4
4.1) tree = (F, F, F, T, F, F, F, F)
4.2) Q = ∅ ? → tidak Hapus x = v4 dari Q
Q : v4
4.3.1) N (x) = {y1, y2}
N(v4) = {v5, v7}
j = 1
4.3.2) 1≤2 ? → ya
y = v5
4.3.3) tree (y) = T ? → tidak
4.3.4) y incident dengan matched edge yz ? → ya (z = v3)
tree (v5) = T
tree (v3) = T
parent (v5) = v4
parent (v3) = v5
tambahkan v3 dalam Q
j = 2
Q : v4 v3 alternating tree
V4
V5
[image:48.595.106.278.690.735.2]V3
Gambar 3.5 Alternating Tree tanpa Augmenting Path
4.3.2 ) 2 ≤ 2 ? → ya
y = v7
4.3.3) tree (y) = T ? → tidak
4.3.4) y incident dengan matched edge yz ? →ya (z = v2)
tree (v7) = T
tree (v2) = T
parent (v7) = v4
parent (v2) = v7
tambahkan v2 dalam Q
j = 3
jadi : tree = (F, T, T, T, T, F, T, F)
Alternating tree
V4
V5 V7
V3 V2
Gambar 3.6 Alternating Tree tanpa Augmenting Path 4.3.2) 3 ≤ 2 ? → tidak
4.2 ) Q = ∅ ? → tidak Hapus x = v3 dari Q
Q : v4 v3 v2
4.3.1) N(x) = {y1, y2}
N(v3) = { v5, v7}
j = 1
4.3.2) 1 ≤ 2 ? → ya
y = v5
4.3.3) tree (y) = T ? → ya
j = 2
4.3.2) 2≤2 ? → ya y = v7
j = 3
4.3.2) 3 ≤ 2 ? → tidak 4.2) Q = ∅ ? → tidak
hapus x = v2
Q : v4 v3 v2
4.3.1) N(x) = {y1, y2, y3}
N(v) = {v5, v7, v8}
j = 1
4.3.2) 1≤3 ? → ya
y = v5
4.3.3) tree (y) = T ? → ya
j = 2
4.3.2) 2≤3 ? → ya
y = v7
4.3.3) tree (y) = T ? → ya j = 3
4.3.2) 3≤3 ? → ya
y = v8
4.3.3) tree (y) = T ? → tidak
4.3.4) y incident dengan matched edge yz ? → tidak
alternating tree
V4
V5 V7
V3 V2
V8
Gambar 3.7 Alternating Tree dengan Augmenting Path
4.3.5) Augmenting Path : v4, v7, v2,v8
5) M = {v1v6, v2 v8, v3 v5, v4 v7}
i = 5
2) 5 < 8 ? → ya i = 6
3) v5 matched ? → ya
i = 6
2) 6 < 8 ? → ya
3) v6 matched ? → ya
i = 7
[image:51.595.105.228.87.394.2]2) 8 < 8 ? → tidak
STOP M = MATCHING MAKSIMUM
V1 V5
V2 V6
V3 V7
V4 V8
[image:52.595.106.236.176.447.2]BAB 4
KESIMPULAN DAN SARAN
4.1 Kesimpulan
Berdasarkan uraian penyelesaian soal pada bab sebelumnya, maka dapat diambil kesimpulan, yaitu:
1. Dengan menggunakan algoritma matching bobot maksimum dalam graf bipartisi lengkap berlabel dalam penelitian ini, masalah penugasan dapat diselesaikan secara efisien.
2. Dengan menggunakan algoritma matching bobot maksimum dalam graf bipartisi lengkap berlabel dalam penelitian ini, dibutuhkan perulangan sebanyak vertex sampai akhirnya berhenti jika telah didapat Alternating Tree dengan Augmenting
Path.
4.2 Saran
DAFTAR PUSTAKA
Boffey, T.B. 1982. Graph Theory in Operations Research. London: The Macmillan Press, Ltd London.
C.L., Liu. 1995. Dasar-dasar Matematika Diskrit. Jakarta: PT Gramedia Pustaka Utama.
Hiller Federick S., Lieberman and Gerald J. 1990. Introduction to Operations
Research. First Edition. Mc Growhill, Inc.
Seymor S., Lipson, and Mare L. 2001. Matematika Diskrit. Jakarta: Salemba Teknika. Supranto, Johannes. 1988. Riset Operasi untuk Pengambilan Keputusan. Jakarta:
Universitas Indonesia.
Theresia, M. H. 1995. Graf. Jakarta: Erlangga.