MASALAH KONTROL OPTIMUM HAMA SECARA HAYATI
CHASTRO SEPTIADI SIMANGUNSONG
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ABSTRAK
CHASTRO SEPTIADI SIMANGUNSONG. Masalah Kontrol Optimum Hama Secara Hayati. Dibimbing oleh TONI BAKHTIAR dan FARIDA HANUM.
Hama merupakan spesies yang dapat menyebabkan kerugian pada hasil panen, serta mengganggu aktivitas petani. Upaya untuk mengurangi kerugian yang disebabkan oleh hama sangat diperlukan, salah satunya dengan melakukan pengendalian kimiawi menggunakan obat pembasmi hama atau melakukan pengendalian hayati dengan melibatkan musuh alami untuk melumpuhkan hama. Pada kasus ini, upaya untuk mengendalikan hama dirumuskan ke dalam model matematika, yakni suatu masalah kontrol optimum hama. Tujuan utama permasalahan ini adalah menentukan upaya pengendalian untuk mempertahankan kepadatan populasi hama pada level kesetimbangan di bawah tingkat kerugian ekonomi. Terdapat dua tahap untuk mengendalikan hama yaitu dengan menggabungkan pengendalian kimiawi dan hayati pada tahap pertama untuk mempercepat pengurangan jumlah hama, dan pada tahap kedua hanya dilakukan pengendalian hayati untuk mempertahankan level yang diinginkan. Untuk mengetahui upaya pengendalian tersebut maka ditinjau suatu model hama-predator yang melibatkan Anticarsia gemmatalis sebagai hama pada tanaman kacang kedelai dan Geocoris sp sebagai predator. Upaya pengendalian yang diperoleh menunjukkan bahwa level yang diinginkan untuk jumlah populasi hama sebesar 20 ulat/m2 dapat dicapai dan kemudian akan dipertahankan.
Kata Kunci: kontrol optimum, pengendalian hama, prinsip minimum Pontryagin.
ABSTRACT
CHASTRO SEPTIADI SIMANGUNSONG. Optimal Biological Pest Control Problems. Supervised by TONI BAKHTIAR and FARIDA HANUM.
Pests are species that can attack crops and interfere farming activity. Effort to reduce the effect of pests is necessary. It can be accomplished either by chemical control through insecticides or by biological control using natural enemy intervention. In this work, pest control effort is formulated by a mathematical model, i.e., an optimal pest control problem. The primary objective of this work is to determine control strategies which maintain the density of the pest population in the equilibrium level below economic losses. Two-step control strategy is proposed by using the combination of chemical and biological controls; in the first step to speed-up pest reduction, and solely by using the biological control in the second step to maintain the admissible level. The control strategy is then applied to a predator-prey model which involves Anticarsia gemmatalis as a pest to soybean and Geocoris sp. as a natural enemy. It shows that the admissible level of 20 pest/m2 can be attained and maintained
subsequently.
MASALAH KONTROL OPTIMUM HAMA SECARA HAYATI
CHASTRO SEPTIADI SIMANGUNSONG
Skripsi
sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains
pada Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Judul : Masalah Kontrol Optimum Hama Secara Hayati
Nama : Chastro Septiadi Simangunsong
NIM : G54080061
Menyetujui,
Mengetahui:
Ketua Departemen
Dr. Berlian Setiawaty, M.S.
NIP. 19650505 198903 2 004
Tanggal Lulus :
Pembimbing I
Dr. Toni Bakhtiar, M.Sc.
NIP. 19720627 199702 1 002
Pembimbing II
PRAKATA
Puji dan syukur penulis panjatkan kepada Tuhan Yesus Kristus atas segala berkat, kasih, kekuatan, serta anugerah-Nya yang tak pernah berhenti sehingga karya ilmiah ini berhasil diselesaikan. Penyusunan karya ilmiah ini juga tidak lepas dari bantuan berbagai pihak. Untuk itu penulis mengucapkan terima kasih yang sebesar-besarnya kepada:
1. Keluargaku tercinta, mamaku Rosjelita Gultom dan bapaku Zainal Abidin Simangunsong atas segala doa, kasih sayang, motivasi, pengorbanan, dan nasihat yang senantiasa mengiringi perjalanan penulis selama ini, kakakku Lestrida Gusniati dan adikku Devi Lusiana atas doa, kasih sayang dan dukungannya,
2. Bapak Dr. Toni Bakhtiar, M.Sc. dan Ibu Dra. Farida Hanum, M.Si. selaku dosen pembimbing atas segala kesabaran, ilmu dan masukannya selama membimbing penulis, Bapak Drs. Siswandi, M.Si. selaku dosen penguji, dan seluruh dosen Departemen Matematika FMIPA IPB,
3. Staf Departemen Matematika: Pak Yono, Mas Heri, Mas Deni, Bu Ade, Bu Susi dan lainnya (terima kasih atas bantuan dan motivasinya),
4. Teman-teman satu bimbingan: Vivi, Wulan, dan Nurhadi atas dukungan, bantuan dan kerjasamanya selama ini,
5. Sahabat-sahabat: Ratna, Lya, Nita, Vonika, Ceant, Gio, Togar, Andreas, Tino, Rocky, Willy, Rido, Amudi, Bolas, Christian, Exas, Jeff, Gunawan, Irwan, Ridwan, Ijun, Khafidz, Beni, Herlan, Dono, Hendri, Fuka, Aci, Mega atas dukungan, suka-duka, nasihat, bantuan dan semangat selama ini,
6. Teman-teman mahasiswa Matematika angkatan 45: Ari, Haryanto, Arbi, Bolo, Wahidi, Wulan, Gita, Fenny, Isna, Santi, Yunda, Putri, Fitriyah, Prama, Dimas, Erik, Ryan, Irma, Maya, Wijay, Edi, Fikri, Vikri, Tiwi, Ade, Fina, Ito, Rianiko, Aisyah, Heru, Ana, Risman, Nurhadi, Nova, Rahma, Dewi, Mya, Dini, Dina, Agustina, Anggun, Rini, Haya, Bramanto, Anissa, Rischa, Nurul, Kunedi atas segenap dukungan, suka-duka dan kebahagiaan selama penulis menempuh studi di Departemen Matematika IPB,
7. Kakak-kakak mahasiswa Matematika: Andrew, Kabil, Sabar, Mora, Faisal, Ali, Tendi, Aswin, Della, Ima, Pandi, Ruhiyat, Aze, Yuyun, Wewe, Denda, Dandi, Fajar, Agung, Cumi, Rofi, Aqil, Slamet, Adi, Apri, Pepi, Elly, Alfred, Ucok, Copi, Toper, Ririh, Imam, Abe, Devina, Selvi, Mutya, Rachma, Lukman, Tyas, Vianey atas segenap nasihat dan dukungan selama ini, 8. Adik-adik mahasiswa matematika: Dian, Bari, Andri, Ivonne, Danti, Fachri, Rudi, Desyi, Ipul,
Amel, Reni, Chou, Rohmat, Jodi, Aditya, Adam, Didi, Karin, Kiki, Lola, Dayat, Widia, Sevira, Reni, Dio, Syahrul, Qowi, Dita atas dukungan dan bantuan selama ini,
9. Kakak-kakak mahasiswa Matematika angkatan 43 dan 44 yang tidak bisa disebutkan satu per satu, adik-adik mahasiswa Matematika angkatan 46 dan 47, dan seluruh pengajar, pegawai, dan staf Departemen Matematika IPB,
10.Pihak-pihak lain yang telah membantu penyusunan skripsi ini, yang tidak dapat disebutkan satu per satu,
Penulis menyadari bahwa dalam tulisan ini masih terdapat kekurangan dan jauh dari kesempurnaan, oleh karena itu penulis mengharapkan kritik dan saran yang membangun dari pembaca. Semoga tulisan ini dapat bermanfaat.
Bogor, Mei 2013
RIWAYAT HIDUP
Penulis lahir di Bekasi pada tanggal 21 September 1990 sebagai anak kedua dari tiga bersaudara, anak dari pasangan Zainal Abidin Simangunsong dan Rosjelita Gultom. Penulis menyelesaikan pendidikan Sekolah Dasar (SD) pada tahun 2002 di SDN Kayuringin Jaya XXI Bekasi Selatan, dilanjutkan pendidikan menengah pertama (SMP) diselesaikan pada tahun 2005 di SMPN 7 Bekasi dan pendidikan lanjutan menengah atas (SMA) diselesaikan pada tahun 2008 di SMAN 3 Bekasi. Penulis diterima sebagai mahasiswa Institut Pertanian Bogor pada tahun 2008 melalui jalur Undangan Seleksi Masuk IPB (USMI). Penulis memilih Program Studi Matematika, Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
DAFTAR ISI
Halaman
DAFTAR GAMBAR ... viii
DAFTAR LAMPIRAN... viii
I PENDAHULUAN 1.1Latar Belakang... 1
1.2Tujuan ... 1
II LANDASAN TEORI 2.1 Sistem Persamaan Diferensial... 2
2.2 Kontrol Optimum ... 2
2.3 Prinsip Minimum Pontryagin... 2
III MODEL HAMA-PREDATOR... 3
IV PEMBAHASAN 4.1 Sistem yang Dikendalikan dengan Kontrol ... 4
4.2 Masalah Kontrol Optimum ... 4
V STUDI KASUS 5.1 Kontrol Optimum Hama untuk Tanaman Kacang Kedelai ... 6
5.2 Pengendalian Hama dengan Memanfaatkan Musuh Alami ... 8
VI SIMPULAN ... 10
DAFTAR PUSTAKA ... 11
LAMPIRAN ... 12
DAFTAR GAMBAR
Halaman
1 Kestabilan sistem hama-predator pada kasus kacang kedelai... 7
2 Dinamika populasi hama pada waktu t
... 7
3 Fungsi kontrol untuk kondisi awal 1 0 = 32 dan 2 0 = 16
... 7
4 Fungsi kontrol ∗ untuk kondisi awal 1 0 = 20,219 dan 2 0 = 12,161
... 9
5 Variasi populasi hama dan predator dengan fungsi kontrol ∗
... 10
DAFTAR LAMPIRAN
Halaman 1 Bukti Teorema 1 (Prinsip Minimum Pontryagin) ... 132 Penurunan persamaan (4.11) ... 14
3 Penurunan persamaan (4.18) dan (4.19). ... 15
4 Penurunan persamaan (4.30) dan (4.31) ... 15
5 Penurunan persamaan (5.3) dan (5.4) ... 16
6 Penurunan persamaan (5.5) dan (5.6) ... 16
7 Program Maple 13 untuk Gambar 1 ... 17
8 Penentuan solusi khusus untuk variabel 1∗( ) dan 2∗( )
... 17
9 Program Mathematica untuk Gambar 2. ... 18
10 Program Mathematica untuk Gambar 3 ... 18
11 Pelinearan sistem (5.18) dan (5.19) ... 18
12 Penurunan persamaan aljabar Riccati. ... 19
13 Penentuan matriks P dengan menggunakan LQR pada software MATLAB ... 20
14 Penurunan persamaan (5.32) dan (5.33) ... 21
15 Program Mathematica untuk Gambar 4. ... 22
16 Program Mathematica untuk Gambar 5 ... 22
I PENDAHULUAN
mengganggu aktivitas hewan lainnya. Banyak metode kontrol hama dalam bidang pertanian yang dapat digunakan untuk mengendalikan hama. Kecekatan petani dalam melakukan kontrol hama dengan menggunakan pembasmi hama sangat diperlukan, karena jika penggunaan pembasmi hama tidak benar akan menimbulkan kerugian. Beberapa kerugian yang disebabkan karena penggunaan pembasmi hama ialah: a) kurang efisien dikarenakan terdapat hama yang kebal terhadap pembasmi hama tertentu; b) berkurangnya populasi serangga yang menguntungkan; c) berkurangnya spesies predator yang dapat mengendalikan hama; d) gangguan pada hasil panen; e) bahaya ekologi; f) berdampak buruk pada ekosistem pertanian; g) tingginya bahaya keracunan pada manusia yang dapat menyebabkan kematian.Pengendalian hayati (biological control) merupakan metode pengendalian hama oleh manusia yang melibatkan musuh alami untuk mengurangi jumlah hama sampai pada batas tertentu. Musuh alami adalah organisme yang ditemukan di alam yang dapat membunuh, melemahkan, dan mengurangi fase reproduktif, sehingga dapat mengakibatkan kematian pada hama. Pengendalian hayati dapat diartikan sebagai pengendalian populasi hama dengan menambahkan sejumlah predator atau musuh alami ke dalam suatu ekosistem (Bosch et al. 1982) . Dalam bidang ekologi, jika jumlah hama berlebih dan menyebabkan kerugian ekonomi, maka perlu dilakukan upaya pengurangan jumlah hama sampai pada level kesetimbangan sehingga dapat menurunkan tingkat kerugian ekonomi.
Terdapat empat pendekatan utama untuk melakukan pengendalian hayati yaitu: 1) pendekatan klasik atau yang sering disebut pendekatan importasi: pendekatan ini dilakukan untuk jenis hama yang hanya bisa dikendalikan dengan predator tertentu; 2) pendekatan augmentasi: pendekatan yang dilakukan pada situasi ketika jumlah predator tidak cukup optimal untuk mengendalikan hama dalam jumlah besar; 3) manipulasi genetik: pendekatan
ini dilakukan untuk meningkatkan resistensi musuh alami terhadap lingkungan; 4) pendekatan konservasi: pendekatan ini dilakukan untuk melindungi, memelihara, dan meningkatkan efektivitas populasi musuh alami dalam suatu habitat (Bin-Yahya 2012). Diperlukan pemahaman yang lebih pada permasalahan dinamika populasi hama dan predator agar upaya pengendalian hayati dapat berhasil. Contoh keberhasilan yang diterapkan dari daerah Mediterranean di Eropa Selatan, bahwa penambahan predator serangga tomcat (Paederus sp) dilakukan untuk mengendalikan hama daun kubis (Plutella xylostella).
Model matematika banyak digunakan pada bidang pertanian, khususnya pada masalah pengendalian hama secara hayati. Pada kasus ini, model matematika dapat membantu dalam penentuan fungsi kontrol atau upaya pengendalian pada sistem hama-predator, sehingga kedua populasi dapat mencapai level kesetimbangan dan tidak menyebabkan kerugian ekonomi. Dalam karya ilmiah ini akan dibahas mengenai upaya pengendalian hama yang dibagi menjadi dua tahap. Pada tahap pertama upaya pengendalian hama dilakukan dengan menentukan dua fungsi kontrol untuk populasi hama dan predator, sedangkan pada tahap kedua upaya pengendalian hama dilakukan dengan menentukan satu fungsi kontrol, yaitu hanya dengan menambahkan sejumlah predator ke dalam sistem hama-predator untuk mencapai level kesetimbangan. Sumber utama karya ilmiah ini ialah artikel Optimal pest control
problem in population dynamics yang ditulis
oleh Marat Rafikov dan Jose Manoel Balthazar tahun 2005.
1.2 Tujuan
Berdasarkan latar belakang tersebut, maka tujuan karya ilmiah ini ialah:
1. memelajari upaya pengendalian hama yang dibagi menjadi dua tahap seperti telah disebutkan di atas,
2. menganalisis peranan fungsi kontrol pada kedua tahap agar populasi hama dan predator mencapai level kesetimbangan, sehingga tidak menyebabkan kerugian ekonomi.
II LANDASAN TEORI
2.1 Sistem Persamaan Diferensial
Sistem persamaan diferensial (SPD) orde satu dengan n persamaan dan m buah fungsi sebaliknya jika tidak linear maka SPD di atas disebut taklinear.
2.2 Kontrol Optimum
Alat yang paling penting dari pengoptimuman dinamis adalah teori kontrol optimum yang berkembang secara pesat pada akhir tahun 1950. Ada dua metode penyelesaian masalah kontrol optimum, yaitu dynamic
programming yang diperkenalkan oleh Bellman
(1957) dan maximum principle yang diperkenalkan oleh Pontryagin (1962). Masalah kontrol optimum adalah memilih peubah kontrol
( ) di antara semua peubah kontrol yang
admissible, yaitu kontrol yang membawa sistem
dari state awal ( 0) pada waktu 0 kepada state
akhir ( ) pada waktu akhir T, sedemikian rupa sehingga memberikan nilai maksimum atau nilai minimum bagi fungsional objektif.
Pada masalah nyata yang berkembang menurut waktu , sistem berada dalam keadaan atau kondisi (state) tertentu, yang dapat diungkapkan dengan peubah keadaan (state variables) 1 , 2 ,…, atau dalam
bentuk vektor ( )∈ ℝ . Dengan nilai yang berbeda, vektor ( ) menempati posisi yang berbeda di ruang ℝ sehingga dapat dikatakan bahwa sistem bergerak sepanjang kurva di ℝ .
Sistem dinamika dapat dinyatakan secara matematik oleh sistem persamaan diferensial:
maka diperoleh sistem persamaan diferensial orde satu dengan peubah taktentu . Karena
0 diberikan, maka persamaan (2.1) memunyai
solusi tunggal.
Solusi yang diperoleh merupakan respon terhadap yang dilambangkan dengan .
Dengan memiliki fungsi kontrol yang sesuai, berbagai solusi dapat diperoleh. Agar solusi yang diperoleh adalah solusi yang diinginkan, diperlukan adanya kriteria bagi solusi yang diinginkan, artinya setiap kontrol ( ) dan yang diperoleh, ditentukan salah satu sehingga mencapai nilai maksimum atau minimum. Kontrol yang bersifat demikian disebut kontrol optimum. Permasalahan kontrol optimum dapat dinyatakan sebagai masalah memaksimumkan atau meminimumkan suatu fungsional (2.2) dengan kendala (2.1).
optimum, maka perlu terdapat fungsi vektor ∗ ≠0 sedemikian sehingga
1. ∗ =�
2. ∗ =−�
tidak diberikan, maka syarat transversalitas berikut harus dipenuhi:
Model yang akan dianalisis merupakan suatu model yang dibangun berdasarkan interaksi antarspesies yang hidup secara bersamaan dalam suatu ekosistem. Dalam sistem hama-predator, ekosistem dibagi menjadi dua subsistem, yaitu subsistem yang dikendalikan tanpa campur tangan manusia dan subsistem yang dikendalikan dengan campur tangan manusia.
Subsistem yang dikendalikan tanpa campur tangan manusia memanfaatkan pengendalian alami (natural control) yang melibatkan agen lain selain predator, seperti cuaca atau makanan. Contoh kasus yang terjadi pada subsistem ini adalah kandungan gossifo atau zat beracun pada kapas sehingga dapat menyebabkan kematian pada hama Helicoverpa (Bin-Yahya 2012).
Subsistem yang dikendalikan dengan campur tangan manusia dibagi menjadi dua yaitu:
1. Pengendalian kimiawi: pengendalian ini dilakukan menggunakan bahan kimia beracun untuk melindungi tanaman atau hasil tanaman dari serangan hama. Contoh pendekatan ini adalah pemanfaatan pestisida COPALD untuk mengurangi hama ulat grayak (Spodoptera litura).
2. Pengendalian hayati: pengendalian yang dilakukan dengan memanfaatkan predator atau musuh alami untuk mengendalikan hama. Contoh pendekatan ini ialah dengan mengintroduksi serangga predator yaitu kumbang vedalia (Rodolia cardinalis) untuk mengendalikan hama serangga pada jeruk (Icerya purcasi) (Hartoyo 2008). Konstruksi model matematika untuk model hama-predator ini menggunakan asumsi:
1. Kontrol yang dilakukan oleh manusia dapat memengaruhi laju pertumbuhan populasi hama-predator secara langsung dan taklangsung, di mana pengaruh taklangsung
dapat memengaruhi laju pertumbuhan dengan memanfaatkan interaksi antara hama dan predator.
2. Bagi populasi hama, kontrol yang dilakukan adalah upaya untuk mengurangi jumlah hama dan bagi populasi predator, kontrol dapat meningkatkan jumlah predator. 3. Semua parameter dan variabel yang
digunakan bernilai positif.
Sistem hama-predator yang terdiri atas populasi, dengan 1 menyatakan banyaknya
populasi hama, dan − 1 menyatakan banyaknya populasi predator, dapat dituliskan sebagai berikut:
= 1, 2,…, , (3.1) dengan = , = 1,2,…, , menyatakan kepadatan populasi pada waktu dan ( )
merupakan fungsi kontinu yang bergantung pada kepadatan populasi hama dan predator.
dengan = menyatakan kepadatan pertumbuhan melalui interaksi dengan populasi hama atau predator, sedangkan suku � menyatakan kontrol langsung pada sistem yang dapat memengaruhi laju pertumbuhan tanpa melalui interaksi antara populasi hama dan predator.
IV PEMBAHASAN
Dalam karya ilmiah ini, model interaksi hama-predator diasumsikan hanya terdiri atas satu populasi hama dan satu populasi predator. Pada kasus ini populasi hama dinyatakan dalam indeks = 1 dan populasi predator dinyatakan dalam indeks = 2.
4.1 Sistem yang Dikendalikan dengan Kontrol
Model interaksi antara hama dan predator yang dikendalikan dengan kontrol diberikan oleh sistem persamaan diferensial berikut:
berupa upaya untuk mengurangi jumlah hama dengan menggunakan pestisida,
2 : fungsi kontrol terhadap populasi
predator berupa upaya untuk mempertahankan atau menambahkan jumlah predator,
�1,�2 : konstanta yang bernilai positif.
4.2 Masalah Kontrol Optimum
Masalah kontrol optimum yang dihadapi adalah menentukan fungsi kontrol 1 dan 2,
yang membawa sistem dari kondisi awal ke kondisi akhir kepadatan populasi hama dan predator agar tidak menimbulkan kerugian ekonomi yang cukup signifikan.
Meminimumkan fungsional objektif pada persamaan (4.3) berarti meminimumkan populasi hama 1 dan memaksimumkan
populasi predator 2 di akhir periode , dan sekaligus meminimumkan fungsi kontrol 1
serta memaksimumkan fungsi kontrol 2.
Dengan demikian masalah kontrol optimum dapat dituliskan sebagai berikut: diselesaikan dengan prinsip minimum Pontryagin. Untuk menyelesaikannya modifikasi dengan fungsional objektif dan kendala baru sebagai berikut:
dengan kendala:
Penurunan persamaan (4.11) dapat dilihat pada Lampiran 2.
Dengan prinsip minimum Pontryagin diperoleh fungsi Hamilton dari masalah kontrol optimum tersebut, ialah sebagai berikut:
Syarat (1) akan menghasilkan kembali kendala pada masalah kontrol optimum tersebut yang dapat dituliskan sebagai berikut:
= 1 1 1 1, 2 − 2 2 2 1, 2 ,
1= 1 1 1, 2 − �1 1, 2= 2 2 1, 2 +�2 2.
Pada fungsi Hamilton juga terdapat peubah adjoin 1, 2, dan 3 yang nilainya ditentukan
melalui syarat (2) berikut:
1=− = 0, (4.15)
2=− 1, (4.16)
3=− 2. (4.17) Peubah adjoin yang dihasilkan merupakan syarat batas yang akan memengaruhi perubahan setiap peubah 1 dan 2 pada waktu ,
sedangkan 1, 2 dan 3 menyatakan laju dari
perubahan peubah tersebut.
Untuk menentukan fungsi kontrol pada masalah kontrol optimum, maka syarat (3) dan (4.19) diperoleh fungsi-fungsi adjoin:
1 = , (4.22)
2 = 2ℯ�1 , (4.23)
3 = 3ℯ�2 . (4.24)
Karena diasumsikan ( ) bebas, maka harus dipenuhi syarat transversalitas berikut (syarat (5) pada Teorema 1):
Fungsi kontrol yang diperoleh pada persamaan (4.32) merupakan upaya pengendalian hama dan predator yang akan membawa sistem pada level kesetimbangan yang diinginkan. Upaya pengendalian hama merupakan pengurangan jumlah hama dengan menggunakan pestisida dan upaya pengendalian predator untuk mempertahankan atau menambahkan jumlah predator.
Dengan menyelesaikan persamaan (4.30) dan (4.31) secara serentak, akan diperoleh 1∗( ) dan 2∗( ). Nilai 1∗( ) dan 2∗( ) yang diperoleh
kemudian disubstitusi kembali ke persamaan (4.32), sehingga dapat dituliskan menjadi: hama-predator Lotka-Volterra, yang melibatkan dua fungsi kepadatan populasi berikut:
1 1, 2 = − 1− 2,
2 1, 2 = 1− 2− . Pada sistem (3.1) diterapkan kontrol 1 dan 2,
sehingga fungsi kepadatan populasi hama predator dituliskan menjadi:
: laju kematian populasi hama karena adanya interaksi dengan predator,
: koefisien tingkat pemangsaan,
: koefisien pertumbuhan predator saat memangsa hama,
: laju penurunan populasi predator,
: tingkat kematian populasi predator tanpa
Solusi dari sistem (5.3) dan (5.4) adalah:
1∗ =
5.1 Kontrol Optimum Hama untuk Tanaman Kacang Kedelai
Sebagai studi kasus akan ditinjau model interaksi hama-predator pada tanaman kedelai, dengan ulat kedelai (Anticarsia gemmatalis) sebagai hama dan kepik mata besar (Geocoris) sebagai predator atau musuh alami.
Nilai parameter-parameter berikut diambil dari Rafikov (1997): = 0,216; = 0,011; = 0,173; = 0,003; 1= 1,030;
2= 1,900; �1= 2; �2= 1; = 0; = 0.
Nilai 1 dan 2 dipilih sedemikian sehingga
ambang batas populasi hama sebesar = 20
ulat/m2 menurut Empresa Brasileira de Pequisa
Agropecuaria (EMBRAPA) atau Pusat
Penelitian Pertanian Brasil. Dengan memasukkan nilai parameter tersebut ke persamaan (5.5) dan (5.6) diperoleh:
1∗( ) = 19,301, (5.7)
2∗( ) = 13,064. (5.8)
Substitusi kedua nilai di atas ke dalam persamaan (4.35) dan (4.36) diperoleh sistem persamaan diferensial yang menggambarkan dinamika populasi hama dan predator yaitu: 1∗( ) = 39,998−2 1∗( ), (5.9)
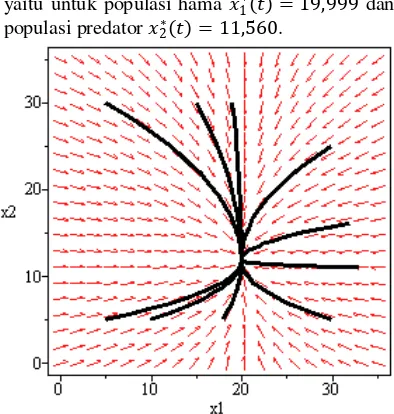
yaitu untuk populasi hama 1∗( ) = 19,999 dan
populasi predator 2∗( ) = 11,560.
Gambar 1 Kestabilan sistem hama-predator pada kasus kacang kedelai.
Gambar 1 menunjukkan bahwa untuk setiap jumlah populasi hama dan predator pada sistem akan menuju level kesetimbangan yang diinginkan. Untuk kondisi awal 1 0 = 32 dan
Gambar 2 Dinamika populasi hama pada waktu .
Gambar 2 menjelaskan dinamika populasi hama dan predator pada kondisi awal sampai kondisi akhir yang mencapai level kesetimbangan. Level kesetimbangan diperoleh karena adanya dua fungsi kontrol untuk populasi hama dan predator yang memengaruhi sistem dinamik.
Substitusi persamaan (5.7), (5.8), (5.11), dan (5.12) ke persamaan (4.33) dan (4.34) akan diperoleh dua fungsi kontrol untuk populasi hama dan predator sebagai berikut:
1∗( ) = 0,698 + 12,001 −2, (5.13)
2∗ = 1,504−4,440 −. (5.14)
Dari persamaan (5.13) dan (5.14) diperoleh nilai kesetimbangan dari dua fungsi kontrol 1∗( ) = 0,698 dan 2∗( ) = 1,504. Nilai fungsi kontrol
1∗ dan 2∗ diinterpretasikan sebagai upaya
pengendalian ulat sebesar 0,698 ulat/m2 dan
upaya pengendalian predator sebesar 1,504 predator/m2.
Gambar 3 Fungsi kontrol untuk kondisi awal
1(0) = 32 dan 2(0) = 16.
Gambar 3 menjelaskan dua fungsi kontrol berhasil membawa sistem pada level kesetimbangan yang diinginkan. Fungsi kontrol
1∗ mengalami penurunan sampai hari ke-2,
namun setelah hari ke-2 populasi hama dapat dikendalikan untuk menuju level kesetimbangan. Fungsi kontrol 1∗ merupakan
upaya pengendalian hama dengan menggunakan pestisida. Penurunan fungsi kontrol 1∗ sampai
hari ke-2 dikarenakan upaya pengendalian hama selanjutnya akan ditambahkan dengan upaya
pengendalian hayati pada hari ke-1 yang dinyatakan dalam fungsi kontrol 2∗, yaitu
dengan mengintroduksi predator ke dalam sistem.
Pada tahap pertama cukup sulit untuk memperoleh pengendalian hama ulat yang sangat kecil sebesar 0,698 ulat/m2, oleh karena itu proses pengendalian hama selanjutnya dibagi menjadi dua tahap. Tahap pertama populasi hama dan predator dapat distabilkan dengan dua fungsi kontrol dan tahap kedua akan diselesaikan pada bagian selanjutnya.
5.2 Pengendalian Hama dengan Memanfaatkan Musuh Alami
Pada bagian ini proses pengendalian hama selanjutnya dilakukan hanya dengan mengintroduksi predator ke dalam sistem, di mana kontrol bergerak mempertahankan sistem pada keadaan setimbang. Masalah ini dituliskan dalam sistem dinamik berikut:
1= 1 1 1, 2 , (5.15)
2= 2 2 1, 2 − 2∗ 2 1∗, 2∗ + . (5.16) Kontrol merupakan upaya pengendalian hama
dengan memanfaatkan predator untuk mempertahankan sistem pada keadaan setimbang, yaitu tingkat populasi hama 1∗=
= 20 dan populasi predator 2∗. Di sini nilai 2
∗ ditentukan melalui persamaan berikut: 1 1∗, 2∗ = 0. (5.17)
Dengan menggunakan nilai parameter Lotka-Volterra = 0,216; = 0,011; = 0,173; = 0,003; = 0, dan = 0, maka dari persamaan (5.17) diperoleh nilai 2∗=
19,636.
Analisis model (5.15) dan (5.16) dilakukan terhadap model linear padanannya. Didefinisikan:
Selanjutnya, akan ditentukan fungsi kontrol yang membawa sistem dari keadaan awal ke level kesetimbangan 1∗, 2∗ , dengan
meminimumkan suatu fungsional objekif, yang dinyatakan dalam masalah kontrol optimum berikut: sebagai masalah regulasi linear kuadratik (linear quadratic regulator, LQR).
Dari permasalahan kontrol optimum tersebut diperoleh fungsi Hamilton sebagai berikut:
=1
Dengan menggunakan kembali prinsip minimum Pontryagin, maka syarat (1)
Untuk menentukan fungsi kontrol pada masalah kontrol optimum persamaan (5.21), maka syarat (3) memberikan: dengan merupakan matriks simetrik berukuran 2 × 2. Dengan menurunkan Pelinearan model (5.15) dan (5.16) di sekitar titik keseimbangan 1∗, 2∗ = (20; 19,636)
memberikan:
= 0 −0,220
0,059 −0,113 . Selanjutnya diambil = 0 1,2
1,2 1,226 .
Dengan menggunakan fungsi LQR dari
software MATLAB, diperoleh solusi persamaan
aljabar Riccati, yaitu:
= 5,723 0
0 1 . (5.28)
Substitusi persamaan (5.25) ke persamaan (5.24) memberikan:
=− �, sehingga dari persamaan (5.20) dan (5.28) fungsi kontrol dapat dituliskan menjadi: ∗ =− 2−19,636 . (5.29)
Fungsi kontrol ∗ pada persamaan (5.29) disubstitusi ke persamaan (5.16), sehingga diperoleh persamaan berikut:
1=−0,220 2−19,636 , (5.30)
2= 1,415 1−20 −0,800 2−19,636 .
(5.31)
Dari persamaan (5.30) dan (5.31) akan diperoleh solusi khusus untuk kondisi awal populasi hama
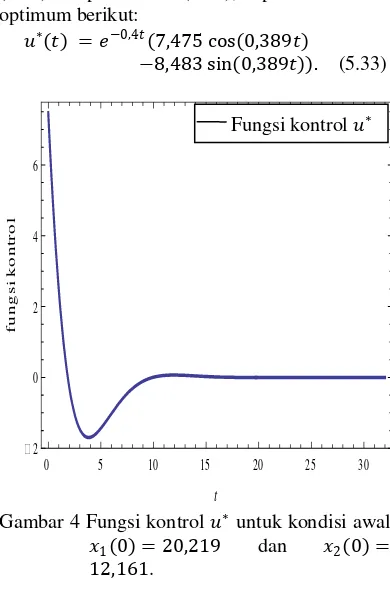
1 0 = 20,219 dan populasi predator 2 0 = Dengan menyubstitusi persamaan (5.32) dan (5.33) ke persamaan (5.29), diperoleh kontrol optimum berikut:
∗( ) = −0,4 (7,475 cos(0,389 )
−8,483 sin(0,389 )). (5.33)
Gambar 4 Fungsi kontrol ∗ untuk kondisi awal
1(0) = 20,219 dan 2(0) =
12,161.
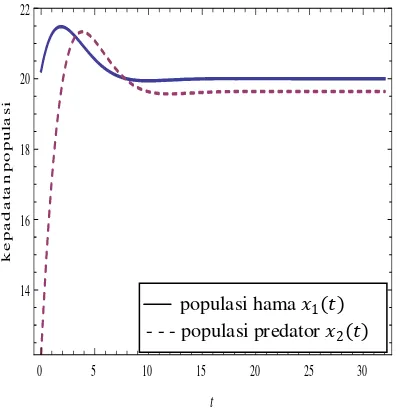
Gambar 5 Variasi populasi hama dan predator dengan fungsi kontrol ∗.
Karena kontrol dilakukan dengan menambahkan sejumlah predator ke dalam sistem (meski dengan jumlah yang terus menurun), maka dari Gambar 5 dapat dilihat bahwa populasi predator terus meningkat hingga mencapai 21,34 predator/m2 pada hari ke-4.
Kepadatan populasi hama kemudian menurun dan mencapai level stabil 20 ulat/m2 setelah hari
ke-8.
VI SIMPULAN
Dalam permasalahan kontrol optimum hama, penyelesaiannya dibagi menjadi dua tahap. Tahap pertama menentukan dua fungsi kontrol untuk populasi hama dan predator dengan menggunakan Prinsip Minimum Pontryagin, dan tahap kedua menentukan satu fungsi kontrol yang dapat mengendalikan populasi hama dan membawa sistem pada level kesetimbangan yang diinginkan, diselesaikan kembali dengan menggunakan Prinsip Minimum Pontryagin.
Penentuan dua fungsi kontrol 1∗( ) = 0,698
dan 2∗( ) = 1,504 mampu mencapai sistem pada level kesetimbangan populasi hama 1∗( )
dan populasi predator 2∗( ) yang diinginkan
agar tidak menyebabkan kerugian ekonomi. Pada tahap pertama, untuk dua hari pertama sulit untuk mengendalikan hama dalam jumlah yang sangat kecil sebesar 0,698 ulat/ 2, sehingga
upaya pengendalian sebaiknya dilakukan dengan
menentukan satu fungsi kontrol ∗ pada tahap kedua, yaitu upaya pengendalian hama dengan mengintroduksi predator sebesar 7,475 predator/ 2 ke dalam sistem. Pada tahap kedua untuk kondisi awal populasi hama yang melebihi nilai ambang batas = 20 hama/ 2, fungsi kontrol ∗ mampu membawa sistem lebih cepat ke level kesetimbangan yang diinginkan (20; 19,636).
DAFTAR PUSTAKA
Bin-Yahya H. 2012. Bentuk pengendalian hama. http://infohamapenyakittumbuhan.blogspot.c om/2012/04/bentuk-bentuk-pengendalian-hama-tanaman.html. [22 Januari 2013].
Bosch R van den, Messenger PS, and Gutierrez AP. 1982. An Introduction to Biological
Control. Plenum Press, New York.
Hartoyo D. 2008. Pengendalian hama nonhayati. http://www.htysite.com/hama musuh alami pengertian.htm. [3 Agustus 2012].
Rafikov M, Balthazar JM. 2005. Optimal pest control problem in population dynamics.
Computational and Applied Mathematics,
25: 65-81.
Rafikov M. 1997. Determinação dos parâmetros de modelos biomatemáticos, Ciência e Natura. UFSM, Santa Maria,19: 7- 20.
Lampiran 1 Bukti Teorema 1 (Prinsip Minimum Pontryagin)
Misalkan akan diminimumkan
= 0 , , + ( , )), (1)
0
dengan kendala : = , , . (2)
Misalkan 0 = 0, = 0, sedangkan ( ) dan keduanya tidak ditentukan. Fungsi “Scrap”
( , ) dapat didefinisikan sebagai
, = 0, 0 + ( , ) 0
, (3)
sehingga persamaan (1) menjadi
= 0, 0 + 0 , , + ( , )
0
= 0, 0 + 0 ∙ + �
� +
� � 0
(4)
dengan ( ), ( ), 0 , , , dan ( , ) secara sederhana dapat dituliskan sebagai , , 0(∙) dan
. Untuk meminimumkan pada persamaan (4) tidak dipengaruhi oleh pada saat = 0 tetapi ditentukan oleh bentuk integral pada suku kedua oleh persamaan (4).
Selanjutnya didefinisikan fungsional objektif yang diperbesar sebagai berikut:
= , , , , ,
0
(5)
dengan
, , , , = 0 ∙ + ∙ − +�
� +
�
� (6)
= , , , − +�
� +
� � .
Bentuk , , , = 0 , , , + ( , , ) disebut fungsi Hamilton. Syarat perlu agar
fungsional (5) memiliki nilai ekstrim adalah = 0. Berdasarkan kalkulus variasi maka diperoleh
= − + + + + ( − ) = = 0.
0
(7)
Agar persamaan (7) dipenuhi, maka persamaan Euler harus dipenuhi, yaitu
− = 0,
sehingga
− = + �
� + −
�
� −
= + + − +
= + (8)
dan berakibat =− . (9)
Variasi dan memberikan sifat saling bebas sehingga koefisiennya bernilai nol, yaitu = 0 dan
= 0. Persamaan (6) memberikan = dan = ∙ − = − , sehingga
= 0 (10)
= . (11)
Selanjutnya syarat batas diberikan oleh suku terakhir persamaan (7), yaitu
+ ( − ) = = 0. (12)
Karena
= −
− = − + + − +
= + ,
maka persamaan (12) menjadi
− = + + =0= = 0, (13)
persamaan ini dikenal sebagai transversality condition atau syarat batas. Apabila (0) dan 0 belum
ditentukan, maka syarat batas menjadi
− =0= + + =0= = 0,
yang menghasilkan teorema Pontryagin.
(Tu 1994)
Lampiran 2 penurunan persamaan (4.11)
Diketahui persamaan (4.1), (4.2), (4.7), (4.8) dan (4.9) sebagai berikut: 1= 1− 1 1 1− 1, 2+ 2 − �1 1
2= 2+ 2 2 1− 1, 2+ 2 +�2 2
( ) = 1 1( )− 2 2( ) + ( 1�1 1 � + 2�2 2 � ) �
0
1= 1− 1
2= 2+ 2
Dengan menurunkan persamaan (4.7) terhadap dan menyubstitusi persamaan (4.1), (4.2), (4.8), dan (4.9) akan diperoleh persamaan (4.11).
= 1 1( )− 2 2( ) + ( 1�1 1 � + 2�2 2 � ) �
0
= 1 1
− 2
2
+ 1�1 1 � 0
�+ 2�2 2 �
0
�
= 1 1 − 2 2+ 1�1 1 � 0
�+ 2�2 2 �
0
�
= 1( 1− 1 1 1− 1, 2+ 2 − �1 1)− 2( 2+ 2 2 1− 1, 2+ 2 +�2 2) + 1�1 1 �
0
�+ 2�2 2 �
0
�
= 1 1 1 1, 2 − 1�1 1− 2 2 2 1, 2 − 2�2 2+ 1�1 1+ 2�2 2 = 1 1 1 1, 2 − 2 2 2 1, 2
Lampiran 3 Penurunan persamaan (4.18) dan (4.19)
Diketahui persamaan (4.8), (4.9), dan (4.14) 1= 1− 1
2= 2+ 2
= 1 1 1 1 1, 2 − 1 2 2 2 1, 2 + 2 1 1 1, 2 − �1 1 + 3 2 2 1, 2 +�2 2
Dengan menurunkan terhadap 1dan 2 menggunakan aturan rantai, sehingga dari syarat (3) Prinsip
Minimum Pontryagin dapat diperoleh sebagai berikut:
1= �
Lampiran 4 Penurunan persamaan (4.30) dan (4.31)
Diketahui persamaan (4.20), (4.21), (4.28) dan (4.29) �
Lampiran 5 Penurunan persamaan (5.3) dan (5.4)
Diketahui persamaan (4.30) , (4.31), (5.1) dan (5.2)
1�( 1 1( 1, 2)
Lampiran 6 Penurunan persamaan (5.5) dan (5.6)
Diketahui persamaan (5.3) dan (5.4)
1 − 2−2 1 − 2 2= 0 1 1+ 2(− + 1−2 2) = 0
Dari persamaan (5.3) dapat disederhanakan sehingga diperoleh nilai 1
1= 1 − 2( 1+ 2)
2 1 …( )
Dengan menyubstitusi persamaan (A) ke persamaan (5.4) sehingga diperoleh persamaan (5.6)
1
Dari persamaan (5.4) dapat disederhanakan sehingga diperoleh nilai 2
2= 1 1 + 2 − 2
2 2 …( )
Dengan menyubstitusi persamaan (B) ke persamaan (5.3) sehingga diperoleh persamaan (5.5)
2 1 2 − 1 1 1 + 2 + 1 2 −2 12 2 1− 2 1 1 + 2 + 2 2 = 0
2 1 2 + 1 2 + 2 2 − 1 1 1 + 1 2 + 1 2 + 2 2 + 4 1 2 = 0
1∗( ) =
1 1 + 2 + 2 1 2
1 + 2 2+ 41 2
Lampiran 7 Program Maple 13 untuk Gambar 1
>
>
Lampiran 8 Penentuan solusi khusus untuk variabel �∗(�) dan �∗(�)
Diketahui persamaan (5.9) dan (5.10)
1( ) = 39,998−2 1( )
2 = 11,56− 2
Dengan menggunakan metode pengintegralan, maka persamaan diferensial orde satu di atas dapat ditentukan solusinya.
Bentuk umum + = di mana merupakan fungsi dalam dan dalah suatu konstanta. Solusi dinyatakan dalam bentuk = −
Maka dari persamaan (5.9) dan (5.10) solusi dari variabel 1∗( ) dan 2∗( ) dapat diselesaikan menjadi: 1
+ 2 1( ) = 39,998
⇔ 2
1 + 2 1 = 239,998… (kedua ruas dikalikan dengan 2 )
atau dapat dituliskan menjadi: ( 2
1( )) = 2 39,998
⇔ ( 2
1( )) = 2 39,998 … (kedua ruas diintegralkan terhadap )
⇔ 2
1( ) = 39,998 2 ⟺ 1 = −2 39,998 2 ⟺ 1 = −2 39,998
1 2
2 + 1
⟺ 1 = −2 19,999 2 + 2 ; 2= 39,998 1 ⟺ 1 = 19,999 + −2 2
Diketahui kondisi awal 1 0 = 32.
Maka solusi khusus dari 1∗( ) diperoleh 1∗( ) = 19,999 + 12,001 −2 . 2
+ 2 = 11,56
⇔ 2 + 2 = 11,56… (kedua ruas dikalikan dengan )
atau dapat dituliskan menjadi: ( 2( )) = 11,56
⇔ ( 2( )) = 11,56 … (kedua ruas diintegralkan terhadap )
Diketahui kondisi awal 2 0 = 16.
Maka solusi khusus dari 2∗ diperoleh 2∗ = 11,56 + 4,440 −.
Lampiran 9 Program Mathematica untuk Gambar 2
Plot[{19.999 + 12.001∗Exp[−2∗ ],11.56 + 4.44∗Exp[−1∗ ]}, { , 0,10}, PlotRange
→{32,10}, PlotStyle→{Dashed, Thick}, Frame→True, FrameLabel→{ , }]
Lampiran 10 Program Mathematica untuk Gambar 3
Plot[{0.698 + 12.001∗Exp[−2∗ ],1.504−4.440∗Exp[− ]}, { , 0,10}, PlotRange
→{0,13}, PlotStyle→{Dashed, Thick}, AxesOrigin→{0,0}, Frame
→True, FrameLabel→{ }
Lampiran 11 Pelinearan sistem (5.18) dan (5.19)
Diketahui persamaan (5.18) dan (5.19)
sehingga pelinearan untuk sistem di atas dapat dituliskan menjadi:
2= 2∗+ 2 1
Dari persamaan (C) dan (D) dapat dituliskan ke dalam bentuk matriks berikut:
1
Prinsip Minimum Pontryagin
1= �1= 1 1− 1∗ + 2 2− 2∗ 2= �2= 3 1− 1∗ + 4 2− 2∗ +
⇔ � = �+
�1=− 1=− 1 1− 1∗ + 2 2− 2∗ + 1�1+ 3�2
�2=− 2=− 2 1− 1
∗ +
3 2− 2∗ + 2�1+ 4�2
⇔ � =− �+ �
= 0
⇔ +�2= 0⇔ =−�2⇔ =− �… (*)
Misalkan �= � , matriks simetrik berukuran 2x2 (konstan).
�= �… (**)
� = �+ �
⇔ � = �+ �+
⇔ � = �+ � − �
⇔ � = �+ � − �
⇔ − �+ � = �+ � − �
⇔ − �+ � = �+ � − �
⇔0 = �+ � − �+ �+ �
⇔0 = + − + + �
⇔ + − + + = 0… (***)
Untuk → ∞ dan konstan, maka →0, sehingga persamaan (***) akan menghasilkan algebraic Riccati equation (ARE) atau persamaan aljabar Riccati berikut:
+ − + = 0.
Substitusi persamaan (**) ke persamaan (*) memberikan fungsi kontrol =− �.
Lampiran 13 Penentuan matriks P dengan menggunakan LQR pada software MATLAB
A=[0 -0.22; 0.059 -0.113]; >> B=[0;1];
>> Q=[0 1.2;1.2 1.226]; >> [P,L,G]=care(A,B,Q) P =
5.7227 0.0000 0.0000 1.0000 L =
-1.1012 -0.0118 G =
0.0000 1.0000
Lampiran 14 Penurunan persamaan (5.32) dan (5.33)
Diketahui persamaan (5.30) dan (5.31)
1=−0,22 2+ 4,319
2= 1,415 1−0,8 2−12,591
= 1
2
= 1,4150 −−0,220,8
1
2 +
4,319
−12,591 = 0 −0,22
1,415 −0,8 ; =
4,319
−12,591
Solusi partikular −1= −2,569 0,707
−4,545 0
=− −1 = 20
19,636 ⇔
1 = 20 2 = 19,636
Solusi homogen
= 1 1 �1 +
2 2 �2
Nilai eigen (�)
− � = 0
1,4150 −−0,220,8 − �0 0� = 0
�2+ 0,8�+ 0,311 = 0 �1,2=−0,4 ± 0,389
Vektor eigen yang berpadanan dengan �1=−0,4−0,389
0,4 + 0,389 −0,22
1,415 −0,8 + 0,4 + 0,389
1
2 = 0
0,4 + 0,389 1−0,22 2= 0⇔ 2 = (1,818 + 1,768 ) 1
1,415 1+ −0,4 + 0,389 2= 0
Misal 1=� ⇔ 2= (1,818 + 1,768 )�
Maka vektor eigen yang berpadanan dengan �1 adalah 1= 1 1,818 + 1,768
Vektor eigen yang berpadanan dengan �2=−0,4 + 0,389
0,4−0,389 −0,22
1,415 −0,8 + 0,4−0,389
1
2 = 0
0,4−0,389 1−0,22 2= 0⇔ 2 = (1,818−1,768 ) 1 1,415 1+ −0,4−0,389 2= 0
Misal 1=� ⇔ 2= (1,818−1,768 )�
Maka vektor eigen yang berpadanan dengan �2 adalah 2= 1 1,818−1,768
= 1 1 �1 + 2 2 �2
= 1
1
1,818 + 1,768 (−0,4−0,389 ) + 2
1
1,818−1,768 (−0,4+0,389 )
= −0,4 1
1
1,818 + 1,768 (cos 0,389 − 0,389 ) + −0,4
2
1
1,818−1,768 (cos0,389 + 0,389 ) = −0,4 1(cos 0,389 − 0,389 )
1(1,818(cos 0,389 − sin(0,389 )) + 1,768 (cos0,389 − sin(0,389 )))
+ −0,4 2(cos 0,389 + 0,389 )
2(1,818(cos0,389 + sin(0,389 ))−1,768 (cos 0,389 + sin(0,389 )))
= −0,4
1cos 0,389 + 2cos 0,389
{ 1(1,818cos 0,389 + 1,768sin(0,389 )) + 2(1,818cos0,389 + 1,768sin(0,389 ))} + −0,4
− 1sin 0,389 + 2sin 0,389
{ 1(−1,818sin 0,389 + 1,768cos(0,389 ))
+ 2(1,818sin0,389 −1,768cos(0,389 ))}
= −0,4
1cos 0,389 + 2sin 0,389
{ 1(1,818cos 0,389 + 1,768sin(0,389 ))
+ 2(1,818cos0,385 −1,768sin(0,389 ))}
; 1= 1+ 2
2=− 1+ 2
1 = −0,4 ( 1cos 0,389 + 2sin 0,389 )
2 = −0,4 1(1,818cos0,389 + 1,768sin(0,389 ))
+ 2(1,818sin 0,389 −1,768cos(0,389 ))
Solusi Umum
1 = 1 + 1 = 20 + −0,4 ( 1cos 0,389 + 2sin 0,389 )
2 = 2 + 2 = 19.636 + −0,4 1(1,818cos0,389 + 1,768sin(0,389 )
+ 2(1,818sin 0,389 −1,768cos(0,389 )))
Kondisi awal
1 0 = 20,219 2 0 = 12,161
1= 0,219
2= 4,453
Solusi Khusus
1 = 20 + −0,4 4,453 sin 0,389 + 0,219 cos 0,389 2 = 19,636+ −0,4 8,483 sin(0,389 )−7,475 cos 0,389
Lampiran 15 Program Mathematica untuk Gambar 4
Plot[{Exp[−0.4∗ ]∗(7.475∗Cos[0.389∗ ]−8.483∗Sin[0.389∗ ])}, { , 0,32}, AxesOrigin
→{0,−1.1}, PlotStyle→Thick, Frame→True, PlotRange→All, FrameLabel
→{ }]
Lampiran 16 Program Mathematica untuk Gambar 5
Plot[{20 + Exp −0.4∗ ∗ 4.453∗Sin0.389∗ + 0.219∗Cos[0.389∗ ],19.636 + Exp[−0.4
∗ ]∗(8.483∗Sin[0.389∗ ]−7.475∗Cos[0.389∗ ])}, { , 0,32}, PlotStyle
→{Thick, Dashed}, Frame→True, AxesOrigin→{0,0}, PlotRange
→{12.161,22}, FrameLabel→{ }]