Studi Penggunaan Algoritma Branch And Bound Untuk Menyelesaikan Persoalan Travelling Salesman Problem (TSP) Pada Graf Lengkap

(1)

STUDI PENGGUNAAN ALGORITMA BRANCH AND BOUND UNTUK MENYELESAIKAN PERSOALAN

TRAVELLING SALESMAN PROBLEM (TSP) PADA GRAF LENGKAP

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

MARCO SIAGIAN NIM : 050803055

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

(2)

PERSETUJUAN

Judul : STUDI PENGGUNAAN ALGORITMA BRANCH

AND BOUND UNTUK MENYELESAIKAN

PERSOALAN TRAVELLING SALESMAN

PROBLEM (TSP) PADA GRAF LENGKAP

Kategori : SKRIPSI

Nama : MARCO SIAGIAN

Nomor Induk Mahasiswa : 050803055

Program Studi : SARJANA (S1) MATEMATIKA

Departemen : MATEMATIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN

ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di

Medan, Desember 2009 Komisi Pembimbing :

Pembimbing 2 Pembimbing 1

Drs. Faigiziduhu Bu’ulolo, M.Si Drs. Ujian Sinulingga, M.Si NIP 195003211980031003 NIP 195603031984031004

Diketahui/Disetujui oleh

Departemen Matematika FMIPA USU Ketua,

Dr. Saib Suwilo, M.Sc. NIP 1964010919880301004

(3)

PERNYATAAN

STUDI PENGGUNAAN ALGORITMA BRANCH AND BOUND UNTUK MENYELESAIKAN PERSOALAN

TRAVELLING SALESMAN PROBLEM (TSP)

PADA GRAF LENGKAP SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.

Medan, Desember 2009

MARCO SIAGIAN 050803055

(4)

PENGHARGAAN

Puji dan syukur penulis ucapkan serta panjatkan kepada Tuhan Yang Maha Kuasa atas kasih, berkat dan karunia-Nya sehingga penulis dapat menyelesaikan skripsi ini.

Skripsi ini berjudul “ Studi Penggunaan Algoritma Branch And Bound Untuk Menyelesaikan Persoalan Travelling Salesman Problem (TSP) Pada Graf Lengkap ” diajukan sebagai salah satu syarat untuk memperoleh gelar sarjana pada Departemen Matematika Fakultas Matematika dan Ilmu Pengetahuan Alam, Universitas Sumatera Utara.

Dalam kesempatan ini, penulis juga didukung dan dibantu oleh orang-orang yang ada di sekitar penulis. Oleh sebab itu penulis ingin mengucapkan terimakasih yang sebesar-besarnya kepada :

1. Ayahanda dan Ibunda yang tersayang dan tercinta M. Siagian dan R. Sihite yang telah mengasuh dan membesarkan penulis dengan rasa kasih dan sayang tulus yang tak terbalas.

2. Adik-ku satu-satunya yang tersayang dan tercinta, Only Christine Siagian yang selalu memberikan dukungan dan dorongan di setiap kondisi dan keadaan apapun. 3. Frety Ginova Ginting yang selalu menemani penulis dalam setiap langkah dan

hari-hari penulis untuk menyelesaikan skripsi ini.

4. Bapak Drs. Ujian Sinulingga, M.Si dan Bapak Drs. Faigiziduhu Bu’ulolo, M.Si selaku dosen pembimbing I dan dosen pembimbing II yang telah banyak memberikan masukan dan bantuan kepada penulis.

5. Bapak Prof. Dr Herman Mawengkang dan Bapak Drs. H Haluddin Panjaitan selaku dosen penguji buat penulis.

6. Teman-teman Stambuk 2005 khususnya Math_05 FC (Jo, Paul, Mama, Sahat, Nixon, Nico, Doni, Cahaya, Opung, Reynold, Paskah, Andre, Firiska),serta Christine, Trisna, Imelda, Ester, Enda, Mei, dll.

Dalam penyusunan skripsi ini mungkin terdapat kekurangan dan kesalahan,untuk itu penulis mengharapkan kritik dan saran yang membangun dari pembaca guna perbaikan untuk skripsi ini.

Akhirnya penulis berharap semoga skripsi ini dapat memberikan manfaat dan guna bagi para pembaca.

(5)

ABSTRAK

Travelling Salesman Problem (TSP) adalah masalah optimisasi, yaitu mengunjungi

setiap tempat dari himpunan tempat-tempat yang ditentukan sekali dan hanya satu kali kemudian kembali ke tempat awal pada akhir dari rute perjalanan dengan jarak, waktu dan biaya yang minimum. Masalah di atas dapat diselesaikan dengan beberapa algoritma seperti, algoritma brute force, algoritma greedy, algoritma genetic, algoritma branch and bound dll. Pada penelitian in, digunakan algoritma Branch and

Bound, yaitu dengan menggunakan pohon untuk penyimpanan berbagai kemungkinan

(6)

STUDY ABOUT THE USED OF BRANCH AND BOUND ALGORITHM TO SOLVED TRAVELLING SALESMAN PROBLEM

ABSTRACT

(7)

DAFTAR ISI

Halaman

Persetujuan ii

Pernyataan iii

Penghargaan iv

Abstrak v

Abstract vi

Daftar Isi vii

Daftar Tabel ix

Daftar Gambar x

Bab 1 Pendahuluan

1.1 Latar Belakang 1

1.2 Perumusan Masalah 3

1.3 Batasan Masalah 3

1.4 Tujuan Penelitian 3

1.5 Manfaat Penelitian 3

1.6 Metodologi Penelitian 4

1.7 Tinjauan Pustaka 4

Bab 2 Landasan Teori

2.1 Konsep Dasar Graf 5

2.1.1 Graf 5

2.1.2 Loop Dan Edge Paralel 6

2.1.3 Graf Sederhana (Simple Graf) 6

2.1.4 Ketetanggaan (Adjacent) 7

2.1.5 Bersisian (Incident) 7

2.1.6 Simpul Terpencil (Isolated Vertex) 7

2.1.7 Graf Kosong (Null Graf) 7

2.1.8 Derajat (Degree)

2.2 Jenis-Jenis Graf 8

2.3 Terminologi Dasar 12

2.3.1 Walk 12

2.3.2 Trail 13

2.3.3 Lintasan (Path) 14

2.3.4 Sirkuit (Cycle) 14

(8)

2.3.6 Graf Berbobot Dan Graf Berlabel 15

2.3.7 Distance 15

2.4 Lintasan Dan Hamilton Cycle 15

2.5 Travelling Salesman Problem 17

Bab 3 Pembahasan

3.1 Algoritma Branch and Bound 18

3.2 Implementasi Metode Branch and Bound Dalam 19 Pemecahan Travelling Salesman Problem (TSP) Pada Graf

Lengkap

3.3 Contoh Penyelesaian Masalah Travelling Salesman Problem 21

(TSP) Dengan Menggunakan Metode Branch and Bound

3.4 Gambar Diagram Pohon Penyelesaian 35

Bab 4 Kesimpulan dan Saran

4.1 Kesimpulan 36

4.2 Saran 36

(9)

DAFTAR TABEL

Halaman

Tabel 3.1 Vehicle Routing Problem 21

(10)

DAFTAR GAMBAR

Halaman

Gambar 2.1 Graf 5

Gambar 2.2 Simple Graf 6

Gambar 2.3 Graf Kosong 7

Gambar 2.4 Graf G(7,8) 8

Gambar 2.5 Graf Berarah dan Graf Ganda Berarah 9

Gambar 2.6 Graf Lengkap 10

Gambar 2.7 Graf Lingkaran 10

Gambar 2.8 Graf Teratur 11

Gambar 2.9 Graf Bipartite 11

Gambar 2.10 Graf Bipartisi Lengkap 12

Gambar 2.11 Graf 13

Gambar 2.12 Graf Berbobot Dan Graf Berlabel 15

Gambar 2.13 Graf Hamilton 16

(11)

ABSTRAK

Travelling Salesman Problem (TSP) adalah masalah optimisasi, yaitu mengunjungi

setiap tempat dari himpunan tempat-tempat yang ditentukan sekali dan hanya satu kali kemudian kembali ke tempat awal pada akhir dari rute perjalanan dengan jarak, waktu dan biaya yang minimum. Masalah di atas dapat diselesaikan dengan beberapa algoritma seperti, algoritma brute force, algoritma greedy, algoritma genetic, algoritma branch and bound dll. Pada penelitian in, digunakan algoritma Branch and

Bound, yaitu dengan menggunakan pohon untuk penyimpanan berbagai kemungkinan

(12)

STUDY ABOUT THE USED OF BRANCH AND BOUND ALGORITHM TO SOLVED TRAVELLING SALESMAN PROBLEM

ABSTRACT

(13)

BAB 1 PENDAHULUAN

1.1 Latar Belakang Masalah

Travelling Salesmen Problem (TSP) merupakan masalah klasik yang mencoba

mencari rute atau jarak terpendek yang dilalui salesmen yang ingin mengunjungi beberapa tempat yang harus mendatangi tempat yang sama lebih dari satu kali. Meskipun persoalan ini bernama persoalan perjalanan pedagang, namun penerapannya tidak hanya pada kasus yang berhubungan dengan pedagang. Banyak penerapan

Travelling Salesmen Problem (TSP) yang muncul dalam kehidupan sehari-hari

misalnya :

a. Efesiensi pengiriman surat dan barang b. Perencanaan pemasangan saluran pipa c. Masalah transportasi

d. Persoalan delivery order (jasa pengantar makanan) e. Analisis rangkaian air atau listrik

f. Dan lain sebagainya

(14)

Terdapat beragam teori algoritma yang dapat digunakan untuk menyelesaikan permasalahan Travelling Salesmen Problem (TSP) seperti, algoritma brute force,

algoritma greedy, algoritma genetic, algoritma branch and bound dll.

Dalam tulisan ini, penulis memilih salah satu algoritma di atas untuk menyelesaikan masalah Travelling Salesmen Problem (TSP) yaitu dengan menggunakan algoritma Branch and Bound.

Metode Branch and Bound diusulkan pertama kali oleh A.H.Land dan A.G.Doig pada tahun 1960. Sebenarnya metode ini dibuat untuk pemrograman linier (linier programming). Namun kenyataannya metode ini mampu menyelesaikan permasalahan seperti Travelling Salesmen Problem (TSP) dan beberapa masalah lain. Metode ini menggunakan pohon pencarian (Search Tree), setiap simpul di pohon merupakan representasi dari sejumlah kemungkinan solusi dari Travelling Salesmen

Problem (TSP). Metode ini hanya dapat digunakan untuk masalah optimasi saja

(optimazion problem).

Algoritma dimulai dengan pengisian sebuah nilai ke akar dari pohon pencarian tersebut. Pencabangan dilakukan dengan memasang sebuah pending node ke pending

node lain yang lebih rendah levelnya. Bobot juga dihitung pada setiap proses dan

ditulis di simpul pohon. Jika sebuah simpul diketahui merupakan solusi yang tidak mungkin bagi persoalan yang dihadapi, simpul tersebut diisi dengan nilai tak terbatas

(infinity). Algoritma berhenti ketika sudah tidak mungkin lagi untuk membentuk

simpul baru di pohon atau hasil terakhir yang ditemukan merupakan hasil yang lebih rendah (minimum) dari isi simpul yang telah ada pada level yang lebih rendah.

Dari uraian di atas maka penulis tertarik untuk membahas algoritma Branch

and Bound sebagai suatu pendekatan dalam menyelesaikan masalah Travelling

(15)

1.2 Perumusan Masalah

Adapun permasalahan yang timbul dari latar belakang adalah memakai algoritma Branch and Bound untuk memecahkan permasalahan Travelling Salesman

Problem (TSP).

1.3 Batasan Masalah

Pada tulisan ini masalah dibatasi hanya sampai pada tahap pencarian nilai optimal dengan menggunakan algoritma Branch and Bound pada permasalahan

Travelling Salesman Problem (TSP).

1.4 Tujuan Penelitian

Tujuan dari penelitian ini adalah mempelajari dan menyelesaikan persoalan pengoptimalan dari Travelling Salesman Problem (TSP) dengan menggunakan algoritma Branch and Bound.

1.5 Manfaat Penelitian

Manfaat dari penelitian ini adalah :

a. Dapat merepresentasikan masalah Travelling Salesman Probem (TSP) ke dalam model graf.

b. Mengatasi masalah perjalanan salesman secara optimal dengan menggunakan algoritma Branch and Bound.

(16)

1.6 Metodologi Penelitian

Metode penelitian yang akan digunakan adalah penelitian literatur dengan prosedur sebagai berikut :

a. Menguraikan teori dasar yang menunjang terhadap pembahasan yang diperoleh dari jurnal, buku, dan artikel internet.

b. Menguraikan penjelasan masalah Travelling Salesman Problem (TSP) dengan menggunakan algoritma Branch and Bound.

c. Menyelesaikan contoh masalah Travelling Salesman Problem (TSP) dengan algoritma Branch and Bound.

1.7 Tinjauan Pustaka

Sebagai pendukung dalam penulisan tugas akhir ini digunakan beberapa buku, yaitu:

(Munir Rinaldi,2005; 355). Persoalan Travelling Salesmen Problem (TSP) adalah persoalan mengunjungi sejumlah kota tepat satu kali dan kembali lagi ke kota asal keberangkatannya.

(Boffey, T, B, 1982; 148). Travelling Salesmen Problem (TSP) adalah persoalan perjalanan dari kota Ti mengunjungi n – 1 kota lainnya T2, T3, … , Tn tepat

satu kali dan kembali lagi ke kota asal Ti. Jika dij menyatakan jarak antara kota Ti dan Tj maka akan dicari cara meminimumkan jarak perjalanan tersebut.

(Johnsonbaugh Richard,2001; 265). Graf G adalah pasangan himpunan (V,E) di mana V adalah himpunan dari vertex dan E adalah himpunan dari edge yang menghubungkan sepasang simpul.

(17)

BAB II

LANDASAN TEORI

2.1 Konsep Dasar Graf

Definisi 2.1.1 Graf

Sebuah graf G adalah pasangan (V,E) dengan V adalah himpunan yang tak kosong yang anggotanya disebut vertex, dan E adalah himpunan yang anggotanya adalah pasangan-pasangan tak berurut dari vertex V dan disebut dengan edge.

Gambaran umum mengenai graf diartikan sebagai diagram, dimana vertex disajikan berupa titik dan dinotasikan dengan vi ; i = 1,2,3,…,m dan edge disajikan

berupa garis lurus atau garis lengkung yang menghubungkan dua buah vertex (vi,,vj )

dan dapat dinotasikan dengan ek ; k = 1,2,3,…,n.

Definisi 2.1 menyatakan bahwa V tidak boleh kosong, sedangkan E boleh kosong. Jadi, sebuah graf dimungkinkan tidak mempunyai sisi satu buah pun, tetapi simpulnya harus minimal ada satu.

Sebagai ilustrasi dapat dilihat gambar 2.1 yaitu :

G1 G2 G3

Gambar 2.1 Graf

G1 adalah graf dengan

V = { 1, 2, 3, 4 }

E = { (1, 2), (1, 3), (2, 3), (2, 4), (3, 4) }

1 1 1

2 3 4 2 3 4 2 4 3 e₁ e₂ e₃ e₄

e₅ e6

e₇

e₁ e₂

e₃ e₄

e₅ e6

e₇

(18)

G2 adalah graf dengan V = { 1, 2, 3, 4 }

E = { (1, 2), (2, 3), (1, 3), (1, 3), (2, 4), (3, 4), (3, 4) = { e1, e2, e3, e4, e5, e6, e7}

G3 adalah graf dengan

V = { 1, 2, 3, 4 }

E = { (1, 2), (2, 3), (1, 3), (1, 3), (2, 4), (3, 4), (3, 4), (3, 3) }

= { e1, e2, e3, e4, e5, e6, e7, e8}

Definisi 2.1.2 Loop dan Edge Paralel

Sebuah edge yang menghubungkan pasangan vertex yang sama yakni (vi,vi)

disebut loop dan dua buah atau lebih edge yang mempunyai vertex -vertex ujung yang sama disebut edge-edge yang paralel atau multiple edge. Pada gambar 2.1 dapat dilihat, gambar G1 tidak memiliki loop maupun edge pararel, sedangkan pada gambar G2 tidak memiliki loop tetapi memiliki edge paralel yaitu e3,e4 dan e1,e6. Dan pada

gambar G3 memiliki loop yaitu e8 dan edge pararel yaitu e3, e4 dan e1, e6.

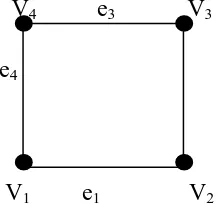
Defenisi 2.1.3 Graf Sederhana (Simple Graf)

Simple graf adalah graf yang tidak memuat loop dan edge-edge yang pararel. V4 e3 V3

e4 e2

V1 e1 V2

(19)

Definisi 2.1.4 Ketetanggaan (Adjacent)

Dua buah simpul pada graf dikatakan bertetangga bila kedua simpul tersebut terhubung langsung. Atau dapat kita sebut, vj bertetangga dengan vk pada graf Gjika (vj,vk ) adalah sisi pada sebuah graf G.

Definisi 2.1.5 Bersisian (Incident)

Untuk sembarang sisi e = ( vj, vk ) dikatakan e bersisian dengan simpul vj, atau e bersisian dengan simpul vk.

Definisi 2.1.6 Simpul Terpencil (Isolated Vertex )

Simpul yang tidak memiliki sisi yang bersisian dengannya atau tidak bertetangga dengan simpul lainnya disebut dengan simpul terpencil.

Definisi 2.1.7 Graf Kosong (Null Graf)

Graf yang himpunan sisinya merupakan himpunan kosong (Nn) disebut graf

kosong, dimana n adalah jumlah simpul.

1 2

3

4

Gambar 2.3 Graf Kosong Defenisi 2.1.8 Derajat (Degree)

Derajat dari sebuah vertex vi dalam graf G adalah jumlah edge yang bersisian

(20)

v1 e1 v2

e4

e2 v3 e6 e7

e3

v4 e5 v5 e8 v6 v7

Gambar 2.4 Graf (7,8) Dari gambar 2.3 tersebut,

V = { v1, v2, v3, v4, v5, v6, v7 } dan E = { e1, e2, e3, e4, e5, e6, e7, e8 }

Simpul 1 bertetangga dengan simpul 2, 3 dan 4 tetapi tidak bertetangga dengan simpul 5 dan 6.

Simpul 5 bertetangga dengan simpul 2 dan 4 tetapi tidak bertetangga dengan simpul 1, 3, 4 dan 6.

Sisi (1,2) bersisian dengan simpul 1 dan simpul 2. Sisi (1,4) bersisian dengan simpul 1 dan simpul 4.

Tetapi sisi (3,4) tidak bersisian dengan simpul 1, 2, 5, 6 dan 7. Simpul terpencil adalah simpul 7.

Derajat, d(1) = d(2) = d(4) = 3 d(3) = d(5) = 2

d(6) = 1 dan d(7) = 0

(21)

1. Graf sederhana (Simple Graf)

Graf yang tidak mengandung gelang maupun sisi-ganda dinamakan graf sederhana. 2. Graf tak-sederhana (Unsimple-Graf)

Graf yang mengandung sisi ganda atau gelang dinamakan graf tak-sederhana

(unsimple graf).

Berdasarkan jumlah simpul pada suatu graf, maka secara umum graf dapat digolongkan menjadi dua jenis:

1. Graf berhingga (Limited Graf)

Graf berhingga adalah graf yang jumlah simpulnya n berhingga. 2. Graf tak-berhingga (Unlimited Graf)

Graf yang jumlah simpulnya n tidak berhingga banyaknya disebut graf tak berhingga.

Berdasarkan orientasi arah pada sisi, maka secara umum graf dibedakan atas 2 jenis:

1. Graf tak-berarah (Undirected Graf)

Graf yang sisinya tidak mempunyai orientasi arah disebut graf tak-berarah. 2. Graf berarah (Directed Graf atau Digraf)

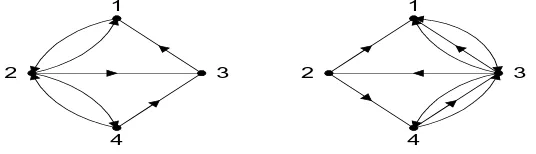
Graf yang setiap sisinya diberikan orientasi arah disebut sebagai graf berarah.

Gambar 2.5 Graf Berarah dan Graf-Ganda Berarah

1 1

2 3

4

2 3

(22)

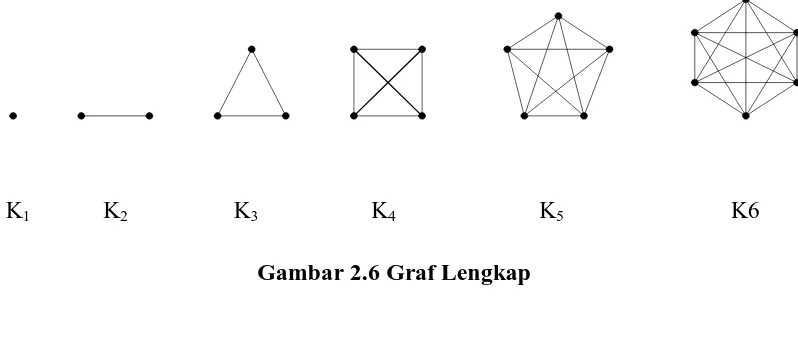
Ada juga graf sederhana khusus yang terdiri dari: a. Graf lengkap (Complete Graf)

Graf lengkap ialah graf sederhana yang setiap simpulnya mempunyai sisi ke semua simpul lainnya. Graf lengkap dengan n buah simpul dilambangkan dengan Kn.

Jumlah sisi pada graf lengkap yang terdiri dari n buah simpul adalah n(n – 1)/2.

K1 K2 K3 K4 K5 K6

Gambar 2.6 Graf Lengkap

b. Graf lingkaran

Graf lingkaran adalah graf sederhana yang setiap simpulnya berderajat dua. Graf lingkaran dengan n simpul dilambangkan dengan Cn.

(23)

c. Graf teratur (Regular Graf)

Graf yang setiap simpulnya mempunyai derajat yang sama disebut graf

teratur. Apabila derajat setiap simpul adalah r, maka graf tersebut disebut sebagai graf

teratur derajat r. Jumlah sisi pada graf teratur adalah nr/2.

Gambar 2.8 Graf Teratur d. Graf bipartisi (Bipartite Graf)

Graf G yang himpunan simpulnya dapat dipisah menjadi dua himpunan bagian

V1 dan V2, sedemikian sehingga setiap sisi pada G menghubungkan sebuah simpul di V1 ke sebuah simpul di V2 disebut graf bipartite dan dinyatakan sebagai G(V1, V2).

V1 V2

Gambar 2.9 Graf Bipartite

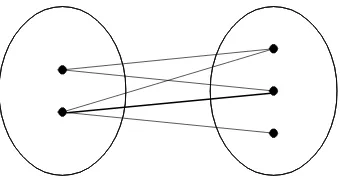
e. Graf bipartisi Lengkap ( Complete Bipartite Graf )

Graf bipartisi yang tiap vertex pada V1 dihubungkan ke setiap vertex dari V2,

maka graf yang demikian disebut graf bipartisi lengkap dan dinotasikan dengan Km,n ;

(24)

Gambar 2.10 Graf Bipartisi Lengkap

2.3 Terminologi Dasar

Definisi 2.3.1 Walk

Suatu walk dalam graf G adalah suatu barisan berhingga dari vertex dan edge secara bergantian yang dimulai dan diakhiri dengan vertex sehingga setiap edge yang bersisian dengan vertex sebelum dan sesudahnya, dimana sebuah edge hanya dilalui satu kali. Di dalam suatu walk pada sebuah graf dapat terjadi bahwa satu vertex dilalui lebih dari satu kali. Pada umumnya penulisan barisan walk biasanya mengikutsertakan edgenya, tetapi boleh juga tidak.

Apabila vertex awal dan akhir dari suatu walk adalah sama, maka walk yang demikian disebut dengan closed walk (walk tertutup). Sedangkan bila vertex awal dan

vertex akhir dari suatu walk berbeda, maka walk yang demikian disebut open walk

(25)

Sebagai contoh diberikan pada gambar berikut : v1

e1 e2

v2 e3 e9 v3

e5 e6

e4 v5 e8

e7

v6

Gambar 2.11 Graf

Pada gambar tersebut dapat diambil beberapa walk diantaranya sebagai berikut :

v1 e1 v2 e4 v6 e7 v5 e6 v3 e2 e1 (closed walk)

v1e2 v3 e6 v5 e7 v6 (open walk)

Walk di atas boleh juga ditulis dengan cara sebagai berikut :

v1 v2 v6 v5 v3 v1 (closed walk)

v1 v3 v5 v6 (open walk)

Definisi 2.3.2 Trail

Walk yang semua sisi di dalam setiap barisan harus berbeda disebut trail. Trail

tertutup adalah suatu trail dengan simpul awal dan simpul akhir yang sama. Dari gambar 2.11, salah satu contoh yang merupakan trail adalah :

(26)

Defenisi 2.3.3 Lintasan (Path)

Path dari suatu graf G adalah suatu walk yang keseluruhan vertex nya berbeda

kecuali vertex awal dan vertex akhir yang boleh sama. Bila dalam suatu path di mana

vertex awal dan akhir sama maka path yang demikian disebut closed path (path

tertutup), sedangkan bila vertex awal dan akhir tidak sama maka disebut open path (path terbuka). Sebagai contoh lihat gambar 2.11

v1 v3 v5 v3 v2 v 6 (open path)

v5 v3 v6 v2 v1 v 5 (closed path)

Defenisi 2.3.4 Sirkuit (Cycle)

Cycle dari suatu graf G adalah suatu closed path (path tertutup). Atau dengan

kata lain cycle merupakan lintasan yang berawal dan berakhir pada simpul yang sama. Dari gambar di atas, yang merupakan cycle diantaranya :

v1 v2 v5 v6 v3 v1

Definisi 2.3.5 Connected Graf dan Disconnected Graf

(27)

Defenisi 2.3.6 Graf Berbobot Dan Graf Berlabel

Graf berbobot graf yang setiap sisinya diberi sebuah bobot sedangkan graf berlabel adalah graf yang tidak memiliki bobot.

Gambar 2.12 Graf Berbobot Dan Graf Berlabel Defeinisi 2.3.7 Distance

Distance antara dua vertex vi dan vj dituliskan d( v1,v2 ) diartikan sebagai

panjang terpendek antara vi dan vj. Sebagai contoh dapat dilihat pada gambar 2.12

yaitu jarak dari a ke b atau d (a,b) adalah 12.

2.4 Lintasan Dan Hamilton Cycle

Lintasan Hamilton adalah lintasan yang melalui tiap vertex di dalam graf G tepat satu kali. Bila lintasan itu kembali lagi ke vertex awal dan membentuk lintasan tertutup (cycle), maka lintasan tertutup itu dinamakan Hamilton Cycle. Jadi, Hamilton

Cycle adalah cycle yang melalui tiap vertex di dalam graf G tepat satu kali, kecuali

vertex awal dan vertex akhir dan graf yang memiliki Hamilton Cycle dinamakan

Hamilton Graf.

(28)

Gambar 2.13 Graf Hamilton

Teorema 2.4.1

Di dalam sebuah graf lengkap G dengan sekurang-kurangnya 3 buah vertex , selalu terdapat suatu hamilton cycle.

Bukti :

Misalkan di dalam suatu graf lengkap terdapat sebuah lintasan dengan p-1

(29)

dengan kedua edge (v1,vx) dan (vx,v2) sehingga vertex vx ada dalam lintasan

gandengannnya. Akan tetapi jika edge (vx,v2) tidak ada, maka pasti edge (v2,vx) ada

didalam graf dan cara diatas diulangi lagi. Pada akhirnya jika ternyata tidak mungkin memasukkan vertex vx ke dalam lintasan gandengan dengan cara mengganti edge (vx,vk+1) di dalam lintasan asalnya dengan kedua edge (vk,vx) dan (vk,vk+1), dengan 1≤k≤p-1, maka dapat disimpulkan pastiada edge (vp,vx) di dalam graf ini. Oleh

karenanya,edge (vp,vx) dapat digandengkan pada lintasan asalnya agar vx berada di

dalam lintasan gandengannya. Langkah-langkah diulangi terus sampai semua vertex yang ada di dalam graf ini tercakup di dalam lintasan.

2.5 Travelling Salesman Problem

Travelling Salesmen Problem (TSP) merupakan masalah klasik yang mencoba

mencari rute atau jarak terpendek yang dilalui salesmen yang ingin mengunjungi beberapa tempat tanpa harus mendatangi tempat yang sama lebih dari satu kali untuk mengoptimalkan waktu dan ongkos yang diperlukan. Masalah Travelling Salesman

Problem (TSP) dapat direpresentasikan ke dalam suatu terminologi graf, yakni sebuah

graf G= (V,E) dengan vertex mewakili kota-kota yang akan diunjungi dan edge mewakili jalan-jalan yang menghubungkan dua kota. Panjang edge (x,y) yakni d(x,y) merupakan jarak, waktu atau biaya dari perjalanan sepanjang edge (x,y).

Hamilton cycle sering dikenal sebagai masalah Travelling Salesman Problem

(TSP) pada graf yang dapat diformulasikan pada directed graf maupun undirected

graf yang mana pada undirected graf umumnya disebut sebagai masalah perjalanan

Travelling Salesman Problem (TSP) yang simetris yakni panjang perjalananan dari

vertex x ke vertex y maupun dari vertex y ke vertex x mempunyai bobot yang sama.

Sedangkan masalah pada directed graf pada umumnya disebut sebagai masalah perjalanan. Travelling Salesman Problem (TSP) yang tidak simetris, yakni bobot dari perjalanan dari vertex x ke vertex y berbeda dengan bobot perjalanan dari vertex y ke

(30)

BAB 3 PEMBAHASAN

3.1 Algoritma Branch And Bound

Metode Cabang dan Batas ( Branch and Bounch ) pertama kali di usulkan oleh A.H.Land dan A.G.Doig pada tahun 1960 untuk menyelesaikan permasalahan Program Bilangan Cacah dan Program Liniear (Linear Programming), namun pada kenyataannya metode ini dapat ini menyelesaikan masalah penugasan (Assignment

Problem), graf (Travelling Salesaman Problem), dan masalah transportasi.

Metode ini menggunakan pohon pencarian (Search Tree) yang mana setiap simpul di pohon merupakan representasi dari sejumlah kemungkinan dari solusi

Travelling Salesaman Problem (TSP) yang ada. Algoritma dimulai dengan pengisian

sebuah nilai ke akar pohon pencarian tersebut. Pencabangan dilakukan dengan memasang sebuah pending node ke pending node yang lain yang lebih rendah levelnya. Bobot juga dihitung pada setiap proses dan ditulis di simpul pohon. Jika sebuah simpul diketahui merupakan solusi yang tidak mungkin bagi persoalan yang dihadapi, simpul tersebut diisi dengan nilai tak terbatas (infinity). Algoritma berhenti ketika sudah tidak mungkin lagi untuk membentuk simpul baru di pohon atau hasil terakhir yang ditemukan merupakan hasil yang lebih rendah (minimum) dari isi simpul yang telah ada pada level yang lebih rendah.

Kita defenisikan S = merupakan kumpulan dari berbagai kemungkinan dari solusi yang ada, dengan ka$ta lain E1,E2,E3, … ,En merupakan himpunan dari

simpul yang membentuk sirkuit Hamilton dan dari sekian banyak kemungkinan sirkuit Hamilton yang tersebut terdapat sebuah solusi untuk Travelling Salesman Problem

(TSP). Kita defenisikan juga S sebagai kardinalitas dari S dan f merupakan fungsi

(31)

3.2 Implementasi Metode Branch and Bound Dalam Pemecahan Travelling Salesman Problem (TSP) Pada Graf Lengkap

Metode Branch and Bound sebenarnya bukan merupakan metode yang mutlak untuk menyelesaikan permasalahan Travelling Salesman Problem (TSP), metode ini merupakan sekumpulan dari berbagai masalah (Class of Solving Problem), hanya saja persamaan karakteristik cara-cara tersebut yang membuat mereka disebut Branch and

Bound.

Graf Lengkap mempunyai jumlah derajat yang sama pada setiap simpul. Solusi Travelling Salesman Problem (TSP) pada graf ini merupakan Sirkuit Hamilton yang mempunyai bobot paling kecil (minimum). Selama pencarian solusi, current

node merupakan simpul pohon yang akan diproses selanjutnya atau yang mendapat

perhatian. Sirkuit dari current node inilah yang nanti akan diproses. Sisi yang tidak boleh dimasukkan ke dalam solusi disebut sisi yang terlarang (forbidden) dan sebaliknya disebut bebas (free). Disetiap simpul pohon kita merekam bobot dari sirkuit yang deperoleh sebagai kemungkinan solusi. Jika sirkuit tersebut mengandung sisi yang terlarang (yang menyebabkan sirkuit tersebut terlarang nantinya), sisi tersebut akan terlarang sampai anak-anak pohon dibawahnya. L0 merupakan batas atas

dari solusi setiap waktu pencarian. Jadi sirkuit yang melebihinya jelas bukan merupakan solusi dari Travelling Salesman Problem (TSP). berikut akan disajikan algoritma dari metode Branch and Bound pada pemecahan Travelling Salesman

Problem (TSP) pada graf lengkap Kn.

Algoritma : Langkah 1.

Ambil salah satu sirkuit bebas, biasanya sirkuit yang merupakan lintasan terluar, hitung bobotnya dan berinama L0. L0 merupakan batas atas awal dari masalah

ini. E0 merupakan himpunan simpul dari sirkuit ini. Akar dari search tree diisi dengan

bobot dari L0. Kemudian simpul ini dipersiapkan untuk dipartisi menjadi 2 simpul

(32)

Langkah 2.

Hitung batas bawah yang baru yaitu l untuk current node dengan mengambil

n simpul yang mempunyai bobot terkecil. Simpan himpunan simpul ini sebagai E. Jika

E bukan sirkuit, langsung ke langkah 3. Jika l = L0 atau l < batas terbawah yang ada

pada pending node bersesuaian, hentikan proses, E adalah solusi TSP-nya. Tetapi jika

l < L0, l diisi dengan L0 dan E diisi dengan E0, kemudian lanjut ke langkah 3.

Langkah 3.

Bersiap untuk mempartisi simpul pohon. Cari pending node yang mempunyai bobot paling kecil (calon simpul yang akan dipartisi). Jika simpul yang sudah dipilih tersebut merupakan sebuah sirkuit, hentikan pencarian. Simpul tersebut merupakan solusinya. Solusinya adalah sirkuit graf lengkap yang berkorespondensi dengan simpul pohon tersebut. Jika E mengandung simpul dari Kn yang mempunyai derajat lebih dari 2. Pilih salah satu sisi yaitu e (yang belum diproses sebelumnya) yang bersisian dengan simpul tersebut. Maju ke langkah 4. Jika tidak ada simpul yang lebih besar dari 2 tetapi mengandung upasirkuit, maka e diisi dengan salah satu simpul yang membangun upasirkuit tersebut.

Langkah 4.

Lakukan Partisi. S0…kl dipartisi menjadi 2 simpul. Satu simpul yaitu S0…kl1

mempunyai E sebagai sebuah solusi. Satu simpul lagi yaitu S0…kl2 menyimpan E

sebagai sisi yang terlarang dan kemudian akan di tutup (closed node). Jika S0…kl

menyimpan sebuah sisi yang membentuk sebuah upasirkuit (Subgraf) di graf lengkap atau membentuk derajat lebih dari 2 di sebuah simpul graf lengkap, isi dari simpul pohon tersebut diisi dengan lambing ∞ (infinity), artinya simpul pohon ini bukan

sebuah solusi yang mungkin dan kemudian akan menjadi closed node. Setelah itu, maka simpan nilai dari simpul S0…kl1 sebagai l yang baru. Kemudian, tutuplah simpul

(33)

3.3 Contoh Penyelesaian Masalah Travelling Salesman Problem (TSP) Dengan Menggunakan Metode Branch and Bound

Diberikan sebuah graf lengkap dengan derajat 12 (K12) dan diminta untuk

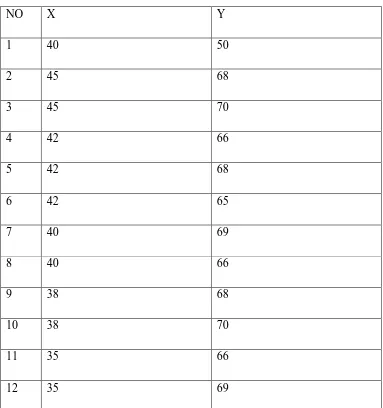
[image:33.595.125.508.277.685.2]

menyelesaikan persoalan Travelling Salesman Problem (TSP) pada graf dengan menggunakan metode Branch and Bound jika diberikan bobot-bobot sisi sebagai berikut :

Tabel 3.1 Vehicle Routing Problem

NO X Y

1 40 50

2 45 68

3 45 70

4 42 66

5 42 68

6 42 65

7 40 69

8 40 66

9 38 68

10 38 70

11 35 66

12 35 69

(34)

Dari table diatas, jarak dari satu kota ke kota lainnya didapat dengan menggunakan

rumus : d = ,

(35)

Maka dengan menggunakan rumus d = , didapat jarak dari satu titik ke titik lain dan direpresentasikan ke dalam matriks di bawah ini

Masalah pencarian rute atau jarak terpendek dari matriks diatas akan diselesaikan dengan menggunakan metode Branch and Bound. Kita mulai dengan mendefinisikan masalah kedalam bentuk graf seperti berikut :

1

2

3 4 5 6

7

8

9

10

11

12

(36)

Berikut akan disajikan algoritma Branch and Bound pada pemecahan

Travelling Salesman Problem (TSP) pada graf lengkap Kn.

Langkah 1.

Ambil E0 yaitu {e(1,6), e(6,4), e(42), e(2,3), e(3,5), e(5,7), e(7,10), e(10,12), e(12,11), e(11,9), e(9,8), e(8,1)}, semua sisinya bebas (free). Bobot dari sirkuit ini adalah L0 = 58,43 dan S = S0.

Langkah 2

Diambil 10 sisi dengan bobot terkecil. Yaitu E = {(1,6), (2,3), (3,5), (4,6), (5,4), (6,8),

(7,9), (8,4), (9,10), (10,12), (11,12), (12,7) } dengan bobot L1 = 43,38

1

2 3

5

4

6 8

7

9 10

12

11

Langkah 3

(37)

Langkah 4

Definisikan sebuah pernyataan untuk partisi simpul pohon.

S01 = {Ej ∈ S0 | e(4,8) ∈ Ej}

S02 = {Ej ∈ S0 | e(4,8) ∉ Ej}

Kemudian ambil edge (4,7),sehingga bobot menjadi 44,99

1

2 3

5

4

6 8

7

9 10

12

11

Langkah 5

S021 = {Ej ∈ S02 | e(12,7) ∈ Ej}

S022 = {Ej ∈ S02 | e(12,7) ∉ Ej}

(38)

1

2 3

5

4

6 8

7

9 10

12

11

Langkah 6

S0221 = {Ej ∈ S022 | e(9,12) ∈ Ej}

S0222 = {Ej ∈ S022 | e(9,12) ∉ Ej}

Kemudian ambil edge (9,8) sehingga bobot menjadi 42,82

2 3

5

4

6 8

7

9 10

12

(39)

Langkah 7

S02211 = {Ej ∈ S0221 | e(9,7) ∈ Ej}

S02212 = {Ej ∈ S0221 | e(9,7) ∉ Ej}

1

2 3

5

4

6 8

7

9 10

12

11

Langkah 8

S022121 = {Ej ∈ S02212 | e(4,7) ∈ Ej}

S022122 = {Ej ∈ S02212 | e(4,7) ∉ Ej}

(40)

1

2 3

5

4

6 8

7

9 10

12

11

Langkah 9

S0221221 = {Ej ∈ S022122 | e(8,4) ∈ Ej}

S0221222 = {Ej ∈ S022122 | e(8,4) ∉ Ej}

2 3

5

4

6 8

7

9 10

12

(41)

Langkah 10

S02212211 = {Ej ∈ S0221221 | e(8,6) ∈ Ej}

S02212212 = {Ej ∈ S0221221 | e(8,6) ∉ Ej}

1

2 3

5

4

6 8

7

9 10

12

11

Langkah 11

S022122121 = {Ej ∈ S02212212 | e(9,11) ∈ Ej}

S022122122 = {Ej ∈ S02212212 | e(9,11) ∉ Ej}

(42)

1

2 3

5

4

6 8

7

9 10

12

11

Langkah 12

S0221221221 = {Ej ∈ S022122122 | e(8,7) ∈ Ej}

S0221221222 = {Ej ∈ S022122122 | e(8,7) ∉ Ej}

2 3

5

4

6 8

7

9 10

12

(43)

Langkah 13

S02212212221 = {Ej ∈ S0221221222 | e(5,4) ∈ Ej}

S02212212222 = {Ej ∈ S0221221222 | e(5,4) ∉ Ej}

1

2 3

5

4

6 8

7

9 10

12

11

Langkah 14

S022122122211 = {Ej ∈ S02212212221 | e(5,8) ∈ Ej}

S022122122212 = {Ej ∈ S02212212221 | e(5,8) ∉ Ej}

(44)

1

2 3

5

4

6 8

7

9 10

12

11

Langkah 15

S0221221222121 = {Ej ∈ S022122122212 | e(7,8) ∈ Ej}

S0221221222122 = {Ej ∈ S022122122212 | e(7,8) ∉ Ej}

2 3

5

4

6 8

7

9 10

12

(45)

Langkah 16

S02212212221221 = {Ej ∈ S0221221222122 | e(9,7) ∈ Ej}

S02212212221222 = {Ej ∈ S0221221222122 | e(9,7) ∉ Ej}

1

2 3 5

4 6 8

7

9 10 12

11

Langkah 17

S022122122212221 = {Ej ∈ S02212212221222 | e(9,11) ∈ Ej}

S022122122212222 = {Ej ∈ S02212212221222 | e(9,11) ∉ Ej}

(46)

1

2 3

5

4

6 8

7

9 10

12

11

(47)

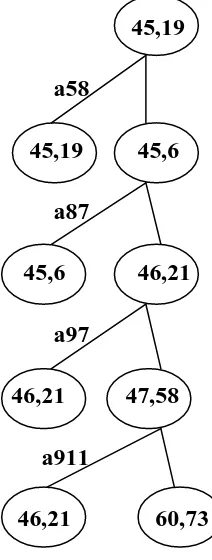
3.4 Gambar Diagram Pohon Penyelesaian

43,38 45,19

a48 a58 43,38 44,99 45,19 45,6

a127 a87

44,99 43,15 45,6 46,21

a129 a97

43,15 42,82 46,21 47,58

a97 a911

43,15 44,19 46,21 60,73 a47

44,19 42,58 a48

42,58 45,97 a86

42,58 46,73 a911

46,73 45,36 a87

45,36 45,19 a54

[image:47.595.339.445.109.389.2]

(48)

BAB 4 KESIMPULAN

4.1 Kesimpulan

Berdasarkan uraian penyelesaian soal pada bab sebelumnya, maka dapat diambil beberapa kesimpulan, yaitu:

1) Dengan menggunakan metode Branch and Bound pada contoh masalah Travelling

Salesman Problem (TSP) dalam penelitian ini, maka didapat rute yang optimal atau

terpendek adalah:

1 6 4 7 5 3 2 8 9 10 12 11 1 dengan panjang rute atau jarak perajalanan sebesar 60,73 satuan panjang.

2) Dengan menggunakan metode Branch and Bound pada contoh masalah Travelling

Salesman Problem (TSP) dalam penelitian ini, maka hanya dibutuhkan partisi

sebanyak 13 kali dan enumerasi sebanyak 29 simpul.

4.2 Saran

Berdasarkan hasil yang diperoleh dalam menyelesaikan masalah Travelling

Salesman Problem (TSP) pada penelitian ini dengan metode Branch and Bound,

(49)

DAFTAR PUSTAKA

Boffey, T.B.1982. Graph Theory in Operations Research. London : The Macmillan Press, Ltd, London,

Deo, Narsingh, 1984. Graph Theory with Applications to Engineering and Computer

Sciense, Printice Hall of India, Private Limited, New Delhi.

Evans, James R dan Edward Minieka,1992. Optimazation Algorithms for Networks

and Graphs, Marcel Dekker, Inc, New York.

Grimaldi, P.Ralph. 2004. Discrete and Combinatorial Mathematics. New York : Pearson Addison Wesley, Comp

Munir, Rinaldi. 2003. Matematika Diskrit. Bandung : Informatika.

R. Thie, Paul.1979. An Introduction to Linear Programming and Game Theory. New York : John Wiley & Sons, Inc.

S.Wolfe, Carvel. 1985. Linear Programming with Basic and Fortran. Virginia : Reston Publishing Company.

Solomon, M. M.,1987, 254-265. A Standard Set of 100-Customer Eucledian,

Algorithm for the Vehicle Routing and Scheduling Problem with Time Window Constraints.

Townsend, Michael,1987. Discrete Mathematics : Applied Combiatorics and Graph