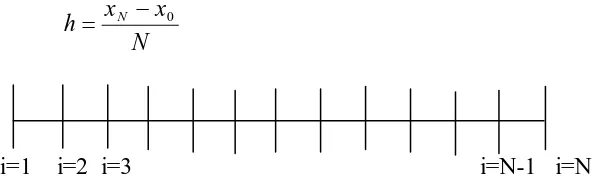Solusi Persamaan Schrodinger Pada Partikel Bebas Dan Partikel Dalam Kotak Dengan Metode Beda Hingga (Finite Difference Methods)

SOLUSI PERSAMAAN SCHRODINGER PADA PARTIKEL BEBAS DAN PARTIKEL DALAM KOTAK DENGAN METODE BEDA HINGGA

(FINITE DIFFERENCE METHODS)

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

TRISNOPENSIA BERUTU 060801011

DEPARTEMEN FISIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

PERSETUJUAN

Judul : SOLUSI PERSAMAAN SCHRODINGER PADA PARTIKEL BEBAS DAN PARTIKEL

DALAM KOTAK DENGAN METODE BEDA HINGGA (FINITE DIFFERENCE METHODS)

MM Kategori : SKRIPSI Nama : TRISNOPENSIA BERUTU Nomor Induk Mahasiswa : 060801011

Program studi : SARJANA(S1) FISIKA Departemen : FISIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM (FMIPA) UNIVERSITAS SUMATERA

UTARA

Diluluskan di Medan, Oktober 2010

Diketahui/Disetujui oleh

Departemen Fisika FMIPA USU Pembimbing

PERNYATAAN

SOLUSI PERSAMAAN SCHRODINGER PADA PARTIKEL BEBAS DAN PARTIKEL DALAM KOTAK DENGAN METODE BEDA HINGGA

(FINITE DIFFERENCE METHODS)

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dari ringkasan yang masing-masing disebutkan sumbernya.

Medan, Oktober 2010

PENGHARGAAN

Puji syukur kepada Tuhan Yesus Kristus atas Segala berkat serta kasihnya senantiasa melindungi, menyertai , memimpin dan membimbing penulis sehingga dapat menyelesaikan skripsi ini dengan kesungguhan.

Dalam kesempatan ini Penulis ingin mengucapkan terima kasih kepada: 1. Drs.Kurnia Sembiring, MS , selaku dosen pembimbing skripsi.

2. Ketua jurusan Departemen Fisika FMIPA USU, Dr.Marhaposan Situmorang beserta sekretaris jurusan Dra.Justinon, MS.

3. Yang tercinta Ayahanda H. Berutu dan Ibunda E. Bancin, kakak Anju Anna, Sutriana, Erni Asti dan abang Chardy, Jhonardi beserta adik Elfrita yang banyak mendorong untuk segera menyelesaikan skripsi ini secara moril dan materil.

4. Keluarga besar Nesli Berutu, Chardy Berutu, Angelika, Vincentia Situmorang dan Adrian Boangmanalu,yang selalu memperhatikan penulis dan selalu meberi nasehat yang luar biasa.

5. Teman-temanku, Khususnya Sulastri Sihotang, Reza, Susan, serta Enteria, Juga rekan-rekan Stambuk ’06 yang selalu memberi semangat.

Semoga Tuhan selalu memberkahi kalian.Amin.

Terima kasih atas semua dukungan, bantuan dan semangat yang selama ini penulis terima guna menyelesaikan skripsi ini. Penulis menyadari sebagai manusia tentunya tidak luput dari khilaf dan kesalahan. Akhir kata penulis mengucapkan terima kasih dan semoga skripsi ini dapat bermanfaat bagi penulis juga pembaca.

SOLUSI PERSAMAAN SCHRODINGER PADA PARTIKEL BEBAS DAN PARTIKEL DALAM KOTAK DENGAN METODE BEDA HINGGA

(FINITE DIFFERENCE METHODS)

ABSTRAK

THE SOLUTION FOR SCHRODINGER EQUATION OF FREE PARTICLES AND PARTICLES IN A BOX USING FINITE DIFFERENT METHODS

(FINITE DIFFERENCE METHODS)

ABSTRACT

DAFTAR ISI

Halaman

Persetujuan………. i

Pernyataan………...…...ii

Penghargaan ……….. .iii

Abstrak …… .……….iv

Abstract …… .………...v

Daftar isi …… .………. …vi

Daftar tabel …… .………...viii

Daftar gambar …… .………...ix

Daftar lampiran…… .………...x

BAB I Pendahuluan 1.1 Latar Belakang Masalah………...1

1.2 Batasan Masalah ………. ...2

1.3 Tujuan.Penelitian………...2

1.4 Manfaat Penelitian ………...2

1.5 Sistematika Penulisan ………..3

BAB II Tinjauan Pustaka 2.1 Persamaan Schrödinger……… 4

2.2 Probabilitas dan Normalisasi………. 6

2.3 Penerapan Persamaan Schrödinger……… 7

2.3.1 Pada Partikel Bebas………... 7

2.4 Metode Numerik ……… 13

2.5 Sistem Tri-diagonal……… 13

2.6 Metode Perbedaan Hingga……… 18

2.7 Persamaan Diffrensial Biasa (PDB) dengan nilai batas……. 20

2.8 Solusi Numerik Persamaan Schrodinger……… 21

2.8.1 Partikel bebas……….. 21

2.8.2 Partikel Dalam Kotak………. 24

2.9 Program Komputer………. 24

2.9.1 Pengantar Pemrograman MATLAB…………. 24

2.9.2 Input-Output………. 26

2.9.3 Kontrol Program……… 26

2.9.4 Grafik MATLAB……….. 28

BAB III Metodologi Penelitian 3.1 Rancangan Penelitian……….. 30

3.2 Teknik Analisis Data………... 30

3.3 Diagram Alir penelitian………... 31

BAB IV Hasil Dan Pembahasan 4.1 Visualisasi Persamaan Schrödinger Pada partikel Bebas ……. 32

4.2 Visualisasi Persamaan Schrodinger Pada Partikel kotak …….. 33

BAB V Kesimpulan 5.1 Kesimpulan………. 40

5.2 Saran……….. 40

DAFTAR GAMBAR

Halaman Gambar 2.1.Sumur potensial yang bersesuaian dengan sebuah kotak

dindingnya keras tak berhingga………. 9

Gambar 2.2. Fungsi gelombang sebuah partikel sumur potensial yang dibatasi x0=0 menuju x=a dengan orde berbeda.………12

Gambar.2.3. Tingkat energi dalam kotak secara konstan………..13

Gambar 2.4. Pembagian Interval antara [

x ,

₀

x

_N]………...19

Gambar 3.1. Diagram Alir Penelitian……….31

Gambar 4.1. Visualisasi fungsi gelombang partikel bebas ……….. 33

Gambar 4.2. Visualisasi fungsi gelombang partikel dalam kotak n=1, N=100dan h=0.01………..34

Gambar 4.3. Visualisasi fungsi gelombang partikel dalam kotak n=2, N=100 dan h=0.01……….. 36

Gambar 4.4. Visualisasi fungsi gelombang partikel dalam kotak n=3, N=100 dan h=0.01………. 37

DAFTAR TABEL

Halaman

Tabel 2.1 Operator Aritmatika……….. 25

Tabel 4.1.Hasil running untuk n=1, N=100 dan h=0.01……… 34

Tabel 4.2..Hasil running untuk n=2, N=100 dan h=0.01……….. 35

Tabel 4.3.Hasil running untuk n=3, N=100 dan h=0.01……… 37

DAFTAR LAMPIRAN

Halaman

Lampiran 1.Kode Pemrograman Visualisasi Gelombang Pada Partikel

Bebas ………. 42 Lampiran 1.Kode pemrograman Visualisasi gelombang pada Partikel

Dalam kotak ………. 43

SOLUSI PERSAMAAN SCHRODINGER PADA PARTIKEL BEBAS DAN PARTIKEL DALAM KOTAK DENGAN METODE BEDA HINGGA

(FINITE DIFFERENCE METHODS)

ABSTRAK

THE SOLUTION FOR SCHRODINGER EQUATION OF FREE PARTICLES AND PARTICLES IN A BOX USING FINITE DIFFERENT METHODS

(FINITE DIFFERENCE METHODS)

ABSTRACT

BAB I PENDAHULUAN

1.1 Latar Belakang Masalah

Metode numerik adalah teknik untuk menyelesaikan permasalahan-permasalahan yang diformulasikan secara matematis dengan cara hitungan (Aritmatika). Berbagai permasalahan dalam bidang ilmu pengetahuan khususnya Fisika dapat digambarkan dalam bentuk persamaan matematik. Apabila persamaan tersebut mempunyai bentuk yang sederhana maka dapat diselesaikan secara analitis (Bambang Triatmodjo, 2002).

Namun ada beberapa persoalan fisika yang cukup rumit dan menghabiskan waktu yang banyak untuk menyelesaikannya, misalnya masalah matematika yang dijumpai bersifat kompleks yang melibatkan banyak variabel dan parameter serta hubungannya saling ketergantungan antara variabel lain dengan yang lainnya sehingga metode analitis sulit diterapkan untuk itu perlu disederhanakan penyelesaiannya dengan menggunakan metode numerik. Karena itu metode numerik sangat membantu dalam mempelajari gejala fisika ( Parwadi Moengin, 2005).

Salah satu gejala fisika yang sangat menarik adalah perilaku gelombang dari partikel. Analisis persamaan Schrödinger dapat dilakukan dengan menggunakan model matematika dan menerapkan metode numerik untuk menyederhanakan penyelesaian matematisnya .

Metode beda hingga akan diterapkan pada persamaan Schrödinger yaitu pada partikel bebas, dan partikel dalam kotak, sehingga diperoleh bentuk persamaan Schrödinger dalam satu dimensi menggunakan metode beda hingga, kemudian Persamaan Schrödinger tersebut diterapkan pada setiap diskresitasi yaitu i = 1, 2,3,…, n-1 sehingga berbentuk sistem persamaan linier (SPL) dengan bentuk

tri-diagonal yang dapat dipecahkan dengan algoritma Thomas sehingga mempermudah pembuatan program dan visualisasi sebagai solusi dari persamaan Schrödinger pada partikel bebas dan partikel dalam kotak tidak bergantung waktu.

1.2 Batasan Masalah

Adapun batasan masalah yang dibahas dalam penelitian ini:

1. Penelitian ini dibatasi untuk membahas bentuk komputasi persamaan Schrödinger pada partikel bebas dan partikel dalam kotak satu dimensi tidak bergantung waktu dengan menggunakan metode beda hingga

2. Bentuk visualisasi persamaan Schrödinger satu dimensi menggunakan MATLAB

1.3 Tujuan Penelitian

1. Untuk mengetahui bentuk komputasi persamaan Schrödinger satu dimensi dengan metode beda hingga

2. Untuk mengetahui bentuk visualisasi persamaan Schrödinger satu dimensi dengan MATLAB

1.4. Manfaat Penelitian

1. Mengetahui bentuk komputasi persamaan Schrödinger satu dimensi dengan metode beda hingga

1.5. Sistematika Penulisan

Sistematika penulisan masing-masing bab adalah sebagai berikut: BAB I Pendahuluan

Bab ini mencakup latar belakang masalah, tujuan penelitian, batasan masalah, manfaat penelitian, dan sistematika penulisan.

BAB II Tinjauan pustaka

Bab ini berisi teori yang mendasari penelitian.

BAB III Metodologi Penelitian

Bab ini membahas tentang diagram alir penelitian, peralatan, bahan-bahan, pembuatan algoritma dan program komputer.

BAB IV Hasil dan pembahasan

Bab ini membahas tentang hasil penelitian dan menganalisis data yang diperoleh dari penelitian.

BAB V Kesimpulan dan Saran

BAB II

TINJAUAN PUSTAKA

2.1 Persamaan Schrödinger

Persamaan Schrödinger merupakan fungsi gelombang yang digunakan untuk memberikan imformasi tentang perilaku gelombang dari partikel. Suatu persamaan differensial akan menghasilkan pemecahan yang sesuai dengan fisika kuantum.Walaupun dihalangi oleh tidak adanya hasil percobaan yang dapat digunakan sebagai bahan perbandingan. Untuk menghasilkan persamaan Schrödinger, maka harus memenuhi 3 kriteria, sebagai berikut :

a. Taat asas dengan kekekalan energi

Hukum kekekalan energi adalah jumlah energi kinetik ditambah energi potensial bersifat kekal, artinya tidak bergantung pada waktu maupun posisi. Persamaan Schrödinger harus konsisten dengan hukum kekekalan energi . Secara matematis, huku m kekekalan energi dapat diungkapkan dengan rumusan:

K + V = Etot

E x V m p

=

+ ( )

2

2

(2.1)

Suku pertama ruas kiri menyatakan energi kinetik, suku kedua menyatakan energi potensial, dan ruas kanan menyatakan suatu tetapan yang biasanya disebut sebagai energi total.

Dimana energi kinetik digunakan bukanlah dalam bentuk 2

2 1

mv

pada saat bersamaan, bahkan ketidakpastian dalam posisi dikalikan dengan ketidakpastian momentum selalu lebih besar nilainya dari konstanta Planck sangat kecil. Sehingga hanya digunakan dalam kawasan mikroskopik misalnya elektron. b. Linear dan bernilai tunggal

Persamaannya haruslah “ Berperilaku Baik” dalam pengertian matematikanya. Pemecahannya harus memberi informasi tentang probabilitas untuk menemukan partikelnya, walaupun ditemukan probabilitas berubah secara kontinu dan partikelnya menghilang secara tiba-tiba dari satu titik dan muncul kembali pada titik lainnya, namun fungsinya haruslah bernilai tunggal, artinya tidak boleh ada dua probabilitas untuk menemukan partikel di satu titik yang sama. Ia harus linear , agar gelombangnya memiliki sifat superposisi yang diharapkan sebagai milik gelombang yang berperilaku baik.

c. Pemecahan partikel bebas sesuai dengan gelombang de Broglie tunggal

Tahun 1924 de Broglie menyatakan bahwa materi mempunyai sifat gelombang disamping sifat partikel. Bentuk persamaan diffrensial apapun, haruslah taat azas terhadap hipotesis de Broglie. Untuk menyelesaikan persamaan matematik bagi sebuah partikel dengan momentum p, maka pemecahannya harus berbentuk fungsi gelombang dengan panjang gelombang λ yang sama dengan h / p . Sesuai dengan persamaan λ = h / p. Maka energi kinetik dari gelombang de Broglie partikel bebas haruslah K = p2 / 2m = ħ2 k2 / 2m.

Bentuk persamaan harus taat azas dengan kekekalan energi seperti yang dijelaskan diatas ( V + K = E ), K muncul dalam pangkat satu dan K = p2 / 2m =

ħ2

k2 / 2m, sehinggga satu-satunya cara untuk memperoleh suku yang mengandung k2 adalah dengan mengambil turunan kedua dari ψ (x) = A sin kx terhadap x. Sehingga dihasilkan Persamaan Schrödinger sebagai berikut:

) ( )) ( ( 2 ) ( 2 ) ( )

(

2 2

2 2

2

x x V E m x

k m x

k dx

x d

ψ ψ

ψ

ψ _{=− =− =− −}

 

) ( )

( ) (

2 2

2 2

x E x V dx

x d

m ψ ψ

ψ _{+ =}

− 

Persamaan Schrödinger (2.2) diatas merupakan persamaan Schrödinger tidak bergantung waktu dalam satu dimensi.

2.2 Probabilitas dan Normalisasi

Fungsi gelombang ψ(x) menyatakan suatu gelombang yang memiliki panjang gelombang dan bergerak dengan kecepatan fase yang jelas. Masalah yang muncul ketika hendak menafsirkan amplitudonya. Apakah yang dinyatakan oleh amplitudo

ψ(x) dan variabel fisika apakah yang bergetar? Ini merupakan suatu jenis gelombang yang berbeda, yang nilai mutlaknya memberikan probabilitas untuk menemukan partikelnya pada suatu titik tertentu. Dimana |ψ(x)|2 dx memberikan probabilitas untuk menemukan partikel dalam selang dx di x. Rapat probabilitas P(x) terhadap

ψ(x) menurut persamaan Schrödinger sebagai berikut:

P(x)dx=|ψ(x)|2dx (2.3) Tafsiran |ψ(x)|2 ini membantu memahami persyaratan kontinu ψ(x), walaupun

amplitudonya berubah secara tidak jelas dan kontinu. Probabilitas untuk menemukan partikel antara x1 dan x2 adalah jumlah semua probabilitas P(x)dx dalam selang antara x1 dan x 2 adalah sebagai berikut:

∫

=

∫

2

1 2 2

1

) ( )

(

x

x x

x

dx x dx

x

P ψ (2.4)

Dari aturan ini, maka probabilitas untuk menemukan partikel disuatu titik sepanjang sumbu x, adalah 100 persen, sehingga berlaku:

∫

( )2 =1

+∞

∞ −

dx x

ψ (2.5)

semua perhitungan yang mempunyai makna fisika. Jika normalisasinya telah dilakukan secara tepat, maka persamaan (2.4) akan selalu menghasilkan suatu probabilitas yang terletak antara 0 dan 1.

Setiap pemecahan persamaan Schrödinger yang menghasilkan |ψ(x)|2 bernilai tak hingga, harus dikesampingkan. Karena tidak pernah terdapat probabilitas tak hingga untuk menemukan partikel pada titik manapun. Maka harus mengesampingkan suatu pemecahan dengan mengembalikan faktor pengalinya sama dengan nol. Sebagai contoh, jika pemecahan matematika bagi persamaan differensial menghasilkan ψ(x) = A + B bagi seluruh daerah x > 0 , maka syaratnya A = 0 agar pemecahannnya mempunyai makna fisika. Jika tidak |ψ(x)| akan menjadi tak hingga untuk x menuju tak hingga ( Tetapi jika pemecahannya dibatasi dalam selang 0 < x < L, maka A tidak boleh sama dengan nol). Tetapi jika pemecahannya berlaku pada seluruh daerah negatif sumbu x < 0, maka B = 0.

Kedudukan suatu partikel tidak dapat dipastikan,dalam hal ini tidak dapat menjamin kepastian hasil suatu kali pengukuran suatu besaran fisika yang bergantung pada kedudukannnya. Namun jika menghitung probabilitas yang berkaitan dengan setiap kooordinat, maka ditemukan hasil yang mungkin dari pengukuran satu kali atau rata-rata hasil dari sejumlah besar pengukuran berkali-kali (Eisberg,1970).

2.3 Penerapan Persamaan Schrödinger

Persamaan Schrödinger dapat diterapkan dalam berbagai persoalan fisika. Dimana pemecahan persamaan Schrödinger, yang disebut fungsi gelombang, memberikan informasi tentang perilaku gelombang dari partikel.

2.3.1. Pada partikel Bebas

Yang dimaksud dengan “Partikel Bebas” adalah sebuah partikel yang bergerak

tanpa dipengaruhi gaya apapun dalam suatu bagian ruang, yaitu, F = - dV(x) / dx = 0 sehingga menempuh lintasan lurus dengan kelajuan konstan.

Partikel bebas dalam mekanika klasik bergerak dengan momentum konstan P, yang mengakibatkan energi totalnya jadi konstan. Tetapi partikel bebas dalam mekanika kuantum dapat dipecahkan dengan persamaan Schrödinger tidak bergantung waktu. Persamaan Schrodinger pada partikel bebas dapat diperoleh dari persamaan (2.2) berikut:

) ( ) ( ) ( 2 2 2 2 x E x V x x

m ψ ψ

ψ _{+ =}

∂ ∂

−  (2.6)

Untuk partikel bebas V = 0, maka persamaannya menjadi

) ( ) ( 2 2 2 2 x E x x m ψ ψ ₌ ∂ ∂

−  (2.7)

Atau: 0 ) ( 2 ) ( 2 2 2 = + ∂

∂ mE _x

x x

ψ ψ

 _(2.8)

Karena:

2

2 2

 mE

k = atau

m k E 2 2 2 

= (2.9)

Dengan demikian diperoleh:

) ( ) ( 2 2 2 x k x x ψ ψ ₌₋ ∂

∂ _(2.10)

Persamaan (2.8) adalah bentuk umum dari persamaan differensial biasa berorde dua, dengan k2 adalah positif, dimana ψ(x) merupakan kuantitas kompleks yang memiliki bagian real (nyata) dan bagian imajiner, sehingga pemecahannnya adalah:

ψ(x)=Asinkx+ B cos kx (2.11)

normalisasi tidak dapat dihitung dari -∞ hingga +∞ , bagi fungsi gelombang itu. (Krane, 1992).

2.3.2. Partikel dalam kotak

Untuk meninjau sebuah partikel yang bergerak bebas dalam sebuah kotak dalam dimensi yang panjangnya L, dimana partikelnya benar-benar terperangkap dalam kotak. Misalnya, sebuah manik-manik yang meluncur tanpa gesekan sepanjang kawat yang ditegangkan antara dua dinding tegar dan bertumbukan secara eksak dengan kedua dinding. Potensial ini dapat dinyatakan

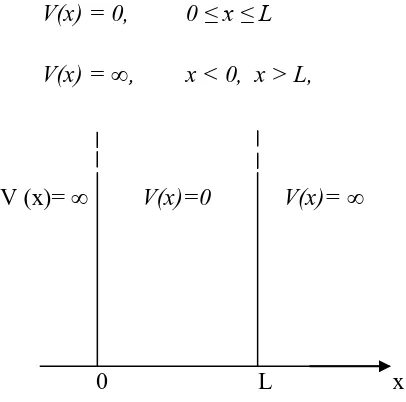
V(x) = 0, 0 ≤ x ≤ L

V(x) = ∞, x < 0, x > L,

V (x)= ∞ V(x)=0 V(x)= ∞

0 L x

Gambar.2.1.Sumur Potensial yang bersesuaian dengan sebuak kotak yang dindingnya keras tak berhingga.

Kita dapat memberi spesifikasi pada gerak partikel dengan mengatakan bahwa gerak itu terbatas pada gerak sepanjang sumbu-x antara x = 0 dan x = L disebabkan oleh dinding keras tak berhingga. Sebuah partikel tidak akan kehilangan Energinya jika bertumbukan dengan dinding, energi totalnya tetap konstan.

adalah nilai ψ di dalam kotak, yaitu antara x = 0 dan x = L . Persamaan Schrodinger menjadi:

0 ) ( 2

2 2

2

= 

     + ∂

∂ m _{E x}

x ψ

ψ

 _(2.12)

Berdasarkan pembuktian persamaan Diatas, didapat pemecahan sebagai berikut:

ψ(x)=Asinkx+B coskx (2.13)

ψ =0 dan x = 0

Dari persamaan (2.13) diperoleh B = 0, maka:

ψ(x) =Asinkx= 0 (2.14) Pemecahan ini belum lengkap, karena belum ditentukan nilai A dan B, juga belum menghitung nilai energi E yang diperkenankan. Untuk menghitungnya, akan diterapkan persyaratan bahwa ψ(x) harus kontinu pada setiap batas dua bagian ruang. Dalam hal ini, akan dibuat syarat bahwa pemecahan untuk x < 0 dan x > 0 bernilai sama di x = 0. Begitu pula pemecahan untuk x > L dan x < L haruslah bernilai sama di x = L. Jika x = 0, Untuk x < 0 Jadi harus mengambil ψ(x) = 0 pada x = 0.

ψ(0) =Asin 0 + B sin 0

ψ(0) = 0 + B.1 = 0 (2.15)

Jadi,didapat B = 0. Karena ψ =0 untuk x > L, maka haruslah berlaku ψ(L) = 0,

Ψ(L) = AsinkL + Bcos kL = 0 (2.16)

Karena telah didapatkan bahwa B = 0,maka haruslah berlaku:

AsinkL = 0 (2.17)

Disini ada dua pemecahan yaitu A = 0, yang memberikan ψ(x) = 0 dan

ψ2

(x) = 0, yang berarti bahwa dalam kotak tidak terdapat partikel (Pemecahan tidak masuk akal) atau sin kL = 0, maka yang benar jika:

Dengan:

(2.19)

Dari persamaan (2.18) dan persamaaan (2.19) diperoleh bahwa energi partikel mempunyai harga tertentu yaitu harga eigen. Harga eigen ini membentuk tingkat energisitas yaitu:

(2.20)

Fungsi gelombang sebuah partikel didalam kotak yang berenergi En ialah:

(2.21)

Untuk memudahkan E0 =ħ2π2/2mL2, yang mana tampak bahwa unit energi ini ditentukan oleh massa partikel dan panjang kotak. Maka E = n2E0 dan demikian partikelnya hanya dapat ditemukan dengan energi E0, 4 E0, 9 E0, 16 E0 dan seterusnya. Karena dalam kasus ini energi yang diperoleh hanya pada laju tertentu yang diperkenankan dimiliki partikel. Ini sangat berbeda dengan kasus klasik, misalnya manik-manik (yang meluncur tanpa gesekan sepanjang kawat dan menumbuk kedua dinding secara secara elastik) dapat diberi sembarang kecepatan awal dan akan bergerak selamanya, bolak-balik, dengan laju tersebut.

Dalam kasus kuantum, hal ini tidaklah mungkin, karena hanya laju awal tertentu yang dapat memberikan keadaan gerak tetap, keadaan gerak khusus ini disebut keadaan stasioner (Disebut keadaan”stasioner”karena ketergantungan pada waktu yang dilibatkan untuk membuat ψ(x,t),ψ(x,t)2 tidak bergantung waktu). Hasil pengukuran energi sebuah partikel dalam sebuah sumur potensial harus berada pada salah satu keadaan stasioner, hasil yang lain tidaklah mungkin. Pemecahan bagi ψ(x)

belum lengkap, karena belum ditentukan tetapan A. Untuk menentukannya, ditinjau

2 2 2 2

2mL n E_n = π 

x mE

A n

n

 2 sin = ψ

k mE

kembali persyaratan normalisasi, yaitu

∫

( )2 =1

+∞

∞ −

dx x

ψ . Karena ψ(x)=0, kecuali untuk

0 ≤ x ≤ Lsehingga berlaku:

1 2

sin

0

2 2 2

=

∫

L n

xdx mE A

 (2.22)

Karena pada persamaan (2.20)

Maka diperoleh A = 2/L. Dengan demikian, Pemecahan lengkap bagi fungsi gelombang untuk 0 ≤ x ≤ L adalah:

L x n L

n

π

ψ = 2sin n=1,2,3,… (2.23)

Dalam gambar 2.2 akan dilukiskan berbagai tingkat energi, fungsi gelombang dan rapat probabilitas ψ 2 yang mugkin untuk beberapa keadaan terendah. Keadaan energi terendah, yaitu pada n =1 , dikenal sebagai keadaan dasar dan keadaan dengan energi yang lebih tinggi (n > 1) dikenal sebagai keadaan eksitasi.

n=1

ψ

n=3

n=2 x =0 x = a

Gambar.2.2. Fungsi gelombang sebuah partikel sumur potensial yang dibatasi x0 = 0 menuju x = a dengan orde berbeda.

2 2 2 2

Partikel itu memiliki peluang untuk didapatkan di luar sumur. Jika sebuah partikel dengan energi E0 dalam suatu daerah (“kawat” untuk manik-manik) dan kemudian akan diukur kedudukannnya dengan pengukuran dilakukan berulang kali. Maka akan ditemukan distribusi hasil pengukuran yang sama seperti ψ 2(x) untuk kasus n=1 hingga probabilitas terbesar x=L/2 dan berangsur-angsur berkurang saat menjauhi pusatnya yang akhirnya menuju nol pada ujung-ujungnya (jika menggunakan fisika partikel klasik, takkuantum, maka probabilitasnya tetap pada semua titik di dalam kotak).

Jika pengukuran diulangi kembali, dengan pengecualian bahwa partikelnya diberi energi sebesar 4E0. Bila diulangi semua pengukuran terhadap kedudukannnya , akan didapati bahwa distribusi ini sesuai dengan ψ2(x) untuk n = 2. Maksimum probabilitas pada x = L/4 dan x = 3L/4, sedangkan probabilitas nol terjadi pada x = L/2. Dengan demikian partikelnya harus bergerak sedemikian rupa sehinggga suatu waktu dapat ditemukan di x = L/4 dan x = 3L/4 tanpa menemukan di x = L/2. Ini merupakan ilustrasi grafis mengenai perbedaan antara fisika klasik dan kuantum. Tetapi bagaimana mungkin terjadi suatu partikel mencapai 3L/4 dari L/4 tanpa melewati L/2 ? Ini adalah hal yang sulit dijawab jika adanya kecenderungan hanya pada partikel, karena fisika kuantum cenderung pada pandangan gelombang.

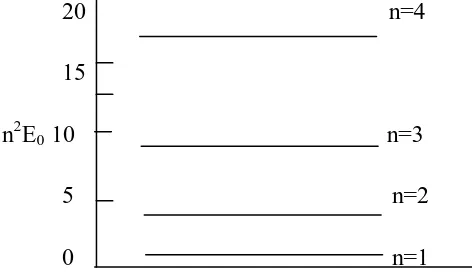
Berbicara tentang kedudukan, fokusnya pada partikel dan berbicara tentang gerak dari L/4 ke 3L/4 fokusnya pada gelombang. Untuk lebih jelasnya dapat memperhatikan gambar 2.3 tentang beberapa tingkat energi terendah yang diperkenankan dari partikel yang terbatas geraknya dalam kotak.

20 n=4 15

n2E0 10 n=3

5 n=2 0 n=1

2.4. Metode Numerik

Penerapan metode numerik pada persamaan Schrödinger dirumuskan dengan persamaan differensial. Langkah pendahuluan yang ditempuh dalam menerapkan metode ini adalah memperkirakan persamaan differensial yang bersangkutan beserta syarat-syarat batasnya dengan seperangkat persamaan aljabar. Dengan mengganti daerah yang kontinu dengan suatu pola titik-titik tersebut. Sistem dibagi menjadi sejumlah subluas yang kecil dan memberi nomor acuan kepada setiap sub luas.

2.5 Sistem Tri-Diagonal

Pemecahan persamaan differensial dengan menggunakan diskretisasi perbedaan hingga (finite difference), seringkali melibatkan sistem persamaan linier (SPL) yang mempunyai bentuk-bentuk khusus. Contoh berikut memberikan dua kemungkinan bentuk SPL berikut;

2 23 2 22 1 21 1 2 12 1 11 b a x a x a b x a x a = + + = +

a32x2 +a33x3 +a34 =b3 (2.24)

4 45 4 44 3

43x a x a b

a + + =

 

N N NN N

NN x a x b

a _{−1 −1}+ =

Dengan menggunakan notasi matriks, sistem persamaan (2.24) dapat dituliskan

Pada sistem tridiagonal tampak bahwa mayoritas dari elemen matriksnya adalah nol. Komputasi dengan komputer dapat menghemat banyak ruang memori dengan hanya menyimpan elemen yang ada di diagonal mayor dan dua sub diagonal lainnya. Untuk sistem tridiagonal, digunakan tiga vektor a, d dan c untuk menyimpan nilai elemen yang bukan nol sepanjang diagonal mayor dan subdiagonalnya sehingga (2.25) menjadi:                     =                                         − − − − − N N N N N N N N N b b b b b x x x x x d a c d a c d a c d a c d 1 3 2 1 1 3 2 1 1 1 1 3 3 3 2 2 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0                 (2.26)

Pemecahan SPL dengan koefisien matriks tridiagonal didasari oleh metode doolittle. Pertama-tama matriks A didekomposisi menjadi LU, yaitu matriks segitiga bawah dan segitiga atas sesuai algoritma Doolittle. Setelah dekomposisi (2.26) menjadi:

                =                                                 − − N N N N N N b b b b x x x x c c c                     3 2 1 3 2 1 1 1 2 2 1 1 3 2 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 δ δ δ δ α α α (2.27)

L U x b

Setelah perkalian matriks persamaan (2.27) menjadi

Inti dari algoritma ini adalah mengubah elemen-elemen pada vektor a, d dan c dengan vektor α, δ dan c yang merupakan elemen-elemen dari L dan U, Jika dibandingkan persamaan (2.28) dengan (2.26) maka tampak bahwa:

1 1 2 3 3 3 2 3 1 2 2 2 1 2 1 1 / / / − − = → = = → = = → = → = N N N N N N a a a a a d δ α α δ α δ α δ αδ α δ α δ   1 1 2 3 3 3 3 3 2 3 1 2 2 2 2 2 1 2 − − + = → = − − = → = + − = → = + N N N N N N N

Nc d d c

c d d c c d d c α δ δ α α δ δ α δ δ α α  

Langkah-langkah di atas dapat dengan mudah diprogram, sebagai ilustrasi, 3 langkah pertama program tersebut dapat dituliskan sebagai berikut:

d(1) = d(1)

a(2) = a(2) / d(1) d(2) = d(2) – a(2)*c(1) a(3) = a(3) / d(2) d(3) = d(3) – a(3)*c(2)

Setelah elemen-elemen pada vektor a dan d dengan α dan δ , persamaan (2.27) dapat diproses lebih lanjut, jika Ux sebut saja g, maka persamaan (2.27) dapat dituliskan

                =                                 N N N b b b b g g g g             3 2 1 3 2 1 3 2 1 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 α α α (2.29)

Dari (2.29) dapat diperoleh: 2 3 3 3 3 3 2 3 1 2 2 2 2 2 1 2 1 1 g b g b g g g b g b g g b g α α α α − = → = + − = → = + = (2.30)  

α_Ng_N−1+g_N =b_N →g_N =b_N −α_Ng_N−1

Dalam proses komputasi g disimpan dalam vektor b, yaitu elemen-elemen awal b diganti dengan yang baru. Tiga langkah pertama dalam program tertulis sebagai berikut:

b(1) = b(1)

b(2) = b(2) – a(2)*b(1) b(3) = b(3) – a(3)*b(2) karena g adalah U x maka:

                =                                 − − N N N N N g g g g x x x x c c c             3 2 1 3 2 1 1 1 2 2 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 δ δ δ δ (2.31)

L x g

2 1 2 2 2 2 1 2 2 2 1 1 1 1 1 1 1 1 / ) ( / ) ( / − − − − − − − − − − − − − − − − − − − = → = + − = → = + = N N N N N N N N N N N N N N N N N N N N N N N x c g x g x c x x c g x g x c x g x δ δ δ

δ δ (2.32)

  1 2 1 1 1 1 2 1 1

1 ( )/δ

Dalam komputasi, tiga langkah pertama berbentuk: x(N) = b(N) / d(N)

x(N-1) = [ b(N-1)-c(N-1)*x(N)] / d(N-1) x(N-1) = [ b(N-2)-c(N-2)*x(N-1)] / d(N-2)

Jika diperhatikan prosedur di atas adalah metode Doolittle yang diterapkan pada sistem tridiagonal. Namun karena elemen dari matriks A kebanyakan nol maka hanya digunakan tiga vektor dengan ukuran 1 x N untuk menyimpan elemen bukan nol matriks A. Tekhnik ini sangat populer dengan algoritma Thomas, sesuai dengan nama penemunya (Kosasih Buyung, 2006).

2.6 Metode Perbedaan Hingga

Metode perbedaan hingga adalah metode yang digunakan mengubah problem PDB nilai batas dari sebuah problem kalkulus menjadi sebuah aljabar. Dengan metode ini persamaan differensial ψ'dan ψ" akan diaproksimasikan dengan menggunakan deret Taylor. Deret Taylor adalah representasi fungsi matematika sebagai jumlahan tak hingga dari suku-suku yang nilainya dihitung dari turunan fungsi tersebut di suatu titik. Bentuk deret taylor dapat dituliskan sebagai berikut:

n k n

k k

R k h x h

x+ =

∑

+

= !

) ( ) ( )

(

0

ψ

ψ (2.33)

Dengan:

1 0

. ),

( !

)

( + < <

= ψ x θh dengan θ

n h

R n

n

n

Jika: n→∞,R_n →0

Maka deret Taylor dapat dituliskan dalam bentuk:

Atau dapat dituliskan dalam bentuk: ... ) ( " ! 2 ) ( ' ) ( ) ( 2 + + + =

+h x h x h x

x ψ ψ ψ

ψ (2.35) ... ) ( " ! 2 ) ( ' ) ( ) ( 2 + − − =

−h x h x h x

x ψ ψ ψ

ψ (2.36)

Jika dikurangi (2.35) dengan (2.36) dan nilai setelah pangkat 2 diabaikan atau dianggap sangat kecil atau sama dengan nol (karena pada persoalan ini kita hanya membutuhkan turunan pertama dan kedua sesuai dengan persamaan diffrensial orde dua pada persamaan Schrodinger partikel bebas dan dalam kotak lihat persamaan (2.8) dan (2.12) maka akan didapat:

h h x h x x 2 ) ( ) ( ) ( ' =ψ + −ψ −

ψ (2.37)

Apabila (2.35) ditambah dengan (2.36) akan diperoleh:

2 ) ( ) ( 2 ) ( ) ( " h h x x h x

x =ψ + − ψ +ψ −

ψ (2.38)

Persamaan (2.37) – (2.38) dapat diterapkan dengan membagi [x ,₀ x_N] (lihat gambar 2.4) menjadi N bagian dengan interval h:

N x x

h= N − 0 (2.39)

i=1 i=2 i=3 i=N-1 i=N

[image:32.595.114.411.591.687.2]

Dengan metode perbedaan hingga yang dicari adalah ψ pada x tertentu:

h x

x_i+1= _i+ (2.40)

Jika i = 0 maka x₁ =x₀ +h dengan menggunakan notasi ini persamaan (2.37) dan (2.38) dapat dituliskan:

h x x

xi i i

2

) ( ) ( ) (

' =ψ +1 −ψ −1

ψ (2.41)

2

1

1) 2 ( ) ( )

( ) ( "

h

x x

x

x_i =ψ i+ − ψ i +ψ i−

ψ (2.42)

Persamaan (2.41) dan (2.42) dikenal dengan aproksimasi perbedaan hingga.

2.7. Persamaan Differensial Biasa (PDB) dengan Nilai Batas

Pada persoalan engineering lebih sering dijumpai PDB tingkat 2 dengan kondisi batas yang diberikan pada dua titik. Umumnya kedua titik ini ada pada batas-batas domain permasalahan. Karena solusi yang dicari berada pada dua batas yang tertutup, maka problem ini dikenal sebagai problem domain tertutup atau PDB dengan nilai batas. Bentuk umum dari PDB dengan nilai batas adalah:

) ( )

( )

(

2 2

x f x q dx d x p dx d

= +

+ ψ ψ

ψ

n

x x

x0 ≤ ≤ (2.43)

Dengan nilai-nilai batas:

α ψ

ψ( 0)+ 1 ( 0)=

1 x

dx d B x

A (2.44)

β ψ

ψ( )+ ₂ ( )=

2 n xn

dx d B x

A (2.45)

Dari kondisi batas (2.44) dan (2.45), ada 3 kemungkinan jenis kondisi batas yang mungkin diterapkan dalam PDB ini

1. Nilai batas konstan (Tipe Dirichlet)

Nilai batas diberikan sebagai sebuah konstan. Contoh, jika A₁ =1 dan B₁ =0 maka ψ(x₀)=α

2. Nilai batas Derivatif (Tipe Neuman)

Nilai batas yang diberikan sebagai sebuah nilai derivatif. Contoh, jika A₁ =0 danB₁ =1 maka ψ'(x₀)=α

3. Nilai batas campuran (Tipe Robin)

Nilai batas terdiri dari nilai konstan derivatif. Contoh, jikaA₁ =1 dan B₁ =1 maka ψ(x₀)+ψ'(x₀)=α

Tergantung dari koefisien-koefisien p(x,y) dan q(x,y), PDB (2.38) dapat diklasifikasikan sebagai berikut:

1. PDB linier , jika p(x,y) dan q(x,y) berupa fungsi dari x saja atau berupa sebuah bilangan konstan p(x,y) = p(x) atau p(x,y) = konstan

2. PDB non linier, jika p(x,y)dan q(x,y) merupakan fungsi dari x dan y.

2.8 Solusi Numerik Persamaan Schrödinger

2.8.1 Partikel bebas

Persamaan Schrödinger pada partikel bebas (2.7) adalah sebagai berikut:

) ( ) ( 2 2 2 x k x x ψ ψ ₌₋ ∂ ∂ Atau 0 ) ( 2 ) ( 2 2 2 = + ∂

∂ mE _x

x x

ψ ψ

 pada persamaan (2.8)

Langkah-langkah yang digunakan untuk memecahkan persamaan Schrödinger dalam berbagai potensial ke dalam bentuk numerik sebagai berikut:

1 Persamaan (2.8) (₂ ) 2 ₂ ( ) 0

2

= +

∂

∂ mE _x

x x

ψ ψ

 dikonversi ke persamaan umum PDB (2.43) (₂ ) ( ) ( ) ( ) ( ) ( )

2 x f x x q x x x p x x = + ∂ ∂ + ∂

∂ ψ ψ _{ψ Sehingga diperoleh koefisien}

dari persamaan (2.8) p(x) = 0 , q(x) = 2 ₂ 

mE

dan f(x) = 0

2 Aproksimasi beda hingga turunan pertama pada persamaan (2.41)

h x x

xi i i

2 ) ( ) ( ) (

' =ψ +1 −ψ −1

ψ dan turunan kedua pada persamaan (2.42)

2

1

1) 2 ( ) ( )

( ) ( " h x x x

x i i i

i

−

+ − +

=ψ ψ ψ

ψ disubstitusikan ke persamaan (2.43) maka

didapatkan:

[

]

( ) ( ) ( ) 2 1 1 ) ( ) ( 2 ) ( ) ( 2 1 1 2 1 2

1 h q x x hp x x h f x

x x

hp _{i i i} =

    + + − −   

 − ψ − ψ ψ + (2.47)

Atau dapat disederhanakan

[

]

( ) ( ) 2 1 1 ) ( 2 ) ( 2 1 1 2 1 2

1 h q x hp x h f x

x

hp _{i i i} =

    + + − −   

 − ψ − ψ ψ + (2.48)

) 0 ( ) 0 ( 2 1 1 2 2 ) 0 ( 2 1

1 2 1 2

2

1 h h

mE h

h i  i + +  i =

   _      − −     − ψ − ψ ψ +

 (2.49)

[ ]

1 2 2 2

[ ]

1 1 0

2

1  + =

   _      − − +

− i i

i

mE

h ψ ψ

ψ

 (2.50)

0 2

2 2 _{2 1}

1  + =

   _      − − +

− i i

i

mE

h ψ ψ

ψ

 (2.51)

Persamaan (2.51) diterapkan pada setiap titik diskresitasi, yaitu i =1, 2,…,N-1 Sehinggga terbentuk sistem persamaan linier (SPL) dengan bentuk tri-diagonal yang dapat dipecahkan dengan algoritma Thomas.

Dari persamaan (2.46) Untuk 1≤ i ≤ N-1 diperoleh:

i =1: 2 2 2 ₂ ψ₁     _      − −  mE

h + ψ₂ + 0 + 0 = −ψ0

i = 2: ψ₁ 2 2 2 ₂ ψ₂     _      − −  mE

h + ψ₃ + 0 = 0

i = 3: 0 + ψ₂ 2 2 2 ₂ ψ₃     _      − −  mE

h + ψ₄ = 0

…

i =N-1: 0 + 0 + ψ_N−2 2 2 2 _{2 −1}     _      − − N mE h ψ

 = −ψN

Bila diambil: 2 2 ₂ 

mE

k =− maka bentuk matriksnya menjadi:

[

]

[

]

[

]

[

]

               − − =                 −                 − − − − − − − − − − − − − N N k h k h k h k h ψ ψ ψ ψ ψψ      0 0 ) ( 2 1 0 0 0 0 0 0 1 ) ( 2 1 0 0 0 1 ) ( 2 1 0 0 0 1 ) ( 2 0 1 3 2 1 2 2 2 2 2 2 2 2 (2.52)

Pemecahan metode numerik menggunakan metode beda hingga pada persamaan (2.52) diatas akan mempermudah pembuatan programnya sehingga akan diperoleh visualisasi dari persamaan Schrodinger pada partikel bebas.

2.8.2 Partikel dalam Kotak

Pada dasarnya persamaan Schrödinger pada partikel bebas identik dengan persamaan Schrödinger dalam kotak sehingga memiliki pemecahan yang sama. Sehingga metode-metode penyelesaian pada partikel bebas juga digunakan untuk mencari solusi persamaan schrodinger pada partikel dalam kotak.

2.9 Program komputer

Program komputer adalah suatu urutan instruksi yang disusun secara sistematis dan logis dengan menggunakan bahasa pemrograman untuk menyelesaikan suatu masalah. Program komputer dapat digunakan untuk perhitungan numerik dan eksprimen simulasi melalui pendekatan fisika komputasi.

2.9.1 Pengantar pemrograman MATLAB

MATLAB diciptakan di Universitas Mexico dan stanford University ditahun 70-an dan saat ini dipasarkan Oleh Math Work Inc.

Elemen dasar :

A. Membuka paket MATLAB

a. Cari ikon MATLAB kemudian klik dengan cepat dua kali, jendela kerja MATLAB akan muncul

b. Perintah (Command) dari MATLAB dituliskan dengan tanda >>

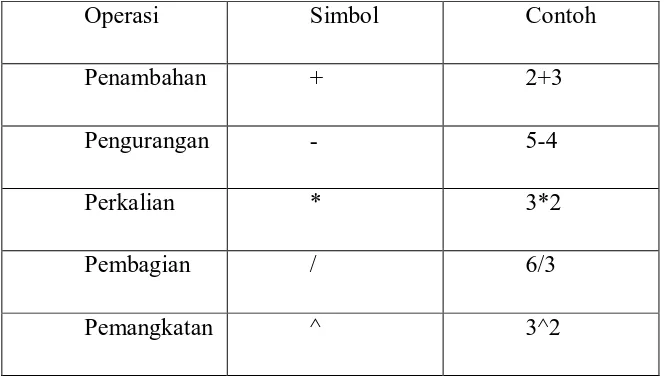
[image:38.595.107.439.372.562.2]

c. Setelah selesai menggunakan MATLAB, ketik quit dan [enter], atau klik File/Exit. B.Operasi Aritmatika

Tabel 2.1 Operator Aritmatika

Operasi Simbol Contoh

Penambahan + 2+3

Pengurangan - 5-4

Perkalian * 3*2

Pembagian / 6/3

Pemangkatan ^ 3^2

C.Variabel

Variabel pada MATLAB harus diberi nama.Nama variabel harus dimulai dengan huruf, dan bisa diikuti dengan huruf lain atau angka maksimum 31 karakter. Nama varibel dengan huruf besar (kapital) dianggap berbeda dengan nama variabel yang ditulis dengan huruf kecil.

D.konstanta/tetapan

pi nilai π = 3,14452…

eps nilai epsilon, bilangan natural e = inf nilai tak berhingga ~

E.Tanda baca

% Digunakan untuk mengawali komentar (command)

, digunakan untuk memisahkan dua pernyataaan dalam sebaris ; digunakan untuk memisahkan dua pernyataan tanpa echo … digunakan untuk melanjutkan statemen ke baris berikutnya.

2.9.2 input-output

MATLAB juga menyediakan instruksi untuk menerima data dari keyboard (input) dan menampilkan nilai variabel ke monitor (output) yaitu:

a.Melakukan input : x =input(‘masukkan nilai x:’) b.Menampilkan nilai:disp(‘nilai dari x adalah’)

2.9.3 Kontrol Program

MATLAB menyediakan beberapa instruksi yang memugkinkan pengguna membuat program atau fungsi, antara lain instruksi pemilihan (seleksi) dan instruksi perulangan (loop)

Instruksi seleksi: a. Pemilihan bersyarat:

else if

instruksi-2 else

instruksi-3 end.

Pemilihan diatas digunakan untuk memilih satu diantara beberapa instruksi sesuai dengan syarat yang dipenuhi. Bila syarat 1 dipenuhi maka laksanakan instruksi 1 , bila syarat 2 dipenuhi, maka laksanakan instruksi 2 bila tidak ada syarat yang dipenuhi maka laksanakan instruksi-3.

b. Pemilihan kasus switch variabel

case 1 {nilai-1} instruksi-1 case 2 {nilai-2} instruksi-2

case 3 {nilai-3} instruksi-3 …

Otherwise instruksi n End.

Instruksi seleksi ini akan memilih satu instruksi berdasarkan nilai yang diberikan pada variabel. Bila nilainya adalah nilai -1 maka instruksi 1 dilaksanakan. Bila nilainya adalah 2 maka instruksi 2 yang dilaksanakan. Bila nilainya adalah 2 maka instruksi 2 yang dilaksanakan.

Instruksi perulangan a. Perulangan dengan for

instruksi-instruksi end

Perulangan yang dibatasi oleh nilai var, mulai dari n1 hingga n3 dengan perubahan nilai sebesar n2 pada setiap putaran. Apakah n2=1 maka n2 tidak perlu ditulis, sehingga bentuknya menjadi:

for var = n1: n3

instruksi-instruksi end

b. Perulangan denganWhile while (syarat)

insruksi-instruksi end

Perulangan yang ditentukan oleh suatu syarat. Selama syarat terpenuhi maka perulangan akan belangsung. (Suarga,2005).

2.9.4. Grafik MATLAB

MATLAB menyediakan fasilitas grafik yang dapat dipanggil dari baris perintah atau perintah yang langsung dituliskan pada command window . Berikut adalah tekhnik untuk memperoleh tampilan grafik yang lebih menarik dengan menggunakan MATLAB.

1. Memberi judul dan Label pada Grafik

Dan untuk menambahkan label sumbu x pada hasil plot harus mengggunakan skrip berikut : xlabel(‘---labelnya---‘);

Dan untuk menambahkan label sumbu y pada hasil plot harus mengggunakan skrip berikut : ylabel(‘---labelnya---‘);

2. Memunculkan Grid pada Grafik

Latar belakang grafik secara default berwarna putih dan polos. MATLAB menyediakan fungsi untuk membuat grid pada latar belakang grafik dengan menggunakan fungsi grid on dan grid off.

3. Mengubah garis, tanda dan warna pada Grafik

Jika diinginkan tampilan data tidak dalam bentuk garis tepi berupa titik, lingkaran atau kotak dan mungkin saja dalam warna yang berbeda-beda. Maka tekhnik yang digunakan adalah memberikan parameter input yang berhubungan dengan fungsi plot, seperti berikut: Plot (z,y,symbol). Dimana x dan y adalah variabel data yang akan diplot.Simbol adalah karakter yang akan digunakan untuk menggantikan format tampilan default grafik.

BAB III

METODOLOGI PENELITIAN

3.1 Rancangan Penelitian

Langkah awal yang dilakukan adalah memecahkan persamaan Schrodinger dengan metode analitik kemudian mencari pemecahannnya dengan metode komputasi, maka langkah-langkah penyusunan program dilakukan sebagai berikut:

a. Membahas Persoalan fisika

b. Mengkonfirmasikan persoalan fisika ke dalam bentuk numerik c. Penyusunan algoritma

d. Pengkodean yaitu menterjemahkan algoritma kedalam kode bahasa pemograman.

e. Menjalankan program f. Analisis hasil visualisasi g. Penulisan laporan

3.2 Teknik Analisis Data

1. Mengumpulkan data yang diperoleh dalam program dan data tersebut dibuat dalam bentuk visualisasi.

2. Hasil visualisasi fungsi gelombang persamaan Schrodinger dengan metode komputasi akan dilihat kesesuaiannya dengan hasil analitik

3.3Diagram Alir Penelitian

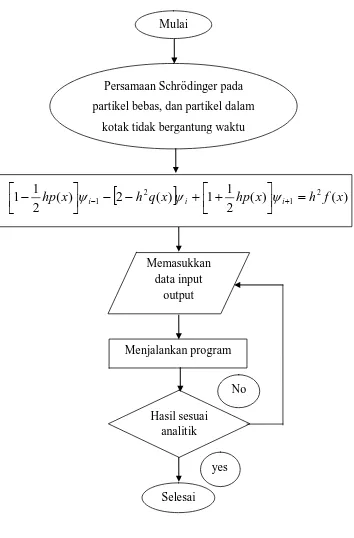
[image:44.595.121.475.127.665.2]

Gambar.3.1. Diagram Alir Penelitian Menjalankan program

Selesai Memasukkan

data input output

Hasil sesuai analitik

Persamaan Schrödinger pada partikel bebas, dan partikel dalam

kotak tidak bergantung waktu

yes Mulai

No

[

]

(

)

(

)

2

1

1

)

(

2

)

(

2

1

1

hp

x

_{i 1}

h

2

q

x

_i

hp

x

_{i 1}

=

h

2

f

x







 +

+

−

−







BAB IV

HASIL DAN PEMBAHASAN

Hasil dari penelitian ini berupa penyelesaian komputasi persamaan Schrödinger menggunakan metode beda hingga (finite difference Methods) yaitu pada partikel bebas, dan partikel dalam kotak. Dengan konversi metode beda hingga ke dalam persamaan Schrödinger, diharapkan akan diperoleh visualisasi gelombang partikel bebas dan kotak dengan menggunakan Sofware MATLAB.

4.1. Visualisasi Persamaan Schrödinger pada partikel bebas

-50 0 50 -0.25

-0.2 -0.15 -0.1 -0.05 0 0.05 0.1 0.15 0.2 0.25

Fungsi Gelombang Partikel Bebas

Posisi x

P

s

i

-50 0 50

0 0.01 0.02 0.03 0.04 0.05 0.06

Posisi x

P

robabi

lit

y

dens

it

y

[image:46.595.106.529.87.398.2]

rapat probabilitas

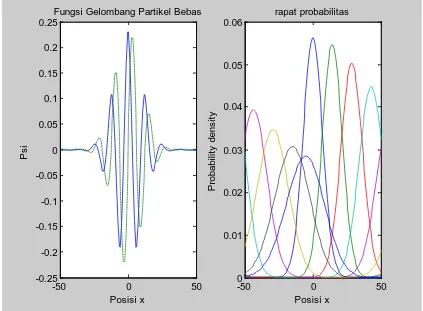
Gambar.4.1.Visualisasi Partikel bebas pada bentangan bidang –L/2 sd L/2 dengan Jumlah Persamaan N= 100 dengan interval h=2.

Pada Gambar 4.1. Visualisasi Gelombang Partikel Bebas pada bentangan bidang –L/2 sampai dengan L/2, dengan L = 50 Jelas terlihat bahwa visualisasi Partikel bebas merupakan sebuah paket gelombang yang dapat dipandang sebagai superposisi sejumlah besar gelombang, yang berinterferensi secara maksimum di sekitar partikel dengan Probabilitas tertinggi ditemukannya partikel berada pada posisi x= 0.

4.2 Visualisasi Persamaan Schrödinger pada partikel dalam kotak

[image:47.595.106.471.163.366.2]

a. Orde gelombang n = 1, jumlah persamaan N = 100 dengan ukuran langkah h = 0.01. Visualisasi gelombangnya sebagai berikut:

Tabel 4.1.Hasil running untuk n = 1, N = 100 dan h = 0.01

x Hasil komput asi (Psi) X Hasil komput asi (Psi)

0.01 0.1658 0.06 0.9894

0.02 0.3314 0.07 1.1521

0.03 0.4967 0.08 1.3138

0.04 0.6616 …

0.05 0.8259 1.00 1.0000

Hasil running kemudian diplot sebagai berikut:

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0 5 10 15 20 25 30 35

Visualisasi Gelombang partikel sumur tak berhingga

x

P

si

(x

)

[image:47.595.108.465.167.362.2]

Komputasi imag probabilitas

[image:47.595.108.530.422.688.2]

Persamaan Schrödinger pada partikel dalam sebuah kotak dalam selang 0 ≤ x

≤ L, dengan L = 1 bila V(x) = 0 dapat diterapkan syarat bahwa ψ (x) harus kontinu pada setiap batas dua bagian ruang. Dalam hal ini disyaratkan bahwa pemechan untuk x<0 dan x>0 bernilai sama di x= 0, begitu juga pemecahan untuk x>0 dan x<L haruslah bernilai sama di x =L

Pada gambar. 4.2 Visualisasi fungsi gelombang partikel dalam sebuah kotak dapat dilihat pada x = 0 untuk x < 0 diperoleh ψ (x) = 0 maka persamaan (2.11) diperoleh ψ(0) = Asin 0 + B cos 0 = 0 jadi B = 0. Karena ψ (x) = 0 untuk x > L maka harus berlaku ψ (L) = 0. Partikel akan selalu berada di dalam kotak jika kedua dinding benar-benar tegar . Sehingga probabilitas untuk menemukan partikel di luar kotak adalah nol, dengan mengambil ψ (x) = 0.

Untuk keadaan energi terendah, yaitu pada n = 1 probabilitas terbesarnya pada x = L/2 artinya partikel berada di dalam kotak dan berangsur-angsur berkurang begitu bergerak menjauhi pusatnya dan akhirnya menuju nol.

[image:48.595.106.445.487.678.2]

b. Orde gelombang n = 2, jumlah persamaan N = 100 dengan ukuran langkah h = 0.01. Visualisasi gelombangnya sebagai berikut:

Tabel 4.2.Hasil running untuk n = 2, N = 100 dan h = 0.01

X Hasil komput asi (Psi) x Hasil komput asi (Psi)

0.01 -0.1687 0.06 -0.9916

0.02 -0.3368 0.07 -1.1480

0.03 -0.5037 0.08 -1.3004

0.04 -0.6689 …

Hasil running kemudian diplot sebagai berikut:

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

-10 -8 -6 -4 -2 0 2 4 6 8 10

Visualisasi Gelombang partikel sumur tak berhingga

posisi(x)

P

si

(x

)

Komputasi imag

[image:49.595.108.528.136.373.2]

rapat probabilitas

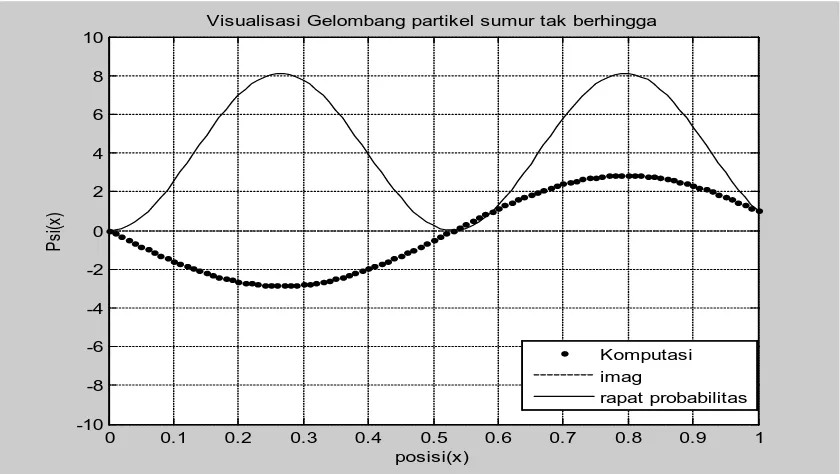
Gambar.4.3. Visualisasi fungsi gelombang partikel dalam kotak orde gelombang n = 2, Jumlah persamaaan N = 100 dan ukuran langkah h = 0.01

[image:50.595.108.468.165.359.2]

c. Orde gelombang n = 3, jumlah persamaan N = 100 dengan ukuran langkah h = 0.01. Visualisasi gelombangnya sebagai berikut :

Tabel 4.3.Hasil running untuk n = 3, N = 100 dan h = 0.01

x Hasil komput asi (Psi) X Hasil komput asi (Psi)

0.01 0.1737 0.06 0.9949

0.02 0.3461 0.07 1.1406

0.03 0.5157 0.08 1.2773

0.04 0.6812 …

0.05 0.8414 1.00 1.0000

Hasil running kemudian diplot sebagai berikut:

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

-4 -3 -2 -1 0 1 2 3 4

Visualisasi Gelombang partikel sumur tak berhingga

posisi(x)

P

si

(x

)

Komputasi imag

[image:50.595.107.529.411.684.2]

rapat probabilitas

Gambar.4.4. Visualisasi fungsi gelombang partikel dalam kotak n=3, maksimum probabilitas dalam selang 0 ≤ x ≤ L, terjadi pada x = L/6, x =L/2, dan x = 5/6 L. Sedangkan probabilitas nol terjadi pada x = L/3 dan x = 4/6 L. Artinya partikel akan ditemukan pada x = L/6, x =L/2, dan x = 5/6 L dan partikel tidak akan pernah ditemukan pada x = L/3 dan x = 4/6 L karena partikel berada diluar kotak dimana

[image:52.595.107.439.166.328.2]

d. Orde gelombang n = 5, jumlah persamaan N = 100 dengan ukuran langkah h = 0.01. Visualisasi gelombangnya sebagai berikut:

Tabel 4.4.Hasil running untuk n = 5, N = 100 dan h = 0.01

X Hasil Komput asi(psi) X Hasil Komput asi(psi)

0.01 0.1908 0.06 1.0034

0.02 0.3774 0.07 1.1126

0.03 0.5558 0.08 1.1974

0.04 0.7219 …

0.05 0.8722 1.0 1.0000

Hasil running kemudian diplot sebagai berikut:

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 -4

-3 -2 -1 0 1 2 3 4

Visualisasi Gelombang partikel sumur tak berhingga

posisi(x)

P

si

(x

)

Komputasi imag

[image:52.595.108.521.387.597.2]

rapat probabilitas

BAB V

KESIMPULAN DAN SARAN 5.1 Kesimpulan

Dari hasil penelitian, dapat diambil kesimpulan:

1. Diperoleh bentuk komputasi persamaan Schrödinger satu dimensi pada partikel bebas dan partikel dalam kotak dengan menggunakan metode beda Hingga.

2. Diperoleh bentuk visualisasi Persamaan Schrodinger pada partikel bebas dan partikel kotak menggunakan MATLAB dimana fungsi gelombang dengan potensial konstan atau dapat dikatakan V(x) = 0 akan membentuk gelombang deBroglie karena arah merambat gelombang partikel bebas dan partikel bebas sama dengan arah kecepatan partikel yaitu menuju Positip. momentum partikel di hubungkan dengan kecepatan partikel p= mv. Dengan hubungan momentum dan panjang gelombang de Broglie p= h/λ. Dengan kecepatan de gelombang de Broglie sama dengan kecepatan Partikel v.

5.2 Saran

Metode beda Hingga (finite difference Methods) juga dapat digunakan untuk memperoleh solusi persamaan Schrodinger tidak bergantung waktu, juga untuk solusi persamaan Scrodinger pada dua dimensi atau tiga Dimensi.

0 2

2 2 1

2

1  + =

 

 _

     −

− +

− i i

i

mE

h ψ ψ

ψ

DAFTAR PUSTAKA

Basaruddin, 1991, Metode Beda Hingga Untuk Persamaan diffrensial, Jakarta, Penerbit Gramedia.

Chapra, 1998, Numerical Methods For Engineers, Singapore, Penerbit M.Graw-Hill Companies,Inc

Eisberg, R, dan Resnick, R, 1970, Quantum Physics, Jhon wiley & Sons,New York,California.

Hartanto dan Prasetyo, 2003, Analisis dan desain Sistem Kontrol Dengan MATLAB, Yogyakarta, Penerbit ANDI

Kosasih, B , 2006, Komputasi Numerik Teori dan Aplikasi, Yogyakarta , Penerbit ANDI.

Krane, K, 1992, Fisika Modern (Modern Physics), Terjemahan, Jakarta, Penerbit UI-press.

Moengin, Parwadi, 2008, Metode Numerik Untuk Teknik, Jakarta, Penerbit Universitas Trisakti

Raymond, D, 2006, Particle in a Box.

Suarga,2005, Fisika Komputasi,Solusi Problema Fisika Dengan MATLAB,Yogyakarta,Penerbit ANDI.

Lampiran 1.Kode Pemrograman Visualisasi Gelombang Pada Partikel Bebas %program persamaan schrodinger pada partikel bebas

%PDB linier dengan Perbedaan Hingga

x0 = input('Batas awal(x0)='); xn = input('Batas akhir(xn)='); N = input('Jumlah Persamaan(N)='); m = 9.1100e-031;

hbar=1.0550e-034; Vx = 0.0;

h = (xn-x0)/N; h2 = 0.5*h; hh = h*h;

E = (((hbar)^2) /(2*m*(h^2)) p = 0*ones(1,N-1);

q =(-(2-h^2)*(-2*m*E)/(hbar^2))*ones(1,N-1); f =0*ones(1,N-1);

%syarat batas

y0= -50.; yn= 50;

x=linspace(x0+h,xn,N);

%elemen-elemen matriks tri-diagonal

a = zeros(1,N-1); b = a;

c = a;

a(2:N-1) = 1-p(1,2:N-1)*h2; d = -(2.-hh*q); c(1:N-2) = 1+p(1,1:N-2)*h2; b(1) = hh*f(1)-(1-p(1)*h2)*y0; b(2:N-2) = hh*f(2:N-2);

b(N-1) = hh*f(N-1)-(1-p(N-1)*h2)*yn; y = tri_diag(a,d,c,b);

xx = [x0 x]; yy = [y0 y yn]; out = [xx' yy'];

plot (xx,yy,'.k',xx,imag(yy),'--k',xx,yy.*conj(yy),'-k'); title('Visualisasi Gelombang partikel bebas');

Lampiran 1.Kode pemrograman Visualisasi gelombang pada Partikel dalam kotak

% program persamaan Schrodinger pada partikel dalam kotak %PDB linier dengan Perbedaan Hingga

x0 = input('Batas awal(x0)='); xn = input('Batas akhir(xn)='); N = input('Jumlah Persamaan(N)='); n =input('Orde Gelombang(n)='); m =9.1100e-031;

hbar =1.0550e-034; L =1.0;

E = ((((hbar)^2)*(pi^2)*(n^2))/(2*m*(L^2))); h =(xn-x0)/N;

h2 =0.5*h; hh =h*h;

p =0*ones(1,N-1);

q =(-(2-h^2)*(-2*m*E))/(hbar^2)*ones(1,N-1); f =0*ones(1,N-1);

%syarat batas y0=0.;

yn=1.0;

x =linspace(x0+h,xn,N);

%elemen-elemen matriks tri-diagonal a=zeros(1,N-1);

b=a; c=a;

a(2:N-1) = 1-p(1,2:N-1)*h2; d = - (2-hh*q); c(1:N-2) = 1+p(1,1:N-2)*h2; b(1) = hh*f(1)-(1-p(1)*h2)*y0; b(2:N-2) = hh*f(2:N-2);

b(N-1) = hh*f(N-1)-(1-p(N-1)*h2)*yn; y = tri_diag(a,d,c,b);

xx = [x0 x]; yy = [y0 y yn]; out = [xx' yy'];

plot (xx,yy,'.k',xx,imag(yy),'--k',xx,yy.*conj(yy),'-k'); title('Visualisasi Gelombang partikel sumur tak berhingga'); xlabel('x');ylabel('Psi(x)');legend('Komputasi','imag','probabilitas'); axis([x0 xn 0 35]);