BAB II
TINJAUAN PUSTAKA
2.1 Metode Beda Hingga
Metode perbedaan beda hingga adalah metode yang sangat popular. Pada intinya metode ini mengubah masalah Persamaan Differensial Biasa (PDB) nilai batas dari sebuah masalah kalkulus menjadi sebuah aljabar. Dengan metode ini persamaan differensial ψ’ dan ψ” akan diaproksimasikan dengan menggunakan deret Taylor sebagai berikut:
( ) ( ) ( ) ( ) (2.1) ( ) ( ) ( ) ( ) (2.2) Kalau dikurangi (2.1) dengan (2.2) dan nilai setelah pangkat 2 diabaikan maka akan didapat:
( ) ( ) ( ) (2.3)
Apabila (2.1) ditambahdengan (2.2) akandiperoleh
( ) ( ) ( ) ( ) (2.4)
Persamaan (2.1) – (2.4) dapat diterapkan dengan membagi [x0,xn], (lihat gambar 2.1)
menjadi n bagian dengan interval h:
(2.5)
i=0 i=1 i=2 i=n-1 i=n
X0 X1 X2
Xn-1 Xn
Gambar 2.1 Pembagian Interval antara [x0,xn]
Dengan metode perbedaan hingga yang dicari adalah pada x tertentu:
(2.6)
Jika i = 0 maka dengan menggunakan notasi ini persamaan (2.3) dan (2.4) dapat dituliskan:
( ) ( ) ( )
( ) ( ) ( ) ( ) (2.8) Persamaan (2.7) dan (2.8) dikenal dengan aproksimasi perbadaan hingga tiga titik (central three points finite difference approximation).
2.2 Persamaan Differensial Biasa (PDB) dengan Nilai Batas
Pada persoalan matematik lebih sering dijumpai PDB tingkat 2 dengan kondisi batas yang diberikan pada dua titik. Umumnya kedua titik ini ada pada batas-batas domain permasalahan. Karena solusi yang dicari berada pada dua batas-batas yang tertutup maka problem ini dikenal sebagai problem domain tertutup atau PDB dengan nilai batas. Bentuk umum dari PDB tingkat 2 dengan nilai batas adalah:
( )
1. Nilai batas konstan (Tipe Dirichlet)
Nilai batas yang diberikan sebagai sebuah konstan. Contoh, jikaA1 = 1 dan
B1 = 0 maka ψ(x0) = α
2. Nilai batas derivatif (Tipe Neuman)
Nilai batas yang diberikan sebagai sebuah nilai derivatif. Contoh, jika A1 = 0
dan B1 = 1 maka ψ’(x0) = α
3. Nilai batas campuran (Tipe Robin)
Nilai batas terdiri dari nilai konstan dan derivatif. Contoh, jika A1 = 1 dan B1
= 1 maka ψ(xo) + ψ’(xo) = α
Tergantung dari koefisien-koefisien p(x) dan q(x), PDB (2.9) dapat diklasifikasikan sebagai berikut:
1. PDB Linier, jika p(x) dan q(x) berupa fungsi dari x saja atau berupa sebuah bilangan kompleks.
2.3 Metode Numerik
Penerapan metode numerik pada persamaan Schrödinger dirumuskan dengan persamaan differensial. Langkah pendahuluan yang ditempuh dalam menerapkan metode ini adalah memperkirakan persamaan differensial yang bersangkutan beserta syarat-syarat batasnya dengan seperangkat persamaan aljabar. Dengan mengganti daerah yang kontinu dengan suatu pola titik tersebut. Sistem dibagi menjadi sejumlah subluas yang kecil dan memberi nomor acuan kepada setiap sub luas.
2.4 Sistem Tri-Diagonal
Pemecahan persamaan differensial dengan menggunakan diskretisasi perbedaan hingga (finite difference), seringkali melibatkan system persamaan linier (SPL) yang mempunyai bentuk-bentuk khusus. Contoh berikut memberikan dua kemungkinan bentuk SPL berikut;
Dengan menggunakan notasi matriks, sistem persamaan (2.13) dapat dituliskan
[
[
Pemecahan SPL dengan koefesien matriks tri-diagonal didasari oleh metode Doolittle. Pertama-tama matriks A didekomposisi menjadi LU, yaitu matriks segitiga bawah dan segitiga atas sesuai algoritma Doolittle. Setelah dekomposisi persamaan (2.15) menjadi: Setelah perkalian matriks persamaan (2.16) menjadi
[
Inti dari algoritma ini adalah mengubah elemen-elemen pada vector a, d, dan c dengan vector α, δ, dan c yang merupakan elemen-elemen dari L dan U, jika dibandingkan persamaan (2.17) dengan (2.15) maka tampak bahwa:
Langkah-langkah di atas dapat dengan mudah diprogram, sebagai ilustrasi, 3 langkah pertama program tersebut dapat dituliskan sebagai berikut:
d(1) = d(1)
a(2) = a(2) / d(1) d(2) = d(2) – a(2)*c(1) a(3) = a(3) / d(2) d(3) = d(3) – a(3)*c(2)
setelah elemen-elemen pada vector a dan d dengan α dan δ, persamaan (2.16) dapat diproses lebih lanjut, jika Ux sebut saja g, maka persamaan (2.16) dapat dituliskan
( ) ⁄
( ) ⁄ Dalam komputasi, tiga langkah pertama berbentuk x(N) = b(N) / d(N)
x(N-1) = [b(N-1) – c(N-1)*x(N)] / d(N-1) x(N-2) = [b(N-2) – c(N-2)*x(N-1)] / d(N-2)
Jika diperhatikan prosedur di atas adalah metode Doolittle yang diterapkan pada sistem tri-diagonal. Namun karena elemen dari matriks A kebanyakan nol maka hanya digunakan tiga vector dengan ukuran 1 x N untuk menyimpan elemen bukan nol matriks A. Teknik ini sangat populer dengan algoritma Thomas, sesuai dengan nama penemunya. (Zettili, 2009)
2.5 Osilator Harmonik
Pada mekanika klasik, salah satu bentuk osilator harmonik adalah sistem pegas massa, yaitu suatu beban bermassa m yang terikat pada salah satu ujung pegas dengan konstanta pegas k. Persamaan gerak adalah
(2.22)
(2.23)
Dengan √ adalah frekuensi angular osilasi.
Persamaan (2.23) adalah persamaan diferensial orde dua dengan akar-akar bilangan kompleks yang berlainan, solusinya adalah
( ) (2.24)
Dan energi potensial sistem adalah ( )
( ) (2.25)
Persamaan Schrödinger merupakan fungsi gelombang yang digunakan untuk memberikan informasi tentang perilaku gelombang dari partikel. Suatu persamaan differensial akan menghasilkan pemecahan yang sesuai dengan fisika kuantum. Untuk membentuk persamaan Schrödinger , maka harus memenuhi 3 (tiga) kriteria, sebagai berikut:
a Taat azas dengan kekekalan energi
Hukum kekekalan energi adalah jumlah energi kinetik ditambah energi potensial bersifat kekal, artinya tidak bergantung pada waktu maupun posisi. Persamaan Schrödinger harus konsisten dengan hukum kekekalan energi. Secara matematis, hukum kekekalan energi dapat dinyatakan dengan rumusan:
( ) (2.27)
Suku pertama ruas kiri menyatakan energi kinetik, suku kedua menyatakan energi potensial, dan ruas kanan menyatakan suatu tetapan yang biasanya disebut sebagai energi total. dimana energi kinetik yang digunakan bukanlah dalam bentuk . Karena pada persamaan Schrödinger berbicara tentang dunia atom, sehingga digunakan “prinsip ketakpastian” , dengan h = 6,63 x 10-34 J.s. Ketidakpastian ini adalah sesuatu yang akurat dan pasti. Pada skala ini memberi makna terhadap gejala fisika dalam dunia atom dan karena momentum itu sebanding dengan kecepatan. Ini berarti partikel tidak dapat memiliki posisi dan kecepatan yang akurat pada saat bersamaan, bahkan ketidakpastian dalam posisi dikalikan dengan ketakpastian momentum selalu lebih besar nilainya dari konstanta Planck, karena nilai konstanta Planck sangat kecil. Sehingga hanya digunakan dalam kawasan mikroskopik misalnya elektron.
b. Linear dan bernilai tunggal
partikelnya, walaupun ditemukan probabilitas berubah secara kontiniu dan partikelnya menghilang secara tiba-tiba dari suatu titik dan muncul kembali pada titik lainnya, namun fungsinya haruslah bernilai tunggal, artinya tidak boleh ada dua probabilitas untuk menemukan partikel di satu titik yang sama. Probabilitas harus liniear, agar gelombangnya memiliki sifat superposisi yang diharapkan sebagai miliki gelombang yang berperilaku baik.
c. Pemecahan partikel bebas sesuai dengan gelombang de Broglie tunggal
Tahun 1924 de Broglie menyatakan bahwa materi mempunyai sifat gelombang disamping sifat partikel. Bentuk persamaan differensial apapun, haruslah taat asas terhadap hipotesis de Broglie. Untuk menyelesaikan persamaan matematik bagi sebuah partikel dengan momentum p, maka pemecahannya harus berbentuk fungsi gelombang dengan panjang gelombang λ yang sama dengan ⁄ . Sesuai dengan persamaan ⁄ . Maka energi kinetik dari gelombang de Broglie partikel bebas haruslah ⁄ ⁄ .
Bentuk persamaan harus taat asas kekekalan energi seperti yang dijelaskan di atas ( ), K muncul dalam pangkat satu dan ⁄ ⁄ , sehingga satu-satunya cara untuk memperoleh suku yang mengandung k2 adalah dengan mengambil turunan kedua dari ( ) terhadap x. Sehingga dihasilkan persamaan Schrödinger sebagai berikut:
( )
( )
( ) ( ( )) ( )
( )
( ) ( ) (2.28)
Persamaan (2.28) merupakan bentuk persamaan Schrödinger tidak bergantung waktu dalam satu dimensi.
2.7 Probabilitas dan Normalisasi
gelombang yang berbeda, yang nilai mutlaknya memberikan probabilitas untuk menemukan partikelnya pada suatu titik tertentu. Dimana | ( )| memberikan probabilitas untuk menemukan partikel dalam selang dx di x. Rapat probabilitas P(x)
terhadap ( ) menurut persamaan Schrödinger sebagai berikut:
( ) | ( )| (2.29)
Tafsiran | ( )| ini membantu memahami persyaratan kontiniu ( ). Walaupun amplitudonya berubah secara tidak jelas dan kontiniu. Probabilitas untuk menemukan partikel antara x1dan x2 adalah jumlah semua probabilitas ( ) dalam
selang antara x1dan x2 adalah sebagai berikut:
∫ ( ) ∫ | ( )| (2.30) dari aturan ini, maka probabilitas untuk menemukan partikel disuatu titik sepanjang sumbu x, adalah 100 persen, sehinga berlaku:
∫ | ( )| (2.31)
Persamaan (2.31) dikenal dengan syarat normalisasi, yang menunjukkkan bagaimana mendapatkan tetapan A. Dimana tetapan A tidak dapat ditentukan dari persamaan differensialnya. Sebuah fungsi gelombang yang tetapan pengalinya ditentukan dari persamaan (2.31) disebut ternormalisasi secara tepat, yang dapat digunakan untuk melakukan semua perhitungan yang mempunyai makna fisika. Jika normalisasinya telah dilakukan secara tepat, maka persamaan (2.30) akan selalu menghasilkan suatu probabilitas yang terletak antara 0 dan 1.
Setiap pemecahan persamaan Schrödinger yang menghasikan | ( )| bernilai tak berhingga, harus dikesampingkan. Karena tidak pernah terdapat probabilitas tak hingga untuk menemukan partikel pada titik manapun. Maka harus mengesampingkan suatu pemecahan dengan mengembalikan faktor pengalinya sama dengan nol. Sebagai contoh, jika pemecahan matematika bagi persamaan differensial menghasilkan ( ) bagi seluruh daerah x >0, maka syaratnya A = 0 agar pemecahannya mempunyai makna fisika. Jika tidak, | ( )| akan menjadi tak hingga untuk x menuju tak hingga (tetapi jika pemecahannya dibatasi dalam selang 0 < x < L, maka A tidak boleh sama dengan nol). Tetapi jika pemecahannya berlaku pada seluruh daerah negatif sumbu x < 0, maka B = 0.
setiap koordinat, maka ditemukan hasil yang mungkin dari pengukuran satu kali atau rata-rata hasil dari sejumlah besar pengukuran berkali-kali. (Krane, 1992)
2.8 Penerapan Persamaan Schrödinger
Persamaan Schrödinger dapat diterapkan dalam berbagai persoalan fisika. Dimana pemecahan persamaan Schrödinger, yang disebut fungsi gelombang, memberikan informasi tentang perilaku gelombang dari partikel.
2.8.1. Pada Partikel Bebas
Yang dimaksud dengan partikel bebas adalah sebuah partikel yang bergerak tanpa dipengaruhi gaya apapun dalam suatu bagian ruang; yaitu, F = -dV(x)/dx = 0
sehingga menempuh lintasan lurus dengan kelajuan konstan. Dalam hal ini, bebas memilih tetapan potensial sama dengan nol. Berikut ini resep Schrödinger diterapkan pada partikel bebas, kembali ke persamaan Schordinger dengan potensial energi yang sesuai, V(x) = 0.
Partikel bebas dalam mekanika klasik bergerak dengan momentum konstan p, yang mengakibatkan energi totalnya juga konstan. Tetapi partikel bebas dalam mekanika kuantum dapat dipecahkan dengan persamaan Schrödinger bergantung waktu, persamaan Schrödinger untuk partikel bebas dapat diperoleh dari persamaan (2.28) berikut:
( ) ( ) ( ) (2.32)
untuk partikel bebas V(x) = 0, maka persamaannya menjadi
( ) ( ) (2.33) ( ) merupakan kuantitas kompleks yang memiliki bagian real dan bagian imajiner. Sehingga pemecahannya adalah
( ) (2.36)
karena integral normalisasi tidak dapat dihitung dari hingga bagi fungsi gelombang itu.(Einsberg, 1970)
2.8.2. Potensial Halang
Apa yang akan terjadi apabila sebuah partikel yang sedang bergerak (satu dimensi) dalam suatu daerah yang berpotensial tetap tiba-tiba bergerak memasuki suatu daerah. Pemecahan pada persoalan seperti ini dilakukan, dengan mengambil E
sebagai energi total (yang tetap) dari partikel dan V0. sebagai nilai energi potensial
tetapnya.
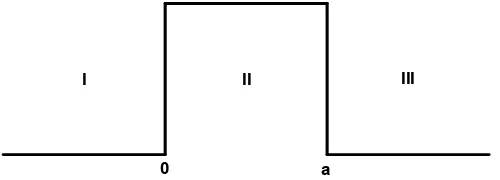
Pada daerah I dan III, nilai Vn = 0 ,dan pada daerah II dengan batas x 0
hingga x = a memiliki energi potensial Vn = V0
II
I III
0 a
Gambar 2.2 Potensial halang
Partikel dengan energi E yang lebih kecil daripada V0 datang dari sebelah
kiri. Daerah x<0 berupa gelombang datang dan pantul berbentuk sinus, dalam daerah 0 ≤ x≤ a dan kembali berbentuk sinus pada daerah x>a yaitu gelombang transmisi.
Pemecahan ini mengilustrasikan perbedaan penting antara mekanika klasik dan mekanika kuantum. Secara klasik, partikelnya tidak pernah dapat ditemukan pada daerah x > 0, karena energi totalnya tidak cukup melampaui potensial tangga. Tetapi, mekanika kuantum memperkenankan fungsi gelombang dan partikel akan menerobos masuk ke dalam daerah terlarang klasik.
1. Padadaerah 1, ≤x ≤ a V=0
( )
(2.37)
Bila diambil
=
(2.38)
2. Pada daerah II, 0≤ x ≤a, danE <V0 V = V0
( )
(2.39)
(
) (2.40)
Dimana:
= ( )
Maka persamaan Schrödingernya menjadi:
(2.41)
3. Pada daerah III, a ≤ x ≤
(
)
(2.42)
(2.43)
Maka solusi dari persamaan (2.38), (2.40) dan (2.43) adalah sebagai berikut:
(2.44)
(2.45)
(2.46)
Dengan
k1= √ (2.47)
Menyatakan bilangan gelombang deBroglie yang membuat partikel di luar perintang, karena:
Ei = cos + i sin (2.48)
e-i = cos + i sin (2.49)
mewakili panjang gelombang sepanjang sumbu x
denganamplitudo A dan mewakili gelombang yang dipantulkan sepanjang sumbu x negatif dengan amplitudo B. Pada persamaan (2.45). mewakili penurunan gelombang eksponensial sepanjang sumbu x dalam potensial halang data gelombang pantul dalam potensial halang. Sedangkan pada persamaan (2.59), mewakili gelombang transmisi yang bergerak sepanjang sumbu x dalam daerah III.
(R. Murugeshan, 2007).
2.8.3 EfekTerobosan
Sebagaimana dari prinsip sumur potensial, secara mekanika klasik sebuah elektron tidak dapat menembus penghalang, karena E < E0, tidak memungkinkan
elektron bisa menembus daerah tersebut, sehingga Ek = E – E0 bernilai negatif. Atau
dengan bahasa lain x > 0 merupakan daerah larangan yang tidakmungkin di temukanelektron, yang terjadi hanya dipantulkan kembali. Namun nyatanya, secara kuantum pada sisi setelah penghalang tersebut, masih bisa ditemukan elektron. Teori kuantum ini juga meramalkan kemungkinan elektron menembus suatu penghalang yang hanya terjadi didunia mikro. Fenomena inilah yang dikenal dengan gejala penerobosan.
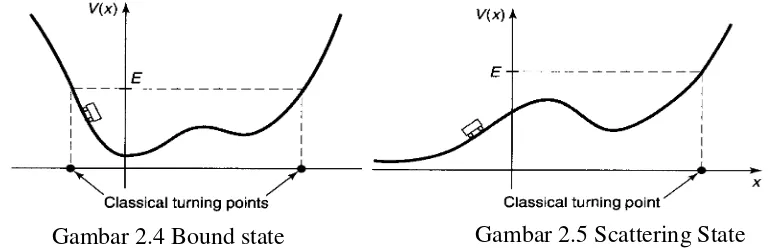
Dalam mekanika klasik sebuah potensial tak bergantung waktu satu dimensi dapat memberikan dua jenis gerak yang berbeda. Jika V(x) meningkat melebihi besar
daripada energi total partikel (E) di kedua sisi (gambar 2.4) maka partikel akan terperangkap pada sumur potensial (terguncang bolak-balik) diantara titik balik, tapi tidak dapat melarikan diri. Keadaan partikel tersebut disebut keadaan terikat (bound state). Jika pada sisi lain E > V(x) pada satu sisi atau keduanya, lalu partikel datang dari ketakterbatasan, memperlambat kecepatan atau menambah kecepatan dibawah pengaruh potensial dan kembali ke keadaan tak hingga(gambar 2.5). Keadaan ini di sebut keadaan hamburan (scattering state).
Kita telah menemui dua jenis solusi persamaan schrödinger tak bergantung waktu, yaitu untuk spektrum diskrit dan kontinu. Persamaan Schrödinger ini menerangkan secara tepat pada bound state dan scattering state. Perbedaannya terlihat sangat jelas pada wilayah kuantum karena fenomena tunneling ini mengijinkan partikel untuk menerobos melalui dinding potensial yang terbatas (finite), jadi satu-satunya permasalahannya adalah pada saat potensial bernilai tak hingga. (Einsberg, 1970)
2.9Program Komputer
Program komputer adalah suatu urutan instruksi yang disusun secara sistematis dan logis dengan menggunakan bahasa pemrograman untuk menyelesaikan suatu masalah. Program komputer merupakan contoh perangkat lunak komputer yang menuliskan aksi komputasi yang akan dijalankan oleh komputer. Komputasi ini biasanya dilaksanakan berdasarkan suatu algoritma atau urutan perintah tertentu. Urutan perintah (algoritma) merupakan suatu perangkat yang sudah termasuk dalam program komputer tersebut. Tanpa algoritma tersebut, program komputer tidak dapat berjalan dengan baik. Program komputer dapat digunakan untuk perhitungan numerik dan eksperimen simulasi melalui pendekatan fisika komputasi dengan menggunakan pemrograman MATLAB.
Matlab adalah singkatan dari Matrix Laboratory, suatu perangkat lunak matematis yang menggunakan vector dan matriks sebagai elemen data utama. Matlab merupakan bahasa pemrograman yang hadir dengan fungsi dan karakteristik yang berbeda dengan bahasa pemrograman lain yang sudah ada lebih dahulu seperti Delphi, Basic, maupun C++. Matlab merupakan bahasa pemrograman level tinggi yang dikhususkan untuk kebutuhan komputasi teknis, visualisasi dan pemrograman seperti komputasi matematik, analisis data, pengembangan algoritma, simulasi, dan pemodelan serta grafik-grafik tertentu. (Aris, 2006)
Matlab menyediakan beberapa instruksi dasar yang memungkinkan pengguna membuat program atau fungsi, antara lain sebagai berikut:
1. Statement if : untuk mengeksekusi sekumpulan instruksi yang diisyaratkan bernilai benar.
2. Statement switch : untuk mengeksekusi sekumpulan instruksi dari suatu ekspresi atau variable.
3. Statement for : digunakan untuk mengulang sekumpulan instruksi.
4. Statement while : untuk mengerjakan sekelompok perintah yang diulang secara tidak terbatas.
5. Statement break : untuk keluar lebih awal dari suatu loop for dan while jika kondisi yang sudah diinginkan sudah tercapai.
6. Grid danlegend : untuk member grid dan legend pada grafik.