Pemodelan Linier Sebaran Gamma dan Pareto Terampat dengan Regularisasi L1 pada Statistical Downscaling untuk Pendugaan Curah Hujan Bulanan Aplikasi Pada Pemodelan Curah Hujan di Kabupaten Indramayu

PEMODELAN LINIER SEBARAN GAMMA DAN PARETO

TERAMPAT DENGAN REGULARISASI L

1

PADA

STATISTICAL DOWNSCALING

UNTUK PENDUGAAN CURAH

HUJAN BULANAN

Aplikasi Pada Pemodelan Curah Hujan di Kabupaten Indramayu

AGUS MOHAMAD SOLEH

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

PERNYATAAN MENGENAI DISERTASI DAN SUMBER

INFORMASI SERTA PELIMPAHAN HAK CIPTA*

Dengan ini saya menyatakan bahwa disertasi berjudul Pemodelan Linier Sebaran Gamma dan Pareto Terampat dengan Regularisasi L1 pada Statistical

Downscaling untuk Pendugaan Curah Hujan Bulanan adalah benar karya saya

dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir disertasi ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

Bogor, September 2015

Agus Mohamad Soleh

AGUS MOHAMAD SOLEH. Pemodelan Linier Sebaran Gamma dan Pareto Terampat dengan Regularisasi L1 pada Statistical Downscaling untuk Pendugaan

Curah Hujan Bulanan. Dibimbing oleh AJI HAMIM WIGENA, ANIK DJURAIDAH dan ASEP SAEFUDDIN.

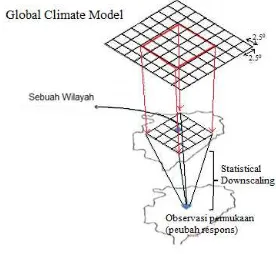
Pemodelan Statistical Downscaling (SDS) merupakan suatu teknik dalam klimatologi yang menggunakan pemodelan statistika untuk menganalisis hubungan antara data iklim skala besar (global) dengan data iklim skala kecil (lokal). Pemodelan SDS umumnya melibatkan kovariat skala besar terkondisi buruk

(ill-conditioned) (tidak bebas/korelasi tinggi). Teknik-teknik seperti pereduksian

dimensi, seleksi peubah, dan penyusutan koefisien (shrinkage) dapat digunakan untuk mengatasinya. Teknik regularisasi L1 merupakan salah satu teknik yang

dikembangkan untuk menangani masalah kovariat terkondisi buruk oleh Tibshirani (1996) dengan cara seleksi peubah dan penyusutan koefisien. Penelitian yang dilakukan merupakan kajian tentang penggunaan dan pengembangan teknik regularisasi L1 pada model linier untuk mendapatkan solusi bagi permasalahan

kovariat terkondisi buruk dalam pemodelan SDS. Dalam hal ini peubah kovariat mengambil nilai dari luaran model GCM dari CMIP5 dan data observasi GPCP versi 2.2 pada grid domain 7_×7 yang ditetapkan di atas wilayah Kabupaten Indramayu. Pemodelan yang digunakan merupakan pemodelan linier berbasis sebaran, yaitu respons diasumsikan berasal dari sebaran normal, sebaran Gamma dan sebaran pareto terampat.

Penelitian dibagi ke dalam dua kelompok, yaitu kelompok kajian pengembangan teknik regularisasi L1untuk pemodelan linier sebaran Gamma dan

sebaran pareto terampat, dan kelompok kajian aplikasi pemodelan SDS untuk pendugaan curah hujan bulanan menggunakan pemodelan linier. Pengembangan teknik regularisasi L1 dilakukan dengan menggunakan teknik optimisasi umum

Nelder-Mead. Pada model linier terampat sebaran Gamma, nilai awal parameter diduga melalui teknik iterative reweighted least square (IRWLS), sedangkan pada model linier sebaran pareto terampat nilai awal diduga menggunakan

metode IRWLS dan

√

6var(y)

π . Teknik optimisasi Nelder-Mead pada pemodelan

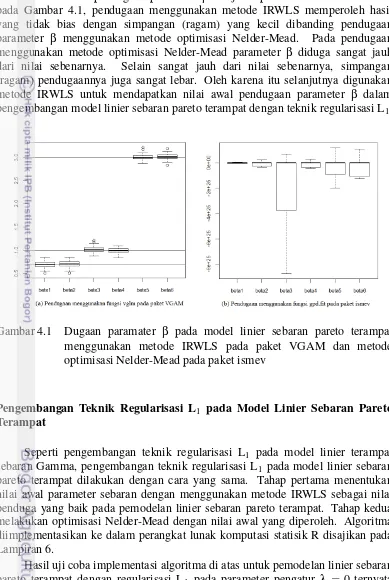
linier terampat sebaran Gamma berhasil mendapatkan penduga parameter yang konvergen, tetapi pada pemodelan linier sebaran pareto terampat penduga parameter tidak konvergen ke parameter sebenarnya dengan menggunakan data simulasi.

Simulasi dilakukan untuk membandingkan teknik regularisasi L1 dengan

dengan 3 nilai parameter simpangan baku (σ) untuk sebaran normal dan 3 nilai parameter bentuk/shape (ξ) untuk sebaran Gamma dan pareto terampat. Hasil simulasi menunjukkan teknik regularisasi L1 memberikan hasil pendugaan yang

lebih baik atau relatif sama baiknya dibanding dengan analisis komponen utama. Teknik lasso (regresi dengan regularisasi L1) pada aplikasi pemodelan SDS

memberikan hasil yang lebih baik dalam memprediksi curah hujan di 11 pos hujan di Indramayu dan sekitarnya dibanding dengan metode regresi komponen utama. Pada pendugaan curah hujan menggunakan model linier terampat sebaran Gamma, penambahan peubah dummy bulan mempengaruhi pendugaan curah hujan secara signifikan. Beberapa hasil menunjukkan nilai RMSE dari pendugaan model linier terampat sebaran Gamma memberikan nilai yang lebih kecil dibanding dengan pendugaan dari regresi komponen utama. Tetapi dalam pendugaan nilai ekstrim di atas batas nilai pencilan, pemodelan linier terampat sebaran Gamma memberikan nilai RMSE yang lebih kecil di banding regresi komponen utama. Pada kasus ini, curah hujan ekstrim bulanan lebih baik diduga menggunakan nilai dugaan pada quantil 0.90 dan 0.95.

Model linier sebaran pareto terampat memberikan nilai RMSE yang lebih besar pada pendugaan rataan curah hujan bulanan di atas nilai ambang, dibanding dengan model linier terampat sebaran Gamma atau metode regresi komponen utama. Tetapi, pada pendugaan curah hujan bulanan di atas pencilan, model linier sebaran pareto terampat memberikan hasil sama baiknya dibanding dua metode lainnya dengan menggunakan pendugaan quantil 0.90 dan 0.95.

Kata kunci: regularisasi L1,statistical downscaling, model linier terampat sebaran

AGUS MOHAMAD SOLEH. Gamma and Generalized Pareto Distribution Linear Modeling with L1 Regularization to Predict Montly Rainfall in Statistical

Downscaling. Supervised by AJI HAMIM WIGENA, ANIK DJURAIDAH and ASEP SAEFUDDIN.

Statistical Downscaling (SDS) modeling is a technique in climatology that uses statistical model to analyze the relationship between large-scale data (global) and small-scale (local) data. SDS models might involve large-scale ill-conditioned covariates (not independent/high correlation). Techniques such as dimensional reduction, selection, and shrinkage could be use to solve this problems. L1

regularization is a technique for selection and shrinkage was proposed by Tibshirani (1996). This research is about the development and the use of L1 regularization

technique on linear model to obtain a solution for ill-conditioned covariates problem faced in SDS modeling. Covariates were taken from the output of CMIP5 and the GPCP version 2.2 in the 7_×7 gridded domain above Indramayu. Linear modeling based on distribution was used in this research using normal, Gamma and generalized pareto distribution.

This study consists of two parts, namely the development of L1regularization

technique for linear modeling with Gamma and generalized pareto distribution, and application of monthly rainfall prediction using SDS modeling. L1 regularization

technique development was done by using the general Nelder-Mead optimization technique. Initial parameter values for the generalized linear model with Gamma distribution estimated by iterative reweighted least squares (IRWLS), while for the

linear modeling with generalized pareto distribution used IRWLS and

√

6var(y)

π .

The parameters estimated for generalized linear modeling with Gamma distribution was convergent to the actual values, but for the linear modeling with generalized pareto distribution did not converge using data of simulations.

Simulations were performed to compare prediction of responses between L1

regularization technique and principal component analysis. Three scenarios were based on covariates, the coefficient of βj and distribution of responses scenarios. Two covariates scenarios were used in this study, namely observational data of GPCP version 2.2 and the outputs of CMIP5. The coefficient ofβjscenarios were taken from the combination of<1; 0 and>1 and a uniform of βj equal to<1. Normal, Gamma and generalized pareto distributions were used for distribution of responses scenario with different parameters, namely 3 different standard deviation (σ) for normal distribution and 3 different shape (ξ) parameters for Gamma and generalized pareto distribution. The simulation showed that L1 regularization

technique provide better prediction or as good as principal component analysis. On SDS modeling application, lasso technique (regression with L1

variables (month) to predict monthly rainfall using generalized linear model with Gamma distribution gave significant impact. Some results of generalized linear model with Gamma distribution showed a smallest root mean square error (RMSE) than principal component regression. However, all of models from generalized linear model with Gamma distribution gave a smaller RMSE values for extreme value prediction above outliers. In this case, quantile 0.90 and 0.95 were better for prediction of extreme monthly rainfall.

Pareto distribution linear models gave RMSE values greater than the Gamma distribution linear models or principal component regression on monthly rainfall average prediction above a threshold. However, the prediction of monthly rainfall above an outlier, the generalized pareto distribution linear models gave smallest RMSE as good as Gamma distribution generalized linear models and principal component regression using quantile 0.90 and 0.95.

Keywords: L1 regularization, statistical downscaling, generalized linear model

Hak Cipta Dilindungi Undang-Undang

Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB

PEMODELAN LINIER SEBARAN GAMMA DAN PARETO

TERAMPAT DENGAN REGULARISASI L

1

PADA

STATISTICAL DOWNSCALING

UNTUK PENDUGAAN CURAH

HUJAN BULANAN

Aplikasi Pada Pemodelan Curah Hujan di Kabupaten Indramayu

AGUS MOHAMAD SOLEH

Disertasi

sebagai salah satu syarat untuk memperoleh gelar Doktor

pada

Program Studi Statistika

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

Dr. Anang Kurnia, MSi

Judul Disertasi : Pemodelan Linier Sebaran Gamma dan Pareto Terampat dengan Regularisasi L1 pada Statistical Downscaling untuk

Pendugaan Curah Hujan Bulanan. Aplikasi Pada Pemodelan Curah Hujan di Kabupaten Indramayu

Nama : Agus Mohamad Soleh NIM : G161100021

Disetujui oleh

Komisi Pembimbing

Dr Ir Aji Hamim Wigena, MSc Ketua

Dr Ir Anik Djuraidah, MS Prof Dr Ir Asep Saefuddin, MSc

Anggota Anggota

Diketahui oleh

Ketua Program Studi Statistika Dekan Sekolah Pascasarjana

Dr Ir I Made Sumertajaya, MSi Dr Ir Dahrul Syah, MScAgr

PRAKATA

Puji dan syukur penulis panjatkan ke hadirat Allah SWT atas segala karunia-Nya sehingga disertasi ini dapat diselesaikan dengan baik. Tema yang dipilih dalam penelitian ini adalah pengembangan metode pemodelan linier, dengan judul ”Pemodelan Linier Sebaran Gamma dan Pareto Terampat dengan Regularisasi

L1padaStatistical Downscalinguntuk Pendugaan Curah Hujan Bulanan. Aplikasi

Pada Pemodelan Curah Hujan di Kabupaten Indramayu”.

Terima kasih penulis ucapkan kepada Bapak Dr Ir Aji Hamim Wigena, MSc, Ibu Dr Ir Anik Djuraidah, MS dan Bapak Prof Dr Ir Asep Saefuddin, MSc selaku pembimbing, Dr Agus Salim (La Trobe University Australia) selaku pendamping/mentor selama program Sandwich-like yang telah banyak memberi bantuan dalam penelitian ini, Bapak Dr. Ir. Dodo Gunawan, DEA dari BMKG dan Bapak Dr. Anang Kurnia, MSi selaku penguji luar komisi pembimbing yang banyak memberikan masukan berharga untuk disertasi ini. Di samping itu, penghargaan penulis sampaikan kepada Bapak Urip Haryoko dari BMKG yang membantu dalam penyediaan data curah hujan di Kabupaten Indramayu, pak Hari Wijayanto selaku ketua departemen yang memberikan izin untuk studi S3, Dian Kusumaningrum & Utami Dyah Syafitri yang membantu dalam terjemahan bahasa Inggris, Bagus Sartono & Prof. Noer Azam Achsani yang memberikan semangat dan informasi berharga sebagai bekal hidup di luar negeri dalam program Sandwich-like, dan Pak Heri yang banyak membantu dalam pengurusan administrasi. Terima kasih juga penulis ucapkan kepada teman sejawat di Departemen Statistika IPB yang telah banyak membantu dan mendorong penulis untuk menyelesaikan studi S3, teman kuliah di S3: pak Setyono dan rekan-rekan mahasiswa pasca Program Studi Statistika & Statistika Terapan IPB. Terakhir, ungkapan terima kasih juga disampaikan kepada seluruh keluarga penulis: istri dan anak, kedua orang tua penulis, ibu mertua, kakak & kakak ipar, keponakan-keponakan atas segala dukungan, do’a dan kasih sayangnya.

Semoga karya ilmiah ini bermanfaat.

Bogor, September 2015

DAFTAR ISI

DAFTAR TABEL vii

DAFTAR GAMBAR viii

DAFTAR LAMPIRAN x

DAFTAR ISTILAH xi

1 PENDAHULUAN 1

Latar Belakang 1

Road MapPenelitian 3

Rumusan Permasalahan 5

Tujuan Penelitian 6

Manfaat Penelitian 6

Ruang Lingkup Penelitian 7

Kebaruan/Novelty 8

2 REGRESI LINIER DENGAN REGULARISASI L1 9

Pendahuluan 9

Tinjauan Pustaka 9

Pendugaan Parameter dengan Metode Iterasi 12 Perbandingan Teknik Regularisasi L1dengan Analisis Komponen Utama 14

Hasil dan Pembahasan 17

Simpulan 19

3 MODEL LINIER TERAMPAT SEBARAN GAMMA DENGAN

REGULARISASI L1 21

Pendahuluan 21

Model Linier Terampat dengan Respons Sebaran Gamma 21

Pendugaan Parameter 22

Perbandingan Teknik Regularisasi L1dengan Analisis Komponen Utama 23

Hasil dan Pembahasan 25

Simpulan 28

4 MODEL LINIER SEBARAN PARETO TERAMPAT 29

Pendahuluan 29

Perbandingan Metode IRWLS dengan Metode Optimisasi Nelder-Mead 30

Simpulan dan Saran 32

5 APLIKASI MODEL LINIER PADASTATISTICAL DOWNSCALING 35

Pendahuluan 35

Model Prediksi Curah Hujan di Pos Hujan Indramayu 36

Model Proyeksi Curah Hujan Ekstrim pada 3 Zona Musim (ZOM)

Indramayu 51

Simpulan 60

6 PEMBAHASAN UMUM 63

Perbandingan Model Linier untuk Pendugaan Respons dari Sebaran

Berbeda 63

7 SIMPULAN DAN SARAN 67

Simpulan 67

Saran 68

DAFTAR PUSTAKA 69

DAFTAR TABEL

2.1 Proporsi keragaman kumulatif untuk luaran GCM CMIP5 dan data

observasi GPCP 16

5.1 Banyaknya parameter model yang diduga menggunakan metode

lasso di luar intersep 45

5.2 Nilai statistik RMSE dan RMSEP menggunakan validasi silang 10-fold untuk setiap penduga model menggunakan data observasi

model GPCP versi 2.2 46

5.3 Koefisien korelasi antara nilai respons dengan dugaan setiap teknik 46 5.4 Nilai RMSE untuk setiap model pendugaan 48 5.5 Koefisien korelasi antara nilai respons dengan dugaan model regresi

komponen utama, model linier terampat sebaran Gamma dengan analisis komponen utama dan regularisasi L1 48

5.6 Banyaknya parameter model yang diduga menggunakan metode model linier terampat sebaran Gamma dengan regularisasi L1

termasuk peubah dummy di luar intersep 49 5.7 Nilai RMSE untuk setiap model pendugaan curah hujan ekstrim

menggunakan metode regresi komponen utama 50 5.8 Nilai RMSE untuk setiap model pendugaan curah hujan ekstrim

menggunakan metode model linier terampat sebaran Gamma dengan analisis komponen utama 51 5.9 Nilai RMSE untuk setiap model pendugaan curah hujan ekstrim)

menggunakan metode model linier terampat sebaran Gamma

dengan regularisasi L1 51

5.10 Nilai RMSE pendugaan model linier untuk masing-masing ZOM 59 5.11 Koefisien korelasi antara respons dengan nilai dugaan pada setiap

model linier untuk masing-masing ZOM 59 5.12 Nilai RMSE untuk pendugaan model linier curah hujan di atas

pencilan setiap ZOM menggunakan model linier sebaran pareto terampat, regresi komponen utama (RKU), dan model linier

terampat sebaran Gamma 60

1.1 Roadmap penelitian pemodelan SDS yang diusulkan dengan

literatur terbaru 4

1.2 Kerangka penelitian yang dilakukan 8

2.1 Grafik screeplot hasil analisis komponen utama luaran model CMIP5 dan data observasi GPCP versi 2.2 15 2.2 Hasil RMSE dengan kovariat data observasi GPCP 18

3.1 Hasil RMSE dengan kovariat data observasi GPCP 26 3.2 Hasil RMSE dengan kovariat data luaran CMIP5 27

4.1 Dugaan paramater β pada model linier sebaran pareto terampat menggunakan metode IRWLS pada paket VGAM dan metode optimisasi Nelder-Mead pada paket ismev 32

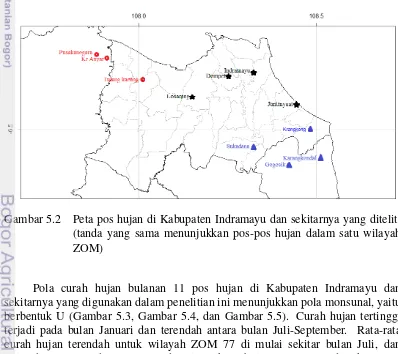
5.1 PemodelanStatistical Downscaling(SDS) 36 5.2 Peta pos hujan di Kabupaten Indramayu dan sekitarnya yang diteliti

(tanda yang sama menunjukkan pos-pos hujan dalam satu wilayah

ZOM) 37

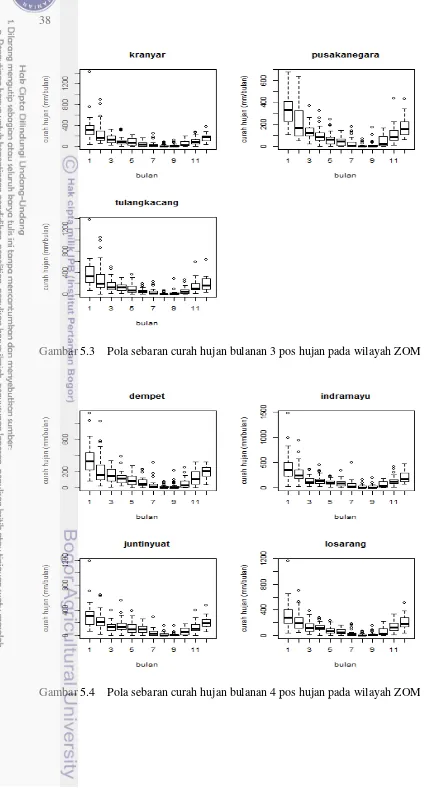
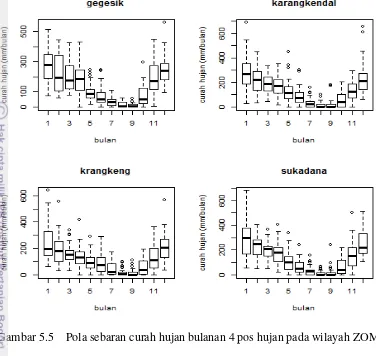
5.3 Pola sebaran curah hujan bulanan 3 pos hujan pada wilayah ZOM 77 38 5.4 Pola sebaran curah hujan bulanan 4 pos hujan pada wilayah ZOM 78 38 5.5 Pola sebaran curah hujan bulanan 4 pos hujan pada wilayah ZOM 79 39 5.6 Domain grid kovariat yang digunakan dalam penelitian 40 5.7 Karakteristik spasial dua komponen utama kovariat GPCP versi 2.2 40 5.8 Grafik plotCpMallows dengan banyaknya parameter yang diduga

untuk pos hujan di wilayah ZOM77 dengan kovariat data observasi

GPCP 44

5.9 Boxplot curah hujan bulanan untuk setiap Zona Musim (ZOM) di Indramayu dan sekitarnya 53 5.10 Grafikmean residual life plotuntuk setiap ZOM 55 5.11 Grafik nilai ambang dan penduga parameter sebaran pareto

terampat untuk ZOM 77 56

5.12 Grafik nilai ambang dan penduga parameter sebaran GP untuk

ZOM 78 56

5.13 Grafik nilai ambang dan penduga parameter sebaran pareto

terampat untuk ZOM 79 57

5.14 Grafik plot verifikasi penduga parameter sebaran pareto terampat

untuk ZOM 77 58

5.15 Grafik plot verifikasi penduga parameter sebaran pareto terampat

untuk ZOM 78 58

5.16 Grafik plot verifikasi penduga parameter sebaran pareto terampat

untuk ZOM 79 59

ix

1 Implementasi algoritma metode iterasi regresi linier dengan regularisasi L1dalam perangkat lunak komputasi statistik R

75

2 Hasil RMSE dengan kovariat data luaran CMIP5 76 3 Hasil RMSEP dengan kovariat data luaran GPCP 77 4 Hasil RMSEP dengan kovariat data luaran CMIP5 78 5 Implementasi algoritma model linier terampat sebaran Gamma

dengan regularisasi L1 dalam perangkat lunak komputasi

statistik R

79

6 Implementasi algoritma model linier sebaran pareto terampat dengan regularisasi L1 dalam perangkat lunak komputasi

statistik R

81

7 Karakteristik spasial enam komponen utama (KU-3 – KU-8) kovariat GPCP versi 2.2

82

8 Grafik plot Cp Mallows dengan banyaknya parameter yang diduga untuk pos hujan di wilayah ZOM 78 dan ZOM 79 dengan kovariat data observasi GPCP

83

9 Karakteristik spasial tiga komponen utama (KU) kovariat CMIP5

84

10 Perbandingan RMSE model dengan respons sebaran normal pada kovariat data luaran CMIP5

85

11 Perbandingan RMSE model dengan respons sebaran Gamma pada kovariat data observasi GPCP

86

12 Perbandingan RMSE model dengan respons sebaran Gamma pada kovariat data luaran CMIP5

87

13 Perbandingan RMSE model dengan respons sebaran pareto terampat pada kovariat data observasi GPCP

88

14 Perbandingan RMSE model dengan respons sebaran pareto terampat pada kovariat data luaran CMIP5

89

DAFTAR ISTILAH

AKU : Analisis Komponen Utama (Principal

Component Analysis)

GCM : General Circulation Models

GLM : generalized linear model/model linier terampat,

suatu rampatan model-model linier dengan respons dari keluarga sebaran eksponensial

ill-conditioned : kovariat terkondisi buruk akibat adanya kolinier

atau korelasi tinggi

IRWLS : Iteratively Re-Weighted Least Square, suatu algoritma untuk mendapatkan solusi penduga koefisien ˆβppada model linier

Kovariat : Peubah bebas/peubah penjelas/peubah prediktor

Lasso : least absolute shrinkage and selection

operator/ regresi dengan regularisasi L1

MKT : metode kuadrat terkecil/(least square method) Model linier terampat : lihat generalized linear model

regularisasi L1 : pemberian kendala dari norm L1 yaitu

∑pj=1|βj| ≤ t, t ≥ 0 pada fungsi tujuan pemodelan linier

RKU : Regresi Komponen Utama/Regresi linier ganda dengan kovariat skor komponen utama

RMSE : Root Mean Square Error, rataan dari kuadrat

simpangan nilai respons dengan nilai dugaan pada data yang digunakan untuk menduga model

RMSEP : Root Mean Square Error Prediction, rataan dari kuadrat simpangan nilai respons dengan nilai dugaan pada data validasi

SDS : Statistical Downscaling

sebaran pareto terampat : generalized pareto distribution

sebaran GP : sebaran pareto terampat

shrinkage : Penyusutan penduga koefisien parameter dalam

model linier ke arah 0

1 PENDAHULUAN

Latar Belakang

Pemodelan Statistical Downscaling (SDS) merupakan suatu teknik dalam klimatologi yang menggunakan pemodelan statistika untuk menganalisis hubungan antara data skala besar (global) dengan data skala kecil (lokal) (Benestad et al.

2008). Metode ini relatif baru walaupun perkembangan penerapan pendugaan menggunakan statistika dalam klimatologi sudah dimulai sejak Klein tahun 1948 (dalam Benestadet al.(2008)). Penggunaan istilah SDS merujuk pada keberadaan model iklim global yang direpresentasikan dengan luaran General Circulation

Model (GCM) sebagai representasi data skala besar untuk pendugaan kasar iklim

lokal seperti curah hujan pada suatu wilayah yang merepresentasi data skala kecil. GCM merupakan model numerik yang menghasilkan sejumlah data dari berbagai parameter iklim seperti presipitasi, temperatur, dan kelembaban untuk keperluan pendugaan iklim. Model GCM merepresentasikan cara kemungkinan terbaik mensimulasi kondisi iklim skala-besar dan memproyeksikan perubahan iklim ke depan akibat pengaruh kekuatan (forcing) yang diketahui seperti pengaruh gas rumah kaca. Kemampuan untuk menduga skala kecil menggunakan GCM sangat terbatas karena resolusi spasial dalam GCM umumnya kasar (_± 300 km

×300 km).

Pengembangan model prediksi curah hujan menggunakan model SDS berbasis GCM sudah banyak dilakukan di IPB seperti dalam Wigena (2006) dan Sutikno (2008). Kajian lain menggunakan SDS di antaranya menggunakan arsitektur jaringan syaraf (neural network) (Buonoet al. 2010), regresi kontinum

(continuum regression) dengan pra-pemrosesan PCA (Sutikno et al. 2010),

Empirical Orthogonal Function/Principal Component (EOF/PC) dengan regresi

linier;Maximum Covariance Analysis(MCA); dan analisis korelasi kanonik (CCA) (Vimontet al.2010), dan teknikpartial least square(PLS) sebagai alternatif dalam pemodelan SDS (Wigena 2011).

Pemodelan SDS menggunakan luaran GCM melibatkan banyak peubah yang tidak bebas (korelasi tinggi/data terkondisi buruk (ill-conditioned)). Teknik-teknik seperti pereduksian dimensi, seleksi peubah, dan penyusutan koefisien (shrinkage) dapat digunakan dalam pendugaan parameter untuk mengatasinya. Analisis komponen utama (principal component analysis) merupakan metode yang umum digunakan di dalam pemodelan pada data dengan kondisi buruk ini. Hammamiet al. (2012) dan Gao et al. (2014) menggunakan teknik baru, yaitu menggunakan metode lasso (least absolute shrinkage and selection operator) untuk pemodelan SDS yang diperbandingkan dengan metode regresi bertatar (stepwise regression).

Metode lasso dikembangkan oleh Tibshirani (1996), digunakan dalam seleksi peubah dan menyusutkan koefisien parameter dalam regresi linier, yaitu dengan cara memberikan penalti yang disebut regularisasi L1. Regularisasi L1adalah pemberian

kendala∑p_j=1|βj| ≤t, t≥0 pada fungsi tujuan pemodelan seperti meminimumkan jumlah kuadrat sisaan pada kuadrat terkecil. Penambahan regularisasi L1 ini

pada metode regresi bertatar dan penduga parameter yang stabil seperti pada regresi gulud (ridge regression). Selain itu, metode lasso masih dapat digunakan pada kasus n_≪p, dalam hal ini n adalah banyaknya observasi dan p adalah banyaknya kovariat, yang tidak dapat dilakukan apabila menggunakan metode regresi bertatar ataupun regresi gulud.

Pola curah hujan di Indonesia memiliki karakteristik berbeda untuk beberapa wilayah yang ditentukan oleh banyak faktor, seperti letak geografis yang berada di antara dua benua dan dua samudera, kejadian ENSO (El-Ni˜no Southern Oscilation), dan kejadianIndian Ocean Dipole(IOD) (As-syakur dan Prasetia 2010). Aldrian dan Susanto (2003) mengidentifikasi tiga wilayah curah hujan dominan (A, B dan C) di Indonesia yang memiliki karakteristik berbeda. Wilayah A meliputi bagian selatan Sumatera sampai kepulauan Timor, bagian selatan Kalimantan, Sulawesi bagian selatan dan sebagian Papua, Wilayah B meliputi bagian utara Sumatera dan bagian utara Kalimantan, dan Wilayah C meliputi Maluku dan Sulawesi bagian utara.

Pola curah hujan di Kabupaten Indramayu termasuk ke dalam pola curah wilayah A (seperti didefinisikan oleh Aldrian dan Susanto (2003)). Pemodelan SDS untuk pendugaan curah hujan di wilayah A yang dilakukan oleh Vimont et al. 2010, pada umumnya sudah cukup baik dalam menduga curah hujan periode Mei-Desember dan tidak baik pada periode Januari-April. Vimont et al. 2010 menggunakan tiga metode dalam pendugaan, yaitu regresi dengan Empirical

Orthogonal Function/Principal Component(EOF/PC), Analisis Korelasi Kanonik

(CCA) dan Analisis Peragam Maksimum (MCA). Pada periode bulan Januari-April merupakan puncak tertinggi terjadinya curah hujan sehingga terdapat kemungkinan terjadinya curah hujan ekstrim. Oleh karena itu pendekatan pemodelan SDS menggunakan pemodelan respons sebaran nilai ekstrim diduga akan memberikan pendugaan yang lebih baik.

Curah hujan ekstrim sebagai respons pada pemodelan tidak dapat didekati dengan pemodelan sebaran normal. Stephenson et al. (1999) melakukan pendugaan curah hujan ekstrim di India pada hari-basah (wet-day) dengan menggunakan sebaran Gamma dan Weibull yang memberikan nilai dugaan yang lebih baik. Menurut Das (1955) (di dalam Krishnamoorthy 2006), sebaran Gamma dipostulatkan dalam aplikasi curah hujan (presipitasi) dikarenakan presipitasi terjadi hanya ketika partikel air dapat terbentuk di sekitar debu dengan massa yang cukup, dan waktu tunggu untuk terjadinya akumulasi debu mirip dengan aspek waktu tunggu sebaran Gamma secara implisit. Oleh karena itu penggunaan model respons menggunakan sebaran Gamma diperkirakan akan mendapatkan pendugaan yang lebih baik untuk menduga curah hujan ekstrim.

Beberapa kajian mengenai curah hujan ekstrim menggunakan pemodelan SDS sudah dilakukan seperti menggunakan metode Artificial Neural Network

(Olsson et al. 2001, Begueria dan Vicente-Serrano 2006), regresi kuantil tersensor (Friederichs dan Hense 2007), analisis korelasi kanonik (Busuioc et al. 2008), dan teori nilai ekstrim dengan menggunakan suatu nilai di atas ambang (Peak Over Thresshold/POT) untuk pemodelan sebaran pareto terampat

(Generalized Pareto Distribution/GPD) serta Blok Maksima untuk pemodelan

3

salah satu pos hujan di Kabupaten Indramayu menggunakan regresi kuantil.

Aplikasi pemodelan teori nilai ekstrim dalam pemodelan SDS saat ini adalah dengan cara memodelkan periode taraf nilai return respons dengan masing-masing kovariat dalam sebaran GEV atau sebaran GP. Periode taraf nilai

return yang digunakan berdasarkan pada nilai persentil tertentu yang dimodelkan

dengan menggunakan metode regresi linier biasa. Yee dan Stephenson (2007) mengembangkan metode pemodelan linier teori nilai ekstrim (sebaran GEV dan sebaran GP) dengan kovariat yang diimplementasikan dalam metode Vector

Generalized Linear and Aditive Models (VGLM/VGAM). Aplikasi pemodelan

linier teori nilai ekstrim untuk pemodelan SDS menggunakan VGLM umumnya terkendala dalam kovariat yang tidak saling bebas, sama seperti pemodelan menggunakan sebaran Gamma. Permasalahan ini dapat ditangani menggunakan teknik pereduksian dimensi seperti analisis komponen utama (AKU) untuk mendapatkan peubah yang saling bebas. Alternatif lain adalah dengan memberikan regularisasi L1pada fungsi tujuan pendugaan parameter modelnya.

Penelitian ini mengembangkan pemodelan linier dengan sebaran Gamma dan Pareto Terampat menggunakan regularisasi L1 dan menerapkannya dalam

pemodelan SDS untuk curah hujan terutama curah hujan ekstrim di Indonesia. Pemodelan linier dengan respons sebaran Gamma termasuk ke dalam model linier terampat (Generalized Linear Model/GLM). Pengembangan regularisasi L1

dalam pemodelan GLM untuk respons diasumsikan sebaran Binom dan Poisson telah dilakukan oleh Park dan Hastie (2007) dan kemudian Friedman et al.

(2010) mengusulkan metodeCoordinate Descent pada kasus yang sama di dalam pendugaannya. Secara umum untuk mendapatkan solusi dari penerapan regularisasi L1 adalah dengan menggunakan metode optimisasi yang merupakan bagian dari

optimisasi convex (Tibshirani 1996, Boyd dan Vandenberghe 2004).

Road MapPenelitian

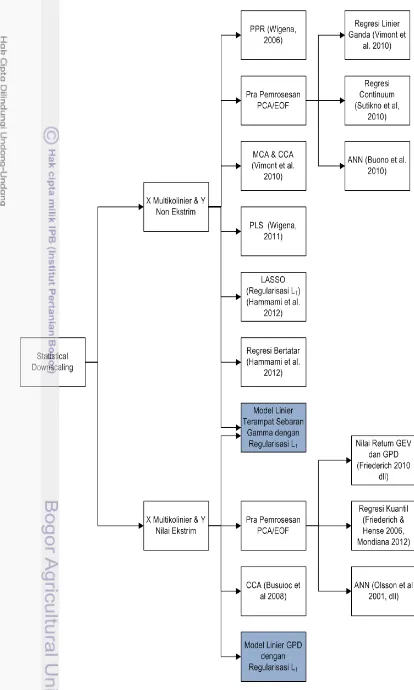
Penelitian ini berdasarkan beberapa penelitian sebelumnya dan kepustakaan yang berkaitan dengan pemodelan SDS seperti telah disampaikan dalam pendahuluan. Road Map pemodelan SDS dan kajian yang diusulkan untuk pemodelan SDS dengan sebaran non-normal disajikan pada Gambar 1.1. Terdapat dua permasalahan dalam pemodelan SDS, yaitu: peubah kovariat yang tidak saling bebas (multikolinier) dan pendugaan respons nilai ekstrim/non-ekstrim. MetodeProjection Pursuit Regression, regresi komponen utama, regresi continuum, jaringan syaraf tiruan, MCA & CCA, PLS, Lasso dan regresi bertatar telah digunakan dalam pemodelan SDS untuk menduga respons non-ekstrim, sedangkan pemodelan dengan pra pemrosesan komponen utama untuk model sebaran GEV dan GP, regresi kuantil, jaringan syaraf tiruan serta CCA telah digunakan untuk pendugaan curah hujan ekstrim. Penelitian yang diusulkan adalah pengembangan teknik pemodelan linier menggunakan model linier sebaran pareto terampat dengan regularisasi L1 untuk menduga curah hujan ekstrim dan non-ekstrim serta

pemodelan linier dengan sebaran pareto terampat dengan regularisasi L1 untuk

5

Rumusan Permasalahan

Kajian tentang pendugaan model curah hujan ekstrim menggunakan teknik pemodelan SDS di Indonesia belum banyak dilakukan. Mondiana (2012) menggunakan regresi kuantil dalam pemodelan SDS untuk menduga curah hujan ekstrim di salah satu pos hujan Kabupaten Indramayu. Penggunaan regresi kuantil untuk eksplorasi pola curah hujan di Kabupaten Indramayu juga sebelumnya telah dilakukan oleh Djuraidah dan Wigena (2011). Teknik pemodelan SDS menggunakan pemodelan sebaran pareto terampat dalam Friederichs (2010) dan Aceroet al.(2010) memodelkan periode taraf nilaireturnsebaran pareto terampat (taraf yang diperkirakan akan melebihi suatu nilai tertentu pada suatu periode) dari respons dengan periode taraf nilai return sebaran pareto terampat dari masing-masing kovariat menggunakan regresi linier ganda.

Pemodelan SDS menggunakan peubah kovariat dari data skala besar seperti luaran GCM. Penggunaan luaran GCM yang memiliki keterkaitan secara spasial dan temporal umumnya terkendala dalam mendapatkan peubah yang saling bebas seperti disyaratkan pada pemodelan linier. Empat teknik telah dikembangkan untuk mengatasi permasalahan ini, yaitu:

1. Teknik seleksi peubah: seperti subset terbaik dan regresi bertatar.

2. Teknik penyusutan (shrinkage): seperti regresi gulud/regresi dengan regularisasi L2.

3. Teknik pereduksian dimensi: seperti regresi komponen utama, dan PLS

(partial least square).

4. Teknik seleksi dan penyusutan: seperti lasso/regresi dengan regularisasi L1.

Teknik seleksi memiliki keunggulan dalam pemilihan kovariat yang mempengaruhi respons, tetapi kelemahannya adalah model yang diduga tidak stabil. Penambahan atau pengurangan dari observasi dapat mengakibatkan model penduga yang berbeda atau kovariat yang terseleksi berbeda. Sebaliknya, teknik penyusutan memiliki keunggulan dalam kestabilan penduga model, tetapi tidak dapat secara otomatis menyeleksi kovariat yang mempengaruhi respons. Keunggulan teknik pereduksian dimensi adalah mempertahankan semua peubah kovariat masuk ke dalam model (menganggap semua kovariat penting). Lasso mempertahankan keunggulan-keunggulan dari teknik seleksi dan penyusutan, yaitu dapat melakukan seleksi peubah yang mempengaruhi respons sekaligus kestabilan dalam menduga model.

Metode pemodelan linier dengan respons sebaran Gamma dan sebaran pareto terampat menggunakan regularisasi L1 sampai saat ini belum memiliki kajian

pengembangannya. Pemodelan linier dari sebaran Gamma dan pareto terampat diduga akan memberikan pendugaan yang lebih baik pada kasus pemodelan SDS untuk curah hujan ekstrim. Penambahan regularisasi L1 pada pemodelan linier

sebaran Gamma diduga akan membuat pendugaan parameter menjadi stabil dan konsisten seperti pada penambahan regularisasi L1di regresi linier (Tibshirani 1996,

Hastieet al.2008, Soleh dan Aunuddin 2013).

Belum semua metode pemodelan linier dikembangkan dengan menggunakan teknik regularisasi L1, seperti model linier terampat sebaran Gamma dan

dengan ekor panjang (menjulur) adalah sebaran curah hujan pada bulan tertentu yang menjadi topik dalam penelitian ini.

Pengembangan teknik regularisasi L1 untuk model linier terampat sebaran

Gamma dan sebaran pareto terampat tidak dapat dilakukan secara deduktif, tetapi menggunakan teknik optimisasi. Teknik optimisasi yang lebih umum adalah metode optimisasi Nelder-Mead yang tidak memerlukan fungsi diferensial dari fungsi tujuannya. Kendala dalam metode optimisasi Nelder-Mead adalah penentuan nilai awal parameter yang akan diduga. Dalam hal ini pemilihan nilai awal parameter yang tidak tepat akan menyebabkan fungsi tujuan konvergen ke maksimum/minimum lokal. Oleh karena itu, penetapan nilai awal yang tepat sangat diperlukan dalam metode optimisasi ini. Pada penelitian ini nilai awal diusulkan dari metode yang menjamin nilai fungsi tujuan pemodelan tanpa regularisasi L1

mencapai maksimum. Dalam pemodelan linier terampat (seperti model untuk respons sebaran Gamma), metode IRWLS (Iteratively Re-Weighted Least Square) menjamin fungsi tujuan dapat dicapai nilai maksimum globalnya apabila konvergen, sedangkan untuk model linier sebaran pareto terampat terdapat dua metode yang digunakan untuk mendapatkan fungsi tujuan maksimum, yaitu metode IRWLS (Yee

dan Stephenson 2007) dan

√

6var(y)

π (Coles 2001).

Hasil pengembangan teknik regularisasi L1 untuk model linier terampat

sebaran Gamma dan model linier sebaran pareto terampat kemudian diaplikasikan untuk menduga curah hujan bulanan. Curah hujan bulanan diduga oleh nilai tengah sebaran dari parameter-parameter sebaran yang diduga oleh model, sedangkan curah hujan ekstrim bulanan diduga menggunakan nilai quantil 0.75, 0.90 dan 0.95 dari parameter-parameter sebaran yang diduga oleh model.

Tujuan Penelitian

Tujuan yang ingin dicapai dalam penelitian ini adalah pengembangan teknik Regularisasi L1 dalam pemodelan linier dengan respons diasumsikan dari sebaran

Gamma dan pareto terampat, yang kemudian diaplikasikan pada pemodelan untuk menduga curah hujan bulanan dan curah hujan ekstrim bulanan di beberapa pos hujan dan Zona Musim (ZOM) Kabupaten Indramayu dan sekitarnya. Secara rinci tujuan penelitian ini adalah:

1. Mengkaji pendugaan curah hujan dengan model regresi regularisasi L1

(lasso).

2. Mengembangkan teknik regularisasi L1 untuk model linier terampat sebaran

Gamma dan mengaplikasikan pada pendugaan model curah hujan bulanan dan curah hujan ekstrim.

3. Mengembangkan teknik regularisasi L1 untuk model linier sebaran pareto

terampat dan mengaplikasikan pada pendugaan model curah hujan ekstrim bulanan.

Manfaat Penelitian

7

1. Keilmuan Statistika:

• Memperkaya kajian teknik regularisasi L1 dalam pendugaan model

regresi linier dengan mengembangkan teknik secara iteratif.

• Mengembangkan teknik regularisasi L1 untuk model linier terampat

sebaran Gamma dan model linier sebaran pareto terampat.

• Kajian perbandingan hasil dugaan menggunakan teknik regularisasi L1

dengan analisis komponen utama pada kasus data terkondisi buruk pada respons sebaran normal, sebaran Gamma dan sebaran pareto terampat.

• Menambah road map teknik pemodelan SDS dengan menggunakan teknik regularisasi L1.

2. Klimatologi:

• Memberikan kajian pendugaan terhadap curah hujan dan curah hujan ekstrim bulanan dengan pemodelan SDS melalui pemodelan linier

Ruang Lingkup Penelitian

Penelitian dikelompokkan ke dalam dua kelompok, yaitu kelompok kajian pengembangan teknik regularisasi L1 untuk pemodelan linier sebaran Gamma dan

sebaran pareto terampat, dan kelompok kajian aplikasi pemodelan SDS untuk pendugaan curah hujan bulanan menggunakan pemodelan linier. Pengembangan teknik regularisasi L1 dilakukan dengan menggunakan teknik optimisasi umum

Nelder-Mead dengan nilai awal parameter yang diduga melalui pendugaan metode

IRWLS untuk sebaran Gamma dan pemilihan metode IRWLS atau

√

6var(y)

π untuk

sebaran pareto terampat.

Pada aplikasi hasil pengembangan teknik pemodelan, penelitian dibagi menjadi tiga bagian kajian yang saling berkaitan (Gambar 1.2). Kajian yang dilakukan adalah mengkaji teknik regularisasi L1 dalam pemodelan linier

dibandingkan dengan teknik analisis komponen utama dalam menduga curah hujan bulanan. Pada kajian pertama, curah hujan dimodelkan menggunakan pendugaan model linier yang mengasumsikan sebaran respons berasal dari sebaran normal. Kajian kedua menggunakan pemodelan linier terampat dengan respons sebaran Gamma untuk menduga curah hujan normal dan curah hujan ekstrim bulanan. Terakhir, bagian ketiga, melakukan aplikasi pemodelan sebaran pareto terampat untuk memodelkan curah hujan pada suatu nilai ekstrim.

Data yang digunakan pada penelitian ini adalah data riil, yaitu data curah hujan bulanan sebagai respons dan data skala besar dari luaran GCM atau data observasi dalam bentuk grid sebagai kovariat. Kebaikan teknik yang dibandingkan ditentukan oleh nilaiRoot Mean Square Error(RMSE) terkecil.

Kajian pengembangan pemodelan linier dengan regularisasi L1 untuk

Indramayu dan sekitarnya yang digunakan untuk pemodelan diambil dari periode tahun 1981 - 2014.

Gambar 1.2 Kerangka penelitian yang dilakukan

Kebaruan/Novelty

Penelitian ini dengan ”Pemodelan Linier Sebaran Gamma dan Pareto Terampat dengan Regularisasi L1 pada Statistical Downscaling untuk Pendugaan

Curah Hujan Bulanan” memiliki kebaruan sebagai berikut:

1. Kajian teknik regularisasi L1 dalam pemodelan SDS merupakan suatu

kebaruan di Indonesia. Saat penelitian mulai di awal tahun 2012, penelusuran literatur pemodelan SDS menggunakan teknik regularisasi L1

belum diperoleh dalam jurnal-jurnal internasional. Saat ini baru ada dua literatur yang menggunakan teknik ini, yaitu oleh Hammami et al. (2012) dan Gaoet al.(2014). Terdapat perbedaan metode yang dibandingkan, dalam hal ini Hammamiet al.(2012) dan Gaoet al.(2014) membandingkan teknik regularisasi L1 dengan metode regresi bertatar (stepwise), sedangkan dalam

penelitian ini dibandingkan dengan teknik analisis komponen utama.

2. Pengembangan metode pemodelan linier terampat sebaran Gamma dan pemodelan linier sebaran pareto terampat dengan teknik regularisasi L1

2 REGRESI LINIER DENGAN REGULARISASI L

₁

Pendahuluan

Seleksi peubah merupakan isu penting dalam regresi terutama ketika jumlah kovariat sangat besar dan tidak saling bebas. Tibshirani (1996) mengusulkan teknik lasso (least absolute shrinkage and selection operator), sebuah metode baru yang saat ini populer untuk seleksi peubah dan penyusutan (shrinkage) koefisien penduga parameter. Lasso menambahkan penalti L1 (disebut juga regularisasi

L1) terhadap fungsi tujuan pendugaan model regresi yang menghasilkan dua

keuntungan: seleksi dan penyusutan. Kegunaan dari penyusutan adalah untuk mencegah timbulnya overfit akibat terjadi kolinieritas dari kovariat (Hastie et al.

2008). Pendugaan parameter pada teknik lasso tidak dapat dilakukan dalam bentuk formula tertutup, tetapi menggunakan optimisasiconvex. Tibshirani (1996) menggunakan pemrograman kuadratik, salah satu metode dalam optimisasiconvex

untuk mendapatkan solusi dari lasso dan Efron et al. (2004) mengembangkan metode LAR (Least Angle Regression) yang menghitung jalur (path) koefisien lebih efisien. Bab ini memberikan kajian literatur metode lasso (regresi linier dengan regularisasi L1) dan melakukan simulasi untuk menentukan metode terbaik

dibandingkan dengan metode regresi komponen utama pada data kovariat yang terkondisi buruk.

Metode regresi komponen utama merupakan salah satu metode yang sering digunakan dalam pemodelan linier dengan kovariat terkondisi buruk. Tahap pertama pada metode regresi komponen utama adalah melakukan analisis komponen utama terhadap peubah-peubah kovariat untuk mendapatkan komponen utama/peubah laten yang ortogonal. Tahap kedua adalah memodelkan antara respons dengan skor komponen utama sebagai peubah kovariat. Banyaknya komponen utama yang digunakan dalam pemodelan ditentukan oleh grafik scree plot, proporsi keragaman, dan nilai akar ciri.

Tinjauan Pustaka

Teknik lasso (least absolute shrinkage and selection operator) yang bertujuan mengatasi masalah dalam keakuratan pendugaan dan interpretasi dengan mempertahankan keuntungan-keuntungan metode regresi bertatar (stepwise) dan regresi gulud (ridge) dikembangkan oleh Tibshirani (1996). Pada regresi linier ganda, teknik lasso meminimumkan jumlah kuadrat sisaan dengan memberikan penalti L1 pada koefisien parameternya. Misalkan terdapat vektor input XT =

(x1,x2, . . . ,xp)digunakan untuk memprediksi luaran nilai Yyang berupa bilangan

riil. Model regresi linier memiliki bentuk:

f(X) =β0+

p

∑

j=1

Untuk menduga β = (β0,β1, . . . ,βp)T, metode kuadrat terkecil meminimumkan

jumlah kuadrat sisaan (Hastie et al. 2008), yaitu dengan meminimumkan persamaan:

JKS(β) =

N

∑

i=1

(yi−f(xi))2=

N

∑

i=1

yi−β0−

p

∑

j=1

xi jβj

!2

(2.2)

yang dapat ditulis dalam catatan matriks, dengan X berukuran N_×(p+1) danyyy

adalah vektor-N, sebagai :

JKS(β) = (yyy₋Xβ)T(yyy₋Xβ). (2.3)

JKS(β) minimum didapatkan dengan cara mendiferensialkan JKS(β) terhadapβ secara kalkulus, yang menghasilkan persamaan dalam bentuk:

XTyyy=XTXβ (2.4)

yang disebut sebagai persamaan normal.

Jika XTX adalah matriks berpangkat penuh, maka dugaan β akan menghasilkan solusi unik, yaitu:

ˆ

β= XTX−1

XTyyy. (2.5)

Apabila XTX tidak berpangkat penuh atau mendekati singular, maka ˆβ yang diperoleh menjadi tidak stabil. Regresi gulud diperkenalkan oleh Hoerl dan Kennard (1970) (dalam Draper dan Smith (1998)) diusulkan sebagai salah satu metode untuk menangani ketidakstabilan penduga kuadrat terkecil ini. Regresi gulud memberikan penalti koefisien regresi dalam norm L2 atau secara spesifik

mendugaβdengan meminimumkan JKS(β)dengan kendala:

p

∑

j=1

β2_{j ≤}t, t_≥0. (2.6)

Masalah regresi gulud ini dapat ditulis dengan cara lain dalam bentuk persamaan lagrange yaitu memininumkan jumlah kuadrat sisaan terkendala:

JKS(β,λ) = (yyy₋Xβ)T(yyy₋Xβ) +λ_kβ_k2₂ λ_≥0. (2.7)

Solusi regresi gulud didapat dengan cara yang sama seperti pada metode kuadrat terkecil, yaitu dengan meminimumkan jumlah kuadrat sisaan JKS(β,λ) sehingga memperoleh persamaan dalam bentuk:

XTyyy= (XTX+λI)β. (2.8)

Dengan cara ini dapat dijamin(XTX+λI)selalu berpangkat penuh walaupunXTX

11

terkecil. Solusi yang unik dapat diperoleh dalam bentuk tertutup:

ˆ

βgulud= XTX+λI−1XTyyy. (2.9)

Penduga koefisien yang diperoleh menggunakan metode regresi gulud tidak

equivariant (Hastie et al. 2008), artinya penduga koefisien tersebut tidak dapat

diperbandingkan hasilnya jika peubah asal tidak dibakukan. Oleh karena itu untuk pendugaan ˆβgulud ini sebelumnya disarankan untuk membakukan skala dari peubah asal sehingga memiliki nilai harapan nol dan ragam satu (Hastie et al. 2008). Penduga koefisien regresi hasil dari regresi gulud akan disusutkan ke arah nol seiring dengan peningkatan nilai λ. Tetapi, penyusutan ini tidak dapat dilakukan untuk seleksi peubah secara otomatis dikarenakan secara simultan koefisien yang diduga mungkin tidak bernilai nol.

Tibshirani (1996) mengembangkan metode lasso yang mengubah kendala dalam regresi gulud menjadi dalam bentuk norm L1, yaitu: ∑p_j=1|βi| ≤t atau disebut juga dengan istilah regularisasi L1. Solusi dari lasso yang dituliskan dalam

bentuk persamaan lagrange adalah meminimumkan:

JKS(β,λ) = (yyy₋β0−Xβ)T(yyy−β0−Xβ) +λkβk1. (2.10)

Untuk mendapatkan solusi penduga koefisien tidak dapat diperoleh dalam bentuk tertutup, tetapi harus menggunakan pemrograman kuadratik (Tibshirani 1996) yang merupakan bagian dari optimisasi convex Boyd dan Vandenberghe (2004). Dampak yang terjadi dari pengubahan kendala ini sangat besar, yaitu menyebabkan koefisien menyusut ke arah nol seperti dalam regresi gulud dan beberapa koefisien menghasilkan nilai nol secara tepat.

Ide dasar metode lasso berasal dari Non-negative Garrotte (Breiman 1995) yang meminimumkan fungsi berikut terhadapc=cj:

N

∑

i=1

(yi− p

∑

j=1

cjxi jβˆj)2 dengan kendala cj≥0, p

∑

j=1

cj≤t, (2.11)

dalam hal ini ˆβj adalah penduga kuadrat terkecil biasa. Metode NN-Garrotte ini tidak terdefinisikan ketika p>N (yang bukan merupakan topik panas pada tahun 1995) (Tibshirani 2011). Pada sekitar tahun tersebut, beberapa metode yang mirip dengan lasso telah dikembangkan berdasarkan penalti L1, sepertibridge regression

oleh Frank dan Friedman tahun 1993 dan basis pursuit oleh Chen et al. (1998) (dalam Tibshirani (2011)). Setelah publikasi pertama tahun 1996 sampai tahun 2002, makalah metode lasso dengan pendekatan pemrograman kuadratik ini tidak mendapatkan perhatian. Tetapi setelah tahun 2002, metode lasso mulai menjadi perhatian setelah dikembangkan algoritma lar (Least Angle Regresion) oleh Efron, Hastie, Johnstone dan Tibshirani yang dipublikasikan tahun 2004 (Tibshirani 2011). Efron et al. (2004) mengembangkan algoritma lar yang digunakan untuk menduga model regresi linier dalam bentuk model umum:

E(Y_|X=x) = f(x) =β0+βMφ1(x) +βMφ2(x) +. . .+βMφM(x), (2.12)

lar untuk lasso menghasilkan efisiensi algoritma dalam menduga solusi penduga koefisien lasso dengan komputasi yang lebih cepat dibandingkan pemrograman kuadratik. Selain untuk menduga koefisien lar dan lasso, algoritma lar ini juga dimodifikasi untuk digunakan dalam menduga koefisien regresiforward stagewise

dan regresi bertatar, sehingga kemudian namanya dikenal sebagai lars (untuk lar, lasso,forward stagewisedan regresi bertatar).

Pendugaan Parameter dengan Metode Iterasi

Perhatikan kembali permasalahan lasso sebagai berikut:

arg min

βk (

(y₋β0−

p

∑

k=1

βkxk)T(y−β0−

p

∑

k=1

βkxk) +λ p

∑

k=1

|βk|

)

.

Misalkan f(βk,λ) = (y−∑_kp₌₁βkxk)T(y−∑_kp₌₁βkxk) +λ ∑_kp₌₁|βk|, solusi dari lasso untuk setiap βj diperoleh dengan mendiferensialkan f(βk,λ) terhadap βj sama dengan nol yang akan memberikan teorema sebagai berikut.

Teorema 1: Terdapatλjyang membuat ˆβjbernilai nol, yaitu: λj≥ |2xT_jr₋j|, dalam hal inir₋j=y−∑_k6=jβˆkxk.

Bukti.

∂ ∂βj

f(βk,λ) =0=

∂ ∂βj

(

yTy₋2yT

p

∑

k=1

βkxk+ ( p

∑

k=1

βkxk)T( p

∑

k=1

βkxk) +λ p

∑

k=1

|βk|

)

=₋2yTxj+2xTj p

∑

k=1

βkxk+λsign(βj)

=₋xT_jy+xT_j

p

∑

k=1

βkxk+

λ

2 sign(βj)

=xT_j

p

∑

k=1

βkxk−y

!

+λ

2 sign(βj)

=βjxTjxj+xTj

∑

k6=j

βkxk−y

!

+λ

2 sign(βj)

=βjxTjxj−xTj y−

∑

k6=j

βkxk

!

+λ

2 sign(βj)

Notasi:xT_jxj=kxjk2, sehingga:

=βjkxjk2−xTj y−

∑

k₆=j

βkxk

!

+λ

13

=βj−

xT_j y₋∑k6=jβkxk

kxjk2

+λsign(βj)

2_kxjk2

Misalkanr₋j=y−∑k=6 jβkxk, maka penduga dariβjadalah:

ˆ

βj=

xT_jr₋j

kxjk2 −

λ

2_kxjk2

sign(βj)

Perhatikan λ dan _kxjk2 selalu positif, sedangkan xTjr−j searah tandanya dengan koefisienβj.

Perhatikan daerah sebagai berikut:

• x

T jr−j

kxjk2 > λ

2kxjk2 ⇒sign(βj) bernilai +. Hal ini berimplikasi

ˆ

βj=

xT_jr₋j

kxjk2 −

λ

2_kxjk2

• x

T jr−j

kxjk2 <− λ

2kxjk2 ⇒sign(βj) bernilai -. Hal ini berimplikasi

ˆ

βj=

xT_jr₋j

kxjk2

+ λ

2_kxjk2

• 0 < x

T jr−j

kxjk2 < λ

2kxjk2 ⇒ sign(βj) bernilai +. Hal ini berimplikasi sign( ˆβj)

memiliki tanda - yang berkebalikan dengan sign(βj). Oleh karena itu, maka ˆ

βjsecara asimtotik sama dengan 0

• −2kxλjk2 <

xT_jr₋j

kxjk2 < 0⇒ sign(βj) bernilai -. Hal ini berimplikasi sign( ˆβj)

memiliki tanda + yang berkebalikan dengan sign(βj). Oleh karena itu, maka ˆ

βjsecara asimtotik sama dengan 0.

Sehinggaλj≥ |2xTjr−j|akan membuat ˆβj bernilai nol.

Teorema 2: Terdapat λ minimum yang membuat semua ˆβj bernilai nol, yaituλ=2max(_|xT_jy_|).

Bukti. Berdasarkan fakta bahwa λj ≥ |2xT_jr−j| menghasilkan ˆβj bernilai nol

Dari pembuktian Teorema 1 diperoleh solusi dari dari lasso sebagai berikut:

ˆ

βj=

        

xT_jr₋j

kxjk2 − λ

2kxjk2 ,λ<2x

T jr−j

xT_jr₋j

kxjk2 + λ

2kxjk2 ,−λ>2x

T jr−j 0 ,λ_{≥ |}2xT_jr₋j|

(2.13)

Perhatikan solusi dari lasso tidak dapat dilakukan dengan cara langsung menggunakan formula tersebut, tetapi harus dilakukan secara iterasi karena masing-masing ˆβjtergantung pada ˆβklain. Algoritma untuk solusi iterasi kemudian diusulkan sebagai berikut:

1. Bakukan kovariat (X) 2. Tetapkan i=0, ˆβ0₌₀

3. Untukλ=0 sampaiλ=2max(_|xT_jy_|)

(a) i = i+1

(b) Untuk j=1 sampai p

i. Hitungr₋j=y−∑k6=jβik−1xk

ii. Hitung ˆβj_{menggunakan formula pada Persamaan 2.13.} (c) ulangi (a) dan (b) sampai(βˆi_−βˆi−1_)<ie−6

4. Penduga akhir ˆβditentukan dengan pendekatan validasi silang.

Implementasi algoritma di atas dalam perangkat lunak komputasi statistik R disajikan pada Lampiran 1.

Perbandingan Teknik Regularisasi L1dengan Analisis Komponen Utama

Data

Dua data kovariat terkondisi buruk digunakan dalam kajian ini, yaitu data presipitasi dari luaran GCM, yaitu luaran ensemble dari banyak model CMIP5

(multi-model ensemble Phase 5 Couple Model Intercomparisson Project) dengan

skenario perubahan iklim moderat RCP (Representative Concentration Pathways) 4.5 (Tayloret al.2012) selanjutnya disingkat sebagai CMIP5, dan data presipitasi hasil interpolasi kombinasi data observasi permukaan dan satelit dalam bentuk grid dari GPCP (Global Precipitation Climatology Project) versi 2.2 (Adleret al.2003) selanjutnya disingkat sebagai GPCP.

Pemilihan data kovariat untuk simulasi didasarkan adanya perbedaan karakteristik kedua data CMIP5 dan GPCP, yaitu berdasarkan nilai koefisien korelasi pasangan kovariat dan hasil pereduksian dimensi menggunakan analisis komponen utama. Banyaknya pasangan yang memiliki nilai mutlak korelasi >

15

Analisis komponen utama digunakan sebagai teknik pra pemrosesan untuk mendapatkan peubah-peubah laten yang saling ortogonal dan merupakan kombinasi linier dari kovariat-kovariatnya. Banyaknya peubah laten yang digunakan untuk analisis lanjut ditentukan umumnya oleh minimal dua dari tiga hal berikut, yaitu: grafik screeplot, proporsi keragaman kumulatif dan besarnya nilai ragam yang ditunjukkan oleh akar ciri. Banyaknya komponen utama menggunakan grafik

screeplot ditentukan oleh perubahan ragam yang tidak signifikan (ditunjukkan

oleh grafik batang/plot yang stasioner), sedangkan proporsi keragaman kumulatif umumnya diambil nilai>75%. Pada penelitian ini digunakan proporsi keragaman kumulatif>90% dan nilai akar ciri mengambil nilai yang>1.

Grafikscreeplot yang diperoleh dari luaran GCM CMIP5 dan data observasi GPCP disajikan pada Gambar 2.1. Pada luaran grafik screeplot, baik untuk luaran GCM CMIP5 maupun data observasi GPCP menyarankan untuk mengambil banyaknya peubah laten yang ortogonal sebanyak 3 komponen utama. Terlihat dalam kedua grafik setelah komponen ketiga, keragaman dari komponen keempat dan selanjutnya sudah menuju stabil.

Gambar 2.1 Grafikscreeplothasil analisis komponen utama luaran model CMIP5 dan data observasi GPCP versi 2.2

[image:38.595.61.481.34.842.2]

Tabel 2.1 Proporsi keragaman kumulatif untuk luaran GCM CMIP5 dan data observasi GPCP

Komponen Utama CMIP5 GPCP

Akar Ciri Proporsi Akar Ciri Proporsi

1 13.33 88.14% 16.82 45.87% 2 3.99 96.04% 12.19 69.97%

3 1.60 97.31% 6.44 76.70%

4 1.57 98.53% 5.30 81.24% 5 0.90 98.93% 4.67 84.77% 6 0.85 99.29% 3.71 87.00% 7 0.49 99.41% 3.10 88.56% 8 0.48 99.53% 3.06 90.08%

9 0.37 99.59% 2.78 91.33% 10 0.31 99.64% 2.40 92.26%

Metode

Tahapan kajian perbandingan teknik lasso dengan regresi komponen utama adalah sebagai berikut:

1. Menetapkan skenario parameterβ

Parameterβdigunakan dua skenario, yaitu:

• kombinasi parameter β= 0.7 (perwakilan<1), 0, dan 3.0 (perwakilan

>1) masing-masing sebanyak 16, 17 dan 16.

• βseragam sebesar 0.7 (perwakilan<1) sebanyak 49. 2. Membangkitkan data respons

Data respons dibangkitkan dari sebaran normal dengan menggunakan persamaan y = Xβ+ε, dalam hal ini ε _∼ Normal(0,σ2_{). Tiga nilai σ}

digunakan dalam simulasi yaituσ=1, 5, dan 10. 3. Menduga nilai dugaan dengan teknik lasso

Nilai dugaan dengan teknik lasso digunakan dengan menggunakan model

y=β0+β1x1+. . .+βkxk dalam hal ini k adalah banyaknya kovariat yang terseleksi dengan menggunakan nilai validasi silang terkecil, dan xk adalah data presipitasi ke-k dari data kovariat luaran CMIP5 atau GPCP.

4. Menduga nilai dugaan dengan regresi komponen utama

Nilai dugaan dengan regresi komponen utama digunakan dengan menggunakan model y = β0 +β1KU1+ . . .+ βkKUk dalam hal ini k adalah banyaknya komponen utama, dan KUk adalah data skor komponen utama ke-k dari data kovariat luaran CMIP5 atau GPCP.

5. Proses pembangkitan data dan pendugaan nilai tengah di ulang sebanyak 100 kali

6. Pemilihan Metode Pendugaan Terbaik

Metode pendugaan terbaik ditentukan melalui nilai penduga galat yang terkecil. Nilai Root Means Square Error (RMSE) dan Root Means Square

17

RMSEP merupakan metode untuk mengukur perbedaan antara nilai prediksi dengan nilai aktual yang didefinisikan sebagai berikut:

RMSE atau RMSEP=

s

∑ni=1(Yi−Yˆi)2

n (2.14)

dalam hal ini Yi adalah nilai observasi/aktual, ˆYi adalah nilai dugaan ke-i dan nadalah banyaknya observasi dalam pendugaan. Nilai RMSEP diduga menggunakan teknik validasi silang 10-fold. Kebaikan dari suatu metode ditentukan oleh nilai RMSE dan RMSEP yang paling kecil.

Hasil dan Pembahasan

Untuk menentukan metode mana yang terbaik dalam menangani data kovariat terkondisi buruk dilakukan simulasi data dengan beberapa skenario. Skenario simulasi memperhatikan berbagai kemungkinan yang akan mempengaruhi hasil pendugaan model. Dua karakteristik kovariat digunakan dalam kajian yaitu luaran CMIP5 mewakili data kovariat yang mengandung kolinier tinggi/berkorelasi tinggi dan data observasi GPCP yang mengandung kolinier rendah/tidak banyak yang berkorelasi. Dua kemungkinan nilaiβdalam simulasi ini mewakili dari kombinasi dari tiga nilai yaitu nilai <1, tidak berpengaruh (0), dan nilai >1, dan koefisien

β seragam dengan nilai < 1. Kemungkinan koefisien β seragam > 1 tidak digunakan karena teknik lasso akan menghasilkan penduga kuadrat terkecil (Soleh dan Aunuddin 2013). Peubah respons dalam simulasi dibangkitkan dari sebaran normal dengan 3 kemungkinan nilai simpangan bakuσ=1, 5, dan 10. Oleh karena itu terdapat 12 skenario yang digunakan dalam kajian ini, yaitu kombinasi antara karakteristik kovariat, kemungkinan nilaiβ, dan simpangan baku dari respons.

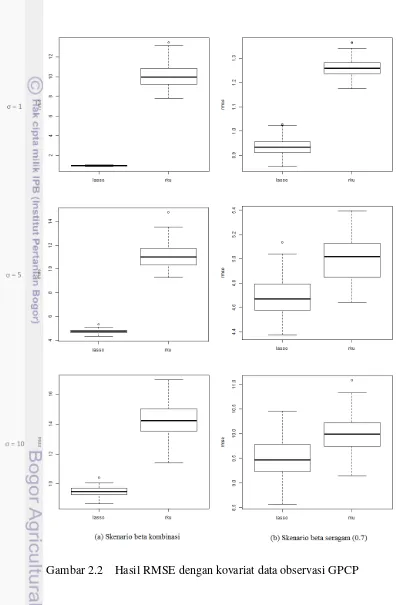
Sebaran hasil nilai statistik RMSE untuk kovariat dari GPCP disajikan pada Gambar 2.2. Secara umum teknik lasso memberikan rataan nilai RMSE yang lebih kecil dibanding dengan metode regresi komponen utama. Pada skenario

β kombinasi, sebaran nilai RMSE dari pendugaan teknik lasso (regularisasi L1)

memiliki keragaman yang lebih kecil dibanding dengan skenarioβ<1. Semakin besar keragaman data (σsemakin besar), keragaman nilai RMSE dari teknik lasso juga semakin membesar. Berbeda dengan teknik lasso, metode regresi komponen utama memberikan keragaman dan rataan nilai RMSE yang stabil. Keragaman dan rataan nilai RMSE dari dugaan menggunakan metode regresi komponen utama lebih besar dibanding teknik lasso, tetapi semakin besar keragaman respons sebenarnya, keragaman dan rataan nilai RMSE dari teknik lasso semakin mendekati keragaman dan rataan nilai RMSE dari metode regresi komponen utama.

Hasil yang relatif sama ditunjukkan oleh nilai RMSE dari kovariat luaran CMIP5 (Lampiran 2). Sebaran nilai RMSE yang diperoleh dari pendugaan dengan skenario β kombinasi memiliki keragaman yang lebih kecil dibanding dengan skenario β seragam<1, dan semakin besar keragaman data respons sebenarnya, maka keragaman nilai RMSE dari penduga teknik lasso juga semakin membesar.

[image:40.595.81.477.125.730.2]

seragam<1, semakin besar ragam respons sebenarnya, metode regresi komponen utama memberikan rataan nilai RMSEP yang lebih kecil dibanding dengan teknik lasso.

19

Simpulan

Pengembangan teknik lasso (regularisasi L1) dapat diimplementasikan ke

dalam bahasa pemrograman R menggunakan teknik iterasi. Hasil simulasi menunjukkan teknik lasso memberikan pendugaan nilai RMSE yang lebih kecil dibanding dengan metode regresi komponen utama, tetapi keragaman dari nilai RMSE dipengaruhi oleh keragaman respons sebenarnya. Semakin besar ragam respons, maka keragaman nilai RMSE dari teknik lasso juga semakin besar. Keragaman nilai RMSE dari metode regresi komponen utama memiliki perubahan yang tidak terlalu signifikan dibanding dengan teknik lasso. Metode regresi komponen utama memberikan nilai RMSEP terkecil pada skenario beta seragam

3 MODEL LINIER TERAMPAT SEBARAN GAMMA

DENGAN REGULARISASI L

₁

Pendahuluan

Beberapa kejadian alam secara alami hanya memiliki nilai non-negatif seperti contohnya curah hujan yang menjadi topik penelitian. Dalam statistika kejadian tersebut dapat dipandang sebagai peubah acak dengan rentang nilai_≥0. Pendugaan nilai peubah acak dalam rentang nilai _≥0 dengan pendekatan pendugaan model linier yang dibangun pada Bab 2 tidak akan secara alami memperoleh dugaan selalu

≥0, dikarenakan teknik-teknik pendugaan tersebut berlandaskan respons berasal dari suatu peubah acak sebaran normal atau sebaran dengan rentang (₋∞,∞). Oleh karena itu pemodelan curah hujan dengan respons sebaran non-normal perlu dipertimbangkan untuk digunakan. Salah satu sebaran dengan rentang nilai _≥0 adalah sebaran Gamma 2-parameter.

Sebaran Gamma 2-parameter dapat dipandang sebagai rampatan

(generalized) dari sebaran eksponensial dengan nilai tengah 1/λ, (λ_≥ 0) yang merepresentasikan waktu tunggu sampai sebanyak a kejadian (Krishnamoorthy 2006). Menurut Das (1955) (di dalam Krishnamoorthy 2006) sebaran Gamma dipostulatkan dalam aplikasi curah hujan (presipitasi) dikarenakan presipitasi terjadi hanya ketika partikel air dapat terbentuk di sekitar debu dengan massa yang cukup, dan waktu tunggu untuk terjadinya akumulasi debu mirip dengan aspek waktu tunggu sebaran Gamma secara implisit. Bentuk dari sebaran Gamma tergantung dari parameter bentuk (shape), semakin mendekati nilai nol, bentuk sebaran akan menjulur ke kanan dan semakin menuju ∞ bentuk sebaran Gamma akan simetrik. Pemodelan linier dengan respons sebaran Gamma 2-parameter termasuk dalam kelas pemodelan linier terampat (Generalized Linear

Model/GLM), yang ditujukan untuk pemodelan dengan respons kontinu dan

menjulur (skewed) (Faraway 2006).

Model Linier Terampat dengan Respons Sebaran Gamma

Model linier terampat (GLM) merupakan rampatan dari model-model linier, dalam hal ini peubah respons berasal dari keluarga sebaran eskponensial dan adanya fungsi hubung yang menghubungkan antara nilai harapan dengan komponen sistematik dari model linier. Aspek penting dari rampatan semua model adalah keberadaan prediktor linier berdasarkan kombinasi linier dari peubah kovariat (peubah bebas/penjelas) dan adanya algoritma bersama untuk pendugaan parameter menggunakan metode kemungkinan maksimum. Komponen-komponen dari model linier terampat adalah sebagai berikut:

1. Komponen acak: Peubah respons (Y) berasal dari keluarga sebaran eksponensial denganE(Y) =µ.

2. Komponen sistematik:η=β0+∑₁pxjβj

Fungsi kepekatan peubah acak dari keluarga sebaran eksponensial dituliskan dalam bentuk natural (McCullagh dan Nelder 1989) sebagai berikut:

fY(y;θ) =exp

(

yθ₋b(θ)

a(φ) +c(y,φ)

)

. (3.1)

dalam hal ini a(_·), b(_·) dan c(_·) adalah fungsi tertentu,θadalah parameter kanonik, danφadalah parameter dispersi.

Perhatikan fungsi kepekatan sebaran Gamma 2-parameter untuk respons y

pada wilayah(0,∞)dituliskan sebagai:

fY(y;ν,ξ) =

νξ Γ(ξ)y

ξ−1_exp(

−νy) (3.2)

dalam hal iniνadalah parameter laju (rate) danξadalah parameter bentuk (shape). Untuk keperluan model linier terampat, nilaiνdiparameterisasi ulang denganν=ξ_µ. Dalam bentuk keluarga eksponensial dengan parameter θ = 1_µ dan φ= 1_ξ, fungsi kepekatan sebaran Gamma dapat ditulis:

fY(y;θ,φ) =exp

(

−ξ y

1 µ −log 1 µ !

+ξlog(ξy)₋log(y)₋log(Γ(ξ))

)

(3.3)

Pendugaan Parameter

Pendugaan parameter model linier terampat dilakukan dengan menggunakan metode kemungkinan maksimum. Parameter βj dalam komponen sistematik digunakan untuk menduga nilai parameter µ sesuai dengan fungsi hubung yang digunakan. Untuk respons sebaran Gamma, fungsi hubung kanoniknya adalah

inverse/reciprocalyaitu 1_µ. Hubunganµ dengan parameter dalam sebaran Gamma

adalahµ= ξ_ν, dalam hal ini parameterξdianggap konstan. Solusi penduga secara numerik diperoleh melalui prosedurIterated Re-Weighted Least Squares(IRWLS) yang merupakan turunan dari aproksimasi metode Newton-Raphson (McCullagh dan Nelder 1989, Dobson 2002). Dengan metode IRWLS, solusi pendugaan dapat mencapai nilai maksimum dari fungsi kemungkinan apabila konvergen. Algoritma metode IRWLS adalah sebagai berikut:

1. Misalkanβr_{adalah penduga ˆβsaat ini, hitung:}

• ηˆr

i :=xtiβr i=1, . . . ,n

• µˆr_i :=g−1(ηˆr i)

• θˆr

i :=h−1(µˆri)

• V_ir :=a(φ)_·b′′(θi)|_θi=θˆr i

• Z_ir:=ηˆr

i+ (yi−µˆri)

dηi

dµi|ηi=ηˆ r i

23

• W_ir:=

V_ird_dµηi

i|ηi=ηˆri 2−1

2. Regresikan Z_ir terhadap X dengan memberikan bobot (Wr

i)−1 untuk mendapatkan penduga baruβr+1_{dan ulangi Tahap 1 sampai}

|βr

−βr+1

|cukup kecil.

Pengembangan Model Linier Terampat dengan Regularisasi L1

Solusi pendugaan parameter dalam pemodelan linier terampat dengan Regularisasi L1adalah (Friedmanet al.2010):

arg min

βk (

−log[L(y;βk)]/n+λ p

∑

k=1

|βk|

)

. (3.4)

dalam hal iniL(y;βk)adalah fungsi kemungkinan keluarga sebaran eksponensial,λ adalahtuningparameter dalam regularisasi L1dannadalah banyaknya observasi.

Untuk mendapatkan nilai penduga parameter tidak dapat dilakukan secara deduktif kalkulus, tetapi dengan menggunakan metode optimisasi. Ada beberapa metode optimisasi numerik umum yang dapat digunakan untuk mendapatkan solusi optimisasi, salah satunya adalah metode Nelder-Mead. Metode Nelder-Mead atau metode downhill simplex merupakan metode yang hanya menggunakan fungsi untuk di-minimisasi/maksimisasi, kekar (robust) tetapi relatif lambat dan dapat konvergen ke titik non-statisioner apabila inisialiasi awal tidak tepat. Oleh karena itu dalam penelitian ini digunakan penggabungan metode IRWLS dan metode optimisasi untuk mendapatkan solusi pendugaan dari model linier terampat dengan Regularisasi L1 respons sebaran Gamma. Metode IRWLS pada nilai λ = 0

digunakan sebagai inisial awal dengan harapan metode optimisasi bergerak di sekitar fungsi kemungkinan yang maksimum. Algoritma yang digunakan adalah:

1. Pendugaan awal dengan metode IRWLS untuk λ = 0. Hasil koefisien pendugaan digunakan sebagai inisial awal metode optimisasi Nelder-Mead. 2. Lakukan pendugaan menggunakan metode optimisasi dengan metode

Nelder-Mead padaλtertentu yang ditetapkan.

Implementasi algoritma di atas dalam perangkat lunak komputasi statistik R disajikan pada Lampiran 5.

Perbandingan Teknik Regularisasi L1dengan Analisis Komponen Utama

Data

Dua data kovariat terkondisi buruk digunakan dalam kajian ini seperti pada Bab 2, yaitu data presipitasi dari model GCM, yaitu luaran ensemble

dari banyak model CMIP5 (multi-model ensemble Phase 5 Couple Model

Intercomparisson Project) dengan skenario perubahan iklim moderat RCP

(Representative Concentration Pathways) 4.5 (Taylor et al. 2012) selanjutnya

Climatology Project) versi 2.2 (Adler et al. 2003) selanjutnya disingkat sebagai GPCP.

Metode

Tahapan kajian perbandingan teknik regularisasi L1 dengan teknik analisis

komponen utama pada model linier terampat sebaran Gamma adalah sebagai berikut:

1. Menetapkan skenario parameterβ

Parameterβdigunakan dua skenario, yaitu:

• kombinasi parameter β= 0.7 (perwakilan<1), 0, dan 3.0 (perwakilan

>1) masing-masing sebanyak 16, 17 dan 16.

• βseragam sebesar 0.7 (perwakilan<1) sebanyak 49. 2. Membangkitkan data respons

Data respons dibangkitkan dari sebaran Gamma dengan cara sebagai berikut:

• Tetapkan parameter shape ξ. Tiga nilai ξ digunakan dalam simulasi yaituξ=0.5, 1, dan 5.

• µ=1/Xβ.

• ν=ξ/µ

• Bangkitkany_∼Gamma(ξ,ν)

3. Menduga nilai dugaan model linier terampat sebaran Gamma dengan regularisasi L1

Nilai dugaan dengan teknik regularisasi L1digunakan dengan menggunakan

model µ = 1/(β0+β1x1+. . .+βkxk) dalam hal ini k adalah banyaknya kovariat yang terseleksi dengan menggunakan nilai validasi silang terkecil, dan xk adalah data presipitasi ke-k dari data kovariat luaran CMIP5 atau GPCP.

4. Menduga nilai dugaan dengan model linier terampat sebaran Gamma dengan analisis komponen utama

Nilai dugaan dengan regresi komponen utama digunakan dengan menggunakan model µ = 1/(β0+β1KU1+. . .+βkKUk) dalam hal ini

k adalah banyaknya komponen utama, dan KUk adalah data skor komponen utama ke-k dari data kovariat luaran CMIP5 atau GPCP.

5. Proses pembangkitan data dan pendugaan nilai tengah di ulang sebanyak 100 kali

6. Pemilihan Metode Pendugaan Terbaik

25

Hasil dan Pembahasan

Untuk menentukan teknik terbaik antara teknik regularisasi L1 dengan

analisis komponen utama, disusun skenario berdasarkan kemungkinan kovariat, nilai koefisien β pada model linier dan sebaran respons menggunakan sebaran Gamma. Skenario kemungkinan kovariat dan nilai koefisien β pada model linier digunakan skenario yang sama seperti pada Bab 2, yaitu skenario kovariat dari dua kemungkinan (data observasi GPCP dan data luaran CMIP5) dan dua skenario kemungkinan koefisien β berupa kombinasi (< 1, 0 dan > 1) dan β seragam

< 1. Tiga kemungkinan sebaran respons dari sebaran Gamma dibangkitkan untuk simulasi. Sebaran Gamma yang digunakan memiliki dua parameter, yaitu parameter bentuk (shape) dan parameter laju (rate). Parameter bentuk diasumsikan bernilai konstan, sedangkan parameter laju merupakan fungsi dari model linier. Pembangkitan respons dari sebaran Gamma disusun berdasarkan skenario pemilihan parameter bentuk yaituξ=0.5, 1, dan 5. Parameter bentukξ_≤

1 memberikan bentuk sebaran seperti bentuk sebaran eksponensial, dan semakin besar nilaiξbentuk sebaran Gamma akan menuju ke bentuk sebaran simetrik seperti sebaran normal. Dengan demikian terdapat 12 skenario yang digunakan untuk menentukan metode/teknik yang terbaik antara teknik regularisai L1dengan analisis

komponen utama.

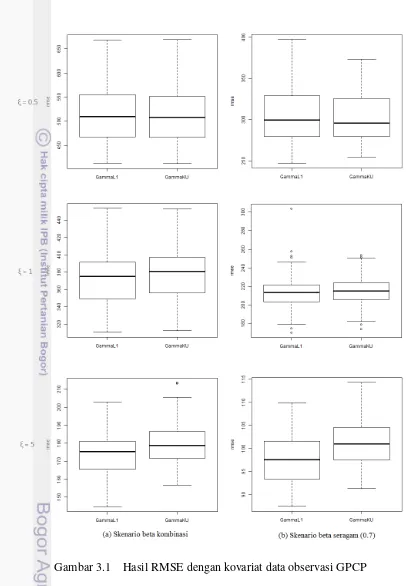
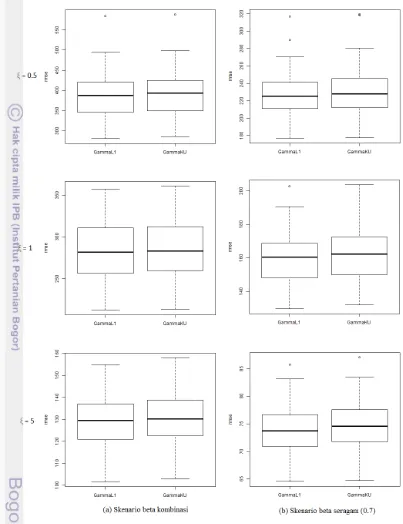
Sebaran nilai RMSE untuk 12 skenario disajikan pada Gambar 3.1 untuk skenario kovariat data observasi GPCP dan Gambar 3.2 untuk skenario kovariat luaran CMIP5. Secara umum sebaran nilai RMSE menunjukkan penggunaan teknik regularisasi L1 memiliki bentuk yang sama dengan sebaran nilai RMSE yang

diperoleh menggunakan analisis komponen utama. Hal ini berbeda sangat nyata dibanding dengan perbandingan antara teknik lasso (regularisasi L1 pada regresi

linier) dengan metode regresi komponen utama pada Bab 2 sebelumnya.

Dari 12 skenario yang dicoba dalam simulasi, rataan nilai RMSE yang diperoleh dari dugaan model dengan teknik regularisasi L1 tampak lebih kecil

dibanding dengan teknik analisis komponen utama tetapi perbedaannya tidak signifikan dan masih dalam selang kepercayaan yang sama. Tidak ada pola sebaran RMSE yang jelas untuk menentukan mana metode yang terbaik antara pemodelan linier terampat sebaran Gamma dengan teknik regularisasi L1 maupun dengan

teknik pereduksian dimensi menggunakan analisis komponen utama. Semua skenario memberikan perbandingan yang sama antara teknik regularisasi L1dengan

teknik analisis komponen utama.

Terdapat perbedaan rataan nilai RMSE yang diperoleh dari dua skenario nilai koefisienβ. Pada skenario nilai koefisienβseragam<1, rataan nilai RMSE selalu lebih kecil dibanding dengan skenario nilai koefisien kombinasi baik pada skenario kovariat GPCP maupun kovariat CMIP5. Tetapi semakin besar nilai parameter bentuk, teknik regularisasi L1 menunjukkan kecenderungan untuk mendapatkan

[image:48.595.73.479.73.659.2]

[image:49.595.101.504.98.622.2]

27