METODE NUMERIK UNTUK MENENTUKAN NILAI OPSI
DENGAN MODEL VOLATILITAS
RISK ADJUSTED PRICING
METHODOLOGY
(RAPM)
ILHAM SYATA
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
PERNYATAAN MENGENAI TESIS DAN
SUMBER INFORMASI SERTA PELIMPAHAN HAK CIPTA*
Dengan ini saya menyatakan bahwa tesis berjudul Metode Numerik untuk Menentukan Nilai Opsi dengan Model Risk Adjusted Pricing Methodology (RAPM) adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.
Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.
RINGKASAN
ILHAM SYATA. Metode Numerik untuk Menentukan Nilai Opsi dengan Model Risk Adjusted Pricing Methodology (RAPM). Dibimbing oleh DONNY CITRA LESMANA dan HADI SUMARNO.
Fisher Black dan Myron Scholes (1973) menunjukkan bahwa harga opsi merupakan solusi dari persamaan diferensial parsial (PDP) yang disebut persamaan Black Scholes. Fisher Black dan Myron Scholes dalam merumuskan persamaan Black-Scholes standar menggunakan asumsi bahwa tidak ada biaya transaksi dalam jual beli aset atau opsi. Asumsi tersebut tidak relevan, karena sebenarnya dalam jual beli aset selalu ada biaya transaksi. Dengan memasukkan biaya transaksi ke dalam model, Jandacka & Sevcovic (2005) menunjukkan bahwa volatilitas menjadi tidak konstan, yaitu suatu fungsi yang bergantung pada harga saham dan turunan parsial kedua harga opsi terhadap harga saham.
Dengan mengasumsikan bahwa terdapat biaya transaksi untuk pembelian dan penjualan aset atau opsi, persamaan Black-Scholes dengan volatilitas konstan berubah menjadi Persamaan Black-Scholes taklinear sebagai berikut adalah waktu jatuh tempo, adalah harga saham.
Jandacka dan Sevcovic (2005) dalam tulisannya berargumentasi bahwa harga opsi adalah solusi dari persamaan diferensial parsial taklinear pada persamaan di atas dengan volatilitas termodifikasi sebagai berikut
dengan
adalah turunan parsial kedua U terhadap S, adalah ukuran biaya transaksi dan adalah ukuran premi risiko, adalah volatilitas sebagai fungsi dari dan .
Secara umum persamaan diferensial parsial taklinear tidak memiliki solusi analitik, termasuk pada kasus ini, sehingga diperlukan metode numerik untuk menyelesaikannya. Persamaan Black-Scholes taklinear diaproksimasi dengan metode implisit untuk diskretisasi waktu, dan metode beda hingga upwind untuk diskretisasi ruang (harga saham). Metode beda hingga upwind adalah suatu metode numerik untuk menyelesaikan persamaan diferensial parsial taklinear dengan cara mengkombinasikan antara beda hingga maju dan beda hingga mundur.
untuk diskretisasi waktu. Orde kekonvergenan opsi call, opsi put, opsi butterfly, dan opsi cashornothing (CoN) yaitu berkisar antara
SUMMARY
ILHAM SYATA. Numerical Method for Determining Option Price with Risk Adjusted Pricing Methodology (RAPM) Model. Supervised by DONNY CITRA LESMANA and HADI SUMARNO.
Fisher Black and Myron Scholes (1973) showed that option price is the solution of partial differential equations (PDE) called Black-Scholes equation. When formulating the standard Black-Scholes equation, they assume that there is no transaction costs on buying and selling either assets or options. This is irrelevant because buying and selling assets always involve transaction costs. By applying the transaction costs into the model, Jandacka and Sevcovic (2005) showed that the volatility becomes a function of stock prices and the second derivative of the option price.
Assuming that the transaction costs exist, the Black-Scholes equation with constant volatility turns into a nonlinear Black-Scholes equation as follow
nonlinear partial differential equations in the equation above with modified volatility as follow
In general, nonlinear partial differential equations do not have analytical solutions, including this one, so we require numerical methods to solve the equations. The nonlinear Black-Scholes equation is approximated using an implicit methods for time discretization and an upwind finite difference method for space discretization. An upwind finite difference method solves the nonlinear partial differential equations in a way that combines forward and backward finite difference. From its discretization scheme, we have an M-matrix for the system matrix. We show that the discretization scheme converges to the viscosity solution to the equation by showing that the scheme is monotone, consistent, and stable.
© Hak Cipta Milik IPB, Tahun 2015
Hak Cipta Dilindungi Undang-Undang
Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumbernya. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah; dan pengutipan tersebut tidak merugikan kepentingan IPB
Tesis
sebagai salah satu syarat untuk memperoleh gelar Magister Sains
pada
Program Studi Matematika Terapan
METODE NUMERIK UNTUK MENENTUKAN NILAI OPSI
DENGAN MODEL VOLATILITAS
RISK ADJUSTED PRICING
METHODOLOGI
(RAPM)
SEKOLAH PASCASARJANA INSTITUT PERTANIAN BOGOR
BOGOR 2015
PRAKATA
Puji syukur penulis panjatkan kehadirat Allah SWT atas limpahan rahmat dan ridho-Nya, kesempatan, dan kesehatan yang dikaruniakan-Nya sehingga karya ilmiah yang berjudul “Metode Numerik untuk Menentukan Nilai Opsi dengan Model Risk Adjusted Pricing Methodology (RAPM)” ini dapat terselesaikan. Terima kasih penulis ucapkan kepada:
1. Ayahanda dan Ibunda tercinta Muhammad Syata dan Sitti Rahman yang telah membesarkan dan mendidik penulis dengan penuh kasih sayang.
2. Bapak Dr Donny Citra Lesmana, MFinMath dan Dr Ir Hadi Sumarno MS selaku pembimbing, atas kesediaan dan kesabaran untuk membimbing dan membagi ilmunya kepada penulis dalam penyusunan karya ilmiah ini.
3. Bapak Dr Jaharuddin, MS selaku Ketua Program Studi Matematika Terapan Institut Pertanian Bogor.
4. Bapak Dr Ir I Gusti Putu Purnaba, DEA selaku penguji luar komisi.
5. Dosen Departemen Matematika Terapan IPB yang telah mengasuh dan mendidik penulis selama di bangku kuliah hingga berhasil menyelesaikan studi, serta seluruh staf Departemen Matematika Terapan IPB atas bantuan, pelayanan, dan kerjasamanya selama ini.
6. Mahasiswa Pascasarjana Departemen Matematika Terapan IPB, Petapa Timbul IPB, dan HIMMPAS IPB atas segala bantuan dan kebersamaannya selama menghadapi masa-masa terindah maupun tersulit dalam menuntut ilmu, serta semua pihak yang telah banyak membantu dan tak sempat penulis sebutkan satu per satu.
Semoga karya ilmiah ini dapat bermanfaat bagi semua pihak yang membutuhkan.
DAFTAR ISI
DAFTAR TABEL vi
DAFTAR GAMBAR vi
DAFTAR LAMPIRAN vi
1 PENDAHULUAN 1
Latar Belakang 1
Tujuan Penelitian 2
2 TINJAUAN PUSTAKA 2
Opsi 2
Aset yang Mendasari Opsi (Underlying Asset) 5
Persamaan Black-Scholes 5
Proses Harga Saham 7
Penurunan Persamaan Black-Scholes 7
Model Volatilitas RAPM 9
Metode Iteratif Newton 9
Matriks M 10
Solusi Viskositas 10
Operator Beda Hingga 11
3 METODE PENELITIAN 12
Langkah-langkah Penelitian 12
4 HASIL DAN PEMBAHASAN 12
Syarat awal dan Syarat Batas 12
Skema Diskretisasi 13
Kekonvergenan Skema Diskretisasi 14
Solusi Sistem Taklinear Skema Diskretisasi 18
Simulasi Numerik 21
5 SIMPULAN DAN SARAN 25
Simpulan 25
DAFTAR PUSTAKA 25
LAMPIRAN 27
DAFTAR TABEL
1 Hasil perhitungan norm dan rasio untuk opsi call 22 2 Hasil perhitungan norm dan rasio untuk opsi put 23 3 Hasil perhitungan norm dan rasio untuk opsi butterfly 24 4 Hasil perhitungan norm dan rasio untuk opsi cash or nothing 25
DAFTAR GAMBAR
1 Payoff untuk opsi call dengan pada 5
2 Payoff untuk opsi put dengan pada 5
3 Payoff untuk opsi butterfly dengan dan pada 5
4 Payoff untuk opsi cash or nothing dengan dan pada 5
5 Harga opsi call Eropa dengan 21
6 Harga opsi call Eropa dengan 21
7 Harga opsi put Eropa dengan 23
8 Harga opsi butterfly Eropa dengan 24
9 Harga opsi cash or nothing Eropa dengan 24
DAFTAR LAMPIRAN
1 PembuktianLemma Ito’ 27
1
PENDAHULUAN
Latar Belakang
Pasar keuangan (financial market) terdiri atas pasar uang (money market) dan pasar modal (capital market). Pasar uang adalah suatu tempat pertemuan di mana para pemilik dana jangka pendek dapat menawarkan kepada calon pemakai yang membutuhkannya, baik secara langsung maupun melalui perantara. Sedangkan yang dimaksud dengan dana jangka pendek adalah dana-dana yang dihimpun dari perusahaan maupun perorangan dengan batasan waktu dari satu hari sampai satu tahun, yang dapat diperjualbelikan di dalam pasar uang. Sedangkan untuk pasar modal terjadi jual beli aset keuangan untuk jangka panjang. Pasar modal terdiri atas pasar obligasi, pasar saham, dan pasar derivatif (Bodie et al 2003).
Derivatif digunakan oleh manajer investasi atau manajer portofolio, perusahaan dan lembaga keuangan, serta investor perorangan untuk mengelola posisi yang mereka miliki terhadap risiko dari pergerakan harga saham, komoditas, suku bunga, atau nilai tukar valuta asing tanpa memengaruhi posisi fisik produk yang menjadi acuannya (underlying). Produk derivatif merupakan suatu instrumen keuangan yang nilainya bergantung pada nilai aset yang mendasarinya seperti saham, obligasi, dan lain-lain. Salah satu produk derivatif adalah opsi. Opsi adalah suatu kontrak antara dua pihak di mana pemegang opsi mempunyai hak untuk membeli atau menjual suatu aset tertentu dengan harga dan waktu yang telah ditentukan.
Fisher Black dan Myron Scholes pada tahun 1973 menunjukkan bahwa harga opsi merupakan solusi dari persamaan diferensial parsial (PDP) yang disebut persamaan Black Scholes (Black & Scholes, 1973). Dalam merumuskan persamaan Black-Scholes, salah satu asumsi yang digunakan adalah tidak ada biaya transaksi dalam jual beli aset atau opsi. Asumsi tersebut sudah tidak relevan, karena sebenarnya dalam jual beli aset selalu ada biaya transaksi. Dengan memasukkan biaya transaksi ke dalam model, volatilitas menjadi tidak konstan yaitu suatu fungsi yang bergantung pada turunan kedua dari harga saham, persamaan Black-Scholes standar menjadi persamaan diferensial parsial taklinear yang disebut persamaan Black-Scholes taklinear (Jandacka & Sevcovic, 2005; Barles & Soner, 1998; Lesmana & Wang, 2013; Ankundinova & Ehrhardt, 2008; Boyle & Vorst, 1992). Secara umum persamaan diferensial parsial taklinear sulit diselesaikan secara analitik, termasuk pada kasus ini, sehingga diperlukan metode numerik.
2
Berdasarkan uraian di atas, pada penelitian ini akan dikaji perilaku dan kecepatan kekonvergenan solusi numerik menggunakan metode beda hingga upwind untuk diskretisasi harga dan metode implisit untuk diskretisasi waktu, untuk model Black-Scholes dengan volatilitas RAPM.
Tujuan Penelitian
Adapun tujuan dalam penelitian ini adalah:
1. mengembangkan metode numerik untuk mencari harga opsi ketika terdapat biaya transaksi. Metode tersebut didasarkan pada metode implisit untuk diskretisasi waktu, serta metode beda hingga upwind untuk diskretisasi harga saham.
2. menentukan orde kekonvergenan solusi hampiran menggunakan metode beda hingga upwind untuk diskretisasi harga saham, serta metode implisit untuk diskretisasi waktu.
2 TINJAUAN PUSTAKA
Opsi
Definisi 1 (Opsi)
Opsi adalah suatu kontrak atau perjanjian antara dua pihak, di mana salah satu pihak (sebagai pembeli opsi) mempunyai hak untuk membeli atau menjual suatu aset tertentu dengan harga yang telah ditentukan, pada atau sebelum waktu yang ditentukan (Hull, 2006).
Nilai Opsi
Nilai opsi adalah besarnya biaya yang dikeluarkan oleh seorang investor untuk mendapatkan kontrak opsi dan pembayarannya dilakukan pada saat kontrak dibuat. Ada beberapa hal yang memengaruhi nilai opsi, yaitu:
a) Harga underlying asset (S)
Underlying asset yang digunakan adalah saham. Harga saham berpengaruh terhadap harga opsi. Jika harga saham naik maka harga opsi call akan meningkat, sedangkan jika harga saham naik maka harga opsi put akan turun. b) Harga strike (K)
3 c) Waktu jatuh tempo (T)
Waktu jatuh tempo akan memengaruhi perubahan harga opsi. Semakin lama jangka waktu jatuh tempo suatu opsi maka akan semakin besar peluang harga saham mempengaruhi harga opsi.
d) Volatilitas (σ)
Volatilitas merupakan suatu ukuran yang menunjukkan seberapa besar harga berfluktuasi dalam suatu periode (Lo 2003). Volatilitas atas saham ini mengukur tingkat ketidakpastian mengenai pergerakan saham tersebut di masa yang akan datang. Jika volatilitas semakin meningkat maka kemungkinan menyimpang dari nilai harapan juga semakin tinggi.
e) Suku bunga bebas risiko ( )
Pada tingkat suku bunga bebas risiko yang tinggi, investor akan lebih tertarik untuk membeli opsi daripada membeli saham karena:
1. pemegang opsi dapat menentukan apakah akan melaksanakan haknya atau tidak hingga masa jatuh tempo berakhir,
2. serta para investor dapat memperoleh keuntungan jika dapat menentukan dengan tepat kapan membeli opsi put atau call. Apabila diperkirakan harga naik maka akan membeli opsi call, dan sebaliknya bila harga cenderung turun maka akan membeli opsi put.
Hal ini akan menyebabkan harga opsi naik. f) Dividen ( )
Dividen merupakan bagian dari keuntungan perusahaan yang dibagikan kepada para pemegang saham. Dividen menyebabkan harga saham turun sesaat setelah pembagian dividen, sehingga memengaruhi harga opsi.
Beberapa istilah yang berhubungan dengan harga saham (S) dan harga strike (K), yaitu:
1. opsi call
a) jika , maka opsi call dikatakan dalam keadaan in the money. Pemegang opsi akan mengeksekusi opsi call, yaitu dengan membeli saham dengan harga strike (K), yang lebih kecil dari harga saham (S), kemudian (K), yang lebih besar dari harga saham (S), kemudian membelinya di pasar dengan harga sebesar (S), sehingga pemegang opsi tersebut akan mendapatkan imbalan sejumlah
b) jika , maka opsi put dikatakan dalam keadaan at the money,
4
Jenis-jenis opsi
Jenis-jenis opsi yaitu:
1. opsi call memberikan hak kepada pembeli untuk membeli suatu aset tertentu dengan jumlah tertentu pada harga eksekusi (strike price, exercise price) pada atau sebelum waktu jatuh tempo.
2. opsi put memberikan hak kepada pembeli untuk menjual suatu aset tertentu dengan jumlah tertentu pada harga eksekusi sampai waktu jatuh tempo. 3. opsi butterfly merupakan strategi spread yang melibatkan kombinasi antara
empat opsi call dengan 2 harga strike yang berbeda dan dua harga strike nothing disebut juga opsi call digital atau opsi biner.
Berdasarkan waktu eksekusinya, opsi dibedakan atas opsi tipe Eropa dan opsi tipe Amerika.
1. opsi tipe Eropa (European option) adalah opsi yang memberikan hak kepada pemegangnya untuk membeli atau menjual underlying asset hanya pada waktu jatuh tempo.
2. opsi tipe Amerika (American option) memberikan hak kepada pemegangnya untuk membeli atau menjual underlying asset pada saat atau sebelum waktu jatuh tempo.
(Hull, 2006).
Payoff harga opsi
Payoff adalah imbalan yang diperoleh dari jual beli opsi ketika opsi tersebut dieksekusi. Payoff opsi tipe Eropa sebagai berikut
5
Aset yang Mendasari (Underlying Asset)
Aset yang mendasari (underlying asset) adalah aset yang dijadikan sebagai objek atau dasar transaksi. Dalam perdagangan opsi terdapat beberapa aset yang dapat digunakan sebagai aset dasar, antara lain indeks (index), valuta asing (foreign currency), surat berjangka (future) dan saham (stock). Opsi indeks adalah suatu opsi dengan aset berbasis indeks pasar saham. Opsi valuta asing adalah suatu opsi dengan aset berbasis mata uang asing dengan kurs tertentu, opsi berjangka adalah suatu opsi dengan aset berbasis kontrak berjangka. Sedangkan opsi saham adalah suatu opsi dengan aset yang mendasarinya adalah saham. Dalam tulisan ini, underlying asset yang digunakan adalah saham.
Bursa Amerika yang memperdagangkan opsi saham antara lain The Chicago Board Option Exchange (CBOE), The Philadephia Stock Exchange (PHLX), The American Stock Exchange (AMEX), dan New York Stock Exchange (NYSE). Bursa Indonesia yang memperdagangkan opsi saham adalah Bursa Efek Jakarta (BEJ).
Persamaan Black-Scholes
6
1. suku bunga bebas risiko ( ) adalah konstan dan sama untuk semua waktu jatuh tempo.
2. dimungkinkan adanya short selling terhadap aset (saham). Short shelling yaitu meminjam suatu aset kepada seseorang kemudian menjualnya dengan harapan bahwa bisa membeli kembali aset tersebut dengan harga yang lebih murah kemudian mengembalikannya.
3. perdagangan dari aset yang mendasari bersifat kontinu. 4. tidak terdapat peluang arbitrage.
5. tidak ada pembayaran dividen selama opsi berlaku.
6. harga dari aset yang mendasari mengikuti proses Wiener yang mempunyai fungsi kepekatan peluang lognormal.
7. tidak ada biaya transaksi dalam pembelian atau penjualan aset atau opsi.
Untuk memodelkan Persamaan Black-Scholes, didefinisikan atau ditentukan beberapa istilah berikut:
Definisi 2 (Proses Stokastik)
Proses stokastik adalah suatu koleksi (gugus, himpunan, atau kumpulan) dari peubah acak (random variables). Untuk setiap t pada himpunan indeks H, W(t) adalah suatu peubah acak dan t sering diinterpretasikan sebagai waktu (Ross, 1996).
Proses Wiener adalah gerak Brown dengan rataan 0 dan variansi 1 (Niwiga 2005).
Definisi 4 (Proses Wiener Umum (Generalized Wiener Process))
Proses Wiener Umum untuk suatu peubah acak S dapat dinyatakan sebagai berikut (Hull 2006):
(1)
dengan disebut sebagai komponen deterministik dan menyatakan komponen stokastik, serta adalah proses Wiener, sedangkan dan masing-masing menyatakan rataan (drift rate) dan standar deviasi (variance rate) dari S.
Definisi 5 (Proses Ito’)
Proses Ito’ adalah proses Wiener umum dengan dan menyatakan suatu fungsi dari
peubah acak S dan waktu t. Secara aljabar proses Ito’ dapat dinyatakan sebagai berikut (Hull, 2006).
7
Dengan kondisi pasar yang tidak menentu menyebabkan terjadinya perubahan harga saham. Harga saham merupakan variabel stokastik karena dipengaruhi oleh faktor-faktor yang tidak dapat ditentukan secara pasti. Sehingga perubahan harga saham dapat dimodelkan menggunakan persamaan diferensial stokastik berikut:
(5)
dengan adalah komponen deterministik, adalah komponen stokastik dan adalah proses Wiener. Sedangkan dan masing-masing menyatakan nilai harapandan volatilitas dari harga saham tersebut. Persamaan ini juga dikenal sebagai model pergerakan harga saham.
8
berdasarkan Lemma Ito’, proses untuk U berubah atas interval waktu dt yang sangat kecil, akan diperoleh
(9)
Versi diskret dari persamaan (8) dan (9) adalah
(10) ini akan menjual satu opsi dan membeli saham sebanyak
. Nilai dari portofolio tersebut adalah sebesar x, dengan
. (12)
Perubahan nilai portfolio dalam selang waktu adalah
. (13)
Substitusi (10) dan (11) ke dalam (13), menghasilkan
. (14)
Portofolio ini dikatakan tidak berisiko karena tidak ada faktor ketidakpastian. Portofolio ini dikatakan konstan sehingga portofolio ini mempunyai pendapatan yang sama dengan saham jangka pendek lainnya yang bebas risiko.
Perubahan nilai portofolio bebas risiko dapat dinyatakan dengan , dengan
9
Dengan mengasumsikan bahwa terdapat biaya transaksi untuk pembelian dan penjualan aset atau opsi, volatilitas menjadi suatu fungsi yang bergantung pada saham dan turunan parsial kedua harga opsi terhadap harga saham. Sehingga persamaan Black-Scholes standar berubah menjadi persamaan Black-Scholes taklinear sebagai berikut
Jandacka dan Sevcovic (2005) dalam tulisannya berargumentasi bahwa harga opsi adalah solusi dari persamaan diferensial parsial taklinear pada persamaan (19) dengan volatilitas termodifikasi sebagai berikut:
(20) Scholes taklinear tersebut yang akan dibahas dalam tesis ini.
Metode Iteratif Newton
Metode iteratif Newton digunakan untuk menyelesaikan sistem persamaan taklinear yang memiliki bentuk sebagai berikut: Berikut ini adalah pendekatan yang dilakukan dengan metode iteratif Newton
(22)
10
dengan metode iteratif Newton, akan dicari vektor yang membuat konvergen ke vektor nol, sehingga
(25)
(26)
(27)
di mana adalah matriks segi dan adalah vektor yang diketahui. Untuk langkah selanjutnya, penentuan solusi memiliki proses berikut: 1. Selesaikan
11 ii. Dikatakan bahwa adalah supersolusi viskositas persamaan (28) pada titik jika dan hanya jika, untuk setiap fungsi uji sedemikian sehingga yang mencapai minimum lokal di , dan
(30) iii. Dikatakan bahwa adalah solusi viskositas pada himpunan terbuka jika
adalah subsolusi viskositas dan supersolusi viskositas, pada setiap titik
(Dragoni, 2009).
Operator Beda Hingga
Persamaan Black-Scholes taklinear akan diaproksimasi dengan diskretisasi menggunakan metode implisit untuk diskretisasi waktu, serta metode beda hingga upwind untuk diskretisasi harga saham. Metode beda hingga upwind adalah suatu metode numerik untuk menyelesaikan persamaan diferensial parsial taklinear dengan cara mengkombinasikan antara beda hingga maju dan beda hingga mundur.
Untuk diskretisasi harga, misalkan dibagi menjadi sub-interval, di mana
dengan , dan untuk setiap dimisalkan . Untuk diskretisasi waktu, misalkan dibagi menjadi sub-interval, di mana
dengan dan untuk setiap dimisalkan .
Aproksimasi turunan parsial pertama dan kedua diperoleh dari ekspansi deret Taylor sebagai berikut:
Untuk sembarang dan dengan dan , didefinisikan turunan pertama dan turunan kedua mengikuti operator beda hingga berikut:
(31)
, (32)
12
3 METODE PENELITIAN
Langkah-langkah Penelitian
Adapun langkah-langkah yang akan dilakukan dalam penelitian ini adalah: 1. melakukan diskretisasi untuk persamaan Black-Scholes taklinear dengan
metode beda hingga upwind untuk diskretisasi harga saham, dan metode implisit untuk diskretisasi waktu.
2. memeriksa kekonvergenan skema diskretisasi yaitu dengan membuktikan Lemma monoton, konsisten, dan stabil.
3. membandingkan hasil numerik yang diperoleh dari metode implisit dan eksplisit.
4. melakukan simulasi numerik untuk menunjukkan akurasi dari metode beda hingga upwind untuk diskretisasi variabel harga saham, dan metode implisit untuk diskretisasi variabel waktu.
4 HASIL DAN PEMBAHASAN
Syarat Awal dan Syarat Batas
Persamaaan Black-Scholes taklinear mempunyai domain . Untuk perhitungan komputasi perlu dibatasi menjadi , dengan merupakan nilai yang cukup besar yang menjamin akurasi dari solusi. Syarat batas untuk persamaaan Black-Scholes taklinear dapat ditentukan sebagai berikut:
(34) Syarat awal dan syarat batas untuk opsi tersebut yaitu sebagai berikut:
13
Dengan menggunakan operator (31-33) dan dengan mengaplikasikan metode beda hingga upwind, persamaan Black-Scholes taklinear (19) diaproksimasi menjadi sebagai berikut: Untuk penyederhanaan, persamaan (40) dapat dituliskan menjadi bentuk berikut:
Berdasarkan (34-36), didefinisikan syarat awal dan syarat batas untuk persamaan (41) sebagai berikut
14
untuk dan Dengan syarat awal dan syarat batas di atas, persamaan (41) dapat dituliskan menjadi bentuk matriks berikut
̂
Untuk membuktikan Teorema 1, harus ditunjukkan bahwa
(47)
Sehingga merupakan matriks M karena matriks tridiagonal memiliki diagonal utama yang bernilai positif dan dua diagonal atas dan bawah bernilai takpositif.
Kekonvergenan Skema Diskretisasi
15 bagian ini akan ditunjukkan bahwa skema diskretisasi memenuhi syarat kekonvergenan tersebut.
Skema diskretisasi (41) akan ditunjukkan monoton melalui Lemma 2.
Lemma 2 Berdasarkan definisi , diperoleh
16
Selanjutnya, diperiksa tanda pada bagian taklinear , di mana didefinisikan sebagai berikut
(55)
maka,
( ) ( )
( ),
(56)
misalkan dan
(57)
(58) Diketahui dan
jelaskarena dan selanjutnya akan dibuktikan bahwa
(59)
karena
maka
( ) (60) Dari persamaan di atas diperoleh bahwa
(61)
Dengan demikian adalah fungsi naik pada dengan syarat bahwa
Dengan demikian untuk sembarang dan diperoleh gabungan bagian linear dan bagian taklinear dari persamaan (50) sebagai berikut:
17
Skema diskretisasi (41) akan ditunjukkan stabil melalui Lemma 3.
Lemma 3
18
‖ ‖
‖ ‖ ‖ ‖ (66) ‖ ‖ ‖ ‖ ‖ ‖ .
Selanjutnya jika ‖ ‖ | | atau ‖ ‖ | |maka berdasarkan persamaan (35), (36) dan (45) dapat dilihat bahwa:
| | | | (67)
Skema diskretisasi (41) akan ditunjukkan konsisten melalui Lemma 4.
Lemma 4
Skema diskretisasi (41) konsisten. Bukti
Teorema ekuivalensi Lax menyatakan bahwa metode beda hingga konsisten untuk persamaan diferensial parsial dengan masalah nilai awal yang diberikan (Strikwerda 1989). ∎
Teorema 2. Kekonvergenan
Solusi numerik dari skema diskretisasi (41) konvergen ke solusi viskositas persamaan (19) dengan syarat batas yang diberikan oleh (34)-(36) ketika .
Bukti:
Barles (1997), membuktikan bahwa jika suatu diksretisasi dari PDP taklinear orde-2 konsisten, stabil dan monoton, maka konvergen ke solusi viskositas. Berdasarkan Lemma 2, Lemma 3, dan Lemma 4 maka diskretisasi terbukti konsisten, stabil dan monoton, maka skema diskretisasi (46) konvergen ke solusi viskositas persamaan (19). ∎
Solusi Sistem Taklinear Skema Diskretisasi
20
4. Jika ‖ ‖ set dan kembali kelangkah 3. Jika sebaliknya, lanjutkan ke langkah berikutnya.
5. Tentukan ̂ Jika . Set dan kembali ke langkah 2. Jika sebaliknya berhenti.
Dengan menggunakan matriks Jacobi , diperoleh Teorema 3 berikut.
Teorema 3
Untuk sembarang dengan , adalah matriks M. Bukti
Untuk membuktikan Teorema 3, harus ditunjukkan bahwa
(68)
| | | | (69)
Untuk matriks , diperoleh
(menggunakan persamaan 61). Hal yang sama untuk
. Selanjutnya karena dan
maka
| | | | | | |
|
untuk sembarang dengan ketentuan bahwa . Oleh karena itu, matriks adalah matriks M. ∎
21
Simulasi Numerik
Simulasi numerik dengan metode beda hingga upwind dan implisit untuk menentukan harga opsi empat jenis tipe Eropa dilakukan dengan mengambil contoh kasus kontrak opsi. Selanjutnya diamati perbandingan harga opsi metode implisit dan metode eksplisit, serta dihitung orde kekonvergenan dari metode implisit dengan memilih serangkaian mesh yang dibangkitkan dengan membagi-dua parameter mesh pada iterasi sebelumnya.
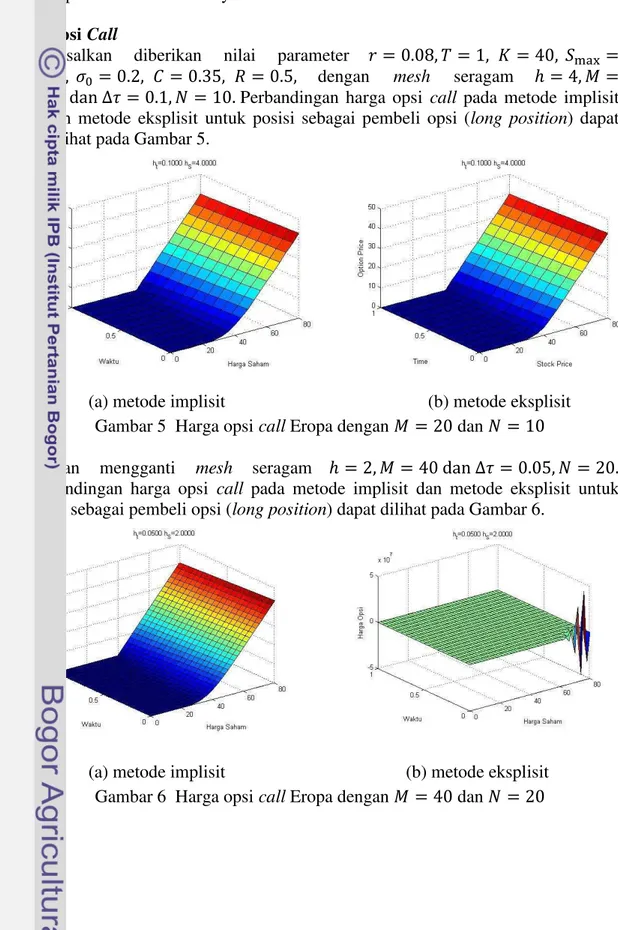
a) Opsi Call
Misalkan diberikan nilai parameter dengan mesh seragam Perbandingan harga opsi call pada metode implisit dan metode eksplisit untuk posisi sebagai pembeli opsi (long position) dapat dilihat pada Gambar 5.
(a) metode implisit (b) metode eksplisit
Gambar 5 Harga opsi call Eropa dengan dan
Dengan mengganti mesh seragam Perbandingan harga opsi call pada metode implisit dan metode eksplisit untuk posisi sebagai pembeli opsi (long position) dapat dilihat pada Gambar 6.
22
Pada Gambar 6, metode implisit masih memberikan solusi, sedangkan metode eksplisit tidak memberikan solusi (tidak stabil).
Untuk menghitung norm dan rasio skema tersebut, dipilih serangkaian mesh yang dibangkitkan secara berurutan dengan membagi dua ukuran mesh sebelumnya. Selanjutnya akan dihitung norm dan rasio metode tersebut dengan membandingkan solusi “eksaknya” (“ ”). Dalam menentukan solusi “eksak” (“ ”) digunakan solusi numerik dengan mengambil ukuran mesh yang sangat kecil, yaitu dan Selanjutnya dengan menggunakan solusi “eksak” tersebut, dihitung rasio dari solusi numerik dari mesh yang berurutan dengan
‖
‖ ‖ ⁄⁄ ‖
di mana adalah solusi pada mesh dengan ukuran mesh saham dan ukuran mesh waktu, serta rumus untuk menghitung norm sebagai berikut
‖ ‖ ‖ ‖ | |.
Orde kekonvergenan metode numerik dihitung dengan menghitung rata-rata dari rasio.
Tabel 1 Hasil perhitungan norm dan rasio untuk opsi call
M N Metode implisit
23
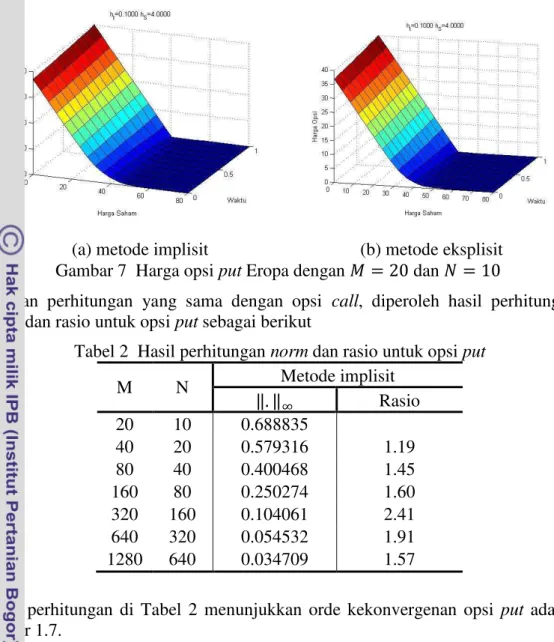
(a) metode implisit (b) metode eksplisit Gambar 7 Harga opsi put Eropa dengan dan
Dengan perhitungan yang sama dengan opsi call, diperoleh hasil perhitungan norm dan rasio untuk opsi put sebagai berikut
Tabel 2 Hasil perhitungan norm dan rasio untuk opsi put
M N Metode implisit
‖ ‖ Rasio
20 10 0.688835
40 20 0.579316 1.19
80 40 0.400468 1.45
160 80 0.250274 1.60
320 160 0.104061 2.41
640 320 0.054532 1.91
1280 640 0.034709 1.57
Hasil perhitungan di Tabel 2 menunjukkan orde kekonvergenan opsi put adalah sekitar 1.7.
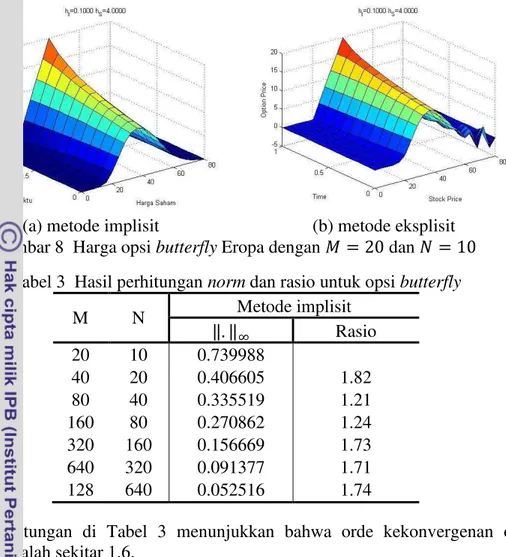
c) Opsi Butterfly
24
(a) metode implisit (b) metode eksplisit Gambar 8 Harga opsi butterfly Eropa dengan dan
Tabel 3 Hasil perhitungan norm dan rasio untuk opsi butterfly
M N Metode implisit
‖ ‖ Rasio
20 10 0.739988
40 20 0.406605 1.82
80 40 0.335519 1.21
160 80 0.270862 1.24
320 160 0.156669 1.73
640 320 0.091377 1.71
128 640 0.052516 1.74
Hasil perhitungan di Tabel 3 menunjukkan bahwa orde kekonvergenan opsi butterfly adalah sekitar 1.6.
d)Opsi Cash or Nothing
Misalkan diberikan nilai parameter dengan mesh seragam Perbandingan harga opsi cash or nothing pada metode implisit dan metode eksplisit untuk posisi sebagai pembeli opsi (long position) dapat dilihat pada Gambar 9.
25 Tabel 4 Hasil perhitungan norm dan rasio untuk opsi cash or nothing
M N Metode implisit
Hasil perhitungan di Tabel 4 menunjukkan bahwa orde kekonvergenan opsi cash or nothing adalah sekitar 1.4.
SIMPULAN
Persamaan Black-Scholes taklinear diaproksimasi dengan metode implisit untuk diskretisasi waktu dan metode beda hingga upwind untuk diskretisasi harga saham diperoleh:
1. suatu sistem matrix yang disebut matriks M yang menjamin solusi bernilai positif.
2. skema diskretisasi terbukti monoton, konsisten, dan stabil. Sehingga, solusi numerik skema diskretisasi konvergen ke solusi viskositas persamaan Black-Scholes taklinear.
3. dengan sub-interval harga saham dan sub-interval waktu menghasilkan orde kekonvergenan opsi call, opsi put, opsi butterfly, dan opsi cashornothing bekisar antara
DAFTAR PUSTAKA
Ankudinova J, Ehrhardt M. 2008. On the numerical solution of nonlinear Black-Scholes equations. Comput. Math. Appl. 56: 799-812.
Barles G. 1997. Convergence of Numerical Schemes for Degenerate Parabolic Equations Arising in Finance, in: L.C.G. Rogers, D. Talay (Eds.), Numerical Methods in Finance. Cambridge: Cambridge University Press. Barles G, Soner HM. 1998. Option pricing with transaction costs and a
non-linear Black-Scholes equation. Finance and Stochastics. 2(4):369-397. Black F, Scholes M. 1973. The pricing of options and corporate liabilities. J.
Political Economy. 81(3):637-659.
26
Boyle P, Vorst T. 1992. Option replication in discrete time with transaction costs. The Journal of Finance. XLVII(1):271-293.
Dragoni F. 2009. Introduction to Viscosity Solutions for Nonlinear PDEs. London: Notes Imperial College London.
Fujimoto T, Ranade R. 2004. Two characterizations of inverse-positive matrices: the Hawkins-Simon condition and the Le Chatelier-Braun principle. Electronic Journal of Linear Algebra 11: 59–65.
Hull J. 2006. Option, Futures and Other Derivatives. 6th Ed. New Jersey: Prentice – Hall.
Jandacka M, Sevcovic D. 2005. On the risk-adjusted pricing-methodology-based valuation of vanilla options and explanations of the volatility smyle. J Appl. Math. 3: 235-258.
Lesmana DC, Wang S. 2013. Numerical method for non-linear partial differential equations and inequalities arising from option valuation under transaction cost. Appl. Math. Comput. 219:8811–8828.
Lo MS. 2003. Generalized Autoregressive Conditional Heterscedasticity Time Series Model [Thesis]. Burnaby: Department of Statistics and Actuaria Science, Simon Fraser University.
Niwiga DB. 2005. Numerical Method for Valuation of Financial Derivatives, [Thesis]. South Africa (tZA): University of Werstern Cape.
Pooley DM, Forsyth PA, Vetzal KR. 2001. Numerical convergence properties of option pricing PDEs with uncertain volatility. IMA J. Numer. Anal. 23: 241-267.
Ross SM. 1996. Sthochastic Process. New York: John Wiley & Son Inc.
Strikwerda JC. 1989. Finite Difference Schemes and Partial Differential Equations. 1st Ed. Madison: Wadsworth & Brooks.
Zang K, Wang S. 2009. A computational scheme for uncertain votality model in option pricing.Appl. Numer. Math. 59:1754–1767.
27
LAMPIRAN
Lampiran 1 Pembuktian Lemma Ito’
Diasumsikan bahwa model dari harga saham dapat dinyatakan sebagai berikut: 1.a) ( Misalkan U(S(t),t)dan berdasarkan ekspansi deret Taylor diperoleh
. ( 1.b) Dengan menguadratkan kedua ruas pada persamaan (1.a), diperoleh sebagai berikut
Beda Hingga Upwind dan Eksplisit
29 % nS : banyak sub-interval dari [0, S_end]
% nt : banyak sub-interval dari [0, T] %
% OUTPUT
30
% entri dari koefisien matrix untuk systems tridiagonal (to be % solved at each time level)
F(1) = A(1,1)*U(m,1) + A(1,2)*Vtemphit(1) +A(1,3)*Vtemphit(2)-rat*Un(1);
31
for k = 2:(nS1-3)
lamb1(k) = J(k,3)/(J(k,2)-J(k,1)*lamb1(k-1));
d(k) = (-F(k)-J(k,1)*d(k-1))/(J(k,2)-J(k,1)*lamb1(k-1)); end
y = zeros(nS1-2,1);
y(nS1-2) = (-F(nS1-2)-J(nS1-2,1)*d(nS1-3))/(J(nS1-2,2)-J(nS1-2,1)*lamb1(nS1-3));
for k = (nS1-3):-1:1
y(k) = d(k) - lamb1(k)*y(k+1); end
%%%%%%%%%%%%% End for Tridiagonal matrix %%%%%%%%%%%%%%%%%%%%
Vtemphit = Vtemphit + y; tol = max(y);
iter = iter + 1;
Vtemp = [U(m,1) Vtemphit' U(m,end)]; end %%%%% End for while
for i = 1:nS1
U(m,i) = Vtemp(i); end
end %%%%%%%%%%%% End untuk time-step iteration
V = zeros(nt1, nS1);
for j = 1:nt1
V(j,:) = U((nt1+1)-j,:); end
%%%%%%% Plot Solusi Numerik
surf(Svec,tvec,V)
xlabel('Harga Saham');
ylabel('Waktu');
zlabel('Harga Opsi');
s1=sprintf('h_t=%6.4f h_S=%6.4f', ht, hS);
32
RIWAYAT HIDUP
Penulis dilahirkan di Balusu Desa Balusu Kec.Balusu Kab.Barru Sul-Sel pada tanggal 09 Agustus 1990, sebagai anak keempat dari pasangan Muh Syata dan Sitti Rahman. Pendidikan sekolah menengah ditempuh di SMA Negeri 1 Soppeng Riaja Program IPA, lulus pada tahun 2008. Pada tahun yang sama penulis diterima di program studi Matematika Universitas Negeri Makassar, dan menyelesaikannya pada tahun 2011.