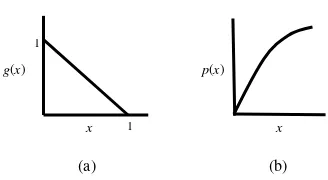LAZUARDI RAMADHAN
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ALI KUSNANTO dan PAIAN SIANTURI.
Mangsa pemangsa merupakan salah satu fenomena alam yang dipelajari untuk studi dampak keseimbangan alam yang diakibatkan oleh dua spesies yang berinteraksi. Oleh karena itu, dibuat beberapa model matematika untuk menggambarkan perkembangan populasi mangsa dan pemangsa. Salah satu model adalah model Holling-Tanner tipe II yang dibahas dalam karya ilmiah ini. Metode yang digunakan dalam pembahasan ini adalah analisis kestabilan titik tetap. Dalam karya ilmiah ini diperoleh dua titik tetap yaitu dan . Kestabilan adalah sadel sedangkan bergantung pada nilai parameter yang dipilih. Ada tiga kasus yang dianalisis untuk titik tetap . Pada salah satu kasus, diperoleh siklus limit dengan mengubah nilai salah satu parameter.
ALI KUSNANTO and PAIAN SIANTURI.
Phenomenon of prey predator is a natural phenomenon which is intended to study the impact of the natural balance caused by two interacting species. Therefore, mathematical models were developed to describe the dynamics of prey and predator populations. One of the models studied in this paper is the model of Holling-Tanner type II. The method used in this paper is the analysis of the stability of a fixed point. There are two fixed points obtained in this study i.e. and . The stability of is saddle while depends on the value of the selected parameter. There are three cases analyzed for the fixed point . For one of the cases, the limit cycle is obtained by changing the value of one parameter.
LAZUARDI RAMADHAN
Skripsi
sebagai salah satu syarat untuk memperoleh gelar
Sarjana Sains pada
Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
Menyetujui
Tanggal Lulus:
Pembimbing I,
Drs. Ali Kusnanto, M.Si.
NIP: 19650820 199003 1 001
Pembimbing II,
Dr. Paian Sianturi
NIP: 19620212 199011 1 001
Mengetahui:
Ketua Departemen,
sehingga penulis mampu menyelesaikan karya ilmiah ini. Shalawat serta salam semoga senantiasa tercurah kepada Rosulullah Muhammad SAW beserta keluarga, sahabat dan pengikutnya hingga akhir zaman Penyusunan karya ilmiah ini juga tidak lepas dari dukungan dan bantuan banyak pihak. Untuk itu penulis mengucapkan terima kasih yang sebesar-besarnya kepada:
1. Keluarga tercinta: Bapak dan Mamah yang senantiasa mencurahkan nasehat, doa serta kasih sayangnya. Untuk ketiga adikku Wilda Fauziannisa, Devi Imanillah Haqiqi, dan Citra Mustika Fazrin yang telah menjadi spirit,
2. Drs. Ali Kusnanto, M.Si. selaku dosen pembimbing I yang telah meluangkan waktu dan pikiran dalam membimbing, memberi motivasi, semangat dan doa,
3. Dr. Paian Sianturi selaku dosen pembimbing II yang telah memberikan ilmu, kritik dan saran, motivasi serta doanya,
4. Dr. Ir. Endar H. Nugrahani, MS selaku dosen penguji yang telah memberikan ilmu, saran dan doanya,
5. Semua dosen Departemen Matematika, terima kasih atas semua ilmu yang telah diberikan,
6. Staf Departemen Matematika: Ibu Susi, Bapak Yono, Ibu Ade, Alm. Bapak Bono, Mas Deni, dan Mas Hery atas semangat dan doanya,
7. Teman-teman satu bimbingan: angkatan 44 (Fajar, Sri, dan Rachma) dan angkatan 45 (Fikri, Ade, James dan Dewi).
8. Teman-teman mahasiswa Matematika angkatan 44: Aswin, Eka, Ali, Pandi, Imam, Aqil, Ihsan, Fajar, Ropi, Denda, Abe, Dian, Wahyu, Ruhiyat, Yogie, Lugi, Olih, Saepur, Hendro, Saepul, Tendi, Yanti, Ririh, Indin, Ndep, Wewe, Istiti, Ayum, Yuyun, Deva, Lilis, Sri, Rachma, Mutia, Ayung, Della, Tyas, Ima, Dora, Ucu, dan teman-teman yang lainnya.
9. Teman-teman mahasiswa Matematika angkatan 45: Hafiz, Fikri, Heru, Herlan, Arbi, Izzudin, Putri, Yunda, Risca, Mia, Fitryah, Finata, Prama, Chastro, Fuka, Ade, Tiwi, Irwan, Bram, Rian, dan teman-teman lainnya,
10. Teman-teman Matematika angkatan 42, 43, 46 dan 47,
11. Sahabat Gumatika, Pamacik (Persatuan Mahasiswa Cikarang) dan Alpatture. 12. Semua pihak yang telah membantu dalam penyusunan karya ilmiah ini.
Semoga karya ilmiah ini dapat bermanfaat bagi dunia ilmu pengetahuan khususnya bidang matematika dan menjadi inspirasi bagi penelitian selanjutnya.
Bogor, Februari 2013
Penulis merupakan putra pertama dari empat bersaudara, tahun 2001 penulis lulus dari SD Negeri Sukaraya 03, tahun 2004 penulis lulus dari SMP Negeri 1 Cikarang Utara, tahun 2007 penulis lulus dari SMA Negeri 1 Cikarang Utara. Penulis diterima sebagai mahasiswa Institut Pertanian Bogor pada tahun 2007 melalui jalur Undangan Seleksi Masuk IPB (USMI), Tingkat Persiapan Bersama. Pada tahun 2009, penulis memilih mayor Matematika pada Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.
Selama mengikuti perkuliahan, penulis menjadi pengajar les privat mata kuliah Pengantar Matematika dan Kalkulus tahun akademik 2009-2011. Tahun 2009-2010 dan 2011-2012 penulis mendapatkan beasiswa PPA (Peningkatan Prestasi Akademik) dari Institut Pertanian Bogor.
viii
DAFTAR ISI
Halaman
DAFTAR GAMBAR ... ix
DAFTAR LAMPIRAN ... ix
I PENDAHULUAN ... 1
1.1 Latar Belakang ... 1
1.2 Tujuan ... 1
1.3 Sistematika Penulisan ……… ... 1
II LANDASAN TEORI ... 2
2.1 Sistem Persamaan Diferensial ... 2
2.2 Titik Tetap ... 2
2.3 Pelinearan ... 2
2.4 Vektor Eigen dan Nilai Eigen ... 2
2.5 Analisis Kestabilan Titik Tetap ... 2
2.6 Limit Cycle ... 3
2.7 Bifurkasi Hopf ... 3
III PEMODELAN ... 4
3.1 Respon Fungsional Model Holling-Tanner ... 4
3.1.1 Model Holling-Tanner tipe I ... 4
3.1.2 Model Holling-Tanner tipe II ... 4
3.1.3 Model Holling-Tanner tipe III ... 4
3.2 Penondimensionalan Model... 4
IV PEMBAHASAN ... 5
4.1 Penentuan dan Analisis Kestabilan Titik Tetap ... 5
4.2 Stabilitas Global dan Bifurkasi Hopf ... 8
4.3 Dinamika Populasi Mangsa-Pemangsa Model Holling-Tanner Tipe II ... 8
4.3.1 Kasus K1 ... 9
4.3.2 Kasus K2 ... 10
4.3.3 Kasus K3 ... 12
SIMPULAN ... 15
DAFTAR PUSTAKA ... 15
ix
DAFTAR GAMBAR
Halaman
1 Ilustrasi (a) H1 dan (b) H2 ... 5
2 Limit cycle... 8
3 Dinamika populasi mangsa dan pemangsa dengan tingkat predasi yang (a) tinggi dan (b) rendah pada K1 ... 9
4 Bidang fase (a) untuk Gambar 3a dan (b) untuk Gambar 3b ... 10
5 Dinamika populasi mangsa dan pemangsa dengan tingkat predasi yang (a) tinggi dan (b) rendah pada K2 ... 11
6 Bidang fase (a) Gambar 5a dan (b) Gambar 5b ... 11
7 Dinamika populasi mangsa dan pemangsa dengan perubahan tingkat predasi yang signifikan pada K3, di mana (a) 0 <β <β1, (b)β1 <β <β2, dan (c) β >β2 ... 13
8 Bidang fase untuk (a) Gambar 7a, (b) Gambar 7b, dan (c) Gambar 7c ... 13
9 Limit cycle 2 ... 13
10 Dinamika populasi mangsa dan pemangsa dengan waktu pencarian singkat dan tingkat predasi yang rendah ... 14
11 Bidang fase untuk Gambar 10 ... 14
DAFTAR LAMPIRAN
Halaman 1 Penondimensionalan model ... 172 Penentuan titik tetap ... 18
3 Penentuan jenis kestabilan titik tetap ... 19
4 Bukti persamaan (4.5) ... 22
5 Program penggambaran dinamika populasi mangsa dan pemangsa dengan tingkat predasi yang tinggi pada K1 (Gambar 3a) ... 23
6 Program penggambaran dinamika populasi mangsa dan pemangsa dengan tingkat predasi yang rendah pada K1 (Gambar 3b) ... 24
7 Program penggambaran bidang fase pada K1... 25
8 Program penggambaran dinamika populasi mangsa dan pemangsa dengan tingkat predasi yang tinggi pada K2 (Gambar 5a) ... 26
9 Program penggambaran dinamika populasi mangsa dan pemangsa dengan tingkat predasi yang rendah pada K2 (Gambar 5b) ... 27
10 Program penggambaran bidang fase pada K2... 28
11 Program penggambaran dinamika populasi mangsa dan pemangsa dengan perubahan tingkat predasi yang signifikan pada K3 di mana (Gambar 7a) ... 29
12 Program penggambaran dinamika populasi mangsa dan pemangsa dengan perubahan tingkat predasi yang signifikan pada K3 di mana (Gambar 7b) ... 30
13 Program penggambaran dinamika populasi mangsa - pemangsa dengan perubahan tingkat predasi yang signifikan pada K3 di mana (Gambar 7c) ... 31
14 Program penggambaran dinamika populasi mangsa - pemangsa pada K3 di mana bernilai besar (Gambar 10) ... 32
15 Program penggambaran bidang fase pada K3 untuk ... 33
16 Program penggambaran bidang fase pada K3 untuk ... 34
17 Program penggambaran bidang fase pada K3 untuk ... 35
18 Program penggambaran bidang fase pada K3 untuk ... 36
19 Program penggambaran limit cycle pada K3 ... 37
I
PENDAHULUAN
1.1Latar Belakang
Predator atau pemangsa merupakan suatu organisme yang mencari, memburu, dan memakan organisme lain. Sedangkan mangsa adalah organisme yang diburu dan dimakan oleh pemangsa. Interaksi antara mangsa dan pemangsa merupakan kejadian berulang yang terjadi secara terus-menerus dan kehadiran keduanya dapat saling mempengaruhi populasi satu sama lain.
Kehadiran pemangsa merupakan faktor yang secara langsung mempengaruhi populasi mangsa. Populasi mangsa berkurang sebanding dengan jumlah konsumsi per satu pemangsa pada lingkungan tersebut. Andaikan setiap pemangsa hanya memiliki satu jenis mangsa, maka konsumsi yang berlebih akan mengakibatkan jumlah mangsa dapat berkurang dengan cepat yang di kemudian hari akan mendorong keduanya kepada kepunahan. Oleh karena itu, tingkat pertumbuhan mangsa diharapkan lebih besar dari pada tingkat pertumbuhan pemangsa. Sehingga, konsumsi pemangsa akan terus terpenuhi oleh populasi mangsa yang jauh lebih banyak.
Oleh karena itu, mangsa-pemangsa menjadi salah satu fenomena alam yang patut dipelajari, bukan hanya untuk upaya pelestarian organisme tersebut tetapi juga dampak keseimbangan alam yang diakibatkan oleh populasi keduanya di masa yang datang. Alfred Lotka (1925) dan Volterra Vito (1927) dalam Beals et al. (1999) mengembangkan sepasang persamaan diferensial yang menggambarkan fenomena mangsa-pemangsa untuk pertama kali. Sepasang persamaan diferensial yang dikenal sebagai model Lotka-Volterra. Dalam model Lotka-Volterra dibuat beberapa asumsi yaitu
1 Populasi mangsa tumbuh secara eksponensial saat ketidakhadiran predator,
2 Populasi pemangsa akan kelaparan tanpa adanya populasi mangsa, 3 Predator dapat mengkonsumsi jumlah
tak terbatas mangsa, dan
4 Tidak ada kompleksitas lingkungan. Selanjutnya, Beals et al. (1999)
menyatakan bahwa salah satu kekurangan dari model Lotka-Volterra adalah ketergantungan pada asumsi yang tidak realistis. Pendapat senada juga disampaikan oleh Gasull et al. (1997) bahwa model
Lotka-Volterra sangat tidak realistis karena populasi mangsa dapat tumbuh tanpa batas banyaknya saat ketidakhadiran pemangsa.
Setelah itu, mulai berkembang beberapa model yang merupakan modifikasi dari model Lotka-Volterra tersebut, yaitu model Holling-Tanner. Gasull et al. (1997) mengungkapkan bahwa model Holling-Tanner memberikan gambaran adanya kompetisi yang terjadi di antara para mangsa saat kepadatan yang tinggi. Pada saat kepadatan yang tinggi, para mangsa akan bersaing untuk mendapatkan sumber daya mereka.
Dalam tulisan ini, penulis merekonstruksi ulang model Holling-Tanner yang dijelaskan oleh Gasull et al. (1997). Dalam model Holling-Tanner ini digunakan respon fungsional yang tidak hanya monoton naik tetapi juga solusi yang terbatas. Dalam karya ilmiah ini, model tersebut disebut sebagai model Holling-Tanner tipe II.
1.2Tujuan
Tujuan dari penulisan karya ilmiah ini adalah sebagai berikut:
1 Merekonstruksi model Holling-Tanner tipe II,
2 Menganalisis perilaku dinamik yang terjadi pada model Holling-Tanner tipe II,
3 Memeriksa kestabilan global pada model Holling-Tanner tipe II, dan 4 Menunjukkan terjadinya bifurkasi
Hopf pada model Holling-Tanner tipe II.
1.3Sistematika Penulisan
II
LANDASAN TEORI
2.1Sistem Persamaan Diferensial
Suatu sistem persamaan diferensial orde 1 dinyatakan sebagai berikut
(2.1) dengan dan adalah fungsi dari waktu t. Jika adalah suatu fungsi matriks A berukuran n × n dengan koefisien konstan dan dinyatakan sebagai vektor konstan b, maka akan diperoleh bentuk-bentuk sistem persamaan diferensial linear sebagai berikut
, x(0)=x0 (2.2) (Farlow 1994) 2.2Titik Tetap
Misalkan diberikan persamaan diferensial sebagai berikut
(2.3)
Titik disebut titik tetap jika memenuhi . Titik tetap disebut juga titik kritis atau titik kesetimbangan.
(Tu 1994) 2.3Pelinearan
Diketahui
(2.4) Dan misalkan adalah titik tetap (2.4). Maka dan . Misalkan, dan , sehingga didapatkan
dalam bentuk matriks
. Matriks disebut matriks
Jacobi pada titik tetap . Karena
, maka dapat
diabaikan, sehingga didapatkan persamaan linear (2.5) (Strogatz 1994) 2.4Vektor Eigen dan Nilai Eigen
Misalkan A matriks berukuran n × n, maka suatu vektor tak nol di Rn disebut vektor eigen dari A jika untuk suatu skalar yang disebut nilai eigen dari A berlaku
Ax = x. (2.6) Vektor x disebut vektor eigen yang bersesuaian dengan nilai eigen . Untuk mencari nilai eigen dari matriks yang berukuran n × n maka persamaan (2.6)dapat dituliskan kembali sebagai berikut
(A – I) x = 0 (2.7) dengan I adalah matriks identitas. Persamaan (2.7) mempunyai solusi tak nol jika dan hanya jika
det (A – I)= |A – I| = 0. (2.8) Persamaan (2.8) disebut persamaan karakteristikdari matriks A.
(Anton 1995) 2.5Analisis Kestabilan Titik Tetap
Misalkan diberikan matriks A berukuran dengan
persamaan karakteristik matriks A tersebut dapat diperoleh dengan menyelesaikan persamaan
. Sehingga diperoleh persamaan
2
0
dengan:. Nilai eigen dari matriks A adalah
2 1,2 4 2 (2.9)
Untuk Δ < 0
Kedua nilai eigen mempunyai akar real yang berbeda tanda, maka titik tetap bersifat titik pelana (saddle point). Untuk Δ > 0.
o Jika τ > 0 maka titik tetap menjadi simpul tidak stabil.
o Jika τ < 0 maka titik tetap menjadi simpul stabil.
o Jika τ > 0 maka titik tetap menjadi spiral tidak stabil.
o Jika τ < 0 maka titik tetap menjadi spiral stabil.
o Jika τ = 0 maka titik tetap menjadi center.
kurva adalah garis batas antara simpul dengan spiral. Star nodes dan degenerate nodes yang terletak pada kurva ini. Jika kedua nilai eigen bernilai negatif maka titik tetap tersebut bersifat simpul sejati. Untuk Δ = 0
Dikarenakan salah satu nilai eigen bernilai nol titik tersebut disebut sebagai titik tetap tak terisolasi.
(Strogatz 1994)
2.6Limit Cycle
Limit cycle adalah orbit tertutup yang terisolasi. Terisolasi artinya bahwa orbit di sekelilingnya menuju atau menjauhi siklus limit.
(Strogatz 1994) 2.7Bifurkasi Hopf
Bifurkasi Hopf adalah kemunculan siklus batas (limit cycle) dari kesetimbangan dalam sistem dinamis yang dihasilkan oleh persamaan diferensial biasa, saat kesetimbangan mengalami perubahan stabilitas yang melalui sepasang nilai eigen murni imajiner. Bifurkasi dapat bersifat superkritis atau subkritis yang mengakibatkan limit cycle menjadi stabil atau tidak stabil.
Misalkan:
= f (x,a), x Rn (2.10) adalah sistem persamaan diferensial mandiri orde-2 yang tergantung pada parameter a ∈ R. Diasumsikan bahwa matriks Jacobi A(a) = fx(x0(a),a) memiliki sepasang nilai eigen kompleks
1,2(a) = (α) ± iω(α)
(2.11)
yang menjadi imajiner murni saat a = 0, yaitu (0) = 0 dan ω(0) = ω0 > 0. Kemudian, ketika a melewati a = 0 stabilitas kesetimbangan berubah.III
PEMODELAN
3.1Respon Fungsional Model Holling-Tanner
Model yang dianalisis dalam karya ilmiah ini adalah sebuah model dinamika mangsa-pemangsa yang diperkenalkan oleh Holling dan Tanner sebagai berikut,
,
, (3.1) dan .
Pada model (3.1), populasi mangsa dinyatakan sebagai x dan populasi pemangsa dinyatakan sebagai y. Hsu & Hwang 1999 mengasumsikan bahwa populasi mangsa tumbuh secara logistik dengan daya dukung (K) dan laju pertumbuhan intrinsik (r). Banyaknya mangsa yang dikonsumsi oleh pemangsa dinyatakan sebagai respon fungsional p(x) di mana pemangsa tumbuh secara logistik dengan laju pertumbuhan intrinsik (s) serta daya dukung yang bergantung pada populasi mangsa, yaitu dengan h menyatakan jumlah mangsa yang dibutuhkan oleh pemangsa.
Model Holling-Tanner terbagi menjadi tiga tipe respon fungsional seperti berikut:
3.1.1Model Holling-Tanner tipe I
,
, (3.2) dengan respon fungsional , di mana m adalah tingkat maksimum predasi yang dilakukan pemangsa. Tipe respon fungsional ini sangat dipengaruhi oleh jumlah populasi mangsa, dengan semakin banyak populasi mangsa maka semakin banyak mangsa yang akan dimangsa oleh pemangsa.
3.1.2Model Holling-Tanner tipe II
,
. (3.3)
Respon fungsional pada model (3.3) dinyatakan dengan
, dengan A merupakan parameter yang sebanding dengan waktu yang dibutuhkan pemangsa untuk menemukan mangsa, ini nampak lebih realistis. Faktor waktu tersebut secara tidak langsung mempengaruhi jumlah yang dimangsa. Semakin singkat waktu pencarian mengindikasikan mudahnya pemangsa mendapatkan mangsa.
3.1.3Model Holling-Tanner tipe III
,
. (3.4) Respon fungsional yang digunakan adalah
yang lebih rumit
dibandingkan dengan tipe-2.
(Hsu & Huang 1995)
3.2Penondimensionalan Model
Di antara ketiga tipe model Tanner, analisis dibatasi pada model Holling-Tanner tipe II (3.3) yang lebih realistis dibandingkan dengan 1, sedangkan tipe-3 nampak lebih rumit dari keduanya. Model Holling-Tanner tipe II dengan banyak parameter ditransformasikan ke bentuk yang lebih sederhana dengan cara penondimensionalan model.
Pada model (3.3) didefinisikan , ,
, ,
, dan (lihat Lampiran 1). Diperoleh:
,
g(x)
x 1
1
IV
PEMBAHASAN
4.1Penentuan dan Analisis Kestabilan Titik Tetap
Titik tetap persamaan (3.5) didapat dari
dan
, sehingga menurut persamaan tersebut diperoleh 2 titik tetap, yaitu dan
dapat dilihat pada Lampiran 2. Masing-masing titik tetap disubstitusikan ke dalam matriks Jacobi persamaan (3.5) agar diperoleh nilai eigen ( ). Matriks Jacobi dari persamaan (3.5) adalah sebagai berikut:
2 2 2 1 2 ( ) . 2
y xy x
x
a x a x a x
J y y x x (4.1)
Kestabilan titik tetap dapat dilihat dari nilai eigen yang dihasilkan oleh matriks Jacobi (4.1) yang dievaluasi pada titik tetap tersebut. Selanjutnya, kestabilan di sekitar titik tetap diperiksa, dimulai dari titik tetap yang pertama . Titik tetap disubstitusikan ke dalam persamaan matriks Jacobi (4.1), sehingga dihasilkan matriks
(1,0) 1 1 1 0 J a
. Diperoleh dua nilai
eigen yang bernilai positif dari , yaitu dan dengan . Selanjutnya, nilai determinan (Δ) dan teras ( ) dicari dari nilai eigen tersebut. Determinan (Δ) merupakan hasil perkalian dari dua nilai eigen ( ) sedangkan teras adalah hasil penjumlahannya ( ). Nilai yang diperoleh adalah dan . Jadi, jenis kestabilan di sekitar titik tetap adalah titik sadel.
Sedangkan titik tetap yang ke dua bergantung pada nilai parameter, sehingga terlebih dahulu ditentukan nilai parameter tersebut. Titik merupakan ekuilibrium persamaan (3.5) di mana dan dengan persamaan (3.5) yang disederhanakan menjadi persamaan bentuk umumnya seperti berikut:
,
(4.2)
dengan dan . Terdapat dua hipotesis untuk g(x) dan p(x), ditulis H1 dan H2, yakni:
(H1) g(1) = 0 dan g’(x) < 0 untuk (H2) p(0) = 0, p(x) > 0 untuk
(a) (b)
Gambar 1 Ilustrasi (a) H1 dan (b) H2.
Teorema 4.1 Misalkan H1 dan H2 terjadi. Solusi dari persamaan (4.2) adalah positif dan terbatas yaitu terdapat T ≥ 0 sehingga x(t) < 1, y(t) < δ/β untuk .
Bukti:
Andaikan untuk setiap T ≥ 0 solusi tidak terbatas atau x(t) ≥ 1 maka p(0) = 0 tidak terjadi sehingga H1 berlaku tetapi H2 tidak. Sedangkan jika y(t) ≥ δ/β maka solusi menjadi tidak terbatas. Jadi, solusi sistem terbatas pada x(t) < 1dan y(t) < δ/β. Sehingga solusi yang memenuhi titik adalah dan , di mana
. (4.3)
Sistem (4.2) memiliki titik ekuilibrium dengan matriks Jacobi
2
( *) '( *) ( *)
( *) .
p x h x p x
J E
(4.4)
Dimisalkan , sehingga diperoleh persamaan karakteristik nilai eigen seperti berikut,
2
( *) '( *) ( *) '( *) 0.
p x h x p x h x
Diasumsikan bahwa persamaan karakteristik nilai eigen di atas setara dengan
Diketahui bahwa
(4.5)
dan
(4.6)
dengan h(x) = (1 - x)(a + x)diperoleh , (4.7)
sehingga diketahui bahwa Δ > 0 (lihat Lampiran 4). Dengan ini, kedua nilai eigen bernilai sama negatif ataukah positif. Sedangkan nilai eigen diperoleh dengan cara
.
(4.8) Berdasarkan (4.8), kestabilan titik tetap yang ke dua bergantung pada nilai P dan D, dengan . Jika P > 0 maka titik tetap yang ke dua menjadi stabil dan menjadi tidak stabil jika P < 0. Kemudian, jika D > 0 titik tetap bersifat simpul dan jika D < 0 titik tetap bersifat spiral. Dengan itu, terlebih dahulu diperiksa kondisi dari P dari persamaan (4.5) yang setara dengan
(4.9)
di mana
. (4.10) Persamaan (4.9) merupakan hasil substitusi ke dalam persamaan (4.5). Dikarenakan sehingga kondisi P setara dengan kondisi dari Q (lihat Lampiran 4).
Berdasarkan persamaan (4.10) maka analisis kestabilan titik tetap yang ke dua terlebih dahulu harus dilihat dari beberapa kasus berikut:
(K1)
(K2) dan , dan
(K3) dan . Pada kasus K1 diperoleh Q > 0 untuk setiap . Pada K2 terdapat syarat perlu dan cukup bagi sifat definit positif suatu persamaan orde dua. Berlakunya sifat definit positif menunjukkan bahwa setiap daerah hasil dari suatu persamaan orde dua bernilai
positif. Sehingga pada kondisi K2 juga diperoleh Q>0. Sedangkan pada K3 terdapat tiga selang nilai dengan dua selang di antaranya bernilai Q>0 dan yang lainnya Q<0. Pada K3 dimisalkan persamaan (4.10) setara dengan dengan
dan
untuk 0 < θ1 < θ2 < 1 sehingga terdapat tiga selang nilai x yang menjadi subkasus pada K3 seperti berikut:
(SK1) , (SK2) , dan
(SK3) .
Pada SK1 dan SK3 diperoleh Q>0 sedangkan SK2 diperoleh Q<0. Sehingga pada SK1 dan SK3 dihasilkan kondisi P>0 sedangkan pada SK2 dihasilkan kondisi P<0.
Pada model (3.5) kondisi
dan dipenuhi oleh (4.11) dan (4.12)
sehingga dari persamaan (4.12) dan (4.11) diperoleh
. (4.13)
Berdasarkan (4.13) kondisi SK1, SK2, dan SK3 masing-masing dapat direpresentasikan melalui paramater β seperti berikut:
, (4.14)
, dan (4.15) (4.16) dengan untuk . Jadi, dinyatakan bahwa titik tetap yang ke dua bersifat stabil pada kondisi (4.14) dan (4.16), sedangkan pada kondisi (4.15) titik tetap yang ke dua bersifat tidak stabil seperti yang diuraikan oleh Hsu dan Huang (1995).
Dipilih , sehingga
(4.17)
dapat ditulis dengan D = R + S, dengan
;
Diketahui bahwa
dan
,
(4.18)
Persamaan (4.18) dinyatakan bahwa S > 0 jika dan hanya jika atau , sedangkan S < 0 jika dan hanya jika atau .
Pada kondisi atau dihasilkan |R| < |S| dikarenakan
. sehingga pada kondisi atau diperoleh D > 0 sedangkan pada kondisi atau diperoleh D < 0. Setelah kondisi P dan D diketahui maka kestabilan titik tetap yang ke dua dapat diklasifikasikan seperti pada Tabel 1.
Tabel 1Jenis kestabilan titik tetap
Kondisi Q Subkasus T1(x,y) P D T2(x,y)
K1 Q>0
Sadel
P>0
D<0 Spiral stabil
Sadel D>0 Simpul
stabil
K2 dan
Q>0
Sadel
P>0
D<0 Spiral stabil
Sadel D>0 Simpul
stabil
K3
dan
Q>0 Sadel P>0 D<0 Spiral stabil Q<0 Sadel P<0 D<0 Spiral
tidak stabil Q>0 Sadel P>0 D<0 Spiral
stabil Q>0 Sadel P>0 D>0 Simpul
stabil Pada Tabel 1 diklasifikasikan jenis
kestabilan titik tetap yang ke dua berdasarkan kondisi atau kasus yang diperoleh. Kasus tersebut merupakan interpretasi dari waktu pencarian untuk pemangsaan. Pada kondisi K1 diambil waktu pencarian yang lebih lama dari pada K2 dan juga K3. Pada K1 dan K2 masing-masing terbagi menjadi dua subkondisi, yaitu dengan tingkat predasi yang tinggi dan rendah. Diketahui bahwa pada K1 dan K2 titik tetap yang ke dua merupakan titik tetap stabil di mana pada subkondisi tingkat
predasi yang tinggi ( ) titik tetap tersebut bersifat spiral stabil, sedangkan pada tingkat predasi yang rendah ( ) titik tetap yang ke dua bersifat simpul stabil. Pada K3, perilaku dinamika populasi mangsa-pemangsa dilihat berdasarkan perubahan tingkat predasi yang kecil (signifikan) dan besar. Saat perubahan tingkat predasi yang kecil titik tetap yang ke dua mengalami perubahan kestabilan, di mana pada saat itu tingkat predasi yang terjadi adalah cukup tinggi. Perubahan tersebut adalah seperti pada
saat kondisi 0 < β < β1 titik tetap yang ke dua bersifat spiral stabil kemudian bersifat spiral tak stabil pada kondisiβ1 < β < β2 dan berubah kembali pada kondisi β2 < β menjadi bentuk spiral stabil. Sedangkan pada saat perubahan β menjadi sangat besar sifat kestabilan titik tetap yang ke dua berubah menjadi simpul stabil.
4.2Stabilitas Global dan Bifurkasi Hopf Berdasarkan kondisi P kestabilan titik tetap yang ke dua dipengaruhi oleh tiga kasus di bawah ini:
(K1)
(K2) dan , dan
(K3) dan . Pada K1 dan K2 akan terjadi kestabilan secara global berdasarkan Teorema 4.2.
Teorema 4.2.
(i) Misalkan K1 atau K2 berlaku, maka ekuilibrium adalah stabil asimtot global di dalam kuadran pertama,
(ii) Misalkan K3 dan SK1 berlaku, maka kesimpulan dari (i) berlaku.
Bukti (i) dan (ii) terdapat pada global stability for class of predator-prey systems (Hsu & Huang 1995) (lihat Lampiran 20). Teorema 4.1 menyatakan bahwa solusi sistem terbatas sehingga pada kondisi tersebut sistem mengalami kestabilan global asimtotik. Sehingga pada kondisi ini populasi mangsa-pemangsa akan stabil menuju ke suatu nilai.
Diketahui bahwa nilai eigen sistem adalah sebagai berikut
dengan persamaan (4.5) dan (4.6). Pada kasus K1 dan K2 diperoleh sehingga kedua nilai eigen bernilai negatif yang diindikasikan sistem menjadi stabil. Sedangkan pada kasus K3 dihasilkan tiga subkasus, seperti berikut:
, (4.14)
, dan (4.15)
(4.16) di mana pada (4.14) dan (4.16) nilai P bernilai positif, sehingga pada kedua subkasus tersebut diperoleh titik tetap stabil. Sedangkan pada (4.15) titik tetap yang ke dua merupakan titik tetap tidak stabil.
Fenomena perubahan kestabilan yang terjadi di sekitar β1 dan β2 pada K3, yaitu saat P = 0, dihasilkan nilai eigen yang bernilai
imajiner murni. Nilai eigen yang bernilai imajiner murni berakibat sifat kestabilan berubah menjadi center. Dalam kasus ini fenomena perubahan kestabilan tersebut dikenal sebagai bifurkasi Hopf.
Bifurkasi Hopf terjadi ketika titik tetap yang semula memiliki kestabilan spiral stabil menjadi spiral tidak stabil atau sebaliknya dan terdapat limit cycle di dalamnya, di mana perubahan kestabilan tersebut terjadi pada (K3). Pada saat kondisi 0 < β < β1 titik tetap yang ke dua merupakan spiral stabil kemudian berubah menjadi spiral tak stabil pada kondisi β1 < β < β2 dan berubah kembali pada kondisi β2 < βmenjadi spiral stabil.
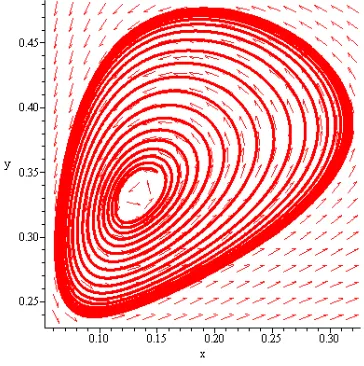
Gambar 2 Limitcycle.
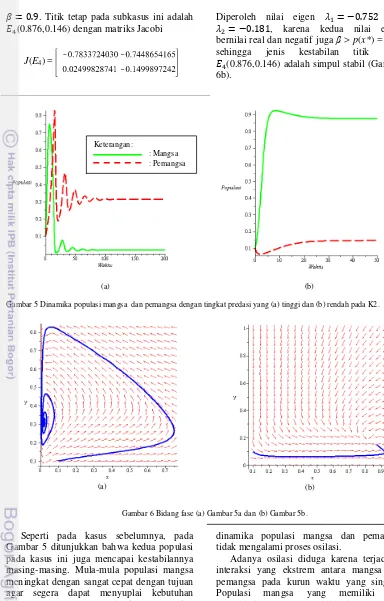
Limit cycle diperkirakan terjadi pada kondisi SK3. Gasull et al. (1997) menyatakan bahwa pada kondisi yang direpresentasikan menjadi β1 < β < β2. adalah pusat tidak stabil. Teorema 4.1 digunakan untuk menarik kesimpulan adanya limit cycle pada kasus ini (lihat Gambar 2).
4.3Dinamika Populasi Mangsa-Pemangsa Model Holling-Tanner Tipe II
Pada saat penondimensionalan model, diketahui bahwa dengan sebanding dengan lamanya waktu pencarian oleh pemangsa (A). Sedangkan secara tidak langsung menyatakan tingkat predasi, dengan s menyatakan laju pertumbuhan intrinsik pemangsa, h adalah jumlah mangsa yang dibutuhkan oleh satu pemangsa, dan m adalah predasi maksimal yang dapat dilakukan oleh pemangsa. Sehingga tingginya tingkat predasi terhadap mangsa direpresentasikan dengan kecilnya nilai dari parameter . Jadi, pada proses simulasi diperlihatkan pengaruh lamanya waktu pencarian dan tingkat predasi yang masing-masing direpresentasikan oleh a dan untuk penggambaran dinamika populasi mangsa-pemangsa.
4.3.1Kasus K1
Pada kasus pertama, pemangsa dihadapkan pada waktu pencarian yang lama dengan kondisi parameter adalah a + δ > 1. Nilai parameter yang diambil adalah 0.15 dan 0.99 serta nilai awal yaitu 0.1 dan
0.1 masing-masing per satuan
populasi. Pada subkasus yang pertama diperlihatkan pengaruh tingkat predasi yang tinggi dengan . Titik tetap pada
subkasus ini adalah (0.06575,0.98633) dengan matriks Jacobi
diperoleh nilai eigen 0.0788+0.37I dan 0.0788-0.37I, karena kedua nilai eigen merupakan bilangan kompleks yang bernilai negatif juga nilai β < p(x*), dengan p(x*) = 0.062 sehingga jenis kestabilan titik tetap (0.06575,0.98633) adalah spiral stabil (Gambar 4a).
Pada subkasus yang ke dua diperlihatkan pengaruh tingkat predasi yang rendah dengan . Titik tetap pada subkasus ini adalah
(0.91973,0.15328) dengan matriks Jacobi
.
Diperoleh nilai eigen 0.86420 dan 0.1668, karena kedua nilai eigen bernilai real negatif juga β > p(x*), di mana p(x*) = 0.48 sehingga jenis kestabilan titik tetap (0.91973,0.15328) adalah simpul stabil (Gambar 4b).
(a) (b)
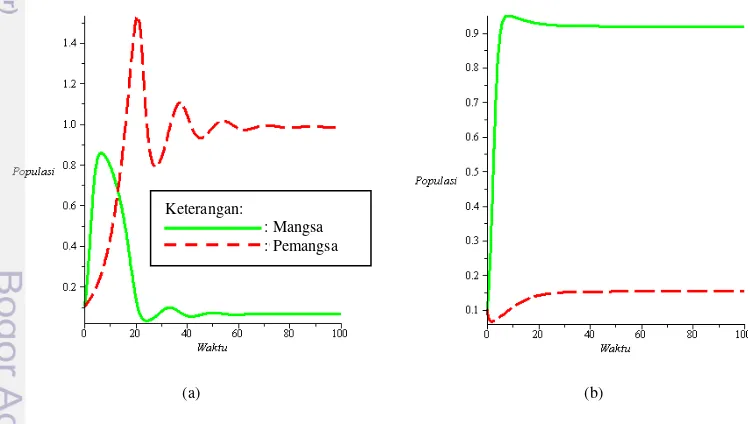
Gambar 3 Dinamika populasi mangsa dan pemangsa dengan tingkat predasi yang (a) tinggi dan (b) rendah pada K1.
Gambar 3a memperlihatkan bahwa di awal waktu populasi mangsa mengalami pertumbuhan yang lebih cepat dibandingkan dengan pertumbuhan populasi pemangsa.
Pertumbuhan populasi mangsa yang cepat akan menyuplai kebutuhan konsumsi pemangsa dengan segera. Selanjutnya, populasi mangsa menyusut drastis ketika Keterangan:
populasi pemangsa mulai berkembang yang kemudian mengalami proses osilasi sebelum kedua populasi tersebut stabil menuju ke suatu nilai. Gambar 3b juga memperlihatkan bahwa di awal waktu populasi mangsa akan mengalami pertumbuhan yang lebih cepat dibandingkan dengan pertumbuhan populasi pemangsa. Perbedaannya adalah perbandingan antara populasi mangsa dan pemangsa, di mana pada Gambar 3a diperlihatkan populasi pemangsa lebih banyak dari pada populasi mangsa, sedangkan pada Gambar 3b diperlihatkan bahwa populasi pemangsa tidak pernah melebihi populasi mangsa.
Berdasarkan persamaan (4.3), diketahui bahwa perbandingan antara parameter
terhadap parameter δ adalah setara dengan perbandingan populasi mangsa terhadap populasi pemangsa saat ekuilibrium. Jadi, ketika tingkat predasi yang tinggi melebihi rasio laju pertumbuhan pemangsa terhadap mangsa, populasi mangsa menjadi lebih sedikit dikarenakan populasi mangsa berkurang dengan drastis seiring bertambahnya populasi pemangsa yang memiliki tingkat predasi yang tinggi. Sebaliknya, populasi pemangsa menjadi lebih sedikit di saat tingkat predasi yang rendah dan dengan waktu pencarian yang lama sehingga populasi mangsa terus bertambah banyak dengan sumber daya yang terbatas.
(a) (b)
Gambar 4 Bidang fase (a) untuk Gambar 3a dan (b) untuk Gambar 3b.
Pada Gambar 4 diberikan ilustrasi bidang solusi di sekitar titik tetap di mana pada kedua subkasus tersebut kedua populasi stabil menuju suatu nilai. Pada bagian (a) diperlihatkan bahwa jenis kestabilan titik tetap pada kondisi tingkat predasi yang tinggi adalah spiral stabil. Sedangkan pada kondisi tingkat predasi yang rendah adalah simpul stabil. Perubahan nilai parameter β yang menjadi besar menyebabkan perubahan jenis kestabilan titik tetap dari jenis spiral stabil menjadi simpul stabil.
4.3.2Kasus K2
Pada kasus yang ke dua ini pemangsa dihadapkan dengan waktu pencarian yang lebih singkat dibandingkan waktu pencarian pada kasus pertama di mana kondisi parameter a + δ < 1 dan (1 - a - δ)2 - 8aδ < 0 dengan nilai parameter 0.15 dan 0.3
serta nilai awal yaitu dan masing-masing per satuan populasi. Sama seperti pada kasus yang pertama, pada subkasus ini juga diperlihatkan pengaruh tingkat predasi yang tinggi dengan . Titik tetap pada subkasus ini adalah
(0.0209,0.3142) dengan matriks Jacobi
J(E3) =
Diperoleh nilai eigen 0.0535+0.37I dan 0.0535-0.37I, karena kedua nilai eigen merupakan bilangan kompleks dan negatif juga β < p(x*), dengan p(x*) = 0.065 sehingga jenis kestabilan titik tetap (0.0209,0.3142) adalah spiral stabil (Gambar 6a).
. Titik tetap pada subkasus ini adalah (0.876,0.146) dengan matriks Jacobi
J(E4) =
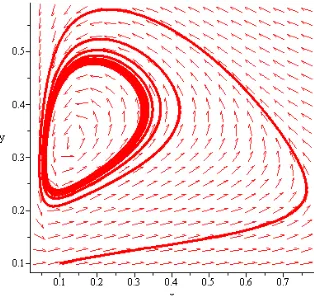
Diperoleh nilai eigen dan , karena kedua nilai eigen bernilai real dan negatif juga β > p(x*) = 0.74 sehingga jenis kestabilan titik tetap (0.876,0.146) adalah simpul stabil (Gambar 6b).
(a) (b)
Gambar 5 Dinamika populasi mangsa dan pemangsa dengan tingkat predasi yang (a) tinggi dan (b) rendah pada K2.
(a) (b)
Gambar 6 Bidang fase (a) Gambar 5a dan (b) Gambar 5b.
Seperti pada kasus sebelumnya, pada Gambar 5 ditunjukkan bahwa kedua populasi pada kasus ini juga mencapai kestabilannya masing-masing. Mula-mula populasi mangsa meningkat dengan sangat cepat dengan tujuan agar segera dapat menyuplai kebutuhan konsumsi pemangsa. Pada kondisi tingkat predasi yang tinggi, populasi pemangsa menjadi lebih banyak dibandingkan populasi mangsa sedangkan dengan tingkat predasi yang rendah populasi pemangsa jauh lebih sedikit dari pada populasi mangsa. Pada kondisi dengan tingkat predasi yang rendah
dinamika populasi mangsa dan pemangsa tidak mengalami proses osilasi.
Adanya osilasi diduga karena terjadinya interaksi yang ekstrem antara mangsa dan pemangsa pada kurun waktu yang singkat. Populasi mangsa yang memiliki laju pertumbuhan yang lebih besar dapat memenuhi kebutuhan konsumsi pemangsa dengan segera. Sehingga diduga penyebab terjadinya osilasi adalah tingkat predasi maksimum (m) yang cukup tinggi dan waktu pencarian yang lebih singkat.
Keterangan:
Pada Gambar 6 diberikan ilustrasi bidang fase di sekitar titik tetap di mana pada kedua subkasus tersebut kedua populasi stabil menuju suatu nilai. Pada bagian (a) diperlihatkan bahwa jenis kestabilan titik tetap pada kondisi tingkat predasi yang tinggi adalah spiral stabil. Sedangkan pada kondisi tingkat predasi yang rendah adalah simpul stabil seperti ditunjukkan pada Gambar 6(b).
4.3.3Kasus K3
Pada proses penggambaran kasus yang ke tiga ini, pemangsa dihadapkan dengan waktu pencarian yang jauh lebih singkat dengan perubahan tingkat predasi yang signifikan, dengan kondisi a + δ < 1 dan (1 - a - δ)2 - 8aδ > 0 dimana a = 0.25 dan δ = 0.15 serta nilai awal yaitu x(0) = 0.1 dan y(0) = 0.1 masing-masing per satuan populasi. Tingkat predasi nilai parameter β disesuaikan berdasarkan kondisi, β = 0.03 untuk 0 <β <β1 dan β = 0.1 untuk β >β2, dan β = 0.06 untuk β1 <β <β2 di mana θ1 = 0.088763, θ2 = 0.21124, β1 = 0.043 dan β2 = 0.087. Hasil komputasi dapat dilihat pada Gambar 7.
Pada subkasus 0 <β <β1 didapatkan titik tetap E5(0.058031,0.290156). Didapatkan matriks Jacobi
J(E5) =
serta dua nilai eigen λ1 = -0.0152+0.35I dan λ2= -0.0152 - 0.35I, dikarenakan kedua nilai eigen bernilai kompleks dan negatif juga β < p(x*) dengan p(x*) = 0.188 sehingga jenis kestabilan E5(0.058031,0.290156) adalah spiral stabil.
Pada subkasus β1 < β < β2 diperoleh titik tetap E6(0.132782,0.331956). Didapatkan matriks Jacobi sebagai berikut:
J(E6) =
dan nilai eigen λ1 = 0.009+0.32I dan λ2 = 0.009 - 0.32I, dikarenakan kedua nilai eigen bernilai kompleks dan positif juga β < p(x*) dengan p(x*) = 0.346 sehingga jenis
kestabilan E6(0.132782,0.331956) adalah spiral tidak stabil.
Sedangkan pada subkasus β > β2 diperoleh titik tetap E7(0.219951,0.36685). Didapatkan matriks Jacobi sebagai berikut:
J(E7) =
Diperoleh nilai eigen λ1 = -0.25+0.305I dan λ2 = -0.25-0.305I. Kedua nilai eigen tersebut bernilai kompleks dan negatif juga β < p(x*) dengan p(x*) = 0.468. Jadi, jenis kestabilan dari titik tetap E7(0.219951,0.36685) adalah spiral stabil.
(a) (b) (c)
Gambar 7 Dinamika populasi mangsa dan pemangsa dengan perubahan tingkat predasi yang signifikan pada K3, di mana (a) 0 <β <β1, (b)β1 <β <β2, dan (c) β >β2.
(a) (b) (c)
Gambar 8 Bidang fase untuk (a) Gambar 7a, (b) Gambar 7b, dan (c) Gambar 7c.
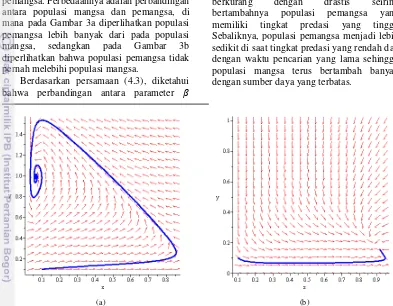
Pada kasus K3 terjadi perubahan kestabilan yang dipengaruhi oleh perubahan parameter β seperti ditunjukkan Gambar 8. Kestabilan titik tetap berubah dari stabil ke tidak stabil dan kemudian kembali stabil dengan parameter acuan β1 dan β2, di mana β1 = 0.43 dan β2 = 0.087. Pada saat β1 dan β2, nilai P = 0 sehingga kestabilan titik tetap ditentukan oleh akar dari determinan sistem di mana determinan sistem bernilai positif sehingga jenis kestabilan sistem menjadi center.
Pada Gambar 8 bagian a ditunjukkan bahwa E5(0.058031,0.290156) dengan kondisi parameter 0 < β < β1 adalah titik tetap stabil dengan jenis spiral stabil, sama seperti E7(0.219951,0.36685) dengan kondisi parameter β > β2 seperti ditunjukkan oleh Gambar 8c. Sedangkan Gambar 8b menunjukkan bahwa titik tetap E6 (0.132782, 0.331956) adalah spiral tidak stabil dengan kondisi parameter β1 <β < β2. Pada ilustrasi titik tetap E6 (0.132782, 0.331956) muncul
limit cycle. Dengan ini, fenomena yang terjadi pada kasus K3 seperti perubahan kestabilan titik tetap dan keberadaan limit cycle dengan berubahnya nilai suatu parameter sistem merupakan sifat bifurkasi Hopf, di mana pada kasus ini terjadi dua kali proses bifurkasi Hopf.
Gambar 9 Limit cycle 2. Keterangan:
Keberadaan limit cycle diperkuat oleh Gambar 9 yang merupakan penggambaran orbit yang terjadi diluar limit cycle tersebut menuju titik tetap. Sedangkan Gambar 8b diilustrasikan orbit bergerak keluar dari titik tetap dengan arah yang sama sehingga dari kedua gambar tersebut orbit akan terus bergerak dan bertemu hingga ada batas yang berbentuk siklus yang dikenal sebagai siklus limit atau limit cycle.
Pada subkasus berikutnya di mana pemangsa memiliki tingkat predasi yang cukup rendah dengan kondisi parameter a + δ < 1 dan (1 - a - δ)2 - 8aδ > 0 di mana a , δ dan β serta nilai awal yaitu dan masing-masing per satuan populasi. Pada subkasus ini diperoleh titik tetap E8 . Didapatkan matriks Jacobi sebagai berikut:
E8 =
di mana nilai eigen λ1 dan λ2 . Kedua nilai eigen tersebut bernilai real dan negatif juga β > p(x*) dengan p(x*) = 0.776. Jadi, jenis kestabilan dari titik tetap E8 adalah simpul stabil.
Pada Gambar 10 dinyatakan bahwa populasi pemangsa menjadi lebih sedikit dibandingkan dengan populasi mangsa seperti pada dua kasus sebelumnya. Interaksi kedua populasi pada kondisi ini terjadi tidak secara ekstrem sehingga kedua populasi masing-masing akan mengalami kestabilan menuju ke suatu nilai setelah mencapai populasi maksimum. Hal ini disebabkan oleh tingkat predasi yang rendah yang juga menyebabkan perubahan jenis kestabilan dari spiral stabil menjadi simpul stabil (Gambar 11).
Gambar 10 Dinamika populasi mangsa dan pemangsa dengan waktu pencarian singkat dan tingkat predasi yang rendah.
Gambar 11 Bidang fase untuk Gambar 10.
Jadi, pada kasus ke tiga titik tetap sistem merupakan spiral stabil yang berubah menjadi spiral tidak stabil ketika parameter melewati β1 dan kembali menjadi spiral stabil ketika parameter melewati β2. Kemudian, saat parameter β semakin besar mendekati satu akan terjadi perubahan jenis kestabilan titik tetap di mana titik tetap yang semula merupakan spiral stabil akan berubah menjadi simpul stabil.
Keterangan:
SIMPULAN
Pada sistem ini diketahui bahwa tingkat predasi dari pemangsa sangat berpengaruh terhadap jenis kestabilan titik tetap. Pada saat tingkat predasi yang sangat tinggi kestabilan titik tetap sistem adalah spiral dan di saat tingkat predasi yang rendah titik sistem menjadi simpul. Tingkat predasi juga berpengaruh terhadap perbandingan kedua populasi di mana pada tingkat predasi yang rendah populasi pemangsa akan menjadi lebih sedikit dari pada populasi mangsa sedangkan pada tingkat predasi yang tinggi populasi pemangsa menjadi lebih banyak dari pada populasi mangsa.
Pada sistem ini diketahui bahwa solusi sistem adalah terbatas dengan satu titik tetap stabil sehingga kestabilan yang terjadi merupakan kestabilan secara global. Jadi, pada kasus pertama dan ke dua, sistem mengalami stabil global, sedangkan pada kasus ke tiga terjadi fenomena perubahan kestabilan titik tetap dan kemunculan limit cycle dengan berubahnya salah satu parameter sistem yang merupakan sifat bifurkasi Hopf.
DAFTAR PUSTAKA
Anton H. 1995. Aljabar Linear Elementer. Ed ke-5. Terjemahan Pantur Silaban dan I Nyoman Susila. Jakarta: Erlangga.
Farlow SJ. 1994. An Introduction to Differential Equations and Their Applications. New York: McGraw-Hill. Gasull A, Kooij RE, Torregrosa J. 1997. Limit
cycles in the Holling-Tanner model. Public Math 41:149-167.
Beals M, Gross L, Harrell S. 1999. Predator-prey dynamics: Lotka-Volterra. http://www.tiem.utk.edu/~gross/bioed/beal smodules/predator-prey.html. [20 Sep 2012].
Hsu SB, Huang TW. 1995. Global stability for a class of predator-prey systems. SIAM J Appl Math 55:763-783.
Hsu SB, Hwang TW. 1999. Hopf bifurcation analysis for a predator-prey system of Holling and Leslie type. Taiwanese Journal of Mathematics 3:35-53.
Strogatz SH. 1994. Nonlinear Dynamics and Chaos, with Application to Physics, Biology, Chemistry, and Engineering. Addison-Wesley Publishing Company. Tu PNV. 1994. Dynamical System, An
Introduction with Application in Economics and Biology. Heidelberg, Germany: Springer-Verlag.
Lampiran 1Penondimensionalan model. Model persamaan (3.3):
1
1
dx
x
mx
rx
y
dt
K
A x
dy
hy
sy
dt
x
Persamaan di atas ditransformasikan menjadi sistem persamaan yang lebih sederhana dengan metode nondimensional seperti berikut:
rt
, ( ) x t( ) K
, ( ) my t( )rK
,
s r
/
, shm
, dan a A K
( ) ( ) ( ) . . ( ) 1 1. 1 .
( )
( ) 1 ( ) ( ) ( ) ( ) ( ) 1 ( ) ( )
( )
d d dx t dt
d dx t dt d
x mx
rx y
K K A x r
A K a (1) ( ) ( ) ( ) . . ( ) 1 1 ( ) ( ) ( ) ( ) ( ) ( )
d d dy t dt
d dy t dt d
m hy
sy
rK x r
s sh r m
(2)
Persamaan hasil transformasi nondimensional dimisalkan kembali dengan dan sehingga menjadi persamaan (3.5) seperti berikut:
(1 )
( )
0 dan 0
dx x
x x y
dt a x
dy y y dt x x y
Lampiran 2 Penentuan titik tetap.
Titik tetap persamaan (3.5) ditentukan dengan membuat persamaan menjadi dx 0
dt dan 0 dy
dt
seperti pada persamaan berikut.
(1 ) x 0
x x y
a x
(4)
( y) 0
y
x
(5)
Dari persamaan (5) akan diperoleh nilai y sebagai berikut,
0
( ) 0
dy dt y y x
0 atau x
y y
(6)
Dari persamaan (6) akan diperoleh nilai x yang memenuhi dx 0
dt sebagai berikut, 0
dx
dt
Untuk
(1 ) 0
x x
x
0 atau
x
1
(7)Untuk
2 2(1 ) 0
(1 )( ) 0
( ) ( ) 0
0
( ( ) 0
x x
x x
a x
x x a x x
x a x a x x x
x a x a x x x
x x x a a
x
0
(8)
x1,2(9)
Titik tetap yang memenuhi solusi adalah
dan
Lampiran 3 Penentuan jenis kestabilan titik tetap. Diketahui matriks Jacobi seperti berikut
2 2 2 1 2 ( ) 2
dX dX ay x
x
dx dy a x a x
J
dY dY y y
dx dy x x
Titik tetap T(1,0)
Pelinearan pada titik tetap T(1,0)
(1,0) 1 2 1 2 1 2 1 1 1 0
( 1 )( )
1 0 1 J a J I
:. Jadi, berdasarkan δ < 0 jenis kestabilan di sekitar titik tetap T(1,0) adalah titik sadel. Titik tetap E*(x*, y*)
Kasus 1 ( ) β < p(x*)
Dipilih , , dan untuk disubstitusikan ke persamaan (10) agar diperoleh titik tetap, yaitu (0.06575, 0.98633). Selanjutnya parameter dan titik tetap disubstitusikan ke matriks Jacobi sistem sehingga dihasilkan nilai eigen sebagai berikut:
=
Jadi, jenis kestabilan titik tetap adalah spiral stabil. β > p(x*)
Dipilih , , dan untuk disubstitusikan ke persamaan (10) agar diperoleh titik tetap, yaitu (0.91973, 0.15328). Selanjutnya parameter dan titik tetap disubstitusikan ke matriks Jacobi sistem sehingga dihasilkan nilai eigen sebagai berikut:
=
Kasus 2 ( dan ) β < p(x*)
Dipilih , , dan untuk disubstitusikan ke persamaan (10) agar diperoleh titik tetap, yaitu (0.020948, 0.314225). Selanjutnya parameter dan titik tetap disubstitusikan ke matriks Jacobi sistem sehingga dihasilkan nilai eigen sebagai berikut:
=
Jadi, jenis kestabilan titik tetap adalah spiral stabil. β > p(x*)
Dipilih , , dan untuk disubstitusikan ke persamaan (10) agar diperoleh titik tetap, yaitu (0.87585, 0.14597). Selanjutnya parameter dan titik tetap disubstitusikan ke matriks Jacobi sistem sehingga dihasilkan nilai eigen sebagai berikut:
=
Jadi, jenis kestabilan titik tetap adalah simpul stabil. Kasus 3 ( dan )
Dipilih , , dan untuk disubstitusikan ke persamaan (10) agar diperoleh titik tetap (0.058031, 0.290156). Selanjutnya parameter dan titik tetap disubstitusikan ke matriks Jacobi sistem sehingga dihasilkan nilai eigen sebagai berikut:
=
Jadi, jenis kestabilan titik tetap adalah spiral stabil.
Dipilih , , dan untuk disubstitusikan ke persamaan (10) agar diperoleh titik tetap (0.132782, 0.331956). Selanjutnya parameter dan titik tetap disubstitusikan ke matriks Jacobi sistem sehingga dihasilkan nilai eigen sebagai berikut:
=
Dipilih , , dan untuk disubstitusikan ke persamaan (10) agar diperoleh titik tetap, yaitu (0.25,0.375). Selanjutnya parameter dan titik tetap disubstitusikan ke matriks Jacobi sistem sehingga dihasilkan nilai eigen sebagai berikut:
=
Jadi, jenis kestabilan titik tetap adalah spiral stabil. p(x*)
Dipilih , , dan untuk disubstitusikan ke persamaan (10) agar diperoleh titik tetap, yaitu (0.8705,0.14508). Selanjutnya parameter dan titik tetap disubstitusikan ke matriks Jacobi sistem sehingga dihasilkan nilai eigen sebagai berikut:
=
Lampiran 4 Bukti persamaan (4.5). Diketahui
dengan mensubstitusikan
ke persamaan
sehingga
dengan
di mana
Sehingga dengan , , , dan .
Jadi, .
Hal serupa juga berlaku terhadap
di mana dan , sehingga kondisi P bergantung pada kondisi Q(x).
Lampiran 5 Program penggambaran dinamika populasi mangsa dan pemangsa dengan tingkat predasi yang tinggi pada K1(Gambar 3a).
Ket:
Lampiran 6 Program penggambaran dinamika populasi mangsa dan pemangsa dengan tingkat predasi yang rendah pada K1(Gambar 3b).
Ket:
Lampiran 7Program penggambaran bidang fase pada K1.
>> Bidang fase Gambar 3a
Lampiran 8 Program penggambaran dinamika populasi mangsa dan pemangsa dengan tingkat predasi yang tinggi pada K2(Gambar 5a).
Ket:
Lampiran 9 Program penggambaran dinamika populasi mangsa dan pemangsa dengan tingkat predasi yang rendah pada K2(Gambar 5b).
Ket:
Lampiran 10 Program penggambaran bidang fase pada K2.
>> Bidang fase Gambar 5a
Lampiran 11 Program penggambaran dinamika populasi mangsa dan pemangsa dengan perubahan tingkat predasi yang signifikan pada K3 di mana (Gambar 7a).
Ket:
Lampiran 12 Program penggambaran dinamika populasi mangsa dan pemangsa dengan perubahan tingkat predasi yang signifikan pada K3 di mana (Gambar 7b).
Ket:
Lampiran 13 Program penggambaran dinamika populasi mangsa-pemangsa dengan perubahan tingkat predasi yang signifikan pada K3 di mana (Gambar 7c).
Ket:
Lampiran 14 Program penggambaran dinamika populasi mangsa-pemangsa pada K3 di mana (Gambar 10).
Ket:
Lampiran 20 Pembuktian Teorema 4.2.
(i) Misalkan:
(1 ) ( , )
( ) ( , )
(0) 0, (0) 0
dx x
x x y f x y
dt a x
dy y
y g x y
dt x x y digunakan
dengan dan diketahui:
2
( , ) (1 2 ) ( , )
( )
f ay
H x y x H x y
x a x
(11) 2 ( , ) ( , ) g y
H x y H x y
y x
(12)
2 2 1 2 2 2
( , ) 1
(1 )
1 (1 )
1
(1 ) (
H x y x x a
f x x y y
x a x x x
x x a x x
x x y y
a x x x a x a x
x x a x
x x y H x
a x x x a x
2 , ) 1 1
(1 ) ( , )
(1 )
(1 ) ( , )
( )
y x
x x y H x y
a x a x x
x x xy y
x H x y
a x a x a x
(13)
1 2 3 1 2 3 1 22 3 2
2 3 ( , ) 2 2 2 2
H x y y x
g y y
y x a x
y x
y y
x a x
y x
y y y y
x a x
y
y y y
x 2 2 1 ( , )
2 ( , )
H x y
y
y y H x y
x (14)
1 2 2 1 1 2 12 1 1 1 1
1 2 (1 ) 2
( )
( , )
2
1 1 1 1
1 2 (1 ) ( ) 2
( )
2 2
ay y xy
x x x y y
x a x x a x a x x
a x
H x y y
y x
y
x x x a x a x y y
a x x a x a x x
y y y x
2 2 2
2 2
2 2
( , )
(1 ) ( )
1 2 (1 ) 2 ( , )
( ) ( ) ( )
(1 )
( , )
( ) ( )
( )(1 ) (1 ) ( )(1 ) ( )(1 )
( ) ( )
H x y
x x ay xy y a x
x x H x y
a x a x a x a x
y x x ay xy
x H x y
a x a x a x a x
a x x x x a a x x x a x x
x
a x a x a x a x
2 2 2 2 2 ( , )
(1 ) (1 ) (1 )
(1 ) ( , )
(1 )
(1 ) ( , )
( , )
( , )
2 (1 )
( , )
(
H x y
x x a x x x
x x H x y
a x a x a x
a x
x x H x y
a x
a x ax x ax x a x a ax
H x y
a x
x ax x x a x
H x y
a x
x x a a
H x y
a x P
x) H x y( , )
a x (ii) Misalkan:
di mana dan telah ditentukan
dengan , di mana
Dipilih , sehingga
atau
di mana
agar untuk , sehingga
; untuk
.
(15)Misalkan
dan
maka
,