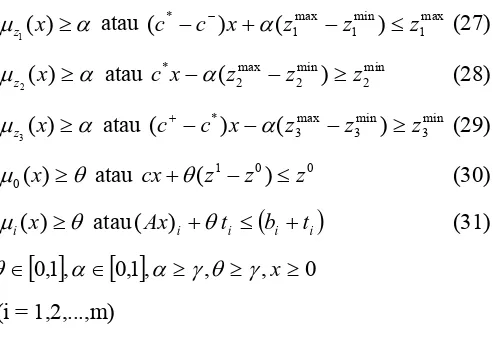Pendekatan Fuzzy Multiobjective Programming Pada Traveling Salesman Problem

ABSTRAK

Traveling salesman problem (TSP) adalah salah satu tantangan nyata-masalah kehidupan, menarik peneliti dari berbagai bidang termasuk Artificial Intelligence, Riset Operasi, dan Algoritma. Desain dan Analisis. Masalahnya telah dipebelajar dengan baik sehingga sekarang di bawah judul yang berbeda dan telah diselesaikan dengan pendekatan yang berbeda termasuk genetik algoritma dan pemrograman linear. Konvensional program linear dirancang untuk menangani dengan parameter garing, tetapi informasi tentang nyata sistem kehidupan sering tersedia dalam bentuk penjelasan kabur. Metode fuzzy yang dirancang untuk menangani hal kabur, dan yang paling sesuai untuk mencari solusi yang optimal untuk masalah dengan parameter kabur. Fuzzy multi-objektif linear program, sebuah tindakan percampuran dari logika fuzzy dan multi - objektif linear program, kesepakatan dengan fleksibel tingkat aspirasi atau tujuan dan kendala fuzzy dengan penyimpangan yang dapat diterima.

ABSTRACT

Traveling salesman problem (TSP) is one of the challenging real-life problems, attracting researchers of many fields including Artificial Intelligence, Operations Research, and Algorithm Design and Analysis. The problem has been well studied till now under different headings and has been solved with different approaches including genetic algorithms and linear programming. Conventional linear programming is designed to deal with crisp parameters, but information about real life systems is often available in the form of vague descriptions. Fuzzy methods are designed to handle vague terms, and are most suited to finding optimal solutions to problems with vague parameters. Fuzzy multi-objective linear programming, an amalgamation of fuzzy logic and multiobjective linear programming, deals with flexible aspiration levels or goals and fuzzy constraints with acceptable deviations.

BAB 1

PENDAHULUAN

1.7.Latar Belakang

Pada awal diciptakan, komputer hanya difungsikan sebagai alat hitung saja. Namun seiring dengan perkembangan zaman, maka peran komputer semakin mendominasi peran kehidupan. Lebih dari itu, komputer diharapkan dapat digunakan untuk mengerjakan segala sesuatu yang bisa dikerjakan oleh manusia baik dalam bidang pendidikan, kesehatan, industri, dan kehidupan sehari – hari sehingga peran komputer dan manusia akan saling melengkapi. Beberapa hal yang menjadi kekurangan manusia diharapkan dapat digantikan oleh komputer. Begitu juga komputer yang tidak akan berguna tanpa sentuhan manusia.

Untuk menggunakan atau memfungsikan sebuah komputer maka harus terdapat program yang terdistribusi didalamnya, tanpa program tersebut komputer hanyalah menjadi sebuah kotak yang tak berguna. Program yang terdapat pada komputer sangat bervariasi dan setiap program tersebut pasti menggunakan algoritma. Algoritma merupakan kumpulan perintah untuk menyelesaikan suatu masalah. Perintah-perintahnya dapat diterjemahkan secara bertahap dari awal hingga akhir. Masalah tersebut dapat berupa apapun dengan catatan untuk setiap masalah, memiliki kriteria kondisi awal yang harus dipenuhi sebelum menjalankan algoritma.

Secara umum, pencarian jalur terpendek dapat dibagi menjadi dua metode, yaitu metode konvensional dan metode heuristik. Metode konvensional cenderung lebih mudah dipahami daripada metode heuristik, tetapi jika dibandingkan, hasil yang diperoleh dari metode heuristik lebih variatif dan waktu perhitungan yang diperlukan lebih singkat.

Yang paling sering dianggap tujuan dari Traveling Salesman Problem selanjutnya dalam tulisan ini disingkat menjadi TSP adalah untuk menentukan secara optimal agar perjalanan semua kota dilalui sehingga total biaya adalah minimal. Mempertimbangkan situasi saat pengambilan keputusan harus menentukan solusi optimal dari TSP dengan meminimalkan biaya, waktu dan jarak keseluruhan.

Dalam pengambilan keputusan untuk memperoleh biaya, waktu dan jarak yang minimum digunakan metode logika fuzzy. Karena logika fuzzy merupakan salah satu dari artificial intelligent yang memiliki kemampuan untuk menyelesaikan masalah perilaku sistem yang kompleks dan memiliki ketidak pastian, sehingga apabila diterapkan pada sebuah kontroller, logika fuzzy dapat mengatasi proses dari suatu sistem yang dinamik, kompleks dan memiliki ketidak pastian yang disebabkan oleh kemampuan mengolah informasi numerik dari variabel yang diukur. Pada sistem logika fuzzy nilai yang diolah tidak hanya nilai yang dapat didefinisikan secara pasti seperti yang dapat dilakukan pada sistem kontrol konvensional yang hanya mengenal logika ‘0’ dan ‘1’ atau bekerja pada dua state sehingga dihasilkan perubahan yang besar, pada sistem logika fuzzy nilai yang berada antara ‘0’ dan ‘1’ juga dapat didefinisikan sehingga akan menghasilkan perubahan yang smooth.

1.8.Perumusan Masalah

dalam lintasan terpendek dibutuhkan suatu metode fuzzy multiobjective dalam menentukan hasil.

Berdasarkan kasus diatas maka dirumuskan masalah sebagai berikut : 1. Analisa pendekatan Fuzzy Multi-Objective dalam menyelesaikan kasus TSP. 2. Melakukan analisa pada TSP dalam menyelesaikan masalah jarak, biaya dan

waktu dengan melakukan beberapa simulasi data.

1.9.Tujuan Penelitian

Penelitian ini bertujuan untuk mengimplementasikan suatu algoritma yang dapat digunakan dalam menyelesaikan persoalan TSP kedalam model pemrograman fuzzy multiobjective sehingga masalah biaya, waktu, dan jarak dapat dioptimalisasi.

1.10. Kontribusi Penelitian

Selain menambah pemahaman dan pengetahuan penulis mengenai metode-metode yang digunakan sebagai alat bantu sistem pendukung keputusan untuk penyelesaian persoalan TSP, hasil penelitian ini juga bermanfaat untuk membantu memformulasikan persoalan dengan tujuan ganda dalam bentuk formulasi fuzzy multiobjective dan pemrograman linier, dan mengimplementasikan algoritma untuk model pemrograman fuzzy multiobjective tersebut.

1.11. Tinjauan Pustaka

dan suatu himpunan E (edge) kecuali E mengandung multiple edge, yaitu beberapa edge yang menghubungkan titik-titik ujung yang sama, dan E mungkin mengandung satu atau lebih loop, yaitu sebuah edge yang titik-titik ujungnya adalah verteks yang sama.

Logika fuzzy, diperkenalkan oleh Zadeh (1965), merupakan superset dari konvensional (Boolean) logika, yang telah diperpanjang untuk menangani konsep kebenaran sebagai nilai-nilai kebenaran antara “sepenuhnya benar” dan “sepenuhnya palsu”. Sebagai peneliti menyarankan, Modus dari logika yang melandasi alasan yang tepat daripada perkiraan. Istilah linguistik dapat mewakili pengalaman yang lebih baik dan subyektif dari sudut pandang keputusan dalam cara lebih intuitif dan format. Sebuah fungsi keanggotaan fuzzy yang ditetapkan, disebut fuzzy fungsi keanggotaan, yang dipetakan pada interval [0,1] yang merupakan nilai kebenaran.

Sebelum sampai pada pendefenisian masalah lintasan terpendek, terlebih dahulu pada bagian ini akan diuraikan mengenai konsep-konsep dasar dari model graph dan representasinya dalam memodelkan masalah lintasan terpendek.

Definisi 1.1. Sebuah graph G adalah pasangan (V,E) dimana V adalah himpunan tak kosong yang anggotanya disebut verteks dan E adalah himpunan yang anggotanya adalah pasangan tak berurut dari verteks V yang disebut edge.

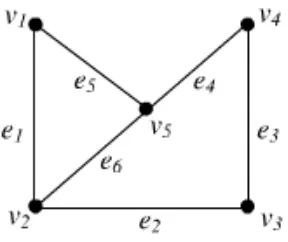
Secara umum graph dapat digambarkan dengan suatu diagram dimana verteks ditunjukkan sebagai titik yang dinotasikan dengan vi , i = 1, 2, …,P dan edge digambarkan dengan sebuah garis lurus atau garis lengkung yang menghubungkan dua verteks (vi, vj) dan dinotasikan dengan ek . Sebagai ilustrasi

Gambar 1.1. Graph dengan lima verteks dan enam edge

Pengambilan keputusan yang terbaik pada permasalahan TSP dalam adalah menggunakan logika fuzzy, dimana menurut Zadeh (1965), merupakan superset dari konvensional (Boolean) logika, yang telah diperpanjang untuk menangani konsep kebenaran sebagian nilai-nilai kebenaran antara “sepenuhnya benar” dan “sepenuhnya palsu”. Sebagian peneliti menyarankan bahwa, modus dari logika yang melandasi alasan lebih tepat daripada perkiraan. Istilah linguistik dapat mewakili pengalaman yang lebih baik dan subyektif dari sudut pandang keputusan dalam cara lebih intuitif dan format. Sebuah fungsi keanggotaan fuzzy yang ditetapkan, disebut fuzzy fungsi keanggotaan, yang dipetakan pada interval [0,1] dengan nilai 0 yang berarti bahwa anggota tidak termasuk dalam himpunan fuzzy dan 1 menggambarkan sepenuhnya termasuk anggota himpunan fuzzy. Notasi untuk fungsi keanggotaan fuzzy yang mengatur adalah :

] 1 , 0 [

→

X

R. Raja dan LA Zaedah pertama mengusulkan tentang konsep pengambilan keputusan dalam lingkungan fuzzy yang melibatkan beberapa tujuan dan Zimmerman HJ (1978) menerapkan pendekatan mereka ke vektor masalah. Setelah di tranformasikan pada fuzzy multiobjective dalam masalah klasik yang tujuannya adalah program linier. Berikut model fuzzy multiobjective pada program linier :

cx Z

terhadap kendala Ax≤b Mengadopsi model fuzzy Zimmerman

>

cx

Max ~ 0

Z

terhadap kendala Ax<~ b

Dimana Zo = (z₁0,z₂0,...,z0_n) adalah tujuan dan tingkatan lebih besar atau lebih kecil dalam fuzzy yang merupakan kesenjangan fuzzifications ≥ dan ≤ dari masing-masing. Dalam pengukuran tingkat pencapaian tujuan dan kendala, Zimmerman menyarankan pada fungsi sederhana dari fungsi keanggotaan. Dari penjelasan diatas, maka program fuzzy multiobjective dapat dituliskan sebagai berikut :

cx Z

Max =

terhadap kendala α ≤1−

(

z_k0 −C_kX

)

/t_k k = 1,…..,n

(

aiX bi

)

/di

1− −

≤

α i = 1,……,m

Dapat disimpulkan bahwa secara keseluruhan akan mencapai tingkat kepuasan terhadap solusi yang dihasilkan.

1.12. Metode Penelitian

Dalam tulisan ini, metode penelitian yang dilakukan adalah metodologi yang berhubungan dengan parameter kabur dan mencapai tingkat optimalisasi aspirasi tertentu untuk TSP dengan mengubahnya menjadi linier menggunakan pemrograman fuzzy linear multiobjective sehingga diperlukan pembahasan yang berkenaan dengan :

1. Traveling Salesman Problem 2. Logika Fuzzy

3. Pemrograman Fuzzy Multiobjective

BAB 2

LANDASAN TEORI

2.4 Teori Graf

Sebelum sampai pada pendefenisian masalah lintasan terpendek, terlebih dahulu pada bagian ini akan diuraikan mengenai konsep-konsep dasar dari model graf dan representasinya dalam memodelkan masalah lintasan terpendek.

Definisi 2.1. Sebuah graf G adalah pasangan (V,E) dimana V adalah himpunan tak kosong yang anggotanya disebut verteks dan E adalah himpunan yang anggotanya adalah pasangan tak berurut dari verteks V yang disebut edge.

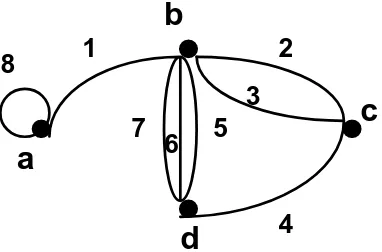
Secara umum graf dapat digambarkan dengan suatu diagram dimana verteks ditunjukkan sebagai titik yang dinotasikan dengan vi , i = 1, 2, …,P dan edge digambarkan dengan sebuah garis lurus atau garis lengkung yang menghubungkan dua verteks (vi, vj) dan dinotasikan dengan ek . Sebagai ilustrasi

dapat dilihat gambar 2.1. yaitu suatu graf yang mempunyai empat verteks dan delapan edge.

a

b

c

d

1

2

3

4

5

6

7

8

2.2.Permasalahan Optimisasi

Secara umum, penyelesaian masalah pencarian jalur terpendek dapat dilakukan dengan menggunakan dua metode, yaitu metode konvensional dan metode heuristik. Metode konvensional diterapkan dengan perhitungan matematik biasa, sedangkan metode heuristik diterapkan dengan perhitungan kecerdasan buatan.

Metode Konvensional

Metode konvensional adalah metode yang menggunakan perhitungan matematik biasa. Ada beberapa metode konvensional yang biasa digunakan untuk melakukan pencarian jalur terpendek, diantaranya: algoritma Djikstra, algoritma Floyd-Warshall, dan algoritma Bellman – Ford.

Metode Heuristik

Metode Heuristik adalah sub bidang dari kecerdasan buatan yang digunakan untuk melakukan pencarian dan optimisasi. Ada beberapa algoritma pada metode heuristik yang biasa digunakan dalam permasalahan optimisasi, diantaranya algoritma genetika, algoritma semut, logika fuzzy, jaringan syaraf tiruan, pencarian tabu, Self-Organizing Map, dan lain-lain. [ Siang, Jong Jek, 2005].

2.3. Lintasan Terpendek (Shortest Path)

Banyak bidang penerapan mensyaratkan untuk menentukan lintasan terpendek berarah dari asal ke tujuan di dalam suatu distribusi aliran berarah. Algoritma yang diberikan dapat dimodifikasi dengan mudah untuk menghadapi lintasan berarah pada setiap iterasinya.

Suatu versi yang lebih umum dari masalah lintasan terpendek adalah menentukan lintasan terpendek dari sembarang verteks menuju ke setiap verteks lainnya. Pilihan lain adalah membuang kendala tak negatif bagi “jarak”. Suatu kendala lain dapat juga diberlakukan dalam suatu masalah lintasan terpendek.

Andaikan diberikan sebuah graf G dalam tiap edge (x,y) dihubungkan dengan verteks a (x,y) mewakili panjang dari edge. Dalam beberapa hal, panjang sebenarnya mewakili biaya atau beberapa nilai lainnya. Panjang dari lintasan adalah menentukan panjang jumlah dari masing-masing edge yang terdiri dari lintasan. Untuk 2 verteks s dan t dalam G, ada beberapa lintasan dari s ke t . Masalah lintasan terpendek meliputi bagaimana pencarian lintasan dari s ke t yang mempunyai lintasan terpendek dan biaya termurah.

Pada persoalan ini akan terdorong bagaimana menyelesaikan suatu persoalan dalam menentukan lintasan terpendek dan biaya termurah pada suatu jaringan dengan mengimplementasikannya ke dalam graf dengan menggunakan penyelesaian beberapa algoritma yang dapat diimplementasikan.

X4 1 3

X3

2 X2

X7 3

Contoh 2.2.

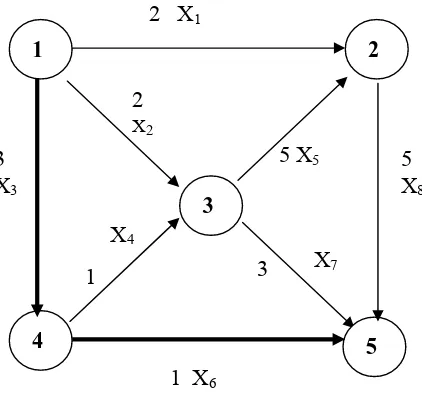
Gambar 2.2. Shortest path (1 – 4, 4 - 5)

Pada gambar 2.2. dapat dilihat bahwa setiap edge terletak pada path-path dari titik 1 ke titik 5. Edge merepresentasikan saluran dengan kapasitas tertentu (contohnya, air) dapat dialirkan melalui saluran. Sedangkan verteks merepresentasikan persimpangan saluran. Air mengalir melalui verteks pada verteks yang dilalui Lintasan terpendek dari verteks pada graf di atas adalah P = {1 – 4, 4 – 5} dengan kapasitas 4.[ L.R, Foulds, 1984].

2.4 Traveling Saleman Problem

Persoalan TSP merupakan salah satu persoalan kombinatorial. Banyak permasalahan yang dapat direpresentasikan dalam bentuk TSP. Persoalan ini sendiri menggunakan representasi graf untuk memodelkan persoalan yang diwakili sehingga lebih memudahkan penyelesaiannya. Diantara permasalahan yang dapat direpresentasikan dengan TSP ialah masalah transportasi, efisiensi pengiriman surat atau barang, perancangan pemasangan pipa saluran, proses pembuatan PCB (Printed Cirtcuit Board) dan lain-lain. Persoalan yang muncul ialah bagaimana cara mengunjungi simpul (node) pada graf dari titik awal ke setiap titik-titik lainnya dengan bobotminimum. Bobot ini sendiri dapat mewakili

5 X5 3

5

1 2

4

1 X6

berbagai hal, seperti biaya, jarak, bahan bakar, waktu, dan lainnya yang semuanya juga berimplikasi pada besarnya biaya.

Persoalan TSP atau pedagang keliling ialah sebuah persoalan optimisasi untuk mencari rute terpendek bagi seorang pedagang keliling (salesman) yang ingin menjajakan produknya di beberapa kota dengan batasan bahwa dia pergi dari sebuah kota ke setiap kota-kota lainnya yang menjadi target penjualan produknya dan harus kembali ke kota asal keberangkatan. Persoalan optimisasi yang ingin dicapai ialah rute yang dilalui, waktu dan biaya yang digunakan paling minimum.

Beberapa metode algoritma telah dikembangkan untuk menyelesaikan persoalan TSP ini. Bila dipandang dari sudut komputasinya, algoritma ini dapat diselesaikan dengan cepat walaupun dengan menggunakan algoritma brute force sekalipun, jika kota-kota yang akan dikunjunginya sedikit. Namun, jika kota-kota yang akan dikunjungi banyak, maka algoritma seperti brute force tidaklah menjadi pilihan lagi. Sebab, algoritma brute force sendiri memiliki kompleksitas O(n!) jika kota-kota yang akan dikunjungi diasumsikan sebagai graf lengkap yang saling terhubung antara satu kota dengan kota yang lainnya.

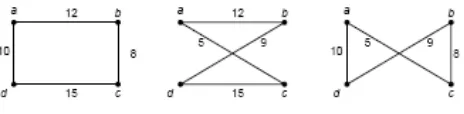
Misalkan diberikan contoh kasus yang diselesaikan dengan brute force seperti di bawah ini:

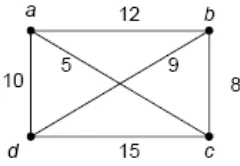
Gambar 2.3 graf yang mempunyai bobot

Gambar 2.4 Alternatif Penyelesaian

• Lintasan pertama = (a → b → c → d → a) atau (a → d → c → b

→ a) memiliki panjang lintasan = 10 + 12 + 8 + 15 = 45

• Lintasan kedua = (a → b → d → c → a) atau (a → c → d → b → a) memiliki panjang lintasan = 12 + 5 + 9 + 15 = 41

• Lintasan ketiga = (a → c → b → d → a) atau (a → d → b → c → a) memiliki panjang lintasan = 10 + 5 + 9 + 8 = 32

Dari hasil ketiga enumerasi di atas didapatkan panjang jalur lintasan paling minimum yaitu 32. Namun, jumlah enumerasi dari algoritma ini ialah (n - 1)! yang akan memerlukan waktu yang sangat lama untuk mendapatkan panjang lintasan paling minimum jika nilai n bernilai sangat besar. Beberapa metode telah dikembangkan untuk memecahkan masalah ini namun belum ditemukan algoritma penyelesaian yang optimal.

2.4.1 Sejarah Permasalahan TSP

persoalan TSP sebagai sebuah topik studi dapat ditemukan pada tulisan Alexander Schriver “On the history ofcombinatorial optimization (till 1960)”.

2.4.2 Perkembangan Penyelesaian Persoalan TSP

Bagaimana kita mengukur kemajuan dalam penyelesaian persoalan TSP? Sebuah penilaian sederhana pasti mengatakan bahwa metode A lebih baik daripada metode B jika A membutuhkan waktu yang lebih singkat atau sumber daya yang lebih sedikit untuk menyelesaikan setiap contoh persoalan. Ini merupakan sebuah aturan yang jelas. Namun, masalah penilaian untuk metode ini akan sulit untuk dilakukan karena metode-metode yang sangat berkaitan erat satu sama lain tidak dapat dinilai hanya melalui perbandingan yang sederhana. Sepertinya perlu dilakukan pertimbangan ulang untuk menentukan kriteria perbandingan antar metode tersebut. Oleh karena itu, penilaian yang lebih baik harus mengesampingkan hasil contoh kasus kecil seperti di atas karena contoh-contoh kasus tersebut dapat diselesaikan oleh seluruh teknik penyelesaian yang baik. Sejauh ini, jika diberikan sejumlah n kota, penilaian seharusnya difokuskan pada n-kota yang benar-benar sulit untuk diselesaikan dengan menggunakan metode-metode yang diajukan yang nantinya akan diuji mana yang lebih baik. Dengan pendekatan ini, kita kemudian dapat menentukan apakah metode A lebih baik daripada metode B jika diberikan persoalan n-kota dengan n sebuah bilangan yang besar. Agar ide perbandingan metode-metode di atas dapat diaplikasikan, kita dapat menganalisis metode-metode penyelesaian yang diberikan untuk dapat memberikan jaminan bahwa setiap n akan memakan waktu sejumlah f

( )

n untuk berapapun n-kota TSP, dimana f

( )

n ialah sebuah fungsi yang menghasilkan waktu yang dibutuhkan untuk menyelesaikan persoalan TSP n-kota.

dibandingkan dengan metode penyelesaian lain yang dianalisis dengan baik. Pada beberapa persoalan komputasi, bagaimanapun juga, studi mengenai algoritma dan fungsi telah memberikan hasil yang baik dan penting bagi pengembangan untuk penyelesaian persoalan praktis. Hal ini telah menjadi subjek studi utama di dalam Bidang Ilmu Komputer. Jadi, dapat kita simpulkan bahwa metode – metode penyelesaian persoalan TSP adalah untuk mengembangkan metode penyelesaian

yang memiliki fungsi, contohnya

( ) ( ) ( ) (

n = n−1!= n−1 × n−2

) ( )

× n−3...×3×2×1

f dan jumlah jalur perjalanan

antar kota yang mungkin terjadi ialah

( )

n−1!/2. Ditemukan hasil yang lebih baik setelah dikembangkan lagi pada tahun 1962 oleh Michael Held dan Richard Karp, ditemukannya algoritma yang menghasilkan f

( )

n yang memiliki proporsi n22n, yaitu n×n×2×2×2×...×2, dimana ada sebanyak n perkalian 2. Untuk setiap n yang bernilai besar, fungsi f

( )

n Held-Karp akan selalu lebih kecil jika dibandingkan dengan

( )

n−1!. Bagi setiap orang yang tertarik untuk menyelesaikan persoalan TSP, adalah sebuah kabar buruk bahwa selama 45 tahun sejak Held dan Karp menemukan fungsi f

( )

n =n22n ternyata tidak ditemukan fungsi f

( )

n yang lebih baik. Hal ini tentu saja mengecewakan karena dengan n = 30 fungsi f

( )

n Held-Karp menghasilkan nilai yang sangat besar. Dan untuk n = 100, adalah suatu hal yang mustahil untuk menyelesaikan persoalan ini dengan kemampuan yang dimiliki komputer yang ada saat ini. Perkembangan fungsi

( )

n

pada kasus dengan tingkat performansi terburuk dari metode penyelesaian masalah TSP.

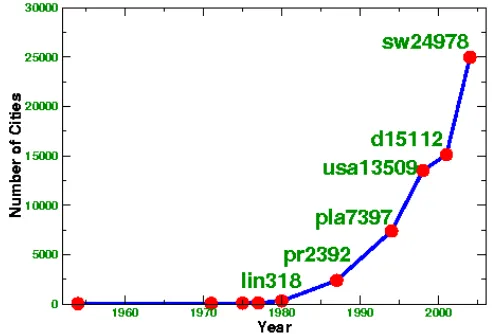
Dengan sedikit informasi yang tersedia, para peneliti TSP telah berusaha untuk mengukur perkembangan dengan cara melihat bagaimana implementasi pada komputer dari metode-metode penyelesaian tersebut untuk menyelesaikan persoalan pada contoh kasus yang diberikan. Maksudnya ialah bahwa dengan memperbesar ukuran dan variasi contoh kasus yang dapat diselesaikan, kita akan memperoleh kemajuan dan solusi praktis dari TSP. Walaupun pergantian proses perbandingan untuk mendapatkan suatu perbandingan yang baik seperti yang kami tawarkan di awal lemah, namun tes komputasi praktis ini telah membawa para peneliti TSP kepada metode penyelesaian TSP berkembang lebih baik. Dan yang lebih penting lagi, usaha-usaha tersebut telah mengarahkan penelitian ke dalam pengembangan alat optimisasi yang bersifat umum. Contoh kasus yang paling umum digunakan dalam studi komputasi sekarang ialah himpunan data tes TSPLIB Gerd Reinelt. TSPLIB yang memiliki lebih dari 100 contoh kasus mulai dari industri, geografi, dan akademi. Untuk melengkapi koleksi ini, contoh kasus lebih jauh tersedia di koleksi National TSP dan VLSI TSP. Sebuah tanda yang mudah dikenali untuk mengukur perkembangan pada data tes ialah perkembangan jumlah data TSP terbesar yang dapat diselesaikan yang terus meningkat selama beberapa tahun, seperti yang ditunjukkan pada gambar 2.5 di bawah ini.

Gambar 2.5 Grafik pemecahan permasalahan TSP dengan n-kota

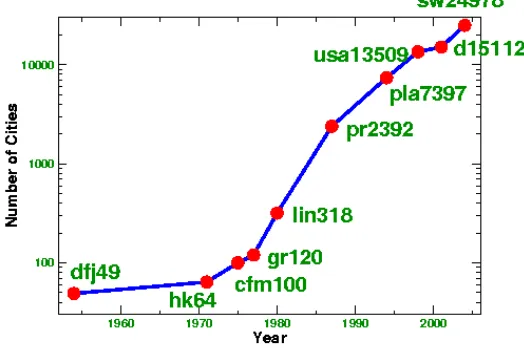
Catatan perkembangan di atas dimulai oleh tulisan klasik Danzig, Fulkerson, dan Johnson pada tahun 1954 dimana mereka menyelesaikan permasalahan TSP 49-kota yang terdiri dari seluruh negara bagian di Negara Amerika (Alaska dan Hawaii belum masuk di dalamnya) termasuk juga Washington, D. C. Daftar perkembangan persoalan yang muncul telah disebutkan pada pembahasan di atas. Perkembangan contoh persoalan TSP, diukur dengan skala logaritma terhadap jumlah kota yang dimodelkan dapat dilihat pada gambar 2.6 di bawah ini.

Gambar 2.6 Grafik pemecahan permasalahan TSP dengan n-kota terhadap

Tahun dielesaikan dengan skala logaritma

Dari gambar 2.5 dan 2.6 di atas kita dapat menarik kesimpulan bahwa perkembangan penyelesaian persoalan TSP telah dicapai selama lebih dari 30 tahun ke belakang. Jika hal ini terus berlanjut, kita dapat memperkirakan bahwa untuk 30 tahun ke depan kita dapat menyelesaikan persoalan TSP dengan jumlah kota yang berjumlah jutaan.

2.5 Model Pemrograman Linier

menggambarkan kontribusi satu satuan variabel keputusan terhadap nilai fungsi objektif. Koefisien fungsi objektif yang selama ini dikenal dalam pembahasan MPL bersifat tegas (crisp), meskipun demikian tetap memiliki satu atau lebih kendala.

Sejak dikembangkan oleh George Dantzig pada tahun 1947, Model Pemrograman Linear (MPL) telah banyak digunakan dalam pemecahan masalah optimisasi di berbagai sektor industri dan jasa. Bahkan telah dilakukan survey kepada perusahaan-perusahaan yang pernah dilakukan oleh Fortune 500 menunjukkan 85% dari respondennya menggunakan MPL (Winston, 2003). MPL tersusun atas dua komponen utama yaitu fungsi objektif dan kendala. Fungsi objektif berkaitan dengan tujuan yang hendak dicapai. Fungsi ini akan dimaksimumkan misalnya bila menyatakan keuntungan, atau diminimumkan bila berkaitan dengan besarnya ongkos produksi yang harusdikeluarkan. Fungsi objektif adalah fungsi dari beberapa variabel yang disebut variabel keputusan. Pada realitanya keseluruhan variabel keputusan ini harus memenuhi satu set pertidaksamaan yang disebut kendala. Setiap MPL memiliki 3 buah parameter, yaitu koefisien fungsi objektif (objective function coefficient atau KFO) yang terdapat pada fungsi objektif, serta koefisien teknologi (technological coefficient) dan koefisien ruas kanan (right-hand side coefficient) yang keduanya terdapat pada kendala. KFO yang selama ini dikenal dalam pembahasan MPL bersifat tegas (crisp), demikian pula halnya dengan kendala.

Secara ringkas MPL beserta kedua komponen utama (fungsi objektif dan kendala) dan ketiga parameternya (KFO, koefisien teknologi serta ruas kanan) dapat dimodelkan sebagai berikut:

maksimasi

∑

=

= n

j j jx

c cx

1

(1)

terhadap kendala Ax≤b (2) 0

≥

x (3)

Pada model (1)-(3) di atas:

ƒ vektor x=

(

x₁Lx_jLx_n

)

T disebut vektor keputusan, sedangkan x_j disebut variabel keputusan ke-j,

ƒ vektor baris c=

(

c₁Lc_jLc_n

)

disebut vektor koefisien fungsi objektif, sedangkan c_j adalah koefisien fungsi objektif (KFO) dari variabel keputusan ke-j

ƒ A=

[ ]

aij _mxn adalah matriks koefisien teknologi, sedangkan aijadalah

koefisien teknologi dari variabel keputusan ke-j pada kendala ke-i,

ƒ vektor b=

(

b1Lb_iLb_n

)

T disebut vektor ruas kanan, sedangkan bi adalah

koefisien ruas kanan pada kendala ke-i

ƒ j = 1,2,.,n (n = jumlah kendala), dan i =1,2,...,m (m = jumlah variabel keputusan)

Salah satu asumsi yang harus dipenuhi oleh suatu MPL adalah Asumsi Ketertentuan (Certainty Assumption). (Winston, 2004). Asumsi ini menuntut tertentunya nilai semua parameter pada MPL. Perumusan MPL dalam hal;

ƒ asumsi ketertentuan tidak dipenuhi, lebih spesifik lagi, dalam hal parameter KFO tidak memenuhi Asumsi Ketertentuan, serta

ƒ kendala bersifat kabur

Untuk memperjelas perumusan MPL, berikut ini akan dibahas konsep bilangan kabur serta konsep kendala kabur.

2.6 Fuzzy Set

himpunan; ini digambarkan dengan bantuan sebuah fungsi keanggotaan dinilai dalam satuan riil interval [0, 1]. Fuzzy set set menggeneralisasikan klasik, karena fungsi indikator set klasik adalah contoh khusus dari fungsi keanggotaan fuzzy set, jika yang terakhir hanya mengambil nilai-nilai 0 atau 1. Klasik bivalen set berada dalam teori himpunan fuzzy biasa disebut renyah set. Para teori himpunan fuzzy dapat digunakan dalam berbagai domain di mana informasi tidak lengkap atau tidak tepat, seperti bioinformatika.

Fuzzy set adalah sepasang (A, m) di mana A adalah suatu himpunan dan

[ ]

0,1 :A→

m . Untuk setiap x∈A, m ( x ) adalah derajat keanggotaan dari x. Jika A = (x 1 ,..., x n) yang fuzzy set (A, m) dapat dinyatakan

(

m

( )

x1 /x1,...,m

(

x n/xn

)

)

Λ

.

Pemetaan elemen dengan nilai 0 berarti bahwa anggota tidak termasuk dalam himpunan fuzzy, 1 menggambarkan sepenuhnya termasuk anggota. Nilai ketat antara 0 dan 1 ciri anggota kabur.

Himpunan

{

x∈Am

( )

x >o

}

disebut dukungan dari fuzzy set (A, m) dan himpunan

( )

{

x∈Am x =1

}

disebut kernel dari fuzzy set (A, m).

Definisi yang lebih umum digunakan, di mana fungsi keanggotaan mengambil nilai-nilai yang tidak tentu dalam aljabar atau struktur L adalah fungsi keanggotaan yang biasa dengan nilai-nilai dalam [0, 1]. Kemudian disebut nilai fungsi keanggotaan [0, 1]. Generalisasi ini dianggap pertama kali pada 1967 oleh Joseph Goguen, yang merupakan murid Zadeh.

2.6.1 Fuzzy Multiobjective

palsu”. Sebagai peneliti menyarankan, modus dari logika yang melandasi alasan yang tepat dari perkiraan. Istilah linguistik dapat mewakili pengalaman yang lebih baik dan subyektif dari sudut pandang keputusan dalam cara lebih intuitif dan format. Sebuah fungsi keanggotaan fuzzy yang ditetapkan, disebut fuzzy fungsi keanggotaan, yang dipetakan pada interval [0,1], dengan nilai 0 yang berarti bahwa anggota tidak termasuk dalam himpunan fuzzy dan 1 menggambarkan sepenuhnya termasuk anggota himpunan fuzzy. Notasi untuk fungsi keanggotaan fuzzy yang mengatur adalah :

] 1 , 0 [

→

X

R. Raja dan LA Zadeh pertama mengusulkan tentang konsep pengambilan keputusan dalam lingkungan fuzzy yang melibatkan beberapa tujuan dan Zimmerman HJ (1978) menerapkan pendekatan mereka ke vektor masalah. Setelah di tranformasikan pada fuzzy multiobjective dalam masalah klasik yang tujuannya adalah program linier. Berikut model fuzzy multiobjective pada program linier :

terhadap kendala Ax≤b

Mengadopsi model fuzzy Zimmerman

>

cx

Max ~ Z0

terhadap kendala Ax<~ b

Dimana Zo = (z₁0,z₂0,...,z0_n) adalah tujuan dan tingkatan lebih besar atau lebih kecil dalam fuzzy yang merupakan kesenjangan fuzzifications ≥ dan ≤ dari masing-masing. Dalam pengukuran tingkat pencapaian tujuan dan kendala, Zimmerman menyarankan pada fungsi sederhana dari fungsi keanggotaan. Dari penjelasan diatas, maka program fuzzy multiobjective dapat dituliskan sebagai berikut :

cx Z

Max =

cx Z

terhadap kendala α ≤1−

(

z_k0 −C_kX

)

/t_k k = 1,…..,n

(

aiX bi

)

/di

1− −

≤

α i = 1,……,m

2.6.2 Fuzzy Multiobjective pada Pendekatan Traveling Salesman Problem

Yang paling sering dianggap tujuan dari TSP adalah untuk menentukan secara optimal agar perjalanan semua kota dilalui sehingga total biaya adalah minimal. Mempertimbangkan situasi saat pengambilan keputusan harus menentukan solusi optimal dari TSP dengan meminimalkan biaya, waktu dan jarak keseluruhan. Fungsi tujuan ndividu dapat dibentuk untuk semua tujuan dari pengambil keputusan.

Andaikan xij merupakan hubungan dari kota i ke kota j yang direpresentasikan dengan:

⎩ ⎨ ⎧ =

kota antar hubungan ada

tidak jika ,

0

i kota dari kunjungan merupakan

j kota jika , 1

ij

x

Jadi c_ij merupakan biaya perjalanan dari kota i ke kota j, keseluruhan biaya tertentu rute adalah jumlah biaya pada link yang terdiri dari rute. Sejak keputusan dibuat telah dilakukan untuk meminimalkan keseluruhan biaya perjalanan, sehingga ia dapat menetapkan tujuan untuk total perkiraan biaya keseluruhan untuk rute tsp denoted oleh z₁0. Tetapi dapat menjadi perkiraan biaya dan tidak memenuhi sehingga keputusan dapat mengatur toleransi untuk perkiraan biaya. Marilah kita menunjukkan toleransi terhadap tujuan ini sebagai t1, fungsi tujuan untuk minimisasi biaya yang diberikan sebagai :

0 1

1:min c x ~z

z

n

j ij ij n

i

≤

∑

∑

0 2

2:min c x ~ z

z

n

j ij ij n

i

≤

∑

∑

Jika tij merupakan lama di perjalanan dari kota i ke kota j, z₃0 menjadi aspirasi tingkat untuk fungsi tujuan untuk minimisasi dari total waktu, dan t3

sesuai toleransi. Fungsi tujuan dapat ditulis sebagai berikut :

0 3

3:min c x ~ z

z

n

j ij ij n

i

≤

∑

∑

Satu aspek yang penting ketergantungan pada setiap fungsi tujuan lain. Sebagian besar dari waktu mereka bergantung, tetapi tepat menentukan bentuk dependensi juga sebuah proses kompleks. Dalam kasus TSP memiliki batasan bahwa untuk setiap kota harus dikunjungi tepat satu kali dari setiap tetangga dan begitu juga sebaliknya. Contohnya yaitu :

∑

n = i

ij

x 1 untuk semua j

∑

n = i

ij

x 1 untuk semua i

Sebuah rute tidak dapat dipilih lebih dari sekali, yaitu : 1

≤ + ij ij x

x untuk semua i dan j, Dan non-kendala sisi negatif, yaitu :

0

≥ ij

x

2.7 Bilangan Kabur dan Pemrograman Linear dengan Koefisien Fungsi

Objektif Kabur

Bilangan kabur atau yang sering disebut Fuzzy number adalah sebuah kuantitas yang nilainya tidak tepat yang menggambarkan ketidakpastian. Setiap bilangan kabur dapat dianggap sebagai fungsi yang domain tertentu. Setiap nilai numerik dalam domain diberikan sebuah spesifik nilai kenaggotaan dimana ”0” mewakili nilai kecil yang mungkin dan ”1000” merupakan nilai terbesar yang mungkin.

Ketika kita berbicara tentang jumlah roda pada semua jendela pada suatu mobil sedan, kita dihadapkan pada jumlah yang sudah tertentu, yaitu tepat 4 (empat) buah. Sangat berbeda halnya ketika kita berbicara tentang:

- jam kedatangan langganan koran, mungkin akan berkata sekitar pukul 5.30 - volume air kemasan dalam botol, mungkin akan berkata kira-kira 500

mililiter.

Banyak hal dalam dunia nyata yang tidak memungkinkan kita untuk menggunakan frase tepat sekian, melainkan harus puas dengan menggunakan frase yang menggambarkan ketidaktepatan, seperti: sekitar sekian, kira-kira sekian, hampir sekian, kurang lebih sekian dan sejenisnya. Dalam hal konsep bilangan kabur atau fuzzy number dapat mengkomodasinya. Himpunan bilangan yang nilainya sekitar 3, atau kira-kira 3, atau hampir 3, atau kurang lebih 3 adalah contoh himpunan kabur, yang sering pula disebut bilangan kabur 3. Terdapat dua jenis bilangan kabur yang sering dipakai dalam praktek, yaitu bilangan kabur segitiga (triangular fuzzy number) dan bilangan kabur trapesium (trapezoidal fuzzy number) (Wang, 1997).

(

)

(

(

) (

) (

)

)

⎪⎩ ⎪ ⎨ ⎧ <

> ≤ <

−

−− − ≤ <

= a x atau d x jika d x c jika c d x d c x a jika a b a x d c a x b , 0 , / , / , , ;

µ (4)

Bilangan kabur segitiga c pada model (4) seringkali pula dilambangkan dengan

(

− +

)

= c c c

c , 0, atau c=

(

a,c,d

)

dalam hal ini c− =a, c0 =cdan c+ =d.

Secara umum, Pemrograman Linear dengan KFO berupa bilangan kabur berbentuk:

maksimasi (minimasi)

∑

= = n j j jx c cx 1

~ _{terhadap kendala (2)-(3), dalam hal ini}

bilangan kabur c~ dicirikan oleh _j fungsi keanggotaan seperti pada model (4) yang menggambarkan derajat keanggotaan suatu bilangan terhadap himpunan bilangan yang nilainya “sekitar c_j” atau “kurang lebih c_j” atau ungkapan kabur lainnya.

Berikut ini diuraikan tentang langkah-langkah pembentukan MPLKFOK untuk kasus dengan fungsi objektif berbentuk minimalisasi:

Langkah-1: Tentukan MPL yang akan diubah kedalam MPLKFOK (yaitu, masalah (1)-(3))

Langkah-2: Tentukan jenis bilangan kabur bagi setiap KFO (yaitu, bilangan kabur segitiga (4))

Langkah-3: Tentukan:

a. c* =c=

(

c₁Lc_jLc_n

)

, yaitu vektor koefisien fungsi objektif yang komponen ke-j-nya adalah koefisien fungsi objektif variabel x_j

b. c− =

(

c₁−Lc_j−Lc_n−

)

, yaitu vektor yang komponen ke-j-nya adalah batas bawah dari bilangan kabur c_j

Langkah-4: Rumuskan pemrograman linear bertujuan majemuk berfungsi objektif

Meminimumkan nilai bilangan kabur segitiga, sebagai berikut: minc−x. minc*x, minc+xdengan kendala (2)-(3).

2.7.1 Kendala Kabur dan Pemrograman Linear dengan Kendala Kabur

Secara umum, Pemrograman Linear dengan Kendala yang Kabur (MPLKK) berbentuk:

max(min)cx (5)

terhadap kendala Ax~≤b, x≥0

Dalam hal ini ≤~ dicirikan oleh fungsi keanggotaan yang menggambarkan “derajat toleransi” seperti di atas. Berikut ini adalah pembentukan fungsi keanggotaan yang merupakan potongan-potongan garis yang kontinu bagian demi bagian.

Misalkan dalam bentuk yang tegas kendala ke-i berbentuk

( )

Ax _i ≤b_i , maka bentuk kaburnya adalah

( )

Ax _i ≤~b_i. Misalkan pula t_iadalah toleransi dari kendala ke-i, maka kendala kabur ini dapat dicirikan dengan fungsi keanggotaan sebagai berikut:

{

}

( )

{

}

( )

(

)

{

i i i

}

i

( ) (

i i i

)

i

i i

i b Ax i

i Ax b t b Ax b t

t

b Ax

Ax Ax

i

i +

⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧

≤ ≤

− − −

< =

= ≤

Lainnya ,

0 , )

( 1

, 1 )

( )

( µ

µ (6)

Berikut ini diuraikan tentang langkah-langkah perumusan dan penyelesaian MPLKK untuk kasus MPL dengan fungsi objektif dari model (5) berbentuk minimalisasi:

sebesar t_i >0, jadi sekalipun untuk kendala ini sebenarnya ditetapkan

( )

Ax _i ≤b_i, namun masih diberi toleransi hingga

( ) (

Ax _i ≤ b_i+t_i

)

, dengan derajat toleransi akan didefinisikan pada Langkah-4.

Langkah 2: Selesaikan pemrograman linear berikut:

maksimasi cxterhadap kendala

( )

Ax _i ≤b_i (i = 1,2,...,m) dan misalkan x0 adalah solusinya, serta definisikan z0 =cx0

Langkah 3: Selesaikan pemrograman linear berikut:

maksimasi cxterhadap kendala

( ) (

Ax _i ≤ b_i+t_i

)

(i = 1,2,...,m)

misalkan x 1 adalah solusinya, definisikan z1=cx1 . (Catatan: jelaslah z1 ≥z0!)

Langkah 4: Berdasarkan nilai z0dan z1yang diperoleh pada Langkah-2 dan 3, definisikan Fungsi keanggotaan berikut yang menggambarkan derajat optimalitas dari setiap nilai fungsi objektif cx:

⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ ≥ ≤ ≤ − − ≥ = 0 1 0 0 1 0 1 0 , 0 , , 1 ) ( z cx z cx z z z z cx z cx x

µ (7)

Definisikan pula fungsi keanggotaan berikut yang menggambarkan derajat toleransi bagi pelanggaran kendala ke-i:

( )

(

)

( )

( )

⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ + ≥ + ≤ ≤ − + < = ) ( , 0 ) ( , ) ( , 1 ) ( i i i i i i i i i i i i i i t b Ax t b Ax b t Ax t b b Ax x

Langkah 5: Definisikan masalah PL berikut ini:

( )

x 0

BAB 3

PEMBAHASAN

Permasalahan Traveling Salesman Problem (TSP) adalah salah satu tantangan masalah yang nyata dalam kehidupan, menarik peneliti dari berbagai bidang termasuk Artificial Intelligence, Riset Operasi, dan Algoritma Desain dan Analisis. Masalah ini telah dipelajari dengan baik hingga judul yang berbeda saat ini telah diselesaikan dengan pendekatan yang berbeda termasuk genetic algoritma dan pemograman linear.

Pemrograman linier konvensional dirancang untuk menangani parameter yang pasti, tetapi informasi nyata tentang sistem kehidupan sering tersedia dalam bentuk penjelasan kabur. Metode Fuzzy yang dirancang untuk menangani hal kabur, dan yang paling sesuai untuk mencari solusi yang optimal untuk masalah dengan parameter kabur. Pemrograman fuzzy linier multiobjective, adalah sebuah percampuran dari logika fuzzy dan linier multiobjective, kesepakatan dengan fleksibel tingkat aspirasi atau tujuan dan kendala fuzzy dengan penyimpangan yang dapat diterima. Dalam tulisan ini, metodologi untuk memecahkan TSP yang tepat dengan parameter yang menggunakan pemrograman fuzzy multiobjective. Salah satu contoh TSP dengan beberapa tujuan dan parameter kabur yang akan dibahas.

Tujuan mengoptimalkan TSP berarti adalah untuk menentukan k-dimensi poin yang akan berkenaan dengan ruang solusi yang layak dan memiliki masalah yang minimal dalam nilai yang mungkin sesuai untuk semua dimensi. Penyimpangan yang diperbolehkan dari nilai sebuah dimensi struktural yang cukup besar karena TSP dapat menghadapi situasi dimana dia tidak dapat mencapai tujuan sepenuhnya. Harus ada satu set alternatif dari yang ia pilih satu yang terbaik memenuhi aspirasi tingkat itu. Pendekatan pemrograman konvensional tidak berurusan dengan situasi ini namun beberapa penelitian telah melakukan secara khusus masalah TSP multiobjektif.

Fischer dan Richter (1982) yang menggunakan pendekatan cabang dan terikat untuk menyelesaikan TSP dengan dua kriteria. Gupta dan Wanaraja (1986) menggunakan 2 dan 3 heuristics untuk memilih maxordering TSP. Sigal (1994) dekomposisi pendekatan yang diusulkan untuk memecahkan TSP terhadap dua kriteria dari rute panjang dan bottlenecking, dimana kedua tujuan tersebut diperoleh dari matriks biaya yang sama. Tung (1994) menggunakan cabang yang terikat dengan beberapa label skema untuk mengetahui kemungkinan pareetooptimal wisata. Melamed dan Sigal (1997) mengusulkan e-terpaksa – berbasis algoritma untuk bi-tujuan TSP. Ehrgott (2000) mengusulkan sebuah pendekatan algoritma dengan kinerja terburuk kasus terikat. Hansen (2000) menerapkan pelarangan algoritma untuk pencarian TSP multi-objektif.

Borges dan Hansen (2002) menggunakan bobot untuk program studi global program multi linier dan TSP. Jaszkiewicz (2002) mengusulkan genetic local pencarian yang menggabungkan gagasan dari algoritma evolusioner, pencarian local dengan modifikasi dan penggabungan tujuan dari fungsi.

tujuan, dimana setiap penggabungan mengkonversi dwi-tujuan masalah menjadi satu tujuan tunggal. Yan dkk (2003) menggunakan memecahkan algoritma evolusioner multi tujuan TSP.

Angel, Bampis dan Gourves (2004) mengusulkan menggunakan algoritma pencarian lokal dengan memperlihatkan ukuran lingkungan yang dapat dicari dalam jumlah waktu yang banyak dengan menggunakan dinamis pemrograman dan teknik pembulatan. Paquete, Chiarandini dan Stutzle (2004) mengemukakan metode Pareto lokal yang membentang lokal untuk Algoritma pencarian satu-satunya tujuan untuk TSP bikasus obyektif. Metode ini menggunakan sebuah arsip untuk terus didominasi non-solusi ditemukan dalam proses pencarian. Selain itu, dalam TSP pedagang yang mengambil keputusan yang optimal dan memilih rute yang layak antara setiap beberapa kota berdasarkan langkah-langkah yang diharapkan.

Dari sebagian besar masalah dunia nyata tidak mungkin untuk memiliki semua kendala dan sumber daya dalam bentuk lebih tepat sesuai dengan keinginan yang diharapkan atau kabur. Hal ini menyebabkan konsep logika fuzzy yang memungkinkan kita untuk memikirkan proses dan membuat keputusan berdasarkan kabur atau tepat data, dan program fuzzy memberikan metodologi dalam menyelesaikan permasalahan di lingkungan fuzzy. Metode yang ideal dalam menyelesaikan setiap masalah TSP yang optimal, tetapi ini tidak praktis dan merupakan masalah paling besar. Walaupun berbagai kemajuan telah dibuat dalam menyelesaikan permasalahan TSP, kemajuan yang telah datang pada biaya yang lebih rumit untuk pengkodean komputer. Kompleksitas tidak hanya melibatkan panjang kode tetapi yang diperlukan nesting dan struktur data.

3.1 Pemrograman Fuzzy

multiobjective dan logika fuzzy Sinopsis yang secara singkat ini akan dibahas dalam bagian melanjutnya.

3.2 Fuzzy dan Fungsi Keanggotaan Logika Fuzzy

Logika fuzzy, diperkenalkan oleh Zadeh (1965), merupakan superset dari konvensional (Boolean) logika, yang telah diperpanjang untuk menangani konsep kebenaran sebagian : nilai-nilai kebenaran antara “sepenuhnya benar” dan “sepenuhnya palsu”. Sebagai peneliti menyarankan, modus dari logika yang melandasi alasan yang tepat dari pada perkiraan. Istilah lingustik dapat mewakili pengalaman yang lebih baik dan subyektif dari sudut pandang keputusan dalam cara lebih intuitif. Itu pentingnya logika fuzzy berasal dari fakta bahwa kebanyakan manusia dari modus pemikiran dan terutama rasa alasan umum adalah perkiraan di alam. Menetapkan teori fuzzy menggunakan variabel lingustik daripada kuantitatif untuk variabel mewakili konsep tepat data. Sebuah fungsi keanggotaan fuzzy yang ditetapkan, disebut fuzzy keanggotaan, yang dipetakan pada interval [0,1] dengan nilai 0 yang berarti bahwa anggota tidak termasuk dalam himpunan fuzzy dan 1 menggambarkan sepenuhnya termasuk anggota himpunan fuzzy. Notasi untuk fungsi keanggotaan fuzzy yang mengatur adalah : X [0,1].

3.3 Pemrograman Linier dan Pemrograman Linier Bertujuan Majemuk

Berfungsi Objektif

Permasalahan program linier pertama kali diselesaikan dengan teknik yang efisien dikembangkan oleh George B. Dantzig (1974) dengan model pemrograman linear, untuk maksimalisasi masalah, diusulkan oleh Dantzig adalah :

Masalah z = _{i i}

n

i

x c

∑

₌₁

dan xij ≥ 0

Di mana z adalah fungsi tujuan X1 adalah variabel keputusan, m adalah nomor dari kendala, n adalah jumlah variabel keputusan, dan b1 yang diberikan sumber daya, pemograman model linear ini dapat diselesaikan dengan metode yang berbeda misalnya solusi grafis, metode simpleks, dll.

Keterbatasan program linier yang dapat menangani hanya dengan satu fungsi tujuan tidak memasukkan kendala lunak. Zeleny di 1974 memperkenalkan konsep Pemrograman fuzzy linier multiobjective. Linier umum dengan beberapa kriteria pengambilan keputusan model dapat disajikan sebagai menemukan vector

x berikut :

Xt = (X1, X2, ….., Xn)

k tujuan yang memaksimalkan fungsi, dengan variabel dan m adalah kendala sebagai berikut.

(

)

⎪ ⎩ ⎪ ⎨ ⎧ ≤ ≤ ≤ − ≤ − − − = 0 0 0 0 0 1 / 1 0 k k k k k k k k k k k k k ik Z X C Z X C t Z t Z X C jika jika jika t X C Z X C µ

Dimana k = 1,….., n dan tk pelanggaran adalah tujuan untuk Zk yang ditentukan oleh pengambil keputusan. Zimmerman membahas fungsi keanggotaan tujuan untuk memaksimalkan fungsi. Dalam kasus minimisasi fungsi tujuan yang fungsi keanggotaan fuzzy akan sebagai berikut

(

)

⎪ ⎩ ⎪ ⎨ ⎧ ≥≤ + ≤ ≥ + − − = 0 0 0 0 0 1 / 1 0 k k k k k k k k k k k k k ik Z X C t Z X C Z t Z X C jika jika jika t Z X C X C µ

Dimana k = 1. …., n lain kelas memiliki fungsi keanggotaan fuzzy µ_2i

( )

a_iX

dimana I = 1,2, …., M dan di adalah untuk pelanggaran fuzzy sumber daya bi untuk kendala keanggotaan ini fungsi ungkapan kepuasan dari keputusan pembuat dengan solusi, sehingga mereka harus maksimal. Akibatnya fungsi tujuan menjadi

( ) (

)

(

) ( ) ( )

(

)

(

C X C X _k C_kX a X a X _m a_mX

)

x 11 1 , 12 2 ,..., 1 21 1 22 2 ,..., 2

max µ µ µ µ µ µ

Menurut Teorema menetapkan fuzzy, fungsi keanggotaan dari persimpangan atas dua atau lebih set minimum adalah fungsi keanggotaan ini set. Oleh menerapkan ini menjadi tujuan dalil :

( ) (

)

(

) ( ) ( )

(

)

(

C X C X _k C_kX a X a X _m a_mX

)

xmin 11 1 , 12 2 ,..., 1 21 1 22 2 ,..., 2

max µ µ µ µ µ µ

Max zi = cijxj

n

i

∑

₌₁ (I = 1,2….,k)

Memenuhi kendala bj

aijxi

n

i

≤

∑

₌₁ (j=1,2,….m)

Dimana parameter Cij, Aij dan Bj diberi nilai. Dalam bentuk yang tepat, yang tujuan beberapa masalah dapat diwakili oleh model Pemrograman fuzzy linier multiobjective :

cx Z maksimasi =

terhadap kendala Ax≤b

Dimana Z = (z1 ,z2,….zn) adalah vektor dari tujuan, C adalah k×n matriks konstan dan X adalah n×1 vektor putusan variabel, yang merupakan

n

m× matriks dan b adalah m×1vektor dari konstan.

3.4 Perumusan Model Pemrograman Linear dengan KFO Kabur dan

Kendala Kabur dan Langkah-langkah Pencarian Solusinya

maksimasi (minimisasi)

∑

=

= n

j j jx

c cx

1 ~

(9)

terhadap kendala

( )

Ax _i ≤~b_i (10) x≥0 (11)

Perumusan MPLKFOK3 lebih lanjut beserta penyelesaiannya dibahas pada 3.4.1 dan 3.4.2 berikut ini.

3.4. 1 Perumusan Model Pemrograman Linear dengan KFO Kabur dan

Kendala Kabur

MPLKFOK3 adalah gabungan dari MPLKFOK dan MPLKK yang berturut-turut, telah dibahas pada 2.6 dan 2.7. Perumusan model MPLKFOK3 pada hakekatnya adalah juga gabungan dari perumusan model MPLKFOK dan MPLKK. Oleh karenanya, masalah MPLKFOK3 pada (9)-(11) menjadi berbentuk masalah optimisasi bertujuan majemuk berikut ini:

x c−

max . maxc*x, maxc+x (12)

( )

x 0

maxµ maxµ₁

( )

x maxµ₂

( )

x ... maxµ_m

( )

x dengan kendala:x≥0

3.4. 2 Langkah-langkah Pencarian Solusi Pemrograman Linear dengan

KFO Kabur dan Kendala Kabur

Fungsi-fungsi objektif pada (12) ekivalen dengan fungsi objektif berikut: x

c c

z ( )

min = *− − maxz=c*x maxz=(c+ −c*)x (12a) sehingga bentuk-bentuk (12) dan (12a) dapat saling menggantikan satu sama lain. Usulan langkah-langkah pencarian solusi selengkapnya bagi MPLKFOK3 (12) adalah sebagai berikut:

Misalkan x={xAx≤b,x≥0}

Langkah 1.1 Tentukan nilai-nilai berikut ini:

o z c c x

X

x ( )

min *

min 1

− ∈ −

= (13)

o z c c x

X

x ( )

max * max

1

− ∈ −

= (14)

o z c x

X x * min 2 min ∈

= (15)

o z c x

X x

* max

2 =max_∈ (16)

o z c c x

X

x ( )

min *

min

3 = −

+

∈ (17)

o z c c x

X

x ( )

max *

max

3 = −

+

∈ (18)

Langkah1.2 Definisikan ketiga fungsi keanggotaan berikut:

⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ ≥ − ≤ − ≤ − − − − ≥ = − − − − max 1 * max 1 * min 1 min 1 max 1 * max 1 min 1 * ) ( jika , 0 ) ( jika , ) ( ) ( jika , 1 ) ( 1 z x c c z x c c z z z x c c z z x c c x z

µ (19)

⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ ≥ ≤ ≤ − − ≥ = max 2 * max 2 * min 2 min 2 max 2 max 2 * min 2 * jika , 0 jika , jika , 1 ) ( 2 z x c z x c z z z z x c z x c x z

µ (20)

⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ ≥ − ≤ − ≤ −− − − ≥ = + + + + max 3 * max 3 * min 3 min 3 max 3 max 3 * min 3 * ) ( , 0 ) ( jika , ) ( ) ( jika , 1 ) ( 3 z x c c z x c c z z z z c c z x c c x z

µ (21)

Langkah1.3 Definisikan fungsi:

min

{

( ), ( ), ( )

}

3 2

1 x z x z x

z µ µ

µ

α = (22)

yang ekivalen dengan ketiga relasi berikut: α

µ ( )≥

1 x

z atau

max 1 min 1 max 1 * ) ( )

(c −c− x+α z −z ≤ z (22a)

α

µ

( )≥

2 x

z atau

min 2 min 2 max 2 * )

(z z z

x

c −α − ≥ (22b)

α µ ( )≥

3 x

z atau

min 3 min 3 max 3 *_{) ( )}

(c+ −c x−α z −z ≥ z (22c) Langkah1.4 Definisikan masalah optimisasi:

maxα (23)

Langkah-2: Menyatakan MPLKK (yang bersifat multiobjektif) kedalam bentuk masalah optimisasi dengan satu fungsi objektif saja, melalui langkah-langkah:

Langkah 2.1 Pecahkan masalah Pemrograman Linear berikut:

maksimasi cxterhadap kendala

( )

Ax _i ≤b_i (i = 1,2,...,m) sebutlah nilai optimal dari fungsi objektifnya 0

z

Langkah 2.2 Pecahkan masalah Pemrograman Linear berikut:

maksimasi cxterhadap kendala

( ) (

Ax _i ≤ b_i+t_i

)

(i = 1,2,.,m) sebutlah nilai optimal dari fungsi objektifnya adalah z1 Langkah 2.3 Definisikan fungsi: µ₀

( )

x seperti pada (7), dan

µ_i

( )

x seperti pada (8) Langkah 2.4 Definisikan fungsi:

θ =min

{

µ₀(x),µ₁(x),µ₂(x),L,µ_m(x)

}

(24) yang ekivalen dengan relasi berikut:

µ₀(x)≥θ atau _cx+θ_(z1−_z0₎≤_z0 _(24a) µ_i(x)≥θ atau (Ax)_i +θt_i ≤

(

b_i+t_i

)

(24b) (i = 1,2,...,m)

Langkah 2.5 Definisikan masalah optimisasi: θ

max (24c)

dengan kendala x≥0

Langkah-3: Menggabungkan MPLKFOK dan MPLKK, yang masing-masing memiliki sebuah fungsi objektif, kedalam bentuk masalah optimisasi dengan satu fungsi objektif saja, hal ini ditempuh melalui langkah-langkah:

Langkah 3.1 Definisikan fungsi:

γ min

{ }

α,θ ) 24 ) 24 ( ), 22 ( ) 22

( a c a c

kendala − −

= (25)

Langkah 3.2 Definisikan dan pecahkan masalah optimisasi:

maxγ (26)

µ ( )≥α

1 x

z atau

max 1 min 1 max 1 *

) (

)

(c −c− x+α z −z ≤z (27) µ ( )≥α

2 x

z atau

min 2 min 2 max 2 *

)

(z z z

x

c −α − ≥ (28)

µ ( )≥α

3 x

z atau

min 3 min 3 max 3 *

) (

)

(c+ −c x−α z −z ≥ z (29) µ₀(x)≥θ atau ₍ 1 0₎ 0

z z z

cx+θ − ≤ (30)

µ_i(x)≥θ atau(Ax)_i +θt_i ≤

(

b_i +t_i

)

(31) θ∈

[ ] [ ]

0,1,α∈ 0,1,α≥γ,θ ≥γ,x≥0

(i = 1,2,...,m)

3. 5 Pendekatan MPLKFOK3 untuk TSP

[image:39.612.245.493.77.249.2] [image:39.612.249.386.535.627.2]

Pada pembahasan MPLKFOK3 dikaji berdasarkan mencari fungsi maksimum, sedangkan persoalan optimisasi TSP adalah mencari nilai minimum dari fungsi tujuan dari lintasan dengan biaya paling murah, lintasan dengan jarak paling pendek dan lintasan dengan waktu tempuh paling cepat sehingga mendapatkan lintasan dengan tingkat efisien paling tinggi. Untuk menyelesaikan persoalan TSP fungsi tujuan pada MPLKOK3 dibuatkan minimum dan tanda pada kendala diubah dari “≥” menjadi “≤” atau “=”.Pandang suatu kasus Pedagang keliling mengunjungi tiga kota tepat sekali dari kota asalnya dengan melihat lintasan terpendek dan biaya yang paling murah serta waktu yang paling cepat. Kota asal dilabelkan 0 dan kota tempat kunjungan dilabelkan dengan 1, 2 atau 3 seperti pada gambar 3.1

Gambar 3.1 hubungan kota asal dengan kota tujuan

Pada permasalahan TSP, dari hubungan antar kota diatas dibatasi dengan bobot biaya, jarak dan waktu seperti pada tabel 3.1.

Tabel 3.1 Biaya, jarak dan waktu (b,j,w) antar kota 1

2

Kota 0

(b,j,w)

1

(b,j,w)

2

(b,j,w)

3

(b,j,w)

0 (0,0,0) (20,5,4) (15,5,5) (11,3,2)

1 (20,5,4) (0,0,0) (30,5,3) (10,3,3)

2 (15,5,5) (30,5,3) (0,0,0) (20,10,2)

3 (11,3,2) (10,3,3) (20,10,2) (0,0,0)

Andaikan xij merupakan hubungan dari kota i ke kota j yang direpresentasikan dengan:

⎩ ⎨ ⎧ =

kota antar hubungan ada

tidak jika ,

0

i kota dari kunjungan merupakan

j kota jika , 1

ij

x

ij

c merupakan koefisien biaya, jarak dan waktu dari kota i ke kota j. fungsi tujuan untuk minimasi biaya, jarak dan waktu adalah :

0 1 1

~ min

: _k

n

i n

j ij ij

i c x z

z

∑∑

≤

= =

Andaikan z₁,z₂,z₃ adalah tiga fungsi tujuan yang dirumuskan untuk biaya, jarak dan waktu. Tingkat aspirasi dari masing-masing ditetapkan sebagai 65, 16, 11 yang diambil dari jumlah minimum biaya, jarak dan waktu dari semua lintasan. Dengan toleransi 5, 2, 1 yang diambil dari selisih antara koefisian variabel keputusan dari biaya, jarak dan waktu.

Perjalanan pedagang keliling pada kasus ini manakala dibuat daftar perjalanan berdasarkan algoritma Bruce Force adalah :

(n-1)! = 3! = 6

Terdapat 6 keputusan lintasan yang dilalui dengan masing-masing pilihan lintasan akan diperoleh total biaya, jarak dan waktu, yakni:

2. x₀₁→x₁₃→x₃₂ →x₂₀ =

(

20,5,4

) (

+ 10,3,3

) (

+ 11,3,2

) (

+ 15,5,5

) (

= 81,23,14

)

3. x₀₂ →x₂₁ →x₁₃ →x₃₀ =

(

15,5,5

) (

+ 30,5,3

) (

+ 10,3,3

) (

+ 11,3,2

) (

= 66,16,15

)

4. x₀₂ →x₂₃ →x₃₁→x₁₀ =

(

15,5,5

) (

+ 20,10,2

) (

+ 10,3,3

) (

+ 20,5,4

) (

= 65,23,14

)

5. x₀₃ →x₃₁→x₁₂ →x₂₀ =

(

11,3,2

) (

+ 10,3,3

) (

+ 30,5,3

) (

+ 15,5,5

) (

= 66,16,13

)

6. x₀₃ →x₃₂ →x₂₁→x₁₀ =

(

11,3,2

) (

+ 20,10,2

) (

+ 30,5,3

) (

+ 20,5,4

) (

= 81,23,11

)

Tingkat aspirasi untuk biaya jatuh pada pilihan lintasan 4, yaitu 65 sedangkan untuk jarak jatuh pilihan pada pilihan lintasan 3 dan 5, yaitu 16 dan untuk waktu jatuh pada pilihan lintasan 1 dan 6, yaitu 11. Kemudian untuk menentukan aspirasi toleransi adalah dengan memilih selisih koefisien objektif dari pilihan lintasan tersebut adalah sebagai berikut:

1. Untuk menetapkan toleransi biaya dari koefisien {15,20, 10, 20} = t1 = 5 2. Untuk menetapkan toleransi jarak dari koefisien {3,3,5,5} atau {5,5,3,3}=

t2 = 2

3. Untuk menetapkan toleransi waktu dari koefisien {2,2,3,4}atau {4,3,2,2}= t3 = 1

Fungsi objketif digambarkan sebagai berikut:

65 ~ 20 10 11 20 30 15 10 30 20 11 15 20 min 32 31 30 23 21 20 13 12 10 03 02 01 1 ≤ + + + + + + + + + + + = x x x x x x x x x x x x z

Toleransi t1 = 5

16 ~ 10 3 3 10 5 5 3 5 5 3 5 5 min 32 31 30 23 21 20 13 12 10 03 02 01 2 ≤ + + + + + + + + + + + = x x x x x x x x x x x x z

Toleransi t2 = 2

Toleransi t3 = 1

fungsi keanggotaan kabur untuk biaya, jarak dan waktu adalah sebagai berikut:

⎪ ⎩ ⎪ ⎨ ⎧ ≥ ≤ ≤ − ≤ = 70 , 0 70 65 , 5 70 65 , 1 ) ( 1 1 1 1 1 z z z z z µ ⎪ ⎩ ⎪ ⎨ ⎧ ≥ ≤ ≤ − ≤ = 18 , 0 18 16 , 2 18 16 , 1 ) ( 2 2 2 2 2 z z z z z µ ⎪⎪⎩ ⎪⎪ ⎨ ⎧ ≥ ≤ ≤ − ≤ = 12 , 0 12 11 , 1 12 11 , 1 ) ( 3 3 3 3 3 z z z z z µ

3.6 Pendekatan fungsi maxmin pemrograman linier tujuan majemuk

dengan kendala kabur

Pemrograman Fuzzy Multiobjective dengan pendekatan linier mak-min diberikan sebagai:

( )

z maksimasi µ

terhadap kendala :

( )

z₁ ≤1−

(

z₁−65

)

/5 µ

( )

z₂ ≤1−

(

z₂−16

)

/2 µ

( )

z₃ ≤1−

(

z₃−11

)

/1 µ

1 03 02 01+x +x = x

1 13 12 10+x +x = x

1 32 31 30+x +x = x

1 30 20 10+x +x = x

1 31 21 01+x +x = x

1 32 12 02+x +x = x

1 23 12 03+x +x = x

1 10 01+x ≤ x

1 20 02+x ≤ x

1 30 03+x ≤ x

1 21 12+x ≤ x

1 31 13+x ≤ x

1 32 23+x ≤ x

( )

z ≥0 µ

0

≥ ij

x

Dari data di atas fuzzy linear program dan varian yang di selesaikan dengan menggunakan program LINDO. Sebagaimana ditampilkan dalam table 3.2. dimana hanya z1 dan z2 dianggap, dan z3 dihilangkan, maka optimal kekalahan dihasilkan dengan a = 0.8.. Bila z3 juga dianggap, solusi menjadi infeasible pada toleransi ini. Jika toleransi z3 ke 4, solusi menjadi layak. Dalam hal ini, jalan yang optimal di capai dengan a = 0.55

[image:44.612.146.498.95.201.2]

Tabel 3.2 Hasil optimal untuk setiap solusi

Solusi Z1, t1 Z2, t2 Z3,t3 a Rute

0 65.5 16.2 Not 0.80 XO3-X31-X20

1 65.5 16.2 11.1 ……. Tidak ada solusi

2 65.5 16.2 11.4 0.55 X03-X31-X12-X19

BAB 4

KESIMPULAN DAN SARAN

4.1. Kesimpulan

Berdasarkan hasil penelitian mengenai Pemrograman Multiobjective dalam penyelesaian kasus Traveling Salesman Problem (TSP) dapat disimpulkan bahwa:

1. TSP Multiobjective tidak tentu ada di lingkungan dimana pilihan rute yang kabur dapat dilakukkan apabila dengan menggunakan parameter ini. 2. Toleransi yang diperkenalkan oleh pengambil keputusan untuk

mengakomodasi ketidakjelasan ini.

3. Dalam menyesuaikan toleransi ini, berbagai solusi dengan tingkat aspirasi yang berbeda ditemukan, maka pengambil keputusan dapat memilih satu yang terbaik dari yang memenuhi tingkat memuaskan dalam domain yang diberikan toleransi.

4. Pemrograman Fuzzy Linier Multiobjective dapat membantu untuk mencapai k-dimensi poin sesuai dengan aspirasi pengambil keputusan ditingkat multi – dimensi ruang solusi.

4.2. Saran

DAFTAR PUSTAKA

Cox, E. D, 1995, Fuzzy Logic for Business and Industry, Newyork : The Metus Systems Group

Jang, J –S. R., Sun, C.T and Mizutani,E, 2004, Neuro-Fuzzy and Soft Computing, Pearson Education Pte Ltd. Singapore.

Kusumadewi, S. & Purnomo, H., 2004, Aplikasi Logika Fuzzy untuk Pendukung Keputusan, Graha Ilmu. Yogyakarta.

Marakas, G. M., 1999, Decision Support System in The Twenty-First Century, Prentice-Hall

Pasaribu, E. D., 2004, Sistem Pendukung Keputusan Pemilihan Jurusan di SMU dengan Logika Fuzzy, Program Studi Ilmu Komputer, Fakultas MIPA, Universitas Gadjah Mada. Yogyakarta

Pressman, R., 1997, SOFTWARE ENGINERING: A Practitioner’s Approach Sixth Edition. McGraw-Hill. New York.

Rugaya, T. I.,2005, Sistem Pendukung Keputusan Pemberian Kredit Menggunakan AHP, Program Studi Ilmu Komputer, Fakultas MIPA, Universitas Gadjah Mada. Yogyakarta

LAMPIRAN A. Listing Program Menggunakan LINDO

1. Nilai Minimum dari Segi Biaya

min 20x01 + 15x02 + 11x03 + 20x10 + 30x12 + 10x13 + 15x20 + 30x21 + 20x23 + 11x30 + 10x31 + 20x32

st

x01 + x02 + x03 = 1 x10 + x12 + x13 = 1 x20 + x21 + x23 = 1 x30 + x31 + x32 = 1 x10 + x20 + x30 = 1 x01 + x21 + x31 = 1 x02 + x12 + x32 = 1 x03 + x13 + x23 = 1 x01 + x10 <= 1

x02 + x20 <= 1 x03 + x30 <= 1 x12 + x21 <= 1 x13 + x31 <= 1 x23 + x32 <= 1 xij >= 0

end

2. Nilai Minimum dari Segi Jarak

min 5x01 + 5x02 + 3x03 + 5x10 + 5x12 + 3x13 + 5x20 + 5x21 + 10x23 + 3x30 + 3x31 + 10x32

st

x01 + x02 + x03 = 1 x10 + x12 + x13 = 1 x20 + x21 + x23 = 1 x30 + x31 + x32 = 1 x10 + x20 + x30 = 1 x01 + x21 + x31 = 1 x02 + x12 + x32 = 1 x03 + x13 + x23 = 1 x01 + x10 <= 1

x02 + x20 <= 1 x03 + x30 <= 1 x12 + x21 <= 1 x13 + x31 <= 1 x23 + x32 <= 1 xij >= 0

3. Nilai Minimum dari segi Waktu

min 4x01 + 5x02 + 2x03 + 4x10 + 3x12 + 3x13 + 5x20 + 3x21 + 3x23 + 2x30 + 3x31 + 2x32

st

x01 + x02 + x03 = 1 x10 + x12 + x13 = 1 x20 + x21 + x23 = 1 x30 + x31 + x32 = 1 x10 + x20 + x30 = 1 x01 + x21 + x31 = 1 x02 + x12 + x32 = 1 x03 + x13 + x23 = 1 x01 + x10 <= 1

x02 + x20 <= 1 x03 + x30 <= 1 x12 + x21 <= 1 x13 + x31 <= 1 x23 + x32 <= 1 xij >= 0

LAMPIRAN B. Output Program Menggunakan LINDO

4. Nilai Minimum dari Segi Biaya

LP OPTIMUM FOUND AT STEP 12

OBJECTIVE FUNCTION VALUE

1) 65.00000

VARIABLE VALUE REDUCED COST X01 0.000000 1279.000000 X02 1.000000 0.000000 X03 0.000000 0.000000 X10 1.000000 0.000000 X12 0.000000 1.000000 X13 0.000000 1.000000 X20 0.000000 0.000000 X21 0.000000 0.000000 X23 1.000000 0.000000 X30 0.000000 0.000000 X31 1.000000 0.000000 X32 0.000000 0.000000 XIJ 0.000000 0.000000

ROW SLACK OR SURPLUS DUAL PRICES 2) 0.000000 9.000000 3) 0.000000 -5.000000 4) 0.000000 0.000000 5) 0.000000 4.000000 6) 0.000000 -15.000000 7) 0.000000 -30.000000 8) 0.000000 -24.000000 9) 0.000000 -20.000000 10) 0.000000 0.000000 11) 0.000000 0.000000 12) 1.000000 0.000000