Aspek Komputasi Solusi Residu Kuadratik

ASPEK KOMPUTASI

SOLUSI RESIDU KUADRATIK

MUHAMMAD MUKAFI

G54103011

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

RINGKASAN

MUHAMMAD MUKAFI. Aspek Komputasi Solusi Residu Kuadratik. Dibimbing oleh SUGI GURITMAN dan SISWANDI.

Dalam menentukan apakah suatu kongruensi x2≡a

(

modp

)

dengan a bilangan bulat dan p

bilangan prima mempunyai solusi atau tidak dapat digunakan Kriteria Euler. Jika

( 1 / 2)

(

)

1 mod

p

a − ≡ p maka _x2_≡a

(

_modp

)

_{mempunyai solusi.}

Jika x2≡a

(

modp

)

mempunyai solusi, maka untuk mementukan solusinya dapat digunakan Algoritma RESSOL (Residue Solver). Algoritma RESSOL adalah algoritma acak (randomized algorithm) dan bukan algoritma deterministic, tetapi prosedur perhitungannya lebih praktis dan cepat.

Algoritma RESSOL hanya dapat digunakan untuk mencari solusi dari 2

(

_mod

)

x ≡a p

dengan p prima ganjil. Tetapi dari Algoritma RESSOL tersebut dapat dikembangkan menjadi beberapa algoritma untuk mencari solusi dari 2

(

)

mod

x ≡a pq dengan p dan q prima ganjil, dan

2

(mod j)

ASPEK KOMPUTASI

SOLUSI RESIDU KUADRATIK

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

Pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Oleh :

MUHAMMAD MUKAFI

G54103011

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

Judul

: Aspek Komputasi Solusi Residu Kuadratik.

Nama

: Muhammad Mukafi

NRP

: G54103011

Menyetujui,

Mengetahui,

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Tanggal Lulus : ………..

Pembimbing II

Drs. Siswandi, M.Si

NIP. 131 957 320

Pembimbing I

Dr. Sugi Guritman

NIP. 131 999 582

PRAKATA

Puji syukur penulis panjatkan kepada Allah SWT atas segala karunianya sehingga penulis dapat menyelesaikan tugas akhir yang berjudul Aspek Komputasi Solusi Residu Kuadratik. Shalawat dan salam semoga senantiasa tercurah kepada Rasulullah Muhammad SAW beserta keluarga, sahabat dan pengikutnya hingga akhir zaman.

Tugas akhir ini saya persembahkan untuk kedua orang tua saya dan ketiga kakakku yang telah banyak memberikan dukungan yang luar biasa (terutama nasehat dan doa-doanya) sehingga karya ilmiah ini dapat terselesaikan.

Keterbatasan dan ketidaksempurnaan membuat penulis membutuhkan bantuan, dukungan dan semangat dari orang-orang secara langsung ataupun tidak langsung berkontribusi besar dalam pembuatan tugas akhir ini. Oleh karena itu penulis ingin mengucapkan rasa terima kasih yang sebesar-besarnya kepada Bapak Sugi Guritman dan Bapak Siswandi yang dengan sabar telah membimbing dan mengarahkan selama penulisan karya ilmiah ini. Ibu Sri Nurdiati atas kesediaannya menjadi penguji luar dalam sidang tugas akhir penulis. Rismanto dan Arie Wijayanto yang telah membantu dalam menyelesaikan program penulis. Rian, Elis, dan Tiwi atas kesediaannya menjadi pembahas dalam seminar penulis.

Tak lupa penulis ingin mengucapkan terima kasih kepada Hepy Purnomo, Syamsuri, Taufik Hidayah, Jaenudin, Indra, Cecep, Engkus, Iim dan para pengajar MCS (Walidah, Rina, Yudi, Nuqi, Novi, Lia, Dian, Arum, Fifi). Kepada Bapak Ridwan Hasan Saputra dan tim KPM (Teh Desi, Bu Anis, Bu Astri, Hirasawa, Dadan, Rahmi). Seluruh Dosen Departemen Matematika atas segala ilmu yang telah diberikan. Staf dan karyawan TU Matematika IPB. Penghuni Villa Merah (Abay, Sanggam, Tyo). Matematika angkatan 40 atas persahabatannya selama ini semoga tidak akan berakhir. Serta seluruh pihak-pihak yang tidak dapat penulis sebutkan satu per satu.

Penulis mengetahui bahwa tugas akhir ini masih jauh dari kesempurnaan. Semoga tugas akhir ini dapat bermanfaat bagi penulis khususnya dan bagi pihak lain yang membutuhkan.

Bogor, Januari 2007

RIWAYAT HIDUP

Nama lengkap penulis adalah Muhammad Mukafi, dilahirkan di Brebes pada tanggal 7 Oktober 1984 sebagai anak keempat dari empat bersaudara. Ayah bernama Fachrur Rozi dan Ibu bernama Siti Aisyah Mu’tamiroh.

Penulis menyelesaikan pendidikan Sekolah Dasar pada tahun 1997 di SD Negeri Jatibarang Kidul 1 Jatibarang Brebes, Sekolah Lanjutan Tingkat Pertama Negeri 2 Brebes tahun 2000, Sekolah Menengah Umum Negeri 1 Slawi Tegal tahun 2003, dan masuk Institut Pertanian Bogor melalui jalur USMI pada tahun 2003.

Selama mengikuti perkuliahan, penulis pernah menjadi asisten dosen untuk mata kuliah Pengantar Matematika, Matematika Dasar, Kalkulus I, Kalkulus II dan Kalkulus III pada tahun 2004 - 2006.

Penulis pernah menjadi anggota aktif dalam himpunan profesi Gugus Mahasiswa Matematika IPB sebagai ketua Departemen Kajian Ilmiah pada tahun 2004-2005 dan menjadi anggota Dewan Legislatif Gugus Mahasiswa Matematika pada tahun 2005-2006.

DAFTAR ISI

Halaman

I. PENDAHULUAN ... 1

1.1. Latar Belakang ... 1

1.2. Tujuan penulisan ... 1

II. LANDASAN TEORI ... 1

2.1 Bilangan Bulat ... 1

2.2 Kongruensi ... 3

III. PEMBAHASAN ... 4

3.1 Teorema – Teorema yang Terkait Solusi Residu Kuadratik. ... 4

3.2 Konstruksi Algoritma RESSOL beserta Analisisnya... 6

3.3 Mengkontruksi Algoritma untuk Mencari Solusi 2

(

)

mod x ≡a pq

dengan

p dan q bilangan prima ganjil ... 10

3.4 Mengkontruksi Algoritma untuk Mencari Solusi x2≡a(modpj) dengan p prima ganjil dan j 2 ... 11

3.5 Membandingkan waktu eksekusi Algoritma 1 dengan Algoritma RESSOL yang terkait bilangan besar... 14

IV. SIMPULAN DAN SARAN ... 15

4.1 Simpulan ... 15

4.2 Saran ... 15

DAFTAR PUSTAKA ... 15

DAFTAR BAGAN

Halaman

Bagan 1 : Algoritma mencari solusi 2

(

)

mod

x ≡a p ... 5 Bagan 2 : Algoritma RESSOL ... 9 Bagan 3 : Algoritma mencari akar kuadrat modulo (pq), p dan q prima ganjil ... 11 Bagan 4 : Algoritma mencari akar kuadrat modpj, dengan p prima ganjil dan j≥2.. 13

DAFTAR TABEL

Halaman

Tabel 1 : Waktu Eksekusi Algoritma 1 dan Algoritma RESSOL ... 14 Tabel 2 : Waktu Eksekusi Algoritma RESSOL ... 14

DAFTAR LAMPIRAN

Halaman

Lampiran 1 : Implementasi Algoritma 1 dengan bantuan perangkat lunak

Mathematica 5.2 ... 17 Lampiran 2 : Implementasi Algoritma RESSOL dengan bantuan perangkat lunak

Mathematica 5.2 ... 18 Lampiran 3 : Implementasi Algoritma 3 dengan bantuan perangkat lunak

Mathematica 5.2 ... 19 Lampiran 4 : Implementasi Algoritma 4 dengan bantuan perangkat lunak

Mathematica 5.2... 20 Lampiran 5 : Waktu Eksekusi Algoritma 1 dan Algoritma RESSOL dengan

I. PENDAHULUAN

1.1 Latar Belakang

Salah satu masalah dalam teori bilangan adalah masalah residu kuadratik yaitu mencari solusi dari kongruensi x2≡a(mod )n dengan

a dan n adalah suatu bilangan bulat.

Untuk mencari solusi dari

(

)

2

mod

x ≡a n terlebih dahulu ditentukan apakah a merupakan residu kuadratik dari n

atau bukan. Masalah residu kuadratik telah dibahas sebelumnya oleh Yuliarti Ningsih (2006). Jika a merupakan residu kuadratik maka 2

(

)

mod

x ≡a n mempunyai solusi.

Mencari solusi dari 2

(mod )

x ≡a n lebih mudah jika n adalah bilangan prima, tetapi jika n adalah bilangan komposit yang tidak diketahui faktor primanya maka akan sulit untuk dicari solusinya.

Pencarian solusi dari 2

(

)

mod

x ≡a n

dapat kita bagi menjadi beberapa kasus yaitu untuk n prima, n = p q dengan p dan q

prima ganjil, dan n = j

p dengan p prima ganjil dan j bilangan bulat dimanaj≥2.

Untuk kasus 2

(

)

mod

x ≡a p dengan p

prima ganjil dan a adalah residu kuadratik, terdapat suatu algoritma yang dapat digunakan untuk mencari solusinya yaitu Algoritma RESSOL (Residue Solver) dan Algoritma 1.

Untuk kasus 2

(

)

mod

x ≡a pq dengan p

dan q prima ganjil, terlebih dahulu dicari solusi kongruensi dari masing-masing faktor prima tersebut dengan Algoritma RESSOL, kemudian digunakan Teorema Sisa Cina untuk menemukan solusinya.

Untuk kasus 2

(

)

mod j

x ≡a p dengan p

prima ganjil dan j≥2, terlebih dahulu diceri solusi dari 2

(

)

mod

x ≡a p dengan Algoritma RESSOL, kemudian digunakan Lemma Hensel’s untuk mencari solusinya.

1.2 Tujuan

Tujuan dari penulisan ini adalah : 1. Mempelajari teorema-teorema yang

terkait dengan solusi residu kuadratik dan mengkonstruksi Algoritma 1 untuk mencari solusinya.

2. Merekonstruksi Algoritma RESSOL beserta analisisnya.

3. Mengkonstruksi Algoritma untuk mencari solusi 2

(

)

mod

x ≡a pq dan

dengan a dan j bilangan bulat

(

j≥2

)

serta p dan q prima ganjil.

4. Membandingkan waktu eksekusi Algoritma 1 dengan Algoritma RESSOL yang terkait bilangan besar.

II. LANDASAN TEORI

Pada bagian ini akan dituliskan beberapa definisi dan teorema yang digunakan sebagai landasan bagi argumen-argumen yang dituliskan pada bab-bab berikutnya.

2.1 Bilangan Bulat

Himpunan Bilangan Bulat dinotasikan .

{

..., 2, 1, 0,1, 2,...

}

= − − .

Definisi 2.1 [Keterbagian]

Bilangan bulat b dikatakan pembagi dari bilangan bulat a(a 0), jika ada bilangan bulat x sedemikian sehinggab axdan ditulis

a | b. Apabila b bukan pembagi dari a, maka ditulis a|/b.

[Niven, 1991]

Definisi 2.2 [Pembagi Bersama Terbesar] Suatu bilangan bulat tak negatif d dikatakan pembagi bersama terbesar dari bilangan bulat

a dan b, jika :

1. d adalah pembagi bersama dari a dan b, dan

2. Jika c dimana c|a dan c|b, maka

c|d.

Biasanya pembagi bersama terbesar dari a

dan b dinotasikan dengan d ( , )a b

.

[Menezes, 1997]

Definisi 2.3 [Relatif Prima]

Bilangan a dan b dikatakan relatif prima jika ( , )a b 1dan bilangan-bilangan a a1, 2,...,an

dikatakan relatif prima jika ( ,a a1 2,...,an) 1.

(

)

2

mod j

Bilangan-bilangan a a1, 2,...,an dikatakan

relatif prima berpasangan jika ( ,a ai j) 1 untuk setiap i 1, 2, 3...,n dan j 1, 2, 3...,n

dengan i j.

[Niven, 1991]

Definisi 2.4 [Bilangan Prima]

Suatu bilangan bulat p > 1 dinamakan prima atau bilangan prima , jika pembagi dari p

adalah 1 dan p itu sendiri.

Bilangan bulat a > 1 yang bukan prima dinamakan bilangan komposit.

[Niven, 1991]

Teorema 2.1

1. Jikap abdan p prima makap aataup b. 2. Jika p a a_{1 2}....andan p prima maka

1

p a atau p a2atau p a3… atau p an.

[Niven, 1991]

Teorema 2.2 [Teorema Dasar Aritmatika]

Setiap bilangan bulat n > 1 dapat difaktorkan secara tunggal ke dalam faktor-faktor yang semuanya prima, tanpa memperhatikan urutan.

[Niven, 1991]

Definisi 2.5 [Fungsi Euler Phi]

Fungsi Euler Phi dari n dengan n = 1, 2, 3, ... dinotasikan dengan φ(n) adalah banyaknya bilangan bulat pada interval [1,n] yang prima relatif dengan n.

[Menezes, 1997]

Teorema 2.3 [Sifat-sifat Fungsi Euler Phi]

1. Jika p prima maka φ(p) = p – 1.

2. Jika (m,n) = 1, maka φ(mn) = φ(m).φ(n). 3. Jika 1 2 3

1 2 3

...

k

e e

e e

k

n= p p p p dengan pi

bilangan prima, maka

1 2

1 1 1

( ) 1 1 ... 1

k

n n

p p p

φ = − − −

[Menezes, 1997]

2.2 Kongruensi

Definisi 2.6

Misalkan a, b dan m bilangan bulat, dengan 0

m . Bilangan a dikatakan kongruen terhadap b modulo m, dinotasikan dengan

(mod )

a b m , jika m pembagi (a b).

Bilangan bulat m disebut modulus dari kongruensi.

[Menezes, 1997]

Teorema 2.4

Jika a, b, c, d, dan m adalah bilangan bulat, dengan m 0maka :

1. Ketiga pernyataan berikut adalah ekuivalen :

i. a b(mod )m , ii. b a(mod )m , dan iii. a b 0(mod )m .

2. Jika a b(mod )m dan b c(mod )m

maka a c(mod )m .

3. Jika a b(mod )m dan c d(mod )m

maka a c(mod )m b d(mod )m . 4. Jika a b(mod )m dan c d(mod )m

maka ac bd(mod )m .

5. Jika a b(mod )m dan d m| , dengan

0

d maka a b(mod )d .

6. Jikaa b(mod )m makaac bc(mod )m

untuk setiap c positif.

[Niven, 1991]

Definisi 2.7 [Himpunan Bilangan Bulat Modulo n]

Himpunan bilangan bulat modulo n, dinotasikan _n, merupakan suatu himpunan dari bilangan-bilangan bulat {0,1,2,3,…, n – 1}.

[Menezes, 1997] Operasi penjumlahan, pengurangan, dan perkalian bilangan bulat modulo n bersifat

tertutup dalam _n.

Definisi 2.8 [Invers Perkalian]

Misalkan a∈ n. Jika ( , )a n =1 maka invers

perkalian dari a

(

modn

)

adalah bilangan bulat x∈ n sedemikian sehingga

(

)

1 mod

ax≡ n . Invers dari a dinotasikan a−1. [Niven, 1991]

Teorema 2.5 [Teorema Euler]

Teorema 2.6 [Teorema Fermat]

1. Jika

(

a p,

)

=1maka _ap−1_{≡1 mod}

(

_p

)

_. 2. ap≡a

(

modp

)

untuk setiap a∈ .

[Niven, 1991]

Definisi 2.9 [Grup Perkalian dari n]

Grup perkalian n adalah

(

)

{

}

*

, 1

n = a∈ n a n = .

[Menezes, 1997] Jika n prima, maka *n =

{

a1≤a≤n−1

}

. Jika a∈ *_n dan b∈ *_n maka a b. ∈ *_n.

*

n bersifat tertutup terhadap perkalian.

Definisi 2.10 [Order]

Misalkan a∈ *_n. Order dari a dinotasikan ord(a) adalah bilangan bulat positif terkecil t

sedemikian sehingga at ≡1 mod

(

n

)

. [Menezes, 1997]

Definisi 2.11 [Generator]

Bilangan g∈ *_n dinamakan generator dari *

n jika ord g

( )

=φ

( )

n . Grup perkalian *

n yang mempunyai generator dinamakan

grup siklik.

[Menezes, 1997]

Teorema 2.7

Jika g adalah generator dari *_n, maka

( )

{

}

* i_{mod 0 1}

n = g n ≤ ≤i φ n − .

[Menezes, 1997]

Teorema 2.8

Jika p prima maka *pmempunyai generator.

[Niven, 1991]

Definisi 2.12 [Residu Kuadratik]

Bilangan * n

c∈ dinamakan residu kuadratik modulo n atau kuadrat modulo n jika ada

* n

m∈ Ζ dengan 2

(

)

mod

m ≡c n . Himpunan semua residu kuadrat modulo n dinotasikan

Qn.

[Menezes, 1997]

Lemma 2.9

(

)

2

1 mod

x ≡ p dengan p prima jika dan hanya jika x≡ ±1 mod

(

p

)

.

[Niven, 1991]

Teorema 2.10

Misalkan p adalah bilangan prima, maka

(

)

2

1 mod

x ≡ − p mempunyai solusi jika dan hanya jika p=2atau p≡1(mod 4).

[Niven, 1991]

Teorema 2.11

Misal a b m, , ∈ dengan m>0, dan

(

,

)

g= a m . Kongruensi ax≡b

(

modm

)

mempunyai solusi jika dan hanya jika g b. Jika kondisi tersebut dipenuhi, solusinya membentuk barisan aritmatika dengan beda

m

g dan memberikan sebanyak g solusi

[Niven, 1991]

Teorema 2.12 [Teorema Sisa Cina]

Jika m m₁, ₂,....,m_r adalah bilangan bulat positif dimana m_i relatif prima dengan m_j

untuk i≠ j, dan a a₁, ₂,....,a_r adalah bilangan bulat sembarang, maka sistem kongruensi

(

)

(

)

(

)

1 1

2 2

mod mod

mod

r r

x a m

x a m

x a m

≡ ≡

≡ mempunyai solusi.

Jika x0 adalah solusi dari sistem tersebut, maka x=x0+km dengan k∈ dan

1. 2. 3... r

m=m m m m juga solusi dari sistem tersebut.

[Niven, 1991]

Lemma 2.13

Misal a∈ *_n

.

Jika ord(a) = h, dan

(

)

1 mod

k

a ≡ n maka h k.

[Niven, 1991]

Akibat 2.14

Jika

(

a m,

)

=1, maka order dari a

(

modm

)

pembagi φ

( )

m .

Lemma 2.15

Jika a memiliki order h

(

modm

)

, maka ak

memiliki order

(

,

)

(

mod

)

h

m

h k .

[Niven, 1991]

III. PEMBAHASAN

Pada bagian pendahuluan telah disebutkan bahwa tujuan dari penulisan ini adalah mempelajari teorema-teorema yang terkait solusi residu kuadratik dan mengkonstruksi algoritma untuk mencari solusinya, merekonstruksi Algoritma RESSOL beserta analisisnya, mengkonstruksi algoritma untuk mencari solusi

(

)

2

mod

x ≡a pq dan 2

(

mod j

)

x ≡a p serta membandingkan waktu eksekusi algoritma yang terkait bilangan besar.

3.1 Teorema – Teorema yang Terkait Solusi Residu Kuadratik.

Definisi 3.1 [Akar kuadrat]

Misalkan a∈Qn. Jika

(

)

* 2

mod

n

x x a n

∃ ∈ Ζ ∋ ≡

,

maka x dinamakan akar kuadrat dari a

modulo n.

[Menezes, 1997]

Mencari solusi dari x2 ≡a

(

modn

)

tidaklah mudah, apalagi jika n adalah bilangan komposit yang tidak diketahui faktor primanya. Jika n adalah bilangan prima, maka ada beberapa teorema yang dapat digunakan untuk mencari solusinya.

Teorema 3.1

Jika p prima, (a,p) = 1 dan

( 1 /) (, 1)

(

)

1 mod

p n p

a − − ≡ p , maka kongruensi n

(

mod

)

x ≡a p …(i) mempunyai (n, p–1) solusi.

Jika ( 1 /) (, 1)

(

)

1 mod

p n p

a − − ≡/ p maka

(

mod

)

n

x ≡a p tidak mempunyai solusi. [Niven, 1991]

Bukti :

Karena p prima maka berdasarkan Teorema 2.8, *

p mempunyai generator. Misal g adalah generator (mod p) maka berdasarkan Teorema 2.7 ada i dimana 0≤ ≤i p−2

sedemikian sehingga gi ≡a(mod )p …(ii)

Jika ada x0 yang merupakan solusi dari

(

mod

)

n

x ≡a p maka

(

x0,p

)

=1, sehingga ada u dimana 0≤u≤ p−2 sedemikian sehingga ₀ u(mod )

x ≡g p …(iii) Dari (i) , (ii) dan (iii) diperoleh

(

mod

)

( )

(mod ) n

n u i

x ≡a p ⇔ g ≡g p

⇔gun ≡gi(mod )p ⇔un≡i(modp−1) Misalkan k = (n, p -1).

Berdasarkan Teorema 2.11, un≡i(modp−1)

mempunyai k solusi jika k i| dan tidak mempunyai solusi jika k |/i.

Jika k i| maka i p( 1) 0(modp 1)

k

−

≡ −

(karena i

k adalah bilangan bulat) sehingga

( )

(

)

(

)

1 ( 1)

1

1 mod

p i p i

p

k k k

a g g p

− −

−

≡ ≡ ≡

Jika k |/i maka i p( 1) 0(modp 1)

k

−

≡/ − dan

berakibat

( )

(

)

1 ( 1)

1 mod

p i p

k k

a g p

− −

≡ ≡/ .

Dari Teorema 3.1 dapat kita ambil kasus khusus untuk n = 2

(

2

(

)

)

mod

x ≡a p .

Akibat 3.2 [Kriteria Euler]

Jika p adalah bilangan prima ganjil,

(

a p,

)

=1

dan ( 1 / 2)

(

)

1 mod

p

a − ≡ p maka 2

(

)

mod

x ≡a p

mempunyai 2 buah solusi. Jika ( 1 / 2)

(

)

1 mod

p

a − ≡ − p maka

(

)

2

mod

x ≡a p tidak mempunyai solusi. [Niven, 1991] Bukti :

Berdasarkan Teorema 3.1 2

(

)

mod

x ≡a p

mempunyai (2,p−1)=2 buah solusi jika

( 1 / 2)

(

)

1 mod

p

a − ≡ p

.

Misal (p1) / 2

2 ( 1)

1(mod ) p

b =a − ≡ p sehingga 1(mod )

b≡ ± p . Jika b=a(p−1) / 2 ≡ −1(mod )p

maka 2

(

)

mod

x ≡a p

tidak mempunyai solusi

berdasarkan Teorema 3.1.

Dalam mencari solusi dari

(

)

2

mod

x ≡a p dengan p prima ganjil ada beberapa hal yang perlu diperhatikan. Jika

0(mod )

a≡ p maka solusinya adalah 0(mod )

x≡ p . Jika a≡/0(mod )p maka

(

)

2

mod

x ≡a p mungkin tidak mempunyai solusi tergantung kriteria Euler.

Jika 2

(

)

mod

x ≡a p mempunyai solusi maka solusinya ada 2. Misal x0 adalah salah

satu solusinya maka −x0 adalah solusi

lainnya, karena 2 2

(

)

0 0

(−x ) =x ≡a modp . Karena p ganjil maka x₀ ≡ −/ x₀(mod )p

sehingga 2

(

)

mod

x ≡a p akan mempunyai 2 solusi yang berbeda.

Dalam hal 2

(

)

mod

x ≡a p mempunyai solusi, dari bukti Teorema 3.1 kita dapat menemukan solusinya apabila generator dari

*

p diketahui.

Dalam bukti tersebut terlihat bahwa solusi dari 2

(

)

mod

x ≡a p adalah

(mod ) u

x≡g p dengan g adalah generator dari *p, dan u adalah solusi dari

2u≡i(modp−1) 2 1 (mod 1) 2

p

u −

i

−

⇔ ≡

dengan i adalah bilangan genap sedemikian sehingga i (mod )

g ≡a p .

Dari uraian di atas dapat dibuat sebuah algoritma untuk mencari solusi dari

(

)

2

mod

x ≡a p .

Algoritma 1 :

Mencari solusi 2

(

)

mod

x ≡a p dengan

terlebih dahulu mencari generator dari *p. INPUT : Bilangan prima ganjil p dan

bilangan bulat a, 1 ≤ a ≤ p-1. OUTPUT : Dua akar kuadrat a modulo p.

1. Hitung a(p−1 2) dengan Kriteria Euleur. Jika (p1 2) 1 mod

(

)

a − p

≡ − maka a tidak

mempunyai akar kuadrat modulo p dan proses berhenti .

Jika ( 1 2)

(

)

1 mod

p

a − ≡ p lanjut ke langkah 2.

2. Cari generator dari *p, misalkan generator tersebut adalah g.

3. Cari i sedemikian sehingga (mod )

i

g ≡a p dengan 4. Cari u sedemikian sehingga

1 1

2 (mod ) 2

p

u≡ −i −

5. Solusinya adalah x≡gu(mod )p

Langkah-langkah dalam algoritma tersebut dapat dilihat melalui bagan berikut ini.

Bagan 1. Algoritma mencari solusi

Tidak Ya

Hitung

( 1 2)

(mod )

p

a − p

Mulai

Bilangan prima panjil p

dan a∈

[

1,p−1

]

Apakah

( 1 2)

(

)

1 mod

p

a − ≡ p

(

)

2

mod

x ≡a p

tak punya solusi

Cari g = generator *

p

(

)

2

mod

x ≡a p

punya solusi

Hitung (mod ) i

g p dengan 0, 2, 4, ..., 1

i= p−

Apakah (mod ) i

g ≡a p

Tidak

Ya

Hitung

1 1

2 (mod )

2

p

u −i −

≡

Solusi adalah (mod ) u

x≡g p

Selesai

(

)

2

mod

x ≡a p

0, 2, 4, ..., 1

Contoh 1:

Tentukan solusi dari 2

(

)

15 mod17

x ≡

.

Jawab :

(17 1 2) 8

15 − ≡15 (mod 17) ≡1 (mod 17) Karena 15(17 1 2−) ≡ 1 (mod 17) maka berdasarkan kriteria Euler 2

(

)

15 mod 17

x ≡ mempunyai solusi.

Generator dari *

17 adalah g = 3.

Mencari nilai i sehingga 3i ≡15(mod17)

i 0 2 4 6

3 (mod17)i 1 9 13 15 Dari tabel diperoleh nilai i adalah 6.

6 17 1

(mod )

2 2

u≡ − ≡3(mod 8)

Solusinya adalah x≡33≡10(mod17). Solusi satunya adalah − ≡ −x 10≡7(mod17). Jadi solusi dari 2

(

)

15 mod17

x ≡ adalah 7 dan 10 .

Algoritma di atas tidak efisien untuk nilai

p yang besar ( p > 1.000.000 ), karena untuk mencari g yaitu generator dari *p untuk nilai

p > 1.000.000 tidaklah mudah, kemudian mencari nilai i sedemikian sehingga

(mod ) i

g ≡a p juga memerlukan waktu yang lama untuk nilai p > 1.000.000.

Oleh karena itu, di bagian berikutnya akan dibahas sebuah algoritma yang lebih efisien untuk mencari solusi dari

(

)

2

mod

x ≡a p yaitu Algoritma RESSOL.

Mencari solusi dari 2

(

)

mod

x ≡a p

memang tidak mudah, tetapi ada beberapa kasus untuk nilai p tertentu yang solusinya sudah dengan ditentukan. Misal untuk

3(mod 4)

p≡ maka solusi dari

(

)

2

mod

x ≡a p adalah ( 1 / 4)

(

)

mod

p

x≡ ±a + p

karena

(

(p 1) / 4

)

2 (p 1 / 2)

a + a +

± = =a(p−1 / 2) .a

≡a

(

modp

)

.

Berdasarkan Teorema 2.9,

(

)

2

1 mod

x ≡ − p mempunyai solusi jika dan hanya jika p=2 atau p≡1(mod 4). Untuk

1(mod 4)

p≡ misalkan x= ±z(p−1) / 4(mod )p

dengan z adalah suatu bilangan non residu

kuadratik yang ambil secara acak dalam *p. Berdasarkan Kriteria Euler diperoleh

(

)

2

(

)

2 ( 1) / 4 ( 1) / 2

1 mod

p p

x ≡ ±z − ≡z − ≡ − p .

Teorema 3.4

Jika a dan b relatif prima terhadap bilangan prima p, dan jika a dan b memiliki order

(

)

2j mod

p dengan j>0, maka ab memiliki order '

(

)

2j mod

p untuk beberapa 'j < j. [Niven, 1991]

Bukti :

2

ord( )a ≡2 (mod )j p ⇔a j ≡1(mod )p …(1), berdasarkan Teorema Fermat,

1

1(mod ) p

a − ≡ p …(2) Dari persamaan (1) dan (2) diperoleh

2 | (j p−1) dan p > 2.

Ambil

1

2j

x a

−

= , karena ord( )a ≡2 (mod )j p

maka

1

2

1(mod ) j

x a p

−

= ≡/ tetapi

2 2

1(mod ) j

x =a ≡ p sehingga berdasarkan

Lemma 2.9 maka

1

2

1(mod ) j

x a p

−

= ≡ − .

Dengan cara yang sama diperoleh

1 2 1(mod ) j b p −

≡ − , dan mengakibatkan

( )

2 1 2 1 2 1

( 1)( 1) 1(mod )

j j j

ab a b p

− − −

= ≡ − − ≡ .

Berdasarka Lemma 2.13 maka order dari ab

membagi 2j−1

sehingga order dari ab adalah '

2j untuk suatu 'j < j.

Teorema-teorema di atas menjadi landasan Algoritma RESSOL untuk mencari solusi dari 2

(

)

mod

x ≡a p dengan a∈Qpdan

p prima ganjil.

3.2 Konstruksi Algoritma RESSOL beserta Analisisnya.

Untuk mencari solusi 2

(

)

mod

x ≡a p

dengan p prima ganjil, ada sebuah algoritma yang dapat digunakan untuk mencarinya yaitu Algoritma RESSOL (Residue Solver).

Langkah pertama menghitung

( 1 2)

(mod )

p

a − p dengan Kriteria Euleur. Jika

( )

(

)

1 2

1 mod

p

a − ≡ − p maka 2

(

)

mod

x ≡a p

tidak mempunyai solusi.

Jika ( 1 2)

(

)

1 mod

p

a − ≡ p maka untuk menentukan solusi dari 2

(

)

mod

x ≡a p

adalah mencari nilai k dan m dengan k > 0 dan

m ganjil sedemikian sehingga 1 2k

p− = m. Kemudian didefinisikan :

( 1 / 2)

(

)

mod

m

r≡a + p

…(1)

Jika kedua ruas persamaan (1) dikuadratkan, maka diperoleh :

2 ( 1)

(

)

mod

m

r ≡a + p

2

(

)

. mod

m

r ≡a a p

.

Misalkan m

(

mod

)

n≡a p , sehingga dapat ditulis : 2

(

)

mod

r ≡na p

…(2)

Jika n≡1 mod

(

p

)

, maka solusinya adalah

x≡ ±r

(

modp

)

.

Jika n≡1 mod

(

p

)

, maka untuk menentukan solusinya diperlukan langkah penyelesaian sebagai berikut.

Ambil secara acak suatu bilangan nonresidu kuadratik di dalam *

p. Misal bilangan tersebut adalah z. Definisikan

m

(

mod

)

c≡z p …(3) Jika kedua ruas persamaan (3) dipangkatkan dengan 2k, maka diperoleh :

2k 2k_m

c =z _=zp−1_{≡1 mod}

(

_p

)

…(4)

Berdasarkan Lemma 2.13, order dari c

membagi 2k

. Sementara itu, karena z adalah nonresidu kuadratik maka

2k1 2k1_m

c − =z − ( 1 / 2)

(

)

1 mod

p

z − p

= ≡ −

…(5)

Jadi order dari c adalah tepat 2k

. Hal ini dapat ditulis ord( ) 2k

c ≡ atau

(

)

2k _{1 mod}

c ≡ p

.

Dengan cara yang sama diperoleh

2k 2k_{m p} 1 _{1 mod}

(

)

n =a =a − ≡ p

…(6)

Dengan demikian order dari n membagi 2k

.

Dengan pengulangan kuadrat dapat ditentukan order dari n adalah 2k'.

Sementara itu n2k−1=a2k−1m=a(p−1 / 2) , karena

a adalah kuadratik residu mod p maka 2k1 (p1 / 2) _{1 mod}

(

)

n − =a − ≡ p …(7)

sehingga k'<k

.

Algoritma ini dimulai dengan proses pengulangan.

Didefinisikan

2 ' 1

(

mod

)

k k

b c p

− −

≡ …(8)

(

)

' mod

r ≡br p …(9) 2

(

)

' mod

c ≡b p …(10) n'≡c n'

(

modp

)

…(11) Dengan melakukan perkalian pada kedua ruas persamaan (2) oleh 2

b diperoleh :

(

)

2 2 2

mod

b r ≡b na p

dengan menggunakan persamaan (9), (10) dan (11) diperoleh :

(

)

2

' ' mod

r ≡an p …(12) Dari persamaan (8) dan (10) diperoleh

(

)

2

' mod

c ≡b p

(

)

' 1 2

2k k _mod

c − − p

≡

_≡c2k k−'

(

_modp

)

_…(13)

Jika kedua ruas persamaan (13) dipangkatkan dengan '

2k

, maka diperoleh :

( )

(

)

' ' ' 2 2 2 ' mod k k k k

c c p

−

≡

2

(

)

(

)

mod 1 mod

k

c p p

≡ ≡ .

Sementara itu

( )

(

)

' 1

'

' 1 2

2 2

' mod

k

k k k

c c p

−

− −

≡

_≡c2k−1

(

_modp

)

_{≡ −1 mod}

(

_p

)

Dengan demikian c ' memiliki order tepat

'

2k

.

Karena ord( )n ≡2k' dan _{ord( ')c ≡2}k'

,

maka berdasarkan Teorema 3.4, order dari

' ' (mod )

n ≡c n p adalah 2k'' dengan k''<k'. Jika ''k =0, maka n'≡1 mod

(

p

)

, dan dengan menggunakan persamaan (12), maka solusi dari 2

(

)

mod

x ≡a p adalah

(

)

' mod

x≡ ±r p .

Jika n'≡1 mod

(

p

)

maka ''k >1, dan kondisi ini serupa dengan ketika pengulangan dimulai, sehingga pengulangan dilakukan kembali sampai solusi diperoleh.

Langkah penyelesaian untuk menentukan solusi dari kongruensi 2

(

)

mod

x ≡a p

Algoritma 2 (Algoritma RESSOL) : Mencari akar kuadrat modulo p prima ganjil.

INPUT : Bilangan prima ganjil p dan bilangan bulat a, 1 ≤ a ≤ p – 1. OUTPUT : Dua akar kuadrat a modulo p.

1. Hitung a(p−1 2) dengan Kriteria Euleur. Jika ( 1 2)

(

)

1 mod

p

a − ≡ − p maka a tidak mempunyai akar kuadrat modulo p dan proses berhenti .

Jika ( 1 2)

(

)

1 mod

p

a − ≡ p lanjut ke langkah 2.

2. Cari k dan m, dengan m ganjil sehingga 1 2k

p− = m. 3. Hitung ( 1 / 2)

(

)

mod

m

r≡a + p

dan

(

mod

)

m

n≡a p

.

4. Definisikan

2

(

)

mod

r ≡an p

…(

i ) Jika n≡1 mod

(

p

)

,

maka solusinya adalah x≡ ±r

(

modp

)

.

Jika n≡1 mod

(

p

)

, lanjut langkah 5.

5. Ambil z∈ *p secara acak yang nonresidu kuadratik, dan tetapkan

(

mod

)

m

c≡z p

. Sehingga ord(

c) = 2k

.

6. Dengan pengulangan kuadrat diperoleh ord(n) = '

2k

.

7. Tetapkan _{b ≡c}2k k− −' 1

(

_modp

)

_,

(

)

' mod

r ≡br p , 2

(

)

' mod

c ≡b p dan

(

)

' ' mod

n ≡c n p dengan k'<k

8. Kalikan kedua ruas (i) dengan c'. Dengan demikian diperoleh 2

(

)

' ' mod

r ≡an p …(ii) 9. Jika n'≡1 mod

(

p

)

, maka solusinya

adalah x≡ ±r' mod

(

p

)

.

Jika n'≡1 mod

(

p

)

, lakukan

pengulangan langkah (6) – (8), sampai diperoleh n'≡1 mod

(

p

)

.

10. Solusinya adalah x≡ ±r' mod

(

p

)

.

Algoritma RESSOL adalah algoritma acak (randomized algorithm) karena langkah ke-5 mensyaratkan untuk memilih bilangan nonresidu kuadratik secara acak dalam *p.

Dalam *p, setengah dari anggotanya adalah non residu kuadratik sehingga pengambilan bilangan nonresidu kuadratik

mempunyai peluang 1

2 dengan rata-rata pengambilan adalah 2 kali percobaan.

Algoritma RESSOL bukanlah algoritma

deterministic, tetapi prosedur perhitungannya lebih praktis dan cepat.

Algoritma RESSOL mempunyai waktu eksekusi (running time) O((lg ) )p 4 bit operasi.

[Menezes, 1997]

Contoh 2.

Tentukan solusi dari 2

(

)

13 mod 23

x ≡

.

Jawab:

(23 1 2) 11

13 − ≡13 (mod 23) ≡ 1 (mod 23). Karena 13(23 1 2−) ≡ 1 (mod 23) maka

(

)

2

13 mod 23

x ≡ mempunyai solusi.

23 – 1 = 22 = 2 .11 1 pilih k = 1 dan m = 11

(11 1 / 2)

13 (mod 23)

r≡ +

≡13 (mod 23)6 ≡6 (mod 23) Karena 2 12

13 (mod 23)

r ≡

≡13 .13 (mod 23)11

dengan n≡1311 (mod 23)≡1 (mod 23) maka solusi dari 2

(

)

13 mod 23

x ≡

adalah

6 (mod 23)

x≡ dan

6 (mod 23) 17 (mod 23)

x≡ − ≡

Jadi solusi dari 2

(

)

13 mod 23

Langkah-langkah dalam Algoritma RESSOL dapat dilihat melalui bagan berikut ini.

Algoritma RESSOL hanya dapat digunakan untuk mencari solusi dari

(

)

2

mod

x ≡a p dengan p prima ganjil. Tetapi Algoritma RESSOL ini dapat dijadikan landasan untuk mencari solusi dari

(

)

2

mod ,

x ≡a pq dengan p dan q prima

ganjil, dan x2≡a(modpj), dengan p prima ganjil dan bilangan bulat j≥2.

Hitung (m1 / 2)

(

mod

)

r≡a + p

dan m

(

mod

)

n≡a p

Tidak

Tetapkan _{b ≡c}2k k− −' 1

(

_modp

)

_,

(

)

' mod

r ≡br p , 2

(

)

' mod

c ≡b p ,

(

)

' ' mod

n ≡c n p dengan k'<k

Ya

Selesai

Tidak Ya

Hitung

( 1 2)

(mod )

p

a − p

Mulai

Bilangan prima ganjil p

dan a∈

[

1,p−1

]

Apakah

( 1 2)

(

)

1 mod

p

a − ≡ p

(

)

2

mod

x ≡a p

tak punya solusi

Apakah

(

)

1 mod

n≡ p

Solusinya adalah

(

mod

)

x≡ ±r p

Misalkan z adalah bilangan nonresidu kuadratik yang diambil secara acak dalam *p. Hitung m

(

mod

)

c≡z p

Hitung

(

)

2

' ' mod

r ≡an p

Apakah

(

)

' 1 mod

n ≡ p

Tidak

Ya Solusinya adalah

(

)

' mod

x≡ ±r p

(

)

2

mod

x ≡a p

punya solusi

3.3 Mengkontruksi Algoritma untuk Mencari Solusi 2

(

)

mod

x ≡a pq dengan

p dan q bilangan prima ganjil.

Untuk mencari solusi kongruensi

(

)

2

mod ,

x ≡a pq dengan p dan q prima ganjil, diawali dengan mencari terlebih dahulu solusi dari 2

(

)

mod

x ≡a p dan

(

)

2

mod

x ≡a q menggunakan Algoritma RESSOL.

Misalkan x2≡a

(

modp

)

mempunyai 2 solusi, yaitu

x≡r

(

modp

)

...(14) x≡ −r

(

modp

)

...(15) Misalkan _x2_≡a

(

_modq

)

_{mempunyai 2} solusi, yaitu

x≡s

(

modq

)

...(16) x≡ −s

(

modq

)

...(17) Kombinasi dari solusi (14), (15), (16), dan (17) menghasilkan 4 buah sistem kongruensi sebagai berikut :

(

)

(

)

( ) mod

mod

i x r p

x s q

≡

≡

(

)

(

)

( ) mod

mod

ii x r p

x s q

≡ ≡ −

(

)

(

)

( ) mod

mod

iii x r p

x s q

≡ −

≡

( ) (mod ) (mod )

iv x r p

x s q

≡ − ≡ −

Dengan menggunakan Teorema Sisa Cina, sistem kongruensi (i), (ii), (iii) dan (iv) menghasilkan 4 solusi kongruensi dari

2 _{(mod )}

x ≡a pq

dan secara berurutan dapat dituliskan sebagai

(

)

1

( )i x ≡u modpq ,

(

)

2

( )ii x ≡v modpq ,

( )

iii x3≡ −u

(

modpq

)

,

(

)

4

( )iv x ≡ −v modpq .

Keempat solusi ini merupakan solusi yang khas dari modulo pq.

Langkah penyelesaian untuk menentukan solusi dari kongruensi 2

(

)

mod

x ≡a pq

dengan p dan q bilanganprima ganjil tersusun dalam algoritma berikut ini.

Algoritma 3 :

Mencari akar kuadrat modulo pq, dengan p

dan q prima ganjil.

INPUT : Bilangan prima ganjil p dan q , dan 1 ≤ a ≤ pq – 1

OUTPUT : Empat akar kuadrat a modulo pq

1. Gunakan Algoritma RESSOL untuk mencari dua akar r dan –r yang merupakan solusi dari x2≡a

(

modp

)

. 2. Gunakan Algoritma RESSOL untuk

mencari dua akar s dan –s yang merupakan solusi dari _x2_≡a

(

_modq

)

_. 3. Gunakan Algoritma Euclidean yang

diperluas untuk mencari bilangan bulat c

dan d sedemikian sehingga cp + dq = 1. 4. x≡(rdq+scp)(modpq)

( )(mod )

y≡ rdq−scp pq

5. Solusinya

adalah±x(modpq)dan±y(modpq)

Algoritma di atas mempunyai waktu eksekusi (running time) O((lg ) )p3 bit operasi.

[Menezes, 1997]

Contoh 3.

Tentukan solusi dari 2

(

)

71 mod 77

x ≡

.

Jawab

Karena 77 = 7 . 11 maka

(

)

(

)

(

)

2 2

2

71 mod 7 ...( ) 71 mod 77

71 mod 11 ...( )

x i x x ii ≡ ≡ ⇔ ≡ (i) 2

(

)

(

)

71 mod 7 1 mod 7

x ≡ ≡

solusiya adalah x≡ ±1 mod 7

(

)

(ii) 2

(

)

(

)

71 mod 11 5 mod 11

x ≡ ≡

solusiya adalah x≡ ±4 mod 11

(

)

Bilangan bulat yang memenuhi persamaan

7c+11d = 1 adalah c = -3 dan d = 2.

x = 1.2.11 + 4.(-3).7 = -62 15 (mod 77)

y = 1.2.11 - 4.(-3).7 = 106 29 (mod 77)

-x = -15(mod 77) 48 (mod 77)

-y = -29 (mod 77) 62 (mod 77)

Jadi 4 solusi dari 2

(

)

71 mod 77

x ≡ yaitu

Langkah-langkah dalam Algoritma 3 dapat dilihat melalui bagan berikut ini.

Bagan 3. Algoritma mencari akar kuadrat modulo (pq), p dan q prima ganjil.

3.4 Mengkonstruksi Algoritma untuk Mencari Solusi 2

(mod j)

x ≡a p dengan

p prima ganjil dan j 2.

Untuk mencari solusi dari

2

(mod j)

x ≡a p , dengan p prima dan j≥2,

dapat kita ubah bentuknya menjadi

2

0(mod j)

x −a≡ p . Kita misalkan f fungsi polinom dengan koefisien bilangan bulat, 2

( )

f x =x −a. Untuk mencari solusi

dari polinom f x( )≡0(modpj) … (18), kita mulai dari solusi modulo p, kemudian p2,

p3, sampai j

p .

Misalkan x=c adalah sebuah solusi untuk f x( )≡0(modpj) maka kita bisa mencari solusi dari 1

( ) 0(mod j )

f x p +

≡ .

Solusi dari f x( )≡0(modpj+1) berbentuk j

x=c+tp , dengan t adalah suatu bilangan bulat yang dapat kita cari menggunakan deret Taylor’s

2 2

3 3 ( )

''( ) ( ) ( ) '( ) 2! '''( ) ( ) . . . 3! ! j j j

j n nj n

t p f c

f c tp f c tp f c

t p f c t p f c

n

+ = + + +

+ + +

dimana n adalah derajat/pangkat dari fungsi polinom f x( ). Karena 2

( )

f x =x −a

polinom berderajat 2 dalam modulus pj+1, maka deret Taylor’s tersebut menjadi

1

( j) ( ) j '( ) (mod j )

f c+tp = f c +tp f c p+

.

Karena 1

( j) 0(mod j )

f c tp p +

+ ≡ maka

persamaan diatas dapat kita ubah menjadi

1

( ) j '( ) 0 (mod j )

f a +tp f c ≡ p + .

Karena ( ) 0(mod j)

f x ≡ p mempunyai solusi

x=c maka kita dapatkan ( ) '( ) f c_j (mod )

tf c p

p

≡ − …(19)

yang merupakan persamaan linear dalam t. Persamaan (19) mungkin tidak mempunyai solusi, mempunyai solusi tunggal atau mempunyai p solusi. Jika f c'( )≡/0(mod )p

maka persamaan tersebut mempunyai tepat satu solusi.

Solusi dari persamaan (18) dapat ditentukan dengan menggunakan Lemma Hensel’s.

Lemma Hensel’s :

Misalkan f x( ) adalah fungsi polinom dengan koefisien-koefisiennya bilangan bulat dan p

prima. Jika ( ) 0(mod j)

f c ≡ p dan

'( ) 0(mod )

f c ≡/ p maka ada bilangan bulat t

(mod )p yang tunggal sedemikian sehingga

1

( j) 0(mod j )

f c+tp ≡ p+ .

[Niven, 1991] Mencari bilangan bulat c

dan d sehingga cp + dq = 1

Ya

Selesai Ya

Tidak Tidak

Mulai

RESSOL [ , ]a p RESSOL [ , ]a q

Bilangan prima p dan q, dan a∈[1,pq−1]

Apakah ada solusi

Apakah ada solusi

(

mod

)

x≡r p

(

mod

)

x≡ −r p

(

mod

)

x≡s q

(

mod

)

x≡ −s q

Solusinya adalah (mod ) (mod ) x n y n ± ±

(

)

( ) mod

x≡ rdq+scp n

(

)

( ) mod

Bukti dari Lemma Hensel’s tidak dicantumkan karena di luar jangkauan pembahasan.

Jika f c'( ) 0(mod )p dan

( ) 0(mod j)

f c ≡ p maka bilangan bulat c

disebut akar nonsingular. Jika '( )

f c 0(mod )p dan f c'( )≡0(mod )p

maka c disebut akar singular.

Dari Lemma Hensel’s kita lihat bahwa sebuah akar nonsingular c(mod )p

menghasilkan sebuah akar c2(modp2).

Karena c₂≡c(mod )p maka

2

'( ) '( ) 0(mod )

f c ≡ f c ≡/ p . Dari akar

2 2(mod )

c p akan dihasilkan sebuah akar

3 3(mod )

c p dan seterusnya sehingga

mendapatkan akar (mod j) j

c p .

Dari persamaan (19) diperoleh sebuah persamaan rekursif untuk mencari solusi yaitu

(

)

1

1 ( ) '( )

j j j

c+ c f c f r

−

= − ,

dengan

(

f '( )r

)

−1 adalah sebuah bilangan bulat sedemikian sehingga

(

)

1

'( ) '( ) 1(mod )

f c f r − ≡ p .

Contoh 4.

Tentukan solusi dari x2≡5(mod11 )3 . Jawab :

2 3 2 3

5(mod11 ) 5 0(mod11 )

x ≡ ⇔x − ≡

Solusi dari x2−5≡0(mod11) adalah x = ±4 (mengunakan Algoritma RESSOL)

2

( ) 5 '( ) 2

f x =x − f x = x

'(4) 8 0(mod11)

f ≡ ≡/

Karena f '(4)≡/0(mod11)maka 4 adalah akar

nonsingular.

'(4) 8 7(mod 11)

f =

≡

2 1 (4) '(4) 4 11.7

c =c − f f = −

= −73≡48(mod11 )2

3 2 (48) '(4) 48 2299.7

c =c − f f = −

= −16045≡1258(mod11 )3

Solusi dari x2≡5(mod11 )3 adalah

3

1258(mod11 )

x≡ ± yaitu x=1258 dan 73

x= .

Jika f c( )≡0(modpj) dan '( ) 0(mod )

f c ≡ p maka berdasarkan deret

Taylor, 1

( j) ( )(mod j )

f c tp f a p +

+ ≡ untuk

semua bilangan bulat t.

Kemudian jika 1

( ) 0(mod j )

f c p+

≡

maka f c( +tpj)≡0(modpj+1), sehingga sebuah akar (modc pj) akan menghasilkan p

buah akar 1

(modpj+). Tetapi jika

1

( ) 0(mod j )

f c ≡/ p+ maka tidak ada solusi untuk 1

(mod j )

p+ .

Contoh 5.

Tentukan solusi dari x2≡9(mod 27). Jawab :

2 2 3

9(mod 27) 9 0(mod 3 )

x ≡ ⇔x − ≡

Solusi dari x2−9≡0(mod 3) adalah x = 0.

2

( ) 9 '( ) 2

f x =x − f x = x

'(0) 0(mod 3)

f ≡

Karena f'(0)≡0(mod 3) maka 0 adalah akar singular.

2

(0) 9 0(mod 3 )

f = − ≡ , maka solusi mod 9 adalah x = 0, x = 0 + 3 = 3, x = 3 + 3 = 6

3

(0) 9 0(mod 3 )

f = − ≡/ , maka tak ada solusi mod 27

3

(3) 0(mod 3 )

f ≡ , maka solusi mod 27 adalah x = 3, x = 3 + 9 = 12, x = 12 + 9 = 21

3

(6) 27 0(mod 3 )

f = ≡ , maka solusi mod 27 adalah x = 6, x = 6 + 9 = 15, x = 15 + 9 = 24.

Jadi solusi dari x2≡9(mod 27) adalah x = 3,

x = 6, x = 12, x = 15, x = 21 dan x = 24.

Langkah penyelesaian untuk menentukan solusi dari kongruensi x2 ≡a

(

modpj

)

Algoritma 4 :

Mencari akar kuadrat modulo pj , dengan p

prima ganjil dan bilangan bulatj≥2.

INPUT : Bilangan prima ganjil p , bilangan bulat j≥2 dan 1≤a≤ pj−1 OUTPUT : Dua akar kuadrat a modulo j

p .

1. Gunakan Algoritma RESSOL untuk mencari dua akar r dan –r yang merupakan solusi dari x2≡a

(

modp

)

. 2. Tetapkan 2

( )

f x =x −a dan f '( )x =2x

3. Jikaf '( )r ≡/0(mod )p , tentukan

dan r_j =

(

r_j−1−f r( _j−1) '( ) (modf r₁

)

pj)

dengan r1=r. Solusinya dari

(

)

2

mod j

x ≡a p adalahx= ±r_j(modpj). Jikaf'( )r ≡0(mod )p lanjut ke langkah 4.

4. Untuk k=2, 3, ...,j−1 berlaku jika

)

( ) 0(mod k

f r ≡ p maka x≡r+tpk dengan t=1, 2, 3, ...,p merupakan solusi dari x2≡a(modpk+1).

Jika f r( )≡/0(modpk) maka tak ada solusi dari x2≡a(modpk+1).

Langkah-langkah dalam Algoritma 4 dapat dilihat melalui bagan berikut ini.

Ya

Tak ada solusi dari x2≡a(modpk+1)

Selesai Tidak

Apakah '( ) 0(mod )

f r ≡ p

Solusinya adalah (mod j)

j

x≡ ±r p

Tetapkan 2

( )

f x =x −a

dan f'( )x =2x

RESSOL [ , ]a p

Mulai

Bilangan prima ganjil p, 2

j≥ dana∈[1,p−1]

Ya Apakah

ada solusi

(

mod

)

x≡r p

(

mod

)

x≡ −r p

Hitung ( '( ))f r −1dan

(

1

)

1 ( 1)( '( )) (mod )

j

j j j

r r f r f r − p

− −

= −

dengan r1=r.

Hitung f r( )(modpk)

untuk k =2, 3, ...,j−1

Apakah

)

( ) 0(mod k

f r ≡ p

Tidak

Ya

k t

x ≡r+tp dengan t=1, 2, 3, ...,p adalah Solusi dari x2≡a(modpk+1) Tidak

Bagan 4. Algoritma mencari akar kuadrat modpj, dengan p prima ganjil dan j≥2.

3.5 Membandingkan waktu eksekusi Algoritma 1 dengan Algoritma RESSOL yang terkait bilangan besar.

Pada bagian ini akan dibandingkan waktu eksekusi Algoritma 1 dengan Algoritma RESSOL. Implementasi dari Algoritma 1 dan Algoritma RESSOL menggunakan perangkat lunak Mathematica 5.2 dapat dilihat di lampiran.

Tabel 1 adalah waktu eksekusi dari Algoritma 1 dan Algoritma RESSOL menggunakan perangkat lunak Mahtematica

5.2. Nilai p adalah bilangan prima yang ditentukan terlebih dahulu, sedangkan a

adalah bilangan bulat positif yang diambil secara acak dalam *p.

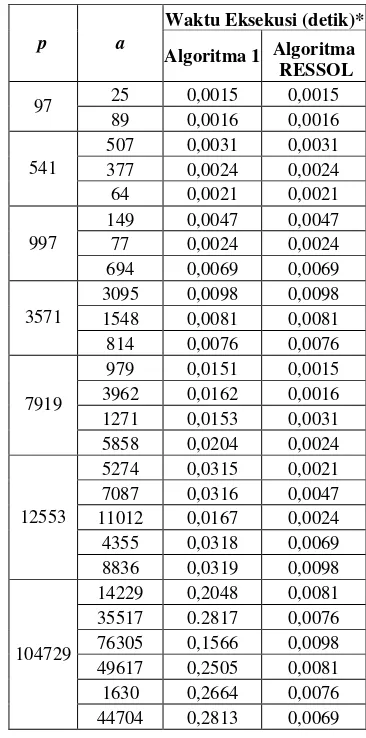
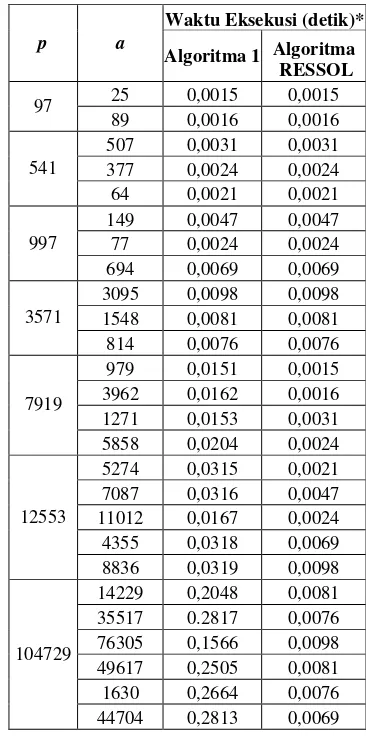
Tabel 1. Waktu Eksekusi Algoritma 1 dan Algoritma RESSOL

Waktu Eksekusi (detik)*

p a

Algoritma 1 Algoritma RESSOL 25 0,0015 0,0015 97

89 0,0016 0,0016 507 0,0031 0,0031 377 0,0024 0,0024 541

64 0,0021 0,0021 149 0,0047 0,0047 77 0,0024 0,0024 997

694 0,0069 0,0069 3095 0,0098 0,0098 1548 0,0081 0,0081 3571

814 0,0076 0,0076 979 0,0151 0,0015 3962 0,0162 0,0016 1271 0,0153 0,0031 7919

5858 0,0204 0,0024 5274 0,0315 0,0021 7087 0,0316 0,0047 11012 0,0167 0,0024 4355 0,0318 0,0069 12553

8836 0,0319 0,0098 14229 0,2048 0,0081 35517 0.2817 0,0076 76305 0,1566 0,0098 49617 0,2505 0,0081 1630 0,2664 0,0076 104729

44704 0,2813 0,0069

592085 0,6092 0,0015 467495 1,6251 0,0016 231000 0,5782 0,0031 96620 1,3753 0,0024 136341 0,8444 0,0021 399632 1,2815 0,0047 611953

541897 0,6256 0,0024 328426 1,2657 0,0069 671944 2,1888 0,0098 231057 1,4539 0,0081 601890 3,8138 0,0076 825496 1,2037 0,0015 290150 3,8286 0,0016 1299709

291949 2,7545 0,0031 3090665 22,0474 0,0024 5210769 42,5473 0,0021 14621620 26,8592 0,0047 14141212 13,9061 0,0024 12920893 31,9062 0,0069 5871391 37,2353 0,0098 15485863

9473376 15,9844 0,0021

Dari data Tabel 1 dapat diambil kesimpulan bahwa waktu eksekusi Algoritma RESSOL lebih cepat dibandingkan Algoritma 1.

Algoritma 1 tidak efisien untuk nilai p

yang besar yaitu p > 1.000.000, sedangkan Algoritma RESSOL lebih efisien untuk nilai p yang besar.

Berdasarkan hasil percobaan (Tabel 2), Algoritma RESSOL masih dapat digunakan untuk mencari solusi x2≡a(mod )p untuk nilai p yang sangat besar, yaitu p =

29.996.224.275.833.

Tabel 2. Waktu Eksekusi Algoritma RESSOL

p a

Waktu Eksekusi

(detik)* 424613597121 0,0159 10878246026665 0,0178 5887477973699 0,0167 20786675373559 0,0206 1574940209207 0,0185 5641355712333 0,0194 10073237724502 0,0153 27504498309348 0,0212 7273523082800 0,0143 29996224275833

IV. SIMPULAN DAN SARAN

4.1 Simpulan

Berdasarkan analisis dari hasil pembahasan, diperoleh beberapa simpulan sebagai berikut :

1. Kriteria Euler menjadi landasan untuk menentukan apakah _x2_≡a

(

_modp

)

dengan p prima ganjil mempunyai solusi atau tidak.

2. Jika x2≡a

(

modp

)

mempunyai solusi maka untuk mencari solusinya dapat digunakan Algoritma 1 atau Algoritma RESSOL.

3. Untuk nilai p yang besar yaitu p > 1.000.000, Algoritma 1 tidak efisien dengan waktu eksekusi yang lama. 4. Algoritma RESSOL tetap stabil meskipun

untuk nilai p yang sangat besar yaitu p = 29.996.224.275.833 dengan waktu eksekusi yang cepat.

5. Dari Algoritma RESSOL dapat dikembangkan menjadi beberapa Algoritma yaitu Algoritma 3 untuk mencari solusi x2≡a(modpq) dengan p

dan q adalah bilangan prima ganjil, dan Algoritma 4 untuk mencari solusi

2

(mod j)

x ≡a p dengan p bilangan prima ganjil dan bilangan bulatj≥2.

4.2 Saran

Tema dalam karya ilmiah ini dapat diteruskan bagi yang berminat, yaitu menentukan solusi dari 2

(mod )

x ≡a n

dengan n bilangan komposit

( 1 2 3

1 2 3 ...

k

e e

e e

k

n=p p p p , denganp_i prima dan

i

e bilangan bulat positif).

DAFTAR PUSTAKA

Hidayat, T. 2005. Analisis Algoritma Kunci Publik Rabin. Skripsi. Departemen Matematika FMIPA IPB, Bogor

Ningsih, Y. 2006. Masalah Residu Kuadratik. Skripsi. Departemen Matematika FMIPA IPB, Bogor

Niven, I. Zuckerman, H. S. dan Montgomery, L. H. 1991. An Introduction to The Theory of Numbers. John Wiley & Sons. Inc: New York.

Lampiran 1.

Implementasi Algoritma 1 dengan bantuan perangkat lunak Mathematica 5.2.

Algoritma 1 :

Mencari solusi 2

(

)

mod

x ≡a p dengan terlebih dahulu mencari generator dari *p. INPUT : Bilangan prima ganjil p dan bilangan bulat a, 1 ≤ a ≤ p-1.

OUTPUT : Dua akar kuadrat a modulo p.

<< NumberTheory`NumberTheoryFunctions` Algoritma1[a_Integer, p_Integer] :=

If[PrimeQ[p] = = False, Print["p bukan prima"], If[JacobiSymbol[a, p] = = -1, Print["Tak ada solusi"], If[JacobiSymbol[a, p] = = 0, {0},

{aa = Mod[a, p]; g = PrimitiveRoot[p] ; For[i = 0, i p - 1, i = 2 + i,

If[PowerMod[g, i, p] = = aa, Break[] ] ;

u = Mod[ 2

i

, 1 2

p− ] ;

x = PowerMod[g, u, p], Mod[-x, p]

} ] ] ]

Contoh :

Input : Algoritma1[24,97]

Output : { 86, 11 }

Input : Algoritma1[541,104729]

Lampiran 2.

Implementasi Algoritma RESSOL dengan bantuan perangkat lunak Mathematica 5.2.

Algoritma 2 (Algoritma RESSOL) Mencari akar kuadrat modulo p prima ganjil

INPUT : Bilangan prima ganjil p dan bilangan bulat a, 1 ≤ a ≤ p – 1. OUTPUT : Dua akar kuadrat a modulo p.

RESSOL[a_Integer, p_Integer] :=

If[PrimeQ[p] = = False, Print["p bukan prima"], If[JacobiSymbol[a, p] = = -1, Print["Tak ada solusi"], If[JacobiSymbol[a, p] = = 0, {0},

{m = p – 1 ; k = 0 ;

While[IntegerQ[ 2

m

], {m = 2

m

, k++}] ;

aInv = PowerMod[a, -1, p] ; z = Random[Integer,{1, p-1}]; While[JacobiSymbol[z, p] 1, z = Random[Integer,{1, p-1}]; ]; c = PowerMod[z, m, p] ;

r = PowerMod[a, 1 2

m+ , p] ;

For[i = 1, i k - 1, i++, {

d = PowerMod[r2 * aInv, 2k - i - 1, p], If[Mod[d, p] = = p - 1, r = Mod[r*c, p] ],

c = Mod[c2, p] } ;

r, Mod[-r, p