Super (a,d) edge antimagic total labeling pada graf petersen

(1)

RAHMAT CHAIRULLOH

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2014

SUPER

(

a

,

d

)

EDGE

ANTIMAGIC TOTAL LABELING

PADA

(2)

(3)

Dengan ini saya menyatakan bahwa skripsi berjudul Super (a,d) Edge Antimagic Total Labeling pada Graf Petersen adalah benar karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apa pun kepada perguruan tinggi mana pun. Sumber informasi yang berasal atau dikutip dari karya yang diterbitkan maupun tidak diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir skripsi ini.

Dengan ini saya melimpahkan hak cipta dari karya tulis saya kepada Institut Pertanian Bogor.

(4)

Petersen. Dibimbing oleh MUHAMMAD ILYAS dan TEDUH WULANDARI MAS’OED.

Karya ilmiah ini membuktikan teorema-teorema untuk memperoleh super (a,d)-edge-antimagic total labeling pada graf Petersen. Pada pelabelan, didefinisikan jumlah label sisi (edge) dan label dua simpul (vertex) yang menempel pada sisi (edge) disebut sebagai bobot sisi (edge-weights). Suatu graf yang memiliki bobot sisi yang berbeda untuk setiap sisi maka graf ini disebut graf dengan antimagic total labeling. Jika semua sisi mempunyai bobot sisi yang berbeda dan himpunan bobot sisi dari semua sisi membentuk barisan aritmatika dengan suku awal a dan beda (selisih) d maka pelabelan tersebut disebut (a,d)-edge-antimagic total labeling. Kemudian, edge-antimagic total labeling disebut super (a,d)-edge-antimagic total labeling jika f(V(G)) = {1, 2, …, v} dan f(E(G)) = {v+1, v+2, …, v+e}. Terdapat dua pembuktian teorema yang dibahas dalam karya ilmiah ini. Teorema pertama membuktikan bahwa graf Petersen P(n,m) dengan n ≥ 3 bilangan bulat ganjil dan m = 1, memiliki super 5 +5, -edge-antimagic total labeling. Teorema kedua membuktikan graf Petersen P(n,m) dengan n ≥ 3, 1 ≤ m ˂ , mempunyai sebuah super � + , -edge-antimagic total labeling.

Kata kunci: (a,d)-edge-antimagic total labeling, antimagic total labeling, graf Petersen, super (a,d)-edge-antimagic total labeling

ABSTRACT

RAHMAT CHAIRULLOH. Super (a,d) Edge Antimagic Total Labeling of Petersen Graph. Supervised by MUHAMMAD ILYAS and TEDUH WULANDARI MAS’OED.

This manuscript proves theorems to obtain super (a,d)-edge-antimagic total labeling of generalized Petersen graph. On labeling, edge-weights is defined as the total labeling of edge and its incident vertices. A graph that has different the edge-weights for each edge is called graph with antimagic total labeling. If each edge on a graph has edge-weights in the form of arithmetic progression starting from a and having common difference d, then its labeling is called (a,d)-edge-antimagic total labeling. An (a,d)-edge-antimagic total labeling f is called super (a,d)-edge-antimagic total labeling if f(V(G)) = {1, 2, …, v} and f(E(G)) = {v+1, v+2, …, v+e}. There are two theorems discussed in this paper. The first theorem proves that generalized Petersen graph P(n,m), n ≥ 3 be an odd integer and m = 1, has a super

5 +5_,

-edge-antimagic total labelings. The second theorem proves that generalized Petersen graph P(n,m), n ≥3, 1 ≤ m ˂ , has a super � + , -edge-antimagic total labeling.

(5)

Skripsi

sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains

pada

Departemen Matematika

RAHMAT CHAIRULLOH

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2014

SUPER

(

a

,

d

)

EDGE

ANTIMAGIC TOTAL LABELING

PADA

(6)

(7)

Disetujui oleh

Diketahui oleh

Dr Toni Bakhtiar, MSc Ketua Departemen

Tanggal Lulus:

Muhammad Ilyas, MSi, MSc Pembimbing I

(8)

SAW sehingga penelitian ini berhasil diselesaikan. Tema yang dipilih dalam penelitian ini ialah Antimagic Total Labeling, dengan judul Super (a,d) Edge Antimagic Total Labeling pada Graf Petersen.

Terima kasih penulis ucapkan kepada Bpk Muhammad Ilyas, MSi, MSc dan Ibu Teduh Wulandari Mas’oed, MSi selaku pembimbing. Ungkapan terima kasih juga disampaikan kepada almarhum ayah, ibu, serta seluruh keluarga, atas segala doa dan kasih sayangnya. Terima kasih juga disampaikan untuk rekan kerja penelitian saya, yaitu Ikhwan Al Amin atas segala saran dan masukan terkait penelitian. Selain itu, tidak lupa rasa terima kasih sebesar-besarnya kepada teman-teman di Departemen Matematika IPB angkatan 47.

Semoga karya ilmiah ini bermanfaat bagi dunia ilmu pengetahuan khususnya dalam bidang matematika dan dapat menjadi inspirasi bagi penelitian-penelitian selanjutnya.

Bogor, Agusrtus 2014

(9)

DAFTAR GAMBAR vi

DAFTAR LAMPIRAN vi

PENDAHULUAN 1

Latar Belakang 1

Tujuan 2

LANDASAN TEORI 2

Teori Graf 2

Pelabelan Graf 5

PEMBAHASAN 7

SIMPULAN DAN SARAN 36

Simpulan 36

Saran 36

DAFTAR PUSTAKA 36

LAMPIRAN 38

(10)

1 Graf G = (V, E) 2

2 Cycle dengan 3 simpul 3

3 Graf Teratur Derajat 3 4

4 Graf Petersen P(3,1) 5

5 Graf Cycle C3 6

6 (8,2)-edge antimagic total labeling pada graf Cycle C3 7

7 Super (8,1)-edge antimagic total labeling pada graf Cycle C3 7

9 Super (15,2)-edge antimagic total labeling pada graf Petersen P(5,1) 17 10 Super (15,2)-edge antimagic total labeling pada graf Petersen P(5,1) 27

12 Super (22,1)-edge antimagic total labeling pada graf Petersen P(5,2) 35

14 Super (20,2)-edge antimagic total labeling pada graf Petersen P(7,1) 39 15 Super (20,2)-edge antimagic total labeling pada graf Petersen P(7,1) 40 16 Super (14,1)-edge antimagic total labeling pada graf Petersen P(3,1) 41

18 Super (18,1)-edge antimagic total labeling pada graf Petersen P(4,1) 43 19 Super (22,1)-edge antimagic total labeling pada graf Petersen P(5,1) 44

DAFTAR LAMPIRAN

1 Pola dan gambar super 5 +5, -edge antimagic total labeling pada graf Petersen P(7,1) dengan menggunakan definisi pelabelan � 38 2 Pola dan gambar super ��+�

� , -edge antimagic total labeling pada graf Petersen P(7,1) dengan menggunakan definisi pelabelan � 40 3 Pola dan gambar super (4n + 2,1)-edge antimagic total labeling pada graf

Petersen P(3,1) dengan menggunakan definisi pelabelan 41 4 Pola dan gambar super (4n + 2,1)-edge antimagic total labeling pada graf

Petersen P(4,1) dengan menggunakan definisi pelabelan 42 5 Pola dan gambar super (4n + 2,1)-edge antimagic total labeling pada graf

(11)

PENDAHULUAN

Latar Belakang

Teori graf merupakan salah satu cabang matematika yang cukup penting untuk dipelajari dan dikembangkan. Pada awalnya, teori graf diperkenalkan oleh seorang ahli matematika asal Swiss, Leonhard Euler pada tahun 1736 untuk mencari solusi permasalahan mungkin tidaknya melewati ketujuh jembatan di kota Königsberg (sekarang dikenal sebagai Kaliningrad, Rusia) dan kembali ke tempat asal semula tepat satu kali. Kemudian, Leonhard Euler memodelkan permasalahan tersebut ke dalam model matematika berupa bagan yang terdiri dari simpul dan garis. Simpul mempresentasikan kota yang dihubungkan oleh jembatan dan garis sebagai jembatan yang menghubungkan kota. Model ini kemudian dikenal sebagai “Teori Graf”.

Daya tarik teori graf adalah penerapannya yang sangat luas, mulai dari ilmu komputer, kimia, fisika, biologi, sosiologi, teknik kelistrikan, linguistik, ekonomi, manajemen, pemasaran, hingga pemecahan teka-teki dan permainan asah otak. Walaupun penerapannya sangat banyak, yang menarik adalah bahwa “Teori Graf” hanya mempelajari simpul dan garis (Wijaya 2011).

Salah satu contoh graf yang paling dikenal dan sangat populer adalah graf Petersen. Graf Petersen diambil dari nama Peter Christian Julius Petersen pada tahun 1898 (Wijaya 2011). Salah satu penerapan graf Petersen diantaranya dalam masalah pewarnaan gambar peta, dimana warna setiap daerah pada peta yang berbatasan dibuat berlainan sehingga mudah untuk dibedakan. Hinga saat ini, teori graf masih terus berkembang selaras dengan pemikiran-pemikiran para ahli yang mengembangkannya. Salah satu masalah yang cukup menarik dalam teori graf adalah pelabelan pada graf.

Pelabelan pada suatu graf merupakan fungsi injektif yang memetakan setiap unsur himpunan simpul (vertex) dan setiap unsur himpunan sisi (edge) ke bilangan asli yang disebut label (Gallian 2009). Pelabelan pada graf terdiri dari pelabelan simpul, pelabelan sisi, dan pelabelan total. Pelabelan simpul adalah pelabelan dengan domain himpunan simpul, pelabelan sisi adalah pelabelan dengan domain himpunan sisi, dan pelabelan total adalah pelabelan dengan domain gabungan himpunan simpul dan sisi. Terdapat beberapa jenis pelabelan pada graf, antara lain pelabelan gracefull, pelabelan harmoni, pelabelan total tak beraturan, pelabelan ajaib (magic labeling), dan pelabelan antiajaib (antimagic labeling).

Antimagic total labeling pada suatu graf merupakan pelabelan total pada simpul dan sisi suatu graf dengan labelnya adalah bilangan asli, dengan jumlah label sisi dan label dua simpul yang menempel pada sisi disebut sebagai bobot sisi dimana untuk setiap sisi pada graf memiliki bobot sisi yang berbeda. Dalam karya ilmiah ini akan dibuktikan beberapa teorema untuk memperoleh super (a,d)-egde-antimagic total labeling pada graf Petersen.

(12)

Tujuan

Tujuan dari penulisan karya ilmiah ini adalah membuktikan teorema-teorema untuk memperoleh super (a,d)-edge-antimagic total labeling pada graf Petersen.

LANDASAN TEORI

Pada bab ini akan dijelaskan beberapa definisi dalam teori graf dan pelabelan graf yang akan digunakan dalam penyusunan karya ilmiah ini.

Teori Graf Definisi 1 (Graf)

Suatu graf G adalah pasangan terurut (V, E) dengan V adalah himpunan takkosong dan berhingga dan E adalah himpunan pasangan takterurut yang menghubungkan elemen-elemen V. Graf G dinotasikan G = (V, E). Elemen V disebut simpul (vertex) sedangkan elemen E disebut sisi (edge). Himpunan dari simpul-simpul pada graf G dinotasikan dengan V atau V(G), sedangkan himpunan dari sisi-sisi pada graf G dinotasikan dengan E atau E(G).

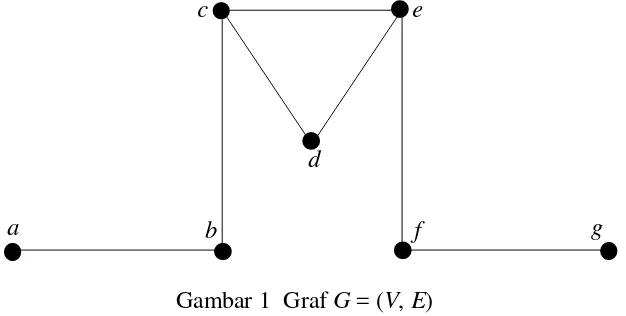
(Foulds 1992) Graf yang dimaksud definisi di atas disebut graf tak berarah. Contoh graf dapat dilihat pada Gambar 1 berikut ini.

Himpunan simpul dan himpunan sisi graf pada Gambar 1 adalah V(G) = {a, b, c, d, e, f, g}

E(G) = {ab, bc, cd, ce, de, ef, fg}. Definisi 2 (Order dan Size)

[image:12.595.128.441.428.586.2]

Misalkan diberikan graf G. Banyaknya simpul pada graf G disebut order dan banyaknya sisi pada graf G disebut size. Order dari graf G dinotasikan dengan |V(G)| dan size dari graf G dinotasikan dengan |E(G)|.

(Chartrand & Oellermann 1993) Pada Gambar 1, nilai dari |V(G)| = 7 dan |E(G)| = 7.

Gambar 1 Graf G = (V, E)

g e

d c

(13)

Definisi 3 (Incident dan adjacent)

Misalkan diberikan graf G. Jika e = uv ∈ E(G) dengan u, v ∈ V(G) maka u dan v dikatakan adjacent di G dan e dikatakan incident dengan u dan v.

(Chartrand & Oellermann 1993) Pada Gambar 1, misalkan e = ab ∈ E(G) maka a dan b dikatakan adjacent di G dan e dikatakan incident dengan a dan b.

Definisi 4 (Derajat)

Derajat (degree) dari suatu simpul v pada graf G adalah banyaknya sisi yang incident dengan v dan dinotasikan dengan deg v.

(Chartrand & Oellermann 1993) Pada Gambar 1, derajat setiap simpulnya ialah deg a = 1, deg b =2, deg c = 3, deg d = 2, dan deg e = 3, deg f = 2 deg g = 1.

Definisi 5 (Walk)

Suatu walk pada graf G adalah suatu barisan simpul dan sisi dari graf G dengan bentuk {v1, v1v2, v2, v2v3, v3, … , vn-1vn, vn} dan dapat dituliskan sebagai

{v1, v2, … , vn} atau v1, v2, … , vn. Suatu walk yang menghubungkan v1 dengan vn

dikatakan tertutup jika v1 = vn. Jika v1 ≠ vn maka walk tersebut dikatakan terbuka.

(Foulds 1992) Pada Gambar 1, terdapat walk terbuka yaitu walk {a, ab, b, bc, c, ce, e, ef, f, fg, g}. Definisi 6 (Cycle)

Cycle pada graf G adalah walk tertutup yang mengandung setidaknya tiga simpul berbeda. Graf G ber-order n dengan n ≥ 3 yang membentuk sebuah cycle disebut graf Cycle ber-order n, dituliskan Cn.

(Chartrand & Oellermann 1993) Pada Gambar 1 sebelumnya, terdapat Cycle pada graf G yang terdiri atas tiga simpul, yaitu

Gambar 2 di atas juga merupakan graf Cycle ber-order 3, dituliskan C3.

Definisi 7 (Graf Teratur)

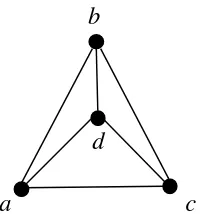
Graf yang setiap simpulnya mempunyai derajat yang sama disebut graf Teratur (Regular graphs). Apabila derajat setiap simpul adalah r, maka graf tersebut disebut sebagai graf Teratur Derajat r (r-Regular graphs).

(Chartrand & Oellermann 1993). Pada Gambar 3, terdapat graf Teratur Derajat 3 dengan derajat setiap simpul adalah 3

e

d c

(14)

Definisi 8 (Graf Petersen)

Graf G disebut graf Petersen, dinotasikan P(n,m), dengan n dan m bilangan bulat, n ≥ 3, 1 ≤ m ˂ , jika graf G tersebut merupakan graf Teratur Derajat 3 dengan 2n simpul dan 3n sisi serta himpunan simpul dan sisi adalah

V(G) = {u1, u2,…, un, v1, v2,…, vn}

E(G) = {uiui+1, uivi, vivi+m}

∀i ∈{1, 2, …, n}

di mana ketika nilai indeks i+1 pada simpul u maupun nilai indeks i+m pada simpul v lebih besar dari n maka nilai indeks tersebut akan di-modulo-kan dengan n.

(Ngurah dan Baskoro 2003) Berikut dijelaskan mengenai contoh graf Petersen berdasarkan Definisi 8 yaitu contoh graf Petersen P(3,1) dengan n = 3 dan m =1.

Pada bagian simpul graf Petersen P(3,1) terdapat 6 simpul dengan 3 simpul pertama pada bagian luar yaitu u1, u2, dan u3 serta 3 simpul kedua pada bagian dalam

yaitu v1, v2, dan v3 sehingga diperoleh himpunan simpul dari graf Petersen P(3,1)

sebagai berikut.

V[P(3,1)] = {u1, u2, u3, v1, v2, v3}

Kemudian, pada bagian sisi dari graf Petersen P(3,1) terdapat 9 sisi. Tiga sisi pertama pada bagian luar menghubungkan antar simpul-simpul u dari graf Petersen P(3,1) dengan himpunan sisi E [P(3,1)] = {uiui+1} untuk setiap i ∈ {1, 2, 3}. Berikut

penjelasan tiga himpunan sisi pertama E [P(3,1)] = {uiui+1} dari graf Petersen

P(3,1).

 Ketika indeks pada simpul u, yaitu i bernilai 1, maka indeks pada simpul u lainnya, yaitu i+1 bernilai 2, sehingga diperoleh sisinya yaitu u1u2.

 Ketika indeks pada simpul u, yaitu i bernilai 2, maka indeks pada simpul u lainnya, yaitu i+1 bernilai 3, sehingga diperoleh sisinya yaitu u2u3.

 Ketika indeks pada simpul u, yaitu i bernilai 3, maka indeks pada simpul u lainnya, yaitu i+1 bernilai 4. Karena indeks i+1 > 3, maka nilai i+1 kan 3, yaitu 4 mod 3 = 1. Sehingga indeks i+1 setelah di-modulo-kan 3 bernilai 1. Akibatnya, diperoleh sisinya yaitu u3u1 bukan u3u4.

Himpunan sisi tersebut dituliskan sebagai berikut. E[P(3,1)] = {u1u2, u2u3, u3u1}

Selanjutnya, tiga sisi kedua yang menghubungkan setiap simpul u pada bagian luar tepat satu dengan setiap simpul v pada bagian dalam dari graf Petersen P(3,1) dengan himpunan sisi sebagai berikut.

d

c b

[image:14.595.234.338.83.190.2]

a

(15)

E [P(3,1)] ={u1v1, u2v2, u3v3}

Terakhir, tiga sisi ketiga pada bagian dalam menghubungkan antar simpul-simpul v dari graf Petersen P(3,1) dengan himpunan sisi E [P(3,1)] = {vivi+m},

dengan m = 1, untuk setiap i ∈ {1, 2, 3}. Dengan cara yang sama seperti tiga sisi pertama pada bagian luar sebelumnya, dapat diperoleh himpunan sisinya sebagai berikut.

E[P(3,1)] = {v1v2, v2v3, v3v1}

Sehingga himpunan sisi secara keseluruhan dari graf Petersen P(3,1) dapat dituliskan sebagai berikut.

E[P(3,1)] = {u1u2, u2u3, u3u1, u1v1, u2,v2, u3v3, v1v2, v2v3, v3v1}

Contoh graf Petersen P(3,1) dapat dilihat seperti pada Gambar 4 dengan n =3 dan m = 1 di mana graf Petersen tersebut merupakan graf Teratur Derajat 3 dengan jumlah simpul sebanyak 6 dan jumlah sisi sebanyak 9

Himpunan simpul dan himpunan sisi graf Petersen P(3,1) pada Gambar 4 adalah V(G) = {u1, u2, u3, v1, v2, v3}

E(G) = {u1u2, u2u3, u3u1, u1v1, u2v2, u3v3, v1v2, v2v3, v3v1}

Pelabelan Graf

Karya ilmiah ini membahas suatu antimagic total labeling untuk mencari super (a,d)-edge antimagic total labeling pada graf Petersen. Berikut dijelaskan beberapa definisi tentang pelabelan graf.

Definisi 9 (Total Labeling)

Total Labeling pada graf G = (V, E) dengan banyaknya simpul v dan banyaknya sisi e adalah pemetaan satu-satu dari himpunan � ∪ � � ke himpunan bilangan bulat positif {1, 2, …, v +e} dengan domain pemetaannya simpul dan sisi.

(Ngurah dan Baskoro 2003) Definisi 10 (Antimagic Total Labeling)

Misalkan G graf dengan himpunan simpul V dan himpunan sisi E serta penjumlahan label sisi dengan label dua simpul yang menempel pada sisi disebut sebagai bobot sisi (edge-weights). Graf G disebut magic total labeling jika memiliki bobot sisi yang sama untuk setiap sisi di G sedangkan graf G disebut antimagic

v3 v2

v1

u3 u2

[image:15.595.234.393.302.405.2]

u1

(16)

total labeling jika memiliki bobot sisi yang berbeda untuk setiap sisi di G.

(Rahman et al. 2012) Definisi 11 ((a,d)-Edge Antimagic Total Labeling)

Misalkan G graf dengan himpunan simpul V dan himpunan sisi E. (a,d)-edge antimagic total labeling pada graf G adalah pemetaan satu-satu dari himpunan simpul dan himpunan sisi ke himpunan bilangan bulat positif {1, 2, …, v+e} sedemikian hingga himpunan bobot sisi dari semua sisi di G membentuk barisan aritmatika seperti berikut {a, a+d, …, a+(e-1)d} dengan suku pertama a dan beda (selisih) d, di mana a ≥ 0 dan d ≥ 0.

(Simanjuntak et al. 2000) Definisi 12 (Super (a,d)-Edge Antimagic Total Labeling)

Sebuah (a,d)-edge antimagic labeling disebut super (a,d)-edge antimagic total labeling jika f(V(G)) = {1, 2,…, v} dan f(E(G)) = {v+1, v+2, …, v+e}.

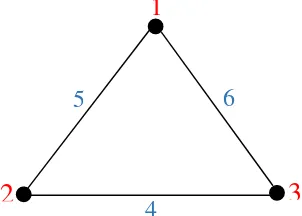
(Simanjuntak et al. 2000) Berikut ini diberikan contoh (a,d)-edge antimagic total labeling pada graf Cycle ber-order 3, yaitu C3, seperti pada Gambar 5. Banyaknya simpul ialah 3 dan

banyaknya sisi ialah 3 dengan himpunan simpul dan sisi sebagai berikut. V(C3) = {a, b, c}

E(C3) = {e1, e2, e3}

serta f(V[C3] ∪ E[C3]) = {1, 2, 3, 4, 5, 6}

Misalkan simpul-simpul pada graf C3 diberi pelabelan, misalnya

f(a) = 1 f(b) = 3 f(c) = 5

kemudian, diberikan pelabelan untuk sisi-sisi pada graf C3, misalnya

f(ab) = f(e1) = 4 f(bc) = f(e2) = 2 f(cd) = f(e3) = 6

maka akan diperoleh bobot sisi dari penjumlahan label tiap sisi yang incident terhadap 2 simpul ujungnya:

f(a) + f(e1) + f(b) + = 1 + 4 + 3 = 8

f(b) + f(e2) + f(c) + = 3 + 2 + 5 = 10

f(c) + f(e3) + f(a) + = 5 + 6 + 1 = 12

Dari cara pelabelan tersebut diperoleh himpunan bobot sisi dari graf Cycle C3

membentuk barisan aritmatika {8, 10, 12} dengan suku awal a = 8 dan beda (selisih) d = 2 sehingga graf Cycle C3 memiliki (8,2)-edge antimagic total labeling dengan

e3

e1

c b

a

e2

(17)

suku pertama a = 8 dan beda (selisih) d = 2. Pelabelan tersebut digambarkan seperti pada Gambar 6.

.

Kemudian, diberikan juga contoh super (a,d)-edge antimagic total labeling pada graf Cycle C3 seperti pada Gambar 5 sebelumya. Banyaknya simpul ialah 3

dan banyaknya sisi ialah 3 dengan f(V[C3]) = {1, 2, 3} dan f(E[C3]) = {4, 5, 6}.

Misalkan simpul-simpul pada graf C3 diberi pelabelan, misalnya

f(a) = 1 f(b) = 2 f(c) = 3

kemudian, diberikan pelabelan untuk sisi-sisi pada graf C3, misalnya

f(ab) = f(e1) = 5 f(bc) = f(e2) = 4 f(cd) = f(e3) = 6

maka akan diperoleh bobot sisi dari penjumlahan label tiap sisi yang incident terhadap 2 simpul ujungnya:

f(a) + f(e1) + f(b) + = 1 + 5 + 2 = 8

f(b) + f(e2) + f(c) + = 2 + 4 + 3 = 9

f(c) + f(e3) + f(a) + = 3 + 6 + 1 = 10

Dari cara pelabelan tersebut diperoleh himpunan bobot sisi dari graf Cycle C3

membentuk barisan aritmatika {8, 9, 10} dengan suku awal a = 8 dan beda (selisih) d = 1 sehingga graf Cycle C3 memiliki super (8,1)-edge antimagic total labeling

dengan suku pertama a = 8 dan beda (selisih) d = 1. Pelabelan tersebut digambarkan seperti pada Gambar 7.

.

Gambar 6 (8,2)-edge antimagic total labeling pada graf Cycle C3

6 4

5 3

1

2

Gambar 7 Super (8,1)-edge antimagic total labeling pada graf Cycle C3

6 5

3

2

1

[image:17.595.234.388.127.234.2] [image:17.595.236.387.562.670.2]

(18)

PEMBAHASAN

Karya ilmiah ini membahas teorema-teorema mengenai super (a,d)-edge antimagic total labeling pada graf Petersen P(n,m). Permasalahan utama dalam karya ilmiah ini adalah bagaimana mencari pola antimagic total labeling sehingga diperoleh definisi formula (rumus) khusus untuk pola super (a,d)-edge antimagic total labeling dari graf Petersen P(n,m).

Antimagic total labeling tidak hanya dilakukan satu kali melainkan dilakukan beberapa kali hingga terlihat beberapa pola pelabelan. Semua pola pelabelan tersebut akan dibentuk menjadi suatu definisi formula (rumus) khusus. Dari definisi formula (rumus) khusus tersebut digunakan untuk mendapatkan super (a,d)-edge antimagic total labeling dari graf Petersen P(n,m).

Kajian antimagic total labeling pada graf Petersen P(n,m) akan disajikan dalam bentuk teorema berikut beserta contoh gambar pola pelabelannya.

Teorema 1

Graf Petersen yang diperumum P(n,m) dengan n bilangan bulat ganjil (n ≥ 3) dan m = 1, memiliki super 5 +5, -edge antimagic total labeling.

(Ngurah dan Baskoro 2003) Bukti :

Misalkan P(n,m) adalah graf Petersen yang mempunyai super (a,d)-edge antimagic total labeling karena |V[P(n,m)]| = 2n dan |E[P(n,m)]| = 3n sehingga

�: V[P(n,m)] → {1, 2, …, 2n} �: E[P(n,m)] → {2n+1, 2n+2, …, 5n}

Semua simpul dan sisi pada graf Petersen P(n,m) dilabelkan dengan menggunakan definisi formula pelabelan � , di mana � didefinisikan sebagai pelabelan simpul dan sisi dari graf Petersen P(n,m). Berikut diberikan definisi fomula pelabelan � .

� � = {

+

, � � � + +

, � �

� � = { � +

, � �

� +

, � �

� � �+ = { � + + ,_{� + ,} _{= �}≤ ≤ � −

� � � = � + , ≤ ≤ �

(19)

misalkan w menyatakan bobot sisi dari graf Petersen P(n,m). Didefinisikan bobot sisi w dari pelabelan total � dari sisi-sisi : { _{� �+} , _{� �}, _{� �+} } pada graf Petersen P(n,m) untuk semua i ∈{1, 2, …, n} sebagai berikut.

� �+ = � � + � � �+ + � �+

� � = � � + � � � + � �

� �+ = � � + � � �+ + � �+

dengan indeks i+1 dan i+m di-modulo-kan dengan n bila i+1, i+m > n.

Dari ketiga persamaan bobot sisi di atas, yaitu _{� �+} , _{� �} , dan � �+ dapat didefinisikan dengan suatu formula bobot sisi dengan cara mensubstitusikan formula pelabelan simpul dan sisi-sisi: {� _� ,� _� , � _{� �} ,

� � �+ } ke masing-masing persamaan bobot sisi yang telah didefinisikan sebelumnya. Berikut definisi formula bobot sisi untuk _{� �+} , _{� �} , dan

� �+ .

a) Definisi formula bobot sisi untuk _{� �+} sebagai berikut. � �+ = � � + � � �+ + � �+

� �+ =

{

+

+ � + + +� + + + , � �

� + +

+ � + + + + + , � �

+

+ � + + , = �

kemudian, definisi formula di atas dapat disederhanakan menjadi seperti berikut.

� �+ =

{

� +

+ , � �

� +

+ , � �

� +

, = �

karena definisi formula untuk i ganjil = i genap maka berlaku 5 +5+ untuk 1 ≤ i ≤ n-1. Sehingga diperoleh definisi formula baku untuk bobot sisi

� �+ , yaitu

� �+ = { � +

+ , ≤ ≤ � −

� +

, = �

(20)

� � = � � + � � � + � �

� � = {

+

+ � + + � + , � �

� + +

+ � + + � + , � �

� � = { � +

+ , � �

� +

+ , � �

karena definisi formula untuk i ganjil = i genap maka berlaku 9 + + untuk 1 ≤ i ≤ n. Sehingga diperoleh definisi formula baku untuk bobot sisi

� � , yaitu

� � = � + + , ≤ ≤ �

c) Definisi formula bobot sisi untuk _{� �+} sebagai berikut.

� �+ = � � + � � �+ + � �+

� �+ = { � +

+ � + + + � + , � �

� +

+ � + + + � + , � �

kemudian definisi formula di atas dapat disederhanakan menjadi seperti berikut.

� �+ = { � +

+ , � �

� +

+ , � �

karena definisi formula untuk i ganjil = i genap maka berlaku +5+ untuk 1 ≤ i ≤ n. Sehingga diperoleh definisi formula baku untuk bobot sisi

� �+ , yaitu

� �+ = � + + , ≤ ≤ �

selanjutnya, misalkan _� adalah himpunan bobot sisi di mana ∈ { , , } dengan penjelasan _� sebagai berikut.

(21)

 t = 2 → menyatakan himpunan bobot sisi untuk _{� �}

 t = 3 → menyatakan himpunan bobot sisi untuk _{� �+}

Jadi, definisi formula himpunan bobot sisi terhadap pelabelan total � dari sisi-sisi { _{� �+} , _{� �}, dan _{� �+} } dari graf Petersen P(n,m) untuk semua i ∈{1, 2, …, n} adalah sebagai berikut.

= { � �+ ; ≤ ≤ �} = { � +

+ , ≤ ≤ � −

� +

, = �

= { � � ; ≤ ≤ �} = � + +

= { � �+ ; ≤ ≤ �} = � + +

dari semua definisi formula himpunan bobot sisi di atas dapat digabungkan menjadi himpunan bobot sisi keseluruhan untuk pelabelan � sehingga akan terbentuk sebuah barisan aritmatika dari himpunan bobot sisi tersebut. Penggabungan semua definisi himpunan bobot sisi di atas, yaitu ∪ ∪ = {5 +5, 5 +5+

,9 + + , + + }, untuk setiap i ∈ {1, 2, …,n}.

Rincian pola barisan aritmatika dari penggabungan himpunan bobot sisi di atas adalah sebagai berikut.

(i) Untuk himpunan bobot sisi :

Ketika indeks i bernilai n, maka definisi formula bobot sisi adalah � +

Ketika indeks i berjalan dari 1, 2, …, n-1, maka diperoleh definisi formula bobot sisi sebagai berikut.

5 +5+ = { 5 +5+ , 5 +5+ , 5 +5+ , … , 5 +5+ � − }

Sehingga diperoleh himpunan bobot sisi sebagai berikut.

= { 5 +5, 5 +5+ , 5 +5+ , 5 +5+ , … , 5 +5+ � − } (ii) Untuk himpunan bobot sisi :

Perhatikan bahwa definisi formula bobot sisi , yaitu � +

+ = � + + � − +

(22)

� +

+ � − +

= { 5 +5+ �, 5 +5+ � + , 5 +5+ � + , … , 5 +5+ � − }

= { 5 +5+ �, 5 +5+ � + , 5 +5+ � + , … , 5 +5+ � − } (iii)Untuk himpunan bobot sisi :

Perhatikan bahwa definisi formula bobot sisi , yaitu � +

+ = � + + � − +

ketika indeks i berjalan dari 1, 2, …, n, maka diperoleh definisi formula sebagai berikut.

� +

+ � − +

= { � + + � , � + + � + , … , � + + � − }

= { 5 +5+ � , 5 +5+ � + , … , 5 +5+ � − } dari rincian yang telah dijabarkan mengenai himpunan bobot sisi , , dan

sudah terlihat jelas pola barisan aritmatika yang dibentuk oleh ∪ ∪ sehingga bisa diperoleh bahwa

∪ ∪

= { 5 +5, 5 +5+ , 5 +5+ , … , 5 +5+ � − , 5 +5+ �, 5 +5+ � + , … 5 +5+ � − , 5 +5+ � , 5 +5+ � + , … , 5 +5+ � − }

= { , + , + , … , + � − , + � , + � + , . . , + � − , + � , + � + , … , + � − }

(23)

antimagic total labeling yang membentuk barisan aritmatika dengan suku awal a = 5 +5

dan selisih d = 2.

Kemudian, untuk menunjukkan bahwa 5 +5, -edge antimagic total labeling tersebut adalah super 5 +5, -edge antimagic total labeling, akan dibuktikan bahwa

� (V[P(n,m)]) = {1, 2, …, 2n} � (E[P(n,m)]) = {2n+1, 2n+2, …, 5n} Bukti:

Misalkan dan berturut-turut menyatakan himpunan simpul _� dan himpunan simpul _�, ∀i ∈ {1, 2, ..., n} . Dengan menggunakan definisi formula pelabelan

simpul � _� dan � _� yang telah diperoleh sebelumnya maka himpunan simpul dan dapat didefinisikan dengan formula sebagai berikut.

= {� � ; ≤ ≤ �} = { +

, � � � + +

, � �

= {� � ; ≤ ≤ �} = { � +

, � �

� +

, � �

dari semua definisi formula himpunan simpul di atas dapat digabungkan menjadi himpunan simpul keseluruhan untuk pelabelan � , yaitu ∪ = { +�, + +�, +�, +� } untuk setiap i ∈ {1, 2, …,n}, sehingga penggabungan himpunan simpul tersebut akan membentuk barisan bilangan untuk label simpul dengan penjelasan sebagai berikut.

(i) Untuk himpunan simpul :

Ketika indeks i bernilai ganjil, dengan i = 1, 3,..n, maka definisi formula himpunan simpul adalah

+

= { , , … ,� + }

Ketika indeks i bernilai genap, dengan i = 2, 4, .., n-1, maka diperoleh definisi formula himpunan simpul sebagai berikut.

� + +

= { � + ,� + , … , �}

(24)

(ii) Untuk himpunan simpul :

Ketika indeks i bernilai ganjil, dengan i = 1, 3,..n, maka definisi formula himpunan simpul adalah

� +

= { � + , � + , … , �}

Ketika indeks i bernilai genap, dengan i = 2, 4, .., n-1, maka diperoleh definisi formula himpunan simpul sebagai berikut.

� +

= { � + , � + , … , � − }

Sehingga diperoleh himpunan simpul sebagai berikut.

= { � + , � + , … , � − , � + , � + , … , � }

dari rincian yang telah dijabarkan mengenai himpunan simpul dan sudah terlihat jelas barisan bilangan untuk label simpul yang dibentuk oleh ∪ sehingga bisa diperoleh bahwa

∪ = { , , … ,� + ,� + , … , �, � + , . . , � − , � + , … , �}

Kemudian, misalkan pula � , � , dan � , berturut-turut menyatakan himpunan sisi � �+ , � � , dan � �+ , ∀i ∈ {1, 2, ..., n} . Dengan menggunakan definisi

formula pelabelan sisi � _{� �+} , � _{� �} , dan � _{� �+} yang telah diperoleh sebelumnya maka himpunan sisi � , � , dan � dapat didefinisikan dengan formula sebagai berikut.

� = {� � �+ ; ≤ ≤ �} = { � + + ,_{� + ,} _{= �}≤ ≤ � −

� = {� � � ; ≤ ≤ �} = � + , ≤ ≤ �

� = {� � �+ ; ≤ ≤ �} = � + , ≤ ≤ �

dari semua definisi formula himpunan sisi di atas dapat digabungkan menjadi himpunan sisi keseluruhan untuk pelabelan � , yaitu � ∪ � ∪ � = { � + +

, � + , � + , � + } untuk setiap i ∈ {1, 2, …,n}, sehingga penggabungan himpunan sisi tersebut akan membentuk barisan bilangan untuk label sisi dengan penjelasan sebagai berikut.

(i) Untuk himpunan sisi � :

Ketika indeks i bernilai n, maka definisi formula himpunan sisi � adalah � +

Ketika indeks i berjalan dari 1, 2, …, n-1, maka diperoleh definisi formula himpunan sisi � sebagai berikut.

(25)

Sehingga diperoleh himpunan simpul � sebagai berikut. � = { � + , � + , � + , … , �}

(ii) Untuk himpunan sisi � :

Ketika indeks i berjalan dari 1, 2, …, n, maka definisi formula himpunan sisi � adalah

� + = { � + , � + , … , � }

Sehingga diperoleh himpunan sisi � sebagai berikut. � = { � + , � + , … , � }

(iii) Untuk himpunan sisi � :

Ketika indeks i berjalan dari 1, 2, …, n, maka definisi formula himpunan sisi � adalah

� + = { � + , � + , … , � }

Sehingga diperoleh himpunan sisi � sebagai berikut. � = { � + , � + , … , � }

dari rincian yang telah dijabarkan mengenai himpunan sisi � , � , dan � sudah terlihat jelas barisan bilangan untuk label sisi yang dibentuk oleh � ∪ � ∪ � sehingga bisa diperoleh bahwa

� ∪ � ∪ � = { � + , � + , … , �, � + , … , �, � + , … , �}

Dari penjabaran mengenai barisan bilangan untuk label himpunan simpul dan label himpunan sisi di atas maka dapat disimpulkan bahwa:

1 ∪ = { , , … , + , + , … , �, � + , . . , − , + , … , �} sehingga � (V[P(n,m)]) = {1, 2, …, 2n}.

2 � ∪ � ∪ � = { � + , � + , … , �, � + , … , �, � + , … , �} sehingga � (E[P(n,m)]) = {2n+1, 2n+2, …, 5n}.

Sehingga dengan menggunakan pelabelan total � , teorema 1 sebeluimnya telah terbukti bahwa untuk graf Petersen yang diperumum P(n,m) dengan n bilangan bulat ganjil (n ≥ 3) dan m = 1, memiliki super 5 +5, -edge antimagic total labeling yang membentuk barisan aritmatika dengan suku awal a = 5 +5 dan selisih d = 2.

(26)

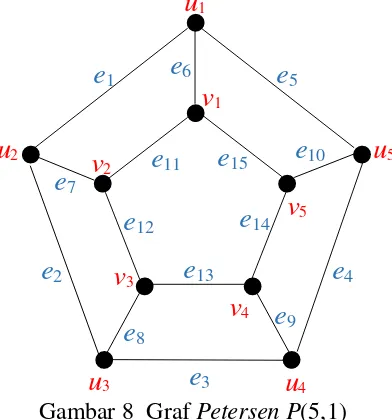
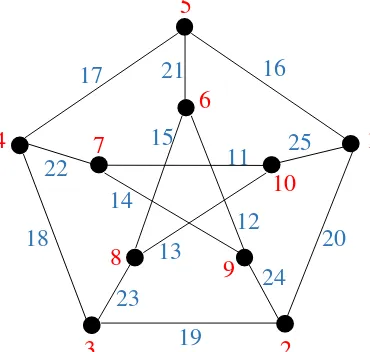
banyaknya sisi ialah 15, dengan dengan � (V[P(5,1)])= {1, 2, …, 10} dan � (E[P(5,1)]) = {11, 12, …, 25} serta himpunan simpul dan sisi sebagai berikut. V[P(5, 1)] = {u1, u2,…, u5, v1, v2,…, v5}

E[P(5, 1)] = {uiui+1, uivi, vivi+1}

∀i ∈ {1, 2, 3, 4, 5}

di mana ketika nilai indeks i+1 pada simpul u maupun nilai indeks i+1 pada simpul v lebih besar dari 5 maka nilai indeks tersebut akan di-modulo-kan dengan 5.

Dengan menggunakan definisi formula pelabelan � , maka untuk graf Petersen

P(5,1) diperoleh label simpul sebagai berikut. � (u1) = 1 � (v1) = 8

� u2) = 4 � (v2) = 6

� (u3) = 2 � v3) = 9

� (u4) = 5 � (v4) = 7

� (u5) = 3 � (v5) = 10

kemudian, diperoleh juga pelabelan untuk sisi sebagai berikut.

� (u1 u2) = � (e1) = 12 � (u1 v1) = � (e6) = 16 � (v1 v2) = � (e11) = 21

� (u2 u3) = � (e2) = 13 � (u2 v2) = � (e7) = 17 � (v2 v3) = � (e12) = 22

� (u3 u4) = � (e3) = 14 � (u3 v3) = � (e8) = 18 � (v3 v4) = � (e13) = 23

� (u4 u5) = � (e4) = 15 � (u4 v4) = � (e9) = 19 � (v4 v5) = � (e14) = 24

� (u5 u1) = � (e5) = 11 � (u5 v5) = � (e10) = 20 � (v5 v6) = � (e15) = 25

sehingga diperoleh bobot sisi dari penjumlahan label tiap sisi yang incident terhadap 2 simpul ujungnya seperti berikut.

� (u1) + � (e1) + � (u2) = 1 + 12 + 4 = 17

� (u2) + � (e2) + � (u3) = 4 + 13 + 2 = 19

� (u3) + � (e3)+ � (u4) = 2 + 14 + 5 = 21

� (u4) + � (e4) + � (u5) = 5 + 15 + 3 = 23

� (u5) + � (e5) + � (u1) = 3 + 11 + 1 = 15

� (u1) + � (e6) + � (v1) = 1 + 16 + 8 = 25

� (u2) + � (e7) + � (v2) = 4 + 17 + 6 = 27

[image:26.595.185.381.190.400.2]

e

10

e

15

e

14

e

13

e

12

e

11

v

5

v

4

v

3

v

2

v

1

e

5

e

9

e

8

e

7

e

6

e

4

e

3

e

2

e

1

u

5

u

4

u

3

u

2

u

1

(27)

� (u3) + � (e8) + � (v3) = 2 + 18 + 9 = 29

� (u4) + � (e9) + � (v4) = 5 + 19 + 7 = 31

� (u5) + � (e10)+ � (v5) = 3 + 20 + 10 = 33

� (v1) + � (e11) + � (v2) = 8 + 21 + 6 = 35

� (v2) + � (e12) + � (v3) = 6 + 22 + 9 = 37

� (v3) + � (e13) + � (v4) = 9 + 23 + 7 = 39

� (v4) + � (e14) + � (v5) = 7 + 24 +10 = 41

� (v5) + � (e15) + � (v1) = 10 + 25 + 8 = 43

Dari cara pelabelan tersebut diperoleh himpunan bobot sisi dari graf Petersen P(5,1) membentuk barisan aritmatika {15, 17, 19, 21,…,39, 41, 43} dengan suku awal a = 5 5 +5 = 15 dan beda (selisih) d = 2 sehingga graf Petersen P(5,1) memiliki super (15,2)-edge antimagic total labeling. Pelabelan graf Petersen P(5,1) dari pelabelan � dapat digambarkan sebagai berikut.

Kemudian, untuk contoh pola dan gambar pelabelan dari graf Petersen P(7,1) dengan menggunakan definisi pelabelan � terlampir pada Lampiran 1.

Selain pembuktian teorema 1 sebelumnya dengan menggunakan definisi formula pelabelan � , berikut juga diberikan pembuktian alternatif dari teorema 1 dengan menggunakan definisi formula pelabelan lainnya.

Alternatif bukti:

Misalkan P(n,m) dengan adalah graf Petersen yang mempunyai super (a,d)-edge antimagic total labeling karena |V[P(n,m)]| = 2n dan |E[P(n,m)]| = 3n sehingga

�: V[P(n,m)] → {1, 2, …, 2n} �: E[P(n,m)] → {2n+1, 2n+2, …, 5n}

Dengan cara yang sama, semua simpul dan sisi pada graf Petersen P(n,m) dilabelkan dengan menggunakan definisi formula pelabelan � , di mana � didefinisikan sebagai formula pelabelan simpul dan sisi dari graf Petersen P(n,m). Berikut diberikan definisi fomula pelabelan � .

20 25 24 23 22 21 10 7 9 6 8 11 19 18 17 16 15 14 13 12 3 5 2 4 1

[image:27.595.219.403.303.471.2]

(28)

� � = { +

, � � � + + +

, � �

� � =

{

� + +

, � �

� + +

, � �

� + , = �

� � �+ = { � + + , ≤ ≤ � −_{� + , = �}

� � � = { � + + , ≤ ≤ � −_{� + , = �}

� � �+ = { � + + , ≤ ≤ � −_{� + + , = � − , �}

Sama seperti pelabelan � sebelumnya, misalkan z menyatakan bobot sisi dari graf Petersen P(n,m). Didefinisikan bobot sisi z dari pelabelan total � dari sisi-sisi: { _{� �+} , _{� �}, _{� �+} } pada graf Petersen P(n,m) untuk semua i ∈ {1, 2, …, n} sebagai berikut.

� � �+ = � � + � � �+ + � �+ � � � = � � + � � � + � � � � �+ = � � + � � �+ + � �+

dengan indeks i+1 dan i+m di-modulo-kan dengan n bila i+1, i+m > n.

Dari ketiga persamaan bobot sisi di atas, yaitu � _{� �+} , � _{� �} , dan � � �+ dapat didefinisikan dengan suatu formula bobot sisi dengan cara mensubstitusikan formula pelabelan simpul dan sisi: {� _� ,� _� , � _{� �} ,

�� + } ke masing-masing persamaan bobot sisi yang telah didefinisikan sebelumnya.Berikut definisi formula bobot sisi untuk � _{� �+} , � _{� �} , dan � � �+ .

a) Definisi formula bobot sisi untuk � _{� �+} sebagai berikut. � � �+ = � � + � � �+ + � �+

� � �+ =

{

+

+ � + + +� + + + , � �

� + +

+ � + + + + + , � �

+

+ � + + , = �

(29)

� � �+ =

{

� +

+ , � �

� +

+ , � �

� +

, = �

karena formula untuk i ganjil = i genap maka berlaku 5 +5+ untuk 1 ≤ i ≤ n-1. Sehingga diperoleh definisi formula baku untuk bobot sisi � _{� �+} , yaitu

� � �+ = { � +

+ , ≤ ≤ � −

� +

, = �

b) Definisi formula bobot sisi untuk � _{� �} sebagai berikut � � � = � � + � � � + � �

� � � =

{

+

+ � + + + � + + + + , � �

� + +

+ � + + + + � + + + , � �

+

+ � + + � + , = �

� � � =

{ � +

+ , � � � +

, = �

karena definisi formula untuk i ganjil = i genap maka berlaku 9 +5+ untuk 1 ≤ i ≤ n-1. Sehingga diperoleh definisi formula baku untuk bobot sisi � � � , yaitu

� � � = { � +

+ , ≤ ≤ � −

� +

, = �

(30)

� � �+ = � � + � � �+ + � �+

� _{� �+} =

{ + +�

+ � + + + ++ + +� , � � + +�

+ � + + + + + +� , � � + +�

+ � + + + + � + , = � − � + + � + + + + , = �

� � �+ =

{ � +

+ , � �

� +

+ , � �

� +

, = � − � +

, = �

karena definisi formula untuk i ganjil = i genap maka berlaku +9+ untuk 1 ≤ i ≤ n-2. Sehingga diperoleh definisi formula baku untuk bobot sisi � � �+ , yaitu

� � �+ =

{

� +

+ , ≤ ≤ � −

� +

, = � − � +

, = �

selanjutnya, misalkan _� adalah himpunan bobot sisi di mana ∈ {1, 2, 3} dengan penjelasan _� sebagai berikut.

 t = 1 → menyatakan himpunan bobot sisi untuk � _{� �+}

 t = 2 → menyatakan himpunan bobot sisi untuk � _{� �}

 t = 3 → menyatakan himpunan bobot sisi untuk � _{� �+}

Jadi, definisi formula himpunan bobot sisi terhadap pelabelan total � dari sisi-sisi � �+ , � �, dan � �+ dari graf Petersen P(n,m) untuk semua i ∈ {1, 2, …, n} adalah sebagai berikut.

= {� � �+ ; ≤ ≤ �} = { � +

+ , ≤ ≤ � −

� +

(31)

= {� � � ; ≤ ≤ �} = { � +

+ , ≤ ≤ � −

� +

, = �

= {� � �+ ; ≤ ≤ �} =

{

� +

+ , ≤ ≤ � −

� +

, = � − � +

, = �

dari semua definisi formula himpunan bobot sisi di atas dapat digabungkan menjadi himpunan bobot sisi keseluruhan untuk pelabelan � sehingga akan terbentuk sebuah barisan aritmatika dari pelabelan bobot sisi tersebut. Penggabungan semua definisi himpunan bobot sisi di atas, yaitu ∪ ∪ = {5 +5, 5 +5+

, 9 +5+ ,9 +5, +9+ , +5, +9 }, untuk setiap i ∈{1, 2, …,n}. Rincian tebentuknya pola barisan aritmatika dari penggabungan himpunan bobot sisi di atas adalah sebagai berikut.

(i) Untuk himpunan bobot sisi :

Ketika indeks i berjalan dari 1, 2, …, n-1, maka diperoleh definisi formula bobot sisi sebagai berikut.

5 +5+ = { 5 +5+ , 5 +5+ , 5 +5+ , … , 5 +5+ � − }

= { 5 +5, 5 +5+ , 5 +5+ , 5 +5+ , … , 5 +5+ � − }

(ii) Untuk himpunan bobot sisi :

= � + + �

untuk indeks i dari 1, 2, …, n-1, maka definisi formula bobot sisi sebagai berikut.

� +

(32)

Ketika indeks i berjalan dari 1, 2, …, n, maka diperoleh formula dari definisi bobot sisi sebagai berikut.

� +

+ � + =

{ � + + � + , � + + � + , … , � + + � − }

= { 5 +5+ �, 5 +5+ � + , 5 +5+ � + , … , 5 +5+ � − }

(iii) Untuk himpunan bobot sisi :

= � + + � +

Ketika indeks i bernilai n-1, maka definisi formula bobot sisi adalah � +

= � + + �

untuk indeks i dari 1, 2, …, n-2, maka definisi formula bobot sisi sebagai berikut.

� +

+ = � + + � + +

ketika indeks i berjalan dari 1, 2, …, n-2, maka diperoleh formula dari definisi bobot sisi sebagai berikut.

� +

+ � + + =

{ 5 +5+ � + , 5 +5+ � + , … , 5 +5+ � − }

= { 5 +5+ � , 5 +5+ � + , … , 5 +5+ � − }

dari rincian yang telah dijabarkan mengenai himpunan bobot sisi , , dan sudah terlihat jelas pola barisan aritmatika yang dibentuk oleh ∪ ∪ sehingga bisa diperoleh bahwa

(33)

= { 5 +5, 5 +5+ , 5 +5+ , … , 5 +5+ � − , 5 +5+ �, 5 +5+ � + , … 5 +5+ � − , 5 +5+ � , 5 +5+ � + , … , 5 +5+ � − }

= { , + , + , … , + � − , + � , + � + , . . , + � − , + � , + � + , … , + � − }

pola barisan yang terbentuk dari ∪ ∪ di atas telah membentuk barisan aritmatika dengan suku awal a = 5 +5 dan selisih d = 2, sehingga dengan menggunakan alternatif pembuktian di atas yaitu menggunakan pelabelan � diperoleh bahwa graf Petersen yang diperumum P(n,m) dengan n bilangan bulat ganjil (n ≥ 3) dan m = 1, memiliki 5 +5, -edge antimagic total labeling yang membentuk barisan aritmatika dengan suku awal a = 5 +5 dan selisih d = 2.

Kemudian, untuk menunjukkan bahwa 5 +5, -edge antimagic total labeling tersebut adalah super 5 +5, -edge antimagic total labeling, akan dibuktikan bahwa

� (V[P(n,m)]) = {1, 2, …, 2n} � (E[P(n,m)]) = {2n+1, 2n+2, …, 5n} Bukti:

simpul � _� dan � _� yang telah diperoleh sebelumnya maka himpunan simpul dan dapat didefinisikan dengan formula sebagai berikut.

= {� � ; ≤ ≤ �} = { +

, � � � + +

, � �

= {� � ; ≤ ≤ �} =

{

� + +

, � � � + +

, � � � + , = �

dari semua definisi formula himpunan simpul di atas dapat digabungkan menjadi himpunan simpul keseluruhan untuk pelabelan � , yaitu ∪ = { +�, + +�, + +�, + +�, � + } untuk setiap i ∈ {1, 2, …,n}, sehingga penggabungan himpunan simpul tersebut akan membentuk barisan bilangan untuk label simpul dengan penjelasan sebagai berikut.

(34)

Ketika indeks i bernilai ganjil, dengan i = 1, 3,..n, maka definisi formula himpunan simpul adalah

+

= { , , … ,� + }

� + +

= { � + ,� + , … , �}

Sehingga diperoleh himpunan simpul sebagai berikut. = { , , … ,� + ,� + ,� + , … , �}

Ketika indeks i bernilai n, maka definisi formula himpunan simpul adalah

� +

Ketika indeks i bernilai ganjil, dengan i = 1, 3,..n-2, maka definisi formula himpunan simpul adalah

� + +

= { � + , � + , … , �}

� + +

= { � + , � + , … , � + }

Sehingga diperoleh himpunan simpul sebagai berikut.

= { � + , � + , … , � + , � + , � + , … , � }

∪ = { , , … ,� + ,� + , … , �, � + , . . , � + , � + , … , �}

Kemudian, misalkan pula , , dan , berturut-turut menyatakan himpunan sisi � �+ , � � , dan � �+ , ∀i ∈ {1, 2, ..., n} . Dengan menggunakan definisi

(35)

= {� � �+ ; ≤ ≤ �} = { � + + , ≤ ≤ � −_{� + , = �}

= {� � � ; ≤ ≤ �} = { � + + , ≤ ≤ � −_{� + , = �}

= {� � �+ ; ≤ ≤ �} = { � + + , ≤ ≤ � −_{� + + , = � − , �}

dari semua definisi formula himpunan sisi di atas dapat digabungkan menjadi himpunan sisi keseluruhan untuk pelabelan � , yaitu ∪ ∪ = { � + +

, � + , � + + , � + , � + + , � + + }, untuk setiap i ∈ {1, 2, …,n} sehingga penggabungan himpunan sisi tersebut akan membentuk barisan bilangan untuk label sisi dengan penjelasan sebagai berikut.

(i) Untuk himpunan sisi :

Ketika indeks i bernilai n, maka definisi formula himpunan sisi adalah � +

Ketika indeks i berjalan dari 1, 2, …, n-1, maka diperoleh definisi formula himpunan sisi sebagai berikut.

� + + = { � + , � + , … , �}

Sehingga diperoleh himpunan simpul sebagai berikut. = { � + , � + , � + , … , �}

(ii) Untuk himpunan sisi :

Ketika indeks i berjalan dari 1, 2, …, n-1, maka definisi formula himpunan sisi adalah

� + + = { � + , � + , … , � }

Sehingga diperoleh himpunan sisi sebagai berikut. = { � + , � + , … , � }

(iii) Untuk himpunan sisi :

Ketika indeks i berjalan dari 1, 2, …, n-2, maka definisi formula himpunan sisi adalah

� + + = { � + , � + , … , � }

Ketika indeks i berjalan dari n-1 sampai n, maka definisi formula himpunan sisi adalah

(36)

Sehingga diperoleh himpunan sisi sebagai berikut. = { � + , � + , … , � }

dari rincian yang telah dijabarkan mengenai himpunan sisi , , dan sudah terlihat jelas barisan bilangan untuk label sisi yang dibentuk oleh ∪ ∪ sehingga bisa diperoleh bahwa

∪ ∪ = { � + , � + , … , �, � + , … , �, � + , … , �}

1 ∪ = { , , … , + , + , … , �, � + , . . , + , + , … , �} sehingga � (V[P(n,m)]) = {1, 2, …, 2n}.

2 ∪ ∪ = { � + , � + , … , �, � + , … , �, � + , … , �} sehingga � (E[P(n,m)]) = {2n+1, 2n+2, …, 5n}.

Sehingga dengan menggunakan pelabelan alternatif, yaitu pelabelan total � , teorema 1 sebeluimnya juga telah terbukti bahwa graf Petersen yang diperumum P(n,m) dengan n bilangan bulat ganjil (n ≥ 3) dan m = 1, memiliki super , -edge antimagic total labeling yang membentuk barisan aritmatika dengan suku awal a = 5 +5 dan selisih d = 2

■ Terbukti Berikut ini juga diberikan contoh super 5 +5, -edge antimagic total labeling pada graf Petersen P(5,1) seperti pada Gambar 8 sebelumnya namun dengan pelabelan yang berbeda, yaitu dengan menggunakan pelabelan � .

Dengan menggunakan definisi formula pelabelan � , maka untuk graf Petersen P(5,1) diperoleh label simpul sebagai berikut.

� (u1) = 1 � (v1) = 9

� (u2) = 4 � (v2) = 7

� (u3) = 2 � (v3) = 10

� (u4) = 5 � (v4) = 8

� (u5) = 3 � (v5) = 6

� (u1 u2) = � (e1) = 12 � (u1 v1) = � (e6) = 17 � (v1 v2) = � (e11) = 23

� (u2 u3) = � (e2) = 13 � (u2 v2) = � (e7) = 18 � (v2 v3) = � e12) = 24

� (u3 u4) = � (e3) = 14 � (u3 v3) = � (e8) = 19 � (v3 v4) = � (e13) = 25

� (u4 u5) = � (e4) = 15 � (u4 v4) = � (e9) = 20 � (v4 v5) = � (e14) = 21

� (u5 u1) = � (e5) = 11 � (u5 v5) = � (e10) = 16 � (v5 v6) = � (e15) = 22

sehingga diperoleh bobot sisi dari penjumlahan label tiap sisi yang incident terhadap 2 simpul ujungnya seperti berikut.

(37)

� (u2) + � (e2) + � (u3) = 4 + 13 + 2 = 19

� (u3) + � (e3) + � (u4) = 2 + 14 + 5 = 21

� (u4) + � (e4) + � (u5) = 5 + 15 + 3 = 23

� (u5) + � (e5) + � (u1) = 3 + 11 + 1 = 15

� (u1) + � (e6) + � (v1) = 1 + 17 + 9 = 27

� (u2) + � (e7) + � (v2) = 4 + 18 + 7 = 29

� (u3) + � (e8) + � (v3) = 2 + 19 + 10 = 31

� (u4) + � (e9) + � (v4) = 5 + 20 + 8 = 33

� (u5) + � (e10) + � (v5) = 3 + 16 + 6 = 25

� (v1) + � (e11) + � (v2) = 9 + 23 + 7 = 39

� (v2) + � (e12) + � (v3) = 7 + 24 + 10 = 41

� (v3) + � (e13) + � (v4) = 10 + 25 + 8 = 43

� (v4) + � (e14) + � (v5) = 8 + 21 + 6 = 35

� v5) + � (e15) + � (v1) = 6 + 22 + 9 = 37

Dari cara pelabelan tersebut diperoleh himpunan bobot sisi dari graf Petersen P(5,1) membentuk barisan aritmatika {15, 17, 19, 21,…,39, 41, 43} dengan suku awal a = 5 5 +5 = 15 dan beda (selisih) d = 2 sehingga graf Petersen P(5,1) memiliki super (15,2)-edge antimagic total labeling. Pelabelan graf Petersen P(5,1) dari pelabelan � di atas dapat digambarkan sebagai berikut.

Kemudian, untuk contoh pola dan gambar pelabelan dari graf Petersen P(7,1) dengan menggunakan definisi pelabelan � terlampir pada Lampiran 2.

Cara pelabelan dengan menggunakan definisi pelabelan � dan � di atas merupakan ilustrasi pembuktian yang digunakan untuk memperoleh super

5 +5_,

-edge antimagic labeling pada graf Petersen P(n,m) dengan n bilangan bulat ganjil (n ≥ 3) dan m = 1. Berikut juga akan dibuktikan teorema 2 untuk memperoleh super (4n + 2,1)-edge antimagic labeling pada graf Petersen P(n,m).

16 22 21 25 24 23 6 8 10 7 9 11 20 19 18 17 15 14 13 12 3 5 2 4 1

[image:37.595.219.402.398.566.2]

(38)

Teorema 2

Setiap graf Petersen yang diperumum P(n, m), (n ≥ 3), 1 ≤ m ˂ , memiliki sebuah super (4n + 2, 1)-edge antimagic total labeling.

(Ngurah dan Baskoro 2003) Bukti :

Misalkan P(n,m) dengan adalah graf Petersen yang diperumum yang mempunyai sebuah super (a,d)-edge antimagic total labeling karena |V[P(n,m)]| = 2n dan |E[P(n,m)]| = 3n sehingga

: V[P(n,m)] → {1, 2, …, 2n} : E[P(n,m)] → {2n+1, 2n+2, …, 5n}

Semua simpul dan sisi pada graf Petersen P(n,m) dilabelkan dengan menggunakan definisi formula pelabelan , di mana didefinisikan sebagai formula pelabelan simpul dan sisi dari graf Petersen P(n, m). Berikut diberikan definisi pelabelan .

� = � − + , ≤ ≤ �

� = � + , ≤ ≤ �

� �+ = { � + + ,_{� + ,} _{= �}≤ ≤ � −

� � = � + , ≤ ≤ �

� �+ = � + − , ≤ ≤ �

misalkan g menyatakan bobot sisi dari graf Petersen P(n,m). Didefinisikan bobot sisi g dari pelabelan total dari sisi : { _{� �+} , _{� �}, _{� �+} } pada graf Petersen P(n,m) untuk semua i ∈{1, 2, …, n} sebagai berikut.

� �+ = � + � �+ + �+

� � = � + � � + �

� �+ = � + � �+ + �+

dengan indeks i+1 dan i+m di-modulo-kan dengan n bila i+1, i+m ≥ n.

Dari ketiga persamaan bobot sisi di atas, yaitu _{� �+} , _{� �} , dan � �+ dapat didefinisikan dengan suatu definisi formula bobot sisi dengan cara mensubstitusikan definisi formula pelabelan simpul dan sisi: { _� , _� ,

� � , dan � �+ } ke masing-masing pesamaan bobot sisi yang telah didefinisikan sebelumnya. Berikut definisi formula bobot sisi untuk _{� �+} ,

� � , dan � �+ .

a) Definisi formula bobot sisi untuk _{� �+} sebagai berikut.

� �+ = � + � �+ + �+

(39)

= { � + − + � + + + � − +_{� + − + � +} _{+ � , = �}+ , ≤ ≤ � −

� �+ = { � + − , ≤ ≤ � −_{� + − , = �}

karena definisi formula untuk 1 ≤ i ≤ n-1 sama dengan i = n maka berlaku � + − untuk 1 ≤ i ≤ n. Sehingga diperoleh definisi formula baku untuk bobot sisi _{� �+} , yaitu

� �+ = � + − , ≤ ≤ �

b) Definisi formula bobot sisi untuk _{� �} sebagai berikut.

� � = � + � � + �

� � = � + − + � + + � + , ≤ ≤ �

Kemudian, definisi formula di atas dapat disederhanakan sehingga diperoleh definisi formula baku untuk bobot sisi _{� �} , yaitu

� � = � + + , ≤ ≤ �

c) Definisi formula bobot sisi untuk _{� �+} sebagai berikut.

� �+ = � + � �+ + �+

� �+

= { � + + � + − + (� + + ), ≤ ≤ � −

� + + � + − + � + , , = �

Kemudian definisi formula di atas dapat disederhanakan sehingga diperoleh definisi formula baku untuk bobot sisi _{� �+} , yaitu

� �+ = { � + + ,_{� + , = �}≤ ≤ � −

selanjutnya, misalkan �_� adalah himpunan bobot sisi di mana ∈ { , , } dengan penjelasan �_� sebagai berikut.

 t = 1 → � menyatakan himpunan bobot sisi untuk _{� �+}

 t = 2 → � menyatakan himpunan bobot sisi untuk _{� �}

 t = 3 → � menyatakan himpunan bobot sisi untuk _{� �+}

Jadi, definisi formula himpunan bobot sisi terhadap pelabelan total dari sisi-sisi � �+ , � �, dan � �+ dari graf Petersen P(n, m) untuk semua i ∈ {1, 2, …, n} adalah sebagai berikut.

(40)

� = { � � ; ≤ ≤ �} = � + +

� = { � �+ ; ≤ ≤ �} = { � + + ,_{� + , = �}≤ ≤ � −

dari semua definisi formula himpunan bobot sisi di atas dapat digabungkan menjadi himpunan bobot sisi keseluruhan untuk pelabelan sehingga akan terbentuk sebuah barisan aritmatika dari pelabelan bobot sisi tersebut. Penggabungan semua definisi himpunan bobot sisi di atas, yaitu � ∪ � ∪ � = { � + − , � +

+ , � + + , � + }, untuk setiap i ∈ {1, 2, …,n}.

Rincian pola barisan aritmatika dari penggabungan himpunan bobot sisi di atas adalah sebagai berikut.

(i) Untuk himpunan bobot sisi � :

Perhatikan bahwa definisi formula bobot sisi � untuk 1 ≤ i ≤ n, yaitu � + − = � + + � −

Ketika indeks i berjalan dari 1, 2, …,n-2, n-1, n, maka diperoleh definisi formula bobot sisi � sebagai berikut.

� + + � −

={ � + + [� − � − [� − ] ], … , � + + � − [� − ] , � + + � − [� − ] , � + + � − � }

= { � + , � + + , � + + , … , � + + [� − ] }

Sehingga diperoleh himpunan bobot sisi � sebagai berikut.

� = { � + , � + + , � + + , … , � + + [� − ] }

(ii) Untuk himpunan bobot sisi � :

Perhatikan bahwa definisi formula bobot sisi � , yaitu � + + = � + + � +

ketika indeks i berjalan dari 1, 2, …, n, maka diperoleh definisi formula � sebagai berikut.

� + + � +

= { � + + � + , � + + � + , … , � + + � + � }

= { � + + � , � + + � + , … , � + + � + � } = { � + + � , � + + � + , … , � + + � − }

(41)

(iii) Untuk himpunan bobot sisi � :

Ketika indeks i bernilai n, maka definisi formula bobot sisi � adalah � + = � + + �

Perhatikan bahwa definisi formula bobot sisi � untuk 1 ≤ i ≤ n-1, yaitu � + + = � + + � +

ketika indeks i berjalan dari 1, 2, …, n-1, maka diperoleh definisi formula � sebagai berikut.

� + + � +

= { � + + � + , � + + � + , … , � + + � + � − } = { � + + � + , � + + � + , … , � + + � − }

� = { � + + �, � + + � + , � + + � + , … , � + + � − }

dari rincian yang telah dijabarkan mengenai bobot sisi � , � , dan � sudah terlihat jelas pola barisan aritmatika yang dibentuk oleh � ∪ � ∪ � sehingga bisa diperoleh bahwa

� ∪ � ∪ �

= { � + , � + + , � + + … , � + + � − , � + + �, � + + � + , … , � + + � − , � + + � , � + + � + , … , � + + � − }

= { , + , + , … , + � − , + � , + � + , . . , + � − , + � , + � + , … , + � − }

pola barisan yang terbentuk dari � ∪ � ∪ � di atas telah membentuk barisan aritmatika dengan suku awal a = � + dan selisih d = 1, sehingga.dengan menggunakan pelabelan total diperoleh bahwa setiap graf Petersen yang diperumum P(n,m), (n ≥ 3), 1 ≤ m ≤ , memiliki sebuah (4n + 2,1)-edge antimagic total labeling yang membentuk barisan aritmatika dengan suku awal a = � + dan selisih d = 1.

Kemudian, untuk menunjukkan bahwa (4n + 2,1)-edge antimagic total labeling tersebut adalah super (4n + 2,1)-edge antimagic total labeling, akan dibuktikan bahwa

(42)

Bukti:

simpul _� dan _� yang telah diperoleh sebelumnya maka himpunan simpul dan dapat didefinisikan dengan formula sebagai berikut.

= { � ; ≤ ≤ �} = � − + , ≤ ≤ � = { � ; ≤ ≤ �} = � + , ≤ ≤ �

dari semua definisi formula himpunan simpul di atas dapat digabungkan menjadi himpunan simpul keseluruhan untuk pelabelan , yaitu ∪ = {� − + , � + }, untuk setiap i ∈ {1, 2, …,n} sehingga penggabungan himpunan simpul tersebut akan membentuk barisan bilangan untuk label simpul dengan penjelasan sebagai berikut.

(i) Untuk himpunan simpul :

Ketika indeks i berjalan dari 1, 2, …, n maka definisi formula himpunan simpul adalah

� − + = {�, � − , � − , … , , } � − + = { , , … , � − , � − , � } Sehingga diperoleh himpunan simpul sebagai berikut.

= { , , … , � − , �}

Ketika indeks i berjalan dari 1, 2, …, n, maka definisi formula himpunan simpul adalah

� + = {� + , � + , … , � } Sehingga diperoleh himpunan simpul sebagai berikut.

= { � + , � + , … , � }

∪ = { , , … , �, � + , � + , … , �}

Kemudian, misalkan pula , , dan , berturut-turut menyatakan himpunan sisi � �+ , � � , dan � �+ , ∀i ∈ {1, 2, ..., n} . Dengan menggunakan definisi

formula pelabelan sisi _{� �+} , _{� �} , dan _{� �+} yang telah diperoleh sebelumnya maka himpunan sisi , , dan dapat didefinisikan dengan formula sebagai berikut.

= { � �+ ; ≤ ≤ �} = { � + + , ≤ ≤ � −_{� + , = �}

(43)

= { � �+ ; ≤ ≤ �} = � + − , ≤ ≤ � dari semua definisi formula himpunan sisi di atas dapat digabungkan menjadi himpunan sisi keseluruhan untuk pelabelan , yaitu ∪ ∪ = { � + +

, � + , � + , � + − } untuk setiap i ∈ {1, 2, …,n}, sehingga penggabungan himpunan sisi tersebut akan membentuk barisan bilangan untuk label sisi dengan penjelasan sebagai berikut.

(i) Untuk himpunan sisi :

Ketika indeks i berjalan dari 1, 2, …, n-1, maka diperoleh definisi formula himpunan sisi sebagai berikut.

� + + = { � + , � + , … , �} Sehingga diperoleh himpunan simpul sebagai berikut.

= { � + , � + , � + , … , �, }

(ii) Untuk himpunan sisi :

Ketika indeks i berjalan dari 1, 2, …, n, maka definisi formula himpunan sisi adalah

� + = { � + , � + , … , � } Sehingga diperoleh himpunan sisi sebagai berikut.

= { � + , � + , … , � }

(iii) Untuk himpunan sisi :

Ketika indeks i berjalan dari 1, 2, …, n, maka definisi formula himpunan sisi adalah

� + − = { �, � − , � − , … , � + , � + } � + − = { � + , � + , … , � − , �}

Sehingga diperoleh himpunan sisi sebagai berikut. = { � + , � + , … , � − , �}

dari rincian yang telah dijabarkan mengenai himpunan sisi , , dan sudah terlihat jelas barisan bilangan untuk label sisi yang dibentuk oleh ∪ ∪ sehingga bisa diperoleh bahwa

∪ ∪ = { � + , � + , … , �, � + , … , �, � + , … , �}

(44)

sehingga (V[P(n,m)]) = {1, 2, …, 2n}.

2 ∪ ∪ = { � + , � + , … , �, � + , … , �, � + , … , �} sehingga (E[P(n,m)]) = {2n+1, 2n+2, …, 5n}.

Sehingga dengan menggunakan pelabelan alternatif, yaitu pelabelan total , teorema 2 sebeluimnya telah terbukti bahwa setiap graf Petersen yang diperumum P(n,m), (n ≥ 3), 1 ≤ m ≤ , memiliki sebuah super (4n + 2, 1)-edge antimagic total labeling yang membentuk barisan aritmatika dengan suku awal a = � + dan selisih d = 1.

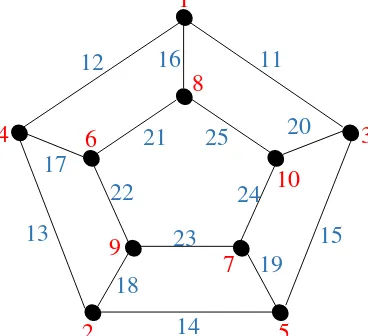
■ Terbukti Berikut ini diberikan contoh super (4n + 2,1)-edge antimagic total labeling pada graf Petersen P(5,2) seperti pada Gambar 11. Banyaknya simpul ialah 10 dan banyaknya sisi ialah 15, dengan (V[P(5,2)])= {1, 2, …, 10} dan (E[P(5,2)]) = {11, 12, …, 25} serta himpunan simpul dan sisi sebagai berikut.

V[P(5,2)] = {u1, u2, u3, u4, u5, v1, v2, v3, v4, v5}

E[P(5,2)] = {uiui+1, uivi, vivi+2}

∀i ∈ {1, 2, 3, 4, 5}

di mana ketika nilai indeks i+1 pada simpul u maupun nilai indeks i+2 pada simpul v lebih besar dari 5 maka nilai indeks tersebut akan di-modulo-kan dengan 5.

Dengan menggunakan definisi formula pelabelan , maka untuk graf Petersen P(5,2) diperoleh label simpul sebagai berikut.

(u1) = 5 (v1) = 6

(u2) = 4 (v2) = 7

(u3) = 3 (v3) = 8

(u4) = 2 (v4) = 9

(u5) = 1 (v5) = 10

(u1 u2) = (e1) = 17 (u1 v1) = (e6) = 21 (v1 v3) = (e11) = 15

(u2 u3) = (e2) = 18 (u2 v2) = (e7) = 22 (v2 v4) = (e12) = 14

e15

e14

e13

e12