DEPARTEMEN
MATEMATIKA
FMIPA
- INSTITUT
PERTANIAN
BOGaR
ISSN:
1412-677X
jihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAC o m p a rfn g O p tim is m o t E rro r R a te E s tIm a to fS In D is c rim in a n t A n a ly s is b y M o n te c a rto S im u la tio n
o n M u ltlv a rfa te N o rm a l D a ta 1
I W a y a n M a n g k uNMLKJIHGFEDCBA
A la m a t R e d a k s f:
D e p a rte m e n M a te m a tik a B ffu rk a s i H o p t p a d a M o d e l S ik lu s B is n ls K a ld o r-F M IP A -/n s titu t P e rta n ia n B o g o r
K a le c k l T a n p a W a k tu T u n d a
N u rra c h m a w a ti d a nihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAA K u s n a n to . 13
JJn. M e ra llti, K a m p u s IP S
D ra m a g a -
Bogor
P e n d u g a a n K o m p o n e n P e rfo d ik F u n g s lln te n s lta sB e rb e n tu k F u n g s i P e rto d ik K a li T re n K u a d ra tik
S u a tu P ro se s P o isso n N o n -H o m o g e n
P h o n e jF a x :(0 2 6 1 ) 8 6 2 5 2 7 6
R a m d a n l, P ., IvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAW.M a n g k u , o e n R . B u d ia rti 19
I
f-m a rt: m a th @ lp b .a c J d M a s a la h D lrfc h le t u n tu k P e tS a m a a n B e d a d a la m H I
iI/)
G m t T e rb o b o ti lll<\'H
Iff.
G a m a d l, A D . d a n E.K h a tJ z a 31 )!l"
F u rth e r E x p lO ra tio n ofth e K le e -M in ty P ro b le m
~ i
IVol. 9, No.2, Desernbcr 2010 ISSN : 1412-677X
Journal of Mathematics
and Its Applications
Jurnal Matematika dan Aplikasinya
PIMPINAN REDAKSI
Dr. Jaharuddin, MS.
EDITOR
Dr. Ir. Sri Nurdiati, MSc. Dr. Ir. Hadi Sumarno, MS. Dr. Ir. I Wayan Mangku, MSc. Dr. Ir. Endar H. Nugrahani, MS.
Dr. Paian Sianturi
ALAMA T REDAKSI:
Departemen Matematika FM[PA - Institut Pertanian Bogor Jln. Meranti, Kampus IPB Dramaga
Bogor
Phone.lFax: (0251) 8625276
Email:math@ipb.ac.idihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAI
IjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA
i'
3T.ffl1!l merupakan media yang mernuat inforrnasi hasil penelitian matematika baik murni maupun
terapan, bagi para matematikawan atau para pengguna matematika. 3TJill\!l diterbitkan dua kali (dua
nomor) setiap tahun (periode Juli dan Desember).
Harga langganan per volume, termasuk biaya pos, Vo1.9, No, I dan 2:
Institusi/Perpustakaan Rp. 350.000,- (dalam IPB), Rp. 500.000,- (luar IPB)
Staf/Perorangan Rp. 200,000,- (dalam IPB), Rp.250.000,- (luar IPB)
Mahasiswa Rp.
75.000,-Penulis makalah yang diterima dikenai biaya administrasi Rp.25.000,- per lernbar
Semua pembayaran biaya dapat ditransfer mclalui:
Retno Budiarti BNI Cabang Bogor No. Rek. 000291007-5
3f:ffl£l,vutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAVol. 9, No.2, Desember 2010 ISS : 1412-677X
Journal of Mathematics
and Its Applications
Jurnal Matematika dan Aplikasinya
1:1ihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA D A F T A R IS I
(I
III,
1 '
C o m p a rin g O p tim is m o fE rro r R a te E s tim a to rs in D is c rim in a n t A n a ly s is b y M o n te C a rlo S im u la tio n
o n M u ltiv a ria te N o rm a l D a ta
1
I W a ya n M a n g k u
B ifu rk a s i H o p f p a d a M o d e l S ik lu s B is n is K a ld o
r-K a /e c k i T a n p a W a k tu T u n d a
N u rra c h m a w a ti d a n A.K u s n a n to .
13
P e n d u g a a n K o m p o n e n P e rio d ik F u n g s i In te n s ita s
B e rb e n tu k F u n g s i P e rio d ik K a li T re n K u a d ra tik
S u a tu P ro s e s P o is s o n N o n -H o m o g e n
R a m d a n i, P ., IW. M a n g k u , d a n R . B u d ia rti 19
I':
M a s a la h D iric h le t u n tu k P e rsa m a a n B e d a d a /a m
G ra fT e rb o b o ti
!
I G a rn a d i, A .D . d a n E. K h a tiz a31
.i. \
F u rth e r E x p lo ra tio n o fth e K le e -M in ty P ro b le m
ABSTRACT. The Klee-Minty problem is explored in this paper. The coordinates formulas of all vertices of the Klee-Minty cube are presented. The subset representation of the vertices of the Klee-Minty cube is discussed. How to construct the Klee-Minty path is showed. It turns out that there are rich structures in the
Klee-Minty path. We explore these structures.edcbaZYXWVUTSRQPONMLKJIHGFEDCBA
K e y w o r d s : Klee-Minty cube, Klee-Minty path, Klee-Minty prob-lem.ihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA
I
\'
FURTHER EXPLORATION OF
THE KLEE-MINTY PROBLEM.
a m PARUHUM SILALAHI
Department of Mathematics,
Faculty of Mathematics and Natural Sciences, Bogar Agricultural University
Jl. Meranti, Kampus IPB Darmaga, Bogar, 16680 Indonesia
1 . INTRODUCTION
The Klee-Minty (KM) problem is a problem that had been presented by Klee and Minty in [3J. The n-dimensional KM problem is given by:
mm Y n
(1) subject to P Y k - l ~ Y k ~ 1 - P Y k - l , k
=
1, ... ,n ,wherejihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAP is small positive number by which the unit cube
[O,lJn
is squashed, and Y o = O. The domain (we denote as e n ), which is called KM-cube, is a perturbation of the unit cube in R". If p = 0 then the domain is the unit cube and for p E (O,~) it is a perturbation of the unit cube which is contained in the unit cube itself. Since the perturbation is small, the domain has the same number of vertices as the unit cube, i.e. 2 n .The KM-problem has become famous because Klee and Minty found a pivoting rule such that the simplex method requires 2n - 1 iterations to sol ve the problem (1).
Y k - l ~ Y k ~ 1 - Y k - l
In this paper, we explore the KM problem further. We provides for-mulas for the coordinates of all vertices of the KM cube, and discuss the subset representation of the vertices of the KM cube. Then we
42ihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAB lB P A I1 U H U d S fL A L A fllvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA
describe the KM path.jihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAV.,Te show that when using the subset represen-tation, the KM path can easily be constructed by using the so-called
flip p in g operation. It, turns out that there are rich structures in the KM path. We explore these structures.
2 . VERTICES OF THE KLEE-MINTY CUBE
With the n-dimensional EM problem as defined in (1), we define the slack vectors 2.. andedcbaZYXWVUTSRQPONMLKJIHGFEDCBAS according to
2 ..k = Y k - P Y k - l , k = l , ,n , (2)
s k = l - Y k - P Y k - l , k = l , , n . (3)
For any vertex of the KM cube we have either Q .k
=
0 or S k=
0, for eachk . As a consequence, each vertex can be characterized by the subset
of the index set J= {I, 2, ... ,n } consisting of the indices k for which
S k vanishes (and hence 2 ..kis positive). Therefore, given a vertex v we
define
S ; = { k : S k = O} == { k : 2 ..k> O} .
Note that the KM cube has 2n vertices. Since 2n is also the number of subsets of the index set J, each subset S of the index set uniquely determines a vertex. We denote this vertex as vS. Given S , the
co-ordinates of vS in the y-space can easily be solved from (2) and (3), because we then have S k = 0 if k E Sand Q .k = 0 if k ~ S , which yields
n equations in the entries of the vector y. When defining Y o
=
0 andy = vS, one easily deduces that.
{
l -P Y k -l, k E S ,
Y k =
P Yk - L, k d'F S .
Since Y o = 0, we have Y 1 E {O,I}. This together with (4) implies that
Y k is a polynomial in P whose degree is at most k - 1. Moreover, the
coefficients of this polynomial take only the values 0, 1 and -1 , and the nonzero coefficients alternate between 1 and -1. Finally ifY k = 1 = 0 then the lowest degree t.erm has coefficient I.
'vVecan be more specific. Let
(4 )
S = {81' 82, ... , 8m }, 80 = 0 < 81 < 82 < ... < 8m < 8m+1 :=n + l.
Then the entries of yare given by the following lemma. In this lemma we define an empty sum to be equal to zero.
Lemma 1. O n e h a s
Y S ;
=
L ( - l ) , + J p - " - s ) ,0:::; i:::;
m,j= 1
(5)
and
JMA, VOL. 9.jihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAN O .2 , DESEMJ3ER, 201.0, 41-53 43
P ro o]. If k
tt
S then the definition of S implies thatedcbaZYXWVUTSRQPONMLKJIHGFEDCBAS iihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA< k < S i + 1 forsome i, with 0 ~ i ~m. It follows from (4) that in that case
Y S i + l = 1 - P Y S i + l - l . At this stage we need to distinguish two cases: and S i + l - 1
tt
S (case II).In case I we must have S i + l -1
=
s . . Since (5) holds forY S i it follows from (7) that(7)
S i + l - 1 E S (case I) _ _ _ k - s i - 1 _ k = s ;
Y k - P Y k - l - .t • - P Y si+ l - P Y Sil proving (6).
So it remains to prove (5). The proof uses induction with respect to the index i in (5). Before entering this proof it may be worth noting that (5) expresses Y Si as a polynomial in P of degree s , - S l . The lowest degree term occurs for j = i , and hence this term equals (-1
)2i
p O = 1.For i = 0 the sum in (5) becomes empty, whence we obtain Y o
=
0,as it should. This proves that (5) holds if i = O. Now assume that (5) holds for some i, with 0 ~ i < m. Since S i + l E S , according to (4) we have
Y.S,+I = 1 - p ys ,, = 1 - r -f),\,i,L ....J = 1 ( _ l ) i + j p S i - S j
= 1 - L ~ = l ( - l ) i + j p S i + l - s j
=
1+
L ~ = 1 (-1)i+l+j p S i + I - S j .In case II we may use (6), which gives
Y,8,+1_1
=
p S i + l - l - s iy s ,,=
p S i + I - 1 - s i ,\,i,L....J=l( _ l ) i + j p s i - S j=
,\,i, ( _ l ) i + j S i + l - l - S j L ....J = 1 P ,whence (7) yields that
I I
i i+l
Y S i - j - 1
=
1+
I)
_ 1 ) i + 1 + j p S i + I - S j=
I)
_ 1 ) i + 1 + j p S i + I - S j ,j= 1 j= l
which completes the proof.
o
Y S i + 1
=
1- P 2 ~ ) _ 1 ) i + j p S i + l - l - S j = 1+
I ) _ l ) i + l +jp s i + I - S j .j = 1 j = 1
We conclude that in both cases we have
3 . THE KLEE-MINTY PATH
is well known in which order the vertices are visited. This can be easily described by using the subset representation of the vertices introduced in the previous section. The. path starts at vertex (0, ... ,0,1) whose
subset is the subsetjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAS 1ihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA= {n }. Thesubsequent subsets are obtained by an operation which we call flip p in g · an index with respect to a subset
S [4]. Given a subset S and an index i, flipping i (with respect to S )
means that we add i to S if i t/:. S , and remove i from S if i E S . Now let S k denote the subset corresponding to the k-th vertex on the KM path. Then S k+ l is obtained from S k as follows:
• if
ISkl
is odd, then flip 1;• if
ISkl
is even, then flip the element. following the smallest ele-ment inedcbaZYXWVUTSRQPONMLKJIHGFEDCBAS i :Denoting the resulting sequence as Pn , we can now easily construct the KM path for small values of n :
P1 :
{I}
- t0
P
2 :{2}
- t{1,2}
-7{I}
- t0
P3 :
{3}
- t{I, 3}
-7{I, 2, 3}
- t{2, 3}
-7 P2P
4:{4}
-t{1,4}
-t{I,2,4}
-7{2,4}
-7{2,3,4}
-t{1,2,3,4}
-t
{1,3,4}
-t{3,4}
-t P3 .
Table 1 shows the subsets and the corresponding vectors y for the KM path for n = 4. The corresponding tables for n = 2 and n = 3 are subtables, as indicated. Note that if subsets S a n d S ' differ only in n ,
and y
=
v s and y '=
V S ' , then we haveY i
=
y ~ , 1 ~ i<
n , u «+
Y : l=
LObviously, the subsets of two subsequent vertices differ only in one element. For the corresponding subsets, S k and S k+ l say, we denote this element by ik . Then we have S ik
=
0 in one of these vertices, and in the other vertex S ik > 0, or equivalently § . i k=
O. On the interior ofthe edge connecting these two vertices we will have § . i k > 0 and S ik > O. If n
=
4 then, when following the KM path, the flipping index ik runs through the following sequence:1, 2, 1, 3, 1, 2, 1, 4, 1, 2, 1, 3, 1, 2, 1.
So if n
=
4 then the flipping index 8 times equals 1, 4 times 2, 2 times3, and once 4.
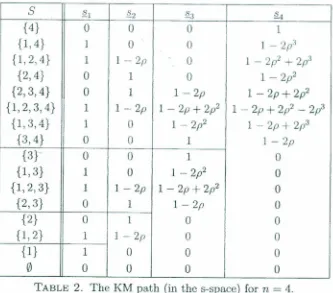
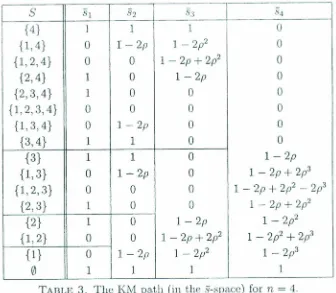
Table 2 shows the slack vector §. and Table 3 the slack vector S [or each of the vertices. For a graphical illustration (with n
=
3) we refer to Figure 1.4. S E Q U E N C E O F V E R T IC E S IN T H E K L E E -M IN T Y P A T H
r - - .edcbaZYXWVUTSRQPONMLKJIHGFEDCBA
SvutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAYi Y 2 Y 3
Y4
{4} 0 0 0 1
{1,4}
1
,p p 21 _
p 3{1,2,4}
1
I - p p _ p 21 -
p 2+
p 3{2,4}
01
P1 _
p 2{2,3,4}
0 1 1 - p 1 _ P+
p 2{1,2,3,4}
1 1 - p ] _ p+
p 2 1 _ p+
p 2 _ p 3{1,3,4}
1jihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAp1 _
p 2 1 - (J+
p 3{3,4}
0 01
I - p{3}
0 01
P{1,3}
1
p1 _
p 2 P _ p 3{1,2,3}
1
I - p 1 _ p+
p 2 P _ p 2+
p 3{2,3}
01
1 - P P _ p 2{2}
01
p p 2{1,2}
1
1 - p p _ p 2 p 2 _ p 3{I}
1
p p 2 P30
0 0 0 0,,
JMA, VOL. 9, NO.2, DESEtvIBER, 2010, 41-53 45
TABLE L The KM path (in the v-space) for n
=
4.sequence. Hence, when denoting the first half of Pn as
P::-l
we havefor n E {2, 3, 4} that Pn =
P ::-
1 ---t Pn -1 . Indeed, when defining P o =0
then this pattern holds for each n ~ 1, as stated in the following lemma.
Lemma 2. fO T ' n ~ 1, o n e h a s
(8)
P r o o f . The proof uses induction with respect to n . We already know
that the lemma holds if n ~ 4. Therefore, (8) holds if n = 1. Suppose
that n ~ 2. Let S k denote the k - t h subset in the sequence Pn -1 . By
the induction hypothesis we have S 1
=
{ n - I} and S 2n-J=
0. Thefirst set in Pn is the set {n}
=
{n} U S2n-J. For 2 ~ k ~ 2n-t, weconsider the set S
=
S k U {n } and we show below that its successoris the set S k-l U {n }. This will imply that the 2n-l_th set in Pn is
S 1 U { n } = { n - 1,n } , whose successor is the set { n - I}, the first set
of Pn -1. This makes clear that it suffices for the proof of the lemma if
we show that for each set S k in Pn -1 the successor of S k U {n } is the
set S k-1 U {n}. This can be shown as follows.
If
ISI
is even then the successor ofS
in Pn arises by flipping theelement following the smallest element in S . If this smallest element
B IB l'A IW H U I\l S IL 1 \L A H IjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA
SedcbaZYXWVUTSRQPONMLKJIHGFEDCBAQ 1 S 2 ~ ~
{4}
vutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA0 0 01
{1,4}
1
0 0 ] - 2 p3{l,2,4}
1
1 -
2 p-
01 -
2 p 2+
2 p3{2,4}
01
0 1 - 2 p 2{2,3,4}
01
1 - 2 p 1 - 2 p+
2 p 2{1,2,3,4}
1
1 - 2 p1 -
2 p+
2 p 21 -
2 p+
2 p 2 - 2 p3{1,3,4}
1
01 -
2 p 2 1 - 2 p+
2 p3{3,4}
0 0 1 1 - 2 p{3}
0a
1 0{1,3}
1a
1 - 2 p 2 0{1,2,3}
1
1 -
2 p 1 - 2 p+
2 p 2 0{2,3}
0 1 1 - 2 p 0{2}
0 1 0 0{l,2}
1 1 - 2 p 0 0{I}
1 0 0 0 [image:9.613.185.518.69.362.2]0 0 0 0 0
TABLE 2. The KM path (in the s-space) for n
=
4.of S is the set { n - 1}
=
S l, which is the first element of Pn -1 .Other-wise the smallest element is at most n - 2, and then, since
ISkl
is odd,the successor of S is equal to S k -l U {n }. The latter follows since S
and S k -1 have the same smallest element and
ISk-ll
is even.If
ISI
is odd then the successor of S in P ; arises by flipping l. SinceISkl
is even flipping 1yields the predecessor of S k in Pn -1, which is S k -1 ' Hence we find again that the successor of S is Sk - l U {n }. Thiscompletes the proof. 0
According to this lemma, the index i that occurs K times as flipping
index in Pn -1 will occur 2 K times in Pn , i.e. K times in
P::-1
and K times in Pn -1 . The index n flips only at the last set inP ::-
1, which givesthe first set in Pn -1 . These sets are { n -l,n} \ {OJ and { n -I} \ {O}
respectively. The complement operation of
{OJ
is applied to adjust for the case where n=
l. As an immediate consequence we have the following corollary.Corollary 1. T h e i n d e x i, 1 ~ i ~T L , n e v e r f l i p s i n P i , f o r 0 S;k < i.
I t f l i p s f o r t h e f i r s t t i m e i n P i w h e n a p p l i e d t o t h e s e t
{i - 1, i} \ {O}
Jw h i c h y i e l d s t h e s e t
{i - I} \ {O} .
From Lemma 2, for 0 ~ i < n , we can obtain
- n - n - l - i + 1
JMA, VOL. 9, NO.2, DESEMBER, 2010, 41-53 47jihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA
S .5ihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA1 82 83
.5
4
{4}
1
1
1
0{l,4}
0 I -edcbaZYXWVUTSRQPONMLKJIHGFEDCBA2 p 1 - 2 p 2 0{1,2,4}
0 0 1 - 2 p+
2 p 2 0{2,4}
1
0 1 - 2 pa
{2,3,4}
1
a
a
a
{1,2,3,4}
a
a
a
a
{1,3,4}
a
1 - 2 pa
0{3,4}
1
1
a
a
{3}
1
1
a
1 - 2 p{1,3}
0 1 - 2 pa
1 - 2 p+
2 p3{1,2,3}
a
a
a
1 - 2 p+
2 p 2 - 2 p3{2,3}
1
0a
1 -
2 p+
2 p 2{2}
1
0 1 - 2 p 1 - 2 p 2{1,2}
0 01 -
2 p+
2 p 21 -
2 p 2+
2 p3{I}
a
1 - 2 p1 -
2 p 21 -
2 p3(/)
1
1 1 1TABLE 3. The KM path (in the s-space) for n
=
4.According to Corollary 1, index i is flipped for the first time in P i ,
hence we have the next corollary.
Corollary 2. T h e i n d e x i f l i p s f o r t h e l a s t t i m e i n Pn a t t h e s e t
{i -
l,i} \ {a }, w h i c h y i e l d s t h e s e t {i - I} \ {O}.The sequence
P::-1
is equal to the sequence which is obtained by reversing the sequenceP- n - 1n - 2 --t ... --t p - H 1i --t pi
and by adding the element n to each sets in the resulting sequence. Thus the next corollary follows.
Corollary 3. T h e i n d e x i f l i p s J O T t h e firs t t i m e i n Pn a t t h e s e t
{i
- 1 , n } \{a},
w h i c h y i e l d s t h e s e t{i
- 1 , i , n } \{a}.
Moreover, by letting J , be any subset of
J\
{I, ... ,i}, we have the following corollary.Corollary 4. T h e i n d e x i f l i p s i n Pn w h e n i t i s a p p l i e d t o e i t h e r
{i-l,i}\{O}UJ
i o r{i-l}\{O}UJ
i.P r o o f . Let us consider Pn as in (9). The flipping indexes of two sets that
connecting two sequences of sets consecutively aren , n-1 , ... , i
+
1 .In [image:10.613.129.465.67.360.2]{3}
48 BIB PARUHUM SILALAHIedcbaZYXWVUTSRQPONMLKJIHGFEDCBA
Y 3
• 1
---~~-ihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA/
" I
/" ,- ,." 1 /~~ ~ ,.:t'<1 .,J'. / - - - -.a.::- - - _""::::0...,.,- '"'"_ I
.'
~SL---:"~1{2,3}
.. / /
~t / / / /
;/// /
'/ • 1 • / " "
.- / 1 / " ,,"
1jihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAr> J
--'-:--y - - - - 1 - - - '/ " '- 1 ' /
1 - p 2 ~-H.-3-} 1 / I /
1 y ~ ' 1 /" 1 ,/
2 1 / 1 1 /
I - p + p ( ;r - - - - ~ - - - - T - - - -
tl,2,3}'/
I-p f . : . . - - - - T - - - - ; A 1 - ~ ---;
{2}
1 1 / 1 1 1 _ --- 1
1 " 1 I 1 -- /'/ I
1 I"1 ,,1 I --I - "1 1 I" 1
0
_ -,..1 .-- 1 ,," 11 r/ -- 1 1 / 1
1 / I 1 I " " • Y 2
1 / " I I / "
I / I // I // //
1 "/ 1 " 1 I /
,-I / I / I 1 //
P
~ - - - - r -
- - - 1 - - '- - 1 '2 / I
P - P v _ - - 7 ~ r - - - I "
1 /" / ' ./
'{1 2}
I "I " •.. 1 ' / I' I /
p 2 ~ "'/-'-{1 } I I //
"'0
;Z- - - _,_- - - -
-1 // 0
p I-p 1Yl
FIGURE 1. Unit cube (red dashed), KM cube (blue
dashed) and KM path (blue solid) for n = 3.
·1
this case there is no index which is equal to i . In P i , flipping an index i
is only applied to the set
{i -
1,i} \
{O} which yield the set{i -
1} \ {O}. Let us call the pair of two sets, where an index iis flipped with respect to one of the sets and another one is its successor, as pair of sets with flipping index i. Generally, the pairs of sets with flipping index i that appear in p ;+ 1 , k ~ i, definitely equal to pairs of sets which is resultedfrom the union of each set of pair of sets with flipping index i in Pk by
{k
+
1}. By taking J , as any subset of:1\
{1, ... ,i},
we obtain that the pairs of sets with flipping index iin Pn are{i -
1,i} \
{O}UJ , and{i -
1} \ {O}U J ; This implies the corollary. 0 The following corollary expresses how many times the index i is Ripped in Pn. \Ve have discussed this number for small value of n previously.
III
Lemma 3. T h e i n d e x i, 1 ~ i ~n , i s f l i p p e d i n Pn e x a c t l y
2n
.JMA, VOL. 9, NO.2, I)J:;SCMDEH, 20JO, -11-5:3 49edcbaZYXWVUTSRQPONMLKJIHGFEDCBA
P r o o f . The index n is Hipped only 1 time injihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAPn . By using the recursive pattern of Pn as in Lemma.2 and Coronary 1, in Pn , the index
n - 1 , is flipped 2 times,
n - 2, is flipped 4 times,
n - k , is flipped 2k times,
1 , is flipped 211-1 times.
The lemma follows by takingihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAi
=
ti - k , 0 When n is given, the set S k is uniquely determined by k , and viceversa. Moreover, for each k (2 ~ k : ~ 211), the sets S k - l and S k
differ only in one element. This means that the sequence Pn defines a so-called G r a y c o d e . Such codes have been studied thoroughly, also
because of their many applications. 1
It may be worth mentioning some results from the literature that make the one-to-one correspondence between k and S k more explicit. The next proposition is the main
result (Theorem 6(ii)) in
[1].2
Proposition 1 . O n e h a s i E S k i f a n d o n l y i f
l
2n
- k
1J
2i
+
2
mod 2 = 1. (10)Given k , by computing the left-hand side expression in
(10)
for i=1,2, ... , n we get the set S k . Conversely, when S k is given we can
find k (also in ti iterations) by using Corollary 24 in [1]. This goes as
follows. V \T e first form the binary representation b .; ... b2bl of S k , with b ,
=
1 if i E S k and b ,=
a
otherwise. We then replace b , bya
if the number of 1's in b ., ... b2b1 to the left ofb , (including b , itself) is even, and by 1 if this number is odd. The resulting binary n-word a n · . . a 2 a lis the binary representation of some natural number, let it be K. Then
k
=
2n - K. For example, let S k=
{2,3} and n=
4. ThenS k == bn · . . b2b1
=
0110 - t a n . . . a 2 a l = 0100 == 4 - t k=
24 - 4=
12, Jlwhich is in accordance with Table 1.
lCray codes were first designed to speed up telegraphy, but now have numerous applications such as in addressing microprocessors, hashing algorithms, distributed systems, detecting/correcting channel noise and in solving problems such as the Towers of Hanoi, Chinese Ring and Brain and Spinout.
50 13IB P;\ RU HedcbaZYXWVUTSRQPONMLKJIHGFEDCBAU l'v [ SlLA LAHIihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA
5 . EDGES OF T H E K L E E -M IN T Y P A T H
An edge of the KM path in e n is a line segment connecting tw o
consecutive vertices of the KM path. As before, we represent the k-th
vertex on the KM path by the set S i : The edge connectingjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAS k and
S k+ 1 is denoted a s e
k.
The set of all edges of the n-dimensional K Mpath, denoted by E n , is therefore given by
,
I'
M
{
y E
en :
}
e k
=
5 j=
0 ifj E S k nS k+ l, . § 'j=
0 ifjtJ.
S k U S k+ 1Further elaborating (iii) we get the following lemma.
Lemma 4. L e t il,; b e t h e f l i p p i n g e le m e n t /0 1 ' S k I t h e n o n e r . [ o r 1 <
j < ik O T I-e h a s
(12) 2"-1
E n
=
U
ek · ( 1 1 )k= l
Remember that S k and S k+ 1 differ only in one element, which we denote as ik . On the interior of the edge connecting these two vertices we have
§ . i k > 0 and 5 ik > O. For any j = 1 = ik , we have s ,
=
0 if j E S k n S k+ 1 and § 'j=
0 otherwise. So it follows that if j = 1 = ik then either § 'j=
0 one
k
or 5 j=
0 on ek .
For ik = 1 = 1, we have either § .1
=
0 or 5 1=
0, which implies eitherY 1
=
0 or Y 1=
1 on ek . Since for any j < ik we have either § 'j=
0 or5 j
=
0 on ek,
we may conclude that Y j is constant on ek·
Summarizing,we may state that on ek we have the following properties:
(i)
u ,
> 0 or s . , > 0,(ii)
j = 1 = ik : 5 j = 0 or § 'j=
0,(iii)
1 ~ j < ik : Y j is constant.Table 4 and Table 5 shows the slack vector § . and 5 on e
k
for n=
4.The subtables show § . and 5 for n
=
1,n=
2 and n = 3.We therefore can describe the edge e
k
as followsek
=
{y Een :
for any j = 1 = ik , S j=
0 ifj E S knS k+ 1, § 'j=
0 otherwise}.Or, in other words, since
s ,
U S k+ 1 = (S I,;n S k+ 1) U {id , we may write{
I, j
=
ik - I,EdgeihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA§ .l § .2 § .J
~
{4} - {1,4} (0, 1) 0 0edcbaZYXWVUTSRQPONMLKJIHGFEDCBA( 1 - 2 p 3 ,1 )
{1,4} - {1,2,4} 1 (0,1 - 2 p ) 0 (1 - 2 p 2
+
2 p 3 , 1 - 2 p 3 ){1,2,4} - {2,4} (0, 1) ( 1 - 2 p ,1 ) 0 (1 - 2 p 2 , 1 - 2 p 2
+
2 p 3 ){2,4} - {2,3,4} 0 1 (0,1 - 2 p ) (1 - 2 p
+
2 p 2 , 1 - 2 p 2 ){2,3,4} - {1,2,3,4} (0, 1) ( 1 - 2 p ,1 ) (1 - 2 p , 1 - 2 p
+
2 p 2 ) (1 - 2 p+
2 p 2 - 2 p 3 , 1 - 2 p+
2 p 2 ){1,2,3,4} - {1,3,4} 1 ( 0 ,1 - 2 p ) (1 - 2 p
+
2 p 2 , 1 - 2 p 2 ) (1 - 2 p+
2 p 3 , 1 - 2 p+
2 p 2 - 2 p 3 ){1,3,4} - {3,4} (0, 1) 0 ( 1 - 2 p 2 , 1) (1 - 2 p , 1 - 2 p
+
2 p 3 ){3, 4} - {3} 0 0 1 ( 0 ,1 - 2 p )
{3} - {1,3} (0, 1) 0 ( 1 - 2 p 2 ,1 ) 0
{1,3} - {I, 2, 3} 1 (0,1-2p) ( 1 - 2 p + 2 p 2 ,1 - 2 p 2 ) 0
{l,2,3} - {2,3} (0,1) ( 1 - 2 p ,1 ) (1 - 2 p , 1 - 2 p
+
2 p 2 ) 0{2, 3} - {2} 0 1 ( 0 ,1 - 2 p ) 0
{2} - {I, 2} (0, 1) ( 1 - 2 p ,1 ) 0 0
{1,2}-{1} 1 (0,1 - 2 p ) 0 0
{I} -
0
(0, 1) 0 0 0
'-:s:
::t>
<
o
r.-e :
z
o
tv
G
l':
u :
L-J
'7
-w
t! r : ,,,,;, o c
"'"",
G'
c ...:
T A B L E 4. Edges of the KM path (in s-space) for n = 4.
[image:14.843.180.756.138.462.2]I ,vutsrqponmlkjihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBA
Edge 81 82 83 84
{4} - {1,4}
(0,1)
edcbaZYXWVUTSRQPONMLKJIHGFEDCBA( 1 - 2 p ,l)11 -
2 p 2 ,1)
0
{1,4} - {1,2,4}
0
( O ,l- 2 p )(1 -
2 p+
2 p 2 ,l- 2 p 2 )0
{1,2,4} - {2,4}
(0,1)
0
(1 -
2 p ,1 -
2 p+
2 p 2 )0
{2,4} - {2,3,4}
1
0
( O ,l- 2 p )0
{2,3,4} - {1,2,3,4}
(0,1)
0
0
0
{1,2,3,4} - {1,3,4}
0
( O ,l- 2 p )0
0
{1,3,4} - {3,4}
(0,1)
( 1 - 2 p ,l)0
0
{3,4} - {3}
1
1
0
( O ,l- 2 p ){3} - {1,3}
(0,1)
( 1 - 2 p ,l)0
(1 -
2 p ,1 -
2 p+
2 p3 ){1,3} - {1,2,3}
0
( O ,l- 2 p )0
(1 -
2 p+
2 p3 ,1 -
2 p+
2 p 2 - 2p3 ){1,2,3} - {2,3}
(0,1)
0
0
(1 -
2 p+
2 p 2 - 2 p3 ,1 -
2 p+
2 p 2 ){2,3} - {2}
1
0
( 0 ,1 - 2 p )(1 -
2 p+
2 p 2 ,1 -
2 p 2 ){2} - {1,2}
(0,1)
0
(1 -
2 p ,1 -
2 p+
2 p 2 )(1 -
2 p 2 ,1 -
2 p 2+
2 p3 ){1,2} - {I}
0
( O ,l- 2 p )(1 -
2 p 2 p 2 ,l- 2 p 2 ) ( 1 - 2 p 2+
2 p3 ,1 -
2 p3 ){l}-0
(0,1)
( 1 - 2 p ,l)(1 -
2 p 2 ,l)(1 -
2 p3 ,1)
[image:15.842.194.761.165.451.2]J1\'lA, VOL. 9, NO.2, DESEI'vfBER, 2010, 41-53 53edcbaZYXWVUTSRQPONMLKJIHGFEDCBA
P r o o f . The only different element injihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAS k and S k+ 1definitely is the index
ik that we flip in the set,sk' According to Corollary 4, the only different
element ik happens in pair of sets { ik - 1,
id \
{O}
Us .;
and { ik - I} \{O}
ihgfedcbaZYXWVUTSRQPONMLKJIHGFEDCBAU Jik , where Jik is any subset of:1\
{I, ... ,id .
This means thaton the edge connecting S k and S k + l we have
.§.l
=
0, .§.2=
0, ... ,. § . ik- 2
=
0, S i k - l=
O.From s,
=
0 we get YI=
O. Then subsequently we get Y 2=
0, ... , Y ik- 2 = 0 , Y i k - l=
1 from .§.2=
0, ... ,. § . i k - 2=
0, S i k - l=
0, which proves thelemma. 0
One may use Table 1 to verify Lemma 4 for n ~ 4.
REFERENCES
[1] M.W. Bunder, K.P. Tognetti, and G.E. Wheeler. On binary reflected Gray codes and functions. D i s c r e t e M a t h e m a t i c s , 308: 1690-1700, 2008.
[2] M. Conder. Explicit definition of the binary reflected Gray codes. D i s c r e t e M a i h -e m a t i c s , 195:245-249, 1999.
[3] V. Klee and G.J. Minty. How good is the simplex algorithm? In I n e q u a l i t i e s ,
III{ P r o c . T h i r d S y m p o s . , U n i v . C a l i f o r n i a , L o s A n g e l e s , C a l i f . , 1969; d e d i c a t e d t o t h e m e m o r y o f T h e o d o r e S. M o t z k i n ) , pages 159-175. Academic Press, New York, 1972.