Peranan Geometri Dalam Mengoptimalkan Fungsi 2 Peubah Atau Lebih

PERAN AN GEOM ETRI D ALAM M EN GOPTI M ALKAN FUN GSI 2 PEUBAH ATAU LEBI H

D r s. R.Joh a n n e s P. M a t a n ia r i; D r s. Gim Ta r iga n

Fa k u lt a s M a t e m a t ik a da n I lm u Pe n ge t a h u a n Ala m Ju r u sa n M a t e m a t ik a

Un ive r sit a s Su m a t e r a Ut a r a

BAB I PEN D AH ULUAN

1 .1 La t a r be la k a n g

St udi t ent ang perilaku fungsi um um nya m encakup hal- hal ant ara lain, penent uan daerah dim ana fum gsi naik/ t urun, m aksim ium / m inim um , t it ik belok, asim t ot dan sebagainy a. Tuj uan y ang ingin dicapai dalam m eny elesaik an fungsi dua peubah adalah unt uk m endapat kan hasil yang opt im al. Hal ini dipengaruhi oleh harga–harga peubah x dan y karena peubah x dan y m erupakan peubah–peubah bebas y ang m enent uk an harga peubah t ak bebas z. Opt im al t idak dit ent uk an oleh m aksim um at au m inim um . Akan t et api yang dim aksudkan dengan hasil yang opt im al ialah bagaim ana m em aksim um kan z= f( x,y) dengan harga peubah x dan y yang m inim um .

Masalah m aksim um / m inim um banyak kit a j um pai dalam kehidupan nyat a, dalam cabang ilm u sepert i ekonom i, st at ist ika, t eknik dan lain- lain. Secara singkat , t eori m aksim um / m inim um sangat bergun unt uk m enyelesaikan m asalah m aksim um / m inim um yam g banyak kit a j um pai dalam berbagai hal. Misalnya, m enghit ung volum e, luas suat u plat dan lain- lain. Salah sat u cara yang dapat digunakan unt uk m encari penyelesaian opt im al dari fungsi dua peubah adalah secara geom et ri diferensial. Dengan geom et ri diferensial, dapat diperoleh harga peubah x dan y yang diinginkan dan harga peubah z yang opt im al apabila peubah z= f( x,y) dan k endala–k endalany a dik et ahui.

Berdasark an uraian di at as adalah m erupak an hal y ang m enarik perhat ian k am i unt uk m em bahas t ent ang “ Peranan Geom et ri dalam m engopt im alkan Fungsi Dua Peubah at au lebih ” . dengan m em akai fungsi diferensial.

Selam a ini kit a t elah m em bicarakan diferensial fungsi hanya dari sat u variabel, yait u dalam fungsi eksplisit nya adalah y = f( x) , at au dalam bent uk im plisit f( x,y) = 0. fungsi yang dem ikian it u m em berikan pengert ian adanya hubungan ant ara dua v ariabel y ait u, x dan y . Ak an t et api bany ak k asus sebenarny a m erupak an hubungan- hubungan dari beberapa variabel yang dinyat akan dalam suat u fungsi. Misalny a, di dalam t eori ekonom i k it a t ahu bahw a perm int aan ak an suat u barang seringkali dipengaruhi t idak hanya oleh harga barang it u, t et api j uga oleh harga barang- barang yang m em punyai hubungan erat ( bisa sebagi barang subsit usi at au barang kom plem ent er) , oleh t ingkat pendapat an konsum en, selera, j um lah penduduk dan sebagainy a y ang dalam huk um perm int aan diasum sik an t et ap k onst an ( cet eris paribus) . Dengan dem ik ian fungsi sepert i it u dapat dit ulis y = f( x1, x2, x2,

...,xn) . Oleh karena it u penurunan dari fungsi t ersebut harus dilakukan secara

t erpisah unt uk set iap v ariabel bebasny a.

1 .2 Ru m u sa n M a sa la h

sesuat u yang t idak diinginkan. Oleh karena it u, akibat t ersebut m erupakan penyim pangan dari apa yang seharusnya.

Dari uraian di at as, m asalah–m asalah y ang dihadapi adalah sebagai berik ut : 1. Apakah hasil yang ingin dicapai dari suat u fungsi dua peubah z= f( x,y) it u

sudah opt im al ?

2. Jik a hasil t ersebut t idak opt im al, berapak ah besarny a peny im pangan y ang t erj adi ?

1 .3 Tu j u a n da n M a n fa a t

Hasil yang opt im al adalah sesuat u yang sangat pent ing dalam hal apapun. Sedikit saj a t erj adi kesalahan dalam m enent ukan langkah aw al, m aka hasilnya akan j auh dari apa yang diharapkan.

Oleh k arena it u, k am i m engharapk an dengan adany a t ulisan ini, m ak a dapat diket ahui cara–cara apa yang harus dit em puh unt uk m encapai suat u hasil yang opt im al dari fungsi dua peubah at au lebih.

1 .4 Alu r / Ke r a n gk a Pe m ik ir a n

Pem bahasan dalam t ulisan ini adalah dengan m enggunak an diferensial parsial, k hususny a pada t eori deferensial geom et ri pada pengopt im alan fungsi dua peubah z= f( x,y) .

Adapun langkah–langkah yang digunakan dalam t ulisan ini adalah sebagai berik ut :

a. Teori t ent ang fungsi dua peubah z= f( x ,y ) .

b. Pengert ian m aksim um dan m inim um suat u fungsi.

c. Mem perk enalkan t eori t ent ang nilai ekst rim dari fungsi dua peubah z= f( x ,y ) dan j enis ekst rim nya.

d. Menguraikan m et ode- m et ode yang akan digunakan unt uk m endapat kan hasil y ang opt im al dari fungsi dua peubah at au lebih z= f( x ,y ) .

e. Menggunakan diferensial parsial dalam beberapa m et ode unt uk m enent ukan luas at au v olum e y ang opt im al.

f. Mencari besarny a ham piran ( peny im pangan) y ang t erj adi pada luas at au v olum e y ang opt im al.

BAB I I M ETOD OLOGI

2 .1 Fu n gsi D u a Pe u ba h

Bila unt uk set iap pasangan ( x ,y) dari harga–harga dua peubah bebas x dan y ( dari beberapa dom ain D) , t erdapat k orespondensi harga–harga t ert ent u, m ak a dik at ak an bahw a z adalah fungsi dari dua peubah bebas x dan y y ang t ert ent u di dalam dom ain D. Secara sim bolis, fungsi dari dua v ariabel dit ulisk an dengan z= f( x ,y ) .

2 .2 Pe n ge r t ia n m a k sim u m da n m in im u m

Suat u fungsu y = f( x) dikat akan m em punyai m aksim um lokal ( m ak sim um relat if) dim ana x = a bila f ( a) lebih besar dari sem barang nilai f( x) lainnya dari x sek it ar a, dan dik at ak an m em puny ai m inim um lok al ( m inim um relat if) pada x = a bila f( a) lebih kecil dari sem barang nilai f( x) lain unt uk x disekit ar a. Maksim um dan m inim um lokal suat u fungsi ini adalah m aksim um dan m inim um unt uk j arak t ert ent u yang berdekat an, sedangkan m aksim um dan m inim um absolut dari suat u fungsi m em puny ai j arak y ang lebih besar lagi dan t erket ak pada t it ik y ang paling t inggi at au paling rendah dari j arak t ersebut , m elebihi m aksim um at au m inim um lokal yang m anapun. Jadi, dapat dik at ak an bahw a f( x ) m em puny ai nilai m ak sim um absolut pada nilai x = a1 dalam bat as

b

≤

x

≤

c

, apabila nilai f( x) pada x = a1 m em punyai

nilai paling t inggi, f( a1) > f( x) . Sedangkan f( x) m em punyai nilai m aksim um lokal

pada dalam bat as

b

≤

x

≤

c

, apabila nilai f( x) pada x= a2. Dengan cara yang sam a

dapat pula k it a t erangk an k onsep m inim um absolut dan m inim um lok al pada gam bar di baw ah. Dengan dem ikian suat u fungsi yang m em punyai t it ik m aksim um kurvanya berbent uk cem bung keat as( convex upw ard) dan fungsi yang m em punyai t it ik m inim um k urvany a berbent uk cem bung k ebaw ah ( conv ex dow nw ard) . Bisa t erj adi bahw a suat u nilai m aksim um lokal dari suat u fungsi lebih kecil dari nilai m inum um lokal dari fungsi t ersebut dalam suat u j arak t ersebut .

f( x) m aksim um

lokal

f( c) m aksim um

lokal

m inim um

lokal

m inim um f( b)

x= b lokal

Apabila f( x) = 0 at au f1( a) t idak t ert ent u j ik a a = 0 , m ak a a m er upakan t it ik kr it is, yait u m aksim um at au m inim um .

2 .3 N ila i Ek st r im

Nilai m aksim um dari fungsi z= f( x,y) dicapai pada pasangan nilai variabel-v ariabel bebas x dan y adalah nilai t erbesar dari fungsi f( x ,y ) dalam suat u lengk ungan dari t it ik ( xo,yo,o) dan nilai m inim um dari z= f( x,y) adalah nilai t erkecil di

lengk ungan dari t it ik ( x1,y1,o) .

Ada beberapa bat asan yang harus kit a perhat ikan unt uk m enget ahui nilai ekst rim suat u fungsi, yakni:

1. Fungsi z= f( x,y) m em punyai nilai m aksim um di ( xo,yo) j ik a t erdapat bilangan –

bilangan posit if S1dan S2 sehingga berlak u :

∀ ( x,y) ∈ H = { ( x,y) | |x- xo| < S1, ( x,y) | |y- yo| < S2 } berlaku f( xo,yo) ≥ f( x,y) .

3. Jika fungsi z= f( x,y) di ( xo,yo) m encapai nilai m inim um at au m inim um m ak a fungsi

z= f( x ,y ) m encapai nilai ekst rim dan t it ik ny a disebut dengan t it ik ekst rim .

4. Misalkan z= f( x ,y ) m erupak an suat u perm uk aan dan andaikan T adalah t it ik pada perm uk aan.

Jika berlaku dz dz

dx T = 0 dan dy T = 0 m ak a T disebut t it ik st asioner pada perm uk aan.

Pandang f suat u fungsi dua peubah yang kont iniu dalam suat u daerah siku em pat t erbuk a H di bidang x y . j ik a ( a,b) suat u t it ik - dalam di dalam H dan j ik a fx( a,b)

dan fy( a,b) ada, m ak a sy arat perlu agar f( a,b) m enj adi suat u nilai ekst rem f adalah

fx( a,b) = fy( a,b) = 0 at au

0

)

,

(

=

∇

f

a

b

Pandang f suat u fungsi dua peubah yang kont iniu yaang m em punyai t urunan parsial pert am a dan k edua y ang k ont iniu j uga dalam suat u daerah sik u em pat t erbuk a Hdi bidang x y . Misalkan ( a,b) suat u t it ik dlam H dengan

0

)

,

(

=

∇

f

a

b

Dan andaikan

∆

=

f

_xx

(

a

,

b

)

f

yy

(

a

,

b

)

−

f

xy2

(

a

,

b

).

Mak a

i. j ika

∆

>

0

dan fx x( a,b) < 0, m aka f( a,b) adalah nilai m aksim um lokal f

ii. j ik a ∆ > 0 dan fx x( a,b) > 0, m aka f( a,b) adalah nilai m inim um lokal f

iii. j ik a

∆

>

0

m ak a f( a,b) adalah buk an suat u nilai ekst rem f iv. j ika

∆

=

0

, m aka uj i ini t ak berkeput usan.

2 .4 La gr a n ge M u lt iplie r

Jika f fungsi t iga peubah x, y, dan z, m em iliki t urunan parsial pert am a t erhadap t iap perubah m ak a suat u sy arat perlu agar f( a,b,c) m enj adi nilai ekst rem f adalah fx( a,b,c) = 0, fy( a,b,c) = 0 dan fz( a,b,c) = 0. Sy arat ini dapat dit ulis dengan

pendek sebagai

∇f( a,b,c) = 0

Tit ik- t it ik ( a,b,c) yang m em enuhi persam aan ini adalah t it ik krit is unt uk f. sem ua t it ik dim ana f m em iliki m aksim um lokal at au m inim um lokal t erm asuk dalam k uk m pulan t it ik k rit is. Nam un dem ik ian, sapert i t elah k it a lihat , t idak sem ua t it ik krit is m em berikan nilai ekst rem .

Dit em ukan nilai ekst r em fungsi dua var iabel F( x,y) = 3x3 + y2 – 9x + 4y . Soal 1: Apabila dim int a unt uk m enent ukan j arak m inim um t it ik P: ( x,y,z ) dari t it ik

asal, dengan sy arat P harus pada perm uk aan z2 = x2y + 4, yait u kit a t ent ukan

BAB I I I PEM BAH ASAN

3 .1 Fu n gsi be r pe r u ba h be ba s le bih da r i sa t u

Suat u fungsi perubah m elibat kan t iga hal: w ilayahnya, D, yait u suat u him punan pasangan t erurut bilangan- bilangan real; j elaj ahnya, R, yait u suat au him punan bilangan real; dan suat u at uran pem adanan yang m em ungkinkan kit a m enet ukan bilangan unik yang m ana dari j elaj ahnya berpadanan dengan t iap pasangan t erurut dalam w ilay ahny a.

Mem ang m ungkin beberapa pasangan t erurut dalam D m em iliki padanan y ang sam a dalam R, t et api t idak m ungk in lebih dari sat u bilangan dalam R berpadanan dengan sat u pasangan t erurut t ert ent u dalam D.

Misalkan f suat u fungsi dua per ubah. Maka f( x,y) , baca “ f( dar i) x,y,” m erupakan suat u bilangan yang unik dalam j elaj ahnya yang m enj adi padanan ( x,y) dalam w ilay ahny a; f( x ,y ) disebut nilai fungsi f di ( x ,y) . perubah x dan y disebut perubah bebas fungsi f it u; j ik a z = f( x ,y ) m ak a z adalah perubah t ak bebasny a, at au perubah t erik at ny a.

Apabila w ilayah t idak dengan j elas dinyat akan dalam defenisi suat u fungsi dua perubah m aka kit a art ikan bahw a w ilayahnya adalah him punan sem ua pasangan t erurut bilangan- bilangan riel( x,y) yang m em buat f( x,y) m ej adi suat u bilangan riel yang unik. Fungsi f suat u fungsi dua perubah x dan y m em bent uk suat u him punan ganda t iga t erurut bilangan- bilangan ( x ,yf( x ,y ) ) , at au ( x ,y,z) dengan z = f( x ,y ) .

Dalam uraian set erusnya, unt uk m udahnya, sering digunakan not asi f( x,y) unt uk m enyat akan fungsi f yang nilainya adalah f( x,y) . Dengan not asi ini dapat segera t erlihat banyaknya perubah bebas dan huruf- huruf yang m enyat akan perubah- perubah it u.

Cont oh 1: Tent ukan lengkungan ket inggian fungsi z = 2

−

2

−

1

y

x

Penyelesaian:

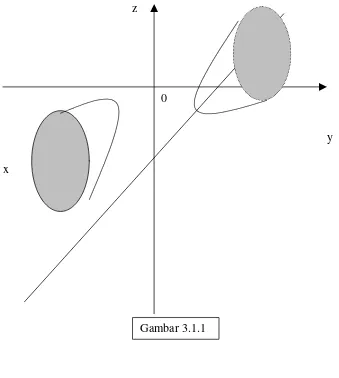
Grafik ini m erupak an bagian at as set engah suat u hiperboloid dua lem bar y ang dit uj uak an pada gam bar 3.1.1 ( dengan a= b= c= 1) . Kit a cari lengkungan- lengkungan dalam bidang xy yang m erupakan proyeksi kurva

perpot ongan perm uk aan z =

x

2

−

y

2

−

1

dengan bidang z = k unt uk

berbagai nilai k negat if. Jik a k it a subsit usikan k unt uk z dalam persam aan lengk ungan k et inggian di bidang x y .

1

1

1

2

2 2

2

=

+

−

+

k

y

k

x

Unt uk t iap nilai k , persam aan ini m eny at ak an suat u hiperbol dalam posisi

st andar. Jadi unt uk k =

3

, hiperbony a adalah

1

4

4

2 2

=

−

y

x

. Kom put asi dapat

diperm udah dengan m em ilih nilai k yang m em berikan k2 + 1 sebagai suat u k uadrat .

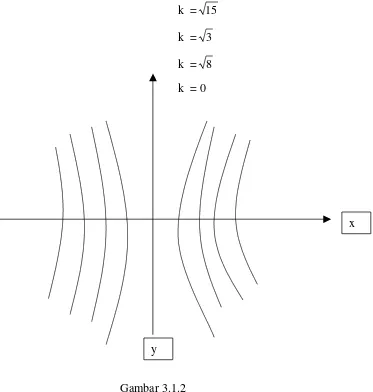
Lengkungan ket inggian unt uk k = 0, k =

3

, k =

8

dan k =

15

diperlihat k an dalam gam bar 3.1.2. Tidak suk ar m em perluas defini k it a at as fungsi sat u perubahan dan fungsi dua perbah unt uk dit erapk an pada fungsi dengan perubah t iga at au lebih.

dalam D , disebut fungsi t iga peubah. Him punan D it u disebut w ilay ah ( daerah defenisi) fungsi t ersebut dan him punan ? j elaj ahnya R ( daerah nilainya) .

x

0

z

[image:6.612.141.480.143.521.2]

y

3 .2 Tu r u n a n Pa r sia l

Jika di dalam f( x,y) nilai y dit ahan agar konst an, m aka f m enj adi fungsi sat u perubah bebas x dan m ungkin dit ent ukan t urunannya t erhadap x dengan m em perlakukan y sebagai konst ant a. Turunan sem acam ini disebut t urunan parsial f

t erhadap x da biasany a dit ulis

x

f

∂

∂

at au fx .

Misalnya, j ika f( x,y) = x2- 3xy + ln( x2+ y2) dit urunk an t erhadap x dengan m em perlakukan y sebagai konst ant a, m aka kit a peroleh nilai t urunan parsial f t erhadap x di t it ik ( x ,y) ,

x

f

∂

∂

f( x,y) = fx( x ,y) = 2x – 3y +

(

2

)

1

2

2

x

y

x

+

[image:7.612.153.526.40.432.2]

Serupa it u pula, t urunan parsial f t erhadap y diperoleh dengan m enurunkannya t erhadap y dan dengan m em perlakukan x sebagai konst ant a.

Gambar 3.1.2

k = 15

k = 8

k = 3

k = 0

x

Turunan ini dit ulis

y

f

∂

∂

at au fy. Sebagai cont oh, j ika f( x,y) = x2- 3xy + ln( x2+ y2)

m aka nilai

y

f

∂

∂

di ( x ,y ) adalah

y

f

∂

∂

f( x,y) = fy( x,y) = – 3y +

(

2

)

1

2

2

y

y

x

+

Turunan parsial m em punyai art i geom et ri yang sederahana. Pandang suat u perm ukaan yang persam aannya z = f( x,y) . bidang y = c m em ot ong perm ukaan ini pada lengk ungan QPR ( gam bar ) dan nilai t urunan parsial f t erhadap x , denagn y bernilai k onst an c, adalah t anj ak an garis singgung pada lengk ungan bidang QPR di t it ik P: ( x , c, f( x ,c) ) . Serupa it u j uga, bidang x = k m em ot ong perm uk aan z = f( x ,y ) pada lengk unagan LPM( gam bar ) dan fy ( k ,y ) adalah t anj ak an garis- singgung pada

lengk ungan bidang LPM ini di t it ik : ( k ,y,f( k ,y) ) .

Con t oh 1 :

volum e V suat u gas t erent u m em iliki hubungan dengan t em perat urnya T dan t ekanannya P m enurut hukum gas

PV = 10 T

Dengan V diuk ur denagn inchi k ubik , T dalam deraj at dan P dalam pon per inci k uadrat . Jik a v olum e gas it u diusahak an k onst an 200 inci k ubik , berapak ah laj u perubahan sesaat t ek anan t erhadap t em perat urny a?

Penyelesaian:

Persam aan gas t ersebut dapat dit ulis P = 10 T/ V. laj u perubahan P t erhadap T, j ik a V k onst an adalah

V

T

P

10

=

∂

∂

(a)

(b)

z

z

y

y

x

x

M

L

P k

c

Q

R

Karena V = 200, m ak a laj u perubahan t ek anan t erhadap t em perat ur adalah 10/ 200 = 0.05.

Con t oh 2 :

Jika f( x,y,z) = xy + 2 yz + 3 zx, t ent ukan fx, fy, dan fz.

Penyelesaian:

Unt uk m endapat fx k it a pandang y dan z sebagai k onst ant a dan k it a t urunk an

f t erhadap perubah x . j adi fx( x,y,z) = y + 3z,

Unt uk m em peroleh fy, k it a perlak uk an x dan z sebagai k onst ant a f dit urunk an

t erhadap y ,

fy( x,y,z) = x + 2z

serupa it u pula

fz( x,y,z) = 2y+ 3x

Con t oh 3 :

Suat u t angk i logam dengan at asny a t erbuk a m uat 256 k ak i k ubik cairan. Bagaim ana ukuran t angki t ersebut yang m em erlukan sesedikit bahan pada pem buat annya?

Penyelesaian:

V = 256 k ak i k ubik

x .y .z = 256

z =

y

x

.

256

L = 2x y + 2y z + x z

= 2x y + 2y

y

x

.

256

+ x

y

x

.

256

L = 2xy +

x

512

+

y

256

x

Sy arat :

*

dx

dL

= 0

2y -

512

₂

x

= 0

2y =

512

₂

x

y =

256

₂

x

………..( 1)

*

dx

dL

= 0

2x -

256

₂

y

= 0

2x =

256

₂

y

x =

128

₂

y

………..( 2)

Subsit usi pers( 1) ke ( 2) :

* y =

256

₂

x

= 2

2

)

128

(

256

y

= ₂

4

)

128

(

256

y

=

64

4

y

y3 = 64 y = 4 kaki

* y = 4

→

x =

128

₂

y

=

4

2

128

x = 8 kaki

* z =

xy

256

=

4

.

8

256

=

32

256

= 8 k ak i

Ukurannya: panj ang = 8 kaki Lebar = 8 kaki Tinggi = 4 kaki m aka: L = 2xy + 2yz + xz

= 2( 8) ( 4) + ( 2) ( 4) ( 8) + ( 8) ( 8) = 64 + 64 + 64

= 192 k ak i persegi

Con t oh 4 :

Penyelesian:

* Sin ( 180-θ) =

y

b

Sin θ =

y

b

b = y Sin θ

* Cos ( 180-θ) =

y

a

- Cos θ =

y

a

a = - y cos θ

lebar = 12 inchi

x + 2y = 12

x = 12- 2y

m ak a:

L = p.l = ( x + a) b = ( 12 – 2y – y cos θ) y sin θ = 12 y sin θ - 2y2sin θ - y2sin θcos θ

sy arat :

*

dy

dL

= 0

dy

d

12 y sin θ - 2y2sin θ - y2sin θcos θ = 0

12 sin θ - 4y sin θ - 2ysin θcos θ = 0 sin θ ( 12- 4 y – 2y cos θ) = 0

12- 4 y – 2y cos θ = 0 4y – 2y cos θ = 12 2y – y cos θ = 6 y( 2 + cos θ) = 6

y =

θ

cos

2

6

+

………( 3)

*

θ

d

dL

= 0

y

b

a

u

θ

θ

d

d

12 y sin θ - 2y2sin θ - y2sin θcos θ = 0

12 y cos θ - 2y2 cos θ + y2sin θ - y2cos2 θ = 0 ( 12 cos θ - 2ycos θ + ysin2θ - ycos2 θ) y = 0 y = 0 t idak m ungk in

12 cos θ - 2ycos θ + ysin2θ - ycos2 θ = 0 12 cos θ - 2ycos θ + y ( 1- cos2 θ) - y cos2 θ = 0 12 cos θ - 2ycos θ + y - y cos2 θ - y cos2 θ = 0

12 cos θ - 2ycos θ + y - 2y cos2 θ = 0 ………( 4)

subsit usikan persam aan ( 3) k e persam aan ( 4)

12 cos θ - 2

θ

cos

2

6

+

cos θ +

2

cos

θ

6

+

- 2

2

cos

θ

6

+

cos

2 _θ

= 0

θ

θ

cos

2

cos

12

+

-

2

cos

θ

6

+

+

θ

θ

cos

2

cos

12

2

+

=

θ

θ

θ

cos

2

)

cos

2

(

cos

12

+

+

12 cosθ - 6 + 12 cos2θ = 24 cos θ + 12 cos2θ 12 cosθ = - 6

cosθ =

-2

1

θ = 1200

besar sudut t alang t ersebut adalah 1200 m aka ukuran- ukurannya:

* y =

θ

cos

2

6

+

y =

2

1

2

6

+

y = 4 kaki * x = 12 – 2y

= 12- 2( 4) x = 4 kaki

Con t oh 5 :

Tent ukan nilai m inim um dari:

f( x,y) dengan kendala g( x,y) = xy – 3 = 0 Penyelesain:

Gradien f dan g adalah v ek t or :

*

v

f( x,y) = fx( x,y) i + fy( x,y) j

= 2xi + 2yj

*

v

g( x,y) = gx( x,y) i + gy( x,y) j

= yi + xj

m ak a:

fx( x,y) = λ gx( x,y)

λ =

y

x

2

………..( 5)

* fx( x,y) = λ gx( x,y)

2y = λx

λ =

x

y

2

………..( 6)

sehingga persam aan 5 dan 6:

λ1 = λ2

y

x

2

=

x

y

2

2x2 = 2y2………..( 7)

subsit usi persam aan ( 7) : x y – 3 = 0

xx = 3 x2 = 3

x =

3

, y =

3

m ak a nilai m inim um f( x,y) = x2 + y2

= (

3

)2 + (

3

)2

= 3 + 3 = 6

Con t oh 6 :

Bagaim ana uk uran suat u k ot ak segi em pat t erbuk a at asny a y ang m em puny ai v olum e m ak sim um apabila luas perm uk aan 48?

Penyelesaian:

x

y

V= x y z

L = x y + 2x z + 2 y z = 48 ………( 8) * Vx( x, y, z) = y z

Vy( x, y, z) = x z

Vz( x, y, z) = x z

* Lx( x, y, z) = y + 2z

Ly( x, y, z) = x + 2z

Lz( x, y, z) = 2x + 2y

Mak a:

* Vx( x, y, z) = λ Lx( x, y, z)

y z = λ( y + 2z)

λ1 =

z

y

yz

2

+

………( 9)

* Vy( x, y, z) = λ Ly( x, y, z)

x z = λ( x + 2z)

λ2 =

z

x

xz

2

+

………( 10)

* Vz( x, y, z) = λ Lz( x, y, z)

x y = λ( 2x + 2y)

λ3 =

y

x

xy

2

2

+

………( 11)

Persam aan( 9) ( 10) : λ1 = λ2

z

y

yz

2

+

=

z

x

xz

2

+

xyz + 2yz2 = xyz + 2xz2 2yz2 = 2xz2

y = z ………( 12) dari persam aan ( 10) ( 11) :

λ2 = λ3

z

x

xz

2

+

=

y

x

xy

2

2

+

2x2z + 2x y z = x2y + 2 xyz 2x2z = x2y

z =

2

1

y ………( 13)

dari persam aan ( 12) ( 13) :

z =

2

1

y =

2

1

x ………( 14)

x.x + 2x.

2

1

x + 2x.

2

1

x = 48

x2 + x2 + x2 = 48

3x2 = 48 → x = 4 m ak a didapat : y = x = 4

z =

2

1

x =

2

1

4 = 2

uk uran k ot ak adalah: x = panj ang = 4 sat uan y = lebar = 4 sat uan z = t inggi = 2 sat uan sehingga :

Vm aksim um = x y z = 4.4.2 = 16 sat uan v olum e

BAB I V

KESI M PULAN D AN SARAN

4 .1 Ke sim pu la n

Berdasarkan hasil yang diperoleh dam pem bahasan BAB I I I dapat kit a lihat bahw a geom et ri sangat berperan dalam m enent uk an nilai opt im al dari dua perubahan at au lebih suat u fungsi. Dalam m enent ukan nilai opt im al t ersebut , digunak an berbagai m et ode sepert i m et ode Lagrange selain daripada it u penulis j uga m enggunakan t urunan parsial unt uk m ancari nilai opt im al dari volum e dan luas, sepert i cont oh- cont oh di at as.

4 .2 Sa r a n

Kit a bisa m em ak ai t eori- t eori di at as dalam k ehidupan sehari- hari, k arena apa yang dipaparkan diat as it u sangat berhubungan erat dengan apa yang kit a gunakan dalam m elakukan akt ivit as kit a. Dan sangat lah pent ing bagi kit a unt uk m enget ahui t ent ang opt im isasi supay k it a t idak m engalam i k erugian.

D AFTAR PUSTAKA

1. Edw in J. Purcell, kalkulus dan geom et ri analit is, edisi ke 3, j ilid 2, penerbit Erlangga, Jak art a.