i
KARAKTERISTIK PERMAINAN ELLO YANG DAPAT DIMENANGKAN
FITRI DURROTUN NAFISAH
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
ii
ABSTRAK
FITRI DURROTUN NAFISAH. Karakteristik Permainan ELLO yang Dapat Dimenangkan. Dibimbing oleh TEDUH WULANDARI MAS’OED dan FARIDA HANUM.
iii
ABSTRACT
FITRI DURROTUN NAFISAH. Characteristics of winnable games of ELLO. Supervised by TEDUH WULANDARI MAS’OED dan FARIDA HANUM.
iv
KARAKTERISTIK PERMAINAN ELLO YANG DAPAT DIMENANGKAN
FITRI DURROTUN NAFISAH
Skripsi
sebagai salah satu syarat untuk memperoleh gelar
Sarjana Sains pada
Departemen Matematika
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
INSTITUT PERTANIAN BOGOR
v
Judul Skripsi : Karakteristik Permainan ELLO yang Dapat Dimenangkan
Nama
: Fitri Durrotun Nafisah
NIM
: G54070057
Menyetujui
Pembimbing I,
Pembimbing II,
Teduh Wuland
ari Mas’oed, M.Si.
Dra. Farida Hanum, M.Si.
NIP 19740915 199903 2 001
NIP 19651019 199103 2 002
Mengetahui:
Ketua Departemen,
Dr. Berlian Setiawaty, M.S.
NIP 19650505 198903 2 004
vi
KATA PENGANTAR
Puji dan Syukur penulis panjatkan ke hadirat Allah SWT atas segala rahmat dan karunia yang telah diberikan hingga karya ilmiah ini dapat diselesaikan. Penyusunan karya ilmiah ini tidak lepas dari bantuan beberapa pihak. Oleh karena itu, penulis mengucapkan terima kasih yang sebesar-besarnya kepada :
1. Keluarga besar, khususnya Mama dan Appa, atas kesabaran, doa dan nasihat-nasihatnya, untuk kakak tercinta, Teh Nina, terima kasih atas dukungan dan doanya dari kejauhan, 2. Teduh Wulandari Mas’oed, M.Si selaku dosen pembimbing I yang telah memberikan ilmu
yang sangat bermanfaat dan kesabaran dalam membimbing penulis,
3. Dra. Farida Hanum, M.Si selaku dosen pembimbing II yang telah memberikan ilmu serta tuntunan dalam menyusun karya ilmiah ini,
4. Drs. Prapto Tri Supriyo, M.Kom. selaku dosen penguji yang telah memberikan ilmunya, 5. seluruh Dosen Departemen Matematika, terima kasih atas ilmu yang telah diberikan kepada
penulis,
6. staf Departemen Matematika: Bapak Yono, Ibu Susi, Ibu Ade, Bapak Bono, Mas Hery, Bapak Deni dan Bapak Epul, atas bantuan dan dukungannya,
7. teman-teman terdekat: Lingga, Ima, Atik, Dini, Yuni, Siva, Dian, dan PMR sixteen, terima kasih telah menjadi teman yang baik bagi penulis,
8. teman-teman Matematika 44: Anis, Ruhi, Siska, Fikri, Yuyun, Lugi, Diana, Yanti, Lilis, Ririh, Eka, Aswin, Wahyu, Aqil, Aze, Wewe, Nurul, Tanto, Rachma, Melon, Lili, Tita, Cita, Nchel, Tendi, Ali, Lina, Tante, Deva, Uchu, Titi, Ayum, Sri, Yuli, Zae, Dian, Eni, Ndep, Yogi, Chopa, Ayung, Sari, Endro, Fajar, Kodok, Masay, Denda, Gan gan, Dika, Fani, Iksan, Della, Pandi, Abe, Tias, Arina, Imem, Nadiroh, Rofi, Indin, Iam, Olih, Ipul, Nurus, Lukman, Puying, Naim, atas kebersamaannya selama kurang lebih 3 tahun,
9. kakak-kakak Matematika 43 dan 42, atas saran dan nasihatnya, 10. adik-adik matematika 45, atas doa dan dukungannya,
11. akang, teteh, sareng rai-rai di UKM LISES Gentra Kaheman atas kehangatan dan kebersamaannya,
12. semua pihak yang telah membantu dalam penyusunan karya ilmiah ini.
Semoga tulisan ini dapat bermanfaat bagi dunia ilmu pengetahuan khususnya dalam bidang matematika.
Bogor, Oktober 2011
vii
RIWAYAT HIDUP
Penulis dilahirkan di Bogor pada tanggal 13 Mei 1989 dari pasangan Bapak Lili Sutisna dan Ibu Latifah. Penulis merupakan anak kedua dari dua bersaudara,
Penulis menempuh pendidikan formal di SDN Panaragan 3 Bogor dan lulus pada tahun 2001. Tahun 2004 penulis lulus dari SMP Negeri 4 Bogor. Tahun 2007 penulis lulus dari SMA Negeri 1 Bogor dan melanjutkan pendidikan ke Institut Pertanian Bogor. Penulis diterima di Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, melalui jalur USMI.
viii
DAFTAR ISI
Halaman
DAFTAR GAMBAR ... ix
I PENDAHULUAN ... 1
1.1 Latar Belakang ... 1
1.2 Tujuan ... 1
II LANDASAN TEORI ... 1
2.1 Definisi-Definisi Dasar pada graf ... 1
2.2 Permainan ELLO ... 3
III PEMBAHASAN ... 7
IV SIMPULAN DAN SARAN ... 17
4.1 Simpulan ... 17
4.2 Saran ... 17
ix
DAFTAR GAMBAR
Halaman
1 Graf G( , )V E ... 1
2 Graf J tak terhubungkan ... 2
3 H subgraf dari graf G ... 3
4 Graf lengkap ber-order 4 ... 3
5 Graf G setelah simpul x diambil ... 3
6 Permainan ( , )G c ... 4
7 Graf G setelah simpul v diambil ... 4
8 Graf G setelah simpul v dan u diambil ... 4
9 Graf G setelah simpul v, u dan x diambil ... 4
10 Graf G setelah simpul w diambil ... 5
11 Graf G setelah simpul x diambil ... 5
12 Graf G setelah simpul x dan u diambil ... 5
13 Graf G setelah simpul x, u dan v diambil ... 5
14 Graf G yang tidak dapat dimenangkan ... 5
15 Graf G setelah simpul u diambil ... 5
16 Graf G setelah simpul u dan v diambil ... 6
17 Graf G setelah simpul u, v dan wdiambil ... 6
18 Graf G setelah simpul u, v dan x diambil ... 6
19 Graf G setelah simpul x diambil ... 6
20 Graf G setelah simpul x dan v diambil ... 6
21 Graf G setelah simpul x, v dan u diambil ... 6
22 Graf G setelah simpul x dan w diambil ... 6
23 Permainan (K c5, ) pada suatu graf lengkap ... 9
24 Graf K5 setelah simpul u diambil ... 9
25 Graf K5 setelah simpul u dan y diambil ... 10
26 Graf K5 setelah simpul u, y dan x diambil ... 10
27 Graf K5 setelah simpul u, y, x dan v diambil ... 10
28 Permainan ( , )G c ... 12
29 Permainan ( , )G c ... 12
30 Permainan ( , )G c yang memenuhi kondisi keseimbangan ... 16
31 Permainan ( , )G c setelah simpul v diambil ... 16
I PENDAHULUAN
1.1 Latar Belakang
Teori graf pertama kali diperkenalkan oleh matematikawan asal Swiss, yaitu Leonard Euler, pada tahun 1736. Euler menemukan penyelesaian untuk permasalahan jembatan Konigsberg (Konigsberg bridge problem). Sejak saat itu, Euler dijuluki The Father of Graph Theory.
Seiring dengan perkembangannya, teori graf tidak hanya dapat menyelesaikan permasalahan transportasi dan riset operasi, tetapi juga mulai dikembangkan di bidang kimia, fisika dan bahkan permainan. Permainan yang pertama kali dikembangkan dari teori graf adalah permainan puzzle oleh W. R. Hamilton pada tahun 1856. Permasalahan graf pada permainan ini adalah bagaimana membuat perjalanan ke setiap sisi dengan melewati setiap simpul tepat satu kali.
Pada tahun 1995, Tiger Electronics memproduksi permainan dengan array berukuran 5 × 5 yang disebut dengan permainan Lights Out. Cara memainkan permainan ini adalah memilih suatu simpul (misalnya simpul x) sehingga warna simpul x dan simpul-simpul yang bersebelahan dengan x berubah warna. Tujuan dari permainan ini adalah menjadikan semua simpul pada array
tersebut memiliki warna yang sama. (Anderson & Feil 1998)
Perkembangan dari permainan Lights Out adalah permainan Elimination-Lit Lights Out (ELLO) yang diperkenalkan pada tahun 2007. Perbedaan antara permainan ELLO dan Lights Out adalah adanya proses penghapusan simpul yang dipilih pada permainan ELLO.
Untuk permainan ELLO yang diberikan, permainan diklasifikasikan menjadi dua, yaitu permainan yang dapat dimenangkan (winnable) dan permainan yang tidak dapat dimenangkan (unwinnable). Terdapat beberapa ciri permainan yang dapat dimenangkan. Ciri-ciri tersebut biasa disebut dengan karakteristik permainan yang dapat dimenangkan. Karya ilmiah ini akan membahas karakteristik graf 2 warna yang dapat dimenangkan dengan rujukan utama Craft et al. (2007).
1.2 Tujuan
Tujuan dari penulisan karya ilmiah ini adalah mengklasifikasikan graf 2 warna yang diberikan menjadi permainan yang dapat dimenangkan dan permainan yang tidak dapat dimenangkan.
II LANDASAN TEORI
2.1 Definisi-Definisi Dasar pada Graf Berikut diberikan definisi-definisi dasar pada graf.
Definisi 1 (Graf)
Suatu graf G adalah pasangan terurut ( , )V E dengan V himpunan takkosong dan berhingga dan E himpunan pasangan takterurut yang menghubungkan elemen-elemen V. Graf G dinotasikan dengan
( , ).
G V E Elemen V disebut simpul (vertex, node) sedangkan elemen E disebut sisi (edge). Himpunan dari simpul-simpul pada graf G dinotasikan dengan V G( ), sedangkan himpunan dari sisi-sisi pada graf
G dapat dinotasikan dengan E G( ).
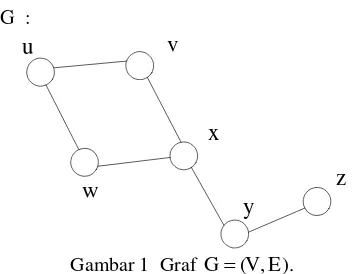
(Foulds 1992) Berikut ini adalah contoh graf dengan 6 simpul dan 6 sisi.
G :
u
v
w
x
y
z
Gambar 1 Graf G( , ).V E
Himpunan simpul pada graf pada Gambar 1 adalah V G( ){ , , , , , }.u v w x y z Himpunan sisi pada graf pada Gambar 1 adalah
( ) {{ , },{ , },{ , },{ , },{ , },{ , }}. E G u v u w v x w x x y y z Definisi 2 (Order dan Size)
2
sisi pada graf G disebut size dari Gdan dinotasikan dengan |E G( ) | .
(Chartrand & Oellermann 1993)
Untuk graf pada Gambar 1, nilai | ( ) | 6V G dan |E G( ) | 6.
Definisi 3 (Incident dan Adjacent)
Misalkan diberikan graf G( , )V E . Jika { , } ( )
e u v E G dengan u v V G, ( ), maka u dikatakan adjacent dengan v di G dan e dikatakan incident dengan u dan .v
(Chartrand & Oellermann 1993) Untuk graf pada Gambar 1, misalkan
{ , } ( ),
e u v E G maka u dikatakan adjacent dengan v dan e incindent dengan u dan v. Definisi 4 (Neighborhood)
Misalkan diberikan grafG( , )V E dan ( ).
vV G Neighborhood dari v atau N v( ) didefinisikan dengan
( ) ( ) | ( ) .
N v uV G uvE G
(Chartrand & Oellermann 1993) Untuk graf pada Gambar 1, neighborhood dari simpul u adalah simpul
v
dan w, sehingga( ) { , }. N u v w Definisi 5 (Derajat)
Derajat atau degree (dinotasikan dengan deg v atau d v( )) merupakan banyaknya simpul yang adjacent dengan v, untuk
( ). vV G
(Chartrand & Oellermann 1993) Untuk graf pada Gambar 1, derajat untuk setiap simpul, yaitu :
deg 2 deg 2
deg 2
deg 3 deg 2 deg 1
u v w x y z
Definisi 6 (Walk)
Suatu walk pada graf G( , )V E adalah suatu barisan simpul dan sisi dari graf G dengan bentuk :
1 1 2 2 2 3 3 1
{ ,{ , },v v v v,{ , }, ,...,{v v v vn, }, }vn vn dan dapat ditulis sebagai { ,v v1 2,..., }vn atau
1, 2,..., n
v v v . Walk yang menghubungkan v1
dan vn dikatakan tertutup jika v1vn. Jika
1 n
v v maka walk tersebut dikatakan terbuka. (Foulds 1992) Untuk graf pada Gambar 1, contoh walk terbuka yang berawal dari simpul u dan berakhir pada simpul z adalah walk
{ ,{ , }, ,{ , }, ,{ , }, ,{ , }, }u u v v v x x x y y y z z dan contoh walk tertutup yang berawal dan berakhir pada simpul u adalah walk { ,{ , }, ,{ , }, ,{ , }, ,{ , }, }.u u v v v x x x y y y u u
Definisi 6 (Path)
Path pada suatu graf G adalah suatu walk dengan semua simpulnya berbeda.
(Foulds 1992) Untuk graf pada Gambar 1, salah satu contoh path yang menghubungkan simpul u dan z adalah u v x y z, , , , .
Definisi 7 (Graf terhubungkan dan tak terhubungkan)
Graf G dikatakan terhubungkan jika setiap 2 simpul yang berbeda pada G dihubungkan oleh suatu path dan dikatakan tak terhubungkan jika pada 2 simpul yang berbeda, tidak ada path yang menghubungkan kedua simpul tersebut.
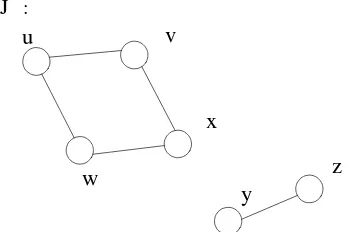
(Foulds 1992) Graf pada Gambar 1 merupakan graf terhubungkan. Berikut adalah contoh graf takterhubungkan.
J :
u
v
w
x
y
z
Gambar 2 Graf J tak terhubungkan. Definisi 8 (Subgraf)
Misal diberikan graf G dan H. Graf H disebut subgraf dari G jika
V H
( )
V G
( )
danE H
(
)
E G
( ).
(Chartrand & Oellermann 1993) Misalkan V H( ){ , , , }u w x y V G( ) dan
( ) {{ , }} ( ),
3
subgraf dari graf G pada Gambar 1. Berikut adalah gambar subgraf H dari graf G.
H :
u
w
x
y
Gambar 3 H subgraf dari graf G. Definisi 9 (Graf Lengkap)
Graf berorder p sehingga setiap dua simpulnya adjacent disebut graf lengkap dan dinotasikan dengan K p.
(Chartrand & Oellermann 1993) Berikut ini adalah contoh graf lengkap ber-order 4.
4 K :
u
w
x
v
Gambar 4 Graf lengkap ber-order 4. Definisi 10 (Penghapusan Simpul)
Misalkan diberikan graf G dan v V G ( ). Jika v adalah simpul pada graf G maka ,
G v merupakan subgraf dari G yang
terbentuk dengan menghapus
(menghilangkan) simpul v dari graf G. Penghapusan simpul pada graf selalu mengakibatkan penghapusan semua sisi yang incident dengan simpul tersebut.
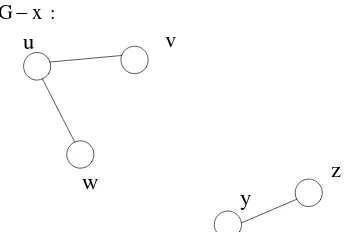
(Deo 1974) Untuk graf pada Gambar 1, penghapusan simpul x mengakibatkan sisi { , },v x { , }w x dan { , }x y terhapus. Berikut adalah graf G setelah penghapusan simpul x.
G x :
u
v
w
y
z
Gambar 5 Graf G setelah simpul x diambil. 2.2 Permainan ELLO
Permainan Elimination-Lit Lights Out (ELLO) dimainkan pada graf dengan inisialisasi pewarnaan 2 warna
: ( ) {hijau, merah}.
c V G Cara memainkan
permainan ini adalah dengan memilih dan mengambil satu per satu simpul pada permainan sedemikian sehinga pengambilan simpul tersebut akan mengakibatkan simpul-simpul yang adjacent dengan simpul-simpul tersebut berubah warna. Pada saat diambil, simpul harus berwarna hijau. Tujuan dari permainan ini adalah mengambil seluruh simpul pada permainan.
Berikut adalah langkah-langkah dalam memainkan permainan ini.
1 Pilih satu simpul berwarna hijau, misalkan simpul x dan hapus simpul tersebut dari graf.
2 Neighborhood dari simpul x diubah warnanya.
3 Graf G diubah menjadi Gx.
4 Prosesnya terus berulang hingga simpul tidak tersisa atau simpul yang tersisa berwarna merah.
Berikut definisi tambahan untuk istilah-istilah yang digunakan pada karya ilmiah ini. Definisi 11 (Permainan (G,c))
Permainan ELLO dari graf G dengan pemetaan warna awal simpul adalah
: ( ) {hijau, merah}
c V G dinotasikan
dengan ( , ).G c Simpul hijau memiliki nilai ( ) 0
c v dan simpul merah memiliki nilai ( ) 1.
c v
(Craft et al.2007)
4
G :
u
w
x
v
Gambar 6 Permainan ( , ).G c
Nilai c v( ) untuk setiap simpul pada Gambar 6 adalah:
( ) 1 ( ) 0 ( ) 0 ( ) 0 c u c v c w c x
Definisi 12 (Strategi)
Permainan ( , )G c dimainkan dengan mengambil satu per satu simpul pada graf G. Susunan simpul yang diambil dalam permainan ini disebut strategi dan dituliskan dengan ( ,v v v1 2, 3,...vp).
(Craft et al. 2007) Pada Gambar 6, salah satu strategi yang dapat digunakan adalah ( , , , ).v u w x
Definisi 13 (Menang dan kalah)
Pada akhir permainan, jika simpul tidak tersisa, maka permainan dikatakan menang. Jika simpul yang tersisa berwarna merah, maka permainan dikatakan kalah.
(Craft et al. 2007) Definisi 14 (Strategi menang)
Diberikan permainan ( , )G c dengan strategi . Strategi dikatakan strategi menang jika susunan simpul pada dapat memenangkan permainan ( , ).G c
(Craft et al. 2007) Definisi 15 (Permainan yang dapat dimenangkan dan tidak dapat dimenangkan)
Permainan ( , )G c dapat dimenangkan jika terdapat setidaknya satu strategi menang. Permainan ( , )G c dikatakan tidak dapat dimenangkan jika tidak memiliki strategi menang.
(Craft et al.2007)
Berikut adalah contoh permainan yang dapat dimenangkan dan permainan yang tidak dapat dimenangkan.
Untuk permainan ( , )G c pada Gambar 6, terdapat beberapa kemungkinan pengambilan simpul yang pertama kali, yaitu :
1 Kasus 1
Jika simpul yang diambil pertama kali adalah simpul u, maka strategi yang digunakan bukan strategi menang, karena simpul u tidak berwarna hijau.
2 Kasus 2
Jika simpul yang diambil pertama kali adalah simpul v, maka simpul u, w, dan x berubah warna sehingga diperoleh graf sebagai berikut.
G v :
u
w
x
Gambar 7 Graf G setelah simpul v diambil. Simpul kedua yang dapat diambil adalah simpul u. Pengambilan simpul u mengakibatkan simpul x berubah warna sehingga diperoleh graf sebagai berikut.
G v u :
w
x
Gambar 8 Graf G setelah simpul v dan u diambil.
Simpul ketiga yang dapat diambil adalah simpul x. Pengambilan simpul x mengakibatkan simpul w berubah warna sehingga diperoleh graf sebagai berikut.
G v u x:
w
Gambar 9 Graf G setelah simpul v, u, dan x diambil
Simpul keempat yang diambil adalah simpul w sehingga tidak ada simpul yang tersisa. Strategi yang digunakan, yaitu
( , , , ),v u x w
5
3 Kasus 3
Jika simpul yang diambil pertama kali adalah simpul w, maka simpul v dan x berubah warna sehingga diperoleh graf sebagai berikut.
Gw:
u
x
v
Gambar 10 Graf G setelah simpul w diambil.
Simpul yang tersisa berwarna merah, sehingga strategi yang digunakan bukan strategi menang.
4 Kasus 4
Jika simpul yang diambil pertama kali adalah simpul x, maka simpul u, v dan w berubah warna sehingga diperoleh graf sebagai berikut.
G x :
u
w
v
Gambar 11 Graf G setelah simpul x diambil.
Simpul kedua yang dapat diambil adalah simpul u. Pengambilan simpul u mengakibatkan simpul v berubah warna sehingga diperoleh graf sebagai berikut.
G x u :
w
v
Gambar 12 Graf G setelah simpul x dan u diambil.
Simpul ketiga yang dapat diambil adalah simpul v. Pengambilan simpul v mengakibatkan simpul w berubah warna sehingga diperoleh graf sebagai berikut.
G x u v :
w
Gambar 13 Graf G setelah simpul x, u, dan v diambil.
Simpul yang diambil keempat adalah simpul w sehingga tidak ada simpul yang tersisa. Strategi yang digunakan, yaitu
( , , , ),x u v w
merupakan strategi menang bagi permainan ( , )G c pada Gambar 6.
Dari uraian terlihat permainan ( , )G c pada Gambar 6 memiliki 2 strategi menang, maka permainan ( , )G c merupakan permainan yang dapat dimenangkan.
Berikut adalah contoh permainan yang tidak dapat dimenangkan.
G :
u
w
x
v
Gambar 14 Graf G yang tidak dapat dimenangkan.
Terdapat beberapa kemungkinan pengambilan simpul yang pertama untuk permainan ( , )G c pada Gambar 14, yaitu : 1 Kasus 1
Jika simpul yang diambil pertama kali adalah simpul u, maka simpul v dan w berubah warna sehingga diperoleh graf sebagai berikut.
G u :
w
x
v
6
Simpul kedua yang diambil adalah simpul v, maka simpul w dan x berubah warna sehingga diperoleh graf sebagai berikut.
G u v :
w
x
Gambar 16 Graf G setelah simpul u dan v diambil.
1.1 Jika simpul ketiga yang diambil adalah simpul w, maka simpul x berubah warna sehingga diperoleh graf sebagai berikut.
G u v w :
x
Gambar 17 Graf G setelah simpul u, v, dan w diambil.
Simpul yang tersisa berwarna merah, sehingga strategi ( , , , )u v w x bukan strategi menang.
1.2 Jika simpul ketiga yang diambil adalah simpul x, maka simpul w berubah warna, sehingga diperoleh graf sebagai berikut.
G u v x :
w
Gambar 18 Graf G setelah simpul u, v, dan x diambil.
Simpul yang tersisa berwarna merah, sehingga strategi ( , , , )u v x w bukan strategi menang.
2 Kasus 2
Jika simpul yang diambil pertama kali adalah simpul x, maka simpul u, v, dan w berubah warna sehingga diperoleh graf sebagai berikut.
G x :
u
w
v
Gambar 19 Graf G setelah simpul x diambil.
2.1 Jika simpul kedua yang diambil adalah simpul v, maka simpul u dan w berubah
warna, sehingga diperoleh graf sebagai berikut.
G x v :
u
w
Gambar 20 Graf G setelah simpul x dan v diambil.
Simpul ketiga yang diambil adalah simpul u, karena simpul u berwarna hijau, sehingga diperoleh graf sebagai berikut.
G x v u :
w
Gambar 21 Graf G setelah simpul x, v, dan u diambil.
Simpul yang tersisa berwarna merah, sehingga strategi ( , , , )x v u w bukan strategi menang.
2.2 Jika simpul kedua yang diambil adalah simpul w, maka simpul v berubah warna, sehingga diperoleh graf sebagai berikut.
G x w :
u
v
Gambar 22 Graf G setelah simpul x dan w diambil.
Semua simpul yang tersisa berwarna merah, sehingga baik strategi
( , , , )x w v u
atau ( , , , )x w u v bukan strategi menang.
3 Kasus 3
Jika simpul v atau w diambil pertama kali, maka strategi yang digunakan bukan strategi menang, karena kedua simpul tersebut berwarna merah.
Dari uraian di atas, permainan ( , )G c pada Gambar 14 tidak dapat dimenangkan karena permainan tersebut tidak mempunyai strategi menang.
7
Definisi 16 (Predegree)
Diberikan permainan ( , )G c dengan strategi . Banyaknya simpul yang adjacent dengan v yang telah mendahului v pada strategi disebut predegree dari v. Predegree dari simpul v dinotasikan dengan
( , ) G
d v atau d( , ) v .
(Craft et al.2007)
Pada Gambar 6, permainan ( , )G c yang dimainkan dengan strategi ( , , , )v u x w memiliki nilai predegree untuk setiap simpul sebagai berikut.
( , ) 1 d u
( , ) 0 d v
( , ) 2 d w
( , ) 2 d x
Simpul yang diambil pertama kali, yaitu simpul v, memiliki nilai predegree 0, karena tidak ada simpul yang adjacent dengan simpul v yang telah diambil sebelumnya. Simpul kedua yang diambil, yaitu simpul u, memiliki nilai predegree 1 karena terdapat 1 simpul yang adjacent dengan simpul u yang telah diambil sebelumnya, yaitu simpul v. Simpul ketiga yang diambil, yaitu simpul x, memiliki nilai predegree 2 karena terdapat 2 simpul yang adjacent dengan simpul x yang telah diambil sebelumnya, yaitu simpul u dan v. Simpul yang keempat diambil, yaitu simpul w, memiliki nilai predgree 2, karena terdapat 2 simpul yang adjacent dengan simpul w yang
telah diambil sebelumnya, yaitu simpul x dan v.
Definisi 17 (Kongruensi Modulo)
Misalkan n adalah bilangan intejer positif dan n1. Jika a dan b adalah bilangan bulat, maka a disebut kongruen ke b modulo n, ditulis ab(mod )n apabila n membagi (ab). Bilangan bulat n disebut modulus dari kongruensi.
(Grimaldi 1994) Salah satu contoh kongruensi modulo yaitu
249(mod 5) karena 24 9 15 3.5. Definisi 18 (Kondisi Seimbang)
Diberikan permainan ( , )G c dari graf G dengan p simpul, q sisi dan simpul hijau. Permainan ( , )G c dikatakan memenuhi kondisi keseimbangan jika dan hanya jika
(mod 2) p q
.
(Craft et al.2007) Untuk permainan pada Gambar 6, permainan ( , )G c memiliki 4 simpul, 5 sisi, dan 3 simpul hijau, sehingga p4, q5, dan
3. Dari nilai-nilai tersebut dapat dilihat bahwa permainan ( , )G c memenuhi kondisi keseimbangan.III PEMBAHASAN
Karya ilmiah ini membahas proposisi, akibat dan teorema yang memberikan karakteristik permainan ( , )G c pada graf G yang dapat dimenangkan.
Proposisi 1
Misalkan G adalah graf, ( , )G c adalah graf G dengan pewarnaan c, dan adalah strategi pada permainan ( , ).G c Strategi dikatakan strategi menang bagi permainan
( , )G c jika dan hanya jika d( , ) v c v( ) bernilai genap untuk setiap simpul yang terdapat pada strategi .
Bukti :
Misalkan v adalah simpul yang diambil pada strategi . Predegree dari simpul v
merupakan banyaknya perubahan warna yang terjadi pada simpul .v
Simpul v yang berwarna merah harus berubah warna sebanyak m kali, dengan m adalah bilangan ganjil sehingga m2k1, dengan kZ, agar v berubah warna menjadi hijau saat diambil pada strategi .
( , ) ( ) ( ) d v c v m c v
(2k 1) 1
2k 2
Dapat dilihat bahwa untuk c v( )1, predegree d( , ) v bernilai ganjil, sehingga
( , ) ( )
d v c v bernilai genap.
8
dengan kZ, agar v berwarna hijau saat diambil pada strategi .
( , ) ( ) ( ) d v c v n c v
2k 0
2k
Dapat dilihat bahwa untuk c v( )0, predegree d( , ) v bernilai genap, sehingga
( , ) ( )
d v c v bernilai genap.
Dapat disimpulkan bahwa d( , ) v c v( ) bernilai genap untuk setiap simpul yang terdapat pada strategi .
Permainan ( , )G c pada Gambar 6 dimainkan dengan strategi menang
( , , , ).v u x w
Nilai c v( ) dan d( , ) v untuk setiap simpul adalah sebagai berikut.
( ) 0 ( ) 1 ( ) 0 ( ) 0 c v c u c x c w
( , ) 0 ( , ) 1 ( , ) 2 ( , ) 2
d v d u d x d w
Dapat dilihat bahwa d( , ) v c v( ) untuk setiap v pada strategi bernilai genap.
Permainan ( , )G c pada Gambar 6 dimainkan dengan strategi ( , , , ).u w v x Nilai c v( ) dan d( , ) v untuk setiap simpul adalah sebagai berikut.
( ) 1 ( ) 0 ( ) 0 ( ) 0 c u c w c v c x
( , ) 0 ( , ) 0 ( , ) 1 ( , ) 3 d u d w d v d x
Dari nilai-nilai tersebut, nilai d( , ) v c v( ) untuk simpul u, v, dan x pada strategi bernilai ganjil. Berdasarkan proposisi 1, bukan strategi menang bagi permainan ( , ).G c
Proposisi 1 mengakibatkan beberapa akibat yang memberikan karakterisktik dari graf yang dapat dimenangkan.
Misalkan diberikan strategi untuk graf ,
G pewarnaan simpul c dari graf G didefinisikan dengan
0 jika ( , ) bernilai genap ( )1 jika ( , ) bernilai ganjil.
d v
c v
d v
Akibat 2
(i) Untuk setiap strategi pada graf G, ( ,G c) adalah permainan yang unik (khas) pada G untuk suatu strategi menang pada ( , ).G c
(ii) Permainan ( , )G c dapat dimenangkan jika dan hanya jika terdapat strategi untuk suatu c c.
Bukti :
(i) Diberikan permainan ( , )G c dan andaikan 1
dan
2 adalah strategi menang bagi permainan ( , ).G c Akan dibuktikan bahwa setiap strategi menang bagi permainan pada graf G unik. Pernyataan ini dibuktikan dalam 2 kasus, yaitu :1
Kasus pertama, jika v berwarna hijau, maka c v( )0. Karena c v( )0, maka untuk strategi menang 1 dan 2, nilai1 ( , )
d v dan d(2, )v bernilai genap agar warna v tetap (hijau). Karena
1 ( , )
d v bernilai genap, maka
1( ) 0
c v . Karena d(2, )v bernilai genap, maka nilai
2( ) 0.
c v Dapat
disimpulkan bahwa
1( ) 2( ).
c v c v 2 Kasus kedua, jika v berwarna merah
maka c v( )1. Karena c v( )1, maka untuk strategi menang 1 dan 2, nilai
1 ( , )
d v dan d(2, )v bernilai ganjil agar warna v berubah menjadi hijau. Karena d(1, )v bernilai ganjil, maka
1( ) 1.
c v Karena d(2, )v bernilai ganjil, maka nilai
2( ) 1.
c v Dapat disimpulkan bahwa
1( ) 2( ).
c v c v Dari kedua kasus di atas dapat disimpulkan bahwa untuk strategi menang 1 dan 2, nilai
1( ) 2( )
c v c v untuk v V G ( ).
(ii) Pernyataan ini akan dibuktikan dengan 2 tahap, yaitu :
1 Diberikan permainan ( , )G c yang dapat dimenangkan dan akan dibuktikan bahwa terdapat strategi untuk suatu
.
c c Karena permainan ( , )G c dapat dimenangkan, maka ada strategi menang bagi ( , ).G c Misalkan adalah strategi menang bagi ( , ),G c dari Proposisi 1, maka c v( )d( , ) v bernilai genap untuk v V G( ). Pernyataan dibuktikan dalam 2 kasus, yaitu :
1.1 Kasus pertama: nilai c v( )1. Karena c v( )1, maka agar
( ) ( , )
9
haruslah d( , ) v bernilai ganjil. Karena d( , ) v bernilai ganjil, maka c v( )1. Oleh karena itu,
( ) ( ) 1. c v c v
1.2 Kasus kedua: nilai c v( )0. Karena ( ) 0,
c v maka agar c v( )d( , ) v bernilai genap haruslah d( , ) v bernilai genap. Karena d( , ) v bernilai genap, maka c v( )0. Oleh karena itu, c v( )c v( )0. Dapat disimpulkan bahwa jika ( , )G c dapat dimenangkan, maka terdapat strategi untuk suatu c c.
2 Diberikan strategi sehingga c c dan akan dibuktikan bahwa permainan
( , )G c dapat dimenangkan. Pernyataan ini dibagi menjadi 2 kasus, yaitu : 2.1 Kasus pertama: c v( )1. Karena
nilai c v( )1, maka c v( )1. Nilai c v( ) akan 1 jika d( , ) v bernilai ganjil. Karena
( ) ( ) 1
c v c v dan d( , ) v bernilai ganjil, maka c v( )d( , ) v bernilai genap.
2.2 Kasus kedua: c v( )0. Karena ( ) 0,
c v maka c v( )0. Nilai ( )
c v akan 0 jika d( , ) v bernilai genap. Karena c v( )c v( )0 dan
( , )
d v bernilai genap, maka ( ) ( , )
c v d v bernilai genap. Dari kedua kasus di atas dapat disimpulkan bahwa untuk strategi sehingga c c, strategi merupakan strategi menang bagi permainan ( , )G c karena c v( )d( , ) v bernilai genap
( ), v V G
sehingga permainan ( , )G c dapat dimenangkan.
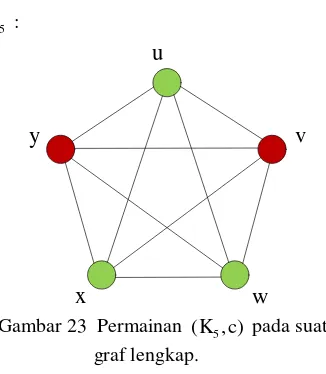
Karakteristik permainan pada graf lengkap lebih mudah diamati, karena setiap simpulnya adjacent dengan simpul lainnya. Berikut adalah contoh permainan pada graf lengkap ber-order 5.
5 K :
u
w
x
v
y
Gambar 23 Permainan (K c5, ) pada suatu graf lengkap.
Simpul yang dapat diambil pertama kali adalah simpul u, w, atau x. Misalkan simpul pertama yang diambil adalah simpul u. Simpul u memiliki nilai c u( )0 dan
( , ) 0.
d u Pada saat simpul u diambil, semua simpul yang adjacent dengan u berubah warna. Karena K5 adalah graf lengkap, maka setiap simpul adjacent dengan simpul lainnya. Oleh karena itu, pada saat pengambilan simpul u, semua simpul lain berubah warna.
5 K u :
w
x
v
y
Gambar 24 Graf K5 setelah simpul u diambil.
Simpul kedua yang dapat diambil adalah simpul v atau y. Misalkan simpul kedua yang diambil adalah simpul y. Simpul y memiliki nilai c y( )1, karena pada awalnya simpul y berwarna merah dan memiliki nilai predegree
( , ) 1
10
5
K u y:
w
x
v
Gambar 25 Graf K5 setelah simpul u dan y diambil.
Simpul ketiga yang dapat diambil adalah simpul w atau x. Misalkan simpul ketiga yang diambil adalah simpul x. Karena warna awal simpul x adalah hijau, maka c x( )0. Simpul-simpul yang adjacent dengan x dan telah diambil sebelumnya adalah simpul u dan y, sehingga d( , ) x 2.
5
K u y x:
w
v
Gambar 26 Graf K5 setelah simpul u, y, dan x diambil.
Simpul keempat yang dapat diambil adalah simpul v. Warna awal simpul v adalah merah, sehingga nilai c v( )1. Simpul-simpul yang adjacent dengan v dan telah diambil sebelumnya adalah u, y, dan x sehingga d( , ) v 3.
5
K u y x v:
w
Gambar 27 Graf K5 setelah simpul u, y, x, dan v diambil.
Simpul kelima yang dapat diambil adalah simpul w. Warna awal simpul w adalah hijau, sehingga nilai c w( )0. Karena terdapat 4 simpul yang adjacent dengan w dan telah diambil sebelumnya, maka d( , ) w 4.
Strategi yang digunakan pada permainan 5
(K c, ) adalah ( , , , , ).u y x v w Karena permainan tersebut dimenangkan dengan strategi
, maka adalah strategi menang bagi (K c5, ).Bentuk umum karakteristik dari permainan pada graf lengkap terdapat pada Akibat 3.
Misalkan c adalah banyaknya simpul yang berwarna hijau dan
c adalah banyaknya simpul yang berwarna merah. Selanjutnya, c dan
c akan ditulis dengan dan .
Akibat 3
Permainan (K c dapat dimenangkan p, ) jika dan hanya jika c p/ 2 , dengan x
adalah bilangan bulat terbesar yang terdekat dengan x.
Bukti :
Pernyataan ini akan dibuktikan dalam 2 tahap, yaitu :
1 Diberikan permainan (K c yang dapat p, ) dimenangkan dan akan dibuktikan bahwa
/ 2 .
c p
Misalkan adalah strategi menang bagi permainan (K c dengan p, ) strategi ( ,v v v1 2, 3,...,vp1,vp). Karena permainan (K c dapat dimenangkan, p, ) maka dari Proposisi 1, c v( )d( , ) v bernilai genap v V G( ). Pembuktian dibagi dalam 2 kasus, yaitu :
1.1 Kasus pertama: p bilangan genap. Simpul yang diambilpertama kali, yaitu
1,
v memiliki nilai d( , v1)0 dan
warna awal hijau sehingga c v( )1 0.
Simpul kedua yang diambil, yaitu v2, memiliki nilai d( , v2)1 dan warna awal merah sehingga c v( 2)1.Simpul ketiga yang diambil, yaitu v3, memiliki nilai d( , v3)2 dan warna awal
hijau sehingga c v( )3 0.Proses terus
berulang hingga simpul ke- .p Simpul ke-pyang diambil, yaitu v memiliki p, nilai d( , vp) p 1 karena simpul yang telah diambil sebelumnya sebanyak (p1) dan semua simpul tersebut adjacent dengan v Simpul p.
p
11
1 1
( , ) 0 ( ) 0 d v c v
2 2
( , ) 1 ( ) 1 d v c v
3 3
( , ) 2 ( ) 0 d v c v
1 1
( , p ) 2 ( p ) 0
d v p c v ( , p) 1 ( p) 1. d v p c v Nilai c v( ) secara bergantian bernilai 0 dan 1. Simpul yang memiliki nilai
( ) 0
c v sebanyak p/ 2. Dapat disimpulkan bahwa banyaknya simpul hijau pada (Kp, )c adalah p/ 2. 1.2 Kasus kedua: p bilangan ganjil.
Simpul yang pertama kali diambil, yaitu v1, memiliki nilai d( , v1)0
dan warna awal hijau sehingga
1
( ) 0.
c v Simpul kedua yang diambil, yaitu v2, memiliki nilai d( , v2)1
dan warna awal merah sehingga 2
( ) 1.
c v Simpul ketiga yang diambil, yaitu v3, memiliki nilai d( , v3)2
dan warna awal hijau sehingga 2
( ) 0.
c v Proses terus berulang hingga simpul ke- .p Simpul yang diambil ke- ,p yaitu v p, memiliki nilai
( , p) 1
d v p karena simpul yang telah diambil sebelumnya sebanyak (p1) simpul dan seluruh simpul tersebut adjacent dengan v Simpul p.
p
v berwarna hijau pada awalnya, karena v telah berubah warna p sebanyak (p1) kali dengan (p1) adalah bilangan genap. Secara umum, proses dalam permainan graf lengkap ditulis dengan
1 1
( , ) 0 ( ) 0 d v c v
2 2
( , ) 1 ( ) 1 d v c v
3 3
( , ) 2 ( ) 0 d v c v
1 1
( , p ) 2 ( p ) 1
d v p c v ( , p) 1 ( p) 0. d v p c v Nilai c v( ) secara bergantian bernilai 0 dan 1. Simpul yang memiliki nilai
( ) 0
c v sebanyak p/ 2 .
D
apat disimpulkan bahwa banyaknya simpul hijau pada (Kp, )c adalah p/ 2 .2 Diberikan graf lengkap K p dengan banyaknya simpul hijau adalah c p/ 2
dan akan dibuktikan bahwa permainan (K c dapat dimenangkan. Misalkan p, ) strategi ( ,v v v1 2, 3,...,vp1,vp) adalah strategi bagi permainan (K c Hal yang p, ). perlu diingat bahwa pengambilan simpul pada graf lengkap akan mengubah warna simpul lainnya.
2.1 Kasus pertama: p bilangan genap. Karena p bilangan genap, maka
/ 2 / 2.
c p p
Agar strategi dapat memenangkan permainan
(K c maka setiap simpul pada p, ), strategi harus memenuhi Proposisi1. Untuk simpul yang pertama diambil pertama kali, nilai c v( )1 0 karena v1 berwarna hijau dan nilai d( , ) v1 0 karena tidak ada simpul yang telah diambil sebelumnya. Untuk simpul kedua yang diambil, nilai c v( )2 1 karena v2 berwarna merah dan nilai
2 ( , ) 1
d v karena simpul yang telah diambil sebelumnya sebanyak 1 simpul. Untuk simpul ketiga yang diambil, nilai c v( )3 0 karena v3 berwarna hijau dan nilai d( , v3)2 karena simpul telah diambil sebelumnya sebanyak 2 simpul. Proses pengambilan simpul terus berulang hingga simpul ke- .p Simpul ke-p yang diambil berwarna merah karena telah berubah warna sebanyak (p1) kali, dengan (p1) bilangan ganjil, sehingga c v( p)1 dan nilai
( , p) 1.
d v p Secara umum, proses tersebut ditulis dengan
1 1
( ) 0 & ( , ) 0 c v d v
2 2
( ) 1& ( , ) 1 c v d v
3 3
( ) 0 & ( , ) 2 c v d v
1 1
( p ) 0 & ( , p ) 2 c v d v p
( p) 1& ( , p) 1. c v d v p
Dapat dilihat bahwa nilai ( )i ( , )i
c v d v bernilai genap dengan 1, 2,3,... .
i p Dapat disimpulkan
12
(K c sehingga permainan (p, ) K c p, ) dapat dimenangkan.
2.2 Kasus kedua: p bernilai ganjil. Karena p bernilai ganjil, maka c p/ 2 .
Agar strategi dapat memenangkan permainan (K c maka setiap simpul p, ), pada strategi harus memenuhi Proposisi 1. Untuk simpul yang diambilpertama kali, nilai c v( )1 0 karena v1 berwarna hijau dan nilai
1 ( , ) 0
d v karena tidak ada simpul yang telah diambil sebelumnya. Untuk simpul yang diambil kedua kalinya, nilai c v( )2 1 karena v2 berwarna merah dan nilai d( , v2)1 karena simpul yang telah diambil sebelumnya sebanyak 1 simpul. Untuk simpul yang ketiga diambil, nilai c v( )3 0 karena
3
v berwarna hijau dan nilai 3
( , ) 2
d v karena simpul telah diambil sebelumnya sebanyak 2 simpul. Proses pengambilan simpul terus berulang hingga simpul ke- .p Simpul ke-p yang diambil berwarna hijau karena telah berubah warna sebanyak (p1) kali dengan (p1) bilangan genap sehingga (c vp)0 dan nilai d( , vp) p 1. Secara umum, proses tersebut ditulis dengan
1 1
( ) 0 & ( , ) 0 c v d v
2 2
( ) 1& ( , ) 1 c v d v
3 3
( ) 0 & ( , ) 2 c v d v
1 1
( p ) 1& ( , p ) 2 c v d v p
( p) 0 & ( , p) 1. c v d v p Dapat dilihat bahwa nilai
( )i ( , )i
c v d v bernilai genap dengan 1, 2,3,... .
i p Dapat disimpulkan
bahwa adalah strategi menang bagi (K c sehingga permainan (p, ) K c p, ) dapat dimenangkan.
Dari kedua kasus tersebut dapat disimpulkan bahwa permainan (K c p, ) dapat dimenangkan.
Pada suatu grafG, jika pewarnaan pada ( )
V G dinotasikan dengan c, maka
c
didefinisikan dengan pewarnaan dari c dengan mengubah warna simpul yang berderajat ganjil, sedangkan warna simpul berderajat genap tidak berubah.
Misalkan ( ,v v v1 2, 3,...,vp1,vp) adalah strategi pada permainan ( , ),G c maka susunan simpul (v vp, p1,vp2,...,v v2, )1 dinotasikan dengan
.
Berikut adalah ilustrasi hubungan antara dan
serta c danc
.
G :
y
x
v
u
z
w
Gambar 28 Permainan ( , ).G c
Dari graf pada Gambar 28, warna dari simpul-simpul yang berderajat ganjil akan diubah. Simpul-simpul yang berderajat ganjil tersebut adalah simpul w dan x. Berikut adalah permainan ( , )G c yang terbentuk dari permainan ( , )G c pada gambar 28.
G :
y
x
v
u
z
w
Gambar 29 Permainan ( , ).G c Simpul pada permainan ( , )G c dan ( , )G c yang berderajat ganjil memiliki warna yang berbeda.
Untuk permainan ( , )G c pada Gambar 27, salah satu strategi menang bagi ( , )G c adalah
( , , , , , ).w v z u x y
Dari strategi diperoleh strategi ( , , , , , ).y x u z v w
13
( , ) 0 ( , ) 1 ( , ) 1 ( , ) 1 ( , ) 2 ( , ) 4
d w d v d z d u d x d y
( , ) 3 ( , ) 3 ( , ) 1 ( , ) 1 ( , ) 1 ( , ) 0
d w d v d z d u d x d y deg 3 deg 4 deg 2 deg 2 deg 3 deg 4 w v z u x y Dari ilustrasi diatas, dapat dilihat bahwa banyaknya sisi yang incident dengan suatu simpul sama dengan penjumlahan predegree pada strategi dan
atau dapat ditulis degvd( , ) v d( , ). v Berikut adalah uraian untuk menunjukkan bahwadegvd( , ) v d( , ). v
Misalkan ( , )G c adalah permainan ELLO pada graf Gyang memiliki p simpul dan adalah strategi pada permainan ( , ).G c Karena terdapat susunan simpul pada
dan strategi
diperoleh dari strategi
, maka terdapat susunan simpul pada
.
Strategi dan
memuat semua simpul yang terdapat pada permainan. Misalkan v adalah simpul pada strategi dan
.
Jika simpul v adalah simpul pertama yang diambil pada strategi
, maka simpul v adalah simpul terakhir yang diambil pada strategi
.
Untuk kasus ini, nilai d( , ) v 0 dan nilai( , ) deg
d v v karena terdapat deg v simpul yang adjacent dengan v yang telah diambil sebelumnya pada strategi
.
Jika v adalah simpul terakhir yang diambil pada strategi
, maka simpul v adalah simpul pertama yang diambil pada strategi
.
Untuk kasus ini, nilai d( , ) v degv karena terdapat deg v simpul yang adjacent dengan v yang telah diambil sebelumnya pada strategi dan nilai d( , ) v 0 karena tidak ada simpul yang adjacent dengan simpul v yang telah diambil sebelumnya pada strategi.
Misalkan v adalah simpul ke-n yang diambil pada strategi dan terdapat t simpul yang telah diambil sebelumnya, maka
( , ) .
d v t Sebanyak t simpul yang telah diambil pada strategi
, merupakan simpul-simpul yang belum diambil sebelumnya pada strategi
, sehingga simpul-simpul yang telah diambil sebelumnya adalah sebanyak degv t . Karena banyaknya simpul yang telah diambil sebanyak deg v t , maka( , ) deg . d v v t
Dari uraian di atas, dapat dilihat bahwa degvd( , ) v d( , ). v
Hubungan antara strategi dan
dituliskan dalam Akibat 4.Akibat 4
(i) Diberikan strategi pada graf G dan v adalah simpul pada G, deg v bernilai genap jika dan hanya jika warna v pada strategi sama dengan warna v pada strategi
dengan dan
adalah strategi menang.(ii) Permainan ( , )G c dapat dimenangkan jika dan hanya jika ( , )G c dapat dimenangkan. Bukti :
(i) Untuk membuktikan pernyataan ini, pembuktian dilakukan dalam 2 tahap. 1.1 Misalkan v adalah simpul pada graf G
dengan deg v bernilai genap dan akan dibuktikan bahwa nilai c v( )c v( ) dengan dan
adalah strategi menang. Pembuktian dibagi dalam dua kasus, yaitu :1.1.1 Kasus pertama: d( , ) v bernilai genap. Karena d( , ) v bernilai genap, maka nilai
( ) 0.
c v Karena d( , ) v bernilai genap dan deg v bernilai genap, maka
( , ) deg ( , ) d v v d v bernilai genap. Karena d( , ) v bernilai genap, maka nilai
( ) 0. c v
1.1.2 Kasus kedua:d( , ) v bernilai ganjil. Karena d( , ) v bernilai ganjil, maka nilai c v( )1. Karena d( , ) v bernilai ganjil dan d v( ) bernilai genap, maka
( , ) ( ) ( , )
d v d v d v bernilai ganjil. Karena d( , ) v bernilai ganjil, maka nilai c v( )1. Dari kedua kasus tersebut dapat disimpulkan bahwa c v( )c v( ). 1.2 Diberikan simpul v yang memiliki
14
pewarnaan simpul v sama pada strategi dan
, maka nilai( ) ( )
c v c v untuk suatu v V G ( ). Pernyataan ini dibagi dalam 2 kasus, yaitu :
1.2.1 Kasus pertama: c v( )0 dan ( ) 0.
c v Pada saat c v( )0, nilai d( , ) v adalah genap. Pada saat c v( )0, nilai
( , )
d v adalah genap. Karena ( , )
d v dan d( , ) v bernilai genap, maka d( , ) v d( , ) v bernilai genap, sehingga deg v bernilai genap.
1.2.2 Kasus kedua: c v( )1 dan ( ) 1.
c v Pada saat c v( ) 1, nilai d( , ) v adalah ganjil. Pada saat c v( ) 1, nilai
( , )
d v adalah ganjil. Karena ( , )
d v dan d( , ) v bernilai ganjil, maka d( , ) v d( , ) v bernilai genap, sehingga deg v bernilai genap.
Dari kedua kasus tersebut dapat disimpulkan bahwa deg v bernilai genap untuk v V G ( ).
(ii)Pernyataan ini digunakan pada simpul yang berderajat ganjil dan untuk simpul yang berderajat genap telah dibahas sebelumnya. Pembuktian pernyataan ini dilakukan dalam 2 tahap.
2.1 Diberikan permainan ( , )G c yang dapat dimenangkan dan akan dibuktikan bahwa permainan ( , )G c dapat dimenangkan. Karena permainan ( , )G c dapat dimenangkan, maka ada strategi menang untuk permainan ( , ).G c Misalkan adalah strategi menang bagi permainan
( , ).G c Pembuktian dibagi dalam 2 kasus, yaitu :
2.1.1 Kasus pertama: d( , ) v bernilai ganjil. Karena deg v bernilai ganjil dan d( , ) v bernilai ganjil, maka diperoleh
( , ) deg ( , ) d v v d v bernilai genap. Karena d( , ) v bernilai ganjil, maka c v( )1.
Karena d( , ) v bernilai genap, maka c v( )0. Dapat dilihat bahwa nilai c v( ) dan c v( ) berbeda.
2.1.2 Kasus kedua, untuk d( , ) v bernilai genap. Karena deg v bernilai ganjil dan d( , ) v bernilai genap, maka diperoleh
( , ) deg ( , ) d v v d v bernilai ganjil. Karena d( , ) v bernilai genap, maka
( ) 0.
c v Karena d( , ) v bernilai ganjil, maka c v( )1. Dapat dilihat bahwa nilai c v( ) dan c v( ) berbeda.
Dari kedua kasus di atas dapat disimpulkan bahwa nilai c v( ) dan
( )
c v berbeda. Karena permainan ( , )G c dapat dimenangkan oleh strategi
, maka berdasarkan Akibat 2, nilai c v( )c v( ). Pewarnaan v pada strategi dan
berbeda untuk v yang berderajat ganjil, sehingga berdasarkan definisi c v( ), nilai( ) ( ).
c v c v Berdasarkan Akibat 2,
adalah strategi menang bagi permainan ( , ).G c2.2 Diberikan permainan ( , )G c yang dapat dimenangkan dan akan dibuktikan bahwa permainan ( , )G c dapat dimenangkan. Karena permainan ( , )G c dapat dimenangkan, maka ada strategi menang untuk permainan ( , ).G c Misalkan
adalah strategi menang bagi ( , ).G c Pembuktian dibagi dalam 2 kasus, yaitu :2.2.1 Kasus pertama: d( , ) v bernilai ganjil. Karena deg v bernilai ganjil dan d( , ) v bernilai ganjil, maka
( , ) ( , ) deg ( , )
d v d v v d v
bernilai genap. Karena d( , ) v bernilai ganjil, maka nilai
( ) 1.
c v Karena d( , ) v bernilai genap, maka
( ) ( ) 0.
15
bahwa nilai c v( ) dan c v( ) berbeda.
2.2.2 Kasus kedua: d( , ) v bernilai genap. Karena deg v bernilai ganjil dan d( , ) v bernilai genap, maka diperoleh
( , ) ( , ) deg ( , )
d v d v v d v
bernilai ganjil. Karena d( , ) v bernilai genap, maka nilai
( ) 0.
c v Karena d( , ) v bernilai ganjil, maka
( ) ( ) 1.
c v c v Dapat dilihat bahwa nilai c v( ) dan c v( ) berbeda.
Dari kedua kasus di atas dapat dilihat bahwa nilai c v( ) dan c v( ) berbeda. Karena permainan ( , )G c dapat dimenangkan oleh strategi
, maka berdasarkan Akibat 2, nilai( ) ( ).
c v c v Pewarnaan v pada strategi dan
berbeda jika v berderajat ganjil, sehingga berdasarkan definisi, nilai( ) ( ) ( ).
c v c v c v Berdasarkan Akibat 2, adalah strategi menang bagi permainan ( , )G c sehingga dapat dimenangkan.
Untuk permainan pada Gambar 28, diketahui bahwa permainan ( , )G c memiliki 6 simpul, 9 sisi dan 3 simpul berwarna hijau, sehingga p6, q9, dan
3. Telah dibahas sebelumnya bahwa permainan ( , )G c dapat dimenangkan. Dari nilai p, q dan , permainan ( , )G c memenuhi kondisi keseimbangan, yaitu p q(mod 2).Hubungan antara kondisi keseimbangan dan permainan ( , )G c yang dapat dimenangkan dituliskan pada Teorema 5. Teorema 5
Diberikan graf G dengan p simpul, q sisi, dan
simpul hijau. Jika permainan( , )G c dapat dimenangkan, maka permainan tersebut memenuhi p q(mod 2).
Bukti :
Misalkan Gi adalah graf dengan i simpul dan (G ci, ) adalah permainan pada graf Gi dengan warna pada V G( ) adalah .c
Teorema ini dibuktikan dengan induksi matematik.
1 Diberikan permainan (G c1, ) yang dapat dimenangkan dan akan dibuktikan bahwa permainan (G c1, ) memenuhi
(mod 2). p q
Karena G1 adalah graf sederhana tanpa loop, maka tidak ada sisi pada graf G1, sehingga p1 dan q0. Karena permainan (G c1, ) dapat dimenangkan, maka simpul pada graf
1
(G c, ) haruslah berwarna hijau, sehingga 1.
1 0 p q
1(mod 2) p q
(mod 2)
p q (Terbukti)
2 Diberikan permainan (G ck, ) yang dapat dimenangkan. Misalkan banyaknya sisi pada graf Gk adalah
l
dan banyaknya simpul hijau adalah m, sehingga nilai,
pk ql dan m. Permainan (G ck, ) dianggap memenuhi kondisi keseimbangan, yaitu p q (mod 2), sehingga k l m(mod 2).
3 Diberikan permainan (Gk1, )c yang dapat dimenangkan. Graf Gk1 merupakan graf
k
G yang ditambahkan satu simpul, misalkan simpul v Penambahan simpul . v akan menambah banyaknya sisi sebanyak deg ,v sehingga q l deg .v Terdapat dua kasus dalam penambahan simpul, yaitu :
3.1 Kasus pertama: simpul v berwarna merah. Karena simpul v berwarna merah, maka dibutuhkan n kali perubahan warna, dengan n bilangan ganjil, agar v menjadi hijau dan dapat diambil dalam permainan. Oleh karena itu, derajat simpul v bernilai ganjil, sehingga degv2t1, t . Karena simpul yang ditambahkan berwarna merah, maka banyaknya simpul hijau tetap, sehingga m. Dari penambahan simpul v diperoleh nilai p k 1, q l degv
2 1
l t
16
( 1) ( (2 1)) p q k l t
(k l) (2t 2)
(mod 2)
Dapat disimpulkan bahwa penambahan simpul merah memenuhi
(mod 2). p q
3.2 Kasus kedua: simpul v berwarna hijau. Karena simpul v berwarna hijau, maka dibutuhkan n kali perubahan, dengan n bilangan genap, agar v dapat diambil dalam permainan. Oleh karena itu, derajat simpul v bernilai genap, sehingga degv2 , tt . Karena simpul yang ditambahkan berwarna hijau, maka banyaknya simpul hijau bertambah, sehingga
m 1. Dari penambahan simpul v diperoleh nilai1,
p k q l degv l 2 ,t dan 1,
m
sehingga ( 1) ( 2 ) p q k l t(k l) (2t 1)
1(mod 2) m
(mod 2)
Dapat disimpulkan bahwa penambahan simpul hijau memenuhi
(mod 2). p q
Berdasarkan kedua kasus tersebut, dapat disimpulkan bahwa penambahan simpul memenuhi p q (mod 2).
Dari (1), (2), dan (3), berdasarkan induksi matematik, dapat disimpulkan bahwa jika permainan ( , )G c dapat dimenangkan maka permainan tersebut memenuhi kondisi keseimbangan, yaitu p q (mod 2).
Misalkan terdapat suatu permainan ( , )G c pada graf G yang memenuhi kondisi keseimbangan dan permainan tersebut dimainkan dengan strategi .
G :
u
v
w
Gambar 30 Permainan (G,c) yang memenuhi kondisi keseimbangan.
Pada Gambar 30, terdapat 3 simpul, 1 sisi, 2 simpul berwarna hijau, dan 1 simpul berwarna merah sehingga p3, q1 dan
2. Permainan ( , )G c memenuhi kondisi keseimbangan.Terdapat beberapa kemungkinan pengambilan simpul yang pertama untuk permainan ( , )G c pada Gambar 30, yaitu : 1 Kasus 1
Jika simpul yang diambil pertama kali adalah simpul u, maka strategi yang digunakan bukan strategi menang karena simpul u berwarna merah.
2 Kasus 2
Jika simpul yang diambil pertama kali adalah simpul v, maka simpul w berubah warna sehingga diperoleh graf sebagai berikut.
: G v
u
w
Gambar 31 Permainan ( , )G c setelah simpul v diambil.
Semua simpul yang tersisa berwarna merah, sehingga strategi yang digunakan bukan strategi merah.
3 Kasus 3
Jika simpul yang diambil pertama kali adalah simpul w, maka simpul v berubah warna sehingga diperoleh graf sebagai berikut.
: G w
u
v
Gambar 32 Permainan ( , )G c setelah simpul w diambil.
17
Proposisi 6
Diberikan strategi untuk permainan ( , ),G c permainan tersebut memenuhi kondisi keseimbangan jika dan hanya jika terdapat m simpul, dengan m adalah bilangan genap, untuk suatu c v( )d( , ) v yang bernilai ganjil.
Bukti :
Diberikan strategi untuk permainan ( , )G c yang memenuhi kondisi keseimbangan dan ( , )G c memiliki p simpul, q sisi, simpul berwarna hijau, dan simpul berwarna merah.
Misalkan
( ) ( ) ( , ) . v V G
s
c v d v Untuk simpul berwarna hijau nilai c v( )0 dan untuk simpul yang berwarna merah nilai( ) 1. c v
( ) ( ) ( , ) v V G
s
c v d v
v V G( ) ( )
v V G( ) ( , )
s c v d v
s
q
( )
s p q
s
p q
Dari perhitungan tersebut,
p q
bernilai genap karena permainan ( , )G c memenuhi kondisi keseimbangan s bernilai genap.Untuk c v( )0 dengan d( , ) v bernilai genap dan c v( )1 dengan d( , ) v bernilai ganjil tidak akan memengaruhi nilai s, karena keduanya menghasilkan c v( )d( , ) v bernilai genap.
Untuk c v( )0 dengan d( , ) v bernilai ganjil dan c v( )1 dengan d( , ) v bernilai genap menghasilkan c v( )d( , ) v bernilai ganjil. Karena nilai s selalu genap, maka banyaknya simpul yang memiliki nilai
( ) ( , )
c v d v genap adalah ganjil.
Dapat disimpulkan bahwa terdapat m simpul, dengan m adalah bilangan genap, untuk suatu c v( )d( , ) v yang bernilai ganjil.
Misalkan permainan ( , )G c pada Gambar 30 dimainkan dengan strategi ( , , ).u v w Permainan ( , )G c memiliki nilai c v( ) dan
( , )
d v sebagai berikut. ( ) 1
( ) 0 ( ) 0 c u c v c w
( , ) 0 ( , ) 0 ( , ) 1
d u d v d w
Simpul-simpul yang memiliki nilai ( ) ( , )
c v d v bernilai ganjil adalah simpul u dan w. Permainan tersebut memiliki 2 simpul yang memiliki nilai c v( )d( , ) v bernilai ganjil.
IV SIMPULAN DAN SARAN
4.1 SIMPULAN
Dalam karya ilmiah ini telah dibuktikan proposisi, akibat, dan teorema yang menunjukkan karakteristik graf yang dapat dimenangkan dan permainan yang tidak dapat dimenangkan.
Untuk setiap strategi pada graf G, ( ,G c) adalah permainan yang unik (khas) pada G untuk suatu strategi menang pada ( , )G c dan permainan ( , )G c dapat dimenangkan jika dan hanya jika terdapat strategi untuk suatu c c.
Pada graf lengkap ber-order p (K ), p permainan (K c dapat dimenangkan jika p, ) dan hanya jika banyaknya simpul hijau adalah pembulatan ke atas dari p/2, atau dinotasikan denganc p/ 2 .
Permainan ( , )G c dapat dimenangkan jika dan hanya jika permainan ( , )G c dapat dimenangkan.
Untuk permainan ( , )G c yang memiliki p simpul, q sisi dan simpul hijau, jika permainan ( , )G c dapat dimenangkan maka memenuhi kondisi keseimbangan, yaitu
(mod 2). p q
4.2 SARAN
18
DAFTAR PUSTAKA
Anderson M, Feil T. 1998. Turning lights out with linear algebra. Mathematics Magazine 71(4):300-303.
Chartrand G, Oellermann OR. 1993. Applied and Algorithmic Graph Theory. New York: McGraw-Hill.
Craft D, Miller Z, Pritikin D. 2007. A solitaire game played on 2-colored graphs. Discrete Mathematics 309: 188-201.
Deo N. 1974. Graph Theory with Applications to Engineering and Computer Science. New Jersey: Prentice-Hall,Inc.
Foulds LR. 1992. Graph Theory Applications. New York: Springer-Verlag.