PENERAPAN ALGORITMA GENETIKA UNTUK
PENYELESAIAN VEHICLE ROUTING PROBLEM WITH
DELIVERY AND PICK-UP (VRP-DP)
SKRIPSI
HERLIN SIMANULLANG
060803023
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM
UNIVERSITAS SUMATERA UTARA
PENERAPAN ALGORITMA GENETIKA UNTUK PENYELESAIAN VEHICLE ROUTING PROBLEM WITH DELIVERY AND PICK-UP
(VRP-DP)
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
HERLIN SIMANULLANG 060803023
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
PERSETUJUAN
Judul : PENERAPAN ALGORITMA GENETIKA UNTUK PENYELESAIAN VEHICLE ROUTING PROBLEM WITH DELIVERY AND PICK-UP (VRP-DP)
Kategori : SKRIPSI
Nama : HERLIN SIMANULLANG
Nomor Induk Mahasiswa : 060803023
Program Studi : SARJANA (S1) MATEMATIKA
Departemen : MATEMATIKA
Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN
ALAM (FMIPA) UNIVERSITAS SUMATERA UTARA
Diluluskan di
Medan, Desember 2012 Komisi Pembimbing :
Pembimbing 2 Pembimbing 1
Drs. James Piter Marbun, M.Kom Drs. Partano Siagian, M.Sc
NIP 19580611 198603 1 002 NIP 13087799 40000 0 000
Diketahui/Disetujui oleh
Departeman Matematika FMIPA USU Ketua Departemen Matematika,
PERNYATAAN
PENERAPAN ALGORITMA GENETIKA UNTUK PENYELESAIAN
VEHICLE ROUTING PROBLEM WITH DELIVERY AND PICK-UP
(VRP-DP)
SKRIPSI
Saya mengaku bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dan ringkasan yang masing-masing disebutkan sumbernya.
Medan, Desember 2012
PENGHARGAAN
Puji dan syukur penulis kepada Tuhan Allah untuk kasih anugerah dan penyertaannya, sehingga penulis dapat menyelesaiakan penulisan skripsi ini.
Ucapan terima kasih penulis ucapkan kepada Drs. Partano Siagian, M.Sc dan Drs. James Piter Marbun M.Kom selaku dosen pembimbing penulis dalam penyelesaian skripsi ini, atas bimbingan, arahan serta meluangkan waktu yang diberikan. Penulis juga mengucapakan terima kasih kepada Drs. Sawaluddin, M.IT dan Drs. Marihat Situmorang, M.Kom selaku dosen penguji/pembanding, atas setiap saran dan masukannya selama penulisan skripsi ini. Ucapan terima kasih juga penulis tujukan kepada Ketua dan Sekretaris Departemen Matematika Prof. Drs. Tulus, Vordip1.Math., M.Si, Ph.D dan Dra. Mardiningsih, M.Si, Dekan dan Pembantu Dekan Fakultas MIPA USU beserta semua Staf Administrasi di FMIPA USU.
ABSTRAK
THE IMPLEMENTATION OF GENETICS ALGORITHM FOR FINISHING VEHICLE ROUTING PROBLEM (VRP-DP)
ABSRACT
DAFTAR ISI
PERSETUJUAN ii
PERNYATAAN iii
PENGHARGAAN iv
ABSTRAK v
ABSRACT vi
DAFTAR ISI vii
DAFTAR GAMBAR ix
DAFTAR TABEL x
BAB 1 PENDAHULUAN 11
1.1 Latar Belakang 11
1.2 Perumusan Masalah 12
1.3 Batasan Masalah 12
1.4 Tujuan Penelitian 12
1.5 Manfaat Penelitian 13
1.6 Konstribusi Penelitian 13
1.7 Metodologi Penelitian 14
1.8 Tinjauan Pustaka 15
BAB 2 LANDASAN TEORI 18
2.1 Pengertian Optimasi 18
2.2 Vehicle Routing Problem 20
2.3 Algoritma Genetika 21
2.3.1 Sejarah Singkat Algoritma Genetika 21
2.3.2 Karakteristik Algoritma Genetika 21
2.3.3 Komponen-komponen Algoritma Genetika 22
2.3.4 Parameter Genetik 28
2.3.5 Mekanisme Kerja Algoritma Genetika 29
BAB 3 ANALISIS DAN PERANCANGAN 31
3.1 Analisis Kebutuhan 32
3.1.1 Analisis Kebutuhan Masukan (Input) 32
3.1.2 Analisis Kebutuhan Proses 32
3.1.4 Kebutuhan Perangkat Lunak 33
3.1.5 Kebutuhan Perangkat Keras 33
1.2 Perancangan Perangkat Lunak 34
3.2.1 Penerapan Algoritma Genetika Untuk Penyelesaian Vehicle
Routing Problem With Delivery And Pick-Up (VRP-DP) 34
1.3 Diagram Alir (Flowchart) 37
BAB 4 HASIL DAN PEMBAHASAN 38
4.1 Pengkodean Kromosom 38
4.2 Inisialisasi Populasi dan Evaluasi Individu 42
4.3 Probabilitas Fitness 46
4.4 Seleksi Roda Roulette (Roulette Wheel Selection) 47
4.5 Order Crossover 51
4.6 Swap Mutation 53
4.7 Hasil Penyelesaian VRP-DP 58
BAB 5 KESIMPULAN DAN SARAN 61
DAFTAR PUSTAKA 63
DAFTAR GAMBAR
Gambar 2.1 Tree Encoding 24
Gambar 2.2 Mekanisme Kerja Algoritma Genetika 30
Gambar 3.1 Model VRP 31
Gambar 3.2 Diagram Alir Penyelesaian VRPD-DP 37
Gambar 4.2.a Subrute 1 58
Gambar 4.2.b Subrute 2 58
Gambar 4.2.c Subrute 3 59
DAFTAR TABEL
Tabel 4.1 Data node beserta jumlah delivery and pick-up 39
Tabel 4.2.a Data jarak antar node 40
Tabel 4.2.b Data jarak antar node (lanjutan) 41
ABSTRAK
THE IMPLEMENTATION OF GENETICS ALGORITHM FOR FINISHING VEHICLE ROUTING PROBLEM (VRP-DP)
ABSRACT
BAB 1
PENDAHULUAN
1.1 Latar Belakang
Optimasi adalah salah satu ilmu dalam matematika yang fokus untuk mendapatkan nilai minimum atau maksimum secara sistematis dari suatu fungsi, peluang maupun pencarian nilai lainnya dalam berbagai kasus. Optimasi sangat berguna dihampir segala bidang dalam rangka melakukan usaha secara efektif dan efisien untuk mencapai target hasil yang ingin dicapai. Pengoptimalan dilakukan untuk menekan pengeluaran untuk menghasilkan output yang maksimal. Optimasi ini juga penting karena persaingan sudah sangat ketat disegala bidang yang ada.
Salah satu permasalahan optimasi yang diangkat oleh penulis adalah permasalahan Vehicle Routing Problem (VRP). Permasalahan Vehicle Routing Problem (VRP) adalah sebuah permasalahan optimasi kombinatorial yang kompleks, yang didefinisikan sebagai berikut: pencarian cara penggunaan sejumlah vehicle (kendaraan) secara efisien yang harus melakukan perjalanan untuk untuk mengantar dan/atau menjemput orang/barang pada sejumlah tempat. Setiap tujuan hanya boleh dilayani oleh satu vehicle saja. Hal ini dilakukan dengan mempertimbangkan kapasitas kendaraan dalam satu kali angkut, untuk meminimalkan biaya yang diperlukan. Asumsi bahwa penentuan biaya minimal erat kaitannya dengan jarak yang minimal.
(VRP-DP). Salah satu solusi untuk penyelesaian Vehicle Routing Problem With Delivery And Pick-Up dapat dilakukan dengan menerapkan metode algoritma genetika.
Berdasarkan uraian singkat tersebut maka penulis mengambil judul ”PENERAPAN ALGORITMA GENETIKA UNTUK PENYELESAIAN VEHICLE ROUTING PROBLEM WITH DELIVERY AND PICK-UP (VRP-DP)”.
1.2 Perumusan Masalah
Permasalahan yang dibahas dalam penulisan ini adalah penyelesaian Vehicle Routing Problem With Delivery And Pick-Up (VRP-DP) dengan menggunakan algoritma
genetika dan pengujiannya dirancang di Matlab.
1.3 Batasan Masalah
Batasan-batasan masalah yang akan dibahas adalah sebagai berikut:
1. Jumlah pelanggan dan jumlah permintaan diinput oleh user, dimana tiap konsumen mempunyai variabel lokasi dan permintaan (Delivery and Pick-Up). 2. Parameter yang digunakan adalah ukuran populasi, peluang crossover, peluang
mutasi, maksimum generasi dan panjang kromosom (jumlah gen).
1.4 Tujuan Penelitian
Tujuan dari tugas akhir ini adalah
1. Mengoptimalkan kinerja salesman dalam menyalurkan barang berdasarkan total biaya pelaksanaan atas jarak dan permintaan barang.
2. Mengetahui dampak dari model penyelesaian VRP-DP terhadap keterlaksanaan tugas pengiriman barang.
1.5 Manfaat Penelitian
Manfaat dari penelitian ini adalah sebagai berikut: 1. Bagi Salesman
a. Membantu salesman memilih jalur yang paling optimal berdasarkan permintaan dan jarak yang ditempuh sehingga akan lebih banyak konsumen yang terlayani.
b. Membantu salesman untuk memenuhi target penjualan dengan waktu yang relatif.
c. Membantu para salesman dalam menganalisa pasar dan memutuskan jumlah barang yang akan dibawa untuk dijual.
2. Bagi Perusahaan
a. Membantu meningkatkan efisiensi dari perusahaan sehingga laba perusahaan meningkat.
b. Membantu perusahaan dalam memanajemen para salesmannya. 3. Bagi Akademik
a. Menambah pengetahuan penjualan dalam bisnis penjualan consumer goods. b. Menambah pengetahuan dalam model penjaluran para salesman dalam bisnis
consumer goods.
1.6 Konstribusi Penelitian
1.7 Metodologi Penelitian
Dalam melakukan penelitian ini, penulis menggunakan beberapa metode penelitian, antara lain:
1. Studi Literatur dan Pemahaman Sistem.
Penulisan ini dimulai dengan studi kepustakaan yaitu dengan membaca buku-buku, jurnal-jurnal dan bahan-bahan referensi dari internet untuk memperoleh pengertian dan pengetahuan mengenai algoritma genetika, analisis dan perancangan sistem, dan pemrograman Matlab 6.1.
2. Analisis
Pada tahap ini dilakukan pengumpulan fakta-fakta yang mendukung penyelesaian VRP-DP dengan mengadakan konsultasi dengan seorang pakar dan membandingkan dengan yang ada pada buku penuntun, membuat metode penjaluran berdasarkan permintaan barang dan jarak tempuh, mendefinisikan gen atau kromosom atau individu dan populasi, membuat algoritma dan flowchart, dan merancang sistem.
3. Perancangan dan Implementasi
Perancangan dan penerapan algoritma genetika untuk penyelesaian Vehicle Routing Problem with Delivery and Pick-Up (VRP-DP) dengan menggunakan
perancangan pemrograman Matlab 6.1.
4. Pengujian
Pada tahap ini sistem yang sudah dirancang diuji oleh pengguna dan membandingkan solusi pada sistem dengan pemikiran seorang pakar.
5. Penyusunan laporan dan kesimpulan akhir.
1.8 Tinjauan Pustaka
Algoritma genetika adalah sebuah teknik optimasi yang berdasarkan pada proses evolusi alam. Di alam, kromosom yang terbaik akan bertahan hidup sehingga generasi berikutnya akan lebih baik karena kromosom pada generasi tersebut diturunkan dari orang tua yang lebih baik pula. Konsep yang sama dikembangkan untuk penyelesaian masalah dengan cara mencari himpunan solusi terbaik yang bertahan hidup dan melakukan rekombinasi solusi yang kurang baik untuk mendapatkan kromosom lain yang lebih baik pada generasi berikutnya.
Proses algoritma terdiri dari berapa langkah, yaitu pengkodean (encoding), seleksi (selection), persilangan (crossover), mutasi (mutation), decoding. Pertama-tama, proses encoding adalah suatu proses kodifikasi atas solusi dari permasalahannya. Hasil encoding adalah berbentuk string yang merupakan representasi dari suatu kromosom.
Proses seleksi menentukan kromosom mana yang tetap tinggal pada generasi berikutnya. Proses crossover akan menghasilkan kromosom baru yang merupakan pengganti dari kromosom yang hilang sehingga total kromosom pada satu generasi berjumlah tetap. Proses mutasi memunginkan terjadinya kromosom baru secara unpredictiable. Proses terakhir adalah decoding yaitu mengambil makna dari hasil
kromosom terbaik untuk menjawab permasalahannya.
Proses Genetic Algorithm untuk perhitungan optimisasi dapat direpresentasikan melalui penjelasan sebagai berikut ini.
1. Inisialisasi
Populasi awal dari solusi kandidat yang dihasilkan secara random, sesuai dengan fungsi-fungsi tujuan dan kendala yang sesuai dengan masalah yang ada.
2. Evaluasi
Salah satu populasi diinisialisasi atau populasi offspring dibuat. Tahap ini berfungi untuk memperoleh fungsi fitness pada masing-masing fitness. Fungsi fitness ini diperoleh dari fungsi tujuan sesuai dengan masalah yang ada. Model
. ·
1; 1,2,3, … ,
1; 1,2,3, … ,
; 1,2,3, … ,
Keterangan:
= biaya yang dibutuhkan dari titik i ke titik j
= jumlah kunjungan ke suatu titik bernilai 1 jika dikunjungi dan bernilai 0 jika tidak dikunjungi
= kebutuhan pada konsumen tujuan j = Total kapasitas kendaraan
3. Seleksi
Pemikiran utama dari seleksi adalah untuk mendapatkan solusi terbaik sampai terburuk. Pada penelitian ini metode yang digunakan adalah roulette wheel. Seleksi ini bertujuan untuk memberikan kesempatan reproduksi lebih besar bagi anggota populasi yang memiliki fitness tinggi. Adapun algoritma seleksi roda roulette adalah sebagai berikut:
a. Hitung total Fitness (F):
Total Fitness ∑ !; " 1,2, . . ., ukuran populasi b. Hitung Fitness Relatif tiap individu:
#! ! / Total fitness c. Hitung Fitness komulatif
- #
- ! !% & #!; " 2,3, . .., ukuran populasi
d. Pilih induk yang akan menjadi kandidat untuk di rekombinasi/crossover dengan cara:
- Bangkitkan bilangan random r.
4. Rekombinasi/Crossover
Crossover merupakan penyilangan induk yang dilakukan untuk membentuk
keturunan yang baru. Crossover dilakukan antar dua individu. Metode yang dipilih dalam penelitian ini adalah order crossover. Penjelasan metode ini dapat dilihat sebagaimana gambar berikut.
Orang Tua 1 2 1 3 4 5 6
Orang Tua 2 5 4 6 3 2 1
Anak 1 5 6 3 4 2 1
Anak 2 1 5 6 3 2 4
Dalam contoh di atas misalkan terpilih dua orang tua, dari hasil random [0,jumlahkons] terpilih dua titik untuk memisahkan rantai DNA pada suatu individu. Kemudian proses bilangan random [0,1] untuk menentukan titik mana yang akan dipindah silangkan.
5. Mutasi
Model mutasi yang dilakukan adalah menggunakan swap mutation, dengan diberikan batasan dengan tipe individu yang sama. Misalkan terjadi konsumen 5 dan konsumen 3 mempunyai pesanan yang sama maka dapat dipertukarkan.
Kromosom Awal 5 6 3 4 2 1
Kromosom Mutasi 3 6 5 4 2 1
BAB 2
LANDASAN TEORI
2.1 Pengertian Optimasi
Optimasi adalah salah satu ilmu dalam matematika yang fokus untuk mendapatkan nilai minimum atau maksimum secara sistematis dari suatu fungsi, peluang maupun pencarian nilai lainnya dalam berbagai kasus. Optimasi sangat berguna dihampir segala bidang dalam rangka melakukan usaha secara efektif dan efisien untuk mencapai target hasil yang ingin dicapai. Pengoptimalan dilakukan untuk menekan pengeluaran untuk menghasilkan output yang maksimal. Optimasi ini juga penting karena persaingan sudah sangat ketat disegala bidang yang ada.
Seperti yang dikatakan sebelumnya, bahwa optimasi sangat berguna bagi hampir seluruh bidang yang ada, maka berikut ini adalah contoh-contoh bidang yang sangat terbantu dengan adanya teknik optimasi tersebut. Bidang tersebut, antara lain: Arsitektur, Data Mining, Jaringan Komputer, Signal and Image Processing, Telekomunikasi, Ekonomi, Transportasi, Perdagangan, Pertanian, Perikanan, Perkebunan, Kehutanan dan sebagainya.
Teknik optimasi secara umum dapat dibagi menjadi dua bagian, yang pertama adalah Mathematical Programing, dan yang kedua adalah Combinatorial Optimization. Dalam bidang mathematical programming dapat dibagi dua, yaitu support vector machines dan gradient descent. Sedangkan pada bidang Combinatorial Optimization
Adapun cara untuk membuat optimasi yang baik, adalah dengan memperhatikaan hal-hal berikut,
- Model dan Starting Poin
- Convergence to global minimum / maximum - Classes of nice optimization problems - Find a threshold
- Constraint give a trade off
Optimasi kombinatorial adalah topik dalam ilmu komputer teroritis dan matematika terapan yang berfungsi untuk mencari solusi dengan biaya yang terkecil untuk masalah matematika dimana setiap solusi dikaitkan dengan numerical cost. Dalam beberapa permasalahan, pencarian menyeluruh tidak dapat dilakukan. Beroperasi pada daerah yang dioptimasi, dimana set solusi yang layak adalah diskrit atau dapat dikurangi menjadi diskrit, dan dimana tujuannya adalah mencari solusi yang terbaik. Beberapa masalah umum yang melibatkan optimasi kombinatorial adalah traveling salesman problem dan the minimum spanning tree problem.
Optimasi kombinatorial adalah bagian dari optimasi yang berhubungan dengan riset operasi, teori algoritma, dan teori kompleksitas komputasi. Ini memiliki aplikasi penting dalam bebrapa bidang termasuk artificial intelligence, matematika dan rekayasa perangkat lunak.
2.2 Vehicle Routing Problem
VRP diperkenalkan pertama kali oleh Dantziq dan Ramser pada tahun 1959 dan semenjak itu dipelajari secara luas. VRP didefnisikan sebagai sebuah pencarian atau penggunaan yang efisien untuk sejumlah kendaraan (vehicle) dimana kendaraan tersebut harus mengunjungi sejumlah tempat untuk mengantar dan/atau menjemput orang/barang. Istilah pelanggan digunakan untuk menunjukkan tempat pemberhentian. Dan seorang pelanggan hanya boleh dilayani oleh sebuah kendaraan (vehicle) saja. Hal ini dilakukan untuk meminimalkan biaya yang diperlukan dengan mempertimbangkan kapasitas sebuah kendaraan dalam satu kali pengantaran.
VRP juga dapat dipandang sebagai kombinasi dari dua permasalahan optimasi lain yaitu Bin Packing Problem (BPP) dan Travelling Salesman Problem (TSP). BPP dapat digambarkan sebagai berikut: “Diberikan sejumlah angka, yang melambangkan ukuran dari sejumlah item, dan sebuah konstanta K, yang melambangkan kapasitas dari bin. Berapa jumlah bin minimum yang diperlukan?”. Tentu saja satu item hanya dapat
berada dalam satu bin saja, dan total kapasitas item pada setiap bin tidak boleh melebihi kapasitas dari bin tersebut. Dan TSP adalah suatu kondisi dimana seorang pedagang keliling yang harus mengunjungi n kota dengan aturan bahwa pedagang tersebut harus mengunjungi setiap kota hanya sebanyak satu kali untuk meminimalisasi total jarak perjalanannya dan pada akhirnya ia harus kembali ke kota asalnya. Hubungan keduanya dengan VRP adalah, vehicle dapat dihubungkan dengan pelanggan menggunakan BPP, dan urutan kunjungan vehicle terhadap tiap konsumen dapat diselesaikan menggunakan TSP.
penyelesaian secara umum yang memperluas ruang solusi untuk mengidentifikasi solusi
yang baik dan sering menyimpan beberapa susunan rute standar serta perbaikan
heuristik.
2.3 Algoritma Genetika
2.3.1 Sejarah Singkat Algoritma Genetika
Algoritma Genetika ditemukan pertama kali oleh John Holland pada tahun 1960-an dan kemudian dikembangkan bersama murid dan rekan kerjanya di Universitas Michigan pada tahun 1960-an sampai 1970-an. Tujuan Holland mengembangkan algoritma genetika saat itu bukan untuk mendesain suatu algoritma yang dapat menyelesaiakna suatu masalah, namun lebih mengarah ke studi mengenai fenomena adaptasi yang terjadi di alam dan mencoba menerapkan mekanisme adaptasi alam tersebut ke dalam sistem komputer.
Algoritma Genetika yang dibuat Holland merupakan sebuah metode untuk memisahkan satu populasi kromosom (terdiri dari bit-bit 1 dan 0) ke populasi baru dengan menggunakan “seleksi alam” dan operator genetik seperti crossover, mutation (mutasi) dan inversion. Crossover menukar bagian kecil dari dua kromosom, mutasi mengganti secara acak nilai gen beberapa lokasi pada kromosom dan inversion membalikkan urutan beberapa gen yang berurutan dalam kromosom. Dasar teori inilah yang menjadi dasar kebanyakan program yang menggunakan Algoritma Genetika saat ini.
2.3.2 Karakteristik Algoritma Genetika
pencarian atau optimasi yang lainnya. Karakteristiknya dapat di asumsikan sebagai berikut.
1. Algoritma Genetika bekerja dengan pengkodean dari himpunan solusi permasalahan berdasarkan parameter yang telah ditetapkan dan bukan parameter itu sendiri.
2. Algoritma Genetika malakukan pencarian pada sebuah populasi dari sejumlah individu-individu yang merupakan solusi permasalahan bukan hanya dari sebuah individu.
3. Algoritma Genetika merupakan informasi fungsi objektif (fitness), sebagai cara untuk mengevaluasi individu yang mempunyai solusi terbaik, bukan turunan dari suatu fungsi.
4. Algoritma Genetika aturan-aturan transisi peluang, bukan aturan-aturan deterministik.
2.3.3 Komponen-komponen Algoritma Genetika
Pada dasarnya algoritma genetika memiliki 7 komponen, antara lain:
a. Pendefenisian Individu
Pendefenisian individu merupakan proses pertama yang harus dilakukan dalam Algoritma Genetika yang menyatakan salah satu solusi yang mungkin dari suatu permasalahan yang diangkat. Pendefenisian individu dilakukan dengan mendefenisikan jumlah dan tipe dari gen yang digunakan dan tentunya dapat mewakili solusi permasalahan yang diangkat. Sebuah kromosom dibentuk dari komponen-komponen penyusun yang disebut sebagai gen dan nilainya dapat berupa bilangan numerik, biner, simbol ataupun karakter tergantung dari permasalahan yang ingin diselesaikan. Menurut Marek Obitko terdapat beberapa macam teknik pengkodean antara lain :
1. Binary Encoding (Pengkodean Biner)
Pada binary encoding, setiap kromosom akan terdiri dari deretan bilangan biner, sehingga allela setiap gen-nya ada dua, yaitu bernilai 0 atau 1.
Kromosom 1
1101100100110110
Kromosom 2
1101011000011110
2. Permutation Encoding (Pengkodean Permutasi)
Pada permutation encoding, setiap kromosom terdiri atas deretan angka yang menyatakan posisi dalam suatu urutan. Nilai dalam suatu lokus yang ada pada satu kromosom tidak boleh ada yang sama. Biasanya digunakan pada permasalahan TSP.
Contohnya:
Pada permasalahan TSP (vehicle routing problem), dimana seorang sales harus mengantarkan barang dengan melewati beberapa kota. Syaratnya dia tidak boleh melewati kota yang sama.
3. Value Encoding (Pengkodean Nilai)
Pada value encoding, setiap kromosom berupa kumpulan dari suatu nilai yang bisa berupa macam-macam nilai sesuai dengan permasalahan yang dihadapi. Seperti bilangan real, char dan lain-lain.
Contohnya:
Kromosom 1
A B E D B C A E D D
Kromosom 2
N W W N E S S W N N
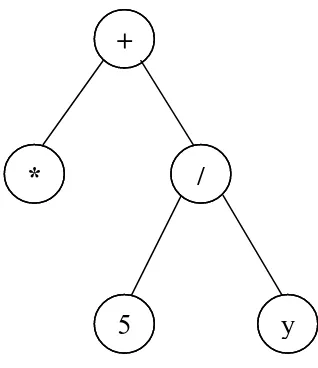
4. Tree Encoding (Pengkodean Pohon)
Pada tree encoding, tiap kromosom adalah pohon dari objek-objek seperti fungsi atau perintah dalam bahasa pemrograman.
Contohnya: (+ x (/5 y))
Gambar 2.1 Tree Encoding
b. Nilai Fitness
Suatu individu dievaluasi berdasarkan suatu fungsi tertentu sebagai ukuran performansinya. Di dalam evolusi alam, individu yang bernilai fitness tinggi yang akan bertahan hidup. Sedangkan individu yang bernilai fitness rendah akan mati. Pengertian nilai fitness ini sendiri adalah nilai yang menyatakan baik tidaknya suatu solusi (individu). Algoritma Genetika bertujuan mencari individu dengan nilai fitness yang paling tinggi. Umumnya kromosom ber-fitness tinggi akan bertahan dan berlanjut kegenerasi berikutnya. Kromosom yang telah terbentuk akan berevolusi secara berkelanjutan yang disebut dengan generasi. Dalam tiap generasi kromosom-kromosom tersebut dievaluasi tingkat keberhasilan nilai solusinya terhadap masalah yang ingin diselesaikan menggunakan ukuran yang disebut dengan nilai fitness. Nilai fitness inilah yang dijadikan acuan dalam mencapai nilai optimal dalam Algoritma Genetika.
c. Seleksi
Proses seleksi adalah proses evaluasi kualitas setiap kromosom di dalam populasi untuk memperoleh peringkat calon solusi. Seleksi bertujuan untuk memberikan kesempatan reproduksi yang lebih besar bagi anggota populasi yang paling fit. Proses seleksi dilakukan dengan mencari kromosom terbaik dalam satu generasi, dimana untuk menentukan suatu kromosom terbaik dapat dilihat dari nilai fitness-nya. Proses seleksi dilakukan dengan mengevaluasi setiap kromosom berdasarkan nilai fitness untuk mendapatkan peringkat terbaik. Selanjutnya dipilih secara acak, kromosom-kromosom yang mengalami proses
+
/
5
y
rekombinasi. Umumnya kromosom ber-fitness tingggi yang berpeluang lebih besar untuk terpilih. Kromosom dengan kualitas yang lebih baik akan memiliki peluang lebih besar untuk terpilih sebagai calon kromosom generasi berikutnya.
Kemampuan Algoritma Genetika untuk memproduksi kromosom yang lebih baik secara progresif tergantung pada penekanan selektif (Selektif Pressure) yang diterapkan ke populasi. Penekanan selektif dapat diterapkan
dalam dua cara yaitu dengan membuat lebih banyak kromosom anak yang dipelihara dalam populasi dan memilih hanya kromosom-kromosom terbaik bagi generasi berikut. Walaupun induk dipilih secara acak, metode ini akan terus menghasilkan kromosom yang lebih baik berhubungan dengan penekanan selektif yang diterapkan pada individu anak tersebut. Cara lainnya adalah dengan memilih induk yang lebih baik ketika membuat keturunan baru. Dengan metode ini, hanya kromosom sebanyak yang dipelihara dalam populasi yang perlu dibuat bagi generasi berikutnya. Walaupun penekanan selektif tidak diterapkan ke level keturunan, metode ini akan terus menghasilkan kromosom yang lebih baik, karena adanya penekanan selektif yang diterapkan ke induk.
Terdapat beberapa metode seleksi untuk mendapatkan calon induk yang baik, namun proses seleksi yang biasa digunakan adalah Roulette Wheel Selection (Seleksi Roda Roulette). Sesuai dengan namanya, metode ini
menirukan permainan roulette-wheel dimana masing-masing kromosom menempati potongan lingkaran pada roda roulette secara proporsional sesuai dengan nilai fitness-nya.
d. Perkawinan Silang (Crossover)
Salah satu komponen paling penting dalam Algoritma Genetika adalah crossover atau perkawinan silang, dikenal juga dengan pindah silang. Crossover
proses ini dilakukan penukaran bagian gen yang telah dipilih posisinya secara acak dalam satu kromosom. Dalam proses ini, perkawinan silang yang terjadi adalah perkawinan antar seluruh gen dalam suatu generasi.
Perkawinan Silang(Crossover) juga dapat berakibat buruk jika ukuran populasinya sangat kecil. Dalam suatu populasi yang sangat kecil, suatu kromosom dengan gen-gen yang mengarah ke solusi akan sangat cepat menyebar ke kromosom-kromosom lainnya. Untuk mengatasi masalah ini digunakan suatu aturan bahwa perkawinan silang hanya bisa dilakukan dengan suatu probabilitas tertentu ρc. Artinya pindah silang bisa dilakukan hanya jika suatu bilangan random yang dibangkitkan kurang dari probabilitas yang ditentukan tersebut. Pada umumnya probabilitas tersebut diset mendekati 1.
Probabilitas crossover ρc merupakan nilai perbandingan jumlah kromosom yang diharapkan akan mengalami perkawinan silang terhadap jumlah kromosom dalam suatu populasi. Probabilitas crossover yang tinggi akan memungkinkan pencapaian alternatif solusi yang lebih bervariasi dan mengurangi kemungkinan menghasilkan nilai optimum yang tidak dikehendaki. Tetapi bila nilai ini terlalu tinggi akan mengakibatkan pemborosan waktu untuk melakukan perhitungan di daerah solusi yang tidak menjanjikan hasil yang optimal.
e. Mutasi
Cara termudah untuk melakukan mutasi adalah dengan mengubah satu atau lebih bagian dalam kromosom dan hal ini tergantung pada probabilitas mutasi. Probabilitas mutasi menentukan probabilitas jumlah gen di dalam satu populasi yang diharapkan mengalami mutasi. Apabila nilai probabilitas mutasi terlalu kecil, banyak kromosom yang berguna mungkin tidak akan muncul dalam populasi, tetapi apabila terlalu tinggi maka keturunan yang dihasilkan akan kehilangan sifat-sifat yang mungkin saja merupakan sifat yang unggul dari induknya dan Algoritma Genetika akan kehilangan kemampuan untuk belajar dari pencarian-pencarian sebelumnya.
f. Elitisme
Proses seleksi dilakukan secara random sehingga tidak ada jaminan bahwa suatu individu yang bernilai fitness tertinggi akan selalu terpilih. Walaupun individu bernilai fitness tertinggi terpilih, mungkin saja individu tersebut akan rusak (nilai fitness-nya menurun) karena proses perkawinan silang. Untuk menjaga agar individu bernilai fitness tertinggi tersebut tidak hilang selama proses evolusi, maka perlu dibuat satu atau beberapa kopinya. Prosedur inilah yang dikenal sebagai elitisme.
Proses ini dilakukan untuk mempertahankan individu yang terbaik dari tiap generasi, karena setelah dilakukan proses perkawinan silang dan mutasi, kemungkinan untuk kehilangan kromosom yang terbaik sangat besar. Proses elitisme ini dilakukan dengan menggantikan kromosom terburuk dari generasi
berikutnya dengan kromosom terbaik dari generasi sebelumnya apabila kromosom yang baru tersebut tidak lebih buruk dari yang lama.
g. Evaluasi Solusi
Proses ini akan mengevaluasi setiap populasi dengan menghitung nilai fitness setiap kromosom dan mengevaluasinya sampai terpenuhi kriteria
berhenti. Beberapa kriteria berhenti yang sering digunakan antara lain:
1. Berhenti pada generasi tertentu.
2. Berhenti setelah dalam beberapa generasi berturut-turut didapatkan nilai fitness tertinggi tidak berubah.
3. Berhenti bila dalam n generasi berikut tidak didapatkan nilai fitness yang lebih tinggi.
2.3.4 Parameter Genetik
Yang disebut dengan parameter disini adalah parameter kontrol Algoritma Genetika, yaitu: ukuran populasi (popsize), probabilitas crossover (peluang
crossover-c
ρ ) dan probabilitas mutasi (peluang mutasi-ρm ). Nilai parameter ini ditentukan juga berdasarkan permasalahan yang akan dipecahkan. Tidak ada aturan pasti tentang berapa nilai setiap parameter ini. (Koza, 2001). Ukuran populasi kecil berarti hanya tersedia sedikit pilihan untuk crossover dan sebagian kecil dari domain solusi saja yang dieksplorasi untuk setiap generasinya. Sedangkan bila terlalu besar, kinerja Algoritma Genetika menurun. Penelitian menunjukkan ukuran populasi besar tidak mempercepat proses pencarian solusi. Disarankan ukuran populasi berkisar antara 20-30, probabilitas crossover umumnya berkisar antara 0,6 sampai dengan 0,9 dan probabilitas mutasi kecil
berkisar 0.5%-1% atau sekitar 1 dibagi dengan jumlah gen. Jumlah generasi besar berarti semakin banyak iterasi yang dilakukan, dan semakin besar domain solusi yang akan dieksplorasi (Nico saputro dan Yento, 2004).
Menurut Kusumadewi dan Purnomo (2005), ada beberapa rekomendasi yang bisa digunakan untuk menentukan nilai parameter tersebut, antara lain :
1. Untuk permasalahan yang memiliki kawasan solusi cukup besar, De Jong merekomendasikan untuk nilai parameter control :
2. Bila rata-rata fitness setiap generasi digunakan sebagai indikator, maka Grefenstette merekomendasikan :
(popsize; ρc; ρm) = (30; 0,95; 0,01)
3. Bila fitness dari individu terbaik dipantau pada setiap generasi, maka usulannya adalah :
(popsize; ρc; ρm) = (80; 0,45; 0,01)
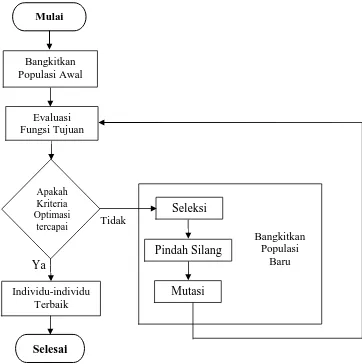
2.3.5 Mekanisme Kerja Algoritma Genetika
Algoritma Genetika dimulai dengan pembentukan sejumlah solusi yang dilakukan secara acak. Sebuah solusi yang dibangkitkan dalam Algoritma Genetika disebut sebagai kromosom, sedangkan kumpulan kromosom-kromosom tersebut disebut sebagai populasi. Sebuah kromosom dibentuk dari komponen-komponen penyusun disebut sebagai gen dan nilainya dapat berupa bilangan numerik, biner, simbol ataupun karakter tergantung dari permasalahan yang ingin diselesaikan.
Kromosom-kromosom tersebut akan berevolusi secara berkelanjutan yang disebut dengan generasi. Dalam tiap generasi, kromosom-kromosom tersebut dievaluasi tingkat keberhasilan nilai solusinya terhadap masalah yang ingin diselesaikan dengan menggunakan ukuran yang disebut dengan nilai fitness. Untuk memilih kromosom yang tetap dipertahankan untuk generasi selanjutnya dilakukan proses yang disebut dengan seleksi. Proses seleksi kromosom menggunakan konsep teori evolusi Darwin yaitu kromosom yang mempunyai nilai fitness tinggi akan memiliki peluang lebih besar untuk terpilih lagi pada generasi selanjutnya.
Ya
Tidak
Bangkitkan Populasi
Baru
beberapa generasi akan dihasilkan kromosom-kromosom yang nilai gen-gennya konvergen ke suatu nilai tertentu yang merupakan solusi terbaik yang dihasilkan oleh Algoritma Genetika terhadap permasalahan yang ingin diselesaikan.
Secara umum, blok diagram dari mekanisme kerja Algoritma Genetika ini adalah seperti yang terlihat pada gambar Gambar 2.3.
Gambar 2.2 Mekanisme Kerja Algoritma Genetika Bangkitkan
Populasi Awal
Mulai
Evaluasi Fungsi Tujuan
Individu-individu Terbaik
Apakah Kriteria Optimasi
tercapai
Selesai
Seleksi
Pindah Silang
BAB 3
ANALISIS DAN PERANCANGAN
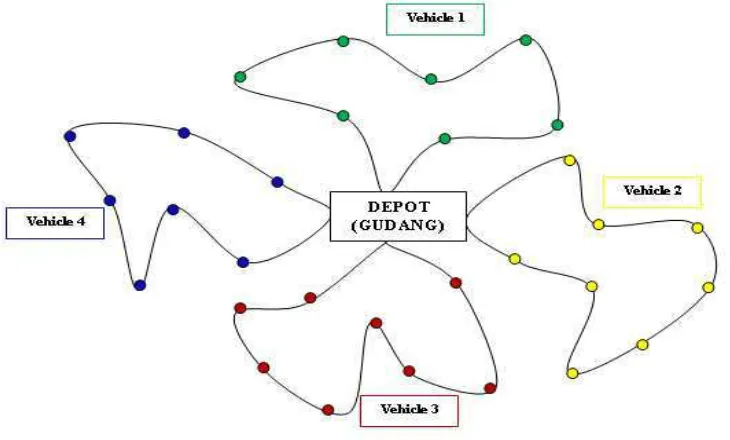
Gambaran umum permasalahan Vehicle Routing Problem with Delivery and Pick-Up adalah sebagai berikut. Andaikan ada satu jenis komuniti ditempatkan di sebuah depot/gudang (i=0) dengan K kendaraan (vehicle) yang berpangkalkan di depot yang mempunyai kapasitas sama yaitu W. Andaikan ada N pelanggan (customer) dinyatakan dengan i=1,2,3, …, N dengan masing-masing permintaan sebesar di, 1 ≤ i ≤ N, jarak
antara dua lokasi i dan j diketahui sebesar Cij, 1 ≤ i≠j ≤ N, jarak tempuh maksimum yang diijinkan adalah T. Masalah utama dalam VRP ini adalah bagaimana menentukan rute untuk K kendaraan tersebut sedemikian sehingga setiap pelanggan terlayani oleh tepat satu kendaraan, permintaan terpenuhi, muatan sepanjang rute tidak melampui kapasitas W, panjang rute dari depot keliling kembali ke depot lagi tidak melampui T dan akhirnya jumlah total panjang rute seluruh K kendaraan minimum (Sarwadi, 1995).
3.1 Analisis Kebutuhan
Implementasi yang dibuat menggunakan metode algoritma genetika, karena dapat merepresentasikan bilangan bulat (integer). Pemakaian algoritma genetika dalam penyelesaian Vehicle Routing Problem with Delivery and Pick-Up (VRP-DP), dilakukan simulasi pada beberapa kasus dengan jumlah node yang bervariasi. Untuk mengetahui bagaimana penerapan algoritma genetika dalam menyelesaiakan VRP-DP, dibuatkan dengan sebuah program Matlab 6.1.
3.1.1 Analisis Kebutuhan Masukan (Input)
Proses input atau masukan dari aplikasi dalam optimasi VRP-DP ini, berupa parameter-parameter yang diperlukan dalam Algoritma Genetika yaitu:
1. Data jumlah node yang digunakan. 2. Data jarak antar node.
3. Parameter-parameter yang diperlukan dalam perhitungan Algoritma Genetika, yaitu:
1. Ukuran Populasi (Popsize) = 50
2. Peluang Crossover (ρc) = 0.6 sampai dengan 0.9 3. Peluang Mutasi (ρm) = 0.03
4. Maksimum Generasi = 100
5. Panjang Kromosom/Jumlah Gen = 31
3.1.2 Analisis Kebutuhan Proses
Kebutuhan proses yang dilakukan pada sistem menentukan jalur terpendek dalam penyelesaian VRP ini antara lain:
1. Proses penentuan jarak antar node
2. Proses penentuan sub-rute dengan memperhatikan kapasitas kendaraan dan delivery demand and pickup demand
4. Proses penggabungan subrute yang terbentuk.
3.1.3 Analisis Kebutuhan Keluaran (Output)
Data keluaran yang diperoleh dari proses penyelesaian VRP-DP dengan Algoritma Genetika ini adalah rute jalur melewati setiap titik yang terdiri dari 31 node (termasuk depot) yang telah ditentukan disertai dengan jarak antar node serta panjang jalur minimumnya dan diperoleh juga grafik fitness rata-ratanya.
3.1.4 Kebutuhan Perangkat Lunak
Untuk penyelesaian VRP-DP dalam meminimalkan total jarak tempuh supaya menghasilkan biaya pengoperasian kendaraan minimal, perancangan aplikasi dilakukan dengan menggunakan bahasa pemrograman Matlab 6.1. Matlab juga sering digunakan pada teknik-teknik komputasi lainnya. Matlab juga menyediakan fasilitas-fasilitas untuk komputasi, visualisasi, dan pemrograman. Matlab juga dapat menghilangkan kesulitan dari pengetikan perintah-perintah yang menyulitkan, karena Matlab merupakan suatu aplikasi yang berbasis matematika.
Perangkat keras komputer tidak berarti tanpa perangkat lunak begitu juga sebaliknya. Jadi perangkat lunak dan perangkat keras saling mendukung satu sama lain. Perangkat keras hanya berfungsi jika diberikan instruksi-intruksi kepadanya. Instruksi-instruksi inilah disebut dengan perangkat lunak. Dalam penelitian ini penyusun menggunakan perangkat lunak MATLAB 6.1 Release 12.1, The Mathworks, Inc.
3.1.5 Kebutuhan Perangkat Keras
terdiri dari 2 bagian yaitu perangkat keras dan perangkat lunak. Perangkat lunak memberikan instruksi-instruksi kepada perangkat keras untuk melakukan suatu tugas tertentu.
Penggunaan komputer sebagai alat bantu suatu kejadian yang benar-benar terjadi dikehidupan nyata sering kali digunakan. Perangkat keras komputer yang digunakan adalah perangkat keras yang dapat mendukung perangkat lunak yang memiliki kemampuan atau tampilan grafis yang cukup baik. Perangkat keras yang digunakan pada program Algoritma Genetika untuk VRP-DP dalam menentukan jalur yang terpendek dari beberapa node yang telah ditentukan adalah sebuah personal notebook dengan spesifikasi sebagai berikut :
1. Processor Intel Celeron CPU @ 2.17GHz 2. RAM 768 MB
3. Hardisk 160 GB
4. O/S Windows XP Profesioanal SP3
5. Aplikasi Matlab 6.1 Release 12.1, The Math Work, Inc.
1.2 Perancangan Perangkat Lunak
Perancangan perangkat lunak dibuat dengan menggunakan bahasa pemrograman Matlab dengan tampilan Figure. Perancangan aplikasi yang dibuat pada dasarnya mengikuti metode Algoritma Genetika yang disajikan oleh penulis. Program yang dibuat berdasarkan langkah demi langkah untuk menyelesaikan VRP-DP dengan Algoritma Genetika.
3.2.1 Penerapan Algoritma Genetika Untuk Penyelesaian Vehicle Routing
Problem With Delivery And Pick-Up (VRP-DP)
1. Pengkodean kromosom
beserta kapasitas kendaraan yang digunakan. Kemudian rute yang terbentuk di representasikan dalam suatu kromosom yang berisi gen-gen. Jumlah gen dari setiap kromosom sama dengan jumlah outlet. Masing-masing nomor urut node muncul sekali di dalam suatu kromosom dan dibangkitkan secara acak dengan menggunakan perintah yang ada pada Matlab.
2. Inisialisasi Populasi
Tahap ini bertujuan untuk membangkitkan sebuah populasi yang berisi sejumlah kromosom. Setiap kromosom berisi sejumlah gen. Masukan untuk fungsi ini adalah ukuran populasi (jumlah kromosom dalam populasi) dan jumlah gen dalam satu kromosom.
3. Menentukan nilai fitness
Dalam penyelesaian VRP-DP yaitu untuk meminimalkan total jarak perjalanan yang dilalui salesman sehingga biaya perjalanan dapat diminimalisasi. Oleh karena itu, nilai fitness yang bisa digunakan adalah 1 dibagi dengan total jarak subrute. Dalam hal ini yang dimaksud dengan total jarak subrute adalah jumlah jarak antara node dengan kota yang lainnya secara melingkar. Misalkan, untuk sejumlah n node, total biaya adalah jarak node 1 ke node 2 ditambah jarak dari node 2 ke node 3 dan seterusnya sampai dengan jarak dari kota n kembali ke node 1.
4. Seleksi
Seleksi yang digunakan pada penyelesaian VRP-DP ini adalah dengan metode roulette wheel (roda roulette). Pada tahap ini masing-masing kromosom
5. Proses Perkawinan Silang (crossover)
Pada tahap ini, akan dimilih dua kromosom induk yang akan mengalami proses perkawinan silang secara acak, kemudian menentukan titik potongnya. Setelah titik potongnya terpilih, maka dilakukan penukaran informasi dari kedua kromosom tersebut berdasarkan titik potong yang telah ditentukan. Pada proses ini, akan dihasilkan kromosom anak hasil dari perkawinan silang kedua induknya, dimana kromosom anak ini berisi gen-gen gabungan dari bagian kromosom parent.
6. Proses mutasi
Proses mutasi yaitu penukaran pasangan gen yang telah terpilih secara random dalam satu kromosom. Penukaran pasangan ini dilakukan pada dua gen dalam suatu kromosom. Untuk semua gen dalam kromosom, jika bilangan random [0,1] yang dibangkitkan kurang dari probabilitas mutasi, maka nilai gen tersebut akan ditukarkan dengan nilai gen lain yang dipilih secara random.
7. Evaluasi
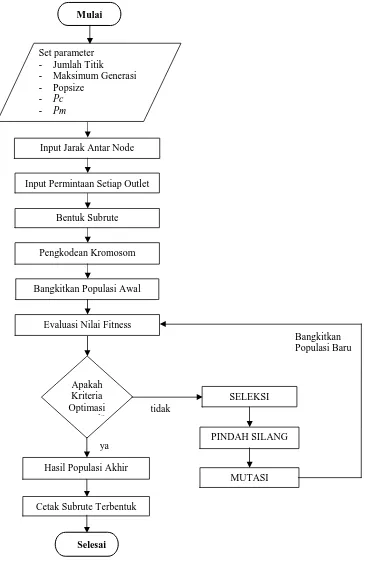
1.3 Diagram Alir (Flowchart)
Diagram alir di bawah ini adalah suatu bagan yang menggambarkan langkah-langkah penyelesaian VRP-DP dengan penerapan Algoritma Genetika.
Gambar 3. 1 Diagram Alir Penyelesaian VRP-DP
Set parameter - Jumlah Titik - Maksimum Generasi - Popsize
- Pc
- Pm
Input Permintaan Setiap Outlet
Pengkodean Kromosom
Bangkitkan Populasi Awal
Evaluasi Nilai Fitness
Apakah Kriteria Optimasi tercapai?
Hasil Populasi Akhir
Cetak Subrute Terbentuk ya
tidak
SELEKSI
PINDAH SILANG
MUTASI
Bangkitkan Populasi Baru Input Jarak Antar Node
Bentuk Subrute
Selesai
BAB 4
HASIL DAN PEMBAHASAN
Pada bab ini akan dilakukan uji coba dan evaluasi terhadap perangkat lunak dengan data yang ada. Uji coba dan evaluasi perangkat lunak dilakukan untuk menyelesaian VRP-DP dengan metode algoritma genetika, mengevaluasi jalannya program, menganalisa dampak, dan memperbaikinya jika ada kekurangan.
4.1 Pengkodean Kromosom
Pada tahap ini pengkodean kromosom yang dilakukan merupakan suatu proses yang sulit dalam algoritma genetika. Hal ini disebabkan karena proses pengkodean untuk setiap permasalahan berbeda-beda dan tidak semua teknik pengkodean cocok untuk setiap permasalahan. Proses pengkodean ini menghasilkan suatu deretan yang kemudian disebut kromosom. Dalam kasus ini yang digunakan adalah pengkodean permutasi (permutation encoding).
Daftar variabel input beserta asumsinya adalah sebagai berikut
1. Data set demand dan pick-up untuk masing-masing node yang ditunjukkan pada
Tabel 4.1.
2. Data jarak antar node dapat dilihat pada Tabel 4.2. 3. Setiap node harus dikunjungi hanya sekali.
Tabel 4.1 Data node beserta jumlah delivery dan pick-up
Outlet Delivery
Ammount
Pick-Up Ummount
Total Ummount
1(Depot) 0 0 0
2 7 7 14
3 5 7 11
4 4 4 8
5 5 3 8
6 7 4 11
7 8 7 15
8 6 4 10
9 5 3 8
10 10 10 20
11 9 6 15
12 18 11 29
13 11 10 21
14 6 4 10
15 10 14 24
16 7 8 15
17 9 11 20
18 12 14 26
19 13 13 26
20 9 7 16
21 8 8 16
22 4 5 9
23 6 10 16
24 10 13 23
25 3 5 8
26 16 11 27
27 5 6 11
28 8 6 14
29 10 7 17
30 7 9 16
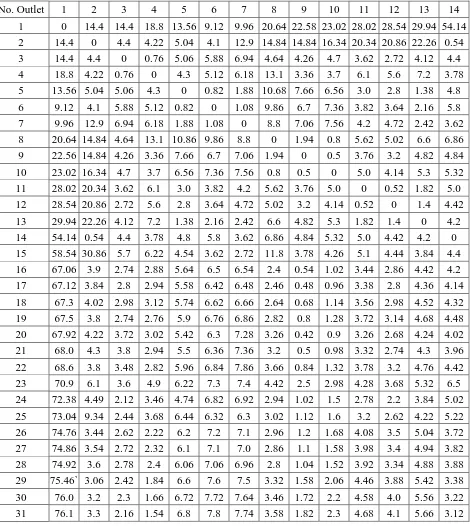
Tabel 4.2. a Data jarak antar node
No. Outlet 1 2 3 4 5 6 7 8 9 10 11 12 13 14
1 0 14.4 14.4 18.8 13.56 9.12 9.96 20.64 22.58 23.02 28.02 28.54 29.94 54.14 2 14.4 0 4.4 4.22 5.04 4.1 12.9 14.84 14.84 16.34 20.34 20.86 22.26 0.54
3 14.4 4.4 0 0.76 5.06 5.88 6.94 4.64 4.26 4.7 3.62 2.72 4.12 4.4 4 18.8 4.22 0.76 0 4.3 5.12 6.18 13.1 3.36 3.7 6.1 5.6 7.2 3.78 5 13.56 5.04 5.06 4.3 0 0.82 1.88 10.68 7.66 6.56 3.0 2.8 1.38 4.8
6 9.12 4.1 5.88 5.12 0.82 0 1.08 9.86 6.7 7.36 3.82 3.64 2.16 5.8 7 9.96 12.9 6.94 6.18 1.88 1.08 0 8.8 7.06 7.56 4.2 4.72 2.42 3.62
8 20.64 14.84 4.64 13.1 10.86 9.86 8.8 0 1.94 0.8 5.62 5.02 6.6 6.86 9 22.56 14.84 4.26 3.36 7.66 6.7 7.06 1.94 0 0.5 3.76 3.2 4.82 4.84 10 23.02 16.34 4.7 3.7 6.56 7.36 7.56 0.8 0.5 0 5.0 4.14 5.3 5.32
11 28.02 20.34 3.62 6.1 3.0 3.82 4.2 5.62 3.76 5.0 0 0.52 1.82 5.0 12 28.54 20.86 2.72 5.6 2.8 3.64 4.72 5.02 3.2 4.14 0.52 0 1.4 4.42 13 29.94 22.26 4.12 7.2 1.38 2.16 2.42 6.6 4.82 5.3 1.82 1.4 0 4.2
14 54.14 0.54 4.4 3.78 4.8 5.8 3.62 6.86 4.84 5.32 5.0 4.42 4.2 0 15 58.54 30.86 5.7 6.22 4.54 3.62 2.72 11.8 3.78 4.26 5.1 4.44 3.84 4.4
16 67.06 3.9 2.74 2.88 5.64 6.5 6.54 2.4 0.54 1.02 3.44 2.86 4.42 4.2 17 67.12 3.84 2.8 2.94 5.58 6.42 6.48 2.46 0.48 0.96 3.38 2.8 4.36 4.14 18 67.3 4.02 2.98 3.12 5.74 6.62 6.66 2.64 0.68 1.14 3.56 2.98 4.52 4.32
19 67.5 3.8 2.74 2.76 5.9 6.76 6.86 2.82 0.8 1.28 3.72 3.14 4.68 4.48 20 67.92 4.22 3.72 3.02 5.42 6.3 7.28 3.26 0.42 0.9 3.26 2.68 4.24 4.02 21 68.0 4.3 3.8 2.94 5.5 6.36 7.36 3.2 0.5 0.98 3.32 2.74 4.3 3.96
22 68.6 3.8 3.48 2.82 5.96 6.84 7.86 3.66 0.84 1.32 3.78 3.2 4.76 4.42 23 70.9 6.1 3.6 4.9 6.22 7.3 7.4 4.42 2.5 2.98 4.28 3.68 5.32 6.5 24 72.38 4.49 2.12 3.46 4.74 6.82 6.92 2.94 1.02 1.5 2.78 2.2 3.84 5.02
25 73.04 9.34 2.44 3.68 6.44 6.32 6.3 3.02 1.12 1.6 3.2 2.62 4.22 5.22 26 74.76 3.44 2.62 2.22 6.2 7.2 7.1 2.96 1.2 1.68 4.08 3.5 5.04 3.72
27 74.86 3.54 2.72 2.32 6.1 7.1 7.0 2.86 1.1 1.58 3.98 3.4 4.94 3.82 28 74.92 3.6 2.78 2.4 6.06 7.06 6.96 2.8 1.04 1.52 3.92 3.34 4.88 3.88 29 75.46` 3.06 2.42 1.84 6.6 7.6 7.5 3.32 1.58 2.06 4.46 3.88 5.42 3.38
Tabel 4.2.b Data jarak antar node (lanjutan)
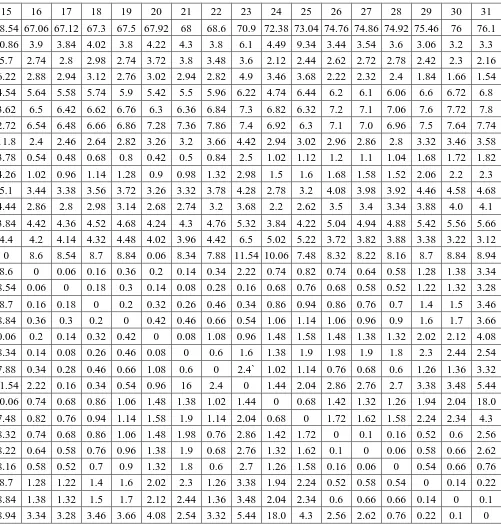
15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31
58.54 67.06 67.12 67.3 67.5 67.92 68 68.6 70.9 72.38 73.04 74.76 74.86 74.92 75.46 76 76.1 30.86 3.9 3.84 4.02 3.8 4.22 4.3 3.8 6.1 4.49 9.34 3.44 3.54 3.6 3.06 3.2 3.3
5.7 2.74 2.8 2.98 2.74 3.72 3.8 3.48 3.6 2.12 2.44 2.62 2.72 2.78 2.42 2.3 2.16 6.22 2.88 2.94 3.12 2.76 3.02 2.94 2.82 4.9 3.46 3.68 2.22 2.32 2.4 1.84 1.66 1.54 4.54 5.64 5.58 5.74 5.9 5.42 5.5 5.96 6.22 4.74 6.44 6.2 6.1 6.06 6.6 6.72 6.8
3.62 6.5 6.42 6.62 6.76 6.3 6.36 6.84 7.3 6.82 6.32 7.2 7.1 7.06 7.6 7.72 7.8 2.72 6.54 6.48 6.66 6.86 7.28 7.36 7.86 7.4 6.92 6.3 7.1 7.0 6.96 7.5 7.64 7.74
11.8 2.4 2.46 2.64 2.82 3.26 3.2 3.66 4.42 2.94 3.02 2.96 2.86 2.8 3.32 3.46 3.58 3.78 0.54 0.48 0.68 0.8 0.42 0.5 0.84 2.5 1.02 1.12 1.2 1.1 1.04 1.68 1.72 1.82 4.26 1.02 0.96 1.14 1.28 0.9 0.98 1.32 2.98 1.5 1.6 1.68 1.58 1.52 2.06 2.2 2.3
5.1 3.44 3.38 3.56 3.72 3.26 3.32 3.78 4.28 2.78 3.2 4.08 3.98 3.92 4.46 4.58 4.68 4.44 2.86 2.8 2.98 3.14 2.68 2.74 3.2 3.68 2.2 2.62 3.5 3.4 3.34 3.88 4.0 4.1 3.84 4.42 4.36 4.52 4.68 4.24 4.3 4.76 5.32 3.84 4.22 5.04 4.94 4.88 5.42 5.56 5.66
4.4 4.2 4.14 4.32 4.48 4.02 3.96 4.42 6.5 5.02 5.22 3.72 3.82 3.88 3.38 3.22 3.12 0 8.6 8.54 8.7 8.84 0.06 8.34 7.88 11.54 10.06 7.48 8.32 8.22 8.16 8.7 8.84 8.94
8.6 0 0.06 0.16 0.36 0.2 0.14 0.34 2.22 0.74 0.82 0.74 0.64 0.58 1.28 1.38 3.34 8.54 0.06 0 0.18 0.3 0.14 0.08 0.28 0.16 0.68 0.76 0.68 0.58 0.52 1.22 1.32 3.28 8.7 0.16 0.18 0 0.2 0.32 0.26 0.46 0.34 0.86 0.94 0.86 0.76 0.7 1.4 1.5 3.46
8.84 0.36 0.3 0.2 0 0.42 0.46 0.66 0.54 1.06 1.14 1.06 0.96 0.9 1.6 1.7 3.66 0.06 0.2 0.14 0.32 0.42 0 0.08 1.08 0.96 1.48 1.58 1.48 1.38 1.32 2.02 2.12 4.08 8.34 0.14 0.08 0.26 0.46 0.08 0 0.6 1.6 1.38 1.9 1.98 1.9 1.8 2.3 2.44 2.54
7.88 0.34 0.28 0.46 0.66 1.08 0.6 0 2.4` 1.02 1.14 0.76 0.68 0.6 1.26 1.36 3.32 11.54 2.22 0.16 0.34 0.54 0.96 16 2.4 0 1.44 2.04 2.86 2.76 2.7 3.38 3.48 5.44 10.06 0.74 0.68 0.86 1.06 1.48 1.38 1.02 1.44 0 0.68 1.42 1.32 1.26 1.94 2.04 18.0
7.48 0.82 0.76 0.94 1.14 1.58 1.9 1.14 2.04 0.68 0 1.72 1.62 1.58 2.24 2.34 4.3 8.32 0.74 0.68 0.86 1.06 1.48 1.98 0.76 2.86 1.42 1.72 0 0.1 0.16 0.52 0.6 2.56
8.22 0.64 0.58 0.76 0.96 1.38 1.9 0.68 2.76 1.32 1.62 0.1 0 0.06 0.58 0.66 2.62 8.16 0.58 0.52 0.7 0.9 1.32 1.8 0.6 2.7 1.26 1.58 0.16 0.06 0 0.54 0.66 0.76 8.7 1.28 1.22 1.4 1.6 2.02 2.3 1.26 3.38 1.94 2.24 0.52 0.58 0.54 0 0.14 0.22
5. Alat transportasi selalu tersedia dalam kondisi baik.
6. Kepadatan lalu lintas dan kondisi jalan setiap harinya adalah normal.
7. Kapasitas kendaraan angkut 130 unit dan biaya sewa Rp.500.000,- dengan asumsi sewa per rute.
8. Biaya BBM kendaraan Rp. 4.500,-/liter dengan asumsi kendaraan tersebut per-liter mampu menempuh jarak 15 km.
9. Dalam permasalahan ini yang mempengaruhi adalah biaya pendistribusian adalah jarak tempuh.
Perhitungan selanjutnya adalah perhitungan-perhitungan fungsi tujuan, kendala dan perhitungan asumsi yang dibutuhkan seperti perhitungan total biaya sewa kendaraan, biaya perjalanan dan total biaya perjalanan. Untuk lebih jelasnya dapat dilihat perhitungan sebagai berikut ini.
1. Biaya sewa kendaraan = jumlah kendaraan dikali biaya sewa per kendaraan dengan jumlah kendaraan ≈ jumlah rute solusi yang dibentuk algoritma genetika. 2. Biaya kendaraan.
Biaya Kendaraan 4=>?8?@A8B 7>?@AC @>; 9D7>;56789 :8;8< E F Harga minyak per liter 3. Total biaya = biaya sewa kendaraan + biaya perjalanan
4.2 Inisialisasi Populasi dan Evaluasi Individu
Pada tahap inisialisasi individu akan dibangkitkan sebuah populasi yang berisi sejumlah kromosom yang berisi sejumlah gen. Masukan untuk fungsi ini adalah ukuran populasi (jumlah kromosom dalam populasi) dan jumlah gen dalam satu kromosom. Ukuran populasi tergantung pada masalah yang akan dipecahkan dan jenis operator genetika yang akan diimplementasikan. Setelah ukuran populasi ditentukan, kemudian harus dilakukan inisialisasi terhadap kromosom yang terdapat pada populasi tersebut. Inisialisasi kromosom dilakukan secara acak, namun demikian harus tetap memperhatikan domain solusi dan kendala permasalahan yang ada. Dalam populasi tersebut terdapat anggota populasi yang disebut dengan kromosom.
permasalahan ini yang dibahas adalah menentukan semua rute dengan jaral minimal dari 31 verteks, oleh sebab itu nilai fitness yang bisa digunakan adalah 1 / total jarak. Dalam hal ini yang dimaksud total jarak adalah jumlah jarak antara node dalam sebuah subrute yang merupakan solusi. Variabel yang digunakan untuk mencari nilai fitness yaitu populasi, jumlah gen, dan jarak antar node dalam suatu kromosom. Dari persoalan diatas maka selanjutnya dilakukan inisialisasi populasi dan evaluasi individu sebanyak ukuran populasi yaitu 50, peluang crossover dan peluang mutasi masing-masing 0.699 dan 0.03 serta maksimum generasinya adalah 100. Untuk membangkitkan kromosom ini, digunakan fungsi random yang telah tersedia dalam Matlab.
Untuk penyelesaian VRP-DP, kromosom dirancang dengan menggunakan prinsip pengacakan, dimana untuk perhitungan dilakukan hanya untuk jalur yang dilalui dari depot ke node dan kembali ke depot, dengan sisa kromosom (node yang tidak dilalui) berfungsi sebagai pelengkap agar kromosom tidak terpotong. Sintak selengkapnya adalah sebagai berikut:
Untuk menyatakan kromosom ke-ii pada populasi yang jumlah kolomnya sama dengan jumlah gen digunakan perintah Populasi(ii,:). Popsize menyatakan ukuran populasi atau jumlah kromosom dalam populasi, dimana nilainya dimasukkan lewat perintah
input ('Masukkan Ukuran Populasi: '). N menyatakan jumlah gen dalam kromosom,
dimana gen ini merepresentasikan jumlah kota yang ada. Nilai dari N dimasukkan melalui perintah input ('Masukkan Jumlah Gen : '). Perintah sort (rand(1,N)) menyatakan pembangkitan matriks berukuran 1 x N yang berisi bilangan random dalam interval 0 – 1 yang terurut dari kecil ke besar. Kemudian disimpan program ini dengan nama InisialisasiPopulasi.m melalui perintah save inisialisasi popsize N Populasi. Dari program di atas terbentuklah kromosom yaitu sebagai berikut.
43 2 16 5 20 30 3 18 27 22 7 8 19 14 31 24 13 10 25 28 1 26 11 17 15 21 9 4 23 6 12 29 0.00646
44 2 5 23 6 19 16 24 1 30 14 20 17 29 21 9 18 12 22 25 11 7 15 10 8 28 13 4 3 27 31 26 0.00883
45 2 12 3 30 25 26 18 22 23 31 4 10 8 28 20 15 9 11 29 24 5 27 6 17 1 16 7 21 13 14 19 0.00600
46 2 19 26 21 20 5 30 8 7 3 28 10 9 23 24 22 31 16 12 6 11 17 27 1 25 4 15 13 14 18 29 0.00649
47 2 6 5 14 16 12 8 1 3 11 27 22 21 29 23 17 19 20 28 15 7 24 25 9 18 4 30 26 10 13 31 0.01759
48 2 10 25 5 28 4 30 14 1 16 20 7 15 6 9 27 3 18 23 24 21 26 22 8 31 12 11 17 29 19 13 0.00938
49 2 12 25 20 13 9 17 15 10 3 29 22 31 5 21 1 30 6 14 28 26 19 7 11 16 18 23 24 4 27 8 0.00658
50 2 9 10 30 16 27 24 3 1 20 4 18 25 21 5 7 28 17 14 23 12
6 15 19 29 31 22 13 26 8 11 0.01939
. . .
4.3 Probabilitas Fitness
Probabilitas fitness adalah perhitungan masing-masing nilai fitness pada setiap kromosom dalam suatu populasi terhadap jumlah total nilai fitness-nya. Rumus yang digunakan nilai fitness dibagi total nilai fitness. Pada tahap ini juga dapat ditentukan nilai kumulatif dari probabilitasnya. Variabel yang digunakan untuk mencari probabilitas fitness yaitu popsize dan MaxGen. Keluarannya adalah probabilitas fitness dan nilai kumulatif dari probabilitasnya.
Probabilitas fitness
4.4 Seleksi Roda Roulette (Roulette Wheel Selection)
2 8 25 27 28 24 18 13 1 23 15 5 9 14 7 21 31 26 19 29 16 30
memindah-silangkan dua buah kromosom. Pada tahap ini, pilih dua kromosom induk yang akan mengalami perkawinan silang secara acak, kemudian tentukan titik potongnya. Setelah itu lakukan pertukaran informasi dari kedua kromosom tersebut berdasarkan titik potong yang telah ditentukan.
1 21821 513 111141729 922302620 61531 310 716 412272824231925 8 0.01802 1
2 22012302722 92625161014 1 3242128191723 6 7113115 4 5291813 8 0.01093 2
3 219 8131626312721 6 9 3 11822 51524 7141217 42028101125232930 0.01478 3
4 2 8252728241813 12315 5 914 7213126192916301011 6 4 322201217 0.01418 5
5 2 9 4 6201415181127 828 7 1263012292423 32521311713 519161022 0.01096 6
6 222181028 323172927 61625 1 5 420211419261524 9313013 71112 8 0.00856 7
7 2131429 6201718222123 7262816 327121024 5 930 4 831251915 111 0.00516 8
8 2 71121131816311424 6 1301528 5 41023121922 317262529 8 92720 0.01431 9
9 2 3 819251315 1 9291714213122 628 724232018 43012111626 51027 0.01064 11
10 21223241729 725 61928301411 12018163122 913 4 32110 526 81527 0.00934 12
11 2211627 3201729 110302326131519 725 6 4141112282218 9 824 531 0.00980 13
12 21910 31630222623311117121829281420 625 927 42421 113 8 5 715 0.00664 14
13 219281310291223 122 31730 4111627212018 5 7263124 6 925 81514 0.00920 18
14 22018 3152924 61719 725 421 922271431 5121026 13011 813281623 0.00585 19
15 222301619241021 9 1152711 72012 3131725 5 823182814 6293126 4 0.02096 20
16 223173028241631291211 4 3 819212610 92214 51325 7 1 615272018 0.01229 21
17 21811101615 8 5 1221729 720233014271225 9 6133119212624 3 428 0.01377 22
18 21729101813223123 62827162421 13019 3151225 520 91126 414 7 8 0.00825 24
19 2 3291721221016 9 130122811 627 4181431231920 71326 5 8251524 0.02050 25
21 2143126272829 9 1102524162022302313 621 4 7 5 8 3111518191217 0.02349 28
22 2 919 6 423 7 117262913102718 528 811 32216212530312012152414 0.01558 29
23 2 81115 5132726241225203123192814 11610 4 3 6 9 7182229213017 0.00808 30
24 21420 6172913273118 8 4 91519232611 32212 725 5 1241028301621 0.00793 32
25 2121122142030 116 72615 8241319 331 410 5182928 9172125 62327 0.00797 33
26 22113241210 32611 11627 5 42214 92923 8182531 7 6281930201715 0.01377 34
27 2 81026 630 922 3132019 1181714 7292127 52825121131 416241523 0.00777 35
28 21218 3 8192820 1 5152726233125241614 730 6112113 922 4291710 0.00842 36
29 212 8 916292315252710 7 11913 524172030 3 626 422111831211428 0.01151 37
30 21928 62322 8292112 41514111718301031162013 7 327 525 9 12426 0.00762 39
31 2162917183128302421 82010 9 711 41527 5 12623 312 61419222513 0.01155 40
32 210202118 4 92325242913 32628 8151714123122 1 52719 7163011 6 0.00614 41
33 219291831 81114 6 11727202124102226 9 32513152328301216 4 5 7 0.01945 42
34 216 52030 3182722 7 81914312413102528 12611171521 9 423 61229 0.00646 43
35 2 523 6191624 1301420172921 91812222511 71510 82813 4 3273126 0.00883 44
36 212 330252618222331 410 8282015 9112924 527 617 116 721131419 0.00600 45
37 219262120 530 8 7 32810 9232422311612 6111727 125 41513141829 0.00649 46
38 2 6 5141612 8 1 31127222129231719202815 72425 918 43026101331 0.01759 47
39 21025 528 43014 11620 715 6 927 3182324212622 831121117291913 0.00938 48
40 212252013 9171510 3292231 521 130 614282619 71116182324 427 8
0.00658 49
. . .
4.6 Swap Mutation
random [0,1] yang dibangkitkan kurang dari probabilitas mutasi, maka nilai gen tersebut akan ditukar dengan nilai gen lain yang dipilih secara random. Hal ini berlaku untuk semua gen dalam kromosom. Nilai dari probabilitas mutasi adalah
gen Jumlah
1
. Untuk kasus diatas maka peluang mutasinya adalah
N 0.0322581 atau bila dibulatkan
2 62216 42123 13028 8191027261418291731 911 3201225 7 5151324 0.010
Proses Mutasi:
Kromosom dihilangkan & Pengganti: hilang:
42
2 919 6 423 7 117262913102718 528 811 32216212530312012152414 0.01558
Ganti : 28
2211627 3201729 110302326131519 725 6 4141112282218 9 824 531 0.00980
hilang: 38
2 523 6191624 1301420172921 91812222511 71510 82813 4 3273126 0.00883
Ganti : 20
216 52030 3182722 7 81914312413102528 12611171521 9 423 61229 0.00646
hilang: 32
21729101813223123 62827162421 13019 3151225 520 91126 414 7 8 0.00825
Ganti : 25
2 3291721221016 9 130122811 627 4181431231920 71326 5 8251524 0.02050
hilang: 17
2162917183128302421 82010 9 711 41527 5 12623 312 61419222513 0.01155
Ganti : 42
0.02349 hilang: 39
2 6 91113231225 7 11828271420262919 4211530 31716 5 824311022 0.01705
Ganti : 50
4.7 Hasil Penyelesaian VRP-DP
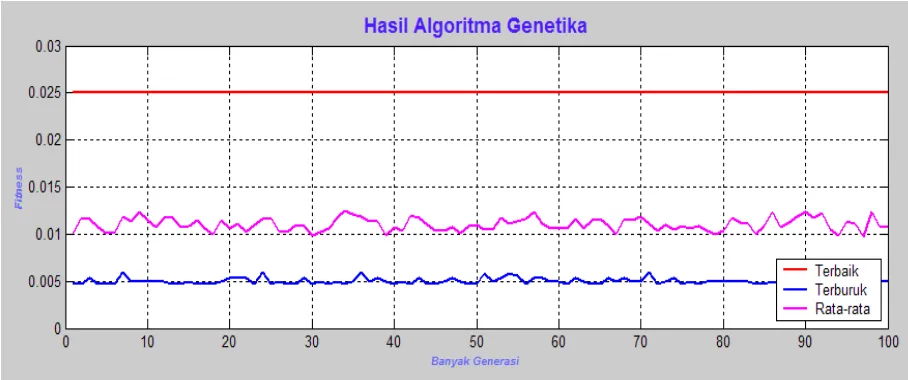
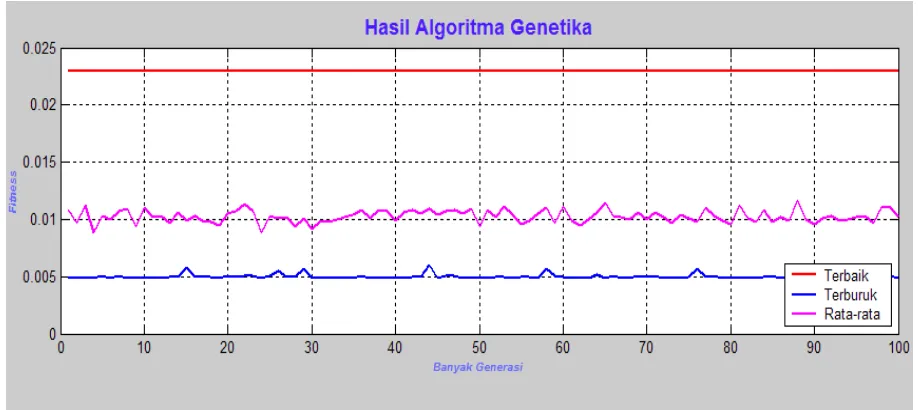
Pada tahap ini, parameter-parameter genetika yang ditentukan berdasarkan setiap subrute, yaitu probabilitas mutasi adalah 0.03, ukuran populasi adalah 50, jumlah gen adalah 31, maksimum generasi adalah 100 dan probabilitas perkawinan silang (ρc) diset 0,690. Hasil yang diperoleh adalah sebuah subrute-subrute dengan jarak minimal dapat dilihat pada Gambar 4.1.a, Gambar 4.2.b, Gambar 4.2.c dan Gambar 4.2.d.
Gambar 4.2.a Subrute 1
Gambar 4.2.c Subrute 3
Gambar 4.2.d Subrute 4
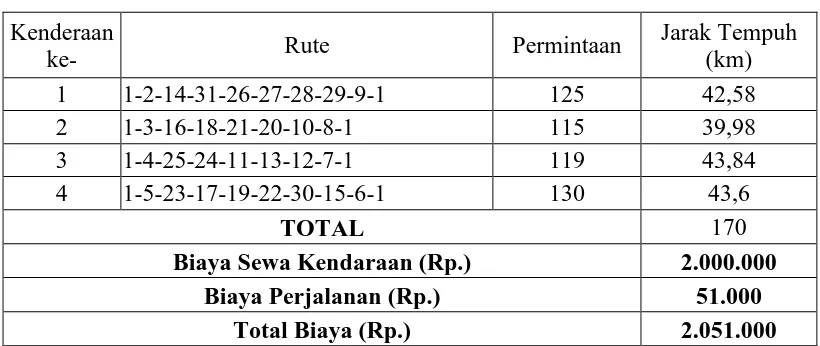
Tabel 4.3 Subrute yang diperoleh melalui proses AG
Kenderaan
ke- Rute Permintaan
Jarak Tempuh (km)
1 1-2-14-31-26-27-28-29-9-1 125 42,58
2 1-3-16-18-21-20-10-8-1 115 39,98
3 1-4-25-24-11-13-12-7-1 119 43,84
4 1-5-23-17-19-22-30-15-6-1 130 43,6
TOTAL 170
Biaya Sewa Kendaraan (Rp.) 2.000.000
Biaya Perjalanan (Rp.) 51.000
Total Biaya (Rp.) 2.051.000
Dari tabel diatas dapat dilihat jumlah total jarak tempuh seluruh subrute yaitu sejauh 170 km dengan perhitungan sebagai berikut.
1. Dari hasil uji coba program dibutuhkan kurang dari 13,5 liter bahan bakar minyak. 2. Jumlah permintaan dari setiap rute tidak lebih dari kapasitas kendaraan yaitu 130. 3. Biaya perjalanan untuk total subrute adalah sebesar Rp.51.000,-.
BAB 5
KESIMPULAN DAN SARAN
Kesimpulan yang diperoleh dari analisa dari bab sebelumnya adalah sebagai berikut:
1. Dalam hasil uji program tersebut diperoleh jarak tempuh kendaraan yang digunakan dalam pengiriman barang menggunakan subrute-subrute yang diusulkan adalah 170 km (Tabel 4.3).
2. Dalam permasalahan ini yang mempengaruhi biaya pendistribusian barang adalah total jarak tempuh. Dengan demikian biaya total pendistribusian barang dapat berkurang karena jaraknya yang lebih minimum.
3. Untuk penyelesaian VRP-DP, kromosom dirancang menggunakan prinsip pengacakan, dimana untuk perhitungan dilakukan hanya untuk node yang dilalui dari depot dan kembali lagi ke depot, dengan sisa kromosom (node yang tidak dilalui) berfungsi sebagai pelengkap agar kromosom tidak terpotong.
Adapun saran–saran yang perlu diperhatikan untuk pengembangan metode ini adalah sebagai berikut:
1. Untuk memperoleh hasil yang lebih akurat, sebaiknya dalam penelitian lebih lanjut perlu mempertimbangkan penggunaan software yang lebih mutakhir yang lebih mempertimbangkan banyak variabel (sesuai kondisi lapangan) selain memperhatikan jarak antar outlet.
2. Aplikasi yang dirancang masih dalam tampilan figure, akan lebih baik jika ditambahkan Graphic User Interface (GUI) sehingga lebih memudahkan pengguna untuk menginputkan parameter-parameter yang diperlukan secara langsung.
DAFTAR PUSTAKA
Arhami, M. dan Desiani, A. 2005. Pemrograman MATLAB. Edisi ke-1. Yogyakarta: Andi.
Away, G. A. 2006. The Shortcut of MATLAB Programming. Jilid 1. Bandung: Informatika Bandung.
Darmanius. 2008. Pemodelan Vehicle Routing Problem Terbuka dengan Keterbatasan Waktu. M.Si. Tesis. Medan, Indonesia: Universitas Sumatera Utara.
Hannawati, Anies., Thiang, dan Eleazar. 2002. Pencarian rute optimum menggunakan algoritma genetika. Jurnal Teknik Elektro Vol.2, No.2, September 2002; hal. 78-83.
Hendarto, Janoe. 2007. “Modul Pengantar Analisis Algoritma”. Jurnal Ilmu Komputer Universitas Gajah Mada. Yogyakarta. Diakses tanggal 18 Januari 2009.
Goldberg, D. E. 1989. Genetic Algorithms in Search, Optimization and Machine Learning. Canada: Addison-Wesley Publishing.
Kusumadewi, S. dan Purnomo, Hari. 2005. Penyelesaian Masalah Optimasi Menggunakan Teknik-teknik Heuristik. Edisi Pertama. Yogyakarta; Penerbit Graha Ilmu.
Prana, Raden. “Aplikasi kombinatorial pada vehicle routing problem”. Makalah If16105.
Robandi, Imam. 2006. Desain Sistem Tenaga Modern, Optimasi, Logika Fuzzy, dan Algoritma Genetika. Yogyakarta: Andi.
Sembiring, A. C. 2008. Penentuan Rute Distribusi Produk Yang Dioptimalkan Dengan Menggunakan Algoritma Heuristik Pada PT. Coca-cola Bootling Indonesia
Medan. Skripsi. Medan, Indonesia: Universitas Sumatera Utara
Sawardi dan Anjar KSW,. Algoritma Genetika untuk Penyelesaian Masalah Vehicle Routing. Jurnal Matematika dan Komputer Vol. 7. No. 2, 1-10, Agustus 2004, ISSN: 1410-8518.
Suyanto. 2005. Algoritma Genetika dalam MATLAB. Yogyakarta: Andi.
LAMPIRAN SINTAK PROGRAM 70.90 72.38 73.04 74.76 74.86 74.92 74.92 75.46 76.00;
% menentukan bobot antar titik
fprintf(fb,'Generasi ke %4d',generasi); fprintf(fb,'\n');
fprintf(fb,'%3d',selek(i,2:N+1));
fprintf(fb,'CROSSOVER ---> Bilangan random:'); fprintf(fb,'\n');
end; end;
fprintf(fb,'Kromosom kena mutasi:'); fprintf(fb,'\n');
%Mengganti kromosom secara acak dengan kromosom terbaik fprintf(fb,'Kromosom dihilangkan & Pengganti:');
fprintf(fb,'\n');
fprintf(fb,'%2d',pop(indek(popsize-no+1),2:N+1)); fprintf(fb,'\n');
fprintf(fb,'%10.5f',pop(indek(popsize-no+1),N+2)); fprintf(fb,'\n');
end;
%Hasil akhir setiap generasi
fprintf(fb,'%10.5f',pop(i,N+2));
xlabel('Banyak Generasi','color',[.4 .4 1],...
'fontweight','bold','fontangle','italic','fontsize',8); ylabel('Fitness','color',[.4 .4 1],...
'fontweight','bold','fontangle','italic','fontsize',8); title('Hasil Algoritma Genetika','color',[.3 .1 1],... 'fontweight','bold','fontsize',14); num2str(JalurBaru) ' ---> Total Jarak = ' num2str(PjgJalur1)]);