1
3. Graph Euler dan Graph Hamilton
Oleh : Ade Nurhopipah
Pokok Bahasan :
1. Masalah Exploring dan Travelling 2. Graph Euler
3. Graph Hamilton
Sumber :
Aldous, Joan M. ,Wilson, Robin J. 2004. Graph and Applications. Springer: UK.
Exploring dan Traveling
Pada bagian ini kita akan memperhatikan dua jenis masalah berkaitan dengan rute yang menghubungkan sejumlah kota dalam peta.
Masalah Exploring
Seorang explorer ingin menemukan suatu perjalanan yang melalui setiap jalan tepat satu kali dan kembali ke tempat semula.
Masalah Traveller
Seorang traveller ingin mengunjungi setiap kota tepat sekali dan kembali ke tempat semula.
Untuk memahami perbedaan antara kedua masalah tersebut, perhatikan peta jalan pada Gambar 3.1 berikut.
Gambar 3.1 Ilustrasi jalan antar kota
Seorang explorer ingin menemukan perjalanan yang dimulai dari kota a, lalu melewati setiap jalan tepat satu kali dan kembali ke kota awal a. Dua contoh perjalanan yang seperti ini adalah sebagai berikut.
a b c d e f b g c e g f a dan a f g c d e g b c e f b a
Selanjutnya traveler ingin menemukan perjalanan yang dimulai dari kota a, lalu melewati semua kota dan kembali ke kota a. Dua contoh perjalanan yang seperti ini adalah sebagai berikut.
2 Catat bahwa explorer melalui setiap jalan tepat satu kali, namun mungkin mengunjungi suatu kota tertentu beberapa kali. Sementara itu traveller menggunjungi kota tepat satu kali, namun mungkin tidak mengunjungi beberapa jalan yang ada.
Mari kita anggap peta jalan pada Gambar 3.1 tersebut sebagai graph terhubung dengan vertex mewakili kota dan edge mewakili jalan yang menghubungkan kota tersebut. Masalah explorer kini merupakan masalah mencari trail tertutup yang mencakup semua edge pada graph. Sedangkan masalah traveller merupakan masalah menemukan cycle yang mencakup semua vertex pada graph. Dengan konsep ini, kita mendapatkan definisi berikut.
Definisi 3.1
Suatu graph terhubung merupakan graph Euler jika ia memiliki trail tertutup yang memuat semua edge. Trail seperti ini disebut trail Euler.
Suatu graph terhubung merupakan graph Hamilton jika ia memiliki cycle yang memuat semua vertex. Cycle seperti ini disebut cycle Hamilton.
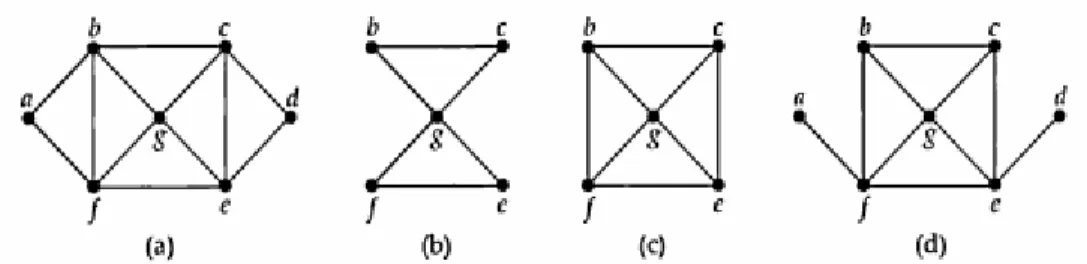
Sebagai contoh, perhatikan graph pada Gambar 3.2.
Graph (a) merupakan graph Euler dan juga graph Hamilton, seperti telah kita lihat pada Gambar 3.1 sebelumnya.
Graph (b) merupakan graph Euler, namun bukan graph Hamilton. Trail Euler yang mungkin adalah :
b c g f e g b
Graph (c) merupakan graph Hamilton, namun bukan graph Euler. Cycle Hamilton yang mungkin adalah : b c g e f b.
Graph (d) bukan merupakan graph Euler maupun graph Hamilton.
3
Latihan 3.1
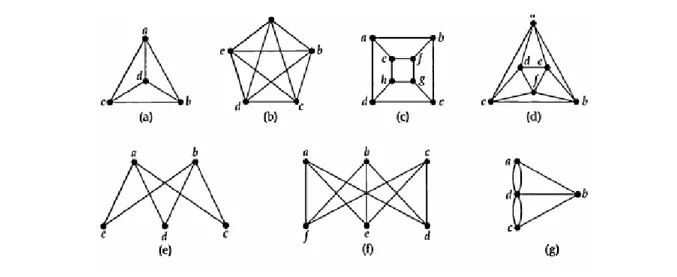
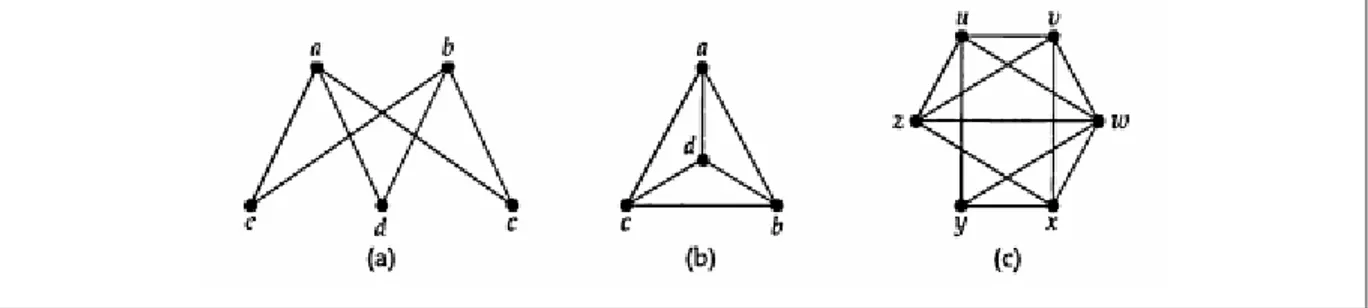
Tentukan graph berikut apakah merupakan graph Euler dan/atau graph Hamilton. Tulis suatu trail Euler atau cyce Hamilton yang anda temukan.
Grap Euler
Pada masalah jembatan Kὂnigsberg sebelumnya, kita merepresentasikan jembatan Kὂnigsberg ke dalam bentuk graph dengan vertex mewakili empat bagian kota dan edge mewakili tujuh jembatan seperti ditunjukan pada Gambar 3.3.
Gambar 3.3 Representasi graph untuk jembatan Kὂnigsberg
Masalah jembatan Kὂnigsberg adalah masalah bagaimana menemukan rute untuk menyebrangi setiap jembatan satu kali ternyata berkoresponden dengan pencarian suatu trail Euler pada graph representasinya. Kita telah mengetahui pula bahwa trail semacam ini tidak akan ada, atau tidak ada solusi untuk permasalahan jembatan Kὂnigsberg tersebut.
Euler menyajikan permasalahan yang sesuai dengan pencarian rute untuk melewati semua jembatan dengan susunan jembatan dan area kota yang lebih umum. Hal ini menuntunnya untuk memperkenalkan suatu aturan yang menunjukan kapan rute semacam itu mungkin ada. Graph dengan rute semacam ini selanjutnya disebut graph Euler.
4 Latihan 3.2
1. Menemukan sebuah rute menyebrangi jembatan satu kali dan kembali ke tempat semula merupakan masalah menemukan trail Euler pada graph yang mewakilinya. Hal ini mungkin terjadi jika kita menyebrangi jembatan menuju suatu bagian kota, kita juga harus bisa meninggalkan kota tersebut dengan jembatan yang lain.
Apa yang anda dapat simpulkan dengan derajat vertex pada graph Euler?
2. Dengan menggunakan hasil bagian 1, tebaklah aturan yang menjelaskan kapan suatu graph adalah graph Euler. Test aturan tersebut untuk graph pada latihan 3.1
Catatan Sejarah
Leonhard Euler (1707-1783), mungkin adalah matematikawan paling produktif sepanjang waktu. Ia memecahkan masalah jembatan Kὂnigsberg dalam sebuah paper penting berjudul Solutio
problematis ad geometriam situs pertinentis (Solusi dari masalah yang berhubungan dengan
posisi geometri)
Teorema 3.1
Misalkan G adalah sebuah graph yang setiap vertex-nya memiliki derajat genap, maka G dapat dibagi menjadi beberapa cycle, tidak ada dari dua cycle yang terbentuk memiliki edge yang sama. Bukti :
Misalkan G adalah graph yang semua vertex-nya memiliki derajat genap. Kita akan memperoleh cycle pertama di G dengan memulai di sebuah vertex u dan menelusuri edge secara sembarang tanpa mengunjungi semua edge dua kali. Karena setiap vertex memiliki derajat genap, ketika kita masuk pada satu vertex, kita akan mampu keluar dari vertex tersebut melalui edge yang berbeda. Karena kita memiliki jumlah vertex yang terbatas, maka kita akan bertemu dengan suatu vertex v yang kita temui sebelumnya. Oleh karena itu trail pada vertex v akan membentuk suatu cycle C1.
Kini kita menghapus semua edge dari cycle C1 sehingga tersisa graph G (mungkin tak terhubung) di mana setiap vertex memiliki derajat genap. Jika G memiliki edge lain selain yang ada di C1, kita dapat mengulangi prosedur tersebut sampai tidak ada edge yang tersisa, dan kita memperoleh C1,C2, C3…, Ck yang bersama-sama memuat setiap vertex di G, dan tidak ada dari dua
cycle tersebut yang memiliki edge yang sama seperti ditunjukan pada Gambar 3.4.
5 Latihan 3.3
Tunjukan bagaimana graph berikut dapat dibagi menjadi beberapa cycle, tidak ada dari dua cycle yang terbentuk, yang memiliki edge yang sama.
Bagaimana cycle ini dapat dikombinasikan untuk membentuk trail Euler?
Teorema 3.2
Sebuah graph adalah graph Euler jika dan hanya jika setiap vertex-nya memiliki derajat yang genap.
Teorema 3.2 memberikan syarat perlu dan syarat cukup untuk sebuah graph terhubung menjadi graph Euler. Hal ini ekuivalen dengan dua pernyataan untuk sebuah graph terhubung G sebagai berikut.
a. Jika G adalah graph Euler, maka setiap vertex G memiliki derajat yang genap. b. Jika setiap vertex G memiliki derajat yang genap, maka G adalah graph Euler. Bukti :
a. Jika G adalah graph Euler, maka setiap vertex G memiliki derajat yang genap.
Misalkan G adalah graph Euler, maka ia memiliki trail Euler. Ketika trail ini melewati sebuah vertex, maka ia memberi kontribusi 2 untuk derajat vertex tersebut. Karena setiap edge hanya dipakai satu kali, maka derajat setiap vertex adalah 2s yang pasti merupakan bilangan genap.
b. Jika setiap vertex G memiliki derajat yang genap, maka G adalah graph Euler.
Misalkan G adalah graph terhubung di mana setiap vertex memiliki derajat genap. Kita mengetahui dari Teorema 3.1 bahwa G dapat dibagi ke dalam beberapa cycle, dan tidak ada cycle yang mempunyai edge yang sama.
Kita tahu bahwa cycle ini bersama-sama membuat sebuah trail Euler. Kita mulai dari vertex manapun di cycle C1. Kelilingi C1 sampai kita bertemu dengan cycle lain, misalnya C2. Kita
melintasi edge pada cycle ini, sehingga kita mendapatkan sebuah trail tertutup yang memuat
C1 dan C2. Lanjutkan prosedur tersebut, seperti ditunjukan pada Gambar 3.5 sampai kita
mendapatkan cycle lain. Ketika kita sampai pada sebuah cycle, karena G terhubung, maka selalu ada setidaknya sebuah cycle untuk ditambahkan pada trail tersebut. Kita lanjutkan proses tersebut sampai semua cycle dikelilingi, atau trail tersebut telah melewati semua edge di G, sehingga kita mendapatkan trail Euler yang diinginkan. Oleh karena terdapat trail Euler, maka G adalah graph Euler.
6 Gambar 3.5 Ilustrasi pembuktian Teorema 3.2
Latihan 3.4
Pakai Teorema 3.2 untuk menentukan graph mana pada graph berikut yang merupakan graph Euler.
a. Graph komplit K8
b. Graph bipartit komplit K8,8
c. Graph cycle C8
d. Graph dodecahedron e. Graph cube Q8
Dengan mengkombinasikan Teorema 3.1 dan 3.2, kita mendapatkan teorema sebagai berikut.
Teorema 3.3
Sebuah graph dapat dibagi menjadi beberapa cycle, tidak ada dari dua cycle tersebut yang memiliki edge yang sama.
Graph Semi-Euler
Terdapat beberapa modifikasi dalam masalah jembatan Kὂnigsberg. Salah satu yang paling penting adalah, jika kita ingin menyebrangi semua jembatan yang dimulai dari suatu tempat, dan kita tidak perlu pulang ke tempat semula. Ide ini mengarah pada definisi 3.2 berikut.
Definisi 3.2
Sebuah graph adalah graph semi-Euler jika terdapat sebuah trail terbuka yang memuat setiap edge. Trail seperti ini disebut trail semi-Euler.
Teorema 3.4
Sebuah graph terhubung adalah graph semi-Euler jika dan hanya jika memiliki tepat dua vertex dengan derajat ganjil.
7 Teorema 3.4 memberikan syarat perlu dan syarat cukup untuk sebuah graph terhubung menjadi graph semi-Euler. Hal ini ekuivalen dengan dua pernyataan untuk sebuah graph terhubung G sebagai berikut.
a. Jika G adalah graph semi-Euler, maka G memiliki tepat dua vertex yang berderajat ganjil. b. Jika G memiliki tepat dua vertex yang berderajat ganjil, maka G adalah graph semi-Euler. Bukti :
a. Jika G adalah graph semi-Euler, maka G memiliki tepat dua vertex yang berderajat ganjil. Misalkan G adalah graph semi-Euler, dan misalnya v dan w menjadi vertex awal dan titik akhir dari sebuah trail terbuka. Perhatikan Gambar 3.6, jika kita menambahkan sebuah edge
e yang menghubungkan v dan w, maka kita mendapatkan sebuah graph Euler dimana setiap
vertex memiliki derajat yang genap. Dengan teorema 3.2, jika kita menghapus edge e, maka kita akan mendapatkan bahwa v dan w adalah dua vertex yang memiliki derajat ganjil.
Gambar 3.6 Ilustrasi penambahan suatu edge pada graph semi-Euler
b. Jika G memiliki tepat dua vertex yang berderajat ganjil, maka G adalah graph semi-Euler. Misalkan G adalah graph yang memiliki tepat dua vertex berderajat ganjil yaitu v dan w. Misalkan kita enambahkan sebuah edge e yang menghubungkan v dan w, maka kita mendapatkan graph terhubung yang setiap vertex-nya memiliki derajat genap. Dengan Teorema 3.2 graph tersebut adalah graph Euler, dan memiliki trail Euler. Penghapusan edge
e dari trail ini menghasilkan sebuah trail terbuka yang memuat semua edge dari G, sehingga
G adalah graph semi-Euler.
Latihan 3.5
Pakai Teorema 3.4 untuk menentukan graph mana pada graph berikut yang merupakan graph semi-Euler.
8
Grap Hamilton
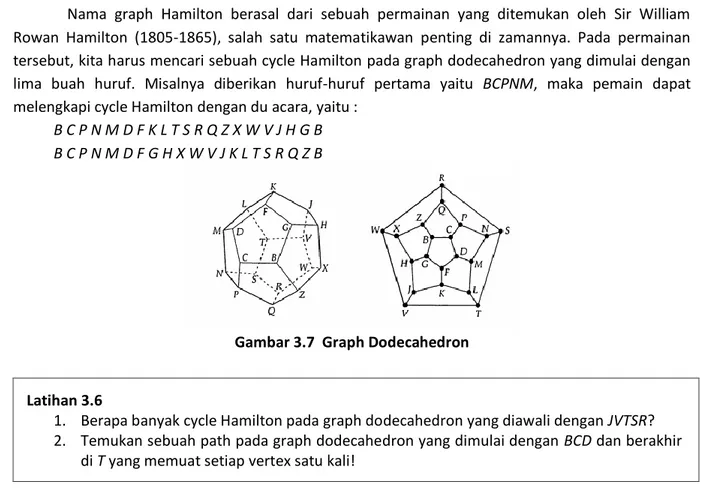
Nama graph Hamilton berasal dari sebuah permainan yang ditemukan oleh Sir William Rowan Hamilton (1805-1865), salah satu matematikawan penting di zamannya. Pada permainan tersebut, kita harus mencari sebuah cycle Hamilton pada graph dodecahedron yang dimulai dengan lima buah huruf. Misalnya diberikan huruf-huruf pertama yaitu BCPNM, maka pemain dapat melengkapi cycle Hamilton dengan du acara, yaitu :
B C P N M D F K L T S R Q Z X W V J H G B B C P N M D F G H X W V J K L T S R Q Z B
Gambar 3.7 Graph Dodecahedron
Latihan 3.6
1. Berapa banyak cycle Hamilton pada graph dodecahedron yang diawali dengan JVTSR? 2. Temukan sebuah path pada graph dodecahedron yang dimulai dengan BCD dan berakhir
di T yang memuat setiap vertex satu kali!
Sifat-sifat Graph Hamilton
Pada graph Hamilton, belum ditemukan suatu syarat cukup dan syarat perlu untuk menentukan suatu graph merupakan graph Hamilton atau bukan. Karena situasi ini, maka hal yang dapat kita lakukan adalah mencari berbagai sifat dari graph yang merupakan graph Hamilton. Sebagai contoh pada Gambar 3.8, sebuah graph Cn adalah graph Hamilton untuk semua nilai n,
demikian pula graph komplit Kn adalah graph Hamilton untuk n≥3.
9 Latihan 3.7
1. Yang mana dari graph berikut yang merupakan graph Hamilton? a. Graph bipartit komplit K4,4
b. Sebuah tree
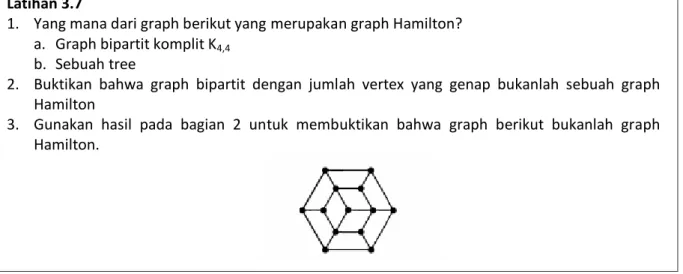
2. Buktikan bahwa graph bipartit dengan jumlah vertex yang genap bukanlah sebuah graph Hamilton
3. Gunakan hasil pada bagian 2 untuk membuktikan bahwa graph berikut bukanlah graph Hamilton.
Jika kita memiliki graph Hamilton dan menambahkan sebuah edge pada graph tersebut, maka kita akan memperoleh graph Hamilton lain, karena kita dapat mengambil cycle Hamilton yang sama seperti sebelumnya. Suatu graph yang memiliki derajat vertex yang besar (insiden dengan banyak edge), lebih berpeluang menjadi graph Hamilton dari pada graph yang memiliki derajat vertex yang kecil. Oystein Ore, membuktikan suatu teori pada tahun 1960 yang mengaitkan derajat vertex dengan graph Hamilton.
Teorema 3.5 : Teorema Ore
Misalnya G adalah graph sederhana yang terhubung dengan n vertex, di mana n≥3 dan derajat v + derajat w ≥ n ,
Untuk setiap pasangan vertex v dan w yang tidak bertetangga, maka G adalah graph Hamilton. Sebagai contoh, pada Gambar 3.9, ditunjukan bahwa derajat v + derajat w ≥ 5, untuk setiap pasangan vertex yang tidak bertetangga, sehingga graph tersebut adalah graph Hamilton menurut teorema Ore.
Gambar 3.9 Contoh graph Hamilton yang memenuhi teorema Ore
Latihan 3.8
1. Misalkan G adalah graph sederhana yang terhubung dan memilki n vertex, dimana n≥3 dan derajat v ≥ n/2 untuk setiap vertex v. Gunakan teorema Ore untuk menunjukan bahwa G graph Hamilton.
10 Seperti pada graph Euler, pada graph Hamilton, terdapat juga variasi ide tentang graph semi-Hamilton sebagai berikut.
Definisi 3.3
Sebuah graph adalah graph semi-Hamilton jika terdapat sebuah path (bukan cycle) yang memuat setiap vertex. Path seperti ini disebut path semi-Hamilton.
Latihan 3.9
Tentukan graph mana yang merupakan graph semi-Hamilton. Jika terdapat path semi-Hamilton, tuliskanlah.
Studi Kasus
Domiino
Graph Euler dapat diterapkan dalam permainan domino. Jika kita kita memiliki graph komplit
K7, seperti ditunjukan pada Gambar 3.10, maka kita memiliki graph Euler di mana setiap vertex
memiliki derajat 6. Misalkan kita memberi label vertex dengan 0,1,2,3,4,5,6 secara berurutan, maka kita dapat memperoleh sebuah contoh trail Euler dengan urutan sebagai berikut.
01, 12, 23, 34, 45, 56, 60, 02, 24, 46, 61, 13, 35, 50, 03, 36, 62, 25, 51, 14, 40.
Gambar 3.10 Graph K7
sebagai representasi domino
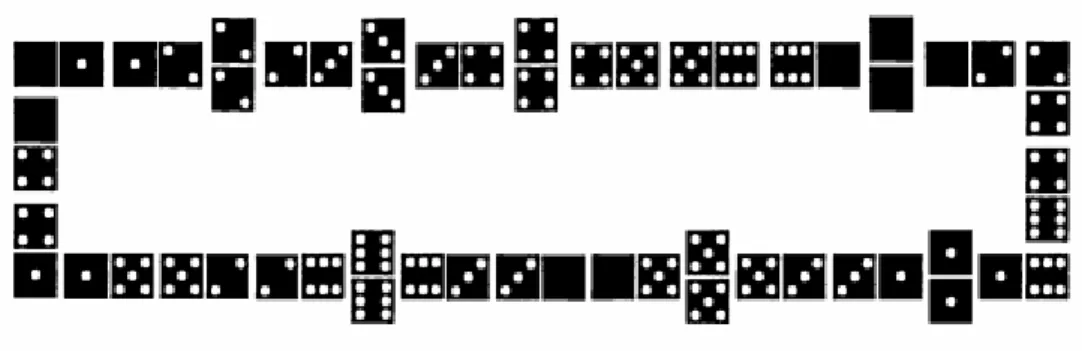
Kita dapat menganggap setiap edge sebagai sebuah domino. Trail Euler yang dihasilkan berkoresponden dengan susunan domino (set 0-0 sampai 6-6), dalam barisan yang kontinu. Saat kita menemukan barisan tersebut, kita dapat menyisipkan kartu double pada tempat yang mungkin, sehingga didapatkan permainan domino yang komplit seperti ditunjukan pada Gambar 3.11.
11 Gambar 3.11 Susunan kartu pada permainan domino
Latihan 3.10
Dengan menemukan sebuah trail Euler dalam K5, susunlah suatu set 50 buah domino (dari 0-0
sampai 4-4) dalam suatu lingkaran.
Diagram-Tracing Puzzle
Salah satu tipe puzzle yang biasa dimainkan adalah permainan menggambar suatu diagram dengan continuous pen-strokes (goresan pena kontinu) seminimal mungkin, tanpa mengangkat pena dari kertas dan tanpa melewati suatu bagian diagram dua kali.
Masalah ini dapat diwakili dengan masalah menentukan jumlah minimal dari trail terbuka tanpa melalui edge yang sama untuk membuat graph tersebut. Pada tahun 1809 Lois Poinsot menunjukan bahwa diagram yang memiliki n titik yang saling terhubung dapat digambar dalam sebuah goresan pena kontinu, jika jumlah n ganjil. Dalam terminologi teori graph, graphini adalah komplit Kn, yang merupakan graph Euler jika memiliki jumlah vertex n yang ganjil. Perhatikan Gambar 3.12.
12 Pada tahun 1847, Johann Listing membahas masalah diagram-tracing puzzle ini. Dalam penelitiannya, ia menyatakan bahwa untuk graph pada Gambar 3.13 terdiri dari delapan vertex dengan derajat ganjil, sehingga tidak dapat digambar dengan goresan pena kontinu lebih kecil dari empat goresan.
Gambar 3.13 Contoh masalah diagram-tracing puzzle
Latihan 3.11
1. Berapa buah goresan pena kontinu yang dibutuhkan untuk menggambar diagram berikut
2. Buktikan bahwa jika graph terhubung G memiliki k vertex yang berderajat ganjil, maka jumlah terkecil dari goresan pena kontinu yang dibutuhkan untuk menggambar semua edge pada graph G adalah k/2.
Knight’s Tour Problem
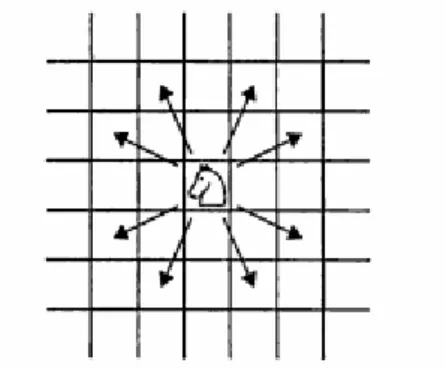
Dalam permainan catur, Knight (kuda) selalu bergerak dua kotak horizontal/vertical dan satu kotak yang tegak lurus dengannya. Ilustrasi pergerakan kuda ditunjukan pada Gambar 3.14. Suatu masalah rekreasional yang telah muncul ratusan tahun lalu adalah bisakah kuda mengunjungi semua kotak pada papan catur tepat satu kali dan kembali lagi ke kotak awal.
13 Pada permasalahn ini, kita dapat merepresentasikan papan catur sebagai sebuah graph di mana vertex mewakili kotak dan pasangan vertex dihubungkan jika ia yang berkoresponden dengan pergerakan kuda. Kita menyimpulkan bahwa masalah ini sama dengan masalah mencari cycle Hamilton pada graph yang sesuai dengan papan catur. Untuk papan catur berukuran 4x4, graph yang dapat dibuat ditunjukan pada Gambar 3.15.
Gambar 3.15 Representasi graph untuk pergerakan kuda
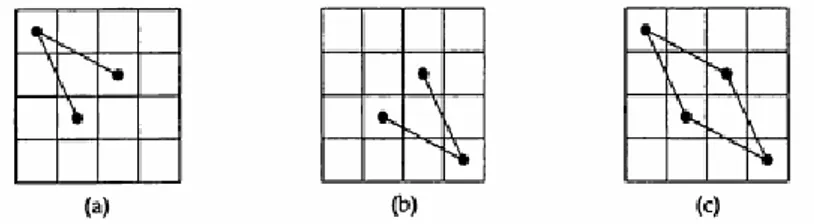
Pada papan catur berukuran 4x4, satu-satunya cara agar kita dapat mengunjungi kotak di bagian kiri atas adalah dengan dua buah pergerakan yang ditunjukan pada Gambar 3.16 (a). Begitu juga jika kita ingin mengunjungi kotak di bagian kanan bawah hanya dapat dipenuhi dengan pergerakan kuda yang ditunjukan pada Gambar 3.16(b). Dengan menggabungkan keduanya pada Gambar 3.16(c) kita dapat melihat bahwa sudah tercipta suatu cycle, sementara kotak yang lain belum dapat dikunjungi. Oleh karena itu, tidak ada solusi untuk masalah perjalanan kuda pada papan catur 4x4.
Gambar 3.16 Masalah perjalanan kuda pada papan catur 4x4
Pada papan catur berukuran 8x8, terdapat solusi untuk masalah perjalanan kuda seperti ditunjukan pada Gambar 3.17. Solusi atas permasalahan ini cukup menarik, karena jika kita menuliskan urutan perjalanan kuda pada setiap kotak, kita akan mendapatkan kotak ajaib di mana jumlah bilangan pada setiap baris dan setiap kolom sama dengan 260.
14 Latihan 3.12
Tunjukan bahwa tidak ada solusi untuk masalah perjalanan kuda pada papan catur 5x5 dan 7x7. Petunjuk : Ingat bahwa sebuah graph bipartit dengan jumlah vertex yang ganjil bukanlah graph Hamilton.
Gray Codes
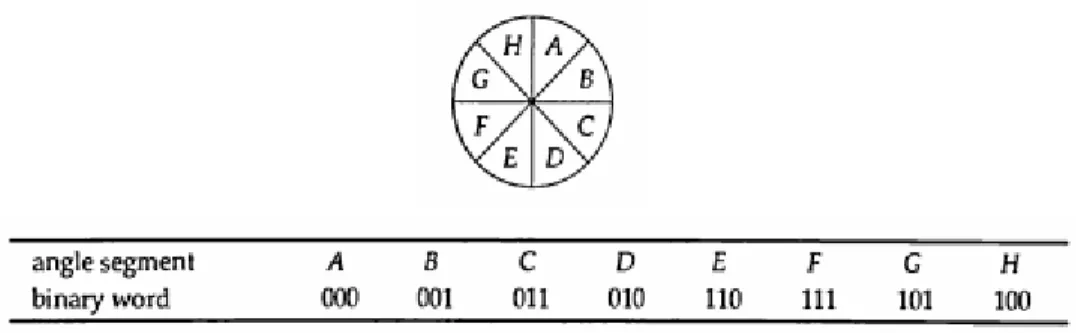
Para insinyur kadang-kadang ingin merepresentasikan posisi sudut ( dalam kelipatan 45o) pada sebuah batang yang berotasi secara kontinu. Segmen sudut pada batang direpresentasikan ke dalam 3 digit bilangan biner ( 0 dan 1) seperti ditunjukan pada Gambar 3.18. Setiap 3-digit bilangan biner mewakili segmen sudut pada posisi tertentu.
Gambar 3.18 Konversi segmen sudut ke dalam bilangan biner
Pada setiap perputaran batang, barisan bilangan biner berubah tepat hanya satu digit pada setiap satuan waktu. Barisan bilangan biner seperti ini disebut Gray code. Keuntungan kode semacam ini adalah meminimalisir ambigusitas yang dapat disebabkan oleh kesalahan pembacaan track. Gray code dapat ditemukan dengan mencari cycle Hamilton pada graph Cube. Sebagai contoh pada Gambar 3.19 merupakan graph 3-cube atau Q3. Gray code yang mungkin dan berkoresponden
dengan cycle Hamilton adalah sebagai berikut.
000 → 001 → 011 → 010 → 110 → 111 → 101 → 100 → 000, dan 000 → 100 → 110 → 010 → 011 → 111 → 101 → 001 → 000
15 Pada gray code dengan 4 digit bilangan biner graph yang mewakili adalah graph 4-cube atau
Q4 yang ditunjukan pada Gambar 3.20. Cycle Hamilton yang dapat dibuat dari graph tersebut
misalnya adalah sebagai berikut.
0000 → 0001 → 0011 → 0010 → 0110 → 0111 → 0101 → 0100 → 1100 → 1101 → 1111 → 1110 → 1010 → 1011 → 1001 →1000 → 0000
Gambar 3.18 Graph cube Q4 merepresentasikan gray code 4 digit
Latihan 3.13