Scrambling Index dari Kelas Digraf Hamilton Dwiwarna dengan n Titik Ganjil

(1)

DIGRAF DWIWARNA PRIMITIF

Pada bab ini akan dibahas mengenai teori-teori yang berhubungan dengan peneli-tian digraf Hamilton dwiwarna dan menjadi landasan berfikir untuk mempermu-dah dalam pembahasan hasil pada bab berikutnya. Adapun teori-teori yang akan dibahas mencakup definisi, primitifitas, scrambling index dan batas scrambling index digraf dwiwarna.

2.1 Definisi Digraf Dwiwarna

Pada subbab ini akan dipaparkan definisi digraf dwiwarna, notasi dan terminologi yang akan digunakan pada pembahasan selanjutnya.

Secara sederhana, suatu digrafD didefinisikan sebagai kumpulan titik ber-hinggaV dan sisi berarah atauarc A. Secara matematika, suatu digrafDadalah sebuah objek yang terdiri atas dua himpunan, yaitu

1. Himpunan berhingga dan tak kosong V = {v₁, v₂, v₃,· · · , vn}, dimana vi dengani= 1,2,3,· · · , n disebut titik dari digraf D.

2. Himpunan A yang merupakan himpunan bagian dari himpunan V × V. Unsur himpunan A disebut sisi berarah atau arc dari digraf D.

Suatu digraf dwiwarna, dinotasikan dengan D(2)_{, adalah sebuah digraf} _D _yang

setiap arc-nya diberi warna merah atau biru (Fornasini dan Valcher, 1997). Bila a = (vi, vj) ∈ V ×V adalah sebuah arc pada digraf dwiwarna D(2), maka titik vi disebut sebagai titik asal dan titikvj disebut titik terminal. Suatu a= (vi, vj) dikatakan arcmerah dinotasikan dengan vi −→vj dana = (vi, vj) dikatakanarc biru dinotasikan dengan vi − →vj.

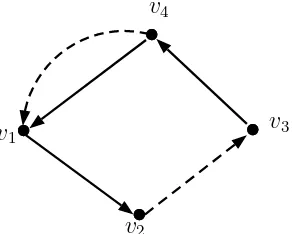
Contoh 2.1.1. Himpunan titik V = {v1, v2, v3, v4} bersama dengan himpunan

arc yang terdiri dari himpunan arc merah R = {(v1, v2),(v3, v4),(v4, v1)} dan

himpunan arc biru B = {(v2, v3),(v4, v1)} merupakan sebuah digraf dwiwarna

(2)

bc

v₁

v₂

v₃ v₄

Gambar 2.1 : Digraf dwiwarna dengan 4 titik dan 5arc

Konsep insidensi antara titik dengan arc pada digraf dwiwarna D(2) di-definisikan sama dengan konsep insidensi pada digraf D. Andaikan a = (vi, vj) adalah sebuaharcpada digraf dwiwarnaD(2). Titikvi dikatakan insiden kearc a dan titikvj dikatakan insiden dariarc a. Sedangkan,arc adikatakan insiden dari titik vi dan arc a dikatakan insiden ke titik vj. Derajat masuk (indegree) dari sebuah titik vi, dinotasikan dengan id(vi), adalah banyaknya arc yang insiden ke titik vi. Derajat keluar (outdegree) dari sebuah titik vi, dinotasikan dengan od(vi), adalah banyaknya arcyang insiden dari titik vi. Pada Gambar 2.1 perha-tikanarc(v₁, v₂), maka titikv₁insiden ke (v₁, v₂) dan titikv₂ insiden dari (v₁, v₂). Selain itu, diperoleh bahwa id(v1) = 2 dan od(v1) = 1, sedangkan id(v2) = 1 dan

od(v2) = 1.

Sebuah (h, ℓ)-walk berarah pada digraf dwiwarna D(2) adalah sebuahwalk berarah dengan panjangh+ℓyang terdiri darih arcmerah danℓ arcbiru. Notasi vi

(h,ℓ)

−→ vj digunakan untuk menyatakan sebuah (h, ℓ)-walk berarah dari titik vi ke titik vj. AndaikanW adalah sebuahwalk berarah, banyaknyaarcmerah dari W dinotasikan dengan r(W) dan banyaknyaarcbiru dariW dinotasikan dengan

b(W). Panjang dariW adalahℓ(W) = r(W)+b(W) dan vektor

[

r(W) b(W)

]

adalah

komposisi dari W.

Sebuahwalk berarah yang memuat setiap titik berbeda kecuali pada titik awal dan titik akhir disebut path. Sebuah (h, ℓ)-path adalah sebuah path yang terdiri dari h arc merah dan ℓ arc biru. Notasi Pvi,vj menyatakan terdapat path

dari titikvike titikvj. AndaikanPvi,vj adalah sebuahpath, banyaknyaarcmerah

dari Pvi,vj dinotasikan dengan r(Pvi,vj) dan banyaknya arc biru dari Pvi,vj

dino-tasikan dengan b(P_v_i_,v_j). Vektor

[

r(Pvi,vj)

b(Pvi,vj) ]

(3)

Perhatikan Gambar 2.1, akan diperlihatkanwalk,path, dan cycleyang ada pada digraf dwiwarna D(2) tersebut.

1. v₁ −→ v₂ − → v₃ −→ v₄ − → v₁ −→ v₂ − → v₃ adalah walk berarah

dengan komposisi

[

3 3

]

dan bukan path karena titik v1, v2, v3 muncul 2

kali.

2. v1 −→v2 − →v3 −→v4 adalahpath dengan komposisi

[

2 1

]

.

3. v1 −→v2 − →v3 −→v4 −→v1 adalah cycle dengan komposisi

[

3 1

]

.

Definisi 2.1.2. Path Hamilton adalah path yang memuat setiap titik yang ada pada digraf dwiwarna D(2) tepat satu kali. Cycle Hamilton adalah cycle yang melalui setiap titik yang ada pada digraf dwiwarna D(2) tepat satu kali, kecuali pada titik awal dan titik akhir.

Suatu digraf dwiwarna D(2) _{yang memuat} _cycle _{Hamilton disebut digraf}

Hamilton dwiwarna, sedangkan digraf dwiwarna D(2) yang memuat path Hamil-ton disebut digraf semi-HamilHamil-ton dwiwarna.

2.2 Matriks Ketetanggaan Digraf Dwiwarna

Suatu digraf dwiwarna D(2) atas n titik dapat direpresentasikan dalam bentuk matriks ketetanggaan(adjacency matrix). Matriks ketetanggaan dari suatu digraf dwiwarna D(2) terbagi menjadi dua, yaitu matriks ketetanggaan merah R dan matriks ketetanggaan biru B.

Matriks ketetanggaan merah dari D(2) _{adalah matriks bujursangkar} _R ₌

(rij) berordon didefinisikan sebagai

rij =







1, jika (vi, vj) adalah arc merah, 0, jika sebaliknya.

Matriks ketetanggaan biru dariD(2) adalah matriks bujursangkarB = (bij) berordo n didefinisikan sebagai

bij =







(4)

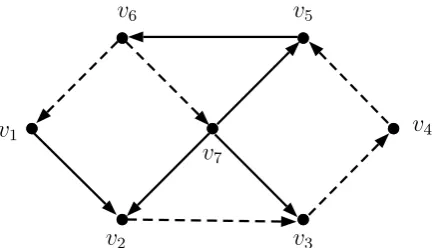
Contoh 2.2.1. Perhatikan digraf dwiwarna D(2) dengan 7 titik dan 10arc beri-kut ini. bc bc bc bc bc bc bc v₁

v₂ v₃

v4

v₅ v₆

v₇

Gambar 2.2 : Digraf dwiwarna dengan 7 titik dan 10 arc

Matriks ketetanggaan merah dan biru dari Gambar 2.2 adalah sebagai berikut. R =           

0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0

          

dan B =

          

0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0

           .

Suatu matriks bujursangkarM = (mij) berordon, untuk setiap i, j = 1,2, . . . , n, dikatakan matriks tak negatif jikamij merupakan bilangan bulat tak negatif dan dikatakan matriks positif jika mij merupakan bilangan bulat positif.

Contoh 2.2.2. Berikut diperlihatkan contoh matriks tak negatif dan matriks positif.

Matriks M =





1 0 5 3 2 7 6 0 9



 adalah matriks tak negatif.

Matriks M =





2 3 5 1 9 6 8 7 4



 adalah matriks positif.

2.3 Primitifitas Digraf Dwiwarna

(5)

dan titik vj terdapatwalk berarah dari titikvi ke titikvj dan walk berarah dari titik vj ke titik vi. Terdapat sifat khusus dari digraf dwiwarna D(2) terhubung kuat yang berkaitan dengan keberadaan cycle.

Proposisi 2.3.1. AndaikanD(2) _{adalah sebuah digraf dwiwarna terhubung kuat.}

Setiap titik di D(2) _{terletak pada sebuah cycle.}

Bukti. Andaikan vi adalah sebarang titik di D(2). Dapat dibentuk sebuah cycle yang memuat titikvi. KarenaD(2) terhubung kuat, maka terdapat titikvj diD(2) sehingga (vi, vj) adalah sebuaharcdiD(2). KarenaD(2)terhubung kuat, terdapat sebuahpath Pvi,vj dari titikvike titikvj. Sekarangarc(vi, vj) dilanjutkan dengan

path Pvi,vj adalah sebuah cycle yang memuat titik vi.

Berikut diperlihatkan contoh digraf dwiwarna D(2) terhubung kuat dan tidak terhubung kuat.

b

b b b

b b

b b b

b

v1 v2 v3 v1 v2 v3

v₄

v₅ v₅ v₄

(a) (b)

Gambar 2.3 : (a) D(2) terhubung kuat, (b) D(2) tidak terhubung kuat

Gambar 2.3(a) merupakan digraf dwiwarna D(2) terhubung kuat karena terdapat walk berarah yang menghubungkan setiap pasangan titik di D(2) atau berdasarkan Proposisi 2.3.1 setiap titik berada pada sebuah cycle, sedangkan Gambar 2.3(b) merupakan digraf dwiwarna D(2) tidak terhubung kuat karena tidak terdapat walk berarah yang menghubungkan titik v2 ke titikv5 atau

ber-dasarkan Proposisi 2.3.1 titik v1 dan v5 tidak berada pada sebuah cycle.

Suatu digraf dwiwarnaD(2) terhubung kuat dikatakan primitif dengan sya-rat terdapat bilangan bulat tak negatif h dan ℓ sehingga untuk setiap pasangan titik vi dan vj di D(2) terdapat vi

(h,ℓ)

−→vj walk dan vj

(h,ℓ)

−→vi walk. Bilangan bu-lat tak negatif h+ℓ terkecil merupakan eksponen dari D(2)_{, dinotasikan dengan}

exp(D(2)_).

(6)

sebagai matriks 2×q yang mana kolom ke-i adalah komposisi dari cycle Ci, i= 1,2, . . . , q yaitu sebagai berikut

M =

[

r(C1) r(C2) · · · r(Cq)

b(C1) b(C2) · · · b(Cq)

]

.

Jika M memiliki rank 1, maka content dari M adalah 0 dan content dari M didefinisikan sebagai pembagi bersama terbesar dari determinan submatriks 2×

2 dari M. Berikut diberikan karakteristik dari sebuah digraf dwiwarna D(2)

primitif.

Teorema 2.3.2. (Fornasini dan Valcher, 1998) AndaikanD(2) adalah digraf dwiwarna terhubung kuat dengan paling sedikit satuarcsetiap warna dan andaikan M adalah matriks cycle dari D(2). Digraf dwiwarna D(2) dikatakan primitif jika dan hanya jika content dari M adalah 1.

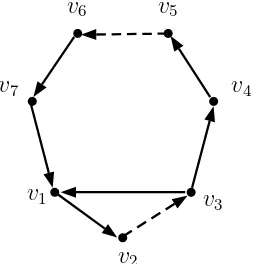
Contoh 2.3.3. Perhatikan digraf dwiwarna D(2) terhubung kuat pada Gambar 2.4. Digraf dwiwarna D(2) tersebut terdiri atas dua cycle sehingga diperoleh matriks cycle M sebagai berikut.

M =

[

r(C₁) r(C₂) b(C₁) b(C₂)

]

=

[

5 2 2 1

]

karena det(M) = 1, berdasarkan Teorema 2.3.2 maka digraf dwiwarna D(2)

ter-sebut adalah primitif.

b b

b

v1

v2

v₃ v4

v5

v6

v7

Gambar 2.4 : Digraf dwiwarna D(2) terhubung kuat primitif

(7)

Untuk sebarang pasangan matriks tak negatif (A, B), suatu (h, ℓ)-Hurwitz productdari matriksAdanB, dinotasikan dengan (A, B)(h,ℓ)_{, didefinisikan secara}

rekursif sebagai berikut. Untuk sebarang bilangan bulat tak negatif h ≥ 1 dan ℓ≥1, (A, B)(h,0) ₌_Ah_,₍_{A, B}₎(0,ℓ) ₌_Bℓ_{, dan}

(A, B)(h,ℓ) =A(A, B)(h−1,ℓ)₊_B₍_{A, B}₎(h,ℓ−1)_.

Lemma 2.3.4. AndaikanD(2)adalah digraf dwiwarna denganntitik dan andaikan R danB adalah matriks ketetanggaan merah dan biru dariD(2). Maka entri (i, j) dari (R, B)(h,ℓ) _{adalah banyaknya} _{(h, ℓ)-walk dari titik} _v

i ke titik vj.

Bukti. Akan dibuktikan induksi pada (h+ℓ) dan (h+ℓ+ 1), jika h = 0 maka ℓ= 1 atau jikah= 1 makaℓ = 0. Jikah= 0 maka entri (i, j) dari (R, B)(0,1) ₌_B

adalah walk dengan kompisisi

[

0 1

]

. Dengan cara yang sama, jika ℓ = 0 maka

entri (i, j) dari (R, B)(1,0) ₌_R _adalah _walk _{dengan kompisisi}

[

1 0

]

diD(2).

Asumsikan Lemma 2.3.4 adalah benar untuk bilangan bulat tak negatif h′

dan ℓ′

dengan h′

+ℓ′

≤ h+ℓ, akan diperlihatkan untuk h+ℓ+ 1 adalah benar dengan catatan sebagai berikut.

(R, B)(h+1,ℓ)=R(R, B)(h,ℓ)+B(R, B)(h+1,ℓ−1)_.

Berdasarkan hipotesis induksi, entri (i, j) pada R(R, B)(h,ℓ) _adalah _walk _dari

ti-tik vi ke titikvj yang dimulai denganarc merah dan diikuti oleh (h, ℓ)-walk dan entri (i, j) padaB(R, B)(h+1,ℓ−1) _adalah_walk _{dari titik}_v

i ke titikvj yang dimulai denganarcbiru dan diikuti oleh (h+ 1, ℓ−1)-walk sedemikian hingga entri (i, j) dariR(R, B)(h+1,ℓ) _{adalah banyaknya (h}_{+ 1, ℓ)-walk} _{dari titik}_v

i ke titikvj. Jadi, entri (i, j) pada (R, B)(h,ℓ)_{adalah banyaknya (h, ℓ)-walk}_{dari titik}_v

i ke titikvj.

2.4 Scrambling Index Digraf Dwiwarna

AndaikanD(2)_{adalah digraf dwiwarna primitif dan andaikan titik}_v

idanvj adalah dua titik berbeda di D(2)_{. Scrambling index lokal dari titik} _v

i dan vj di titik vt ∈ V(D(2)), kvi,vj(vt), adalah bilangan bulat positif terkecil h+ℓ dari seluruh

pasangan bilangan bulat tak negatif (h, ℓ) sedemikian hingga terdapat sebuah vi

(h,ℓ)

−→vt walk dan vj

(h,ℓ)

(8)

D(2) didefinisikan sebagai,

k_v_i_,v_j(D(2)) = min

vt∈V(D(2)₎{kvi,vj(vt)}.

Scrambling index dari D(2)_{, dinotasikan dengan} _k₍_D(2)_{), adalah bilangan bulat}

positif terkecil h+ℓ dari seluruh pasangan bilangan bulat tak negatif (h, ℓ) se-demikian hingga untuk setiap pasangan titik vi dan vj di D(2) terdapat sebuah titik vt dengan sifat bahwa terdapat vi

(h,ℓ)

−→vt walk dan vj

(h,ℓ)

−→vt walk. Berdasarkan definisi scrambling index, diperoleh hubungan sebagai berikut

max vi,vj∈V(D(2))

{kvi,vj(D

(2)₎_{} ≤}_k(D(2)_).

Contoh 2.4.1. Representasi digraf dwiwarnaD(2) primitif dengan 3 titik, 2arc merah, dan 2 arc biru seperti pada Gambar 2.5. Scrambling index lokal dari digraf dwiwarna D(2) tersebut sebagai berikut.

kv1,v2(D(2)) = min{kv1,v2(v1), kv1,v2(v2), kv1,v2(v3)}

= min{(1,1),(2,1),(3,1)}= min{2,3,4}= 2,

kv1,v3(D(2)) = min{kv1,v3(v1), kv1,v3(v2), kv1,v3(v3)}

= min{(2,2),(3,2),(4,2)}= min{4,5,6}= 4, kv2,v3(D

(2)_{) = min}_{_k

v2,v3(v1), kv2,v3(v2), kv2,v3(v3)}

= min{(0,1),(1,1),(2,1)}= min{1,2,3}= 1.

Dari definisi, maka diperolehk(D(2)₎_≥_max_{_k

v1,v2(D(2)), kv1,v3(D(2)), kv2,v3(D(2))} = max{2,4,1}= 4 dengan komposisi 2 arc merah dan 2 arc biru.

Selanjutnya, akan diperlihatkan bahwak(D(2)₎_≤_{4 dengan komposisi 2}_arc

merah dan 2 arc biru, yaitu akan diperlihatkan untuk setiap dua pasang titik (vi, vj) yang berbeda diD(2) terdapat titikvtdiD(2) sedemikian hingga terdapat vi

(2,2)

−→ vt walk dan vj

(2,2)

−→ vt walk. Pada Contoh 2.4.1, diperoleh setiap dua pasang titik yang berbeda, yaitu (v1, v2),(v2, v3),(v1, v3) di D(2).

1. Untuk pasangan titik (v1, v2) terdapatv1sedemikian hingga terdapatv1 (2,2) −→

v1 walk dan v2 (2,2)

−→v1 walk, yaitu

v₁ −→v₂ − →v₁ −→v₂ − →v₁ dan v₂ −→v₃ − →v₁ −→v₂ − →v₁.

2. Untuk pasangan titik (v1, v3) terdapatv1sedemikian hingga terdapatv1 (2,2) −→

v1 walk dan v3 (2,2)

−→v1 walk, yaitu

(9)

b

v1 v2

v₃

Gambar 2.5 : Digraf dwiwarna D(2) primitif

3. Untuk pasangan titik(v₂, v₃) terdapatv₁ sedemikian hingga terdapatv₂ −→(2,2)

v₁ walk dan v₃ −→(2,2) v₁ walk, yaitu

v₂ −→v₃ − →v₁ −→v₂ − →v₁ dan v₃ − →v₁ −→v₂ −→v₃ − →v₁.

Telah diperlihatkan bahwak(D(2)₎_≤_{4 dan} _k(D(2)₎_≥_{4 dengan kompisisi 2}

arc merah dan 2 arc biru. Jadi, dapat disimpulkan scrambling index dari digraf dwiwarna D(2) primitif pada Gambar 2.5 adalah 4.

Berdasarkan Lemma 2.3.4, scrambling index dari suatu digraf dwiwarna D(2) _{primitif dapat dicari dengan menggunakan (}_{h, ℓ}_)-_{Hurwitz product}_dari

mat-riks ketetanggaan merah R dan matriks ketetanggaan biru B. Jika untuk setiap dua baris pada (R, B)(h,ℓ) _{terdapat paling sedikit satu entri bernilai positif pada}

kolom yang sama, maka k(D(2)_{) =}_h₊_ℓ.

Contoh 2.4.2. Matriks ketetanggaan merah dan biru dari digraf dwiwarna D(2) primitif pada Gambar 2.5 diberikan sebagai berikut.

R =





0 1 0 0 0 1 0 0 0



 dan B =





0 0 0 1 0 0 1 0 0



,

maka untuk h+ℓ= 1, diperoleh

1. (R, B)(1,0) ₌_R₌





0 1 0 0 0 1 0 0 0



.

Scrambling index dari digraf dwiwarna D(2) _{pada Gambar 2.5 tidak sama}

dengan 1 karena baris pertama dan baris kedua pada matriks (R, B)(1,0)

tidak memiliki entri positif pada kolom yang sama.

2. (R, B)(0,1) ₌_B ₌





0 0 0 1 0 0 1 0 0



(10)

Scrambling index dari digraf dwiwarna D(2) pada Gambar 2.5 tidak sama dengan 1 karena baris pertama dan baris kedua pada matriks (R, B)(0,1)

Untuk h+ℓ= 2, diperoleh

1. (R, B)(2,0) ₌_R2 ₌





0 0 1 0 0 0 0 0 0



.

dengan 2 karena baris pertama dan baris kedua pada matriks (R, B)(2,0)

2. (R, B)(0,2) ₌_B2 ₌





0 0 0 0 0 0 0 0 0



.

dengan 2 karena untuk setiap dua baris pada matriks (R, B)(0,2) _tidak

memiliki entri positif pada kolom yang sama.

3. (R, B)(1,1) ₌_{R(R, B)}(0,1)₊_{B(R, B)}(1,0) ₌





1 0 0 1 1 0 0 1 0



.

Scrambling index dari digraf dwiwarna D(2) pada Gambar 2.5 tidak sama dengan 2 karena baris pertama dan baris ketiga pada matriks (R, B)(1,1)

1. (R, B)(3,0) ₌_R3 ₌





0 0 0 0 0 0 0 0 0



.

Scrambling index dari digraf dwiwarna D(2) pada Gambar 2.5 tidak sama dengan 3 karena untuk setiap dua baris pada matriks (R, B)(3,0) _tidak

2. (R, B)(0,3) ₌_B3 ₌





0 0 0 0 0 0 0 0 0



.

(11)

3. (R, B)(2,1) ₌_{R(R, B)}(1,1)₊_{B(R, B)}(2,0) ₌





1 1 0 0 1 1 0 0 1



.

Scrambling index dari digraf dwiwarna D(2) pada Gambar 2.5 tidak sama dengan 3 karena baris pertama dan baris ketiga pada matriks (R, B)(2,1)

4. (R, B)(1,2) ₌_{R(R, B)}(0,2)₊_{B(R, B)}(1,1) ₌





0 0 0 1 0 0 1 0 0



.

Scrambling index dari digraf dwiwarna D(2) pada Gambar 2.5 tidak sama dengan 3 karena baris pertama dan baris kedua pada matriks (R, B)(1,2)

1. (R, B)(4,0) ₌_R4 ₌





0 0 0 0 0 0 0 0 0



.

2. (R, B)(0,4) ₌_B4 ₌





0 0 0 0 0 0 0 0 0



.

3. (R, B)(3,1) ₌_R₍_{R, B}₎(2,1)₊_B₍_{R, B}₎(3,0) ₌





0 1 1 0 0 1 0 0 0



.

dengan 4 karena baris pertama dan baris ketiga pada matriks (R, B)(3,1)

4. (R, B)(1,3) ₌_{R(R, B)}(0,3)₊_{B(R, B)}(1,2) ₌





0 0 0 0 0 0 0 0 0



.

(12)

5. (R, B)(2,2) ₌_{R(R, B)}(1,2)₊_{B(R, B)}(2,1) ₌





1 0 0 2 1 0 1 1 0



.

Scrambling index dari digraf dwiwarnaD(2) pada Gambar 2.5 sama dengan 4 karena untuk setiap dua baris pada (R, B)(2,2) _{terdapat paling sedikit satu}

entri positif pada kolom yang sama. Jadi, diperoleh k(D(2)_{) = 4 dengan}

komposisi

[

2 2

]

.

2.5 Batas Scrambling Index Digraf Dwiwarna

Pada subbab ini akan dibahas mengenai batas atas dan batas bawah untuk scram-bling index dari digraf dwiwarna D(2) primitif, terkhusus digraf dwiwarna D(2) primitif yang terdiri atas dua cycle (Mulyono dan Suwilo, 2014).

Setiapwalkberarah pada suatu digraf dwiwarnaD(2) _{dapat diuraikan}

men-jadi sebuahpath dan beberapacycle. Hal ini berarti untuk setiapvi

(h,ℓ)

−→vj walk memiliki hubungan sebagai berikut.

[

h ℓ

]

=

[

r(Pvi,vj)

b(Pvi,vj) ]

+z1

[

r(C₁) b(C₁)

]

+z2

[

r(C₂) b(C₂)

]

+· · ·+zq

[

r(Cq) b(Cq)

]

=

[

r(Pvi,vj)

b(P_v_i_,v_j)

]

+Mz

untuk beberapa path Pvi,vj dari titik vi ke titik vj dan beberapa vektor bilangan

bulat tak negatif z.

Proposisi berikut ini digunakan untuk menentukan batas atas scrambling index digraf dwiwarna.

Proposisi 2.5.1. (Mulyono dan Suwilo, 2014) Andaikan D(2) adalah digraf dwiwarna primitif yang terdiri atas dua cycle C1 dan C2. Andaikan vj adalah sebuah titik yang berada pada kedua cycle. Jika untuk beberapa bilangan bulat positif h dan ℓ, terdapat sebuah path P_v_i_,v_j dari titik v_i ke titik v_j sedemikian hingga sistem

Mz+

[

r(Pvi,vj)

b(P_v_i_,v_j)

]

=

[

h ℓ

]

(2.1)

(13)

Bukti. Asumsikan bahwa solusi dari sistem (2.1) adalah z =

[

z1

z2

]

. Terdapat

empat kemungkinan nilai z1 dan z2 sebagai berikut.

Jika z1 > 0 dan z2 >0, maka walk berarah bergerak mulai dari titik vi ke vj melalui sepanjang (r(Pvi,vj), b(Pvi,vj))-path Pvi,vj dan akhirnya bergerak

meng-elilingicycle C1 sebanyak z1 kali dan bergerak mengelilingi cycle C2 sebanyak z2

kali, dan kembali ke titikv_j adalah sebuah (h, ℓ)-walk berarah dari titikv_i kev_j.

Jika z₁ = 0 dan z₂ >0, maka walk berarah bergerak mulai dari titik vi ke vj melalui sepanjang (r(Pvi,vj), b(Pvi,vj))-path Pvi,vj dan akhirnya bergerak

meng-elilingi cycle C₂ sebanyak z₂ kali. Dengan cara yang sama, Jika z₁ > 0 dan z₂ = 0, maka walk berarah bergerak mulai dari titik vi ke vj melalui sepanjang (r(Pvi,vj), b(Pvi,vj))-path Pvi,vj dan akhirnya bergerak mengelilingi cycle C1

seba-nyak z1 kali dan kembali ke titikvj adalah sebuah (h, ℓ)-walk berarah dari titik vi ke vj.

Jika z1 = z2 = 0, maka (r(Pvi,vj), b(Pvi,vj))-path Pvi,vj dari titik vi ke vj

adalah sebuah (h, ℓ)-walk berarah.

Lemma berikut ini digunakan untuk menentukan batas bawah scrambling index digraf dwiwarna. Didefinisikan bahwa ℓ(C₁) adalah panjang dari cycle C₁ dan ℓ(C₂) adalah panjang dari cycle C₂.

Lemma 2.5.2. (Mulyono et al. ₂₀₁₅₎ _Andaikan_D(2) _{adalah digraf dwiwarna} primitif yang terdiri atas dua cycle C₁ dan C₂ dengan matriks cycle

M =

[

r(C1) r(C2)

b(C1) b(C2)

]

,

dan andaikan vi dan vj adalah sebarang dua titik yang berbeda di D(2). Jika kvi,vj(vt) diperoleh dari sebuah (h, ℓ)-walk berarah, maka

[

h ℓ

]

≥M

[

b(C₂)r(P_v_i_,v_t)−r(C₂)b(P_v_i_,v_t) r(C1)b(Pvj,vt)−b(C1)r(Pvj,vt)

]

.

Oleh karena itu,

kvi,vj(vt)≥ℓ(C1)[b(C2)r(Pvi,vt)−r(C2)b(Pvi,vt)]+ℓ(C2)[r(C1)b(Pvj,vt)−b(C1)r(Pvj,vt)]

(14)

Bukti. KarenaD(2) adalah primitif, maka berdasarkan Teorema 2.3.2 diperoleh det(M) = 1 atau det(M) = −1. Tanpa menghilangkan keumuman diasumsikan bahwa det(M) = 1. Karena det(M) = 1, terdapat bilangan bulat e1 dan e2

sedemikian hingga

[

h ℓ

]

=M

[

e₁ e₂

]

. (2.2)

Karena setiap walk berarah dapat diuraikan menjadi sebuah path dan beberapa cycle, maka

[

h ℓ

]

=

[

r(Pvi,vt)

b(Pvi,vt) ]

+Mz, (2.3)

untuk beberapa path Pvi,vt dari titik vi kevt dan beberapa vektor bilangan bulat

tak negatif z. Bandingkan persamaan (2.2) dan (2.3), maka diperoleh

z=

[

e1

e2

]

−M−1

[

r(Pvi,vt)

b(Pvi,vt) ]

≥0.

Oleh karena itu,

[

e₁ e₂

]

≥M−1

[

r(P_v_i_,v_t) b(P_v_i_,v_t)

]

=

[

b(C₂)r(P_v_i_,v_t)−r(C₂)b(P_v_i_,v_t) r(C₁)b(P_v_i_,v_t)−b(C₁)r(P_v_i_,v_t)

]

.

Sehingga, diperolehe₁ ≥b(C₂)r(Pvi,vt)−r(C2)b(Pvi,vt) untuk beberapapath Pvi,vt

dari titik vi ke vt dan e2 ≥ r(C1)b(Pvj,vt)−b(C1)r(Pvj,vt) untuk beberapa path

Pvj,vt dari titikvj ke vt. Jika kvi,vj(vt) diperoleh dari sebuah (h, ℓ)-walk berarah,

maka

[

h ℓ

]

=M

[

e₁ e₂

]

≥M

[

b(C₂)r(P_v_i_,v_t)−r(C₂)b(P_v_i_,v_t) r(C₁)b(P_v_j_,v_t)−b(C₁)r(P_v_j_,v_t)

]

dan diperoleh

kvi,vj(vt)≥ℓ(C1)[b(C2)r(Pvi,vt)−r(C2)b(Pvi,vt)]+ℓ(C2)[r(C1)b(Pvj,vt)−b(C1)r(Pvj,vt)]