Soal Olimpiade Sains Tingkat Kabupaten/Kota 2017 Bidang Fisika SMA Waktu : 3 jam

(1)

Davit Sipayung | 1 Sekolah Online Fisika Indonesia

davitsipayung.com

Davit Sipayung

davitsipayung@gmail.com

Soal Olimpiade Sains Tingkat Kabupaten/Kota 2017 Bidang Fisika SMA

Waktu : 3 jam

1. Sebuah pegas telah di desain sedemikian untuk diletakan di dasar lantai suatu kolom lift pada sebuah gedung bertingkat (lihat gambar di bawah). Pegas ini berfungsi untuk mengamankan orang yang di dalam lift ketika kabel lift putus dan kemudian lift terjatuh. Diketahui massa total lift dan penumpangnya adalah M dan percepatan gravitasi g. Jika pada saat lift berada pada ketinggian

h di atas puncak pegas, kabel lift putus dan kemudian lift terjatuh, tentukan:

a. konstanta pegas k agar penumpang lift merasakan percepatan yang tidak lebih besar dari pada 5g pada saat lift akan berhenti untuk pertama kali!

b. amplitudo osilasi dinyatakan dalam h, jika setelah berhenti pegas itu kemudian berosilasi.

2. Sebuah benda bermassa M bergerak secara vertikal pada sebuah poros (seperti gambar di bawah) akibat pengaruh dari sebuah gaya F yang besarnya konstan namun arahnya berubah setiap waktu. Diketahui bahwa θ =bt, dimana b merupakan sebuah konstanta dan t adalah waktu dalam detik . Jika koefisien gesek antara benda dan poros adalah μk dan bila benda itu bergerak dari keadaan diam (yaitu θ =00

), tentukan besar gaya F yang menyebabkan benda berhenti setelah θ =π/2 .

3.

Sebuah piringan pejal bermassa M, dan berjari-jari R ( I = ½ MR2) dipasang pada ujung sebuah batang tak bermassa dengan panjang L. Ujung batang lainnya diberi poros tetap yang licin. Mula-mula batang disimpangkan dengan sudut α =π/3 radian terhadap garis vertikal. Jika piringan dilepaskan tanpa kecepatan awal, tentukanlah kecepatan pusat massa piringan v di titik terendahnya dengan kondisi (lihat gambar di bawah) :

a. Piringan di lem ke batang (lihat gambar A). b. Piringan dipasang dengan poros licin (Gambar B).

c. Sama dengan (b), hanya saja terdapat lintasan lingkaran berjari-jari (L+R) yang cukup kasar sehingga piringan tidak slip pada permukaan tersebut (Gambar C).

k

h

M M θ F

(2)

2 | Davit Sipayung

Sekolah Online Fisika Indonesia

davitsipayung.com

Davit Sipayung

4. Sebuah bola A bermassa m menumbuk bola B dengan massa 2m yang mula-mula diam (seperti yang ditunjukkan gambar di bawah). Sesaat setelah tumbukan , bola B meluncur pada lintasan yang berbentuk seperempat lingkaran berjari-jari R dan kemudian pada sudut β, gerakan bola B menjadi gerakan proyektil. Diketahui bahwa tumbukan antara kedua bola bersifat lenting sebahagian dengan koefisien restitusi e, dan kedua bola dapat dianggap sebagai benda titik. Tentukan besar kecepatan bola A sesaat menumbuk bola B.

5. Sebuah balok kecil (massa m1) berada di atas suatu bidang miring (massa m2, sudut kemiringan θ) yang diletakkan di atas alat timbangan berat (lihat gambar). Diketahui bidang miring memiliki keringgian h dan titik pusatnya berada pada ketinggian h/3 dari alas bidang miring. Sementara itu pada saat awal, titik pusat massa balok m1 berada di ketinggian h dari alas bidang miring. Asumsikan bidang miring licin dan terikat pada timbangan. Tentukan : a. letak posisi vertikal pusat massa sistem balok-bidang miring tersebut.

b. komponen vertikal kecepatan pusat massa sistem tersebut dinyatakan sebagai fungsi waktu t, saat balok kecil tergeser/bergerak ke bawah di atas permukaan bidang miring. c. posisi vertikal pusat massa sistem tersebut sebagai fungsi waktu.

A B β R α L M Poros Tetap A α L M Poros Tetap B α L M Poros Tetap C

(3)

davitsipayung.com

Davit Sipayung

d. nilai pembacaan pada alat timbangan berat saat balok kecil mulai bergeser.

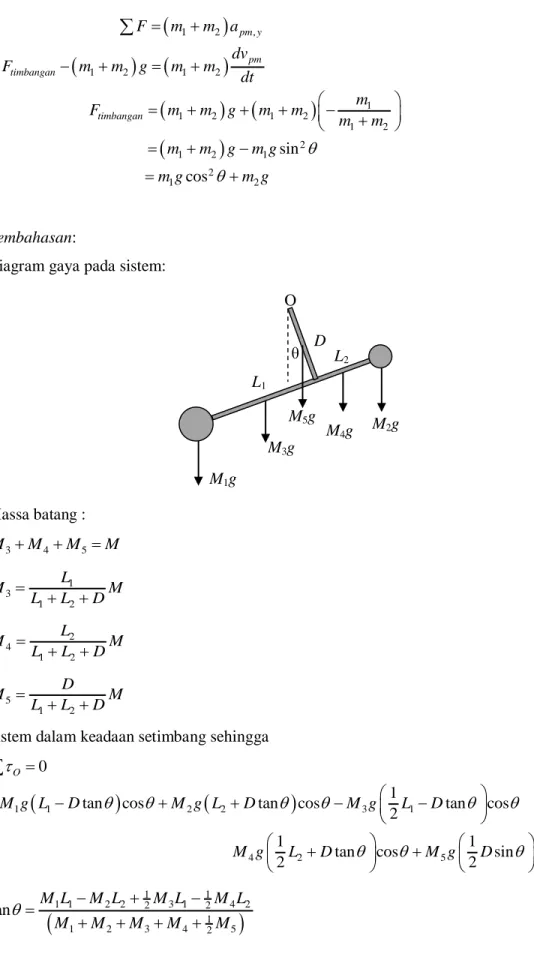
6. Diketahui dua batang seragam yang disusun seperti pada gambar berikut. Batang dengan panjang D dipasang tegak lurus terhadap batang dengan pamjang L1+ L2 (lihat gambar). Massa total batang adalah M. Ujung batang D diletakkan pada poros O yang licin, sedangkan pada ujung batang L1 dan batang L2 dipasang massa masing-masing berturut-turut M1 dan M2. Ternyata pada keadaan setimbang,batang D membentuk sudut θ terhadap vertikal. Percepatan gravitasi g ke bawah.Tentukan tanθ dinyatakan dalam besaran-besaran di atas.

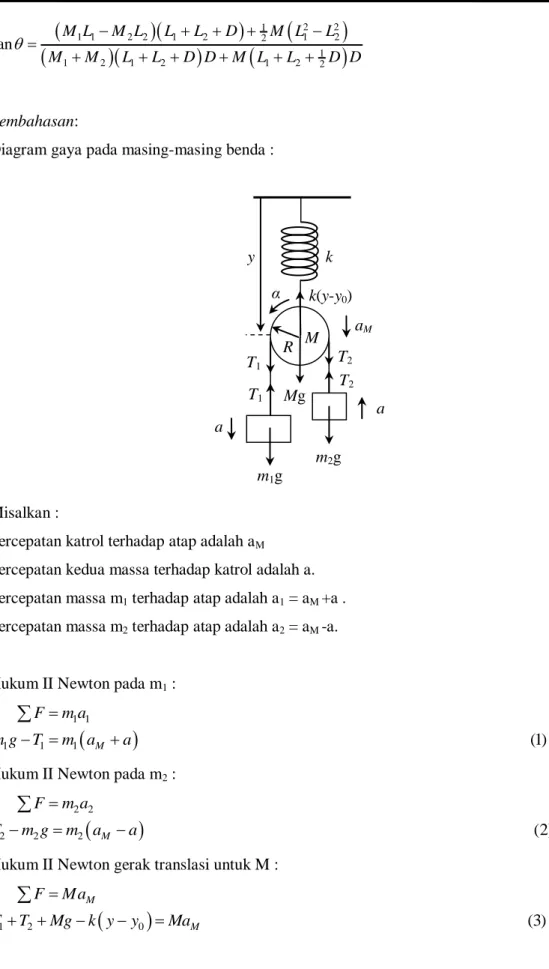
7. Pada sistem massa-pegas-katrol di bawah ini, diketahui pegas tak bermassa dengan tetapan k digantung vertikal pada atap tetap. Panjang pegas mula-mula dalam keadaan tidak tertarik atau tertekan adalah y0. Di bawah pegas tergantung sebuah katrol silinder bermassa M dan berjari-jari R dengan momen inersia I = ½ MR2 . Pada katrol tersebut terdapat tali tak bermassa yang tidak dapat mulur yang menghubungkan massa m1 dan m2 . Jika m1 ≠ m2, tentukan kecepatan sudut osilasi pegas.

O θ M2 M1 D L2 L1 h m1 m2 θ k m1 m2 M R

(4)

davitsipayung.com

Davit Sipayung

Pembahasan Olimpiade Sains Tingkat Kabupaten/ Kota 2017 Bidang Fisika SMA

1. Pembahasan:

a. Misalkan kompresi maksimum pegas adalah x. Pilih energi potensial nol di titik terendah benda. Kekekalan energi mekanik :





2 2 1 2 1 0 2 awal akhir EM EM Mg h x kx kx Mgx Mgh       Solusi x adalah 2 2 ₂ Mg M g Mghk x k   

Pilih solusi x positif sebagai solusi yang mungkin. 2 2 ₂ Mg M g Mghk x k   

Hukum II Newton pada lift saat akan terangkat ke atas (a ≤ 5g) :

2 2 2 5 12 F ma kx Mg Ma Mg M g Mghk k Mg Mg k Mg k h     _ _           

b. Posisi setimbang pegas dari ujung atas pegas mula-mula adalah 0

Mg x

k



(5)

davitsipayung.com Davit Sipayung davitsipayung@gmail.com 0 2 2 2 2 2 2 2 2 12 2 12 5 12 A x x Mg M g Mghk Mg k k M g Mghk k Mg M g Mgh h Mg h h            _ _           2. Pembahasan:

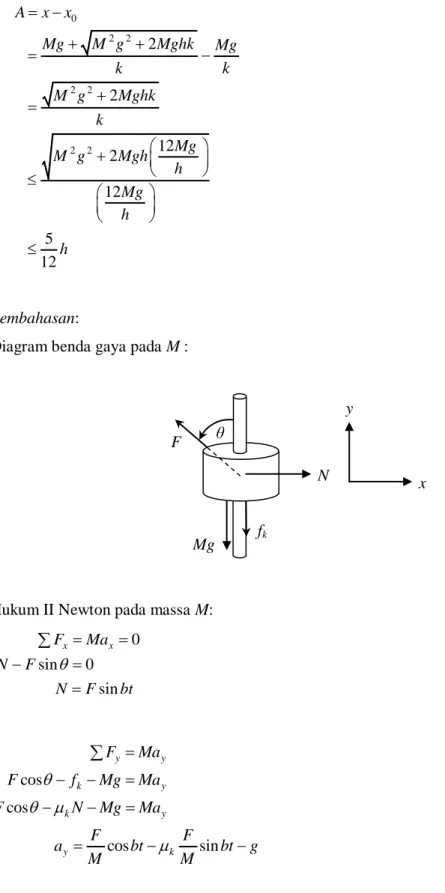
Diagram benda gaya pada M :

Hukum II Newton pada massa M: 0 sin 0 sin x x F Ma N F N F bt        cos cos cos sin y y k y k y y k F Ma F f Mg Ma F N Mg Ma F F a bt bt g M M              



Sudut antara gaya dan poros adalah θ = bt .

x y N fk θ F Mg

(6)

davitsipayung.com

Davit Sipayung

Kecepatan benda sebagai fungsi waktu :

0 0 0 0 0 0 0 0 0 cos sin sin cos sin cos y y y y y y v _t y y v t y y y t k y t k y k y k dv a dt dv a dt dv a dt v v a dt F F v bt bt g dt M M F F v bt bt gt Mb Mb F F F v bt bt gt Mb Mb Mb              _   _      _   _           

Kecepatan awal benda nol, v0y=0, ketika θ0 =0 atau t = 0. Kecepatan akhir benda nol, vy=0, ketika θ=π/2 atau t = π/2b.

sin cos k y k F F F v bt bt gt Mb Mb Mb       0 sin cos 2 2 2 k k F F F b b g Mb b Mb b b Mb   _            _ _ __ _ _ __ _ _          





2 1 k F  Mg    3. Pembahasan:

a. Pilih acuan energi potensial sama dengan nol di titik terendah lintasan piringan. Energi mekanik awal sistem



1 cos



1 cos 3 2 awal EM MgL MgL MgL





     _  _   

Piringan berotasi terhadap poros tetap dengan kecepatan sudut setiap titik pada piringan bernilai sama atau dengan kata lain piringan berotasi murni. Energi mekanik akhir pendulum di titik terendah lintasannya ,

(7)

davitsipayung.com Davit Sipayung davitsipayung@gmail.com 2 2 2 2 1 2 1 1 2 2 akhir poros pm EM I v MR ML L        _  __ _   

Hukum kekekalan energi mekanik:

2 2 2 3 2 2 1 1 2 2 2 2 2 awal akhir pm pm EM EM v MgL MR ML L gL v R L       _  __ _     

b. Piringan berotasi terhadap poros tetap dengan kecepatan linier setiap titik pada piringan bernilai sama atau dengan kata lain piringan translasi murni. Energi mekanik akhir pendulum di titik terendah lintasannya ,

2 1 2

akhir pm

EM  Mv

Hukum kekekalan energi mekanik:

2 1 2 2 awal akhir pm pm EM EM MgL Mv v gL   

Piringan akan menggelinding tanpa slip dengan pusat rotasi di pusat massa piringan. Hukum kekekalan energi mekanik:

2 2 2 2 2 1 1 2 2 2 1 1 1 2 2 2 2 2 3 awal akhir pm pm pm pm EM EM MgL Mv I v MgL Mv MR R gL v         _ _   

(8)

davitsipayung.com

Davit Sipayung

4. Pembahasan:

Gambar gerakan bola A dan bola B.

Tinjau tumbukan antara bola A dan bola B. Hukum kekekalan momentum :

0 0 1 1 0 1 1 1 1 0 0 2 2 (1) awal akhir A A B B A A B B A A B A B A p p m v m v m v m v mv mv mv v v v         



Koefisien restitusi: 1 1 0 0 1 1 0 (2) akhir awal B A B A A B A v e v v v v v v v ev   _       

Eliminasi vA1 menggunakan persamaan (1) dan persamaan (2) untuk mendapatkan





1 0 1 3 B A e v   v

Tinjau gerakan bola B sesaat setelah tumbukan dan sesaat sebelum lepas dari lintasannya. Pilih energi potensial nol di posisi bola B lepas dari lintasannyanya. Hukum kekekalan energi mekanik :









_

_

2 2 1 2 2 2 2 2 0 1 1 2 2 1 cos 2 0 2 2 1 2 1 cos 9 awal akhir

awal awal akhir akhir

B B B A EM EM EK EP EK EP m v mgR m v e v v gR                   vA0 vB1 vB2 vB0 = 0 A B β R Mg N

(9)

davitsipayung.com

Davit Sipayung

Hukum II Newton sesaat B meninggalkan lintasannya, N =0 :





_

_





2 2 2 2 0 0 cos 1 cos 0 2 1 cos 9 3 3cos 2 1 sp B A A F ma mv mg N R e m mg v gR R v gR e         _             _ 



5. Pembahasan:

a. Pilih pusat koordinat di titik siku bidang miring seperti ditunjukkan gambar di bawah ini.

Posisi vertikal pusat massa balok dan bidang miring berturut-turut adalah y1 = h dan y2 = h/3. Posisi vertikal pusat massa sistem balok-bidang miring :

1 1 3 2 1 1 2 2 1 2 1 2 pm m m m y m y y h m m m m      _{ } _  _  _

b. Diagram gaya pada balok :

m1g a1 N θ θ x y h y x m2 θ m1

(10)

davitsipayung.com

Davit Sipayung

Hukum II Newton pada balok searah bidang miring : 1 1 1 sin sin F ma mg ma a g     



Komponen vertikal pusat massa balok :

1 1 2 sin sin y a a g      

Komponen vertikal kecepatan pusat massa balok sebagai fungsi waktu: 1 01 1 2 sin y y y v v a t g t    

Komponen vertikal kecepatan pusat bidang miring sebagai fungsi waktu: 2y 0

v 

Kecepatan vertikal pusat massa sistem balok-bidang miring sebagai fungsi waktu : 1 1 2 2 , 1 2 1 2 1 2 sin y y pm y m v m y v m m m g t m m       

c. Komponen vertikal posisi pusat massa balok sebagai fungsi waktu : 1 2 1 01 01 2 1 1 2 2 2 sin y y y y v a t h g t     

Komponen vertikal posisi pusat bidang miring sebagai fungsi waktu: 2

3

h

y 

Posisi vertikal pusat massa sistem balok-bidang miring sebagai fungsi waktu :





 

1 1 2 2 1 2 2 2 1 1 1 2 2 3 1 2 1 1 3 2 1 2 2 1 2 1 2 sin 1 sin 2 pm m y m y y m m m h g t m h m m m m m h g t m m m m     _    _      _ _  _ _  _  _  

(11)

davitsipayung.com Davit Sipayung davitsipayung@gmail.com

























1 2 , 1 2 1 2 1 1 2 1 2 1 2 2 1 2 1 2 1 2 sin cos pm y pm timbangan timbangan F m m a dv F m m g m m dt m F m m g m m m m m m g m g m g m g               _ _        



6. Pembahasan:

Diagram gaya pada sistem:

Massa batang : 3 4 5 M M M M 1 3 1 2 L M M L L D    2 4 1 2 L M M L L D  _ _ 5 1 2 D M M L L D  _ _

Sistem dalam keadaan setimbang sehingga









1 1 2 2 3 1

4 2 5

0

1

tan cos tan cos tan cos

2

1 1

tan cos sin 0

2 2 O M g L D M g L D M g L D M g L D M g D                   _  _    _  _  _        







1 1 1 1 2 2 2 3 1 2 4 2 1 1 2 3 4 2 5 tan M L M L M L M L M M M M M          O θ M2g M1g M3g L1 M5g L2 M4g D

(12)

davitsipayung.com Davit Sipayung davitsipayung@gmail.com





















2 2 1 1 1 2 2 1 2 2 1 2 1 1 2 1 2 1 2 2 tan M L M L L L D M L L M M L L D D M L L D D              7. Pembahasan:

Diagram gaya pada masing-masing benda :

Misalkan :

Percepatan katrol terhadap atap adalah aM Percepatan kedua massa terhadap katrol adalah a. Percepatan massa m1 terhadap atap adalah a1 = aM +a . Percepatan massa m2 terhadap atap adalah a2 = aM -a.

Hukum II Newton pada m1 :





1 1 1 1 1 M (1) F m a m g T m a a    



Hukum II Newton pada m2 :





2 2 2 2 2 M (2) F m a T m g m a a    



Hukum II Newton gerak translasi untuk M :





1 2 0 (3) M M F Ma T T Mg k y y Ma      



k m1g T2 M R m2g T2 T1 T1 y k(y-y0) a a aM α Mg

(13)

davitsipayung.com

Davit Sipayung

Hukum II Newton gerak rotasi untuk M :

2 1 2 1 2 1 2 1 (4) 2 I a T R T R MR R T T Ma        _{ }    



Gabungan persamaan (1) sampai persamaan (4) akan menghasilkan

























1 1 2 2 0 2 1 1 2 1 2 1 2 2 0 2 2 0 (5) M k m m M a y y g m m M m m M m m g y y y y                    _   _      

Kecepatan sudut osilasi pegas adalah

















1 1 2 2 2 1 1 2 1 2 1 2 (6) k m m M m m M m m M m m         

dan posisi setimbang katrol dari atap adalah

0 0 2 (7)

g y  y _