SKRIPSI
Oleh :
ARIEFIANI RACHMALINA NINGSIH
0734010058
J URUSAN TEKNIK INFORMATIKA
FAKULTAS TEKNOLOGI I NDUSTRI
UNIVERSITAS PEMBANGUNAN NASIONAL “VETERAN”
J AWA TIMUR
SKRIPSI
Diajukan Untuk Memenuhi Persyaratan Dalam Memperoleh Gelar Sarjana Komputer
Program Studi Teknik Informatika
Oleh :
ARIEFIANI RACHMALINA NINGSIH 07340101058
PROGRAM STUDI TEKNIK INFORMATIKA FAKULTAS TEKNOLOGI INDUSTRI
UNIVERSITAS PEMBANGUNAN NASIONAL “VETERAN” J AWA TIMUR
PENENTUAN NILAI OPTIMAL DENGAN VARIABEL DAN
KONSTRAIN YANG DINAMIS
Disusun Oleh :
ARIEFIANI RACMALINA NINGSIH NPM : 0734010058
Telah dipertahankan dihadapan dan diter ima oleh Tim Penguji Skr ipsi Pr ogram StudiTeknik Infor matika, Fakultas Teknologi Industri
Univer sitas Pembangunan Nasional “Veteran” J awa Timur Pada tanggal 15 J uni 2012
PEMBIMBING :
PENERAPAN PEMROGRAMAN LINEAR PADA APLIKASI
PENENTUAN NILAI OPTIMAL DENGAN VARIABEL DAN
KONSTRAIN YANG DINAMIS
Disusun Oleh :
ARIEFIANI RACMALINA NINGSIH NPM : 0734010058
Telah disetujui mengikuti Ujian Negar a Lisan
Gelombang VI Tahun Akademik 2011/2012
Menyetujui,
Pembimbing Utama
Ir . Kindr iar i Nur ma Wahyusi, MT
NIP. 196 002 281 988 032 001
Pembimbing Pendamping
Achmad J unaidi, S.Kom
NPT. 37881.040.1991
Mengetahui,
Kepala Pr ogr am Studi Teknik Infor matika
Fakultas Teknologi Industr i
Univer sitas Pembangunan Nasional “Veter an” J awaTimur
telah melimpahkan Rahmat dan Hidayah-NYA kepada penulis sehingga dapat menyelesaikan laporan tugas akhir ini dengan baik dan benar.
Penyusunan laporan tugas akhir ini merupakan prasyarat dalam mengambil tugas akhir. Adapun judul laporan tugas akhir ini adalah “Penerapan nilai optimal dengan variable dan konstrain yang dinamis”.
Skripsi dengan beban 4sks ini disusun guna diajukan sebagai salah satu syarat untuk menyelesaikan program strata satu (S1) pada program studi Teknik Informatika, Fakultas Teknologi Industri, UPN ”Veteran” Jawa Timur.
Tidak lupa pada kesempatan ini pe ulis menyampaikan ucapan terimakasih yang sebesar-besarnya kepada semua pihak yang telah membantu dalam penyelesaian laporan skripsi ini. Ucapan Terimakasih yang sebesar-besarnya penulis sampaikan kepada:
1. Sang penguasa alam semesta Allah Subhanallah Wata’ala yang telah melimpahkan Rahmat dan Hidayah kepada penulis sehingga dapat menyelesaikan tugas skripsi sampai tuntas, memberikan kemudahan disaat mengalami kesulitan dan selalu memberikan petunjuk agar dapat menyelesaikan skripsi ini.
iii
3. Bapak Prof.Dr.Ir Teguh Soedarto, MP, Selaku Rektor UPN “Veteran” Jawa Timur.
4. Bapak Soetiyono,MT, Selaku DEKAN FTI UPN ”Veteran” Jawa Timur. 5. Ibu Dr. Ir. Ni Ketut Sari, MT, Selaku Kepala Jurusan Teknik Informatika, FTI
UPN “Veteran” Jawa Timur.
6. Ibu Ir.Kindriari Nurma Wahyusi,MT, Selaku dosen pembimbing 1 yang telah banyak meluangkan begitu banyak waktu dan pikiran serta memberikan motivasi, tenaga, solusi terbaik, perhatian, dukungan, nasehat-nasehat dalam memberikan bimbingan dengan sabar selama proses tugas akhir ini.
7. Bapak Achmad Junaidi,S.Kom. Selaku dosen pembimbing 2 yang juga telah meluangkan begitu banyak waktu, tenaga, dan pikiran serta memberikan motivasi, nasehat-nasehat dalam memberikan bimbingan selama proses tugas akhir ini.
8. Para Dosen Teknik Informatika, Sistem Informasi, serta semua staff yang telah membantu dan mendukung dalam kesuksesan tugas akhir ini.
mengerjakan tugas akhir ini dengan baik.
11. Terimakasih banyak untuk Mbah Mad yang telah membantu dalam segi spiritual dan doa sehingga diberi kemudahan dalam mengerjakan skripsi ini. 12.Special to: My Best Boy Friend Aryo Puguh Prakoso (Manies ku) yang telah
memotivasi, mendoakan, menghibur saat bosan dengan sabar, memberi masukkan dan selalu setia menemani, sehingga semua yang dikerjakan dapat berjalan dengan baik.
13.Untuk teman-teman seperjuangan yang selalu menghibur, membantu dan berbagi dalam memberikan informasi serta memotivasi dalam mengerjakan laporan tugas akhir ini.
Penulis sebagai manusia biasa pasti mempunyai keterbatasan dan banyak sekali kekurangan, terutama dalam pembuatan laporan tugas akhir ini. Oleh sebab itu kritik dan saran yang membangun dalam memperbaiki laporan tugas akhir ini.
Akhirnya dengan Ridho Allah Subhanallahu Wata’ala penulis berharap semoga skripsi ini memberikan manfaat bagi pembaca sekalian terutama untuk mahasiswa dibidang Informatika
Surabaya, Juni 2012
v
2.2. Pemrograman Linier………..12
2.2.1. Kateristik Pemrograman Linier……….13
2.2.2. Pemodelan Pemrograman Linier………...15
2.3.2. Level–level DFD………...………....36
2.3.3. Bentuk Data Flow Diagram ( DFD )……….38
2.4. Rekayasa Perangkat Lunak………...39
2.4.1. Kategori Rekayasa Perangkat Lunak………39
BAB III ANALISIS DAN PERANCANGAN 3.1. Desain Sistem………52
3.6. Algoritma Penyelesaian Program Linier………...73
3.6.1. Sub Rutin Penentuan Bentuk Persamaan……….74
3.4.2. Sub Rutin Penentuan Nilai Kanan………...75
vii
4.1. Penggunaan Perangkat………..81
4.2. Implementasi Aplikasi………..82
4.2.1. Prosedure BtnHitungClick………...85
4.2.2. Prosedure TableSizeChange……….88
4.2.3. Prosedure TableDrawCell………88
4.2.4. Prosedure BtnBaruClick………..89
4.3. Pengujian Sistem………..89
4.3.1. Pengujian Kasus Pertama………...91
4.3.1. Pengujian Kasus Kedua………...94
BAB V PENUTUP 5.1. Kesimpulan………….………..98
5.2. Saran……..………….………..99
Pembimbing 2 : Achmad Junaidi, S.Kom
ABSTRAK
Makalah ini membahas bagaimana cara menentukan nilai optimal pada pemrograman linier agar dapat menentukan variabel dan konstrain yang dinamis. Masih banyak mahasiswa yang mengalami kesulitan dalm penerapan perhitungan program linier tersebut. Kendala yang sering dialami oleh pengguna dalam menggunakan program linear adalah waktu yang diperlukan untuk menghitung nilai optimal tergantung pada jumlah variabel dan konstrain yang selalu berubah sesuai dengan pemodelan matematikanya.
Solusi dari penyelesaian program linier tersebut dengan cara menggunakan metode simpleks, untuk penyelesaiannya membuat tabel permasalahan dan bentuk matematika terlebih dahulu dari permasalahan yang ada, kemudian mencari kolom yang mempunyai nilai pertama (X1) pada baris F(z) dan memilih baris, Pemilihan
baris yang mempunyai nilai kedua (X4) pada baris F(z). Nilai-nilai baris dan
kolom tersebut dibagi dengan titik perpotongan. Langkah berikutnya adalah mengkalikan kolom kedua (X2) dengan baris pertama sehingga nilai-nilai kolom
(selain baris) sama dengan 0 atau 1.
1 1.1. Latar Belakang
Mata pelajaran Matematika perlu diberikan kepada semua peserta didik mulai dari sekolah dasar untuk membekali peserta didik dengan kemampuan berpikir logis, analitis, sistematis, kritis, dan kreatif, serta kemampuan bekerjasama. Kompetensi tersebut diperlukan agar peserta didik dapat memiliki kemampuan memperoleh, mengelola, dan memanfaatkan informasi untuk bertahan hidup pada keadaan yang selalu berubah, tidak pasti, dan kompetitif.
Salah satu materi yang dapat mengantar siswa untuk mampu berpikir logis, kritis, analitis dan kreatif adalah Program Linier, sekaligus mengurangi anggapan bahwa program linier itu sulit. Untuk itu guru sebagai fasilitator diharapkan mampu menciptakan suatu kondisi pembelajaran dengan menggunakan pendekatan, strategi serta model pembelajaran yang mampu mengantarkan siswa kepada tujuan pembelajaran.
penjumlahan, pengurangan, perkalian serta membandingkan banyaknya benda. Di Sekolah Menengah Pertama (SMP) konsep diperluas melalui pembelajaran materi Sistem Persamaan Linier Satu Variabel, kemudian ditingkatkan melalui materi Sistem Persamaan Linier Dua Variabel. Di Sekolah Menengah Atas (SMA) telah diperkenalkan sistem pertidaksamaan linier dan materi khusus program linier yang menyajikan persoalan sehari-hari, kemudian menerjemahkan permasalahan ke dalam model matematika. Menyelesaikan sistem pertidaksamaan yang merupakan kendala atau pembatas mencari penyelesaian optimum dan menjawab permasalahan. Metode yang digunakan adalah metode grafik dengan menggunakan uji titiksudut dan garis selidik. Pada tingkat universitas, terdapat mata kuliah khusus program linier yang membahas metode penyelesaian program linier yang tujuannya mencari keuntungan maksimum dan mengeluarkan biaya minimum. Metode yang diberikan pada universitas adalah metode grafik, metode simpleks, metode analisis dual, metode transportasi.
Dengan melihat pengalaman dan kenyataan tersebut, tampak menarik apabila dikaji secara khusus mengenai materi yang berkaitan dengan program linier. Pada kesempatan ini penulis akan membahas pada materi yang berkaitan dengan program linier di satuan pendidikan tingkat Universitas dan materi-materi yang terkait pada program linier dengan menggunakan metode simpleks saja yang bertujuan untuk mencari nilai optimal pada suatu variabel dan constraint yang dinamis.
tersebut. Kendala yang sering dialami oleh pengguna dalam menggunakan program linear adalah waktu yang diperlukan untuk menghitung nilai optimal relatif lama dalam proses interasinya tergantung pada jumlah variabel dan konstrain yang selalu berubah sesuai dengan pemodelan matematikanya. Oleh karena itu, dalam tugas akhir ini, mendapatkan ide untuk membuat aplikasi yang mampu menentukan nilai optimal dengan variabel dan konstrain yang dinamis dengan mudah.
1.2. Rumusan Masalah
Rumusan masalah yang digunakan dalam tugas akhir ini adalah :
1. Penyebab seorang siswa atau mahasiswa melakukan kesalahan dalam menyelesaikan soal pemrograman linier.
2. Bagaimana cara menerapkan pemrograman linier ke dalam aplikasi untuk mencari nilai optimal tersebut sehingga dapat memudahkan pengguna mencari nilai optimal sesuai fungsi kendala dan fungsi tujuan yang dimasukkan.
1.3. Batasan Masalah
Adapun batasan masalah yang dipergunakan dalam tugas akhir ini adalah: 1. Aplikasi penentuan nilai optimal pemrograman linear ini menggunakan
metode simpleks sesuai bentuk ekspresi model matematika yang dimasukkan oleh user.
3. Cara pemrosesan nilai variabel dan konstrain sesuai format yang digunakan pada sistem aplikasinya. Disesuaikan dengan nilai operator dan Constantnya. 4. Aplikasi ini juga dapat langsung menginput nilai variabel dan kostraint,
sehingga apabila yang diinputkan bukan angka, sistem akan memberikan pesan peringatan bahwa nilai yang diinputkan tidak valid
1.4. Tujuan
Tujuan yang ingin dicapai pada pengerjaan tugas akhir ini adalah:
1. Dapat menggunakan model matematika dalam pemrograman linear sesuai kasus yang diinputkan user.
2. Membuat aplikasi yang dapat menentukan nilai optimal dalam pemrograman linear dengan variabel dan konstrain yang dinamis.
3. Mengetahui apa saja yang menyebabkan siswa melakukan kesalahan dalam menyelesaikan soal program linear.
1.5. Manfaat
Adapun manfaat yang ingin diperoleh dari pengerjaan tugas akhir ini adalah dapat membuat perangkat lunak untuk mempermudah pengguna dalam menentukan nilai optimal pada pemrograman linear dengan fungsi kendala yang bersifat dinamis.
1.6. Metodologi Penelitian
alur yang sistematis. Metodologi penelitian in digunakan sebagai pedoman penelitian dalam pelaksanaan penelitian ini agar hasil yang dicapai tidak menyimpang dari tujuan yang telah ditetapkan sebelumnya.
Adapun metode penelitian yang dipergunakan dalam pengerjaan tugas akhir ini adalah :
a. Studi Literatur
Dilakukan dengan cara mencari segala macam informasi secara riset ke perpustakaan dan mempelajari buku – buku yang berkaitan dengan masalah yang di hadapi.
b. Pengumpulan dan Analisa Data
Pengumpulan data dilakukan dengan cara : observasi, identifikasi, dan klasifikasi melalui studi literatur. Dari pengumpulan data tersebut dapat dilakukan analisa data yaitu sistem pemodelan program linier.
c. Perancangan Sistem
Melakukan analisa awal tentang system yang akan dibuat yaitu pemecahan masalah yang dilakukan melalui bahasa pemrograman untuk mengetahui nilai optimasi dari persamaan program linier.
d. Pembuatan Aplikasi
e. Pengujian Aplikasi
Merupakan tahap pengujian terhadap perangkat lunak yang telah dibangun.
1.7. Sistematika Penulisan
Sistematika penulisan tugas akhir ini disusun untuk memberikan gambaran umum tentang penelitian yang dijalankan. Sistematika penulisan tugas akhir ini adalah sebagai berikut :
BAB I PENDAHULUAN
Bab ini berisi latar belakang masalah, identifikasi masalah, maksud dan tujuan yang ingin dicapai, batasan masalah, metodologi penelitian yang diterapkan dalam memperoleh dan mengumpulkan data, waktu dan tempat penelitian, serta sistematika penulisan.
BAB II TINJ AUAN PUSTAKA
Membahas berbagai konsep dasar dan teori-teori yang berkaitan dengan topik masalah yang diambil dan hal-hal yang berguna dalam proses analisis permasalahan.
BAB III ANALISIS DAN PERANCANGAN
BAB IV IMPLEMENTASI DAN PENGUJ IAN
Membahas mengenai pengimplementasian aplikasi yang telah dibuat ke perangkat yang akan digunakan serta melakukan pengujian terhadap aplikasi yang telah diimplementasikan tersebut.
BAB V PENUTUP
2.1. Pemr ograman Matematika
Pemrograman matematika adalah ilmu manajemen yang menentukan suatu optimasi, atau efisiensi yang sangat tinggi, dengan menggunakan sumber daya untuk mencapai tujuan individu pada suatu bisnis.
Cabang ilmu pemrograman matematika mulai berkembang sejak pasca revolusi industri. Hal tersebut membuat dunia usaha mengalami perubahan dalam
hal ukuran (besarnya) dan kompleksitas organisasi-organisasi perusahaan. Bagian yang mengalami perubahan yang cukup terlihat adalah perkembangan dalam pembagian kerja dan segmentasi tanggung jawab manajemen dalam organisasi tersebut, termasuk pengaturan sumber daya. Disisi lain, organisasi-organisasi (perusahaan) pada saat ini harus beroperasi di dalam situasi dan kondisi lingkungan bisnis yang dinamis dan selalu berbeda satu dengan yang lainnya, serta siap untuk berubah-ubah.
langkah-langkah dan strategi yang tepat serta target yang sesuai secara sistematis dalam rangka mencapai tujuan yang telah ditentukan, yakni hasil yang memuaskan. Hasil yang memuaskan tersebut adalah hasil yang optimal yang berarti dampak yang positive maksimum dan dampak negative minimum.
Pemrograman matematika lebih berkaitan dengan permasalahan optimasi. Dalam dunia industri, cabang ilmu ini lebih dikenal dengan nama riset operasional. Arti riset operasi (operations research) telah banyak didefinisikan oleh beberapa ahli. Diantaranya :
1. Morse dan Kimball mendefinisikan riset operasi sebagai metode ilmiah (scientific method) yang memungkinkan para manajer mengambil keputusan
mengenai kegiatan yang mereka tangani dengan dasar kuantitatif. Definisi ini kurang tegas karena tidak tercermin perbedaan antara riset operasi dengan disiplin ilmu yang lain. (Morse,Philip M. 2005).
2. Churchman, Arkoff dan Arnoff pada tahun 1950-an mengemukakan pengertian riset operasi sebagai aplikasi metode-metode, teknik-teknik dan peralatan-peralatan ilmiah dalam menghadapi masalah-masalah yang timbul di dalam operasi perusahaan dengan tujuan ditemukannya pemecahan yang optimum masalah-masalah tersebut. (Churchman, et. al. 1957).
Dari ketiga definisi tersebut dapat disimpulkan bahwa riset operasi berkenaan dengan pengambilan keputusan yang optimal dalam, dan penyusunan model dari sistem-sistem baik yang diterministik maupun probabilistik yang berasal dari kehidupan nyata. Atau dunia pengelolaan atau dunia usaha yang memakai pendekatan ilmiah atau pendekatan sistematis.
Dengan demikian dapat juga disimpulkan bahwa riset teknologi informasi adalah metode untuk memformulasikan dan merumuskan permasalahan sehari-hari baik mengenai bisnis, ekonomi, sosial maupun bidang lainnya ke dalam pemodelan matematis untuk mendapatkan solusi yang optimal dengan menggunakan perangkat teknologi informasi.
Bagian terpenting dari riset teknologi informasi adalah bagaimana menerjemahkan permasalahan sehari-hari ke dalam model matematis. Faktor-faktor yang mempengaruhi pemodelan harus disederhanakan dan apabila ada data yang kurang, kekurangan tersebut dapat diasumsikan atau diisi dengan pendekatan yang bersifat rasional. Dalam membuat pemodelan matematika diperlukan ketajaman berpikir dan logika. Untuk mendapatkan solusi yang optimal dan memudahkan kita mendapatkan hasil, kita dapat menggunakan komputer sebagai alat utama pendukungnya.
Dalam hal ini termasuk menentukan pilihan dari alternatif-alternatif yang ada secara umum meliputi langkah-langkah :
1. Identifikasi masalah.
keputusan yang dapat dikendalikan maupun yang tidak dapat dikendalikan. Kumpulkan data tentang kendala-kendala yang menjadi syarat ikatan terhadap perubah-perubah dalam fungsi tujuan sistem model yang dipelajari.
2. Penyusunan model.
Penyusunan model yang terdiri dari, memilih model yang cocok dan sesuai dengan permasalahannya. Merumuskan segala macam faktor yang terkait di dalam model yang bersangkutan secara simbolik ke dalam rumusan model matematika. Menentukan perubah-perubah beserta kaitan-kaitannya satu sama lainnya. Tetapkan fungsi tujuan beserta kendala-kendalanya dengan nilai-nilai dan perameter yang jelas.
3. Analisa model.
Didalam analisa model terdapat hal yang penting diantaranya yaitu, Melakukan anlisis terhadap model yang telah disusun dan dipilih. Memilih hasil-hasil analisis yang terbaik (optimal). Melakukan uji kepekaan dan anlisis postoptimal terhadap hasil-hasil terhadap analisis model.
4. Pengesahan model.
Analisis pengesahan model menyangkut penilaian terhadap model tersebut dengan cara mencocokannya dengan keadaan dan data yang nyata, juga dalam rangka menguji dan mengesahkan asumsi-asumsi yang membentuk model tersebut secara struktural. Yang termasuk dengan struktural tersebut yaitu perubahnya, hubungan-hubungan fungisionalnya, dan lain-lain. 5. Implementasi hasil
merupakan hasil-hasil analisis yang kiranya dapat dipakai dalam perumusan keputusan yang kiranya dapat dipakai dalam perumusan strategi-strategi, target-target, langkah-langkah kebijakan guna disajikan kepada pengambilan keputusan dalam bentuk alternatif-alternatif pilihan. (Njotowidjojo, Yoko. 2003).
2.2. Pemr ograman Linier
Linier Programming adalah suatu model yang dipakai dalam pemecahan
masalah pengalokasian sumber-sumber yang terbatas secara optimal. untuk menyelesaikan masalah optimisasi, yaitu memaksimumkan atau meminimumkan fungsi tujuan yang bergantung pada sejumlah variabel input.
Dalam persoalan program linear memberikan lebih dari satu pemecahan yang mungkin terjadi. Pemecahana terbaik adalah pemecahan yang mencapai hasil maksimum melalui pembatas-pembatasnya. Pembatas-pembatas tersebut dinyatakan secara sistematis dalam bentuk persamaan linier. Sehingga persoalan ini dinamakan persoalan program linier
Hal terpenting yang perlu kita lakukan dalam menyelesikan permasalahan optimasi adalah mencari tujuan penyelesaian masalah dan apa penyebab masalah tersebut. Di dalam Linier Programming terdapat dua fungsi yaitu :
1. Fungsi tujuan (Objective Function) merupakan Fungsi yang menggambarkan tujuan dalam permasalahan Linier Programming yang berkaitan dengan pengaturan secara optimal sumber daya-sumber daya untuk memperoleh keuntungan yang maksimal atau biaya yang minimum F(z).
2. Fungsi batasan (Subjective To Constraint) merupakan Bentuk penyajian secara sistematis batasan-batasan kapasitas yang tersedia yang akan dialokasikan secara optimal ke berbagai kegiatan.
2.2.1. Karakteristik Pemrograman Linier
Pemrograman Linier atau Linier Programming biasa disingkat PL, merupakan metode matematik dalam mengalokasikan sumber daya yang terbatas untuk mencapai suatu tujuan seperti memaksimumkan keuntungan dan meminimumkan biaya, banyak pula diterapkan dalam masalah ekonomi, industri, militer, sosial dan lain-lain. Terdapat beberapa kateristik atau sifat dalam pemrograman linier yaitu sebagai berikut.
1. Sifat Linearitas
hipotesa. Secara teknis, linearitas ditunjukkan oleh adanya sifat proporsionalitas, additivitas, divisibilitas dan kepastian fungsi tujuan dan pembatas.
2. Sifat Proporsional
Sifat proposional dapat dipenuhi jika kontribusi setiap variabel pada fungsi tujuan atau penggunaan sumber daya yang membatasi proporsional terhadap level nilai variabel. Jika harga per unit produk misalnya adalah sama berapapun jumlah yang dibeli, maka sifat proporsional dipenuhi. Atau dengan kata lain, jika pembelian dalam jumlah besar mendapatkan diskon, maka sifat proporsional tidak dipenuhi. Jika penggunaan sumber daya per unitnya tergantung dari jumlah yang diproduksi, maka sifat proporsionalitas tidak dipenuhi.
3. Sifat Additivitas
volume penjualan produk lainnya dalam pasar yang sama, maka sifat
additivitas tidak terpenuhi.
4. Sifat Divisibilitas
Sifat Divisibilitas berarti unit aktivitas dapat dibagi ke dalam sembarang level fraksional, sehingga nilai variabel keputusan non integer dimungkinkan.
5. Sifat Kepastian
Sifat Kepastian dapat menunjukkan bahwa semua parameter model berupa konstanta. Artinya koefisien fungsi tujuan maupun fungsi pembatas merupakan suatu nilai pasti, bukan merupakan nilai dengan peluang tertentu.
Dari penjelsan kelima kateristik atau sifat ini dalam dunia nyata tidak selalu dapat dipenuhi. Untuk meyakinkan dipenuhinya kelima kateristik atau sifat ini, dalam pemrograman linier diperlukan analisis sensitivitas terhadap solusi optimal yang diperoleh sehingga mendapatkan hasil yang optimal dan sesuai dengan perhitungan pemrogramn linier tersebut. . (http://repository.usu.ac.id/bitstream/123456789/26289/3/Chapter%20II.pdf)
2.2.2. Pemodelan Pemr ograman Linier
Tahap berikutnya yang harus dilakukan setelah memahami permasalahan optimasi adalah membuat model yang sesuai untuk analisis. Pendekatan konvensional riset operasional untuk pemodelan adalah membangun model
diterjemahkan ke model matematik. Model matematik merupakan representasi kuantitatif tujuan dan sumber daya yang membatasi sebagai fungsi variabel keputusan. Model matematika permasalahan optimal terdiri dari dua bagian.
Bagian pertama memodelkan tujuan optimasi. Model matematik tujuan selalu menggunakan bentuk persamaan. Bentuk persamaan digunakan karena kita ingin mendapatkan solusi optimum pada satu titik. Fungsi tujuan yang akan dioptimalkan hanya satu. Bukan berarti bahwa permasalahan optimasi hanya dihadapkan pada satu tujuan. Tujuan dari suatu usaha bisa lebih dari satu. Tetapi pada bagian ini kita hanya akan tertarik dengan permasalahan optimal dengan satu tujuan.
Bagian kedua merupakan model matematik yang merepresentasikan sumber daya yang membatasi. Fungsi pembatas bisa berbentuk persamaan ( = ) atau pertidaksamaan (≤ atau ≥). Fungsi pembatas disebut juga sebagai konstra in. Konstanta (baik sebagai koefisien maupun nilai kanan) dalam fungsi pembatas maupun pada tujuan dikatakan sebagai parameter model. Model matematika mempunyai beberapa keuntungan dibandingakan pendeskripsian permasalahan secara verbal. Salah satu keuntungan yang paling jelas adala model matematika menggambarkan permasalahan secara lebih ringkas. Hal ini cenderung membuat struktur keseluruhan permasalahan lebih mudah dipahami, dan membantu mengungkapkan relasi sebab akibat penting.
keterhubungannya secara dinamis. Terakhir, model matematik membentuk jembatan ke penggunaan teknik matematik dan komputer kemampuan tinggi untuk menganalisis permasalahan.
Di sisi lain, model matematika mempunyai kelemahan. Sehingga tidak semua karakteristik sistem dapat dengan mudah dimodelkan menggunakan fungsi matematik. Meskipun dapat dimodelkan dengan fungsi matematik, kadang-kadang penyelesaiannya sulit diperoleh karena kompleksitas fungsi dan teknik yang dibutuhkan tidak dapat terpecahkan. Dalam pemodelan linier tersebut ada beberapa langkah-langkah yang harus dipenuhi dalam formulasi model program linier adalah sebagai berikut :
1. Memahami masalah dan mengidentifikasi variabel keputusan
2. Penentuan fungsi tujuan sebagai kombinasi linier dari variabel keputusan 3. Menentukan konstrain sebagai kombinasi linier dari variabel keputusan 4. Identifikasi batas atas dan batas bawah dari variabel keputusan.
Tabel 2.1. Data Untuk Model Pemrograman Linier
Pertambahan laba
/ biaya per unit C1 C2 C3 …… Cn Tingkat kegiatan X1 x 2 x 3 …… x n
Dalam membangun atau membuat model dari formulasi dalam tabel 2.1. digunakan kateristik-kateristik yang biasa digunakan dalam persoalan Program Linier, yaitu :
1. Variabel keputusan
Variabel keputusan merupakan suatu variabel yang menguaraikan secara lengkap keputusan-keputusan yang akan dibuat. Dalam tabel diatas, variabel keputusannya adalah X1, X2, X3 …. Xn.
2. Fungsi Tujuan
Fungsi Tujuan merupakan variabel kepuutusan yang akan dimaksimumkan atau diminimumkan. Dalam tabel 2.1. fungsi tujuannya adalah C1X1 + C2X2 + C3X3 + …. + CnXn.
3. Pembatas
Pembatas merupakan kendala yang dihadapi sehingga untuk dapat menentukan harga-harga variabel keputusan secara sembarang atau acak-acakan. Dimana tabel diatas tersebut pembatasnya adalah b1, b2, b3 ….. bn.
4. Pembatas Tanda
keputusannya tersebut boleh positif, boleh juga negatif (tidak terbatas dalam tanda), misalnya tanda ≥ atau tanda ≤.
Maximize problem yaitu fungsi tujuan yang berorientasi pada laba atau
keuntungan.
Fungsi Tujuan (Objective Function) :
Maximize Z = C1X1 + C2X2 + C3X3 + …… + CnXn.
Batasan-batasan (Subject To Constraint) :
a11X1 + a12X2 + a13X3 + …… + a1nXn ≤ b 1.
a21X1 + a22X2 + a23X3 + …… + a2nXn ≤ b 2.
a31X1 + a32X2 + a33X3 + …… + a3nXn ≤ b 3.
am1X1 + am2X2 + am3X3 + …… + amnXn ≤ b m.
X1, X2, X3, … , Xn ≥ 0
Minimize problem yaitu fungsi tujuan yang berorientasi pada biaya
Fungsi Tujuan (Objective Function)
Minimize Z = C1X1 + C2X2 + C3X3 + …… + CnXn.
Batasan-batasan (Subject To Constraint) :
a11X1 + a12X2 + a13X3 + …… + a1nXn ≤ b 1.
a21X1 + a22X2 + a23X3 + …… + a2nXn ≤ b 2.
a31X1 + a32X2 + a33X3 + …… + a3nXn ≤ b 3.
am1X1 + am2X2 + am3X3 + …… + amnXn ≤ b m.
2.2.3. Metode Simplek
Kasus pemrograman linier sangat beragam. Dalam setiap kasus, hal yang penting adalah memahami setiap kasus dan memahami konsep permodelannya. Meskipun fungsi tujuan misalnya hanya mempunyai kemungkinan bentuk maksimisasi atau minimisasi, keputusan untuk memilih salah satunya bukan pekerjaan mudah. Tujuan pada suatu kasus bisa menjadi batasan pada kasus yang lain. Harus hati-hati dalam menentukan tujuan, koefisien fungsi tujuan, batasan dan koefisien pada fungsi pembatas.
Agar lebih memahami permasalahan dalam program linier, khususnya dalam pencarian nilai optimasi, berikut ini dalah contoh kasus dan cara penyelesaiannya. Ada perusahaan yaitu PT. GUNDAR saat ini telah memproduksi 2 jenis pipa, yaitu : Aqua dan Hydro, dengan rincian sumber daya sebagai berikut:
Tabel 2.2. Sumber Daya PT. Gundar Aqua Hydro
Pompa 1 1
Jam Kerja 9 jam 6 jam Pipa 12 meter 16 meter Laba/Unit $350 $300
Berikut ini adalah langkah penyelesaian dari permasalahan diatas : 1. Memahami masalah.
2. Identifikasi variabel keputusan :
X1=jumlah pipa Aqua yang dihasilkan.
X2=jumlah pipa Hydro yang dihasilkan.
3.Penentuan Fungsi Tujuan Sebagai Kombinasi Linier dari variabel keputusan : MAX: 350 X1 + 300 X2
4. Menentukan konstrain sebagai kombinasi linier dari variabel keputusan : 1X1 + 1X2 <= 200 } pompa
9X1 + 6X2 <= 1566 } jam kerja
12X1 + 16X2 <= 2880 } pipa
5. Identifikasi batas atas atau bawah dari variabel keputusan : X1 >= 0
Seberapa besar hal tersebut dapat terjadi? Misalkan X2 = 0
Konstrain-2: 9X1 <=1566 or X1 <=174
Konstrain-3: 12X1 <= 2880 or X1 <= 240
Jika X2=0, nilai maksimum X1 adalah 174 keuntungan totalnya adalah
$350*174 + $300*0 = $60,900
Solusi tersebut layak (feasible), tapi apakah optimal ?
Beberapa konstrain atau kendala suatu Perangkat Lunak mendefinisikan daerah feasiblenya?
Titik terbaik dari daerah feasible adalah solusi optimal masalah tersebut. Untuk Perangkat Lunak dengan 2 variabel, sangatlah mudah untuk memplot daerah feasible dan menentukan solusi optimalnya.
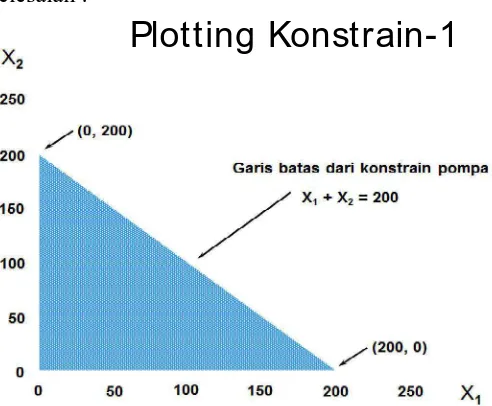
Daerah penyelesaian :
Gambar 2.1. Daerah penyelesaian persamaan linier berdasarkan konstrain 1
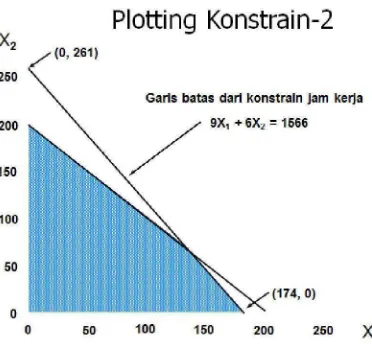
Gambar 2.2. Daerah penyelesaian persamaan linier berdasarkan konstrain 2
Gambar 2.3. Daerah penyelesaian persamaan linier berdasarkan konstrain 3
Gambar 2.5. Daerah penyelesaian plotting kurva tingkat kedua
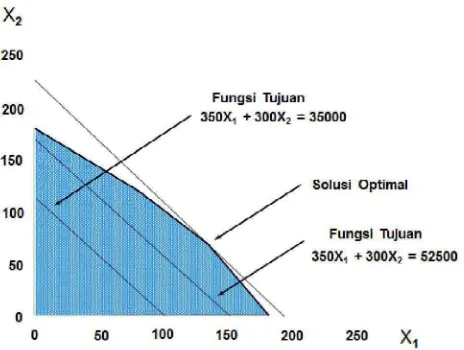
Gambar 2.6. Daerah penyelesaian lokalisasi area optimal Sedangkan perhitungan solusi optimal adalah sebagai berikut :
Solusi optimal terjadi dimana kendala pompa dan jam kerja beririsan. Hal ini terjadi ketika:
X1 + X2 = 200 (1)
dan 9X1 + 6X2 = 1566 (2)
Subtitusi (3) ke dalam (2), dan kita punyai : 9X1 + 6 (200 -X1) = 1566
yang menghasilkan X1 = 122
Sehingga solusi optimalnya adalah : X1=122, X2=200-X1=78
Total Keuntungan = $350*122 + $300*78 = $66,100
Hasil perhitungan diatas, dapat dibuktikan dengan metode grafik yang tampak seperti gambar 2.7 berikut ini :
Gambar 2.7. Pembuktian titik yang menjadi nilai optimal
Sehingga dapat disimpulkan, bahwa cara penyelesaian masalah program linier yang menggunakan grafik adalah sebagai berikut :
1. Plot garis batas setiap konstrain 2. Identifikasi daerah feasible atau layak
3. Lokalisasi solusi optimal dengan melakukan: a. Plotting Kurva bertingkat
= 0; = 0; = 0;……,, = 0; k = 0, 1, 2, 3,…,m 2.3. Polinomial
Proses penentuan suatu fungsi dekatan menggambarkan kecenderungan data dengan simpangan minimum antara nilai fungsi dengan data regresi linier. Regresi linear adalah salah satu cara penyajian data dengan fungsi pendekatan linear.
y = a0 + a1 x + e
dengan
a0 dan a1 : koefisien fungsi
e : simpangan kesalahan
jika dipilih penyajian data dalam fungsi polynomial derajat n, maka fungsi dapat dinyatakan sebagai
Pn (x) = a0 + a1 x + a1 x2 + a1 x3 + ……+ an xn = ah xh
Dan simpangan kesalahan yang terjadi anatara setiap data dengan nilai fungsi adalah
Ci = Pn (xi) – yi, i = 1, 2, 3,…,m
Apabila ditetapkan fungsi S = ei2 , maka S adalah fungsi dan koefisien
polynomial Pn (x), yaitu S = S (a0, a1, a2,……,an). Supaya nilai S minimum,
haruslah ditetapkan koefisien ai sehingga turunan parsial S terhadap setiap
koefisien sama dengan nol. Dengan koefisien ai, dengan i = 0, 1, 2, 3,…,m,
= 0 = 2(a0 + a1x1 + a2x12 + a3x13 – y1)(1) + 2(a0 + a1x2 + a2x22 + a3x23 – y2)(1) +…+
2(a0 + a1xi + a2xi2 + a3xi3 – yi )(1)+…+ 2( a0 + a1xm + a2xm2 + a3xm3 – ym )(1)
= 0 = 2(a0 + a1x1 + a2x12 + a3x13 – y1)(x1) + 2(a0 + a1x2 + a2x22 + a3x23 – y2)(x2) +…+
2(a0 + a1xi + a2xi2 + a3xi3 – yi )(xi)+…+ 2( a0 + a1xm + a2xm2 + a3xm3 – ym )(xm)
= 0 = 2(a0 + a1x1 + a2x12 + a3x13 – y1)(x12) + 2(a0 + a1x2 + a2x22 + a3x23 – y2)(x22) +…+
2(a0 + a1xi + a2xi2 + a3xi3 – yi )(xi2)+…+ 2( a0 + a1xm + a2xm2 + a3xm3 – ym )(xm2)
Untuk menurunkan rumusan regresi, ditinjau fungsi polynomial pangkat tiga sebagai fungsi dekatan
P3 (x) = a0 + a1 x + a1 x2 + a1 x3
Fungsi simpangan S menjadi
S = { P3 (x1) – y1}2 + { P3 (x2) – y2}2 + { P3 (x3) – y3}2+…+ { P3 (xm) – ym}2
= ( a0 + a1x1 + a2x12 + a3x13 – y1 )2 + ( a0 + a1x2 + a2x22 + a3x23 – y2 )2 +…+ ( a0 +
a1xi + a2xi2 + a3xi3 – yi )2 +…+ ( a0 + a1xm + a2xm2 + a3xm3 – ym )2
Turunan parsial S terhadap a0 :
Penyelesaian
a0m + a1 xi + a2 xi 2 + a3 xi 3 = yi
Memberikan
= 0 = 2(a0 + a1x1 + a2x12 + a3x13 – y1)(x13) + 2(a0 + a1x2 + a2x22 + a3x23 – y2)(x23) +…+
2(a0 + a1xi + a2xi2 + a3xi3 – yi )(xi3)+…+ 2( a0 + a1xm + a2xm2 + a3xm3 – ym )(xm3)
Memberikan
a0 xi2 + a1 xi3 + a2 xi 4 + a3 xi 5 = xi2yi
Memberikan
a0 xi3 + a1 xi4 + a2 xi 5 + a3 xi 6 = xi3yi
Terlihat hasil turunan parsial fungsi S memberikan empat persamaan dengan empat variabel yang tidak diketahui. Persamaan ini dibuat persamaan normal yang merupakan persamaan linear simultan
m xi xi2 xi3
xi xi2 xi3 xi4
xi2 xi3 xi4 xi5
xi2 xi3 xi4 xi5
m xi xi2 xi3 ……… xin
xi xi2 xi3 xi4……… xin+1
xi2 xi3 xi4 xi5……… xin+2
xi2 xi3 xi4 xi5……… xin+3
2.4. Data Flow Diagr am (DFD)
Data Flow Diagram (DFD) adalah alat pembuatan model yang memungkinkan profesional sistem untuk menggambarkan sistem sebagai suatu jaringan proses fungsional yang dihubungkan satu sama lain dengan alur data, baik secara manual maupun komputerisasi.
DFD ini adalah salah satu alat pembuatan model yang sering digunakan, khususnya bila fungsi-fungsi sistem merupakan bagian yang lebih penting dan kompleks dari pada data yang dimanipulasi oleh sistem. Dengan kata lain, DFD adalah alat pembuatan model yang memberikan penekanan hanya pada fungsi sistem.
bagi seorang analis sistem. Penggunaan DFD Sebagai Modeling Tool dipopulerkan oleh Demacro and Yordan (1979) dan Gane and Sarson (1979) dengan menggunakan pendekatan Metode Analisis Sistem Terstruktur.
DFD (Data Flow Diagram) merupakan data yang tersimpan dan proses dengan proses yang terhubung dengan data tersebut. DFD bukan termasuk flowchart dikarenakan dalam proses DFD bisa berjalan secara parallel, DFD juga
menggambarkan aliran data dalam sebuah sistem. Dalam proses membuatan DFD tidak ada loop ataupun cabang tetapi dapat menggambarkan semua proses, meskipun proses tersebut terjadi dalam waktu yang berbeda.
Ada beberapa peraturan-peraturan yang penting dalam membuatan DFD tersebut.
1. Semua objek harus mempunyai nama.
2. Aliran data harus diawala dan diakhiri oleh proses.
3 Semua aliran data harus mempunyai tanda panah. (Howard anton, 2000).
2.3.1. Komponen-Komponen dalam DFD
Menurut Gene dan Serson didalam DFD terdapat komponen-komponen yang banyak digunakan agar dapat membentuk atau membuat suatu DFD secara utuh, berikut adalah macam-macam komponen-komponen yang umum digunakan.
1. Entity
Entity dapat digambarkan dengan simbol bujur sangkar. Entity Merupakan
sumber atau tujuan dari aliran data. Bisa juga menggambarkan secara fisik, yaitu seseorang atau sekelompok orang atau system lain. Kadang-kadang diperlukan untuk menduplikasinya agar dapat menghindari anak panah yang simpang siur.
Ditandai dengan garis diagonal disudut kanan bawah yang menyatakan jiks suatu entity tersebut lebih dari satu. Dalam Entity terdapat 2 jenis entity yaitu :
a. Entity sumber merupakan entitas yang menjadi sumber
b. Entity tujuan merupakan entitas yang menjadi tujuan data atau informasi suatu sistem.
Gambar 2.2. Jenis–jenis Entity
Entity dapat berupa orang, sekelompok orang, organisasi, perusahaan atau
departemen yang berada diluar sistem yang akan dibuat, diberi Data Flow Diagram nama yang berhubungan dengan sistem tsb dan biasanya menggunakan kata benda.
Contoh : Dosen, Mahasiswa.
Hal yang perlu diperhatikan tentang Entity:
1. Alur data yang menghubungkan entity dengan sistem, menunjukkan hubungan sistem dgn dunia luar.
2. Profesional sistem tidak dapat mengubah isi atau cara kerja, prosedur yang berkaitan dengan entity.
3. Hubungan yang ada antar entity tidak digambarkan dalam DFD.
2. Aliran Data
Gambar 2.3. Aliran Data
Aliran Data menggambarkan aliran data dari suatu proses ke proses lainnya. Merepresentasikan dengan menggunakan anak panah. Nama proses dapat ditulis untuk menjelaskan arti dalam aliran tersebut dan ditulis untuk mengidentifikasi aliran tersebut. Aliran data juga dapat menyebar atau menyatu. Didalam aliran data masih ada 4 konsep tentang alur data :
1. Packets of data
Apabila terdapat dua data atau lebih yg mengalir dari satu sumber yg sama menuju pada tujuan yg sama dan mempunyai hubungan dapat digambarkan dengan 1 alur.data.
2. Diverging data flow
Apabila ada sejumlah paket data yg berasal dari sumber yg sama menuju pada tujuan yang berbeda atau paket data yang kompleks dapat dibagi menjadi beberapa elemen data yang akan dikirim ke tujuan yang berbeda pula.
Gambar 2.5. Diverging data flow 3. Converging data flow
Dalam Converging data flow ini terdapat beberapa alur data yang berbeda–beda sumber yang menuju ke tujuan yang sama.
Gambar 2.6. Converging data flow 4. Source and Objective
Gambar 2.7. Source And Objective 3. Proses
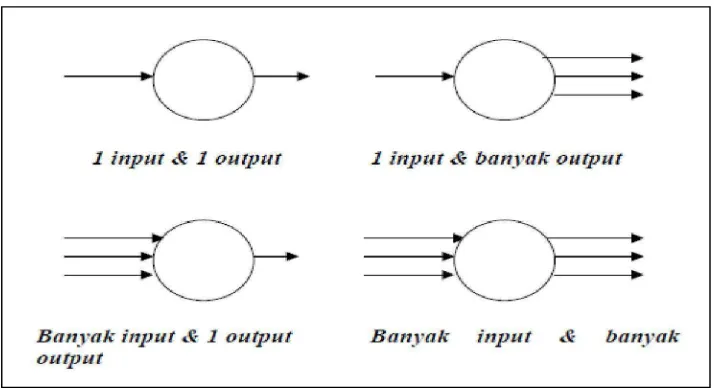
Gambar 2.8. Proses
Gambar 2.9. Input Dan Output Dari Proses
Dari penjelasan diatas, dalam pembuatan proses ada beberapa hal yang perlu diperhatikan tentang suatu proses :
a. Proses harus memiliki input dan output.
b. Proses dapat dihubungkan dengan komponen entity, data store atau proses melalui alur data.
c. Sistem atau bagian atau divisi yang sedang dianalisis oleh professional sistem dan akan digambarkan dengan komponen proses.
4. Storage atau Penyimpan
Gambar 2.10. Storage atau penyimpanan
Storage atau Penyimpanan merupakan komponen yang berfungsi untuk
Data store dapat berupa file atau database yang tersimpan dalam disket, harddisk atau bersifat manual seperti buku alamat, file folder. Ada pula hal yang perlu diperhatikan tentang data store :
1. Alur data dari proses menuju data store, hal ini berarti data store berfungsi sebagai tujuan atau tempat penyimpanan dari suatu proses (proses write). 2. Alur data dari data store ke proses, hal ini berarti data store berfungsi sebagai
sumber atau proses memerlukan data (proses read).
3. Alur data dari proses menuju data store dan sebaliknya berarti berfungsi sebagai sumber dan tujuan.
Gambar 2.11. Proses Dalam Penyimpanan
2.3.2. Level-level DFD
level 1, 2 dan seterusnya sesuai dengan kebutuhan tetapi penurunan tidak dilakukan pada semua bagian sistem.
1. Diagram level Nol.
Pada diagram level Nol ini merupakan diagram awal suatu program yang digunakan agar dapat melanjutkan ke diagram level selanjutnya. Perlihatkan data store yang digunakan.
- Pada proses yang tidak diperrinci, tambahkan tanda * pada akhir penomoran proses.
- Keseimbangan antara diagram kontex dan diagram nol harus Dipelihara. 2. Diagram level Satu
Keseimbangan data store yang digunakan diagram ini merupakan dekomposisi dari diagram level zero. Dengan cara sebagai berikut:
- Keseimbangan aliran data antara diagram nol dan diagram rinci.
- Pada proses yang tidak dirinci lagi, tambahkan tanda * pada akhir penomoran proses.
- Tentukan proses yg lebih kecil (sub-proses) dari proses utama yg ada di level zero.
- Tentukan apa yg diberikan atau diterima masing-masing sub-proses pada atau dari sistem dan perhatikan konsep keseimbangan.
- Apabila diperlukan, munculkan data store (transaksi) sebagai sumber maupun tujuan alur data.
- Beri nomor pada masing-masing sub-proses yg menunjukkan dekomposisi dari proses sebelumnya. Contoh : 1.1, 1.2, 2.1.
3. DFD level dua, tiga, ..
Diagram ini merupakan dekomposisi dari level sebelumnya. Proses dekomposisi dilakukan sampai dg proses siap dituangkan ke dalam program. Aturan yg digunakan sama dgn level satu. (Jogiyanto H-M).
2.3.3. Bentuk Data Flow Diagram
Menurut Jogiyanto (1999), Terdapat dua bentuk DFD, yaitu Diagram Alur Data Fisik, dan Diagram Alur data Logika. Diagram alur data fisik lebih menekankan pada bagaimana proses dari sistem diterapkan, sedangkan Diagram alur data logika lebih menekankan proses-proses apa yang terdapat di sistem. Berikut ini merupakan penjelasan lebih rinci tentang bentuk DFD tersebut
1. Diagram Alur Data Fisik (DADF).
DADF lebih tepat digunakan untuk menggambarkan sistem yang ada (sistem yang lama). Penekanan dari DADF adalah bagaimana prosesproses dari sistem diterapkan (dengan cara apa, oleh siapa dan dimana), termasuk proses-proses manual.
2. Diagram Alur Data Logika (DADL).
2.4. Rekayasa Perangkat Lunak
Rekayasa perangkat lunak atau yang sering disebut dengan RPL merupakan metode pengembangan perangkat lunak dengan menggunakan pendekatan yang sistematis, disiplin, bisa terukur untuk pengembangan operasional dan pembuatan software.
Yang menjadi pondasi dalam Rekayasa Perangkat Lunak adalah lapisan proses karena memiliki keterkaitan dengan teknologi dan waktu pengembangan. Proses mendefinisikan framework Key Prosess Area (KPA) yang harus dibuat untuk penekanan teknologi Rekayasa Perangkat Lunak yang efektif. Metode Rekayasa Perangkat Lunak memberikan teknik bagaimana membangun software.
Yang termasuk dalam metode Rekayasa Perangkat Lunak adalah Analisa, desain, pembuatan program, dan pengujian.
2.4.1. Kategori Rekayasa Perangkat Lunak
Pekerjaan yang berhubungan dengan Rekayasa Perangkat Lunak dapat dikategorikan ke dalam 3 fase umum tanpa memandang area aplikasi, ukuran proyek atau kompleksitas. Fase tersebut yaitu:
a. Definition Phase
b. Development Phase
Selama fase ini, software developer berusaha untuk mendefinisikan bagaimana data disusun, bagaimana fungsi bisa diimplementasikan sesuai dengan arsitektur software, bagaimana prosedur detail untuk implemetasi, bagaimana
karakter interface, bagaimana hasil desain bisa ditranslasikan ke bahasa pemrograman dan bagaimana cara pengujiannya.
Ada tiga aktifitas teknis yang selalu terjadi:
1. Desain software, merupakan awal sebelum membuat program sehingga diperlukan rancangan atau desain suatu aplikasi yang akan dibuat.
2. Pembuatan Program, merupakan implementasi dari desain atau rancangan yang sebelumnya telah dibuat sehingga dapat memudahkan dalam pembuatan program.
3. Pengujian Software, langkah terakhir dari aktifitas teknis yaitu pengujian untuk mengeluarkan hasil dari pembuatan program tersebut apakah program yang telah dirancang dan dibuat berhasil atau tidak. Kemungkinan terjadi kegagalan dalam pengujian.
c. Maintenance Phase
Maintenance Phase bertujuan untuk memfokuskan pada suatu perubahan
2.4.2. Pengujian Perangkat Lunak
Pengembangan sistem perangkat lunak melibatkan sederetan aktifitas produksi di mana peluang terjadinya kesalahan manusia sangat besar. Kesalahan dapat mulai terjadi pada permulaan proses dimana sasaran ditetapkan secara tidak sempurna, kemudian dalam desain dan tahapan pengembangan selanjutnya. Karena ketidakmampuan manusia untuk melakukan dan berkomunikasi dengan sempurna, maka pengembangan perangkat lunak harus selalu diiringi dengan aktifitas jaminan kualitas.
Pengujian perangkat lunak adalah elemen kritis dari jaminan kualitas Perangkat Lunak, dan mempresentasikan kajian pokok dari spesifikasi, desain, dan pengkodean. Dengan meningkatnya visibilitas perangkat lunak sebagai suatu elemen sistem, dan biaya yang muncul akibat kegagalan perangkat lunak, maka memotivasi dilakukakannya perencanaan yang baik melalui pengujian yang teliti. Adalah hal yang wajar jika organisasi pengembangan Perangat Lunak meningkatkan 30 – 40 % dalam usaha proyek pengembangan Perangkat Lunak pada tahap pengujian. (Pressman, Roger S. 2003).
2.5. Borland Delphi 7
pemrograman Pascal yang merupakan bahasa pemrograman yang bersifat prosedural.
Dengan penggunaan pascal sebagai programming language atau notasi sekunder, membuat Borland Delphi lebih mudah dipelajari untuk programmer yang telah terbiasa memakai bahasa pascal atau programmer yang awam sekalipun dengan bantuan dan petunjuk dari fitur help (dokumentasi) nya yang terintegrasi dan mudah di akses. IDE Delphi pun lebih mudah digunakan dan memungkinkan adaptasi yang lebih cepat secara visual karena di lengkapi dengan penggunaan alat bantu visual berupa tombol-tombol dan icon yang mudah di akses dan di ingat.
Saat ini Borland Delphi telah mengalami beberapa perubahan versi, yang terakhir adalah Codegear Delphi 2009 yang mendukung teknologi .Net 3.5 dari Microsoft dan komponen-komponen grafis yang mendukung trend antarmuka pengguna (user interface). Pada courseware ini digunakan Borland Delphi versi 7 yang cukup lengkap dan masih cukup banyak pemakaiannya di industri-industri pengembang aplikasi perangkat lunak.
2.5.1. Pengenalan IDE Borland Delphi
Borland Delphi merupakan aplikasi pengembangan visual dengan lingkungan pengembangan yang terintegrasi (IDE – Intergrated Development Environment). IDE Borland Delphi terdiri dari beberapa bagian sebagai berikut:
1. Main Menu
Dalam terdapat aplikasi-aplikaksi yang dapat digunakan untuk membuat suatu aplikasi, dan terdapat komponen yang berfungsi untuk menjalankan suatu aplikasi yang telah dibuat sebelumnya.
Gambar 2.12. Main Menu
Main menu berfungsi untuk membuat semua komponen-komponen yang dapat digunakan oleh sebuah program yang sedang dikembangkan. Dalam main menu juga terdapat komponen Run untuk menjalankan suatu aplikasi yang telah dibuat dan dapat menyimpah data atau aplikasi tersebut.
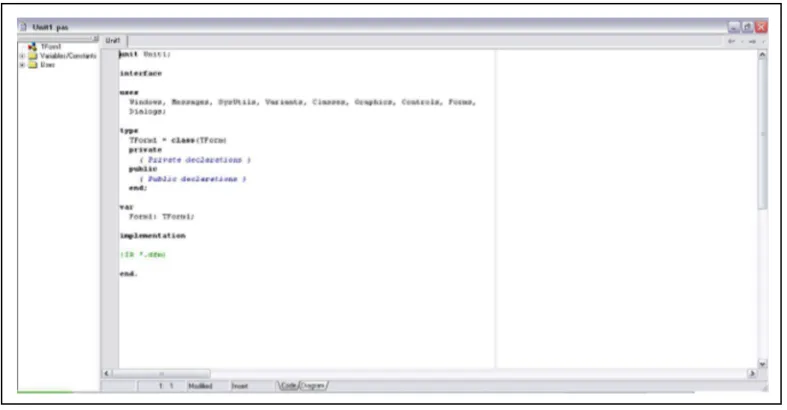
2. Code Editor
Code Editor berfungsi untuk menambahkan notasi sintaksis sekunder
berupa teks kode program, pascal.
Code Editor ini dilengkapi dengan fitur code completion yaitu sebuah fitur
dimana kita bisa menyisipkan deklarasi kelas, object, properties, tipe data, dan lain sebagainya dalam bentuk teks.
3. Component Palette
Component palette merupakan kumpulan icon yang digunakan untuk
merancang suatu aplikasi untuk membentuk sebuah aplikasi user interface. Component Palette menampung berbagai macam notasi simbolis berupa
icon-icon yang mewakili fungsi-fungsi tertentu sebuah komponen.
Gambar 2.14. Component Palette
Dalam Component Palette terdapat beberapa tab yang terdiri dari Tab Standart, Additional, Win32, System, Data Access, Data Controls, dbExpress dan
lain-lain. Didalam Tab tersebut masih terdapat tombol-tombol yang berfungsi untuk menunjang pembuatan aplikasi, misalnya dalam Tab Standart terdapat Component button, radio box, label, Edit, Memo, ListBox, Panel dan lain-lain.
4. Form View
Form view merupakan area kerja visual anda. Anda dapat menambahkan
Gambar 2.15. Form View
Dapat dilihat pada Gambar 2.15. Form View diatas merupakan contoh untuk menampilkan teks “Hello Word” yang terdiri atas satu komponen button dan satu label.
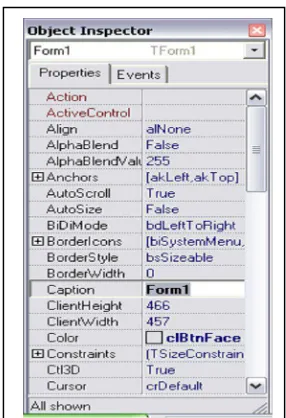
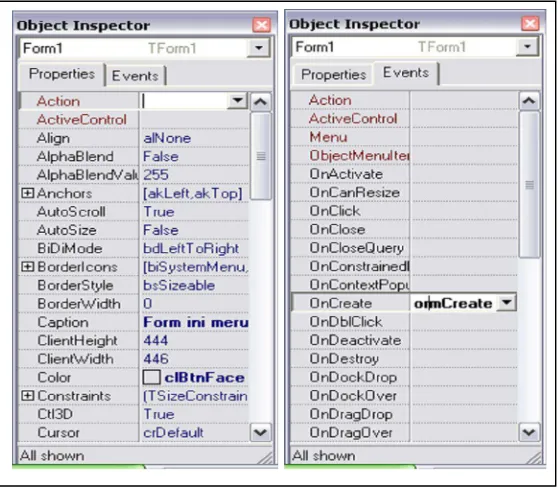
5. Object Inspector
Setiap komponen yang mempunyai representasi visual seperti button, label, edit, numedit dan lain-lain memiliki atribut-atribut seperti warna, ukuran, tipe font dan lain sebagainya yang bisa di ubah sesuai dengan kebutuhan di Object Inspector.
Object Inspector digunakan untuk melakukan perubahan atribut dari
komponen. Saat ingin mengganti nama yang diinginkan dapat diubah melalui object inspector tersebut, begitu juga saat ingin member texr atau kalimat. Didalam Object Inspector tersebut terbagi dua komponen yang digunakan untuk membantu dalam pembuatan suatu sistem atau aplikasi. Komponentersebut yaitu Properties dan Event
Gambar 2.17. Properties dan Event Pr operties
Setiap komponen di dalam delphi diperlakukan sebagai objek, objek tentunya memiliki atribut, dan method yang bisa dijalankan pada dirinya. Setiap atribut yang bisa diubah oleh programmer disebut properties, contoh properties untuk sebuah form adalah caption (nama di title bar), ukuran (width x height), anchor (jangkar), cursor, warna latar (color), visibility (tampak atau tidak), dan
Event
Event adalah sebuah kejadian atau yang lebih tepat adalah sebuah aksi
yang dilakukan ketika aplikasi menemui sebuah kondisi tertentu, misal ketika sebuah form pertama kali ditampilkan maka sebuah event bernama onCreate milik form tersebut dieksekusi, nah event onCreate memiliki notasi tekstual berupa
prosedur di code editor nah sebagai contoh jika anda ingin mengeksekusi sebuah program pada event on create, anda bisa mengaktifkan nya dengan cara klik ganda di bagian event onCreate yang teradapat di Object Inspector, dan Delphi akan secara otomatis menyediakan kerangka untuk prosedur tersebut di dalam unit yang terdapat di code editor.
2.5.2. File Project, Unit dan For m Bor land Delphi
Dalam sebuah project yang kita buat dalam Borland Delphi, secara default terdapat file-file yang diciptakan pada saat project tersebut di buat.
1. Project File
File .dpr adalah file pusat atau utama dari sebuah project Delphi (satu file .dpr per project). File berekstensi *.dpr ini sebenarnya merupakan file sumber
2. Unit File
File berekstensi .pas ini berisi source code program dalam bahasa Object Pascal. File source ini merupakan impelementasi fungsi dari event yang ada di
form atau sebuah file source yang digunakan untuk unit lain. 3. Form File
File berekstensi .frm ini berisi seluruh informasi mengenai form, baik itu ukuran, caption, warna, event dan bahkan informasi komponen-komponen child yang berada di dalam form tersebut.
2.5.3. Kelebihan Delphi
Delphi memiliki beberapa kelebihan yang dimiliki didalam komponan atau fitur- fiturnya berikut ini ada beberapa kelebihan yang dimiliki oleh Borland Delphi 7 ini antara lain :
1. Delphi dibangun dengan menggunakan arsitektur native compiler, sehingga proses kompilasi instruksi menjadi bahasa mesin menjadi lebih cepat.
2. Semua file yang disertakan saat proses kompilasi, digabungkan menjadi satu sesuai dengan arsitektur native compiler, sehingga mengurangi ketergantungan terhadap library ataupun file-file pendukung lainya, sesuai dengan prinsip build once, runs everywhere.
kemampuan seperti itu. Dengan adanya kemampuan tersebut, maka file eksekusi yang dihasilkan delphi menjadi lebih optimal.
4. Lingkungan pengembangan Delphi sangat mudah karena semua komponen yang menjadi alat utama desain visual telah ditampilkan saat pertama kali langsung dapat diamati oleh user dan dapat digunakan secara langsung.
Berikut ini adalah Tampilan Awal Delphi :
Gambar 2.18. Tampilan Awal Delphi
Dalam delphi seperti halnya bahasa visual lainnya menyediakan komponen. Komponen adalah “jantung” bagi pemograman visual. Component Palette telah terbagi menjadi berbagai jenis komponen, diantaranya adalah
2.5.4. Kata-kata Baku
Kata-kata baku yang digunakan dalam pemrograman dan sudah terintergrated dalam pascal dan juga mempunyai bentuk serta kegunaan tertentu
yang didefinisikan oleh Delphi. Kata-kata baku tersebut disebutkan seperti pada tabel 2.3. dibawah ini.
Tabel 2.3. Kata-Kata Baku Yang Digunakan Pada Delphi
And Except Label Resourcestring
Array Exports Library Set
As File Mod Shl
Asm Finalization Nil Shr
Begin Finally Not String
Case For Object Then
Class Function Of Threadvar
Const Goto Or To
Constructor If Out Try
Destructor Implementation Packed Type Dispinterface In Procedure Unit
Div Inherited Program Until
Do Initialization Property Uses
Downto Inline Raise Var
Else Interface Record While
End Is Repeat With
Pada tabel 2.3 diatas merupakan macam-macam kata-kata baku yang tidak boleh didefinisakn kembali oleh pemakai, seperti And, Array, As, End dan lain-lain sehingga tidak dapat digunakan sebagai pengenal (Identifier). (Nugroho, E., 2005)
Tabel 2.4. Jenis-jenis file dalam Delphi
J enis File Keterangan
.dproj File proyek, fungsinya untuk linking object
.dfm File form, fungsinya menyimpan nilai properti form .pas File unit, berisi source code prosedur dan fungsi .dpk File package, berisi instalasi komponen
.res File resource
.cfg File konfigurasi proyek .dof File pilihan proyek .dcu Hasil kompilasi file .pas
.exe File executable (yang dapat dijalankan) .~* File cadangan (back up)
Didalam bab ini akan dijelaskan tentang tata cara perancangan sistem yang akan dibuat. Didalam bab ini juga akan membahas tentang cara perancanagan untuk aplikasi pemrograman linear berbasis kasus pada aplikasi penentuan nilai optimal dengan variabel dan konstrain yang dinamis yang didalamnya akan terdapat perancangan sistem, Flowchart, Data Flow Diagram yang dibuat.
.
3.1. Desain Sistem
Didalam bab ini akan dijelaskan tentang cara perancangan sistem yang akan dibuat. Didalam perangcangan ini juga akan dibahas tentang cara hardware dan software untuk aplikasi pemrograman linear berbasis kasus pada aplikasi penentuan nilai optimal dengan variabel dan konstrain yang dinamis, alur kerja system yaitu memasukkan angka yang akan dihitung dan hasil dari angka yang
dimasukkan sebelumnya. Terdiri atas beberapa tahap antara lain meliputi perancangan.
a. Data
Perangcangan data yang dimaksudkan adalah perancangan data-data yang berkaitan dengan pembuatan perangkat lunak, meliputi :
1. Data Input
dalam Delphi7.0. 2. Data Output
Dari data input diatas, sistem akan menggunakannya hingga didapatkan kesimpulan sebagai output sistem. Dalam aplikasi ini hasil proses perhitungan dapat disimpan ke dalam bentuk file exe, dpr, pas, dfm. b. Proses
Perancangan proses yang dimaksudkan adalah bagaimana sistem akan bekerja. Proses-proses yang digunakan, mulai dari masuknya angka masukkan yang kemudian diproses atau dihitung oleh sistem hingga menjadi informasi. c. Antar Muka
Perancangan antarmuka yang mengandung penjelasan tentang desain antar muka dari aplikasi pemrograman linier.
3.2. Analisa Sistem
Dalam bab ini akan dibahas mengenai analisa dari sistem aplikasi Pemrograman Linier, khususnya pencarian nilai optimal bagian terpenting adalah bagaimana menerjemahkan permasalahan sehari-hari ke dalam model matematis. Faktor-faktor yang mempengaruhi pemodelan harus disederhanakan dan apabila ada data yang kurang, kekurangan tersebut dapat diasumsikan atau diisi dengan pendekatan yang bersifat rasional.
desain sistem yang akan dibuat. Berapa bagian penting dalam melakukan analisa maupun desain sistem, antara lain melakukan perancangan dan pembuatan flowchart, DFD (Data Flow Diagram), langkah-langkah perhitungan metode simplek.
Hal terpenting yang perlu kita lakukan adalah mencari tahu tujuan penyelesaian masalah dan apa penyebab masalah tersebut. Jika suatu persamaan program linier hanya mempunyai dua variabel maka dapat diselesaikan dengan menggunakan penyelesaian persamaan garis linier dalam mencari nilai optimumnya Adapun cara mendapatkan nilai optimum jika menggunakan penyelesaian persamaan garis linier adalah :
1. Dengan mencari nilai fungsi tujuan setiap titik ekstrim atau titik perpotongan antara baris dan kolom.
2. Dengan cara menggeser garis fungsi tujuan.
3.3. Perancangan Sistem
dilakukan. Adapun tahapan-tahapan dalam perancangan sistem yang dilakukan adalah Flowchart Sistem, Data Flow Diagram (DFD), Diagram Berjenjang dan perancangan Antar Muka (Interface).
3.3.1. Langkah–langkah Perhitungan Metode Simpleks
Untuk mengghitung suatu permasalahan program linier, dapat diselesaikan dengan menggunakan metode simpleks, dalam hal ini terdapat langkah-langkah yang harus dilakukan agar dapat menyesaikan permasalahan tersebut.
a. Jika variabel keputusan yang cukup besar atau lebih dari dua, maka untuk menyelesaikannya digunakan Metode Simpleks, beberapa ketentuan yang perlu diperhatikan, antara lain:
1. Nilai kanan (NK) fungsi tujuan harus nol (0).
2. Nilai kanan (NK) fungsi kendala harus positif. Apabila negatif, nilai tersebut harus dikalikan –1.
3. Fungsi kendala dengan tanda “≥” harus diubah ke bentuk “=” dengan menambahkan variabel slack atau surplus. Variabel slack atau surplus disebut juga variabel dasar.
b. Langkah-langkah perhitungan metode simplek adalah sebagai berikut :
1. Mengubah fungsi tujuan dan fungsi kendala (lihat beberapa ketentuan yang harus diperhatikan di atas).
pertama (X1) pada baris F(z).
4. Memilih baris, Pemilihan baris adalah baris yang mempunyai nilai kedua (X4) pada baris F(z).
5. Mengubah nilai-nilai baris atau dapat disebut dengan baris baru kunci, dengan cara membaginya dengan titik perpotongan. Baris baru = baris kunci kedua dibagi titik perpotongan.
6. Langkah berikutnya adalah mengkalikan kolom kedua (X2) dengan baris
pertama sehingga nilai-nilai kolom (selain baris) sama dengan 0. Sebelumnya masukkan hasil perhitungan baris baru terlebih dahulu dalam tabel.
7. Masukkan hasil nilai di atas ke dalam tabel, sehingga tabel tersebut berubah menjadi hasil dari perhitungan langkah 6 yang merupakan hasil akhir untuk menentukan nilai X1 dan X2.
3.3.2. Implementasi Langkah–langkah Metode Simpleks
Dari langkah–langkah yang telah dijelaskan diatas, dapat di implementasikan agar dapat memahami langkah–langkah tersebut dengan lebih jelas dapat dijelaskan menggunakan contoh kasus berikut ini :
tersebut dimaksudkan agar pasien tersebut tidak cepat merasa bosan. Setiap unit A mengandung 2 mg vitamin 1 dan 6 mg vitamin 2. Sedangkan setiap unit B mengandung 3 mg vitamin 1 dan 2 mg vitamin 2. Menurut dokter, setiap tahun pasien harus menelan paling tidak 3.500 mg vitamin 1 dan 7.000 mg vitamin 2. Setelah dihitung–hitung oleh pasien yang bekerja sebagai pegawai negeri tersebut, biaya per unit A sebesar Rp. 10,- dan B sebesar Rp. 4,-. Bagaimana sebaiknya kombinasi tablet A dan tablet B yang harus ditelan pasien tersebut dalam setahun agar syarat kesehatannya terpenuhi tetapi sakunya mengijinkan ?
Penyelesaian :
Diketahui fungsi minimize Z = 10X1 + 4X2
Dengan fungsi kendala : 1. 2X1 + 3X2 ≥ 3.500
2. 6X2 + 2X2 ≥ 7000
3. X1, X2 ≥ 0
Bila diubah menjadi bentuk matematika : Diketahui fungsi minimize Z = 10X1 + 4X2
Dengan fungsi kendala : 1. -2X1 + 3X2 ≤ -3.500
2. -6X2 + 2X2 ≤ -7000
3. X1, X2 ≥ 0
Z = 10X1 + 4X2 + 0X3 + 0X4
Z = 10X1 – 4X2 – 0X3 – 0X4
Subject to constraints:
-2X1 + 3X2 + X3 ≤ -3.500
-6X2 + 2X2 + X4 ≤ -7000
X1, X2, X3, X4 ≥ 0
Maka langkah-langkah penyelesaian metode simplex: 1. Mengubah fungsi tujuan dan fungsi kendala.
Z = 10X1 + 4X2 => Z – 10X1 – 4X2 = 0
Fungsi kendala
1) 2X1 + 3X2 ≤ -3.500 => -2X 1 – 3X2 ≤ -3.500
2) 6X2 + 2X2 ≤ -7000 => -6X 2 – 2X2 ≤ -7000
3) X1, X2, X3, X4 ≥ 0
2. Menyusun persamaan-persamaan ke dalam tabel.
Tabel 3.1. Persamaan Linier Dalam Bentuk Tabel
Tablet A (X1) Tablet B (X2)
Kebutuhan per Tahun (mg) Biaya / Unit Rp.10,- Rp.4,- ??
Vitamin I 2 3 3500
pertama (X1) pada baris Z.
4. Memilih baris, Pemilihan baris adalah baris yang mempunyai nilai kedua (X4)
pada baris F(z).
5. Mengubah nilai-nilai baris atau dapat disebut dengan baris baru kunci, dengan cara membaginya dengan titik perpotongan. Baris baru = baris kunci kedua dibagi titik perpotongan.
Tabel 3.4. Perhitungan Baris Baru
Baris I + Baris II (2) Cara II :
Baris F(z) -10 -40 0 0 0 -10 ( 1 1/3 0 -1/6 3500/3 ) 0 -2/3 0 -5/3 3500/3
Baris I -2 -3 1 0 -3500 -2 ( 1 1/3 0 -1/6 3500/3 )
0 -7/3 1 -1/3 -3500/3 Tabel 3.5. Hasil baris baru
F(z)
Z X1 X2 X3 X4 NK
1 -10 -4 0 0 0
X3 0 -2 -3 1 0 3.500
X1 0 1 1/3 0 -1/6 3500/3
6. Langkah berikutnya adalah mengkalikan kolom kedua (X2) dengan baris
pertama sehingga nilai-nilai kolom (selain baris) sama dengan 0. Sebelumnya masukkan hasil perhitungan baris baru terlebih dahulu dalam tabel, seperti Tabel 3.6. dibawah ini.
–
F(z)
Z x1 x2 x3 x4 NK
1 0 -2/3 0 -5/3 35000/3
x3 0 0 -7/3 1 -1/3 3500/3
x1 0 1 1/3 0 -1/6 3500/3
Cara I : Baris F(z) + Baris I (2/3) Baris II + Baris I (-1/3) Cara II :
Baris F(z) 0 -2/3 0 -5/3 35000/3 -2/3 ( 1 1 -3/7 1/7 500 ) 0 0 -2/7 -11/7 12000
Baris II 1 1/3 0 -1/6 3500/3 1/3 ( 0 1 -3/7 1/7 500 )
1 0 1/7 -3/14 1000
7. Masukkan hasil nilai di atas ke dalam tabel, sehingga tabel tersebut berubah menjadi tabel 3.7 yang merupakan hasil akhir untuk menentukan nilai X1 dan
X2 seperti tabel berikut ini.
–
–
-3500/3 x -3/7 = 500
F(z)
z X1 X2 X3 X4 NK
1 0 0 -2/7 -11/7 12000
X3 0 0 1 -3/7 1/7 500
X1 0 1 0 1/7 -3/14 1000
Sehingga nilai untuk X1 = 1000, X2 = 500 dan Z = 12000,-
Kesimpulan :
Setiap tahun pasien tersebut harus memakan 1000 tablet A dan 500 tablet B agar syarat kesehatannya terpenuhi juga sakunya mengijinkan dengan biaya sebesar Rp.12.000,-
Dalam perhitungan model matematikanya dapat disimpulkan sebagai berikut : Diperoleh hasil: X1 = 1000, X2 = 500, sehingga bila nilai tersebut dimasukkan ke
dalam fungsi tujuan : Z = 10X1 + 4X2
Z = 10 (1000) + 5 (500) Zmax = 12500
3.3.3. Langkah-lagkah Polinomial
= –2 ( yi – a0 – a1xi – a2xi2 –……– amxim )
= –2 xi ( yi – a0 – a1xi – a2xi2 –……– amxim )
= –2 xi2 ( yi – a0 – a1xi – a2xi2 –……– amxim )
= –2 xim ( yi – a0 – a1xi – a2xi2 –……– amxim )
terhadap polinom derajat ke-m : y = a0 + a1x+a1x2+……+ amxm+e
untuk kasus ini jumlah kuadrat dari sisa-sisanya adalah
Sr = ( yi – a0 – a1xi – a2xi2 –……– amxim)2
2. Dengan mengikuti procedure sebelumnya, dapat diambil turunan persamaan terhadap masing-masing koefisien polinom, seperti berikut :
3. Persamaan-persamaan ini dapat ditetapkan sama dengan nol dan disusun ulang untuk mengembangkan himpunan persamaan normal yang berikut ini:
a0n + a1 xi + a2 xi2+…...+ am xim = yi
a1 xi + a2 xi2+ a2 xi3+……+ am xim+1 = xiyi
a1 xi2+ a2 xi3+ a2 xi4+……+ am xim+2 = xi2yi
a1 xim+ a2 xim+1+ a2 xim+2+……+am xi2m = ximyi
pengamatan. Jadi, masalah penentuan polinom kuadrat terkecil derajat m setara dengan pemecahan sistem m + 1 persamaan linier yang simultan.
4. Sama seperti untuk regresi linier, galat untuk polinom regresi dapat diukur
juga dapat dihitung koefisien korelasi untuk regresi polinom dengan cara yang sama
seperti untuk kasus linier:
r2 =
3.3.4. Uji Kasus Polinomial Yang Diselesaikan