DAFTAR ISI
LEMBAR PERSETUJUAN DAN PENGESAHAN ...
PERNYATAAN …………...
ABSTRAK ...
KATA PENGANTAR ...
UCAPAN TERIMA KASIH ...
DAFTAR ISI ...
B. Rumusan Masalah ...
C. Tujuan Penelitian ...
D. Manfaat Penelitian ...
E. Definisi Operasional …...
BAB II KAJIAN PUSTAKA
A. Pemahaman Matematis ...
B. Pembelajaran Reciproc (Reciprocal Teaching) ...
D. Pembelajaran Langsung (Direct Intruction) ...
E. Analisis Pembelajaran Reciproc, Pembelajaran
Kooperatif tipe NHT, dan Pembelajaran Langsung
(Direct Instruction) ...
F. Hipotesis ...
BAB III METODE PENELITIAN
A. Disain Penelitian ...
B. Tempat dan Waktu Penelitian ...
C. Subjek Penelitian …...
D. Variabel Penelitian ………...
E. Instrumen Penelitian ……...
1. Analisis Reliabilitas Tes ……...
2. Analisis Validitas Tes ...
3. Analisis Daya Pembeda ...
4. Analisis Tingkat Kesukaran ...
F. Bahan Ajar ...
G. Teknik Pengumpulan Data ...
G. Teknik Pengolahan Data ...
H. Prosedur Penelitian ...
BAB IV HASIL PENELITIAN DAN PEMBAHASAN
1. Pengolahan Data Kuantitatif ...
1.1. Analisis Skor Awal (UTS) ………..
1.2. Analisis Kemampuan Pemahaman Matematis ...
2. Pengolahan Data Kualitatif ...
2.1. Sikap Siswa Ketiga Kelas Eksperimen ...
2.2. Aktivitas Siswa Ketiga Kelas ……….
2.3. Penilaian Pengjaran Guru selama Penelitian …..
B. Pembahasan ...
1. Analisis Model Pembelajaran Reciproc(PR) tehadap
Model Pembelajaran Kooperatif tipe NHTdan
Langsung (PL) ……….
a. Peringkat rerata PR lebih tinggi dibandingkan
peringkat rerata NHT ………...
b. Peringkat rerata PR lebih tinggi dibandingkan
peringkat rerata PL ………...
2. Analisis Model Pembelajaran Kooperatif tipe
NHTdenganModel Pembelajaran Langsung (PL)
DAFTAR PUSTAKA ...
LAMPIRAN ...
RIWAYAT HIDUP ... 87
232
Halaman
Indikator Pemahaman Matematis dan Indikator Materi ...
Analisis Ketiga Model Pembelajaran dalam Penelitian ...
Kisi-kisi Soal Kemampuan Pemahaman Matematis ...
Kriteria Penskoran Kemampuan Pemahaman Matematis ...
Klasifikasi Koefisien Reliabilitas ...
Rekapitulasi Reliabilitas Butir Soal ...
Klasifikasi Koefisien Validitas ...
Rekapitulasi Validitas Butir Soal ...
Kriteria Penafsiran Daya Pembeda ...
Analisis Daya Pembeda dan Kriteria ...
Kriteria Penafsiran Tingkat Kesukaran ...
Analisis Tinakat Kesukaran dan Kriteria ...
Kategori ungkapan kata-kata Skala Likert ...
Kriteria Interpretasi Skor Skala Likert ...
Statistik Deskriptif Skor Awal (UTS) ...
Hasil Uji Normalitas Kemampuan Awal ...
Rekapitulasi Uji Normalitas Kemampuan Awal ketiga kelas ...
Hasil Uji Homogenitas Kemampuan Awal ...
Hasil Uji ANOVA Satu-Jalur ...
4.7.
Hasil uji NormalitasKemampuan Pemahaman Matematis...
Rekapitulasi Uji Normalitas Kemampuan Pemahaman Matematis
Ketiga Kelas ...
Hasil Uji ANOVA Satu-Jalur ...
Multiple Comparisons ...
Peringkat (Rank) ...
Hasil uji Kruskal-Wallis ...
Nilai Perbedaan Absolute (Mutlak) …...
Rekapitulasi Skala Sikap Kelas Pembelajaran Reciproc(PR) ……
Rekapitulasi Skala Sikap Kelas Pembelajaran Kooperatif tipe NHT
(NHT) ...
Veny Triana Andika Sari, 2012
Halaman Gambar
DAFTAR GAMBAR
2.1.
3.1.
Dampak instruksional dan pengiring dari Model Pengajaran
Langsung ………..
Bagan Prosedur Penelitian ... 29
52 Gambar
Halaman
Rencana Pelaksanaan Pembelajaran (RPP) Untuk
PembelajaranReciproc
………...
Rencana Pelaksanaan Pembelajaran (RPP) Untuk Pembelajaran
Kooperatif tipe NHT ………
Rencana Pelaksanaan Pembelajaran (RPP) Untuk Pembelajaran
Langsung ……….
Lembar Kerja Siswa (LKS) Untuk Pembelajaran Reciproc ………
Lembar Kerja Siswa (LKS) Untuk Pembelajaran Kooperatif tipe
NHT ……….
Daftar Nama Siswa ………..
Lembar Observasi Siswa ……….
Lembar Observasi Guru ………..
Jadwal Kegiatan Pembelajaran ………
Kisi-kisi Skala Sikap ………
Lembar Skala Sikap ………
Kisi-kisi Soal Kemampuan Pemahaman Matematis ………
Lembar Soal Kemampuan Pemahaman Matematis ……….
Penskoran Soal Kemampuan Pemahaman Matematis ………
Analisis Daya Pembeda (DP) dan Tingkat Kesukaran (TK) ……..
Perhitungan Daya Pembeda (DP) Butir Soal Kemampuan
Pemahaman Matematis ………
Perhitungan Tingkat Kesukaran (TK) Butir Soal Kemampuan
Pemahaman Matematis ………
Analisis Reliabilitas Soal Kemampuan Pemahaman Matematis ….
D.7
Rekapitulasi Reliabilitas Soal Kemampuan Pemahaman Matematis
Analisis Validitas Soal Kemampuan Pemahaman Matematis …….
Perhitungan Validitas Soal Kemampuan Pemahaman Matematis ...
Rekapitulasi Validitas Soal Kemampuan Pemahaman Matematis ..
Rekapitulasi Skor & Nilai Awal (UTS) Ketiga Kelas Eksperimen .
Rekapitulasi Skor & Nilai Akhir (Postes) Ketiga Kelas
Eksperimen ………..
Analisis Skala Sikap Ketiga Kelas Eksperimen ………..
Rekapitulasi Penilaian Skala Sikap Ketiga Kelas Eksperimen ……
Rekapitulasi Penilaian Aktivitas Siswa ………...
Rekapitulasi Penilaian Guru Selama Penelitian ………..
Perhitungan Uji Normalitas dan Homogenitas Skor dari Nilai
Awal (UTS) menggunakan program SPSS 16.0 ………..
Perhitungan Uji ANOVA satu-jalur menggunkan program SPSS
16.0 ...
Perhitungan Uji Normalitas dan Homogenitas Skor dari Nilai
Akhir (Postes) menggunakan program SPSS 16.0 ………..
Perhitungan Uji Non-Parametrik dengan Uji
Kruskal-Wallismenggunakan program SPSS 16.0
………..
Dokumentasi Ketiga Kelas Eksperimen ………..
BAB I PENDAHULUAN
A. Latar Belakang
Matematika merupakan ilmu dasar yang memiliki peranan penting
dalam proses kehidupan manusia. Dapat dikatakan bahwa perkembangan ilmu
pengetahuan dan teknologi dewasa ini dilandasi oleh matematika. Hal ini
sesuai dengan pernyataan Suherman, dkk. (2003: 25) bahwa matematika
tumbuh dan berkembang sebagai penyedia jasa layanan untuk pengembangan
ilmu-ilmu yang lain sehingga pemahaman konsep suatu materi dalam
matematika haruslah ditempatkan pada prioritas yang utama.
Mata pelajaran matematika diberikan kepada siswa untuk membekali
kemampuan berpikir logis, kritis, kreatif, dan inovatif. Selain itu, mata
pelajaran matematika juga membekali siswa untuk memiliki kemampuan
bekerjasama. Kompetensi tersebut diperlukan agar siswa dapat memiliki
kemampuan memperoleh, mengelola, dan memanfaatkan informasi untuk
bertahan hidup pada keadaan yang selalu berubah, tidak pasti, dan kompetitif
(Depdiknas, 2006).
Departemen Pendidikan Nasional (2007) menyatakan ada beberapa
aspek yang perlu dikembangkan dalam pembelajaran matematika, diantaranya
adalah pemahaman matematis, pemecahan masalah, serta penalaran dan
komunikasi. Pemahaman matematis dapat dikatakan sebagai fondasi dalam
mengembangkan pembelajaran matematika. Pernyataan tersebut sesuai dengan
matematis, siswa akan lebih mudah dalam memecahkan permasalahan karena
siswa akan mampu mengaitkan serta memecahkan permasalahan tersebut
dengan berbekal konsep yang sudah dipahaminya.
Kemampuan siswa dalam bernalar serta berkomunikasi juga akan lebih
baik jika siswa mempunyai pemahaman matematis yang baik karena menurut
Arends (2007: 322) konsep adalah dasar untuk berpikir dan berkomunikasi,
sehingga dengan adanya pemahaman matematis siswa tidak hanya akan
sekedar berkomunikasi tetapi siswa akan berkomunikasi secara baik dan benar
karena mereka mempunyai pemahaman tentang konsep yang mereka
komunikasikan. Sebaliknya, jika pemahaman matematis masih kurang maka
siswa akan cenderung mengalami kesulitan dalam melakukan pemecahan
masalah ataupun dalam bernalar serta mengkomunikasikan suatu konsep.
Menyadari pentingnya pemahaman matematis dalam pembelajaran
matematika, maka pembelajaran matematika perlu direncanakan sedemikian
rupa sehingga pada akhir pembelajaran, siswa bisa memahami konsep yang
dipelajarinya. Hal tersebut sesuai dengan salah satu tujuan Kurikulum Tingkat
Satuan Pendidikan (KTSP) untuk mata pelajaran matematika di tingkat
Sekolah Menengah Pertama yaitu agar siswa memiliki kemampuan
memahami konsep matematika, menjelaskan keterkaitan antara konsep dan
mengaplikasikan konsep atau alogaritma, secara luwes, akurat, efisien, dan
tepat dalam pemecahan masalah. Jika tujuan KTSP tersebut dapat diterapkan
Adapun indikator yang menunjukkan pemahaman matematis menurut
Skemp (dalam Sumarmo, 2000) dibedakan menjadi dua jenis, yaitu
pemahaman instrumental dan relasional. Pemahaman instrumental adalah
menghafal sesuatu secara terpisah atau dapat menerapkan sesuatu pada
perhitungan sederhana dan mengerjakan sesuatu secara alogaritmatik.
Pemahaman relasional adalah kemampuan mengaitkan beberapa konsep yang
saling berhubungan, meliputi mengaitkan antara konsep yang satu dengan
konsep lainnya, menginterpretasi grafik atau gambar, mengabstraksi
pernyataan verbal ke formula atau simbol matematika dan kemahiran siswa
menggunakan strategi untuk menyelesaikan soal.
Pemahaman matematis siswa dapat ditingkatkan melalui berbagai cara,
salah satunya dengan menerapkan model pembelajaran yang dinilai efektif
dalam menunjang pembelajaran. Pembelajaran yang dinilai efektif dapat
terlaksana jika setiap pengajar mampu mengetahui, memahami, memilih, dan
menerapkan model pembelajaran yang dinilai efektif sehingga dapat
menciptakan suasana kelas yang kondusif dalam menunjang proses
pembelajaran yang optimal.
Wahyudin (2008: 394) menyatakan upaya menjadikan matematika
bermakna serta dapat diterapkan bagi para siswa memerlukan restrukturisasi
yang secara praktis bersifat mendasar pada seluruh aspek pengajaran, seperti:
materi kurikulum, lingkungan belajar, tanggung jawab guru, dan
metodologi-metodologi untuk menyelenggarakan assessment terhadap pemahaman
menjadikan matematika bermakna adalah membiarkan siswa yang melakukan
pembelajaran mandiri dengan cara saling berdiskusi antara siswa, sehingga
siswa lebih memahami pembelajaran matematika.
Higgins (dalam O’Connell, 2007: 85) menyatakan bahwa siswa akan
lebih dapat memahami dan memaknai konsep yang menjadi tujuan
pembelajaran jika dalam proses pembelajaran yang berlangsung siswa
melakukan kegiatan berdiskusi, saling menjelaskan, dan berelaborasi. Dewey
(Oxford, 1997) juga menyatakan bahwa konsep akan dapat dipahami siswa
jika konsep tersebut dikonstruksikan sendiri oleh siswa melalui pembelajaran
dalam suatu kelompok sehingga siswa akan melakukan proses sosial. Proses
sosial yang terjadi pada setiap kelompok tersebut menjadikan pembelajaran
matematika yang aktif, karena Wahyudin (2008) menyatakan pembelajaran
matematika yang pasif memiliki kemungkinan besar mengalami kegagalan.
Berkaitan dengan uraian di atas maka inovasi-inovasi dalam
pembelajaran matematika haruslah menciptakan siswa aktif dalam proses
pembelajaran sehingga memunculkan kemampuan pemahaman matematis
siswa, sesuai pernyataan Furner (2007) bahwa cara penyampaian materi bisa
berpengaruh pada pemahaman konsep atau matematis siswa. Dalam hal ini,
peneliti dituntut untuk memilih bentuk pengalaman belajar siswa yaitu
metode, media, situasi kelas, dan segala sesuatu yang mendukung
keberhasilan proses pembelajaran sehingga proses pembelajaran berlangsung
Model pembelajaran yang akan digunakan dalam penelitian ini adalah
pembelajaran reciproc (reciprocal teaching). Menurut Palinscar and Brown
(1986) bahwa reciprocal teaching dapat meningkatkan kemampuan
pemahaman matematis siswa. Sehingga, reciprocal teaching merupakan salah
satu model pembelajaran yang diduga kuat bisa mengembangkan kemampuan
pemahaman matematis siswa.
Reciprocal teaching merupakan salah satu model pembelajaran yang
dilaksanakan melalui proses belajar mandiri dan siswa mampu menyajikannya
di depan kelas. Hal ini sesuai dengan pendapat Palincsar (1986) bahwa model
reciprocal teaching menggunakan empat strategi, yaitu membuat pertanyaan
(question generating), mengklarifikasi istilah-istilah yang sulit dipahami
(clarifying), memprediksi materi lanjutan (predicting), dan merangkum
(summarizing). Menurut Pannen (dalam Suyitno, 2006), melalui model
pembelajaran reciprocal ini siswa dapat mengembangkan kemauan belajar
mandiri, siswa memiliki kemampuan mengembangkan pengetahuannya
sendiri dan guru berperan sebagai fasilitator, mediator, dan manager dalam
proses pembelajaran. Sehingga siswa diharapkan dapat meningkatkan
pemahaman konsep matematika mereka sendiri.
Siswapun mampu mengembangkan langkah-langkah dalam reciprocal
teaching seperti mengkaji dan menyelidiki materi yang dibahas secara mandiri
sehingga hasil yang diperoleh akan bermakna sehingga tidak mudah dilupakan
oleh siswa. Kemandirian dalam pembelajaran reciprocal, tidak diartikan
mereka dapat mendiskusikan materi tersebut dengan siswa lainnya. Dengan
mengkaji materi yang dipelajari secara mandiri, pengertian siswa tentang
suatu konsep merupakan pengertian yang benar-benar dipahami oleh siswa.
Selain pembelajaran reciproc (reciprocal teaching), model
pembelajaran kooperatif (cooperative learning) diduga dapat memunculkan
kemampuan pemahaman matematis karena pembelajaran kooperatif salah satu
pembelajaran kelompok yang mendorong siswa untuk aktif berdiskusi, agar
siswa saling bertukar pendapat atau ide, sehingga dapat menghubungkan
konsep satu dengan konsep yang lainnya. Model-model pembelajaran
kooperatif telah terbukti efektif di kelas heterogen (Wahyudin, 2008: 405).
Model pembelajaran kooperatif mempunyai beberapa teknik,
diantaranya pembelajaran kooperatif tipe Student-Teams Achievement
Devision (STAD), Group Investigation, Jigsaw dan pembelajaran kooperatif
tipe NHT. Dari ketiga teknik pembelajaran kooperatif tersebut, teknik yang
paling sederhana untuk kelompok kelas yang heterogen menurut beberapa
pernyataan buku model-model pembelajaran dan penulis memilih model
pembelajaran kooperatif tipe NHT. Number-Heads-Together (NHT) adalah
teknik belajar mengajar kepala bernomor yang dikembangkan oleh Kagan
(1992). Teknik ini memberikan kesempatan kepada siswa untuk saling
membagikan ide-ide dan mempertimbangkan jawaban yang paling tepat;
mendorong siswa untuk meningkatkan semangat kerjasama mereka; serta
dapat digunakan dalam semua mata pelajaran dan untuk semua tingkatan
kooperatif tipe NHT dipilih peneliti sebagai pembelajaran yang akan
dibandingkan dengan pembelajaran reciproc dalam mengembangkan
kemampuan pemahaman matematis siswa.
Dari model pembelajaran reciproc dan model kooperatif tipe NHT
yang dijabarkan di paragaraf sebelumnya, model pembelajaran lainnya yang
dianggap dapat memunculkan kemampuan pemahaman matematis pada siswa
adalah pembelajaran langsung (direct instruction). Pembelajaran tersebut
merupakan pembelajaran langsung yang berpusat kepada guru. Guru
menjelaskan suatu materi dalam kelompok besar, kemudian menguji
pemahaman siswa dengan praktik atau latihan ke depan kelas dibawah
bimbingan guru, dan siswa melanjutkan praktik atau latihan di tempat duduk
mereka masing-masing di bawah bimbingan guru.
Pengajaran langsung merupakan suatu model pembelajaran yang
kegiatannya terfokus pada aktivitas akademik. Di dalam implementasi
kegiatan pembelajaran guru melakukan kontrol yang ketat terhadap kemajuan
belajar siswa, pendayagunaan waktu serta iklim kelas, pemberian arahan dan
pengembangan model pembelajaran langsung ini terutama dilakukan ketika
guru menjelaskan tentang tugas-tugas belajar dan materi pelajaran (Jihad,
2008). Dengan demikian pembelajaran tersebut juga diduga dapat
mengembangkan kemampuan pemahaman matematis.
Berdasarkan penjelasan di atas tentang tiga model pembelajaran yang
diduga dapat meningkatkan kemampuan pemahaman matematis. Selain dapat
model pembelajaran kooperatif tipe NHT karena kedua model pembelajaran
tersebut sama-sama menggabungkan beberapa siswa menjadi satu kelompok,
sedangkan model pemebelajaran langsung (direct instruction) dalam proses
pembelajarannya mengecek pemahaman siswa dengan menyuruh beberapa
siswa untuk mempresentasikannya di depan kelas sama seperti dua model
pembelajaran sebelumnya yaitu model pembelajaran reciproc dan model
pembelajaran kooperatif tipe NHT.
Oleh karena itu, peneliti tertarik ingin mengetahui perbedaan dan
model pembelajaran mana yang memiliki pengaruh lebih baik terhadap
kemampuan pemahaman matematis dengan melakukan penelitian dengan
judul “Pengaruh Pembelajaran Reciproc, Kooperatif tipe NHT, dan Langsung
terhadap Kemampuan Pemahaman Matematis Siswa SMP”.
B. Rumusan Masalah
Rumusan masalah dalam penelitian ini adalah:
1. Apakah terdapat perbedaan kemampuan pemahaman matematis antara
siswa yang belajar dengan model pembelajaran reciproc, model
pembelajaran kooperatif tipe NHT, dan model pembelajaran langsung?
2. Jika terdapat perbedaan, manakah dari model pembelajaran reciproc,
model pembelajaran kooperatif tipe NHT, dan model pembelajaran
langsung yang memiliki pengaruh lebih baik terhadap kemampuan
3. Bagaimana sikap siswa terhadap model pembelajaran reciproc, model
pembelajaran kooperatif tipe NHT, dan model pembelajaran langsung ?
C. Tujuan Penelitian
Sejalan dengan rumusan masalah yang telah dikemukakan di atas,
maka secara umum penelitian ini bertujuan untuk:
1. Mengetahui perbedaan pembelajaran reciproc, kooperatif tipe NHT, dan
langsung terhadap kemampuan pemahaman matematis siswa SMP.
2. Mengetahui model pembelajaran yang lebih baik dalam meningkatkan
kemampuan pemahaman matematis siswa SMP.
3. Mengetahui sikap siswa terhadap pembelajaran reciproc, kooperatif tipe
NHT, dan langsung.
D. Manfaat Penelitian
Penelitian ini diharapkan dapat dijadikan referensi guru dalam memilih
model pembelajaran yang tepat untuk digunakan dalam usahanya
mengembangakan kemampuan pemahaman matematis siswa, kreativitas siswa
dalam membuat soal-soal matematika, melatih siswa mengkaji dan
menggeneralisasi atau menyimpulkan materi yang dipelajari.
E. Definisi Operasional
Agar tidak terjadi kesalahpahaman pengertian dalam penelitian ini,
1. Kemampuan pemahaman matematis adalah kemampuan siswa untuk
menyatakan ulang sebuah konsep; mengklasifikasi objek-objek menurut
sifat-sifat tertentu (sesuai dengan konsepnya); menyajikan konsep dalam
berbagai bentuk representasi; dan mengaplikasikan konsep atau algoritma
pemecahan masalah.
2. Reciprocal teaching merupakan model pembelajaran yang dilakukan
dengan mengelompokkan siswa menjadi kelompok-kelompok kecil yang
masing-masing kelompok terdiri dari 4-5 orang siswa, yang diawali
dengan tugas membaca bahan ajar oleh siswa dan dilanjutkan dengan
melaksanakan empat kegiatan yaitu: mengerjakan LKS yang diberikan
kepada masing-masing kelompok; membuat pertanyaan; memberikan
penjelasan; pembahasan dalam kelompok dipimpin oleh siswa. Sedangkan
guru berperan sebagai fasilitator dan pembimbing dalam menyimpulkan
materi yang telah dibahas.
3. Cooperative learning tipe Numbered-Heads-Together (NHT) merupakan
model pembelajaran berkelompok, setiap kelompok terdiri dari tiga sampai
lima siswa dan memiliki kemampuan akademik yang berbeda, dengan
langkah awal guru melakukan presentasi dalam kelas yang berkaitan
dengan pokok-pokok materi yang akan dipelajari serta penjelasan tentang
teknik pembelajaran yang akan digunakan. Kemudian dilanjutkan dengan
melaksanakan empat kegiatan yaitu: siswa mempelajari materi dan
mengerjakan LKS, berdiskusi secara berkelompok; guru melakukan
kelompok untuk menjawab pertanyaan yang diajukan oleh guru; dan guru
memberikan penghargaan kepada siswa yang menjawab benar.
4. Direct instruction (Pembelajaran Langsung) merupakan model
pembelajaran yang secara langsung dijelaskan secara menyeluruh oleh
guru sehingga dikatakan pembelajaran yang berpusat kepada guru.
Langkah-langkah dalam penelitian, guru menyampaikan tujuan
pembelajaran; memberikan motivasi siswa; memulai mempresentasikan
materi yang dipelajari; siswa diberikan latihan untuk mengetahui
pemahaman siswa terhadap materi yang disampaikan; guru mengecek
pemahaman siswa dengan membahas latihan yang telah diberikan; dan
BAB III
METODE PENELITIAN
A. Disain Penelitian
Jenis penelitian ini adalah penelitian kuantitatif. Disain penelitian ini
adalah disain kuasi eksperimen berbentuk disain kelompok kontrol hanya
postes (post-test only control group), sebanyak 3 kelompok. Kelompok
pertama belajar menggunakan pembelajaran reciprocal teaching (PR),
kelompok kedua belajar menggunakan pembelajaran cooperative tipe NHT
(NHT), dan kelompok ketiga belajar menggunakan pembelajaran langsung
(PL).
Dalam pelaksanaannya sebelum melakukan penelitian, ketiga kelas
dipastikan mempunyai kemampuan awal yang sama, dengan melakukan uji
kesamaan rerata. Skor awal tersebut diperoleh dari skor ujian tengah semester
(UTS) ketiga kelas, dan peneliti percaya akan validitas serta reliabilitas soal
UTS kepada guru bidang studi matematika di sekolah tersebut. Dikarenakan
kompetensi guru tersebut dalam membuat soal-soal matematika sudah teruji.
Berikut ilustrasi disain penelitiannya:
X1 O --- X2 O ---
X3 O (Ruseffendi, 2005: 49) Keterangan:
X1 = kelompok pertama dengan pembelajaran reciprocal teaching (PR)
X3 = kelompok ketiga dengan pembelajaran langsung (PL)
O = postes (tes akhir) kemampuan pemahaman matematis dan skala sikap dari
model pembelajaran masing-masing kelas
---- = subjek tidak dipilih secara acak
B. Tempat dan Waktu Penelitian
Penelitian ini dilakukan di SMP Negeri 37 Bekasi, Jalan Padi Raya
Perum Deptan Kaliabang Tengah – Bekasi Utara. Penelitian dilaksanakan
pada semester genap, pada awal Mei sampai pertengahan Mei tahun pelajaran
2011 – 2012 tepatnya pada tanggal 01 – 21 Mei 2012.
C. Subjek Penelitian
Populasi dalam penelitian ini adalah seluruh siswa kelas VIII yang
terdiri dari enam kelas di SMP Negeri 37 Bekasi yang terdaftar sebagai siswa
di semester genap pada tahun 2011/2012 dengan jumlah keseluruhan siswa
kelas VIII 320 orang. Untuk sampel, peneliti memilih tiga kelas dari enam
kelas yang ada dengan ketentuan kemampuan siswa yang heterogen, artinya
siswa dalam satu kelas terdiri dari siswa yang mempunyai kemampuan
akademik tinggi, sedang, dan rendah.
Peneliti memilih kelas VIII dikarenakan siswa kelas VIII SMP sudah
cukup beradaptasi sebagai siswa SMP dibanding kelas VII SMP. Selain itu
IX SMP yang harus mempersiapkan diri untuk Ujian Nasional (UN). Teknik
pengambilan sampel yang peneliti lakukan adalah kuasi eksperimen.
D. Variabel Penelitian
Penelitian ini memuat empat variabel terdiri dari tiga variabel bebas
dengan perlakuan berbeda serta memuat variabel terikat, diantaranya sebagai
berikut:
1. Variabel bebas 1: Pembelajaran reciproc yang diterapkan kepada siswa
kelas eksperimen pertama.
2. Variabel bebas 2: Pembelajaran kooperatif tipe NHT yang diterapkan
kepada siswa kelas eksperimen kedua.
3. Variabel bebas 3: Pembelajaran langsung (direct instruction) yang
diterapkan kepada siswa kelas eksperimen ketiga.
4. Variabel terikat : Kemampuan pemahaman matematis.
E. Instrumen Penelitian
Variabel terikat yang digunakan dalam penelitian ini memuat satu
aspek kognitif. Aspek kognitif dalam penelitian yaitu kemampuan pemahaman
matematis siswa, menggunakan tes. Tes yang digunakan dalam penelitian ini
adalah postes (tes akhir). Tes yang digunakan berbentuk uraian, dengan
maksud untuk melihat proses pengerjaan siswa agar dapat diketahui
kemampuan pemahaman matematis baik siswa yang belajar dengan model
kooperatif tipe nht, maupun siswa yang belajar dengan model pembelajaran
langsung. Sebelum soal tes disusun, kisi-kisi soal dibuat terlebih dahulu,
seperti pada tabel di bawah ini:
Tabel 3.1
Kisi-kisi Soal Kemampuan Pemahaman Matematis
Aspek Indikator Pemahaman
Matematis
Selanjutnya dengan menentukan kriteria penskoran yang akan
Kriteria penskoran, untuk tes pemahaman berpedoman pada Holistics Scoring
Rubics yang dikemukakan oleh Cai, Lane, dan Jakcobsin (dalam Setiadi,
2010), sebagai berikut:
Tabel 3.2
Kriteria Penskoran Kemampuan Pemahaman Matematis
Skor Kriteria Jawaban dan Alasan
4 Menunjukkan kemampuan pemahaman konsep dan prinsip terhadap soal matematika secara lengkap, penggunaan istilah dan notasi secara tepat, penggunaan alogaritma secara lengkap dan benar.
3 Menunjukkan kemampuan pemahaman konsep dan prinsip terhadap soal matematika hampir lengkap, penggunaan istilah dan notasi hampir benar, penggunaan alogaritma secara lengkap, perhitungan secara umum benar, namun mengandung sedikit kesalahan.
2 Menunjukkan kemampuan pemahaman konsep dan prinsip terhadap soal matematika kurang lengkap dan perhitungan masih terdapat sedikit kesalahan.
1 Menunjukkan kemampuan pemahaman konsep dan prinsip terhadap soal matematika sangat terbatas dan sebagian besar jawaban masih mengandung perhiungan yang salah.
0 Tidak ada jawaban, kalaupun ada tidak menunjukkan kemampuan pemahaman konsep dan prinsip terhadap soal matematika.
Instrumen penelitian ini berupa tes tertulis pada pokok bahasan kubus
dan balok berbentuk soal uraian yang terdiri dari 8 butir soal dengan skor
maksimal 4 setiap butir soal. Skor total siswa jika menjawab benar seluruh
soal adalah 32, sedangkan perhitungan dari skor ke nilai guna kepentingan
kelengkapan penilaian guru bidang studi sekolah tersebut terhadap kepada
siswa yang bersangkutan yaitu Nilai = � � ℎ �
� × 10.
Agar memenuhi syarat sebagai instrumen yang baik, soal tes
Negeri 14 Bekasi kelas X. Hasil ujicoba tersebut untuk mengetahui
reliabilitas, validitas, indeks kesukaran, dan daya pembeda, sebagai berikut:
1. Analisis Reliabilitas Tes
Untuk mengukur sejauh mana suatu alat ukur memberikan
gambaran yang benar-benar dapat dipercaya tentang kemampuan
seseorang maka dilakukan uji reliabilitas. Tes yang diujikan berbentuk
uraian perhitungan reliabilitas tes dapat digunakan rumus Cronbach’s
Alpha, yaitu:
: jumlah variansi skor butir soal,
2
: variansi skor total.
Kemudian dari hasil perhitungan derajat reliabilitas soal
diinterpretasikan dengan menggunakan klasifikasi derajat reliabilitas pada
Tabel 3.3, berikut:
Tabel 3.3
Klasifikasi Koefisien Reliabilitas
Besarnya ��� Interpretasi
Perhitungan reliabilitas didapat dari 8 butir soal yang
diujicobakan pada siswa yang sudah mendapat materi kubus dan balok.
Perhitungan skor setiap siswa dapat dilihat pada lembar lampiran.
Berikut tabel rekapitulasi reliabilitas:
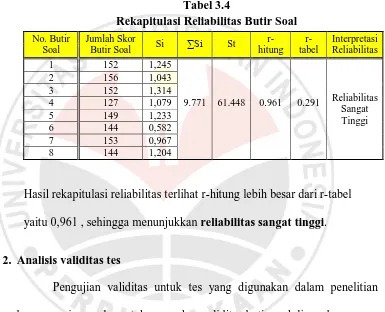
Tabel 3.4
Rekapitulasi Reliabilitas Butir Soal No. Butir
Hasil rekapitulasi reliabilitas terlihat r-hitung lebih besar dari r-tabel
yaitu 0,961 , sehingga menunjukkan reliabilitas sangat tinggi.
2. Analisis validitas tes
Pengujian validitas untuk tes yang digunakan dalam penelitian
berupa uraian, maka untuk mengukur validitas butir soal digunakan rumus
korelasi Product Moment Pearson, yaitu:
: skor total,
�: jumlah siswa.
Kemudian dari hasil perhitungan koefisien korelasi
diinterpretasikan dengan menggunakan klasifikasi koefisien validitas yang
dapat dilihat pada Tabel 3.5, berikut:
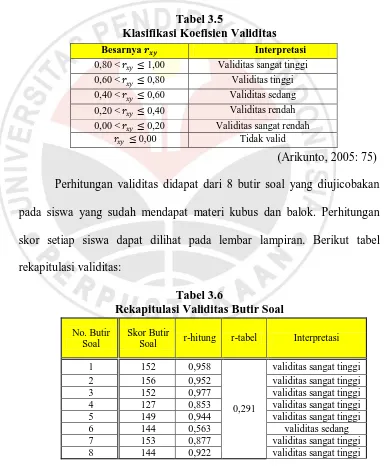
Tabel 3.5
Klasifikasi Koefisien Validitas
(Arikunto, 2005: 75)
Perhitungan validitas didapat dari 8 butir soal yang diujicobakan
pada siswa yang sudah mendapat materi kubus dan balok. Perhitungan
skor setiap siswa dapat dilihat pada lembar lampiran. Berikut tabel
rekapitulasi validitas:
Tabel 3.6
Rekapitulasi Validitas Butir Soal No. Butir
Soal
Skor Butir
Soal r-hitung r-tabel Interpretasi
1 152 0,958
Besarnya � Interpretasi
Hasil rekaputulasi validitas yang terlihat pada Tabel 3.6 bahwa dari
8 butir soal uraian yang diujicobakan terbukti valid. Klasifikasi validitas
terdiri dari validitas sangat tinggi pada butir soal nomer 3, validitas tinggi
pada butir soal nomer 1, 2, 4, dan 5, serta validitas sedang pada butir soal
nomer 6, 7, dan 8.
Apabila diambil rerata dari nilai r-hitung yang diperoleh, rerata
validitas dari seluruh butir soal yang diteskan adalah 0,881. Hal tersebut
mempunyai makna bahwa soal dari instrumen tes ini valid dengan
interpretasi validitas sangat tinggi.
3. Analisis Daya Pembeda
Untuk menentukan daya pembeda digunakan rumus:
A B
A
S S
DP
I
(Sundayana, 2010: 77) keterangan:
DP = indeks daya pembeda suatu butir soal
A
S
= jumlah skor kelompok atas pada butir soal yang diolahB
S
= jumlah skor kelompok bawah pada butir soal yang diolahA
I
= jumlah skor ideal kelompok atas pada butir soal yang diolahHasil perhitungan daya pembeda diinterpretasikan dengan
menggunakan kriteria penafsiran menurut Sundayana (2010: 78) dalam
Tabel 3.7
Kriteria Penafsiran Daya Pembeda
Besarnya �� Interpretasi
��≤ 0,00 Sangat Jelek
untuk mengukur kemampuan pemahaman matemtis setelah perlakuan atau
setelah pembelajaran berlangsung. Sebelum menganalisis daya pembeda
tersebut, skor hasil uji coba dikelompokan menjadi skor kelompok atas
yaitu skor dari siswa yang mendapat skor tertinggi dan skor kelompok
bawah yaitu skor dari siswa yang mendapat skor terendah. Pengelompokan
masing-masing kelompok diambil dari 27% dari 46 siswa yang
mengerjakan soal uji coba tersebut, pengelompokan tersebut dapat dilihat
pada lembar lampiran. Berikut tabel hasil analisis daya pembeda 8 butir
soal:
Tabel 3.8
4. Analisis Tingkat Kesukaran
Rumus yang digunakan untuk menghitung tingkat kesukaran adalah:
�= +
� +�
(Sundayana, 2010: 77)
dengan,
TK : Tingkat Kesukaran,
: jumlah skor siswa kelompok atas pada butir soal yang diolah,
: jumlah skor siswa kelompok bawah pada butir soal yang diolah,
� : jumlah skor ideal siswa kelompok atas, � : jumlah skor ideal siswa kelompok bawah,
Hasil perhitungan tingkat kesukaran diinterpretasikan dengan
menggunakan Tabel 3.9 berikut, (Sundayana, 2010: 78):
Tabel 3.9
Kriteria Penafsiran Tingkat Kesukaran
Besarnya �� Interpretasi
TK = 0,00 Terlalu Sukar
0,00 < �≤ 0,30 Sukar
0,30 < �≤ 0,70 Sedang
0,70 < �≤ 1,00 Mudah
TK = 0,00 Terlalu Mudah
Analisis Tingkat Kesukaran dari butir soal yang akan dipakai
berguna untuk mengukur kemampuan pemahaman matemtis setelah
perlakuan atau setelah pembelajaran berlangsung. Sebelum menganalisis
indeks kesukaran tersebut, skor hasil uji coba dikelompokan menjadi skor
kelompok atas yaitu skor dari siswa yang mendapat skor tertinggi dan skor
kelompok bawah yaitu skor dari siswa yang mendapat skor terendah.
Pengelompokan masing-masing kelompok diambil dari 27% dari
dapat dilihat pada lembar lampiran. Berikut tabel hasil analisis tingkat
kesukaran 8 butir soal:
Tabel 3.10
Analisis Tingkat Kesukaran dan Kriteria Butir
Soal
Tingkat
Kesukaran (TK) Kriteria
1 0,69 Sedang
2 0,74 mudah
3 0,67 Sedang
4 0,66 Sedang
5 0,70 Sedang
6 0,77 mudah
7 0,74 mudah
8 0,67 Sedang
Selain instrumen di atas masih ada lagi instrumen yang digunakan,
yaitu:
1. Skala sikap digunakan untuk mengetahui sikap siswa terhadap proses
pembelajaran selama penelitian.
Jenis skala sikap dalam penelitian ini yaitu skala Likert, skala
likert sendiri berguna untuk mengukur sikap, pendapat, dan persepsi
seseorang atau sekelompok tentang kejadian atau gejala sosial. Dengan
menggunakan skala likert, maka variabel yang akan dijabarkan menjadi
dimensi, dimensi dijabarkan menjadi sub variabel kemudian sub
variabel dijabarkan lagi menjadi indikator-indikator yang dapat diukur.
Akhirnya indikator-indikator yang terukur ini dapat dijadikan titik tolak
untuk membuat item instrumen yang berupa pertanyaan atau pernyataan
Setiap jawaban responden dihubungkan dengan bentuk
pernyataan atau dukungan sikap yang diungkapkan dengan kata-kata
Sangat Setuju (SS), Setuju (S), Netral (N), Tidak Setuju (TS), dan
Sangat Tidak Setuju (STS). Namun, dalam penelitian ini peneliti
menggunakan empat kategori kata-kata ungkapan saja yaitu:
Tabel 3.11
Kategori ungkapan kata-kata Skala Likert Pernyataan Positif Pernyataan Negatif
Sangat Setuju (SS) 4 Sangat Setuju (SS) 1
Setuju (S) 3 Setuju (S) 2
Tidak Setuju (TS) 2 Tidak Setuju (TS) 3
Sangat Tidak Setuju (STS) 1 Sangat Tidak Setuju (STS) 4
Untuk perhitungan skala likert ini, Pertama merekapitulasi hasil
jawaban responden sesuai dengan mengelompokkan kategori yang ada.
Kedua, setiap frekuensi yang sudah direkap dari jawaban responden
dikalikan dengan nilai sesuai kategori ungkapan yang ada pada Tabel
3.11. Kemudian untuk yang terakhir hitung persentase setiap kelas
dengan menggunakan rumus � ℎ �
� ℎ � × 100%.
Setelah diketahui persentase yang diperoleh, maka persentase
dapat diartikan sesuai kriteria interprestasi skor pada Tabel 3.12 berikut,
(Riduwan, 2008):
Tabel 3.12
Kriteria Interpretasi Skor Skala Likert Interval Persentase Interpretasi
0% - 20% Sangat Lemah
21% - 40% Lemah
41% - 60% Cukup
61% - 80% Kuat
Skala sikap ini digunakan setelah dinyatakan valid dan reliabel
oleh ahli, dalam hal ini dosen pembimbing. Skala sikap diberikan
sesudah pembelajaran. Bentuk skala sikap tersebut dapat dilihat pada
lampiran C.
2. Lembar observasi digunakan untuk mengontrol aktivitas siswa dan guru
selama penelitian berlangsung. Lembar observasi dan guru, hasilnya di
hitung persentase dan rerata dari ketiga kelas yang diteliti.
Kedua tes ini bertujuan untuk menjaga kemungkinan munculnya
hal lain yang dapat mempengaruhi hasil penelitian.
F. Bahan Ajar
Bahan ajar yang digunakan dalam penelitian ini adalah rencana
pelaksanaan pembelajaran (RPP) dan lembar kerja siswa (LKS) yang
berkaitan dengan materi akhir semester 2 kelas VIII yaitu Bangun Ruang Sisi
Datar khususnya pada Kubus dan Balok.
RPP yang dirancang dalam penelitian ini ada tiga macam. RPP
pertama merupakan RPP yang digunakan untuk mengajar kelas eksperimen
yang memperoleh pembelajaran reciproc (PR), RPP kedua merupakan RPP
yang digunakan untuk mengajar kelas eksperimen yang memperoleh
pembelajaran kooperatif tipe numbered-head-together (NHT), dan RPP ketiga
merupakan RPP yang digunakan untuk mengajar kelas eksperimen yang
memperoleh pembelajaran langsung (PL). Bentuk format RPP yang disusun
LKS dirancang sesuai tahapan-tahapan pada model PR dan model
NHT. Sedangkan untuk model PL, peneliti (guru) tidak menggunakan LKS
karena cukup dengan memberikan pertanyaan-pertanyaan dan latihan-latihan
secara langsung kepada siswa. semuanya tergambar dalam pembelajaran pada
RPP dan LKS yang digunakan terdapat pada lampiran A.
G. Teknik Pengumpulan Data
Pengumpulan data dilakukan melalui tes dan angket. Tes yang
digunakan hanya postes, postes yang diberikan berupa tes kemampuan
pemahaman matematis. Angket yang digunakan berupa skala sikap untuk
menjaga kemungkinan munculnya hal lain yang dapat mempengaruhi hasil
penelitian. Postes dan angket (skala sikap) diberikan setelah pembelajaran
dalam penelitian selesai.
H. Teknik Pengolahan Data
Data yang diperoleh dalam penelitian ini berasal dari dua instrumen.
Yaitu skor awal dari hasil ujian tengah semester (UTS) dan postes (tes akhir).
Data yang diperoleh dari skor awal dari hasil ujian tengah semester (UTS) dan
postes (tes akhir) diolah melalui tahap-tahap sebagai berikut:
1. Menghitung skor yang diperoleh siswa dari postes kemampuan
2. Melakukan uji normalitas untuk mengetahui kenormalan data, baik yang
diperoleh dari skor kemampuan awal (UTS) atau skor kemampuan akhir
(postes). Uji normlitas ini diawali dengan hipotesis. Hipotesisnya adalah:
H0 : data berdistribusi normal
H1 : data tidak berdistribusi normal
Dengan ketentuan tolak H0 jika nilai sinifikansi yang diperoleh lebih kecil
(<) dari taraf signifikansi yang diperbolehkan (0,05). Karena jumlah
sampel pada penelitian ini 50 orang siswa maka uji yang digunakan untuk
menguji normalitas adalah uji Kolmogorov-Smirnov dengan program
SPSS.
3. Menguji homogenitas varians data, baik yang diperoleh dari skor
kemampuan awal (UTS) atau skor kemampuan akhir (postes). Uji ini
diawali dengan hipotesis. Hipotesisnya adalah:
H0 : data bervariansi homogen.
H1 : data tidak bervariansi homogen.
Dengan ketentuan tolak H0 jika taraf signifikansi yang diperoleh lebih
kecil (<) dari taraf signifikansi yang diperbolehkan (0,05). Untuk
mengetahui apakah setiap kelas mempunyai kesamaan kemampuan maka
dilakukan uji Homogeneity of Variance dengan program SPSS.
4. Jika sebaran data normal dan homongen, akan dilakukan uji perbedaan dua
atau lebih rerata. Uji statistik yang digunakan adalah Compare Means
One-Way ANOVA dengan tes Post Hoc jenis uji HSD Tuckey, karena uji
Uji ANOVA yang dapat menghasilkan hasil yang lebih signifikan
dibandingkan jenis uji ANOVA lainnya.
5. Jika salah satu data tidak berdistribusi normal, maka uji yang dilakukan
adalah uji statistik Non-parametric Tests K Independent Sample yaitu uji
Kruskal-Wallis dan jika hipotesis nol ditolak maka dilakukan uji lanjutan
Kruskal-Wallis.
I. Prosedur Penelitian
Prosedur penelitian ini dirancang untuk memudahkan dalam
pelaksanaan penelitian. Prosedur penelitian yang dilakukan dalam penelitian
ini adalah:
1. Tahap Persiapan
a. Menyusun jadwal penelitian
b. Membuat rencana penelitan
c. Menyusun instrumen penelitian
2. Tahap Pelaksanaan
a. Menentukan kelas eksperimen yang memperoleh model
pembelajaran reciproc, model pembelajaran kooperatif tipe NHT,
dan model pembelajaran langsung dari sampel yang telah dipilih.
b. Melakukan perlakuan dengan model pembelajaran sesuai Rencana
Pelaksanaan Pembelajaran (RPP) yang telah dirancang untuk
c. Memberikan postes dan skala sikap di akhir pembelajaran.
3. Tahap Pengumpulan data
4. Tahap analisis data
Gambar 3.1. Bagan Prosedur Penelitian Perlakuan pada kelas eksperimen
(reciprocal teaching)
Pemberian Postes dan Skala sikap terhadap
pembelajaran di kelas Pengidentifikasikan masalah &
tujuan penelitian
Penyusunan instrumen dan bahan ajar
uji coba instrumen
Perbaikan instrumen
Perlakuan pada kelas ekssperimen (cooperative learning tipe NHT)
Kesimpulan Analisis
Memilih tiga kelas yang akan diteliti dengan menguji normalitas dan homogenitas dari ketiga kelas dari
nilai UTS siswa ketiga kelas.
Perlakuan pada kelas eksperimen (direct instruction) Analisis
BAB V
KESIMPULAN DAN SARAN
A. Kesimpulan
Berdasarkan hasil analisis penelitian yang telah disampaikan pada Bab IV
sebelumnya, membuktikan pengaruh pembelajaran reciproc, kooperatif tipe NHT,
dan langsung terhadap kemampuan pemahaman matematis, diperoleh beberapa
kesimpulan sebagai berikut:
1. Terdapat perbedaan kemampuan pemahaman matematis antara siswa yang
memperoleh model pembelajaran reciproc, model pembelajaran kooperatif
tipe NHT, dan model pembelajaran langsung.
2. Kemampuan pemahaman matematis siswa yang memperoleh model
pembelajaran reciproc lebih baik daripada kemampuan pemahaman
matematis siswa yang memperoleh model pembelajaran kooperatif tipe NHT
dan model pembelajaran langsung, tetapi model pembelajaran langsung lebih
baik daripada model pembelajaran kooperatif tipe NHT.
3. Sikap siswa selama pembelajaran baik pembelajaran reciproc dan
pembelajaran kooperatif tipe NHT berjalan dengan cukup baik. Selama
pembelajaran siswa terlibat secara aktif baik dalam berdiskusi,
mengemukakan pendapat serta dalam menyelesaikan tugas yang diberikan
oleh guru. Begitu juga pada siswa yang memperolah model pembelajaran
langsung terlihat cukup aktif untuk membahas soal-soal pemahaman di depan
kelas. Sehingga secara keseluruhan sikap siswa terhadap ketiga pembelajaran
B. Saran
Dari hasil penelitian penulis mengajukan saran sebagai berikut:
1. Model pembelajaran yang terbaik dalam penelitian ini hendaknya dijadikan
referensi setiap pengajar dalam memilih model pembelajaran yang tepat,
untuk digunakan dalam usahanya mengembangkan kemampuan pemahaman
matematis siswa, kreativitas siswa dalam membuat soal-soal matematika,
melatih siswa mengkaji dan menggeneralisasi atau menyimpulkan materi
yang dipelajari.
2. Dalam menerapkan model pembelajaran yang diteliti, setiap pengajar
disarankan untuk menyediakan bahan ajar yang dirancang secara khusus
sesuai dengan indikator pemahaman matematis sehingga kemampuan tersebut
dapat dimiliki siswa.
3. Untuk penelitian lebih lanjut hendaknya penelitian ini dapat dilengkapi
dengan meneliti aspek lain secara lebih terperinci yang belum terjangkau oleh
DAFTAR PUSTAKA
Arends, R. I. (2007). Learning To Teach. New York : McGraw Hill Companies.
Arikunto, S. (2005). Dasar-dasar Evaluasi Pendidikan. Jakarta: Bumi Aksara.
Aunurrahman. (2008). Belajar Dan Pembelajaran: Memadukan Teori-teori Klasik dan Pandangan-pandangan Kontemporer. Bandung: ALFABETA.
Depdiknas.(2006). Peraturan Menteri Pendidikan Nasional Republik Indonesia tentang Standar Isi untuk Satuan Pendidikan Dasar dan Menengah. Jakarta: Depdiknas
Depdiknas.(2007). Kajian Kebijakan Kurikulum Mata Pelajaran Matematika. Jakarta: Pusat Kurikulum Balitbang Depdiknas
Furner, M. J. dan Kumar D. D. (2007). The Mathematics and Science Integration Argument : A Stand for Teacher Education. Eurasia Journal of Mathematics, Science & Technology Education, Vol 3 Number 3, (185-189)
Irianti. (2007). Upaya Peningkatan Hasil Belajar Matematika tentang Program Linier melalui Pembelajaran Kooperatif tipe Numbered Heads Together Untuk Siswa Kelas XII IPA 1 SMA Negeri 1 Wanadadi Banjarnegara.
Joyce, B. and Marsha with Beverly S. (2004). Models of Teaching. Boston: Allyn and Bacon.
Lie, A. (2005). Cooperative Learning Mempraktikkan Cooperative Learning di Ruang-ruang Kelas. Jakarta: PT Gramedia.
Martadiputra, B. A. P. (2011). “Pelatihan Pengolahan Data Menggunakan SPSS
untuk Mahasiswa S2& S3 Pendidikan PPs UPI”. Makalah pada Pelatihan,
Bandung
Minium, E. W., Bruce M. K. and Gordon B. Statistical Reasoning In Psychology and Education. New York: JOHN WILLEY.
Oxford, L. R. (1997). “Cooperative Learning, Collaborative Learning, and Interaction: Three Communicative Strands in the Language Classroom ”.
The Modern Language Journal, Vol. 81, No. 4
O’Connel, S. (2007). Introduction to Connection. Boston: Heinemann.
Palincsar. (1986). Reciprocal Teaching [online]. Tersedia: http://www.ncrel.org/sdrs/areas/issues/students/atrisk/at6lk38.htm. [20 November 2010].
________ & Brown, A. (1986). Teacher’s corner: what is reciprocal teaching.
[Online]. Tersedia:
http://team.lacoe.edu/documentation/classroom/patti/2-3/teacher/resources/reciprocal.html. [21 desember 2010]
Qohar, A. (2010). Mengembangkan Kemampuan Pemahaman, Koneksi Dan Komunikasi Matematis Serta Kemandirian Belajar Matematika Siswa SMP Melalui Reciprocal Teaching. Disertasi Sps UPI Bandung: Tidak diterbitkan.
Ridwan. (2008). Belajar Mudah Penelitian untuk Guru-Karyawan dan Penelitian Pemula. Bandung: ALFABETA.
Rosdiana & Lambertus. (2006). Meningkatkan Prestasi Belajar Matematika Siswa Kelas VIII pada Pokok Bahasan Faktorisasi Suku Aljabar melalui Pembelajaran Kooperatif tipe NHT di SMP Negeri 15 Kendari. [Online]. Tersedia: http://isjd.pdii.lipi.go.id/admin/jurnal/142074954.pdf. [13 Februari 2012]
Ruseffendi, E. T.(2005). Dasar-dasar Penelitian Pendidikan dan Bidang Non-Eksakta lainnya. Bandung: Tarsito.
Sanjaya, W. (2009). Stategi Pembelajaran Berorientasi Standar Proses Pendidikan. Jakarta: Kencana.
_____________. (2008). Perencanaan dan Desain Sistem Pembelajaran. Jakarta: Kencana.
Setiadi, Y. (2010). Meningkatkan Kemampuan Pemahaman dan Komunikasi Matematis Siswa SMP melalui Pembelajaran Kooperatif dengan Teknik Think-Pair-Square. Tesis Sps UPI Bandung: Tidak diterbitkan.
Sundayana, R. (2010). Statistika Penelitian Pendidikan. Garut: STKIP Garut Press.
Suherman, E. dkk. (2003). Strategi Pembelajaran Matematika Kontemporer. Bandung: JICA-Universitas Pendidikan Indonesia.
Sumarmo, U. (2000). Proses Belajar dan Pemahaman Materi Kuliah. Makalah disampaikan pada lokakarya Peran Pedagogi dalam peningkatan Proses Pembelajaran TPB ITB di Bandung pada tanggal 4 Desember 2000.
Suprijono, A. (2012). Cooperative Learning: Teori & Aplikasi PAIKEM. Yogyakarta: Pustaka Pelajar.
Trianto. (2007). Mode-model Pembelajaran Inovatif Berorientasi Konstruktivistik. Jakarta: Prestasi Pustaka.