On
l
-majority voting paradoxes
* ´
Jozsef Mala U ´ ´
Budapest University of Economics, Fovam ter 8, Budapest, H-1093, Hungary
Received 27 February 1997; received in revised form 23 October 1997; accepted 3 February 1998
Abstract
A new supplement to McGarvey’s wellknown theorem is given. Namely, we prove that for each
lwith 1 / 2,l ,1 there exists a tournament T on some finite set of alternatives A such that for every profile of A there exists an arc (a, b) of T such that the proportion of voters that prefer a to b is less thanl. In other words, there exist tournaments that cannot be al-majority relation of any profile. Lower and upper bounds for the minimal majority with which we can generate all tournaments on n alternatives are also given. 1999 Elsevier Science B.V. All rights reserved.
Keywords: McGarvey’s theorem; Tournament; Alternatives
1. Introduction
The history of studying voting paradoxes goes back to Condorcet (1785) who was among the first to observe that the majority relation can ‘‘cycle’’. Namely, consider three voters: 1, 2 and 3, and three alternatives: a, b and c among which our voters are to choose. Let the linear preferences of our voters be given by the following way:
1: a b c 2: b c a; 3: c a b.
which should be read as voter 1 prefers a most, b second and so on. Then a is preferred to b by the 2 / 3 majority of the voters, b is preferred to c by the 2 / 3-majority of the voters and c is preferred to a by the 2 / 3-majority of the voters.
It is a natural question then what can be said about the simple majority relation in general. The answer can be found in McGarvey (1953). He proved that if T is a tournament on the n-element alternative set A (that is, T is a binary relation on A such that aTb if and only if not bTa, for each a, b in A) then there is a profile u of n(n21)
*E-mail: [email protected]
voters (that is, it is an n(n21)-tuple of linear orders of A), such that the corresponding
majority relation M (that is, for which aM b if and only if at least the half of the votersu u
prefer a to b, for each a, b in A) coincides with T. McGarvey raised a question about the least integer f(n) such that any tournament on an n-element alternative set can be obtained as the simple majority relation from some profile of at most f(n) voters. So McGarvey’s result can be read as f(n)#n(n21).
Improving on McGarvey’s method, Stearns (1959) showed that f(n)#n12 if n is
n
In 1964 Erdos and Moser (1964) showed that
n
]]
f(n)#c , (1)
2 log n
for some positive constant c .2
f (n)log n ]]
The question that if the limit of n exists is open.
Hollard and Le Breton (1996) have shown that if we restrict ourselves to separable complete relations then McGarvey’s result remains true, that is, every separable complete relation on a finite set of alternatives can be generated by some separable profile.
Now we can approach the topic from the following point of view: we seek a lwith
1 / 2,l#1, such that for each tournament T there exists a profile u5(P ,...,P ) with the
the l-majority profile u.
In this context many interesting questions arise so just to mention a few:
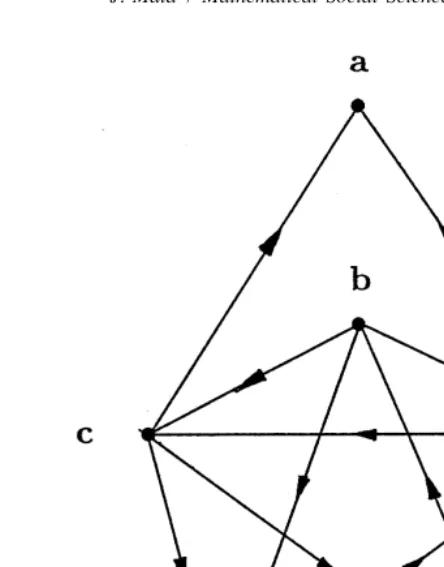
If given a tournament on n alternatives (that can be regarded, for example as the expected majority result of some election), what is the maximal majority of the voters (if it exists at all) that can generate that tournament? What is the minimal number of voters that can produce that maximal majority? If given the electorate with possible set of (linear) preferences (think of for instance the various conditions on profiles in Arrow and Raynaud, 1986 that guarantee the transitivity of the majority relation) and the finite set of alternatives, then what kind of majority relations can occur and with what majority? Our paper may be regarded as a first step towards such investigations. To illustrate the first two questions let us consider the tournament T on 6 nodes (Fig. 1) where not all the arcs have been included in the drawing; arcs (a, b), (a, d ) and a, e) are has not been drawn for the sake of clearness.
One can check that the following 3-voter profile is a 2 / 3-majority profile for T : 1: a d e f b c
Fig. 1. A relatively complex tournament.
It can be seen easily that if a tournament contains a 3-cycle (like ours does) then it cannot be generated by a l-majority profile if l.2 / 3. So, for T above the maximum
value of the majority that can generate it, it is 2 / 3 and the minimum number of voters necessary for it is clearly 3.
One may expect that it is true that there exists alwith 1 / 2,l#2 / 3 such that every
tournament is generated by somel-majority profile. Unfortunately, as the main result of
our paper shows, this is not true.
2. The results
U
We will make use of the following theorem due to Erdos and Moon (1965):
U
11´ n ]]
S D
w(n), .
2 2
for any positive ´and sufficiently large n. h
It is easy to see that the previous theorem is equivalent to saying that for each´ .0
and sufficiently large n there exists a tournament T on n alternatives such that 11´ n
Now we are ready to prove the main result of our paper:
Theorem 2. If l.1 / 2 then there exists an integer n5n(l) and a tournament T on n
alternatives such that T is not generated by any l-majority profile.
Proof. Letl.1 / 2 be arbitrary. By Theorem 1 there exists a tournament T on n5n(l)
n
S D
alternatives such thatuT>Pu,l . holds for every linear order P. We state that T is
2 not generated by any l-majority profile.
Otherwise let T be generated by the l-majority profile u5(P , P ,...,P ).
Theorem 3. Letl denote the supremum of the numberslsuch that any tournament on
n
n alternatives is generated by some l-majority profile. Then the sequence (l ) is
n decreasing and lim l 51 / 2.
n→` n
Proof. If tournament T on the set of alternatives A is generated by thel-majority profile
u then any subtournament T9of T (that is, T9is the restriction of T to some subset A9of
A) is generated by the l-majority profile u9 which is obtained from u by deleting the
elements of A\A9 from each component of u. This shows that l #l if n,m. By
m n
1 ]
McGarvey’s theorem it is true that for every tournament there exists al . such that it
1 ]
can be generated by some l-majority profile, that is, l . for each n. Now using
n 2
Theorem 2 we obtain our theorem. h
U
The following result is stronger than Theorem 1 and can also be found in Erdos and Moon (1965):
U
Theorem 4. (Erdos and Moon) For any ´ .0 the proportion of tournaments on n
alternatives that contain some acyclic relation with more than
1 / 2
1 n 1 3
]
S D
1(11´)S
]n log nD
2
2 2
arcs tends to zero as n tends to infinity. h
By the aid of Theorem 4 we can estimate the sequencel :
n
Proof. From (1) it easily follows that every tournament on n alternatives can be 1 2 log n
] ]]
generated by a 1 -majority profile, that is, d 52 /c will do for our purpose.
1 2 cn
By Theorem 4, with ´ 51, we have that for sufficiently large n there exists a
tournament T on n alternatives such that T does not contain acyclic relations with atn n
least
arcs. Following the proof of Theorem 2 with
1 / 2
and T5T we have that for n sufficiently large there is a tournament that cannot be
n
generated by l-majority profiles if
1 / 2
So, there exists a constant d such that for each n2
]]
alter-natives. By using that list one can check that if T is a tournament on 6 alternatives then6
T is generated by a 3-voter profile. From this it follows that the maximum majority that6
can generate those tournaments is exactly 2 / 3. Hence, we can state
Theorem 6.
l 52 / 3 if i53, 4, 5, 6.
i
h
It is interesting to note that it seems very hard to construct tournaments that cannot be generated by any l-majority profiles for l close to 1 / 2. Those tournaments are rather
‘‘random’’ tournaments.
Acknowledgements
U ´
The author is indebted to Erno Zalai and Jozsef Temesi for the moral support during the work on this paper. The author also thanks Michel Le Breton and Nick Baigent and the two referees for helpful comments.
References
Arrow, K.J., Raynaud, H., 1986. Social Choice and Multicriterion Decision-Making. MIT Press, Cambridge, MA.
´ Condorcet, M.J.A.M., Caritat, Marquis de, 1785. Essai sur l’Application de l’ Analyse a la Probabilite des
´ ´
Decisions rendues a la pluralite des voix L’Imprimerie Royale, Paris. U
Erdos, P., Moon, J.W., 1965. On sets of consistent arcs in a tournament. Canadian Mathematical Bulletin 8, 269–271.
U
Erdos, P., Moser, L., 1964. On the representation of directed graphs as unions of orderings. Publications of the Mathematical Institute of the Hungarian Academy of Sciences 9, 125–132.
Hollard, G., Le Breton, M., 1996. Logrolling and a McGarvey theorem for separable tournaments. Social Choice and Welfare 13 (4), 451–455.
McGarvey, D.C., 1953. A theorem on the construction of voting paradoxes. Econometrica 21, 608–610. Moon, J.W., 1968. Topics on Tournaments. Holt, Rinehart and Winston.