ANalisis DAta dan GRAfik dengan R

(1)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 1 dari 234

Cari Halaman Kembali Layar Penuh

(2)

UNEJ

Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 2 dari 234

Tutup

ANalisis DAta dan GRAfik dengan R

(ANDAGRAR

-

Versi Elektronik)

Prof. Drs. I. M. Tirta, Dip.Sc, M.Sc., Ph.D.

itirta@unej.ac.id

(3)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 3 dari 234

(4)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 1 dari 234

Tutup

DAFTAR ISI

I STATISTIKA INFERENSIAL DENGAN R 13

1 PROGRAM STATISTIKA R 15

1.1 Sekilas Program Statistika R . . . 19

1.2 RGUI dengan R-Commander . . . 21

1.3 RCommander dengan Menu Bahasa Indonesia . . . 25

1.4 Editor Skrip dengan Tinn-R . . . 28

(5)

UNEJ

Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 2 dari 234

Tutup

1.6 Bacaan Lebih Lanjut . . . 31

1.7 Soal-soal Latihan . . . 32

2 KONSEP DASAR STATISTIKA 35 2.1 Statistika dan Data Statistik . . . 37

2.2 Jenis Data . . . 42

2.3 Distribusi Data . . . 46

2.4 Ukuran Pemusatan dan Penyebaran . . . 50

2.4.1 Ukuran Pemusatan . . . 50

2.4.2 Ukuran Penyebaran . . . 53

3 EXPLORASI DATA 63 3.1 Menyiapkan Data pada R . . . 66

3.1.1 Mengedit langsung data . . . 67

3.1.2 Memanggil Data dari Database R . . . 68

3.1.3 Mengimpor data dari file . . . 71

3.1.4 Membangkitkan Data Simulasi . . . 73

(6)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 3 dari 234

Tutup

3.2.1 Deskripsi Data . . . 77

3.2.2 Visualisasi Data Univariat . . . 80

3.2.3 Visualisasi Data Multivariat . . . 84

4 UJI RATA-RATA DAN PROPORSI 99 4.1 Interval Keyakinan dan Uji Rata-rata . . . 101

4.1.1 Hasi-hasil Statistika . . . 101

4.1.2 Tingkat Interval Keyakinan dan Peluang Penutup108 4.1.3 Distribusi Beda Rata-rata Kelompok Saling Bebas . . . 110

4.1.4 Distribusi Beda Sampel/ Kelompok Tidak Saling Bebas . . . 112

4.2 Uji hipotesis rata-rata . . . 117

4.2.1 Menggunakan menu R-Commander . . . 120

4.3 Interval Keyakinan dan Uji Proporsi . . . 123

4.3.1 Interval keyakinan proporsi . . . 123

4.3.2 Interval keyakinan beda proporsi . . . 124

(7)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 4 dari 234

Tutup

4.4 Fungsi-fungsi R . . . 127

5 ANALISIS VARIANSI (ANAVA) 131 5.1 Konsep Dasar Anava . . . 133

5.2 Uji Anava Faktor Tunggal . . . 136

5.2.1 Alternatif Formula untuk perhitungan secara semi manual . . . 140

5.2.2 Uji Anava dengan R atau R-Commander . . 141

5.3 Anava Multi Faktor . . . 144

5.3.1 Eksplorasi Grafik Beda Rata-rata . . . 147

6 DASAR-DASAR PEMODELAN STOKASTIK 155 6.1 Prinsip Pemodelan . . . 159

6.2 Langkah-langkah Penting Dalam Pemodelan . . . . 166

(8)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 5 dari 234

Tutup

6.2.2 Langkah penting dalam Pemodelan Stokastik167

6.3 Metode Mengestimasi Parameter . . . 172

6.3.1 Metode kuadrat terkecil . . . 172

6.3.2 Metode likelihood maksimum . . . 173

6.3.3 Mencari maksimum dengan metode numerik 174 6.4 Model Linier dan Perkembangannya . . . 178

6.4.1 Model linier klasik . . . 179

6.4.2 Model linier tercampur . . . 181

6.4.3 Model linier tergeneralisasi . . . 184

6.4.4 Model linier campuran tergeneralisasi . . . . 187

6.5 Pengembangan Lain Model Linier . . . 189

6.6 Outline Buku . . . 192

6.7 Latihan Soal- soal . . . 193

7 REGRESI LINIER SEDERHANA 195 7.1 Bentuk dan Asumsi . . . 197

7.2 Estimasi Parameter . . . 198

(9)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 6 dari 234

Tutup

7.3 Uji Inferensial dari βˆj . . . 205

7.3.1 Distribusi βˆj . . . 205

7.3.1.1 Distribusi βˆj bila σ2 diketahui . . 205

7.3.1.2 Distribusi βˆj bila σ2 tidak diketahui207 7.3.2 Estimasi selang dari βj . . . 208

7.3.3 Uji Hipotesis . . . 209

7.3.4 Interval Prediksi Rata-rata dan Nilai Tunggal 210 7.3.5 Melaporkan nilai probabilitas p . . . 211

7.3.6 Menentukan Model dengan R . . . 212

7.3.7 Menggunakan fungsi lm() . . . 212

7.3.8 Menggunakan Menu R-Commander . . . 216

7.5 Latihan Soal- Soal . . . 218

(10)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 7 dari 234

Tutup

DAFTAR GAMBAR

1.1 Tampilan RGUI versi 2.2.1 Standar untuk Windows 23 1.2 Tampilan Menu R-Commander Asli . . . 24 1.3 Tampilan Menu R-Commander Menu Bahasa

In-donesia . . . 26 1.4 Tampilan Editor Skrip Tinn-R . . . 29

2.1 Sebaran Data dengan Mean Berbeda tetapi

(11)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 8 dari 234

Tutup

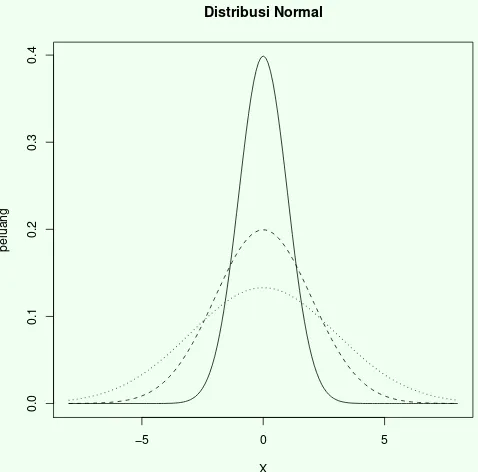
2.2 Sebaran Data dengan Mean Sama tetapi Dispersi

Berbeda . . . 56 2.3 Sebaran Data dengan Mean Sama tetapi Dispersi

Berbeda . . . 57 2.4 Perspektif dan Kontur Dua Peubah dengan r = 0

(atas) dan r = 0.8 (bawah) . . . 58

3.1 Menu Dialog Membaca Data . . . 72 3.2 Contoh Histogram, Boxplot, QQPlot dan

Dia-gram Lingkaran . . . 87 3.3 Komponen Boxplot . . . 88 3.4 Histogram dan Denstias Berat Ayam . . . 89 3.5 Contoh Diagram boxplot dengan mempertimbangkan

kelompok. Diagram menunjukkan bahwa distribusi keliling batang pohon berhubungan dengan jenis

pohon . . . 90 3.6 Contoh Diagram Pencar . . . 91 3.7 Contoh Matriks Diagram Pencar dengan

(12)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 9 dari 234

Tutup

3.8 Contoh Diagram Permukaan 3 Dimensi yang

men-gandung Peubah Kualitatif . . . 93

3.9 Contoh Representasi Tiga Dimensi Regresi de-ngan dua Peubah Penjelas . . . 94

3.10 Contoh CoPlot . . . 95

4.1 Ilustrasi distribusi rata-rata sampel . . . 115

4.2 Grafik Simulasi Interval Keyakinan . . . 116

4.3 Menu Uji Rata-rata . . . 121

4.4 Menu Uji Beda rata-rata . . . 122

4.5 Menu R-Commander untuk uji proporsi . . . 126

5.1 Ilustrasi konsep Anava . . . 134

5.2 Ilustrasi konsep Anava . . . 135

5.3 Menu dialog anova satu arah . . . 143

5.4 Menu dialog anova multi arah . . . 146

5.5 Contoh Mean Plot untuk ilustrasi uji anava . . . 149

5.6 Contoh Mean Plot untuk ilustrasi interaksi . . . . 150

5.7 Contoh Mean Plot untuk ilustrasi uji anava . . . 151

(13)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 10 dari 234

Tutup

(14)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 11 dari 234

Tutup

DAFTAR TABEL

3.1 Penulisan Data pada R . . . 68

3.2 Perintah Untuk Data Acak . . . 74

3.3 Tabel Fungsi Eksplorasi Data . . . 86

5.1 Tabel Anava Faktor Tunggal . . . 139

5.2 Tabel Anava Faktor Ganda . . . 145

(15)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 12 dari 234

(16)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 13 dari 234

Tutup

Bagian I

(17)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 14 dari 234

(18)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 15 dari 234

Tutup

BAB

1

PROGRAM STATISTIKA R

(19)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 16 dari 234

(20)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 17 dari 234

Tutup

Indikator Kompetensi

Setelah menyelesaikan materi pada bab ini pembaca menguasai kemampuan yang ditandai oleh indikator seperti berikut:

❼ memahami R dan kenapa perlu menggunakan R;

❼ dapat menginstal R dengan beberapa pustaka yang diper-lukan;

❼ dapat membuka R dan mengaktifkan pustaka RComman-der;

❼ dapat memanggil fungsi yang diperlukan baik melalui skrip maupun menu;

❼ dapat memangil dokumentasi bantuan untuk fungsi yang diperlukan.

(21)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 18 dari 234

Tutup

(22)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 19 dari 234

Tutup

1.1.

Sekilas Program Statistika R

Program R atau biasa disebut R adalah salah satu paket ana-lisis data dan pemrograman, yang merupakan paket open source yang dapat diperoleh secara cuma-cuma pada situs

http://cran.r-project.org/. Sebenarnya R adalah paket pemrograman yang

(23)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 20 dari 234

Tutup

(24)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 21 dari 234

Tutup

1.2.

RGUI dengan R-Commander

Sebenarnya ada beberapa GUI atau interface yang dapat di-pakai untuk mengaktifkan R melalui menu. GUI untuk pro-gram R biasa disebut RGUI. Salah satu RGUI dikembangkan oleh R-Development Corre Team (RDCT). Dibandingkan de-ngan program-program komersial berbasis Windows, interface RGUI ini memang masih sangat sederhana. Menu yang terse-dia hanya empat kelompok yaitu: File, Edit, Misc, Package dan Help seperti ditunjukkan Gambar 1.1. RGUI standar ini dapat difungsikan dengan beberapa cara yaitu:

1. memberikan perintah-perintah pendek satu-baris (Command line) yang iikuti dengan enter; dengan cara ini perintah pen-dek ini akan langsung ditafsirkan dan dikerjakan R;

2. menulis perintah panjang pada suatu file yang selanjutnya dipanggil melalui pilihan source file.

(25)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 22 dari 234

Tutup

S-Plus. Untuk mengatasi hal ini dapat dilakukan dengan men-ginstall suatu interface RGUI yang lain diantaranya adalah R-Commander. Untuk R versi 2.2. ke atas dan RCommander versi 1.2.7 ke atas, tersedia RCommander dengan menu bahasa Inggris dan menu bahasa Indonesia, yang merupakan kontribusi penulis (Lihat Gambar 1.2 dan Gambar 1.3). Untuk mengak-tifkan menu berbahasa Indonesia, pada properties dari shortcut R di desktop ditulis

"C:\Program Files\R\R-2.2.1\bin\Rgui.exe" LANGUAGE=id

R-Commander adalah salah satu RGUI yang tampilannya sederhana sehingga sangat cocok bagi pemula. Untuk dapat menggunakan RGUI RCommander kita harus menginstal pus-takaRCmdrdengan cara terlebih dahulu mendownloadRCmdr.zip

selanjutnya menginstal pustaka tersebut dalam R. Untuk men-gaktifkannya kita lakukan perintah

(26)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 23 dari 234

Tutup

Gambar 1.1: Tampilan Jendela Pembukaan RGUI untuk Windows.

(27)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 24 dari 234

Tutup

(28)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 25 dari 234

Tutup

1.3.

RCommander dengan Menu Bahasa Indonesia

Rcommander ini pada dasarnya merupakan modifikasi menu RCommander asli. Salah satu tampilan dapat dilihat pada Gam-bar 1.3. Menu RCommander ini terutama diperuntukkan bagi pengguna pemula dari R atau bagi mereka yang tidak mem-punyai cukup dasar dalam pemrograman komputer. Untuk da-pat mengaktifkan menu Bahasa Indonesia, maka yang harus di-lakukan adalah langkah-langkah berikut.

1. Dapatkan skrip menu berbahasa Indonesia dari Lab Sta-tistika Jurusan Matematika FMIPA UNEJ

2. Salin/copy file yang diperoleh pada direktori yang dimak-sud yaitu:

❼ ...\library\Rcmdr\etc, untuk menyimpan menu

❼ ...\library\Rcmdr\docuntuk menyimpan dokumen-tasi dan

(29)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 26 dari 234

Tutup

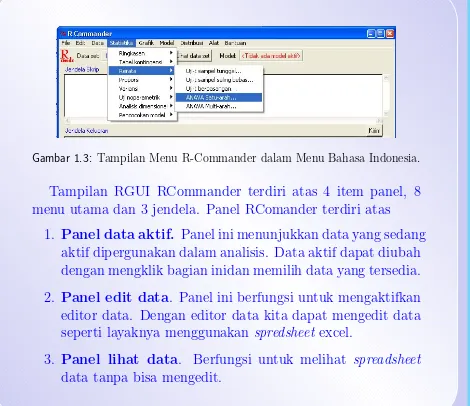
Gambar 1.3: Tampilan Menu R-Commander dalam Menu Bahasa Indonesia.

Tampilan RGUI RCommander terdiri atas 4 item panel, 8 menu utama dan 3 jendela. Panel RComander terdiri atas

1. Panel data aktif. Panel ini menunjukkan data yang sedang aktif dipergunakan dalam analisis. Data aktif dapat diubah dengan mengklik bagian inidan memilih data yang tersedia.

2. Panel edit data. Panel ini berfungsi untuk mengaktifkan editor data. Dengan editor data kita dapat mengedit data seperti layaknya menggunakan spredsheet excel.

(30)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 27 dari 234

Tutup

4. Panel model aktif. Panel ini menunjukkan model yang sedang aktif dipergunakan dalam analisis regresi (model li-nier). Bila kita telah melakukan lebih dari sekali analisis regresi pada data yang sama, kita dapat membandingkan model-model tadi.

(31)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 28 dari 234

Tutup

1.4.

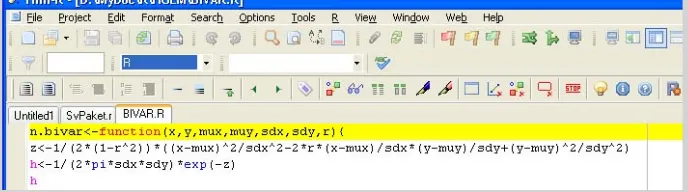
Editor Skrip dengan Tinn-R

(32)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 29 dari 234

Tutup

(33)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 30 dari 234

Tutup

1.5.

Data untuk Ilustrasi

R menyediakan banyak koleksi data sebagai ilustrasi. Data yang ada pada R dapat diperiksa melalui salah satu perintah berikut.

data()

data(package = .packages(all.available = TRUE))

(34)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 31 dari 234

Tutup

1.6.

Bacaan Lebih Lanjut

(35)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 32 dari 234

Tutup

1.7.

Soal-soal Latihan

Diskusikan dalam kelompok terdiri atas 3-4 orang.

1. Tentang prospek pemanfaatan program open source untuk mengatasi maraknya kasus pembajakan program kompu-ter, bagaimana komentar anda terhadap pendapat bahwa Indonesia merupakan salah satu negara yang banyak mela-kukan pembajakan program komputer dan pendapat yang mengatakan bahwa untuk kepentingan pendidikan dan pen-gajaran tidak perlu ragu-ragu melakukan pembajakan.

2. Lakukan eksplorasi R menjalankan beberapa demo yang ada.

3. Lakukan eksplorasi RCommander baik dalam menu Ba-hasa Inggris maupun BaBa-hasa Indonesia dengan mengak-tifkan salah satu data yang ada pada paket R.

(36)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 33 dari 234

Tutup

(37)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 34 dari 234

(38)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 35 dari 234

Tutup

BAB

2

KONSEP DASAR STATISTIKA

(39)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 36 dari 234

Tutup

Indikator Kompetensi

Setelah menyelesaikan materi pada bab ini pembaca menguasai kemampuan yang ditandai oleh indikator seperti berikut:

❼ dapat menjelaskan lingkup statistika deskriptif dan sta-tistika inferensial;

❼ menjelaskan pengaruh ukuran pemusatan dan penyebaran terhadap distribusi data;

(40)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 37 dari 234

Tutup

2.1.

Statistika dan Data Statistik

Untuk memahami prinsip dasar statistika ada baiknya kita mengikuti definisi tentang statistika diantaranya seperti berikut ini.

1. MenurutWebster’s New Collegiate Dictionarystatistika di-definisikan sebagai “cabang matematika yang berkaitan de-ngan pengumpulan, analisis, interpretasi, dan penyajian dari sejumlah data numerik ”.

2. Kendal dan Stuart (1977) mengatakan: “ Statistika ada-lah cabang dari metode ilmiah yang berhubungan dengan pengumpulan data yang dikumpulkan dengan mencacah atau mengukur sifat- sifat dari populasi.”

3. Fasher (1958), mengatakan bahwa “ statistika berhubungan dengan metode untuk menarik kesimpulan dari hasil per-cobaan atau proses.”

(41)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 38 dari 234

Tutup

5. Mood, Graybill dan Boes (1974) mendefinisikan statistika sebagai “teknologi dari metode ilmiah” dan menambahkan bahwa statistika berhubungan dengan :“(1) rancangan per-cobaan dan penyelidikan, (2) penarikan kesimpulan statis-tik.”

6. Mendenhall bk:Mendenhall79 mendefinisikan statistika se-bagai suatu “bidang sains yang berkaitan dengan ekstraksi informasi dari data numerik dan menggunakannya untuk membuat keputusan tentang populasi dari mana data terse-but diperoleh.”

Jadi secara umum dapat dikatakan bahwa statistika adalah su-atu teori informasi, dengan penarikan kesimpulan sebagai tu-juannya.

(42)

de-UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 39 dari 234

Tutup

ngan biaya minimal, dari sejumlah informasi tertentu, dan meng-gunakan informasi ini untuk membuat kesimpulan- kesimpulan. Pembuatan kesimpulan terhadap populasi yang tidak diketahui adalah prosedur yang terdiri atas dua langkah. Pertama, kita menentukan prosedur- prosedur penarikan kesimpulan yang co-cok dari situasi yang dihadapi; dan kedua, kita mencari ukuran kecocokan dari kesimpulan yang dihasilkan.

Jadi informasi merupakan bagian yang sangat penting da-lam menggunakan statistik sebagai alat mengambil keputusan. Demikian juga sebaliknya statistika adalah salah satu alat yang dapat dipergunakan untuk memanfaatkan informasi sebagai ba-han pengambilan keputusan. Selain karena menggunakan in-formasi sebagai landasan pengambilan keputusan, pengambilan keputusan dengan statistika juga memiliki keunggulan lain yaitu statistika juga memberikan ukuran kecocokan atau ukuran kesa-lahan dari kesimpulan yang dibuat (Mendenhall [15]). Informasi yang dijadikan dasar pengambilan keputusan biasa disebut se-bagai data statistik.

(43)

pengambi-UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 40 dari 234

Tutup

lan keputusan dari sejumlah kecil informasi pada sampel, untuk digeneralisasikan pada lingkungan yang lebih luas yaitu populasi. Prosedur ini meliputi, mengorganisir, mer-ingkas, menyajikan data dan menguji dugaan. Karena luas-nya cakupan statistika, maka statistika dibedakan menjadi dua kelompok besar yaitu Statistika Deskriptif yaitu prose-dur yang meliputi mengorganisir, meringkas dan menya-jikan data. Sedangkan prosedur lebihlanjut terkait dengan pengolahan data untuk pendugaan, peramalan atau pen-gujian dugaan disebut Statistika Inferensial.

Populasi pada umumnya diartikan sebagai keseluruhan indi-vidu atau subjek yang menjadi kepentingan dalam suatu studi atau penelitian. Jika penelitian tentang berat dan tinggi badan mahasiswa suatu perguruan tinggi, maka pop-ulasinya adalah seluruh mahasiswa perguruan tinggi terse-but.

(44)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 41 dari 234

Tutup

sampel (dalam jumlah dan dengan prosedur yang memenuhi syarat) untuk dipelajari.

Data adalah informasi dari populasi atau sampel yang menjadi kepentingan studi.

Variabel/Peubah adalah bagian dari data yang merupakan karakteristik populasi dan sampel yang menjadi perhatian atau kepentingan studi (misalnya, jenis kelamin, pendidikan, tinggi badan dan sebagainya)

Parameter adalah nilai atau ukuran yang menggambarkan deskripsi populasi (misalnya rerata, variansi, korelasi dan sebagainya)

(45)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 42 dari 234

Tutup

2.2.

Jenis Data

Data numerik pada umumnya dapat dibedakan menjadi dua kelompok besar yaitu data hasil pencacahan (disebut data enu-merasi) dan data dari hasil pengukuran disebut data metrik. Pengukuran (meassurement) menghasilkan data numerik yang disebut data metrik. Data ini disajikan dalam bentuk angka atau bilangan. Secara umum data ini dapat dikelompokkan kedalam beberapa jenis sekala yaitu nominal, ordinal, interval dan rasio yang dapat dijelaskan seperti berikut ini (Lihat Guil-ford & Fruchter [7] ).

(46)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 43 dari 234

Tutup Ordinal Dalam beberapa hal hasil pengukuran kontinu

dikelom-pokkan menjadi beberapa kategori yang termasuk kategori kuantitatif. Misalnya dalam hasil belajar pembaca bukan perolehan angkanya yang diperhatikan tetapi rankingnya. Demikian juga sesungguhnya perubahan skor ujian pem-baca dari skala seratus ke skala lima (0-4) sesungguhnya menghasilkan skala ordinal yang bisa dilabel E-A. Sesung-guhnya angka-angka ini juga belum bisa dimanipulasi se-cara aritmatik (dalam arti dijumlah, dirata-rata dan sjenis-nya). Skala ordinal belum memiliki unit pengukuran yang sama, yaitu jarak antara 0 ke 1 belum, tentu sama dengan jarak 1 ke 2 dan seterusnya.

(47)

pem-UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 44 dari 234

Tutup

baca yang mendapat skor 0 tidak berarti tidak memiliki pengetahuan sama sekali. Demikian juga suhu 0 derajat tidak berarti suatu benda tidak memiliki panas atau suhu sama sekali.

Rasio Rasio merupakan skala yang paling sempurna. Skala ini telah memiliki 0 mutlak, dapat dibandingkan secara rasio. Contoh misalnya berat suatu benda. bilangan 0 menun-jukkan tidak ada berat. Suatu objek yang berat 10 satuan dapat dikatakan beratnya dua kali berat objek yang berat-nya 5 satuan. Rasio berat objek yang beratberat-nya 75 unit dan 50 unit adalah 3:2 dan seterusnya.

(48)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 45 dari 234

Tutup

yang tidak menunjukkan perbedaan tingkat kualitas satu de-ngan lainnya misalnya: jenis kelamin (Laki-Perempuan), jenis pekerjaan, kebangsaan dan sebagainya. Untuk data kategorik, hasil pencacahan dapat disajikan dalam bentuk frekuensi atau proporsi.

Dalam kenyataannya suatu data sampel dapat terdiri atas beberapa peubah yang masing-masing memiliki skala berbeda, misalnya data mahasiswa dapat terdiri atas: (i) jenis kelamin dan agama yang bersitaf nominal, (ii) nilai matakuliah yang bersifat ordinal, (A-E) atau interval (0-100) (iii) umur, tinggi dan berat badan yang bersifat rasio dan sebagainya.

(49)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 46 dari 234

Tutup

2.3.

Distribusi Data

Sebagaimana disampaikan sebelumnya bahwa statistika terkait dengan prosedur pengambilan keputusan berdasarkan data yang ada. Prosedur dalam statistika diturunkan menggunakan teori peluang dan distribusi serta kaidah-kaidah deduktif yang ber-laku dalam matematika. Penurunan prosedur dalam statistika menggunakan pendekatan deduktif. Sedangkan aplikasi prose-dur dalam pengolahan data untuk mengambil keputusan dapat dianggap sebaga pendekatan induktif (dari kuhusus/sampel ke umum/populasi). Oleh karena itu memiliki gambaran menge-nai distribusi data sangat penting sebelum seseotang melangkah lebih jauh dalam menggunakan statistik untuk pengambilan kepu-tusan. Pembahasan yang lebih rinci dan matematis merupakan bagian dariStatistika Matematikasedangkan dalam Metode Sta-tistika lebih dilihat dari sisi kebutuhan praktis dalam melihat kondisi data.

(50)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 47 dari 234

Tutup

fungsi distribusi ini dengan sumbu X dan batas atas dan bawah-nya meliputi daerah dengan luas 1, yaitu memiliki probabilitas 100%. Jenis distribusi data dapat dikelompokkan dalam bebe-rapa jenis dan dalam diktat ini hanya dibahas jenis distribusi yang banyak dipakai atau dijumpai di lapangan.

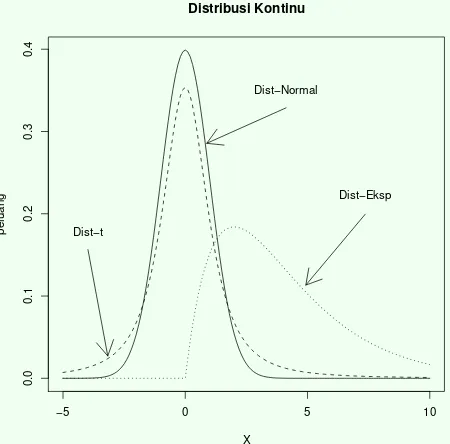
1. Distribusi Kontinu. Distribusi ini adalah untuk data yang bersifat kontinu, yang biasaya merupakan hasil pen-gukuran (tinggi badan, berat badan, tonnase produksi sawah perhektar dan sebagainya). Dilihat dari sekala pengukuran, distribusi kontinu cocok diasumsikan untuk data dengan skala interval atau rasio. Ada beberapa distribusi kontinu yang penting diantaranya adalah:

(a) Distribusi Normal. Selain bersifat kontinu, distribusi ini memiliki ciri-ciri penting diantaranya: (i) rentang data terbuka secara infinit ke kiri dan ke kanan Rx =

(_−∞,_∞), (ii) bersifat simetris dan unimodal (memiliki maksimum tunggal)

(51)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 48 dari 234

Tutup

tinggi dan lebarnya kurva. Dalam kondisi tertentu dis-tribusi t dapat berimpit dengan distribusi Normal. (c) Distribusi Eksponensial. Distribui ini meliputi

bebe-rapa jenis termasuk eksponensial, Chi-kuadrat, dan Gamma. Distribusi-distribusi ini mempunyai sifat rentang data nonnegatif 0 _≤x dan umumnya bersifat tidak simetris. (d) Distribusi F. Distribusi ini juga memiliki sifat hampir sama dengan distribusitdalam hal rentang dan bentuk kurva.

2. Distribusi Diskrit. Distribusi ini adalah untuk data diskrit yang biasanya merupakan hasil pencacahan. Ada bebe-rapa distribusi penting yang banyak dipakai untuk jenis distribusi diskrit ini, diantaranya adalah:

(a) Distribusi Binomial dan Multinomial. Distribusi ini se-suai untuk data yang bersifat nominal dengan rentang terbatas, misalnya laki-perempuan, kaya-menengah-miskin, dan sejenisnya.

(52)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 49 dari 234

Tutup

(53)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 50 dari 234

Tutup

2.4.

Ukuran Pemusatan dan Penyebaran

Secara umum karakteristik distribusi ditentukan oleh dua hal penting yaitu ukuran pemusatan tendensi sentral dan ukuran penyebaran dispersi. Ukuran pemusatan ditentukan oleh bebe-rapa ukuran diantaranya adalah: Mean atau rerata atau rata-rata, Median, Kuantil dan Modus. Sedangkan dispersi diten-tukan oleh beberapa ukuran diantaranya adalah: Range (rentang), deviasi baku, variansi.

2.4.1. Ukuran Pemusatan

Ada beberapa ukuran emusatan yang biasa dipakai diantaranya adalah seperti berikut ini.

Mean atau Rerata. Mean atau Rerata biasanya dinotasian dengan µX atau µY adalah istilah yang dipergunakan

un-tuk parameter populasi, sedangkan unun-tuk statistik sampel biasa disebut rata-rata sampel dan dinotasikan dengan ¯X

(54)

de-UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 51 dari 234

Tutup

ngan menggunakan rumus

¯

X = 1

N

X

xi

Median. Median adalah nilai yang membagi frekuansi data men-jadi dua bagian yaitu 50% bagian bawah dan 50% bagian atas. Untuk distribusi yang bersifat simetris (Normal dan

t), nilai mean dan median berimpit. Secara manual cara menghitung median adalah sebagai berikut:

1. urut data dari rendah ke tinggi

2. Jika banyaknya data ganjil, tentukan nilai data yang menempati urutan di tengah-tengah. Misalnya jika

N = 11 setelah diurut, median adalah nilai yang men-empati urutan ke 6.

3. jika banyaknya data genap, median dihitung dari rata-rata dua nilai yang dekat di tengah. Misalnya untuk

(55)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 52 dari 234

Tutup Kuantil. Kuantil adalah nilai yang membagi frekuansi data

menjadi empat bagian yaitu

Kuantil 1 adalah nnilai yang membatasi 25% bagian bawah dan 75% bagian atas.

Kuantil 2 = Median adalah nilai yang membatasi 50% bagian bawah dan 50% bagian atas.

Kuantil 2 = Median adalah nilai yang membatasi 75% bagian bawah dan 25% bagian atas.

Prinsip menghitung kuantil secara manual sama dengan cara menghitung median.

(56)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 53 dari 234

Tutup

2.4.2. Ukuran Penyebaran

Ada beberapa karakteristik yang biasa dijadikan ukuran penye-baran diantaranya adalah sepertri berikut ini.

Range. Range adalah selisih antara nilai tertinggidengan nilai terendah

RX = max(X)−min(X)

Variansi dan Deviasi Baku. Deviasi baku menunjukkan lebar sebaran suatu data, variansi merupakan kuadrat dari de-viasi baku. Notasi untuk variansi populasi adalah σ2 se-dangkan untuk variansi sampel dinotasikan denganS2.Jadi harus dicatat bahwa deviasi baku dan variansi adalah uku-ran yang bersifat nonnegatif

S_X2 =

N

X

i=1

xi −X¯

2

N ₋1

(57)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 54 dari 234

Tutup

peubah yang satu menaik atau menurun. Derajat asosiasi populasi dinotasikan dengan ρ dan derajat asosiasi sampel dinotasikan dengan r. Dapat dibuktikan (dalam statistika matematika) bahwa ₋1_≤ r _≤ 1.

rXY =

hPN

i=1 xi−X¯

i hPN

i=1 yi −Y¯

i s

(xi−X¯) 2

N−1

(xi−X¯) 2

N−1

(58)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 55 dari 234

Tutup

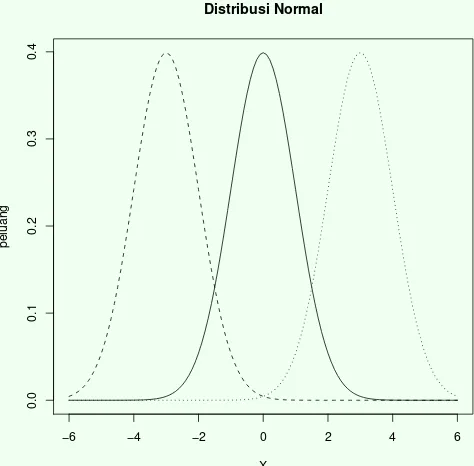
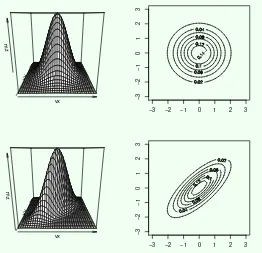
menggambarkan pengaruh korelasi terhadap sebaran dua peu-bah dilihat dari bentuk perspektif dan konturnya.

−6 −4 −2 0 2 4 6

0.0

0.1

0.2

0.3

0.4

Distribusi Normal

X

peluang

(59)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 56 dari 234

Tutup

−5 0 5

0.0

0.1

0.2

0.3

0.4

Distribusi Normal

X

peluang

(60)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 57 dari 234

Tutup

−5 0 5 10

0.0

0.1

0.2

0.3

0.4

Distribusi Kontinu

X

peluang Dist−t

Dist−Normal

Dist−Eksp

(61)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 58 dari 234

Tutup

vx

vy

mz

−3 −2 −1 0 1 2 3

−3

−2

−1

0

1

2

3

vx

vy

mz

−3 −2 −1 0 1 2 3

−3

−2

−1

0

1

2

3

Gambar 2.4: Perspektif dan Kontur Dua Peubah dengan r = 0 (atas) dan

(62)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 59 dari 234

Tutup

2.5.

Bacaan Lebih Lanjut

Ada cukup banyak referensi yang dapat dibaca untuk lebih mema-hami materi pada bab ini. Beberapa referensi dalam Bahasa Indonesia diantaranya Hadi bk:Hadi82, Sudjana bk:Sudjana96. Dalam Bahasa Inggris beberapa referensi yang direokemdasikan

(63)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 60 dari 234

Tutup

2.6.

Soal-soal Latihan

Diskusikan soal-soal berikut secara berkelompok (3-4 orang).

1. diketahui 11 data berikut. Tentukan, minimum, maksi-mum, rentang, rata-rata, median, kuantil ke-1 dan kuantil ke-3

56.11208 51.79550 48.14551 50.78253 46.47393 59.46114 47.52536 51.04185 49.66142 51.25023 45.84077

2. Seseorang ingin memiliki data tentang mahasiswa suatu perguruan tinggi yang meliputi (i) penghasilan orang tua, (ii) asal provinsi, (iii) jumlah saudara kandung dalam kelu-arga, (iv) nilai UAN. Tentukan jenis distribusi yang mung-kin diberlakukan untuk masing-masing peubah tadi.

(64)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 61 dari 234

Tutup

(65)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 62 dari 234

(66)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 63 dari 234

Tutup

BAB

3

EXPLORASI DATA

(67)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 64 dari 234

Tutup

tidak diilustrasikan dengan tampilan menu aslinya, tetapi diilus-trasikan dengan => yang menyatakan pemilihan menu, submenu atau item dari menu (Diagram pohon menu RCommander yang lebih lengkap dapat dilihat pada Lampiran ??).

(68)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 65 dari 234

Tutup

Indikator Kompetensi

Pembaca , dengan menggunakan pendekaran GUI atau CLI, da-pat:

1. menyusun data dalam worksheet R

2. mengimpor data dari format program lain

3. membangkitkan data melalui simulai

4. melalkukan eksplorasi data secara grafis sesuai kebutuhan (melalui boxplot, diagram pencar, diagram rata-rata dan sebagainya)

(69)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 66 dari 234

Tutup

3.1.

Menyiapkan Data pada R

Sebelum melakukan analisis statistika, data yang akan dianal-isis harus sudah siap terlebih dahulu. Dilihat dari sumbernya data dibedakan atas dua jenis yaitu data riil dan data simu-lasi. Data riil diperoleh dari hasil penelitian dengan mengikuti prosedur yang telah ditetapkan. Data simulasi diperoleh de-ngan membangkitkannya dede-ngan menggunakan komputer. Data bangkitan atau data simulasi sangat baik dipergunakan untuk mempelajari atau memahami prosedur statistika, karena be-sarnya parameter dan jenis distribusinya dapat dikendalikan. Data yang akan dianalisis dapat terlebih dahulu disimpan/ dit-ulis dengan program lain dalam berbagai format (misalnya file tex, file SPSS, Minitab), atau langsung dituliskan dalam work-sheet/datasheet dari R. Disamping itu R juga dilengkapi dengan database yang dapat dipanggil untuk dianalisis.

(70)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 67 dari 234

Tutup

(misalnya jumlah penghasilan masyarakat perbulan), sedangkan data kualitatif biasanya diperoleh dari hasil mencacah (misalnya jumlah masyarakat yang termasuk kategori miskin di desa atau di perkotaan).

3.1.1. Mengedit langsung data

Untuk memasukkan data langsung melalui datasheet dilakukan perintah berikut:

NamaDataSheet<-edit(as.data.frame(NULL))

selanjutnya worksheet dapat diisi sesuai banyaknya data dan banyaknya peubah. Dengan menu R-Commander, editing, mau-pun penulisan data dapat dilakukan dengan memilih menu ber-ikut.

Data => data set baru ...

(71)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 68 dari 234

Tutup

Tabel 3.1: Penulisan Data pada R No Subjek Faktor Peubah1 Peubah2

1 K1 x11 y11

2 K1 x12 y12

... ... ... ...

n1 K1 x1n1 y1n1 ... ... .... ...

N Kk xknk yknk

3.1.2. Memanggil Data dari Database R

Data riil yang telah ada pada R dapat dipanggil dengan perintah

data()

(72)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 69 dari 234

Tutup

Data Deskripsi

...

AirPassengers Monthly Airline Passenger Numbers 1949-1960 BJsales Sales Data with Leading Indicator

BOD Biochemical Oxygen Demand

CO2 Carbon Dioxide uptake in grass plants ChickWeight Weight versus age of chicks on different diets

DNase Elisa assay of DNase

EuStockMarkets Daily Closing Prices of Major European Stock Indices, 1991-1998

Harman23.cor Harman Example 2.3 Harman74.cor Harman Example 7.4

Indometh Pharmacokinetics of Indomethicin

JohnsonJohnson Quarterly Earnings per Johnson & Johnson Share

LakeHuron Level of Lake Huron 1875-1972

(73)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 70 dari 234

Tutup

Nile Flow of the River Nile Orange Growth of orange trees ...

Selanjutnya jika kita ingin memanggil salah satu data yang ada, maka yang perlu dilakukan adalah mengkatifkan pustaka dan datanya,, secara berturutan.

library(NamaLibrary) data(Namadata)

attach(Namadata)

Dengan menggunakan R-Commander pemilihan data dapat dilakukan dengan

Data => Data Pada Paket => Baca data set dari paket aktif ...

Selanjutnya tinggal pilih nama paket dan datanya.

(74)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 71 dari 234

Tutup Data => Data pada Paket => Baca data pada peket aktif

=> paket stats

=> data ChickWeight

Sedangkan dengan CLI dapat dilakukan

library(stats) data(ChickWeight)

atau dengan lebih singkat

data(ChickWeight, package="stats") attach(ChickWeight)

Untuk selanjutnya data ChickWeight dapat dieksplorasi ma-upun dianalisis.

3.1.3. Mengimpor data dari file

(75)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 72 dari 234

Tutup

Gambar 3.1: Menu Dialog Membaca Data

data tersebut maka kita perlu melakukan langkah-langkah ber-ikut.

1. Buka data dengan program aslinya (Minitab, Excell) lalu simpan/eksport data dalam bentukplain/ascii texbiasanya dengan ekstensi txt. Selanjutnya dibuka dengan perintah read.table

read.table(Namafile, header = FALSE, sep = "", quote = "\"✬", dec= ".",...)

(76)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 73 dari 234

Tutup

kolom. Untuk tanda desimal, bisa dipergunakan titik atau koma sesuai kondisi data yang dimiliki.

2. Bagi yang menggunakan R-Commander dapat melakukan-nya dengan menggunakan menu Data dengan memilih sub-menu . Pilihan jenis data tersedia diantaranya dari Minitab SPSS dan dalam bentuk teks.

3. Dengan menggunakan R-Commander pemilihan data dapat dilakukan dengan

=> Impor Data => Dari file tex/SPSS/Minitab

selanjutnya ikuti pemilihan direktori dan file yang diinginkan.

3.1.4. Membangkitkan Data Simulasi

(77)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 74 dari 234

Tutup

parameter (mean, varians, korelasi) sesuai dengan yang dibu-tuhkan yang nantinya dapat dicocokkan kembali dengan hasil analisis yang diperoleh. Perintah untuk membangkitkan data dari berbagai distribusi dapat dilihat pada Tabel 3.2sedang daf-tar yang lebih lengkap dapat dilihat pada Tirta bk:TirtaR1.

Tabel 3.2: Perintah Untuk Data Acak No Distribusi Perintah R

1 Normal rnorm(n.sampel,mean,sd)

2 Eksponensial rexp(n.sampel, 1/mean)

2 Poisson rpois(n.sampel,mean)

3 Binomial rbinom(n.sampel,n.binom,prob)

Simulasi data tidak bisa dilakukan melalui menu R-Commader, tetapi data yang sudah masuk data.frame dapat dianalisis melalui menu R-Commander.

Contoh 3.1.

(78)

ber-UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 75 dari 234

Tutup

ikut untuk membangkitkan data yang dapat dipergunakan se-bagai ilustrasi berikutnya.

Faktor1<-rep(rep(c("A","B","C","D"),each=20),4) Faktor2<-rep(rep(c("L","P"),each=10),4)

Y1<-as.numeric(rnorm(80,c(85,80,80,75,90,70,60,55),5)) Y2<-as.numeric(rnorm(80,c(80,85,80,85,85,80,60,75),3)) Y3<-Y1-rnorm(80,10,2)

Y4<-(Y1+Y2)/2-rnorm(80,5,3)

(79)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 76 dari 234

Tutup

3.2.

Explorasi Data

Eksplorasi data mendasar dapat dilakukan melalui R-Commander pada menu statistik (untuk eksplorasi statistik) atau menu gra-fik (untuk eksplorasi grafis). Untuk dapat menggunakan menu R-Commander, terlebih dahulu data harus diaktifkan dengan memilih kotak data aktif atau melalui menu data. Untuk eks-plorasi ikuti petunjuk berikut

Statsistik => Ringkasan => Dataset Aktif => Ringkasan numerik Grafik => Boxplot

=> Diagram Rata-rata

(80)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 77 dari 234

Tutup

standar R tanpa perlu memanggil pustaka khusus. Uraian lebih lengkap dari eksplorasi data ini diberikan pada sub berikutnya.

3.2.1. Deskripsi Data

Untuk data yang bersifat kuantitatif, ada beberapa hal yang dapat diukur yang menjadi karakteristik dari kelompok data bersangkutan. Ukuran data dibedakan menjadi dua macam yaitu ukuran pemusatan (rata-rata, median dan kuantil) dan ukuran penyebaran (rentang dan deviasi baku). Untuk data kuantitatif R-Commander dapat membuat deskripsi data yang meliputi min, max, mean dan median data dapat dieksplorasi dengan perintah summary(data). Cetakan lengkap data dapat diperoleh melalui perintah print(data). Data berikut diambil dari pustaka stats, data ChickWeight yang dapat dilakukan baik melalui menu maupun CLI.

summary(ChickWeight)

weight Time Chick Diet

(81)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 78 dari 234

Tutup 1st Qu.: 63.0 1st Qu.: 4.00 9 : 12 2:120

Median :103.0 Median :10.00 20 : 12 3:120 Mean :121.8 Mean :10.72 10 : 12 4:118 3rd Qu.:163.8 3rd Qu.:16.00 17 : 12

Max. :373.0 Max. :21.00 19 : 12 (Other):506

Sedangkan cetakan lengkap datanya adalah

>print(ChickWeight)

weight Time Chick Diet

1 42 0 1 1

2 51 2 1 1

3 59 4 1 1

4 64 6 1 1

5 76 8 1 1

6 93 10 1 1

(82)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 79 dari 234

Tutup

576 234 18 50 4

577 264 20 50 4

578 264 21 50 4

Untuk data simulasi di atas (Data.sim) diperoleh ringkasan yang bisa dipanggil langsung melalui CLI ataupun melalui menu R-Commander

> summary(Data.sim)

Faktor1 Faktor2 Y1 Y2 Y3

A:80 L:160 Min. :43.72 Min. :56.23 Min. :32.05 B:80 P:160 1st Qu.:63.93 1st Qu.:76.58 1st Qu.:52.64 C:80 Median :75.78 Median :81.09 Median :66.35 D:80 Mean :73.80 Mean :78.81 Mean :63.55 3rd Qu.:83.11 3rd Qu.:84.69 3rd Qu.:73.58 Max. :96.75 Max. :90.26 Max. :86.65

(83)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 80 dari 234

Tutup

3.2.2. Visualisasi Data Univariat

Paket Statistika R dilengkapi dengan kemampuan membuat dan menyajikan grafik yang sangat baik. Bahkan, kemampuan gra-fik S (yaitu Splus dan R) diakui melebihi paket statistika lain-nya Sebagian besar kemampuan grafik R (baik untuk univariat maupun multivariat) sudah dapat dimanfaatkan melalui menu RCommander . Beberapa jenis grafik untuk eksplorasi dan vi-sualisasi data univariate diataranya seperti berikut ini.

Histogram dan kurva distribusi untuk menggambarkan se-baran data dan frekuensi atau peluangnya. Dengan his-togram dan kurva distribusi seseorang dapat melihat apakah data yang dimiliki sebarannya cukup simetris, Unimodal atau Multimodal

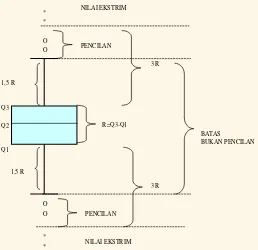
Boxplot untuk menggambarkan posisi data dilihat dari quantil-nya (Q1, median, Q3). Dengan boxplot dapat juga dilihat apakah ada data yang tergolong sebagai pencilan;

(84)

dis-UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 81 dari 234

Tutup

tribusi teoritisnya. Hubungan yang mengikuti garis lurus menunjukkan kesesuaian antara quantil data dengan quan-til distribusi teoritisnya. Dengan kata lain data berdis-tribusi sama dengan disberdis-tribusi teoritis yang diperiksa. Un-tuk distribusi normal grafiknya isebut QQ-norm.

Diagram rata-rata untuk menggambarkan rata-rata dengan interval keyakinannya.

Diagram lingkaran untuk menggambarkan prosentase sebaran data dilihat dari salah satu pengelompokan yang ada pada data.

ACF untuk mmeriksa ada tidaknya autokorelasi pada data.

(85)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 82 dari 234

Tutup

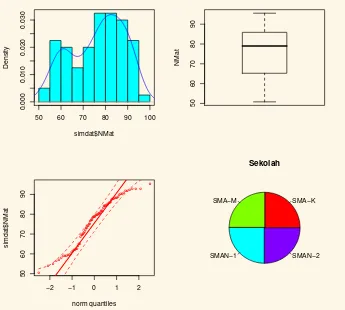
histogram, qqnorm, dan diagram densitas. Data normal akan memiliki densitas yang relatif simetrik dan diagram qq yang relatif mengikuti garis lurus. Untuk data yang tidak berdis-tribuai normal diantaranya ditunjukkan oleh ketidaksimetrisan yang mencolok serta diagram qq yang tidak mengikuti garis lu-rus.

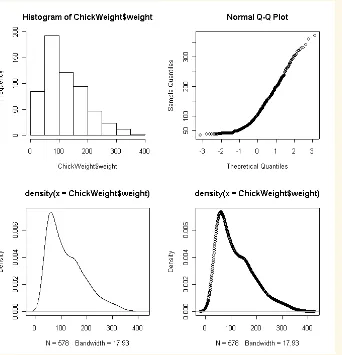
Contoh 3.2. Untuk contoh riil, misalkan dari data “Chicken Weight” kita ingin memeriksa distribusi beratnya ayam. Grafik histogram, qqnorm dan densitas dari data tersebut dapat dili-hat pada Gambar 3.4. Gambar menunjukkan bahwa data berat tidak cukup simetris untuk memenuhi asumsi distribusi normal.

par(mfrow=c(2,2))

hist(ChickWeight$weight) qqnorm(ChickWeight$weight)

(86)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 83 dari 234

Tutup

Jika menggunakan menu R-Commander, kita juga dapat memilih apakah ploting yang dilakukan memperhatikan adanya kelom-pok atau tidak. Perhatian terhadap kelomkelom-pok bermanfaat se-bagai gambaran kasar apakah kira-kira ada beda yang mencolok dari distribusi peubah yang kita amati dilihat dari kelompok-kelompok yang ada (misalnya Jender, Status sosial dan lain se-bagainya). Untuk mengilustrasikan hal ini kita dapat mengam-bil suatu data yang juga ada pada pustaka stats, yaitu data “Or-ange”, baik melalui CLI maupun R-Commander. Data Orange terdiri atas dua peubah yaitu: Age (usia pohon) dan Circum-ference (keliling batang) dan satu faktor/ kelompok yaitu: Tree (Jenis pohon). Untuk memperoleh grafik (misalnya tentang Cir-cumference) yang memperhatikan kelompok (Tree) Pada saat pembentukan grafik boxplot pilih

(87)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 84 dari 234

Tutup

3.2.3. Visualisasi Data Multivariat

Selain gambaran distribusinya, kita juga memerlukan gambaran data dilihat dari hubungan antara peubah satu dengan lainnya, atau sebaran kelompok satu dengan lainnya. Diagram yangbi-asa dipakai untuk menggambarkan kondisi ini adalah diagram pencar (untuk dua peubah), diagram pencar tiga dimensi (un-tuk tiga peubah) dan matriks diagram pancar maupun coplot (untuk lebih dari tiga peubah). Berikut adalah contoh berba-gai variasi diagram pencar, termasuk yang datanya mengandung vpeubah kualitatif. Selain itu R juga dilengkapi dengan paket RGL yang mampu menyajikan animasi dari grafik tiga dimensi. Untuk data multivariat, misalnya data yang terdiri dari tiga peubah acak (X, Y, Z), masing-masing terdiri atas tiga subpop-ulasi (P1, P2, P3). Sebelum melakukan analisis lebih jauh ada

beberapa pertanyaan mendasar yang dapat dieksplorasi melalui grafik, diantaranya:

1. adakah hubungan (korelasi) antara ketiga peubah?

(88)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 85 dari 234

Tutup

Gambaran informasi data seperti di atas dapat diakses melalui grafik trellis _{yaitu dengan perintah} _xyplot()_, _coplot() _atau denganpairs(). Untuk memahami penggunaan coplot dan pair kita ambil data yang merupakan data simulasi nilai ujian dari beberapa sekolah. Dari Gambar 3.7 dan Gambar 3.2.3 terli-hat bahwa kelima jenis pohon memiliki hubungan yang relatif berbeda antara ukuran lingkaran jeruk dengan usianya. Dalam konteks regresi, beberapa subkelompok data memiliki garis re-gresi yang berbeda.

Dengan R-Commander fasilitas di atas dapat diakses dengan memilih menu berikut:

(89)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 86 dari 234

Tutup Keluar

Tabel 3.3: Tabel Fungsi Eksplorasi Data Fungsi Pustaka Data Deskripsi Deskriptif

print() RPackages uni/multivariatmencetak data secara

keselu-ruhan

summary() univariat memperoleh ringkasan data

Grafik

hist() mencetak histogram data

stem() graphics stem & leaf plot (mode teks)

density() menggambar sebaran data

qqnorm() memeriksa normalitas data

dengan diagram quan-til(QQPlot)

qqline() menambah garis lurus pada

diagram qq(QQPlot)]

boxplot() menggambar quantil data

[Boxplot]

dotchart() RPackages multivariat histogram berganda

coplot() grahics menggambar sebaran data

de-ngan kondisi peubah tertentu

xyplot() lattice menggambar sebaran

pa-sangan data

pair() graphics menggambar pasangan

se-baran data

plot() RPackages mengambar sebaran data

de-ngan 2 peubah

biplot() stats multivariat biplot multivariat data

hclust() analisis klaster bertingkat

(90)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 87 dari 234

Cari Halaman Kembali Layar Penuh Tutup simdat$NMat Density

50 60 70 80 90 100

0.000 0.010 0.020 0.030 50 60 70 80 90 NMat ● ● ●●● ●●●●●●● ●●●●●● ●●● ●●●●● ●●● ●●●●● ●●●●●●●●● ●●●●●●●●●● ●●●●●●●●●●●●●● ●●●●●● ●●●●● ● ●

−2 −1 0 1 2

50 60 70 80 90 norm quantiles simdat$NMat SMA−K SMA−M SMAN−1 SMAN−2 Sekolah

(91)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 88 dari 234

Tutup

NILAI EKSTRIM *

Q3

Q2 R=Q3-Q1

O O O O *

PENCILAN

3 R

3 R 1,5 R

BATAS BUKAN PENCILAN Q1

1,5 R

*

NILAI EKSTRIM *

(92)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 89 dari 234

Tutup Keluar

(93)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 90 dari 234

Tutup Keluar

3 1 5 2 4

50

100

150

200

Tree

circumference

(94)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 91 dari 234

Tutup

50 60 70 80 90

50 60 70 80 90 NMat NFis ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●

50 60 70 80 90

50 60 70 80 90 NMat NFis ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●SMA−K SMA−M SMAN−1 SMAN−2

(95)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 92 dari 234

Cari Halaman Kembali Layar Penuh Tutup | | | | | | | || || | | |||| ||||| ||| ||||| | ||||| || |||||| ||||||||||| || ||||||| | ||||||||| |||||| NFis

60 70 80 90 100

● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 50 60 70 80 90 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●● ● ● ● ● ● ● ● ● ● ● ● ● ● 60 70 80 90 100 ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● | || ||| | ||| || | | | | | || ||| | || ||| | | |||| || || |||| | || ||||||||||||||||| ||| | ||||||| || ||||| NIng ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●

50 60 70 80 90

● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●

50 60 70 80 90

50 60 70 80 90 | ||| ||| | || || | | | | | || | || | | || || || | ||||||| |||||| ||||||||||| || ||||||| ||||||||| ||||||| NMat

(96)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 93 dari 234

Tutup

(97)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 94 dari 234

Tutup

(98)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 95 dari 234

Cari Halaman Kembali Layar Penuh Tutup Keluar ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 50 60 70 80 90 ● ● ● ● ● ●● ● ● ● ● ● ● ● ● ● ● ● ● ●

50 60 70 80 90

● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ●

50 60 70 80 90

● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● ● 50 60 70 80 90 NMat NFis SMA−K SMA−M SMAN−1 SMAN−2

Given : Sekolah

(99)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 96 dari 234

Tutup

3.3.

Bacaan Lebih Lanjut

(100)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 97 dari 234

Tutup

3.4.

Soal-soal Latihan

Diskusikan soal-soal berikut dalam kelompok 2-3 orang.

1. Aktifkan salah satu data pada R, misalnya Orange, CO2, Prestige dan lain lainnya. Selanjutnya lakukan eksplorasi sebagai berikut:

(a) buat ringkasan numerik dari data (b) buat grafik histogram data

(c) buat grafik boxplot dengan atau tanpa mempertim-bangkan kelompok yang ada

(d) buat grafik plot rerata (mean plot) (e) buat grafik qq

(f) buat matrksdiagram pencar

(101)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 98 dari 234

(102)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 99 dari 234

Tutup

BAB

4

UJI RATA-RATA DAN PROPORSI

(103)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 100 dari 234

Tutup

Indikator Kompetensi

Pembaca dapat menggunakan R untuk mengiluskrasikan kon-sep interval keyakinan, menghitungnya, serta melakukann uji hipotesis tentang mean dan proporsi yang ditandai dengan ke-mampuan

1. mengilustrasikan konsep interval keyakinan

2. menghitung interval keyakinan

3. melakukan uji rata-rata untuk berbagai jenis sampel

(104)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 101 dari 234

Tutup

4.1.

Interval Keyakinan dan Uji Rata-rata

4.1.1. Hasi-hasil Statistika

Berikut adalah hasil-hasil dalam statistika matematika yang men-dasari analisis statistika. Hasil-hasil ini dapat dijumpai pada buku-buku teks tentang statistika matematika, seperti pada Wack-erlyWackerly Wackerly et al.bk:WMS96, Meyer[16, Bab 13], dan Hogg dan Craig bk:HoggCraig95

Definisi 4.1 (Populasi). Populasi adalah Himpunan Semesta dari peubah yang menjadi perhatian peneliti

(105)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 102 dari 234

Tutup Definisi 4.2 (Sampel). Sampel adalah sebagian dari himpunan

semesta yang benar-benar diobservasi, mewakili keseluruhan ob-jek yang menjadi perhatian.

Dalam hal nilai suatu mata kuliah, jika ada 200 peserta mata kuliah tersebut, maka populasinya adalah 200 nlai mata ku-liah. Jika dari 200 nilai tersebut diambil 50 untuk diteliti, maka kumpulan 50 nilai yang mewakili tersebut disebut sampel.

Sampel harus representatif, benar-benar mewakili populasi sehingga sering disebut sebagai miniatur dari populasi. Un-tuk dapat mengaplikasikan tehnik-tehnik statistika dalam sam-pel, maka sampel harus diambil dengan memperhatikan teknik sampling, salah satu diantaranya yang menjadi syarat penting adalah pengambilan secara acak/random. Syarat lain sangat bergantung apakah dalam populasi ada strata, klaster atau pe-ngelompokan yang perlu mendapat perhatian.

Hasil 4.1(Sifat Reproduktif Distribusi Normal).Jika X1, X2,· · · ,

(106)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 103 dari 234

Tutup

saling independen (secara berpasangan (Xi_||Xj, i 6= j), maka:

Y =

n

X

i=1

aiXi ∼ N n

X

i=1

aiµi, n

X

i=1

a2_iσ_i2

!

Definisi 4.3 (Sampel Acak). Jika Xi, i = 1,· · · , n berasal

dari distribusi normal N(µ, σ2) yang diambil secara saling be-bas, maka dikatakan Xi merupakan sampel acak dari N(µ, σ2).

Syarat utama sampel acak ini adalah berdistribusi sama dan saling independen sehingga sering dinotasikan dengan Xi i.i.d.

N(µ, σ2).

Definisi 4.4 (Statistik Sampel). Statistik adalah fungsi yang diperoleh dari sampel. Dua statistik yang sangat terkenal dan banyak dipakai adalah Rata-rata sampel (X¯) dan Varians sampel (S2₎

¯

X = 1

n

N

X

i=1

Xi dan S2 =

Pn

i=1 Xi −X¯

2

n₋1

(107)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 104 dari 234

Tutup Hasil 4.2 (Distribusi Mean Sampel, jika σ diketahui). Jika

Xi, i= 1,· · · , n adalah sampel acak dari N(µ, σ2), dan σ

dike-tahui maka X¯ _∼ N(µ, σ2/√n).

Hasil 4.3. Jika sampel diambil dari populasi berdistribusi

nor-mal maka

n₋1

σ2

S2 _∼χ2_n₋₁

Hasil 4.4. Jika Z _∼N(0,1) dan V _∼χ2

k, maka

t = pZ

V /k ∼ tk

Hasil di atas diperoleh dari sifat reproduktif dari distribusi normal dengan ai = 1/n. Dikatakan bahwa ¯X merupakan

pen-duga titik dari mean µ. Jika σ2 tidak diketahui maka σ2 diganti dengan σb2 ₌ _S2_. _{Distribusi yang dihasilkan menjadi seperti}

ber-ikut ini.

Hasil 4.5 (Distribusi Mean Sampel σ tak diketahui). Jika

Xi, i= 1,· · · , n adalah sampel acak dari N(µ, σ2), dan σ tidak

(108)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 105 dari 234

Tutup

1. jika n relatif kecil (n < 60) maka _S/X¯−√µ

n ∼ tn−1.

2. jika n relatif besar (n _≥ 60) maka tn−1 ≈ N(0,1) dengan

kata lain _S/X¯−√µ_n _∼ _N₍₀_,_1).

Besaran S/√n disebut standar kesalahan rata-rata, yaitu

S_X¯ = √S

n

Pemahaman terhadap distribusi statistik (khususnya rata-rata sampel) dapat diilustrasikan melalui simulasi. Misalkan sampel berukuran n = 25 diambil secara acak dari populasi berdistribusi N(50,9). Dari sampel yang diambil dihitung rata-rata sampel ¯x. Jika pengambilan sampel diulang sampai 60 kali dan semua rata-rata dicatat, maka kita dapat membuat his-togram atau diagram densitas dari kumpulan rata-rata tadi. Secara teoritis sampling ini akan menghasilkan kesalahan baku atau deviasi baku semua rata-rata sebesar σ/√25 = 0.6

(109)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 106 dari 234

Tutup

sigma<-3

vr<-seq(0,0,length=m) for(i in 1:m){

x<-rnorm(n,mu,sigma) vr(i)<-mean(x)

}

print(mean(vr)) # mencetak rata-rata dari semua rata-rata print(sqrt(vr)) # mencetak deviasi baku dari semua rata-rata summary(vr)

Salah satu eksekusi skrip di atas menghasilkan keluaran berikut dengan grafik (histogram, boxplot, densitas dan diagram quantil) seperti pada Gambar 4.1

> print(mean(vr)) # mencetak rata-rata dari semua rata-rata [1] 50.04896

> print(sqrt(var(vr))) # mencetak deviasi baku dari semua rata-rata [1] 0.5951607

> summary(vr)

Min. 1st Qu. Median Mean 3rd Qu. Max. 48.64 49.64 50.04 50.05 50.50 51.53

Selanjutnya dari distribusi statistik (dalam hal ini rata-rata sampel) dapat dihitung peluang mean populasi berada pada suatu interval tertentu. Jikaσ dike-tahui, maka

P

−1,96_≤ X¯ −µ

σ/√n ≤1,96

(110)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 107 dari 234

Tutup

dengan cara yang sama

P

−2,58_≤ X¯ −µ

σ/√n ≤2,58

= 0,99

atau secara umum

P

−z_α/₂ _≤ X¯−µ

σ/√n ≤zα/2

= (1₋α) (4.1)

Demikian juga meski σ tidak diketahui, tetapi ukuran sampel dapat dianggap cukup besar (n_{→ ∞}) makatn−1 ≈Z dan

¯

X₋µ

S/√n ≈N(0,1). Untuk sampel yang

relatif kecil dan σ tidak diketahui maka:

P

−t_α/₂_,n−₁ ≤

¯

X₋µ

S/√n ≤tα/2,n−1

= (1₋α) (4.2)

Dalam bentuk yang lain (disebut metode Pivot) dan mengganti notasi S/√n de-ngan S_X¯ diperoleh hasil yang disebut Interval/Selang Keyakinan seperti berikut

ini.

Hasil 4.6 (Interval Keyakinan sampel besar). Dari suatu sampel yang berasal dari distribusi normal dengan statistik sampel, masing-masing rata-rata X¯ dan varians sampel S2, jika sampel dianggap cukup besar, maka interval keyakinan

(1₋α)_×100%)untuk penduga mean populasi (µ) adalah

¯

X₋z_α/₂S_X¯ ≤µ≤X¯ +zα/2S_X¯ (4.3)

(111)

UNEJ Daftar Isi

Judul

◭◭ ◭ ◮ ◮◮

Hal. 108 dari 234

Tutup

Hasil 4.7 (Interval Keyakinan sampel kecil). Dari suatu sampel, berukuran n,

yang berasal dari distribusi normal dengan statistik sampel, masing-masing rata-rata X¯ dan varians sampel S2, jika sampel dianggap cukup besar, maka interval keyakinan (1₋α)_×100%) untuk penduga mean populasi (µ) adalah

¯

X₋t_α/₂_,₍_n−₁₎S_X¯ ≤µ≤X¯ +t_α/₂_,₍_n−₁₎S_X¯ (4.4)

Sejauh in