BAB 2
LANDASAN TEORI
2.1.Kriptografi
Kriptografi berasal dari gabungan dua suku kata yang berasal dari bahasa Yunani, yaitu
Kryptos dan Graphein. Kryptos memiliki makna tersembunyi, misterius, atau rahasia.
Graphein sendiri berarti tulisan. Kriptografi adalah seni dan ilmu dalam menyimpan pesan – pesan yang berisi rahasia dan itu dilakukan oleh Cryptographer. Cryptanalysts adalah orang yang mempraktekkan cryptanalysis, seni dan ilmu dalam memecahkan ciphertext. Cabang matematika yang meliputi baik kriptografi maupun kriptoanalisis adalah Cryptology dan orang yang mempraktekkannya disebut Cryptologists (Schneier, 1996).
Jadi secara sederhana, kriptografi dapat didefinisikan sebagai ilmu atau pelajaran
yang menggunakan tulisan dan memiliki makna yang tersembunyi atau rahasia didalamnya.
Terdapat pengertian lain di dalam buku lama (sebelum tahun 1980-an) yang menyatakan
bahwa kriptografi merupakan ilmu dan seni untuk menjaga kerahasiaan pesan dengan cara
menyandikannya ke dalam bentuk yang tidak dapat dimengerti lagi maknanya (Munir, 2006).
2.2.Pembangkit Bilangan Acak
Pembangkit Bilangan Acak atau Random Number Generator (RNG) adalah sebuah sumber dari nomor - nomor yang tidak dapat diprediksi, yang berarti bahwa tidak mungkin
memprediksi hasil yang keluar. Dalam banyak hal seperti kriptografi, simulasi model,
pemgambilan sampel, permainan yang menggunakan kesempatan, dan lainnya dibutuhkan
pembangkitan serangkaian nomor acak (Bhaskar, 2013). RNG juga seringkali digunakan untuk membangkitkan seed yang akan digunakan dalam algoritma block cipher atau membangkitkan bilangan prima untuk algoritma RSA (Lietara, 2009).
2.3.Pembangkit Bilangan Acak Semu
Pembangkit Bilangan Acak Semu atau yang biasa disebut dengan Pseudo Random Number Generator (PRNG) adalah sebuah algoritma yang umum digunakan pada kriptografi. Dengan memberikan angka – angka acak yang pendek, PRNG mengkalkulasi dan mengembalikan
tes yang membandingkan mereka (angka) ke urutan true random numbers. Jika sebuah PRNG dapat memproduksi urutan yang mana tidak ada tes statistik yang dapat
membedakannya dari urutan angka acak yang benar, maka PRNG itu dapat disebut sebagai
Cryptographically Secure Pseudo Random Generator (CSPRNG). Yang ingin diperoleh dari PRNG adalah untuk menciptakan nilai dengan cepat, dari seed yang pendek, ke urutan yang panjang yang muncul dalam setiap cara untuk dihasilkan oleh putaran-putaran koin yang adil
(Blum, 1986).
2.4.Algoritma Blum-Blum-Shub
Blum-Blum-Shub adalah algoritma pembangkit bilangan acak yang dibuat pada tahun 1986. Algoritma yang termasuk dalam kategori Cryptographically Secure Pseudo-Random Number Generator (CSPRNG) ini dapat dikatakan sangat sederhana dan mangkus. BBS sendiri merupakan singkatan dari ketiga nama penemunya, yaitu Lenore Blum, Manuel Blum, dan
Michael Shub. Berikut rumus pada algoritma Blum-Blum Shub :
2.4.1.Cara kerja algoritma Blum-Blum-Shub
Langkah – langkah pembangkitan bilangan acak BBS adalah sebagai berikut : (munir, 2006)
1. Pilih dua buah bilangan prima rahasia p dan q, masing – masing kongruen
Terhadap 3 modulo 4. dan (dalam praktek bilangan
prima yang digunakan cukup besar).
2. Temukan hasil bilangan bulat blum n dengan menghitung
3. Pilih bilangan bulat acak s sebagai umpan. Adapun bilangan yang dipilih harus memenuhi kriteria sebagai berikut :
a.
b. s dan n adalah bilangan prima.
4. Hitung nilai
5. Temukan hasil bilangan bit acak dengan melakukan literasi berikut :
a. Hitung
2.4.2.Flowchart algoritma Blum-Blum-Shub
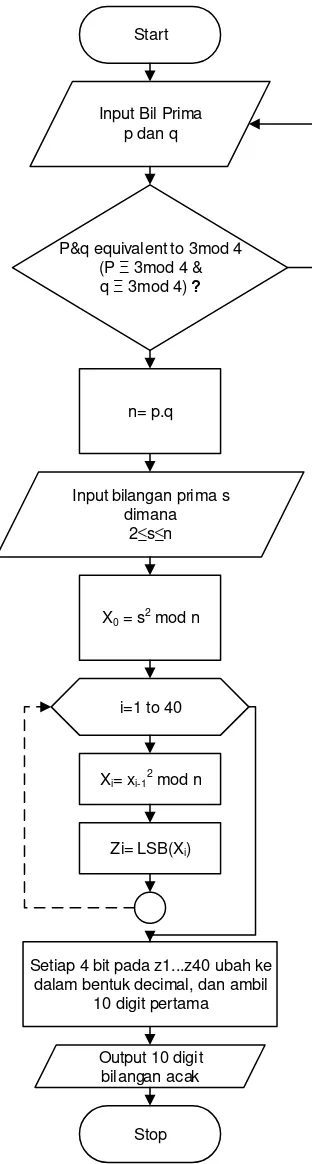
Gambar 2.1 dibawah adalah flowchart untuk algoritma Blum-Blum-Shub.
Start
Input Bil Prima p dan q
P&q equivalent to 3mod 4 (P Ξ 3mod 4 & q Ξ 3mod 4) ?
Input bilangan prima s dimana
2 s n n= p.q
X0 = s2 mod n
i=1 to 40
Xi= xi-12 mod n
Zi= LSB(Xi)
Setiap 4 bit pada z1...z40 ubah ke dalam bentuk decimal, dan ambil
10 digit pertama
Output 10 digit bilangan acak
Stop
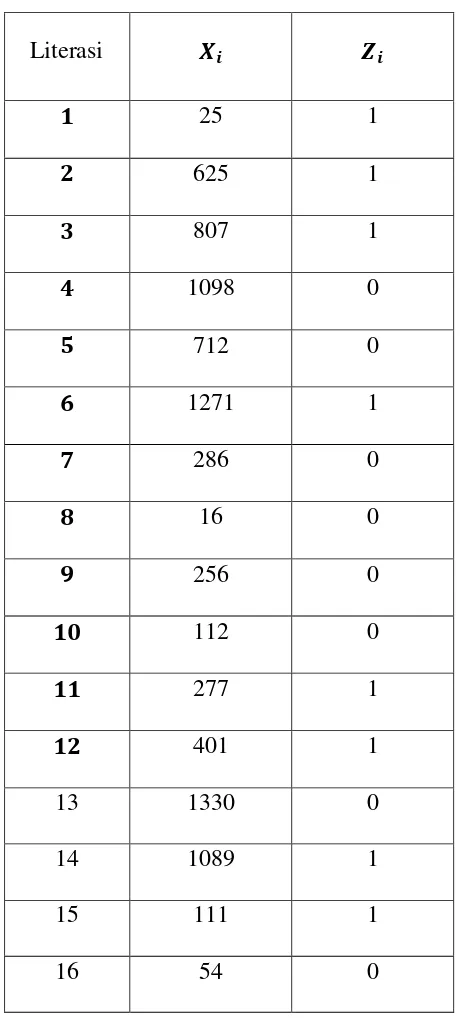
Misal p=29, q=47, n=1363, s=5, x0=25, maka perhitungan algoritma Blum-Blum-Shub bisa dilihat pada tabel 2.1.
Literasi
25 1
625 1
807 1
1098 0
712 0
1271 1
286 0
16 0
256 0
112 0
277 1
401 1
13 1330 0
14 1089 1
15 111 1
16 54 0
Tabel 2.1. Contohperhitungan algoritma Blum-Blum-Shub
Keamanan pada algoritma Blum-Blum-Shub ini terletak pada landasan teori bilangan yang kuat, yaitu sulitnya memfaktorkan bilangan bulat yang besar menjadi faktor-faktor
prima dan juga sulitnya memecahkan Quadratic Residuosity Problem (Yuliawan, 2006).
barisan bit yang dihasilkan oleh CSPRNG ini, kriptanalisi tidak dapat menganalisa barisan bit sebelumnya dan barisan bit sesudahnya dalam urutan bilangan acak yang dihasilkan (Bilqis,
2012). BBS aman selama masalah memfaktorkannya tetap sulit (Sinai, 2011). BBS juga tidak
dapat diprediksi keacakannya (Wibowo, 2015).
2.5.Algoritma Quadratic Linear Congruential Generator
Quadratic Linear Congruential Generator (QLCG) merupakan salah satu algoritma pembangkit bilangan acak dengan rumus sebagai berikut :
( )
Dimana dan (Gille-Ginest, 2009).
Dijelaskan lebih rinci, dimana m adalah bilangan bulat positif dan , a, b, c adalah bilangan bulat non-negative yang lebih kecil daripada m. Knuth (1981) memberikan kondisi yang diperlukan untuk dapat mencapai panjang periode maksimal m yang dapat dihasilkan. Kondisi ini berlaku jika m bukanlah bilangan prima (Eichenauer, 1986).
2.5.1.Cara kerja algoritma Quadratic Linear Congruential Generator
Langkah-langkah pembangkitan bilangan acak pada algoritma Quadratic Linear
Congruential Generator adalah sebagai berikut :
1. Pilih bilangan untuk , a, b, c, serta m dimana : a. m adalah bilangan bulat positif.
b. , a, b, c adalah bilangan bulat non-negative yang lebih kecil dari m. 2. Temukan hasil bilangan bit acak dengan melakukan literasi berikut :
a. Hitung nilai Xi= (aXi-12 + bXi-1+ c ) mod n
b. Temukan hasil bit LSB (Least Significant Bit) yang diambil dari 3. Barisan bit acak yang dihasilkan adalah
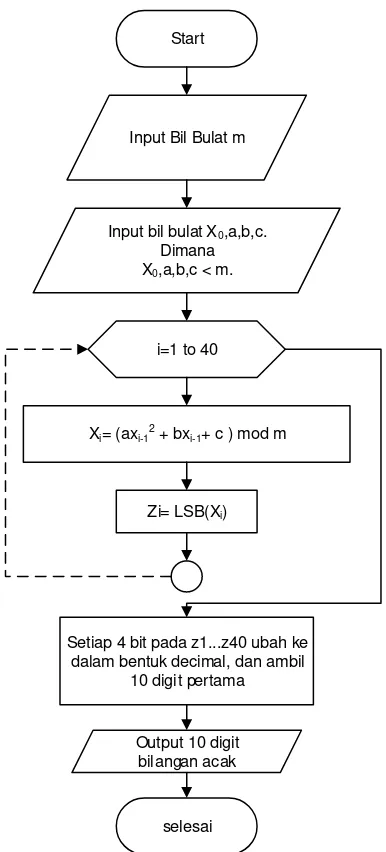
2.5.2.Flowchart algoritma Quadratic Linear Congruential Generator
Start
Input Bil Bulat m
i=1 to 40
Xi= (axi-12 + bxi-1+ c ) mod m
Zi= LSB(Xi)
Setiap 4 bit pada z1...z40 ubah ke dalam bentuk decimal, dan ambil
10 digit pertama
Output 10 digit bilangan acak
selesai Input bil bulat X0,a,b,c.
Dimana X0,a,b,c < m.
Gambar 2.2. Flowchart algoritma Quadratical Linear Congruential Generator
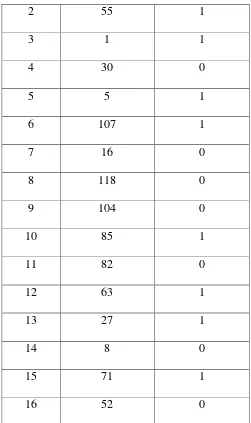
2.5.3.Contoh perhitunganalgoritma Quadratic Linear Congruential Generator
Misal a=69, b=59, c=23, m=121, dan =13, maka perhitungan algoritma Quadratic Linear Congruential Generator bisa dilihat pada tabel 2.2.
Literasi
2 55 1
3 1 1
4 30 0
5 5 1
6 107 1
7 16 0
8 118 0
9 104 0
10 85 1
11 82 0
12 63 1
13 27 1
14 8 0
15 71 1
16 52 0
Tabel 2.2. Contoh perhitungan algoritma Quadratical Linear Congruential Generator
Keunggulan yang terdapat pada algoritma Quadratic Linear Congruential Generator