MODIFIKASI ALGORITMA PLAYFAIR DAN MENGGABUNGKAN DENGAN
LINEAR FEEDBACK SHIFT REGISTER (LFSR)
E. Haodudin Nurkifli
Teknik Informatika, Ilmu Komputer, Universitas Singaperbangsa Karawang Jl. H.S. Ronggo Waluyo / Teluk Jambe Karawang
ABSTRAK
Playfair Cipher merupakan metoda enkripsi klasik yang sangat sulit untuk dikriptanalisis secara manual. Meskipun demikian Playfair dapat dipecahkan dengan menggunakan informasi frekuensi kemunculan bigram. Komponen yang penting pada algoritma playfair adalah tabel cipher yang digunakan untuk melakukan enkripsi dan dekripsi diperkenalkan oleh playfair merupakan matrik berukuran (5x5) yang berisi huruf kapital dari A-Z. Tabel bawaan yang ada pada playfair cipher tidak dapat mengenkripsi Plainteks yang berisi huruf kecil (a-z), angka (0-9) dan simbol-simbol. Mekanisme mengganti huruf J dengan I pada persiapan enkripsi menjadi kelemahan dari playfair karena pada proses dekripsi akan terjadi ambigu pada kata yang memiliki huruf I. Modifikasi tabel playfair chiper yang dapat digunakan untuk melakukan enkripsi huruf kapital, huruf kecil, angka dan simbol. Penggunaan tabel 12 x 12 yang sangat acak memiliki Confusion yang bagus sehingga membuat hubungan statistik antara plainteks, cipherteks, dan kunci menjadi sangat rumit. Perubahan satu bit enkripsi pada plaintek berpengaruh terhadap bit yang lainnya sehingga menggabungkan dengan LFSR menjadi lebih baik juga dari sisi Diffusionya.
Kata Kunci: Playfair, Tabel Cipher, Confusion, Diffusion
1. PENDAHULUAN
Playfair Cipher merupakan metoda enkripsi klasik yang sangat sulit untuk dikriptanalisis secara
manual. Meskipun demikian Playfair dapat
dipecahkan dengan menggunakan informasi
frekuensi kemunculan bigram. Komponen yang penting pada algoritma playfair adalah tabel cipher yang digunakan untuk melakukan enkripsi dan dekripsi tabel bawaan yang diperkenalkan oleh playfair adalah tabel yang berbentuk matrik berukuran (5x5) yang berisi huruf kapital dari A-Z dengan menghilangkan J.
Menurut Aftab (2013), Chaoudhary (2013), Vatsa (2012) Ciphertek hasil enkripsi relatif mudah
dipecahkan ketika kriptanalisis mengetahui
cipherteks dan tabel ciphernya, walaupun kriptanalis hanya mengetahui cipherteks tanpa mengetahui tabel chiper kriptanalis dapat menebak bigram berdasakan huruf yang bermakna dari sebuah kata.
Menurut Harris dan Attia (2013), Kumar (2013), Nidhal dan Wasfi (2013), Shakti dan Gupta (2011) Tabel bawaan yang ada pada playfair cipher tidak dapat mengenkripsi Plainteks yang berisi huruf kecil (a-z), angka (0-9) dan simbol-simbol. Kelemahan yang lain pada playfair adalah terjadinya ambigu pada hasil dekripsi karena pada persiapan enkripsi playfair cipher memiliki mekanisme mengganti J dengan I. Perlunya modifikasi tabel playfair chiper yang dapat digunakan untuk melakukan enkripsi huruf kapital, huruf kecil, angka dan simbol. Mengacak isi tabel diperlukan agar cipherteks yang dihasilkan menjadi acak.
2. TINJAUAN PUSTAKA
Aftab (2013), Chaoudhary (2013) memodifikasi tabel cipher menjadi 7x4 dan menambahkan dua simbol yaitu * dan #. menampilkan semua huruf (A-Z) Agar tidak terjadi ambigu saat melakukan dekripsi. semakin meningkatnya confusion dan diffusion akan mempersulit kriptanalis memecahkan cipherteks.
Harris dan Attia (2013), Shakti dan Gupta (2013) Memodifikasi ukuran tabel cipher menjadi 8x8 yang berisi huruf kapital (A-Z), angka (0-9) dan simbol.
Selain memodifikasi tabel proses enkripsi
digabungkan dengan algortima Linear Feedback Shift Register (LFSR). Ujicoba dengan cipherteks only attack, known Plainteks attack dan cipherteks attack tidak dapat memecahkan cipherteks dari playfair modifikasi. kekuatan tidak hanya substitusi dari matrik 8x8 akan tetapi karena digabungkan dengan cara mengacak bit menggunakan LFSR.
Khumar (2013) Memodifikasi tabel cipher menjadi 6x6 yang berisi (A-Z) dan (0-9). Menggabungkan pengacakan bit dengan LFSR setelah bit teracak baru melakukan enkripsi dengan playfair cipher tabel 6x6. Menggabungkan LFSR dan Playfair tabel cipher 6x6 dapat meningkatkan keamanan dari cipherteksnya.
Vatsa (2012) Memodeifikasi proses enkripsi pada Caesar cipher dengan membuat tabel up (4x4) dan tabel down (4x4). Menghindari brute force attack karena dengan tabel yang dibuat setiap huruf yang sama ketika dienkripsi tidak menghasilkan huruf ciperteks yang sama. Pembentukan cipher dengan tabel dapat memperkuat cipherteks dari Caesar cipher.
Khumar (2013), Ravindra (2011) Membahasa beberapa kelemahan algoritma klasik: Caesar, playfair, vigenere, cipher hill. Kelemahan playfair cipher mudah ditebak jika kriptanalisis menemukan cipher dan kuncinya. Jika kriptanalisis hanya menemukan chiperteks maka kriptanalisis dapat menebak digram yang terbentuk dari cipherteksnya. Playfair dengan tabel cipher 5x5 tanpa modifikasi akan membuat cipher mudah dipecahkan.
Menurut Nidhal (2013) Pembuatan tabel playfair baru dengan ukuran 11x11 yang berisi (A-Z), (a-z),
(0-9), beberapa simbol aritmatik. Lebih
mengamankan di kombinisai dengan LFSR.
Semakin meningkatnya confusion dan diffusion
akan mempersulit kriptanalis memecahkan
cipherteks.
Shrivastava (2013) Memodifikasi ukuran tabel cipher menjadi (8x8) dan menggunakan multi round untuk mengacak isi tabel cipher. Mempersulit pemechana analisis digram dan frekuensi analisis karena semakin acak isi tabel akan menghasilkan cipherteks yang acak.
Berdasarkan beberapa ide dari penelitian terdahulu, menganalisis tabel cipher yang dapat digunakan untuk enkripsi dan dekripsi. membuat tabel cipher dengan ukuran 12 x 12 mengacak isi dari tabel sehingga dapat menghasilkan cipherteks yang sukar untuk dipecahkan oleh analisis frekuensi. Selain itu cipherteks yang dihasilkan dixor dengan kunci yang dibentuk dengan Linear Feedback Sift Ragister (LFSR).
3. LANDASAN TEORI
Menurut Stallings (2010) Playfair Cipher
menggunakan papan kunci yang berbentuk
bujursangkar dalam melakukan penyandian. Papan kunci ini berukuran 5x5, dimana setiap bagian dalam papn kunci mewakili huruf-huruf dalam alfabet (abjad) dengan menghilangkan huruf J dari abjad. Setiap elemen bujursangkar berisi huruf yang berbeda satu sama lain.
Tabel 1. Tabel cipher playfair (5x5)
R X C N Y
E D W I G
O T A M V
F B U Z S
H P Q K L
3.1 Algoritma Persiapan Enkripsi Playfair
Cipher
Menurut Stallings (2010) Sebelum melakukan
enkripsi, pesan yang akan dienkripsi (plainteks) diatur terlebih dahulu sebagai berikut :
1. Semua spasi dan karakter yang bukan alfabet
harus dihilangkan dari plainteks (jika ada).
2. Jika ada huruf J pada palinteks maka ganti huruf
tersebut dengan huruf I.
3. Pesan yang akan dienkripsi ditulis dalam
pasangan huruf (bigram).
4. Jika ada huruf yang sama dalam pasangan huruf,
maka sisipkan huruf X atau Z di tengahnya.
Huruf yang disisipkan sebaiknya huruf X karena
sangat kecil kemungkinan terdapat huruf X yang
sama dalam bigram, tidak seperti huruf Z,
contohnya dalam kata FUZZY.
5. Jika jumlah huruf pada plainteks adalah ganjil
maka pilih sebuah huruf tambahan yang dipilih oleh orang yang mengenkripsi dan tambahkan di akhir plainteks. Huruf tambahan dapat dipilih
sembarang misalnya huruf Z atau X.
3.2 Algoritma Enkripsi Playfair Cipher
Algoritma enkripsi untuk setiap bigram adalah
sebagai berikut:
1. Jika ada dua huruf terdapat pada baris kunci yang
sama maka tiap huruf diganti dengan huruf di kanannya
2. Jika ada dua huruf terdapat pada kolom yang
sama maka tiap huruf diganti dengan huruf di bawahnya
3. Jika dua huruf tidak pada baris yang sama atau
kolom yang sama, maka huruf pertama diganti dengan huruf pada perpotongan baris huruf pertama dengan kolom huruf kedua.
4. Huruf kedua diganti dengan huruf pada titik sudut
keempat dari persegi panjang yang dibentuk dari huruf yang digunakan
3.3 Algoritma dekripsi Playfair Cipher
Algoritma dekripsi merupakan kebalikan dari
algoritma enkripsi untuk setiap bigram adalah sebagai
berikut:
1. Jika ada dua huruf terdapat pada baris kunci yang
sama maka tiap huruf diganti dengan huruf di kirinya
2. Jika ada dua huruf terdapat pada kolom yang
sama maka tiap huruf diganti dengan huruf di atasnya.
3. Jika dua huruf tidak pada baris yang sama atau
kolom yang sama, maka huruf pertama diganti dengan huruf pada perpotongan baris huruf pertama dengan kolom huruf kedua.
4. Huruf kedua diganti dengan huruf pada titik sudut
keempat dari persegi panjang yang dibentuk dari huruf yang digunakan
3.4 Contoh enkripsi dan dekripsi
Menurut Stallings (2010) Plaintek: IT IS FULL
MOON. Buat bigram dari Plainteks gantikan j dengan i, tambahkan X jika pasangan huruf ganjil. “IT IS FU LX LM OX ON”. Enkripsi dengan cara megnacu pada tabel cipher matrik 5x5 dengan isi tabel sembarang. Tabel acuan enkripsi tabel 2.
Tabel 2. Tabel cipher playfair (5x5)
R X C N Y
E D W I G
O T A M V
F B U Z S
H P Q K L
Cipherteks yang dihasilkan: DM GZ BZ PY KV TR MR Proses dekripsi merupakan kebalikan dari
proses enkripsi. Cipherteks yang dihasilkan “DM GZ BZ PY KV TR MR” dilihat berdasarkan tabel DM sehingga pasangan bigram plaintek “IT”. Hasil pasangan bigram menjadi “IT IS FU LX LM OX ON”. Hilangkan X menjadi “IT IS FU L LM OON” palinteks “IT IS FULL MOON” [10].
4. METODE PENELITIAN
Metode penelitian berdasarkan skema kriptografi disajikan pada gambar 1 .
Enkipripsi Dekripsi
Plainteks Cipherteks Plainteks
Kunci Kunci
Gambar 1. Skema enkripsi dan dekripsi Gambar 1 memperlihatkan beberapa hal yang akan dibahas: penentuan kunci, proses enkripsi dan proses
dekripsi. penelitian ini menyajikan bagaimana
melakukan proses modifikasi terhadap algoritma playfair dan menggabungkan dengan LFSR. Skema baru disajikan pada bab 5.
5. USULAN SKEMA BARU ALGORITMA
PLAYFAIR
Usulan ini mengemukakan bentuk skema baru dari algoritma playfair dan digambungkan dengan LFSR. Gambar 2 diperlihatkan bentuk usulan skema baru dari algoritma flayfair. Plainteks1 Enkirpsi1 Menggunakan tabel playfair 12x12 Enkripsi2 Cipherteks1 Kunci1 Kunci2 Pembentukan Kunci Dekripsi2 Kunci2 Pembentukan Kunci Cipherteks2 Dekripsi1 Menggunakan tabel playfair 12x12 Plainteks2 Kunci1 Plainteks1
Gambar 2. Usulan Skema enkripsi dan dekripsi Gambar 2 memperlihatkan beberapa proses yang ada: Plainteks1 dienkripsi dengan algoritma playfair
menggunakan kunci berdasarkan tabel playfair
modifikasi menghasilkan cipherteks1. Cipherteks1 dienkripsi kembali dengan cara cipherteks1 dixor dengan kunci yang dibentuk berdasarkan LSFR 8 bit
sehingga menghasilkan cipherteks2. Proses
mengembalikan pesan dilakukan dengan terlebih
dahulu cipherteks2 didekripsi menghasilkan
cipherteks1 dan cipherteks1 didekripsi sehingga menjadi Plainteks kembali. Proses yang lebih detil disajikan pada subbab 5.1.
5.1 Proses enkripsi dan dekripsi dengan
playfair
Beberapa hal yang harus dipersiapkan untuk melakukan proses enkripsi dan dekripsi yang mengacu pada stalling (2010).
Enkirpsi Menggunakan tabel playfair 12x12 Dekripsi Menggunakan tabel playfair 12x12
Plainteks Cipherteks Plainteks
Gambar 3. Skema enkripsi dan dekripsi playfair
Gambar 3 Memperlihatkan skema dari algoritma playfair. Enkripsi terhadap palinteks membutuhkan tabel playfair. Tabel playfair dimodifikasi sehingga menjadi tabel playfair 12x12. Modifikasi tabel disajikan pada subab 6. Plainteks di enkripsi
menghasilkan cipherteks, Proses untuk
mengembalikan dilakukan dengan mendekripsi cipherteks sehingga menjadi Plainteks.
5.2 Proses enkripsi dan dekripsi dengan xor
menggunakan pembentukan kunci LFSR Proses enkripsi dan dekripsi terdapat beberapa tahapan: pembentukan kunci, enkripsi dan dekripsi diperlihatkan gambar 4 dan gambar 5.
Bit Keluaran
b7 b6 b5 b4 b3 b2 b1
b8
Gambar 4. Pembentukan kunci LFSR 8 bit
Gambar 4 memperlihatkan mekanisme
pembentukan kunci dengan LFSR 8 bit. b1, b2, ..b8
merupakan bit masukan b1 xor b8 kemudian b8
digeser dan ditempatkan di bit keluaran.
Pembentukan Kunci Pembentukan Kunci Plainteks Enkripsi Plainteks Dekripsi Kunci Kunci Cipherteks
Gambar 5. Xor enkripsi dan dekripsi
Gambar 5 memperlihatkan setelah kunci
terbentuk dengan menggunakan LFSR kemudian masing-masing bit di xorkan dengan Plainteks.
6. PEMBAHASAN
Pembahasan menyajikan proses enkripsi dan dekripsi menggunakan playfair dengan tabel yang dimodifikasi dan xor menggunakan kunci yang dihasilkan dengan LFSR. Pembahasan disajikan pada sub bab 6.1 dan 6.2.
6.1 Modifikasi tabel playfair (12x12)
Tabel yang dibentuk tidak berdasarkan kunci, tabel terdiri dari 12 baris dan 12 kolom berisi huruf kapital (A-Z), huruf kecil (a-z), angka (0-9) dan simbol. Tabel bentukan diperlihatkan pada tabel 3. Tabel 3. Tabel cipher (12 x 12)
A B C D E F G H I /J K L M N O P Q R S T U V W X Y Z A b c d E f G h i/j k l m N o p q R s T u V w x y Z 0 1 2 3 4 5 6 7 8 9 # $ % ^ & * ( ) - = + [ ] ; „ : “ \ , . / < > ? £ ¥ @ 𝜷 𝝅 𝝈 𝝁 𝝉 ∞ ± ≥ ≤ ÷ À Á Â Ä È É Ê Ë Ì Í Î Ï Ð Ñ Ò Ó Ô Õ Ö Ø Ù Ú Ü Ý À á â ä Å æ Ç è É ê ë ì Í î ï ð Ñ ò Ó ô Õ ù ü
Tabel 3 memperlihatkan tabel hasil modifikasi yang terdiri dari huruf kapital, huruf kecil angka dan simbol.
6.2 Proses enkripsi dan dekripsi dengan Algoritma Playfair
Proses enkripsi dan dekripsi sama halnya dengan playfair cipher biasa. Misalkan plaintek: “Temui aku di kampus jam 7 atau jam 9 pagi”. Bigram yang terbentuk “Te mu ia ku di ka mp us ia m7 at au ia m9 pa gi” pada bigram ada huru j sehingga setiap j harus diganti dengan i. pembentukan bigram tidak tersisa huruf ganjil dan bigram tidak memiliki huruf sama sehingga tidak perlu menggantikan atau menambahkan dengan X.
Proses enkripsi mengacu pada tabel cipher sehingga cipherteksnya “Sf nv kb hw ek lb nq tv kb vy gn hn kb xy nc”. Proses dekripsi akan menghasilkan bigram “Te mu ia ku di ka mp us ia m7 at au ia m9 pa gi”. Terjadinya ambigu saat dekripsi dikarenakan ada mekanisme menggantikan j dengan i, misalkan jam menjadi iam.
Pembuktian penerapan playfair dengan kunci dan
isi tabel tidak terlalu acak. Kunci: M@h@∞15wa
buat tabel cipher berdasarkan kunci. Isikan tabel dengan huruf, angka, simbol yang belum ada mengacu pada isi tabel 3. Sehingga membentuk tabel 4
Tabel 4. Tabel cipher (12 x 12)
M @ h
∞
1 5 W A A B C D E F G H I/J K L N O P Q R S T U V W X Y Z b c d e f g i/j k l m n O p q r s t u v x y z 0 2 3 4 6 7 8 9 # $ % ^ & * ( ) - = + [ ] ; „ : “ \ , . / < > ? £ ¥ 𝜷 𝝅 𝝈 𝝁 𝝉 ± ≥ ≤ ÷ À Á Â Ä È É Ê Ë Ì Í Î Ï Ð Ñ Ò Ó Ô Õ Ö Ø Ù Ú Ü Ý à á â ä å Æ ç è é ê ë ì í î ï ð ñ Ò ó ô õ ù üEnkripsi plaintek “Temui aku di kampus jam 7 atau jam 9 pagi”. Buat bigram “Te mu ia ku di ka mp us ia m7 at au ia m9 pa gi” menghasilkan
cipherteks “ Us gz oh gx Ur o
∞
nq 7g oh sz M2 @2oh g^ oA ik ”. Proses dekripsi bermula ditemukanya
bigram “Te mu ia ku di ka mp us ia m7 at au ia m9 pa gi”. Masih terjadi ambigu terhadap i yang mana yang akan dirubah menjadi j. tidak terlalu mengacak isi tabel sehingga penambahan angka dan simbol pada isi tabel tidak berpengaruh.
Pembuktian modifikasi tabel cipher yang disi
secara acak Kunci: M@h@∞15wa buat tabel cipher
berdasarkan kunci. Isikan tabel dengan huruf, angka, simbol yang belum ada mengacu pada isi tabel 3 cara pengisiannya dilakukan dengan cara acak. Sehingga membentuk tabel 5
Tabel 5. Tabel cipher (12 x 12)
M @ h
∞
1 5 W a = B C D 𝜷 𝝅 G H ] K L N < P ≥ R S T 3 4 [ X * Z b ÷ Í ) f & i/j k l 𝝉 \ o p Ï r . t “ v x y Ë 0 2 F W 6 7 8 9 # $ % ^ g Y ( e - A + U V ; „ : u n , s / O > ? £ ¥ I/J E 𝝈 𝝁 m ± Q ≤ c À Á Â Ä È É Ê z Ì d Î q Ð Ñ Ò Ó Ô Õ Ö Ø Ù Ú Ü Ý à á â ä Å Æ ç è é ê ë ì í î ï ð Ñ Ò ó ô õ ù üEnkripsi Plainteks “Temui aku di kampus jam 7 atau jam 9 pagi”. Buat bigram “Te mu ia ku di ka mp us ia m7 at au ia m9 pa gi” menghasilkan
cipherteks “÷9 𝝈, oh \; Ár o∞ zF n/ oh ≤F M2 Wn
oh ?( o= #\”. Proses dekripsi bermula ditemukannya bigram “Te mu ia ku di ka mp us ia m7 at au ia m9 pa gi”. Masih terjadi ambigu terhadap i yang mana yang akan dirubah menjadi j. Isi tabel yang sangat acak menghasilkan cipherteks yang sangat acak.
Pembuktian menghilangkan ambigu saat proses
dekripsi . Kunci: M@h@∞15wa buat tabel cipher
berdasarkan kunci. Isikan tabel dengan huruf, angka, simbol yang belum ada mengacu pada isi tabel 3 cara pengisiannya dilakukan dengan cara acak. Sehingga membentuk tabel 6
Tabel 6. Tabel cipher (12 x 12)
M @ h
∞
1 5 W a = B C D 𝜷 𝝅 G H ] K L N < P ≥ R S T 3 4 [ X * Z b ÷ Í ) f & j k l 𝝉 \ o p Ï r . t “ v x y Ë 0 2 F W 6 7 8 9 # $ % ^ g Y ( e - A + U V ; „ : u n , s / O > ? £ ¥ J E 𝝈 𝝁 m ± Q I c À Á i Ä È ≤ Ê z Ì d Î q Ð Ñ Ò Ó Ô Õ Ö Ø Ù Ú Ü Ý à á â ä å Æ ç è é ê ë ì í î ï ð ñ Ò ó ô õ ù üEnkripsi plainteks “Temui aku di kampus jam 7 atau jam 9 pagi”. Buat bigram “Te mu ia ku di ka mp us ja m7 at au ja m9 pa gi” menghasilkan
cipherteks “÷9 𝝈, Ê∞ \; Ár o∞ zF n/ oh ≤F M2 Wn
oh ?( o= #\”. Proses dekripsi bermula ditemukanya bigram “Te mu ia ku di ka mp us ja m7 at au ja m9 pa gi”. Isi tabel yang lengkap dapat menghilangkan ambigu dalam proses dekripsi. Tabel yang acak akan menghasilkan cipher yang acak.
6.3 Pembentukan kunci dengan LFSR 8 bit
Pembentukan kunci diperlihatkan pada tabel dengan bit inputan adalah 11111111.
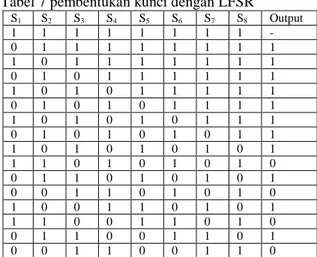
Tabel 7 pembentukan kunci dengan LFSR
S1 S2 S3 S4 S5 S6 S7 S8 Output 1 1 1 1 1 1 1 1 - 0 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 0 1 1 1 1 1 1 1 0 1 0 1 1 1 1 1 0 1 0 1 0 1 1 1 1 1 0 1 0 1 0 1 1 1 0 1 0 1 0 1 0 1 1 1 0 1 0 1 0 1 0 1 1 1 0 1 0 1 0 1 0 0 1 1 0 1 0 1 0 1 0 0 1 1 0 1 0 1 0 1 0 0 1 1 0 1 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 1 0 1 0 0 1 1 0 0 1 1 0
1 0 0 1 1 0 0 1 1 Tabel 7 memperlihatkan kunci dibentuk oleh LFSR yang diambil sebagai kunci adalah bit output.
S1, S2 … S8 diisi dengan bit. Tabel kunci yang
disajikan hanya terdiri 8 bit kunci. Pembentukan kunci berikutnya sesuai dengan mekanisme yang disajikan pada skema LFSR
6.4 Enkripsi dan dekripsi dengan LFSR 8 bit
Enkripsi dengan menggunakan LFSR 8 bit terdiri dari beberapa mekanisme: cipherteks yang dihasilkan enkripsi playfair dibuat matrik 2x9, masing-masing karakter dirubah kedalam bit, kunci yang dibentuk dengan LFSR dibuat matrik 2x9. Xorkan cipherteks dengan kunci yang dihasilkan oleh LFSR. Cipherteks yang dihasilkan oleh playfair
“÷9 𝝈, Ê∞ \; Ár o∞ zF n/ oh ”.
Tabel 8 matrik cipherteks dari playfair (2x9)
÷ 9 𝝈 , Ê ∞ \ ; Á r o ∞ z F n / o h
Tabel 8 memperlihatkan cipherteks yang dihasilkan oleh algoritma playfair dibentuk matrik ukuran 2 x 9. Masing-masing karakter dirubah menjadi bit diperlihatkan pada tabel 9.
Tabel 9 bit dari cipherteks playfair
11110110 00111001 11100101 00101100 10010000 11101100 01011100 00111011 10110101 01110010 01101111 11101100 01111010 01000110 01101110 00101111 01101111 01101000
Tabel 9 memperlihatkan bit dari masing-masing karakter yang ada pada tabel 8.
Tabel 10 bit kunci dari LFSR 8 bit.
11111111 01010101 10011001 00010001 11100001 01000001 10000001 00000000 11111111 01010101 10011001 00010001 11100001 01000001 10000001 00000000 11111111 01010101
Tabel 10 merupakan kunci matrik kunci yang terbentuk dari LFSR. Proses enkripsi cipherteks hasil enkripsi playfair dixor dengan kunci. Berikut contoh dari enkripsi : 11110110 xor 11111111 =
00001001 ascii dari bit tersebut adalah HT (Horizontal Tab), 00111001 xor 01010101 = 01101100 = l, 11100101 Xor 10011001 = 01111100 = | (vertical bar). Enkripsi dilakukan untuk semua bit. Cipherteks yang diperoleh adalah “ HT, l, |, 9, q, ¡ , ¦, ; , J , ' , û, ´ , /, É, - “.
Proses dekripsi dilakukan dengan cara
merubah masing-masing karakter cipherteks
kemudian dixorkan dengan kunci.
7. KRIPTANALISIS
Confusion merupakan prinsip yang
menyembunyikan hubungan apapun yang ada antara plainteks, cipherteks, dan kunci. Prinsip confusion akan membuat kriptanalis sukar untuk mencari pola-pola statistik yang muncul pada cipherteks. Penggunaan tabel 12 x 12 yang acak memiliki Confusion yang bagus sehingga membuat hubungan statistik antara plainteks, cipherteks, dan kunci menjadi sangat rumit.
Diffusion merupakan prinsip yang menyebarkan pengaruh satu bit plainteks atau kunci ke sebanyak mungkin cipherteks dan menyembunyikan hubungan statistik antara plainteks, cipherteks, dan kunci dan membuat kriptanalisis menjadi sulit. Perubahan terjadi pada pembentukan kunci LFSR dan proses xor kunci dengan Plainteks sehingga perubahan
cipherteks tidak dapat diprediksi dan
menyembunyikan hubungan statistik antara
Plainteks, cipherteks, dan kunci.
8. KESIMPULAN
Berdasarkan pembahasan dan analisis kriptanalis ada beberapa kesimpulan sebagai berikut:
a. Tabel cipher pada algoritma playfair menjadi
komponen penting untuk enkripsi dan dekripsi
b. Tabel cipher dapat dimodifikasi menjadi ukuran
tabel sembarang minimal menampung huruf kapital (A-Z).
c. Isi tabel dapat di isi dengan huruf-huruf dan
simbol yang diisikan secara acak sehingga dapat memperkuat cipherteks
d. Pembentukan kunci dengan LFSR 8 bit
menghasilkan kunci bit yang acak.
e. Menggabungkan playfair dengan modifikasi
tabel dan LFSR menghasilkan cipherteks yang susah untuk dipecahkan.
DAFTAR PUSTAKA
Aftab, A. A., Shah, B. K., dan Muhammad, C. S., A
Modified Version of Playfair Cipher Using 7×4 Matrix., International Journal of Computer Theory and Engineering., Volume 5., No. 4., Agustus., 2013
Choudhary, J., Kumar, R. G dan Singh, S., A Generalized Version of Play Fair Cipher., international journal of advanced computer technology., Volume 2., PP 2-6, Juni., 2013 Harris, J., dan Attia, A., Modified Version of
Cryptography Playfair Cipher with 8x8 Linear Feedback Shift Register., European Journal of Industrial and System Engineering., Volume 11., 2013
Kumar, D. M., dan Jain, D., The Problem Analysis on Encryption Technique in Cryptography., International Journal of Societal Applications of Computer Science., Volume 2., Mei., 2013 Kumar, V., et al., Modified Version of Playfair
Cipher Using Linear Feedback Shift Register and Transpose Matrix Concept., International Journal of Innovative Technology and Exploring Engineering., Volume 3., Juni., 2013
Nidhal, O. A. H., dan Wasfi, B. A., 11 × 11 Playfair Cipher based on a Cascade of LFSRs., IOSR Journal of Computer Engineering., Volume 12., PP 29-35., Mei-Juni., 2013
Ravindra, K. B., Udaya, S. K., dan Vina, A. B., A Survey on Recently Modernized Cryptographic Algorithms and Analysis on The Block Cipher Generation Using Play Color Cipher Algorithm., International Journal of Mathematical., Volume 2., November., 2011
Shakti, S. S., dan Gupta, N., A Novel Approach to Security using Extended Playfair Cipher., International Journal of Computer Applications., Volume 20.,c No.6., April., 2011
Shrivastava, G., Chouhan, M., dan Dhawan, M., A Modified Version Of Extended Plafair Cipher (8x8)., International Journal Of Engineering And Computer Science., Volume 2., No. 956 -961., April., 2013
Stallings, W., Cryptography and Network Security: Principles and Practice., 5thedition, Prentice Hall., January 24., 2010.
Vatsa, S., Mohan, T., dan Vatsa, A. K., Novel Cipher Technique Using Subtitution Method.,
International Journal of Information and
Network Security., Volume 1., No.4., PP 313-320., Oktober., 2012