ANALISIS MODEL MATEMATIKA PERAN PENAMBAHAN MAKANAN DALAM SISTEM EKO-EPIDEMIOLOGI DENGAN PENYAKIT PADA
PREY
SKRIPSI
FAIDAH ALIMATUL FITRIAH
PROGRAM STUDI S-1 MATEMATIKA DEPARTEMEN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS AIRLANGGA 2016
ANALISIS MODEL MATEMATIKA PERAN PENAMBAHAN MAKANAN DALAM SISTEM EKO-EPIDEMIOLOGI DENGAN PENYAKIT PADA
PREY
SKRIPSI
FAIDAH ALIMATUL FITRIAH
PROGRAM STUDI S-1 MATEMATIKA DEPARTEMEN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
PEDOMAN PENGGUNAAN SKRIPSI
Skripsi ini tidak dipublikasikan, namun tersedia di perpustakaan dalam lingkungan Universitas Airlangga, diperkenankan untuk dipakai sebagai referensi kepustakaan, tetapi pengutipan harus seizin penulis dan harus menyebutkan sumbernya sesuai kebiasaan ilmiah. Dokumen skripsi ini merupakan hak milik Universitas Airlangga.
KATA PENGANTAR
Alhamdulillahirabbil’alamin. Segala puji syukur penulis panjatkan kepada Allah SWT karena hanya dengan rahmat dan karunia-Nya, sehingga skripsi yang berjudul “Analisis Model Matematika Peran Penambahan Makanan dalam Sistem Eko-epidemiologi dengan Penyakit pada Prey” ini dapat diselesaikan dengan baik. Shalawat serta salam bahagia semoga senantiasa tercurahkan kepada junjungan kita, Nabi Besar Muhammad SAW, pemimpin sekaligus sebaik-baiknya suri tauladan bagi kehidupan umat manusia.
Keberhasilan penulis dalam menyusun skripsi ini tentunya tidak lepas dari dukungan berbagai pihak. Oleh karena itu, tak lupa penulis ucapkan terima kasih kepada semua pihak yang telah membantu dalam menyelesaikan skripsi ini. Ucapan terima kasih penulis sampaikan kepada:
1. Universitas Airlangga yang telah memberikan kesempatan penulis untuk menempuh pendidikan tinggi.
2. Direktorat Jendral dan Pendidikan Tinggi yang telah memberikan beasiswa bidikmisi.
3. Badrus Zaman, S.Kom., M.Cs. selaku Ketua Departemen Matematika Universitas Airlangga yang selalu memberikan motivasi.
4. Dr. Mohammad Imam Utoyo, M.Si. selaku Koordinator Program Studi S-1 Matematika Fakultas Sains dan Teknologi Universitas Airlangga yang selalu memberikan saran dan motivasi.
5. Auli Damayanti, S.Si., M.Si. selaku dosen wali yang telah memberi masukan serta saran selama proses pembelajaran.
6. Dr. Fatmawati, M.Si. selaku dosen pembimbing I yang telah banyak memberikan masukan, tenaga, serta nasehat kepada penulis.
7. Dr. Miswanto, M.Si. sebagai pembimbing II yang telah banyak memberikan arahan, tenaga dan fikiran.
8. Ahmadin, S.Si., M.Si. selaku dosen penguji yang telah memberikan koreksi serta masukan demi perbaikan skripsi ini.
9. Seluruh dosen Universitas Airlangga yang telah menyampaikan banyak ilmu kepada penulis.
10.Alm. Bapak dan Ibu tercinta Samsuri dan Safiatun, adik tercinta Firda Ulfatul Kholida, mas Chairul Anwar beserta keluarga besar saya yang menjadi sumber motivasi, memberikan kasih sayang, do’a, tenaga, dan perhatian kepada penulis.
11.Teman-teman tangguh yaitu Ais Fatkhiyah, Anik Zainurrifah, Endrawati, Alvianita Tri Utami dan teman kos seperjuangan Nisrina, Neni, Mbak Zizah, Nike, Ria, Dewi, Fatim, Mety, Lintang serta adik kos Ayu, Nuril, Sri, Binti, Sofi yang memberi dukungan, saling mengajari dalam membantu penyelesaian skripsi ini.
12.Teman-teman Matematika Angkatan 2012 yang memberikan banyak inspirasi dan motivasi.
Dengan segala kerendahan hati, penulis menyadari bahwa skripsi ini masih jauh dari kesempurnaan mengingat keterbatasan pengetahuan yang penulis peroleh hingga saat ini, namun penulis sudah berupaya agar tidak terjadi kesalahan pada penulisan ini. Oleh karena itu, penulis mengharapkan kritik dan saran yang bersifat membangun guna terciptanya kesempurnaan skripsi ini. Semoga skripsi ini dapat bermanfaat bagi pihak-pihak yang membacanya dan bagi penulis sendiri.
Surabaya, Juli 2016
Faidah Alimatul Fitriah, 2016, Analisis Model Matematika Peran Penambahan Makanan dalam Sistem Eko-epidemiologi dengan Penyakit pada Prey.
Skripsi ini dibawah bimbingan Dr. Fatmawati, M.Si. dan Dr. Miswanto, M.Si. Departemen Matematika, Fakultas Sains dan Teknologi, Universitas Airlangga, Surabaya.
ABSTRAK
Eko-epidemiologi adalah ilmu yang mempelajari tentang penyebaran penyakit menular pada sebuah populasi dalam interaksi di suatu lingkungan. Sistem eko-epidemiologi dengan penyakit pada prey menyediakan makanan alternatif sebagai penambahan makanan untuk predator. Tujuan dari skripsi ini adalah untuk menganalisis model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey serta memperlihatkan peran dari penambahan makanan pada sistem eko-epidemiologi.
Pada skripsi ini membahas analisis kestabilan dari titik setimbang yang terdapat pada model dan syarat eksistensinya. Dari analisis model diperoleh empat titik setimbang yaitu titik setimbang kepunahan 𝐸0 , titik setimbang aksial 𝐸1 , titik setimbang bebas penyakit atau kepunahan prey yang terinfeksi 𝐸2 , dan titik setimbang koeksistensi prey dan predator 𝐸3 . Titik setimbang 𝐸0 tidak stabil, sedangkan titik setimbang 𝐸1, 𝐸2, dan 𝐸3 stabil asimtotis dengan syarat tertentu. Kestabilan lokal dari keempat titik setimbang tersebut dikaji dengan menggunakan kriteria Routh-Hurwitz. Berdasarkan hasil simulasi numerik menggambarkan bahwa adanya makanan alternatif sebagai penambahan makanan yang sesuai dapat memaksimumkan populasi prey yang rentan dan predator serta meminimumkan prey yang terinfeksi meskipun tingkat infeksinya tinggi. Penggunaan makanan alternatif sebagai penambahan makanan untuk predator dengan penyakit pada prey memperkenalkan metode baru non-kimia pada sistem eko-epidemiologi.
Kata Kunci : Sistem eko-epidemiologi, Prey yang terinfeksi, Penambahan makanan, Titik setimbang, Kestabilan.
Faidah Alimatul Fitriah, 2016, Analysis Mathematical Model Role of Additional Food in Eco-epidemiological System with Disease in the Prey. This undergraduate thesis is supervised by Dr. Fatmawati, M.Si. and Dr. Miswanto, M.Si. Mathematics Department, Faculty of Science and Technology, Airlangga University, Surabaya.
ABSTRACT
Eco-epidemiologi is study the spread of infectious diseases in a population in the interaction in an environment. An eco-epidemiological system with disease in the prey supplying alternative food be that of additional food to predator. The aims of this thesis is to analyze mathemathical model role of additional food in eco-epidemiological system with disease in the prey as well as to show the role additional food in an eco-epidemiological system.
In this thesis discussed analyze stability of the equilibrium point contained in the model and condition of existence. Based on the analysis of model, four equilibriums are obtained. Those are extinction (𝐸0), axial (𝐸1), infected prey extinction or disease free (𝐸2), and the coexistence between prey and predator (𝐸3). The 𝐸0 equilibrium is unstable; while 𝐸1, 𝐸2, and 𝐸3 are stable asymptotically under certain conditions. Local stability of four equilibriums using Routh-Hurwitz criteria. Based on numerical simulation results illustrate that what looked like altenative food be that of additional food correspond to can maximize population susceptible prey and predator as soon as minimize population infected prey although the level high infection. The use alternative food be that of additional food for predators to prey disease in introducing new non-chemical methods in eco-epidemiological system.
Keywords : Eko-epidemiological system, infected prey, Additional food, Equilibrium, Stability
DAFTAR ISI
LEMBAR JUDUL ... i
LEMBAR PERNYATAAN ... ii
LEMBAR PENGESAHAN ... iii
PEDOMAN PENGGUNAAN SKRIPSI ... iv
SURAT PERNYATAAN TENTANG ORISINALITAS ... v
KATA PENGANTAR ... vi
ABSTRAK ... ix
ABSTRACT ... x
DAFTAR ISI ... xi
DAFTAR TABEL ... xiv
DAFTAR GAMBAR ... xv
DAFTAR LAMPIRAN ... xvi
BAB I PENDAHULUAN ... 1
1.1 Latar Belakang ... 1
1.2 Rumusan Masalah... 5
BAB II TINJAUAN PUSTAKA ... 7
2.1 Eko-epidemiologi ... 7
2.2 Model Logistik ... 8
2.3 Model Predator-Prey Lotka Volterra ... 8
2.4 Model Holling... 9
2.5 Sistem Persamaan Diferensial ... 11
2.6 Kestabilan Sistem Linier ... 13
2.7 Kriteria Routh-Hurwitz ... 16
2.4 Bilangan Reproduksi Dasar ... 18
BAB III METODOLOGI PENELITIAN ... 21
BAB IV PEMBAHASAN ... 23
4.1 Analisis Model Matematika Peran Penambahan Makanan dalam Sistem Eko-Epidemiologi dengan Penyakit pada Prey ... 23
4.1.1 Titik Setimbang Model ... 30
4.1.2 Analisis Kestabilan Asimtotis Lokal ... 35
4.2 Simulasi Model Matematika Peran Penambahan Makanan dalam Sistem Eko-epidemiologi dengan Penyakit pada Prey ... 44
BAB V PENUTUP ... 54
5.1 Kesimpulan ... 54
DAFTAR PUSTAKA ... 56 LAMPIRAN
DAFTAR TABEL
Tabel Judul Tabel Halaman
4.1 Keterangan parameter-parameter yang digunakan pada model matematika peran penambahan dalam sistem eko-epidemiologi dengan penyakit pada prey
25
4.2 Keterangan parameter-parameter setelah adanya perskalaan pada model
29
4.3 Nilai Awal Simulasi Titik Setimbang Koeksistensi 𝐸3 42 4.4
4.5
Nilai Parameter Simulasi Titik Setimbang Koeksisitensi
𝐸3
Nilai parameter simulasi numerik
43
DAFTAR GAMBAR
Gambar Judul Halaman
4.1 Simulasi Bidang Fase 𝑆 − 𝐼 untuk Titik Setimbang Koeksistensi 𝐸3
43
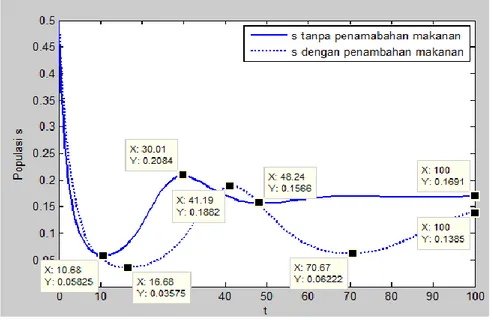
4.2 Dinamika populasi prey yang rentan untuk 𝛽 = 1,25 dengan 𝛼= 0,𝜉 = 0 dan 𝛼= 0,8,𝜉 = 0,4
46
4.3 Dinamika populasi prey yang rentan untuk 𝛽 = 0,1 dengan 𝛼= 0,𝜉 = 0 dan 𝛼= 0,8,𝜉 = 0,4 47 4.4 4.5 4.6 4.7
Dinamika populasi prey yang terinfeksi untuk 𝛽 = 1,25 dengan 𝛼= 0,𝜉 = 0 dan 𝛼= 0,8,𝜉 = 0,4
Dinamika populasi prey yang terinfeksi untuk 𝛽 = 0,1 dengan 𝛼= 0,𝜉 = 0 dan 𝛼= 0,8,𝜉 = 0,4
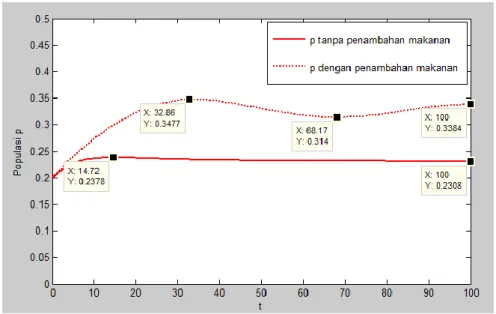
Dinamika populasi predator untuk 𝛽= 1,25 dengan
𝛼 = 0,𝜉= 0 dan 𝛼= 0,8,𝜉= 0,4
Dinamika populasi predator untuk 𝛽 = 0,1 dengan
𝛼 = 0,𝜉= 0 dan 𝛼= 0,8,𝜉= 0,4
48
50
51
DAFTAR LAMPIRAN
Lampiran Judul
1. Analisis Perskalaan
2. Perhitungan Titik Setimbang E0 3. Perhitungan Titik Setimbang E1
4. 5. 6. 7. 8. 9. 10. 11. 12. 13.
Perhitungan Titik Setimbang E2 Perhitungan Titik Setimbang E3
Perhitungan Basic Reproduction Number
Pencarian Persamaan Karakteritik Titik Setimbang E0
Pencarian Persamaan Karakteritik Titik Setimbang E1 Pencarian Persamaan Karakteritik Titik Setimbang E2 Pencarian Persamaan Karakteritik Titik Setimbang E3
Kode Program untuk Simulasi Bidang Fase dan Grafik Dinamika Simulasi Dinamika Model Matematika Peran Penambahan Makanan dalam Sistem Eko-epidemiologi dengan Penyakit pada Prey (𝛼= 0 dan 𝜉= 0)
Simulasi Dinamika Model Matematika Peran Penambahan Makanan dalam Sistem Eko-epidemiologi dengan Penyakit pada Prey(𝛼= 0.8 dan 𝜉= 0.4)
BAB I PENDAHULUAN
1.1 Latar Belakang
Hubungan timbal balik antara makhluk hidup dengan makhuk hidup lain serta dengan benda tak hidup di lingkungannya membentuk ekosistem. Ilmu yang mempelajari ekosistem disebut ekologi. Ekologi berasal dari dua kata dalam bahasa Yunani, yaitu oikos dan logos. Oikos artinya rumah atau tempat tinggal, dan logos artinya ilmu. Istilah ekologi pertama kali dikemukakan oleh Ernst Haeckel. Ekologi mempelajari bagaimana makhluk hidup dapat mempertahankan kehidupannya dengan mengadakan hubungan antar makhluk hidup dan dengan benda tak hidup di dalam tempat hidupnya atau lingkungannya (Syamsuri, 2007).
Pada dasarnya makhluk hidup dan habitatnya tidak dapat dipisahkan satu dengan yang lain, keduanya saling mempengaruhi. Setiap kelompok makhluk hidup menetap di tempat tertentu yang dinamakan habitat, seperti daratan, perairan, hutan, dan sawah (Aryulina, 2004). Antara makhluk hidup yang satu dengan yang lain terjadi hubungan, baik antara sesama spesies maupun antar spesies, sesama komponen biotik maupun antara komponen biotik dan abiotik. Hubungan timbal balik dikenal pula dengan istilah interaksi atau aksi interaksi (Syamsuri, 2007).
predasi umumnya suatu spesies memakan spesies lain, meskipun beberapa hewan memangsa sesama jenisnya. Pada predasi antar hewan, predator kebanyakan berukuran lebih besar daripada prey (Aryulina, 2004). Interaksi antar dua populasi ini sangat penting karena kelangsungan hidup makhluk hidup tergantung pada keseimbangan lingkungan di sekitarnya. Dengan demikian keseimbangan tersebut dapat tercapai jika jumlah rata-rata populasi dari mangsa dan pemangsa yang sedang berinteraksi sesuai dengan ukuran dan proporsinya.
Pada bidang ekologi, eko-epidemiologi sangat penting dalam pemahaman munculnya penyakit. Bidang tersebut mempelajari mengenai dinamika populasi, epidemi, dan penyakit yang terinfeksi pada komunitas yang ada di lingkungan masyarakat. Oleh karena itu dalam pemodelan matematika dikaji berbagai macam model matematika untuk mengetahui terjadi atau tidaknya suatu epidemi dalam populasi pada ekologi yang nyata. Hal ini didasarkan pada beberapa sifat spesifik dari aturan penyebaran penyakit menular dan faktor-faktor sosial yang terkait untuk membangun model matematika. Faktor penyakit pada sistem predator-prey pertama kali diperkenalkan oleh Anderson dan Mei. Anderson dan Mei meneliti faktor utama pengacauan yang terjadi pada interaksi predator-prey serta menemukan studi faktor pengendalian penyakit tersebut (Sahoo, 2015).
Selama 50 tahun terakhir, pengendalian penyakit sangat bergantung pada penggunaan bahan kimia seperti fungisida, bakterisida, dan fumigants tanah. Penggunaan bahan kimia untuk mengendalikan penyakit telah terbukti memiliki efek
lingkungan. Oleh karena itu metode non-kimia pengendalian penyakit menjadi perhatian besar (Sahoo dan Poria, 2014).
Penggunaan makanan altenatif adalah salah satu yang penting dalam pengobatan non-kimia untuk pengendalian penyakit dalam sistem eko-epidemiologi. Beberapa penelitian melakukan penambahan makanan dengan cara adanya makanan alternatif untuk predator dalam program pengendalian biologis. Sahoo dan Poria (2013) menyatakan bahwa makanan alternatif untuk predator dalam sistem predator-prey yang sakit. Sahoo dan Poria memberikan penjelasan bahwa meningkatnya populasi predator dengan adanya makanan alternatif dapat menghapus infeksi dari sistem (Sahoo dan Poria, 2013).
Adanya makanan alternatif sebagai penambahan makanan untuk predator dapat membantu pelestarian predator pada sistem eko-epidemiologi dengan penyakit pada prey, karena dalam sistem tersebut jumlah prey lebih sedikit daripada jumlah predator dan predator akan lebih survive jika tedapat lebih dari satu prey. Akibatnya, predator dapat memangsa makanan alternatif sebagai penambahan makanan yang telah tersedia sehingga kelestarian populasi predator akan tetap terjaga. Oleh karena itu, penambahan makanan dengan adanya makanan alternatif dapat memberikan keseimbangan antara populasi prey dan predator.
ikan tilapia mengalami kekosongan oksigen. Akibatnya, ikan tilapia yang terinfeksi akan berenang menuju permukaan air dan menjadi rentan dipredasi oleh burung pelikan. Apabila burung pelikan memakan ikan tilapia terinfeksi yang masih hidup, maka mereka akan mengalami keracunan dan mati, karena di dalam jaringan tubuh ikan tilapia terinfeksi masih terdapat racun botulism yang dihasilkan oleh bakteri Avian botulism(Chattopadhyay dan Bairagi, 2011).
Para ilmuwan telah mengembangkan model matematika untuk menggambarkan peran penambahan makanan tersebut. Hal ini ditunjukkan dengan banyaknya penelitian yang membahas tentang makanan alternatif sebagai peran penambahan makanan dengan penyakit pada prey. Salah satunya adalah Sahoo dan Poria (2015) dengan penelitiannya yang berjudul “Effects of additional food in a delayed predator-prey model”. Pada model tersebut interaksinya bertipe Holling.
Berdasarkan uraian di atas penulis tertarik untuk mengkaji ulang model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey. Dari model tersebut akan dianalisa kestabilan dari titik setimbang. Materi dalam penelitian ini bukanlah sesuatu yang baru karena diambil dari jurnal yang berjudul “Role of additional food in eco-epidemiological system with
disease in the prey” yang telah dikembangkan oleh Sahoo pada tahun 2015. Dalam
hal ini, analisis kestabilan titik setimbang digunakan untuk mengetahui peran penambahan makanan sebagai pengendalian penyakit pada prey.
1.2 Rumusan Masalah
Berdasarkan latar belakang yang telah penulis uraikan di atas, maka permasalahan yang akan diselesaikan dalam penelitian ini adalah:
1. Bagaimana analisis kestabilan titik setimbang model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey?
2. Bagaimana simulasi dan interpretasi dari model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey?
1.3 Tujuan
Berdasarkan rumusan masalah yang telah diuraikan di atas, tujuan dari penelitian ini adalah:
1. Menganalisis kestabilan titik setimbang model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey.
2. Mensimulasikan dan menginterpretasikan model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey.
1.4 Manfaat
Beberapa manfaat yang bisa diambil dari penelitian ini adalah sebagai berikut:
1. Memberikan kontribusi terhadap perkembangan ilmu pengetahuan khususnya di bidang pemodelan matematika yang terkait dengan bidang biologi terutama ekologi.
2. Memberikan gambaran kesetimbangan dari peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey.
3. Dapat digunakan sebagai acuan untuk penelitian selanjutnya.
1.5 Asumsi
Asumsi dari penelitian ini adalah sebagai berikut:
1. Penyakit menyebar hanya diantara populasi prey dan tidak diwariskan secara genetik.
2. Mangsa yang rentan menjadi terinfeksi ketika bersentuhan dengan mangsa yang terinfeksi.
BAB II
TINJAUAN PUSTAKA
Pada bab ini akan dibahas mengenai model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey, oleh karena itu akan diberikan beberapa definisi dan teorema yang mendukung pada pembahasan selanjutnya.
2.1 Eko-epidemiologi
Secara harfiah, epidemiologi berasal dari kata epi (permukaan di atas, menimpa), demo (orang, populasi, manusia), dan ologi (ilmu tentang) (Efendi dan Majhfudli, 2009). Dengan demikian, istilah epidemiologi berarti ilmu yang mempelajari tentang distribusi penyakit pada manusia, serta faktor-faktor resiko atau masalah kesehatan yang dapat menimbulkan terjadinya kesakitan pada sekelompok orang atau masyarakat. Menurut WHO pada Regional Commite Meeting ke-42 tahun 1989 di Bandung telah membuat definisi mengenai epidemiologi yaitu ilmu yang mempelajari distribusi dari peristiwa kesehatan dan peristiwa lainnya yang berhubungan dengan kesehatan yang menimpa sekelompok masyarakat, dan menerapkan ilmu tersebut untuk memecahkan masalah-masalah kesehatan (Chandra
2.2 Model Logistik
Teori pertumbuhan populasi dikemukakan pertama kali oleh Malthus pada tahun 1798. Malthus menuturkan bahwa petumbuhan populasi tumbuh secara eksponensial dan akhirnya melampaui produksi makanan. Pada 1883, teori ini disanggah oleh Verhulst. Verhulst menuturkan bahwa pertumbuhan populasi tidak naik secara eksponensial melainkan dibatasi oleh ukuran dan kesuburan dari daerah yang menjadi tempat tinggal dari populasi. Sebagai hasilnya populasi semakin mendekati ke keadaan tetap (steady state). Model seperti ini dinamakan model logistik yang dinyatakan dalam bentuk
𝑑𝑃
𝑑𝑡 =𝑟𝑃 1− 𝑃
𝐾 , (2.3)
dengan 𝑃 =𝑃(𝑡) adalah jumlah populasi pada saat 𝑡, 𝑟 adalah laju pertumbuhan intrinsik, yaitu nilai yang menggambarkan daya tumbuh suatu populasi. Dalam hal ini diasumsikan 𝑟> 0 karena setiap populasi memiliki potensi untuk berkembang biak, dan 𝐾 menyatakan kapasitas tampung yaitu ukuran maksimum dari suatu populasi yang dapat diokong oleh suatu lingkungan.
(Hofbauer dan Sigmund, 1998)
2.3 Model Predator-Prey Lotka Volterra
Model predator-prey Lotka-Volterra pertama kali diperkenalkan oleh Alfred J. Lotka pada tahun 1926. Model tersebut menggambarkan persaingan antara predator dengan prey. Apabila tidak ada interaksi yang terjadi diantara prey dan
predator serta lingkungan tidak membatasi maka populasi prey akan meningkat tak terbatas yang disebut dengan model pertumbuhan eksponensial. Akan tetapi, populasi predator akan turun secara eksponensial tanpa adanya prey. Hal ini terjadi karena prey tersebut adalah makanan utama bagi pemangsa.
Misalkan 𝑥= 𝑥(𝑡) mewakili total populasi prey pada saat 𝑡 dan 𝑦= 𝑦(𝑡) mewakili total populasi predator pada saat 𝑡, maka model predator-prey Lotka Volterra dinyatakan dalam bentuk
𝑑𝑥
𝑑𝑡 = 𝑎𝑥 − 𝑏𝑥𝑦 (2.1)
𝑑𝑦
𝑑𝑡 =−𝑐𝑦+𝑑𝑥𝑦, (2.2)
dengan 𝑎,𝑏,𝑐,𝑑 adalah konstanta positif, 𝑑𝑥
𝑑𝑡 adalah laju perubahan populasi prey
pada saat 𝑡dan 𝑑𝑦
𝑑𝑡 adalah laju perubahan populasi predator pada saat 𝑡. Parameter 𝑎
adalah laju pertumbuhan prey ketika tidak ada predator dan 𝑐 adalah laju penurunan dari predator ketika tidak ada prey, sedangkan – 𝑏𝑥𝑦 adalah laju berkurangnya populasi prey saat berinteraksi dengan populasi predator dan 𝑑𝑥𝑦 adalah laju bertambahnya populasi predator saat berinteraksi dengan populasi prey.
(Bacaer, 2011) 2.4 Model Holling
1. Mencari prey
2. Menangani prey yang terdiri dari: mengejar, memangsa, dan mencerna. Laju konsumsi predator dalam model ini dibatasi waktu. Hal ini terjadi karena saat jumlah prey berlimpah predator tidak perlu waktu untuk mencari, tetapi tetap menghabiskan waktu untuk menangani prey.
Total waktu adalah jumlah waktu yang dibutuhkan oleh predator untuk mencari dan menangani prey yakni
𝑇= 𝑇𝑠+𝑇 (2.4)
dengan 𝑇𝑠 adalah waktu untuk mencari prey dan 𝑇 adalah waktu untuk menangani prey. Diasumsikan bahwa predator menangkap 𝑁 prey selama waktu 𝑇 dengan
𝑁 > 0. Waktu untuk menangani prey sebanding dengan jumlah prey yang tertangkap
𝑇 =𝑁 (2.5)
adalah waktu untuk menangani satu prey.
Setelah menghabiskan 𝑇𝑠 untuk mencari, seekor predator menjelajah area sebanyak 𝑘𝑇𝑠, dengan 𝑘 adalah konstanta positif, 𝑥 adalah populasi prey per unit area dan 𝑘𝑥𝑇𝑠 yaitu waktu menangkap prey, sehingga
𝑁 =𝑘𝑥𝑇𝑠 (2.6)
dengan mensubstitusikan persamaan (2.4) dan (2.5) ke persamaan (2.6) diperoleh:
𝑁 =𝑘𝑥 𝑇 − 𝑇
⟺ 𝑁 =𝑘𝑥 𝑇 − 𝑁
⟺ 𝑁+𝑘𝑥𝑁 =𝑘𝑥𝑇
⟺ 𝑁 1 +𝑘𝑥 =𝑘𝑥𝑇
dari sini jumlah prey per satuan waktu atau laju predasi adalah
𝑁 𝑇 =
𝑘𝑥
1+𝑘𝑥 (2.7)
(Logan, 2006)
2.5 Sistem Persamaan Diferensial
Persamaan diferensial didefinisikan sebagai persamaan yang mengandung satu atau lebih variabel dependen dan turunannya yang berhubungan satu atau lebih variabel independen (Zill dan Cullen, 2009). Model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey ini dinyatakan dalam bentuk sistem persamaan diferensial nonlinier, karena adanya interaksi antar komponen. Secara umum sistem persamaan diferensial nonlinear sulit ditentukan secara analitik. Oleh karena itu, digunakan solusi khusus yang biasanya disebut titik setimbang, sehingga untuk mengetahui dinamika model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey dapat diketahui melalui solusi khusus model tersebut. Berikut ini diberikan beberapa definisi serta teorema yang berhubungan dengan titik setimbang pada sistem persamaan diferensial adalah sebagai berikut:
Definisi 2.1 Sebuah sistem persamaan diferensial linier dapat dinyatakan sebagai:
𝑑𝑥
𝑑𝑡 = 𝑥 (𝑡) =𝐴𝑥(𝑡) (2.8)
dengan 𝑥 𝑡 ∈ ℝ𝑛 dinamakan vektor keadaan (state). Penyelesaian dari sistem (2.8) adalah 𝑥 𝑡 = 𝑒𝐴𝑡𝑥0 dengan 𝑒𝐴𝑡 =𝐼+𝐴𝑡+𝐴2𝑡 2 2!+⋯+𝐴 𝑘𝑡 𝑘 𝑘!+⋯= 𝐴 𝑘𝑡 𝑘 𝑘! ∞ 𝑘=0
dan 𝑥 𝑡0 =𝑥0 dinamakan nilai awal dari sistem.
(Bronson dan Costa, 2007)
Definisi 2.2 Sebuah sistem persamaan diferensial orde satu dalam 𝑛 persamaan dinamakan sebagai sistem autonomous jika sistem tersebut ditulis dalam bentuk
𝑑𝑥1 𝑑𝑡 = 𝑔1(𝑥1,𝑥2,…,𝑥𝑛) 𝑑𝑥2 𝑑𝑡 =𝑔2 𝑥1,𝑥2,…,𝑥𝑛 . . . 𝑑𝑥𝑛 𝑑𝑡 = 𝑔𝑛 𝑥1,𝑥2,…,𝑥𝑛 ,
dengan variabel t tidak muncul secara eksplisit di setiap persamaan diferensial. Jika variabel t muncul secara eksplisit pada persamaan diferensial maka dinamakan sistem non-autonomous
(Zill dan Cullen, 2009)
Definisi 2.3 Diberikan sistem persamaan diferensial autonomous, 𝑑𝑥
𝑑𝑡 =𝑓(𝑥). Titik 𝑥
dikatakan titik setimbang jika memenuhi 𝑓 𝑥 = 0.
(Olsder, 2003)
2.6 Kestabilan Sistem Linier
Setelah didapatkan titik setimbang model, selanjutnya dilakukan analisis pada titik setimbang model, guna untuk mengetahui dinamika perilaku solusi disekitar titik setimbang. Solusi khusus disekitar titik setimbang akan diaproksimasi menggunakan garis linear (linearisasi) yang akan mewakili model dalam bentuk sistem persamaan diferensial linear menggunakan matriks jacobian. Nilai eigen dari matriks Jacobian digunakan untuk menganalisis kestabilan dari titik setimbang. Kestabilan tersebut bersifat lokal karena hanya berlaku disekitar titik setimbang. Berikut ini diberikan definisi maupun teorema yang berhubungan dengan linearisasi sistem persamaan diferensial dan kestabilan lokal pada titik setimbang.
Definisi 2.4 Diberikan sistem persamaan diferensial autonomous sebagai berikut: 𝑑𝑥1(𝑡) 𝑑𝑡 = 𝑔1(𝑥1,𝑥2,…,𝑥𝑛) 𝑑𝑥2(𝑡) 𝑑𝑡 = 𝑔2 𝑥1,𝑥2,…,𝑥𝑛 . . . 𝑑𝑥𝑛(𝑡) 𝑑𝑡 = 𝑔𝑛 𝑥1,𝑥2,…,𝑥𝑛
Matriks Jacobian dari sistem di atas adalah:
𝜕𝑔1 𝜕𝑥1 𝜕𝑔1 𝜕𝑥2 … 𝜕𝑔1 𝜕𝑥𝑛 𝜕𝑔2 𝜕𝑥1 𝜕𝑔2 𝜕𝑥2 … 𝜕𝑔2 𝜕𝑥𝑛 … … ⋱ … 𝜕𝑔𝑛 𝜕𝑥1 𝜕𝑔𝑛 𝜕𝑥2 … 𝜕𝑔𝑛 𝜕𝑥𝑛
(Zill dan Cullen, 2009)
Definisi 2.5 Jika 𝐴 adalah matriks berukuran 𝑛×𝑛, maka vektor tak nol 𝑥 di dalam
ℝ𝑛 dinamakan vektor eigen dari 𝐴 jika 𝐴𝑥 adalah kelipatan skalar dari 𝑥, yaitu:
𝐴𝑥 =𝜆𝑥
skalar 𝜆 dinamakan nilai eigen dari 𝐴 dan 𝑥 dikatakan vektor eigen yang bersesuaian dengan 𝜆.
Teorema 2.6 Jika 𝐴 adalah matriks berukuran 𝑛×𝑛, maka pernyataan di bawah ini ekivalen satu sama lain:
a. 𝜆 adalah nilai eigen dari 𝐴.
b. Sistem persamaan 𝜆𝐼 − 𝐴 𝑥 = 0 mempunyai solusi tak trivial.
c. Untuk 𝜆 ∈ ℝ𝑛 maka ada vektor tak nol 𝑥 di dalam ℝ𝑛 sehingga 𝐴𝑥 =𝜆𝑥. d. 𝜆 adalah solusi dari persamaan karakteristik det 𝜆𝐼 − 𝐴 = 0.
(Anton, 2005)
Definisi 2.7 Sistem 𝑥 = 𝐴𝑥(𝑡) dikatakan stabil asimtotis jika lim
𝑡→∞𝑥 𝑡 = 0
dengan 𝑥(𝑡) penyelesaian dari sistem tersebut, 𝑥 𝑡 ∈ ℝ𝑛 dan 0 adalah titik
setimbang dari 𝑥 = 𝐴𝑥(𝑡).
(Zill and Cullen, 2009)
Teorema 2.8 Sistem 𝑥 =𝐴𝑥(𝑡) dikatakan stabil asimtotis jika dan hanya jika semua nilai eigen dari 𝐴, yakni 𝜆𝑖 𝐴 mempunyai bagian real negatif dan dinotasikan sebagai 𝑅𝑒(𝜆𝑖(𝐴)) < 0.
2.7 Kriteria Routh-Hurwitz
Pada akhir 1800-an, A. Hurwitz dan E.J. Routh menerbitkan sebuah metode yang menyelidiki tentang stabilitas sistem yang disebut Kriteria Routh Hurwitz. Metode ini dilakukan untuk menunjukkan tanda bagian rea negatif dari nilai eigen tanpa menghitung akar-akar persamaan karrakteristik secara langsung.
(Levine, 2000)
Diberikan peramaan karakteristik dengan derajat 𝑛 sebagai berikut:
𝜆𝑛 +𝑎1𝜆𝑛−1+𝑎2𝜆𝑛−2+⋯+𝑎𝑛−1𝜆+𝑎𝑛 = 0, (2.9)
dengan koefisien 𝑎𝑖 adalah bagian real, dan 𝑖= 1,2,3,…,𝑛. Dari sini dapat dibentuk matriks 𝐻𝑛, dengan 𝐻𝑛 adalah matriks Hurwitz yang berisi koefisien 𝑎𝑖 dari persamaan karakteristik (2.9) yang didefinisikan sebagai berikut:
𝐻𝑛 = 𝑎1 1 0 0 ⋯ 0 𝑎3 𝑎2 𝑎1 1 ⋯ 0 𝑎5 𝑎4 𝑎3 𝑎2 ⋯ 0 ⋮ ⋮ ⋮ ⋮ ⋱ ⋮ 𝑎2𝑛−3 𝑎2𝑛−4 𝑎2𝑛−5 𝑎2𝑛−6 ⋯ 𝑎𝑛−2 𝑎2𝑛−1 𝑎2𝑛−2 𝑎2𝑛−3 𝑎2𝑛−4 ⋯ 𝑎𝑛 , dengan 𝑎𝑗 = 𝑎𝑗 , 𝑗 ≤ 𝑛 0 , 𝑗> 𝑛 .
Teorema 2.9 Akar-akar dari persamaan karakteristik (2.9) bernilai negatif atau mempunyai bagian real negatif jika dan hanya jika semua determinan dari matriks Hurwitz bernilai positif atau
det 𝐻𝑗 > 0,𝑗 = 1,2,…,𝑛.
Berikut ini akan diberikan contoh kriteria Routh-Hurwitz dengan derajat 𝑛= 3. Untuk 𝑛= 3, bentuk persamaan karakteristiknya adalah:
𝜆3+𝑎
1𝜆2 +𝑎2𝜆+𝑎3 = 0. (2.10)
Dari persamaan (2.10) maka dibentuk matriks Hurwitz sebagai berikut:
𝐻1 = 𝑎1 𝐻2 = 𝑎1 1
0 𝑎2 𝐻3 =
𝑎1 1 0
𝑎3 𝑎2 𝑎1
0 0 𝑎3
Berdasarkan kriteria Routh-Hurwitz, akar-akar persamaan (2.10) mempunyai bagian real negatif jika dan hanya jika det 𝐻1 > 0, det 𝐻2 > 0, dan det 𝐻3 > 0. Dengan demikian didapatkan kondisi sebagai berikut:
i. det 𝐻1 = 𝑎1 > 0 didapatkan 𝑎1 > 0.
ii. det 𝐻2 = 𝑎1 1
0 𝑎2 > 0 didapatkan 𝑎1𝑎2 > 0. Karena 𝑎1 > 0 maka
𝑎2 > 0. iii. 𝑑𝑒𝑡(𝐻3) = 𝑎1 1 0 𝑎3 𝑎2 𝑎1 0 0 𝑎3 > 0 sehingga 𝑎1𝑎2𝑎3− 𝑎32 > 0.
Akibatnya 𝑎3(𝑎1𝑎2− 𝑎3) > 0, dengan demikian didapatkan dua kondisi yaitu a. 𝑎3 > 0 dan 𝑎1𝑎2− 𝑎3 > 0
b. 𝑎3 < 0 dan (𝑎1𝑎2− 𝑎3) < 0
Untuk kondisi (b) tidak mungkin terjadi, sebab jika 𝑎3 < 0 maka tidak mungkin
2.8 Bilangan Reproduksi Dasar
Bilangan reproduksi dasar, dinotasikan dengan ℛ0, merupakan suatu ukuran
potensi penyebaran penyakit dalam suatu populasi. Bilangan reproduksi dasar didefinisikan sebagai nilai harapan banyaknya populasi rentan yang menjadi terinfeksi selama masa infeksi berlangsung.
Kondisi yang timbul adalah:
1. Jika ℛ0 < 1, maka satu individu yang terinfeksi akan menginfeksi kurang dari
satu indvidu rentan sehingga penyakit akan hilang dari populasi.
2. Jika ℛ0 > 1, maka satu individu terinfeksi akan menginfeksi lebih dari satu individu rentan, sehingga penyakit akan bertahan dalam populasi.
ℛ0 dalam skripsi ini ditentukan dari nilai eigen taknegatif dengan modulus
terbesar the next generation matriks. Matriks ini merupakan suatu matriks yang konstruksi dari sub-subpopulasi yang menyebabkan infeksi saja. Untuk model umum dapat ditulis sebagai berikut:
𝑎 𝑖 =ℱ𝑖 𝑎,𝑏 − 𝒱𝑖 𝑎,𝑏 ,𝑖 = 1,2,…,𝑛
𝑏 𝑗 =𝑔𝑗 𝑎,𝑏 , 𝑗 = 1,2,…,𝑚
maka sistem persamaan diferensial taklinear 𝑥 =𝑓 𝑥 ,𝑥 ∈ ℝ𝑛 dapat ditulis sebagai
berikut:
𝑀 =𝜕𝑀𝑖
𝜕𝑎𝑗 0,𝑏0 𝑑𝑎𝑛 𝐷 =
𝜕𝐷𝑖
𝜕𝑎𝑗(0,𝑏0); (0,b0) adalah titik tetap tanpa penyakit.
The next generatiom matriks K untuk suatu sistem persamaan diferensial pada titik tetap tanpa penyakit terbentuk
K=MD-1
Nilai eigen taknegatif dengan modulus terbesar matriks K, yaitu 𝜌(𝑀𝐷−1), yang nantinya dapat digunakan sebagai nilai ℛ0, sehingga dapat ditulis
𝜌(𝑀𝐷−1 =ℜ0).
BAB III
METODOLOGI PENELITIAN
Metode penelitian yang digunakan dalam penelitian ini adalah sebagai berikut:
1. Melakukan studi literatur melalui buku referensi, jurnal maupun artikel yang berkaitan dengan model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey.
2. Mengkaji model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey.
3. Menganalisis kestabilan model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey, dengan langkah-langkah sebagai berikut:
a. Menentukan titik setimbang dari model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey. b. Menganalisis kestabilan lokal dengan langkah-langkah sebagai berikut:
i. Linearisasi model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey dengan menggunakan matriks Jacobian.
ii. Menentukan sifat kestabilan dari titik setimbang yang telah diperoleh dari model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey.
4. Melakukan simulasi numerik dari model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey dengan menggunakan software pemrograman yaitu MATLAB atau MAPLE.
5. Melakukan interpretasi dari model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey.
6. Menarik kesimpulan dari model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey berdasarkan langkah pertama hingga langkah terakhir.
BAB IV PEMBAHASAN
Pada bab ini dibahas mengenai analisis kestabilan dan simulasi model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey. Pertama kali model dianalisis kestabilan dari titik setimbang yang telah diperoleh. Selanjutnya model tersebut disimulasikan ke dalam sebuah program MATLAB R2009a untuk mengetahui pengaruh prey dan penambahan makanan pada predator.
4.1 Analisis Model Matematika Peran Penambahan Makanan dalam Sistem Eko-Epidemiologi dengan Penyakit pada Prey
Pada bagian ini dijelaskan model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey. Model matematika tersebut mengacu pada model yang dikembangkan oleh Sahoo (2015).
Asumsi yang digunakan dalam pembentukan model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey adalah sebagai berikut:
1. Populasi dibagi menjadi tiga subpopulasi, yaitu:
a. Subpopulasi prey suspectible atau rentan terhadap penyakit yang dinyatakan dengan S.
b. Subpopulasi prey infectious atau terinfeksi dan dapat menularkan penyakit yang dinyatakan dengan I.
c. Subpopulasi predator yang dapat dinyatakan dengan P.
2. Populasi mangsa yang rentan tumbuh secara logistik dengan tingkat pertumbuhan intrinsik dan kapasitas pendukung.
3. Diasumsikan bahwa penyakit ini menyebar hanya di antara populasi mangsa dan tidak diwariskan secara genetik. Populasi yang terinfeksi tidak sembuh atau menjadi kebal.
4. Mangsa yang rentan menjadi terinfeksi ketika mereka sampai bersentuhan dengan mangsa yang terinfeksi. Proses kontak diasumsikan mengikuti kinetika kejadian saturasi (kejenuhan), dengan 𝑊1 mengukur kekuatan infeksi, 𝐸1 konstanta saturasi (titik jenuh) dan 𝑊2 efek penghambatan. 5. Terdapat makanan alternatif sebagai penambahan makanan untuk Predator
bernilai konstan 𝐴 yang terdistribusi secara merata di habitat.
6. Jumlah pertemuan per predator dengan makanan alternatif sebagai penambahan makanan sebanding dengan kepadatan makanan alternatif sebagai penambahan makanan.
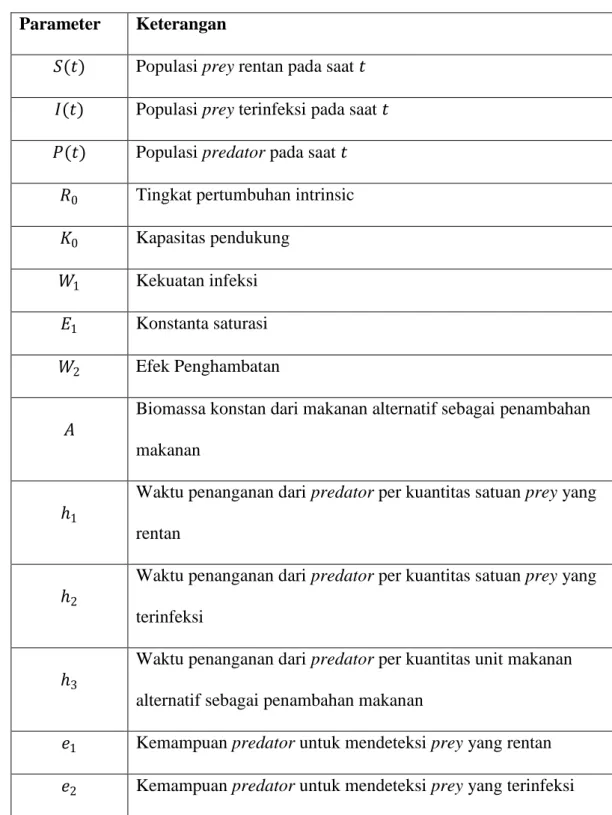
7. Proporsionalitas konstan mencirikan kemampuan predator untuk mengidentifikasi makanan alternatif sebagai penambahan makanan. Pada Tabel 4.1 berikut merupakan keterangan parameter-parameter yang digunakan pada model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey.
Tabel 4.1 Keterangan parameter-parameter yang digunakan pada model matematika peran penambahan dalam sistem eko-epidemiologi dengan penyakit pada prey
Parameter Keterangan
𝑆(𝑡) Populasi prey rentan pada saat 𝑡 𝐼(𝑡) Populasi prey terinfeksi pada saat 𝑡 𝑃(𝑡) Populasi predator pada saat 𝑡
𝑅0 Tingkat pertumbuhan intrinsic
𝐾0 Kapasitas pendukung
𝑊1 Kekuatan infeksi
𝐸1 Konstanta saturasi
𝑊2 Efek Penghambatan
𝐴
Biomassa konstan dari makanan alternatif sebagai penambahan makanan
1
Waktu penanganan dari predator per kuantitas satuan prey yang rentan
2
Waktu penanganan dari predator per kuantitas satuan prey yang terinfeksi
3
Waktu penanganan dari predator per kuantitas unit makanan alternatif sebagai penambahan makanan
𝑒1 Kemampuan predator untuk mendeteksi prey yang rentan
𝑒3
Kemampuan predator untuk mendeteksi makanan alternatif sebagai penambahan makanan
𝑛1 Nilai gizi prey yang rentan
𝑛2 Nilai gizi prey yang terinfeksi
𝑛3 Nilai gizi makanan alternatif sebagai penambahan makanan
𝐷1 Tingkat kematian prey yang terinfeksi
𝐷2 Tingkat kematian predator
Diasumsikan jumlah populasi bernilai positif maka 𝑠 𝑡 ≥0,𝑖 𝑡 ≥
0,𝑝 𝑡 ≥0. Berdasarkan asumsi dan parameter di atas maka diperoleh model matematika sebagai berikut:
𝑑𝑆 𝑑𝑇 =𝑅0𝑆 1− 𝑆+𝐼 𝐾0 − 𝑊1𝑆𝐼 𝐸1+𝑊2𝐼− 𝑒1𝑆𝑃 1+𝑒33𝐴+𝑒11𝑆 (4.1) 𝑑𝐼 𝑑𝑇 = 𝑊1𝑆𝐼 𝐸1+𝑊2𝐼− 𝑒1𝐼𝑃 1+𝑒33𝐴+𝑒22𝐼− 𝐷1𝐼 (4.2) 𝑑𝑃 𝑑𝑇 = (𝑛1𝑒1𝑆+𝑛3𝑒3𝐴)𝑃 1+𝑒33𝐴+𝑒11𝑆 + (𝑛2𝑒2𝐼+𝑛3𝑒3𝐴)𝑃 1+𝑒33𝐴+𝑒22𝐼 − 𝐷2𝑃 (4.3)
Persamaan (4.1) menggambarkan tentang laju pertumbuhan mangsa yang rentan. Populasi mangsa yang rentan bertambah karena pertumbuhan secara logistik dengan tingkat pertumbuhan intrinsik dan kapasitas pendukung yang akan berkurang karena adanya interaksi antara mangsa yang rentan dengan mangsa yang terinfeksi terhadap konstanta saturasi dan efek penghambatan yang mengikuti fungsi respon Holling tipe II serta berkurang karena adanya interaksi
tipe II terhadap biomassa konstan dari makanan alternatif sebagai penambahan makanan.
Persamaan (4.2) menjelaskan tentang laju pertumbuhan mangsa yang terinfeksi. Populasi mangsa yang terinfeksi bertambah karena adanya interaksi antara mangsa yang rentan dengan mangsa yang terinfeksi terhadap konstanta saturasi dan efek penghambatan yang mengikuti fungsi respon Holling tipe II dan berkurang karena adanya interaksi antara mangsa yang terinfeksi dengan predator yang mengikuti fungsi respon Holling tipe II terhadap biomassa konstan dari makanan alternatif sebagai penambahan makanan serta berkurang karena kematian alami mangsa yang terinfeksi.
Persamaan (4.3) menjelaskan tentang laju pertumbuhan predator. Populasi predator bertambah karena adanya kemampuan predator untuk mendeteksi mangsa yang rentan terhadap nilai gizi dan kuantitas pada makanan alternatif sebagai penambahan makanan yang mengikuti fungsi respon Holling tipe II dan bertambah karena adanya kemampuan predator untuk mendeteksi mangsa yang terinfeksi terhadap nilai gizi dan kuantitas pada makanan alternatif sebagai penambahan makanan yang mengikuti fungsi respon Holling tipe II serta berkurang karena kematian alami predator.
Selanjutnya pada persamaan (4.1) – (4.3) dilakukan perskalaan, sehingga model dapat ditulis dalam bentuk sebagai berikut:
𝑑𝑆 𝑑𝑇 =𝑅0𝑆 1− 𝑆+𝐼 𝐾0 − 𝑊1𝑆𝐼 𝐸1+𝑊2𝐼− 𝐴1𝑆𝑃 𝐵1+𝛼1𝜇1𝐴+𝑆 (4.4) 𝑑𝐼 𝑑𝑇 = 𝑊1𝑆𝐼 𝐸1+𝑊2𝐼− 𝐴2𝐼𝑃 𝐵2+𝛼2𝜇2𝐴+𝐼− 𝐷1𝐼 (4.5)
𝑑𝑃 𝑑𝑇 =𝐴1𝐶1 (𝑆+𝜇1𝐴)𝑃 𝐵1+𝛼1𝜇1𝐴+𝑆+𝐴2𝐶2 (𝐼+𝜇2𝐴)𝑃 𝐵2+𝛼2𝜇2𝐴+𝐼− 𝐷2𝑃, (4.6) dengan 𝐴1 = 1 1,𝐴2 = 1 2,𝐵1 = 1 𝑒11, 𝐵2 = 1 𝑒22,𝛼1 = 𝑛1 𝑛3 3 1,𝛼2 = 𝑛2 𝑛3 3 2, 𝜇1 =𝑛3 𝑛1 𝑒3 𝑒1,𝜇2 = 𝑛3 𝑛2 𝑒3 𝑒2,𝐴1𝐶1 = 𝑛1 1,𝐴2𝐶2 = 𝑛2 2.
Untuk mempermudah, diasumsikan 𝛼1 =𝛼2 =𝛼, 𝜇1 = 𝜇2 = 𝜇, dan 𝐵1 = 𝐵2.
Oleh karena itu, model di atas direduksikan dengan persamaan diferensial biasa sebagai berikut, 𝑑𝑆 𝑑𝑇 =𝑅0𝑆 1− 𝑆+𝐼 𝐾0 − 𝑊1𝑆𝐼 𝐸1+𝑊2𝐼− 𝐴1𝑆𝑃 𝐵1+𝛼𝜇𝐴+𝑆 (4.7) 𝑑𝐼 𝑑𝑇 = 𝑊1𝑆𝐼 𝐸1+𝑊2𝐼− 𝐴2𝐼𝑃 𝐵1+𝛼𝜇𝐴+𝐼− 𝐷1𝐼 (4.8) 𝑑𝑃 𝑑𝑇 =𝐴1𝐶1 (𝑆+𝜇𝐴)𝑃 𝐵1+𝛼𝜇𝐴+𝑆+𝐴2𝐶2 (𝐼+𝜇𝐴)𝑃 𝐵1+𝛼𝜇𝐴+𝐼− 𝐷2𝑃 (4.9) Kemudian, dari persamaan (4.7) – (4.9) dilakukan perskalaan menggunakan
𝑠 = 𝑆
𝐾0,𝑖=
𝐼 𝐾0,𝑝=
𝑃
𝐾0, dan 𝑡= 𝑅0𝑇, sehingga diperoleh model sebagai berikut:
𝑑𝑠 𝑑𝑡 =𝑠 1− 𝑠 − 𝑖 − 𝛽𝑠𝑖 1+𝛾𝑖− 𝑎𝑠𝑝 1+𝛼𝜉+𝑏𝑠 (4.10) 𝑑𝑖 𝑑𝑡 = 𝛽𝑠𝑖 1+𝛾𝑖− 𝜂𝑖𝑝 1+𝛼𝜉+𝑏𝑖 − 𝑑1𝑖 (4.11) 𝑑𝑝 𝑑𝑡 = 𝜖1 𝑠+𝑐𝜉 𝑝 1+𝛼𝜉+𝑏𝑠 + 𝜖2 𝑖+𝑐𝜉 𝑝 1+𝛼𝜉+𝑏𝑖 − 𝑑2𝑝, (4.12) dengan 𝛽= 𝑊1𝐾0 𝐸1𝑅0,𝛾= 𝑊2𝐾0 𝐸1 ,𝑎= 𝐴1𝐾0 𝑅0𝐵1,𝜉= 𝜇𝐴 𝐵1,𝑏 = 𝐾0 𝐵1,𝜂 = 𝐴2𝐾0 𝑅0𝐵1,𝜖1 = 𝐶1𝐴1𝐾0 𝑅0𝐵1 , 𝜖2 = 𝐶2𝐴2𝐾0 𝑅0𝐵2 ,𝑐 = 𝐵1 𝐾0,𝑑1 = 𝐷1 𝑅0, dan 𝑑2 = 𝐷2 𝑅0 (Lampiran 1).
penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey, diasumsikan:
𝛼,𝛽,𝛾,𝜖1,𝜖2,𝜉,𝜂,𝑎,𝑏,𝑐,𝑑1,𝑑2 ≥0.
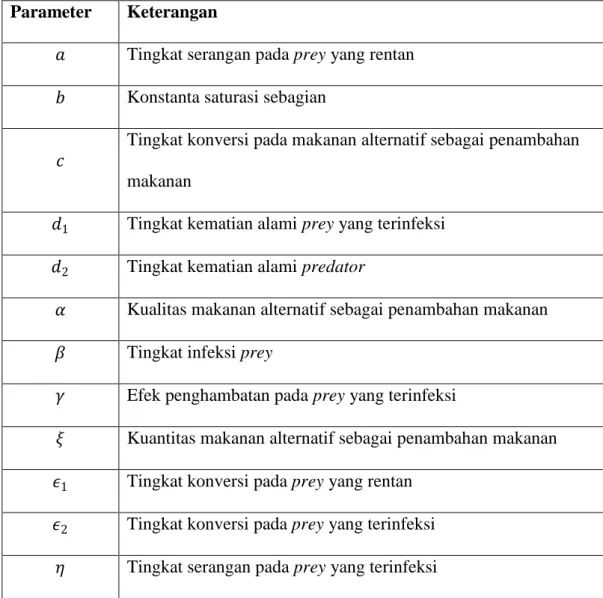
Pada Tabel 4.2 berikut merupakan keterangan parameter-parameter setelah adanya perskalaan pada model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey.
Tabel 4.2 Keterangan parameter-parameter setelah adanya perskalaan pada model
Parameter Keterangan
𝑎 Tingkat serangan pada prey yang rentan
𝑏 Konstanta saturasi sebagian
𝑐
Tingkat konversi pada makanan alternatif sebagai penambahan makanan
𝑑1 Tingkat kematian alami prey yang terinfeksi
𝑑2 Tingkat kematian alami predator
𝛼 Kualitas makanan alternatif sebagai penambahan makanan
𝛽 Tingkat infeksi prey
𝛾 Efek penghambatan pada prey yang terinfeksi
𝜉 Kuantitas makanan alternatif sebagai penambahan makanan
𝜖1 Tingkat konversi pada prey yang rentan
𝜖2 Tingkat konversi pada prey yang terinfeksi
4.1.1 Titik Setimbang Model
Karena model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey tersebut berbentuk non linear maka solusi umum akan sulit dicari, sehingga penulis hanya akan mendapatkan solusi khusus melalui titik setimbang yang stabil asimtotis. Berikut merupakan penjelasan mengenai pencarian titik setimbang pada model matematika sistem eko-epidemiologi dengan mempertimbangkan prey terinfeksi dan makanan alternatif sebagai penambahan makanan pada predator.
Berdasarkan Definisi 2.3, model matematika di atas akan memiliki titik setimbang jika memenuhi 𝑑𝑠 𝑑𝑡 = 𝑑𝑖 𝑑𝑡 = 𝑑𝑝 𝑑𝑡 = 0, sehingga: 𝑑𝑠 𝑑𝑡 = 𝑠 1− 𝑠 − 𝑖 − 𝛽𝑠𝑖 1+𝛾𝑖 − 𝑎𝑠𝑝 1+𝛼𝜉+𝑏𝑠 = 0 (4.13) 𝑑𝑖 𝑑𝑡 = 𝛽𝑠𝑖 1+𝛾𝑖− 𝜂𝑖𝑝 1+𝛼𝜉+𝑏𝑖− 𝑑1𝑖= 0 (4.14) 𝑑𝑝 𝑑𝑡 = 𝜖1 𝑠+𝑐𝜉 𝑝 1+𝛼𝜉+𝑏𝑠 + 𝜖2 𝑖+𝑐𝜉 𝑝 1+𝛼𝜉+𝑏𝑖 − 𝑑2𝑖= 0 (4.15)
Dari persamaan (4.13) – (4.15) didapat:
1. Titik setimbang kepunahan, yakni kondisi ketika populasi prey yang rentan, prey yang terinfeksi, dan predator dalam kepunahan. Kondisi ini terjadi ketika 𝑠 = 0,𝑖 = 0 dan 𝑝= 0. Dari sini diperoleh titik setimbang kepunahan 𝐸0 = 𝑠0,𝑖0,𝑝0 = (0,0,0). Uraian lengkap perhitungan titik setimbang 𝐸0 dapat dilihat pada Lampiran 2.
𝑖= 0 dan 𝑝= 0 maka dari persamaan (4.13) diperoleh 𝑠 1− 𝑠 − 𝑖 −
𝛽𝑠𝑖 1+𝛾𝑖 −
𝑎𝑠𝑝
1+𝛼𝜉+𝑏𝑠 = 0 sehingga 𝑠 = 1. Dari sini diperoleh titik setimbang
aksial 𝐸1 = 𝑠1,𝑖1,𝑝1 = (1,0,0). Uraian lengkap perhitungan titik setimbang 𝐸1 dapat dilihat pada Lampiran 3.
3. Titik setimbang bebas penyakit, yakni kondisi ketika tidak adanya prey yang terinfeksi. Kondisi ini terjadi ketika 𝑠 ≠0,𝑖= 0 dan 𝑝 ≠0. Jika 𝑖= 0 maka dari persamaan (4.15) diperoleh
𝑝 𝜖1 𝑠+𝑐𝜉 1+𝛼𝜉+𝑏𝑠+ 𝜖2 𝑖+𝑐𝜉 1+𝛼𝜉+𝑏𝑖− 𝑑2 = 0, sehingga 𝑠= 𝑑2(1+𝛼𝜉)−𝜖2𝑐𝜉 −𝜖1𝑐𝜉 𝜖1−𝑑2𝑏+1+𝛼𝜉𝜖2𝑐𝜉𝑏
, sedangkan dari persamaan (4.13)
diperoleh 𝑠 1− 𝑠 − 𝑖 − 𝛽𝑖 1+𝛾𝑖 − 𝑎𝑝 1+𝛼𝜉+𝑏𝑠 = 0, sehingga 𝑝 =1−𝑠
𝑎 1 +𝛼𝜉+𝑏𝑠 . Dari sini diperoleh titik setimbang bebas
penyakit 𝐸2 = 𝑠2,𝑖2,𝑝2 = 𝑑2(1+𝛼𝜉)−𝜖2𝑐𝜉 −𝜖1𝑐𝜉 𝜖1−𝑑2𝑏+1+𝛼𝜉𝜖2𝑐𝜉𝑏 , 0,1−𝑠2 𝑎 1 +𝛼𝜉+𝑏𝑠2 .
Titik setimbang 𝐸2 eksis jika 𝑠2 < 1 dan
𝑑2(1+𝛼𝜉)−𝜖2𝑐𝜉 −𝜖1𝑐𝜉
𝜖1−𝑑2𝑏+1+𝛼𝜉𝜖2𝑐𝜉𝑏
> 0 terdapat
dua kondisi yaitu
𝑑2 >𝑐𝜉(𝜖2+𝜖1) 1+𝛼𝜉 dan 𝜖1+ 𝜖2𝑐𝜉 (1+𝛼𝜉)𝑏> 𝑑2𝑏 atau 𝑑2 < 𝑐𝜉(𝜖2+𝜖1) 1+𝛼𝜉 dan 𝜖1+ 𝜖2𝑐𝜉 (1+𝛼𝜉)𝑏< 𝑑2𝑏 .
Selanjutnya, berdasarkan nilai parameter yang telah diketahui dimasukkan ke dua kondisi tersebut dengan bantuan MAPLE. Sehingga didapat kondisi yang memenuhi titik setimbang 𝐸2 sebagai berikut:
𝑑2 >
𝑐𝜉(𝜖2+𝜖1)
1+𝛼𝜉 dan 𝜖1+ 𝜖2𝑐𝜉
(1+𝛼𝜉)𝑏>𝑑2𝑏.
Oleh karena itu, titik setimbang 𝐸2 eksis jika: (i) 𝑠2 < 1,
(ii) 𝑑2 > 𝑐𝜉(𝜖2+𝜖1)
1+𝛼𝜉 , dan
(iii) 𝜖1+ 𝜖2𝑐𝜉
(1+𝛼𝜉)𝑏> 𝑑2𝑏
Uraian lengkap perhitungan titik setimbang 𝐸2 dapat dilihat pada Lampiran 4. 4. Titik setimbang koeksistensi, yakni kondisi ketika populasi prey yang
rentan, prey yang terinfeksi, dan predator hidup berdampingan. Kondisi ini terjadi jika 𝑠 ≠0,𝑖 ≠0 dan 𝑝 ≠0. Dari persamaan (4.15) diperoleh
𝑝 𝜖1 𝑠+𝑐𝜉 1+𝛼𝜉+𝑏𝑠+ 𝜖2 𝑖+𝑐𝜉 1+𝛼𝜉+𝑏𝑖− 𝑑2 = 0, Sehingga 𝑖= 𝑑2 1+𝛼𝜉 1+𝛼𝜉+𝑏𝑠 −𝜖1 𝑠+𝑐𝜉 −𝜖1 𝑠+𝑐𝜉 𝛼𝜉 −𝜖2𝑐𝜉 1+𝛼𝜉+𝑏𝑠 𝜖2 1+𝛼𝜉+𝑏𝑠 −𝑑2𝑏 1+𝛼𝜉+𝑏𝑠 +𝜖1 𝑠+𝑐𝜉 𝑏 , sedangkan dari persamaan (4.13) diperoleh
𝑠 1− 𝑠 − 𝑖 − 𝛽𝑖 1+𝛾𝑖 − 𝑎𝑝 1+𝛼𝜉+𝑏𝑠 = 0, sehingga 𝑝= 1+𝛼𝜉+𝑏𝑠 1−𝑠−𝑖 1+𝛾𝑖 −𝛽𝑖 1+𝛼𝜉+𝑏𝑠 𝑎 1+𝛾𝑖 ,
sehingga 𝑠= 1+𝛾𝑖 𝛽
𝜂𝑝
1+𝛼𝜉+𝑏𝑖+𝑑1 . Dari sini diperoleh titik setimbang
koeksistensi 𝐸3= 𝑠3,𝑖3,𝑝3 sebagai berikut
𝑠3= 1+𝛾𝑖3 𝛽 𝜂 𝑝3 1+𝛼𝜉+𝑏𝑖3+𝑑1 , 𝑖3 = 𝑑2 1+𝛼𝜉 1+𝛼𝜉+𝑏𝑠3 −𝜖1 𝑠3+𝑐𝜉 −𝜖1 𝑠3+𝑐𝜉 𝛼𝜉 −𝜖2𝑐𝜉 1+𝛼𝜉+𝑏𝑠3 𝜖2 1+𝛼𝜉+𝑏𝑠3 −𝑑2𝑏 1+𝛼𝜉+𝑏𝑠3 +𝜖1 𝑠3+𝑐𝜉 𝑏 , 𝑝3= 1+𝛼𝜉+𝑏𝑠3 1−𝑠3−𝑖3 1+𝛾𝑖3 −𝛽𝑖3 1+𝛼𝜉+𝑏𝑠3 𝑎 1+𝛾𝑖3 .
Titik setimbang 𝐸3 eksis jika
(i) 𝑑2 1+𝛼𝜉 1+𝛼𝜉+𝑏𝑠3 −𝜖1 𝑠3+𝑐𝜉 −𝜖1 𝑠3+𝑐𝜉 𝛼𝜉 −𝜖2𝑐𝜉 1+𝛼𝜉+𝑏𝑠3
𝜖2 1+𝛼𝜉+𝑏𝑠3 −𝑑2𝑏 1+𝛼𝜉+𝑏𝑠3 +𝜖1 𝑠3+𝑐𝜉 𝑏 > 0 dan (ii) 1+𝛼𝜉+𝑏𝑠3 1−𝑠3−𝑖3 1+𝛾𝑖3 −𝛽𝑖3 1+𝛼𝜉+𝑏𝑠3
𝑎 1+𝛾𝑖3 > 0. Dari sini terdapat dua kondisi yaitu
a. 𝑑2 >𝜖1 𝑠3+𝑐𝜉 1+𝛼𝜉 +𝜖2𝑐𝜉 1+𝛼𝜉+𝑏𝑠3 1+𝛼𝜉 1+𝛼𝜉+𝑏𝑠3 dan 𝜖2 1+𝛼𝜉+𝑏𝑠3 +𝜖1 𝑠3+𝑐𝜉 𝑏 𝑏 1+𝛼𝜉+𝑏𝑠3 >𝑑2 atau 𝑑2 < 𝜖1 𝑠3+𝑐𝜉 1+𝛼𝜉 +𝜖2𝑐𝜉 1+𝛼𝜉+𝑏𝑠3 1+𝛼𝜉 1+𝛼𝜉+𝑏𝑠3 dan 𝜖2 1+𝛼𝜉+𝑏𝑠3 +𝜖1 𝑠3+𝑐𝜉 𝑏 𝑏 1+𝛼𝜉+𝑏𝑠3 <𝑑2.
Selanjutnya, berdasarkan nilai parameter yang telah diketahui dimasukkan ke kondisi tersebut dengan bantuan MAPLE. Sehingga diperoleh kondisi yang memenuhi titik setimbang 𝐸3 sebagai berikut: 𝑑2> 𝜖1 𝑠3+𝑐𝜉 1+𝛼𝜉 +𝜖2𝑐𝜉 1+𝛼𝜉+𝑏𝑠3 1+𝛼𝜉 1+𝛼𝜉+𝑏𝑠3 dan 𝜖2 1+𝛼𝜉+𝑏𝑠3 +𝜖1 𝑠3+𝑐𝜉 𝑏 𝑏 1+𝛼𝜉+𝑏𝑠3 >𝑑2.
atau
1− 𝑠3− 𝑖3 1 +𝛾𝑖3 < 𝛽𝑖3 dan 𝑎 1 +𝛾𝑖3 < 0.
Selanjutnya, berdasarkan nilai parameter yang telah diketahui dimasukkan ke kondisi tersebut dengan bantuan MAPLE. Sehingga diperoleh kondisi yang memenuhi titik setimbang 𝐸3 sebagai berikut:
1− 𝑠3− 𝑖3 1 +𝛾𝑖3 > 𝛽𝑖3 dan 𝑎 1 +𝛾𝑖3 > 0 dengan syarat
1 >𝑠3+𝑖3.
Oleh karena itu, titik setimbang 𝐸3 eksis jika:
(i) 𝑑2> 𝜖1 𝑠3+𝑐𝜉 1+𝛼𝜉 +𝜖2𝑐𝜉 1+𝛼𝜉+𝑏𝑠3 1+𝛼𝜉 1+𝛼𝜉+𝑏𝑠3 dan 𝜖2 1+𝛼𝜉+𝑏𝑠3 +𝜖1 𝑠3+𝑐𝜉 𝑏 𝑏 1+𝛼𝜉+𝑏𝑠3 >𝑑2, dan (ii) 1− 𝑠3− 𝑖3 1 +𝛾𝑖3 >𝛽𝑖3 dan 𝑎 1 +𝛾𝑖3 > 0 dengan syarat 1 > 𝑠3 +𝑖3.
Uraian lengkap perhitungan titik setimbang 𝐸3 dapat dilihat pada Lampiran 5. Oleh karena itu, nilai-nilai 𝐸2 dan 𝐸3 tergantung pada kualitas (𝛼) dan (𝜉)
makanan alternatif sebagai penambahan makanan. Eksistensi kondisi 𝐸2 dan 𝐸3
juga tergantung pada 𝛼 dan 𝜉. Setelah diperoleh titik setimbang kepunahan (𝐸0),
Selanjutnya, ditentukan basic reproduction number yang akan digunakan untuk parameter ambang batas penentuan kriteria koeksistensi penyakit pada populasi. Nilai 𝑅0 diperoleh dengan menggunakan metode Van den Driessche.
Dalam kasus ini, hanya memperhatikan kompartemen yang terkena penyakit sebagai berikut: i. 𝑑𝑠 𝑑𝑡 = 𝑠 1− 𝑠 − 𝑎𝑠𝑝 1+𝛼𝜉+𝑏𝑠 𝑑𝑝 𝑑𝑡 = 𝜖1 𝑠+𝑐𝜉 𝑝 1+𝛼𝜉+𝑏𝑠 + 𝜖2𝑐𝜉𝑝 1+𝛼𝜉 − 𝑑2𝑝
Dari perhitungan, didapatkan nilai 𝑅0𝑝 yaitu 𝑅0𝑝 = 1 𝑑2 𝜖1 1+𝑐𝜉 1+𝛼𝜉+𝑏 + 𝜖2𝑐𝜉 1+𝛼𝜉 ii. 𝑑𝑠 𝑑𝑡 = 𝑠 1− 𝑠 − 𝑖 − 𝛽𝑠𝑖 1+𝛾𝑖 𝑑𝑖 𝑑𝑡 = 𝛽𝑠𝑖 1+𝛾𝑖− 𝑑1𝑖
Dari perhitungan, didapatkan nilai 𝑅0𝑖 yaitu 𝑅0𝑖 = 𝛽 𝑑1 Perhitungan 𝑅0 secara lengkap dapat dilihat pada Lampiran 6.
4.1.2 Analisis Kestabilan Asimtotis Lokal
Berdasarkan persamaan (4.10) - (4.12) terlihat bahwa sistem tersebut merupakan sistem autonomous non linear, maka untuk mendapatkan kestabilan asimtotis lokal dari model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey di titik-titik setimbang 𝐸0, 𝐸1, 𝐸2, dan 𝐸3perlu dilakukan linearisasi dengan menggunakan matriks Jacobian.
Persamaan (4.10) - (4.12) dapat dinyatakan sebagai fungsi dari variabel 𝑠,𝑖
𝑑𝑠 𝑑𝑡 =𝑓1(𝑠,𝑖,𝑝) 𝑑𝑖 𝑑𝑡=𝑓2(𝑠,𝑖,𝑝) 𝑑𝑝 𝑑𝑡 =𝑓3(𝑠,𝑖,𝑝)
Berdasarkan Definisi 2.4, maka matriks Jacobian dari persamaan (4.10) – (4.12) adalah 𝐽= 1−2𝑠 − 𝑖 −𝛽𝑖 𝐾 − 𝑎𝑝 𝑀 + 𝑎𝑠𝑝𝑏 𝑀 2 −𝑠 − 𝛽𝑠 𝐾 + 𝛾𝛽𝑠𝑖 (𝐾)2 − 𝑎𝑠 𝑀 𝛽𝑖 𝐾 𝛽𝑠 𝐾 − 𝛽𝑠𝑖 (𝐾)2− 𝜂𝑝 𝑁 + 𝜂𝑖𝑝𝑏 (𝑁)2− 𝑑1 − 𝜂𝑖 𝑁 𝜖1𝑝 𝑀 − 𝜖1 𝑠+𝑐𝜉 𝑝𝑏 𝑀 2 𝜖2𝑝 𝑁 − 𝜖1 𝑖+𝑐𝜉 𝑝𝑏 𝑁 2 𝜖1 𝑠+𝑐𝜉 𝑀 + 𝜖1 𝑖+𝑐𝜉 𝑁 − 𝑑2 (4.16) dengan 𝑀= 1 +𝛼𝜉+𝑏𝑠, 𝑁= 1 +𝛼𝜉+𝑏𝑖, 𝐾=1 +𝛾𝑖.
Berdasarkan penjelasan Teorema 2.6, untuk menganalisis kestabilan dari titik setimbang, dapat dilihat melalui nilai eigen matriks Jacobian model yang ada. Berikutnya akan dianalisis kestabilan asimtotis lokal dari titik setimbang
𝐸0, 𝐸1, 𝐸2, dan 𝐸3.
A. Kestabilan Asimtotis Lokal pada Titik Setimbang Kepunahan (𝑬𝟎)
Langkah pertama menentukan kestabilan pada titik setimbang 𝐸0 yaitu dengan mensubstitusikan nilai titik setimbang 𝐸0 = 𝑠0,𝑖0,𝑝0 = (0,0,0) ke
matriks Jacobian pada (4.16), dengan demikian diperoleh:
Dari sini diperoleh persamaan karakteristik untuk matriks 𝐽 𝐸0 adalah sebagai berikut: 𝜆 −1 𝜆+𝑑1 𝜆 − 𝜖1𝑐𝜉 1 +𝛼𝜉 + 𝜖2𝑐𝜉 1 +𝛼𝜉 − 𝑑2 = 0
Dengan demikian diperoleh nilai-nilai eigen dari 𝐽 𝐸0 sebagai berikut:
𝜆1 = 1,𝜆2 = −𝑑1,𝜆3 = 𝜖1𝑐𝜉 1 +𝛼𝜉+
𝜖2𝑐𝜉 1 +𝛼𝜉− 𝑑2
Dari matriks Jacobian 𝐽 𝐸0 , diperoleh satu nilai eigen positif yaitu 1. Oleh karena itu titik setimbang 𝐸0 tidak stabil. Dari sudut pandang biologi, ini menunjukkan
bahwa dalam model ini tidak akan terjadi kepunahan meskipun dalam dunia nyata semua populasi berpeluang terjadi kepunahan. Uraian lengkap pencarian persamaan karakteristik dari titik setimbang 𝐸0 bisa dilihat pada Lampiran 7.
B. Kestabilan Asimtotis Lokal pada Titik Setimbang Aksial (𝑬𝟏)
Pada bagian ini ditentukan kestabilan dari titik setimbang 𝐸1 dengan langkah yang serupa pada bagian A dengan mensubstitusikan 𝐸1 = 𝑠1,𝑖1,𝑝1 = (1,0,0). Dengan demikian matriks Jacobian dari titik setimbang 𝐸1 adalah sebagai berikut: 𝐽 𝐸1 = −1 −(𝛽+ 1) −𝑎 1 +𝛼𝜉+𝑏 0 𝛽 − 𝑑1 0 0 0 𝜖1 1 +𝑐𝜉 1 +𝛼𝜉+𝑏+ 𝜖2𝑐𝜉 1 +𝛼𝜉− 𝑑2
Dari sini diperoleh persamaan karakteristik untuk matriks 𝐽 𝐸1 adalah sebagai berikut:
𝜆+ 1 𝜆 −(𝛽 − 𝑑1) 𝜆 − 𝜖1 1 +𝑐𝜉
1 +𝛼𝜉+𝑏+ 𝜖2𝑐𝜉
1 +𝛼𝜉− 𝑑2 = 0
Dengan demikian diperoleh nilai-nilai eigen dari 𝐽 𝐸1 sebagai berikut:
𝜆1 =−1,𝜆2 =𝛽 − 𝑑1, dan 𝜆3 =
𝜖1 1+𝑐𝜉
1+𝛼𝜉+𝑏 + 𝜖2𝑐𝜉
1+𝛼𝜉 − 𝑑2
Dari matriks Jacobian 𝐽 𝐸1 , diperoleh satu nilai eigen negatif 𝜆1 = −1 dan dua nilai eigen 𝜆2 =𝛽 − 𝑑1dan 𝜆3 =
𝜖1 1+𝑐𝜉
1+𝛼𝜉+𝑏 + 𝜖2𝑐𝜉
1+𝛼𝜉− 𝑑2. Berdasarkan Teorema 2.8, titik setimbang 𝐸1 stabil asimtotis jika :
(i) 𝛽< 𝑑1 atau 𝑅0𝑖 < 1 dan (ii) 𝜖1 1+𝑐𝜉
1+𝛼𝜉+𝑏 + 𝜖2𝑐𝜉
1+𝛼𝜉 < 𝑑2 atau 𝑅0
𝑝 < 1.
Dari sudut pandang biologi, hal ini menunjukkan bahwa akan terjadi kepunahan pada populasi prey yang terinfeksi dan populasi predator. Uraian lengkap pencarian persamaan karakteristik dari titik setimbang 𝐸1 bisa dilihat pada Lampiran 8.
C. Kestabilan Asimtotis Lokal pada Titik Setimbang Bebas Penyakit (𝑬𝟐)
Pada bagian ini ditentukan kestabilan dari titik setimbang 𝐸2 dengan langkah yang serupa pada bagian A dan B. Dengan demikian matriks Jacobian dari titik setimbang 𝐸2 dan kondisi kesetimbangan adalah sebagai berikut:
𝐽 𝐸2 = −𝑠2+ 𝑎𝑠2𝑝2𝑏 1+𝛼𝜉+𝑏𝑠2 2 −𝑠2(1 +𝛽) − 𝑎𝑠2 1+𝛼𝜉+𝑏𝑠2 0 𝛽𝑠2− 𝜂𝑝2 1+𝛼𝜉− 𝑑1 0 𝜖1𝑝2 −𝜖1 𝑠2+𝑐𝜉 𝑝2𝑏 𝜖2𝑝2 − 𝜖2𝑐𝜉𝑝2𝑏 0
Berdasarkan matrik Jacobian 𝐽 𝐸2 , dapat dibentuk persamaan karakteristik sebagai brtikut:
det 𝐽 𝐸2 − 𝜆𝐼 = 0.
Dari sini diperoleh persamaan karakteristik sebagai berikut:
𝜆 − 𝛽𝑠2−
𝜂𝑝2
1 +𝛼𝜉− 𝑑1 𝜆
2+𝑞
1𝜆+𝑞2 = 0,
dengan 𝑞1 dan 𝑞2 adalah sebagai berikut:
𝑞1 = 𝑠2− 𝑎𝑠2𝑝2𝑏 1+𝛼𝜉+𝑏𝑠2 2, 𝑞2 = 𝑎𝑠2𝜖1𝑝2 1+𝛼𝜉+𝑏𝑠2 2− 𝑎𝑠2𝜖1 𝑠2+𝑐𝜉 𝑝2𝑏 1+𝛼𝜉+𝑏𝑠2 3 .
Dengan demikian diperoleh nilai-nilai eigen dari 𝐽 𝐸2 adalah sebagai berikut:
𝜆1 =𝛽𝑠2−
𝜂𝑝2
1 +𝛼𝜉− 𝑑1.
Karena semua parameter bernilai positif dan syarat eksistensi titik setimbang bebas penyakit, 𝐸2 adalah 𝛽𝑠2<
𝜂 𝑝2
1+𝛼𝜉+𝑑1, maka cukup jelas bahwa 𝜆1 < 0. Sedangkan
nilai eigen yang lain diperoleh dari akar-akar persamaan karakteristik berikut: 𝜆2+𝑞1𝜆+𝑞2 = 0.
Menurut kriteria Routh-Hurwitz, persamaan 𝜆2+𝑞
1𝜆+𝑞2= 0 akan memiliki akar-akar dengan bilangan real negatif jika dan hanya jika 𝑞1> 0 dan 𝑞2> 0. Akan ditentukan syarat untuk 𝑞1> 0 dan 𝑞2> 0 sebagai berikut:
Pandang 𝑞1 = 𝑠2− 𝑎𝑠2𝑝2𝑏 1+𝛼𝜉+𝑏𝑠2 2 > 0 ⇔ 𝑠2 1− 𝑎𝑝2𝑏 1 +𝛼𝜉+𝑏𝑠2 2 > 0 ⇔1− 𝑎𝑝2𝑏 1 +𝛼𝜉+𝑏𝑠2 2 > 0
⇔ 𝑎𝑝2𝑏 1 +𝛼𝜉+𝑏𝑠2 2 < 1. Pandang 𝑞2 = 𝑎𝑠2𝜖1𝑝2 1+𝛼𝜉+𝑏𝑠2 2− 𝑎𝑠2𝜖1 𝑠2+𝑐𝜉 𝑝2𝑏 1+𝛼𝜉+𝑏𝑠2 3 > 0 ⇔ 𝑎𝑠2𝜖1𝑝2 1 +𝛼𝜉+𝑏𝑠2 2 1− 𝑠2+𝑐𝜉 𝑏 1 +𝛼𝜉+𝑏𝑠2 > 0 ⇔1− 𝑠2+𝑐𝜉 𝑏 1 +𝛼𝜉+𝑏𝑠2 > 0 ⇔ 𝑠2+𝑐𝜉 𝑏 1 +𝛼𝜉+𝑏𝑠2 < 1.
Dari sini dapat disimpulkan bahwa titik setimbang bebas penyakit (𝐸2) stabil asimtotis jika 1+𝛼𝜉𝑎𝑝2𝑏
+𝑏𝑠2 2< 1 dan
𝑠2+𝑐𝜉 𝑏
1+𝛼𝜉+𝑏𝑠2 < 1. Uraian lengkap pencarian
persamaan karakteristik dari titik setimbang 𝐸2 dan syarat kestabilannya bisa
dilihat pada Lampiran 9. Dari sudut pandang biologi, hal ini menunjukkan bahwa sistem menjadi bebas penyakit yang artinya tidak ada prey yang terinfeksi.
D. Kestabilan Asimtotis Lokal pada Titik Setimbang 𝑬𝟑
Pada bagian ini ditentukan kestabilan dari titik setimbang 𝐸3 dengan langkah yang serupa pada bagian A, B, dan C. Dengan demikian matriks Jacobian dari titik setimbang 𝐸3 dan kondisi kesetimbangan adalah sebagai berikut:
𝐽 𝐸3 = −𝑠3+ 𝑎𝑠3𝑝3𝑏 1+𝛼𝜉+𝑏𝑠32 −𝑠3− 𝛽 𝑠3 1+𝛾𝑖3+ 𝛽 𝑠3𝛾𝑖3 (1+𝛾𝑖3)2 − 𝑎𝑠3 1+𝛼𝜉+𝑏𝑠3 𝛽 𝑖3 1+𝛾𝑖3 − 𝛽 𝑠3𝑖3𝛾 (1+𝛾𝑖3)2+ 𝜂 𝑖3𝑝3𝑏 1+𝛼𝜉+𝑏𝑖32 − 𝜂𝑖3 1+𝛼𝜉+𝑏𝑖3 𝜖1𝑝3 1+𝛼𝜉+𝑏𝑠3− 𝜖1(𝑠3+𝑐𝜉)𝑝3𝑏 (1+𝛼𝜉+𝑏𝑠3)2 𝜖2𝑝3 1+𝛼𝜉+𝑏𝑖3− 𝜖2(𝑖3+𝑐𝜉)𝑝3𝑏 (1+𝛼𝜉+𝑏𝑖3)2 0 dengan
𝐴12 =−𝑠3− 𝛽𝑠3 1 +𝛾𝑖3 + 𝛽𝑠3𝛾𝑖3 (1 +𝛾𝑖3)2 , 𝐴13 =− 𝑎𝑠3 1 +𝛼𝜉+𝑏𝑠3, 𝐴21 = 𝛽𝑖3 1 +𝛾𝑖3 , 𝐴22 = − 𝛽𝑠3𝑖3𝛾 (1 +𝛾𝑖3)2 + 𝜂𝑖3𝑝3𝑏 1 +𝛼𝜉+𝑏𝑖3 2 , 𝐴23 = − 𝜂𝑖3 1 +𝛼𝜉+𝑏𝑖3 , 𝐴31 = 𝜖1𝑝3 1 +𝛼𝜉+𝑏𝑠3− 𝜖1(𝑠3+𝑐𝜉)𝑝3𝑏 (1 +𝛼𝜉+𝑏𝑠3)2, 𝐴32 = 𝜖2𝑝3 1 +𝛼𝜉+𝑏𝑖3 − 𝜖2(𝑖3+𝑐𝜉)𝑝3𝑏 (1 +𝛼𝜉+𝑏𝑖3)2 , 𝐴33 = 0.
Dari sini diperoleh persamaan karakteristik untuk matriks 𝐽 𝐸3 adalah sebagai berikut: 𝜆3+𝛺1𝜆2+𝛺2𝜆+𝛺3 = 0, dengan 𝛺1 =− 𝐴11 +𝐴22 , 𝛺2 = 𝐴11𝐴22− 𝐴12𝐴21 − 𝐴13𝐴31 − 𝐴23𝐴32, 𝛺3 = 𝐴11𝐴23𝐴32 − 𝐴12𝐴23𝐴31 − 𝐴13𝐴21𝐴32 +𝐴13𝐴22𝐴31.
Titik setimbang koeksistensi (𝐸3) stabil asimtotis jika dan hanya jika akar-akar dari persamaan karakteristik bernilai negatif. Berdasarkan kriteria Routh-Hurwitz, persamaan karakteristik tersebut akan memiliki akar-akar yang negatif jika dan hanya jika memenuhi:
a. 𝛺1, 𝛺2, dan 𝛺3 > 0 b. 𝛺1𝛺2− 𝛺3 > 0
Persamaan 𝛺1, 𝛺2, dan 𝛺3 mengandung banyak parameter yang sulit untuk disederhanakan. Oleh karena itu, untuk menentukan syarat agar 𝜆𝑖 < 0 untuk
𝑖= 1,2 dan 3 rumit ditentukan secara manual. Dari sini dilakukan simulasi numerik untuk menentukan sifat kestabilan dari titik setimbang koeksistensi 𝐸3
menggunakan bidang fase software MATLAB. Kode pogram untuk simulasi numerik dapat dilihat pada Lampiran 11.
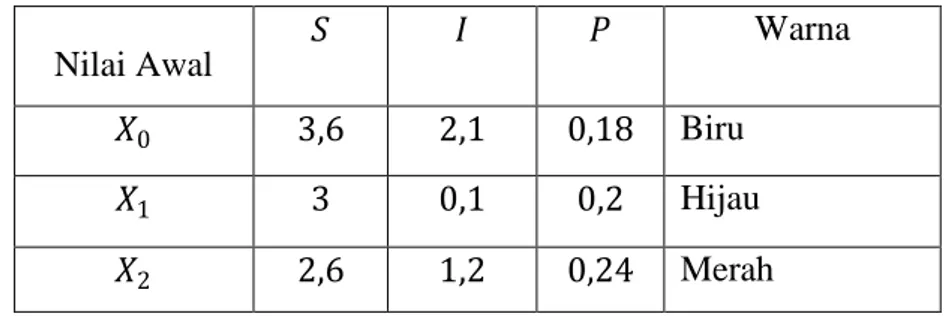
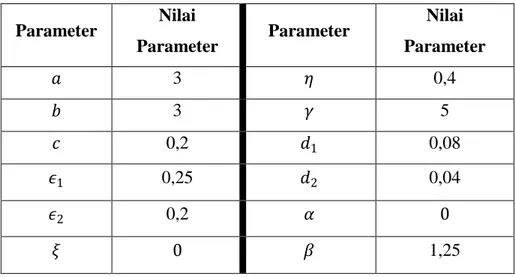
Simulasi ini dilakukan dengan memberi nilai parameter dan tiga nilai awal yang berbeda untuk masing – masing subpopulasi 𝑆, 𝐼, dan 𝑃 yang dinotasikan dengan 𝑋0,𝑋1, dan 𝑋2. Hal ini bertujuan untuk mengetahui kekonvergenan solusi dari masing – masing nilai awal dan parameter yang digunakan. Berikut ini adalah tabel untuk nilai awal pada model matematika peran penambahan makanan dalam sistem eko-epidemiologi dengan penyakit pada prey. Nilai parameter yang digunakan merujuk dari jurnal yang ditulis oleh Sahoo (2015) pada Tabel 4.4. Simulasi ini dilakukan untuk 𝑡 = 0 sampai 𝑡 = 150 hari.
Tabel 4.3 Nilai Awal Simulasi Titik Setimbang Koeksistensi 𝐸3
Nilai Awal
𝑆 𝐼 𝑃 Warna
𝑋0 3,6 2,1 0,18 Biru
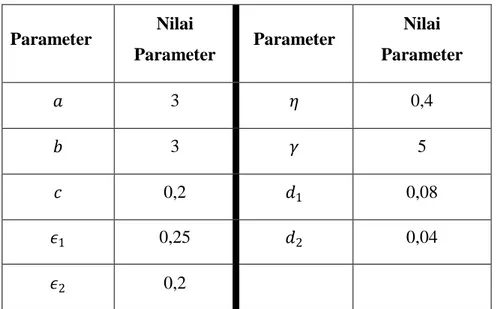
Tabel 4.4 Nilai Parameter Simulasi Titik Setimbang Koeksisitensi 𝐸3 Parameter Nilai Parameter Parameter Nilai Parameter 𝑎 3 𝜂 0,4 𝑏 3 𝛾 5 𝑐 0,2 𝑑1 0,08 𝜖1 0,25 𝑑2 0,04 𝜖2 0,2 𝛼 0 𝜉 0 𝛽 1,25
Hasil simulasi untuk melihat sifat kestabilan lokal titik setimbang koeksistensi 𝐸3 terdapat pada Gambar 4.1.
Gambar 4.1 Simulasi Bidang Fase 𝑆 − 𝐼 untuk Titik Setimbang Koeksistensi 𝐸3
Pada Gambar 4.1 merupakan grafik pada ruang dua dimensi dari populasi