Masalah maksimisasi dapat ditinjau dari metode minimisasi, karena

(1)

Lecture 2: Optimization of Function of One Variable A. Pendahuluan

Ide dasar dari masalah optimisasi adalah mengoptimumkan (memaksimumkan/ meminimumkan) suatu besaran skalar yang merupakan harga suatu fungsi dari n variabel , , … , .

Bentuk masalah minimisasi: Minimumkan:

= ( , , … , ). (2.1) Masalah maksimisasi dapat ditinjau dari metode minimisasi, karena

Maksimum ( , , … , ) =− minimum − ( , , … , ) . (2.2) Sehingga tanpa mengurangi keumuman, pada penyelesaian masalah optimasi berikutnya hanya dibahas masalah minimisasi.

Jika jumlah variabel = 1, maka (2.1) menjadi

Minimumkan: = ( ) (2.3) yang merupakan masalah optimasi fungsi satu variabel.

B. Fungsi Unimodal dan Fungsi Konveks

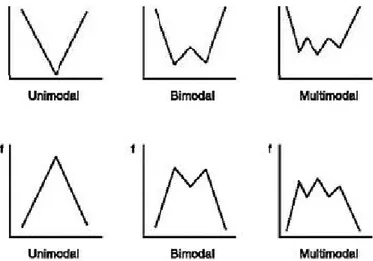
Unimodal. Fungsi satu variabel adalah unimodal jika pada selang (daerah definisi) kurvanya hanya mempunyai satu titik minimum/maksimum relatif ∗.

(2)

Himpunan Konveks.

Definisi 2.1 Suatu himpunan S dikatakan konveks jika dan hanya jika ∀ , ∈ dan ∀ ⋋ ∈[0,1] berlaku

=⋋ + (1−⋋) ∈ .

Dengan kata lain merupakan himpunan konveks jika garis hubung (line segment) antara sebarang dua titik di juga berada di . Untuk selanjutnya, titik =⋋ + (1−⋋) dengan 0≤⋋≤1 disebut kombinasi konveks (convex combination) dari titik dan .

(a) Konveks (b) Tidak konveks Gambar 2.2 Ilustrasi himpunan konveks The following are some examples of convex sets. 1. Hyperplane

= {( , , ): + 2 − = 4}⊂ This is an equation of a plane in . In general, = { : = }

is called a hyperplane in , where is a nonzero vector in , usually referred to as the normal to the hyperplane, and is a scalar.

= [ + 2 − == 4, ]

3 [ [ /. ], { ,−50,50}, { ,−50,50}]

(3)

2. Halfspace

= {( , , ): + 2 − ≤4}⊂

These are points on one side of the hyperplane defined above. These points form a half space. In general

= { : ≤ } in is a convex set.

3 [ + 2 −

≤4, { ,−10,10}, { ,−10,10}, { ,−10,10}]

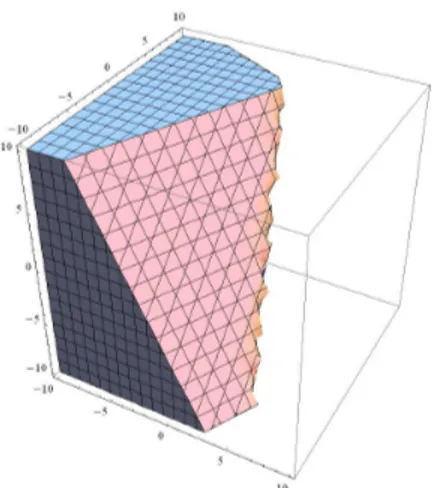
Gambar 2.4 Illustration of half space. 3. Polyhedral set

= ( , , ): + 2 − ≤4, 2 − + ≤6 ⊂

This set is the intersection of two half spaces. In general, the set = { : ≤ }

is a convex set, where is an × matrix, and is an vector. This set is the intersec-tion of half spaces and is usually called a polyhedral set.

3 [ + 2 − ≤4&&2 − +

(4)

Department of Mathematics FMIPA UNS

Gambar 2.5 Illustration of polyhedral set. 4. Convex cone

= {( , ): ≥| |}⊂ This set represents a convex cone in .

[ ≥ [ ], { ,−10,10}, { ,−10,10}]

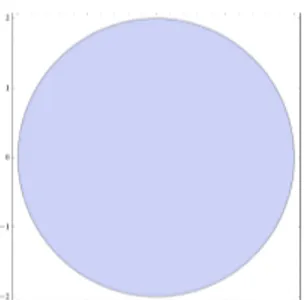
Gambar 2.6 Illustration of convex cone. 5. Points on and inside a circle

= {( , ): + ≤4}⊂

This set represents points on and inside a circle with center (0,0) and radius 2.

(5)

Gambar 2.7 Illustration of points on and inside a circle 6. Linear programming problem

= { : solves below} Problem P

Minimize Subject to =

≥0

Here is an n vector, is an m vector, is an × matrix, and is an n vector. The set gives all optimal solutions of the linear programming problem of minimizing the linear function over the polyhedral region defined by

= and ≥0.

The following lemma is an immediate consequence of the definition of convexity. It states that the intersection of two convex sets is convex and that the algebraic sum of two convex sets is also convex.

Lema 2.2 Misal and merupakan himpunan konveks di . Maka 1. ∩ konveks

2. + = { + : ∈ , ∈ } konveks

3. − = { − : ∈ , ∈ } konveks.

Fungsi Konveks.

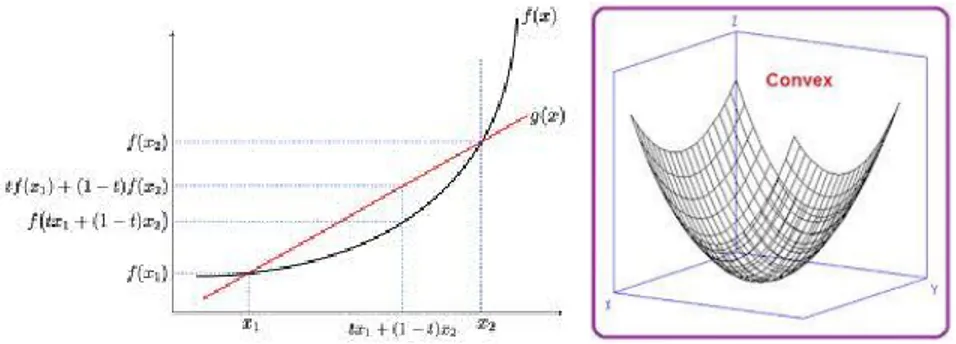
Definisi 2.3 Suatu fungsi adalah konveks pada suatu selang S (berhingga ataupun tidak), jika ∀ 1, 2∈ dan ∀ ⋋ ∈[0,1] berlaku

(6)

Gambar 2.8 Ilustrasi fungsi konveks

Fungsi Konveks Tegas. Jika (2.4) berlaku dengan tanda ketidaksamaan tegas (strict inequality), yaitu

(⋋ + (1−⋋) ) <⋋ ( ) + (1−⋋) ( ) (2.5) untuk ≠ dan ⋋ ∈(0,1), maka fungsi tersebut dikatakan konveks tegas (strictly convex).

Fungsi Konkav. Jika (2.4) berlaku dengan tanda ketidaksamaan terbalik, yaitu (⋋ + (1−⋋) )≥⋋ ( ) + (1−⋋) ( ). (2.6) maka fungsi dikatakan konkav (concave).

Gambar 2.9 Ilustrasi fungsi konkav

Fungsi Konveks Tegas. Jika (2.6) berlaku dengan tanda ketidaksamaan tegas (strict inequality), yaitu

(⋋ + (1−⋋) ) >⋋ ( ) + (1−⋋) ( ) (2.7) untuk ≠ dan ⋋ ∈(0,1), maka fungsi tersebut dikatakan konkav tegas (strictly concave).

(7)

Jadi berlaku pernyataan berikut:

Jika fungsi konveks, maka – konkav.

dan Jika fungsi konveks tegas, maka – konkav tegas. Demikian juga sebaliknya.

Catatan.

1. Fungsi konveks/konkav adalah fungsi yang unimodal.

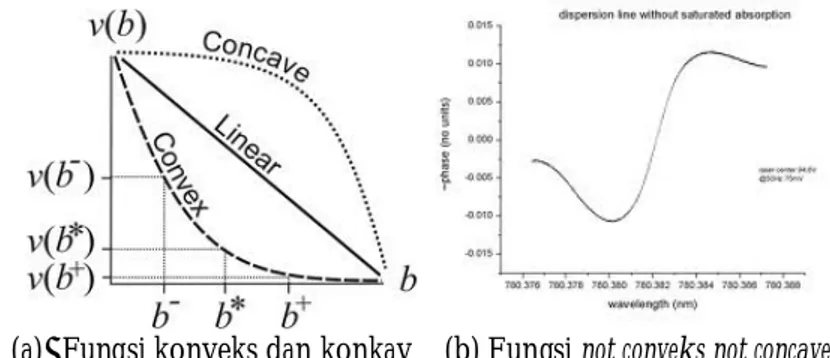
2. Fungsi linear (linear function) merupakan fungsi konveks dan fungsi konkav.

(a) Fungsi konveks dan konkav (b) Fungsi not conveks not concave Gambar 2.10 Ilustrasi fungsi konveks dan fungsi konkav serta tidak keduanya

C. Minimum Mutlak (Global) dan Minimum Relatif (Lokal)

Definisi 2.4. Fungsi dikatakan memiliki minimum relatif (minimum lokal) di ∗ ∈ jika terdapat > 0 sedemikian sehingga

( )≥ ( ∗_),_{∀ ∈} _\{ ∗_{} dan}_| ₋ ∗_{| <} _{. (2.8)}

Definisi 2.5. Fungsi dikatakan memiliki minimum mutlak (minimum global) di ∗ ∈ jika ∀ ∈ ,

( )≥ ( ∗_{). (2.9)}

Definisi maksimum lokal dan maksimum global berturut-turut dengan membalik tanda Ketidaksamaan (2.8) dan (2.9), yaitu "≥" diganti "≤".

Catatan: Suatu minimum/maksimum global juga merupakan minimum/maksimum lokal, sebab D juga merupakan persekitaran dari ∗. Tetapi, tidak setiap minimum lokal adalah minimum global.

(8)

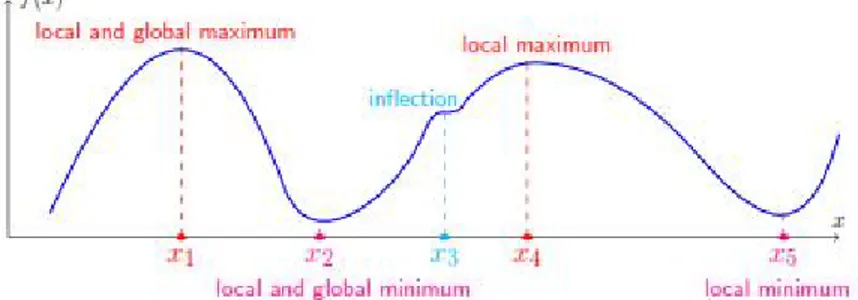
Gambar 2.11 Ilustrasi minimum lokal minimum global D. Beberapa Metode Optimasi

Menentukan letak optimum dengan kalkulus pada prakteknya ada yang tidak berhasil. Hal ini dimungkinkan karena fungsi objektifnya tidak analitik sehingga diferensiasinya tidak mungkin dihitung, atau titik-titik stasionernya tidak dapat diperoleh secara aljabaris. Dalam kasus-kasus seperti ini, maka metode-metode numerik digunakan untuk menghitung nilai-nilai pendekatan terhadap satu atau beberapa optimum relatif hingga suatu toleransi yang dapat diterima.

Terdapat 2 jenis metode optimasi fungsi satu variabel, yaitu 1. Metode Penyelidikan (search method).

Dapat diaplikasikan untuk sembarang fungsi unimodal tanpa menggunakan derivatif fungsi. Ide dasar: Penyusutan selang yang mengandung minimum lokal hingga mencapai selang yang dibatasi dalam limit-limit yang dapat diterima (toleransi yang diberikan).

2. Metode Pendekatan (approximation method).

Hanya dapat diaplikasikan untuk fungsi-fungsi unimodal yang diferensiabel kontinu, yaitu menggunakan derivatif fungsi tersebut.

E. Metode Penyelidikan

Asumsi. Perhatikan fungsi : → ℝ dengan ⊆ ℝ. Jadi f adalah fungsi satu variabel yang didefinisikan pada domain D.

Diasumsikan f mempunyai minimum, yaitu untuk setiap [ , ]⊂ (= [ , ]) terdapat suatu

∗ _∈_{[ , ] sehingga}

( ∗_{) = min}

∈[ , ] ( ). (2.10)

Jadi ada suatu minimum untuk f pada [ , ]. Ide dasar. Diberikan suatu fungsi : [ , ]→ ℝ dengan asumsi (2.10) dan ditentu-kan suatu bilangan kecil > 0 (sebagai toleransi). Akan dicari suatu selang

= [ , ] dengan | | = − ≤ yang mempunyai suatu titik minimum lokal.

(9)

Teorema. Ditentukan : [ , ]→ ℝ yang memenuhi asumsi (2.10) dan < < < . Maka

i. Jika ( )≥ ( ), maka ( , ] mempunyai titik minimum lokal. ii. Jika ( )≤ ( ), maka [ , ) mempunyai titik minimum lokal. Bukti:

i. Andai ( ) > ( )

Dari asumsi (2.10): ∃ ∗ _∈_{[ , ] sehingga} ₍ ∗_{) = min}

∈[ , ] ( ), maka

∗ _≠ _{. Sehingga} ∗_∈_{( , ] yang berarti} ∗_{adalah titik minimum lokal.}

Andai ( ) = ( ) Dari asumsi (2.10):

1. Jika ( ∗_{) = ( ), maka dapat ditulis juga} ₍ ∗_{) = ( ), sehingga dapat}

ditentukan ∗= ∈( , ] yang berarti q adalah titik minimum lokal. 2. Jika ( ∗_{) > ( ), dari asumsi (2.10) hal ini tidak mungkin terjadi.}

3. Jika ( ∗) < ( ), maka ∗∈( , ], berarti ∗_{titik minimum lokal.}

ii. Bukti analog.

Langkah untuk mengerjakan proses pengurangan selang.  [ , ] : selang awal yang mengandung minimum lokal.

, : pasangan titik yang diselidiki untuk menentukan minimum lokal. 1. Jika ( )≤ ( ), maka [ , ] adalah selang kedua: pilih titik

= , = , = ,

dan pilih titik baru < . ( ) ( ) --- ai pi qi bi ---|

ai+1 pi+1 qi+1 bi+1

Gambar 2.12 Ilustrasi untuk ( ) < ( ) 2. Jika ( )≥ ( ), maka [ , ] adalah selang kedua: pilih titik

(10)

--- ai pi qi bi

---|

ai+1 pi+1 qi+1 bi+1

Gambar 2.13 Ilustrasi untuk ( ) > ( )

 Misal interval pada iterasi ke-i, yaitu [ , ] mempunyai panjang . Panjang seharusnya independen (tidak bergantung) terhadap pemilihan interval pa-da iterasi ke- (iterasi sebelumnya). Oleh karena itu titik pa-dan pa-dapat dipilih sedemikian sehingga panjang interval [ , ] sama dengan [ , ], yaitu = − = − . (2.11) Karena − = ( − ) + ( − ) − = ( − ) + ( − ), akibatnya − = − . Perhaikan ilustrasi berikut.

− −

--- ai pi qi bi

−

−  Perhatikan ilustrasi berikut.

--- ai pi qi bi

---|

ai+1 pi+1 qi+1 bi+1

(11)

--- ai pi qi bi

---|

ai+1 pi+1 qi+1 bi+1

Gambar 2.15 Ilustrasi untuk ( ) > ( )