Bumbung gelombang atau waveguide adalah saluran transmisi yang berupa

Modul 6

EE2323

Elektromagnetika Telekomunikasi

Bumbung Gelombang

Oleh :

Organisasi

Organisasi

Modul 5

Bumbung Gelombang

•

A. Pendahuluan

page 3

•

B. Penurunan Persamaan Medan

page 9

•

C. Bumbung Gelombang Rektangular

page 15

•

D. Bumbung Gelombang Sirkular

page 17

•

E. Cavity Resonator

page 19

A. Pendahuluan

Bumbung gelombang

atau waveguide adalah saluran transmisi yang berupa

pipa berongga yang terbuat dari konduktor yang baik. Rongga diisi dengan bahan dielektrik tak merugi yang umumnya adalah udara kering.

Bumbung gelombang umumnya digunakan untuk saluran transmisi frekuensi gelombang mikro ( orde GHz ) , sebagai saluran dari antena parabola menuju ke transmitter atau receiver, atau sebagai feed element. Saluran transmisi lain untuk orde GHz (kecuali serat optik) akan memiliki redaman yang cukup besar, disamping itu akan terjadi absorbsi, radiasi, dan skin effect.

B. Bumbung Gelombang Rektangular

Bahan di dalam waveguide bisa berupa udara atau gas kering yang merupakan dielektrik sempurna, sehingga dapat

dinyatakan dalam persamaan gelombang Helmholtz

disamping :

H

Karena gelombang merambat dalam arah sumbu z saja, maka dinyatakan sbb :

Bumbung Gelombang Rektangular

Untuk mempermudah pembahasan

, ditinjau untuk arah z positif saja, dengan anggapan bahwa analisis untuk arah z negatif sama dengan untuk arah z positif, sehingga :

z

didapat ....

Untuk melihat struktur medan dalam

waveguide,

persamaan diatas dimasukkan dalam

persamaan gelombang Helmholtz....

H

Asumsi :

medan sinusoidal, dielektrik sempurna dalam WG

Bumbung Gelombang Rektangular

Persamaan diatas dapat dituliskan dengan sederhana sebagai berikut :





E

Dengan mendefinisikan LAPLACIAN TRANSVERSAL terhadap sumbu z,

2

Bumbung Gelombang Rektangular

Sedangkan menurut persamaan Maxwell I dan II

tentang hukum Faraday dan hukum Ampere, dinyatakan sbb :

H

Substutusikan persamaan dibawah ke persamaan Maxwell di atas ...

Bumbung Gelombang Rektangular

y x

T

a

ˆ

y

a

ˆ

x

















Ingat kembali operator transversal

H

j

E

a

ˆ

E

_z

T





























_T



E







a

ˆ

_z



E







j



H



Persamaan di atas dapat ditulis sbb :

Karena medan

E

maupun

H

adalah fungsi terhadap z maka

komponen-komponen itu dapat dinyatakan dalam

E

_z

dan

H

_z

, sehingga dengan

menghitung komponen di arah z, komponen di arah lainnya akan dapat

Bumbung Gelombang Rektangular

Lihat kembali

persamaan di

samping yang

sudah kita

dapatkan !!

y

substitusikan !!

Bumbung Gelombang Rektangular

Kemudian ...

y

substitusikan !!

Bumbung Gelombang Rektangular

Lalu untuk

medan magnet

diperoleh dengan

cara yang sama

sbb ...

substitusikan !!

Bumbung Gelombang Rektangular

substitusikan !!

Bumbung Gelombang Rektangular



























y

E

γ

x

H

j

ωω

με

ω

γ

1

E

_{y 2 2} z z







































x

E

y

H

j

1

E

_{x 2 2} z z







































y

H

x

E

j

1

H

_{y 2 2} z z





































x

H

y

E

j

1

H

_{x 2 2} z z

Jadi ...

Didapatkan 4 buah

persamaan umum

WG

rektangular yang jika E

_z

, H

_z

,

dan



diketahui ...maka

Bumbung Gelombang Rektangular

Karakterisasi E

_z

dan H

_z

Lihat kembali penurunan dari persamaan gelombang Helmholtz pada slide 5-6 :





z

Bumbung Gelombang Rektangular

Misalkan E_z merupakan fungsi satu variabel yang saling terpisah atau independen





z



























_{2 2}

2 2

2 2

y

)

y

(

Y

)

y

(

Y

1

x

)

x

(

X

)

x

(

X

1

Bumbung Gelombang Rektangular

Karena ruas kanan adalah konstanta, maka hasil dari ruas kiri juga pasti konstanta, sehingga dapat dituliskan :

2 2

2

M

x

X(x)

X(x)

1

_

_





2 2

2

N

y

Y(y)

Y(y)

1









Sehingga,



γ

ω

με



N

M

2



2





2



2

με

ω

N

M

γ



2



2



2

Bumbung Gelombang Rektangular

2 2

2

M

x

X(x)

X(x)

1









2 2

2

N y

Y(y) Y(y)

1 _{ }

 

0

X(x)

M

x

X(x)

₂

2 2









0

Y(y)

N

y

Y(y)

₂

2 2









Diketahui dari pemisalan terdahulu ,





z

z

x

y

z

X

x

Y

y

e

E

,

,



(

)

(

)



Persamaan diferensial orde 2 yang solusinya adalah :

Ny cos Y

Ny sin Y Y(y)

Mx cos X

Mx sin X

X(x)

2 1

2 1

 

 



 





z

2 1

2 1

z

x

,

y

,

z

X

sin

Mx

X

cos

Mx

Y

sin

Ny

Y

cos

Ny

e

E









Dengan cara yang sama didapat,

Bumbung Gelombang Rektangular

Mode Gelombang Dalam Waveguide

Terdapat 2 kemungkinan konfigurasi medan dalam waveguide :

(1) Transverse Electric ( mode TE )

0

,

0





_z

z

H

E

Medan listrik transversal terhadap sumbu bumbung _gelombang

(2) Transverse Magnetic ( mode TM )

0

,

0





_z

z

E

H

Medan magnet transversal terhadap sumbu bumbung _gelombang

Mode Transverse Electromagnetic ( mode TEM ) TIDAK MUNGKIN ADA pada waveguide karena :

• Jika E_z dan H_z = 0, maka semua komponen medan yang lain juga akan = 0

• Disamping itu, mode TEM tak mungkin ada pada waveguide karena medan magnet pada bidang X-Y (z konstan) harus merupakan loop tertutup,



H





d

L





I

_c



I

_d

0

H











dan menyebabkan semua komponen

Bumbung Gelombang Rektangular

Mode TM (Transverse Magnetic)

0

,

0





_z

z

E

H







z

2 1

2 1

z

X

sin

Mx

X

cos

Mx

Y

sin

Ny

Y

cos

Ny

e

E









y = b x = a

x

y

, 

 = 0

 = 

0

H

_z



b y pada 0

E (4) a

x pada 0

E (2)

0 y pada 0

E (3) 0

x pada 0

E (1)

z z

z z

 

 

 

 

Syarat batas :

z z

C

sin

Mx

sin

Ny

e

E



 _{dimana, C = X}

1Y1

Dari syarat batas (1) dan (3)

Dari syarat batas (2) dan (4)

0

Ma

sin



0

Nb

sin



...dst 0,1,2,

m , mπ

Ma  

st 0,1,2,...d n

π,

Bumbung Gelombang Rektangular

dan

Sehingga

konstanta propagasi didapat ...

με

• Terjadi perambatan energi untuk,

2

• Tidak terjadi perambatan energi untuk,

Bumbung Gelombang Rektangular

Pada suatu bumbung gelombang rektangular

yang memiliki dimensi

tertentu (a dan b tertentu), serta m dan n tertentu pula, maka akan memiliki parameter

yang disebut sebagai “

Frekuensi Cut Off “

2 2

mn , CO

b

n

a

m

2

1

f











 













 







Frekuensi Cut Off2 terjadi ketika,2 2

b n a

m

   

   

   

   

 

Jadi, ketika ….

mn , CO ops

f

f



Terjadi perambatan energi, _waveguide gelombang berjalan dalam



Tidak terjadi perambatan energi, “mode evanescent” Jika,



1



v

Maka,

2 2

mn , CO

b

a

2

v

f



Bumbung Gelombang Rektangular

Jadi, untuk mode propagasi TM ...

2

• Konstanta fasa didalam WG, _mn

• Kecepatan fasa didalam WG, v_mn :

soperposisi gelombang datar uniform dalam WG

Kecepatan fasa diarah z adalah kecepatan muka gelombang di dalam WG, dinyatakan :

• Kecepatan group didalam WG, v_g,mn :

Bumbung Gelombang Rektangular

Adalah kecepatan perambatan energi di dalam WG

mn mn

, g

d

d

v







2

mn , CO mn

, g

f

f

1

v

v

_















• Panjang gelombang didalam WG, v_g,mn :

mn mn

2









2 mn , CO mn

f

f

1

_



















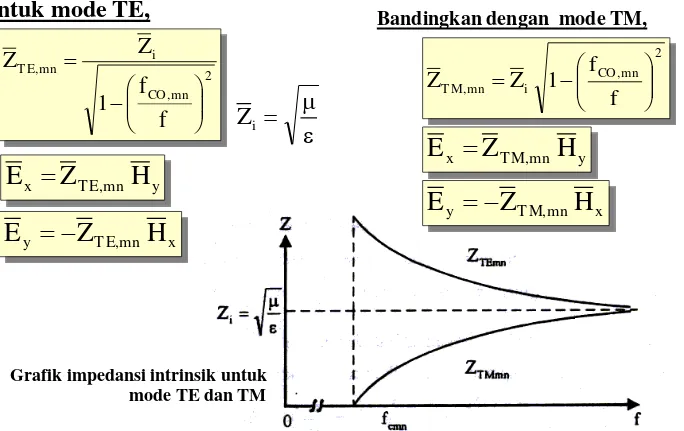
• Impedansi intrinsik didalam WG, v_g,mn :

2 mn , CO i

mn , T M

f

f

1

Z

Z

_















 

Z

y mn

, T M

x

Z

H

E



H

Z

Bumbung Gelombang Rektangular

Persamaan-persamaan medan di dalam waveguide ...

Untuk mode TM

0

H

_z



z

z

C

sin

Mx

sin

Ny

e

E





• Substitusikan untuk mode TM !



























y

E

γ

x

H

ωμ

j

με

ω

γ

1

E

_{y 2 2} z z







































x

E

y

H

j

1

E

_{x 2 2} z z







































y

H

x

E

j

1

H

_{y 2 2} z z





































x

H

y

E

j

1

H

_{x 2 2} z z

Bumbung Gelombang Rektangular

sin

Mx

cos

C

cos

Mx

sin

C

cos

Mx

sin

C

cos

Mx

sin

C

Dengan mengalikan

persamaan dengan ejt _{dan mengambil}

realnya, akan didapat persamaan bentuk waktu



cos

a































sin

t

2

z

b

y

n

cos

a

x

m

sin

C

b

n

h

E

mn 2

mn y

Bumbung Gelombang Rektangular

































sin

t

2

z

b

y

n

cos

a

x

m

sin

C

b

n

h

H

mn 2

x

0

H

_z



Sedangkan untuk medan magnetnya ...































sin

t

2

z

b

y

n

sin

a

x

m

cos

C

a

m

h

H

mn 2

y

Bumbung Gelombang Rektangular

Menggambar konfigurasi medan dalam WG ...

Untuk mode TM

Bentuk medan dapat digambarkan pada bidang transversal arah perambatan, dengan menulis persamaan medan untuk bidang transversal,

y

cos

a

x

m

sin

b

sin

a

x

m

cos

a

sin

a

x

m

cos

a

cos

a

x

m

sin

b

Bumbung Gelombang Rektangular

Cara menggambar ...







































_











ˆ

sin

t

2

z

b

y

n

cos

a

x

m

sin

b

n

ˆ

b

y

n

sin

a

x

m

cos

a

m

C

h

E

mn 2

mn

T

a

x

a

y

1 z

2 t

sin

mn

     

 

   

• Pilih t dan z sehingga :

• Gambar medan E_x , E_y , H_x , dan H_y , sehingga terjadi medan maksimum dan minimum. Untuk TM₁₁ terjadi pada :

b , 2 b , 0 y a

, 2 a , 0

Bumbung Gelombang Rektangular

• Untuk menggambar medan pada bidang yz, pilih pada harga fungsi maksimumnya. Untuk TM₁₁ pada bidang yz :

Untuk t tertentu, seperti t = 0 , persamaan komponen medan sebagai berikut :

 cos b

y sin C

sin

b

y

cos

C

sin y cos C

Terlihat medan berubah sebagai fungsi jarak dalam , sehingga titik-titik yang harus digambar

pada arah z adalah :

Bumbung Gelombang Rektangular

Mode TE (Transverse Electric)

0

pada 0 pada 0

E (2)

0 x pada 0 pada 0

Masukkan syarat batas :



Bumbung Gelombang Rektangular

Didapat persamaan-persamaan syarat :

0 y

H_{z }

 

untuk y = 0

0 y

H_z

  

untuk y = b

0 x

H_{z }

 

untuk x = 0

0 x

H_{z }

 

untuk x = a

Jika didiferensiasi terhadap x dan y, dan syarat-syarat diatas dimasukkan, didapat :

_H

_z

z j z

m n

e

Ny

cos

Mx

cos

C

H



 

_E

_z



₀

_{(mode TE)}

Persamaan-persamaan medan di dalam waveguide ...

Untuk mode TE

• Substitusikan untuk mode TE !



• Dari 4 buah persamaan umum yang sudah kita dapatkan untuk WG rektangular ...

Bumbung Gelombang Rektangular

z

cos

Mx

cos

C

H



 

Bumbung Gelombang Rektangular







j z 2

2 x

m n

e

Ny

sin

Mx

cos

C

N

M

N

j

E

 













j z 2

2 mn x

m n

e

Ny

cos

Mx

sin

C

N

M

M

j

H

 













j z 2

2 y

m n

e

Ny

cos

Mx

sin

C

N

M

M

j

E

 















j z 2

2 mn y

m n

e

Ny

sin

Mx

cos

C

N

M

N

j

H

 









•

M, N, dan



_mn sama seperti pada mode TM !!

•

Dengan mengalikan

persamaan dengan ejt _{dan mengambil realnya, akan}

didapat

persamaan bentuk waktu

. Silakan dicari sendiri !!

• Parameter-parameter sekunder yang lain :

f

_{cut off}

, v

_mn

,



_mn sama seperti pada mode TM !!

Bumbung Gelombang Rektangular

Untuk mode TE,

2 mn , CO i

mn , T M

f

f

1

Z

Z

_





















i

Z

y mn

, T M

x

Z

H

E



x mn

, T M

y

Z

H

E





2 mn , CO

i mn

, T E

f

f

1

Z

Z

















y mn

, T E

x

Z

H

E



x mn

, T E

y

Z

H

E





Bandingkan dengan mode TM,

Bumbung Gelombang Rektangular

•

Pada umumnya, waveguide direncanakan untuk

mendukung mode terendah dan mode lainnya yang lebih

tinggi dihindarkan

•

Untuk bumbung gelombang rektangular, mode terendah

adalah mode TE

₁₀

atau TE

₀₁

tergantung dari dimensi

bumbung gelombang. Hal ini karena mode-mode tersebut

kemungkinan memiliki frekuensi cutoff terendah.

•

Jika a > b

, mode terendah adalah TE

₁₀

, sedangkan

jika a < b

, mode terendah adalah TE

₀₁

•

Untuk mode TM, mode terendah adalah TM

₁₁

, karena

jika salah satu m atau n sama dengan 0, maka semua

2 2

mn , CO

b

n

a

m

2

1

f











 













 







a

Bumbung Gelombang Rektangular

Persamaan medan untuk mode TE

₁₀

,







j z

sin

Mx

cos

C

cos

Mx

sin

C

cos

Mx

sin

C

sin

Mx

cos

C. Konsiderasi Daya

Daya rata-rata yang menembus bidang z konstan...

Perambatan gelombang dihitung dari vektor rapat daya rata-rata,



*



av

Re

E

H

2

1

P











Contoh :

Dicari vektor rapat daya rata-rata untuk TE₁₀ :

z j z

10

e

a

x

cos

C

H





 

0

E

_z



E

_x



0

z j 10

x

10

e

a

x

sin

C

a

j

H



 







z j y

10

e

a

x

sin

C

a

j

E



 









0

H

_y



•

E

ada pada arah sumbu y

•

Konsiderasi Daya

Sehingga,









x

ajiner Im

cos

a

x

sin

C

sin

C

sin

C

Jadi, rumus umum untuk vektor rapat daya rata-rata dapat diturunkan ...

Konsiderasi Daya

Sedangkan daya total rata-rata

yang menembus bidang z konstan (kearah z) adalah :

 





















_







 

 

 

  mn

2 y 2

x b

0 y

a

0 x b

0 y

a

0 x

z z

av av

Z

E

E

2

1

a

ˆ

dxdy

a

ˆ

P

W



Contoh :

Kerjakan soal berikut !

Diketahui bumbung gelombang persegi dengan dimensi a = 2,29 cm dan b = 1,02 cm terisi udara kering

Ditanyakan :

Rugi-rugi pada bumbung gelombang ...

Konsiderasi Daya

• Rugi-rugi terjadi pada bumbung gelombang untuk kasus _c   dan   0 terjadi disebabkan : (1) redaman pada dielektrik pengisi waveguide, dan juga karena adanya (2) gelombang EM yang merambat pada konduktor waveguide.

• Redaman pada dielektrik pengisi bumbung gelombang dapat dihitung dengan mengganti ...

_

_

_

_

_



_

_



tan

j

1

• Sehingga persamaan untuk konstanta propagasi dapat dituliskan :











































1

j

tan

b

n

π

a

m

π

γ

2

2 2

• Akibat redaman oleh dinding, maka gelombang akan diredam sekalipun

f

_ops

> f

_co

• Daya yang merambat sepanjang bumbung gelombang :

z 2

0 av

mn

e

W

W



 

Dalam persamaan di atas, tan 

adalah loss tangent untuk bahan dielektrik

dimana,

Konsiderasi Daya

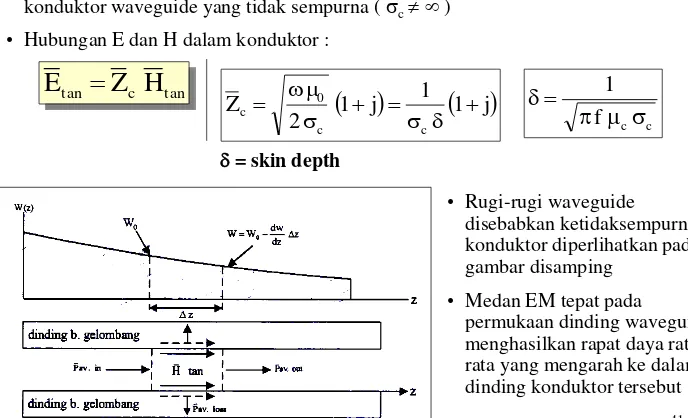
• Rugi-rugi juga disebabkan karena adanya gelombang EM yang merambat pada konduktor waveguide yang tidak sempurna ( _c   )

• Hubungan E dan H dalam konduktor :

tan c

tan

Z

H

E



 

1

j

1

 

1

j

2

Z

c c

0

c

_





_

_







 = skin depth

c c

f

1











• Rugi-rugi waveguide

disebabkan ketidaksempurnaan konduktor diperlihatkan pada gambar disamping

• Medan EM tepat pada

Konsiderasi Daya

• Rugi-rugi rata-rata waveguide disebabkan ketidak-sempurnaan konduktor

dapat dituliskan sebagai berikut :

2 tan c

c 2

tan loss

,

• Untuk satuan panjang ke arah z, rugi-rugi daya rata-rata adalah integrasi dari persamaan di atas untuk keempat dindingnya !









loss

D. Pencatuan Waveguide

•

Perhatikanlah bahwa untuk waveguide

, selalu dicatu pada titik dimana terjadi medan maksimumnya.

• Lihat persamaan medan listriknya, cari titik maksimumnya dan waveguide dicatu pada titik maksimum tersebut !

• Pencatuan bisa dilakukan dengan kabel koaxial dengan ujung dikupas dimasukkan ke dalam waveguide.

•

Contoh

untuk TE₁₀ :

Terdapat satu komponen medan untuk medan listrik E, yaitu komponen ke arah sumbu y :







































 

z

2

t

sin

a

x

sin

C

a

e

a

x

sin

C

a

j

E

10 z

j y

10

Untuk t = 0,

maka harga medan listrik maksimum terjadi pada :

a

x



_{, y = sembarang, dan}

z





10







Pencatuan Waveguide

Jika terdapat dua maksimum

x

y

z

2

a

4

10

