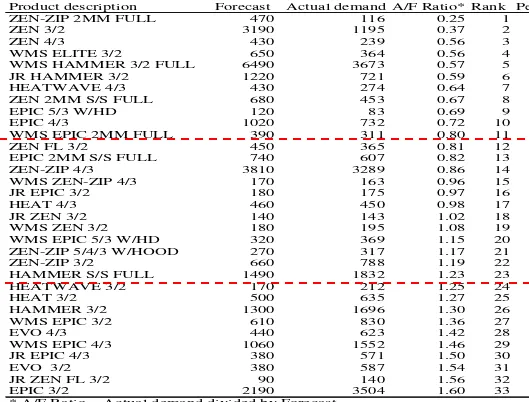
W13 service inventory (continued)
Teks penuh
Gambar
Garis besar
Dokumen terkait
Kebudayaan fisik itu membentuk suatu lingkungan hidup tertentu yang semakin menjauhkan manusia dari lingkungan aslinya sehingga mempengaruhi pula pola-pola
Materi yang disajikan sesuai dengan RPP yang ada. Guru menyampaikan materi dengan sangat komunikatif dan di sisipi dengan lelucon sehingga membuat siswa tidak terlalu kaku
Penelitian ini bertujuan untuk melihat upaya pemberdayaan masyarakat melalui forum kesehatan desa dalam pencapaian cakupan jamban di Desa Jatipurus Kecamatan Poncowarno
- Melakukan entry data rencana studi yang sudah diisikan pada FPRS ke dalam komputer sesuai dengan jadwal dan ruang yang tercantum padaa. KETENTUAN UMUM
faktor yang berhubungan dengan kejadian infeksi nosokomial adalah tindakan invasif yang dapat menembus barier, contohnya pemasangan infus, kateterisasi, intubasi, ruangan
Berdasarkan SPTPD sebagaimana dimaksud dalam Pasal 11 ayat (1), BBNKAA dihitung dan ditetapkan oleh Gubernur dengan mengacu kepada perhitungan sebagaimana
Sedangkan dalam buku “ Het Staatsrecht van Indonesia “ ia mengatakan bahwa negara adalah suatu organisasi artinya sekelompok orang-orang yang dengan bekerja
Evaluasi perubahan mikroskopis pada bursa Fabricius dilakukan dengan menghitung rasio luas seluruh folikel limfoid yang terdapat pada satu plika dengan luas plika