BAB 2. PROGRAM LINEAR
2.1. Pengertian Program Linear
Pemrograman Linier disingkat PL merupakan metode matematik dalam
mengalokasikan sumber daya yang terbatas untuk mencapai suatu tujuan seperti
memaksimumkan keuntungan dan meminimumkan biaya. PL banyak diterapkan dalam
masalah ekonomi, industri, militer, sosial dan lain-lain. PL berkaitan dengan penjelasan
suatu kasus dalam dunia nyata sebagai suatu model matematik yang terdiri dari sebuah
fungsi tujuan linier dengan beberapa kendala linier.
a. Formulasi Permasalahan
Urutan pertama dalam penyelesaian adalah mempelajari sistem relevan dan
mengembangkan pernyataan permasalahan yang dipertimbangakan dengan jelas.
Sistem dalam pernyataan ini termasuk pernyataan tujuan, sumber daya yang
membatasi, alternatif keputusan yang mungkin (kegiatan atau aktivitas), batasan waktu
pengambilan keputusan, hubungan antara bagian yang dipelajari dan bagian lain dalam
perusahaan, dan lain-lain.
Penetapan tujuan yang tepat merupakan aspek yang sangat penting dalam formulasi
masalah. Untuk membentuk tujuan optimalisasi, diperlukan identifikasi anggota
manajemen yang benar-benar akan melakukan pengambilan keputusan dan
mendiskusikan pemikiran mereka tentang tujuan yang ingin dicapai.
b. Pembentukan model matematik
Tahap berikutnya yang harus dilakukan setelah memahami permasalahan optimasi
adalah membuat model yang sesuai untuk analisis. Pendekatan konvensional riset
operasional untuk pemodelan adalah membangun model matematik yang
menggambarkan inti permasalahan. Kasus dari bentuk cerita diterjemahkan ke model
matematik. Model matematik merupakan representasi kuantitatif tujuan dan sumber
permasalahan optimal terdiri dari dua bagian. Bagian pertama memodelkan tujuan
optimasi. Model matematik tujuan selalu menggunakan bentuk persamaan. Bentuk
persamaan digunakan karena kita ingin mendapatkan solusi optimum pada satu titik.
Fungsi tujuan yang akan dioptimalkan hanya satu. Bukan berarti bahwa permasalahan
optimasi hanya dihadapkan pada satu tujuan. Tujuan dari suatu usaha bisa lebih dari
satu. Tetapi pada bagian ini kita hanya akan tertarik dengan permasalahan optimal
dengan satu tujuan.
Bagian kedua merupakan model matematik yang merepresentasikan sumber daya
yang membatasi. Fungsi pembatas bisa berbentuk persamaan (=) atau pertidaksamaan
( atau ). Fungsi pembatas disebut juga sebagai konstrain. Konstanta (baik sebagai
koefisien maupun nilai kanan) dalam fungsi pembatas maupun pada tujuan dikatakan
sebagai parameter model. Model matematika mempunyai beberapa keuntungan
dibandingkan pendeskripsian permasalahan secara verbal. Salah satu keuntungan yang
paling jelas adalah model matematik menggambarkan permasalahan secara lebih
ringkas. Hal ini cenderung membuat struktur keseluruhan permasalahan lebih mudah
dipahami, dan membantu mengungkapkan relasi sebab akibat penting. Model
matematik juga memfasilitasi yang berhubungan dengan permasalahan dan
keseluruhannya dan mempertimbangkan semua keterhubungannya secara simultan.
Terakhir, model matematik membentuk jembatan ke penggunaan teknik matematik dan
komputer kemampuan tinggi untuk menganalisis permasalahan.
Di sisi lain, model matematik mempunyai kelemahan. Tidak semua karakteristik
sistem dapat dengan mudah dimodelkan menggunakan fungsi matematik. Meskipun
dapat dimodelkan dengan fungsi matematik, kadang-kadang penyelesaiannya sulit
diperoleh karena kompleksitas fungsi dan teknik yangdibutuhkan.
c. Bentuk umum pemrograman linier adalah sebagai berikut :
1. Fungsi tujuan :
Maksimumkan atau minimumkan z = c1x1 + c2x2 + ... + cnxn
a11x1 + a12x2 + ... + a1nxn = / / b1
a21x1 + a22x2+ … + a2nxn = / / b2 …
am1x1 + am2x2+ … + amnxn = / / bm
x1, x2, …, xn 0
Simbol x1, x2, ..., xn (xi) menunjukkan variabel keputusan. Jumlah variabel keputusan
(xi) tergantung dari jumlah kegiatan atau aktivitas yang dilakukan untuk mencapai
tujuan. Simbol c1,c2,...,cn merupakan kontribusi masing-masing variabel keputusan
terhadap tujuan, disebut juga koefisien fungsi tujuan pada model matematiknya. Simbol
a11, ...,a1n,...,amn merupakan penggunaan per unit variabel keputusan akan sumber daya
yang membatasi, atau disebut juga sebagai koefisien fungsi kendala pada model
matematiknya. Simbol b1,b2,...,bm menunjukkan jumlah masing-masing sumber daya
yang ada. Jumlah fungsi kendala akan tergantung dari banyaknya sumber daya yang
terbatas.
Pertidaksamaan terakhir (x1, x2, …, xn 0) menunjukkan batasan non negatif.
Membuat model matematik dari suatu permasalahan bukan hanya menuntut
kemampuan matematik tapi juga menuntut seni permodelan. Menggunakan seni akan
membuat permodelan lebih mudah dan menarik.
Kasus pemrograman linier sangat beragam. Dalam setiap kasus, hal yang penting
adalah memahami setiap kasus dan memahami konsep permodelannya. Meskipun
fungsi tujuan misalnya hanya mempunyai kemungkinan bentuk maksimisasi atau
minimisasi, keputusan untuk memilih salah satunya bukan pekerjaan mudah. Tujuan
pada suatu kasus bisa menjadi batasan pada kasus yang lain. Harus hati-hati dalam
menentukan tujuan, koefisien fungsi tujuan, batasan dan koefisien pada fungsi
pembatas.
2.2. Model Perogram Linear
Pada Model Program Linear ada 2 Metode yang dipakai yaitu : Metode Grafik dan
permasalahan dimana hanya terdapat dua variabel keputusan. Untuk menyelesaikan
permasalahan tersebut, langkah pertama yang harus dilakukan adalah memformulasikan
permasalahan yang ada ke dalam bentuk Linear Programming (LP). Langkah-langkah
dalam formulasi permasalahan adalah :
1. Pahamilah secara menyeluruh permasalahan manajerial yang dihadapi.
2. Identifikasikan tujuan dan kendalanya
3. Definisikan variabel keputusannya
4. Gunakan variabel keputusan untuk merumuskan fungsi tujuan dan fungsi kendala
secara matematis.
Sebagai contoh dalam memformulasikan permasalahan, berikut ini akan dibahas
perusahaan Furniture yang akan membuat meja dan kursi. Keuntungan yang diperoleh
dari satu unit meja adalah Rp 70.000,- sedangkian keuntungan yang diperoleh dari satu
unit kursi adalah Rp. 50.000,-. Namun untuk meraih keuntungan tersebut Perusahaan
menghadapi kendala keterbatasan jam kerja. Untuk pembuatan 1 unit meja memerlukan
4 jam kerja. Untuk pembuatan 1 unit kursi membutuhkan 3 jam kerja. Untuk pengecatan
1 unit meja dibutuhkan 2 jam kerja, dan untuk pengecatan 1 unit kursi dibutuhkan 1 jam
kerja. Jumlah jam kerja yang tersedia untuk pembuatan meja dan kursi adalah 240 jam
per minggu sedang jumlah jam kerja untuk pengecatan adalah 100 jam per minggu.
Berapa jumlah meja dan kursi yang sebaiknya diproduksi agar keuntungan perusahaan
maksimum ?
Dari kasus di atas dapat diketahui bahwa tujuan perusahaan adalah
memaksimumkan profit. Sedangkan kendala perusahaan tersebut adalah terbatasnya
waktu yang tersedia untuk pembuatan dan pengecatan. Apabila permasalahan tersebut
diringkas dalam satu tabel akan tampak sebagai berikut:
Mengingat produk yang akan dihasilkan adalah meja dan kursi, maka dalam rangka
memaksimumkan profit, perusahaan harus memutuskan berapa jumlah meja dan kursi
yang sebaiknya diproduksi. Dengan demikian dalam kasus ini, yang merupakan variabel
keputusan adalah meja (X1) dan kursi (X2). Setelah kita mendefinisikan variabel
keputusan, maka langkah selanjutnya adalah menuliskan secara matematis fungsi tujuan
dan fungsi kendala.
1. Fungsi Tujuan
Tujuan perusahaan adalah maksimisasi keuntungan, sehingga kita dapat menuliskan
fungsi tujuan sebagai berikut : P = (Rp. 70.000 x jumlah meja + Rp. 50.000 x jumlah kursi)
yang diproduksi atau secara matematis dapat dituliskan :
Maksimumkan Z = 70.000 X1 + 50.000 X2
2. Fungsi kendala
Berkaitan dengan sumber daya yang digunakan, perusahaan tidak bisa
memperkirakan secara tepat kebutuhan sumber daya yang digunakan untuk mencapai
keuntungan tertentu. Biasanya perusahaan menyediakan sumber daya tertentu yang
merupakan kebutuhan minimum atau maksimum. Kondisi seperti ini secara matematis
diungkapkan dengan pertidaksamaan. Kendala yang pertama adalah waktu yang
tersedia di departemen pembuatan. Total waktu yang diperlukan untuk pembuatan X1
(meja) dimana untuk membuat satu unit meja diperlukan waktu 4 jam kerja dan untuk
pembuatan X2 (kursi) diperlukan waktu 3 jam kerja. Total waktu pembuatan yang
tersedia adalah 240 jam.
Kendala : Waktu pembuatan
1 unit meja memerlukan 4 jam untuk pembuatan -> 4 X1
1 unit kursi memerlukan 3 jam untuk pembuatan -> 3 X2
Total waktu yang tersedia per minggu untuk pembuatan -> 240 Jam
Dirumuskan dalam pertidaksamaan matematis -> 4 X1 + 3 X2 240
Seperti halnya pada kendala yang pertama, maka pada kendala kedua dapat
diperlukanwaktu 2 jam kerja dan untuk pengecatan X2 (kursi) dibutuhkan waktu 1 jam
kerja. Total waktu pengecatan yang tersedia adalah 100 jam. Kendala : Waktu pengecatan
1 unit meja memerlukan 2 jam untuk pengecatan -> 2 X1
1 unit kursi memerlukan 1 jam untuk pengecatan -> 1 X2
Total waktu yang tersedia per minggu untuk pengecatan -> 100 Jam
Dirumuskan dalam pertidaksamaan matematis -> 2 X1 + X2 100
Salah satu syarat yang harus dipenuhi dalam Linear Programming adalah asumsi nilai
X1 dan X2 tidak negatif. Artinya bahwa X1 0 (jumlah meja yang diproduksi adalah lebih
besar atau sama dengan nol) . X2 0 (jumlah kursi yang diproduksi adalah lebih besar
atau sama dengan nol)
Dari uraian di atas dapat dirumuskan formulasi permasalahan secara lengkap sebagai
berikut :
1. Fungsi tujuan :
Maksimumkan Z = 70.000 X1 + 50.000 X2
2. Fungsi kendala :
4X1 + 3X2 240
2X1 + 1X2 100
X1, X2 0 (kendala non negatif pertama)
Setelah formulasi lengkapnya dibuat, maka Kasus Furniture tersebut akan
diselesaikan dengan metode grafik. Keterbatasan metode grafik adalah bahwa hanya
tersedia dua sumbu koordinat, sehingga tidak bisa digunakan untuk menyelesaikan
kasus yang lebih dari dua variabel keputusan.
Langkah pertama dalam penyelesaian dengan metode grafik adalah menggambarkan
fungsi kendalanya. Untuk menggambarkan kendala pertama secara grafik, kita harus
merubah tanda pertidaksamaan menjadi tanda persamaan seperti berikut.
Untuk menggambarkan fungsi linear, maka cari titik potong garis tersebut dengan
kedua sumbu. Suatu garis akan memotong salah satu sumbu apabila nilai variabel yang
lain sama dengan nol. Dengan demikian kendala pertama akan memotong X1, pada saat
X2 = 0, demikian juga kendala ini akan memotong X2, pada saat X1 = 0.
Kendala I :
4 X1 + 3 X2 = 240
memotong sumbu X1 pada saat X2 = 0
4 X1 + 0 = 240
X1 = 240 / 4
X1 = 60.
memotong sumbu X2 pada saat X1 = 0
0 + 3 X2 = 240
X2 = 240/3
X2 = 80
Kendala I memotong sumbu X1 pada titik (60, 0) dan memotong sumbu X2 pada titik
(0, 80).
Kendala II :
2 X1 + 1 X2 = 100
memotong sumbu X1 pada saat X2 = 0
2 X1 + 0 = 100
X1 = 100/2
X1 = 50
memotong sumbu X2 pada saat X1 =0
0 + X2 = 100
X2 = 100
Kendala I memotong sumbu X1 pada titik (50, 0) dan memotong sumbu X2 pada titik
Gambar 2.1. Area Layak
Titik potong kedua kendala bisa dicari dengan cara substitusi atau eliminasi
2 X1 + 1 X2 = 100 → X2 = 100 - 2 X1
4 X1 + 3 X2 = 240 X2 = 100 - 2 X1
4 X1 + 3 (100 - 2 X1) = 240 X2 = 100 - 2 * 30
4 X1 + 300 - 6 X1 = 240 X2 = 100 - 60
- 2 X1 = 240 - 300 X2 = 40
- 2 X1 = - 60
X1 = -60/-2 = 30.
Sehingga kedua kendala akan saling berpotongan pada titik (30, 40).
Tanda pada kedua kendala ditunjukkan pada area sebelah kiri dari garis kendala.
Feasible region (area layak) meliputi daerah sebelah kiri dari titik A (0; 80), B (30; 40),
dan C (50; 0).
Untuk menentukan solusi yang optimal, ada dua cara yang bisa digunakan yaitu
1. Dengan menggunakan garis profit (iso profit line)
2. Dengan titik sudut (corner point)
Penyelesaian dengan menggunakan garis profit adalah penyelesaian dengan
menggambarkan fungsi tujuan. Kemudian fungsi tujuan tersebut digeser ke kanan
sampai menyinggung titik terjauh dari dari titik nol, tetapi masih berada pada area layak
sembarang nilai yang mudah dibagi oleh koefisien pada fungsi profit. Pada kasus ini
angka yang mudah dibagi angka 7 (koefisien X1) dan 5 (koefisien X2) adalah 35. Sehingga
fungsi tujuan menjadi 35 = 7 X1 + 5 X2. Garis ini akan memotong sumbu X1 pada titik (5,
0) dan memotong sumbu X2 pada titik (0, 7).
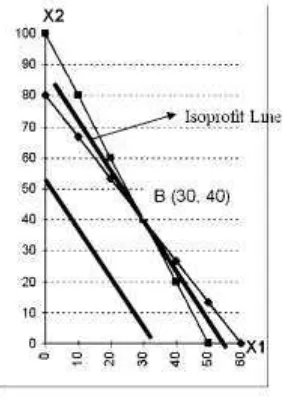
Gambar 2.2. Iso profit line
Iso profit line menyinggung titik B yang merupakan titik terjauh dari titik nol. Titik B
ini merupakan titik optimal. Untuk mengetahui berapa nilai X1 dan X2, serta nilai Z pada
titik B tersebut, kita mencari titik potong antara kendala I dan kendala II (karena titik B
merupakan perpotongan antara kendala I dan kendala II). Dengan menggunakan
eliminiasi atau substitusi diperoleh nilai X1 = 30, X2 = 40 dan Z = 410. Dari hasil
perhitungan tersebut maka dapat disimpulkan bahwa keputusan perusahaan yang akan
memberikan profit maksimal adalah memproduksi X1 sebanyak 30 unit, X2 sebanyak 40
unit dan perusahaan akan memperoleh profit sebesar 4.100.000.
Penyelesaian dengan menggunakan titik sudut (corner point) artinya kita harus
mencari nilai tertinggi dari titik-titik yang berada pada area layak (feasible region). Dari
peraga 1, dapat dilihat bahwa ada 4 titik yang membatasi area layak, yaitu titik 0 (0, 0), A
(0, 80), B (30, 40), dan C (50, 0).
Keuntungan pada titik O (0, 0) adalah (70.000 x 0) + (50.000 x 0) = 0
Keuntungan pada titik A (0; 80) adalah (70.000 x 0) + (50.000 x 80) = 4.000.000
Keuntungan pada titik C (50; 0) adalah (70.000 x 50) + (50.000 x 0) = 3.500.000
Karena keuntungan tertinggi jatuh pada titik B, maka sebaiknya perusahaan
memproduksi meja sebanyak 30 unit dan kursi sebanyak 40 unit, dan perusahaan
memperoleh keuntungan optimal sebesar 4.100. 000.
2.2.1. Solusi Grafis
Untuk mencari solusi suatu persoalan program linier dengan cara grafis, berikut ini
dikemukakan dua buah contoh, yaitu persoalan maksimasi dan minimasi.
a. Solusi grafis untuk persoalan maksimasi
Contoh:
Maksimumkan z = 3x1 + 5x2
Berdasarkan x1
2x2
3x1 + 2x2 8
x1, x2
Gambar 2.3 Titik D sebagai titik optimum
b. Solusi grafis untuk persoalan minimasi
Contoh:
PT Auto Indah memproduksi dua jenis mobil, yaitu mobil sedan dan truk. Untuk
dapat meraih konsumen berpenghasilan tinggi, perusahaan ini memutuskan untuk
melakukan promosi dalam dua macam acara TV, yaitu pada acara hiburan dan acara
dan 2 juta pemirsa pria. Promosi pada acara olah raga akan disaksikan oleh 2 juta
pemirsa wanita dan 12 juta pemirsa pria. Biaya promosi pada acara hiburan adalah 5
jutarupiah/menit, sedangkan pada acara olah raga biayanya adalah 10 juta/menit.
Jika perusahaan menginginkan promosinya disaksikan sedikitnya oleh 28 juta
pemirsa wanita dan sedikitnya oleh 24 juta pemirsa pria, bagaimanakah strategi
promosi itu sebaiknya?
Penyelesaian:
Variabel keputusan:
x1 lamanya promosi dalam acara hiburan
x2 lamanya promosi dalam acara olah raga
Formulasi persoalan:
Minimumkan z = 5x1 + 10x2
Berdasarkan 7x1 + 2x2 8
2x1 + 12x2
x1, x2
Gambar 2.4 Solusi persoalan untuk PT Auto Indah
2.2.2. Kasus Khusus
Contoh soal yang telah dibahas di atas mempunyai hanya satu titik optimal. Berikut
ini ada persoalan program linier yang mempunyai kasus khusus seperti:
1. Mempunyai solusi optimal yang tidak terbatas, biasa disebut juga mempunyai solusi
2. Tidak mempunyai solusi fisibel atau persoalan progama linier yang infisibel.
3. Mempunyai ruang solusi yang tidak terbatas, yaitu kasus dimana ada titik-titik pada
daerah fisibel dengan harga z yang sangat besar (pada persoalan maksimasi).
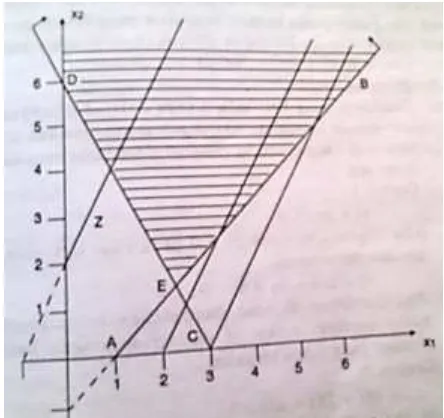
2.2.2.1. Solusi alternatif atau solusi optimal banyak
Contoh:
Maksimumkan z = 3x1 + 2x2
Berdasarkan (1/40)x1 + (1/60)x2
(1/50)x1 + (1/50)x2
X1, x2
Solusi grafis pada persoalan diatas adalah:
Gambar 2.5 Solusi alternatif
2.2.2.2. Persoalan programa linier tanpa solusi fisibel
Dalam hal ini solusi fisibelnya kosong sehingga dengan sendirinya tidak ada solusi
optimal.
Contoh:
Maksimumkan z = 3x1 +2x2
Berdasarkan (1/40)x1 + (1/60)x2 1
(1/50)x1 + (1/50)x2
x1
x2
x1, x2
Gambar 2.6 Tidak ada ruang fisibel
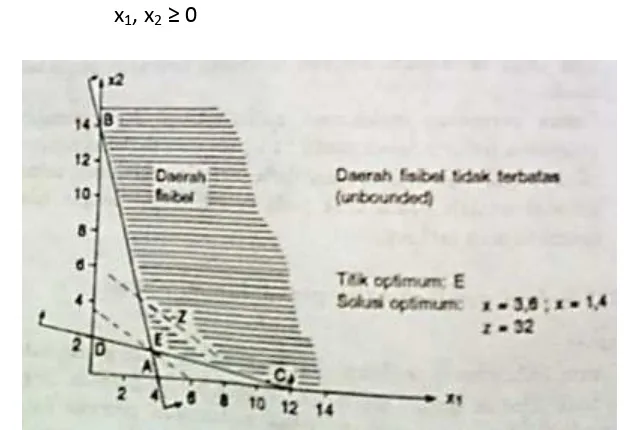
2.2.2.3. Persoalan program linier dengan ruang solusi yang tidak terbatas (unbounded)
Kasus ini terjadi apabila ruang solusi tidak terbatas sehingga nilai fungsi tujuan dapat
meningkat/menurun secara tidak terbatas. Pada umumnya, kasus ini terjadi karena
kesalahan dalam memformulasikan persoalan.
Contoh:
Maksimumkan z = 2x1– x2
Berdasarkan x1– x2
2x1 + x2 6
X1, x2
Solusi grafis pada persoalan ini adalah:
Latihan soal:
1. Sebuah industri kecil, memproduksi 2 macam hiasan dinding dari tripleks yang proses
pengerjaannya dilakukan di 2 stasiun kerja yaitu pemotongan dan perakitan. Hiasan
model A mula-mula dikerjakan di bagian pemotongan selama 5 menit kemudian dirakit
selama 10 menit. Hiasan model B dikerjakan di bagian pemotongan selama 8 menit
kemudian dirakit selama 8 menit. Dalam 1 hari kerja, waktu yang tersedia di bagian
pemotongan 3 jam 20 menit, sedang di bagian perakitan tersedia waktu 4 jam. Jika
harga jual hiasan model A $ 500/unit dan hiasan model B $ 600/unit. Berapakah
masing-masing model harus dibuat agar diperoleh total pendapatan yang optimal?
2. Sebuah pabrik akan mengirimkan hasil produksinya dengan menggunakan 120 kotak
berukuran besar (L) dan 180 kotak berukuran sedang (M). Pabrik tsb akan menyewa truk
besar dan kecil untuk mengangkut barang-barang itu. Sebuah truk besar dapat memuat
10 kotak L dan 20 kotak M. Sebuah truk kecil dapat memuat 8 kotak L dan 4 kotak M.
Ongkos angkutan truk besar sekali jalan Rp. 150.000 dan ongkos truk kecil sekali jalan
Rp. 100.000. Berapa truk besar dan kecil yang harus digunakan supaya total ongkos
angkutnya optimal?
3. Sebuah perusahanaan sepatu membuat 2 jenis sepatu yaitu sepatu I bersol karet dan
sepatu II bersol kulit. Untuk membuat sepatu, perusahaan mempunyai 3 macam mesin.
Mesin 1 untuk membuat sol dari karet, mesin 2 untuk membuat sol dari kulit, mesin 3
untuk membuat bagian atas sepatu dan memasangkan dengan sol sepatu. Setiap lusin
sepatu I dikerjakan mesin 1 selama 2 jam, kemudian mesin 3 selama 6 jam. Sepatu II
dikerjakan mesin 2 selama 3 jam kemudian mesin 3 selama 5 jam. Jam kerja maksimum
setiap hari untuk mesin 1 selama 8 jam, mesin 2 selama 15 jam, dan mesin 3 selama 30
jam. Sumbangan laba untuk setiap lusin sepatu I adalah Rp. 30.000 dan sepatu II adalah
Rp. 50.000. Berapakah masing2 model harus dibuat, agar laba yang diperoleh optimal?
4. Sebuah industri perakitan komputer, memproduksi 2model komputer yaitu model
DeskTop dan model Tower. Pabrik tersebut mampu memproduksi 1000 unit komputer
per bulan. Berdasarkan informasi dari bagian penjualan, dinyatakan bahwa untuk model
per bulan. Jika keuntungan yang diperoleh dari penjualan 1 unit komputer model
DeksTop adalah $ 120 dan komputer model Tower adalah $ 130. Berapakah
masing-masing model harus dibuat agar diperoleh keuntungan yang optimal?. (diasumsikan