www.elsevier.com/locate/dsw
A branch-and-cut algorithm for the maximum cardinality
stable set problem
F. Rossi
∗, S. Smriglio
Dipartimento di Matematica Pura ed Applicata, Universita di L’Aquila, Via Vetoio, 67010 Coppito (L’Aquila), Italy
Received8 April 1999; receivedin revisedform 13 July 2000; accepted24 July 2000
Abstract
We propose a branch-and-cut algorithm for the Maximum Cardinality Stable Set problem. Rank constraints of general structure are generatedby executing clique separation algorithms on a modiedgraph obtainedwith edge projections. A branching scheme exploiting the available inequalities is also introduced. A computational experience on the DIMACS benchmark graphs validates the eectiveness of the approach. c 2001 Elsevier Science B.V. All rights reserved.
Keywords:Branch-and-cut; Stable set; Rank inequality
1. Introduction
LetG= (V; E) be an undirected graph, whereV is the set of vertices andEthe set of edges. Astable set
(also referredto asvertex packing) inGis a subset of pairwise non-adjacent vertices of G. The Maximum
Cardinality Stable Set (MSS) problem consists of
nding a stable set inGof maximum cardinality. The cardinality of a maximum stable set is calledstability
numberofGandis denotedby(G). The
neighbour-hood N(v) of a vertexvis the set of all the vertices adjacent tov, andwe denedegG(v) =|N(v)|. Anal-ogously, for any subset W⊆V we denote by N(W)
∗Corresponding author. Tel.: 0862-433139; fax:
+39-0862-433180.
E-mail addresses: [email protected] (F. Rossi), smriglio@ univaq.it (S. Smriglio).
the set of vertices {u ∈ V:∃v ∈ W such thatu ∈ N(v)}. Thedensityof a graphG= (V; E) is the ratio 2|E|=|V|2− |V|.
Given a setW⊆V, the graphG[W] = (W; E[W]), where E[W] is the set of the edges of G with both the endpoints inW, is calledthe subgraphinducedby
W inG. An induced subgraph ofG such that all its vertices are pairwise adjacent is calledcliqueofG. A
partitioning (covering) of G is a family of induced
subgraphs such that each vertex ofGis containedin exactly (at least) one subgraph of the family.
The MSS problem is known to be NP-hard[9] for arbitrary graphs andit is a known fact that unstructured stable set problems are dicult integer programming problems. Even if several classes of validinequali-ties are known (see [10]), the computation time re-quiredfor generating constraints andfor solving Lin-ear Programs (LPs), is often not justiedby the bound improvement. In fact, the branch-and-cut algorithms
devisedso far [2,14] have been outperformedby com-binatorial algorithms [12,13,16].
On the contrary, several reasons motivate the investigation of ecient polyhedral methods for the stable set problem. One reason is that other combi-natorial problems may be formulatedas a stable set problem with possible transfer of results [7]. An-other recent application is proposedin [1] where preprocessing andprobing techniques for general Mixed Integer Programs (MIP) are devised address-ing their vertex packaddress-ing relaxation (conict graph). In addition, special stable set problems may arise in dierent application areas (see [8,15]), where integer programming often turns out to be eective.
In this paper we propose a branch-and-cut algo-rithm for the MSS problem which attempts to smooth the aforementionedlack of eciency. Two aspects are prominent to accomplish this purpose: (i) the e-ciency of the constraint generation procedure and the quality of the cuts; (ii) the eectiveness of the enu-meration strategy.
As for (i), we introduce a technique to reduce the identication ofrankinequalities of general structure to the identication of clique inequalities on a modi-edgraph (Section 2). This approach is motivatedby the following observations. The family of clique in-equalities gives an important contribution in reducing the integrality gap [1,14]. Although the relatedsepara-tion problem is NP-hard, the identicarelatedsepara-tion of violated clique inequalities can be carriedout by fast andeec-tive heuristics [11]. The proposedconstraint genera-tion procedure combines a clique detecgenera-tion algorithm with a graph reduction operation (edge projection) al-lowing an ecient detection of cliques and other rank inequalities.
For what concerns (ii), we implement the enumera-tion scheme due to Balas and Yu [4]. In their algorithm an upper boundis obtainedby computing a clique par-titioning andthe smaller the gap between the upper boundandthe current lower bound, the smaller the size of the branching set. In our implementation, the upper boundis obtainedby using, besides cliques, all the subgraphs associatedto the generatedrank con-straints (Section 3).
The performance of the branch-and-cut algorithm incorporating rank inequalities is comparedwith the ones of three other algorithms: a branch-and-cut incor-porating pure clique inequalities, the branch-and-cut
by Balas et al. [2] andthe branch-and-boundby Man-nino andSassano [13] (Section 4). The test bedcon-sists of the DIMACS challenge benchmark graphs and sparse uniform random graphs.
2. Rank inequalities
In this section we describe the separation procedure. Let STAB(G) = conv{W ∈ R|V|:W⊆V is a stable
set}be the stable set polytope, i.e., the convex hull of the incidence vectors of all stable sets of vertices of
G. Arank inequalityis an inequality of the form
x(W) =
i∈W
xi6(G[W]) (1)
where, for a givenW⊆V; G[W] is the subgraph ofG
induced byW. It is satisedby the incidence vector of every stable set inG, andso it is validfor STAB(G). In general, a rank inequality is not facet dening even forG[W]. The latter condition holds in special cases, for instance, whenever W induces an odd hole in G
(odd hole inequalities), an odd antihole or a web [3]. The oddhole inequalities have been usedas cutting planes in [14] (in which inequalities are liftedby a sequential lifting procedure) and in [6,11].
A rank inequality which is facet dening for STAB(G) is also obtainedwhenever W induces a maximal clique in G (clique inequalities) [3]. Al-though the separation problem associatedwith the clique inequalities is NP-hard, being equivalent to determining a maximum weight clique, the identica-tion of violatedcliques can be carriedout by fast and eective heuristics [11]. Moreover, clique inequalities have been proven to give an important contribution in reducing the integrality gap [1,14]. In our algorithm, according to known experiences [2,14], a suitable ini-tial linear relaxation of the MSS problem is quickly obtainedby a greedy algorithm which computes a covering of G into maximal cliques. In particular, the initial formulation is given by P(C0) = {x ∈ Rn:x(C)61; ∀C ∈ C0; x¿0}, where C0 is a set
of maximal cliques such that each edge ofGis con-tainedin at least one clique ofC0. Our approach is to
strengthen the formulationP(C0).
During its execution, the branch-and-cut algorithm stores the setRof all the non-dominated constraints
constraintc:x(W)6(G[W]) is generated, it may oc-cur thatcdominates some constraints inR. If this is
the case, the dominated constraints are discarded be-fore adding ctoR. We denote by LPt the linear
re-laxation of the current formulation in a given nodet
of the enumeration tree. Hence, LP0 is the linear re-laxation{maxni=1xi:x∈P(C0)}.
In a given nodetof the enumeration tree let us de-note by xt the optimal solution of LPt foundby the LP solver. The constraint generation procedure works on the subspace Ft ={i= 1; : : : ;|V|: xt
i ∈ {0;1}}.
In the following, when no confusion arises, we let
GF =G[Ft]. The procedure is based on a
polyhe-dral investigation of a graph operation called edge
projection, introducedby Mannino andSassano [13]
as a specialization of Lovasz andPlummer’s clique projection.
2.1. Edge projection and strong projectability
Lete=uv∈Ebe an edge ofG. LetNuv=N(u)∩ N(v), denote by Euv⊆E the set of the edges with at least one endpoint in Nuv∪ {u; v}, andlet Euv= {ij:i; j∈V\({u; v} ∪Nuv); N({i; j})⊇{u; v}}.
Denition 2.1. The graphG|e= (V|e; E|e), in which
V|e=V\({u; v}∪Nuv) andE|e=E\Euv∪Euv, is called
projectionofeinG.
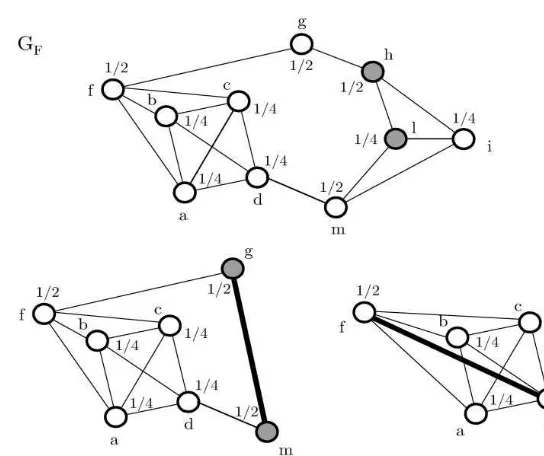
In Fig. 2, the graph G(1)F is the projection ofhl in
GF. As for the stability number of the reduced graph, we have (G)¿(G|e) + 1, for alle∈E. Mannino andSassano [13] noticedthat, for some special edges, this holds at equality.
Denition 2.2. An edgee=uv∈E is projectable in
G if andonly if there exists a maximum stable setS
inGsuch thatS∩ {u; v} =∅.
Lemma 2.3(Mannino andSassano [13]). Let G =
(V; E)be a graph ande=uv∈Ea projectable edge
in G. Then; (G) =(G|e) + 1.
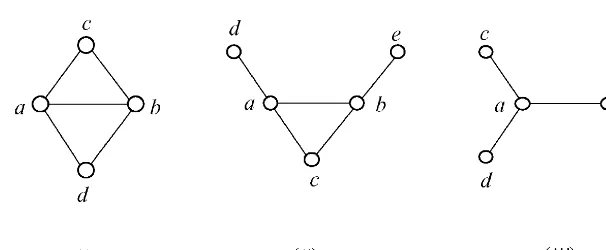
In [13] a sucient condition of projectability is given. Consider the graphs in Fig. 1: Diamond= ({a; b ; c; d};{ab; ac; ad; bc; bd});Bull= ({a; b ; c; d; e}; {ab; ac; ad; bc; be}); Double Fork= ({a; b ; c; d; e; f};
{ab; ac; ad; be; bf}). Let us indicate ab as central edge. The following lemma holds:
Lemma 2.4(Mannino andSassano [13]). Let G =
(V; E) be a graph and let e=uv ∈ E. If e is not
the central edge of an induced subgraph isomorphic
to a diamond or a bull or a double fork; then e is
projectable in G.
Our separation procedure needs to identify some particular projectable edges. We therefore introduce the notion ofstrong projectability.
Denition 2.5. LetG=(V; E) be a graph. An edgee=
uv∈Eisstrongly projectableinGif it is projectable in every induced subgraph of G containing both u
andv.
The next result provides a characterization of strongly projectable edges.
Theorem 2.6. Let G= (V; E) be a graph and e=
uv ∈ E.Then;e is strongly projectable in G if and
only if it is not the central edge of an induced sub-graph isomorphic to a diamond or a bull or a double fork.
Proof(Only if ). Supposeuvis the central edge of an induced subgraphG′ of G isomorphic to a diamond
or a bull or a double fork. Then, there does not exist a maximum stable setS′ofG′such thatS′∩ {u; v} =∅. Therefore, by denition,eis not projectable inG′and it is not strongly projectable inG.
(if). Suppose uv is not the central edge of an in-duced subgraphG′ of Gisomorphic to a diamond or a bull or a double fork. Then the result follows from applying Lemma 2.4 to all induced subgraphs of G
containing bothuandv.
2.2. The separation procedure
The constraint generation is carriedout by heuris-tically solving the separation problem associatedwith general rank inequalities. The procedure consists of two basic ingredients:
(i) the edge projection operation;
Fig. 1. (i) Diamond, (ii) bull, (iii) double fork.
In particular, violatedrank inequalities are identied by executing a clique detection algorithm on a reduced graph obtainedfrom GF by a sequence of edge pro-jections.
More formally, we denote by GF(i)= (V(i); E(i)) a
graph obtainedfromGF by asequenceofiedge
pro-jections andindicate as P(i) ={u
0v0; u1v1; u2v2; : : : ; ui−1vi−1}the sequence of the projectededges, where uhvh ∈E(h) for h= 0; : : : ; i−1. To identify the
cor-responding sequence of graphs we letGF(0)=GF and
GF(h)=G(hF−1)|uh−1vh−1, forh¿1. At thehth
projec-tion step edges andvertices are removedfromGF(h−1), but also new edges, referred to asfalse edges, can be introduced. It turns out that, even if there does not ex-ist a clique inG(hF−1) violatedby xt, the introduction the false edges in Euh−1vh−1 can leadto a clique vio-latedby xt inGF(h); h¿1.
The rst phase of the procedure (reduction phase) iteratively selects an edge uh−1vh−1 in the current
graph GF(h−1) andbuilds its projection G(h)F . The se-quence stops, after isteps, when either (a)GF(i) con-tains a clique, induced by a setC⊆V(i) andviolated by xt, or (b)GF(i)does not contain edges. The reduc-tion phase is detailed in Secreduc-tion 2.2.1.
In case (a), the detected clique inequality is valid for STAB(G(i)F ), but, in general,notfor STAB(GF).
In particular,x(C)61 is validfor STAB(GF) if and
only if GF(i)[C] does not contain false edges (i.e.,C
induces a clique onGF). Hence, the secondphase of the procedure performs a lifting which extends the setCto a setW⊆VF such thatx(W)6(GF[W]) is validfor STAB(GF). The lifting phase is detailed in Section 2.2.2.
2.2.1. Sequence of projections
In this section we explain how to perform the re-duction phase. As will be shown in Section 2.2.2, in order to guarantee the validity of the lifted inequali-ties, we require that, at the (h+ 1)th step of the pro-jection sequence,uhvh is a strongly projectable edge
inGF(h).
Although Theorem 2.6 allows us to check the strong projectability of an edge in polynomial time (notice that deciding the projectability of an edge is NP-complete), the resulting procedure is computa-tionally too expensive to be executed, in any node of the search tree, for every edge in the sequence. In or-der to overcome this diculty, a relaxation technique is introducedso as to make the currently selectededge strongly projectable before constructing its projection. At the (h+ 1)th iteration it consists of removing from
G(h)F a suitable set of edges R(uhvh)⊆E(h), so that
uhvh becomes strongly projectable in the new graph
˜
G(h)F = (V(h); E(h)−R(u
hvh)). One such possible set R(uhvh) can be founddue to the following corrollary
to Theorem 2.6.
Corollary 2.7. Let G= (V; E) be a graph and e=
uv∈E.IfN(u)− {v}is a clique;then uv is strongly projectable in G.
Hence, if Q is a clique containedeither in
N(uh)\{vh} (orN(vh)\{uh}) a possible choice is to
setR(uhvh) ={e∈E(h):ehas an endpoint inuh and
not in Q}.
reduce this drawback we look for the largest clique
Q⊆N(uh)\{vh}, where deg(uh)6deg(vh). The pro-cedure builds the next graph of the sequence assuming
GF(h+1)= ˜G(h)F |uhvh. After the projection ofuhvh, we try
to detect violated clique inequalities on GF(h+1). The separation routine can be either a greedy algorithm or a complete enumeration depending on the size of the graphs [11]. Since the call of this routine at each step can produce an excessive computational workload, the clique separation is executedeveryKprojections.
2.2.2. Lifting
Suppose that the separation routine is successful af-ter i projections, i.e., it returns at least one violated cliqueGF(i)[C] ofGF(i). In this section, a lifting proce-dure is described able to extendCto a setW such that
• (GF[W]) can be computedeasily;
• the inequalityx(W)6(GF[W]) is violatedby xt.
Let us start with a denition.
Denition 2.8 (Anti-projection). Let G(h+1)F be the reduction of GF obtainedby the sequence of projec-tionsP(h+1)andlet wz∈E(h+1)be a false edge gen-ing the edge wz with the path {wuk; ukvk; vkz} (i.e., even subdivision of wz), adding the edges {tuk; tvk}
for eacht∈Nukvk, andremoving all other false edges
ofGF(h+1)generatedbyukvk.
In Fig. 2, GF is the anti-projection ofgm inG(1).
Let ˆNuv=Nuv∪{u; v}. The following lemma describes
a generic anti-projection step, capturing the role of strong projectability.
Lemma 2.9. Let GF(h+1) be the reduction ofGF
ob-tained by the sequence of projections P(h+1)and let
wz ∈ E(h+1) be a false edge generated by
projec-tion of ukvk ∈ P(h+1) in G(k)
kvk, generatedby projec-tions of{uk+1vk+1; : : : ; uhvh}. These false edges
can-not have eitherukor vk as endpoint, sinceukvk is
re-movedfromGk
F by its projection. Moreover,ukvk is
strongly projectable inGF(k). Hence,ukvkis projectable
inGF(h+1)↑wz[Z∪Nˆu inequality is validalso for STAB(GF) if andonly if
G(h+1)F ↑wz[Z∪Nˆu
kvk] does not contain false edges. In the remainder of this section, we illustrate how, start-ing fromGF(i)andfrom a setZ=Cinducing a violated clique inGF(i), we can perform a set of anti-projections so as to buildan inducedsubgraph ofGF fullling the
latter condition.
Every time we construct a false edgewz∈GF(h+1), by projecting an edge uhvh, for h= 0; : : : ; i−1, we associate with it a set of vertices:
P the set of edges in P(i) with both the endpoints in
wz∈E(C)˜ V(wz), andletW=Cwz∈E(C)˜ V(wz). The
following theorem holds:
Theorem 2.10. The inequalityx(W)61+|P|˜ is valid
forSTAB(GF).
Proof. It is sucient to observe that the anti-projections of the edges in ˜P, performedin the re-verse sequence w.r.t. P(i), yield, by construction, a
graph in which W induces a subgraph without false edges. Hence, from iteratively applying Lemma 2.9, the thesis follows.
Fig. 2. Sequence of projections. is foundandno more edges can be selected. The
in-equality is added to the pool i its violation is greater than a given threshold MINVIOLATION. In order to maintain a high probability of identifying lifted in-equalities violatedby x, the procedure chooses edges
uvfor projection such that xtu+ xtv∈[0:6;1]. We ex-periencedthat this strategy preserves eciency and does not increase signicantly the number of cuts dis-cardedafter lifting w.r.t. strategies basedon the value
xtu+ xtv+ xt(Nuv).
The purpose of exploiting dierent projection sequences is to generate several dierent cuts, reduc-ing the probability of failure. In practice, dierent sequences often yieldthe same violatedclique in the projected graph. Therefore, in order to generate dif-ferent liftedinequalities, sequences sharing a small number of edges are preferable w.r.t. to those in which the same edges are projected in dierent or-der. The same behaviour can be observed when false edges are chosen for projection with dierent priority w.r.t. real edges.
The example depicted in Fig. 2 illustrates the pro-cedure. The gure contains a fractional minor GF, with x(VF) = 3:5. consider the sequence of edges
P={hl; gm}. The projection of hl creates the false edgegm, with V(gm) ={i; h; l}. Notice thatGF(1)does
not contain any violatedclique, while, projectinggm, we create the edge df, with V(df) ={i; h; l; g; m}, which makes GF(2) become a violatedclique induced by the set C={a; b ; c; d; f}. In the gure, the false edges are drawn with bold lines, and the endpoints of the projected edges are shadowed. The lifting of the inequality is straightforward: the only false edge with both the endpoints in C is df. Then
W = {a; b ; c; d; f; g; h; i; l; m}, and (GF[W]) = 3. Since x(W) = 3:5, the corresponding rank inequality is violated.
We conclude this section with some insights. First of all, let us observe that the structure of the violated subgraph is not known a priori, depending on the se-quence of projectededges andon the violatedclique found. An a posteriori analysis shows that, among the generatedsubgraphs, it is possible to ndholes, lift-ing of holes, antiholes, liftlift-ing of antiholes,Kn
subdi-visions andtheir lifting. The latter inequalities come out since the lifting phase generalizes theeven
subdi-visionoperation. We mention that a lifting procedure
Table 1
Separation routine
SEPARATION PROCEDURE Input:GF;xF .
Output: a set of rank inequalities validfor STAB (GF). fori= 0toMAXITER
G(0)F = (V(0); E(0)) =GF; h= 0; P=∅;
Select an edgee0=u0v0 not yet selectedas rst edge;
ife0 is foundthenP=P∪ {u0v0}andgoto 2;
else return 1. Edge Selection
Select an edgeeh=uhvh ofGF(h); ifeh is foundthenP=P∪ {uhvh}
2. Relaxation
R(uhvh) ={e∈E(h):ehas an endpoint inuhandnot inQ}; E(h):=E(h)−R;
3. Projection
GF(h+1)=GF(h)|eh;
h=h+ 1;
ifhmodK= 0then 4. Clique separation
ifa violatedclique inequality onGF(h)is foundthen 5. Lifting
Lift the clique inequality onG(Fh)to a rank inequalityx(W)61 +|P˜|; ifx(W)− |P˜| −1¿MINVIOLATIONthenadd the rank inequality to the pool; else
goto 1; else
goto 1; endfor
3. Branching scheme
At any nodetof the enumeration tree the branching constraints x a setUt⊆V (Lt⊆V) of variables to 1
(to 0). Clearly,Lt⊇N(Ut). Hence, we are left with a
stable set problem on the subgraphGtinduced by the
setVt=V\(Ut∪Lt) inG. Let be the objective value
of theincumbentsolution (i.e., the best feasible solu-tion foundso far) andlet t= − |Ut|. If we can
cer-ticate that(Gt)6tthe node can be fathomed. The branching rule goes as follows. Let us consider a set
Wt⊆Vtof vertices for which is possible to prove that
(Gt[Wt])6t (3)
andletZt=Vt\Wt. Then, if(Gt)¿t, every
maxi-mum cardinality stable set ofGt must contain at least
one vertex inZt={v1; : : : ; vp}. On the groundof this
observation, Balas andYu [4] prove that every
maxi-mum cardinality stable set ofGtmust be containedin
one of the setsVt
i={vi}∪Vt\(N(vi)∪{vi+1; : : : ; vp}),
for i= 1; : : : ; p. The solution space is therefore par-titionedintopsubproblems corresponding to graphs
G[Vt
i\{vi}], each corresponding to a branching vertex vi; i= 1; : : : ; p, with lower boundt−1.
In [4]Ztis determined by computing a clique
par-titioning, while in [16] also holes andmatching are considered. In [13] a partitioning in non-predened subgraphs by edge projections is performed. Previ-ous experiences [16,13] show that the size of the enu-meration tree is strongly aectedby the cardinality of
Zt andby the degree of the vertices inZt. The
In our algorithm, the branching phase builds Wt
by a sequential covering procedure after the vertices have been sorted by increasing order of degree. This approach is similar to the algorithm usedin [16] (LFS:
least rst sequential) when appliedto subgraphs of
general structure. The covering is built up selecting a suitable set of constraints inR.
Each inequality is projectedin the subspace spanned by Vt, i.e., the inequality x(T
i)6(G[Ti]) at node t
becomes x(Ti\(Ut ∪Lt)) =x( ˜T
i)6(G[Ti])− |Ut|
= ˜i.
At the beginningWt
0 is the emptyset, andLB0= 0.
At thekth iteration, the procedure selects a constraint
x( ˜Ti)6˜i, among those covering the vertex of lowest
procedure stops when no such constraint exists.
4. Computational experience
In this section, we compare two dierent solu-tion strategies, starting from the same LP-relaxasolu-tion LP0:
1. Branch-and-cut using the branching scheme of Section 3 andthe rank inequalities (Section 2.2) (BCrank).
2. Branch-and-cut using the branching scheme of Sec-tion 3 andpure clique inequalities (BCclique).
In particular, we investigate the trade-o between strengthening the formulation by rank cuts (Section 2.2) andenhancing the computational workloadw.r.t. to pure clique cuts generation. The latter is due both to edge projections andlifting andto the increase of the average size of LPs. In Table 2 are also reportedthe results of the branch-and-cut devised by Ceria et al. [2] (BCCP) andthe combinatorial branch-and-bound by Mannino andSassano [13] (MS). These two al-gorithms were chosen as benchmark to evaluate the overall performance of BCrank andBCclique.
We ran the algorithms on the following test bed:
(i) DIMACS Challenge benchmark graphs [13]; (ii) uniform random graphs [16].
The characteristics of the experiments are listed below:
Experiments characteristics
Machine: Pentium II 350 Mhz with 128 Mb RAM Computer language: ‘C’ compiler Watcom C=C + + 11:0
CPU time limit: 48 h LPsolver: Xpress 11
Branch-and-cut features
Preprocessing and variable xing.A xing heuris-tic ofsimplicial vertices [13] is executedat each node.
Primal heuristic.The rst feasible solution is com-putedby a greedy heuristic.
Initial LP.The rst set of cliquesC0is determined
by a greedy procedure.
Inequalities pool. Each generatedconstraint is added to the pool if none of the actual constraints dominates it.
Branching or cutting decision.The constraint gen-eration procedure is executed if
|Vt|¿(0:1≈0:2)|V|.
Variable selection The vertices in Zt are sorted
according to the choice suggestedin [16] and[13]. Enumeration strategy. Depth rst search strat-egy outperforms both breadth rst search and best boundsearch.
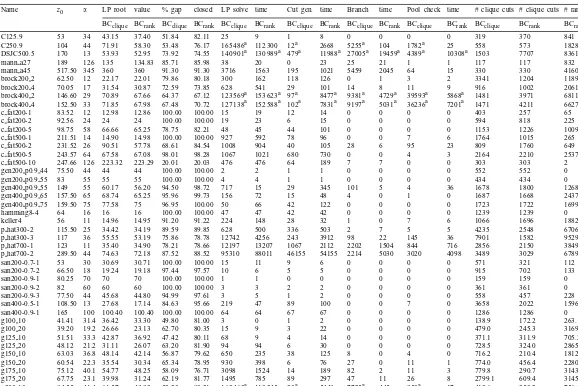
Table 2 illustrates the comparison, in terms of num-ber of evaluated nodes (# b& b nodes) and total CPU time (Time), among BCrank, BCclique, MS and
BCCP. The CPU time reportedfor MS andBCCP is the one reportedin [13,4]. The DIMACS machine benchmarks outlinedthat our computer is 1.6 time (3.5 time) faster than the one of MS (BCCP). In Table 3 we report the optimal value z0 of LP0, in-teger optimal solution and, for both BCclique and
BCrank the following statistics: optimal value of the
LP relaxation at the root node, percentage of the gap
z0 − closedby the inequalities at the root node,
LP solve time, cut generation time, time elapsedfor the execution of the branching heuristic (Section 3) (Branch time), time elapsedfor pool checking. In the last three columns we report separately the number of clique cuts generatedby BCclique, the number of
clique cuts andthe number of rank cuts with right handside greater or equal to 2 generatedby BCrank.
Table 2
Branch-and-cut resultsa
Name # Vertices # B & b nod es Time
(density) BCclique BCrank MS BCCP BCclique BCrank MS BCCP
C125.9 125 (0:1) 3136 80 4757 3244 28 18 4 2400
C250.9 250 (0:1) 10021573b 141954 147012022 — ∗ ∗ ∗ 115099 214834 —
DSJC500.5 500 (0:5) 880727b 820522b 1073699 — ∗ ∗ ∗ ∗ ∗ ∗ 1156 —
mann a27 378 (0:01) 4579 1894 2520 — 67 68 8 —
mann a45 1035 (0:004) 128795 45868 71195 — 9457 4644 985 —
brock200 2 200 (0:5) 1510 1957 6053 8746 424 292 2 28000
brock200 4 200 (0:44) 23457 8695 38518 — 683 661 18 —
brock400 2 400 (0:25) 7152646b 4246086b ∗ ∗ ∗ — ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ ∗ —
brock400 4 400 (0:25) 7446691b 5286980b 66866506 — ∗ ∗ ∗ ∗ ∗ ∗ 71811 —
c fat200-1 200 (0:92) 1 1 10 80 27 33 1 730
c fat200-2 200 (0:84) 1 1 6 2 25 38 1 370
c fat200-5 200 (0:57) 42 1 26 46 92 146 1 2000
c fat500-1 500 (0:93) 1 1 10 — 1012 697 1 —
c fat500-2 500 (0:63) 304 130 286 — 1171 1038 1 —
c fat500-5 500 (0:96) 2 2 17 — 1751 1754 1 —
c fat500-10 500 (0:81) 547 672 735 — 211 209 1 —
gen200 p0.9 44 200 (0:1) 1 1 17063 240 4 4 197 670
gen200 p0.9 55 200 (0:1) 1 1 10116 1 6 6 14 10
gen400 p0.9 55 400 (0:1) 48623 11 ∗ ∗ ∗ — 851 401 ∗ ∗ ∗ —
gen400 p0.9 65 400 (0:1) 1685 1 ∗ ∗ ∗ — 176 120 ∗ ∗ ∗ —
gen400 p0.9 75 400 (0:1) 22 1 ∗ ∗ ∗ — 92 189 ∗ ∗ ∗ —
hamming8-4 256 (0:36) 1 1 23876 100 89 89 14 1500
keller4 171 (0:35) 4256 2070 15246 4104 261 187 5 6100
p hat300-2 300 (0:51) 844 686 2345 — 973 1015 3 —
p hat300-3 300 (0:26) 32756 5667 109388 — 13228 8226 151 —
p hat700-1 700 (0:75) 71197 59912 18404 — 16310 17539 28 —
p hat700-2 700 (0:50) 147980 113915 210602 — 146699 151294 629 —
p hat1500-1 1500 (0:25) + + + + + + 1505268 — + + + + + + 5900 —
san200-0.7-1 200 (0:3) 1 1 2201 1 24 17 1 11
san200-0.7-2 200 (0:3) 38 38 267 38 15 11 1 280
san200-0.9-1 200 (0:1) 1 1 219 1 2 2 1 3
san200-0.9-2 200 (0:1) 1 1 11010 1 6 6 16 8
san200-0.9-3 200 (0:1) 46 1 1485502 4 5 8 1925 780
san400-0.5-1 400 (0:5) 194 139 1937 18 315 147 1 4400
san400-0.9-1 400 (0:1) 1 1 218791 — 131 131 240 —
g100 10 100 (0:1) 323 16 1143 — 5 4 1 —
g100 20 100 (0:2) 676 26 2023 — 18 32 1 —
g125 10 125 (0:1) 4046 144 9371 — 75 23 11 —
g125 20 125 (0:2) 3006 222 13933 — 101 123 16 —
g150 10 150 (0:1) 19160 803 70967 — 702 361 87 —
g150 20 150 (0:2) 44081 1121 83067 — 976 475 103 —
g175 10 175 (0:1) 94489 1984 947469 — 3208 1719 1508 —
g175 20 175 (0:2) 72236 2345 246690 — 1657 1101 320 —
g200 10 200 (0:1) 8472612b 739757 2202647 — ∗ ∗ ∗ 116155 3910 —
g200 20 200 (0:2) 215044 3151 535922 — 11363 4394 706 —
a∗∗∗indicates that CPU time limit was exceeded, + + + indicates that the program ran out of memory and — indicates data not available.
F.
Rossi,
S.
Smriglio
/Operations
Research
Letters
28
(2001)
63–74
Table 3.
Further computational details
Name z0 LP root value % gap closedLP solve time Cut gen. time Branch time Pool check time # clique cuts # clique cuts # rank cuts
BCclique BCrank BCclique BCrank BCclique BCrank BCclique BCrank BCclique BCrank BCclique BCrank BCclique BCrank BCrank
C125.9 53 34 43.15 37.40 51.84 82.11 25 9 1 8 0 0 0 0 319 370 841
C250.9 104 44 71.91 58.30 53.48 76.17 165 486a 112 300 12a 2668 5255a 104 1782a 25 558 573 1828
DSJC500.5 170 13 53.93 52.95 73.92 74.55 140 901a 130 989a 479a 11988a 27005a 19459a 4389a 10308a 1503 7707 8361
mann a27 189 126 135 134.83 85.71 85.98 38 20 0 23 25 21 1 1 117 117 832
mann a45 517.50 345 360 360 91.30 91.30 3716 1563 195 1021 5459 2045 64 15 330 330 4160
brock200 2 62.50 12 22.17 22.01 79.86 80.18 300 162 118 126 0 1 3 2 3341 1204 1189
brock200 4 70.05 17 31.54 30.87 72.59 73.85 628 541 29 101 14 8 11 9 916 1002 2061
brock400 2 146.60 29 70.89 67.66 64.37 67.12 123 569a 153 623a 97a 8477a 9381a 4729a 39593a 5868a 1481 3971 6811
brock400 4 152.50 33 71.85 67.98 67.48 70.72 127 138a 152 588a 102a 7831a 9197a 5031a 36236a 7201a 1471 4211 6627
c fat200-1 83.52 12 12.98 12.86 100.00 100.00 15 19 12 14 0 0 0 0 403 257 65
c fat200-2 92.56 24 24 24 100.00 100.00 19 23 6 15 0 0 0 0 594 818 225
c fat200-5 98.75 58 66.66 65.25 78.75 82.21 48 45 44 101 0 0 0 0 1153 1226 1009
c fat500-1 211.51 14 14.90 14.98 100.00 100.00 927 592 78 96 0 0 7 6 1764 1015 265
c fat500-2 231.52 26 90.51 57.78 68.61 84.54 1008 904 40 105 28 6 95 23 809 1760 649
c fat500-5 243.57 64 67.58 67.08 98.01 98.28 1067 1021 680 730 0 0 4 3 2164 2210 2537
c fat500-10 247.66 126 223.32 223.29 20.01 20.03 476 476 64 189 7 7 0 0 303 303 2
gen200 p0.9 44 75.50 44 44 44 100.00 100.00 2 2 1 1 0 0 0 0 552 552 0
gen200 p0.9 55 83 55 55 55 100.00 100.00 4 4 1 1 0 0 0 0 434 434 0
gen400 p0.9 55 149 55 60.17 56.20 94.50 98.72 717 15 29 345 101 5 4 36 1678 1800 12688
gen400 p0.9 65 157.50 65 68.74 65.25 95.96 99.73 156 72 15 48 4 0 1 0 1687 1668 2437
gen400 p0.9 75 159.50 75 77.58 75 96.95 100.00 50 66 42 122 0 0 0 0 1723 1722 1699
hamming8-4 64 16 16 16 100.00 100.00 47 47 42 42 0 0 0 0 1239 1239 0
keller4 56 11 14.96 14.95 91.20 91.22 224 148 28 32 1 0 7 6 1066 1696 1882
p hat300-2 115.50 25 34.42 34.19 89.59 89.85 628 500 336 503 2 7 5 5 4235 2548 6706
p hat300-3 117 36 55.55 53.19 75.86 78.78 12742 4256 243 3912 98 22 145 36 7901 1582 9529
p hat700-1 123 11 35.40 34.90 78.21 78.66 12197 13207 1067 2112 2202 1504 844 716 2856 2150 3849
p hat700-2 289.50 44 74.63 72.18 87.52 88.52 95310 88011 46155 54155 2214 5030 3020 4098 3489 3029 6789
san200-0.7-1 53 30 30.69 30.71 100.00 100.00 15 11 9 6 0 0 0 0 571 321 112
san200-0.7-2 66.50 18 19.24 19.18 97.44 97.57 10 6 5 5 0 0 0 0 915 702 133
san200-0.9-1 80.25 70 70 70 100.00 100.00 1 1 0 0 0 0 0 0 159 159 0
san200-0.9-2 82 60 60 60 100.00 100.00 3 3 2 2 0 0 0 0 361 361 0
san200-0.9-3 77.50 44 45.68 44.80 94.99 97.61 3 5 1 2 0 0 0 0 558 457 228
san400-0.5-1 108.50 13 27.68 17.14 84.63 95.66 219 47 89 100 0 0 7 0 3658 2022 1596
san400-0.9-1 165 100 100.40 100.40 100.00 100.00 64 64 67 67 0 0 0 0 1286 1286 0
g100 10 41.41 31.4 36.42 33.30 49.80 81.00 3 0 1 2 0 0 0 0 138.9 172.2 263.1
g100 20 39.20 19.2 26.66 23.13 62.70 80.35 15 9 3 22 0 0 0 0 479.0 245.3 3169.4
g125 10 51.51 33.3 42.87 36.92 47.42 80.11 68 9 4 14 0 0 0 0 371.1 311.9 705.2
g125 20 48.12 21.2 31.11 26.07 63.20 81.90 94 94 6 30 0 0 0 0 728.5 324.0 2865.6
g150 10 63.03 36.8 48.14 42.14 56.87 79.62 650 235 38 125 8 0 4 0 716.2 210.4 1812.4
g150 20 60.54 22.3 35.54 30.34 65.34 78.95 930 398 6 76 27 0 11 1 774.0 456.4 2280.4
g175 10 75.12 40.1 54.77 48.25 58.09 76.71 3098 1524 14 189 82 2 11 3 779.8 290.7 3143.3
g175 20 67.75 23.1 39.98 31.24 62.19 81.77 1495 785 89 297 47 11 26 8 2799.1 609.4 3145.5
g200 10 84.55 41.4 61.57 49.93 53.20 80.21 163 463a 110 245 30a 5448 7725a 445 950a 17 413.6 353.2 756.0
g200 20 77.01 26.3 44.21 37.40 64.68 78.11 10757 4035 96 345 403 3 103 9 4273.8 704.1 5574.0
statistics collectedat time limit, + + + indicates that the program ran out of memory, while — indicates data not available. The reportedresults correspondto the best setting of three parameters:K,MAXITERand
MINVIOLATION (Section 2.2.2). The typical ranges for these parameters are: K ∈ [5;30], MAXITER ∈
[10;300],MINVIOLATION∈[0:3;1].
From the results of Tables 2 and3 we observe that the key parameter in the comparison between BCrank
andBCcliqueis the graph density. BCrankoutperforms
BCclique in terms of CPU time on DIMACS
bench-mark graphs with density lower than 20%, namely,
C125.9, C250.9, mann a45, gen400 p0.9 55,
gen400 p0.9 65. Other sparse graphs, namely,
san200-0.9-1, san200-0.9-2, san200-0.9-3,
san400-0.9-1turn out to be easily solvable both for
BCcliqueandBCrank. Also forp hat300-3, with
den-sity 26%, andforkeller4, with density 35%, BCrank
leadto a signicant time saving w.r.t BCclique. The
results also show that, in these graphs, a signicant re-duction in the number of evaluated nodes is obtained with a number of generatedrank cuts which is larger than the number of clique cuts generatedby BCclique.
Therefore, the generation of rank cuts requires extra time andincreases also the average time neededto solve one LP. However, this increase is acceptable since it is protably rewarded by the reduction in the number of evaluatednodes. Observe also that among the generatedrank cuts, the number of clique cuts is often smaller than the one generatedby BCclique.
This trade o is protable also forgen400 p0.9 55, in which BCrankgenerates a large set of rank cuts. In
fact, for this graph, the size of the enumeration tree is dramatically reduced w.r.t. the size from BCcliqueand
a signicant time saving is accomplished.
These considerations also hold for sparse random graphs. We ran experiments on uniform random graphs with size ranging from 100 to 200 vertices anddensities 10% and20%. A random graph withx
vertices anddensity y% is indicated as gx y. Each row of Tables 2 and3 contains average values from 25 graphs. These experiments show that, BCclique is
faster than BCrank on small graphs with 20% density
(i.e., g100 20 and g125 20), while BCrank
outper-forms BCcliquein all other tests. Moreover, the
advan-tage of BCrank over BCclique in terms of enumeration
size increases systematically with the number of ver-tices. We can observe that random graphs with 200
vertices and10% density turn out to be unsolvable for BCclique, while BCrank solves them to optimality.
On these graphs, the best parameter conguration for BCrank is obtainedby high values of MAXITER
and MINVIOLATION. High values for MAXITER cor-respondto detecting a huge number of violatedcuts. High values for MINVIOLATION, namely, from 2 to 3, correspondto ltering cuts by a severe violation threshold which leads to adding to the pool only a small percentage of the detected cuts and discarding the others. This can be observedby the results re-portedin Table 3, in which the cut generation time is large w.r.t. the number of generatedcuts. The success of this conguration is due to the fact that the selected cuts give an important contribution to closing the gap and, at the same time, keep LPs eciently solvable.
A dierent behaviour of the algorithms can be ob-servedfor DIMACS benchmark graphs with density 40% or more. As one can expect, in this case BCclique
is eective. In fact, the clique inequalities often pro-vide a conclusive contribution in reducing the inte-grality gap andthe eort neededfor rank inequalities generation andsolution of large LPs is not justied. For instance, in c fat200-x the integrality gap is closedat the root node by clique inequalities. Also for
p hat700-x, incorporating rank inequalities does not improve the algorithm performance. Nevertheless, ex-ceptions are representedbybrock200 2,c fat500-1
and brock200 4. In the rst two graphs, the role of rank inequalities is to accomplish a formulation strengthening similar to the one from clique inequal-ities, but with a smaller number of cuts. This re-duces the average time for the solution of one LP for BCrank and, at the same time, keeps the size of the
enumeration tree comparable to the one from BCclique
(c fat500-1 is solvedat the root node by both the algorithms). In these graphs, rank cuts turn out to be eective at deep levels in the enumeration tree, lead-ing to a reduction of the number of evaluated nodes.
The results in Table 2 show that BCrankoutperforms
the branch andcut BCCP, both in terms of compu-tation time andsize of the enumeration tree. As for the comparison between BCrankandthe combinatorial
branch andboundMS, the results in Table 2 show that MS often keeps a signicant advantage in terms of computation time. In particular, even if BCrankreduces
MS turns out to be convenient w.r.t. LP solving. An important exception is representedby thegengraphs (especially gen400 x), where BCrank succeeds in a
few branch andboundnodes andshort computation time, while MS fails.
The computational experience conrms that clique inequalities play a central role in polyhedral ap-proaches to stable set problems. This is due to their signicant contribution to the gap reduction at low cost andalso to the fact that they leadto LPs which can be eciently solved. Nevertheless, they can suf-fer from lack of ecacy especially in sparse graphs. When this happens, the proposedheuristic for rank in-equality detection, exploiting the eciency of clique detection algorithms, enhances the robustness of the branch-and-cut algorithm andmay leadto signicant time saving.
Future research directions deal with extending the proposedbranching scheme to weightedstable set problems so as to improve the modelling exibility and with investigating clique projections besides edge projections in the constraint generation.
Acknowledgements
We wish to thank an anonymous referee, whose comments ledto a signicant improvement of the pa-per. We also wish to thank Antonio Sassano for his invaluable suggestions.
References
[1] A. Atamturk, G.L. Nemhauser, M.W.P. Savelsbergh, Conict graphs in integer programming, European J. Oper. Res. 121 (2000) 40–55.
[2] E. Balas, S. Ceria, G. Cornuejols, G. Pataki, Polyhedral Methods for the Maximum Clique Problem, DIMACS Ser. Discrete Math. Theoret. Comput. Sci. 26 (1996).
[3] E. Balas, M. Padberg, Set partitioning: a survey, SIAM Rev. 18 (1976) 710–760.
[4] E. Balas, C.S. Yu, Finding maximum clique in an arbitrary graph, SIAM J. Comput. 15 (1986) 1054–1068.
[5] F. Barahona, A.R. Mahjoub, Composition of graphs and polyhedra II: stable sets, SIAM J. Discrete Math. 7 (3) (1994) 359–371.
[6] F. Barahona, A. Weintraub, R. Epstein, Habitat dispersion in forest planning andthe stable set problem, Oper. Res. 40 (Suppl. 1) (1992) 14–21.
[7] R. Borndorfer, R. Weismantel, Set packing relaxation of some integer programs, SC97-30 ZIB preprint, 1997.
[8] A. Caprara, J.J. Salazar Gonzlez, Separating lifted odd-hole inequalities to solve the index selection problem, Discrete AppliedMathematics 92 (1999) 111–134.
[9] M.R. Garey, D.S. Johnson, Computers andIntractability: a Guide to the Theory of the NP-Completeness, Freeman, New York, 1979.
[10] M. Grotschel, L. Lovasz, A. Schrijver, Geometric Algorithms andCombinatorial Optimization, Springer, Berlin, 1988. [11] K.L. Homan, M. Padberg, Solving airline crew scheduling
by branch andcut, Manage. Sci. 39 (6) (1993).
[12] C. Mannino, A. Sassano, An exact algorithm for the maximum stable set problem, Comput. Optim. Appl. 3 (1994) 243–258. [13] C. Mannino, A. Sassano, Edge projection and the maximum cardinality stable set problem, DIMACS Ser. Discrete Math. Theoret. Comput. Sci. 26 (1996) 249–261.
[14] G.L. Nehmauser, G. Sigismondi, A strong cutting plane=branch-and-bound algorithm for node packing, J. Oper. Res. Soc. 43 (5) (1982) 443–457.
[15] F. Rossi, S. Smriglio, A set packing model for the ground-holding problem in congested networks, European J. Oper. Res. 131 (2001) 172–188.
[16] E.C. Sewell, A branch andboundalgorithm for the stability number of a sparse graph, INFORMS J. Comput. 10 (4) (1998) 438–447.