BAB II TINJAUAN PUSTAKA

(1)

7

BAB II

TINJAUAN PUSTAKA

Pada Bab ini menjelaskan teori dasar yang membantu dalam penyelesaian masalah antara lain Gelombang Harmonik, Hukum Kekekalan Massa,Persamaan Laplace, Hukum Kekekalan Momentum, Persamaan Bernoulli, Kondisi Batas dan Metode Pemisah Variabel.

2.1 Gelombang Harmonik

Sebuah gangguan yang berasal dari kondisi kesetimbangan yang merambat dari satu daerah ke daerah lainnya disebut gelombang. Jika terjadi gerakan yang berulang dalam selang waktu yang sama atau yang disebut gerak periodik maka terjadi pula gerak periodik di suatu partikel pada gelombang merambat sehingga menyebabkan terjadinya gelombang periodik. Gelombang periodik dapat dimisalkan dengan gelombang yang bergerak ke atas dan ke bawah dalam gerak harmonik sederhana. Disebut gerak harmonik sederhana adalah gerak periodik yang mempunyai lintasan yang selalu sama (tetap) dan mempunyai persamaan gerak dalam bentuk sinusoidal dan digunakan untuk menganalisis suatu gerak periodik tertentu [8].

Dalam fungsi gelombang terdapat kecepatan partikel dalam suatu titik pada gelombang sinusoidal, sebagai contoh pada titik 𝑥. Dalam menentukan kecepatan gelombang tersebut dilakukan penurunan fungsi gelombang𝑦(𝑥, 𝑡) terhadap 𝑡 dengan mempertahankan 𝑥 yang konstan. Dimisalkan fungsi gelombang tersebut dengan

𝑦(𝑥, 𝑡) = 𝐴 sin(𝜔𝑡 − 𝑘𝑥) maka,

𝑢(𝑥, 𝑡) =𝜕𝑦(𝑥, 𝑡)

(2)

8

dengan 𝑢(𝑥, 𝑡) adalah laju gelombang.

Pada persamaan (2.1) terlihat bahwa kecepatan partikel akan berubah beriringan dengan waktu, sama halnya dengan gerak harmonik sederhana. Laju partikel maksimum diberikan oleh 𝐴𝜔 yang dimana dapat lebih kecil, lebih besar maupun sama dengan laju gelombang 𝑢 hal ini bergantung pada nilai frekuensi dan besar ampitudo dari gelombang.

Tinggi permukaan gelombang harmonik dapat dimisalkan dalam fungsi 𝜂 dalam bentuk khusus yang mengasumsikan permukaan yang berbentuk gelombang dengan amplitudo, bilangan gelombang dan frekuensi gelombang. Fungsi tersebut dapat dinyatakan sebagai berikut:

𝜂(𝑥, 𝑡) = 𝐴𝑒−𝑖(𝑘𝑥−𝜔𝑡) dimana, 𝐴 = ampitudo gelombang 𝑘 = bilangan gelombang 𝜔 = frekuensi gelombang 𝑡 = waktu

2.2 Hukum Kekekalan Massa

Hukum kekekalan massa menyatakan bahwa suatu partikel fluida harus kontinu dan massa dari partikel fluida tersebut harus kekal (tidak dapat diciptakan maupun dimusnahkan)[9]. Hukum kekekalan massa menyatakan bahwa massa partikel akan selalu konstan meskipun terjadi beberapa proses pada partikel tersebut akibatnya laju perubahan massa sama dengan nol [10]. Hukum kekekalan massa diperoleh dari laju perubahan massa dalam elemen luas terhadap waktu sama dengan nilai perbedaan

(3)

9

massa yang masuk dan yang keluar pada elemen fluida yang sama dan waktu yang sama.

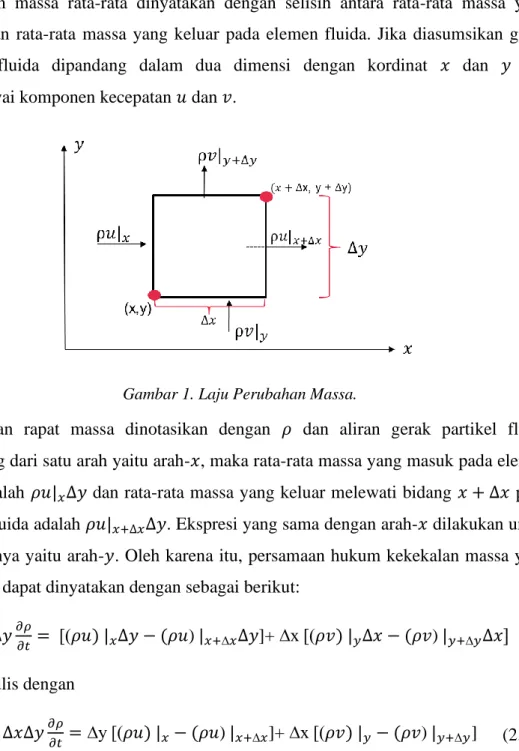
Perubahan massa rata-rata dinyatakan dengan selisih antara rata-rata massa yang masuk dan rata-rata massa yang keluar pada elemen fluida. Jika diasumsikan gerak partikel fluida dipandang dalam dua dimensi dengan kordinat 𝑥 dan 𝑦 dan mempunyai komponen kecepatan 𝑢 dan 𝑣.

Gambar 1. Laju Perubahan Massa.

Dimisalkan rapat massa dinotasikan dengan 𝜌 dan aliran gerak partikel fluida dipandang dari satu arah yaitu arah-𝑥, maka rata-rata massa yang masuk pada elemen fluida adalah 𝜌𝑢|_𝑥∆𝑦 dan rata-rata massa yang keluar melewati bidang 𝑥 + ∆𝑥 pada elemen fluida adalah 𝜌𝑢|_𝑥+∆𝑥∆𝑦. Ekspresi yang sama dengan arah-𝑥 dilakukan untuk arah lainnya yaitu arah-𝑦. Oleh karena itu, persamaan hukum kekekalan massa yang diperoleh dapat dinyatakan dengan sebagai berikut:

∆𝑥∆𝑦𝜕𝜌

𝜕𝑡 = [(𝜌𝑢) |𝑥∆𝑦 − (𝜌𝑢) |𝑥+∆𝑥∆𝑦]+ ∆x [(𝜌𝑣) |𝑦∆𝑥 − (𝜌𝑣) |𝑦+∆𝑦∆𝑥]

dapat ditulis dengan ∆𝑥∆𝑦𝜕𝜌

𝜕𝑡 = ∆y [(𝜌𝑢) |𝑥− (𝜌𝑢) |𝑥+∆𝑥]+ ∆x [(𝜌𝑣) |𝑦− (𝜌𝑣) |𝑦+∆𝑦]

Dengan membagi kedua ruas dengan ∆𝑥∆𝑦 maka diperoleh persamaan sebagai berikut:

(2.4) (2.3)

(4)

10 𝜕𝜌 𝜕𝑡 = (𝜌𝑢|𝑥− 𝜌𝑢𝑥+∆𝑥) ∆𝑥 + (𝜌𝑣|𝑦 − 𝜌𝑣𝑦+∆𝑦) ∆𝑦

lalu mengambil limit menuju nol dikarenakan partikel fluida yang akan dipandang sangat kecil maka dapat mengasumsuikan ∆𝑥 → 0 dan ∆𝑦 → 0 maka menghasilkan sebagai berikut: lim ∆𝑥→0 (𝜌𝑢|_𝑥− 𝜌𝑢_𝑥+∆𝑥) ∆𝑥 = − 𝜕(𝜌𝑢) 𝜕𝑥 lim ∆𝑦→0 (𝜌𝑣|𝑦− 𝜌𝑣𝑦+∆𝑦) ∆𝑦 = − 𝜕(𝜌𝑣) 𝜕𝑦 maka memperoleh persamaan

𝜕𝜌 𝜕𝑡 = − 𝜕(𝜌𝑢) 𝜕𝑥 − 𝜕(𝜌𝑣) 𝜕𝑦 Atau dapat dinyatakan dengan

𝜕𝜌 𝜕𝑡 = −𝜌 ( 𝜕(𝑢) 𝜕𝑥 + 𝜕(𝑣) 𝜕𝑦 )

Diasumsikan fluida tak termampatkan yang artinya bahwa fluida mengalir tanpa mengalami perubahan volume atau massa jenis yang menyebabkan rapat massa fluida (𝜌) konstan yang artinya seluruh turunan 𝜌 adalah nol. Sehingga persamaan (2.5) tereduksi menjadi:

𝜕𝑢 𝜕𝑥+

𝜕𝑣 𝜕𝑦= 0

Persamaan (2.6) adalah persamaan yang disebut dengan hukum kekekalan massa yang dimana rapat massa (𝜌) seperti telah menghilang.

(2.6) (2.5)

(5)

11 2.3 Persamaan Laplace

Diasumsikan bahwa aliran pada fluida tidak termampatkan maka menghasilkan persamaan seperti berikut:

𝜌(∇ ∙ 𝑞) = 0

Sedangkan aliran fluida tak berotasi maka kecepatan partikel fluida dapat dinyatakan dalam fungsi kecepatan potensial 𝜙(𝑥, 𝑦, 𝑡) yang didefenisikan sebagai berikut[11]:

𝑞⃗ = ∇𝜙

yang dimana 𝑞⃗ adalah vektor kecepatan yang memiliki komponen antara lain (𝑢, 𝑣), maka persamaan (2.8) dapat didefenisikan sebagai berikut:

𝑢 = 𝜕𝜙

𝜕𝑥, 𝑣 = 𝜕𝜙 𝜕𝑦

maka dilakukan subsitusi persamaan (2.9) ke persamaan hukum kekekalan massa pada persamaan (2.6) menghasilkan:

𝜕2𝜙 𝜕𝑥2 +

𝜕2𝜙 𝜕𝑦2 = 0

Atau dapat ditulis dalam bentuk notasi vektor ∇2_{𝜙 = 0. Persamaan (2.10) adalah}

persamaan Laplace pada fluida. Persamaan (2.10) merupakan turunan dari persamaan hukum kekekalan massa.

Pada fungsi 𝜙(𝑥, 𝑦) yang dapat membentuk persamaan Laplace bersifat harmonik dan fungsi kecepatan potensial yang dapat menggambarkan aliran tak berotasi tertentu. Komponen kecepatan pada aliran fluida diperoleh dari persamaan 𝑢 dan 𝑣. Persamaan Laplace memiliki solusi yang tidak terbatas, maka dalam mendapatkan solusi yang sesuai harus menggunakan kondisi batas yang sesuai pula. Namun secara analitis, solusi dari persamaan Laplace hanya dapat diselesaikan dengan solusi khusus dikarenakan pengaruh dari kondisi batas yang dibentuk dan dipengaruhi oleh

(2.10) 0)

(2.9) (2.8) (2.7)

(6)

12

bentuk dari daerah asal persamaan Laplace yang ditetapkan sehingga jika secara analitis dapat diselesaikan dengan menggunakan metode pemisahan variabel [12].

2.4 Hukum Kekekalan Momentum

Pada hukum Newton kedua menyatakan bahwa momentum hanya menerapkan gaya-gaya yang berasal dari luar partikel yang kemudian hasilnya dapat digunakan untuk menyelesaikan suatu proses tanpa memperhatikan hal-hal terperinci proses internal yang terjadi di dalam fluida tersebut. Teorema momentum dapat dipakai dalam menyelesaikan kasus aliran baik aliran steady atau unsteady, dalam dimensi satu, dua atau tiga, dalam fluida termampatkan maupun tidak termampatkan. Seperti halnya pada kasus partikel padat, fluida yang menjurus meneruskan keadaan dalam diam maupun gerak beriringannya terkecuali adanya gangguan dari gaya-gaya yang berasal dari luar[10].

Dalam ilmu fisika, momentum merupakan besaran vektor yang memiliki bobot (m) dan memiliki vektor kecepatan (𝑣)[13]. Secara matematis rumus momentum adalah

𝑝 = 𝑚𝑣 dimana,

𝑝 = momemtum 𝑚 = massa partikel 𝑣 = kecepatan partikel

Dari persamaan (2.11), dapat dilihat jika terjadi perubahan pada massa dan kecepatan maka momentum akan mengalami perubahan juga. Perubahan momentum dengan perubahan massa/kecepatan berbanding lurus yang artinya jika momentum besar maka massa/kecepatan pasti bernilai besar. Begitu pula sebaliknya, semakin besar

(7)

13

nilai pergerakan dari partikel/semakin besar nilai massa partikel maka momentum yang dihasilkan akan besar pula.

Dalam hubungan antara massa jenis dan massa dalam fisika terdapat rumus yaitu, 𝜌 =𝑚

𝑉

yang dimana 𝜌 adalah notasi dari massa jenis, m adalah notasi dari massa dan 𝑉 adalah notasi dari luas penampang partikel. Hal itu menyebabkan persamaan diatas dapat berubah menjadi sebagai berikut:

𝑝 = (𝑉𝜌)𝑣 atau dapat ditulis dengan

𝑝 = ∆𝑥∆𝑦 𝜌 𝑣 yang dimana 𝑉 = ∆𝑥∆𝑦 merupakan luas partikel fluida.

Perubahan momentum pada partikel fluida merupakan hasil pengurangan dari jumlah momentum yang masuk dengan momentum yang keluar pada partikel yang ditambahi oleh gaya yang bekerja pada luar partikel. Secara matematis dalam mencari rata-rata perubahan momentum dalam satuan waktu dapat ditulis sebagai berikut:

𝜕 𝜕𝑡𝑝 =

𝜕

𝜕𝑡(∆𝑥∆𝑦 𝜌 𝑣) − ∫ 𝐹𝑙𝑎𝑖𝑛𝑛𝑦𝑎𝑑𝑡

Jika pada persamaan (2.12) disubsitusikan komponen kecepatan seperti

(𝑢|_𝑥− (𝑢|_𝑥+∆𝑥) =∆𝑥

∆𝑡 = 𝑘𝑒𝑐𝑒𝑝𝑎𝑡𝑎𝑛 𝑦𝑎𝑛𝑔 𝑡𝑒𝑟𝑗𝑎𝑑𝑖 𝑝𝑎𝑑𝑎 𝑠𝑢𝑚𝑏𝑢 𝑥 (𝑣|_𝑦− (𝑣|_𝑦+∆𝑦) = ∆𝑦

∆𝑡 = 𝑘𝑒𝑐𝑒𝑝𝑎𝑡𝑎𝑛 𝑦𝑎𝑛𝑔 𝑡𝑒𝑟𝑗𝑎𝑑𝑖 𝑝𝑎𝑑𝑎 𝑠𝑢𝑚𝑏𝑢 𝑦

Komponen yang mempengaruhi perubahan momentum adalah pengaruh dari kontribusi massa komponen itu sendiri. Perubahan momentum dapat berasal dari arah 𝑥 maupun dari arah 𝑦. Komponen 𝜌𝑢2|𝑥∆𝑦 adalah komponenn massa yang bergerak

(2.13) (2.12)

(8)

14

masuk dari arah 𝑥 yang dimana 𝑢 adalah komponen kecepatan yang melintasi bidang 𝑥 dan komponen 𝜌𝑢𝑣|_𝑦∆𝑥 adalah kontribusi massa yang masuk dari arah 𝑦 yang memiliki kecepatan 𝑢. Komponen massa yang keluar melintasi sisi 𝑥 + ∆𝑥 dinyatakan dengan 𝜌𝑢2|_𝑥+∆𝑥∆𝑦 dan komponen massa yang keluar melintasi 𝑦 + ∆𝑦 dinyatakan dengan 𝜌𝑢𝑣|𝑦+∆𝑦∆𝑦.

Gaya tekan yang diberikan pada setiap fluida dalam satuan luas bidang dapat ditulis dengan

𝑓𝑡𝑒𝑘𝑎𝑛𝑎𝑛 = 𝑃|𝑥∆𝑦

Dengan melihat hubungan antara gaya gravitasi dengan percepatan gravitasi, maka persamaan dapat ditulis dengan

𝑓_{𝑔𝑟𝑎𝑣𝑖𝑡𝑎𝑠𝑖} = 𝜌𝑔_𝑥∆𝑥∆𝑦

maka, gaya eksternal pada arah 𝑥 yang terjadi pada komponen fluida dapat ditulis dengan:

[𝑃_𝑥− 𝑃_𝑥+∆𝑥]∆𝑦 + 𝜌𝑔_𝑥∆𝑥∆𝑦

𝑃_𝑥 adalah gaya tekan yang melintasi sisi 𝑥 dan 𝑔 adalah gaya gravitasi yang terjadi pada komponen fluida.

(9)

15

Lalu diambil limit

menuju nol dimana (∆𝑥∆𝑦) → 0 maka

lim

(∆𝑥∆𝑦)→0

[(𝜌𝑢

2

_|

𝑥

)∆𝑦 − (𝜌𝑢

2

|

𝑥+∆𝑥

)]

∆𝑥

+

[(𝜌𝑢𝑣 |

_𝑦

)∆𝑥 − (𝜌𝑢𝑣 |

_𝑦+∆𝑦

)]

∆𝑦

+

(𝑃 |

𝑥

− 𝑃 |

𝑥+∆𝑥

)

∆𝑥

+

𝜌𝑔

_𝑥

∆𝑥

Sehingga didapatkan persamaan gerak dalam arah 𝑥 adalah 𝜕𝜌𝑢 𝜕𝑡 = − [ 𝜕(𝜌𝑢2) 𝜕𝑥 ] − [ 𝜕(𝜌𝑢𝑣) 𝜕𝑦 ] − 𝜕𝑃 𝜕𝑥+ 𝜌𝑔𝑥 = −𝜌 [𝜕(𝑢 2₎ 𝜕𝑥 + 𝜕(𝑢𝑣) 𝜕𝑦 ] − 𝜕𝑃 𝜕𝑥 + 𝜌𝑔𝑥 atau persamaan (2.19) dapat ditulis dengan

𝜌 [𝜕𝑢 𝜕𝑡 + 𝜕(𝑢2) 𝜕𝑥 + 𝜕(𝑢𝑣) 𝜕𝑦 ] = − 𝜕𝑃 𝜕𝑥+ 𝜌𝑔𝑥 Jika kedua ruas persamaan dibagi dengan 1

𝜌 akan memperoleh [𝜕𝑢 𝜕𝑡 + 𝜕(𝑢2₎ 𝜕𝑥 + 𝜕(𝑢𝑣) 𝜕𝑦 ] = − 1 𝜌 𝜕𝑃 𝜕𝑥+ 𝑔𝑥

Jadi, persamaan (2.21) merupakan hukum kekekalan momentum pada arah 𝑥 maka pada arah 𝑦 adalah

[𝜕𝑣 𝜕𝑡 + 𝜕(𝑢𝑣) 𝜕𝑥 + 𝜕(𝑣2₎ 𝜕𝑦 ] = − 1 𝜌 𝜕𝑃 𝜕𝑦+ 𝑔𝑦

Dari dua persamaan di atas (2.21) dan (2.22) dapat disimpulkan kembali ke bentuk vektor yaitu, 𝜕𝑞̅ 𝜕𝑡 + (𝑞̅. ∇)𝑞̅ = − 1 𝜌∇𝑃 + 𝑔𝑦 (2.23) (2.22) (2.21) (2.20) (2.19) (2.18)

(10)

16

Gaya gravitasi berlaku hanya pada arah 𝑦. Notasi ∇ merupakan (𝜕

𝜕𝑥, 𝜕

𝜕𝑦) dan notasi 𝑞̅

merupakan (𝑢, 𝑣).

2.5 Persamaan Bernoulli

Persamaan yang memiliki hubungan antara laju aliran, tekanan, tinggi dan fluida yang memiliki kerapatan massa yang konstan atau sulit diubah sering dinyatakan dengan persamaan Bernoulli. Persamaan Bernoulli diturunkan dari Hukum Kekekalan Momentum yang berbentuk vektor seperti berikut

𝜕𝑞̅

𝜕𝑡+ (𝑞̅ ∙ ∇)𝑞̅ = − 1

𝜌∇𝑃 − 𝑔∇𝑦

Berdasarkan operator turunan total 𝐷

𝐷𝑡= 𝜕 𝜕𝑡+ 𝑢 𝜕 𝜕𝑥+ 𝑣 𝜕

𝜕𝑦 maka suku pertama dari

ruas kiri dalam persamaan (2.24) dapat menjadi 𝐷𝑞̅

𝐷𝑡 = −∇ ( 𝑃

𝑞+ 𝑔𝑦) + 𝑓

yang dimana 𝑓 = 0 dikarekan aliran fluida yang diperhatikan adalah aliran fluida yang tak termampatkan. Sedangkan suku kedua pada ruas kiri persamaan (2.24) telah memenuhi hubungan sebagai berikut

𝑞̅ × (∇ × 𝑞̅) = (𝑞̅ ∙ 𝑞̅)∇ − (𝑞̅ ∙ ∇)𝑞̅ = (1

2|𝑞̅|

2_{) ∇ − (𝑞̅ ∙ ∇)𝑞 ̅}

Kemudian dikarenakan yang diperhatikan adalah fluida yang seragam dan fluida yang tak berotasi yang dimana (∇ × 𝑞̅) = 0, maka persamaan (2.26) dapat menjadi

𝑞̅ × 0 = (1 2|𝑞̅| 2_{) ∇ − (𝑞̅ ∙ ∇)𝑞 ̅} 0 = (1 2|𝑞̅| 2_{) ∇ − (𝑞̅ ∙ ∇)𝑞 ̅} (2.24) (2.25) (2.26)

(11)

17

Dapat ditulis juga dengan

(1 2|𝑞̅|

2_{) ∇ = (𝑞̅ ∙ ∇)𝑞 ̅}

Sehingga hukum kekekalan momentum pada persamaan (2.27) dapat menjadi 𝜕𝑞̅ 𝜕𝑡 + ∇ ( 1 2|𝑞̅| 2_{) = −}1 𝜌∇𝑃 − ∇𝑔𝑦

jika disubsitusikan 𝑞̅ = ∇𝜙(𝑥, 𝑦) yang dimana ∇𝜙(𝑥, 𝑦) = (𝜙_𝑥, 𝜙_𝑦) = (𝑢, 𝑣) dan nilai kecepatan (nilai laju) |𝑞̅| = √𝑢2_{+ 𝑣}2_{, maka persamaan (2.28) dapat ditulis}

dengan 𝜕 𝜕𝑡(∇𝜙) + ∇ ( 1 2|𝑞̅| 2_{) = −}1 𝜌∇𝑃 − ∇𝑔𝑦 𝜕 𝜕𝑡(∇𝜙) + ∇ ( 1 2|𝑞̅| 2_{) +}1 𝜌∇𝑃 + ∇𝑔𝑦 = 0 ∇ (𝜕𝜙 𝜕𝑡 + ( 1 2|𝑞̅| 2_{) +}1 𝜌𝑃 + 𝑔𝑦) = 0

Lalu mengintegralkan persamaan (2.29) dengan integral batas (mengintegralkan terhadap variabel 𝑥dan 𝑦), persamaan diatas menjadi

𝜕𝜙 𝜕𝑡 + 1 2|𝑞̅| 2₊1 𝜌𝑃 + 𝑔𝑦 = 𝑓(𝑡)

dengan fungsi 𝑓(𝑡) adalah fungsi sebarang dari 𝑡 yang didapatkan dari integrasi yang dilakukan terhadap 𝑥 dan 𝑦. Lalu fungsi 𝑓(𝑡) digabungkan dengan fungsi 𝜙 yang berbentuk 𝜙 − 𝑓(𝑡)𝑑𝑡, yang akan menghasilkan sebuah persamaan sebagai berikut.

𝜕𝜙 𝜕𝑡 + 1 2|𝑞̅| 2₊1 𝜌𝑃 + 𝑔𝑦 = 0

Persamaan yang diatas sering dikenal dengan persamaan Bernoulli.

(2.27)

(2.28)

(2.29)

(12)

18 2.6 Kondisi Batas

Pada umumnya dalam menyelesaikan suatu model matematika, kondisi batas dapat dijadikan alat. Kondisi batas terbagi menjadi dua jenis, yaitu kondisi batas kinematik dan kondisi batas dinamik. Dalam defenisinya, kondisi batas kinematik merupakan kondisi batas yang muncul dikarenakan adanya gerak dari partikel-partikel fluida dan kondisi batas dinamik merupakan kondisi batas yang terjadi dikarenakan adanya gaya yang bekerja pada fluida tersebut[11].

2.6.1 Kondisi Batas Kinematik Permukaan Fluida

Kondisi batas kinematik merupakan turunan dari sifat kontinum sebuah fluida yang jika digambarkan dalam suatu ilustrasi gelombang sebagai berikut

Gambar 2. Kondisi Batas Fluida

Pada gambar di atas 𝑥 dan 𝑦 adalah posisi dari partikel fluida, pada 𝑦 = −ℎ menyatakan dasar fluida, 𝑦 = 0 menyatakan posisi kesetimbangan permukaan fluida dan 𝑦 = 𝜂(𝑥, 𝑡) menyatakan batas permukaan fluida yang menyebabkan persamaan permukaan fluida pada gambar diatas dapat ditullis secara implisit sebagai berikut 𝑓(𝑥, 𝑦, 𝑡) = 𝑦 − 𝜂(𝑥, 𝑡) = 0 Udara air y= 𝜂(𝑥, 𝑡) y=0 y = -h (2.31)

(13)

19

Dimisalkan letak partikel pada koordinat yaitu (𝑥, 𝑦) dan diasumsikan partikel yang berada pada batas akan tetap pada batas contohnya partikel yang berada permukaan akan tetap pada permukaan tersebut. Permukaan 𝑓 dinyatakan dalam persamaan 𝑓(𝑥, 𝑦, 𝑡) = 0 dapat dinyatakan dalam bentuk operator turunan total yaitu

𝐷𝑓 𝐷𝑡 = 0 Defenisi turunan total adalah

𝐷𝑓 𝐷𝑡 = 𝜕𝑓 𝜕𝑡 + 𝜕𝑓 𝜕𝑥 𝑑𝑥 𝑑𝑡 + 𝜕𝑓 𝜕𝑦 𝑑𝑦 𝑑𝑡

jika kecepatan vektor didefenisikan dengan 𝑞̅ = (𝑢, 𝑣), maka persamaan (2.32) dapat ditulis dengan 𝐷𝑓 𝐷𝑡 = 𝜕𝑓 𝜕𝑡 + 𝑢 𝜕𝑓 𝜕𝑥+ 𝑣 𝜕𝑓 𝜕𝑦

Dilakukan subsitusi persamaan (2.33) ke persamaan (2.31), menyebabkan 𝜕(𝑦 − 𝜂(𝑥, 𝑡)) 𝜕𝑡 + 𝑢 𝜕(𝑦 − 𝜂(𝑥, 𝑡)) 𝜕𝑥 + 𝑣 𝜕(𝑦 − 𝜂(𝑥, 𝑡)) 𝜕𝑦 = 0 −𝜂_𝑡− 𝑢𝜂_𝑥+ 𝑣 = 0

dengan menyatakan 𝜙 merupakan komponen kecepatan. Jika pada arah x dinyatakan dengan 𝜙_𝑥= 𝑢 dan pada y dinyatakan dengan 𝜙_𝑦 = 𝑣, sehingga persamaan (2.34) dapat ditulis dengan

−𝜂𝑡− 𝜙𝑥𝜂𝑥+ 𝜙𝑦 = 0

Persamaan (2.35) diatas adalah persamaan kondisi batas kinematik pada permukaan fluida.

(2.32)

(2.33)

(2.34)

(14)

20 2.6.2 Kondisi Batas Kinematik pada Dasar

Pada dasar fluida, kondisi batas yang terjadi hanya kondisi batas kinematik saja dikarenakan pada dasar tidak ada gaya yang terjadi atau tidak adanya pergerakan pada dasar fluida. Kondisi batas kinematik pada dasar secara implisit ditulis dengan

𝑓 = 𝑦 + ℎ = 0

yang dimana persamaan dasar fluida ditulis dengan 𝑦 = −ℎ.

Dimisalkan letak partikel fluida berada pada koordinat (𝑥, 𝑦) dan partikel tetap berada pada batas, yang dapat ditulis dengan operator turunan total yaitu

𝐷𝑓 𝐷𝑡 = 0 Operator turunan total didefenisikan dengan

𝐷𝑓 𝐷𝑡 = 𝜕𝑓 𝜕𝑡 + 𝜕𝑓 𝜕𝑥 𝑑𝑥 𝑑𝑡 + 𝜕𝑓 𝜕𝑦 𝑑𝑦 𝑑𝑡

yang komponen kecepatan vektor dilambangkan dengan 𝑞̅ = (𝑢, 𝑣), sehingga defenisi operator turunan total berubah menjadi

𝐷𝑓 𝐷𝑡 = 𝜕𝑓 𝜕𝑡 + 𝑢 𝜕𝑓 𝜕𝑥+ 𝑣 𝜕𝑓 𝜕𝑦

Kemudian dilakukan subsitusi persamaan (2.37) terhadap persamaan (2.36) yang menyebabkan persamaan menjadi

𝜕(𝑦 + ℎ) 𝜕𝑡 + 𝑢 𝜕(𝑦 + ℎ) 𝜕𝑥 + 𝑣 𝜕(𝑦 + ℎ) 𝜕𝑦 = 0 0 + 0 + 𝑣 = 0

dengan mengubah komponen kecepatan (𝑢, 𝑣) menjadi komponen kecepatan 𝜙 yang dimana 𝑢 = 𝜙_𝑥 dan 𝑣 = 𝜙_𝑦, sehingga

(2.36)

(2.37)

(15)

21

𝜙𝑦 = 0

Persamaan diatas adalah persamaan kondisi batas kinematik pada dasar.

2.6.3 Kondisi Batas Dinamik pada Permukaan

Pada kondisi batas dinamik permukaan fluida memakai turunan dari persamaan Bernoulli yang dinyatakan dengan fungsi potrensial sebagai berikut.

𝜙𝑡+

1 2|𝑞̅|

2₊1

𝜌𝑃 + 𝑔𝑦 = 𝑓(𝑡)

dengan fungsi 𝑓(𝑡) adalah fungsi sebarang 𝑡 yang didapatkan dari hasil integral terhadap 𝑥 dan 𝑦. Diasumsikan persamaan permukaan fluida 𝑦 = ℎ + 𝜂(𝑥, 𝑡) dan tekanan udara dianggap sangat kecil (tekanan referensi) dan dapat diabaikan yang mengakibatkan 𝑃 = 0. Persamaan Bernoulli (2.30) dapat ditulis dengan

𝜙𝑡+

1 2(𝜙𝑥

2_{+ 𝜙}

𝑦2) + 𝑔(ℎ + 𝜂(𝑥, 𝑡)) = 𝑓(𝑡)

Dalam keadaan seragam (uniform) maka ruas kiri dari persamaan (2.39) akan berlaku kecepatan vertikal 𝜙_𝑦 = 0, kecepatan horizontal pada 𝜙_𝑥= 𝑎 dengan 𝑎 merupakan kecepatan awal dan dianggap 𝜙_𝑡 = 0 dikarenakan tidak akan ada perubahan terhadap waktu[], maka persamaan (2.39) menjadi

𝜙_𝑡+1 2(𝜙𝑥 2_{+ 𝜙} 𝑦2) + 𝑔(ℎ + 𝜂(𝑥, 𝑡)) = 𝑓(𝑡) 0 +1 2(𝑎 2_{+ 0) + 𝑔(ℎ) = 𝑓(𝑡)} 1 2𝑎 2_{+ 𝑔(ℎ) = 𝑓(𝑡)}

Lalu dengan mensubsitusikan persamaan (2.39) ke persamaan (2.30), sehingga

𝜙_𝑡+1 2|∇𝜙| 2 ₊1 𝜌𝑝 + 𝑔(ℎ + 𝜂(𝑥, 𝑡)) = 1 2𝑎 2 _{+ 𝑔(ℎ)} (2.39) (2.40)

(16)

22 𝜙_𝑡+1 2|∇𝜙| 2_{+ 𝑔(ℎ) + 𝑔𝜂(𝑥, 𝑡) =}1 2𝑎 2_{+ 𝑔(ℎ)} 𝜙_𝑡+1 2|∇𝜙| 2_{+ 𝑔𝜂(𝑥, 𝑡) =}1 2𝑎 2

Jika diasumsikan kecepatan awal 𝑎 = 0, maka persamaan di atas dapat menjadi menjadi

𝜙𝑡+

1 2|∇𝜙|

2_{+ 𝑔𝜂(𝑥, 𝑡) = 0}

pada persamaan permukaan 𝑦 = 𝜂(𝑥, 𝑡) .

Persamaan (2.41) diatas merupakan persamaan kondisi batas dinamik fluida pada permukaan.

2.7 Teori Gelombang Linear

Fenomena gelombang yang terjadi di dunia nyata sangat beragam dan tidak dapat dirumuskan dengan mudah dan akurat. Namun dalam memahami fenomena alam yang terjadi dapat dilakukan beberapa asumsi yang dimana dari beberapa asumsi akan menyebabkan beberapa teori-teori yang mendekati perumusan. Salah satunya adalah teori gelombang linear yang dimana teori ini adalah teori gelombang yang paling sederhana.

Teori gelombang linear merupakan turunan dari persamaan Laplace untuk fluida

irrotational. Dalam menyelesaikan persamaan Laplace tersebut membutuhkan

kondisi batas dalam mencari solusi dari permasalahan. Kondisi batas dibutuhkan pada penyelesaian permasalahan teori gelombang linear. Kondisi batas di permukaan membutuhkan penurunan dari persamaan Bernoulli yang dilinearkan, sedangkan untuk kondisi batas pada dasar digunakan kecepatan aliran searah vertikal sama dengan nol.

(17)

23

2.7.1 Kondisi Batas Kinematik pada Permukaan

Pada persamaan (2.35) memiliki sifat yang nonlinear yang diakibatkan oleh terdapat suku-suku 𝜙𝑥, 𝜂𝑥 namun dalam persamaan (2.35) bentuk 𝜙𝑦 dapat dievaluasi di

sepanjang garis 𝑦 = 0 pada saat dilinearisasi. Hal ini menyebabkan kondisi batas kinematik permukaan fluida dapat berubah menjadi

𝜕𝜙 𝜕𝑦 =

𝜕𝜂 𝜕𝑡

2.7.2 Kondisi Batas Dinamik Permukaan Fluida

Gelombang yang memiliki kecuraman yang rendah maka akan memiliki suku nonlinear yang kecil[14]. Hal ini menyebabkan adanya linearisasi yang mengabaikan kuadrat dan orde suku yang tinggi pada 𝜂 dan 𝜙 agar mendapatkan pendekatan yang baik terhadap sifat gelombang.

Sehingga pada aliran fluida unsteady, persamaan Bernoulli linear (2.41) menjadi

𝜙_𝑡+𝑃

𝜌+ 𝑔𝑦 = 0

Dikarenakan fluida yang diamati adalah fluida tak termampatkan yang mengakibatkan rapat massa fluida tersebut adalah konstan maka persamaan Bernoulli dapat menjadi kondisi batas dinamik pada permukaan 𝑦 = 𝜂(𝑥, 𝑡) dan dianggap 𝜌 = 0. Hal ini menyebabkan persamaan (2.43) dapat ditulis sebagai berikut.

𝜕_𝑡+ 𝑔𝜂 = 0

2.7.3 Kondisi Batas Kinematik Dasar Fluida

Kondisi Batas Kinematik Dasar Fluida yang digunakan yaitu

(2.42)

(2.43)

(2.44)

(18)

24

𝜙𝑦 = 0

pada 𝑦 = −ℎ.

Kondisi batas ini didapatkan dari penurunan pada subbab Kondisi Batas Kinematik pada Dasar sebelumnya. Tidak ada perubahan pada subbab ini dikarenakan persamaan (2.38) sudah linear.

2.8 Metode Pemisahan Variabel

Pemisahan variabel merupakan salah satu metode dalam penyelesaian beberapa jenis persamaan diferensial parsial yang memakai teknik klasik yang efektif. Metode ini menggunkan teknik subsitusi persamaan diferensial parsial dengan beberapa persamaan diferensial biasa yang dalam pengerjaannya harus memakai kondisi awal dan kondisi batas yang sesuai[15]. Dalam penyelesaian 𝑦(𝑥, 𝑡) dalam mencari solusi yang tepat dapat ditulis dengan variabel yang terpisah. Contohnya (𝑥, 𝑡) , yang pertama dilakukan asumsi 𝑦(𝑥, 𝑡) = 𝑋(𝑥)𝑇(𝑡). Lalu dilakukan proses subsitusi ke persamaan diferensial, selanjutnya dipisahkan antara variabel 𝑥 dan variabel yang menghasilkan sebuah fungsi persamaan diferensial[16]. Dalam menyelesaikan permasalahan persamaan gelombang yakni:

𝑦(𝑥, 𝑡) = 𝐹(𝑥)𝑇(𝑡)

Selanjutnya persamaan (2.45) yang bergantung pada 𝑡 diturunkan sekali dan yang bergantung pada 𝑥 diturunkan sebanyak dua kali, maka menghasilkan

𝑦_𝑡= 𝐹(𝑥)𝑇_𝑡(𝑡) 𝑦_𝑥𝑥(𝑥, 𝑡) = 𝐹_𝑥𝑥(𝑥)𝑇(𝑡)

Lalu persamaan (2.46) disubsitusikan terhadap persamaan (2.45) 𝑋(𝑥)𝑇𝑡(𝑡) = 𝑘𝑋𝑥𝑥(𝑥)𝑇(𝑡)

(19)

25

Selanjutnya, kedua ruas persamaan di atas dibagi dengan 𝑋(𝑥)𝑇(𝑡), maka menghasilkan

𝑇_𝑡(𝑡) 𝑇(𝑡) =

𝑋_𝑥𝑥(𝑥) 𝑋(𝑥)

Akibatnya pada ruas kiri persamaan (2.47) terdapat fungsi yang bergantung pada t dan pada ruas kanan bergantung pada x. Kemudian pilih −𝜆2 untuk mendapatkan solusi trivial. 𝑇𝑡(𝑡) 𝑇(𝑡) = 𝑋𝑥𝑥(𝑥) 𝑋(𝑥) = −𝜆 2

Lalu didapatkan 2 solusi yaitu terhadap t dan terhadap x, 𝑇_𝑡(𝑡) + 𝑘𝜆2_{𝑇(𝑡) = 0}

𝑋𝑥𝑥(𝑥) + 𝜆2𝑋(𝑥) = 0

Pertama menyelesaikan persamaan 𝑇_𝑡(𝑡) + 𝑘𝜆2_{𝑇(𝑡) = 0 yang dimana persamaan ini}

adalah persamaan diferensial biasa yang memiliki orde satu. Solusi umum dari 𝑇(𝑡) adalah

𝑇(𝑡) = 𝐴 𝑐𝑜𝑠 𝜆𝑡 + 𝐵𝑠𝑖𝑛𝜆𝑡

Kedua, menyelesaikan persamaan 𝑋𝑥𝑥(𝑥) + 𝜆2𝑋(𝑥) = 0 yang dimana persamaan ini

adalah persamaan diferensial ordo dua. Oleh karena itu, untuk menyelesaikan persamaan ini dapat menggunakan metode karakteristik. Dalam metode karakteristik memiliki tiga jenis kasus antara lain:

1. Saat λ < 0

Jika λ < 0 maka persamaan karakteristik dengan 𝑚2− 𝜆 = 0

Akan memiliki dua solusi yaitu 𝑚₁ = √𝜆 dan 𝑚₂ = √−𝜆. Maka menghasilkan solusi umum

𝑋(𝑥) = 𝐶1𝑒√𝜆𝑥+ 𝐶2𝑒√−𝜆𝑥

(20)

26

2. Saat λ = 0

Pada saat λ = 0, persamaan karakteristik dengan 𝑚2− 𝜆 = 0

𝑚2− 0 = 0

Maka akan menghasilkan akar real kembar yaitu 𝑚1,2 = 0, yang

menyebabkan solusi umumnya adalah

𝑋(𝑥) = 𝐶1+ 𝐶2

3. Saat λ > 0

Ketika λ > 0 maka persamaan karakteristik dengan 𝑚2_{+ 𝜆 = 0}

yang dimana akan memiliki akar kompleks yaitu 𝑚1,2 = ±√−𝜆.

Sehingga solusi untuk permasalahan λ > 0 adalah 𝑋(𝑥) = 𝐶1𝑐𝑜𝑠√−𝜆𝑥 + 𝐶2𝑠𝑖𝑛√𝜆𝑥

Setelah melihat ketiga kasus diatas, maka solusi umum yang tepat untuk persamaan 𝑋(𝑥) adalah

𝑋(𝑥) = 𝐶1𝑐𝑜𝑠√−𝜆2𝑥 + 𝐶2𝑠𝑖𝑛√𝜆2𝑥

𝑋(𝑥) = 𝐶₁cos (𝜆𝑥) + 𝐶₂sin (𝜆𝑥)