THE DEVELOPMENT OF NAPOLEON’S
THEOREM ON QUADRILATERAL WITH
CONGRUENCE AND TRIGONOMETRY
Chitra Valentika, Mashadi, Sri Gemawati
Abstract. This thesis discusses about Napoleon’s theorem on a quadrilateral that
has is two pairs of parallel side with two cases: (i) square built toward outside and (ii) square built toward inside. The Napoleon’s theorem is proved by using congruence approach and trigonometric concepts. At the end of the discussion, the Napoleon’s theorem is developed by using the concept of intersecting parallel lines and using Geogebra applications.
1. INTRODUCTION
Remarkable math statements have been attributed to Napoleon Bona-parte (1769-1821) although his relation to the theorems and their proofs is questioned in most of the sources available to our knowledge. Nevertheless, the mathematics flourished in post-revolutionary France and mathemati-cians were held in great esteem in the new Empire [10]. Napoleon’s theorem states that if equilateral triangles are drawn on the sides of any triangle, either all outward, or all inward, the centroids of those equilateral triangles are the vertices of an equilateral triangle [8]. Napoleons theorem on triangle can be proved by elementary [9], and several articles discussing Napoleons
Received 12-07-2016, Accepted 20-07-2016.
2010 Mathematics Subject Classification: 51F20, 51H10, 97G60
Key words and Phrases: Napoleon’s theorem, Napoleon theorem on quadrilateral, square, con-gruence, trigonometry.
theorem proof with trigonometry [3][7]. There are two cases in the triangle, which is as follow.
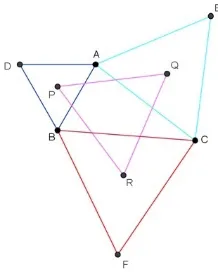
Case 1. Napoleon’s theorem in first case describes an equilateral triangle called the outer Napoleon triangle constructed on each side of any trian-gle △ABC toward the outside [2]. Let P, Q, and R is centroids of triangle △ABD, △ACE, and △BCF, the third of centroids form an equilateral triangle called the external Napoleon triangle [1]. Illustrations shown in the Figure 1.
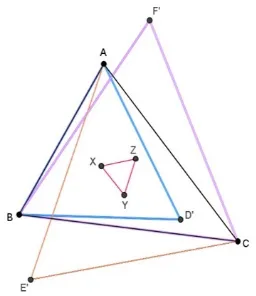
Case 2. Napoleon’s theorem in second case explain an equilateral triangle constructed on each side of any triangle △ABC toward the inside. Let X, Y, and Z is centroids of triangle △ABD,△ACE, and △BCF the third of centroids form an equilateral triangle called the internal Napoleon triangle [8]. Illustrations shown in the Figure 2.
Figure 1: External Napoleon triangle
Figure 2: Internal Napoleon triangle
2. NAPOLEON’S THEOREM ON THE QUADRILATERAL
Napoleon’s theorem on the triangle is the development of theorem Napoleon on the triangle. Several experiments conducted found for square, rhombuses, rectangles, and parallelograms forming a square, for an isosceles trapezium forming kites, and for any quadrilateral forming any quadrilat-eral. There are two cases of Napoleon’s theorem on the quadrilateral shaped parallelogram is as follows.
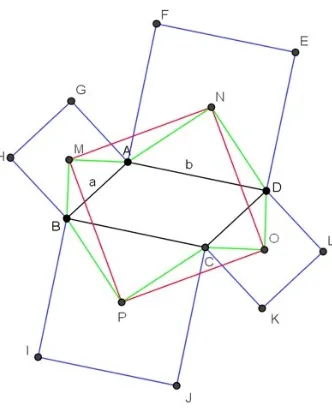
Case 1. In case 1, LetABCD denote any parallelogram, square construc-tion on each side of the parallelogram outwards, shown in the Figure 3.
Teorema 2.1 If M, N, O, and P is the centroid of each square ABHG, squareADEF, squareCDKL, and squareBCIJ which constructed on each side of the parallelogram outwards. The fourth centroids of the square con-nected so form a square M N OP.
Proof 1. By△GADand△BAF, obtainedAG=AB,∠GAD=∠F AB, AD= AF, so △GAD ≈ △BAF [6]. Perform △GQT and △BAT in Figure 4
∠T GQ=∠T BAand ∠GT Q=∠BT A, then∠GQT =∠BAT = 90o
. Then
∠GQT = ∠QSR = ∠M RN = 90o
, similarly ∠M RN = ∠QSR = 90o
Figure 3: Square construction on each side of the parallelogram outwards
RN, similarly forOR=P R, therefore△M RP ≈ △N RO. Since△M RP ≈
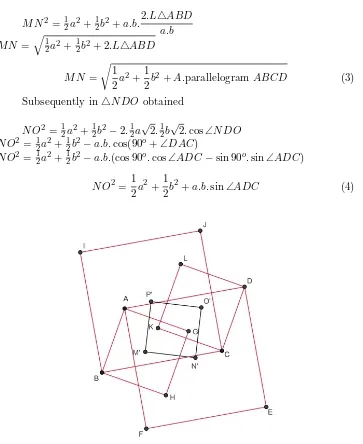
M N2 = 1 Subsequently in△N DO obtained
N O2 = 12a2+12b2−2.12a√2.12b√2.cos∠N DO
Figure 6: Square construction on each side of the parallelogram inwards
Teorema 2.2 Since t = A.parallelogramABCD
b and sin∠ADC =
t
a then
apply
sin∠ADC = A.parallelogramABCD
Substituting equation 5 to 4 in order to obtain
2+A.parallelogramABCD (6) Since M N = N O similarly M N = OP and N O =M P, thereforeM N = OP = N O = M P, and the second diagonal intersect perpendicularly [8]. This completes the proof of theorem 1.
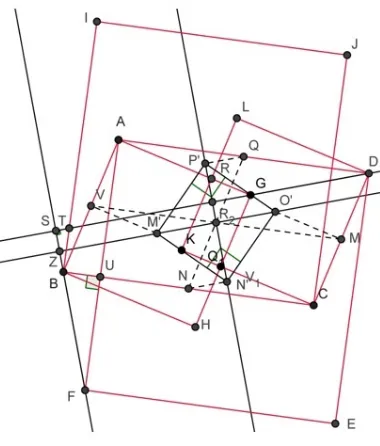
Case 2. In case 2, letABCDdenote any parallelogram, square construction on each side of the parallelogram inwards, shown in the Figure 6.
IfM , N , O,andP is the centroid of each squareABHG, squareADEF, squareCDKL, and squareBCIJ which constructed on each side of the par-allelogram inwards. The fourth centroids of the square connected so form a square M N OP.
Figure 7: Squares which constructed on each side of the parallelogram in-wards
△T SB,∠T BS = ∠BF U,∠F BU = ∠ST B, therefore △BU F ≈ △T SB, then∠F U B =∠T SB = 90o
. SinceV M′ =O′M,∠V M′R=∠M O′R, V R=
RM therefore△V M′R ≈ △M RO′, thenM′R=O′R, similarly for△P′QR≈
△N′N R, thenN′R=P′R. LetP′N′ and O′M′ are diagonal on the square
M′N′O′P′ so dividing the same diagonal length and intersect
perpendicu-larly at the point R. Then proved O′M′N′P′ is square.
3. THE DEVELOPMENT OF NAPOLEON’S THEOREM ON QUADRILATERAL
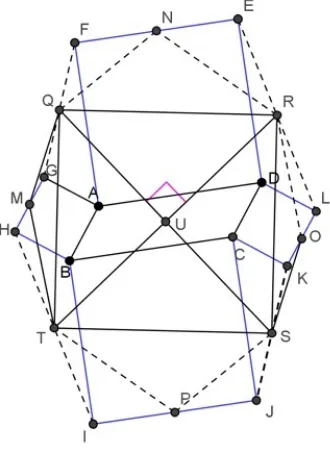
Napoleon’s theorem on quadrilateral developed based Napoleon’s the-orem on quadrilateral for case square built leads outward.
Teorema 3.3 If Q, R, S, and T is the midpoint of the line F G, EL, KJ, and HI, then QRST is a square.
Figure 8: Napoleon’s theorem on quadrilateral
ER, therefore △N ER ≈ △P IT then N R =T P. Since QN =P S, N R = T P and∠QN R=∠SRT, therefore△QN R∠△SP T, thenQR=T S. Sim-ilarly △T M Q and △SOR, T M =OR,∠T M Q =∠SOR, and OM = OS, therefore △T M Q ≈ △SOR then T Q= SR. Since ∠QU R =∠T U S, and
∠QU T = ∠RU S therefore ∠QU T = ∠RU S = ∠QU R = ∠T U S = 90o
, then proved QRST is square.
The following corollary proves statements 1, 2, and 3 from theorem 3.
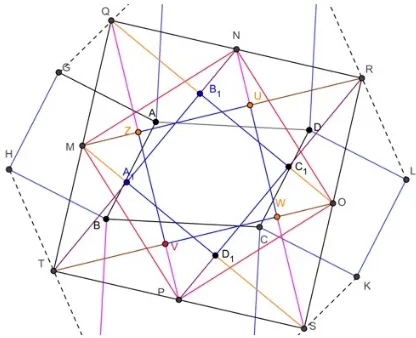
Corollary 3.1 On the square M N OP and T QRS formed parallel lines P Q//SN and M R//T O, then formed a square V W ZU, and if formed parallel lines M S//QO and T N//P R, then formed a square A1B1C1D1. Illustrations in Figure 9.
Figure 9: Parallel lines P Q//SN and M R//T O
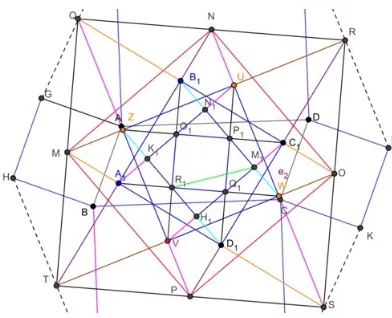
Corollary 3.2 On the squareV W ZU andA1B1C1D1 formed parallel lines U A1//V C1 and ZD1//W B1, then formed a square K1N1M1H1, and if formed parallel lines V B1//U D1 and ZD1//W B1, then formed a square O1P1Q1R1. Illustrations in Figure 10.
Figure 10: Parallel linesV B1//U D1 and ZD1//W B1
4. CONCLUSION
Napoleon’s theorem at quadrilateral only to the quadrilateral that has two pairs of parallel side, such as square, rectangle, rhombus, parallelogram. Then development with two cases: (i) square built toward outside and (ii) square built toward inside then the fourth centroids of the square connected so form a square.
REFERENCES
1. B.J.Mc. Cartin, Mysteries of the Equilateral Triangle, Hikari Ltd, 978-954-91999-5-6(2010), 36-37.
2. G.A. Venema, Exploring Advanced Euclidean Geometry with Geometer’s Sketchpad, Grand Rapids, Michigan 49546 (2009), 84-85.
3. J.A.H. Abed, A Proof of Napoleon’s Theorem, The General Science Jour-nal, 1(2009), 2-4.
4. J. Baker, Napoleon’s Theorem and Beyond, Spread Sheets in Educations (eJSiE), 1[4], Bond University’s Repository, 2005.
5. M. Corral, Trigonometry, Schoolcraft collage, GNU Free Documentation License, Version 1.3, Livonia, Michigan, 2009.
6. Mashadi, Buku Ajar Geometri, PUSBANGDIK UNRI, Pekanbaru, 2012.
7. N. A.A. Jariah,Pembuktian Teorema Napoleon dengan Pendekatan Trigonometri, [http://www.academia.edu/12025134/ Isi NOVIKA ANDRIANI AJ 06121008018], accessed 6 October 2015
8. P. Bredehoft, Special Cases of Napoleon Triangles, Master of Science, University of Central Missouri, 2014.
9. P. Lafleur,Napoleons Theorem, Expository paper, [http://www.Scimath.unl.edu/ MIM/files/MATEexamFiles], accessed 24 November 2015.
10. V. Georgiev and O. Mushkarov, Around Napoleon’s Thorem, Lifelong Learning Progamme, 510028, Dyna Mat, 2010.
11. Y. Nishiyama, Beatiful Geometry As Van Aubel’s Theorem, 533-8533, Univ. Osaka, Dept. Business information, 2010.
Chitra Valentika: Magister Student, Department of Mathematics, Faculty of
Mathematics and Natural Scinces Uneversity of Riau, Bina Widya Campus, Pekan-baru 28293, Indonesia.
Mashadi: Analysis group, Department of Mathematics, Faculty of Mathematics
and Natural Scinces Uneversity of Riau, Bina Widya Campus, Pekanbaru 28293, Indonesia.
E-mail: [email protected]
Sri Gemawati: Analysis group, Department of Mathematics, Faculty of
Mathe-matics and Natural Scinces Uneversity of Riau, Bina Widya Campus, Pekanbaru 28293, Indonesia.