BAB II
TEORI DASAR
II.1. Pengenalan Desain Struktur Baja
II.1.1. Desain Konstruksi
Desain Konstruksi dapat didefenisikan sebagai perpaduan antara seni (artistik /
keindahan) dan ilmu pengetahuan (science) untuk menghasilkan suatu struktur yang aman dan
ekonomis serta memenuhi fungsi tertentu dan persyaratan estetika. Untuk mencapai tujuan ini, seorang perencana/desainer harus mempunyai pengetahuan yang baik tentang :
1. Sifat – sifat fisis material. 2. Sifat – sifat mekanis material. 3. Analisa Struktur.
4. Hubungan antara fungsi rancangan dan fungsi struktur.
II.1.2. Prosedur Desain
Prosedur perencanaan / desain terdiri dari 6 langkah utama, yaitu : 1. Pemilihan tipe dan rancangan struktur.
2. Penentuan besarnya beban – beban yang bekerja pada struktur
3. Menentukan gaya – gaya dalam dan momen yang terjadi pada struktur.
4..Pemilihan komponen – komponen struktur beserta sambungannya yang memenuhi kriteria kekuatan, kekakuan dan ekonomis.
II.1.3. Keunggulan Baja Sebagai Material Konstruksi
II.1.3.1. Kekuatan Tinggi ( High Strength )
Baja struktural umumnya mempunyai daya tarikan (tensile strength) antara 400 s/d 900 Mpa. Hal ini sangat berguna untuk dipakai pada struktur – struktur yang memiliki bentang panjang dan struktur pada tanah lunak.
II.1.3.2. Keseragaman ( Uniformity )
Sifat – sifat baja tidak berubah karena waktu. Hampir seluruh bagian baja memiliki sifat – sifat yang sama sehingga menjamin kekuatannya.
II.1.3.3. Elastisitas ( Elasticity )
Baja mendekati perilaku seperti asumsi yang direncanakan oleh perencana, karena mengikuti hukum Hooke, walaupun telah mencapai tegangan yang cukup tinggi. Modulus elastisitasnya sama untuk tarik dan tekan.
II.1.3.4. Daktalitas ( Ductility )
Daktalitas adalah kemampuan struktur atau komponennya untuk melakukan deformasi inelastik bolak – balik berulang diluar batas titik leleh pertama, sambil mempertahankan sejumlah besar kemampuan daya dukung bebannya. Manfaat daktalitas ini bagi kinerja struktural adalah pada saat baja mengalami pembebanan yang melebihi kekuatannya, baja tidak langsung hancur tetapi akan meregang sampai batas daktalitas. Demikian juga pada beban siklik, daktalitas yang tinggi menyebabkan baja dapat menyerap energi yang besar.
Baja dalah material yang sangat ulet sehingga dapat memikul beban yang berulang – ulang. Komponen struktur baja yang dibebani sampai mengalami deformasi besar,
masih mampu menahan gaya – gaya yang cukup besar tanpa mengalami fraktur. Keuletan ini dibutuhkan jika terjadi konsentrasi tegangan walaupun tegangan yang masih dibawah batas yang diizinkan. Pada bahan yang tidak memiliki keuletan yang tinggi, keruntuhan dapat terjadi pada tegangan yang rendah dan akan bersifat getas ( keruntuhan secara langsung ).
II.1.4. Kelemahan Baja Sebagai Material Konstruksi
II.1.4.1. Biaya Perawatan ( Maintenance Cost )
Baja bisa berkarat karena berhubungan dengan air dan udara. Oleh sebab itu, baja harus dicat secara berkala
II.1.4.2. Biaya Penahan Api ( Fire Proofing Cost )
Kekuatan baja dapat berkurang drastis pada temperatur tinggi. II.1.4.3. Kelelahan ( Fatigue )
Kelelahan pada baja tidak selalu dimulai dengan yielding ( leleh ) atau deformasi yang sangat besar, tetapi dapat juga disebabkan beban siklik ataupun pembebanan berulang – ulang dalam jangka waktu yang lama. Kejadian ini sering terjadi dengan adanya konsentrasi tegangan karena adanya lubang.
II.1.4.4. Rekah Kerapuhan
Struktur baja ada kalanya tiba – tiba runtuh tanpa menunjukkan tanda – tanda deformasi yang membesar. Kegagalan ini sangat berbahaya dan harus dihindari. Berbeda dengan kelelahan, rekah kerapuhan disebabkan oleh beban statik.
II.1.5. Sifat – Sifat Mekanis Baja Struktural
perencanaan suatu struktur bangunan harus memenuhi persyaratan minimum yang diberikan.
II.1.5.1. Tegangan Putus ( Ultimate Stress )
Tegangan Putus untuk perencanaan (Fu) tidak boleh diambil melebihi nilai yang ditetapkan oleh tabel 1.1
II.1.5.2. Tegangan Leleh ( Yielding Stress )
Tegangan Leleh untuk perencanaan (Fy) tidak boleh diambil melebihi nilai yang ditetapkan oleh tabel 1.1
II.1.5.3. Sifat – Sifat Mekanis Lainnya
Sifat – sifat mekanis lain baja struktural untuk maksud perencanaan ditetapkan sebagai berikut :
• Modulus Elastisitas : E = 200.000 Mpa • Modulus Geser : G = 80.000 Mpa • Poisson Ratio : µ = 0.3
Koefisien Pemuaian : α = 12 x 10 ^ -6 / ºC
II.1.6. Jenis – Jenis Baja Struktural yang Umum Digunakan
II.1.7. Hubungan Antara Tegangan dan Regangan pada Konstruksi Baja
Dalam peraturan AISC 2005, perhitungan rumus kekuatan nominal (Rn)
menggunakan tegangan leleh (Fy) maupun tegangan ultimate (Fu), pemilihan tegangan baik itu Fy maupun Fu didasarkan atas kemampuan struktur mempertahankan stabilitasnya setelah beban maksimum diberikan.
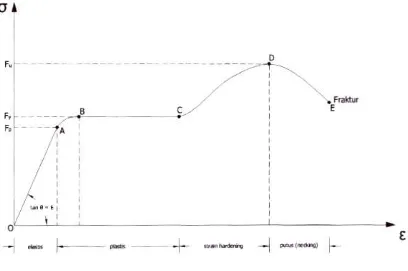
Grafik diatas menunjukkan hasil pengukuran hubungan tegangan - regangan dalam percobaan tarik baja. Tipikal grafik tersebut hanya dapat diperoleh pada percobaan tarik baja lunak (mild).
dengan titik A disebut juga daerah elastis yang artinya jika suatu bahan baja mengalami tegangan tidak melewati titik A dan apabila dilepaskan, maka baja masih dapat kembali ke bentuk atau panjang semula.
Ketika beban diperbesar sehingga tegangan baja sampai ke titik B, maka hubungan tegangan regangan tidak linear lagi. Titik B merupakan titik leleh (Fy) dari baja yang ditandai dengan tegangan yang relatif tidak naik dan regangan yang meningkat. Daerah antara titik A dan titik C merupakan daerah plastis, dimana jika suatu batang baja mengalami tegangan sampai melewati titik A ( masuk kedalam daerah A s/d C ) dan beban dilepaskan, maka baja tidak akan kembali ke panjang semula. Dengan demikian terdapat regangan residu yang disebabkan karena inelastis dari bahan tersebut.
Apabila beban diperbesar lagi, maka yang terjadi adalah regangan akan terus
meningkat tanpa disertai tegangan. Titik C disebut dengan pengerasan regangan, pada titik C terdapat kenaikan tegangan yang disebabkan karena regangan bahan sudah hampir mencapai maksimum. Bahan masih mampu menahan tegangan tambahan sampai pada titik D, yang disebut dengan tegangan ultimate (Fu). Daerah anatara titik C dan titik D merupakan daerah strain hardening yang ditandai dengan peningkatan tegangan dan regangan setelah melewati batas plastis.
II.2. Struktur Statis Tertentu dan Statis Tak-tentu
Dalam analisa struktur kita mengenal tiga jenis permodelan struktur yaitu balok (beams), portal (rigid frames), atau rangka batang (trusses). Balok adalah jenis struktur yang ditujukan hanya untuk memikul beban transversal. Penyelesaian analisa terhadap suatu balok berupa diagram lintang dan diagram momen.
Portal adalah jenis struktur yang tersusun dari elemen-elemen yang terhubung oleh penghubung kaku (misalnya: hubungan las). Penyelesaian analisa terhadap suatu portal berupa variasi gaya aksial, gaya lintang dan momen pada sepanjang elemen-elemennya. Sedangkan rangka batang adalah jenis struktur dimana semua anggota/elemennya dianggap terhubung pada perletakan sendi; dalam hal ini momen dan gaya geser pada setiap elemen diabaikan. Penyelesaian analisa terhadap rangka /batang berupa gaya aksial pada setiap anggota/elemennya.
Diagram lintang dan momen balok dapat digambar apabila semua reaksi luarnya telah diperoleh. Dalam telaah tentang keseimbangan sistem gaya-gaya sejajar yang sebidang, telah dibuktikan bahwa jumlah gaya yang tak diketahui pada sembarang benda bebas (free body) yang dapat dihitung dengan prinsip statika tidak bisa lebih dari dua buah.
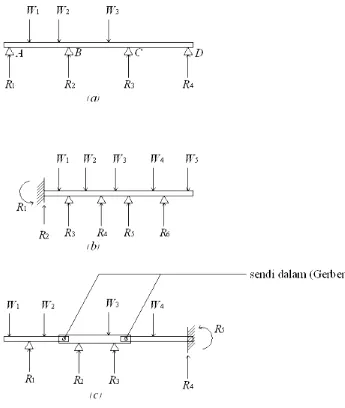
Gambar II.2.2 Balok Statis Tak Tentu
oleh jumlah reaksi kelebihannya tersebut. Balok pada Gambar II.2.2a bersifat statis tak-tentu berderajat dua karena jumlah Gambar II.2.2 Balok statis tak-tak-tentu. reaksi yang tak diketahui ada empat dan statika hanya bisa memenuhi dua kondisi atau dua persamaan keseimbangan; balok pada Gambar II.2.2b bersifat statis tak-tentu berderajat empat; balok pada Gambar II.2.2c bersifat statis tak-tentu berderajat satu karena balok memiliki lima reaksi dan dua sendi-dalam. Pada kenyataannya, jarang sekali suatu balok dibangun dengan sendi-dalam. Namun, keadaan semacam itu dapat terjadi pada perilaku balok dengan beban yang melebihi daya pikulnya.
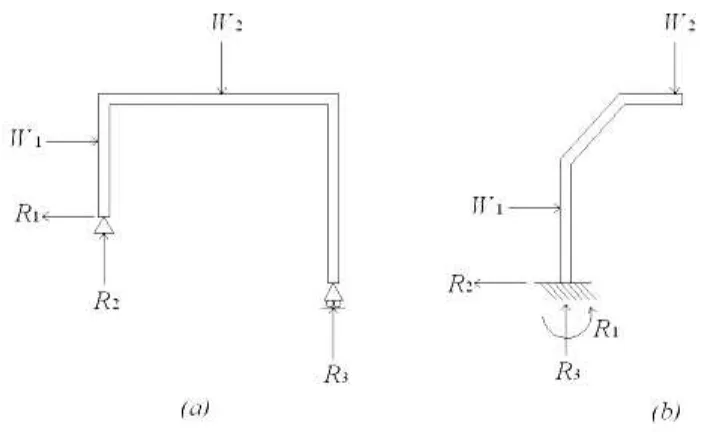
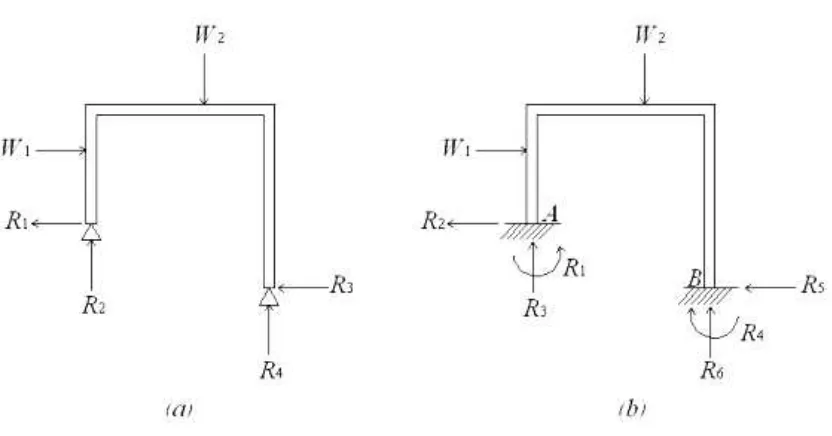
ke-taktentu-annya sama dengan jumlah reaksi kelebihannya. Portal bertingkat satu pada Gambar II.2.4a bersifat statis tak-tentu berderajat satu; pada Gambar II.2.4b adalah berderajat tiga. Sebagian besar portal kaku umumnya bersifat statis tak-tentu, sesuai dengan tuntutan efisiensi dan kekokohannya. Semakin banyak tingkat kerangka kaku, semakin bertambah derajat ke-taktentu-annya.
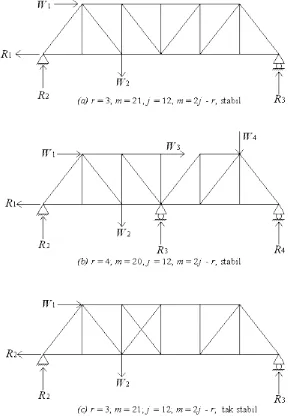
Syarat agar suatu rangka batang bersifat statis tertentu adalah bahwa jumlah gaya yang tidak diketahui sekurang-kurangnya tiga dan jumlah batang di dalam rangka batang tersebut adalah 2j – r, dimana j sama dengan jumlah titik hubungnya (joints) dan r sama dengan jumlah reaksinya. Jika m adalah jumlah batangnya, kondisi perlu untuk keadaan statis tertentu dapat dituliskan:
m = 2j – r (II.2.1)
Keabsahan persamaan diatas dapat diamati dengan mengubah persamaan tersebut menjadi m + r = 2j, dimana m + r adalah jumlah gaya yang tidak diketahui dan 2j adalah jumlah persamaan yang bisa diperoleh dengan prinsip statika apabila setiap titik hubungnya kita pandang sebagai suatu benda bebas (free body).
Gambar II.2.5 Rangka batang yang memenuhi kondisi perlu untuk bangunan statis tertentu.
demikian, agar suatu rangka batang bersifat statis tertentu dan stabil. m buah anggota yang dimaksudkan di dalam persamaan m = 2j – r haruslah diatur secara bijaksana, artinya semua reaksi dan gaya aksial di dalam setiap batang harus dapat ditentukan. Maka pada Gambar II.2.5a dan b bersifat statis tertentu dan stabil, sedangkan pada Gambar II.2.5c rangka batang meskipun memenuhi persamaan, tetapi bersifat statis tak stabil.
Apabila suatu rangka batang memiliki sekurang-kurangnya tiga reaksi yang tak diketahui dan jumlah batangnya, m dan lebih besar dari 2j – r maka rangka batang bersifat statis tak tentu dan derajat ke-taktentu-annya, yakni i, menjadi
i = m – (2j – r) (II.2.2)
Jadi, rangka batang pada Gambar II.2.6a merupakan rangka batang statis tak-tentu berderajat dua, pada Gambar II.2.6b dan c merupakan rangka batang statis tak-tentu berderajat tiga.
II.3. Kinematisme struktur
Selain pengklasifikasian struktur statis tertentu atau statis tak-tentu, kita juga dapat mengklasifikasikan permodelan struktur berdasarkan kinematismenya.
titik B, akibat gaya W1akan menyebabkan titik B berpindah sebesar u1 dan akibat W2 dan W3 akan mengakibatkan putaran sudut pada titik B sebesar θ1. Demikian juga pada titik C, terjadi dua jenis perpindahan yaitu u2 dan θ2. Dengan demikian, jumlah
perpindahan yang mungkin terjadi adalah empat sehingga permodelan struktur ini memiliki 4 derajat ke-taktentu-an secara kinematis. Derajat ke-taktentu-an kinematis sering juga disebut juga sebagai Degree Of Freedom (DOF).
II.4. Metode Perencanaan Konstruksi Baja
II.4.1. Metode ASD ( Allowable Stress Design )
Metode ASD (Allowable Stress Design) merupakan metode yang paling konvensional dalam perencanaan konstruksi. Metode ini menggunakan beban servis sebagai beban yang harus dapat ditahan oleh material konstruksi. Agar konstruksi aman maka harus direncanakan bentuk dan kekuatan bahan yang mampu menahan beban tersebut. Tegangan maksimum yang diizinkan terjadi pada suatu konstruksi saat beban servis bekerja harus lebih kecil atau sama dengan tegangan leleh (σy). Untuk memastikan
bahwa tegangan yang terjadi tidak melebihi tegangan leleh (σy) maka diberikan faktor
keamanan terhadap tegangan izin yang boleh terjadi.
𝝈𝝈′
≥
𝝈𝝈
𝑭𝑭𝑭𝑭
𝛀𝛀
≥
𝝈𝝈
(II.4.1)Dimana :
𝝈𝝈
= Tegangan Terjadi (MPa)𝝈𝝈′
= Tegangan Izin (MPa)...
𝛀𝛀
=
𝑭𝑭𝑭𝑭
=
Tegangan Leleh Baja (Mpa)Besaran faktor keamanan yang diberikan lebih kurang sama dengan 1,5 ; sehingga boleh dipastikan bahwa tegangan maksimum yang diizinkan terjadi adalah 2/3 Fy yang berarti juga akan terletak pada daerah elastis. Perencanaan memakai ASD akan memberikan penampang yang lebih konvensional.
II.4.2. Metode LRFD ( Load Resistance Factor Design )
Metode LRFD ( Load Resistance Factor Design ) lebih mementingkan perilaku bahan atau penampang pada saat terjadinya keruntuhan. Seperti kita ketahui bahwa suatu bahan (khususnya baja) tidak akan segera runtuh ketika tegangan yang terjadi melebihi tegangan leleh (Fy), namun akan terjadi regangan plastis pada bahan tersebut. Apabila tegangan yang tejadi sudah sangat besar maka akan terjadi strain hardening yang mengakibatkan terjadinya peningkatan tegangan sampai ke tegangan runtuh / tegangan ultimate (FU). Pada saat tegangan ultimate dilampaui maka akan terjadi keruntuhan bahan. Metode LRFD umumnya menggunakan perhitungan dengan menggunakan tegangan ultimate (FU) menjadi tegangan izin, namun tidak semua perhitungan metode LRFD menggunakan tegangan ultimate (FU) ada juga perhitungan yang menggunakan tegangan leleh (Fy), terutama pada saat menghitung deformasi struktur yang mengakibatkan ketidakstabilan struktur tersebut.
sebagai faktor reduksi akibat dari ketidak sempurnanya pelaksanaan dilapangan maupun di pabrik.
𝝃𝝃𝝃𝝃
=
𝝓𝝓𝑹𝑹
𝒏𝒏(II.4.2)Dimana : 𝜉𝜉= 𝐿𝐿𝐿𝐿𝐿𝐿𝐿𝐿𝐹𝐹𝐿𝐿𝐹𝐹𝐹𝐹𝐿𝐿𝐹𝐹
P = Beban Servis (kN)
𝜙𝜙 = Faktor Resistansi
𝑅𝑅𝑛𝑛 = Kekuatan Nominal Bahan (kN)
Besaran faktor resistansi berbeda – beda untuk setiap perhitungan kekuatan yang ditinjau, misalnya : untuk kekuatan tarik digunakan faktor reduksi 0,9 dan untuk kekuatan tekan digunakan faktor reduksi 0,75. Dapat dilihat bahwa untuk penampang yang sama hasil kekuatan nominal yang akan didapat dari metode LRFD akan lebih tinggi dari metode ASD.
II.5. Teori Metode Elemen Hingga (FEM)
perpindahan. Nonlinear FEM digunakan untuk memperbaiki parameter materialdari pandangan pelat elastis yang tinggi. Dalam bab ini, dikembangkan model FEM nonlinear untuk deformasi geometri yang besar. dalam hal ini akan digunakan suatu model untuk memperbaiki deformasi yang ada pada struktur balok.
Suatu balok merupakan suatu batang, yang berarti satu dimensi lebih besardari dua elemen struktur yang dapat menahan gaya transversal pada perletakan yangada. Balok yang umum dapat digunakan sebagai struktur tersendiri ataudikombinasikan untuk membentuk struktur portal bangunan yang umum digunakan pada bangunan dan dapat digunakan pada varisai beban secara luas dengan berbagaiarah. Karena kita bekerja pada gambaran struktur 2D , maka digunakan suatu balok sederhana yang membentuk suatu balok 3D di bawah pengaruh gaya yang dipakai pada balok.
II.5.1. Deskripsi Model Matematis.
Euler-Bernoulli beam (EB) teori secara luas digunakan untuk memodelkandeformasi yang kecil. Timoshenko beam (TB) teori memperluas persamaan EB untukmemperjelas untuk efek nonlinear seperti geser. Untuk lebih teliti, elemen kinematikpada balok dijelaskan dengan 3 dof per node yaitu perpindahan aksial pada sumbu X(Ux), perpindahan transversal pada sumbu Y (Uy) dan rotasi pada penampangmelintang (θ). Teori EB mengasumsikan bahwa penampang melintang
akibat perpindahan dan perputaran yang besar. walaupun lebih kompleks teori TB yang muncul agar lebih efisien dalam hal perhitungan FEM.
Balok tersebut dibagi menjadi beberapa bagian ( elemen hingga ). elemenelemenbalok lurus dan memiliki 2 node. Maka dikumpulkan semua nodal dof kedalam sistem vektor dof yang dinamakan vektor tetap :
𝑈𝑈= [𝑢𝑢𝑢𝑢1 𝑢𝑢𝑢𝑢1 𝜃𝜃1 …𝑢𝑢𝑢𝑢𝑛𝑛𝑢𝑢𝑢𝑢𝑛𝑛𝜃𝜃𝑛𝑛]𝑇𝑇 (II.5.1.1)
Dalam hal ini, diasumsikan untuk mengetahui material properti dari modelyang ada seperti E modulus elastisitas, G yaitu modulus geser. Materialnya masihtetap linear elastis . gaya-gaya yang ada bekerja pada node balok yang dikumpulkan untuk membentuk vektor gaya yaitu :
𝑓𝑓 = [𝑓𝑓𝑢𝑢1 𝑓𝑓𝑢𝑢1 𝑓𝑓𝜃𝜃1 …𝑓𝑓𝑢𝑢𝑛𝑛𝑓𝑓𝑢𝑢𝑛𝑛𝑓𝑓𝜃𝜃𝑛𝑛]𝑇𝑇 (II.5.1.2)
dengan n adalah total jumlah node yang ada pada model balok
Regangan merupakan suatu ukuran untuk mengubah bentuk objek, dalam halini yaitu panjang, sebelum dan sesudah terjadi deformasi yang diakibatkan beberapabeban yang ada. Tegangan adalah distribusi gaya-gaya dalam per satuan luas yangseimbang dan bereaksi terhadap gaya luar yang terjadi pada balok. Dalam kasus teoriTB , ada tiga perbedaan komponen tegangan per elemen balok : regangan aksial yangdiukur berdasarkan besar ukuran balok ( e ), regangan geser yang diukur berdasarkanperubahan sudut antara dua garis pada balok sebelum dan sesudah deformasi ( γ ) ,dan ukuran
perubahan kurva ( k ). Dari hal di atas , dapat dikumpulkan menjadi suatuvektor regangan balok secara umum :
Resultan tegangan pada teori TB ditentukan gaya aksial N , gaya lintang Vdan momen lentur M per satuan luas dari penampang melintang. Resultan tegangansecara umum :
𝑧𝑧= [ 𝑁𝑁1𝑉𝑉1𝑀𝑀1 … 𝑁𝑁𝑛𝑛−1𝑉𝑉𝑛𝑛−1𝑀𝑀𝑛𝑛−1] (II.5.1.4)
Di mana n-1 adalah jumlah dari elemen balok.
Energi regangan dalam model sepanjang balok dapat ditulis sebagai integralpanjang:
𝑈𝑈 = ∫𝐿𝐿𝑍𝑍𝑇𝑇ℎ𝐿𝐿𝑋𝑋 (II.5.1.5)
Di mana L adalah panjang balok. Vektor gaya dalam bisa didapat dengan mengambilvariasi pertama dari energi regangan sehubungan dengan perpindahan nodal :
𝑃𝑃= 𝜕𝜕𝑈𝑈𝜕𝜕𝑢𝑢 = ∫𝐿𝐿𝐵𝐵𝑇𝑇(𝑢𝑢)𝑧𝑧𝐿𝐿𝑋𝑋 (II.5.1.6)
Persamaan ini dievaluasi dengan penggabungan satu titik Gauss. B adalahmatrik regangan-perpindahan . akhirnya, variasi pertama pada gaya dalammendefinisikan matriks kekakuan tangensial :
𝐾𝐾𝑇𝑇 = 𝜕𝜕𝜕𝜕𝜕𝜕𝑢𝑢 =∫𝐿𝐿�𝐵𝐵𝑇𝑇 𝜕𝜕𝑧𝑧𝜕𝜕𝑢𝑢 + 𝜕𝜕𝐵𝐵𝜕𝜕𝑢𝑢 𝑍𝑍� 𝐿𝐿𝑋𝑋= (𝐾𝐾𝑀𝑀 + 𝐾𝐾𝐺𝐺) (II.5.1.7)
Di mana KT adalah kekakuan material dan KG adalah kekakuan geometri. Kekakuanmaterial adalah konstan dan identik dengan matriks kekakuan linear pada balokEuler-Bernoulli C1 . kekakuan geometri mendatangkan variasi dari B dimanaresultan tegangan tetap dan membawa balok nonlinear pada deformasi geometri yangbesar.
II.6. Pembebanan
lokasi dari struktur dapat diketahui secara pasti, namun distribusi beban dari elemen ke elemen lainnya umumnya memerlukan asumsi dan pendekatan. Jenis beban yang biasa diperhitungkan pada perencanaan struktur bangunan antara lain sebagai berikut:
II.6.1Beban Mati
Menurut (peraturan pembebanan Indonesia,1983), beban mati merupakan berat dari semua bagian dari suatu struktur yang bersifat tetap selama masa layannya, termasuk segal unsur tambahan, penyelesaian-penyelesaian, mesin-mesin serta peralatan tetap yang merupakan bagian yang tidak terpisahkan dari struktur tersebut. Yang termasuk beban mati adalah berat struktur sendiri dan juga semua benda yang tetap pada posisinya selama struktur berdiri. Beban mati tetap berada pada struktur dan tidak berubah sesuai dengan sistem struktur dan material yang digunakan.
Tabel II.6.1.1 berat bangunan berdasarkan SNI 03-1727-1989-F
II.6.2Beban Hidup
Menurut (Peraturan Pembebanan Indonesia, 1983), beban hidup adalah semua beban yang terjadi akibat penghunian atau penggunaan suatu struktur termasuk beban-beban pada lantai yang berasal dari berat manusia, barang-barang yang dapat berpindah, mesin-msin serta peralatan yang tidak merupakan bagian yang tidak terpisahkan dari struktur dan dapat diganti selama masa layan dari struktur tersebut sehingga menyebabkan perubahan dalam pembebanan lantai dan atap tersebut. Khusus untuk atap, beban hidup dapat termasuk beban yang berasal dari air hujan, baik akibat genangan maupun akibat tekanan jatuh butiran air.
Tabel II.6.1.2 beban hidup menurut kegunaan Berdasarkan SNI 03-1727-1989F
Beban Hidup Lantai Bangunan Besar Beban
Perkantoran, Ruang kuliah, Hotel, Asrama, Dll 250 Kg/m2 Tangga dan Bordes 300 Kg/m2
Beban Pekerja 100 Kg/m2
Lantai Atap 100 Kg/m2
II.6.3Beban Angin
• Pinggir laut hingga 5 km dari pantai minimum tekanan tiup 40 kg/m2
• Bangunan di daerah yang tekanan tiupnya lebih dari 40 kg/m2, harus
diambil sebesar P= -v2/16 Kg/m2. V adalah kecepatan angin dalam m/s • Untuk cerobong, tekanan tiup dalam kg/m harus ditentukan dengan rumus
(42,4+0,6h) dengan h adalah tinggi cerobong seluruhnya.
• Koefisien angin yang diambil untuk struktur tertutup dengan sudut pangkal atap dinyatakan dengan β adalah sebagai berikut:
o β < 22` untuk bidang lengkung dipihak angin
- Pada seperempat busur pertama -0,6 - Pada seperempat busur kedua -0.7
o β < 22` untuk bidang dibelakang angin
- Pada seperempat busur pertama -0,5 - Pada seperempat busur kedua -0.2
o β < 22` untuk bidang lengkung dipihak angin
- Pada seperempat busur pertama -0,5 - Pada seperempat busur kedua -0.6
o β < 22` untuk bidang lengkung dibelakang angin
II.7. Castellated Beam
Castellated beam merupakan suatu profil baja yang mempunyai bukaan berbentuk segi enam. Castellated mengalami proses pemotongan pada bagian badan profil dengan pola zigzag salah satu bagian yang telah dipotong lalu diangkat dan disatukan bagian badannya dan terakhir dilakukan pengelasan pada bagian badan yang menempel; hal ini dilakukan untuk meningkatkan tinggi dari profil awal (h) dengan tinggi potongan yang ada (d). Bentuk castellated beam ditampilkan dalam gambar II.7.1
Gambar II.7.1. proses pembentukan castellated beam
portal. Keuntungan balok castellated juga mencakup penampilan mereka yang mengesankan dan memungkinkan penggunaan daerah bukaan untuk pelayanan instalasi.
Adapun juga kerugian dari penggunaan balok castellated. Akibat adanya bukaan pada bagian badan profil, perilaku struktur dari balok casatellated akan berbeda dari balok baja yang biasa. Karena perbedaan kemungkinan moda kegagalan atau moda kegagalan yang baru, mereka merupakan struktur nonlinear, dimana tidak bisa dianalisi dengan metode sederhana. Kapasitas geser pada bagian badan profil adalah suatu faktor yang terbatas, dan balok acstellated tidak cocok untuk bentang pendek yang dibebani dengan berat. Deformasi geser pada bagian T nya sangat signifikan dan abalisa lendutan lebih kompleks daripada balok yang bagian badan profil padat
II.7.1 Analisa dan perencanaan balok castellated
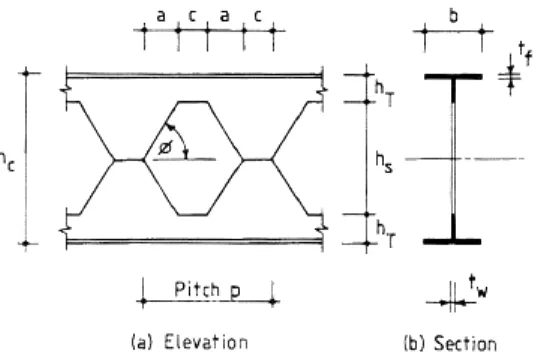
Geometri dari balok castellated terdapat tiga parameter yaitu sudut potongan pada bukaan badan profil (Ø). Rasio ekspansi (α), dan panjang pengelasan (c) yang
ditungukkan pada gambar II.6.2
GambarII.7.2.2. Castellated Beam di lapangan
• Sudut potongan (Ø)
Sudut potongan mempengaruhi jumlah proses pemotongan balok castellated (N) per unit panjang dari balok N akan kecil ketika suduit itu rata dan akan besar ketika bertahap. Percobaan telah menunjukkan bahwa peningkatan jumlah N mempunyai pengaruh yang kecil untuk kekakuan elastis pada balok castellated, itu akan meningkatkan daktilitas dan kapasitas rotasim percobaan yang ada menunjukkan bahwa penyesuaian pada sudut 60 adalah suatu sudut standart yang efisien terhadap bangunan industri.
• Rasio ekspansi (α)
dapat hampir dua kali lipat, tetapi tinggi seluruhnya dari profil T adalah suatu faktor batas dalam pelasanaan, tinggi dari potongan ‘d’ adalah setengah bagian dari tinggi hs , maka:
ℎ𝑇𝑇 =ℎ𝑠𝑠
Jika panjang pengelasan terlalu pendek, kemudian las pada bagian badan yang disambung akan mengalami kegagalan geser horizontal, dan apabila terlalu panjang akan mengalami kegagalan dalam lentur vierendeel, jadi keseimbangan yang beralasan antara dua moda kegagalan ini yaitu c = hs / 4.
Balok harus memiliki kekuatan yang cukup untuk memikul momen lentur dan gaya geser yang ditimbulkan oleh beban-beban yang bekerja. Kinerja dari balok bergantung kepada geometri, dimensi fisik, dan bentuk dari penampangnya. Hingga saat ini, masih belum tersedia metode desain yang dapat diterima secara luas karena kerumitan dari perilaku balok castella serta bentuk kerusakan yang menyertainya. Kekuatan dari balok dengan berbagai jenis bukaan pada pelat badan ditentukan berdasarkan interaksi antara lentur dan geser pada bukaannya. Terdapat beberapa jenis bentuk kerusakan yang perlu diperhitungkan di dalam desain balok dengan bukaan yang meliputi mekanisme
Vierendeel, mekanisme lentur, tekuk torsi lateral, patah pada sambungan las dan tekuk pada badan yang disambung (web post). Did alam perencanaan balok castella, beberapa kriteria berikut perlu diperhitungkan:
1. Kapasitas lentur balok
Momen maksimum akibat beban luar MU tidak boleh melebihi kapasitas plastis Mp
U
dimana ALT adalah luas dari penampang T bawah, FY adalah tegangan leleh baja dan
HU adalah jarak antara pusat berat penampang T atas dan bawah.
2. Kapasitas geser balok
Di dalam perencanaan balok castella, terdapat dua bentuk kerusakan geser yang perlu diperiksa. Yang pertama adalah kapasitas geser vertikal yang akan dipikul oleh penampang T atas dan bawah. Jumlah dari kapasitas geser dari penampang T atas dan bawah perlu diperiksa dengan persamaan (2).
WUL
Yang kedua adalah kapasitas geser horisontal yang timbul pada web post karena adanya perubahan gaya aksial di dalam penampang T seperti ditunjukkan pada
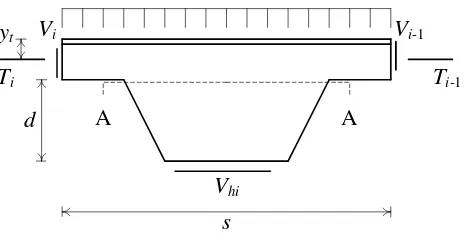
Gambar 5. Web post dengan panjang las yang terlalu pendek dapat mempercepat terjadinya kerusakan pada saat gaya geser horisontal melebihi kekuatan leleh. Kapasitas geser horisontal perlu diperiksa dengan persamaan(3).
Vhi
Gambar 5Gaya geser horisontal di dalam webpost pada balok castella
Dengan mengasumsikan gaya geser vertikal Vi dan Vi+1 adalah sama dan garis kerja gaya aksial Ti dan Ti+1 berada pada titik pusat penampang T, gaya geser horisontal dapat ditentukan dengan menggunakan persamaan keseimbangan berdasarkan pada diagram free-body yang ditunjukkan pada Gambar 5.
(
S t)
dimana HS adalah tinggi total balok castella seperti ditunjukkan pada Gambar
1.2(b).
3. Kekuatan lentur dan tekuk dari web post
Dengan mengasumsikan pelat sayap tertekan dari balok castella terkekang secara lateral oleh pelat lantai, kekuatan tekuk torsi lateral balok castella dapat diabaikan dalam perencanaan. Kapastis lentur dan tekuk dari webpost pada balok castella dapat dihitung dengan menggunakan persamaan (5).
2
potongan dari bukaan, tw adalah tebal pelat badan.
4. Mekanisme Vierendeel
Bentuk kerusakan ini diakibatkan oleh gaya internal lokal di sekitar satu bukaan. Kekuatan balok terhadap kerusakan melalui mekanisme Vierendeel ini dapat dihitung dengan menggunakan metode desain untuk penampang T. Kapasitas momen plastis dari penampang T di atas dan di bawah bukaan akan dihitung secara terpisah. Interaksi antara momen tahanan dan gaya geser lokal serta gaya aksial pada penampang T perlu diperhitungkan. Total kapasitas tahanan terhadap lentur
VierendeelMvrd, adalah jumlah dari kapasitas tahanan Vierendeel dari penampang T
atas dan bawah harus memenuhi ketentuan pada persamaan(9).
eff sd
vrd V l
M > (9)
dimana Vsd adalah gaya geser yang yang perlu disalurkan melalui bukaan, dan leff