BAB II
TINJAUAN PUSTAKA
Dalam bab ini akan dikemukakan teori-teori yang mendukung pembahasan penyelesaian persamaan diferensial linier tak homogen dengan menggunakan metode fungsi green antara lain: persamaan diferensial, orde dan derajat suatu persamaan diferensial, persamaan diferensial linear, persamaan diferensial linear homogen dengan koefisien konstan, persamaan diferensial linier orde-n tak homogen dengan koefisien konstan,determinan wronski, selesaian khusus persamaan tak homogen dengan metode variasi parameter, dan sistem fisis persamaan osilasi harmonik teredam
2.1 Persamaan Diferensial
Persamaan diferensial adalah persamaan yang memuat turunan dari satu (atau beberapa) fungsi yang tidak diketahui. Ada dua macam persamaan diferensial, yaitu:
a. Persamaan diferensial biasa yaitu persamaan dimana fungsi yang belum diketahui hanya memuat satu variabel bebas saja.
Contoh 1. 𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑 =𝑑𝑑+ 6, (dimana hanya mengandung satu variabel bebas yaitu 𝑑𝑑)
2. 𝑑𝑑2𝑑𝑑 𝑑𝑑𝑑𝑑2+ 3
𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑 + 2𝑑𝑑 = 0
3. 𝑑𝑑𝑑𝑑′+𝑑𝑑= 3
4. 𝑑𝑑′′′+ 2(𝑑𝑑′′)2+𝑑𝑑′=𝑐𝑐𝑐𝑐𝑐𝑐𝑑𝑑
b. Persamaan diferensial parsial yaitu persamaan diferensial dimana fungsi yang belum diketahui memuat dua atau lebih variabel bebas. Contoh:
1. 𝜕𝜕𝜕𝜕
2. .𝜕𝜕
2.2 Orde dan Derajat Suatu Persamaan Diferensial
Orde persamaan diferensial adalah tingkat tertinggi turunan yang timbul. Sedangkan derajat persamaan diferensial dapat ditulis sebagai polynomial dalam turunan, adalah derajat turunan tingkat tertinggi yang terjadi.
Contoh: 1. 𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑 =𝑑𝑑+ 6 (merupakan persamaan diferensial biasa orde 1 derajat 1). 2. 𝑑𝑑2𝑑𝑑
𝑑𝑑𝑑𝑑2+ 3 𝑑𝑑𝑑𝑑
𝑑𝑑𝑑𝑑 + 2𝑑𝑑= 0 (merupakan persamaan diferensial biasa orde 2 derajat 1). 3. 𝑑𝑑𝑑𝑑′+𝑑𝑑= 3 (merupakan persamaan diferensial biasa orde 1 derajat 1).
𝜕𝜕𝑑𝑑 (merupakan persamaan diferensial parsial orde 1 derajat 1). 7. 𝜕𝜕𝜕𝜕2
𝜕𝜕𝑑𝑑2+ 𝜕𝜕𝜕𝜕2 𝜕𝜕𝑑𝑑2 =𝑑𝑑
2+𝑑𝑑 (merupakan persamaan diferensial parsial orde 2 derajat 1).
2.3 Persamaan Diferensial Linier
Sebuah persamaan diferensial termasuk persamaan diferensial linier jika memenuhi dua hal berikut:
1. Variabel-variabel terikat dan turunannya tertinggi berpangkat 1
2. Tidak mengandung bentuk perkalian antara sebuah variabel terikat dengan variabel terikat lainnya, atau turunan yang satu dengan turunan yang lainnya, atau variabel terikat dengan sebuah turunan.
Jadi istilah linier berkaitan dengan kenyataan bahwa tiap suku dalam persamaan diferensial itu, peubah-peubah y, y',…, y(n) berderajat 1 atau nol.
Contoh:
1. 𝑑𝑑𝑑𝑑′+𝑑𝑑= 3
2. 𝑑𝑑′′′ + 2�𝑑𝑑′ ′�2+𝑑𝑑′ = 𝑑𝑑
jadi bentuk umum persamaan diferensial linier orde- n adalah
keterangan:
Jika 𝑓𝑓(𝑑𝑑) = 0, maka persamaan (2.3.1) disebut persamaan diferensial linier homogeny orde−𝑛𝑛
Jika 𝑓𝑓(𝑑𝑑) ≠ 0, maka persamaan (2.3.1) disebut persamaan diferensial linier non homogen orde−𝑛𝑛. jika semua koefisien 𝑎𝑎0(𝑑𝑑),𝑎𝑎1(𝑑𝑑), … ,𝑎𝑎𝑛𝑛(𝑑𝑑) adalah tetap, maka persamaan (2.3.1) disebut persamaan diferensial linier dengan koefisien konstan. jika semua koefisien
𝑎𝑎0(𝑑𝑑),𝑎𝑎1(𝑑𝑑), … ,𝑎𝑎𝑛𝑛(𝑑𝑑) adalah berupa fungsi, maka persamaan (2.3.1) disebut persamaan
diferensial linier dengan koefisien variabel (peubah).
2.4 Persamaan Diferensial Linear Homogen dengan Koefisien Konstan
Bentuk umum persamaan diferensial linear homogen dengan koefisien konstan:
𝑎𝑎0𝑑𝑑𝑛𝑛 +𝑎𝑎1𝑑𝑑(𝑛𝑛−1)+⋯+𝑎𝑎𝑛𝑛−1𝑑𝑑′ +𝑎𝑎𝑛𝑛𝑑𝑑 = 0 (2.4.1) dimana 𝑎𝑎0,𝑎𝑎1,…,𝑎𝑎𝑛𝑛 adalah konstanta.
Untuk menentukan selesaiannya yaitu dengan mensubstitusi y = etx, kemudian menentukan bilangan tetap t sehingga etx sehingga persamaan (2.4.1) karena y = etx , y’ = t etx , y”=t2 etx
dan seterusnya hingga yn =tn etx. Bila disubstitusikan ke persamaan (2.4.1) akan didapatkan suatu persamaan dalam t, yaitu:
𝑒𝑒𝑡𝑡𝑑𝑑(𝑎𝑎0𝑡𝑡𝑛𝑛 +𝑎𝑎1𝑡𝑡𝑛𝑛−1+𝑎𝑎2𝑡𝑡𝑛𝑛−2 +⋯+𝑎𝑎𝑛𝑛) = 0 (2.4.2) karena etx≠0, maka
(𝑎𝑎0𝑡𝑡𝑛𝑛 +𝑎𝑎1𝑡𝑡𝑛𝑛−1+𝑎𝑎2𝑡𝑡𝑛𝑛−2+⋯+𝑎𝑎𝑛𝑛) = 0 (2.4.3)
Persamaan (2.4.3) tersebut disebut persamaan karakteristik dari persamaan diferensial (2.4.1) dan akar-akarnya disebut akar-akar karakteristik. Ada tiga kemungkinan selesaian yang bebas linier dari persamaan (2.4.1), yaitu:
1. Bila akar-akarnya real dan berlainan, maka selesaian bebas liniernya yaitu: 𝑒𝑒𝑡𝑡1𝑑𝑑,𝑒𝑒𝑡𝑡2𝑑𝑑, … ,𝑒𝑒𝑡𝑡𝑛𝑛𝑑𝑑
2. Bila akar-akarnya real dan sama, maka selesaian bebas liniernya yaitu:
𝑒𝑒𝑡𝑡𝑑𝑑,𝑑𝑑𝑒𝑒𝑡𝑡𝑑𝑑, … ,𝑑𝑑𝑛𝑛−1𝑒𝑒𝑡𝑡𝑑𝑑
3. Bila akar-akarnya kompleks, maka selesaian bebas liniernya yaitu:𝑒𝑒(𝑎𝑎−𝑏𝑏𝑏𝑏)𝑑𝑑 atau
𝑒𝑒𝑎𝑎𝑑𝑑(cos𝑏𝑏𝑑𝑑+ sin𝑏𝑏𝑑𝑑)
Bentuk umum persamaan diferensial tak homogeny orde-n adalah sebagai berikut : 𝐴𝐴𝑛𝑛𝑑𝑑𝑛𝑛 + 𝐴𝐴𝑛𝑛−1𝑑𝑑𝑛𝑛−1+ 𝐴𝐴𝑛𝑛−2𝑑𝑑𝑛𝑛−2 +⋯+ 𝐴𝐴1𝑑𝑑′+ 𝐴𝐴0𝑑𝑑 =𝑟𝑟(𝑑𝑑) (2.5.1)
Solusi umum 𝑑𝑑(𝑑𝑑) akan didapatkan bila solusi umum 𝑑𝑑ℎ𝑑𝑑 dari Persamaan Diferensial Homogen diketahui, dimana bentuk umum persamaan diferensial homogenya orde-n adalah sebagai berikut :
𝐴𝐴𝑛𝑛𝑑𝑑𝑛𝑛 + 𝐴𝐴𝑛𝑛−1𝑑𝑑𝑛𝑛−1+ 𝐴𝐴𝑛𝑛−2𝑑𝑑𝑛𝑛−2 +⋯+ 𝐴𝐴1𝑑𝑑′+ 𝐴𝐴0𝑑𝑑= 0 (2.5.2)
Kemudian 𝑑𝑑(𝑑𝑑) dibentuk dengan penambahan 𝑑𝑑ℎ𝑑𝑑 sembarang solusi 𝑑𝑑 termasuk konstanta tak tetapnya. Sehingga,
𝑑𝑑(𝑑𝑑) = 𝑑𝑑ℎ(𝑑𝑑) +𝑑𝑑𝑝𝑝(𝑑𝑑) (2.5.3)
Dalam hal ini kita membahas penyelesaian untuk mendapatkan persamaan partikulirnya dengan melalui metode fungsi green dan dengan melalui metode koefisien tak tentu.
2.6 Determinan Wronski
tiap fungsi yang muncul dalam determinan ini dihitung pada x.
Contoh
Diketahui𝑓𝑓1(𝑑𝑑) =𝑑𝑑2 dan 𝑓𝑓
Penyelesaian: Dari defenisi di atas dan dari fungsi-fungsi yang telah diketahui, maka dapat dihitung:
𝑊𝑊(𝑑𝑑2, cos𝑑𝑑;𝑑𝑑) =�𝑑𝑑2 cos𝑑𝑑
2𝑑𝑑 −sin𝑑𝑑�= −𝑑𝑑
2sin𝑑𝑑 −2𝑑𝑑cos𝑑𝑑
Misalkan bahwa 𝑑𝑑1,𝑑𝑑2, … ,𝑑𝑑𝑛𝑛 merupakan n buah penyelesaian persamaan diferensial (2.4.1). Misalkan juga bahwa fungsi-fungsi tersebut bebas linier pada selang defenisi persamaan diferensial ini. Dikatakan bahwa fungsi-fungsi itu membentuk himpunan fundamental (atau sistem fundamental) penyelesaian persamaan diferensial tersebut. Sebagai contoh fungsi cos𝑑𝑑 dan fungsi sin𝑑𝑑 merupakan suatu himpunan fundamental penyelesaian persamaan diferensial 𝑑𝑑′′ +𝑑𝑑 = 0 . Juga fungsi 𝑒𝑒𝑑𝑑dan 𝑒𝑒−𝑑𝑑 membentuk suatu himpunan fundamental penyelesaian persamaan diferensial 𝑑𝑑′′ − 𝑑𝑑= 0.
2.7 Selesaian Khusus Persamaan Takhomogen: Penyelesaian Dengan Metode Variasi
Parameter
Metode variasi parameter adalah metode yang dapat digunakan untuk menentukan selesaian khusus PD linier takhomogen dengan koefisien variabel, sehingga lebih umum daripada metode koefisien tak tentu.
Perhatikan PD linier orde 2 yang mempunyai bentuk
𝑑𝑑′′ +𝑝𝑝(𝑑𝑑)𝑑𝑑′ +𝑞𝑞(𝑑𝑑)𝑑𝑑=𝑟𝑟(𝑑𝑑) (2.7.1)
dengan p, q, dan r fungsi-fungsi kontinu pada suatu interval buka I. Kita akan menentukan selesaian khusus dari (2.7.1) dengan metode variasi parameter seperti berikut. Kita mengetahui bahwa PD homogen yang bersesuaian, yaitu
𝑑𝑑′′ +𝑝𝑝(𝑑𝑑)𝑑𝑑′ +𝑞𝑞(𝑑𝑑)𝑑𝑑= 0 (2.7.2)
mempunyai suatu selesaian umum 𝑑𝑑ℎ(𝑑𝑑) pada I yang berbentuk
𝑑𝑑ℎ(𝑑𝑑) =𝑐𝑐1𝑑𝑑1(𝑑𝑑) +𝑐𝑐2𝑑𝑑2(𝑑𝑑) (2.7.3)
Metode variasi parameter terdiri dari penggantian 𝑐𝑐1dan 𝑐𝑐2dengan fungsi 𝑢𝑢(𝑑𝑑) dan 𝑣𝑣(𝑑𝑑)
yang akan ditentukan sedemikian hingga fungsi penggantinya, yaitu
merupakan selesaian khusus dari (2.7.1) pada I. dengan menurunkan (2.7.3) diperoleh
𝑑𝑑𝑝𝑝′ = 𝑢𝑢′𝑑𝑑1+𝑢𝑢𝑑𝑑1′ +𝑣𝑣′𝑑𝑑2+𝑣𝑣𝑑𝑑2′ (2.7.5)
Persamaan (2.7.3) memuat dua fungsi 𝑢𝑢 dan 𝑣𝑣, tetapi syarat bahwa 𝑑𝑑𝑝𝑝 memenuhi (2.7.1) mengakibatkan bahwa hanya ada satu syarat pada 𝑢𝑢 dan 𝑣𝑣. . Karena itu kita bisa menerapkan kondisi (syarat) sebarang yang ke dua. Perhitungan berikut akan menunjukkan bahwa kita dapat menentukan 𝑢𝑢 dan 𝑣𝑣 sedemikian hingga 𝑑𝑑𝑝𝑝 memenuhi (2.7.1) dan 𝑢𝑢 dan 𝑣𝑣 memenuhi, sebagai syarat ke dua, hubungan:
𝑢𝑢′𝑑𝑑1+𝑣𝑣′𝑑𝑑2 = 0 (2.7.6) Ini mereduksi ekspresi untuk 𝑑𝑑𝑝𝑝’ ke bentuk
𝑑𝑑𝑝𝑝’ = 𝑢𝑢𝑑𝑑1’ +𝑣𝑣𝑑𝑑2’
. (2.7.7)
Dengan menurunkan fungsi ini diperoleh
𝑑𝑑𝑝𝑝” = 𝑢𝑢’𝑑𝑑1’ +𝑢𝑢𝑑𝑑1” +𝑣𝑣’𝑑𝑑2’ +𝑣𝑣𝑑𝑑2” (2.7.8)
Dengan mensubstitusikan (2.7.3), (2.7.5) dan (2.7.6) ke dalam (2.7.1) dan mengumpulkan suku-suku yang memuat 𝑢𝑢 dan 𝑣𝑣 akan diperoleh
𝑢𝑢(𝑑𝑑1” +𝑝𝑝𝑑𝑑1’ +𝑞𝑞𝑑𝑑1) +𝑣𝑣(𝑑𝑑2” +𝑝𝑝𝑑𝑑2’ +𝑞𝑞𝑑𝑑2) +𝑢𝑢’𝑑𝑑1’ +𝑣𝑣’𝑑𝑑2’ = 𝑟𝑟 (2.7.9)
Karena 𝑑𝑑1dan 𝑑𝑑2selesaian dari PD homogen (2.7.6), maka persamaan di atas mereduksi ke bentuk
(i) 𝑢𝑢’𝑑𝑑1’ +𝑣𝑣’𝑑𝑑2’ = 𝑟𝑟 (ii)𝑢𝑢’𝑑𝑑1+𝑣𝑣’𝑑𝑑2 = 0
Persamaan (i) dan (ii) merupakan sistem dua persamaan aljabar linier dari fungsi-fungsi
𝑢𝑢’ dan 𝑣𝑣’ yang tidak diketahui. Selesaian diperoleh dengan aturan Cramer:
𝑢𝑢′ = −𝑑𝑑2𝑟𝑟
𝑊𝑊
𝑣𝑣′ =𝑑𝑑1𝑟𝑟
𝑊𝑊 (2.7.10) Dengan
𝑊𝑊 =𝑑𝑑1𝑑𝑑2′+𝑑𝑑1′𝑑𝑑2 (2.7.11)
𝑢𝑢 =− ∫𝑑𝑑𝑊𝑊2𝑟𝑟 𝑑𝑑𝑑𝑑
𝑣𝑣= ∫𝑑𝑑1𝑟𝑟
𝑊𝑊 𝑑𝑑𝑑𝑑 (2.7.12)
Integral ini ada karena 𝑟𝑟(𝑑𝑑) kontinu. Substitusikan ekspresi untuk 𝑢𝑢 dan 𝑣𝑣 ini ke dalam (2.7.3), untuk memperoleh selesaian dari (2.7.1).
𝑑𝑑𝑝𝑝(𝑑𝑑) =−𝑑𝑑1∫𝑑𝑑2𝑟𝑟
𝑊𝑊 𝑑𝑑𝑑𝑑+𝑑𝑑2∫𝑑𝑑𝑊𝑊1𝑟𝑟 𝑑𝑑𝑑𝑑 (2.7.13)
2.8 Konsep Fungsi Green
Dari suatu sistem persamaan diferensial linear tak homogen orde-n:
𝑎𝑎0(𝑑𝑑)𝑑𝑑(𝑛𝑛)+𝑎𝑎1(𝑑𝑑)𝑑𝑑(𝑛𝑛−1)+⋯+𝑎𝑎𝑛𝑛−1(𝑑𝑑)𝑑𝑑′ +𝑎𝑎𝑛𝑛(𝑑𝑑)𝑑𝑑=𝑓𝑓(𝑑𝑑) (2.8)
dengan fungsi 𝑓𝑓(𝑑𝑑) merupakan fungsi yang kontinyu. Fungsi 𝐺𝐺(𝑑𝑑,𝑡𝑡) dikatakan sebagai fungsi green untuk masalah nilai awal persamaan diferensial di atas jika memenuhi kondisi berikut ini:
a) 𝐺𝐺(𝑑𝑑,𝑡𝑡) terdefenisi pada daerah R=I x I dari semua titik (𝑑𝑑,𝑡𝑡) dimana 𝑑𝑑dan 𝑡𝑡 terletak dalam selang I.
b) 𝐺𝐺(𝑑𝑑,𝑡𝑡),𝜕𝜕𝐺𝐺
𝜕𝜕𝑑𝑑 , 𝜕𝜕2𝐺𝐺
𝜕𝜕𝑑𝑑2 , … ,
𝜕𝜕𝑛𝑛𝐺𝐺
𝜕𝜕𝑑𝑑𝑛𝑛 merupakan fungsi kontinu pada R=I x I c) Untuk setiap 𝑑𝑑0 dalam selang I , fungsi 𝑑𝑑𝑝𝑝(𝑑𝑑) =∫ 𝐺𝐺𝑑𝑑𝑑𝑑 (𝑑𝑑,𝑡𝑡)𝑓𝑓(𝑡𝑡)𝑑𝑑𝑡𝑡
0 adalah solusi
persamaan diferensial di atas yang memenuhi kondisi awal 𝑑𝑑𝑝𝑝(𝑑𝑑0) =𝑑𝑑𝑝𝑝′(𝑑𝑑0) =
𝑑𝑑𝑝𝑝′′(𝑑𝑑0) =⋯= 𝑑𝑑𝑝𝑝(𝑛𝑛−1)(𝑑𝑑0) = 0
2.9 Metode koefisien tak tentu
Ide dasar dari metode koefisien tak tentu adalah menduga dengan cerdas solusi 𝑑𝑑𝑝𝑝 berdasarkan bentuk fungsi 𝑟𝑟(𝑑𝑑) di ruas kanan.
Bentuk persamaan umum:
Fungsi 𝑟𝑟(𝑑𝑑) yang merupakan bentuk solusi pertikular 𝑑𝑑𝑝𝑝(𝑑𝑑) diperoleh dengan cara menebak, seperti misalnya: fungsi cos, fungsi sin, fungsi exponensial atau jumlah dari beberpa fungsi
𝑟𝑟(𝑑𝑑) berisikan koefisien tak tentu
Turunkan 𝑑𝑑𝑝𝑝 sesuai persamaan umum di atas
Subtitusikan 𝑑𝑑𝑝𝑝 dan seluruh turunannya ke dalam persamaan
Bentuk 𝑟𝑟(𝑑𝑑) Pilihan untuk 𝑑𝑑𝑝𝑝
𝑒𝑒𝑎𝑎𝑑𝑑 𝐴𝐴𝑒𝑒𝑎𝑎𝑑𝑑
𝑘𝑘𝑑𝑑𝑛𝑛 (𝑛𝑛 = 0,1, … ) 𝑘𝑘
𝑛𝑛𝑑𝑑𝑛𝑛 +𝑘𝑘𝑛𝑛−1𝑑𝑑𝑛𝑛−1+⋯+𝑘𝑘1𝑑𝑑+𝑘𝑘0
𝑑𝑑𝑒𝑒𝑎𝑎𝑑𝑑 𝐴𝐴𝑒𝑒𝑎𝑎𝑑𝑑 + 𝐵𝐵𝑑𝑑𝑒𝑒𝑎𝑎𝑑𝑑
sin𝑎𝑎𝑑𝑑 𝐴𝐴sin𝑎𝑎𝑑𝑑+𝐵𝐵cos𝑎𝑎𝑑𝑑
cos𝑎𝑎𝑑𝑑 𝐴𝐴sin𝑎𝑎𝑑𝑑+𝐵𝐵cos𝑎𝑎𝑑𝑑
Tabel 2.1 Metode Koefisian Tak Tentu
Misal 𝑓𝑓(𝑑𝑑) merupakan fungsi polinom, eksponen, sinus atau cosines. Maka solusi 𝑑𝑑𝑝𝑝 dimisalkan sebagai jumlah dari 𝑓𝑓(𝑑𝑑) dan semua turunannya. Selanjutnya 𝑑𝑑𝑝𝑝 𝑑𝑑𝑝𝑝′ dan 𝑑𝑑𝑝𝑝′′ disubstitusikan ke persamaan awal untuk menghitung nilai dari koefisiennya.
2.10 Sistem Fisis Persamaan Osilasi Harmonik Teredam
gesekan sebanding dengan kecepatan, tetapi arahnya berlawanan. Contoh dari osilasi teredam misalnya adalah pada shock absorber mobil.
Shock absorber merupakan komponen penting suatu kendaraan yaitu dalam sistem suspensi, yang berguna untuk meredam gaya osilasi dari pegas. Shock absorber berfungsi untuk memperlambat dan mengurangi besarnya getaran gerakan dengan mengubah energi kinetik dari gerakan suspensi menjadi energi panas yang dapat dihamburkan melalui cairan hidrolik.
Peredam kejut (shockabsorber) pada mobil memiliki komponen pada bagian atasnya terhubung dengan piston dan dipasangkan dengan rangka kendaraan. Bagian bawahnya, terpasang dengan silinder bagian bawah yang dipasangkan dengan as roda. Fluida kental menyebabkan gaya redaman yang bergantung pada kecepatan relatif dari kedua ujung unit tersebut. Hal ini membantu untuk mengendalikan guncangan pada roda.
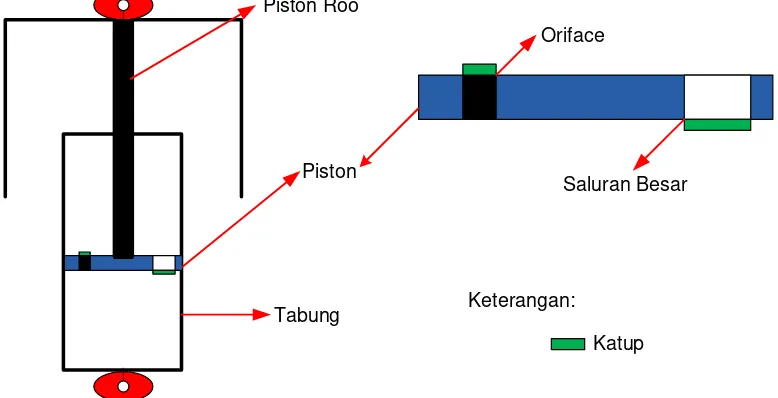
Konstruksi shock absorber itu terdiri atas piston, piston rod dan tabung. Piston adalah komponen dalam tabung shock absorber yang bergerak naik turun di saat shock absorber bekerja. Sedangkan tabung adalah tempat dari minyak shock absorber dan sekaligus ruang untuk piston bergerak naik turun. Dan yang terakhir adalah piston rod adalah batang yang menghubungkan piston dengan tabung bagian atas (tabung luar) dari shock absorber. Untuk lebih jelasnya dapat dilihat pada gambar berikut:
Piston Roo
Piston
Tabung
Oriface
Saluran Besar
Keterangan:
Katup
Shock absorber bekerja dalam dua siklus yakni siklus kompresi dan siklus ekstensi.
Siklus kompresi (penekanan)
Saat shock absorber ditekan karena gaya osilasi dari pegas suspensi, maka gerakan yang terjadi adalah shock absorber mengalami pemendekan ukuran. Siklus kompresi terjadi ketika piston bergerak ke bawah, menekan fluida hidrolik di dalam ruang bawah piston. Dan minyak shock absorber yang berada dibawah piston akan naik keruang atas piston melalui lubang yang ada pada piston. Sementara lubang kecil (orifice) pada piston tertutup karena katup menutup saluran orifice tersebut. Penutupan katub ini disebabkan karena peletakan katup yang berupa membran (plat tipis) dipasangkan dibawah piston, sehingga ketika minyak shock absorber berusaha naik ke atas maka katup membran ini akan terdorong oleh shock absorber dan akilbatnya menutup saluran orifice. Jadi minyak shock absorber akan menuju ke atas melalui lubang yang besar pada piston, sementara minyak tidak bisa keluar melalui saluran oriface pada piston. Pada saat ini shock absorber tidak melakukan peredaman terhadap gaya osilasi dari pegas suspensi, karena minyak dapat naik ke ruang di atas piston dengan sangat mudah.
Siklus ekstensi (memanjang)
Tipikal mobil atau truk ringan akan memiliki lebih banyak perlawanan selama siklus ekstensi daripada siklus kompresi. Semua peredam kejut modern adalah kecepatan-sensitif – suspensi semakin cepat bergerak, semakin banyak perlawanan yang shock breker sediakan. Hal ini memungkinkan guncangan untuk menyesuaikan diri dengan kondisi jalan dan untuk mengontrol semua gerakan yang tidak diinginkan yang dapat terjadi dalam kendaraan yang bergerak. Secara sederhana shock absorber merupakan pengaplikasian dari gerak osilasi harmonik yang teredam.
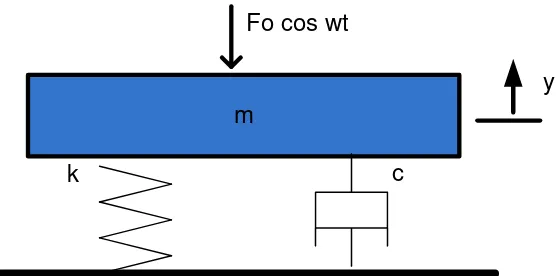
m
k c
y Fo cos wt
Gambar 2.2 Sistem fisis pada shock absorber
Bila peredaman diperhitungkan, maka gaya peredam juga berlaku pada massa. Bila bergerak dalam fluida benda akan mendapatkan redaman karena kekentalan fluida. Gaya akibat kekentalan ini sebanding dengan kecepatan benda. Konstanta akibat kekentalan (viskositas) adalah c dengan satuan N s/m (SI)
Persamaan osilasi teredam diberikan oleh hokum gerak kedua,𝐹𝐹 =𝑚𝑚𝑎𝑎 , dengan F merupakan jumlah dari gaya pemulih – 𝑘𝑘𝑑𝑑 dan gaya redaman –𝑐𝑐𝑑𝑑𝑑𝑑/𝑑𝑑𝑡𝑡 ; dalam hal ini c
adalah konstanta positif. Kita peroleh bahwa
𝛴𝛴𝐹𝐹= 𝑚𝑚𝑎𝑎 (2.10.1)
atau
−𝑘𝑘𝑑𝑑 − 𝑐𝑐𝑑𝑑𝑑𝑑𝑑𝑑𝑡𝑡 =𝑚𝑚𝑑𝑑2𝑑𝑑
𝑑𝑑𝑡𝑡2 (2.10.2)
atau
𝑚𝑚𝑑𝑑
2𝑑𝑑
𝑑𝑑𝑡𝑡2 +𝑐𝑐
𝑑𝑑𝑑𝑑
Dalam osilasi teredam sebenarnya masih terdapat gaya lain yang bekerja berupa gaya paksaan. Dalam hal ini, dimisalkan gaya paksaan yang diberikan terhadap sistem yang telah disebutkan adalah𝐹𝐹0cos𝜔𝜔𝑡𝑡. Di sini 𝐹𝐹0 adalah harga dari gaya eksternal dan 𝜔𝜔 adalah frekuensi sudutnya. Untuk jelasnya, dapat kita bayangkan bahwa gaya eksternal tersebut diberikan langsung pada massa yang digantungkan pada pegas. Maka kita peroleh persamaan:
𝛴𝛴𝐹𝐹= 𝑚𝑚𝑎𝑎
diperoleh
−𝑘𝑘𝑑𝑑 − 𝑐𝑐𝑑𝑑𝑑𝑑
𝑑𝑑𝑡𝑡 +𝐹𝐹0cos𝜔𝜔𝑡𝑡 =𝑚𝑚 𝑑𝑑2𝑑𝑑
𝑑𝑑𝑡𝑡2 (2.10.4)
atau
𝑚𝑚𝑑𝑑2𝑑𝑑 𝑑𝑑𝑡𝑡2 +𝑐𝑐
𝑑𝑑𝑑𝑑