APLIKASI FUNGSI GREEN PADA DINAMIKA SISTEM FISIS-MASSA PEGAS DENGAN SHOCK ABSORBER SKRIPSI MANGARA TUA SITANGGANG

(1)

APLIKASI FUNGSI GREEN PADA DINAMIKA SISTEM FISIS-MASSA PEGAS DENGAN SHOCK ABSORBER

SKRIPSI

MANGARA TUA SITANGGANG 080801035

DEPARTEMEN FISIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN

2013

(2)

APLIKASI FUNGSI GREEN PADA DINAMIKA SISTEM FISIS-MASSA PEGAS DENGAN SHOCK ABSORBER

SKRIPSI

Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains

MANGARA TUA SITANGGANG 080801035

DEPARTEMEN FISIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA

MEDAN

2013

(3)

PERSETUJUAN

Judul : APLIKASI FUNGSI GREEN PADA DINAMIKA

SISTEM FISIS-MASSA PEGAS DENGAN SHOCK ABSORBER

Kategori : SKRIPSI

Nama : MANGARA TUA SITANGGANG

Nomor Induk Mahasiswa : 080801035

Program Studi : SARJANA (SI) FISIKA

Departemen : FISIKA

Fakultas : MATEMATIKA DAN ILMU PENGETAHUAN ALAM

(FMIPA) UNIVERSITAS SUMATERA UTARA

Diluluskan di

Medan, Juli 2013

Pembimbing I Pembimbing II

Drs. Tenang Ginting, MS Tua Raja Simbolon S.Si, M.Si NIP. 194806101976031003 NIP. 197211152000121001

Departemen Fisika FMIPA USU Ketua

Dr. Marhaposan Situmorang

NIP. 195510301980031003

(4)

PERNYATAAN

APLIKSI FUNGSI GREEN PADA DINAMIKA SISTEM FISIS-MASSA PEGAS DENGAN SHOCK ABSORBER

SKRIPSI

Saya mengakui bahwa skripsi ini adalah hasil kerja saya sendiri, kecuali beberapa kutipan dari ringkasan yang masing-masing disebutkan sumbernya.

Medan, Juli 2013

Mangara Tua Sitanggang

NIM 080801035

(5)

PENGHARGAAN

Puji, syukur serta hormat penulis haturkan kepada Tuhan Yesus Kristus yang atas berkat dan rahmatNya penulis dapat menyelesaikan kajian tulisan ini dalam waktu yang telah ditetapkan.

Sesungguhnya hanya Karena berkat dan rahmat yang telah dicurahkanNyalah sehingga tulisan dengan judul APLIKSI FUNGSI GREEN PADA DINAMIKA SISTEM FISIS- MASSA PEGAS DENGAN SHOCK ABSORBER dapat diselesaikan dengan baik.

Penulis juga menyadari akan bimbingan, dukungan, motivasi, saran serta doa dari berbagai pihak yang membantu penulis dalam menyelesaikan tulisan ini. Ucapan terimakasih yang sebesar-besarnya penulis sampaikan kepada:

1. Yth. Bapak Dr. Sutarman selaku dekan Fakultas Matematika dan Ilmu Pengetahuan Alam beserta seluruh jajaran staff dan pegawai Fakultas Matematika dan Ilmu Pengetahuan Alam

2. Yth. Bapak Dr. Marhaposan Situmorang selaku ketua Departemen Fisika beserta seluruh dosen, staff dan pegawai departemen Fisika FMIPA USU

3. Bapak Drs. Tenang Ginting, MS dan Bapak Tua Raja Simbolon S.Si, M.Si selaku dosen pembimbing penulis dalam menyelesaikan penulisan skripsi ini. Penulis sangat berterimakasih buat setiap bimbingan, masukan, saran serta waktu yang senantiasa diberikan kepada penulis sampai pada akhir penulisan skripsi ini.

4. Bapak Drs. Kurnia Sembiring, MS, Ibu Dra.Ratna Askiah S,M.Si, Ibu Dra.Manis Sembiring, MS selaku dosen penguji. Penulis mengucapkan terimakasih yang sebesar-besarnya atas saran-saran yang diberikan kepada penulis dalam penulisan skripsi ini.

5. Tidak terlupakan Orangtua yang sangat saya cintai yakni Bapak ( Alm. H.Sitanggang) dan mamak ( K. Br. Sipakkar),buat kakak tersayang ( Seselia Dormauli Sitanggang) dan adek tersayang (Parsaoran Paulinus Sitanggang). Penulis mengucapkan terimakasih buat setiap dukungan, doa, dan motivasi yang diberikan kepada penulis di setiap waktu, kiranya Tuhan semakin melimpahkan berkat dan sukacita bagi kita semua. Serta buat seluruh keluarga yang selalu mendukung penulis dalam menyelesaikan skripsi ini. Semoga Tuhan senantiasa melimpahklan berkatNya kepada kita semua.

6. Sahabat seperjuangan Fisika 2008 ( bro Roni Sinaga, appara Hiras Sitanggang, appara

Albert Daniel Saragih, Appara Rolas D Nainggolan, appara Aryon Simbolon, Lek

Donal Edison Sijabat, Lek Triandes Sinaga, Lek Asman Marpaung, Lek Zulkarnaen

Manalu, Lek, Ebenezer A Situmorang, Pal Indra Tarigan, Sina Bheng an Ginting, Lek

Sudiaman Mabun, Perdana O Manik, Lyri Martin Simorangkir, Metar Y Hutauruk,

Nya Daniati Malau, Borasida Sihombing, Nyta Efhelzen tampubolon, Melati Putri

Duha, Elda Desi Panjaitan, Elisabeth Situmorang, Yosephin Romania Sinabutar,

(6)

Ervina Novaria Tambunan dan tante Theresia Novita Pangaribuan) yang turut serta membantu penulis dalam menyelesaikan skripsi ini.

7. Abang-abang dan kakak-kakak senior Fisika yang tak dapat penulis sebutkan satu per satu. Penulis mengucapkan terimakasih banyak buat setiap kebersamaan dan cinta kasih yang abang/kakak berikan selama ini.

8. Kelompok MANA KUNCI (Bg Jona Benhart Hutajulu, Bg Anderson Ginting, Bg Erick Rumahorbo, Roni Sinaga, Istas Pratama Manalu, Andico Sihaloho, Natanael Saragih, Zainaludin Rambe dan Timbul Mulya David Panjaitan). Penulis mengucapkan terimakasih buat kebersamaan, motivasi dan doa yang diberikan kepada penulis.

9. Ito-ito yang sangat penulis sayangi ( Rieni Kalesta Sitanggang, Widya Susanti Sitanggang, Roindah Simbolon, Valentina Ginting, Silviana Simbolon, Sermauli Sitanggang dan Ancela Simbolon). Penulis mengucapkan terimakasih buat seluruh dukungan yang diberikan selama perkuliahan, motivasi dan kebersamaan dalam suka duka selama ini.

10. Adek-adek junior yang tersayang : stambuk 2009 ( Poltak Simarmata, Agus P Siahaan, Sabam Simbolon, Sony Togatorop, Endra Tambunan, Ferdi A, Monora Panca Bakara, Emi A Tarigan, Stevani A Sigiro, Helen M Manurung, Agus Ningsih, Sukria Novianti,dkk), stambuk 2010 ( Juan Roy Saragih, Roni Tambi, Faisal Sibuea, Ronald Naibaho, michu/Rumianto Manurung, Lamhot Sihaloho, Jantiber siburian, Gunawan B sitorus, Riady P Sitanggang, Jakson Sitanggang, Fransiskus Waruwu, Rika E, dkk), stambuk 2011( Dosni sipahutar, Simon Sihombing, Steven Sitorus, Intan, dkk), stambuk 2012 ( Marta M Nainggolan, dkk)

11. Teman-teman alumni SMA N 1 Berastagi , SMP N 2 Berastagi dan SDN Sindang Sari I Bandung yang senantiasa memberikan motivasi kepada penulis dalam penulisan skripsi ini.

12. Teman-teman kost KCC ( Robin Siregar, Haendri, Salman dan Ranto). Terimakasih buat doa-doa nya.

Penulis

(7)

ABSTRAK

Telah dilakukan perhitungan secara analitik mengenai sistem persamaan fisis pada massa pegas shock absorber dengan menggunakan metode fungsi green dan metode koefisien tak tentu. Dalam hal ini akan didapatkan solusi yang sama dari persamaan fisis massa pegas dengan shock absorber dengan menggunakan metode yang berbeda tersebut. Perbedaannya hanya terletak pada nilai konstanta yang dihasilkan dari penyelesaian tersebut. Telah dilakukan juga verifiksi terhadap hasil yang didapat dengan menggunakan perangkat lunak mathematica 8.

Kata kunci: fungsi green, koefisien tak tentu

(8)

ABSTRACT

Analytical calculated about shock absorber physical system form had been done by green function method and indeterminate coefficients method. The same solution of shock absorber physical system form had been obtained by use this different methods. The difference lies only in the constant value resulting from the settlement. Verification has been carried out also on the results obtained by using the software Mathematica 8.

Key words: green function, indeterminate coefficients

(9)

DAFTAR ISI

Halaman

Persetujuan ii

Pernyataan iii

Penghargaan iv

Abstrak vi

Abstract vii

Daftrar isi viii

Daftar gambar x

Daftar tabel xi

Daftar simbol xii

BAB I PENDAHULUAN

1.1 Latar Belakang 1

1.2 Rumusan Masalah 2

1.3 Tujuan Penelitian 3

1.4 Manfaat Penelitian 3

1.5 Batasan Masalah 3

1.6 Metode Penulisan 4

1.7 Sistematika Penulisan 5

BAB II TINJAUAN PUSTAKA

2.1 Persamaan Diferensial 6

2.2 Orde dan Derajat Suatu Persamaan Diferensial 7

2.3 Persamaan Diferensial linier 7

2.4 Persamaan Diferensial Linear Homogen dengan Koefisien Konstan 8 2.5 Persamaan Diferensial Linier Orde-n Tak Homogen Dengan

Koefisien Konstan 9

2.6 Determinan Wronski 10

2.7 Selesaian Khusus Persamaan Takhomogen: Penyelesaian Dengan

Metode Variasi Parameter 11

2.8 Metode Fungsi Green 13

2.9 Metode Koefisien Tak Tentu 13

2.10 Sistem Fisis Persamaan Osilasi Harmonik Teredam 14

BAB III METODOLOGI PENELITIAN

3.1 Rancangan Penelitian 20

3.2 Diagram Alir Penelitian 21

BAB IV HASIL DAN PEMBAHASAN

4.1 Penyelesaian Dengan Menggunakan Metode Fungsi Green 22 4.2 Penyelesaian Dengan Menggunakan Metode Koefisien Tak Tentu 25 4.3 Perbandingan Antara Metode Fungsi Green dengan Metode

Koefisien Tak Tentu 27

4.4 Verifikasi Dengan Menggunakan Program Mathematica 8 28 BAB V KESIMPULAN

5.1 Kesimpulan 29

5.2 Saran 30

DAFTAR PUSTAKA 31

(10)

DAFTAR GAMBAR

Halaman

Gambar 2.1 Detail struktur shock absorber 16

Gambar 2.2 Gambaran fisis pada shock absorber 18

(11)

DAFTAR TABEL

Halaman

Tabel 2.1 Tabel Metode Koefisian Tak Tentu 14

(12)

DAFTAR SIMBOL

𝜮𝜮𝜮𝜮 : Resultan gaya 𝒌𝒌 : konstanta pegas 𝒄𝒄 : konstanta redaman

𝜮𝜮

𝟎𝟎

: Gaya luar yang diberikan kepada sistem 𝒚𝒚 : simpangan

𝝎𝝎 : kecepatan sudut 𝒕𝒕 : waktu

𝑾𝑾 : wronskian

𝑮𝑮(𝒚𝒚, 𝒕𝒕) : fungsi green

(13)

BAB I

PENDAHULUAN

1.1 Latar Belakang

Di dalam berbagai permasalahan fisika, matematika memegang peranan yang sangat penting.

Banyak permasalahan fisika yang harus diselesaikan dengan menggunakan model matematika. Salah satu model matematika yang cukup penting adalah persamaan differensial.

Persamaan diferensial adalah persamaan yang memuat turunan satu (atau beberapa) fungsi yang tidak diketahui. Persamaan diferensial seringkali muncul dalam permasalahan fisika yang mencoba menggambarkan keadaan kehidupan nyata. Banyak hukum-hukum alam dan hipotesa-hipotesa yang dapat diterjemahkan ke dalam persamaan yang mengandung persamaan diferensial. Sebagai contoh, turunan-turunan dalam fisika muncul sebagai kecepatan dan percepatan, dalam geometri sebagai kemiringan. Keadaan inilah yang merupakan persoalan pada banyak kasus fisika, sehingga untuk memperoleh suatu persamaan diferensial yang melukiskan suatu persoalan dalam kehidupan nyata, biasanya diambil permisalan bahwa keadaan sebenarnya diatur oleh hukum-hukum yang sangat sederhana yang biasanya sering dibuat permisalan yang ideal.

Persamaan diferensial yang terbentuk dari permasalahan yang ada tersebut juga bermacam-macam. Ada dua macam persamaan diferensial yaitu persamaan diferensial biasa dan persamaan diferensial parsial. Berdasarkan bentuknya, terdapat persamaan diferensial homogen dan persamaan diferensial tak homogen. Di samping itu, berdasarkan orde (tingkat)-nya, terdapat persamaan diferensial orde satu, persamaan diferensial orde dua, persamaan diferensial orde tiga, sampai dengan persamaan diferensial orde-n (orde tinggi).

Sedangkan berdasarkan koefisiennya, terdapat persamaan diferensial dengan koefisien konstan dan persamaan diferensial dengan koefisien variabel (peubah). Serta berdasarkan kelinearannya, terdapat persamaan diferensial linear dan persamaan diferensial tidak linear.

Oleh karena banyaknya jenis persamaan diferensial, maka banyak pula cara mencari

penyelesaiannya. Sebagai contoh, persamaan diferensial biasa orde satu, selesaiannya dapat

dicari dengan pengintegralan. Sedangkan persamaan diferensial linear homogen, misalnya

(14)

persamaan diferensial linear homogen dengan koefisien konstan, dapat diubah menjadi masalah pencarian akar persamaan karakteristik untuk persamaan diferensial itu. Akan tetapi, masalahnya sekarang pada persamaan diferensial linear tak homogen, untuk mencari selesaian umumnya, selain harus mencari selesaian persamaan homogen pautannya, juga harus dicari selesaian khususnya. Oleh karena itu diperlukan suatu metode tertentu.

Dalam penulisan proposal ini, akan dikemukakan suatu metode untuk menyelesaikan persamaan diferensial linear tak homogen yaitu dengan mengkonstruksi fungsi green.

Kemudian akan kita selesaikan suatu permasalahan fisika yaitu pada sistem fisis massa pegas dengan shock absorber dengan mempergunakan fungsi green. Dalam hal ini, permasalahan tersebut juga akan diselesaikan dengan metode lain, yakni dengan metode koefisien tak tentu sehingga kita mendapatkan perbandingan dari kedua metode tersebut.

Dari uraian di atas, maka dalam penulisan skripsi ini, penulis mengambil judul

“APLIKASI FUNGSI GREEN PADA DINAMIKA SISTEM FISIS-MASSA PEGAS DENGAN SHOCK ABSORBER”.

1.2. Permasalahan

Berdasarkan latar belakang tersebut, maka rumusan masalah dalam penulisan skripsi ini adalah sebagai berikut:

• Bagaimana menyelesaikan persamaan diferensial linear tak homogen dengan mengkonstruksi fungsi green.

• Bagaimana menyelesaikan persamaan diferensial linear tak homogen dengan metode koefisien tak tentu.

• Sangat rumitnya untuk menyelesaikan beberapa persamaan differensial

1.3. Tujuan Penulisan

Penulisan skripsi ini bertujuan untuk:

• Menyelesaikan kasus osilasi harmonik teredam dengan mengkonstruksi fungsi green

• Membuat perbandingan solusi persamaan yang dihasilkan dengan menggunakan

metode fungsi green dengan solusi persamaan yang dihasilkan dengan menggunakan

metode koefisien tak tentu

(15)

1.4 Manfaat Penulisan

Manfaat penulisan skripsi ini untuk mengemukakan suatu metode baru sebagai alternatif untuk menyelesaikan persamaan diferensial linear tak homogen yaitu dengan mengkonstruksi fungsi green.

1.5. Batasan Masalah

Dalam penulisan skripsi ini, pembahasannya hanya dibatasi pada:

• Masalah yang diselesaikan hanya persamaan diferensial linear tak homogen dengan koefisien konstan yang dikhususkan pada osilasi teredam pada shock absorber mobil

• Fungsi green yang dimaksud adalah fungsi green khusus pada suatu integral transformasi atau substitusi yang dapat digunakan untuk menyelesaikan persamaan diferensial linear tak homogen.

• Metode yang digunakan untuk mengkonstruksi fungsi green adalah metode variasi parameter.

• Metode pembanding yang dipergunakan adalah metode koefisien tak tentu

1.6. Metode Penulisan

Metode merupakan cara utama yang akan ditempuh untuk menemukan jawaban dari suatu permasalahan. Berdasarkan hal tersebut, maka dalam penulisan proposal ini, penulis menggunakan metode kajian literatur atau kepustakaan, yaitu penelitian yang dilakukan di perpustakaan yang bertujuan untuk mendapatkan informasi dengan bermacam materiil yang terdapat di perpustakaan. Buku-buku fisika yang relevan dengan pembahasan merupakan referensi pendukung yang digunakan oleh penulis.

Adapun langkah-langkah penulisan yang dilakukan adalah sebagai berikut:

• Merumuskan masalah. Sebelum penulis memulai kegiatannya, penulis membuat rancangan terlebih dahulu mengenai suatu permasalahan yang akan dibahas.

• Mengumpulkan sumber informasi. Dengan menggunakan metode kepustakaan,

penulis mengumpulkan bahan atau sumber dan informasi dengan cara membaca dan

memahami literatur yang berkaitan dengan persamaan diferensial dan tentang fungsi

green.

(16)

• Menyelesaikan contoh. Di sini, penulis menyelesaikan soal dengan cara mengaitkan materi yang sedang dikaji.

• Membuat kesimpulan. Kesimpulan merupakan gambaran langkah dari pembahasan atas apa yang sedang ditulis. Kesimpulan didasarkan pada data yang telah dikumpulkan dan merupakan jawaban dari permasalahan yang dikemukakan.

• Membuat laporan

1.7 Sistematika penulisan

Sistematika penulisan masing-masing bab adalah sebagai berikut:

BAB I Pendahuluan

Bab ini mencakup latar belakang penelitian, rumusan masalah, tujuan penelitian, manfaat penelitian, dan sistematika penulisan tugas akhir ini.

BAB II Tinjauan pustaka

Bab ini berisi teori yang mendasari penelitian.

BAB III Metodologi Penelitian

Bab ini membahas tentang metode yang digunakan dan diagram alir penelitian.

BAB IV Hasil dan pembahasan

Bab ini membahas tentang hasil penelitian BAB V Kesimpulan dan Saran

Menyimpulkan hasil-hasil yang didapat dari penelitian dan

memberikan saran pada peneltian berikutnnya.

(17)

BAB II

TINJAUAN PUSTAKA

Dalam bab ini akan dikemukakan teori-teori yang mendukung pembahasan penyelesaian persamaan diferensial linier tak homogen dengan menggunakan metode fungsi green antara lain: persamaan diferensial, orde dan derajat suatu persamaan diferensial, persamaan diferensial linear, persamaan diferensial linear homogen dengan koefisien konstan, persamaan diferensial linier orde-n tak homogen dengan koefisien konstan,determinan wronski, selesaian khusus persamaan tak homogen dengan metode variasi parameter, dan sistem fisis persamaan osilasi harmonik teredam

2.1 Persamaan Diferensial

Persamaan diferensial adalah persamaan yang memuat turunan dari satu (atau beberapa) fungsi yang tidak diketahui. Ada dua macam persamaan diferensial, yaitu:

a. Persamaan diferensial biasa yaitu persamaan dimana fungsi yang belum diketahui hanya memuat satu variabel bebas saja.

Contoh 1.

^{𝑑𝑑𝑑𝑑}

𝑑𝑑𝑑𝑑

= 𝑑𝑑 + 6, (dimana hanya mengandung satu variabel bebas yaitu 𝑑𝑑)

2.

^𝑑𝑑²^𝑑𝑑

𝑑𝑑𝑑𝑑²

+ 3

^{𝑑𝑑𝑑𝑑}_{𝑑𝑑𝑑𝑑}

+ 2𝑑𝑑 = 0

3. 𝑑𝑑𝑑𝑑′ + 𝑑𝑑 = 3

4. 𝑑𝑑′′′ + 2(𝑑𝑑

^′

′)

²

+ 𝑑𝑑′ = 𝑐𝑐𝑐𝑐𝑐𝑐𝑑𝑑

b. Persamaan diferensial parsial yaitu persamaan diferensial dimana fungsi yang belum diketahui memuat dua atau lebih variabel bebas. Contoh:

1.

^{𝜕𝜕𝜕𝜕}

𝜕𝜕𝑑𝑑

= 𝜕𝜕 + 𝑑𝑑

_{𝜕𝜕𝑑𝑑}^{𝜕𝜕𝜕𝜕}

(18)

2. .

^𝜕𝜕²^𝜕𝜕

𝜕𝜕𝑑𝑑²

+

^𝜕𝜕_{𝜕𝜕𝑑𝑑}²^𝜕𝜕₂

= 𝑑𝑑

²

𝑑𝑑

2.2 Orde dan Derajat Suatu Persamaan Diferensial

Orde persamaan diferensial adalah tingkat tertinggi turunan yang timbul. Sedangkan derajat persamaan diferensial dapat ditulis sebagai polynomial dalam turunan, adalah derajat turunan tingkat tertinggi yang terjadi.

Contoh:

1.

^{𝑑𝑑𝑑𝑑}

𝑑𝑑𝑑𝑑

= 𝑑𝑑 + 6 (merupakan persamaan diferensial biasa orde 1 derajat 1).

2.

𝑑𝑑𝑑𝑑²

+ 3

^{𝑑𝑑𝑑𝑑}_{𝑑𝑑𝑑𝑑}

+ 2𝑑𝑑 = 0 (merupakan persamaan diferensial biasa orde 2 derajat 1).

3. 𝑑𝑑𝑑𝑑′ + 𝑑𝑑 = 3 (merupakan persamaan diferensial biasa orde 1 derajat 1).

4. 𝑑𝑑

^′′′

+ 2�𝑑𝑑

^{′ ′}

�

²

+ 𝑑𝑑

^′

= 𝑐𝑐𝑐𝑐𝑐𝑐𝑑𝑑 (merupakan persamaan diferensial biasa orde 3 derajat 1).

5. (𝑑𝑑′′)

²

+ (𝑑𝑑′)

²

+ 3𝑑𝑑 = 𝑑𝑑

²

(merupakan persamaan diferensial biasa orde 2 derajat 2).

6.

^{𝜕𝜕𝜕𝜕}

𝜕𝜕𝑑𝑑

= 𝜕𝜕 + 𝑑𝑑

^{𝜕𝜕𝜕𝜕}_{𝜕𝜕𝑑𝑑}

(merupakan persamaan diferensial parsial orde 1 derajat 1).

7.

^{𝜕𝜕𝜕𝜕}²

𝜕𝜕𝑑𝑑²

+

_{𝜕𝜕𝑑𝑑}^{𝜕𝜕𝜕𝜕}²₂

= 𝑑𝑑

²

+ 𝑑𝑑 (merupakan persamaan diferensial parsial orde 2 derajat 1).

2.3 Persamaan Diferensial Linier

Sebuah persamaan diferensial termasuk persamaan diferensial linier jika memenuhi dua hal berikut:

1. Variabel-variabel terikat dan turunannya tertinggi berpangkat 1

2. Tidak mengandung bentuk perkalian antara sebuah variabel terikat dengan variabel terikat lainnya, atau turunan yang satu dengan turunan yang lainnya, atau variabel terikat dengan sebuah turunan.

Jadi istilah linier berkaitan dengan kenyataan bahwa tiap suku dalam persamaan diferensial itu, peubah-peubah y, y',…, y(n) berderajat 1 atau nol.

Contoh:

1. 𝑑𝑑𝑑𝑑′ + 𝑑𝑑 = 3

2. 𝑑𝑑

^′′′

+ 2�𝑑𝑑

^{′ ′}

�

²

+ 𝑑𝑑

^′

= 𝑑𝑑

jadi bentuk umum persamaan diferensial linier orde- n adalah

𝑎𝑎

0

(𝑑𝑑)𝑑𝑑

^𝑛𝑛

+ 𝑎𝑎

1

(𝑑𝑑)𝑑𝑑

^{(𝑛𝑛−1)}

+ ⋯ + 𝑎𝑎

𝑛𝑛−1

(𝑑𝑑)𝑑𝑑

^′

+ 𝑎𝑎

𝑛𝑛

(𝑑𝑑)𝑑𝑑 = 𝑓𝑓(𝑑𝑑) (2.3)

(19)

keterangan:

Jika 𝑓𝑓(𝑑𝑑) = 0, maka persamaan (2.3.1) disebut persamaan diferensial linier homogeny orde −𝑛𝑛

Jika 𝑓𝑓(𝑑𝑑) ≠ 0, maka persamaan (2.3.1) disebut persamaan diferensial linier non homogen orde −𝑛𝑛. jika semua koefisien 𝑎𝑎

₀

(𝑑𝑑), 𝑎𝑎

1

(𝑑𝑑), … , 𝑎𝑎

𝑛𝑛

(𝑑𝑑) adalah tetap, maka persamaan (2.3.1) disebut persamaan diferensial linier dengan koefisien konstan. jika semua koefisien 𝑎𝑎

₀

(𝑑𝑑), 𝑎𝑎

₁

(𝑑𝑑), … , 𝑎𝑎

_𝑛𝑛

(𝑑𝑑) adalah berupa fungsi, maka persamaan (2.3.1) disebut persamaan diferensial linier dengan koefisien variabel (peubah).

2.4 Persamaan Diferensial Linear Homogen dengan Koefisien Konstan

Bentuk umum persamaan diferensial linear homogen dengan koefisien konstan:

𝑎𝑎

₀

𝑑𝑑

^𝑛𝑛

+ 𝑎𝑎

₁

𝑑𝑑

^{(𝑛𝑛−1)}

+ ⋯ + 𝑎𝑎

_𝑛𝑛−1

𝑑𝑑

^′

+ 𝑎𝑎

_𝑛𝑛

𝑑𝑑 = 0 (2.4.1)

dimana 𝑎𝑎

₀

, 𝑎𝑎

_1,…,

𝑎𝑎

_𝑛𝑛

adalah konstanta.

Untuk menentukan selesaiannya yaitu dengan mensubstitusi y = e

^tx

, kemudian menentukan bilangan tetap t sehingga e

^tx

sehingga persamaan (2.4.1) karena y = e

^tx

, y’ = t e

^tx

, y”=t

²

e

^tx

dan seterusnya hingga y

ⁿ

=t

ⁿ

e

^tx

. Bila disubstitusikan ke persamaan (2.4.1) akan didapatkan suatu persamaan dalam t, yaitu:

𝑒𝑒

^{𝑡𝑡𝑑𝑑}

(𝑎𝑎

0

𝑡𝑡

^𝑛𝑛

+ 𝑎𝑎

₁

𝑡𝑡

^𝑛𝑛−1

+ 𝑎𝑎

₂

𝑡𝑡

^𝑛𝑛−2

+ ⋯ + 𝑎𝑎

_𝑛𝑛

) = 0 (2.4.2) karena e

^tx

≠0, maka

(𝑎𝑎

₀

𝑡𝑡

^𝑛𝑛

+ 𝑎𝑎

₁

𝑡𝑡

^𝑛𝑛−1

+ 𝑎𝑎

₂

𝑡𝑡

^𝑛𝑛−2

+ ⋯ + 𝑎𝑎

_𝑛𝑛

) = 0 (2.4.3)

Persamaan (2.4.3) tersebut disebut persamaan karakteristik dari persamaan diferensial (2.4.1) dan akar-akarnya disebut akar-akar karakteristik. Ada tiga kemungkinan selesaian yang bebas linier dari persamaan (2.4.1), yaitu:

1. Bila akar-akarnya real dan berlainan, maka selesaian bebas liniernya yaitu: 𝑒𝑒

^𝑡𝑡¹^𝑑𝑑

, 𝑒𝑒

^𝑡𝑡²^𝑑𝑑

, … , 𝑒𝑒

^𝑡𝑡^𝑛𝑛^𝑑𝑑

2. Bila akar-akarnya real dan sama, maka selesaian bebas liniernya yaitu:

𝑒𝑒

^{𝑡𝑡𝑑𝑑}

, 𝑑𝑑𝑒𝑒

^{𝑡𝑡𝑑𝑑}

, … , 𝑑𝑑

^𝑛𝑛−1

𝑒𝑒

^{𝑡𝑡𝑑𝑑}

3. Bila akar-akarnya kompleks, maka selesaian bebas liniernya yaitu: 𝑒𝑒

(𝑎𝑎−𝑏𝑏𝑏𝑏)𝑑𝑑

atau 𝑒𝑒

^{𝑎𝑎𝑑𝑑}

(cos 𝑏𝑏𝑑𝑑 + sin 𝑏𝑏𝑑𝑑)

2.5 Persamaan Diferensial Linier Orde-n Tak Homogen Dengan Koefisien Konstan

(20)

Bentuk umum persamaan diferensial tak homogeny orde-n adalah sebagai berikut : 𝐴𝐴

𝑛𝑛

𝑑𝑑

^𝑛𝑛

+ 𝐴𝐴

𝑛𝑛−1

𝑑𝑑

^𝑛𝑛−1

+ 𝐴𝐴

𝑛𝑛−2

𝑑𝑑

^𝑛𝑛−2

+ ⋯ + 𝐴𝐴

1

𝑑𝑑

^′

+ 𝐴𝐴

0

𝑑𝑑 = 𝑟𝑟(𝑑𝑑) (2.5.1)

Solusi umum 𝑑𝑑(𝑑𝑑) akan didapatkan bila solusi umum 𝑑𝑑

_ℎ

𝑑𝑑 dari Persamaan Diferensial Homogen diketahui, dimana bentuk umum persamaan diferensial homogenya orde-n adalah sebagai berikut :

𝐴𝐴

_𝑛𝑛

𝑑𝑑

^𝑛𝑛

+ 𝐴𝐴

_𝑛𝑛−1

𝑑𝑑

^𝑛𝑛−1

+ 𝐴𝐴

_𝑛𝑛−2

𝑑𝑑

^𝑛𝑛−2

+ ⋯ + 𝐴𝐴

₁

𝑑𝑑

^′

+ 𝐴𝐴

₀

𝑑𝑑 = 0 (2.5.2)

Kemudian 𝑑𝑑(𝑑𝑑) dibentuk dengan penambahan 𝑑𝑑

ℎ

𝑑𝑑 sembarang solusi 𝑑𝑑 termasuk konstanta tak tetapnya. Sehingga,

𝑑𝑑(𝑑𝑑) = 𝑑𝑑

_ℎ

(𝑑𝑑) + 𝑑𝑑

_𝑝𝑝

(𝑑𝑑) (2.5.3)

Dalam hal ini kita membahas penyelesaian untuk mendapatkan persamaan partikulirnya dengan melalui metode fungsi green dan dengan melalui metode koefisien tak tentu.

2.6 Determinan Wronski

Misalkan 𝑓𝑓

₁

, 𝑓𝑓

₂

, … , 𝑓𝑓

_𝑛𝑛

kumpulan n buah fungsi yang semuanya dan turunan- turunannya sampai dengan turunan yang ke n-1kontinyu pada selang a ≤ x ≤ b. Wronski dari 𝑓𝑓

₁

, 𝑓𝑓

₂

, … , 𝑓𝑓

_𝑛𝑛

dihitung pada x dinyatakan oleh 𝑊𝑊(𝑓𝑓

₁

, 𝑓𝑓

₂

, … , 𝑓𝑓

_𝑛𝑛

; 𝑑𝑑) dan ditentukan sebagai determinan

𝑊𝑊(𝑓𝑓

₁

, 𝑓𝑓

₂

, … , 𝑓𝑓

_𝑛𝑛

; 𝑑𝑑) =

⎣ ⎢

⎢ ⎢

⎡ 𝑓𝑓

₁

𝑓𝑓

₂

𝑓𝑓

₁

′ 𝑓𝑓

₁

′′ 𝑓𝑓

₂

′

𝑓𝑓

₂

′′

⋯ ⋯

⋯ 𝑓𝑓

_𝑛𝑛

𝑓𝑓

_𝑛𝑛

′ 𝑓𝑓

_𝑛𝑛

′′

⋮ ⋮ ⋮ ⋮

𝑓𝑓

₁^𝑛𝑛−1

𝑓𝑓

₂^𝑛𝑛−1

⋯ 𝑓𝑓

_𝑛𝑛^𝑛𝑛−1

⎦ ⎥ ⎥ ⎥ ⎤

(2.6.1)

tiap fungsi yang muncul dalam determinan ini dihitung pada x.

Contoh

Diketahui 𝑓𝑓

₁

(𝑑𝑑) = 𝑑𝑑

²

dan 𝑓𝑓

₂

(𝑑𝑑) = cos 𝑑𝑑 , cari 𝑊𝑊(𝑓𝑓

₁

, 𝑓𝑓

₂

; 𝑑𝑑)

(21)

Penyelesaian: Dari defenisi di atas dan dari fungsi-fungsi yang telah diketahui, maka dapat dihitung:

𝑊𝑊(𝑑𝑑

²

, cos 𝑑𝑑; 𝑑𝑑) = �𝑑𝑑

²

cos 𝑑𝑑

2𝑑𝑑 − sin 𝑑𝑑 � = −𝑑𝑑

²

sin 𝑑𝑑 − 2𝑑𝑑 cos 𝑑𝑑

Misalkan bahwa 𝑑𝑑

₁

, 𝑑𝑑

₂

, … , 𝑑𝑑

_𝑛𝑛

merupakan n buah penyelesaian persamaan diferensial (2.4.1). Misalkan juga bahwa fungsi-fungsi tersebut bebas linier pada selang defenisi persamaan diferensial ini. Dikatakan bahwa fungsi-fungsi itu membentuk himpunan fundamental (atau sistem fundamental) penyelesaian persamaan diferensial tersebut. Sebagai contoh fungsi cos 𝑑𝑑 dan fungsi sin 𝑑𝑑 merupakan suatu himpunan fundamental penyelesaian persamaan diferensial 𝑑𝑑

^′′

+ 𝑑𝑑 = 0 . Juga fungsi 𝑒𝑒

^𝑑𝑑

dan 𝑒𝑒

^−𝑑𝑑

membentuk suatu himpunan fundamental penyelesaian persamaan diferensial 𝑑𝑑

^′′

− 𝑑𝑑 = 0.

2.7 Selesaian Khusus Persamaan Takhomogen: Penyelesaian Dengan Metode Variasi Parameter

Metode variasi parameter adalah metode yang dapat digunakan untuk menentukan selesaian khusus PD linier takhomogen dengan koefisien variabel, sehingga lebih umum daripada metode koefisien tak tentu.

Perhatikan PD linier orde 2 yang mempunyai bentuk

𝑑𝑑

^′′

+ 𝑝𝑝(𝑑𝑑)𝑑𝑑

^′

+ 𝑞𝑞(𝑑𝑑)𝑑𝑑 = 𝑟𝑟(𝑑𝑑) (2.7.1)

dengan p, q, dan r fungsi-fungsi kontinu pada suatu interval buka I. Kita akan menentukan selesaian khusus dari (2.7.1) dengan metode variasi parameter seperti berikut. Kita mengetahui bahwa PD homogen yang bersesuaian, yaitu

𝑑𝑑

^′′

+ 𝑝𝑝(𝑑𝑑)𝑑𝑑

^′

+ 𝑞𝑞(𝑑𝑑)𝑑𝑑 = 0 (2.7.2)

mempunyai suatu selesaian umum 𝑑𝑑

ℎ

(𝑑𝑑) pada I yang berbentuk

𝑑𝑑

_ℎ

(𝑑𝑑) = 𝑐𝑐

1

𝑑𝑑

₁

(𝑑𝑑) + 𝑐𝑐

₂

𝑑𝑑

₂

(𝑑𝑑) (2.7.3)

Metode variasi parameter terdiri dari penggantian 𝑐𝑐

₁

dan 𝑐𝑐

₂

dengan fungsi 𝑢𝑢(𝑑𝑑) dan 𝑣𝑣(𝑑𝑑) yang akan ditentukan sedemikian hingga fungsi penggantinya, yaitu

𝑑𝑑

ℎ

(𝑑𝑑) = 𝑢𝑢(𝑑𝑑)𝑑𝑑

1

(𝑑𝑑) + 𝑣𝑣(𝑑𝑑)𝑑𝑑

2

(𝑑𝑑) (2.7.4)

(22)

merupakan selesaian khusus dari (2.7.1) pada I. dengan menurunkan (2.7.3) diperoleh 𝑑𝑑

_𝑝𝑝^′

= 𝑢𝑢

^′

𝑑𝑑

₁

+ 𝑢𝑢𝑑𝑑

₁^′

+ 𝑣𝑣

^′

𝑑𝑑

₂

+ 𝑣𝑣𝑑𝑑

₂

′ (2.7.5)

Persamaan (2.7.3) memuat dua fungsi 𝑢𝑢 dan 𝑣𝑣, tetapi syarat bahwa 𝑑𝑑

𝑝𝑝

memenuhi (2.7.1) mengakibatkan bahwa hanya ada satu syarat pada 𝑢𝑢 dan 𝑣𝑣. . Karena itu kita bisa menerapkan kondisi (syarat) sebarang yang ke dua. Perhitungan berikut akan menunjukkan bahwa kita dapat menentukan 𝑢𝑢 dan 𝑣𝑣 sedemikian hingga 𝑑𝑑

_𝑝𝑝

memenuhi (2.7.1) dan 𝑢𝑢 dan 𝑣𝑣 memenuhi, sebagai syarat ke dua, hubungan:

𝑢𝑢

^′

𝑑𝑑

₁

+ 𝑣𝑣

^′

𝑑𝑑

₂

= 0 (2.7.6) Ini mereduksi ekspresi untuk 𝑑𝑑

𝑝𝑝

’ ke bentuk

𝑑𝑑

_𝑝𝑝

’ = 𝑢𝑢𝑑𝑑

₁

’ + 𝑣𝑣𝑑𝑑

₂

’

. (2.7.7) Dengan menurunkan fungsi ini diperoleh

𝑑𝑑

_𝑝𝑝

” = 𝑢𝑢’𝑑𝑑

₁

’ + 𝑢𝑢𝑑𝑑

₁

” + 𝑣𝑣’𝑑𝑑

₂

’ + 𝑣𝑣𝑑𝑑

₂

” (2.7.8)

Dengan mensubstitusikan (2.7.3), (2.7.5) dan (2.7.6) ke dalam (2.7.1) dan mengumpulkan suku-suku yang memuat 𝑢𝑢 dan 𝑣𝑣 akan diperoleh

𝑢𝑢(𝑑𝑑

1

” + 𝑝𝑝𝑑𝑑

1

’ + 𝑞𝑞𝑑𝑑

1

) + 𝑣𝑣(𝑑𝑑

2

” + 𝑝𝑝𝑑𝑑

2

’ + 𝑞𝑞𝑑𝑑

2

) + 𝑢𝑢’𝑑𝑑

1

’ + 𝑣𝑣’𝑑𝑑

2

’ = 𝑟𝑟 (2.7.9)

Karena 𝑑𝑑

₁

dan 𝑑𝑑

₂

selesaian dari PD homogen (2.7.6), maka persamaan di atas mereduksi ke bentuk

(i) 𝑢𝑢’𝑑𝑑

₁

’ + 𝑣𝑣’𝑑𝑑

₂

’ = 𝑟𝑟 (ii) 𝑢𝑢’𝑑𝑑

1

+ 𝑣𝑣’𝑑𝑑

2

= 0

Persamaan (i) dan (ii) merupakan sistem dua persamaan aljabar linier dari fungsi-fungsi 𝑢𝑢’ dan 𝑣𝑣’ yang tidak diketahui. Selesaian diperoleh dengan aturan Cramer:

𝑢𝑢

^′

= − 𝑑𝑑

₂

𝑟𝑟 𝑊𝑊

𝑣𝑣

^′

=

^𝑑𝑑_𝑊𝑊¹^𝑟𝑟

(2.7.10) Dengan

𝑊𝑊 = 𝑑𝑑

1

𝑑𝑑

2

′ + 𝑑𝑑

1

′𝑑𝑑

2

(2.7.11)

adalah Wronski dari dari 𝑑𝑑

₁

dan 𝑑𝑑

₂

. Jelas bahwa W≠0 karena 𝑑𝑑

₁

, 𝑑𝑑

₂

membangun basis

selesaian. Pengintegralan (2.7.7) menghasilkan

(23)

𝑢𝑢 = − ∫

^𝑑𝑑_𝑊𝑊²^𝑟𝑟

𝑑𝑑𝑑𝑑

𝑣𝑣 = ∫

𝑑𝑑𝑑𝑑 (2.7.12)

Integral ini ada karena 𝑟𝑟(𝑑𝑑) kontinu. Substitusikan ekspresi untuk 𝑢𝑢 dan 𝑣𝑣 ini ke dalam (2.7.3), untuk memperoleh selesaian dari (2.7.1).

𝑑𝑑

_𝑝𝑝

(𝑑𝑑) = −𝑑𝑑

₁

∫

^𝑑𝑑_𝑊𝑊²^𝑟𝑟

𝑑𝑑𝑑𝑑 + 𝑑𝑑

₂

∫

𝑑𝑑𝑑𝑑 (2.7.13)

2.8 Konsep Fungsi Green

Dari suatu sistem persamaan diferensial linear tak homogen orde-n:

𝑎𝑎

0

(𝑑𝑑)𝑑𝑑

^(𝑛𝑛)

+ 𝑎𝑎

1

(𝑑𝑑)𝑑𝑑

^{(𝑛𝑛−1)}

+ ⋯ + 𝑎𝑎

𝑛𝑛−1

(𝑑𝑑)𝑑𝑑

^′

+ 𝑎𝑎

𝑛𝑛

(𝑑𝑑)𝑑𝑑 = 𝑓𝑓(𝑑𝑑) (2.8)

dengan fungsi 𝑓𝑓(𝑑𝑑) merupakan fungsi yang kontinyu. Fungsi 𝐺𝐺(𝑑𝑑, 𝑡𝑡) dikatakan sebagai fungsi green untuk masalah nilai awal persamaan diferensial di atas jika memenuhi kondisi berikut ini:

a) 𝐺𝐺(𝑑𝑑, 𝑡𝑡) terdefenisi pada daerah R=I x I dari semua titik (𝑑𝑑, 𝑡𝑡) dimana 𝑑𝑑 dan 𝑡𝑡 terletak dalam selang I.

b) 𝐺𝐺(𝑑𝑑, 𝑡𝑡),

^{𝜕𝜕𝐺𝐺}_{𝜕𝜕𝑑𝑑}

,

^𝜕𝜕_{𝜕𝜕𝑑𝑑}²^𝐺𝐺₂

, … ,

^𝜕𝜕_{𝜕𝜕𝑑𝑑}^𝑛𝑛^𝐺𝐺_𝑛𝑛

merupakan fungsi kontinu pada R=I x I

c) Untuk setiap 𝑑𝑑

0

dalam selang I , fungsi 𝑑𝑑

𝑝𝑝

(𝑑𝑑) = ∫ 𝐺𝐺(𝑑𝑑, 𝑡𝑡)𝑓𝑓(𝑡𝑡)𝑑𝑑𝑡𝑡

_𝑑𝑑^𝑑𝑑₀

adalah solusi persamaan diferensial di atas yang memenuhi kondisi awal 𝑑𝑑

_𝑝𝑝

(𝑑𝑑

0

) = 𝑑𝑑

𝑝𝑝′

(𝑑𝑑

0

) = 𝑑𝑑

_𝑝𝑝^′′

(𝑑𝑑

₀

) = ⋯ = 𝑑𝑑

_𝑝𝑝^{(𝑛𝑛−1)}

(𝑑𝑑

₀

) = 0

2.9 Metode koefisien tak tentu

Ide dasar dari metode koefisien tak tentu adalah menduga dengan cerdas solusi 𝑑𝑑

𝑝𝑝

berdasarkan bentuk fungsi 𝑟𝑟(𝑑𝑑) di ruas kanan.

Bentuk persamaan umum:

𝐴𝐴

_𝑛𝑛

𝑑𝑑

^𝑛𝑛

+ 𝐴𝐴

_𝑛𝑛−1

𝑑𝑑

^𝑛𝑛−1

+ 𝐴𝐴

_𝑛𝑛−2

𝑑𝑑

^𝑛𝑛−2

+ ⋯ + 𝐴𝐴

₁

𝑑𝑑

^′

+ 𝐴𝐴

₀

𝑑𝑑 = 𝑟𝑟(𝑑𝑑) (2.9.1)

(24)

 Fungsi 𝑟𝑟(𝑑𝑑) yang merupakan bentuk solusi pertikular 𝑑𝑑

_𝑝𝑝

(𝑑𝑑) diperoleh dengan cara menebak, seperti misalnya: fungsi cos, fungsi sin, fungsi exponensial atau jumlah dari beberpa fungsi

 𝑟𝑟(𝑑𝑑) berisikan koefisien tak tentu

 Turunkan 𝑑𝑑

_𝑝𝑝

sesuai persamaan umum di atas

 Subtitusikan 𝑑𝑑

_𝑝𝑝

dan seluruh turunannya ke dalam persamaan

Bentuk 𝑟𝑟(𝑑𝑑) Pilihan untuk 𝑑𝑑

𝑝𝑝

𝑒𝑒

^{𝑎𝑎𝑑𝑑}

𝐴𝐴𝑒𝑒

^{𝑎𝑎𝑑𝑑}

𝑘𝑘 𝑑𝑑

^𝑛𝑛

(𝑛𝑛 = 0,1, … ) 𝑘𝑘

𝑛𝑛

𝑑𝑑

^𝑛𝑛

+ 𝑘𝑘

𝑛𝑛−1

𝑑𝑑

^𝑛𝑛−1

+ ⋯ + 𝑘𝑘

1

𝑑𝑑 + 𝑘𝑘

0

𝑑𝑑 𝑒𝑒

^{𝑎𝑎𝑑𝑑}

𝐴𝐴𝑒𝑒

^{𝑎𝑎𝑑𝑑}

+ 𝐵𝐵𝑑𝑑 𝑒𝑒

^{𝑎𝑎𝑑𝑑}

sin 𝑎𝑎𝑑𝑑 𝐴𝐴 sin 𝑎𝑎𝑑𝑑 + 𝐵𝐵 cos 𝑎𝑎𝑑𝑑

cos 𝑎𝑎𝑑𝑑 𝐴𝐴 sin 𝑎𝑎𝑑𝑑 + 𝐵𝐵 cos 𝑎𝑎𝑑𝑑

Tabel 2.1 Metode Koefisian Tak Tentu

Misal 𝑓𝑓(𝑑𝑑) merupakan fungsi polinom, eksponen, sinus atau cosines. Maka solusi 𝑑𝑑

𝑝𝑝

dimisalkan sebagai jumlah dari 𝑓𝑓(𝑑𝑑) dan semua turunannya. Selanjutnya 𝑑𝑑

_𝑝𝑝

𝑑𝑑

_𝑝𝑝

′ dan 𝑑𝑑

_𝑝𝑝

′′

disubstitusikan ke persamaan awal untuk menghitung nilai dari koefisiennya.

2.10 Sistem Fisis Persamaan Osilasi Harmonik Teredam

Sampai saat ini masih banyak anggapan bahwa tidak ada gaya gesekan yang

bekerja pada osilator. Jika anggapan ini dipegang, maka bandul atau beban pada pegas akan

berosilasi terus menerus. Pada kenyataannya, amplitudo osilasi berkurang sedikit demi sedikit

sampai akhirnya menjadi nol karena pengaruh gesekan. Dikatakan bahwa geraknya teredam

oleh gesekan dan disebut osilasi teredam. Gesekan seringkali muncul dari gesekan udara atau

gaya dalam. Besar gaya gesekan biasanya bergantung kepada laju. Dalam banyak hal, gaya

(25)

gesekan sebanding dengan kecepatan, tetapi arahnya berlawanan. Contoh dari osilasi teredam misalnya adalah pada shock absorber mobil.

Shock absorber merupakan komponen penting suatu kendaraan yaitu dalam sistem suspensi, yang berguna untuk meredam gaya osilasi dari pegas. Shock absorber berfungsi untuk memperlambat dan mengurangi besarnya getaran gerakan dengan mengubah energi kinetik dari gerakan suspensi menjadi energi panas yang dapat dihamburkan melalui cairan hidrolik.

Peredam kejut (shockabsorber) pada mobil memiliki komponen pada bagian atasnya terhubung dengan piston dan dipasangkan dengan rangka kendaraan. Bagian bawahnya, terpasang dengan silinder bagian bawah yang dipasangkan dengan as roda. Fluida kental menyebabkan gaya redaman yang bergantung pada kecepatan relatif dari kedua ujung unit tersebut. Hal ini membantu untuk mengendalikan guncangan pada roda.

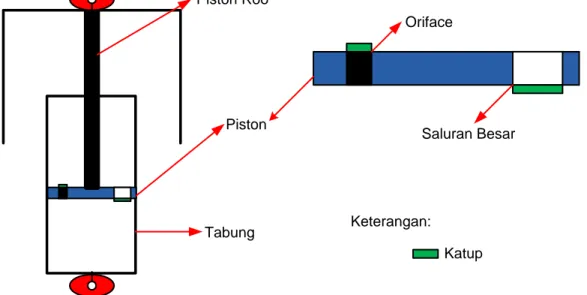
Konstruksi shock absorber itu terdiri atas piston, piston rod dan tabung. Piston adalah komponen dalam tabung shock absorber yang bergerak naik turun di saat shock absorber bekerja. Sedangkan tabung adalah tempat dari minyak shock absorber dan sekaligus ruang untuk piston bergerak naik turun. Dan yang terakhir adalah piston rod adalah batang yang menghubungkan piston dengan tabung bagian atas (tabung luar) dari shock absorber. Untuk lebih jelasnya dapat dilihat pada gambar berikut:

Piston Roo

Piston

Tabung

Oriface

Saluran Besar

Keterangan:

Katup

Gambar 2.1 Detail struktur shock absorber

(26)

Shock absorber bekerja dalam dua siklus yakni siklus kompresi dan siklus ekstensi.

Siklus kompresi (penekanan)

Saat shock absorber ditekan karena gaya osilasi dari pegas suspensi, maka gerakan yang terjadi adalah shock absorber mengalami pemendekan ukuran. Siklus kompresi terjadi ketika piston bergerak ke bawah, menekan fluida hidrolik di dalam ruang bawah piston. Dan minyak shock absorber yang berada dibawah piston akan naik keruang atas piston melalui lubang yang ada pada piston. Sementara lubang kecil (orifice) pada piston tertutup karena katup menutup saluran orifice tersebut. Penutupan katub ini disebabkan karena peletakan katup yang berupa membran (plat tipis) dipasangkan dibawah piston, sehingga ketika minyak shock absorber berusaha naik ke atas maka katup membran ini akan terdorong oleh shock absorber dan akilbatnya menutup saluran orifice. Jadi minyak shock absorber akan menuju ke atas melalui lubang yang besar pada piston, sementara minyak tidak bisa keluar melalui saluran oriface pada piston. Pada saat ini shock absorber tidak melakukan peredaman terhadap gaya osilasi dari pegas suspensi, karena minyak dapat naik ke ruang di atas piston dengan sangat mudah.

Siklus ekstensi (memanjang)

Pada saat memanjang piston di dalam tabung akan begerak dari bawah naik ke atas.

Gerakan naik piston ini membuat minyak shock absorber yang sudah berada diatas menjadi tertekan. Minyak shock absorber ini akan mencari jalan keluar agar tidak tertekan oleh piston terus. Maka minyak ini akan mendorong katup pada saluran oriface untuk membuka dan minyak akan keluar atau turun ke bawah melalui saluran oriface. Pada saat ini katup pada lubang besar di piston akan tertutup karena letak katup ini yang berada di atas piston. Minyak shock absorber ini akan menekan katup lubang besar, piston ke bawah dan mengaakibat katup ini tertutup. Tapi letak katup saluran oriface membuka karena letaknya berada di bawah piston, sehingga ketika minyak shock menekan ke bawah katup ini membuka. Pada saat ini minyak shock absorber hanya dapat turun ke bawah melalui saluran orifice yang kecil.

Karena salurannya yang kecil, maka minyak shock absorber tidak akan bisa cepat turun ke

bawah alias terhambat. Di saat inilah shock absorber melakukan peredaman terhadap gaya

osilasi pegas suspensi.

(27)

Tipikal mobil atau truk ringan akan memiliki lebih banyak perlawanan selama siklus ekstensi daripada siklus kompresi. Semua peredam kejut modern adalah kecepatan-sensitif – suspensi semakin cepat bergerak, semakin banyak perlawanan yang shock breker sediakan.

Hal ini memungkinkan guncangan untuk menyesuaikan diri dengan kondisi jalan dan untuk mengontrol semua gerakan yang tidak diinginkan yang dapat terjadi dalam kendaraan yang bergerak. Secara sederhana shock absorber merupakan pengaplikasian dari gerak osilasi harmonik yang teredam.

m

k c

y Fo cos wt

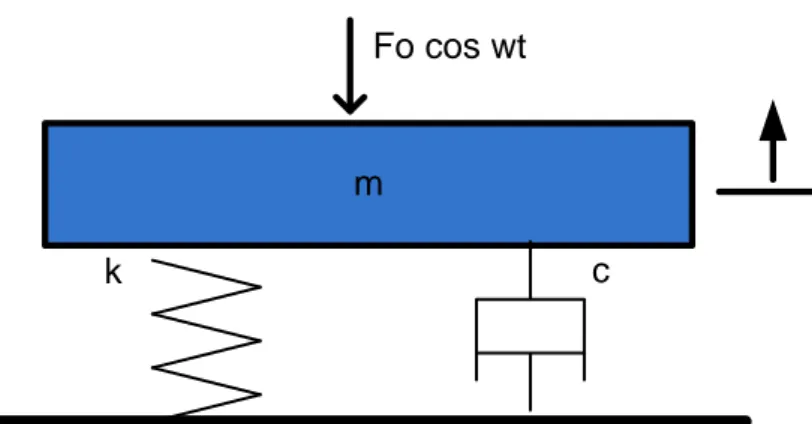
Gambar 2.2 Sistem fisis pada shock absorber

Bila peredaman diperhitungkan, maka gaya peredam juga berlaku pada massa. Bila bergerak dalam fluida benda akan mendapatkan redaman karena kekentalan fluida. Gaya akibat kekentalan ini sebanding dengan kecepatan benda. Konstanta akibat kekentalan (viskositas) adalah c dengan satuan N s/m (SI)

Persamaan osilasi teredam diberikan oleh hokum gerak kedua, 𝐹𝐹 = 𝑚𝑚𝑎𝑎 , dengan F merupakan jumlah dari gaya pemulih – 𝑘𝑘𝑑𝑑 dan gaya redaman – 𝑐𝑐 𝑑𝑑𝑑𝑑/𝑑𝑑𝑡𝑡 ; dalam hal ini c adalah konstanta positif. Kita peroleh bahwa

𝛴𝛴𝐹𝐹 = 𝑚𝑚𝑎𝑎 (2.10.1)

atau

−𝑘𝑘𝑑𝑑 − 𝑐𝑐

^{𝑑𝑑𝑑𝑑}_{𝑑𝑑𝑡𝑡}

= 𝑚𝑚

^𝑑𝑑_{𝑑𝑑𝑡𝑡}²^𝑑𝑑₂

(2.10.2)

atau

𝑚𝑚

+ 𝑐𝑐

+ 𝑘𝑘𝑑𝑑 = 0 (2.10.3)

(28)

Dalam osilasi teredam sebenarnya masih terdapat gaya lain yang bekerja berupa gaya paksaan. Dalam hal ini, dimisalkan gaya paksaan yang diberikan terhadap sistem yang telah disebutkan adalah 𝐹𝐹

₀

cos 𝜔𝜔𝑡𝑡. Di sini 𝐹𝐹

₀

adalah harga dari gaya eksternal dan 𝜔𝜔 adalah frekuensi sudutnya. Untuk jelasnya, dapat kita bayangkan bahwa gaya eksternal tersebut diberikan langsung pada massa yang digantungkan pada pegas. Maka kita peroleh persamaan:

𝛴𝛴𝐹𝐹 = 𝑚𝑚𝑎𝑎 diperoleh

−𝑘𝑘𝑑𝑑 − 𝑐𝑐

+ 𝐹𝐹

0

cos 𝜔𝜔𝑡𝑡 = 𝑚𝑚

(2.10.4) atau

𝑚𝑚

+ 𝑐𝑐

+ 𝑘𝑘𝑑𝑑 = 𝐹𝐹

0

cos 𝜔𝜔𝑡𝑡 (2.10.5)

(29)

BAB III

METODOLOGI PENELITIAN

3.1 Rancangan Penelitian

Langkah awal yang dilakukan adalah memecahkan permasalahan fisika dengan menggunakan metode fungsi green dan juga metode koefisien tak tentu dan kemudian membandingkan kedua hasil yang didapat dari kedua metode tersebut. Pada bagian akhir, akan digunakan program mathematic 8 untuk membuktikan hasil yang didapatkan sebelumnya.

3.2 Diagram Alir Penelitian

Gambar 3.1 Diagram alir penelitian Metode Fungsi Green

Sistem Dinamis Osilasi Persamaan Fisis

pada shock

Metode Koefisien Tak Tent

Solusi

(30)

BAB IV

HASIL DAN PEMBAHASAN

4.1 Penyelesaian Dengan Menggunakan Metode Fungsi Green

Persamaan yang kita dapatkan dari system fisis-massa pegas shock absorber yang telah dibahas sebelumnya adalah:

𝑚𝑚

+ 𝑐𝑐

+ 𝑘𝑘𝑑𝑑 = 𝐹𝐹

₀

cos 𝜔𝜔𝑡𝑡 (4.1.1) Atau dapat kita tuliskan dalam bentuk lain yakni:

𝑑𝑑𝑡𝑡²

+

_𝑚𝑚^𝑐𝑐 ^{𝑑𝑑𝑑𝑑}_{𝑑𝑑𝑡𝑡}

+

_𝑚𝑚^𝑘𝑘

𝑑𝑑 =

^𝐹𝐹⁰^{cos 𝜔𝜔𝑡𝑡}_𝑚𝑚

(4.1.2) Maka untuk mendapatkan solusi dari persamaan (4.1.2) di atas kita selesaikan terlebih dahulu penyelesaian homogennya

𝑃𝑃

²

+

_𝑚𝑚^𝑐𝑐

𝑃𝑃 +

_𝑚𝑚^𝑘𝑘

= 0 (4.1.3) 𝑃𝑃

_1,2

=

⁻

𝑐𝑐

𝑚𝑚±��_𝑚𝑚^𝑐𝑐�²−4�_𝑚𝑚^𝑘𝑘�

2

(4.1.4) 𝑃𝑃 =

_2𝑚𝑚^−𝑐𝑐

±

^�

𝑐𝑐2 𝑚𝑚 2−^4𝑘𝑘_𝑚𝑚

2

(4.1.5) Untuk gerak teredam kritis,maka

^𝑐𝑐²

𝑚𝑚²

−

^4𝑘𝑘_𝑚𝑚

= 0 (4.1.6) 𝑃𝑃

1,2

=

_2𝑚𝑚^−𝑐𝑐

(4.1.7) Sehingga:

𝑑𝑑

ℎ

= 𝑒𝑒

^2𝑚𝑚^−𝑐𝑐^𝑡𝑡

(𝑐𝑐

1

+ 𝑡𝑡𝑐𝑐

2

) (4.1.8)

𝑑𝑑

ℎ

= 𝑐𝑐

1

𝑒𝑒

+ 𝑐𝑐

2

𝑡𝑡𝑒𝑒

(4.1.9) Kemudian kita selesaikan persamaan partikulernya melalui metode fungsi green:

Mis

^𝑐𝑐

2𝑚𝑚

= 𝛾𝛾

𝑑𝑑

_𝑝𝑝

= 𝑢𝑢

₁

𝑒𝑒

^{−𝛾𝛾𝑡𝑡}

+ 𝑢𝑢

₂

𝑡𝑡𝑒𝑒

(4.1.10) Dari sini kita dapatkan:

𝑑𝑑

₁

= 𝑒𝑒

(4.1.11) 𝑑𝑑

₂

= 𝑡𝑡𝑒𝑒

(4.1.12)

𝑊𝑊 = � 𝑒𝑒

^{−𝛾𝛾𝑑𝑑}

𝑑𝑑𝑒𝑒

−𝛾𝛾𝑒𝑒

𝑒𝑒

− 𝛾𝛾𝑑𝑑𝑒𝑒

�=𝑒𝑒

^{−2𝛾𝛾𝑑𝑑}

(4.1.13) 𝑣𝑣

1

(𝑑𝑑) = �0 𝑑𝑑𝑒𝑒

1 𝑒𝑒

− 𝛾𝛾𝑑𝑑𝑒𝑒

�=−𝑑𝑑𝑒𝑒

(4.1.14) 𝑣𝑣

₂

(𝑑𝑑) = � 𝑒𝑒

0 −𝛾𝛾𝑒𝑒

1� = 𝑒𝑒

(4.1.15) 𝐺𝐺(𝑑𝑑, 𝑡𝑡) =

^𝑑𝑑¹^{(𝑡𝑡)𝑣𝑣}¹^{(𝑑𝑑)+𝑑𝑑}_𝑊𝑊 ²^{(𝑡𝑡)𝑣𝑣}²^(𝑑𝑑)

(4.1.16)

=

^𝑒𝑒^{−𝛾𝛾𝑡𝑡}^{−𝑑𝑑𝑒𝑒}^{−𝛾𝛾𝑑𝑑}^{+𝑡𝑡𝑒𝑒}^{−𝛾𝛾𝑡𝑡}^𝑒𝑒^{−𝛾𝛾𝑑𝑑}

𝑒𝑒^{−2𝛾𝛾𝑑𝑑}

(4.1.17)

(31)

= −𝑑𝑑𝑒𝑒

𝑒𝑒

^{𝛾𝛾𝑑𝑑}

+ 𝑡𝑡𝑒𝑒

𝑒𝑒

^{𝛾𝛾𝑑𝑑}

(4.1.18) = −𝑑𝑑𝑒𝑒

^{(𝑑𝑑−𝑡𝑡)𝛾𝛾}

+ 𝑡𝑡𝑒𝑒

(4.1.19) 𝐺𝐺(𝑑𝑑, 𝑡𝑡) = 𝑒𝑒

(𝑡𝑡 − 𝑑𝑑) (4.1.20) 𝑑𝑑

_𝑝𝑝

= ∫ 𝐺𝐺(𝑑𝑑, 𝑡𝑡). ℎ(𝑑𝑑)

_𝑡𝑡^𝑡𝑡₀

𝑑𝑑𝑑𝑑 (4.1.21) Dengan:

ℎ(𝑑𝑑) =

^𝐹𝐹⁰ 𝑐𝑐𝑐𝑐𝑐𝑐𝜔𝜔𝑡𝑡

𝑚𝑚

(4.1.22) Sehinga dengan mensubstitusikan persamaan (4.20) dan (4.22) ke dalam persamaan (4.21) didapatkan:

𝑑𝑑

_𝑝𝑝

= ∫ 𝑒𝑒

(𝑡𝑡 − 𝑑𝑑)

^𝐹𝐹⁰ 𝑐𝑐𝑐𝑐𝑐𝑐𝜔𝜔𝑡𝑡 𝑚𝑚

𝑑𝑑𝑑𝑑

𝑡𝑡

𝑡𝑡₀

(4.1.23) 𝑑𝑑

_𝑝𝑝

=

^𝐹𝐹_𝑚𝑚⁰

∫ (𝑡𝑡 − 𝑑𝑑 )

. 𝑒𝑒

cos 𝜔𝜔𝑡𝑡 𝑑𝑑𝑑𝑑 (4.1.24)

𝑑𝑑

𝑝𝑝

=

∫ (𝑡𝑡 − 𝑑𝑑)

. 𝑒𝑒

^{𝛾𝛾𝑑𝑑}

. 𝑒𝑒

cos 𝜔𝜔𝑡𝑡 𝑑𝑑𝑑𝑑 (4.1.25) 𝑑𝑑

_𝑝𝑝

=

𝑒𝑒

∫ (𝑡𝑡 − 𝑑𝑑 )

𝑒𝑒

^{𝛾𝛾𝑑𝑑}

cos 𝜔𝜔𝑡𝑡 𝑑𝑑𝑑𝑑 (4.1.26) ∫(𝑡𝑡 − 𝑑𝑑) 𝑒𝑒

^{𝛾𝛾𝑑𝑑}

cos 𝜔𝜔𝑡𝑡 𝑑𝑑𝑑𝑑 (4.1.27) Sebagaimana diketahui bahwa

∫ 𝑢𝑢 𝑑𝑑𝑣𝑣 = 𝑢𝑢𝑣𝑣 − 𝑣𝑣𝑑𝑑𝑢𝑢 (4.1.28) Maka dari persamaan (2.27) diketahui bahwa:

𝑢𝑢 = 𝑡𝑡 − 𝑑𝑑 (4.1.29) 𝑑𝑑𝑢𝑢 = −𝑑𝑑𝑑𝑑 (4.1.30)

𝑑𝑑𝑣𝑣 = 𝑒𝑒

^{𝛾𝛾𝑑𝑑}

cos 𝜔𝜔𝑡𝑡 𝑑𝑑𝑑𝑑 (4.1.31) 𝑣𝑣 = ∫ 𝑒𝑒

^{𝛾𝛾𝑑𝑑}

cos 𝜔𝜔𝑡𝑡 𝑑𝑑𝑑𝑑 =

^𝑒𝑒^{𝛾𝛾𝑑𝑑}(𝜔𝜔 sin 𝜔𝜔𝑡𝑡+𝛾𝛾 cos 𝜔𝜔𝑡𝑡)

𝜔𝜔²+𝛾𝛾²

(4.1.32) Maka:

∫(𝑡𝑡 − 𝑑𝑑) 𝑒𝑒^{𝛾𝛾𝑑𝑑} cos 𝜔𝜔𝑡𝑡 𝑑𝑑𝑑𝑑 =^{(𝑡𝑡−𝑑𝑑)𝑒𝑒}^{𝛾𝛾𝑑𝑑}⁽^𝜔𝜔^sin^𝜔𝜔𝑡𝑡+ 𝛾𝛾 cos 𝑑𝑑)

𝜔𝜔²+𝛾𝛾² − ∫^𝑒𝑒^{𝛾𝛾𝑑𝑑}⁽^𝜔𝜔^sin_𝜔𝜔^𝜔𝜔2+𝛾𝛾^{𝑡𝑡+𝛾𝛾 cos}² ^𝜔𝜔^𝑡𝑡(−𝑑𝑑𝑑𝑑)

(4.1.33)

=^{(𝑡𝑡−𝑑𝑑)𝑒𝑒}^{𝛾𝛾𝑑𝑑}(𝜔𝜔 sin 𝜔𝜔𝑡𝑡 + 𝛾𝛾 cos 𝑑𝑑)

𝜔𝜔²+𝛾𝛾² +_𝜔𝜔₂¹_+𝛾𝛾₂[∫ 𝜔𝜔𝑒𝑒^{𝛾𝛾𝑑𝑑}sin 𝜔𝜔𝑡𝑡 𝑑𝑑𝑑𝑑 + ∫ 𝛾𝛾𝑒𝑒^{𝛾𝛾𝑑𝑑}cos 𝜔𝜔𝑡𝑡 𝑑𝑑𝑑𝑑]

(4.1.34)

𝜔𝜔²+𝛾𝛾² +_𝜔𝜔₂^𝜔𝜔_+𝛾𝛾₂∫ 𝑒𝑒^{𝛾𝛾𝑑𝑑}sin 𝜔𝜔𝑡𝑡 𝑑𝑑𝑑𝑑 +_𝜔𝜔₂^𝛾𝛾_+𝛾𝛾₂∫ 𝑒𝑒^{𝛾𝛾𝑑𝑑}cos 𝜔𝜔𝑡𝑡 𝑑𝑑𝑑𝑑

(4.1.35)

𝜔𝜔²+𝛾𝛾² +_𝜔𝜔2^𝜔𝜔+𝛾𝛾²∫ 𝑒𝑒^{𝛾𝛾𝑑𝑑}sin 𝜔𝜔𝑡𝑡 𝑑𝑑𝑑𝑑 +_𝜔𝜔2^𝛾𝛾+𝛾𝛾²∫ 𝑒𝑒^{𝛾𝛾𝑑𝑑}cos 𝜔𝜔𝑡𝑡 𝑑𝑑𝑑𝑑

(4.1.36)

=^{(𝑡𝑡−𝑑𝑑)𝑒𝑒}^{𝛾𝛾𝑑𝑑}(𝜔𝜔 sin 𝜔𝜔𝑡𝑡 + 𝛾𝛾 cos 𝑑𝑑

𝜔𝜔²+𝛾𝛾² +_𝜔𝜔₂^𝜔𝜔_+𝛾𝛾₂�𝑒𝑒𝛾𝛾𝑑𝑑 (𝛾𝛾 sin 𝜔𝜔𝑡𝑡 + 𝜔𝜔 cos 𝑑𝑑)

𝜔𝜔²+𝛾𝛾² � +_𝜔𝜔₂^𝛾𝛾_+𝛾𝛾₂�𝑒𝑒𝛾𝛾𝑑𝑑 (𝜔𝜔 cos 𝜔𝜔𝑡𝑡 + 𝛾𝛾 cos 𝑑𝑑)

𝜔𝜔+𝛾𝛾² �

(4.1.37)

=_𝑤𝑤^𝑒𝑒2^{𝛾𝛾𝑑𝑑}+𝛾𝛾²�(𝑡𝑡 − 𝑑𝑑)(𝜔𝜔 sin

𝜔𝜔

𝑡𝑡 + 𝛾𝛾 cos 𝑑𝑑 +_𝜔𝜔2^𝜔𝜔+𝛾𝛾²(𝛾𝛾 sin 𝜔𝜔𝑡𝑡 + 𝜔𝜔 cos 𝑑𝑑) +_𝜔𝜔2^𝛾𝛾+𝛾𝛾²(𝛾𝛾 cos 𝜔𝜔𝑡𝑡 + 𝜔𝜔 sin 𝜔𝜔𝑡𝑡)�

(4.1.38)

∫ (𝑡𝑡 − 𝑑𝑑)𝑒𝑒_𝑡𝑡^𝑡𝑡₀ ^{𝛾𝛾𝑑𝑑}cos

𝜔𝜔

^{𝑡𝑡 𝑑𝑑𝑑𝑑 =}_𝜔𝜔^𝑒𝑒2^{𝛾𝛾𝑡𝑡}+𝛾𝛾²�_𝜔𝜔2^𝜔𝜔+𝛾𝛾²(𝛾𝛾 sin

𝜔𝜔

^{𝑡𝑡 +}

𝜔𝜔

^cos

𝜔𝜔

^{𝑡𝑡) +}_𝜔𝜔2^𝛾𝛾+𝛾𝛾²(𝛾𝛾 cos

𝜔𝜔

^{𝑡𝑡 +}

𝜔𝜔

^sin

𝜔𝜔

^𝑡𝑡)�

(4.1.39)

=

₍_𝜔𝜔₂^𝑒𝑒_+𝛾𝛾^{𝛾𝛾𝑡𝑡}₂₎₂

[ 𝜔𝜔 𝛾𝛾 sin 𝜔𝜔 𝑡𝑡 + 𝜔𝜔

²

cos 𝜔𝜔 𝑡𝑡 + 𝛾𝛾

²

cos 𝜔𝜔 𝑡𝑡 + 𝜔𝜔 𝛾𝛾 sin 𝜔𝜔 𝑡𝑡)] (4.1.40)

=

₍_𝜔𝜔₂^𝑒𝑒_+𝛾𝛾^{𝛾𝛾𝑡𝑡}₂₎₂

�2 𝜔𝜔 ^{𝛾𝛾 sin} 𝜔𝜔 ^{𝑡𝑡 + (} 𝜔𝜔

²

^{+ 𝛾𝛾}

²

^{) cos} 𝜔𝜔 𝑡𝑡� (4.1.41) Maka di dapatkan:

𝑑𝑑

_𝑝𝑝

=

𝑒𝑒

^{−𝛾𝛾𝑡𝑡}_(𝜔𝜔₂^𝑒𝑒_+𝛾𝛾^{𝛾𝛾𝑡𝑡}₂₎₂

[2𝜔𝜔𝛾𝛾 sin 𝜔𝜔𝑡𝑡 + (𝜔𝜔

²

+ 𝛾𝛾

²

) cos 𝜔𝜔𝑡𝑡] (4.1.43)

(32)

𝑑𝑑

_𝑝𝑝

=

_{𝑚𝑚(𝜔𝜔}₂^𝐹𝐹_+𝛾𝛾⁰ ₂₎₂

[2𝜔𝜔𝛾𝛾 sin 𝜔𝜔𝑡𝑡 + (𝜔𝜔

²

+ 𝛾𝛾

²

) cos 𝜔𝜔𝑡𝑡] (4.1.44) Dengan:

𝑑𝑑 = 𝑑𝑑

ℎ

+ 𝑑𝑑

𝑝𝑝

(4.1.45) Sehingga:

𝑑𝑑 = 𝐶𝐶

1

𝑒𝑒

+ 𝐶𝐶

2

𝑡𝑡𝑒𝑒

+

_𝑚𝑚(_𝜔𝜔^𝐹𝐹₂⁰_+𝛾𝛾₂₎₂

�2 𝜔𝜔 𝛾𝛾 sin 𝜔𝜔 𝑡𝑡 + ( 𝜔𝜔

²

+ 𝛾𝛾

²

) cos 𝜔𝜔 𝑡𝑡� (4.1.46) Dengan 𝑑𝑑 merupakan solusi dari persamaan (4.1.2) yang didapatkan melalui metode fungsi green

4.2 Penyelesaian Dengan Menggunakan Metode Koefisien Tak Tentu

Sebagaimana diketahui bahwa persamaan dari gerak osilasi teredam pada schok mobil adalah sebagai berikut:

𝑚𝑚

+ 𝑐𝑐

+ 𝑘𝑘𝑑𝑑 = 𝐹𝐹

₀

cos 𝜔𝜔𝑡𝑡 (4.2.1) Dari persamaan (4.1.9),maka

𝑑𝑑

ℎ

= 𝑐𝑐

1

𝑒𝑒

^{2𝑚𝑚𝑡𝑡}^−𝑐𝑐

+ 𝑐𝑐

2

𝑡𝑡𝑒𝑒

^{2𝑚𝑚𝑡𝑡}^−𝑐𝑐

Untuk persamaan partikulirnya:

𝑑𝑑

_𝑝𝑝

= 𝑃𝑃 cos 𝜔𝜔𝑡𝑡 + 𝑄𝑄 sin 𝜔𝜔𝑡𝑡 (4.2.2) 𝑑𝑑

_𝑝𝑝^′

= −𝜔𝜔𝑃𝑃 sin 𝜔𝜔𝑡𝑡 + 𝜔𝜔𝑄𝑄 cos 𝜔𝜔𝑡𝑡 (4.2.3) 𝑑𝑑

𝑝𝑝′′

= −𝜔𝜔

²

cos 𝜔𝜔𝑡𝑡 − 𝜔𝜔

²

𝑄𝑄 sin 𝜔𝜔𝑡𝑡 (4.2.4) Maka ketiga persamaan (4.2.2),(4.2.3) dan (4.2.4) kita substitusikan ke persamaan (4.2.1) sehingga didapatkan:

𝑚𝑚(−𝜔𝜔²cos 𝜔𝜔𝑡𝑡 − 𝜔𝜔²𝑄𝑄 sin 𝜔𝜔𝑡𝑡) + 𝑐𝑐( − 𝜔𝜔𝑃𝑃 sin 𝜔𝜔𝑡𝑡 + 𝜔𝜔𝑄𝑄 cos 𝜔𝜔𝑡𝑡) + 𝑘𝑘(𝑃𝑃 cos 𝜔𝜔𝑡𝑡 + 𝑄𝑄 sin 𝜔𝜔𝑡𝑡) = 𝐹𝐹0cos 𝜔𝜔𝑡𝑡

(4.2.5)

(−𝜔𝜔

²

𝑚𝑚𝑃𝑃 + 𝜔𝜔𝑐𝑐𝑄𝑄 + 𝑘𝑘𝑃𝑃) cos 𝜔𝜔𝑡𝑡 + (− 𝜔𝜔

²

𝑚𝑚𝑄𝑄 − 𝜔𝜔𝑐𝑐𝑃𝑃 + 𝑘𝑘𝑄𝑄) sin 𝜔𝜔𝑡𝑡 = 𝐹𝐹

0

cos

𝜔𝜔

𝑡𝑡 (4.2.6) Dari persamaaan (4.2.6) ini didapatkan bahwa:

−𝜔𝜔

²

𝑚𝑚𝑃𝑃 + 𝜔𝜔𝑐𝑐𝑄𝑄 + 𝑘𝑘𝑃𝑃 = 𝐹𝐹

₀

(4.2.7) −𝜔𝜔

²

𝑚𝑚𝑄𝑄 − 𝜔𝜔𝑐𝑐𝑃𝑃 + 𝑘𝑘𝑄𝑄 = 0 (4.2.8) (−𝜔𝜔

²

𝑚𝑚 + 𝑘𝑘)𝑃𝑃 + 𝜔𝜔𝑐𝑐𝑄𝑄 = 𝐹𝐹

₀

(4.2.9) (−𝜔𝜔

²

𝑚𝑚 + 𝑘𝑘)𝑄𝑄 − 𝜔𝜔𝑐𝑐𝑃𝑃 = 0 (4.2.10)

𝜔𝜔𝑐𝑐𝑃𝑃 = (−𝜔𝜔

²

𝑚𝑚 + 𝑘𝑘)𝑄𝑄 (4.2.11) 𝑃𝑃 =

^{�−𝜔𝜔}²_{𝜔𝜔𝑐𝑐}^{𝑚𝑚+𝑘𝑘�𝑄𝑄}

(4.2.12) Kemudian persamaan (4.2.12) ini disubstitusikan ke persamaan (4.2.9), sehingga didapatkan:

(−𝜔𝜔

²

𝑚𝑚 + 𝑘𝑘)

+ 𝜔𝜔𝑐𝑐𝑄𝑄 = 𝐹𝐹

₀

(4.2.13)

^{�−𝜔𝜔}²^{𝑚𝑚+𝑘𝑘�}

2𝑄𝑄

𝜔𝜔𝑐𝑐

+ 𝜔𝜔𝑐𝑐𝑄𝑄 = 𝐹𝐹

₀

(4.2.14) (−𝜔𝜔

²

𝑚𝑚 + 𝑘𝑘)

²

𝑄𝑄 + (𝜔𝜔𝑐𝑐)

²

𝑄𝑄 = 𝐹𝐹

₀

𝜔𝜔𝑐𝑐 (4.2.15) ((−𝜔𝜔

²

𝑚𝑚 + 𝑘𝑘)

²

+ (𝜔𝜔𝑐𝑐)

²

)𝑄𝑄 = 𝐹𝐹

0

𝜔𝜔𝑐𝑐 (4.2.16) 𝑄𝑄 =

_(−𝜔𝜔₂_{𝑚𝑚+𝑘𝑘)}^𝐹𝐹⁰^{𝜔𝜔𝑐𝑐}₂_{+(𝜔𝜔𝑐𝑐 )}₂

(4.2.17) Nilai P dan Q yang telah didapatkan seperti pada persamaan (4.2.12) dan (4.2.17) kemudian disubstitusikan ke persamaan (4.2.2) untuk mendapatkan nilai 𝑑𝑑

_𝑝𝑝

sebagai berikut:

𝑑𝑑

_𝑝𝑝

=

cos 𝜔𝜔𝑡𝑡 +

_(−𝜔𝜔₂_{𝑚𝑚+𝑘𝑘)}^𝐹𝐹⁰^{𝜔𝜔𝑐𝑐}₂_{+(𝜔𝜔𝑐𝑐 )}₂

sin 𝜔𝜔𝑡𝑡 (4.2.18)

𝑑𝑑_𝑝𝑝 =^(−𝜔𝜔_{𝜔𝜔𝑐𝑐}²^{𝑚𝑚+𝑘𝑘)}_(−𝜔𝜔₂_{𝑚𝑚+𝑘𝑘)}^𝐹𝐹⁰^{𝜔𝜔𝑐𝑐}₂_{+(𝜔𝜔𝑐𝑐 )}₂cos 𝜔𝜔𝑡𝑡 +_(−𝜔𝜔₂_{𝑚𝑚+𝑘𝑘)}^𝐹𝐹⁰^{𝜔𝜔𝑐𝑐}₂_{+(𝜔𝜔𝑐𝑐 )}₂sin 𝜔𝜔𝑡𝑡