Membangun aturan kabur dari data numeris.

A B S T R A K

Membangun aturan kabur dari data numeris dapat dicari dengan beberapa cara, yaitu metode penyebaran balik, metode kuadrat terkecil dan metode bentuk tabel. Metode bentuk tabel dipilih karena metode ini lebih mudah dan lebih sederhana daripada kedua metode lainnya.

ABSTRACT

Generating fuzzy rules from numerical data can be found with many ways, like back-propagation algorithm, orthogonal least squares algorithm, and table-lookup scheme. Table-lookup scheme method is a simple method and more easier than other methods.

MEMBANGUN ATURAN KABUR DARI DATA NUMERIS

Skripsi

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Oleh:

Athanasia Anisa Angki P NIM : 003114018

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

GENERATING FUZZY RULES OF NUMERICAL DATA

Thesis

Presented as Partial Fulfillment of Requirements to Obtain the Sarjana Sains Degree

In Mathematics

By

Athanasia Anisa Angki P Student Number : 003114018

MATHEMATICS DEPARTEMENT SCIENCE AND TECHNOLOGY FACULTY

SANATA DHARMA UNIVERSITY YOGYAKARTA

!

"

#

$%

&'()*+

"

,

,

'

#

"

,

-,

)

#

.

,

PERNYATAAN KEASLIAN KARYA

Saya menyatakan dengan sesungguhnya bahwa skripsi yang saya tulis ini tidak

memuat karya atau bagian karya orang lain, kecuali yang telah disebutkan dalam

kutipan daftar pustaka, sebagaimana layaknya karya ilmiah.

Yogyakarta, 2008

Penulis

KATA PENGANTAR

Dengan mengucap puji dan syukur kepada Tuhan Yang Maha Esa yang

telah memberikan rahmat-Nya sehingga skripsi yang berjudul “ Membangun

Aturan Kabur dari Data Numeris” ini dapat diselesaikan dengan baik.

Penyusunan skripsi ini dimaksudkan untuk memenuhi salah satu

persyaratan untuk memperoleh gelar Sarjana Sains (S.Si) pada Fakultas Sains dan

Teknologi Universitas Sanata Dharma.

Pada kesempatan ini juga penulis mengucapkan banyak terima kasih pada

berbagai pihak yang telah ikut membantu dalam menyelesaikan Skripsi ini,

khususnya pada:

1. Bapak Eko Hari Parmadi, S.Si.,M.Kom, selaku dosen pembimbing dan

Dosen Ilmu Komputer Universitas Sanata Dharma

2. Ibu Lusia Krismiyati, S.,Si, M.,Si selaku Ketua Program Studi

Matematika.

3. Ibu M. V. Any Herawati, S.Si.,M.Si, selaku pembimbing akademik dan

dosen FMIPA, Bapak Y.G. Hartono, S.Si. M.Sc, Bapak Ir. Ig. Aris

Dwiatmoko, M.Sc dan juga seluruh Dosen Fakultas Matematika dan Ilmu

Pengetahuan Alam Universitas Sanata Dharma yang tidak bisa disebutkan

satu persatu.

4. Ibu Warni, Pak Tukijo, dan Mbak Linda selaku staf administrasi FMIPA

5. Bapak Paulus Salam, Ibu Yohana Sri Aryani, Hendy dan Yoga. Terima

kasih banyak atas dukungan, motivasi dan kasih sayang yang kalian

berikan selama ini, semua itu tidak bisa diungkapkan dengan kata-kata.

6. Untuk semua pihak yang tidak dapat disebutkan satu persatu yang turut

membantu dalam penyelesaian Tugas Akhir ini.

Penulis menyadari bahwa tugas akhir ini jauh dari sempurna, oleh sebab

itu penulis mengharapkan saran dan kritik yang membangun. Akhir kata penulis

berharap semoga dengan tersusunnya skripsi ini dapat bermanfaat bagi mahasiswa

Jurusan matematika khususnya dan bagi Mahasiswa Universitas Sanata Dharma

pada umumnya.

Yogyakarta, Maret 2008

Penulis

DAFTAR ISI

HALAMAN JUDUL ... i

HALAMAN PERSETUJUAN PEMBIMBING ... ii

HALAMAN PENGESAHAN... iii

HALAMAN PERSEMBAHAN... iv

PERNYATAAN KEASLIAN KARYA ... v

LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI KARYA ILMIAH UNTUK KEPENTINGAN AKADEMIS... vi

KATA PENGANTAR ... vii

DAFTAR ISI ... ix

DAFTAR GAMBAR... xi

DAFTAR TABEL ... xiii

ABSTRAK ... xiv

ABSTRACT... xv

BAB I PENDAHULUAN A. Latar belakang masalah... 1

B. Perumusan Masalah ... 2

C. Pembatasan Masalah ... 2

D. Tujuan Penulisan ... 2

E. Manfaat Penulisan... 2

BAB II LANDASAN TEORI

A. Himpunan Kabur ... 5

B. Operasi pada Himpunan Kabur ... 12

C. Perampatan Operasi Baku pada Himpunan Kabur ... 19

D. Logika Proposisi ... 21

E. Logika Kabur... 26

F. Relasi Kabur ... 29

G. Proposisi Kabur ... 34

H. Implikasi Kabur ... 36

I. Basis Pengetahuan ... 39

BAB III MEMBANGUN ATURAN KABUR DARI DATA NUMERIS... 43

BAB IV PENERAPAN ATURAN KABUR DARI DATA NUMERIS PADA SISTEM KENDALI TRUK A. Permasalahan pada Kontrol Sistem Kendali Truk... 50

B. Membangun Aturan Kabur dari Data Numeris untuk Sistem Kendali Truk... 51

BAB V KESIMPULAN DAN SARAN... 72

DAFTAR GAMBAR

Gambar 2.1.1. Grafik Fungsi Keanggotaan Hinpunan Kabur A~ ... 9

Gambar 2.1.2. Fungsi Keanggotaan Segitiga

(

x;a,b,c

)

... 11

Gambar 2.1.3. Fungsi Keanggotaan Trapesium

(

x;a,b,c,d

)

... 12

Gambar 2.2.1. Grafik Fungsi Keanggotaan Hinpunan Kabur A~ ... 15

Gambar 2.2.2. Grafik Fungsi Keanggotaan Hinpunan Kabur B~ ... 16

Gambar 2.2.3. Grafik Fungsi Keanggotaan Hinpunan Kabur A′~ ... 18

Gambar 2.2.4. Grafik Fungsi Keanggotaan Hinpunan Kabur B′~ ... 18

Gambar 2.5.1. Gambar Kecepatan Mobil ... 28

Gambar 2.9.1. Fungsi Keanggotaan Himpunan-himpunan Kabur yang terkait dengan Nilai-nilai Linguistik untuk Variabel y pada Semesta

[

−a,a

]

... 40

Gambar 3.1 Himpunan Kabur Input ... 44

Gambar 3.2 Himpunan Kabur Output... 45

Gambar 3.3. Membagi Input dan Output menjadi Himpunan Nilai Linguistik dan Korespondensi Fungsi Keanggotaan ... 46

Gambar 3.4. Ilustrasi tabel Look-up dari Aturan Dasar Kabur ... 48

Gambar 4.1. Diagram Simulasi Truk dan Daerah Muatan... 50

Gambar 4.2. Fungsi Keanggotaan Kabur untuk µ

( )

φ ... 52

Gambar 4.4. Fungsi Keanggotaan Kabur untuk µ

( )

θ ... 55

Gambar 4.5. Hasil Akhir Membangun Aturan Kabur dari Data

DAFTAR TABEL

Tabel 2.4.1.1. Tabel Nilai Kebenaran Negasi ... 22

Tabel 2.4.1.2. Tabel Nilai Kebenaran Konjungsi ... 23

Tabel 2.4.1.3. Tabel Nilai Kebenaran Disjungsi ... 24

Tabel 2.4.1.4. Tabel Nilai Kebenaran Implikasi... 25

Tabel 2.4.1.5. Tabel Nilai Kebenaran Biimplikasi ... 26

Tabel 4.1. Panjang Lintasan Dimulai dari

(

)

(

0

)

0 0,φ = 1,0 x ... 51

A B S T R A K

Membangun aturan kabur dari data numeris dapat dicari dengan beberapa cara, yaitu metode penyebaran balik, metode kuadrat terkecil dan metode bentuk tabel. Metode bentuk tabel dipilih karena metode ini lebih mudah dan lebih sederhana daripada kedua metode lainnya.

ABSTRACT

Generating fuzzy rules from numerical data can be found with many ways, like back-propagation algorithm, orthogonal least squares algorithm, and table-lookup scheme. Table-lookup scheme method is a simple method and more easier than other methods.

BAB I

PENDAHULUAN

A. Latar Belakang Masalah

Di dalam membangun aturan kabur dari data numeris terdapat beberapa

metode antara lain metode penyebaran balik, metode kuadrat terkecil ortogonal

dan metode bentuk tabel. Konsep dasar dari metode penyebaran balik adalah

metode ini dapat dipakai pada berbagai jaringan arus-maju. Jika sistem logika

kabur digambarkan sebagai jaringan arus-maju maka dapat digunakan metode ini

untuk menyelesaikannya. Sedangkan metode kuadrat terkecil ortogonal digunakan

untuk menentukan fungsi basis kabur dan parameter sisa. Metode ini

menggunakan prosedur one-pass dan ini lebih cepat dibandingkan metode

penyebaran balik. Sehingga pada metode penyebaran balik dan metode kuadrat

terkecil ortogonal, metode-metode tersebut tidak cukup sederhana karena

membutuhkan perhitungan secara intensif.

Di dalam membangun aturan kabur dari data numeris kita menemukan

metode yang sangat sederhana untuk merancang sistem kabur yang sesuai yang

ditunjukkan dengan operasi nilai tunggal pada pasangan terurut numeris dan

aturan bahasa kabur JIKA-MAKA.

Tulisan ini akan membahas tentang membangun aturan kabur dari data

pasangan berurutan, mengumpulkan aturan yang dibangun dan aturan bahasa

menjadi sebuah dasar aturan kabur pada umumnya dan untuk membentuk akhir

B. Perumusan Masalah

Pokok permasalahan yang akan dibahas dalam tulisan ini dapat

dirumuskan sebagai berikut :

1. Bagaimana membangun aturan kabur dari data numeris?

2. Bagaimana penerapan membangun aturan kabur dari data numeris?

C. Pembatasan Masalah

Dalam topik ini masalah dibatasi pada data yang dimasukkan yaitu data

berupa pasangan terurut dan aturan yang digunakan yaitu implikasi kabur

Mamdani.

D. Tujuan Penulisan

Tujuan penulisan skripsi ini adalah menjawab masalah-masalah yang

terdapat pada perumusan masalah yaitu :

1. Dapat membangun aturan kabur dari data numeris

2. Implementasi membangun aturan kabur dari data numeris

E. Manfaat Penulisan

Manfaat yang diperoleh dari mempelajari topik ini adalah diperoleh cara

F. Metode Penulisan

Metode yang digunakan penulis adalah studi pustaka, yaitu dengan

mempelajari buku-buku yang berkaitan dengan membangun aturan kabur dari

data numeris.

G. Sistematika Penulisan

BAB I : PENDAHULUAN

A. Latar Belakang Masalah

B. Rumusan Masalah

C. Pembatasan Masalah

D. Tujuan Penulisan

E. Manfaat Penulisan

F. Metode Penulisan

G. Sistematika Penulisan

BAB II : LANDASAN TEORI

A. Himpunan Kabur

B. Operasi pada Himpunan Kabur

C. Perampatan Operasi Baku pada Himpunan Kabur

D. Logika Proposisi

E. Logika Kabur

F. Relasi Kabur

H. Implikasi Kabur

I. Basis Pengetahuan

BAB III : MEMBANGUN ATURAN KABUR DARI DATA

NUMERIS

BAB IV : PENERAPAN ATURAN KABUR DARI DATA

NUMERIS PADA SISTEM KENDALI TRUK

A. Permasalahan pada Kontrol Sistem Kendali Truk

B. Membangun Aturan Kabur dari Data Numeris untuk

Sistem Kendali Truk

BAB V : KESIMPULAN DAN SARAN

A. Kesimpulan

BAB II

LANDASAN TEORI

A. Himpunan Kabur

Banyak situasi di dalam kehidupan sehari-hari yang kita jumpai terdefinisi

secara tidak tegas, misalnya himpunan orang miskin, himpunan orang pandai,

himpunan orang yang tinggi, dan sebagainya. Misalnya, murid yang

mempunyai nilai rata-rata 8 mempunyai derajat keanggotaan 0.9, yaitu

( )

8 =0.9

pandai

µ , dan murid yang mempunyai nilai rata-rata 6 mempunyai

derajat keanggotaan 0.5, yaitu µpandai

( )

6 =0.5, dalam himpunan kabur

“pandai” tersebut.

Teori himpunan kabur diperkenalkan oleh Lotfi A. Zadeh pada tahun

1965. Zadeh membuat suatu terobosan baru dengan memperluas konsep

“himpunan” klasik menjadi himpunan kabur untuk mengatasi permasalahan

himpunan dengan batas yang tidak tegas itu. Zadeh juga mengaitkan himpunan

semacam itu dengan suatu fungsi yang menyatakan derajat kesesuaian

unsur-unsur dalam semestanya dengan konsep yang merupakan syarat keanggotaan

himpunan tersebut. Fungsi itu disebut fungsi keanggotaan dan nilai fungsi itu

disebut derajat keanggotaan suatu unsur dalam himpunan itu (Susilo, 2003).

Definisi 2.1.1

Fungsi karakteristik dari suatu himpunan Aadalah suatu fungsi dari himpunan

{

0,1

}

:X →

A

χ

Definisi 2.1.2

Himpunan kabur adalah himpunan di mana nilai fungsi karakteristik untuk tiap

elemennya ada di dalam selang tertutup

[

0,1

]

.

Definisi 2.1.3

Diberikan himpunan semesta X . Suatu himpuanan kabur A~ dalam semesta X

adalah pemetaan µ_A~ dari X ke selang

[

0,1

]

, yaitu ~ :X →

[

0,1

]

A

µ

dimana nilai fungsi µ_A~

( )

x menyatakan derajat keanggotaan unsur x∈X dalam

himpunan kabur A~.

Nilai fungsi sama dengan 1 menyatakan keanggotaan penuh, dan nilai

fungsi sama dengan 0 menyatakan samasekali bukan anggota himpunan kabur

tersebut. Jadi fungsi keanggotaan dari suatu himpunan tegas Adalam semesta X

adalah pemetaan dari X ke himpunan

{ }

0,1 , yang tidak lain daripada fungsi

karakteristik χ_A, yaitu:

( )

∉ ∈ =

A x

A x x

A

jika 0

jika 1 χ

Suatu himpunan kabur A~ dalam semesta pembicara X dapat dinyatakan

sebagai himpunan pasangan terurut

( )

(

)

{

x x x X

}

A= , _A~ ∈

~

dimana µ_A~ adalah fungsi keanggotaan dari himpunan kabur A~, yang merupakan

suatu pemetaan dari himpunan semesta X ke selang tertutup

[ ]

0,1 .

Apabila semesta X adalah himpunan yang kontinu, maka himpunan kabur

A~ seringkali dinyatakan dengan:

( )

x x A

X x

A

∈

= ~

~ µ

dimana tanda pengintegralan bukan notasi pengintegralan seperti yang dikenal

dalam kalkulus, melainkan menyatakan himpunan semua unsur x∈X bersama

dengan derajat keanggotaannya dalam himpunan kabur A~.

Contoh 2.1.1

Misalkan A adalah himpunan bilangan asli yang dekat dengan 10, dimana R

adalah himpunan bilangan asli dari 1≤r≤15 dan himpunan kabur A~ merupakan

himpunan bilangan real yang dekat dengan 10 yang dapat dinyatakan sebagai

(

−

)

=

+ =

∈

x x

A

R x

2

10 1

1 ~

14 / 1 . 0 13 / 1 . 0 12 / 2 . 0 11 / 5 . 0 10 / 1 9 / 5 . 0 8 / 2 . 0 7 / 1 . 0 6 / 1 .

0 + + + + + + + +

=

Dalam penyajian himpunan kabur, derajat keanggotaan 0 biasanya tidak

dituliskan.

Apabila semesta X adalah himpunan yang diskret, maka himpunan kabur

( )

x x A

X x

A

∈

= ~

~

µ

dimana tanda sigma bukan menyatakan operasi jumlahan seperti yang dikenal

dalam aritmatika, tetapi menyatakan himpunan semua unsur x∈X bersama

dengan derajat keanggotaannya dalam himpunan kabur A~.

Contoh 2.1.2

Dalam semesta X =

{

−5,−4,−3,−2,−1,0,1,2,3,4,5

}

dimana X adalah

himpunan bilangan bulat dari −5≤ x≤5, himpunan kabur A~ adalah himpunan

bilangan bulat yang dekat dengan nol yang dapat dinyatakan sebagai

( )

x x A

X x

A

∈

= ~

~

µ =

= 0/-5 + 0.1/-4 + 0.3/-3 + 0.5/-2 + 0.7/-1 + 1/0 + 0.7/1 + 0.5/2 + 0.3/3 + 0.1/4 +

0/5

Contoh 2.1.3

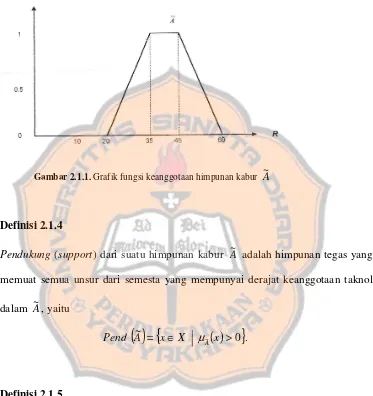
Diberikan himpunan kabur A~ dengan fungsi keanggotaan didefinisikan sebagai

berikut :

( )

≤ ≤ −

≤ ≤

≤ ≤ −

≤ ≤ ≤

≤

=

60 45

jika 15

60

45 35

jika 1

35 20

jika 15

20

100 60

atau 20 0

jika 0

~

x x

x x x

x x

x

A

Maka grafik fungsi keanggotaannya dilukiskan sebagai berikut :

Gambar 2.1.1. Grafik fungsi keanggotaan himpunan kabur A~

Definisi 2.1.4

Pendukung (support) dari suatu himpunan kabur A~ adalah himpunan tegas yang

memuat semua unsur dari semesta yang mempunyai derajat keanggotaan taknol

dalam A~, yaitu

( )

A~ =

{

x∈X ~

( )

x >0

}

Pend µ_A .

Definisi 2.1.5

Tinggi (height) dari suatu himpunan kabur A~ didefinisikan sebagai

( )

A

{

( )

x

}

Tinggi _A

X x

~

sup ~

µ ∈

= .

Definisi 2.1.6

• Jika nilai purata (pusat rata-rata) dari semua titik di mana fungsi

keanggotaan himpunan kabur itu mencapai nilai maksimum adalah

berhingga, maka pusat himpunan kabur itu adalah nilai purata (pusat

rata-rata) tersebut.

• Jika nilai purata itu takhingga positif (negatif), maka pusat himpunan

kabur itu adalah yang terkecil (terbesar) di antara semua titik yang

mencapai nilai fungsi keanggotaan maksimum.

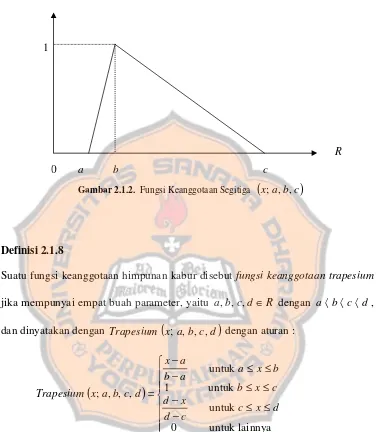
Definisi 2.1.7

Suatu fungsi keanggotaan himpunan kabur disebut fungsi keanggotaan segitiga

jika mempunyai tiga buah parameter, yaitu a,b,c∈R dengan a b c, dan

dinyatakan dengan Segitiga

(

x;a,b,c

)

dengan aturan :

(

)

− ≤ ≤

−

≤ ≤ −

−

=

lainnya untuk

0

untuk untuk

c b, a, x;

Segitiga c b b x c

x c

b x a a

b a x

Fungsi keanggotaan tersebut juga bisa dinyatakan dengan persamaan

sebagai berikut :

(

; , ,

)

max min , ,0 .

− − − − =

b c

x c a b

a x c

Definisi 2.1.8

Suatu fungsi keanggotaan himpunan kabur disebut fungsi keanggotaan trapesium

jika mempunyai empat buah parameter, yaitu a,b,c,d∈R dengan a b c d,

dan dinyatakan dengan Trapesium

(

x;a,b,c,d

)

dengan aturan :

(

)

≤ ≤ −

−

≤ ≤

≤ ≤ −

−

=

lainnya untuk

0

untuk untuk 1

untuk

, , , ;

d x c c

d x d

c x b

b x a a

b a x

d c b a x Trapesium

Fungsi keanggotaan tersebut juga bisa dinyatakan dengan persamaan

sebagai berikut :

(

; , , ,

)

max min ,1, ,0 .

− − −

− =

c d

x d a b

a x d

c b a x Trapesium

0 a b c

1

R

B. Operasi pada Himpunan Kabur

Seperti halnya pada himpunan tegas, kita dapat mendefinisikan operasi

uner “komplemen” dan operasi-operasi biner “gabungan” dan “irisan” pada

himpunan kabur. Karena suatu himpunan tegas dapat dinyatakan secara lengkap

dengan fungsi karakteristiknya, maka ketiga operasi pada himpunan tegas itu

dapat didefinisikan dengan menggunakan fungsi karakteristik itu.

Definisi 2.2.1

Komplemen dari suatu himpunan kabur A~adalah himpunan kabur A′~ dengan

fungsi keanggotaan

( )

x _A

( )

x

A~ 1 µ~

µ _′ = −

1

[image:30.612.133.509.101.586.2]

0 a b c d R

Contoh 2.2.1

Diberikan semesta X adalah nilai-nilai ujian, X=

{

10,20,30, ,100

}

.

Himpunan kabur A~ didefinisikan himpunan kabur “Tinggi” yang dinyatakan :

=

A~ 0.1/50 + 0.3/60 + 0.5/70 + 0.8/80 +1/90 + 1/100

dan himpunan kabur B~ didefinisikan himpunan kabur “Sedang” yang dinyatakan

=

B~ 0.1/30 + 0.5/40 + 0.5/50 + 1/60 + 0.8/70 + 0.5/80

Maka komplemen dari himpunan kabur A~ adalah

= ′

A~ 1/10 + 1/20 + 1/30 + 1/40 + 0.9/50 + 0.7/60 + 0.5/70 + 0.2/80

dan komplemen dari himpunan kabur B~ adalah

= ′

B~ 1/10 + 1/20 + 0.9/30 + 0.5/40 + 0.5/50 + 0.2/70 + 0.5/80 + 1/90 +

1/100

dimana komplemen dari himpunan kabur A~ didefinisikan sebagai himpunan

kabur “Tidak Tinggi” dan komplemen dari himpunan kabur B~ didefinisikan

sebagai himpunan kabur “Tidak Sedang”.

Definisi 2.2.2

Gabungan dua buah himpunan kabur A~ dan himpunan kabur B~ adalah himpunan

kabur A~∪B~ dengan fungsi keanggotaan:

( )

x

{

_A

( )

x _B

( )

x

}

B

A~ ~ max µ~ ,µ~

µ _∪ =

Contoh 2.2.2

Dari contoh 2.2.1, gabungan dari himpunan kabur A~ dan himpunan kabur B~

adalah 100 / 1 90 / 1 80 / 8 . 0 70 / 8 . 0 60 / 1 50 / 5 . 0 40 / 5 . 0 30 / 1 . 0 ~ ~ + + + + + + + = ∪B A Definisi 2.2.3

Irisan dua buah himpunan kabur A~ dan himpunan kabur B~ adalah himpunan

kabur A~∩B~ dengan fungsi keanggotaan

( )

x

{

_A

( )

x _B

( )

x

}

B

A~ ~ min µ~ ,µ~

µ _∩ =

untuk setiap x∈X .

Contoh 2.2.3

Dari contoh 2.2.1, irisan dari himpunan kabur A~ dan himpunan kabur B~ adalah

80 / 5 . 0 70 / 5 . 0 60 / 3 . 0 50 / 1 . 0 ~ ~ + + + = ∩B A Contoh 2.2.4

Misalkan dalam semesta Χ = {-4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6} diketahui

himpunan-himpunan kabur =

~

A 0.3/-3 + 0.5/-2 + 0.7/-1 + 1/0 + 0.7/1 + 0.5/2

+0.3/3 dan =

~

B 0.1/-1 + 0.3/0 + 0.8/1 + ½ + 0.7/3 + 0.4/4 + 0.2/5, maka

~ ~

B

A∪ = 0.3/-3 + 0.5/-2 + 0.7/-1 + 1/0 + 0.8/1 + ½ + 0.7/3 + 0.4/4 + 0.2/5

~ ~

B

A∩ = 0.1/-1 + 0.3/0 + 0.7/1 + 0.5/2 + 0.3/3

Contoh 2.2.5

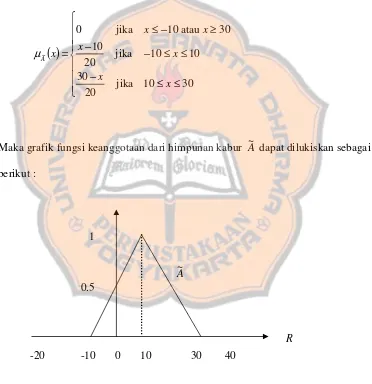
Misalkan A~ adalah himpunan kabur dengan fungsi keanggotaan :

( )

≤ ≤ −

≤ ≤ − −

≥ −

≤

=

30 10

jika 20

30

10 10

jika 20

10

30 atau 10 jika

0

~

x x

x x

x x

x

A

µ

Maka grafik fungsi keanggotaan dari himpunan kabur A~ dapat dilukiskan sebagai

[image:33.612.135.507.245.629.2]

berikut :

Gambar 2.2.1. Grafik fungsi keanggotaan himpunan kabur A~

1

0.5

A~

-20 -10 0 10 30 40

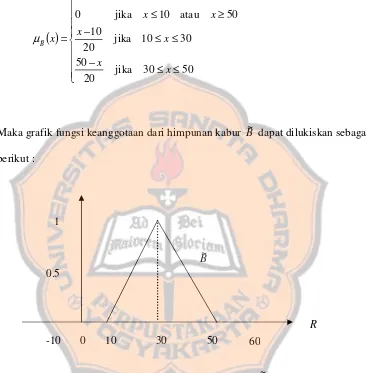
dan B~ adalah himpunan kabur dengan fungsi keanggotaan sebagai berikut :

( )

≤ ≤ −

≤ ≤ −

≥ ≤

=

50 30

jika 20

50

30 10

jika 20

10

50 atau

10 jika

0

~

x x

x x

x x

x

B

µ

Maka grafik fungsi keanggotaan dari himpunan kabur B~ dapat dilukiskan sebagai

[image:34.612.136.503.167.540.2]

berikut :

Gambar 2.2.2. Grafik fungsi keanggotaan himpunan kabur B~

Dengan menggunakan definisi komplemen himpunan kabur dapat diperoleh

fungsi keanggotaan komplemen dari himpunan kabur A~ sebagai berikut : 1

0.5

B~

-10 0 10 30 50

R

( )

≤ ≤ − − ≤ ≤ − − − ≥ − ≤ − = ′ 30 10 jika 20 10 1 10 10 jika 20 10 1 30 atau 10 jika 0 1 ~ x x x x x x x A µ

( )

≤ ≤ − ≤ ≤ − − ≥ − ≤ = ′ 30 10 jika 20 10 10 10 jika 20 10 30 atau 10 jika 1 ~ x x x x x x x A µ

dan fungsi keanggotaan komplemen dari himpunan kabur B~ sebagai berikut :

( )

≤ ≤ − − ≤ ≤ − − ≥ ≤ − = ′ 50 30 jika 20 50 1 30 10 jika 20 10 1 50 atau 10 jika 0 1 ~ x x x x x x x B µ

( )

≤ ≤ − ≤ ≤ − ≥ ≤ = ′ 50 30 jika 20 30 30 10 jika 20 30 50 atau 10 jika 1 ~ x x x x x x x B µ

Grafik fungsi keanggotaan komplemen dari himpunan kabur A~ dan B~ dapat

[image:35.612.135.488.95.616.2]

[image:36.612.146.464.106.554.2]

Gambar 2.2.3. Grafik fungsi keanggotaan himpunan kabur A′~

Gambar 2.2.4. Grafik fungsi keanggotaan himpunan kabur B′~

Ketiga operasi yang didefinisikan di atas disebut operasi baku

C. Perampatan Operasi Baku pada Himpunan Kabur

Definisi 2.31

Suatu pemetaan k:

[

0,1

]

→

[

0,1

]

disebut komplemen kabur jika memenuhi

aksioma sebagai berikut:

1. k

( )

0 =1dank

( )

1 =0 (syarat batas)

2. Jikax y, makak

( )

x ≥k

( )

y untuksemuax,y∈

[

0,1

]

(syarat

taknaik)

Suatu kelas pemetaan yang merupakan komplemen kabuar adalah kelas Sugeno

yang didefinisikan sebagai berikut:

( )

x x x

k

λ λ

+ − =

1 1

dengan parameter λ∈

(

−1,∞

)

.

Untuk setiap nilai parameter λ diperoleh suatu komplemen kabur. Untuk λ =0,

diperoleh operasi komplemen baku, yaitu k₀

( )

x =1−x, di mana x adalah derajat

keanggotaan suatu elemen dalam suatu himpunan kabur A~ dan k₀

( )

x adalah

derajat keanggotaan elemen tersebut dalam himpunan kabur A′~ (komplemen dari

himpunan kabur A~).

Definisi 2.3.2

Suatu pemetaan s:

[

0,1

] [

× 0,1

]

→

[

0,1

]

disebut gabungan kabur (norma-s) jika

memenuhi aksioma-aksioma sebagai berikut:

2. s

(

x,y

)

=s

(

y,x

)

(syarat komutatif)

3. Jika x≤ x′ dan y ≤ y′, maka s

(

x,y

)

≤s

(

x′,y′

)

untuk semua

[

0,1

]

,y∈

x (syarat takturun)

4. s

(

s

(

x,y

)

,z

)

=s

(

x,s

(

y,z

))

(syarat asosiatif)

Operasi gabungan baku, yaitu s

(

x,y

)

=max

{

x,y

}

, merupakan norma-s.

Definisi 2.3.3

Suatu pemetaan t:

[

0,1

] [

× 0,1

]

→

[

0,1

]

disebut irisan kabur (norma-t) jika

memenuhi aksioma-aksioma sebagai berikut:

1. t

(

x,1

)

=t

(

1,x

)

=x dan t

(

0,0

)

=0 (syarat batas)

2. t

(

x,y

)

=t

(

y,x

)

(syarat komutatif)

3. Jika x≤ x′ dan y≤ y′, maka t

(

x,y

)

≤t

(

x′,y′

)

untuk semua

[

0,1

]

,y∈

x (syarat takturun)

4. t

(

t

(

x,y

)

,z

)

=t

(

x,t

(

y,z

))

(syarat asosiatif)

Operasi irisan baku, yaitu t

(

x,y

)

=min

{

x,y

}

, merupakan suatu norma-t.

Contoh-contoh lain dari norma-t adalah sebagai berikut:

a. Darab aljabar: t_da

(

x,y

)

= xy

b. Darab Einstein:

(

)

(

x y xy

)

xy y

x t_de

− + − =

2 ,

c. Darab drastis:

(

)

= = =

lainnya jika

0

1 jika

1 jika

, y x

y x

D. Logika Proposisi

Logika proposisi mempelajari penalaran manusia dengan menggunakan

proposisi yaitu kalimat yang mempunyai nilai benar atau salah. Logika yang

hanya mengenal dua nilai kebenaran ini juga disebut logika dwinilai. Suatu

proposisi disebut proposisi atomik bila proposisi itu memuat proposisi lain

sebagai komponennya.

Contoh 4.1

• Matahari terbit pada pagi hari

• Bilangan 5 habis dibagi 2

Proposisi atomik dapat disajikan dengan menggunakan lambang huruf

kecil, seperti a, b, c, dst. Apabila lambang-lambang huruf itu menyajikan

proposisi yang tidak tertentu, maka lambang itu disebut variabel proposisi(Susilo,

2003).

2.4.1 Perangkai Logis

Semua proposisi bukan atomik merupakan proposisi majemuk dan semua

proposisi majemuk memiliki minimal satu perangkai logis. Perangkai logis yang

hanya melibatkan satu proposisi atomik disebut perangkai uner, sedangkan

perangkai logis yang melibatkan dua proposisi atomik disebut perangkai biner.

Ada lima buah perangkai logis yang akan dibahas, yaitu negasi, konjungsi,

2.4.1.1 Negasi

Negasi dari proposisi lain adalah proposisi yang diperoleh dengan

menambahkan kata “tidak” atau menyisipkan kata “bukan” pada proposisi semula.

Negasi dari suatu proposisi p disajikan dengan lambang ¬p.

Contoh 2.4.1.1

R x x

p= 2 ≥0, ∈

maka ¬p= x2 <0, x∈R atau ¬p= tidak benar bahwa x2 ≥0, x∈R

Definisi 2.4.5

Jika p suatu proposisi maka proposisi “tidak p” mempunyai nilai kebenaran

[image:40.612.131.506.232.558.2]

“salah” bila proposisi semula bernilai “benar” atau sebaliknya.

Tabel 2.4.1.1 Tabel Nilai Kebenaran Negasi

p ¬p

1 0

0 1

2.4.1.2 Konjungsi

Konjungsi dua buah proposisi adalah proposisi yang diperoleh dengan

menghubungkan kedua proposisi itu dengan menggunakan kata perangkai “dan”.

Contoh 2.4.1.2

3

=

p adalah bilangan prima ganjil

2

=

q adalah bilangan prima genap

maka p∧q =3 adalah bilangan prima ganjil dan 2 adalah bilangan prima

genap.

Definisi 2.4.6

Jika p dan q adalah dua buah proposisi maka proposisi majemuk “p danq”

bernilai “benar” bila keduanya bernilai benar.

Tabel 2.4.1.2 Tabel Nilai Kebenaran Konjungsi

p ¬p p∧q

1 1 1

1 0 0

0 1 0

0 0 0

2.4.1.3 Disjungsi

Disjungsi dua buah proposisi adalah proposisi yang diperoleh dengan

menghubungkan kedua proposisi itu dengan menggunakan kata perangkai“atau”

dan disajikan dengan lambang “∨”.

Contoh 2.4.1.3

7

=

7

=

q merupakan bilangan ganjil

maka p∨q =7 merupakan bilangan prima atau bilangan ganjil

Definisi 2.4.7

Jika p dan q adalah dua buah proposisi maka proposisi majemuk “patauq”

bernilai “benar” bila sekurang-kurangnya salah satu dari kedua proposisi itu

bernilai benar.

Tabel 2.4.1.3 Tabel Nilai Kebenaran Disjungsi

p ¬p p∨q

1 1 1

1 0 1

0 1 1

0 0 0

2.4.1.4Implikasi

Implikasi dua buah proposisi adalah proposisi yang diperoleh dengan

menghubungkan kedua proposisi itu dengan menggunakan kata perangkai “jika

… maka … (if … then …)” dan disajikan dengan lambang “p →q”. Proposisi

“ p” disebut dengan anteseden sedangkan proposisi “q” konsekuen.

Contoh 2.4.1.4

=

0 4

2

> −

=b ac

q .

=

→q

p jika persamaan kuadrat ax2+bx+c =0 mempunyai akar-akar

real maka b2−4ac>0.

Definisi 2.4.8

Jika p dan q adalah dua buah proposisi maka suatu implikasi bernilai “benar”

[image:43.612.133.475.250.522.2]

bila antesedennya bernilai salah atau konsekuennya bernilai benar.

Tabel 2.4.1.4 Tabel Nilai Kebenaran Implikasi

p q p→q

0 0 1

0 1 1

1 0 0

1 1 1

2.4.1.5Biimplikasi

Biimplikasi dua buah proposisi adalah proposisi yang diperoleh dengan

menghubungkan kedua proposisi itu dengan menggunakan kata perangkai

“…jhj…“ dan disajikan dengan lambang “p↔ q”.

Contoh 2.4.1.5

=

p dua garis saling berpotongan tegak lurus.

=

q dua garis saling membentuk sudut 0

Maka p ↔q adalah dua garis saling berpotongan tegak lurus jika dan

hanya jika kedua garis itu saling membentuk sudut 0

90 .

Definisi 2.4.9

Jika p dan q adalah dua buah proposisi maka proposisi majemuk

“ p jikadanhanya jikaq”bernilai “benar” jika kedua proposisi bernilai benar

atau kedua-duanya bernilai salah.

Tabel 2.4.1.5 Tabel Nilai Kebenaran Biimplikasi

p q p↔q

0 0 1

0 1 0

1 0 0

1 1 1

E. Logika Kabur

Logika yang biasanya kita pakai dalam kehidupan sehari-hari maupun

dalam penalaran ilmiah, yaitu logika dimana setiap proposisi (pernyataan)

mempunyai dua kemungkinan nilai, yaitu nilai benar atau nilai salah dan tidak

kedua-duanya (Susilo, 2003). Yang menjadi dasar dari logika kabur adalah logika

dengan tak berhingga banyak nilai kebenaran yang dinyatakan dengan bilangan

Definisi 2.5.1

Variabel linguistik adalah variabel yang nilainya bukan merupakan

bilangan tetapi kata-kata atau kalimat-kalimat dalam bahasa sehari-hari.

Variabel linguistik ditentukan oleh suatu rangkap-5

(

x,T, X,G,M

)

di mana x

adalah lambang variabelnya, T adalah himpunan nilai-nilai linguistik yang dapat

menggantikan x, X adalah semesta numeris dari nilai-nilai linguistik dalam T,

G adalah himpunan aturan-aturan sintakis yang mengatur pembentukan

istilah-istilah anggota T, dan M adalah himpunan aturan-aturan simantik yang

mengaitkan setiap istilah dalam T dengan suatu himpunan kabur dalam semesta

X (Susilo, 2003).

Contoh 2.5.1

Kecepatan sebuah mobil adalah variabel x yang mempunyai interval

[

0,V_max

]

,

dimana V_max adalah kecepatan maksimum mobil tersebut. Kita tentukan 3

himpunan kabur “lambat”, “sedang”, dan “cepat” dalam

[

0,V_max

]

seperti pada gambar 2.4.1. Jika kita lihat x sebagai variabel linguistik, maka “lambat”,

“sedang”, dan “cepat” juga sebagai variabel linguistik.

Maka bisa dikatakan “x adalah lambat”, “x adalah sedang”, dan “x adalah

[image:45.612.133.505.254.551.2]

Contoh 2.5.2

Bila variabel linguistik adalah “umur”, maka sebagai himpunan nilai-nilai

linguistik dapat diambil himpunan istilah-istilah T ={muda, sangat muda, agak

muda, tidak muda, tidak sangat muda, tidak muda dan tidak tua, agak tua, tua,

tidak sangat tua, sangat tua}, dengan semesta X =

[

0,100

]

, aturan semantik yang

mengaitkan setiap istilah dalam T dengan suatu himpunan kabur dalam semesta

X .

Definisi 2.5.2

Pengubah linguistik adalah suatu kata yang dipergunakan untuk mengubah

suatu kata/istilah menjadi kata/istilah yang baru dengan makna yang baru pula.

Dua peubah linguistik yang paling sering dipakai adalah “sangat” dan “agak”.

Contoh 2.5.3

Misalkan X =

{

1,2, ,5

}

dan himpunan kabur kecil didefinisikan

slow medium fast

Speed of car (mph)

Vmax

75 55

35 0

[image:46.612.133.509.113.519.2]

1

Maka menurut definisi diatas

sangat kecil=1/1+0.64/2+0.36/3+0.16/4+0.04/5

(

)

5 / 0016 . 0 4 / 0256 . 0

3 / 1296 . 0 2 / 4096 . 0 1 / 1

+ +

+ +

=

= sangat sangat kecil

kecil sangat

sangat

5 / 4472 . 0 4 / 6325 . 0 3 / 7746 . 0 2 / 8944 . 0 1 /

1 + + + +

= kecil agak

Definisi 2.5.3

Misal A himpunan kabur dalam X , maka sangat A adalah himpunan kabur

dalam X dengan fungsi keanggotaan

( )

[

( )

]

2

x x

A _A

sangat µ

µ =

Definisi 2.5.4

Misal A himpunan kabur dalam X, maka agak A adalah himpunan kabur dalam

X dengan fungsi keanggotaan

( )

[

( )

]

1 2

x x

A _A

agak µ

µ =

F. Relasi Kabur

Definisi 2.6.1

Misalkan R₁⊆ X×Y dan R₂⊆Y×Z adalah dua buah relasi tegas.

Z X R

R_{1 2} ⊆ ×

sedemikian sehingga

(

x,z

)

∈R₁ R₂ bila dan hanya bila terdapat

Y

y∈ sedemikian sehingga

(

x,y

)

∈R₁ dan

(

y,z

)

∈R₂.

Definisi 2.6.2

Relasi kabur R~ adalah relasi antara elemen-elemen dalam himpunan X

dengan elemen-elemen dalam himpunan Y yang didefinisikan sebagai bagian

kabur dari darab Cartesius X×Y, dapat dinyatakan dengan

(

)

(

)

(

)

(

)

{

x y x y x y X Y

}

R~= , ,µ_R~ , , ∈ × .

Jika X =Y, maka R~ disebut relasi kabur pada himpunan X .

Contoh 2.6.1

Misalkan X =

{

31,78,205

}

,Y =

{

1,27,119

}

dan R~ adalah relasi kabur “jauh

lebih besar dari” antara elemen-elemen X dan Y maka

(

)

(

)

(

)

(

)

(

)

(

)

(

205,119

)

4

. 0

27 , 205 7 . 0 1 , 205 9 . 0 27 , 78 3 . 0 1 , 78 5 . 0 27 , 31 1 . 0 1 , 31 3 . 0 ~

+

+ +

+ +

+ =

R

Contoh 2.6.2

Relasi kabur “hampir sama” antara bilangan-bilangan real dapat dinyatakan

dengan

(

)

(

)

( )

(

)

(

)

{

x y x y e x y R R

}

R~ = , , _R , = −x−y2 , ∈ ×

1

~

1 µ

(

)

(

)

_{( )}

(

)

∈ × +

=

= _{− −} x y R R

e y

x y x

R _{R x y} ,

1 1 ,

, , ~

2

~

2 µ

Definisi 2.6.3

Bila R~ adalah suatu relasi kabur pada semesta X×Y , maka invers dari R~ yang

dinyatakan dengan R~−1, adalah relasi kabur pada semesta Y×X dengan fungsi keanggotaan

(

y x

)

_R

(

x y

)

R~ 1 , µ~ ,

µ − =

untuk setiap

(

x,y

)

∈Y×X.

Maka

( )

R~−1 −1 ₌R~

untuk setiap relasi kabur R~.

Bila himpunan X dan Y keduanya berhingga, maka relasi kabur R~

antara elemen-elemen dalam himpunan X dengan elemen-elemen dalam

himpunan Y dapat dinyatakan dalam bentuk suatu matriks berukuran mxn

sebagai berikut

=

mn m

m

n n

a a

a

a a

a

a a

a

R

2 1

2 22

21

1 12

11

~

Definisi 2.6.4

Jika R~₁ adalah relasi kabur pada X×Y dan R~₂ adalah relasi kabur pada Y×Z,

maka komposisi relasi kabur R~₁dan R~₂, yang dinotasikan dengan R₁ R₂, adalah relasi kabur pada X×Z dengan fungsi keanggotaan

(

x z

)

t

(

_R

(

x y

)

_R

(

y z

)

)

Y y R

R1 2 , sup 1 , , 2 ,

~ ~

~

~ µ µ

µ

∈

=

di mana t adalah suatu norma-t.

Definisi 2.6.5

Komposisi sup-min diperoleh jika operator “min” sebagai norma-t, maka

diperoleh relasi komposit R₁ R₂ dengan fungsi keanggotaan

(

x z

)

{

_R

(

x y

)

_R

(

y z

)

}

Y y R

R1 2 , supmin 1 , , 2 ,

~ ~

~

~ µ µ

µ

∈

=

Definisi 2.6.6

Komposisi sup-darab diperoleh jika operator “darab aljabar” sebagai

norma-t, maka diperoleh relasi komposit R₁ R₂ dengan fungsi keanggotaan

(

x z

)

{

_R

(

x y

)

_R

(

y z

)

}

Y y R

R1 2 , sup 1 , , 2 ,

~ ~

~

~ µ µ

µ

∈

=

Contoh 2.6.3

Misalkan X =

{

31,78,205

}

,Y =

{

1,27,119

}

dan Z =

{

10,225,94

}

, dan relasi

= 4 . 0 7 . 0 9 . 0 0 . 0 3 . 0 5 . 0 0 . 0 1 . 0 3 . 0 ~ 1 R

Dan R~₂ adalah relasi kabur “jauh lebih kecil” antara elemen-elemen dalam Y

dengan Z dengan matriks sebagai berikut

= 0 . 0 5 . 0 0 . 0 3 . 0 8 . 0 0 . 0 5 . 0 9 . 0 1 . 0 ~ 2 R

Jika menggunakan komposisi sup-min, diperoleh

(

31,10

)

supmin

{

(

31,

)

,

(

,10

)

}

2 1 2 1 ~ ~ ~

~ y y

R R

Y y R

R µ µ

µ

∈

=

(

)

(

)

{

}

{

(

)

(

)

}

{

min 31,1 , 1,10 ,min 31,27 , 27,10 , max 2 1 2 1 ~ ~ ~ ~ R R R

R µ µ µ

µ

=

(

)

(

)

{

31,119 , 119,10

}

min 2 1 ~ ~ R R µ µ

}

{

}

{

}

{

}

{

min 0.3,0.1 ,min 0.1,0.0 ,min 0.0,0.0

}

max

=

{

0.1,0.0,0.0

}

max = 1 . 0 =

Relasi kabur komposit R₁ R₂ dengan komposisi sup-min dapat disajikan dengan matriks sebagai berikut

= = 5 . 0 9 . 0 1 . 0 5 . 0 5 . 0 1 . 0 3 . 0 3 . 0 1 . 0 0 . 0 5 . 0 0 . 0 3 . 0 8 . 0 0 . 0 5 . 0 9 . 0 1 . 0 4 . 0 7 . 0 9 . 0 0 . 0 3 . 0 5 . 0 0 . 0 1 . 0 3 . 0 ~ ~ 2 1 R R

Jika menggunakan komposisi sup-darab, diperoleh

(

31,10

)

sup

{

(

31,

)

,

(

,10

)

}

2 1 2 1 ~ ~ ~

~ y y

R R

Y y R

R µ µ

µ

∈

=

(

)

(

)

(

)

(

)

(

)

(

)

{

31,1 , 1,10 , 31,27 , 27,10 , 31,119 , 119,10

}

max 2 1 2 1 2 1 ~ ~ ~ ~ ~ ~ R R R R R

R µ µ µ µ µ

µ

( )( ) ( )( ) ( )( )

{

0.3 0.1, 0.1 0.0 , 0.0 0.0

}

max

=

{

0.03,0.0,0.0

}

max = 03 . 0 = .

Relasi kabur komposit R₁ R₂ dengan komposisi sup-darab dapat disajikan dengan matriks sebagai berikut

= = 45 . 0 81 . 0 09 . 0 25 . 0 45 . 0 05 . 0 15 . 0 27 . 0 03 . 0 0 . 0 5 . 0 0 . 0 3 . 0 8 . 0 0 . 0 5 . 0 9 . 0 1 . 0 4 . 0 7 . 0 9 . 0 0 . 0 3 . 0 5 . 0 0 . 0 1 . 0 3 . 0 ~ ~ 2 1 R R .

G. Proposisi Kabur

Definisi 2.7.1

Proposisi kabur adalah kalimat yang memuat predikat kabur, yaitu

predikat yang dapat direpresentasikan dengan suatu himpunan kabur.

Bentuk umum dari proposisi kabur

x adalah A

dimana x adalah suatu variabel linguistik dan predikat A adalah suatu nilai

linguistik dari x.

Definisi 2.7.2

Peryataan kabur adalah proposisi kabur yang mempunyai nilai kebenaran

Definisi 2.7.3

Nilai kebenaran dari suatu peryataan kabur disajikan dengan suatu

bilangan real dalam selang

[

0,1

]

dan disebut juga derajat kebenaran dari

peryataan kabur.

Derajat kebenaran dari peryataan kabur

0

x adalah A

Bila A~ adalah himpunan kabur yang dikaitkan dengan nilai linguistik A dan x₀

adalah suatu elemen titik dalam semesta X dari himpunan kabur A~, maka x₀

mempunyai derajat keanggotaan ~

( )

x₀

A

µ dalam himpunan kabur A~.

Definisi 2.7.4

Jika x adalah variabel linguistik dengan semesta numeris X dan y

adalah variabel linguistik dengan semesta numeris Y maka konjungsi kabur

x adalah A dan yadalah B

dimana A dikaitkan dengan himpunan kabur A~ dalam X , dan B dikaitkan

dengan himpunan kabur B~ dalam Y, dapat dipandang sebagai suatu relasi kabur

∧ dalam X ×Y dengan fungsi keanggotaan

(

x,y

)

t

(

µ_A~

( )

x ,µ_B~

( )

y

)

µ_∧ =

Definisi 2.7.5

Jika x adalah variabel linguistik dengan semesta numeris X dan y

adalah variabel linguistik dengan semesta numeris Y maka disjungsi kabur

x adalah A atau yadalah B

dimana A dikaitkan dengan himpunan kabur A~ dalam X , dan B dikaitkan

dengan himpunan kabur B~ dalam Y, dapat dipandang sebagai suatu relasi kabur

∨ dalam X×Y dengan fungsi keanggotaan

(

x,y

)

s

(

µ_A~

( )

x ,µ_B~

( )

y

)

µ_∨ =

dengan s adalah suatu norma-s.

H. Implikasi Kabur

Bentuk umum suatu implikasi kabur adalah

Bila x adalah A, maka y adalah B

dimana A dan B adalah predikat-predikat kabur yang dikaitkan dengan

himpunan-himpunan kabur A~ dan B~ dalam semesta X dan Y berturut-turut.

Sama seperti konjungsi dan disjungsi kabur, implikasi kabur juga

dipandang sebagai suatu relasi kabur dalam X×Y yang dilambangkan dengan

→.

dapat diganti dengan proposisi kabur "y adalahB". Implikasi kabur tersebut

dapat diinterpretasikan sebagai relasi kabur → dalam X×Y dengan fungsi

keanggotaan

(

x,y

)

s

(

k

(

µ_A~

( )

x

)

,µ_B~

( )

y

)

µ_→ =

dimana s adalah norma-s dan k adalah suatu komplemen kabur.

Definisi 2.8.1

Implikasi Dienes-Rescher diperoleh bila norma-s dan komplemen kabur

diambil operasi-operasi gabungan dan komplemen baku dan fungsi

keanggotaannya sebagai berikut

(

x y

)

(

_A

( )

x _B

( )

y

)

dr , max1 µ~ ,µ~

µ_→ = − .

Karena implikasi tegas p→q juga ekivalen dengan

(

p∧q

)

∨¬p, maka

implikasi kabur di atas juga dapat diinterpretasikan sebagai relasi kabur → dalam

Y

X× dengan fungsi keanggotaan

(

x,y

)

s

(

t

(

µ_A~

( )

x

)

,µ_B~

( )

x ,k

(

µ_A~

( )

y

)

)

µ_→ =

dimana s adalah norma-s, t adalah suatu norma-tdan k adalah suatu

komplemen kabur.

Definisi 2.8.2

Implikasi Zadeh diperoleh bila norma-s, norma-t dan k diambil

operasi-operasi gabungan, irisan dan komplemen baku sehingga diadapat fungsi

(

x y

)

(

(

_A

( )

x _B

( )

y

)

_A

( )

x

)

z , maxmin µ~ ,µ~ ,1 µ~

µ_→ = − .

Definisi 2.8.3

Implikasi Mamdani adalah implikasi kabur yang dapat juga dipandang

sebagai suatu konjungsi kabur, sehingga diperoleh

(

x,y

)

t

(

µ_A~

( )

x ,µ_B~

( )

y

)

µ_→ =

Bila sebagai norma-t diambil operasi baku “min”, maka diperoleh

(

x y

)

(

_A

( )

x _B

( )

y

)

mm , min µ~ ,µ~

µ_→ =

dan bila sebagai norma-t diambil operasi “darab aljabar”, maka diperoleh

(

x y

)

_A

( )

x _B

( )

y

md , µ~ µ~

µ_→ =

Contoh 2.8.1:

Misalkan diketahui semesta X =

{

1,2,3,4,5

}

dan Y =

{

50,60,70

}

dan implikasi

kabur cepat y maka banyak x Jika ,

dimana predikat “banyak” dan “cepat” berturut-turut dikaitkan dengan himpunan

kabur 5 / 1 4 / 8 . 0 3 / 6 . 0 2 / 4 . 0 1 / 2 . 0 ~ + + + + = A 70 / 1 60 / 1 . 0 50 / 4 . 0 ~ + + = B

Maka jika digunakan implikasi Dienes-Rescher, diperoleh

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

Jika digunakan implikasi Zadeh, diperoleh

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

5,50

)

0.7

(

5,60

)

1

(

5,70

)

4 . 0 70 , 4 8 . 0 60 , 4 7 . 0 50 , 4 4 . 0 70 , 3 6 . 0 60 , 3 6 . 0 50 , 3 4 . 0 70 , 2 6 . 0 60 , 2 6 . 0 50 , 2 6 . 0 70 , 1 8 . 0 60 , 1 8 . 0 50 , 1 8 . 0 + + + + + + + + + + + + + + = →_z

Dan jika digunakan implikasi Mamdani diperoleh

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

5,50

)

0.7

(

5,60

)

1

(

5,70

)

4 . 0 70 , 4 8 . 0 60 , 4 7 . 0 50 , 4 4 . 0 70 , 3 6 . 0 60 , 3 6 . 0 50 , 3 4 . 0 70 , 2 4 . 0 60 , 2 4 . 0 50 , 2 4 . 0 70 , 1 2 . 0 60 , 1 2 . 0 50 , 1 2 . 0 + + + + + + + + + + + + + + = →_mm atau

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

)

(

5,50

)

0.7

(

5,60

)

1

(

5,70

)

4 . 0 70 , 4 8 . 0 60 , 4 56 . 0 50 , 4 32 . 0 70 , 3 6 . 0 60 , 3 42 . 0 50 , 3 24 . 0 70 , 2 4 . 0 60 , 2 28 . 0 50 , 2 16 . 0 70 , 1 2 . 0 60 , 1 14 . 0 50 , 1 08 . 0 + + + + + + + + + + + + + + = →_md

I. Basis Pengetahuan

Basis pengetahuan dari suatu sistem kendali logika kabur terdiri dari basis

data dan basis kaidah. Basis data adalah himpunan fungsi-fungsi keanggotaan dari

himpunan-himpunan kabur yang terkait dengan nilai-nilai linguistik dari

variabel-variabel yang terlibat dalam sistem itu.

Contoh 2.9.1

Misal dalam suatu sistem kendali logika kabur, variabel ydengan semesta selang

tertutup

[

−a,a

]

mempunyai tujuh nilai linguistik sebagai berikut:

Sedang Negatif, yang dikaitkan dengan himpunan kabur S~−

Kecil Negatif, yang dikaitkan dengan himpunan kabur K~−

Mendekati Nol, yang dikaitkan dengan himpunan kabur 0~

Kecil Positif, yang dikaitkan dengan himpunan kabur K~+

Sedang Positif, yang dikaitkan dengan himpunan kabur S~+

Besar Positif, yang dikaitkan dengan himpunan kabur B~+

Maka basis data dari sistem itu memuat fungsi keanggotaan dari

himpunan-himpunan kabur yang terkait itu, misalnya berbentuk segitiga, sebagai berikut:

Basis kaidah adalah himpunan implikasi-implikasi kabur yang berlaku

sebagai kaidah dalam sistem itu. Bila sistem itu mempunyai mbuah kaidah

dengan

(

n+1

)

variabel, maka bentuk umum kaidah ke-i

(

i=1, ,n

)

adalah

sebagai berikut:

a a

−

−

B~ S~− K~− ~0 K~+ S~+ B~+

[image:58.612.135.504.237.524.2]

0

Gambar 2.9.1. Fungsi keanggotaan himpunan-himpunan kabur yang terkait dengan nilai-nilai linguistik untuk variabel y pada semesta

[

−a,a

]

Bila x₁ adalah A_i1 dan dan x_n adalah A_in, maka y adalah B_i

di mana x_j adalah variabel linguistik dengan semesta numeris X_j

(

j=1, ,n

)

.

Suatu basis kaidah diharapkan memenuhi beberapa kriteria sebagai

berikut:

1. Lengkap, yaitu untuk setiap

(

x₁, ,x_n

)

∈X₁× X_n terdapat i∈

{

1, ,m

}

sedemikian sehingga ~

( )

_j ≠0

Aij x

µ untuk semua j∈

{

1, ,n

}

. dengan

perkataan lain, untuk setiap nilai masukan terdapat sekurang-kurangnya satu

kaidah yang “tersulut”.

2. Konsisten, yaitu tidak terdapat kaidah-kaidah yang mempunyai anteseden

yang sama tetapi konsekuaennya berbeda.

3. Kontinu, yaitu tidak terdapat kaidah-kaidah dengan himpunan-himpunan

kabur yang terkait dala anteseden beririsan, tetapi himpunan-himpunan

kabur yang terkait dalam konsekuennya saling asing.

Contoh 2.9.2

Misalkan implikasinya melibatkan tiga variabel sebagai berikut:

Bila x adalah A dan y adalah B , maka z adalah C

di mana x, y,dan z adalah variabel-variabel dengan semesta selang tertutup

[

−a,a

] [

, −b,b

]

,dan

[

−c,c

]

berturut-turut, dan dengan tujuh nilai linguistik seperti

dalam Conto 2.9.1. maka basis kaidah dari sistem ini terdiri dari 49 kaidah, yang

y

z

−

B~ S~− K~− ~0 K~+ S~+ B~+

−

B~

−

S~

+

B~ S~+ 0~

−

K~ S~+ K~+ 0~

0

~ +

K~ 0~ K~−

+

K~

+

S~

0

~ −

K~ S~−

−

S~

+

S~

x

+

B~

0

~ −

S~ B~−

Misalnya salah satu kaidahnya berbunyi:

Bila x sedang negatif dan y kecil positif, maka z sedang positif

BAB III

MEMBANGUN ATURAN KABUR DARI DATA NUMERIS

Misal diberikan suatu himpunan input A=

{

x₁,x₂ ,x_n

}

dan himpunan

output B=

{

y₁,y₂ ,y_m

}

, sehingga diperoleh suatu himpunan pasangan terurut seperti di bawah ini

( ) ( ) ( ) ( ) ( ) ( )

(

1 1

)

2 1 1 1 1

2 1

1 ,x , , xn ;y , y , ,ym

x

( ) ( ) ( ) ( ) ( ) ( )

(

2 2

)

2 2 1 2 2

2 2

1 ,x , ,xn ; y , y , ,ym

x

( ) ( ) ( ) ( ) ( ) ( )

(

k

)

m k

k k n k

k

y y

y x x

x₁ , ₂ , , ; ₁ , ₂ , , (3.1) di mana k =1,2, ,l.

Misalkan kita berikan suatu contoh himpunan pasangan terurut dua input dan satu

output itu seperti di bawah ini:

( ) ( ) ( )

(

_{x ,x ;y}

)

_,

(

_x( )_,x( )_;y( )

)

_{, ,}

(

_x( )i _,x( )i _;y( )i

)

2 1 2

2 2 2 1 1 1 2 1

1 (3.2)

di mana i=1,2, ,l.

Tugas di sini adalah untuk membangun aturan kabur JIKA-MAKA dari

suatu himpunan pasangan berurutan dari (3.2).

Terdapat empat langkah dalam membangun aturan kabur dari data

3.1 Mendefinisikan Himpunan Kabur pada Ruang Semesta Input dan

Output

Misalkan kita mempunyai himpunan pasangan berurutan

(

x₁,x₂;y

)

. x₁

dan x₂ adalah sebuah input yang mempunyai interval

[

x₁−,x₁+

]

dan

[

x₂−,x₂+

]

dan y

adalah sebuah output dengan interval

[

y−,y+

]

, yang ditunjukkan oleh S3 (Besar

Negatif), S2 (Sedang Negatif), 1S (Kecil Negatif), CE (tengah atau mendekati

nol), 1B (Kecil Positif), B2 (Sedang Positif), dan B3 (Besar Positif).

Didefinisikan himpunan kabur untuk x₁ dan x₂ seperti pada gambar 3.1 di bawah ini.

Sedangkan himpunan kabur untuk y didefinisikan seperti pada gambar 3.2

seperti di bawah ini.

S2 S1 CE B1

( )x2

µ

B3 1.0

0.0

+

2

x

−

2

x

2

x

B2 1.0

0.0

S2 S1 CE B1 B2

( )

x1

µ

1

x

−

1

x +

1

[image:62.612.131.509.245.556.2]

x

3.2 Membangun Aturan Kabur dari Data Pasangan Berurutan

Langkah kedua dalam membangun aturan kabur dari data numeris adalah

membangun aturan kabur dari data pasangan berurutan yang diperlukan tiga

langkah.

Pertama, menentukan derajat keanggotaan dari x₁( )i ,x₂( )i, dan y ( )i pada

himpunan kabur yang berbeda. Sebagai contoh, x₁( )1 mempunyai derajat keanggotaan 0.8 di B1, mempunyai derajat keanggotaan 0.5 di B2, dan

mempunyai derajat keanggotaan 0 untuk semua himpunan kabur yang lain. Secara

sama, ( )2 2

x mempunyai derajat keanggotaan 1 di CE, mempunyai derajat

keanggotaan 0.8 di 1S dan derajat keanggotaan 0 untuk himpunan kabur yang

lain. Begitu juga dengan y( )1 mempunyai derajat keanggotaan 0.9 di CE, mempunyai derajat keanggotaan 0.8 di 1B , dan mempunyai derajat keanggotaan 0

untuk semua himpunan kabur yang lain seperti yang ditunjukkan pada gambar

3.3.

S2 S1 CE B1 B2

1.0

0.0

y

( )

y

µ

−

y y+

[image:63.612.132.506.272.550.2]

Kedua, menetapkan x₁( )i ,x₂( )i, atau y( )i sebagai himpunan kabur dengan derajat keanggotaan yang maksimum atau himpunan kabur yang mempunyai

derajat keanggotaan paling tinggi. Karena derajat keanggotaan ( )1 1

x pada

himpunan kabur 1B lebih besar daripada himpunan kabur B2 maka yang dipilih

adalah himpunan kabur 1B , sedangkan derajat keanggotaan x₂( )2 pada himpunan kabur CE lebih tinggi daripada derajat keanggotaan pada himpunan kabur 1S

maka yang dipilih adalah himpunan kabur CE dan derajat keanggotaan _y( )1 _pada

S2 S1 CE B1 B2

1.0

0.0

y

( )

y

µ

−

y y( )1 y( )2 y+

S2 S1 CE B1

( )x2

µ

B3 1.0

0.0

( )1 2

x x₂( )2 x2+

−

2

x

2

x

B2 1.0

0.0

S2 S1 CE B1 B2

( )

x1

µ

1

x

−

1

x ( )2

1

x x₁( )1 x₁+

0.8 0.5

[image:64.612.144.492.104.555.2]

himpunan kabur CE lebih tinggi daripada derajat keanggotaan pada B1 maka

yang dipilih adalah himpunan kabur CE.

Ketiga, setelah menentukan dan menetapkan derajat keanggotaannya maka

kita bisa menyusun aturan kabur dari data pasangan berurutan sebagai berikut:

JIKA x1 adalah A dan x2 adalah B, MAKA yadalah C

Sebagai contoh, kita tentukan derajat keanggotaan lalu ( )1 1

x , ( )2 2

x , dan _y( )1 _{lalu kita}

tetapkan x₁( )1 di 1B karena himpunan kabur 1B mempunyai derajat keanggotaan

paling tinggi dibandingkan dengan 2B atau yang lainnya, x₂( )2 di CE dan y( )1 di

CE. Sehingga bisa kita susun sebuah aturan sebagai berikut: JIKA x₁adalahB1 dan x₂adalahCE, MAKA yadalahB1.

3.3 Menentukan Derajat Kebenaran dari Masing-masing Aturan

Meskipun menggunakan beberapa pasangan data berurutan dan

masing-masing pasangan data berurutan membangun satu aturan, ada kemungkinan

terdapat beberapa aturan yang konflik, yaitu aturan yang mempunyai bagian JIKA

sama tetapi bagian MAKA berbeda. Salah satu cara untuk menyelesaikannya

adalah dengan menetapkan sebuah derajat kebenaran pada masing-masing aturan

yang membangun pasangan data berurutan dan hanya menerima aturan dari

kelompok aturan yang konflik yang mempunyai derajat maksimum.

Kita menggunakan implikasi Mamdani untuk menetapkan sebuah derajat

adalah B, MAKA yadalah C,” derajat dari aturan ini dinotasikan dengan

(