MODEL OPTIMISASI PENGGUNAAN BINATANG BURUAN SECARA KONSUMTIF AHDIANI FEBRIYANTI G

AHDIANI FEBRIYANTI

G54104020

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2008

ABSTRAK

AHDIANI FEBRIYANTI. Model Optimisasi Penggunaan Binatang Buruan secara Konsumtif. Dibimbing oleh FARIDA HANUMdan DONNY CITRA LESMANA.

Dalam suatu peternakan binatang buruan (game ranch), binatang buruan dikelola oleh suatu manajemen ranch. Dalam mengelola binatang buruan timbul beberapa permasalahan yang harus dihadapi, yakni memaksimumkan pendapatan dari hasil pemanenan. Terdapat dua pemodelan yang digunakan.

Model pertama digunakan untuk mencari solusi optimal dari pemanenan. Model ini terbagi ke dalam dua subproblem. Subproblem pertama menyelesaikan masalah optimisasi pendapatan dari hasil pemanenan spesies tunggal. Hasil ini kemudian digunakan sebagai input subproblem kedua yakni model optimisasi pendapatan dari pemanenan beberapa spesies.

Model kedua digunakan untuk menghitung pendapatan pada masa pembangunan ranch. Pendapatan pada model ini diperoleh dari modal pada akhir pembangunan peternakan. Dalam tugas akhir ini model diselesaikan dengan metode branch-and-bound, menggunakan software Lingo 8.0.

ABSTRACT

AHDIANI FEBRIYANTI. Optimisation Model Of Consumptive Use of Hunting Animals. Supervised byFARIDA HANUMandDONNY CITRA LESMANA.

On a game ranch, hunting animals are managed by a ranch management. In managing game ranch, there are some problems that have to be solved by management, such as maximizing return of harvesting hunted animals. There are two mathematical models that are used to accomplish these problems.

The first model is to obtain the optimal solution from harvesting games. This model is divided into two subproblems. The first subproblem is to obtain optimum return of harvesting one species. Further, the value was input into the second subproblem which is a model to optimize returns of harvesting multispecies.

The second model is to determine the capitals in the end of setting up the game ranch. Here, all models were solved using the branch and bound method using a computer software Lingo 8.0.

MODEL OPTIMISASI PENGGUNAAN BINATANG BURUAN SECARA

KONSUMTIF

Skripsi

Sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains pada Fakultas Matematika dan Ilmu Pengetahuan Alam

Institut Pertanian Bogor

Oleh :

AHDIANI FEBRIYANTI

G54104020

DEPARTEMEN MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

INSTITUT PERTANIAN BOGOR

BOGOR

2008

Judul : Model Optimal Penggunaan Binatang Buruan secara Konsumtif Nama : Ahdiani Febriyanti

NIM : G54104020

Menyetujui,

Mengetahui,

Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Institut Pertanian Bogor

Dr. Drh. Hasim, DEA NIP 131 578 806

Tanggal Lulus :

Pembimbing II

Donny Citra Lesmana, M.Fin.Math. NIP 132 311 927

Pembimbing I

Dra. Farida Hanum, M.Si. NIP 131 956 709

KATA PENGANTAR

Puji dan syukur penulis panjatkan ke hadirat Allah SWT atas segala nikmat, karunia, izin, dan pertolongan-Nya sehingga penulisan skripsi ini berhasil diselesaikan. Tema yang dipilih adalah Riset Operasi dengan judul Model Optimisasi Penggunaan Binatang Buruan secara Konsumtif. Skripsi ini merupakan syarat untuk menyelesaikan studi pada Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam, Institut Pertanian Bogor.

Terima kasih penulis ucapkan kepada :

1. Ibu Dra. Farida Hanum, M.Si. dan Bapak Donny Citra Lesmana, M.Fin.Math. selaku dosen pembimbing, atas segala kesabaran dan masukannya selama membimbing penulis; tak lupa kepada Bapak Prapto Tri Supriyo, M.Kom. selaku penguji;

2. Ibunda Siti Muktiyati dan Ayahanda Masir Saini yang banyak memberi wejangan dan nasihat serta dukungan yang tak terkira. Budhe (Alm.) Rie Suryaningsih yang sudah mengajarkan dan memberikan banyak hal yang sangat berharga dalam kehidupan penulis. Adikku Ginanjar Febrianto, atas semangat belajar dan mengingatkan yang tiada henti, semoga cepat menyusul;

3. keluarga besar (Alm.) Siti Solehah, terutama Bu Ii, Mbak Yanti, Mas Ujang, Jiyhaan, Iqbal, Lia, MbakYudi; keluarga besar (Alm.) Saini Nusu;

4. teman-teman mahasiswa matematika angkatan 41: Ndhit, Situl, Rite, Didutz, Liay, V3, Sifa, Mukti, Abangkh, Uwie, Ani, Liam, Hashi, Jannah, Ami, Iyank, Enyon, Echi, Ria, Enny, Roma, Titis, Tia, Nene’, Ayu, Ika, Mahar, Mami Eli, Rizul, Eeph, Roro, Mba’e, Nyid2, Zali, Majid, Cocom, Iboy, Aji, Amin, Great, Yadi, Dika, Yaya, Racil, Fred, Mimin, Mabok, Idris, Momo, Udin, Deni, Chumi, Chubby, Yos atas segenap dukungan, suka-duka dan kebahagiaan selama penulis menempuh studi di Departemen Matematika IPB;

5. kakak-kakak mahasiswa matematika angkatan 40: TehMita, TehWalida, dkk. atas segala bantuan dan motivasinya; adik-adik mahasiswa matematika angkatan 42 dan 43, terutama Hapsari yang telah bersedia menjadi pembahas; seluruh pengajar, pegawai, dan staf Departemen Matematika IPB;

6. teman-temanku di Paprica House: Pam Pam, Simaw, dan Epoy, terima kasih atas dukungan dan bantuan selama setahun ke belakang, semoga cepat menyusul;

7. staf dan pengajar MSC: Kak Taufik, Kak Hepy, Kak Syam, Engkus, Ikang, Basir, dkk. terima kasih atas bantuannya selama ini;

8. keluarga besar Klinik Pendidikan MIPA: MbakDesi, Pak Ridwan, TehIis, Teh Ema, Teh Mira, MbakAfni, dkk. yang telah memberikan pandangan dan pengalaman baru dalam hidup penulis;

9. keluarga besar Primagama Cimanggu, terima kasih atas kesempatan langka yang diberikan;

10. keluarga besar BEM FMIPA IPB angkatan 2006-2007: Bos, Dewi, Ona, dkk.; GUMATIKA IPB periode 2004-2005 dan 2005-2006 yang banyak memberi suka-duka dan pengalaman hidup;

11. juga pihak-pihak lain yang telah membantu penyusunan skripsi ini, yang tidak dapat disebutkan satu per satu.

Penulis menyadari bahwa dalam tulisan ini masih terdapat kekurangan dan jauh dari kesempurnaan, oleh karena itu penulis mengharapkan kritik dan saran yang membangun dari pembaca. Semoga tulisan ini dapat bermanfaat.

Bogor, Juli 2008

RIWAYAT HIDUP

Penulis dilahirkan di Jakarta Timur pada tanggal 22 Pebruari 1987 dari pasangan Masir Saini dan Siti Muktiyati. Penulis merupakan anak pertama dari dua bersaudara.

Pada tahun 2004 penulis lulus dari SMA Negeri 1 Purwokerto dan pada tahun yang sama lulus seleksi masuk IPB melalui jalur Undangan Seleksi Masuk IPB. Penulis memilih Program Studi Matematika, Departemen Matematika, Fakultas Matematika dan Ilmu Pengetahuan Alam.

Selama mengikuti perkuliahan, penulis aktif dalam kegiatan kemahasiswaan, di antaranya pada tahun 2004-2005 menjabat sebagai anggota seksi Kewirausahaan Gugus Mahasiswa Matematika (GUMATIKA) IPB periode 2004-2005 dan pada tahun 2005-2006 sebagai Kepala Departemen Sosial, Informasi, dan Komunikasi GUMATIKA IPB, serta mengikuti kepanitiaan dari beberapa kegiatan selama rentang waktu 2004-2007. Pada tahun 2006 penulis menjadi staf pengajar matematika pada Lembaga Bimbingan Belajar MSC dan tahun 2007 menjadi asisten tutorial Pengantar Matematika, asisten mata kuliah Kalkulus III dan Pemrograman Taklinear. Tahun 2008 penulis aktif menjadi staf pengajar Lembaga Bimbingan Belajar Klinik Pendidikan MIPA dan Primagama Cimanggu.

DAFTAR ISI

Halaman

DAFTAR TABEL ... viii

DAFTAR GAMBAR ... viii

DAFTAR LAMPIRAN ... viii

1 PENDAHULUAN Latar Belakang ... 1

Tujuan ... 1

2 LANDASAN TEORI Fungsi Linear dan Pertidaksamaan Linear ... 1

Pemrograman Linear ... 2

Integer Programming... 3

Pemrograman Linear Relaksasi ... 3

Metode Branch-and-Bound ... 3

3 DESKRIPSI DAN FORMULASI MASALAH... 7

4 PENYELESAIAN MASALAH MODEL OPTIMAL PENGGUNAAN HEWAN BURUAN ... 13

5 SIMPULAN DAN SARAN Simpulan ... 14

Saran ... 14

DAFTAR PUSTAKA ... 15

LAMPIRAN... 17

DAFTAR TABEL

Halaman

1 Data hidup rata-rata dari spesies 1 ... 13

2 Pendapatan pada model spesies tunggal (dalam $) ... 13

3 Data variabel pada model spesies campuran ... 13

4 Data proporsi kelas pakan spesies j... 13

5 Data tingkat tumbuh, carrying capacity, dan banyaknya AU dari setiap spesies ... 14

6 Tingkat suku bunga dan inflasi terhadap waktu ... 14

7 Data banyaknya hewan yang tersedia untuk dibeli ... 14

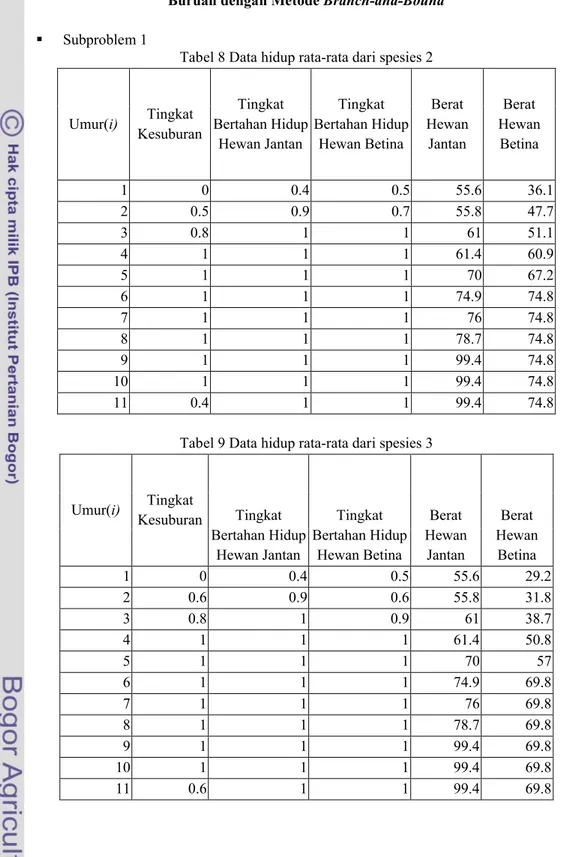
8 Data hidup rata-rata dari spesies 2 ... 20

9 Data hidup rata-rata dari spesies 3 ... 20

DAFTAR GAMBAR

Halaman 1 Daerah fisibel untuk PL-relaksasi dari IP ... 5

2 Daerah fisibel untuk subproblem 2 dan subproblem 3 ... 5

DAFTAR LAMPIRAN

Halaman 1 Syntax Program LINDO 6.1 untuk Menyelesaikan Masalah Pemrograman Linear dengan Metode Branch-and-Boundbeserta Hasil yang Diperoleh ... 17

2 Data Hipotetik untuk Implementasi Penyelesaian Masalah Desain Network Takberkapasitas dengan Metode Branch-and-Bound ... 20

3 Syntax dan Hasil Komputasi Program LINGO 8.0 untuk Masalah Optimisasi Penggunaan Binatang Buruan untuk Keperluan Konsumtif... 21

I PENDAHULUAN

1.1 Latar Belakang

Peternakan didefinisikan sebagai suatu usaha untuk membudidayakan hewan ternak. Jika dilihat dari jenis hewan yang diternakkan, terdapat berbagai jenis peternakan, salah satunya adalah peternakan hewan buruan (game ranch). Jenis hewan yang diternakkan pada peternakan hewan buruan di antaranya adalah rusa, babi hutan, badak bercula satu, dan sapi liar. Jika dilihat dari kepemilikannya, terdapat peternakan milik swasta (pribadi) dan peternakan milik pemerintah. Di beberapa negara, seperti Afrika Selatan, Kenya, dan Namibia, hewan buruan (games) dibudidayakan oleh sektor swasta di peternakan (ranch) untuk kebutuhan konsumtif. Penggunaan hewan buruan untuk kebutuhan konsumtif ini terbagi ke dalam dua kategori, yaitu:

 perburuan untuk memperoleh daging hewan (meat hunting);

 perburuan untuk tujuan olahraga (sport hunting), yakni perburuan untuk memperoleh bagian tertentu yang merupakan ciri khas dari suatu hewan, misalnya kulit, kepala, ataupun tanduk hewan.

Agar dapat memenuhi kebutuhan perburuan dibutuhkan pengelolaan ranchyang berada di bawah suatu manajemen (wildlife management). Manajemen yang baik diharapkan akan mampu menghasilkan pendapatan bagi pemilik ranch. Terdapat dua buah tujuan dalam pengelolaan ranch oleh manajemen, yaitu:

 memaksimumkan pendapatan dari hasil pemanenan ranch baik yang berasal dari meat hunting maupunsport hunting;

 memaksimumkan penggunaan modal pada tahap awal pembangunan ranch.

Permasalahan yang timbul dari tujuan manajemen ranch untuk memaksimumkan pendapatan dari hasil pemanenan ranch kemudian terbagi menjadi dua submasalah, yakni:

1. maksimisasi pendapatan dari hasil pemanenan suatu spesies hewan dalam ranch;

2. maksimisasi pendapatan dari hasil pemanenan semua spesies hewan dalam ranch.

Permasalahan yang harus ditangani oleh manajemen ini dimodelkan dengan suatu pemrograman linear. Pemrograman linear yang telah dibuat sebelumnya digunakan untuk menyelesaikan permasalahan yang dihadapi manajemen ranch (Jordie & Peddie, 1988). Dalam tulisan ini pendapatan dari hasil pemanenan suatu spesies hewan yang dikombinasikan dengan pendapatan dari hasil pemanenan spesies lain tidak digunakan sebagai salah satu faktor input dalam penyelesaian submasalah maksimisasi pendapatan dari hasil pemanenan semua spesies hewan dalam ranch

Dalam karya ilmiah ini akan dibahas permasalahan manajemen pada ranch, dengan pendapatan dari hasil pemanenan suatu spesies digunakan sebagai salah satu faktor input dalam penyelesaian dari submasalah maksimisasi pendapatan dari hasil pemanenan semua spesies hewan dalam ranch (Hearne et al., 2000) menggunakan bantuan software LINGO 8.0.

1.2 Tujuan

Tujuan penulisan karya ilmiah ini adalah menunjukkan peranan pemrograman linear dalam membantu manajemen ranchmengatasi permasalahan pokok yang ada dalam ranch.

II LANDASAN TEORI

Untuk memahami masalah optimisasi penggunaan binatang buruan untuk tujuan konsumtif dan teknik pemecahan yang digunakan dalam karya tulis ini, diperlukan beberapa konsep berikut ini.

Fungsi Linear dan Pertidaksamaan Linear Fungsi linear dan pertidaksamaan linear merupakan salah satu konsep dasar yang harus dipahami terkait dengan konsep pemrograman linear

Definisi 1 (Fungsi Linear)

Misalkan f x x( , ,..., )1 2 xn menyatakan suatu fungsi dalam variabel-variabel

1, ,..., .2 n

x x x Fungsi f x x( , ,..., )_{1 2} x_n dikatakan linear jika dan hanya jika untuk suatu himpunan konstanta c c1, ,..., ,2 cn 1 2 ( , ,..., )_n f x x x  c x_{1 1}c x_{2 2} ... c x_{n n}. (Winston, 2004) Sebagai gambaran, f x x( , )_{1 2}  x₁ 3x₂ merupakan fungsi linear, sementara

2

1 2 1 2

( , )

f x x x x bukan fungsi linear. Misalkan

b sembarang bilangan, suatu persamaan b x x x f( 1, 2,..., n) merupakan persamaan linear.

Definisi 2 (Pertidaksamaan Linear)

Untuk sembarang fungsi linear )

,..., , (x1 x2 xn

f dan sembarang bilangan ,b pertidaksamaan f(x1,x2,...,xn)b dan b x x x f( 1, 2,..., n) adalah pertidaksamaan linear. (Winston, 2004) Pemrograman Linear

Menurut Winston (2004), pemrograman linear (PL) atau linear programming adalah suatu masalah optimisasi yang memenuhi ketentuan-ketentuan sebagai berikut.

a) Tujuan masalah tersebut adalah memaksimumkan atau meminimumkan suatu fungsi linear dari sejumlah variabel keputusan. Fungsi yang akan dimaksimumkan atau diminimumkan ini disebut fungsi objektif.

b) Nilai variabel-variabel keputusannya harus memenuhi suatu himpunan kendala. Setiap kendala harus berupa persamaan linear atau pertidaksamaan linear.

c) Ada pembatasan tanda untuk setiap variabel dalam masalah ini. Untuk sembarang variabel xi, pembatasan tanda

menentukan xi harus taknegatif (xi 0)

atau tidak dibatasi tandanya (unrestricted in sign).

Suatu PL mempunyai bentuk standar seperti yang didefinisikan sebagai berikut.

Definisi 3 (Bentuk Standar PL) Pemrograman linear maks terhadap T z   c x Ax b x 0 (2.1)

dikatakan PL dalam bentuk standar, dengan x

dan c vektor-vektor berukuran n, vektor b

berukuran m, dan Amatriks berukuran m  n yang disebut sebagai matriks kendala, dengan m≤ n.

(Nash & Sofer, 1996) Sebagai catatan, yang dimaksud dengan vektor berukuran n adalah vektor yang memiliki dimensi (ukuran) n × 1.

Solusi Pemrograman Linear

Suatu masalah PL dapat diselesaikan dalam berbagai teknik, salah satunya adalah metode simpleks. Metode ini dapat menghasilkan suatu solusi optimal bagi masalah PL dan telah dikembangkan oleh Dantzig sejak tahun 1947, dan dalam perkembangannya merupakan metode yang paling umum digunakan untuk menyelesaikan PL. Metode ini berupa metode iteratif untuk menyelesaikan PL berbentuk standar.

Pada masalah PL (2.1), vektor x yang memenuhi kendala Ax b disebut solusi PL (2.1). Misalkan matriks A dapat dinyatakan sebagai A



B N



, dengan B adalah matriks berukuran m  m yang elemennya berupa koefisien variabel basis dan N merupakan matriks berukuran m (n m) yang elemen-elemennya berupa koefisien variabel nonbasis pada matriks kendala. Dalam hal ini matriks Bdisebut matriks basis untuk PL (2.1).

Misalkan x dapat dinyatakan sebagai vektor _{  }    B N x x

x , dengan xB adalah vektor variabel basis dan xN adalah vektor variabel nonbasis, maka Ax b dapat dinyatakan sebagai 





_ _   B N x Ax B N x . Bx + Nx_{B N} b (2.2) Karena matriks B adalah matriks taksingular, maka B memiliki invers, sehingga dari (2.2)

B

x dapat dinyatakan sebagai:

- .

 -1 -1

B N

x B b B Nx (2.3) Definisi 5 (Solusi Basis)

Solusi dari suatu PL disebut solusi basis jika memenuhi syarat berikut:

ii. kolom-kolom dari matriks kendala yang berpadanan dengan komponen taknol dari solusi tersebut adalah bebas linear.

(Nash & Sofer, 1996) Menurut Garfinkel & Nemhauser (1972), solusi dari suatu PL disebut solusi basis jika memenuhi  -1 ,

B

x B b x_N 0. Definisi 6 (Solusi Basis Fisibel)

Vektor x disebut solusi basis fisibel jika x merupakan solusi basis dan x0.

(Nash & Sofer, 1996) Ilustrasi solusi basis dan solusi basis fisibel diberikan dalam Contoh 1.

Contoh 1

Misalkan diberikan PL (2.4) berikut:

1 3 1 2 3 1 2 4 1 5 1 2 3 4 5 min 2 4 terhadap 2 4 2 10 5 , , , , 0, z x x x x x x x x x x x x x x x             (2.4) dari PL (2.4) diperoleh: 2 1 1 0 0 4 1 2 0 1 0 , 10 1 0 0 0 1 5          _{ } _{ }         A b . Misalkan dipilih



x3 x4 x5



dan



x1 x2



,  T  T B N x x

maka matriks basisnya adalah 1 0 0 0 1 0 0 0 1            B .

Dengan menggunakan matriks basis di atas didapatkan



0 0 ,







4 10 5 .



 T  1  T

N B

x x B b (2.5)

Solusi (2.5) merupakan solusi basis, karena memenuhi kendala pada PL (2.4) dan kolom-kolom pada matriks kendala yang berpadanan dengan komponen taknol dari (2.5), yaitu B bebas linear (kolom yang satu bukan merupakan kelipatan dari kolom yang lain). Solusi (2.5) juga merupakan solusi basis fisibel, karena nilai-nilai variabelnya lebih dari atau sama dengan nol.

Hal yang juga penting dalam konsep pemrograman linear untuk model ini adalah daerah fisibel dan solusi optimal yang didefinisikan sebagai berikut.

Definisi 7 (Daerah Fisibel)

Daerah fisibel suatu PL adalah himpunan semua titik yang memenuhi semua kendala dan pembatasan tanda pada PL tersebut.

(Winston, 2004) Definisi 8 (Solusi Optimal)

Untuk masalah maksimisasi, solusi optimal suatu PL adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terbesar. Untuk masalah minimisasi, solusi optimal suatu PL adalah suatu titik dalam daerah fisibel dengan nilai fungsi objektif terkecil.

(Winston, 2004)

Integer Programming (Pemrograman

Integer)

Integer programming (IP) atau pemrograman integer adalah suatu model pemrograman linear dengan variabel yang digunakan berupa bilangan bulat (integer). Jika semua variabel harus berupa integer, maka masalah tersebut dinamakan pure integer programming. Jika hanya sebagian yang harus berupa integer, maka disebut mixed integer programming. IP dengan semua variabelnya harus bernilai 0 atau 1 disebut 0-1 IP.

(Garfinkel & Nemhauser, 1972) Definisi 9 (Pemrograman Linear Relaksasi)

Pemrograman linear relaksasi atau sering disebut PL-relaksasi merupakan suatu pemrograman linear yang diperoleh dari suatu IP dengan menghilangkan kendala integeratau kendala 0-1 pada setiap variabelnya.

Untuk masalah maksimisasi, nilai optimal fungsi objektif PL-relaksasi lebih besar atau sama dengan nilai optimal fungsi objektif LP, sedangkan untuk masalah minimisasi, nilai optimal fungsi objektif PL-relaksasi lebih kecil atau sama dengan nilai optimal fungsi objektif LP.

(Winston, 1995) Metode Branch-and-Bound

Pemecahan masalah pemrograman integer dapat dilakukan dengan metode branch-and-bound. Prinsip dasar metode ini adalah memecah daerah fisibel suatu masalah PL-relaksasi dengan membuat subproblem-subproblem. Ada dua konsep dasar dalam algoritme branch-and-bound.

 Cabang (Branch)

Membuat partisi daerah solusi dari masalah utama (PL-relaksasi) dengan membentuk

subproblem-subproblem, tujuannya untuk menghapus daerah solusi yang tidak fisibel. Hal ini dicapai dengan menentukan kendala yang penting untuk menghasilkan solusi IP, secara tidak langsung titik integer yang tidak fisibel terhapus. Dengan kata lain, hasil pengumpulan lengkap dari subproblem-subproblem ini menunjukkan setiap titik integer yang fisibel dalam masalah asli. Karena sifat partisi tersebut, maka prosedur ini dinamakan pencabangan (branching).

 Batas (Bound)

Misalkan masalah utamanya berupa masalah maksimisasi. Nilai objektif yang optimal untuk setiap subproblem dibuat dengan membatasi pencabangan dengan batas atas dari nilai objektif yang dihubungkan dengan sembarang nilai integer yang fisibel. Hal ini sangat penting untuk mengatur dan menempatkan solusi optimal. Operasi pembatasan ini dinamakan pembatasan (bounding).

(Taha, 1975) Metode branch-and-bound diawali dari menyelesaikan PL-relaksasi dari suatu integer programming. Jika semua nilai variabel keputusan solusi optimal sudah berupa integer, maka solusi tersebut merupakan solusi optimal IP. Jika tidak, dilakukan pencabangan dan penambahan batasan pada PL-relaksasinya kemudian diselesaikan.

Winston (2004) menyebutkan bahwa nilai fungsi objektif optimal untuk IP  nilai fungsi objektif optimal untuk PL-relaksasi (masalah maksimisasi), sehingga nilai fungsi objektif optimal PL-relaksasi merupakan batas atas bagi nilai fungsi objektif optimal untuk masalah IP. Diungkapkan pula oleh Winston (2004) bahwa nilai fungsi objektif optimal untuk suatu kandidat solusi merupakan batas bawah nilai fungsi objektif optimal untuk masalah IP asalnya. Suatu kandidat solusi diperoleh jika solusi dari suatu subproblem sudah memenuhi kendala integer pada masalah IP, artinya fungsi objektif dan semua variabelnya sudah bernilai integer.

Berikut ini adalah langkah-langkah penyelesaian suatu masalah maksimisasi dengan metode branch-and-bound.

 Langkah 0

Didefinisikan zsebagai batas bawah dari nilai fungsi objektif (solusi) IP yang optimal. Pada awalnya ditetapkan z dan i0.

 Langkah 1

Subproblem LP( )i dipilih sebagai bagian masalah berikutnya untuk diteliti. Subproblem

( )i

LP diselesaikan dan diukur dengan kondisi yang sesuai.

a) Jika LP( )i terukur, batas bawah z diperbarui jika solusi IP yang lebih baik ditemukan. Jika tidak, bagian masalah (subproblem) baru idipilih dan langkah 1 diulangi. Jika semua subproblem telah diteliti, maka proses dihentikan.

b) Jika LP_{( )i} tidak terukur, proses dilanjutkan ke langkah 2 untuk melakukan pencabangan LP( )i .

Menurut Winston (2004), suatu subproblem dikatakan terukur (fathomed) jika terdapat situasi sebagai berikut.

1. Subproblem tersebut takfisibel, sehingga tidak dapat menghasilkan solusi optimal untuk IP.

2. Subproblem tersebut menghasilkan suatu solusi optimal dengan semua variabelnya bernilai integer. Jika solusi optimal ini mempunyai nilai fungsi objektif yang lebih baik daripada solusi fisibel yang diperoleh sebelumnya, maka solusi ini menjadi kandidat solusi optimal dan nilai fungsi objektifnya menjadi batas bawah nilai fungsi objektif optimal bagi masalah IP pada saat itu. Bisa jadi subproblem ini menghasilkan solusi optimal untuk masalah IP.

3. Nilai fungsi objektif optimal untuk subproblem tersebut tidak melebihi (untuk masalah maksimisasi) batas bawah saat itu, maka subproblem ini dapat dieliminasi.

 Langkah 2

Dipilih salah satu variabel x_j yang nilai optimalnya adalah x*j yang tidak memenuhi

batasan integer dalam solusi LP_i. Bidang 1

] [ ]

[x*_j x_j  x*_j  disingkirkan dengan membuat dua subproblem PL yang berkaitan menjadi dua subproblem yang tidak dapat dipenuhi secara bersamaan, yaitu

* [ ] j j x  x dan _{[ ] 1}* j j x  x  , dengan [ *] j

x didefinisikan sebagai integer terbesar yang kurang dari atau sama dengan

. *

j

x Kembali ke langkah 1.

(Taha, 1996) Untuk memudahkan pemahaman metode branch-and-bound diberikan contoh sebagai berikut.

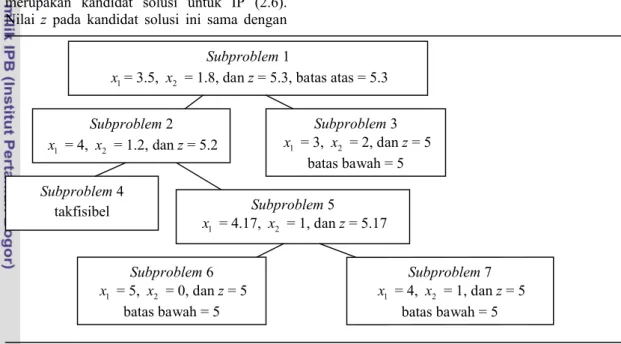
Contoh 2 (Metode Branch-and-Bound) Misalkan diberikan pemrograman integer (IP) berikut maks z x1 x2 terhadap 2x₁5x₂16 6x15x230 (2.6) x x₁, ₂ 0 x x integer. 1, 2

Solusi optimal PL-relaksasi dari masalah IP (2.6) adalah x13.5, x2 1.8, dan

5.3

z (lihat pada Lampiran 1). Batas atas nilai optimal fungsi objektif masalah ini adalah z5.3. Daerah fisibel masalah (2.6) ditunjukkan pada Gambar 1. Solusi optimal berada pada titik perpotongan dua garis yang berasal dari kendala pertidaksamaan masalah (2.6).

Gambar 1 Daerah fisibel untuk PL-relaksasi dari IP (2.6)

Langkah berikutnya adalah memartisi daerah fisibel PL-relaksasi menjadi dua bagian berdasarkan variabel yang berbentuk pecahan (non-integer). Karena nilai dari kedua variabel yang diperoleh bukan integer, maka dipilih salah satu variabel untuk dasar pencabangan. Misalkan dipilih x1 sebagai dasar pencabangan. Jika masalah PL-relaksasi diberi nama Subproblem 1, maka pencabangan tersebut menghasilkan 2 subproblem, yaitu:

 Subproblem 2: Subproblem 1 ditambah kendala x14;

 Subproblem 3: Subproblem 1 ditambah kendala x13.

Hal ini diilustrasikan secara grafis pada Gambar 2.

Gambar 2 Daerah fisibel untuk Subproblem 2 dan Subproblem 3.

Setiap titik (solusi) fisibel dari IP (2.6) termuat dalam daerah fisibel Subproblem 2 atau Subproblem 3. Setiap subproblem ini saling lepas. Subproblem 2 dan Subproblem 3 dikatakan dicabangkan oleh x1.

Sekarang dipilih subproblem yang belum diselesaikan. Misalkan dipilih Subproblem 2, kemudian diselesaikan. Solusi optimal untuk Subproblem 2 ini adalah x₁ 4, x₂ 1.2, dan

5.2

z (lihat Lampiran 1).

Karena solusi optimal yang dihasilkan Subproblem 2 bukan solusi integer, maka dipilih pencabangan pada Subproblem 2 atas

2,

x sehingga diperoleh dua subproblem lagi, yakni:

 Subproblem 4: Subproblem 2 ditambah kendala x₂ 2;

 Subproblem 5: Subproblem 2 ditambah kendala x₂ 1.

Saat ini subproblem yang belum diselesaikan adalah Subproblem 3, 4, dan 5. Salah satu subproblem dipilih, misalnya dengan aturan LIFO (Last In First Out). Dengan adanya aturan ini berarti dipilih Subproblem 4 atau Subproblem 5. Karena Subproblem 4 takfisibel (lihat pada Lampiran 1), maka subproblem ini tidak dapat menghasilkan solusi optimal, yang tersisa adalah Subproblem 3 dan Subproblem 5.

Karena aturan LIFO, dipilih Subproblem 5, yang kemudian menghasilkan solusi optimal

1 4.17, 2 1

x  x  , dan z5.17 (lihat pada Lampiran 1).

Karena x₁4.17 bukan integer, maka dilakukan kembali pencabangan atas x1, sehingga diperoleh:

 Subproblem 6: Subproblem 5 ditambah kendala x₁5;

Subproblem 2 Subproblem 3

 Subproblem 7: Subproblem 5 ditambah kendala x14.

Selanjutnya berdasarkan aturan LIFO, dipilih Subproblem 7. Subproblem yang dipilih menghasilkan solusi optimal yang berupa integer, dengan x14, x2 1, dan

5

z . Diperoleh kandidat solusi optimal yang baru dari Subproblem 7. Nilai z baru merupakan batas bawah baru bagi nilai optimal IP (2.6).

Tersisa dua buah subproblem yaitu, Subproblem 3 dan Subproblem 6. Misalkan dengan aturan LIFO dipilih Subproblem 6. Diperoleh solusi optimal yang bernilai integer, yaitu x15,x2 0, dan z5, sehingga merupakan kandidat solusi untuk IP (2.6). Nilai z pada kandidat solusi ini sama dengan

nilai z pada Subproblem 7, sehingga merupakan batas bawah bagi nilai optimal IP. Penyelesaian Subproblem 3 menghasilkan solusi optimal x13, x22, dan z5 (lihat pada Lampiran 1).

Batas bawah yang ditetapkan dari solusi optimal Subproblem 7 dan 6 bernilai sama dengan nilai z optimal yang dihasilkan oleh Subproblem 3. Semua solusi optimal dari Subproblem 7, 6, dan 3 telah berupa integer dan tidak perlu lagi dilakukan pencabangan, sehingga terdapat 3 solusi optimal dari Subproblem 7, 6, dan 3. Pohon pencabangan yang menunjukkan penyelesaian masalah IP (2.6) secara keseluruhan ditunjukkan pada Gambar 3.

Gambar 3 Seluruh pencabangan pada metode Branch-and-Bound untuk menentukan solusi optimal dari IP (2.6).

Model Matriks Leslie

Penggunaan matriks dalam pertumbuhan populasi dikembangkan oleh Leslie (1948) yang sebelumnya telah dikemukakan Lewis (1942). Matriks Leslie digunakan untuk meramalkan keadaan populasi suatu organisme pada waktu tertentu (t1) berdasarkan keadaan populasi sebelumnya (t).

Dengan menggunakan matriks Leslie, jika populasi menurut struktur umur pada suatu saat telah diketahui maka dimungkinkan untuk dapat meramalkan struktur umur atau banyaknya individu dalam setiap kelompok umur pada waktu berikutnya. Dalam model matriks Leslie, pertumbuhan populasi (reproduksi dan kematian) merupakan fungsi dari umur individu dalam populasi.

Variabel dan parameter yang digunakan dalam model ini antara lain:

Nx = banyaknya makhluk hidup pada kelompok umur x;

sx = tingkat bertahan hidup makhluk hidup pada interval kelompok umur (x) ke (x+1) atau dengan kata lain peluang banyaknya makhluk hidup akan bertahan hidup dari umur (x) ke (x+1); fx = tingkat perkembangbiakan makhluk hidup

pada interval kelompok umur (x) ke (x+1) atau dengan kata lain rataan banyaknya makhluk hidup yang dilahirkan oleh 1 induk yang berusia (x) sampai dengan (x+1).

Terdapat dua buah persamaan pada model matriks Leslie: 1 . x x x N _ N s (a) Subproblem1 1

x = 3.5, x2 = 1.8, dan z= 5.3, batas atas = 5.3 Subproblem3 1 x = 3, x2 = 2, dan z= 5 batas bawah = 5 Subproblem5 1 x = 4.17, x2 = 1, dan z= 5.17 Subproblem4 takfisibel Subproblem7 1 x = 4, x₂ = 1, dan z= 5 batas bawah = 5 Subproblem2 1 x = 4, x₂ = 1.2, dan z= 5.2 Subproblem6 1 x = 5, x₂ = 0, dan z= 5 batas bawah = 5

1 N 1 . n x x x N f  



(b) (2.7) Persamaan (a) menggambarkan perkembangan banyaknya makhluk hidup kelompok umur x ke x1. Persamaan (b) menggambarkan banyaknya makhluk hidup pada kelompok umur pertama.

Persamaan (a) dan (b) dapat dimodelkan dalam suatu persamaan matriks, dengan A adalah matriks Leslie dan Nt adalah banyaknya makhluk hidup pada kelompok umur x pada waktu t,sebagai berikut.

1 .

t t

N_  A N (2.8)

Berikut ini adalah contoh matriks Leslie pada kelompok umur x= 1,2,…,5 dan selang waktu



t t, 1



A N_t N_t1 1,t 1 2 3 4 5 1,t+1 2,t 1 2,t+1 1,t 1 3,t 2 3,t+1 2,t 2 4,t 3 4,t+1 3,t 3 5,t 4 5,t+1 4,t 4 N N . N 0 0 0 0 N N . N 0 0 0 0 = N N . N 0 0 0 0 N N . N 0 0 0 0 N N . x x f f f f f N f s s s s s s s s              _                                 _      



(Getz & Haight, 1989)

Metabolic Body Size (MBS)

Metabolic body size merupakan suatu persamaan yang menyatakan hubungan antara metabolisme energi suatu hewan dengan berat hewan tersebut. Persamaan ini diformulasikan:

0.75

MBS = m ; mmassa rata-rata hewan(kg); 0.75 adalah konstanta metabolisme energi. MBS dapat digunakan sebagai faktor yang mengonversi banyaknya suatu jenis hewan ke banyaknya hewan jenis lain yang memiliki massa rata-rata yang berbeda, dengan membagi MBS hewan tersebut dengan MBS hewan hasil konversi. Jika faktor pengonversi tersebut dikalikan dengan banyaknya hewan yang akan dikonversi, akan didapatkan banyaknya hewan hasil konversi.

(Ruyle & Ogden, 1993)

III DESKRIPSI DAN FORMULASI MASALAH

Seperti telah disebutkan sebelumnya, manajemen ranch mempunyai dua buah tujuan, yaitu:

1. memaksimumkan pendapatan dari hasil pemanenan ranch baik yang berasal dari meat hunting maupun sport hunting, yang terbagi menjadi:

a) maksimisasi pendapatan dari hasil pemanenan suatu spesies dalam ranch; b) maksimisasi pendapatan dari hasil

pemanenan semua spesies yang ada dalam ranch;

2. memaksimumkan penggunaan modal pada tahap awal pembangunan ranch.

Misalkan peternakan (ranch) hanya terdiri atas herbivora yang memiliki tanduk dan tidak terdapat pemangsa hewan buruan di dalamnya. Hal ini memunyai dampak bertambahnya sejumlah hewan buruan dalam waktu relatif singkat, yang kemudian berimbas negatif pada vegetasi, yaitu berkurangnya sejumlah pakan yang tersedia bagi hewan. Dampak negatif ini dapat diatasi dengan pemanenan sejumlah hewan buruan dalam ranch. Pemanenan inilah yang kemudian menjadi sumber pendapatan ranch.

Pemanenan hewan buruan dilakukan melalui dua jenis perburuan, yaitu:

 perburuan hewan (jantan dan betina) untuk mendapatkan daging hewan tersebut pada saat hewan mencapai umur tertentu (meat hunting);

 perburuan hewan jantan untuk mengambil bagian tertentu dari hewan (misalnya: kulit, kepala, dan tanduk) saat hewan mencapai umur tertentu (sport hunting). Untuk mengetahui umur hewan yang siap dipanen pada sport hunting, dalam karya ilmiah ini panjang tanduk tertentu digunakan sebagai acuan (misalnya: badak bercula satu dipanen saat panjang tanduknya mencapai 89.9 cm).

Pada meat hunting, pemanenan dilakukan agar banyaknya pakan yang tersedia di ranch dapat mencukupi kebutuhan pakan semua hewan. Sejumlah hewan betina membutuhkan pakan yang cukup untuk melahirkan sejumlah hewan (jantan dan betina), sedangkan pada saat yang sama sejumlah hewan jantan yang berada di ranchjuga membutuhkan pakan agar hewan-hewan tersebut mencapai panjang tanduk tertentu untuk keperluan sport hunting. Agar kebutuhan pakan tetap tersedia untuk

hewan-hewan tersebut, maka satu tahun setelah kelahiran, sebagian hewan bisa langsung dipanen sedangkan sebagian hewan yang lain dipertahankan di ranch.

Akan dibahas mengenai permasalahan maksimisasi pendapatan dari hasil pemanenan suatu spesies, yang selanjutnya disebut sebagai Subproblem 1, terlebih dahulu. Terdapat dua macam komponen pendapatan pada Subproblem 1, yakni:

1. pendapatan dari penjualan daging hewan hasil perburuan (jantan dan betina);

2. pendapatan dari penjualan hak berburu hewan jantan yang telah mencapai panjang tanduk tertentu (sport hunting).

Asumsi-asumsi yang digunakan pada Subproblem 1 antara lain:

1. pemburu memperoleh hak hanya untuk berburu, sedangkan dagingnya merupakan hak pemilik ranch;

2. tambahan biaya dikenakan apabila pemburu menginginkan daging hewan yang telah diburu;

3. pemanenan semua buruan betina yang masih tersisa di ranch dilakukan ketika tingkat kesuburannya menurun;

4. hewan berumur 0-1 tahun dinyatakan oleh kelompok umur ke-1, hewan berumur 1-2 tahun dinyatakan kelompok umur ke-2, dan seterusnya;

5. pemanenan semua buruan jantan yang masih tersisa di ranch dilakukan ketika telah mencapai panjang tanduk tertentu yang diperbolehkan untuk dipanen;

6. proporsi kelahiran hewan jantan dan betina pada ranchdiasumsikan sama.

Masalah utama dari Subproblem 1 adalah menentukan pendapatan dari penjualan daging hewan dan penjualan hak berburu yang optimal. Pendapatan optimal dari hasil pemanenan suatu spesies kemudian digunakan sebagai salah satu variabel input untuk menghitung pendapatan optimal dari pemanenan semua spesies dalam ranch.

Permasalahan maksimisasi pendapatan dari pemanenan semua spesies dalam ranch, yang selanjutnya disebut Subproblem 2, mempunyai komponen pendapatan yang berasal dari hasil pemanenan optimal suatu spesies hewan yang disusun bersama dengan pendapatan dari hasil pemanenan yang optimal dari spesies hewan lain yang ada di dalam ranch. Pada Subproblem 2 akan ditentukan kombinasi optimal banyaknya hewan yang dipanen dari semua spesies dalam ranch.

Terdapat beberapa asumsi yang digunakan pada Subproblem 2 antara lain:

1. Terdapat sejumlah hewan yang harus ada dalam ranch, hal ini dinyatakan dengan banyaknya pakan yang harus ada dalam ranch;

2. pakan yang digunakan dalam ranch terdiri atas 3 jenis: rumput berdaun pendek (bulk graze), rumput berdaun sedang (concentrate graze), dan rumput berdaun panjang (browse);

3. proporsi banyaknya pakan setiap spesies berbeda;

Selain menangani permasalahan optimisasi pendapatan dari hasil pemanenan hewan buruan, manajemen ranch juga menangani permasalahan maksimisasi penggunaan modal akhir pada tahap awal pembangunan ranch. Pada tahun awal pembangunan dimisalkan ranch baru selesai dibangun sehingga ranch belum terisi oleh hewan buruan. Hal ini mengharuskan manajemen untuk melakukan pembelian sejumlah hewan untuk mengisi ranch. Setelah beberapa tahun hewan-hewan tersebut mencapai ukuran yang menandakan kesiapan hewan untuk dipanen (misalnya: massa rata-rata ataupun panjang tanduk tertentu) dan kemudian dijual. Untuk menjaga ketersediaan sejumlah hewan yang optimal dalam ranch yang berkurang setelah proses penjualan, pembelian sejumlah hewan tetap dilakukan pada tahun-tahun berikutnya.

Modal awal pendirian ranch berasal dari pemilik. Modal awal berfluktuasi terhadap tingkat bunga modal. Hal lain yang juga berpengaruh terhadap fluktuasi modal:  banyaknya pembelian hewan dalam waktu

tertentu;

 banyaknya penjualan sejumlah hewan dalam kurun waktu tertentu.

Pembelian sejumlah hewan akan mengurangi banyaknya modal, sedangkan penjualan akan menambah banyaknya modal, sehingga pada permasalahan optimisasi penggunaan modal akan ditentukan banyaknya hewan yang diperjualbelikan dalam rangka memaksimumkan modal.

Untuk menyelesaikan permasalahan yang berasal dari tujuan manajemen ranchterdapat dua buah pemodelan, sebagai berikut.

1 Maksimisasi pendapatan dari hasil pemanenan binatang buruan

Dalam rangka memaksimumkan pendapatan, terdapat dua buah pemodelan, yaitu:

1) Model Spesies Tunggal

Model ini menentukan strategi pemanenan pada suatu spesies tertentu dan menghitung pendapatan per unit pakan yang dihasilkan

dari spesies tersebut. Fungsi objektif model spesies tunggal terbagi menjadi dua bagian. Dalam fungsi objektif pertama akan dimaksimumkan pendapatan dari perburuan untuk memperoleh daging yang dinyatakan dalam J1. Dalam fungsi objektif pertama

terdapat faktor pengulitan (dress weight factor). Faktor ini adalah suatu faktor yang mengubah berat kotor hewan menjadi berat bersih (berat hewan yang sudah dikuliti dan dibersihkan serta siap untuk dijual). Sedangkan pada fungsi objektif kedua akan dimaksimumkan pendapatan yang berasal dari sport hunting.

Hewan betina dipanen antara kelompok umur pertama sampai kelompok umur ke-n. Kelompok umur awal sampai kelompok umur

1

n merupakan kelompok umur hewan yang harus dipanen karena tingkat kesuburannya tidak mencukupi untuk melahirkan sejumlah hewan. Kelompok umur ke-n merupakan kelompok umur saat tingkat kesuburan suatu hewan mulai berkurang. Tingkat kesuburan hewan betina dipengaruhi antara lain oleh umur dan pola makan. Pemanenan hewan betina dilakukan dengan meat hunting. Pemanenan hewan jantan terdiri atas pemanenan dengan meat hunting dan sport hunting. Pemanenan dengan meat hunting dilakukan antara kelompok umur pertama sampai kelompok umur ke-2n, sedangkan untuk sport hunting, hewan buruan jantan dipanen antara umur n sampai kelompok umur ke-2n saat tanduk hewan mencapai panjang tertentu. Dalam formulasi model terdapat suatu konstanta a, yaitu konstanta yang mewakili kelompok umur hewan jantan yang siap dipanen.

Terdapat empat buah kendala, kendala ketersediaan pakan, dua kendala dinamika populasi, dan kendala ketaknegatifan. Kendala pertama menyatakan banyaknya pakan untuk hewan buruan harus kurang dari atau sama dengan banyaknya pakan yang tersedia dalam ranch (carrying capacity). Satuan pakan adalah AU (Animal Unit), yang menyatakan banyaknya pakan yang dikonsumsi seekor sapi yang memiliki massa rata-rata 455 kg per tahun. Banyaknya pakan yang tersedia pada kendala ketersediaan pakan, untuk Subproblem 1 diasumsikan sebesar 100 AU atau setara dengan banyaknya pakan yang dibutuhkan oleh 100 ekor sapi yang memunyai massa rata-rata 455 kg/ekor selama 1 tahun. Pada kendala pertama terdapat faktor pengonversi massa rata-rata hewan ke dalam satuan AU yang dilambangkan sebagai wi

dengan _{( / 455)}0,75 i i

w  m ; mi= massa rata-rata hewan yang berada pada kelompok umur i. Formula ini diperoleh dengan persamaan MBS (lihat pada Metabolic Body Size). Faktor pengonversi ini menentukan banyaknya pakan yang dibutuhkan hewan berdasarkan massa rata-rata hewan tersebut.

Kendala kedua dan ketiga merupakan kendala dinamika populasi, yang dimodelkan dengan matriks Leslie. Dinamika populasi mencakup pertambahan populasi melalui proses kelahiran dan pengurangan sejumlah anggota populasi dengan adanya penjualan sejumlah hewan hasil pemanenan.

Pada kendala kedua, banyaknya hewan pada kelompok umur pertama (kelompok umur hewan yang baru lahir) diperoleh dari banyaknya hewan betina (induk) yang melahirkan hewan jantan ataupun betina. Banyaknya hewan betina yang dilahirkan di ranch (berdasarkan asumsi Subproblem 1) adalah setengah dari banyaknya kelahiran yang terjadi pada kelompok umur pertama, demikian juga hewan jantan. Suatu angka yang menyatakan kemampuan hewan betina untuk melahirkan disebut tingkat kesuburan. Banyaknya kelahiran hewan jantan dan betina pada kelompok umur pertama dipengaruhi oleh tingkat kesuburan hewan betina pada kelompok umur berikutnya.

Kendala ketiga menyatakan banyaknya hewan yang bertahan hidup pada kelompok umur selanjutnya bergantung pada tingkat bertahan hidup suatu hewan dan banyaknya penjualan hewan hasil pemanenan pada kelompok umur sebelumnya. Tingkat bertahan hidup suatu hewan adalah suatu angka yang menyatakan kemampuan hewan tersebut untuk tetap bertahan hidup pada suatu waktu tertentu.

Banyaknya hewan yang bertahan hidup pada kelompok umur berikutnya dinyatakan dengan xi1. Misalkan akan dihitung banyaknya hewan betina yang dapat bertahan hidup sampai kelompok umur ke-n. Maka harus diketahui banyaknya hewan betina yang bertahan hidup sampai dengan kelompok umur

1

n . Banyaknya hewan jantan yang bertahan hidup pada kelompok umur berikutnya dihitung dengan cara yang serupa dengan yang terdapat pada kendala ketiga.

Kendala selanjutnya adalah kendala ketaknegatifan, yang memastikan banyaknya hewan jantan dan betina pada semua kelompok umur i1, 2,...,2n dan banyaknya hewan jantan dan betina yang dipanen pada

kelompok umur i1, 2,...,2n tidak bernilai negatif.

Masalah model spesies tunggal dapat dimodelkan sebagai berikut.

Model spesies tunggal

2 2 1 2 1 2 1 2 1 1 2 1 maks ; . . . ; . terhadap . 1 . 2 . ; 1,..., 1 n n i i i i i a n i i i n i i i i i i i J J J J dwf mp m h J tp h x w W x x f x x s h i n               









xi 0,hi 0; i1,..., 2n Keterangan:

n banyaknya kelompok umur binatang buruan dengan n = 1, 2,3,...

J1 pendapatan yang diperoleh dari perburuan untuk memperoleh daging (dalam $)

mp harga daging hewan per kilogram (dalam $)

mi massa rata-rata (kg) hewan pada kelompok umur i

hi banyaknya hewan hasil perburuan pada kelompok umur i

dwf dress weight factor (diasumsikan 58% untuk semua spesies)

J2 pendapatan yang diperoleh dari perburuan hewan jantan yang telah mencapai panjang tanduk tertentu (dalam $)

tp harga satu tanduk hewan buruan (dalam $), dimisalkan harga setiap jenis hewan tidak selalu sama J pendapatan total (dalam $)

xi banyaknya hewan yang terdapat pada kelompok umur i

wi faktor pengonversi massa hewan ke dalam banyaknya pakan yang dibutuhkan hewan tersebut pada kelompok umur i

W banyaknya pakan yang tersedia dalam ranch (dalam AU)

fi tingkat kesuburan hewan betina pada kelompok umur i (dalam persen)

si tingkat bertahan hidup binatang pada kelompok umur i (dalam persen)

2) Model Spesies Campuran

Model spesies campuran menentukan pendapatan maksimum dari hasil pemanenan

semua spesies dalam ranch. Model ini juga sekaligus menentukan kombinasi optimal banyaknya hewan yang ada di ranch. Tujuan dari model ini tercermin dari fungsi objektifnya. Dalam fungsi objektif, pendapatan suatu spesies dikombinasikan dengan pendapatan spesies yang lain sedemikian sehingga pendapatan dari semua spesies maksimum. Terdapat tiga fungsi kendala pada model spesies campuran, yaitu kendala ketersediaan pakan, kendala keminimuman, dan kendala kemaksimuman (kendala keberagaman).

Kendala pertama memastikan banyaknya pakan yang dikonsumsi hewan buruan spesies j tidak melebihi banyaknya pakan yang tersedia pada lahan peternakan. Setiap spesies hewan dalam ranch memiliki tipe (kelas) pakan dengan proporsi yang berbeda satu sama lain. Terdapat 3 kelas pakan dalam ranch, yakni:

1. pakan berupa rumput yang berdaun pendek (bulk graze);

2. pakan berupa rumput yang berdaun sedang (concentrate graze);

3. pakan berupa rumput yang berdaun panjang (browse).

Sejumlah hewan yang memiliki tipe pakan yang sama, harus mempunyai kebutuhan pakan yang kurang dari atau sama dengan 100 AU, sesuai banyaknya pakan yang tersedia untuk setiap kelas pakan dalam ranch (carrying capacity).

Kendala keberagaman terdiri atas kendala keminimuman dan kemaksimuman. Banyaknya hewan pada kendala ini direpresentasikan dengan banyaknya pakan yang dibutuhkan oleh hewan tersebut.

Kendala keminimuman menyatakan banyaknya hewan yang terdapat di ranch

harus lebih dari atau sama dengan banyaknya hewan minimum yang harus ada dalam ranch. Sedangkan kendala berikutnya, yaitu kendala kemaksimuman memastikan tidak adanya kelebihan pada banyaknya spesies hewan

tertentu. Oleh karenanya, banyaknya pakan pada hewan dari setiap spesies dibatasi. Model spesies campuran dapat ditulis sebagai berikut.

Model spesies campuran

1 1 maks . terhadap . min , 1, 2,..., max , 1, 2,..., s j j j s f f j j j j j j j J r u u K u j s u j s         





Keterangan:

s banyaknya spesies dalam ranch J pendapatan total (dalam $)

rj pendapatan dari hasil pemanenan spesies j pada penghitungan model spesies tunggal (dalam $)

uj banyaknya pakan yang digunakan oleh spesies j(dalam satuan AU) f kelas pakan (bulk graze, concentrate

graze, dan browse)

f j



proporsi dari kelas pakan f pada susunan pakan spesies j

f

K

banyaknya pakan yang tersedia untuk kelas pakan f(satuan AU) min _j banyaknya pakan dari spesies

j

yang minimum ada di ranch (satuan AU)

maxj banyaknya pakan dari spesies

j

yang maksimum ada di ranch (satuan AU)

2 Pengaturan game ranchyang optimal Permasalahan selanjutnya adalah penyusunan suatu rencana agar peternakan dapat beroperasi penuh pada waktu yang telah ditentukan. Langkahnya adalah dengan mengoptimalkan banyaknya stok binatang buruan j yang diperjualbelikan dan banyaknya modal C pada tahun T. Pada saat yang bersamaan pengaturan tersebut juga memerhatikan penyusunan variasi sejumlah binatang buruan dan beberapa kendala lain.

Dalam fungsi objektif model ini akan dimaksimumkan modal pada akhir periode pengaturan (pembangunan game ranch). Kendala pertama menyatakan perubahan modal tahun berikutnya dipengaruhi oleh

fluktuasi tingkat bunga dan banyaknya hewan yang diperjualbelikan pada tahun sebelumnya. Semakin banyak hewan hasil pemanenan yang dijual akan menambah banyaknya modal. Demikian pula dengan tingkat bunga, tingkat bunga yang tinggi pada suatu tahun akan menambah banyaknya modal pada tahun berikutnya. Sedangkan pembelian sejumlah hewan pada tahun sebelumnya, akan mengurangi banyaknya modal tahun berikutnya.

Kendala kedua dan ketiga merupakan kendala penentuan harga jual dan harga beli hewan. Harga jual seekor hewan pada suatu tahun tertentu dipengaruhi oleh inflasi yang terjadi pada tahun tersebut. Harga jual tahun sebelumnya kemungkinan berbeda dengan tahun berikutnya karena dipengaruhi inflasi yang seringkali berubah setiap tahun. Hal yang sama juga berlaku untuk harga beli.

Kendala berikutnya menyebutkan banyaknya pengeluaran modal dari pembelian sejumlah hewan buruan pada suatu tahun tertentu harus kurang dari besarnya modal yang tersedia pada tahun tersebut. Besarnya modal setiap tahun haruslah bernilai taknegatif. Kendala ini memastikan tidak ada kerugian yang ditanggung oleh manajemen ranch.

Kendala selanjutnya terkait dengan ketersediaan pakan. Banyaknya pakan untuk setiap kelas pakan tidak boleh melebihi banyaknya pakan yang tersedia untuk kelas pakan tersebut. Kelas pakan pada hewan terbagi menjadi 3 kelas pakan, sama seperti kelas pakan pada model spesies campuran.

Kendala keenam merupakan kendala keterbatasan ketersediaan sejumlah hewan tertentu. Oleh karenanya, kendala ini menyatakan banyaknya spesies hewan yang

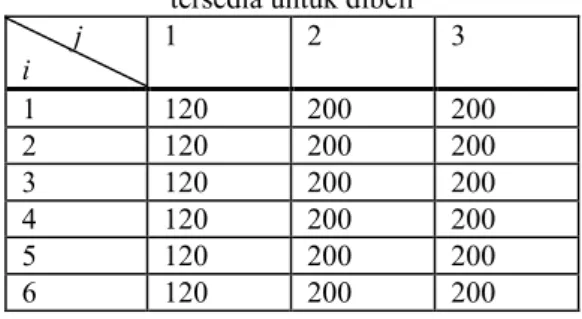
dibeli harus kurang dari atau sama dengan banyaknya hewan yang tersedia untuk dibeli.

Kendala berikutnya merupakan kendala dinamika populasi. Kendala ini menyatakan banyaknya binatang pada tahun ke-i1. Faktor-faktor yang memengaruhi perubahan banyaknya hewan pada tahun berikutnya antara lain:

 banyaknya hewan yang dijual pada tahun ke-i;

 banyaknya hewan yang dibeli oleh manajemen ranch pada tahun ke-i;  banyaknya hewan yang bertahan hidup

pada tahun ke-i.

Banyaknya hewan yang dijual pada suatu tahun akan mengurangi banyaknya hewan pada tahun berikutnya. Banyaknya hewan yang dibeli pada suatu tahun akan menambah populasi hewan pada tahun berikutnya. Banyaknya hewan yang berhasil bertahan hidup pada suatu tahun akan menambah

banyaknya hewan pada tahun berikutnya. Banyaknya hewan yang berhasil bertahan hidup pada tahun ke-i dipengaruhi oleh tingkat tumbuh spesifik (spesific growth rate) dari hewan tersebut. Tingkat tumbuh spesifik merupakan suatu angka yang menyatakan banyaknya hewan dari spesies tertentu yang berhasil bertahan hidup pada suatu waktu tertentu.

Kendala terakhir memastikan banyaknya hewan buruan yang ada pada akhir tahun pengaturan harus sama dengan banyaknya hewan yang telah ditargetkan pada akhir tahun pengaturan. Hal ini karena diasumsikan banyaknya hewan yang ditargetkan sama dengan nol, untuk semua spesies hewan buruan.

Model pengaturan game ranch yang optimal dapat dituliskan sebagai berikut.

1 , , , , , 1, , 1, , , maks terhadap (1 ) ( . ) ( . ) .(1 ) .(1 ) ( . T i i i j i j i j i j i j i j i j i j i j i J C C C I sp h pp b sp sp k pp pp k sp h             , , 1 ) ( . ) dan 0 s j i j i j i i j pp b C C    



, 1 . . s f f j j i j j u x K   



, , 1, , , , , , , 1,..., ; 1,..., . , 1,..., ; 1,..., i j i j i j i i j i j i j T j G j b a i T j s x sgr x b h i T j s x x           Keterangan

T periode pembangunan (banyaknya tahun yang dibutuhkan untuk pendirian ranch secara lengkap, biasanya antara 3-5 tahun

Ci modal yang tersedia pada tahun i (dalam $)

I tingkat bunga modal (dalam %) spi,j harga jual dari spesies j pada tahun

i (dalam $)

hi,j banyaknya hewan dari spesies j yang dipanen pada tahun i

ppi,j harga beli dari spesies j pada tahun i (dalam $)

bi,j banyaknya binatang dari spesies j yang dibeli pada tahun i

k tingkat kenaikan harga/fraksi inflasi (dalam %)

ai,j banyaknya binatang yang tersedia untuk dibeli dari spesies j pada tahun i

sgrj tingkat tumbuh spesifik dari spesies j(dalam %)

, i j

x banyaknya hewan dari spesies j yang ada dalam ranch pada tahun ke-i

, G j

x banyaknya hewan dari spesies j yang ada dalam ranch pada tahun yang menjadi target akhir pendirian ranch

f kelas pakan (bulk graze, concentrate graze, dan browse)

f j



proporsi dari kelas pakan f pada susunan pakan spesies j

f

K

banyaknya pakan yang tersedia untuk kelas pakan f(satuan AU)

uj banyaknya pakan yang digunakan oleh spesies j(dalam satuan AU)

IV PENYELESAIAN MASALAH MODEL OPTIMAL PENGGUNAAN

HEWAN BURUAN

Masalah model optimal penggunaan hewan buruan terbagi ke dalam 3 buah model sebagai berikut.

a. Model Spesies Tunggal

Model spesies tunggal bertujuan menyelesaikan masalah maksimisasi pendapatan dari setiap spesies hewan dalam ranch. Akan digunakan 3 jenis spesies hewan (jantan dan betina) pada kelompok umur 1-11 tahun. Data yang digunakan pada model ini untuk spesies kedua dan ketiga ditentukan oleh penulis, sedangkan data hidup rata-rata dari spesies 1 berasal dari data dalam pustaka utama.

Terdapat beberapa asumsi baru yang digunakan untuk lebih memudahkan penghitungan, di antaranya:

1 penghitungan hewan jantan dan betina dipisahkan;

2 batas atas bagi sejumlah hewan yang terdapat dalam ranch serta sejumlah hewan yang dipanen ditentukan;

3 hewan jantan digunakan untuk sport huntingpada tahun ke-10.

Berikut ini akan ditampilkan salah satu contoh data hidup rata-rata dari spesies 1 (data selengkapnya dapat dilihat pada Lampiran 2).

Tabel 1 Data hidup rata-rata dari spesies 1 Kelom pok Umur (i) Tingkat Kesubur an Tingkat Bertahan Hidup Jantan Tingkat Bertahan Hidup Betina Berat seekor Hewan Jantan Berat seekor Hewan Betina 1 0 0.4 0.4 43 22.3 2 0.4 0.9 0.9 75.8 55.3 3 0.9 1 1 95.7 58.4 4 1 1 1 104.9 59.2 5 1 1 1 109.1 59.2 6 1 1 1 111 59.2 7 1 1 1 111.8 59.2 8 1 1 1 112.1 59.2 9 1 1 1 112.3 59.2 10 1 1 1 112.4 59.2

Syntax program LINGO 8.0 untuk menyelesaikan masalah maksimisasi

pendapatan dari hasil pemanenan setiap spesies hewan dalam ranch dapat dilihat pada Lampiran 3. Penyelesaian program dengan software LINGO 8.0 menghasilkan pendapatan dari hasil pemanenan setiap spesies dalam ranch yang dapat dilihat pada tabel berikut.

Tabel 2 Pendapatan pada model spesies tunggal (dalam $) Spesies Pendapatan dari hewan jantan Pendapatan dari hewan betina Pendapatan total 1 123 96.3 229.3 2 222.34 179.07 401.41 3 357.67 249.55 607.22

b. Model Spesies Campuran

Model ini mempunyai tujuan untuk memaksimumkan pendapatan dari semua spesies hewan yang ada dalam ranch.Dalam model ini dapat diketahui banyaknya hewan optimal yang harus dipanen. Berikut ditampilkan data-data yang dibutuhkan dalam penyelesaian masalah model spesies campuran.

Tabel 3 Data variabel pada model spesies campuran

Spesies Pendapatan Carrying

CapacityMinimum Jumlah AU Jumlah Maksimum AU 1 229.3 100 100 300 2 401.41 100 100 300 3 607.22 100 100 300

Tabel 4 Data proporsi kelas pakan spesies j Spesies

( j) bulk Proporsi Kelas Pakan graze concentrate graze browse graze 1 0 0.4 0.6 2 0.9 0.1 0 3 0.3 0 0.7

Dengan menyelesaikan pemrograman linear menggunakan software LINGO 8.0 diperoleh pendapatan total sebesar $ 310223.3, selain itu juga diperoleh

banyaknya spesies optimal yang harus dipanen sebesar:

 spesies 1: 150 AU;  spesies 2: 233 AU;  spesies 3: 300 AU.

c. Pengaturan game ranchyang optimal Tujuan model ini adalah memaksimumkan perolehan modal pada pembangunan ranch. Asumsi-asumsi baru yang digunakan untuk lebih memudahkan penghitungan antara lain:

1 waktu pembangunan adalah 5 tahun, dengan tahun awal pembangunan adalah tahun ke-0;

2 modal awal sebesar $4000000;

3 terdapat kendala pembatasan banyaknya hewan yang dipanen, dijual, dan banyaknya hewan yang ada dalam ranch. Data-data yang digunakan dalam penghitungan model ini dapat dilihat pada tabel berikut.

Tabel 5 Data tingkat tumbuh, carrying capacity, dan banyaknya AU dari setiap

spesies Spesies Tingkat

tumbuh Carryingcapacity Banyaknya AU

1 0.95 150 150

2 0.98 300 200

3 0.93 150 100

Tabel 6 Tingkat suku bunga dan inflasi terhadap waktu

tahun (i) suku bunga inflasi

1 0.059 0.02 2 0.06 0.05 3 0.061 0.07 4 0.065 0.08 5 0.0.67 0.09 6 0.07 0.12

Tabel 7 Data banyaknya hewan yang tersedia untuk dibeli

j i 1 2 3 1 120 200 200 2 120 200 200 3 120 200 200 4 120 200 200 5 120 200 200 6 120 200 200

Penyelesaian model pengaturan game ranch yang optimal dengan menggunakan software LINGO 8.0 menghasilkan modal akhir yang optimal sebesar $ 5408705 (dapat dilihat pada Lampiran 3).

V SIMPULAN DAN SARAN

5.1 Simpulan

Masalah optimisasi penggunaan binatang buruan secara konsumtif memunyai dua tujuan pokok, yaitu:

1. memaksimumkan pendapatan baik dari satu jenis maupun banyak spesies dalam ranch, yang terbagi lagi ke dalam 2 subtujuan:

1) maksimisasi pendapatan dari satu jenis spesies yang terdiri dari hewan jantan dan betina;

2) maksimisasi pendapatan dari kombinasi semua spesies dalam ranch;

2. memaksimumkan modal terhadap inflasi dan aktivitas jual-beli hewan.

Terdapat dua kendala pokok pada masalah maksimisasi pendapatan dari satu jenis spesies yaitu kendala ketersediaan pakan hewan dan dinamika populasi (fluktuasi banyaknya hewan dalam ranch). Selain kendala ketersediaan pakan, pada masalah maksimisasi pendapatan dari kombinasi semua spesies

dalam ranchterdapat kendala tambahan, yaitu kendala keberagaman yang menjaga kelangsungan hidup hewan dalam peternakan. Kendala–kendala baru pada penyelesaian masalah maksimisasi pendapatan dari hasil pemanenan hewan buruan ditambahkan untuk memudahkan penghitungan.

Pada masalah maksimisasi modal pada akhir waktu pembangunan peternakan, kendala yang harus dipenuhi di antaranya fluktuasi modal, fluktuasi harga jual-beli hewan, keterbatasan modal, ketersediaan pakan, dinamika populasi, dan target hewan pada tahun terakhir.

Hasil yang diharapkan diperoleh dengan metode branch-and–boundyang diaplikasikan melaluisoftware Lingo 8.0

5.2 Saran

Karena kesulitan dalam pencarian data, data yang digunakan adalah data hipotetik. Saran untuk penulisan selanjutnya adalah

penggunaan data asli. Selain itu dapat juga dibuat implementasi untuk studi kasus di Indonesia, dengan peternakan berupa taman buru.

Permasalahan baru yang masih dapat dikembangkan antara lain:

 studi kasus maksimisasi pendapatan dari sport hunting;

 penggabungan model spesies tunggal dan campuran.

DAFTAR PUSTAKA

Garfinkel RS, GL Nemhauser. 1972. Integer Programming. John Willey & Sons, New York.

Getz W, Haight R. 1989. Population Harvesting – Demographic Models of Fish, Forest, and Animal Resources. Princeton University Press, Princeton. Hearne JW, Korrubel JL, Koch KJ. 2000.

Modelling to Optimise Consumptive Use of Games. Annals of Operations Research. 95:268-284.

Jordie K, Peddie D. 1988. A Wildlife Management Problem. A Case Study in Multiple Objective Linear Programming. Journal of the Operational Research Society. 39:1011-1020.

Nash SG, A Sofer. 1996. Linear and Nonlinear Programming. McGraw-Hill, New York.

Ruyle G, Ogden P. 1993. What is an A.U.M. The University of Arizona, Tucson.

Taha HA. 1975. Integer Programming: Theory, Applications, and Computations. Academic Press, New York.

Taha HA. 1996. Pengantar Riset Operasi. Alih Bahasa: Drs. Daniel Wirajaya. Binarupa Aksara, Jakarta. Terjemahan dari: Operations Research.

Winston WL. 1995. Introduction to Mathematical Programming 2nd _ed. Duxbury, New York.

Winston WL. 2004. Operations Research Applications and Algorithms 4th ed. Duxbury, New York.

Lampiran 1

SyntaxProgram Lindo 6.1 untuk Menyelesaikan Masalah Pemrograman Linear dengan Metode

Branch-and-Bound Beserta Hasil yang Diperoleh

1) PL-relaksasi masalah (2.6) max z x₁ x₂ terhadap 2x15x2 16 6x15x2 30

x x1, 2 0.

Syntaxprogram pada Lindo 6.1: max x1+x2

subject to 2x1+5x2<=16 6x1+5x2<=30

x1>=0 x2>=0 Hasil yang diperoleh:

LP OPTIMUM FOUND AT STEP 2 OBJECTIVE FUNCTION VALUE

1) 5.300000

VARIABLE VALUE REDUCED COST X1 3.500000 0.000000 X2 1.800000 0.000000

ROW SLACK OR SURPLUS DUAL PRICES 2) 0.000000 0.050000 3) 0.000000 0.150000 4) 3.500000 0.000000 5) 1.800000 0.000000 NO. ITERATIONS= 2 2) Subproblem 2 max z x₁ x₂ terhadap 2x15x2 16 6x15x2 30 x₁4,x₂0. Syntaxprogram pada Lindo 6.1:

max x1+x2

subject to 2x1+5x2<=16 6x1+5x2<=30

x1>=4 x2>=0 Hasil yang diperoleh:

LP OPTIMUM FOUND AT STEP 2 OBJECTIVE FUNCTION VALUE

1) 5.200000

VARIABLE VALUE REDUCED COST X1 4.000000 0.000000 X2 1.200000 0.000000

ROW SLACK OR SURPLUS DUAL PRICES 2) 2.000000 0.000000 3) 0.000000 0.200000 4) 0.000000 -0.200000 5) 1.200000 0.000000 NO. ITERATIONS= 2 3) Subproblem 4 max zx₁x₂ terhadap 2x15x216 6x15x230 x14,x2 2.

Syntaxprogram pada Lindo 6.1: max x1+x2

subject to 2x1+5x2<=16 6x1+5x2<=30

x1>=4 x2>=2

Hasil yang diperoleh: takfisibel, sebagaimana ditunjukkan di bawah ini

4) Subproblem 5

max z x₁ x₂ terhadap 2x₁5x₂16

x₁4,x₂1.

Syntaxprogram pada Lindo 6.1: max x1+x2

subject to 2x1+5x2<=16 6x1+5x2<=30

x1>=4 x2<=1 Hasil yang diperoleh:

LP OPTIMUM FOUND AT STEP 2 OBJECTIVE FUNCTION VALUE

1) 5.166667

VARIABLE VALUE REDUCED COST X1 4.166667 0.000000 X2 1.000000 0.000000

ROW SLACK OR SURPLUS DUAL PRICES 2) 2.666667 0.000000 3) 0.000000 0.166667 4) 0.166667 0.000000 5) 0.000000 0.166667 NO. ITERATIONS= 2 5) Subproblem 6 max z x1 x2 terhadap 2x₁5x₂ 16 6x₁5x₂ 30 x15,x2 1.

Syntaxprogram pada Lindo 6.1: max x1+x2

subject to 2x1+5x2<=16 6x1+5x2<=30

x1>=5 x2<=1 Hasil yang diperoleh:

LP OPTIMUM FOUND AT STEP 2 OBJECTIVE FUNCTION VALUE

1) 5.000000

VARIABLE VALUE REDUCED COST X1 5.000000 0.000000 X2 0.000000 0.000000

ROW SLACK OR SURPLUS DUAL PRICES 2) 6.000000 0.000000 3) 0.000000 0.200000 4) 0.000000 -0.200000 5) 1.000000 0.000000 NO. ITERATIONS= 2 6) Subproblem 7 max z x₁ x₂ terhadap 2x₁5x₂16 6x15x230 x₁4,x₂ 1. Syntaxprogram pada Lindo 6.1:

max x1+x2

subject to 2x1+5x2<=16 6x1+5x2<=30

x1<=4 x2<=1 Hasil yang diperoleh:

LP OPTIMUM FOUND AT STEP 2 OBJECTIVE FUNCTION VALUE

1) 5.000000

VARIABLE VALUE REDUCED COST X1 4.000000 0.000000 X2 1.000000 0.000000

ROW SLACK OR SURPLUS DUAL PRICES 2) 3.000000 0.000000 3) 1.000000 0.000000 4) 0.000000 1.000000 5) 0.000000 1.000000 NO. ITERATIONS= 2 7) Subproblem 3 max z x1 x2 terhadap 2x15x216 6x15x230 x₁3,x₂ 0. Syntaxprogram pada Lindo 6.1:

max x1+x2

subject to 2x1+5x2<=16 6x1+5x2<=30

x1<=3 x2>=0

Hasil yang diperoleh:

LP OPTIMUM FOUND AT STEP 2 OBJECTIVE FUNCTION VALUE

1) 5.000000

VARIABLE VALUE REDUCED COST X1 3.000000 0.000000